Control of Ion Distortion in Field Asymmetric Waveform Ion Mobility Spectrometry via Variation of Dispersion Field and Gas Temperature

Abstract

Field asymmetric waveform ion mobility spectrometry (FAIMS) has emerged as an analytical tool of broad utility, especially in conjunction with mass spectrometry. Of particular promise is the use of FAIMS and 2-D ion mobility methods that combine FAIMS with conventional IMS to resolve and characterize protein and other macromolecular conformers. However, FAIMS operation requires a strong electric field and ions are inevitably heated by energetic collisions with buffer gas molecules. This may induce ion isomerization or dissociation that distort the separation properties of FAIMS (and subsequent stages) and/or reduce instrumental sensitivity. As FAIMS employs a periodic waveform, whether those processes are controlled by ion temperature at maximum or average field intensity has been debated. Here we address this issue by measuring the unfolding of compact ubiquitin ion geometries as a function of waveform amplitude (dispersion field, E_D) and gas temperature, T. The field heating is quantified by matching the dependences of structural transitions on E_D and T: increasing E_D from 12 to 16 or from 16 to 20 kV/cm is equivalent to heating the (N₂) gas by ∼15 – 25 °C. The magnitude of field heating for any E_D can be estimated using the two-temperature theory, and raising E_D by 4 kV/cm augments heating by ∼15 – 30 °C for maximum and ∼4 – 8 °C for average field in the FAIMS cycle. Hence, isomerization of ions in FAIMS appears to be determined by the excitation at waveform peaks.

Introduction

Separation and structural elucidation of gas-phase ions by mass spectrometry (MS) or ion mobility spectrometry (IMS) is central to many analytical applications.^1,2 To accurately characterize the present species and particularly solution structures, one usually seeks to minimize their destruction or distortion during ionization and subsequent analysis. As in MS the determination of ion m/z is performed in vacuum and thus does not change ion structure (except for spontaneous decay), one generally needs to preserve species only during ionization and transfer through high pressure regions. This has motivated development of electrospray (ESI),^3,4 sonic spray,⁵ and other sources that can ionize large biomolecules, including proteins, protein complexes, and DNA “softly” - without changes to the primary or quaternary structure (i.e., dissociation) and with limited distortion of secondary and tertiary structure (i.e., isomerization). The resulting ions often retain key aspects of their solution conformation.^6–11

In IMS, ions are separated while pulled through gas by electric field,² which may influence their structure. Ion - molecule chemistry is normally avoided by use of He, N₂, or other inert gases that do not react with ions under experimental conditions, but “field heating” of ions by above-thermal collisions with molecules is not preventable. The ion-molecule collision velocity (v_I-M) is the vector sum of the random component due to Brownian motion of both particles (v_Br) and ion drift motion (v) directed by electric field, hence in IMS exceeds that for freely diffusing ions defined by gas temperature, T. As v is constant for all collisions, the distribution of v_I-M (unlike v_Br) is not rigorously Maxwellian, but may be approximated as such when v << v̅_Br. This underlies the two-temperature theory^12,13 where the “ion temperature”, T_I, is

$$T_{\mathrm{I}}=T+T_{\mathrm{H}}=T+M(KE{)}^2/(3k_{\mathrm{B}})$$ (1)

Here M is the gas molecule mass, K is the ion mobility, E is the electric field intensity, and k_B is the Boltzmann constant. While eq (1) has been derived for the translational temperature, on the timescale of IMS and particularly FAIMS separations all degrees of freedom are equilibrated and the ion vibrational temperature is also set by eq (1). For polyatomic ions, this heating by T_H may cause dissociation or isomerization that would change the IMS separation properties.

In drift tube IMS (DTIMS) at conventional pressures (P) of >∼1 Torr,^2,12 the field is usually so weak that T_H is insignificant. For example, the reduced mobility K₀ [equal to K at standard T and P] is <3 cm²/(V×s) even for smallest ions and ∼1 – 2 cm²/(V×s) for most medium-size ones, and typical E in atmospheric-pressure DTIMS systems is ∼200 – 700 V/cm. Then T_H is a negligible ∼0.1 °C even for highest K₀ and E, and routinely is lower. Somewhat stronger but still generally immaterial heating may occur in reduced-pressure IMS used in some IMS/MS systems. For example, the IMS stage in tandem quadrupole - drift tube instruments^14,15 is commonly operated at P ∼5 Torr and E ∼15 V/cm, meaning T_H = 0.15 – 1.3 °C for K₀ = 1 – 3 cm²/(V×s).

The mobility of ions in gases is a function of E. This allows field asymmetric waveform IMS (FAIMS)¹⁶ or differential IMS¹⁷ to separate and identify species based on the difference between mobilities at two unequal E. In practice, FAIMS employs a periodic field E(t) that alternates segments of higher E and lower E of opposite polarity. This field and a superimposed compensation field E_C are established by applying a waveform U(t) and “compensation voltage” U_C to a gap between two electrodes through which ions are carried by gas flow. The amplitudes of E(t) and U(t) are termed the “dispersion field”, E_D, and “dispersion voltage”, U_D. At any given E_C, only species with certain K(E) profile remain balanced and pass to the detector or following analytical stage. The deviation of K from K(0) approximately scales as E³ and thus is negligible at moderate E typical of DTIMS, but rapidly rises at high E. The change of K at higher E is due to several factors. The major is that K equals:¹²

$$K=K_0\frac{N_0}{N}=\frac{3}{16}{\left(\frac{2\pi (m+M)}{mM{k}_B{T}_I}\right)}^{1/2}\frac{q}{N\Omega (T_I)}$$ (2)

where m and q are the ion mass and charge, N is the gas number density, N₀ is N at STP, and Ω is the ion-molecule collision cross section that depends on the v_I-M distribution and thus on T_I in a way governed by the interaction potential. Hence, by requiring K to materially depend on E, FAIMS operation necessitates T_I in one or both E(t) segments to substantially differ from T. Thus field heating is unavoidable during at least the high-field segment.

The heating may fragment ions entering the gap, with FAIMS characterizing the product ions.^18–21 Though this regime may improve the specificity similarly to in-source decay in MS, one usually desires the ability to study intact precursors. In FAIMS, the ion activation is caused by the separation mechanism itself and thus cannot be switched off without altering its outcome. The trivial solution of decreasing E is hardly acceptable²² because it reduces the resolving power (scaling as ∼E³) more than heating that scales as E² by eq (1). In FAIMS/MS systems, one may instantly detect the ion dissociation in FAIMS by switching E(t) off. More subtle is the thermal isomerization, particularly for macroions such as most proteins that denature (i.e., significantly change conformation) upon modest collisional or thermal heating.^22–28 This process is not easily assessed by MS but alters FAIMS separation parameters, which is of concern for the characterization of conformers including misfolded proteins relevant to biomedical problems.^28–34 A dramatic expansion of FAIMS separation space and thus peak capacity, ascribed to the alignment of ion macrodipoles by electric field, was recently reported³³ for proteins with m >∼30 kDa, and might be extendable to lower m. This raises the utility of FAIMS for analysis of macromolecular conformations, motivating the effort to better understand their distortion in FAIMS and devise approaches to its mitigation.

Unlike in DTIMS, |E| in FAIMS is not fixed but oscillates from 0 to E_D and the proper choice of E in eq (1) is not obvious. In the studies of ubiquitin and cytochrome c, where isomerization of ions induced by field heating in FAIMS was first discussed,^30,31 the process was assumed to be controlled by mean |E| over the E(t) cycle. This and the adoption of too low K values²² produced T_H <10 °C, and conformations were not expected to change significantly.^30,31 This issue could not be probed using only FAIMS or FAIMS/MS operating at fixed T for the lack of a priori means to deduce ion structures from FAIMS data.

Positive-mode ESI produces protonated proteins with a distribution of z sensitive to the solution composition. For ubiquitin (m ∼8.6 kDa) in acidic media,^{22–24,28,35} charge states of z ∼5 – 13 are observed. Proteins in either solution or the gas phase may adopt many 3-D structures depending on the present and past conditions. Proteins with no disulfide links like ubiquitin are free to adopt any conformation. In the gas phase, they assume compact near-native geometries at low z and elongated geometries lacking tertiary structure at high z because the Coulomb repulsion between charged sites (scaling as ∼z² for fixed geometries) overcomes the hydrogen bonds.^{22–26,28,35} At intermediate z, one usually encounters the broadest diversity of geometries, including compact, partly folded, and unfolded conformers.

Compact and partly folded proteins gradually unfold at higher T_I as the thermal energy exceeds the dissociation barrier of specific bonds, while elongated conformers change little. The needed T_I decreases for higher z as the folds are destabilized by Coulomb repulsion, so the isomer population over a range of z covering the transition from compact to elongated geometries provides a reliable ion thermometer with laddered overlapping scales. Prominent structural differences between intermediates on the protein unfolding pathway frequently make them distinguishable (and thus the thermometer readable) by either DTIMS or FAIMS. This allows extracting T_H in high-field IMS by matching the resulting populations with those produced by thermal heating at low E where T_H is negligible. In general, heat-denatured protein ions do not spontaneously refold upon cooling,^{22,23,25,26,28} and, as medical thermometers for measuring the body temperature, the “protein unfolding thermometer” registers the highest temperature ever experienced rather than the instantaneous temperature. This feature permits characterizing T_H in high-field IMS by analyses of conformer populations in subsequent stages producing less or no ion heating.

In contrast to FAIMS data, the drift times (t_d) in DTIMS can be related to ion geometries by physical modeling: greater t_d signifies more open structures. At room T, ubiquitin ions generated by ESI under gentle conditions are^22–24,35 compact for z ≤ 6 and elongated for z 11. For z = 7 – 10, both families and/or partly folded species co-exist. Insertion of a FAIMS stage prior to DTIMS raises t_d (summed over the FAIMS spectra), indicating some unfolding by FAIMS.²² The resulting t_d distributions resemble those obtained without FAIMS for ions heated²⁴ to ∼70 – 75 °C, i.e., by ∼50 – 55 °C over room T. This value greatly exceeds T_H ∼15 °C calculated using eq (1) for average |E| but is only slightly less than T_H ∼55 – 70 °C obtained for E = E_D, suggesting that ion isomerization in FAIMS is governed by the maximum²² rather than the average E. It was proposed to avoid the isomerization or dissociation caused by such field heating via cooling the buffer gas by relevant T_H below T_I of entering ions, so that T_I during separation never exceeds the initial value.²² However, the FAIMS (the “Selectra” device of dome geometry previously manufactured by Ionalytics) and DTIMS stages in those experiments had dissimilar ion inlets - a curtain plate and capillary, respectively. So the distortion caused by FAIMS might have reflected stronger ion excitation at the source inlet.²² Also, ions spend a substantial time in FAIMS: ∼200 ms in Selectra vs. ∼60 – 90 ms in DTIMS and <100 ms in the ion funnel trap at DTIMS entrance.²² Hence adding the FAIMS stage raises the “age” of ions characterized by DTIMS by several times, which might promote unfolding by delayed (spontaneous) rather than a heating-driven mechanism.²²

The recent introduction of heated FAIMS devices³⁶ enables analyses at T up to ∼110 °C. This allows comparing isomer populations as a function of E or T without involving other stages, which excludes the effects of inlet conditions and different reaction time scales. The field heating for any ion also depends on the gas identity through the value of K in eq (1): in general, K in gases of smaller molecules is higher,¹² leading to greater T_H. Here we explore the ubiquitin ion conformers resolved by FAIMS in N₂ as a function of both E_D and T, and confirm that the ion structure in FAIMS is largely determined by T_I given by eq (1) using the maximum E.

Experimental method

Measurements were performed using the TSQ Quantum Ultra triple quadrupole MS system with FAIMS option³⁶ and Ion Max ESI source (Thermo Fisher, San Jose, CA). A 10 µM solution of bovine ubiquitin (Sigma Aldrich) in 50:49:1 water/methanol/acetic acid was infused at 2 µL/min to the ESI emitter biased at 4 kV. The FAIMS unit has transverse or “side-to-side” cylindrical configuration with the gap width of g = 2.5 mm (inner and outer radii of 6.5 and 9 mm) and allows |U|≤ 5 kV. With proper U_D sign, curved FAIMS gaps focus ions to the median, which provides high sensitivity but limits resolution.³⁷ All ubiquitin conformers with z = 5 – 14 generated by ESI belong^28–30 (with N₂ carrier gas) to type C,³⁸ meaning a negative derivative of K(E). Such species are focused in the P2 mode³⁷ (U_D <0; U_C <0). Though the E_D value in curved FAIMS varies across the gap,³⁸ here we define E_D = U_D/g (approximating E_D at the median)³⁹ to compare the data at different E_D/N. We used U_D of −3, −4, and −5 kV that correspond to E_D of −12, −16, and −20 kV/cm. The total (carrier and curtain plate) gas flow was 3 L/min. The FAIMS spectra for z = 6 – 13 were acquired by stepping U_C in 0.3 V increments with MS in the selected ion monitoring mode scanning 5 amu-wide windows around pertinent m/z. All data were collected over the T = 35 – 80 °C range with 5 °C step. The FAIMS electrodes were at equal T, creating no thermal gradient across the gap.

Results and Discussion

Apparent and intrinsic temperature dependences of FAIMS spectra

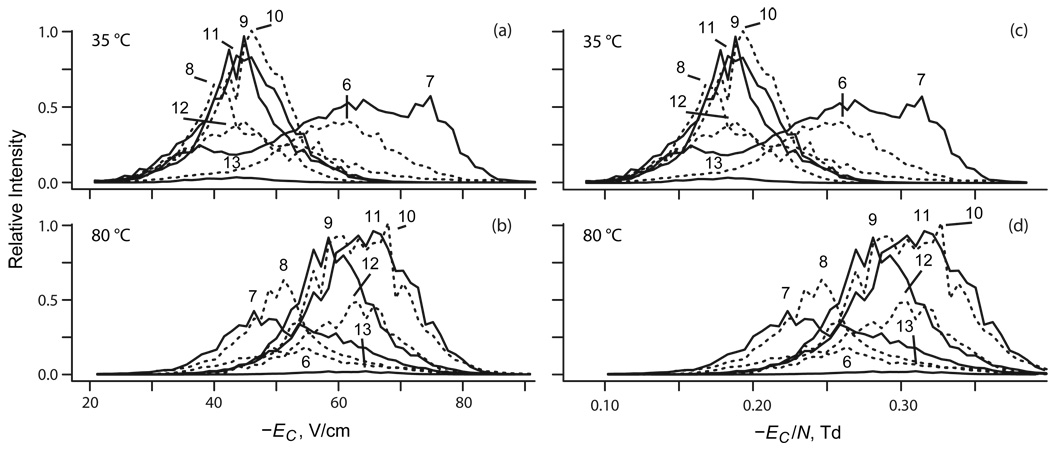
The FAIMS spectra for ubiquitin ions at E_D = −20 kV/cm and minimum T = 35 °C (Figure 1a) are close to those measured^28,37 at same E_D and ∼20 °C using Selectra with g = 2 mm. The spectra for z = 6 and 7 are broad, with major peaks for compact geometries at E_C ∼−60 V/cm for 6+ and ∼−75 V/cm for 7+ and minor features for elongated conformers at ∼−35 – 40 V/cm. For 7+, there also are wide features for partly folded structures at intermediate E_C.³⁷ The results for 8+ resemble those for 6+, but the peak at ∼−40 V/cm becomes dominant as the protein unfolds. For z = 9 – 13, a single peak at E_C ∼−(40 – 45) V/cm indicates full unfolding.^28,37 The absence of more compact geometries at higher |E_c| for 9+ and abundance of unfolded species for 7+ and 8+ point to T_I exceeding that in earlier work,²⁸ possibly reflecting higher T in present experiments.

Fig. 1.

Divergent temperature dependences of FAIMS spectra for protein ions of low and high charge states. Data for ubiquitin with z = 6 – 13 measured using E_D = −20 kV/cm at T = 35 °C (top row) and 80 °C (bottom row).

With T increasing to 80 °C, the raw spectra move to higher |E_c| for z of 8 – 13 but not 6 or 7, and the spectrum for 7+ changes from the signature three-peak shape seen in FAIMS or DTIMS to a single feature (Figure 1b). This pattern remains when data are plotted vs. E_C/N (Figure 1 c, d). The non-uniformity of changes indicates a structural transition upon heating for some z, including 7. To isolate it, we must remove the thermal shift of E_C due to the dependence of N on T.³⁶ Indeed, K₀ for rigid ions generally depends not on E but on E/N:

$$K_0(E/N)=K_0(0)[1+a_1(E/N{)}^2+a_2(E/N{)}^4+\dots a_n(E/N{)}^{2_n}]$$ (3)

where a_n are fixed coefficients characterizing the ion/gas pair.¹² Hence, graphing the spectra acquired at equal E_D/N vs. E_C/N eliminates³⁶ the trivial effect of T within the relative error of ideal gas law which, for N₂ over T = 35 – 80 °C, is a negligible <0.1 % (according to the Van der Waals equation of state). Presently, E_D was not scaled with inverse temperature. In this case, we can exploit the dependence⁴⁰ of E_C/N on E_D/N:

$$E_C/N=-\left({\displaystyle \sum _{n=1}^{\infty }{a}_n{(E_D/N)}^{2n+1}\langle F_{2n+1}\rangle }\right)/\left(1+{\displaystyle \sum _{n=1}^{\infty }(2n+1)a_n{(E_D/N)}^{2n}}\langle F_{2n}\rangle \right)$$ (4)

where 〈F_n〉 are dimensionless properties of the E(t) profile. For bisinusoidal E(t), eq (4) for n = 1 and 2 is equivalent to:¹⁶

$$\frac{E_C}{N}=-\frac{a_1}{N^3}\left(\frac{{E_D}^3}{9}+\frac{5{E_D}^2{E}_C}{6}+{E_C}^3\right)-\frac{a_2}{N^5}\left(\frac{55{E_D}^5}{486}+\frac{55{E_D}^4{E}_C}{72}+\frac{10{E_D}^3{E_C}^2}{9}+\frac{25{E_D}^2{E_C}^3}{9}+{E_C}^5\right)$$ (5)

The highest |E_c / E_D| value for present data is ∼0.004 (with E_C ∼−80 V/cm at E_D = −20 kV/cm for 7+), hence omitting the terms containing E_C on the rhs of eq (5) changes the quantity in either parentheses by <3%. Further, all E_C values are negative at any E_D with |E_c| increasing at higher E_D (Figure 1), which confirms that all ubiquitin ion species in N₂ are³⁸ type C where a₁ <0. For such species, the terms with n ≥2 usually contribute little to the K₀(E/N) and thus E_C(E_D) functions (at moderate E/N of present experiments), and eq (5) may be approximated as

$$E_C/N=-a_1\langle F_3\rangle (E_D/N{)}^3$$ (6)

Indeed, for two most abundant conformers for 11+ or 12+ that are “unfolded” even at E_D = 0 and thus should largely retain the same structure at any E_D, the E_C(E_D) curves measured³⁰ (in N₂) up to |E_D| = 22 kV/cm can be fit by a₁ = −(3.2 – 3.7) × 10⁻¹¹ (cm/V)² and a₂ = (0 ± 3) × 10⁻²¹ (cm/V)⁴: the n = 2 term in eq (3) is <4% of the n = 1 term even at highest |E_D| used here.

Thus the quantity (E_C/N)/(E_D/N)³ (which we call “normalized E_C” or E_CN) for various spectral features should be largely independent of T to the extent a₁ is independent of T. That is never rigorous because K₀ by eq (2) depends on T (i) directly as T_I ^−1/2 and (ii) through Ω(T_I) function. However, the effect of (i) decreases K₀ between 35 and 80 °C by just 7%, which is partly offset by (ii) because Ω for fixed geometries decreases at higher T. So K₀ values for rigid medium-size and large ions in N₂ tend to decrease by just a few percent over the T_I ∼50 – 150 °C range sampled here.⁴¹ Further, the K₀(T) dependence is approximately additive¹² to K₀(E/N) and thus mostly cancels from the ratio of K at high and low E measured in FAIMS. In contrast, unfolding of proteins commonly raises Ω and thus drops K₀ by several times.^{22–26,28,35} Hence, most of the temperature-dependent variation of FAIMS spectra plotted vs. E_CN must reflect changes of ion structure.

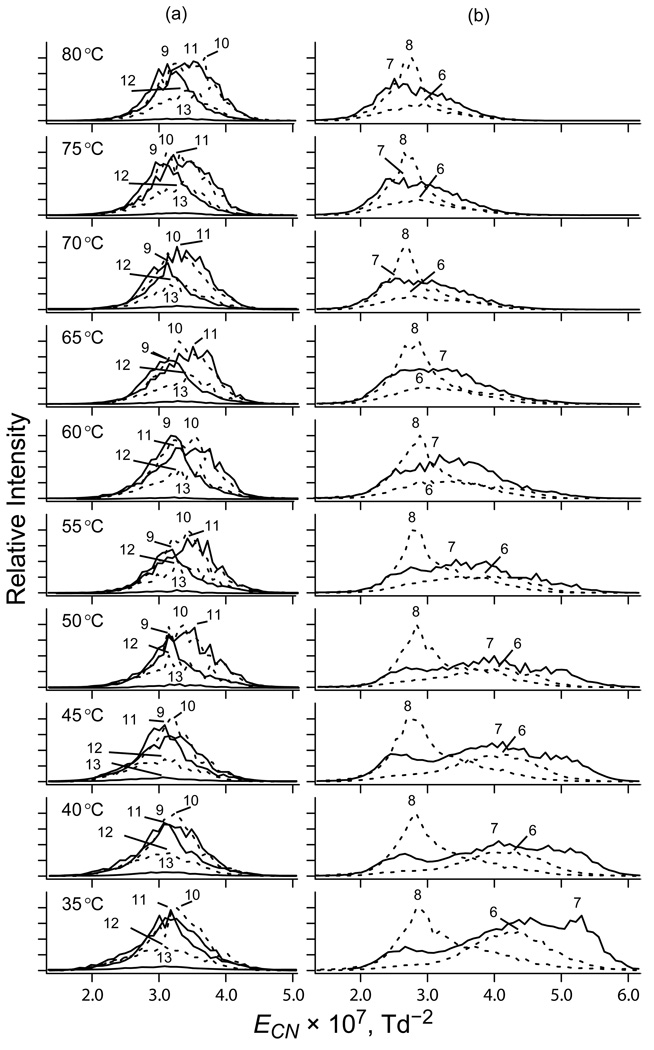
The data for ubiquitin ions at T = 35 – 80 °C support this hypothesis. The redrawn spectra at T = 35 °C (Figure 2) appear the same as in Figure 1a, with E_CN (in 10⁻⁷ Td⁻²) of ∼(5 – 5.5), ∼(4 – 4.5), ∼(3.5 – 4.5), and ∼(2.5 – 3.5) for compact (7+), compact (6+), partly folded (7+), and elongated (z = 8 – 13) conformers, respectively. However, the temperature dependence differs from that in Figure 1. For z = 9 – 13 that are already unfolded at T = 35 °C, the peaks are nearly fixed with a tiny shift to the right at higher T for z = 10 – 13 (Figure 2a). For z = 6 – 8 (Figure 2b), the peaks shift to lower E_CN and greatest changes occur for 6+ and 7+: the compact and partly folded conformers disappear by T ∼80 °C, leaving only the features at ∼(2.5 – 3) × 10⁻⁷ Td⁻² that indicate elongated geometries. As the “isomer population thermometry” requires observable interconversions over the relevant temperature range, we shall focus on structures with z = 6 – 8 that unfold in present experiments.

Fig. 2.

Removing the dependence of spectra on the gas number density. Normalized spectra of ubiquitin ions with z = 9 – 13 (a) and 6 – 8 (b) at E_D = −20 kV/cm as a function of gas temperature (labeled).

Quantification of field heating in FAIMS

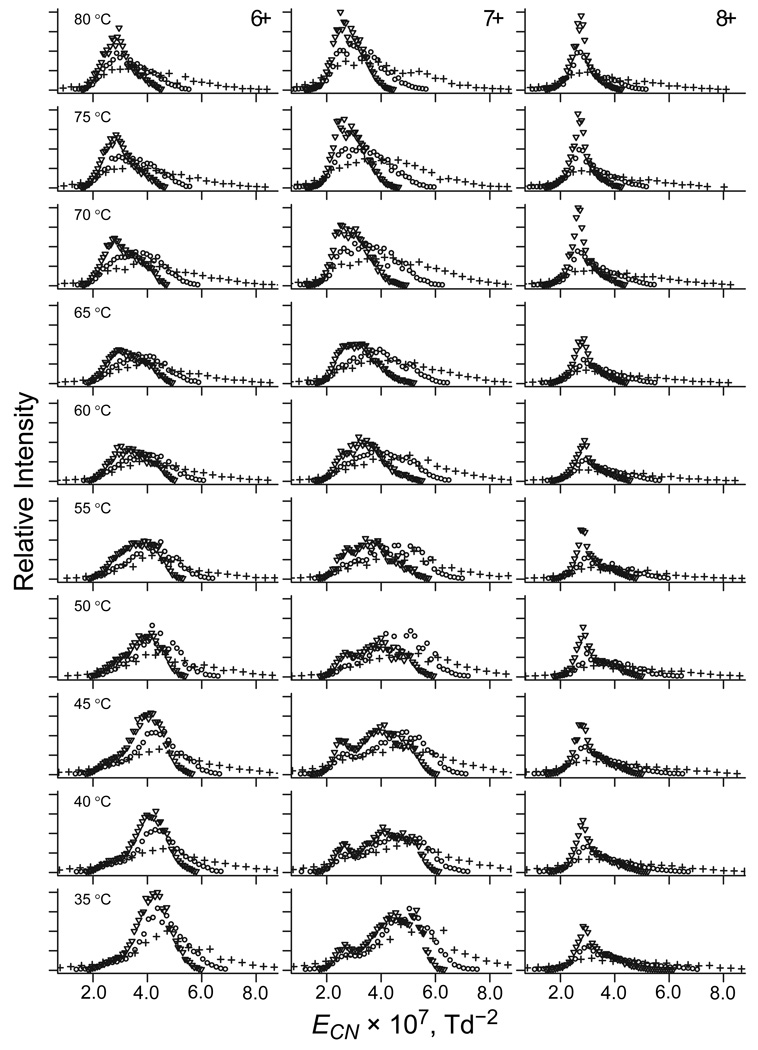
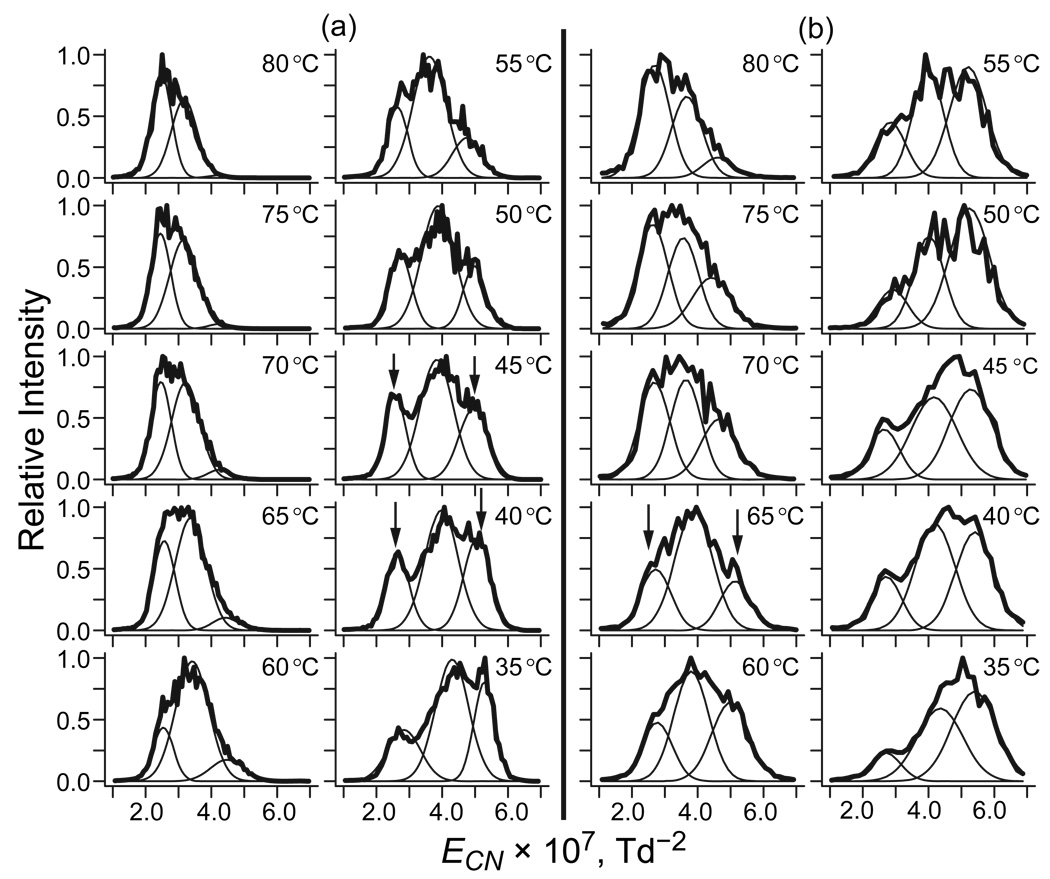
As discussed above, no FAIMS separation is possible at E low enough for negligible T_H. Thus, unlike with DTIMS,²² comparisons of the spectra in Figure 2 with those at other E_D and T values cannot determine absolute T_H. However, they can reveal the difference (ΔT) between T_H at unequal |E_D| values, such as 12, 16, and 20 kV/cm used here. The temperature dependences of spectra at 12 and 16 kV/cm (Figure 3) resemble that at 20 kV/cm described above, but are dwarfed by systematic increase of |E_C| at greater |E_D|. That increase is standard for rigid geometries and must be offset to isolate the spectral changes reflecting isomerization due to stronger field heating at higher E_D. Within the approximations made to isolate the structural part of E_C(T) function, we can express the trivial E_C(E_D) dependence using eq (6) and, again, remove it by plotting the spectra vs. E_CN (Figure 4). This largely aligns the peaks for same isomers at different E_D, as is most clearly seen for 8+. For 6+ and 7+ with multiple features, the same spectral shape changes and E_C shifts occur at higher T as |E_D| drops. For example, in the spectra for 7+ that comprise three peaks (Figure 5), that at the highest |E_C| for compact geometries vanishes, but that at the lowest |E_C| for elongated geometries grows at higher T (at least on the relative scale). While this happens at any |E_D|, the two peaks reach equal height at different T: ∼40 – 45 °C in the data for 20 kV/cm (Figure 5a) but ∼65 °C for 16 kV/cm (Figure 5b), suggesting ΔT ∼20 – 25 °C.

Fig. 3.

Spectra of ubiquitin 6+ ions as a function of gas temperature (labeled) at E_D = −20 kV/cm (▽), −16 kV/cm (○), and −12 kV/cm (+).

Fig. 4.

Removing the dependence of spectra for same geometries on the dispersion field. Normalized spectra of ubiquitin ions with z = 6 – 8 as a function of gas temperature (labeled) at E_D = −20 kV/cm (▽), −16 kV/cm (○), and −12 kV/cm (+).

Fig. 5.

Normalized spectra of ubiquitin 7+ at E_D = −20 kV/cm (a) and −16 kV/cm (b) as a function of gas temperature, fitted assuming three conformers with Gaussian peak profiles. The compared features are marked by arrows.

When the shift of E_C upon isomerization during FAIMS analysis compares to or exceeds the peak width set by instrumental resolving power for the remaining ion residence time in the gap, the products may be filtered out in part or in full.²² Hence spectral changes upon heating may reflect either the reduction/elimination of reactants and growth/emergence of products or just the reactant loss, with other features appearing to increase in relative terms. As the total ion count in these experiments depends on the gas temperature (because of varying efficiency of ion desolvation in front of FAIMS and of focusing in the analytical gap), the two effects are hard to disentangle. However, this does not matter for our goal of measuring the extent of ion heating by electric field via comparison of its consequences by whatever mechanism with those due to known thermal heating.

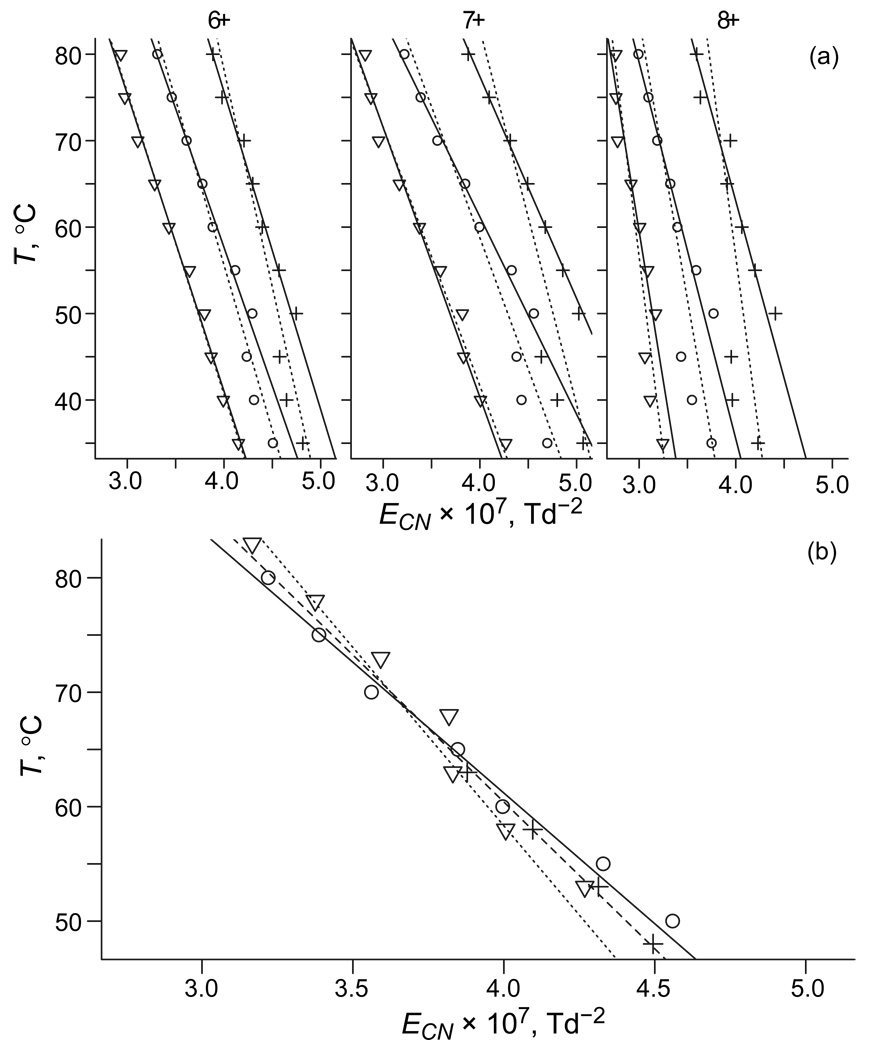
In most cases, the diversity of protein conformers and their consequent poor resolution by FAIMS precludes robust peak fitting to extract isomer abundances. However, given a uniform decrease of E_C with protein unfolding, its overall extent is quantifiable by mean E_CN values, E̅_CN (Figure 6a). As expected, E̅_CN decreases with increasing T for all z = 6 – 8 at any E_D, but the T(E̅_CN) curves move to the right and up at lower E_D: the geometries are more folded at equal T and higher T is needed for equal unfolding. The value of ΔT for two E_D values can be deduced by transposing one curve along the T axis to minimize its deviation from the other. All curves are near-linear for T 50 °C, but those for |E_D| = 12 and 16 kV/cm have breaks of unclear origin at ∼45 °C. Regardless of whether the data for T 45 °C are included in the sets, the linear regressions at |E_D| of 20 and 12 kV/cm match those at 16 kV/cm upon shifting up and down by ∼15 – 25 °C, respectively (Figure 6b). This is consistent with ΔT ∼20 – 25 °C obtained by matching intensities of specific features, as illustrated above. We will now compare these estimates with the two-temperature theory.

Fig. 6.

Comparison of the effects of thermal and field heating on FAIMS spectra measured for ubiquitin ions. (a) Dependences of mean normalized E_C on gas temperature for z = 6 – 8 at E_D = −20 kV/cm (▽), −16 kV/cm (○), and −12 kV/cm (+). First-order regressions through each set including points for T = 35 – 80 °C and 50 – 80 °C are marked by solid and dashed lines, respectively. (b) For z = 7, the minimum scatter of data for three E_D values is achieved via displacements by +18 °C for −20 kV/cm and −17 °C for −12 kV/cm. The needed shifts are 16 – 19 °C for 6+ and 24 – 26 °C for 8+. Lines are 1^st-order regressions through sets for T = 50 – 80 °C, at E_D of −20 kV/cm (dotted), −16 kV/cm (solid), and −12 kV/cm (dashed).

Modeling of field heating and comparison with measurements

By eq (1), changing E from E₁ to E₂ produces:

$$\Delta T=M[(K_2{E}_2{)}^2-(K_1{E}_1{)}^2]/(3k_{\mathrm{B}})$$ (7)

where K₁ and K₂ are mobilities at E₁ and E₂. When E₁ and E₂ are E_D values for two FAIMS waveforms, eq (7) provides the maximum ΔT at waveform peaks (ΔT_max). The variation of K over the sampled E range for ubiquitin species studied is ∼1%, which is negligible compared to the difference between E_D values used. Hence eq (7) can be reduced to:

$$\Delta T_{\max }=MK[{E_2}^2-{E_1}^2]/(3k_{\mathrm{B}})$$ (8)

The average ΔT in FAIMS depends on the integral of eq (8) over E(t) period and thus on the E(t) profile. The TSQ FAIMS system employs a bisinusoidal waveform comprising two harmonics with 2:1 frequency ratio:^39,42–44

$$E(t)=E_{\mathrm{D}}[f\sin wt+\sin (2wt-\text{π/2})]/(f+1)$$ (9)

where f is the ratio of harmonic amplitudes. Substituting this into eq (8) and averaging, we obtain

$$\Delta \overline{T}=\frac{f^2+1}{2{(f+1)}^2}M{K}^2({E_2}^2-{E_1}^2)$$ (10)

As most studies, present experiments use a near-optimum^42–44 f = 2 and eq (10) converts to

$$\Delta \overline{T}=5M{K}^2({E_2}^2-{E_1}^2)/18$$ (11)

Hence ΔT̅ under any conditions equals ΔT_max scaled by ≈0.278. This factor determined by averaging ΔT is more accurate than the published value^22,30,31 of ≈0.218 derived³⁰ by substituting the mean |E| into eq (8), i.e., the mean of the square is not the square of the mean. To calculate ΔT_max and ΔT̅ for specific ions, we need to know the values of K.

The mobilities of ubiquitin ions with z = 6 – 8 in N₂ span a broad range,^22,28 but only compact and partly folded geometries can unfold upon field heating and thus only their mobilities are relevant here. At T = 20 °C, the measured²² values for those species are K₀ ∼0.9 – 1.2 cm²/(V×s) or K ∼0.97 – 1.29 cm²/(V×s). For macroions such as proteins, the cross section of a rigid geometry may be assumed independent of temperature. Then K is proportional to T^1/2 by eq (2), and the values of K, T_H by eq (1), ΔT_max by eq (8), and by eq (11) are listed in Table 1. Reflecting a narrow temperature range, the results at T = 35 and 80 °C are close and we can use average values, especially as unfolding mostly occurs at intermediate T ∼ 50 – 60 °C (Figure 2). The computed ΔT_max or ΔT̅ for |E_D| of 12 and 16 kV/cm are lower than the corresponding values for 16 and 20 kV/cm by 22%. This difference is also not critical to the present discussion, and we can estimate ΔT_max as ∼13 – 30 °C while equals ∼4 – 8 °C only.

Table 1.

Mobilities (in N₂ at 1 Atm) and calculated magnitudes of field heating in FAIMS for compact and partly folded conformers of ubiquitin ions (z = 6 – 8) at E₁ = −12, E₂ = −16, and E₃ = −20 kV/cm.

T, °C	K, cm2/(V×s)	TH, °C			ΔTmax (E2–E1)	ΔTmax (E3–E2)	ΔT̅ (E2–E1)	ΔT̅ (E3–E2)
		E1	E2	E3
35	0.99–1.32	16–28	28–50	44–78	12–22	16–28	3.4–6.1	4.4–7.8
80	1.03–1.38	17–31	30–55	48–85	13–24	17–31	3.7–6.6	4.8–8.6

This ΔT_max range is in agreement with measured ΔT ∼15 – 25 °C, particularly as the maximum T_H and thus ΔT_max apply instantly at E = E_D, while isomerization takes finite time and T_H and ΔT available over finite segments around E(t) peaks are lower.²² An (admittedly arbitrary) discount of 10% in terms of E would reduce ΔT_max at any two E_D by ∼20% - presently, to ∼10 – 25 °C. The calculated ΔT̅ values are much lower than measured ΔT and such small shifts of T(E̅_CN) curves would hardly even be noticed in present experiments with T incremented in 5 °C steps. Accordingly, isomerization of protein ions in FAIMS is controlled by maximum rather than average ion temperature.

The magnitude of ion heating depends on the value of K for particular species, but those for compact ions of proteins generated by ESI are rather insensitive to the protein size and stay close to 1 cm²/(V×s) over a broad mass range.^22–26,28 This happens because the cross sections of macroions scale as or slightly slower than (volume)^2/3 and thus m^2/3, while the typical charging of near-spherical protein geometries by ESI is proportional⁴⁵ to ∼m^1/2. Then K by eq (2) would scale as or slower than m^−1/6, meaning a mobility change of ≤1.5 times over the range of m ∼8.6 – 100 kDa that comprises most proteins.³³ Still, decreasing K by 1.5 times reduces T_H by 2.25 times, e.g., from the maximum of ∼80 °C (Table 1) to ∼35 °C.

Conclusions

We have explored the dependence of FAIMS spectra for ubiquitin ions on the temperature (T) of the N₂ carrier gas and waveform amplitude. For charge states of 6+ to 8+, those ions adopt compact geometries at room temperature but unfold at elevated internal temperatures that may be raised by either heating of the gas or collisional (field) heating of ions by rapid drift in electric field of high intensity (E) that separates ions in FAIMS. This allows quantifying the changes (ΔT) in field heating by comparing the increases of E at waveform peaks (E_D) and gas temperature needed for equal extent of unfolding determined from FAIMS spectra adjusted for trivial (non-structural) shifts as a function of both gas temperature and E_D. The field heating for a given E may be calculated using the two-temperature theory. However, as E in FAIMS cycle oscillates from zero to E_D, the field heating (that scales as E²) and thus ΔT similarly oscillate and their maxima exceed the means by several (here 3.6) times. The measurements of ΔT over a broad E_D range for all three charge states match the computed maximum but not mean values. Hence, the structure of ions in FAIMS is dictated primarily by their highest rather than average internal temperatures. This conclusion is consistent with findings from FAIMS/IMS experiments,²² but is more reliable as it excludes possible artifacts due to unequal ion excitation in FAIMS and IMS inlets, different timescales of IMS and FAIMS/IMS analyses, as well as comparisons with thermal heating measured on other platforms.

It has been suggested that isomerization or dissociation of ions in FAIMS can be avoided if the gas is cooled by the magnitude of field heating of ions.²² Though here the gas was heated, we have directly demonstrated that the nature of ions is controlled by the sum of gas temperature and (maximum) field heating. This should equally apply with a cooled gas, opening the path to non-destructive FAIMS and FAIMS/IMS analyses of fragile macromolecules. At the highest dispersion field used here, cooling to ∼−60 °C should suffice for most protein ions.