Infrared Monitoring of Interlayer Water in Stacks of Purple Membranes

Abstract

The thermodynamic behavior of films of hydrated purple membranes from Halobacterium salinarum and the water confined in it was studied by FTIR spectroscopy in the 180–280 K range. Unlike bulk water, water in the thin layers sandwiched between the biological membranes does not freeze at 273 K but will be supercooled to ~256 K. The melting point is unaffected, leading to hysteresis between 250 and 273 K. In its heating branch a gradually increasing light-scattering by ice is observed with rate-limiting kinetics of tens of minutes. IR spectra decomposition provided extinction coefficients for the confined water vibrational bands and their changes upon freezing. Due to the hysteresis, at any given temperature in the 255–270 K range the inter-bilayer water could be either liquid or frozen, depending on thermal history. We find that this difference affects the dynamics of the bacteriorhodopsin photocycle in the hysteresis range: the decay of the M and N states and the redistribution between them are different depending on whether or not the water was initially pre-cooled to below the freezing point. However, freezing of inter-bilayer water does block the M to N transition. Unlike the water, the purple membrane lipids do not undergo any IR-detectable phase transition in the 180–280 K range.

Introduction

Purple membranes, natural two-dimensional crystals formed in Halobacterium salinarum, contain besides the lipids a single photosensitive protein, bacteriorhodopsin (bR), which, upon illumination, undergoes a cycle of dark transformations that result in transport of a proton across the membrane (see (1,2) for recent reviews). In simplified form, this cycle could be presented as a linear sequence of transient intermediate states, denoted as bR -> K <-> L <-> M <-> N <-> O –> bR. These intermediates were extensively characterized both functionally and structurally. In the latter studies the intermediates were trapped at low temperatures, and this in turn gave rise to a new interest in low-temperature functional studies. The latter revealed peculiarities in the kinetics of the photocycle at cryogenic temperatures (3,4), which had to be separated from thermally-induced processes in water and lipids. The thermodynamics of these is complicated by the confined geometry in the stacks of purple membranes, i.e. 2D crystals, used in many functional studies, and in the 3D crystals used in structural studies. Here we present infrared (IR) studies of the kinetics and the thermodynamics of water confined between stacks of purple membrane sheets, and the protein and the lipids forming these membranes. This model system provides new insights into the thermally-induced behavior of stacks of biological membranes.

The vibrational spectrum of bulk water in the 900–4000 cm⁻¹ region consists of four main bands: bending at ~1645 cm⁻¹, combination of bending and rock/libration at ~2130 cm⁻¹, symmetric stretch at ~3280 cm⁻¹ and antisymmetric stretch at ~3490 cm⁻¹ (5). Under sterically confined conditions a fifth band at ~3120 cm⁻¹ becomes prominent (6). These bands are hundreds of cm⁻¹ wide (~50 cm⁻¹ for the bending vibration), as they reflect a complex pattern of hydrogen-bonding and cluster formation (7). Phase transitions strongly affect these vibrations (7,8), and lead to shifts in band positions and changes in widths, as well as amplitude redistribution between different modes of oscillation (7–10), making IR spectroscopy a useful tool for in situ monitoring. Not only are the IR spectra of water in vapor, liquid and ice distinctly different (7,8,10–12), but the IR spectra readily identify the much smaller changes between different types of ice, e.g., between ice I and ice II (7).

In the bulk, water molecules always exist as clusters (7), and their physical features, including the IR spectra, are dominated by interaction with the immediate neighbors. In the bulk these are predominantly other water molecules. In proteins, pores, or other confined conditions, the immediate environment might be different from that in the bulk. Once out of direct contact with aqueous solutions, highly hydrated stacks of biological membranes (relative humidity near 100%) do not contain bulk water but rather thin layers of water between the lipid bilayers. Unlike bulk water, these are quasi two-dimensional structures, several monolayers thick, whose physical properties might be quite different from those in the bulk. The difference is mainly due to the same factors that are responsible for the differences between macroscopic materials and nanostructures created out of them. The structure and the thermodynamic behavior of the thin layers of water, when sandwiched between the membrane stacks (13,14) or in thin pores (15), differ from those of bulk water, and this is reflected in the IR spectra, which also differ from those for the bulk water (7,11,12). For example, in such cases water does not freeze at 273 K but remains liquid below its normal freezing point (15). This should affect both the structure and the functional peculiarities of proteins embedded in membranes when studied below the expected freezing point at 273 K. Besides a general interest in the properties of such materials, this might have impact on data obtained by methods that require low temperature, e.g., X-ray crystallography, cryo-trapping for NMR, EPR or optical spectroscopy, etc. as well as on biomaterial storage.

In the region of freezing/thawing, the thermal behavior of water in the confined space between biological membranes is complex (16–19). Because of hysteresis in the freezing and melting process in the 260–273 K temperature range, the thermodynamic state of inter-bilayer water is determined not only by temperature but also by the thermal history of the sample. As we report here, the freezing of water is reflected in the altered behavior of the embedded protein, bacteriorhodopsin, but the corresponding changes are surprisingly small.

In the 180–350 K temperature region a stack of highly hydrated membranes might experience at least five distinct phase transitions: i) water freezing at or below 273 K, ii) the main phase transition in the lipids, i.e., the freezing of the hydrophobic lipid tails, which could be as low as at ~260 K for phosphatidylcholine (20) or as high as at ~350 K in purple membranes (21–23) with most lipids between these two extremes; iii) a phase transition in the protein, e.g., at ~240 K (4) in bacteriorhodopsin, the only protein in the purple membrane; iv) the dynamic phase transition, which takes place at or below 230 K in purple membranes (13,18,24–26); and v) the glass transition of lipids, which takes place at or below 210 K (27,28). The dynamic phase transition would have been expected to be a phenomenological consequence of either a thermodynamic phase transition in the protein or its immediate environment, the water and/or lipid. However, it takes place in the purple membrane samples at or below 230 K (13,18,24– 26), i.e., at least 15 K below the transition in the protein (4) or at least some 25 K below the freezing of water (4), and still father away from any known transition in the surrounding lipids (21,29). While the infrared changes observed during the freezing of bulk water (7,11,12) and lipid tails (30–32) are well documented, the infrared signatures of the other three transitions are virtually unknown.

Most of the published IR data on water are focused on its bulk properties, and IR studies of water in biological membranes are mostly done above 273 K, i.e., in the physiologically-relevant temperature range. Here, we focus on the IR characterization of thin layers of water found in well-hydrated stacks of biological membranes, and we extend the temperature region from ambient down to 180 K to cover the region of all of the above-mentioned phase transitions in an attempt to separate the phase transitions in water, or induced directly by water, from those in lipids and the embedded protein bacteriorhodopsin.

Materials and Methods

Phosphatidylcholine was from Avanti (# 840051, Avanti Polar Lipids Inc, Alabama), purple membranes from Halobacterium salinarum, containing bacteriorhodopsin were isolated according to (33). A D96N mutant was used, which, due to the absence of the primary proton donor, Asp-96, perturbs the reprotonation of the Schiff-base and simplifies the observable events in the second half of the photocycle, as recently described at low temperatures in more detail (4).

Samples for IR were prepared by deposition and air-drying of either purple membranes suspension in 1 mM HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid) or lipids from chloroform solution on 13 or 15 mm diameter CaF₂ infrared windows. The lipid samples were humidified by ~90 hours equilibration with a 100% relative humidity atmosphere. Purple membrane films stored under room humidity were further humidified by adding a 2 µL drop of water near but not touching the sample immediately before sealing, and then allowing additional ~48 hours for final equilibration. The samples were sealed with the second IR window, separated from the first by a 0.8 mm Teflon spacer, which was compressed by the cold-block. The humidity of the samples, as monitored by IR, was constant for hundreds of hours, which included repeated changes of temperature in the 1800-300 K range. In the purple membrane samples, for which the protein:lipid ratio is fixed and known (34,35), and the protein concentration is easily estimated spectroscopically in the visible, using ε_VIS = 63,000 M⁻¹cm⁻¹ for the extinction coefficient at 570 nm (36) corrected by a factor of 1.31 (37) for the orientation of purple membranes in the plane of the IR window, the composition in terms of ratio of the number of molecules is approx. 1:10:1600 of bacteriorhodopsin:lipid:H₂O; consistent with published data on such samples at 100% relative humidity. The IR spectra of pure lipid samples were also consistent with the stoichometric ratio of water to lipid molecules, ~3 at 100% humidity (38).

Infrared measurements were performed at a 2 cm⁻¹ resolution on Bruker IFS-66/s Fourier-transform IR (FTIR) spectrometer equipped with an MCT detector (D15D22-M204B-S01M-60-D315/6, Judson, Montgomeryville, PA, USA) and a water-cooled Globar source, operating at 1500 K. The IR beam was restricted by a 5-mm aperture, and the IR flux reaching the sample was <10 mW. The data were collected at 40 kHz scan-rate for the 0–5200 cm⁻¹ wavenumber range. At least two consecutive spectra, with co-adding of 1119 interferograms for each spectrum during the 10 min collection time, were measured at each temperature to verify temperature stability.

Kinetics of the photocycle was monitored, after a single-flash excitation of the second harmonics Nd:YAG laser (10 ns, 532 nm, ~2mJ/cm²) until full recovery of the initial state, in the rapid-scan mode at 240 kHz scan rate with appropriate averaging. For details on time-resolved low-temperature monitoring of the photocycle and kinetic data analysis see (4). Photocycle measurements were performed on highly humidified (see below) samples at pH 6.9.

The IR samples in a ~130 g home-made cold-block were placed in the Optistat DM cryostat equipped with an ITC601 temperature controller (both from Oxford Instruments, Abingdon, UK). This system was able to maintain the temperature stability, as measured with HH81A digital thermometer with a K-type thermocouple (both by Omega Engineering, Stamford, CT, USA) attached directly to the cold-block, with an accuracy better than 0.1 K for >5 hours. Full equilibration to a new temperature point after a temperature jump required ~60 minutes, which was always allowed before collection of spectra. See (3,4) for further details on both low-temperature and photocycle measurements.

All IR bands discussed below are much wide than the 2 cm⁻¹ resolution used in this study. Therefore, they might have been expected to be Lorentzian in shape if it were not for the perturbing influence of the limiting integration in FFT and of the folding with apodization functions. IR bands are best simulated with a weighted sum of Gaussian and Lorentzian profiles (39), where the ratio between the two contribution is an additional adjustable parameter for each of the individually fitted bands. We used such Gaussian/Lorentzian mixtures for deconvolution of the spectra in Figure 1 and Figure 5.

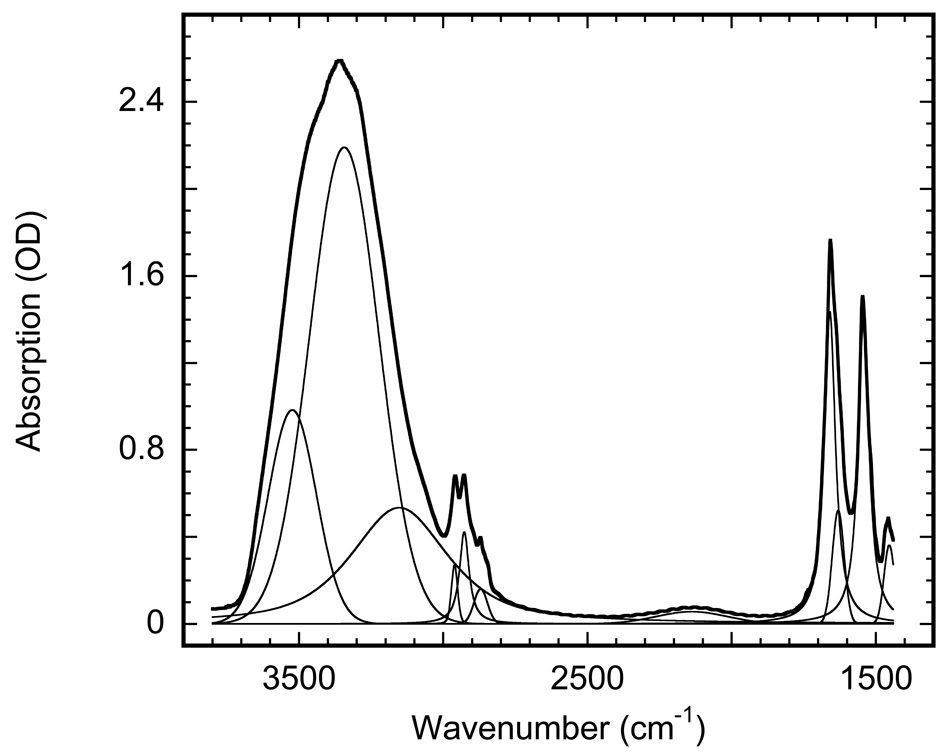
Figure 1.

Absorption spectrum of a purple membrane film (wild-type bacteriorhodopsin) at pH 6.9 deposited on an IR window from 1 mM HEPES solution. The bold line is the measured spectrum, the thin lines are the result of fitting (r⁻¹≥0.999) with weighted sum of Gaussian and Lorentzian bands, which contain12 peaks: (i) five for water at 3523, 3340, 3137, 2131, 1628 cm⁻¹;, (ii) four for methyl and methylene bands of lipids at 2961, 2927, 2871 and 2846 cm⁻¹; and (iii) three for amide bands of the retinal at 1658, 1543 and 1453 cm⁻¹. The band at 2846 cm⁻¹ is barely seen in the figure, since its amplitude is ~1/5 of that of the already small neighboring band at 2871 cm⁻¹.

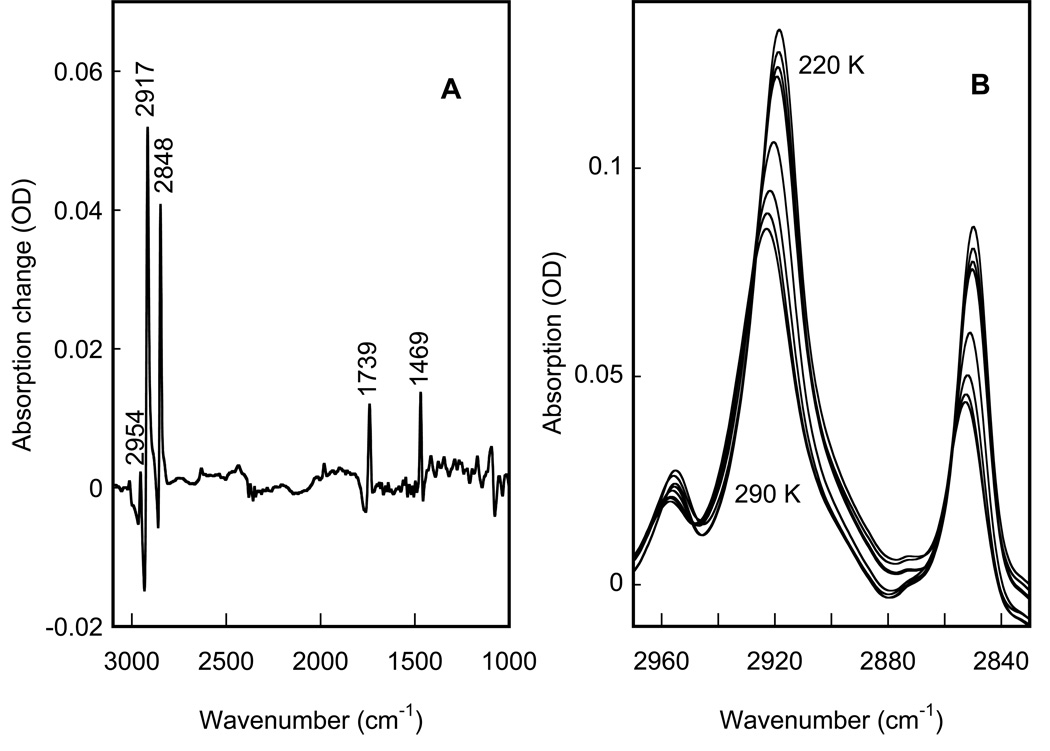
Figure 5.

IR spectral changes in the main phase transition in a hydrated phosphatidylcholine film, shown to define the changes during a phase transition in lipids. A: difference spectrum between 290 and 220 K. B: corresponding absorption spectra in the methyl and methylene stretch region, with the IR bands that increase in amplitude as the temperature is decreased from 290 K in 10 K steps, and down-shift in frequency.

The phase transitions were monitored in IR by either the shifts of characteristic bands positions, or by the changes in the overall transmittance. The latter was measured as the amplitude of the raw IR signal on the detector prior to Fourier transform, and reflects an integral over the whole IR region from ~800 to ~5500 cm⁻¹.

To evaluate the parameters of the phase transition, the IR data were fitted to transition-type dependence:

$$\mathit{\nu }(T)={\mathit{\nu }}_{\mathit{\text{RT}}}-\mathit{\Delta }\mathit{\nu }/\{1+{[T/T_C]}^N\},$$ (1)

where ν(T) is a value (a band position or its width or the amplitude of the IR transmittance) at a given temperature T, ν_RT is the corresponding room temperature value, Δν is its change in the course of the transition, T_C is the transition’s critical temperature, and N is the size of the cooperativity cluster.

To quantitate the protein and the water in our samples, 3.7 OD˙ml of bacteriorhodopsin, i.e., ~ 1.5 mg was resuspended in a 1 mM HEPES at pH 6.9, and evenly spread on a ∅ 25 mm CaF₂ window, forming after partial evaporation a ∅ 23 mm semi-dry film. If it were unoriented as suspension, it would have had ~0.89 OD at 570 nm. However, because the thickness of the purple membrane is 1/100 of its diameter, this film is highly oriented and its apparent optical density is higher due to the retinal-chromophore forming a 21° cone from the plain of the membrane (40,41). Such orientation effectively increases the absorption by a factor of 1.5˙cos²(21°) = 1.31 (37), i.e. to 1.16 OD, in accord with the measured value. The calculated values for extinction coefficients of bacteriorhodopsin in the IR, and as a result, the mol ratio of water to bacteriorhodopsin and the number of effective monolayers of bacteriorhodopsin in each particular sample, would be affected by the degree of orientation of the monolayers relative to the IR window surface. If a minor fraction of the membranes did not lie flat relative to the supporting window, the density of the bacteriorhodopsin in the film but not that of the water, would be underestimated. We believe that such non-ideal orientation causes less than 10% error in the calculated values.

OPUS (Bruker, Geramny), GRAMS (Galactic Industries Corp., Salem, NH), Matlab (The MathWorks Inc., Natick, MA), CurveExpert (42), Fitexp (43), and KaleidoGraph (Reading, PA) software were used for data evaluation and presentation.

Results

Water content and IR extinction coefficients

The spectrum of a typical purple membrane film at room temperature is presented in Figure 1. As a result of humidification it developed an apparent absorption of 2.64 OD in the region of the main water absorption band at ~3360 cm⁻¹ , and 1.55 OD in the region of the protein amide II band at 1543 cm⁻¹ . For the 1443–3778 cm⁻¹ range it was fitted with 12 peaks, yielding 5 bands for water, 4 bands for lipid and 3 bands for amide absorption, with r² ≥ 0.999. Based on previous assignments for bulk water (see (44) for review) the five water bands correspond to the following vibrations: i) the 1628±1 cm⁻¹ band is bending, ii) the 2130±10 cm⁻¹ band is a combination of bending and rock/libration, the latter being at ~690 cm⁻¹ and not shown in Figure 1, iii) the 3140±20 cm⁻¹ band is probably a second overtone of bending and Fermi resonance from symmetric stretch, iv) the 3340±3 cm⁻¹ band is symmetric stretch, and v) the 3522±2 cm⁻¹ band is antisymmetric stretch. We note that the IR peak positions for water in the confined inter-bilayer space in Figure 1 are somewhat different from those of the bulk water (11,44).

Taking the bending vibration band at 1628±1 cm⁻¹, which is least affected by any possible redistributions in intensity, as a reference, and based on its ε_bending = 20.8 M⁻¹ cm⁻¹ (5,7,45), we obtain for the following extinction coefficients for water confined in the inter-bilayer space at room temperature:

Vibration	antisymmetric	symmetric	2nd overtone	combination	bending
position	3522 cm−1	3340 cm−1	3140 cm−1	2130 cm−1	1628 cm−1
Width	195 cm−1	285 cm−1	400 cm−1	290 cm−1	50 cm−1
extinction	43.9 M−1cm−1	96.3 M−1cm−1	20.6 M−1cm−1	3.2 M−1cm−1	20.8 M−1cm−1

The band positions and the extinction coefficients are different from those of bulk water, which are 62.7 M⁻¹cm⁻¹ at ~3490 cm⁻¹ and 54.5 M⁻¹cm⁻¹ ~3280 cm⁻¹, respectively (5,7).

The four bands in the 2845–2961 cm⁻¹ region are from the antisymmetric and the symmetric stretch of methyl groups at 2961 and 2870 cm⁻¹, and the antisymmetric and the symmetric stretch of the methylene, at 2927 and 2845 cm⁻¹ respectively (46). We obtain the following extinction coefficients (not corrected for orientation):

Vibration	amide I	amide II	amide III
position	1658 cm−1	1543 cm−1	1451 cm−1
width	46 cm−1	46 cm−1	43 cm−1
extinction	105,000−1cm−1	98,000 M−1cm−1	28,000 M−1cm−1

These values are in accord with the earlier published ratio of extinctions of amide I to amide II (45). Using the extinction coefficients for amide II at 1543 cm⁻¹ and for water bending vibration at 1628 cm⁻¹, we calculate the ratio of the number of water molecules per bacteriorhodopsin for the sample in Figure 1 to be ~1660, which corresponds to a 1.15 weight ratio. The latter means that ~49%, by volume, of the sample thickness is water i.e., ~4.27 µm of H₂O vs. ~4.3 µm of purple membrane, in accord with buoyant density of bacteriorhodopsin ~1.18 (47). Water contains ~3.3˙10²⁵ molecules per liter, and some 118 water molecules are needed to cover the 1140 Ų (48) surface of each bacteriorhodopsin molecule, leading to ~14 water monolayers for each inter-membrane space for the sample in Figure 1, which is effectively a stack of ~962 individual membrane sheets, each with a thickness of ~45 Å (49).

Since each bacteriorhodopsin molecule is surrounded by ~10 lipids (34,35,50), the sample in Figure 1 consists of three components bacteriorhodopsin/lipid/H₂O in the 1:10:1660 ratio. Usually, a purple membrane sample incubated at a relative humidity near 100% contains ~2–3 times less water (18,19,25,51). We attribute this difference to the additional water uptake by the ~30–50 mM buffer, present from partial evaporation of water from the 1 mM buffer in solution, from which the sample is prepared.

Thermodynamics of phase behavior of inter-bilayer water

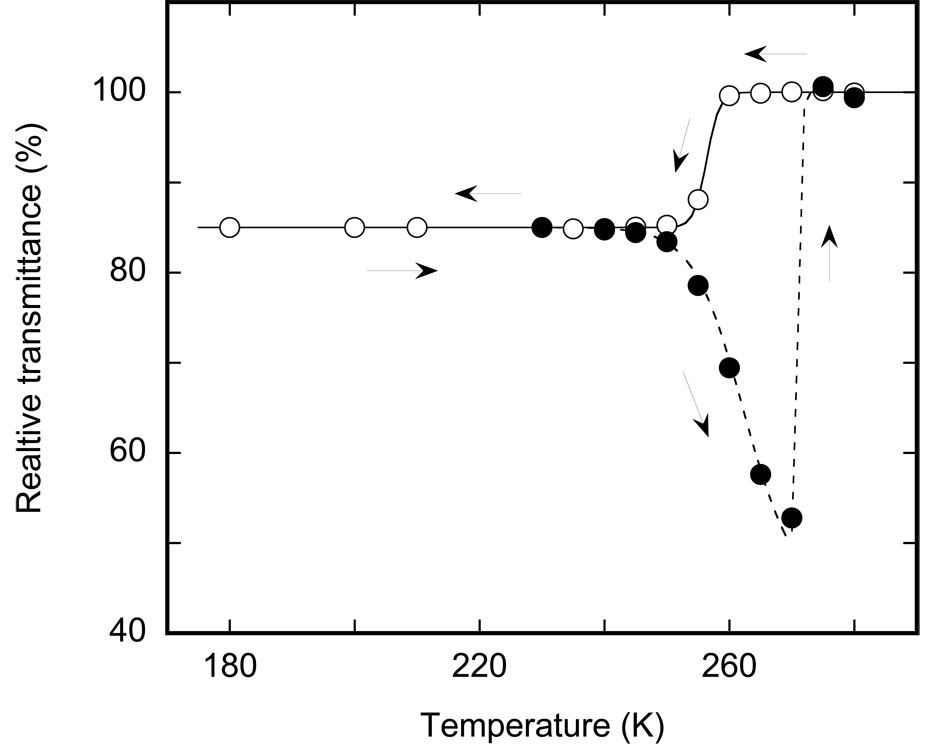
The phase behavior of inter-bilayer water is different from that of the bulk (16–19). We find that the temperature affects both the IR absorption and IR scattering of the highly hydrated membranes. The corresponding changes in transmittance, which include contributions from both the IR absorption and the IR scattering of purple membranes, are presented in Figure 2. The corresponding IR absorption changes are in Figure 3. When considered together, Figure 2 and Figure 3 include four temperature regions that might indicate thermodynamic phase transitions. The thermal behavior of confined water upon cooling is different from that of during the heating, and, therefore, these are presented as two distinct branches in Figure 2, a solid curve for cooling and a broken line for heating.

Figure 2.

Temperature dependence of the overall IR transmittance, measured as the raw amplitude of the signal from the IR detector prior to Fourier transformation. The solid line and open circles depict the cooling branch from 280 to 180 K; the broken line and filled circles illustrate the heating of the sample after the previous cooling to 180 K (see arrows). Cooling and heating between 180 and 240 K do not noticeably affect the overall transmittance despite a change in the absorption below 220 K (see Figure 3).

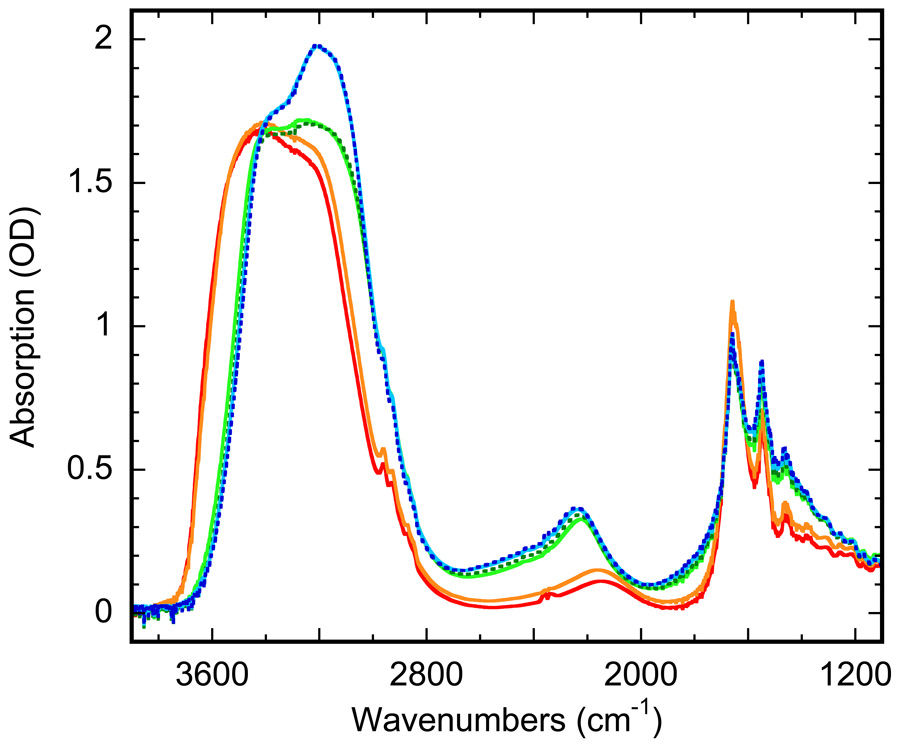
Figure 3.

Absorption spectra of highly hydrated PM film, upon cooling: with non frozen water at 280 (red) and 260 K (orange), and with ice at 250 K (green), 220 K (cyan) and 180 K (blue). The spectra for liquid water are nearly indistinguishable between 280 and 260 K. They are changed in a transition-like manner at ~256 K, reflecting the freezing. Below 250 K the changes in the spectra of ice are gradual, and does not form a sigmoidal curve, which might have been associated with a distinct transition. See text for details.

The cooling curve in Figure 2 includes only one region indicative of a phase-transition type behavior. When fitted with Eq. 1, the cooling curve reproduces a transition centered at ~256 K with a cooperativity parameter N~250 (r²>0.999). As judged from the absorption spectra (compare spectra in (5,7,10–12) and in Figure 3), this is the freezing of inter-bilayer water, which is supercooled to 256 K due to confined conditions (15). The freezing is rapid and accomplished within the temperature equilibration time. Additional waiting, up to several hours at any temperature in the 180–260 K temperature range on the cooling branch, did not lead to further change in the IR transmittance.

Upon further cooling below 250 K, smaller changes, seen in the absorption spectra in Figure 3 but not in the overall transmittance in Figure 2, develop gradually. The corresponding IR changes are small and are not coupled to a significant shift of the water vibration bands (Figure 3) as occurs in freezing. Unlike the phase transitions in Figure 2, these changes do not produce the characteristic sigmoidal curve described by Eq. 1. However, these spectral changes (Figure 3) are characteristic, and with decreasing temperature their shape shifts more and more toward the spectral shape in bulk ice.

The heating branch for the sample pre-cooled to ≤240 K is different from the cooling branch (Figure 2) reflecting thermal hysteresis. Similarly to the cooling branch, the heating branch also includes two regions of changes but these are different changes and take place at different temperatures than during cooling.

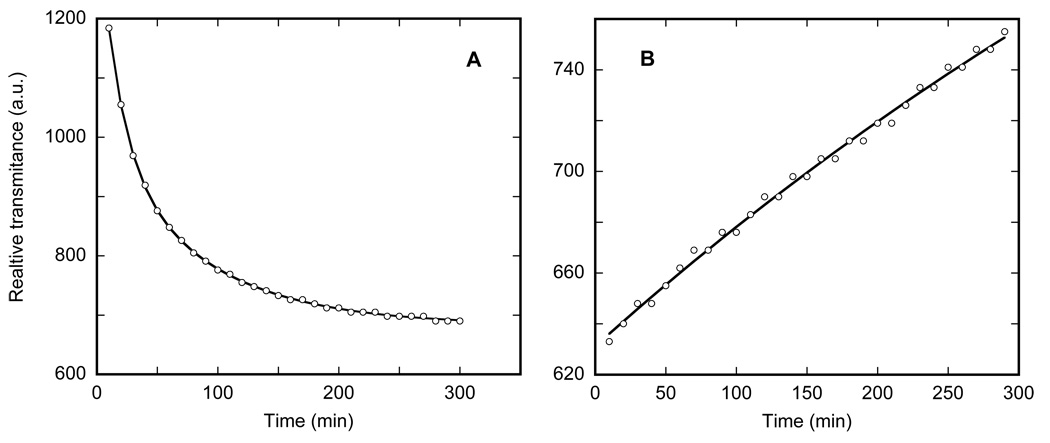
Incremental heating results in progressively decreasing transmittance in the 250–270 K range. This change in IR transmittance is interesting from two points of view. First, it strongly affects scattering without any noticeable effect on IR absorption. Second, unlike freezing, the increase in scattering displays a kinetics of its own, measurable far beyond the time needed for temperature equilibration. The kinetics are shown in Figure 4A. The rates are not strongly temperature dependent and could be represented by two-exponential fits (r² >0.998) with time-constants of 10–20 and 60–90 min at temperature in the 250–265 K range. Comparing the pronounced change in transmittance with virtually no change in absorption in the 250–265 range, we assume that this reflects progressive increase in scattering, most probably from micro-cracking in the ice layers induced by heating. Since it is not coupled to any significant shifts of the vibration bands, we consider that it is not associated with a phase-state change. Note that these changes appear long before the actual thawing above 270 K, and, while to a first approximation their rates are temperature independent, the extent of the temperature-induced change is not, varying from ~11% at 250 K to ~24% at 265 K.

Figure 4.

Kinetics of the overall transmittance changes at 260 K, measured as the raw amplitude of the signal on the IR detector prior to Fourier transform. It could be represented as a bi-exponential increase in scattering with the time-constants: τ₁~17 min, accounting for ~55% of the amplitude of the change, and τ₂~82 min.

The thawing of inter-bilayer ice appears as a jump just above 270 K. In the IR it is characterized by an up-shift by >100 cm⁻¹ of the entire main absorption band of water (Figure 3) and a nearly two-fold increase in the overall IR transmittance. The up-shift is an IR signature of thawing, well-known from studies of bulk water (5,7,10–12), and provides an unambiguous assignment. When the measured transmittance changes are fitted with Eq. 1, they indicate a transition centered at ~273 K and characterized by a cooperativity parameter N ~ 900. As with freezing, the corresponding changes at 273 K are rapid and complete within the time needed for temperature equilibration.

However, unlike in freezing, upon thawing we were able to observe an additional, yet unassigned, process at 270 K, i.e. 3 K below the critical temperature for melting, with very slow kinetics on the time-scale of tens of hours. This process is much slower, with an estimated time-constant of 5–15 hours, than the preceding changes in scattering in the 255–265 K range, with time-constants <100 min. On the other hand, both processes appeared long after the temperature equilibration, unlike the actual freezing and thawing processes. This slow process is observed only in a very limited range close to 270 K, and further studies will be needed for its assignment.

It is possible, in principle, that the IR beam of the spectrometer heats the sample sufficiently to cause kinetic artefacts. A rough estimate would be a temperature elevation in the IR beam by 0.001–0.1 K, which could be responsible for the above-mentioned slow kinetics. To test for this, we repeated the time-resolved experiments in the 255–270 K range, using an IR beam attenuated by a factor of ~4 with thin Ge wafers. There were no noticeable change in the observed rates, and we conclude that temperature gradients created by the measuring IR beam are not responsible for the observed kinetics.

IR monitoring of the main lipid transition

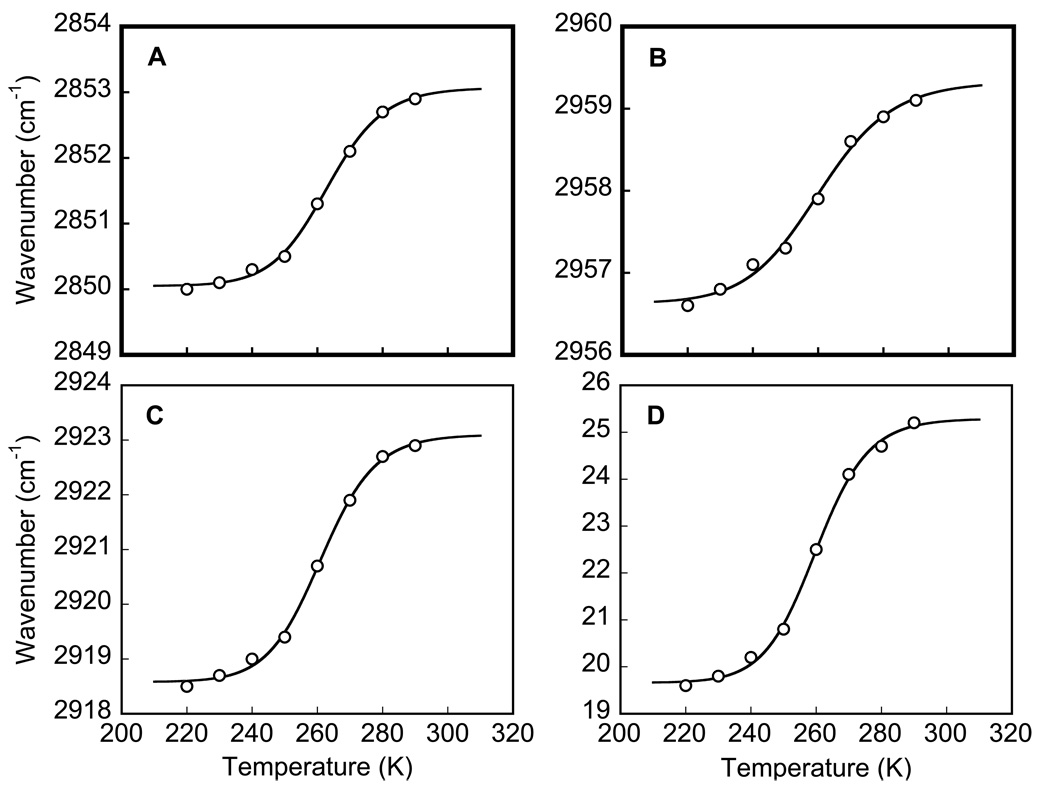
Besides the protein and the water, the purple membrane sample contains only lipids. Most pure lipids undergo a main phase transition in the 250–350 K range (20,52), which is primarily the freezing and immobilization of the hydrophobic lipid tails. This transition leads to specific changes of the methyl, methylene, and carbonyl bands (30–32). Figure 5A represents a difference spectrum for the main (gel-to-liquid crystal) transition calculated between spectra of a phosphatidylcholine film at 290 and at 220K. It contains sharp spectral features from perturbation of the symmetric (~2848 cm⁻¹) and antisymmetric (~2917 cm⁻¹) methylene stretches, methyl antisymmetric stretch (~2954 cm⁻¹), carbonyl antisymmetric stretch (~1739 cm⁻¹), and methylene scissoring and/or methyl bending (~1469 cm⁻¹). Our IR spectra are in accord with earlier data from other lipids (30–32,53) for this transition. The strongest changes are in the region of the methyl and methylene stretch vibrations at 2830–2970 cm⁻¹ (Figure 5B). For their evaluation, the spectra were at first fitted (in GRAMS) with a weighted sum of Gauss and Lorentz band-shapes (with r² ≥ 0.997, data not shown), and then the band position (Figure 6A–C) or their widths (Figure 6D) were fitted with Eq. 1.

Figure 6.

Temperature-dependence of infrared changes in a hydrated phosphatidylcholine film at its main phase transition. A: symmetric methylene stretch frequency; B: antisymmetric methyl stretch frequency; C: antisymmetric methylene stretch frequency, respectively. D shows line-width change for the antisymmetric methylene stretch. Solid lines are the fits (r²≥ 0.994) of Eq. 1 to the data points (open circles), which yielded the following parameters: for symmetric methylene stretch (A), ν_RT = 2853.1 cm⁻¹, Δν=3.0 cm⁻¹; for antisymmetric methyl stretch (B), ν_RT = 2923.1 cm⁻¹, Δν=4.5 cm⁻¹; for antisymmetric methylene stretch (C), ν_RT = 2959.3 cm⁻¹, Δν=2.7 cm⁻¹; and for narrowing of the antisymmetric methylene stretch band characterized by its full width at half maximum, FWHM, (D), FWHM_RT = 25.3 cm⁻¹, ΔFWHM_RT = 5.6 cm⁻¹.

Thus, the IR data for phosphatidylcholine characterize a transition that leads upon freezing to a down-shift of 3.6±0.9 cm⁻¹ in the position of (i) the symmetric (Figure 6A) and (ii) antisymmetric (Figure 6B) methylene stretch bands, (iii) methyl antisymmetric stretch band (Figure 6C), as well as (iv) to a substantial narrowing (by 22%) of the antisymmetric methylene stretch band (Figure 6D). The infrared changes take place at T=261±2 K, in accord with the earlier reported values, 263±7 K for the gel-to-liquid crystal transition determined by calorimetric methods for this lipid (53–63). The corresponding average size of the cooperativity cluster, N, includes according to our estimate 28±5 molecules, in accord with the previously reported domain size (although in different lipids) N=40±5 (64) or N=50±30 (65) or N=37 (66), determined for the gel-to-liquid crystal transition with atomic force microscopy (64,65) or by fluorescence anisotropy measurements (66).

Unlike for pure lipids (see (52) for review), not much is known about the phase behavior of purple membrane between 180–280 K. No evidence for thermodynamic phase transitions were found by either differential scanning calorimetry in the 240–350 K range (23,67) or by X-ray diffraction in the 195–350 K range (21,22). In accord with this, unlike in phosphatidylcholine, we did not find in the 180–280 K range any IR-detectable change in the methyl and methylene bands of purple membrane films (data not shown), at the accuracy of ~1 cm⁻¹, as compared to the 3–4 cm⁻¹ shifts in Figure 6.

The ~261 K temperature point of the IR-detectable phase transition in phosphatidylcholine in Figure 6 is uncomfortably close to the freezing point of inter-bilayer water at 256 K in Figure 2 but its presence in the lipids vs. its absence in the purple membrane sample, and its coincidence with the calorimetrically-detected transition in phosphatidylcholine (20) indicates that this is an intrinsic property of the lipids rather than a slaving effect forced by freezing of the water.

Bacteriorhodopsin kinetics in the region of thermal hysteresis

The kinetics of the photocycle of the D96N mutant at pH 6.9 in the 180–280 K temperature range were described recently in detail (4), in the same samples as those used in this study. At temperatures in the range of 250–280 K a mixture of M and N intermediates is formed within 0.1 s, and this mixture decays to the bR state on the time scale from 0.1 to 10³ seconds with 2-exponential kinetics (see (4) for more details). Thus, the general pattern of the photocycle above 250 K is not different from that at room temperature but with slower overall kinetics. However, the data in (4) was measure on the cooling branch of the hysteresis curve in Figure 2, and the thermal hysteresis (Figure 2) creates a possibility to examine the photocycle in the 250–270 K region, at a fixed given temperature but with the protein surfaces in different environments, of either liquid or frozen water, depending on the thermal history of the sample.

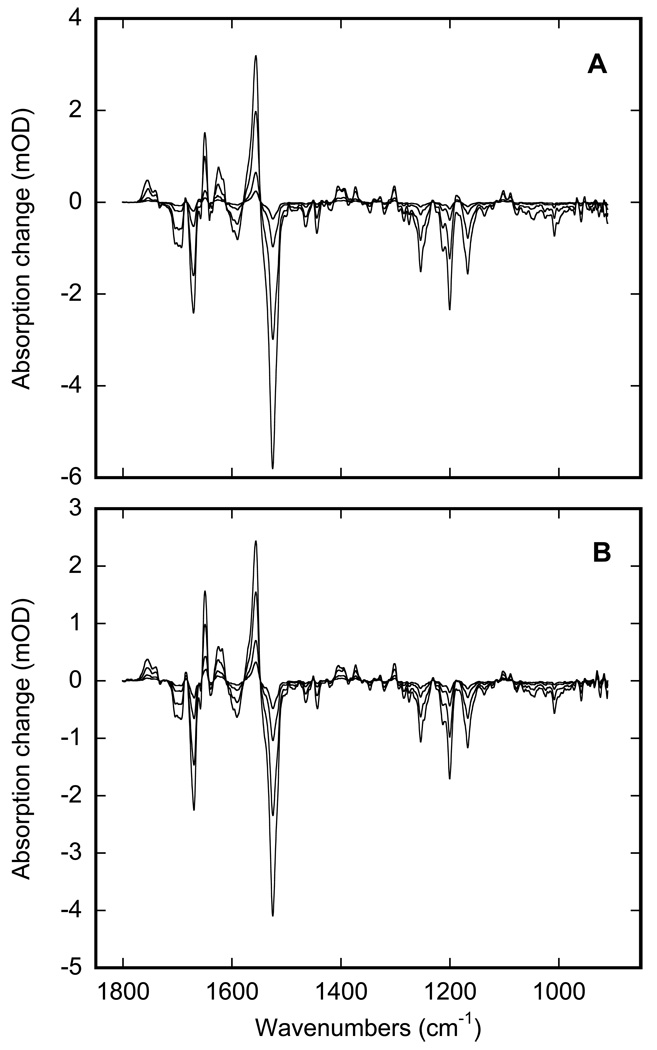
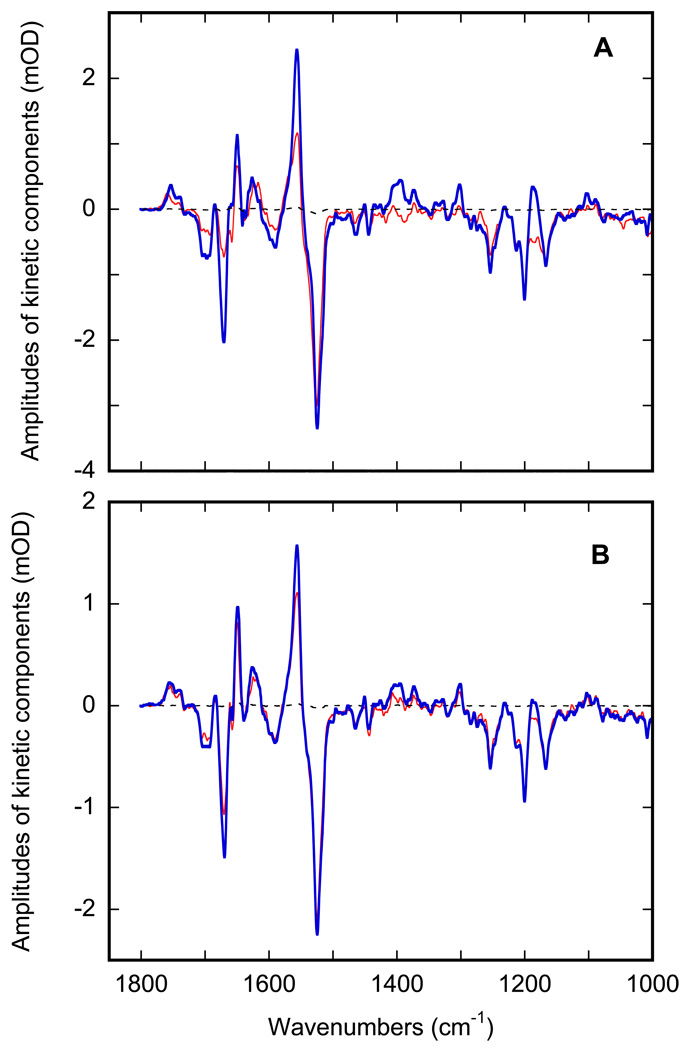
Thus, the photocycle reactions in the D96N mutant at pH 6.9 were monitored after two different thermal pre-treatments. Figure 7 presents the result of rapid-scan IR monitoring of the thermal decay of the mixture of M and N states produced at 270 K after flash excitation. The two panels present the time-resolved spectra for the two options provided by the hysteresis. In panel A the spectra were measured on the sample cooled from 280 K to 270 K, where the water is still in a fluid state (see Figure 2), and in panel B the same sample was first cooled to 240 K to freeze the inter-bilayer water, and then heated to 270 K, ~3 K short of thawing the water (see Figure 2). In both cases the measured kinetics consist of the decay of both M and N intermediates (Figure 7) but the contributions of M and N are different. To explore the differences in more detail, data like those in Figure 7 were subjected to global fitting with multi-exponentials at all wavenumbers (43). In both cases, the IR changes in Figures 7A and 7B are composed of two kinetic components. The two sets of corresponding apparent time-constants at 270 K are 1.9±0.1 and 7.7±0.2 sec for the case of liquid water and 2.2±0.2 and 12.2 ±0.3 sec for the case of ice. Evidently, only the second kinetic component is affected by the phase-state of the inter-bilayer water. The calculated spectra of the two components (Figure 8) indicate that in both cases they are not pure intermediates but are rather mixtures of M and N states.

Figure 7.

Stacks of time-resolved IR spectra measured at 0.3, 3, 10 and 20 seconds after photocycle excitation by 5 ns laser flash at 532 nm, measured on light-adapted (at 280 26 K) D96N bacteriorhodopsin mutant at pH 6.9. A: sample containing liquid water at 270 K, cooled from 280 to 270 K. B: sample containing frozen water at 270 K, first cooled to 240 K to freeze the inter-bilayer water, and then heated to 270, i.e., ~3 K short of reaching the thawing point at 273 K.

Figure 8.

Spectra for the two distinct kinetic components at 270 K, the faster one (red) and the slower one (blue), obtained by global fit of data in Figure 7A and 7B, correspondingly. A: purple membranes surrounded by liquid water, i.e. reached along the cooling branch in Figure 2. B: purple membranes surrounded by frozen water, i.e. reached along the heating branch in Figure 2.

Discussion

The water content in a particular preparation of biological membrane is most commonly characterized by relative humidity. While varying the relative humidity allows to study water-induced effects (46,68), this information per se might be not sufficient for samples such as purple membranes. When equilibrated with water vapor of the same partial pressure, films containing salt absorb water differently, dependent on the amount of salt. We present here direct monitoring of water by IR spectroscopy. Comparing absorption in the visible for protein concentration with IR absorption, we obtained the IR extinction of purple membrane, which allowed us to calculate the ratio of protein to water molecules. This ratio in our preparations was 2–3 higher than that of the usually used IR samples (see (51,69) for example). This excess water, amounting to ~1500 water molecules per bacteriorhodopsin was intentional and important for our further studies of water-protein interaction during the freezing and thawing of water confined in the inter-bilayer space.

The complex pattern of freezing and thawing of water in biological samples has been noted previously by a variety of techniques (16–18). The thermal hysteresis in Figure 2 might seem contra-intuitive at first sight. However, according to the theory of homogeneous nucleation, the stability of nuclei depends on two competing forces proportional to its volume and to its surface, respectively, resulting in its instability below a certain size (70). Therefore, size restrictions as in pores, layers, or any other confined geometry, should impede homogeneous nucleation and depress the freezing point, as is indeed the case for thin surface layers, thin pores in soils, and nano-tubes (15). Our measured depression by ~17 K in samples, in which the inter-bilayer water is ~ 4.5 nm thick, is in accord with the theoretical estimates (70), from which a value of ~15 K should be expected for this geometry. The fact that the freezing point could be depressed for confined water without a corresponding effect on the thawing point has been shown previously by X-ray diffraction studies (16). The result is hysteresis, as in Figure 2, which appears because, unlike freezing, thawing does not require a nucleation step.

Unlike the previous reports on thermal hysteresis in inter-bilayer water by X-ray (16) and by electron spin resonance (17), which measure not the phase transition per se but rather secondary effects that accompany the phase transitions, IR spectra with its information about the frequencies and amplitude distributions of the thermal vibrations, provides more direct evidence on the phase state under study. In particular, the IR data allowed us to unambiguously distinguish two different processes that give rise to the complex behavior of the heating branch in Figure 2: ice thawing at 273 K, and an increase in scattering in the 250–270 K, a change not coupled to a phase state change. The thermodynamic hysteresis enabled comparing the influence of the state of water on the photocycle dynamics at a constant temperature.

The IR spectra of inter-bilayer water in the 180–280 K range (Figure 3) indicate two distinct regions of changes during cooling. The first is the freezing at ~256 K, well described by Eq. 1. It induces a dramatic downshift of the entire main absorption band of water, characterized by a shift of the apparent maximum from ~3400 to ~ 3200 cm⁻¹, well known from the difference in the IR spectra between liquid water and solid ice in the bulk (5,7,10–12). While this >100 cm⁻¹ down-shift unambiguously indicates freezing, the IR spectra of the confined inter-bilayer ice in the 250–180 K range in Figure 3 are still different from those of the bulk ice (7,12). With decreasing temperature these spectra are gradually transformed, although without forming a distinct transition like the one described by Eq. 1, towards the spectrum of bulk ice: compare the trend in the spectral changes between 250 and 180 K in Figure 3 to the bulk ice spectra in (7,12). However, this latter change is only a result of redistribution of the intensities of the three strong IR components, the antisymmetric stretch at 3522 cm⁻¹, the symmetric stretch at 3340 cm⁻¹, and the 2^nd overtone at 3140 cm⁻¹ that form the main water absorption band with an apparent maximum at ~3200 cm⁻¹ for inter-bilayer ice (Figure 3), and it does not include the downshift of the absorption bands, which is an IR signature when the bulk water freezes (5,7,10–12). The spectral change below 250 K could indicate a gradual shift between differently organized ice and reflects some specific re-arrangements in the thin, virtually two-dimensional, layers of ice confined between the membrane bilayers.

We report elsewhere a strong temperature-induced effect on the kinetic of the bacteriorhodopsin photocycle centered at ~245 K (4), which we attributed to a phase transition of the protein. This kinetically-detectable transition is ~10 K below the freezing point of water, and this discrepancy indicated that the two phase transitions are not coupled (4). However, either of those two transitions, in the water or in the protein, could be separately coupled to a transition in the lipids. Any phase transition in lipids is normally accompanied by IR-detectable changes (30–32,71). However, our search by IR spectroscopy for a phase transition in purple membranes in the 180–280 K range did not succeed. The data on the main phase transition in phosphatidylcholine (Figure 5 and Figure 6) are included here as an example for the magnitude of the IR-detectable changes, which should have been expected if there indeed was a thermodynamic phase transition in the purple membrane lipids. As a result of the comparison, we conclude that the 180–280 K temperature range does not include any transition in purple membrane lipids. This is in accord with an early calorimetric and X-ray data on purple membrane, which failed to detect phase transitions in the 195–350 K range (21–23,67).

In general, phase transitions do influence the kinetics of protein functions. For bacteriorhodopsin, both photocycle kinetics and chromophore motions were shown to depend on lipid microviscosity (72). Furthermore, when reconstituted with dipalmitoyl phosphatidylcholine, the temperature dependence of M decay followed an S-shaped curve centered at ~ 308 K (72). The Arrhenius plots are qualitatively different between: (i) these reconstituted membranes that undergo a main phase transition at ~314 K (20,52), and (ii) samples with lipids that do not undergo the main transition in that temperature range, i.e., the native purple membranes (21–23,67) or egg phosphatidylcholine reconstituted samples (20,52). Recently, we observed a similar S-shaped temperature dependence for photocycle kinetics in a sample with native purple membrane lipids. It occurs at ~245 K (4), some 60 K below the transition described by Sherman at el (72) in the dipalmitoyl phosphatidylcholine reconstituted membranes. We assigned it to a transition in bacteriorhodopsin, and, unlike the one described in (72), it was not coupled to transitions in either lipids or water (4).

Here we explore the question whether the bacteriorhodopsin kinetics is sensitive to the phase-state of water confined to the intermembrane space. The kinetics of the bacteriorhodopsin photocycle is know to be sensitive to the environment, being affected by pH (73), ionic strength (73), reduced hydration (74), crystalline structure environment (75), solvent viscosity (76), etc. This is especially dramatic for the transitions in the second half of the photocycle, from M decay to regeneration of the initial state of bacteriorhodopsin, which involve large-scale conformational changes (77,78). The cytoplasmic surface of bR projects out of the lipid bilayer and is exposed to water (35). It might have been expected, therefore, that the extensive conformational changes in the cytoplasmic region of the protein (79) that were linked to the proton transfer from Asp96 to the Schiff base in the M to N reaction (80) would be affected by the water-to-ice transition. We have found that although the second phase of the two-component decay is slower in ice than in liquid water at the same temperature, it is a small (less than 2-fold) effect, and the M to N reaction is not blocked by immobilization in a frozen environment.

The relatively minor effect of the freezing of water is evident in the calculated spectra in Figure 8. They indicate that the relative contribution of the N state increases with time, and that this redistribution is less pronounced in ice (Figure 8A). The opposite should have been true if the reactions of M and N were unidirectional, since the first of the two apparent rates are the same in both frozen and non-frozen states of water (2.2±0.2 vs. 1.9±0.1 sec) but the second rate constant is >50% slower in the former case (12.2 ±0.3 vs. 7.7±0.2 sec). However, the M-to-N transition is a reversible reaction (81) and, to a first approximation, the observable rate constant is the sum of the corresponding forward and reverse rates. Thus, the stronger redistribution coupled to the faster apparent rate (Figure 8A) most probably indicates that rather than N decay itself, it is the rate-constant of the N-to-M back reaction that is affected by the freezing of inter-bilayer water, shifting the balance between M and N states and decreasing the apparent redistribution pattern in Figure 8B.