Combining assays for estimating prevalence of human herpesvirus 8 infection using multivariate mixture models

SUMMARY

For many diseases, it is difficult or impossible to establish a definitive diagnosis because a perfect “gold standard” may not exist or may be too costly to obtain. In this paper, we propose a method to use continuous test results to estimate prevalence of disease in a given population and to estimate the effects of factors that may influence prevalence. Motivated by a study of human herpesvirus 8 among children with sickle-cell anemia in Uganda, where 2 enzyme immunoassays were used to assess infection status, we fit 2-component multivariate mixture models. We model the component densities using parametric densities that include data transformation as well as flexible transformed models. In addition, we model the mixing proportion, the probability of a latent variable corresponding to the true unknown infection status, via a logistic regression to incorporate covariates. This model includes mixtures of multivariate normal densities as a special case and is able to accommodate unusual shapes and skewness in the data. We assess model performance in simulations and present results from applying various parameterizations of the model to the Ugandan study.

1. Introduction

This article was motivated by the problem of estimating prevalence of infection with human herpesvirus 8 (HHV-8) and quantifying the effects of factors that influence prevalence of HHV-8 infection in several African populations. HHV-8, also called Kaposi’s sarcoma (KS)–associated herpesvirus, is the generally accepted infectious cause of KS (Chang and others, 1994). Prevalence of HHV-8 infection and KS risk shows distinctive geographical variations. They are highest in sub-Saharan Africa, intermediate in Mediterranean countries, and lowest in the United States and northern Europe, where most KS cases are AIDS related (Martin, 2003). The modes of HHV-8 transmission are not well understood and appear to differ in high- and low-HHV-8 incidence regions. In African and Mediterranean countries, HHV-8 infection occurs during childhood, most likely via nonsexual modes of transmission, but in the United States and northern Europe, infection is essentially restricted to homosexual men and associated with sexual exposures (Martin, 2003).

Infection status with HHV-8 can be assessed by several serological assays, but it is impossible to establish a definitive diagnosis of infection status as a perfect gold standard measure does not exist. Standard statistical approaches to investigating factors that affect the prevalence of HHV-8 infection, such as contingency table analyses and logistic regression, employ an operational definition of “infected”, namely that the optical density (OD) reading of a given assay exceeds a prespecified cutoff value. Cutoff values are commonly determined based on previous experimental results and a visual inspection of histograms of the OD readings for the given study. To avoid having to use predefined cutoff values for an operational definition of infected, Pfeiffer and others (2000) fitted a 2-component mixture model to the results of continuous assay readings to estimate the prevalence of infection with Helicobacter pylori, with the components corresponding to “infected” and “uninfected” subpopulations. Letting y to denote the OD readings for immunoglobulin G, the model that treats the true infection status as a latent variable has a density function given by

$$g(y)=(1-p)f_0(y)+p{f}_1(y),$$ (1.1)

where f₁ is the density function corresponding to the test results for infected and f₀ for uninfected subjects. To assess the x factors that influence infection with H. pylori, Pfeiffer and others modeled the mixing probability p, the probability of being infected, by a logistic regression, p = p(x;β) = exp(β'x)/{1 + exp( β'x)}.

We will extend model (1.1) to the multivariate setting to address a second problem, that is, how to combine the information from several assays that capture different but not necessarily independent indicators of HHV-8 infection. This is important because a combination of assays may provide a better diagnostic tool and yield more accurate estimates of prevalence. Developments in the area of multivariate mixtures are mostly concentrated on mixtures of multivariate normals because of their computational convenience (McLachlan and others, 2003). However, the fit of multivariate normal densities to the log-transformed assay readings in our data was poor, leading to unreasonably large estimates of the key parameter of interest p, the prevalence, in model (1.1). To improve the fit and obtain unbiased estimates of p, we developed more flexible models to accommodate skewness and heavy tails in the OD readings. First, we incorporate the parameters of the Box–Cox transformation into the model and estimation. Second, we use densities from a flexible class introduced by Gallant and Nychka (1987) as the mixture components. This model includes multivariate normal mixture models as a special case. Covariates are incorporated into the mixing probability via logistic regression.

In Section 2, we define the bivariate logistic mixture models before assessing the performance of the models in simulations (Section 3). We apply the models to data from a cross-sectional study of blood-borne transmission of HHV-8 in Ugandan children afflicted with sickle-cell anemia (Section 4). We compare prevalence estimates from the bivariate mixture model to prevalence estimates obtained by averaging estimates from univariate mixtures fitted to each assay separately. We also compare logistic estimates from the bivariate mixture to those based on predefined cutoff values for the assays. Section 5 contains concluding remarks.

2. The data and model formulation

Inference is based on cross-sectional data on disease status and covariates at the time of examination. The data are (Y_j,X_j) for j = 1,⋯, n, where Y_j = (Y_j1,⋯, Y_jl) and Y_jk denotes the observed measurement for the kth assay on the jth subject. The p×1 vector X_j contains measured covariates. In our application, 2 immunoassays were used to determine HHV-8 infection status, and hence Y_j = (Y_j1, Y_j2). The first component, Y_j1, stands for measurements on the K8.1 assay that detects antibodies expressed during lytic infection, in serum. The second component, Y_j2, corresponds to serological measurements on the orf73 assay that tests for antibodies expressed during latency (Mbulaiteye and others, 2003).

2.1 Mixture model

There is an extensive literature on mixture models (McLachlan and Peel, 2000; Fraley and Raftery, 2002) that were developed to analyze the data that arise from 2 or more distinct data-generation processes. One major problem in mixture models concerns estimation of the number of component densities. However, in our application, we are confident that there are precisely 2 distinct populations that give rise to the data, an infected and an uninfected population. Thus, we assume that each person is in one of the 2 latent true infection states, which we label as state I_j = 1 (infected) and state I_j = 0 (uninfected) with p = pr(I_j = 1) for the jth subject. The probability of infection can depend on covariates x_j, for example, through logistic regression models pr(I_j = 1|x_j) = p(x_j;β). Other parameterizations of p have been used in the context of survival data in Pfeiffer and others (2004). Given x_j, the probability density function of Y_j is modeled as

$$g({\mathbf{y}}_j|{\mathbf{x}}_j,\theta )=f({\mathbf{y}}_j;{\mathbf{\alpha }}_0)\{1-p({\mathbf{x}}_j;\mathbf{\beta })\}+f({\mathbf{y}}_j;{\mathbf{\alpha }}_1)p({\mathbf{x}}_j;\mathbf{\beta }),$$ (2.1)

where f(·; α₀) is a bivariate parametric density function that corresponds to the OD measurements of the uninfected subpopulation and f(·; α₁) is the density of the OD readings for the infected subpopulation.

2.2 Choice of component densities

In previous work (Pfeiffer and others, 2000), we log-transformed the positive OD readings to remove asymmetry in the measurements and used normal densities for the components in model (2.1). However, the transformation was determined by visual inspection. We now incorporate the data transformation indexed by an unknown parameter λ into the likelihood. We choose the Box–Cox power transformation

$$y_i^{({\lambda }_i)}=\mathbf{\{}\begin{array}{cc}(y_i^{{\lambda }_i}-1)/{\lambda }_i,\hfill & {\lambda }_i\ne 0,\hfill \\ \log (y_i),\hfill & {\lambda }_i=0,\hfill \end{array}$$ (2.2)

for the components of y = (y₁, y₂). In the univariate density setting, coupling the Box–Cox power transformation to likelihood methods for normal mixtures has been used previously (e.g. Gutierrez and others, 1995). We use the same transformation for both components of the mixture for each assay, that is λ₀ = λ₁. Transformation ignores the scale of the observed data, and thus for different values of λ, the parameters of the component densities are not directly comparable (Carroll and Ruppert, 1981). Unlike parameters of the component densities, the mixing proportion p(x;β) in (2.1) has a physical meaning independent of the transformed scales, namely the percentage of the subpopulation with x that is infected.

To allow for more flexible shapes compared to normal densities, we choose the component densities in model (2.1) from a general class introduced by Gallant and Nychka (1987), called the semi-nonparametric densities. These densities have been studied, for example, by Zhang and Davidian (2001) and are defined as follows. Let φ(y, μ, Σ) be the bivariate normal density with mean vector μ, covariance matrix Σ, and argument y = (y₁, y₂). Then, the semi-nonparametric density is

$$f(\mathbf{y},\mathbf{\mu },\mathrm{\Sigma },\mathbf{a})={\mathbf{\left(}{\displaystyle \sum _{0\le i+j\le K}{a}_{ij}{y}_1^i{y}_2^j}\mathbf{\right)}}^2\phi (\mathbf{y},\mathbf{\mu },\mathrm{\Sigma }).$$ (2.3)

In (2.3), K = 0 reduces to the bivariate normal density. For K ≥ 1, the polynomial part of the density has d = (K + 1)(K + 2)/2 distinct terms. Using the standard normal density and z = Σ⁻¹/²(y – μ) in (2.3), Zhang and Davidian (2001) showed that ∫ f(y)dy = 1 can be guaranteed by imposing the condition a'Aa = 1 on the coefficients a = (a_ij) of (2.3), where A is a matrix with (i,j)th element $E(U_1^{i_1+j_1})E(U_2^{i_2+j_2})$ for 2 standard normal variables U₁ and U₂ and the superscripts correspond to a_i and a_j. Because A is a positive definite matrix, there exists a matrix B such that A = B², and letting c = Ba, the constraint a'Aa = 1 reduces to c'c = 1. They represent c in terms of polar coordinates as c₁ = sin(ϕ₁),c₂ = cos(ϕ₁) sin(ϕ₂), ⋯, cd = cos(ϕ₁) cos(ϕ₂) ⋯ cos(ϕ_d−1), for –π/2 ≤ ϕ < π/2. Note that the dimension of ϕ = (ϕ₁, ⋯, ϕ_d-1) is now d − 1. The constraints are automatically satisfied, and standard unconstrained optimization techniques can be used to find the maximum likelihood estimates of the parameters.

Combining (2.2) and (2.3), the semi-nonparametric mixtures (model I) are

$$g(\mathbf{y}|\mathbf{x},\mathit{\theta })={\displaystyle \sum _{d=0}^{1}J(\mathbf{\lambda })p^{1-d}(\mathbf{x};}\mathit{\beta }){\{1-p(\mathbf{x};\mathit{\beta })\}}^{d}f({\mathbf{y}}^{(\mathbf{\lambda })},\text{}{\mathit{\mu }}_d,{\mathrm{\Sigma }}_d,{\mathit{\varphi }}_d),$$ (2.4)

where $J(\mathbf{\lambda })=y_1^{{\lambda }_1-1}{y}_2^{{\lambda }_2-1}$ is the Jacobian of the transformation y→ y(^λ) and θ = (β,λ,μ₀, Σ₀,ϕ₀, μ₁, Σ₁,(ϕ₁). Following the recommendations by Zhang and Davidian (2001), we limit the model to K ≤ 2. This model contains the mixture of multivariate normal densities as a special case. Two other special cases of interest are the situation of model I, K = 0, that results in a model that combines the Box–Cox transformation with multivariate normal densities, and a model that fits the mixture (2.4) with K ≥ 1 to untransformed data (model II):

$$g(\mathbf{y}|\mathbf{x},\theta )=\{1-p(\mathbf{x};\mathit{\beta })\}f(\mathbf{y},{\mathit{\mu }}_0,{\mathrm{\Sigma }}_{\text{0}},{\mathit{\varphi }}_0)+P(\mathbf{x};\mathit{\beta })f(\mathbf{y},{\mathit{\mu }}_1,{\mathrm{\Sigma }}_{\text{1}},{\mathit{\varphi }}_1).$$ (2.5)

For a fixed number of mixing components, models (2.4) with increasing K are nested, and thus formal likelihood-ratio tests can be applied to assess goodness of fit. Testing models of increasing complexity allows one to choose a parsimonious but well-fitting model within the class. While model (2.5) is also nested within the more general model (2.4) for the same K, model I, K = 0, and (2.5) are not nested within each other, and we thus also use the Akaike information criterion (AIC) for model comparison.

2.3 Estimation

The log-likelihood for n individuals based on model (2.4) is given by

$$\begin{array}{cc}L(\mathit{\theta }){\displaystyle \sum _{i=1}^{n}g({\mathbf{y}}_i|{\mathbf{x}}_i,\theta )=}\hfill & {\displaystyle \sum _{i=1}^n\{\log [\{1-p({\mathbf{x}}_i;\mathit{\beta })\}f({\mathbf{y}}_i^{(\mathit{\lambda })},{\mathit{\mu }}_0,{\mathrm{\sum }}_0,{\mathit{\varphi }}_0)}\hfill \\ \hfill & +p({\mathbf{x}}_i;\mathit{\beta })f({\mathbf{y}}_i^{(\mathbf{\lambda })},{\mathit{\mu }}_1,{\sum }_1,{\mathit{\varphi }}_1)]+({\lambda }_1-1)\log (y_{i1})+({\lambda }_2-1)\log (y_{i2})\}.\hfill \end{array}$$

We maximized L (θ) directly with respect to θ using a dual quasi-Newton method (NLPQN in PROC IML, SAS 8.2), subject to the constraints det(Σ_i) > 0, i = 0,1. We also implemented an Expectation and Maximization (EM) algorithm (supplemental material available at Biostatistics online). In every case we tested, the EM and quasi-Newton method agreed. To obtain convergence to a global maximum, we choose 100, 600, and 1000 starting values for the optimization for model I, K = 0,1, and 2, respectively. For model II, 200 (K = 1) and 300 (K = 2) starting values were used.

For independent and identically distributed (Y_j,X_j), the maximum likelihood estimate θ̂ satisfies $\sqrt{n}(\widehat{\mathbf{\theta }}-\mathbf{\theta })$ → Normal (0̱ Q⁻¹, where θ denotes the true parameters and Q = - E[∂²log{g(y|x;θ)}/ (∂θ_i∂θ_j)]. The expectation is taken with respect to the joint distribution of (Y, X). We estimate Q by ${\widehat{Q}}_n=n^{-1}{\displaystyle {\sum }_{i=1}^n{H}_i}$, where H_i denotes the negative Hessian of log{g(y_i|x_i,θ)} obtained through numerical differentiation at θ̂.

Local identifiability of model I (2.4) can be shown to hold at a given point in the inside of the parameter space as the information matrix at any point is nonsingular under the correctly specified model (Rothenberg, 1971). However, issues relating to global identifiability and stability of the models can still arise. For K = 2, a single semi-nonparametric density can accommodate heavy tails and skewness as well as multiple modes. This very flexibility can lead to identifiability problems, for example, when multiple modes are present in the data. For a specific realization, either component density, the one corresponding to the infected and the one corresponding to the uninfected population, can capture modes located roughly in the center, which would greatly affect estimates of the mixing proportion. A second related issue is that a single density alone may provide an excellent fit to the data. To our knowledge, there are no published references that address what general shapes the semi-nonparametric densities can accommodate. We aimed to address identifiability of model (2.4) in several numerical experiments based on simulated data (supplemental material available at Biostatistics online) and the real data (Section 4).

3. Simulations

To assess the performance of the various models and numerical issues, we fit the models (2.4) and (2.5) to data from several simulated scenarios. One hundred data sets with 1000 or 2000 data points were generated for 3 sets of simulations presented in this section (further simulations are in the supplemental material available at Biostatistics online). The tables show mean estimates of λ and p over the simulations that converged.

In Table 1, we study the performance for estimating p based on data that arose from a mixture of bivariate normal distributions with constant mixing proportion, p = 0.25, and to assess the robustness of the models to small p, p = 0.05. This case corresponds to a linear Box-Cox transformation, that is, λ₁ = λ₂ = 1. The means of the normal components were μ₀ = (10,10) and μ₁ = (11,11) and the covariance matrices were Σ₀ = [0.25 0.1; 0.1 0.25] and Σ₁ = [0.25 0.05; 0.05 0.5], where Σ = [(Σ)₁₁ (Σ)12; (Σ)12 (Σ)22]. For these 2 settings, we also compared the coverage of a 95% confidence interval for p based on asymptotic normality of the estimate to likelihood-ratio test-based confidence intervals.

Table 1.

Mean estimates of p and λ for models I and II over 100 simulations for N = 1000 observations simulated from “a mixture of 2 bivariate normal distributions with constant p.” μ₀ = (10,10), μ₁ = (11, 11), Σ₀ = [0.25 0.1; 0.1 0.25], and Σ₁ = [0.25 0.05; 0.05 0.50]. Empirical standard errors are given in parenthesis

Model	λ1 = 1	λ2 = l	p = 0.25	Coverage† for p	Coverage‡ for p	Log-likelihood
I, K = 0	1.00 (0.03)	1.00 (0.02)	0.25 (0.06)	0.93	0.94	−2010.71 (32.9)
I, K= 1	1.00 (0.02)	1.02 (0.01)	0.25 (0.06)	0.91	0.93	−2009.69 (32.7)
I, K= 2	1.00 (0.02)	1.00 (0.02)	0.27 (0.11)	0.72	0.71	−2006.68 (32.8)
II, K= 1			0.25 (0.07)	0.93	0.90	−2009.50 (32.6)
II, K= 2			0.10 (0.14)	0.71	0.75	−2007.83 (30.9)
Model	λ1 = 1	λ2 = l	p = 0.25	Coverage for p	Coverage for p	Log-likelihood
I, K = 0	1.00 (0.02)	1.00 (0.02)	0.06 (0.06)	0.78	0.89	−1865.70 (31.0)
I, K = 1	1.00 (0.02)	1.02 (0.02)	0.06 (0.05)	0.85	0.84	−1864.69 (30.9)
I, K = 2	1.00 (0.02)	1.00 (0.02)	0.08 (0.10)	0.64	0.68	−1860.14 (31.2)
II, K = 1			0.08 (0.10)	0.54	0.50	−1860.14 (31.2)
II, K = 2			0.08 (0.17)	NA	0.35	−1862.83 (31.3)

^†Coverage of confidence intervals based on the asymptotic normality of p^.

^‡Coverage of likelihood-ratio test-based confidence intervals.

For the simulations with p = 0.25, the corresponding mean estimates of p (with empirical standard errors in parenthesis) were 0.25(0.06), 0.25(0.06), and 0.27(0.11) for models I, K = 0,1,2, and 0.25(0.07) and 0.10(0.14) for models II, K = 1 and K = 2, respectively. While all models yielded unbiased estimates of p, the standard error of p for model I, K = 2, was nearly twice as large as the standard error of the simpler models I, K = 0 and K = 1. The coverage of the confidence intervals was close to the nominal 95% level for models I, K = 0 and K = 1 and for model II, K = 1, for which p was well estimated, but it was low for model I, K = 2, and model II, K = 2, ranging from 71% to 75% (Table 1). This illustrates the need to choose a parsimonious but well-fitting model. Based on the likelihood-ratio test, in 85/100 simulations, both models I, K = 1 and K = 2, did not fit the data statistically significantly better than the simpler model I, K = 0. Similarly, model II, K = 2, did not provide a better fit than model II, K = 1. Not surprisingly, as the data were generated from a mixture of normals, the simplest model provided unbiased estimates of p with smaller variance and the best fit in most of the runs, as is also reflected by the mean log-likelihood values for each model (Table 1).

For the simulations with p = 0.05, the estimates of p were 0.06(0.06), 0.06(0.05), and 0.10(0.11) for models I, K = 0, 1, 2, and 0.08(0.10) and 0.08(0.17) for models II, K = 1 and K = 2, respectively. The estimates of the parameters of the component densities were nearly unbiased for all models (data not shown). Based on the likelihood-ratio test, for 83/100 simulations, the more complex models did not provide a better fit than the simplest model I, K = 0. While the models estimated the small mixing probabilities without bias, the coverage of all confidence intervals was below the nominal 95% level, with the likelihood-ratio-based confidence intervals yielding slightly better coverage for models I, K = 0 and K = 2. We attribute the lower-than-nominal coverage to the fact that p was close to the boundary zero of the parameter space. The asymptotic normal confidence intervals for model II, K = 2, are not shown as 90/100 runs resulted in singular Hessian matrices.

For the second set of simulations (Table 2), we generated data from the same bivariate normal distributions as Table 1, but with mixing probability p = exp(β₀ + β₁ X)/{1 + exp(β₀ + β₁X)}, with β₀ = −2, β₁ = 1, and a Bernoulli covariate X∈ {0,1} with probability 0.5. For these parameters, E(p) = 0.19.

Table 2.

Mean estimates for models I and II over 100 simulations for N = 1000 or N = 5000 observations simulated from “a mixture of 2 bivariate normal distributions with logistic p (X, β) = exp(β₀ + β₁x)/{1 + exp(β₀ + β₁x)},” X ∈ {0, 1} with probability 0.5. μ₀ = (10, 10), μ₁ = (11,11), Σ₀ = [0.25 0.1; 0.1 0.25], and Σ₁ = [0.25 0.05; 0.05 0.50]. Empirical standard errors are given in parenthesis

Model	λ1 = 1	λ2 = l	β0 = −2.0	β1 = 1.0	Coverage† (β0, β1)	Log-likelihood
N = 1000
I, K= 0	1.02 (0.01)	1.01 (0.09)	−1.89 (0.53)	1.27 (1.038)	(0.94, 0.96)	−1976.37 (32.1)
I, K= 1	1.02 (0.01)	1.03 (0.01)	−1.85 (0.69)	1.02 (0.25)	(0.97, 0.98)	−1975.20 (32.6)
I, K= 2	1.01 (0.09)	1.01 (0.02)	−1.81 (0.69)	1.22 (0.95)	(0.75, 1.00)	−1971.33 (34.9)
II, K= 1			−1.88 (0.52)	1.11 (0.089)	(0.92, 0.96)	−1975.36 (31.5)
II, K= 2			−1.96 (1.53)	1.23 (1.38)	NA	−1970.26 (33.8)
N = 2000
I, K= 0	0.99 (0.03)	1.00 (0.003)	−1.98 (0.21)	1.00 (0.15)	(0.98, 0.95)	−3960.01 (42.8)
I, K= 1	1.00 (0.003)	1.00 (0.004)	−2.00 (0.21)	0.99 (0.15)	(0.99, 0.94)	−3959.96 (42.8)
I, K= 2	1.00 (0.003)	1.00 (0.004)	−2.00 (0.23)	1.00 (0.15)	(0.97, 0.97)	−3959.62 (42.9)
I, K= 1			−1.99 (0.27)	1.00 (0.17)	(0.97, 0.95)	−3959.77 (42.7)
I, K= 2			−1.96 (0.35)	1.01 (0.17)	NA	−3959.11 (42.9)

^†Coverage of confidence intervals based on the asymptotic normality of p^.

For the logistic mixture, all models estimated the parameters β of the mixing proportion as close to (−2.0, 1.0), with similar standard errors for N = 1000, with the exception of model II, K = 2. For N = 2000 data points, the estimates of β were virtually unbiased with comparable standard errors for all models. Models I, K = 0, K = 1, and K = 2, also resulted in similar parameter estimates of λ. The estimated mean vectors and covariance matrices were also nearly unbiased for all models. The asymptotic normal confidence intervals had approximately 95% coverage for all models with the exception of model I, K = 2, where the coverage for β₁ was only 75% for N = 1000. For N = 2000, however, all models but model II, K = 2, had nominal coverage. For model II, K = 2, again nearly all runs resulted in singular Hessian matrices. Based on likelihood-ratio test, model I, K = 0, was preferable to the more complex models in nearly all simulations.

The last set of simulations (Table 3) assessed the performance of the models for highly skewed data with constant mixing proportions p = 0.5 and p = 0.05. The components y₀₁ and y₀₂ of the first subpopulation were independent ${\chi }_1^2$ variables, and the components of the second subpopulation y₁₁ and y₁₂ were independent ${\chi }_3^2$ variables. For the data simulated with p = 0.5, the mean estimated mixing proportions were 0.51(0.05), 0.51(0.05), and 0.48(0.12) for models I with K = 0, K = 1, and K = 2, respectively, with the standard error for K = 2 being more than twice as large as for the simpler models. The estimates of p for model II, K = 2, and model II, K = 1, yielded a lower average estimate of p of 0.44(0.06). Models I, K = 0 and K = 1, resulted in very similar parameter estimates, and the estimates of the polynomial coefficients of models I, K = 1 and K = 2, did not provide evidence for a statistically significant polynomial component. The likelihood-ratio-based confidence intervals for models I, K = 0 and K = 1, had 94% coverage, while it was only 74% for model I, K = 2. For both models II, the coverage was much lower, 39% and 38% for K = 1 and K = 2, respectively. Again, these models did not fit the data as well as model I, K = 0, which has fewer parameters but allows for a Box-Cox transformation. All models correctly estimated the correlation terms in the mixing densities close to zero. All runs converged for models I, K = 0 and K = 1, and 97/100 runs converged for K = 2. For model II, 91/100 simulations converged for K = 1 and 89/100 for K = 2. The simulations with p = 0.05 illustrate well that a lack of fit of the mixing components can lead to severe bias in the estimates of p. The mean estimates of p were 0.04(0.05), 0.05(0.07), and 0.08(0.09) for models I with K = 0, K = 1, and K = 2, respectively, and, highly biased, 0.60(0.05) and 0.59(0.06) for models II, K = 1 and K = 2, respectively. The coverage of likelihood-ratio-based confidence intervals, however, was below the 95% nominal level for all models. For model I, 99/100 runs converged for K = 0, 95/100 for K = 1, and 94/100 for K = 2. For model II, all runs converged for K = 1 and 99/100 for K = 2. As indicated by the log-likelihood-ratio test, model I, K = 2, fits the data better than model I, K = 0 or K = 1, for p = 0.5, but not for p = 0.05. For all values of K, however, model I fits the data significantly better than model II.

Table 3.

Mean estimates ofp and λ for models I and II over 100 simulations for N = 1000 observations simulated from “a mixture of 2 chi-square distributions, constant p”: $y_{01}\sim {\chi }_1^2,y_{02}\sim {\chi }_1^2,y_{11}\sim {\chi }_3^2$, and $y_{12}\sim {\chi }_3^2$. Empirical standard errors are given in parenthesis

Model	λ1	λ2	p = 0.5	Coverage† for p	Log-likelihood
I, K= 0	0.20 (0.02)	0.20 (0.02)	0.51 (0.05)	0.94	−3152.49 (66.9)
I, K= 1	0.20 (0.02)	0.20 (0.02)	0.51 (0.05)	0.94	−3152.47 (66.9)
I, K= 2	0.19 (0.03)	0.18 (0.03)	0.48 (0.12)	0.74	−3138.60 (67.8)
II, K= 1			0.44 (0.06)	0.39	−3893.36 (56.6)
II, K= 2			0.44 (0.06)	0.38	−3862.35 (69.3)
Model	λ1	λ2	p = 0.5	Coverage† for p	Log-likelihood
I, K= 0	0.31 (0.03)	0.30 (0.03)	0.04 (0.05)	0.77	−4061.50 (39.3)
I, K= 1	0.30 (0.03)	0.30 (0.03)	0.05 (0.07)	0.67	−4061.64 (40.3)
I, K= 2	0.28 (0.06)	0.27 (0.06)	0.08 (0.09)	0.66	−4054.07 (40.7)
II, K= 1			0.60 (0.05)	0.00	−4327.55 (40.5)
II, K= 2			0.59 (0.06)	0.00	−4253.37 (40.6)

^†Coverage for likelihood-ratio-based confidence intervals.

4. Application to the Ugandan HHV-8 study

We applied the bivariate mixture models (2.4) and (2.5) to data collected from 599 children aged 0–16 years, at Mulago Hospital, Kampala, from November 2001 to April 2002. Interviewers obtained a blood sample from each child for the K8.1 and the orf73 immunoassays. The main predictors of infection status were age (younger than 5 years, 5 ≤ age < 10, older than 10 years), transfusion status (ever/never transfused), and water source (tap water versus surface water). Details about the study and related HHV-8 epidemiology are in Mbulaiteye and others(2003).

4.1 Analysis using mixture models with constant p

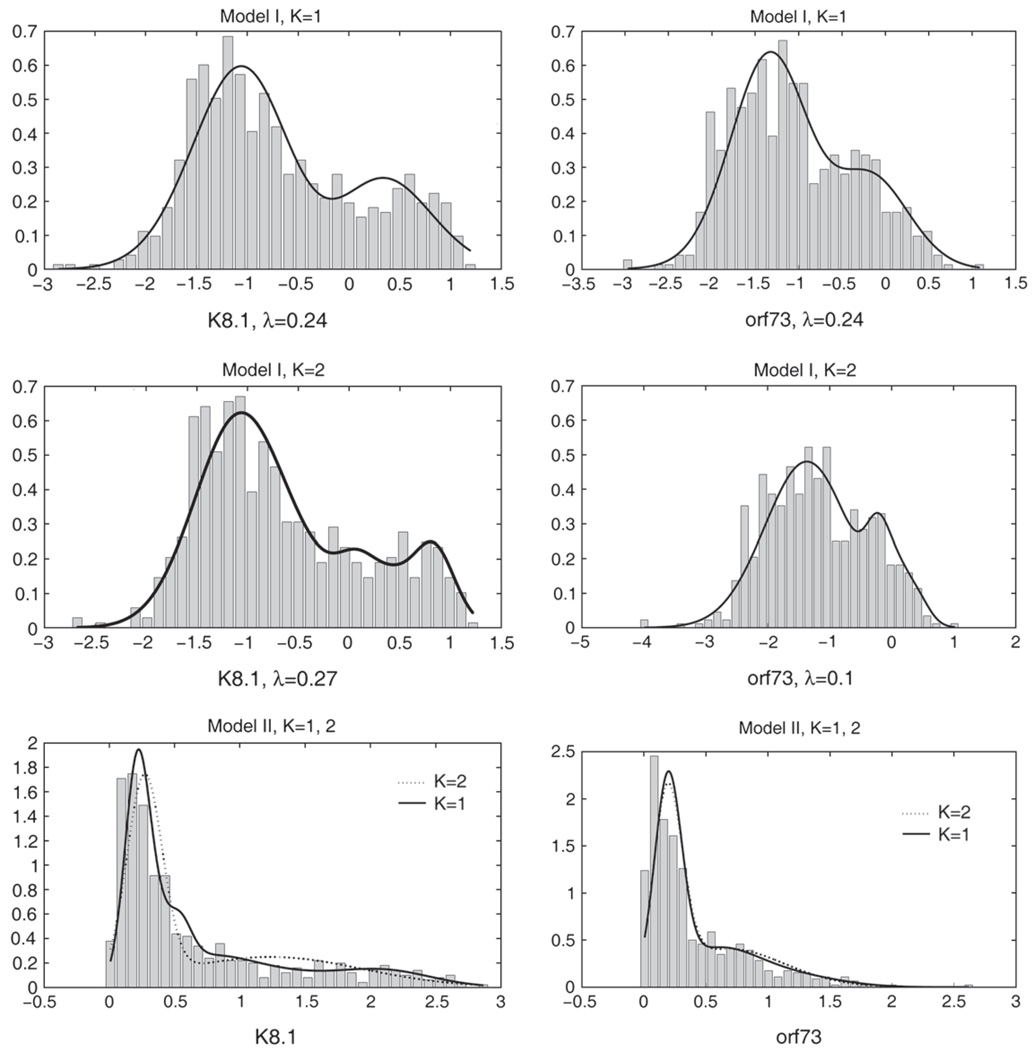
Table 4 shows the estimates of λ, p, and the value of the log-likelihood for models I and II with constant mixing probability p and for single semi-nonparametric densities. Model I, K = 2, had a significantly better fit than all other models based on the likelihood-ratio test and also had the largest AIC value. Model I, K = 1, also fit the data significantly better than model I, K = 0, and both models II, based on the likelihood-ratio test. Histograms of the K8.1 and orf73 OD readings on the λ scales for model I and on the original scale for model II, with the corresponding fits from models I and II for K = 1 and K = 2 superimposed are presented in Figure 1, respectively. Model parameter estimates are presented in the supplemental material available at Biostatistics online. The prevalence estimates based on model I were p = 0.19(0.03) for K = 1 and p = 0.18(0.02) for K = 2, while they were much larger for the models with poor fit, p = 0.49(0.06) for model I, K = 0, and p = 0.44(0.03) and p = 0.43(0.06) for model II with K = 1 and K = 2. Models with poorer fit exhibited higher collinearity in parameter estimates. The correlation of p̂ with the other model parameters was largest for model I, K = 0; for example, the correlations of p̂ with μ̂₀₀ and μ̂₁₀ were 0.71 and 0.85, respectively, which made the estimates of p very sensitive to the fit of the mixing components. For model I, K = 2, however, the largest correlation was 0.35 between p̂ and (Σ̂₁)₁₁. Estimates of p were insensitive to the choice of starting values.

Table 4.

“Uganda HHV-8 study”: Results for mixture models I and II with constant p for bivariate and univariate data, and single Semi-nonparametric density fit to bivariate data; model-based standard errors given in parenthesis

Model	λ1	λ2	p	Log-likelihood	AIC
Bivariate models
I, K= 0	0.43 (0.07)	0.35 (0.05)	0.49 (0.06)	−172.48	−370.96
I, K= 1	0.24 (0.03)	0.24 (0.04)	0.19 (0.03)	−160.13	−354.26
I, K= 2	0.27 (0.05)	0.10 (0.05)	0.18 (0.02)	−145.98	−337.96
II, K= 1			0.44 (0.03)	−258.25	−546.50
II, K= 2			0.43 (0.03)	−210.26	−462.52
Single density, K= 0	0.07 (0.16)	0.03 (0.03)		−232.39	−478.78
Single density, K= 1	0.09 (0.16)	0.03 (0.03)		−224.28	−466.56
Single density, K= 2	0.32 (0.04)	0.20 (0.05)		−181.10	−386.20
Univariate models for K8.1 assay
I, K= 0	0.11 (0.05)		0.17 (0.03)	−302.36	−308.36
I, K= 1	0.04 (0.04)		0.16 (0.02)	−293.30	−301.30
I, K= 2	0.41 (0.08)		0.16 (0.03)	−288.59	−298.59
II, K= 1			0.39 (0.03)	−329.14	−336.14
II, K= 2			0.42 (0.03)	−293.26	−302.26
Univariate models for orf73 assay
I, K= 0	0.28 (0.11)		0.35 (0.11)	−47.29	−53.29
I, K= 1	0.08 (0.06)		0.18 (0.04)	−43.01	−51.01
I, K= 2	0.24 (0.10)		0.35 (0.09)	−38.78	−48.78
II, K= 1			0.41 (0.03)	−81.72	−88.72
II, K= 2			0.42 (0.03)	−50.78	−59.78

Fig. 1.

Histograms and fits from bivariate mixture densities on λ scale for Uganda HHV-8 study.

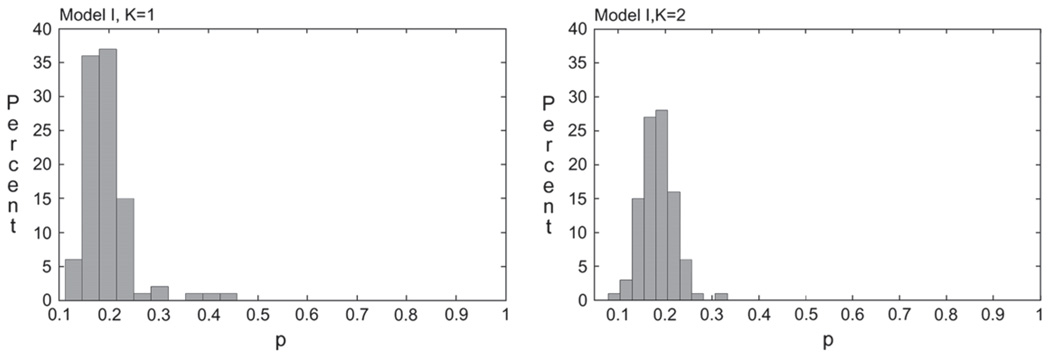
To study the stability and possible identifiability problems of the estimates of p in the Uganda data set, we sampled 100 data sets with replacement and fit models I, K = 1 and K = 2 with 600 and 1000 starting values, respectively. The mean estimates of p over 100 bootstrap repetitions (bootstrap standard deviation in parenthesis) were 0.19(0.05) and 0.18(0.03) for models I, K = 1 and K = 2, respectively. The standard deviations estimated from the bootstrap were very close to the model-based estimates of the standard deviations (Table 4), indicating that the information matrix was well defined and asymptotic theory could be used for inference. Histogram plots of the bootstrap p̂ (Figure 2) showed a unimodal distribution very narrowly centered around 0.2 for models I, K = 1 and K = 2.

Fig. 2.

Histogram of bootstrap estimates of p for Uganda HHV-8 data.

For all choices of K, and even for K = 0, the 2-component mixture fits the Uganda data better than a single semi-nonparametric density as assessed by the AIC (Table 4).

We compared the prevalence estimate from the bivariate model to estimates obtained by averaging prevalence estimates from univariate mixture models that were fitted separately to the K8.1 and orf73 assays (Table 4). To account for the dependence between the univariate estimates, we computed the standard errors of the averaged estimates using a bootstrap procedure, assuming that the weights were known and fixed for the inverse variance–weighted estimate.

Based on the likelihood-ratio test, model I, K = 2, had a significantly better fit than all other models and also the largest AIC value. The simple average of the prevalence estimates from the best fitting models was 0.26(0.08), while the inverse variance–weighted estimate was 0.18(0.06). The inverse variance–weighted estimate thus agreed with the prevalence estimate from the bivariate model. However, the bootstrap standard error of this estimate was 3 times larger than the estimated standard error of p from the bivariate mixture model and twice as large as the bootstrap estimate of the standard error of p from that model. The bivariate mixture model thus provided a much more precise estimate of prevalence.

4.2 Analysis with logistic mixture models

We then modeled the mixing component p by a logistic function that included age in 2 categories, transfusion status, and water source as covariates. We could incorporate covariates by regressing the means of the component densities on covariates, but in our problem, the covariates considered were thought to influence the chance of being infected, but not the antibody distributions conditional on infection status. To verify this, we first fit the constant p models to data stratified on the categories of age, transfusion status, and water source. The stratified component density estimates were very similar, and thus the more general model was not needed in our data.

The estimates for the parameters in the logistic component and the values of the likelihood and AIC are given in Table 5. Again, the fit of model I, K = 2, was significantly better than the fits of the other models based on the likelihood-ratio test. Model I, K = 2, also had the largest AIC value. The parameters of the mixing components for model I, K = 0, and model II did not change much compared to the model with constant p. For models I, K = 1 and K = 2, the parameters of the mixing components, however, were more affected. For example, for K = 1, λ changed from (0.24, 0.24) for constant p to λ = (0.41, 0.33) for the logistic mixture. The parameters of the logistic mixing probability were similar: age and surface water source were associated with significantly elevated risk of infection for all models and transfusion status was not significantly associated. Model I, K = 2, resulted in slightly larger estimates for the log-odds parameters than the other models. Model I, K = 2, also provided the best univariate fits when applied separately to the K8.1 and orf73 OD readings (data not shown).

Table 5.

Uganda HHV-8 Study: Estimation of parameters in “logistic p ” and logistic regression based on fixed cutoff values for the assays; model-based standard errors given in parentheses

Parameter	Bivariate mixture model					Standard logistic regression Infected defined based on fixed cutoff values for
	Model I			Model II
	K = 0	K = 1	K = 2	K = 1	K = 2	K8.1	orf73	Combined
Intercept	−1.65	−1.73	−2.05	−1.65	−1.68	0.01	−0.35	0.15
	(0.28)	(0.29)	(0.39)	(0.25)	(0.24)	(0.23)	(0.23)	(0.21)
5 ≤ age < 10	1.56	1.55	1.72	1.32	1.35	0.94	1.49	1.17
	(0.28)	(0.28)	(0.33)	(0.24)	(0.24)	(0.30)	(0.32)	(0.26)
Age ≥ 10	1.63	1.63	1.94	1.39	1.40	1.75	1.36	1.46
	(0.29)	(0.29)	(0.35)	(0.25)	(0.25)	(0.30)	(0.32)	(0.27)
Ever transfused	0.31	0.30	0.50	0.32	0.32	0.31	0.30	0.21
	(0.23)	(0.22)	(0.25)	(0.19)	(0.19)	(0.22)	(0.22)	(0.20)
Surface water	0.80	0.79	1.09	0.63	0.69	0.55	0.93	0.81
	(0.24)	(0.23)	(0.27)	(0.20)	(0.20)	(0.22)	(0.22)	(0.20)
Log-likelihood	−142.61	−136.67	−117.66	−231.32	−181.46	−271.00	−267.49	−310.21
AIC	−319.22	−315.34	−289.32	−500.64	−412.92	−372.92	−552.00	−544.98

The mixture model allows one to calculate the posterior probability of infection, I_j = 1, given x_j and y_j. Indeed, from (2.4), we get

$$\text{pr}(I_j=1|{\mathbf{y}}_j,{\mathbf{x}}_j)=\frac{p(\mathbf{x};\mathit{\beta })f({\mathbf{y}}^{(\mathit{\lambda })},{\mathit{\mu }}_1,{\mathrm{\Sigma }}_{\text{1}},{\mathit{\varphi }}_1)}{\{1-p(\mathbf{x};\mathit{\beta })\}f({\mathbf{y}}^{(\mathit{\lambda })},{\mathit{\mu }}_0,{\mathrm{\Sigma }}_{\text{0}},{\mathit{\varphi }}_{\text{0}})+p(\mathbf{x};\mathit{\beta })f({\mathbf{y}}^{(\mathit{\lambda })},{\mathit{\mu }}_1,{\mathrm{\Sigma }}_{\text{1}},{\mathit{\varphi }}_1)}.$$

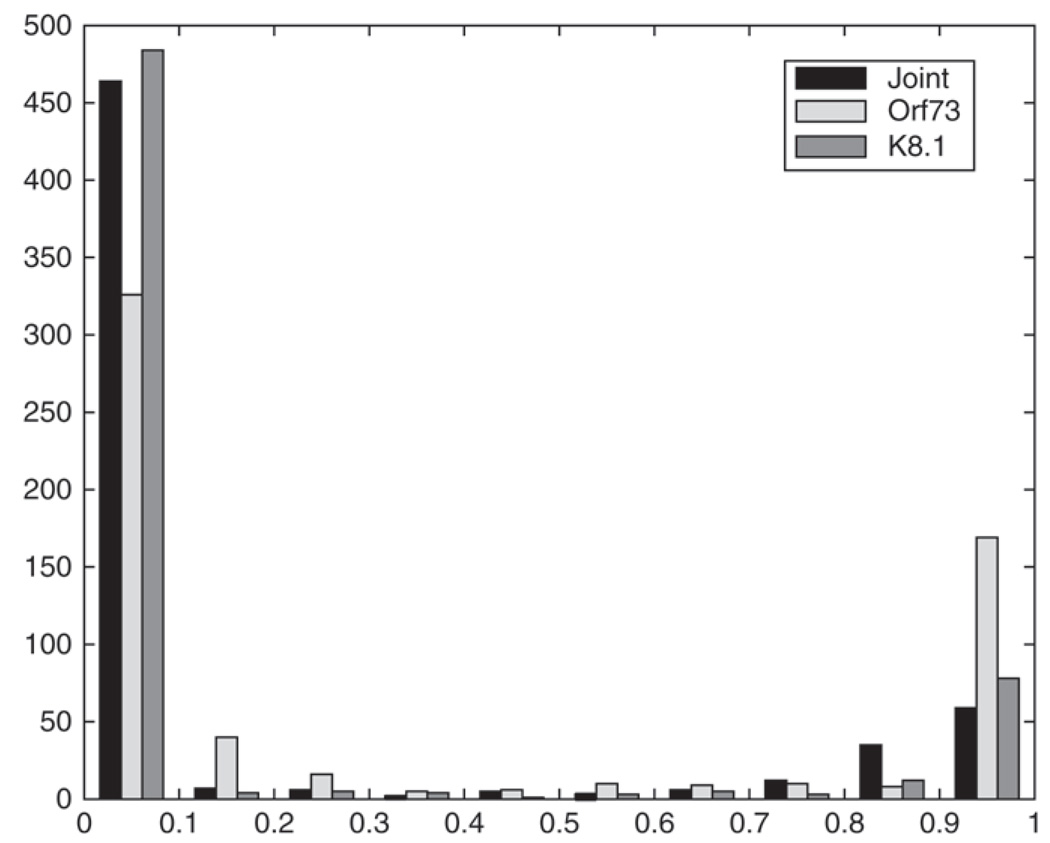
Figure 3 shows histograms of the posterior probabilities of infection computed based on model I, K = 2, fit to the bivariate data as well as to the marginal K8.1 and orf73 data. To minimize the overall misclas-sification probability based on the mixture model when discriminating infected from uninfected subjects, one sets I_j = 1 if pr(I_j = 1|y_j, x_j) ≥ 0.5 and I_j = 0 otherwise. For all models, fewer than 5% of the estimates were between 0.3 and 0.7.

Fig. 3.

Posterior probabilities of infection for the Uganda children.

4.3 Analysis with infection status assumed to be known

We compared the estimates from the mixing probability of the multivariate mixture models with several marginal logistic models, based on operational definitions of infected. The coefficients in this model have a different interpretation than the parameters in the logistic part of the mixture, however. They are based on the observable events T_i = I(y_i ≥ c_i),i = 1,2, whereas the mixture models estimate the probability of the latent, unobservable infection state. To define infected, we applied the cutoff points used by Mbulaiteye and others (2003), with OD for the K8.1 ≤0.90 corresponding to uninfected, OD > 1.20 to infected, and, somewhat arbitrarily, OD reading in the range 0.90–1.20 labeled as “indeterminate”. The prevalence of infection (excluding 38 indeterminate children) was 117/561= 20.9%. The operational definition for the orf73 assay was that a child was HHV-8 negative for OD readings ≤0.5, indeterminate for OD readings in the range 0.5–0.7, and infected if OD ≥0.7. Fifty children were indeterminate and 127 (23.1%) of the remaining 549 were classified as infected, based on their orf73 OD readings. These estimated prevalences agree well with the estimates of p̂ for models I (K = 1,2) in Table 4. Often results from both assays are combined by assuming that a child that is positive on either one of the 2 assays is infected, T = max(T₁, T₂). After excluding 3 children who were indeterminate on both assays, the prevalence based on this criterion was 23%. The corresponding prevalence estimate based on the mixture model is the posterior probability of infection given that the assay readings were not in the indeterminate region, pr(I = 1\y₁ ∉ [0.9, 1.2], y₂ ∉ [0.5, 0.7]), estimated to be 0.19 and 0.18 for models I, K = 1 and K = 2, respectively. The estimates for the models with poor fit were again much higher, 0.48 for model I, K = 0, and 0.43 and 0.42 for models II, K = 1 and K = 2. As only 3 children had OD readings in the joint indeterminate region, these estimates differed only slightly from p̂ in Table 4.

Estimates of log-odds ratios based on the various definitions for infected (Table 5) are close to those obtained from the mixture models, leading us to conclude that the operational definitions of infected capture the true latent infection status well.

4.4 Estimation and comparison of cutoff points

The multivariate mixture can also be used to find the cutoff values that in some sense best separate the uninfected from the infected population. To determine optimal cutoff points for the assays, we minimize the probability of misclassification under the mixture model as a function of cut-points (c₁, c₂),

$$p{\displaystyle {\int }_{c_1}^{\infty }{\displaystyle {\int }_{c_2}^{\infty }f(\mathbf{y};{\alpha }_0)\mathrm{d}y+(1-p){\displaystyle {\int }_{-\infty }^{c_1}{\displaystyle {\int }_{-\infty }^{c_2}f(\mathbf{y};}}}}{\alpha }_1)\mathrm{d}y,$$ (4.1)

where the α_i, i = 0, 1, and p are replaced by their estimates. Reported on the original OD scale, minimizing (4.1) for model I, K = 2, yields c₁ = 0.79 and c₂ = 0.79 with misclassification probability 0.02. While this would not change the number of children that falls above the cutoff value for K8.1 compared to the cutoff values which the investigators used previously, 39 more children would be classified as infected based on the orf73 if c₂ = 0.79 was used.

5. Discussion

In this paper, we present a new class of multivariate mixture models that combines the Box–Cox transformation with a class of semiparametric densities for the mixing components. This class contains mixtures of normals as a special case and, for a fixed number of mixing components, allows for formal testing of models of increasing complexity. Covariates can be incorporated into the mixing probabilities by logistic regression or other generalized linear models. The motivation for our work was the desire to combine 2 different assays to assess infection status with HHV-8 and factors that influence prevalence. Although we are fairly certain that there are 2 distinct subpopulations in the data, one infected and the other uninfected, the assay measurements are not always well separated and the data have heavy tails. The main interest in our applications was the estimation of the parameters relating to the mixing proportion or prevalence, while the parameters of the mixing components were nuisance parameters in the model. An attractive feature of our model is that it can accommodate skewness and multimodality in the data, but this very flexibility can lead to identifiability problems. To study the identifiability aspects of the models, we examined the behavior and stability of estimates of p in simulations (supplemental material available at Biostatistics online), using a bootstrap procedure for the Uganda data. In summary, to avoid identifiability problems in using our proposed class of models, it is necessary to try numerous starting values for maximization to ensure convergence to a global maximum and, most importantly, to avoid overfitting by testing nested models of increasing complexity as recommended for a single semi-nonparametric density (Liu and Zhang, 1998).

Choosing well-fitting but parsimonious models is also important as the use of more flexible models for the component densities, while reducing bias, has the potential to increase the variance of key parameters, such as prevalence. Such a tendency was seen in simulations (Table 1 and Table 2) where all the models, even the simpler ones, fit the data well, but the simpler models yielded more precise estimates of prevalence. However, in data from the Uganda study, we found that more complex but better fitting models yielded more precise estimates of prevalence than a simpler, poorly fitting models (Table 4).

Application of the models to the Uganda data highlights the importance of including both the Box–Cox transformations and the polynomial components in the densities to provide adequate fit to the data and thus stable estimates of prevalence. Estimates of HHV-8 prevalence were insensitive to the choice of starting values for p, and bootstrap replications yielded a tight distribution of p̂ centered about the original estimate. Bootstrap standard errors were close to model-based standard errors, indicating that p was well identified in our data and that inference based on asymptotic theory was valid.

We compared prevalence estimates p from the bivariate mixture model to estimates obtained by averaging prevalence estimates from univariate mixtures fit to each assay separately. While the inverse variance–weighted prevalence estimate was identical to p from the bivariate mixture model, the estimated standard error of the inverse variance–weighted estimate (assuming fixed and known weights) was 3 times larger than the model-based standard error of p from the bivariate mixture model and twice as large as its bootstrap standard error. Computing prevalence by averaging estimates from the marginal models thus resulted in an estimated loss of efficiency of at least 75% for this data set.

Our work relates to other approaches for evaluating diagnostic tests without gold standards. Rindskopf and Rindskopf (1986) among others fitted 2-component multivariate mixture models with the components corresponding to “diseased” and “non-diseased” subjects. However, the results of the K tests applied to the same person were assumed to be independent conditional on disease status. We relax the independence assumption by allowing joint densities for each component. In our application, 2 immunoassays that detect 2 different types of antibodies were used to assess infection status. In case of infection, both types of antibodies can be present, and thus independence likely does not hold.

The mixture model approach has several potential advantages compared to standard epidemiologic approaches to define infection status. We need not rely on an external definition of a cutoff value to classify each observation. The continuous nature of the data is used to its full extent, and we obtain a complete description of the distribution of the OD values (y₁, y₂) in the presence of covariates X. This enables us to calculate pr(infected|y₁, y₂, X), the probability of being truly infected given the OD readings and covariates X.