A Brief Taxometrics Primer

Abstract

Taxometric procedures provide an empirical means of determining which psychiatric disorders are typologically distinct from normal behavioral functioning. Although most disorders reflect extremes along continuously distributed behavioral traits, identifying those that are discrete has important implications for accurate diagnosis, effective treatment, early identification of risk, and improved understanding of etiology. This article provides (a) brief descriptions of the conceptual bases of several taxometric procedures, (b) example analyses using simulated data, and (c) strategies for avoiding common pitfalls that are often observed in taxometrics research. To date, most taxometrics studies have appeared in the adult psychopathology literature. It is hoped that this primer will encourage interested readers to extend taxometrics research to child and adolescent populations.

Among the most long-standing debates in the psychopathology literature is whether mental disorders are best characterized as categorical entities or as extreme expressions of continuously distributed traits (see, e.g., Beauchaine, 2003; Kendell, 1989; Meehl, 1995a). Although many who study psychopathology prefer dimensional models (see Krueger, Watson, & Barlow, 2005; Widiger & Trull, 2007), current convention clearly favors the categorical perspective. The Diagnostic and Statistical Manual of Mental Disorders (DSM; American Psychiatric Association, 2000), which defines pathological behavioral syndromes, provides categorical cutoffs when symptom thresholds are exceeded. Following the DSM model, one either has or does not have a disorder, which serves as a basis for decisions regarding the necessity of intervention and regarding access to sometimes scarce treatment resources.

Nevertheless, most users of the DSM, whether in clinical or research contexts, recognize that diagnostic syndromes affect people to varying degrees and that large numbers of individuals exhibit incipient signs of psychopathology in the absence of debilitating functional impairment (Widiger, 2001). For this reason and others, advocates of the developmental psychopathology perspective have been particularly critical of categorical diagnostic systems. In addition to the issue of arbitrarily dichotomizing psychopathology, such dissatisfaction arises from assertions that the DSM framework largely ignores contextual influences on behavior, assumes biological bases for nearly all psychiatric syndromes, provides few developmental guidelines for diagnosis, overlooks cultural differences in the expression of mental health and mental illness, is clinically confounding because of symptom overlap across diagnostic categories, and assumes discrete etiologic substrates for disorders (e.g., Cantwell, 1996; Clark, Watson, & Reynolds, 1995; Cummings, Davies, & Campbell, 2000; Hinshaw, Lahey, & Hart, 1993; Hinshaw & Park, 1999; Jensen & Hoagwood, 1997; Richters & Cicchetti, 1993; Richters & Hinshaw, 1999; Sonuga-Barke, 1998; Sroufe, 1997). As a result of such concerns, discussions regarding the merits of a dimensional diagnostic system have accelerated as behavioral scientists contemplate the next revision of the DSM (e.g., Cuthbert, 2005; First, 2005; Krueger, Markon, Patrick, & Iacono, 2005; Kupfer, 2005; Watson, 2005; Widiger & Samuel, 2005; Widiger & Trull, 2007).

As we have noted elsewhere (Beauchaine, 2003; Beauchaine & Marsh, 2006), arguments questioning the construct validity of categorical models of psychopathology are often applied to the entire DSM, at times quite derisively. Yet growing evidence suggests that some diagnostic entities, such as schizophrenia, endogenous depression, and narcissistic personality disorder, may indeed be distributed as discrete latent classes, thereby representing typological distinctions from—rather than quantitative shifts in—normal personality (see Ambrosini, Bennett, Cleland, & Haslam, 2002; Beach & Amir, 2003; Blanchard, Gangestad, Brown, & Horan, 2000; Fossati et al., 2005; Golden & Meehl, 1979; Grove et al., 1987; Haslam & Beck, 1994; Korfine & Lenzenweger, 1995; Lenzenweger, 1999; Lenzenweger & Korfine, 1992, 1995; Tyrka et al., 1995; Tyrka, Haslam, & Cannon, 1995).

When a psychiatric disorder is distributed discretely, identifying the proper diagnostic threshold can have very important implications for our basic understanding of etiology and for improvements in prevention and intervention programs (see Beauchaine, 2003; Beauchaine & Beach, 2006; Beauchaine & Marsh, 2006; Meehl, 1992, 1995a). For example, early identification of genetic risk for schizophrenia (i.e., schizotypy; Meehl, 1962), which has repeatedly emerged as a discretely distributed trait affecting about 5% of the population, can provide for targeted prevention programs that substantially reduce prospective risk of psychosis (see Beauchaine & Marsh, 2006). Thus, a threshold model of schizophrenia liability more accurately captures the nature of the disorder, with significant implications for outcome. Other conditions for which threshold models may identify liability for psychopathology among children and adolescents include autism spectrum disorders (e.g., Beauchaine, 2003; Munson et al., 2007), melancholic depression (Ambrosini et al., 2002; Beach & Amir, 2003; Haslam & Beck, 1994), behavioral inhibition that may mark future risk for anxiety disorders (e.g., Kotov, Schmidt, Lerew, Joiner, & Ialongo, 2005; Woodward, Lenzenweger, Kagan, Snidman, & Arcus, 2000), and severe conduct problems that may mark future risk for psychopathy (e.g., Harris, Rice, & Quinsey, 1994; Skilling, Quinsey, & Craig, 2001).

These examples illustrate the importance of determining the appropriateness of categorical versus dimensional models of psychopathology on disorder-by-disorder basis, rather than rejecting an entire diagnostic system (see also Flanagan & Blashfield, 2002; Meehl, 1995a). Even though most disorders probably do reflect behavioral extremes along continuously distributed traits (Beauchaine & Beauchaine, 2002; Klein & Riso, 1993), identifying those that are typologically distributed will advance clinical science.¹

Discussions over the advantages of accurately specifying the latent structure of psychopathology can be quite lengthy (see, e.g., Beauchaine, 2003; Beauchaine & Marsh, 2006). Rather than present such an account here, I seek to provide a brief primer for researchers who are interested in performing taxometric analyses, which represent one of several approaches to searching for typologies. My objectives are to provide accessible examples and to highlight common mistakes and potential pitfalls in both the execution and interpretation of taxometric analyses. Accordingly, I do not present full details regarding the mathematical and statistical underpinnings of taxometric procedures nor do I provide a comprehensive review of all such techniques. Readers are referred to other sources for such accounts (Beauchaine, 2003; Beauchaine & Marsh, 2006; Lenzenweger, 2004; Meehl & Yonce, 1994, 1996; J. Ruscio & Ruscio, 2004a, 2004b; Schmidt, Kotov, & Joiner, 2004; Waller & Meehl, 1998). My primary goal is to promote increased conceptual understanding of taxometric procedures among readers who are minimally familiar with the approach. Nevertheless, I believe this presentation will also be of value for readers with some expertise in the area.

The term taxometrics applies to a set of 13 interrelated procedures invented by Meehl and colleagues, sometimes referred to collectively as coherent cut kinetics. Each of these procedures searches for abrupt changes in the structure of data (e.g., slopes, covariances, Eigenvalues) that may indicate latent subgroups within a larger distribution of scores (Grove & Meehl, 1993; Meehl, 1999, Meehl & Yonce, 1994, 1996; Waller & Meehl, 1998). Although taxometric analyses are not the only approach used to search for typologies (henceforth referred to as taxa), they offer certain advantages (and disadvantages) compared with alternatives. In the sections to follow, I explain the inherent difficulties faced when identifying taxa, regardless of the approach chosen, and I provide guidelines for conducting taxometric analyses. Along the way, I describe pros and cons of using the techniques as opposed to other methods. I begin with discussion of the imprecise nature of most psychological data.

Searching for Typologies: The Problem with Fallible Indicators

Among P. E. Meehl’s most significant contributions to the discourse on latent structure analysis was his emphasis on the nature of the data that psychologists and other behavioral scientists typically collect. Because we usually cannot observe the causes of mental disorders directly, we are forced to infer psychopathology from manifest indicators (symptoms) of latent (unobservable) psychopathological traits (Meehl, 1973, 1995a). Behavioral symptoms are far removed from the genetic, neural, and physiological substrates of psychopathology (Beauchaine & Marsh, 2006) and are therefore characterized by significant measurement error when used as indicators of these substrates. Furthermore, symptoms are typically rated on Likert scales, which are subject to a number of additional error sources, including halo effects (e.g., Saal, Downey, & Lahey, 1980) and response biases (e.g., Macmillan & Creelman, 1990; Rajendar, 1996). As a result, as much as 50% of the variance in ratings of behavioral symptoms is attributable to measurement error (see Hoyt & Kerns, 1999).

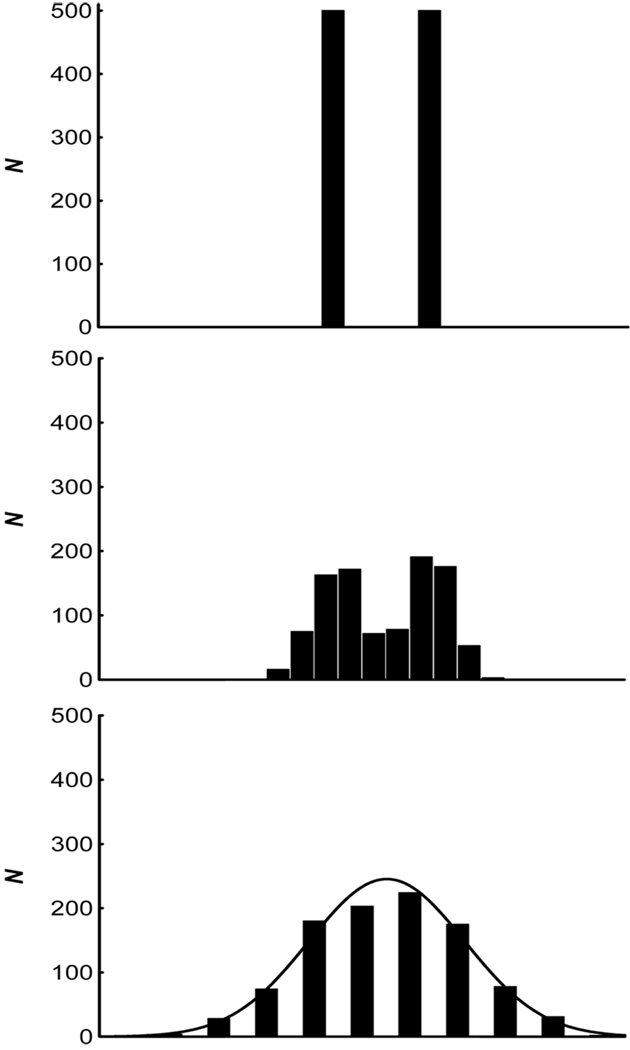
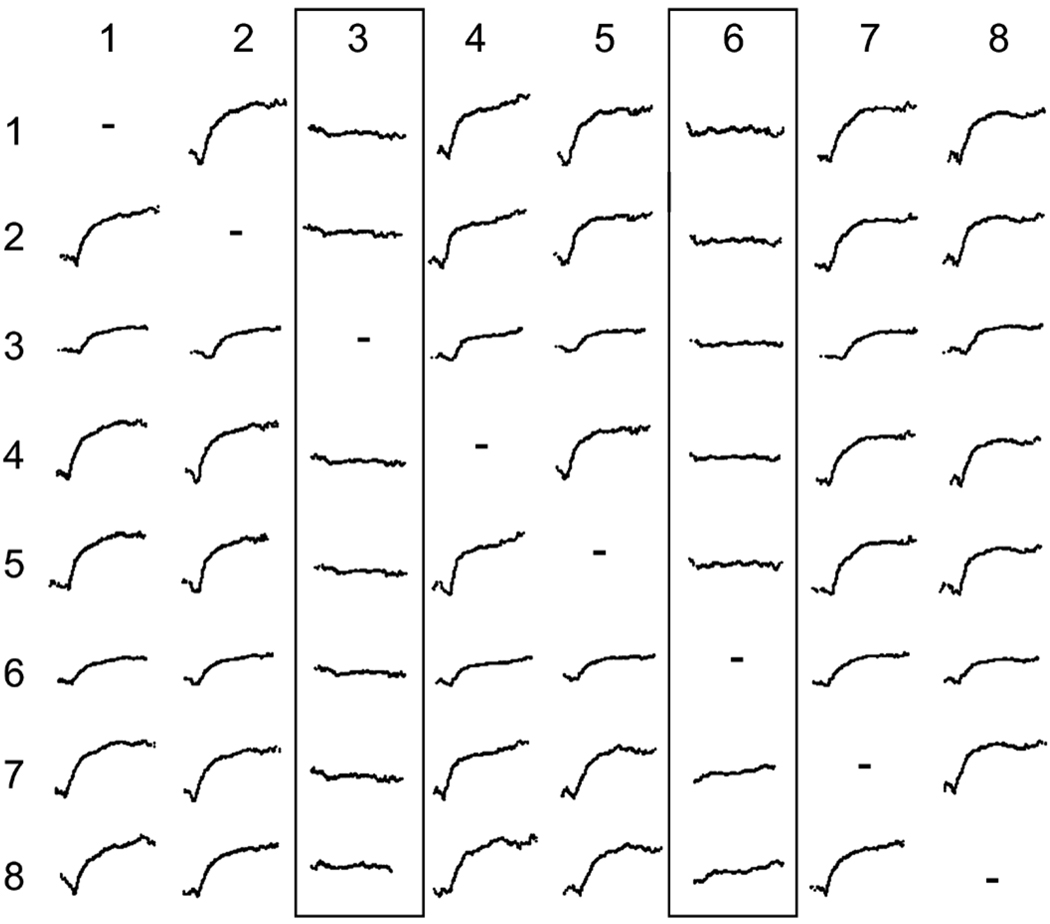
The impact of these different sources of variability on a dichotomously distributed variable is presented in Figure 1. The top panel represents a discrete variable measured with perfect precision (i.e., without error), with 500 members in each of only two classes. Near error-free measurement would be the case when genotyping a psychiatric disorder that is determined by a single genetic locus, such as Huntington’s chorea (although population proportions would not be 50:50 as in the example provided).

Figure 1.

The effect of measurement error on the distribution of a discretely distributed variable. The top panel depicts perfect measurement of a dichotomous trait of equal proportions (50:50) within an overall sample of 1,000. This level of precision would be associated with genotyping of a trait with a single locus. The middle panel illustrates the effect of extremely precise measurement of behavioral phenotypes, or symptoms. Because phenotypes are far removed from the genetic and neurobiological substrates of behavior, individual differences are always observed in symptoms. The bottom panel represents the effect of an additional 50% increase in variance associated with imprecise Likert measurement. Note that the bottom panel is unimodal despite the admixture of two discrete groups. All figures have equivalent x-axis scaling

The middle panel represents the same discrete variable measured with some degree of normally distributed error contributing to the observed score. Such a distribution would be expected given accurate assessment of phenotypic, or behavioral indicators of the same single-gene trait. Example phenotypes of Huntington’s chorea include symptoms of depression and irritability. Note that even with near-perfect assessment of phenotypes, individual differences (variability) in symptom expression, depicted as normally distributed dispersion around the mean for each discrete outcome, is observed. This is because fluctuations in symptom expression are introduced at many levels of influence between genes and behavior (see, e.g., Lenzenweger, 2004). Note also that the effect size (Cohen’s d) separating the two distributions in the middle panel of Figure 1 is 4.0 standard deviation units, an extremely large effect by psychological standards (Cohen, 1988).² For most phenomena studied, considerably more error variance is likely to be added during the measurement process, resulting in smaller effect sizes.

The bottom panel of Figure 1 depicts the same dichotomous variable, with an additional 50% variance in measurement error added, which is not uncommon for Likert-type data (Hoyt & Kerns, 1999). Note that the overall distribution appears to be unimodal, despite the fact that it contains two discrete distributions. Although the effect size (d = 1.6) is still quite large by Cohen’s standards, the admixed distribution is unimodal. Because psychological data are characterized by considerable imprecision, detecting latent taxa is a formidable enterprise (J. Ruscio & Ruscio, 2004a), and bimodality provides a weak criterion for testing typological models (Beauchaine & Beauchaine, 2002; Waller & Meehl, 1998). Note also that the opposite problem—induction of bimodality into a distribution of scores—can result from stereotypes and response biases of raters (Beauchaine & Waters, 2003), an issue that is addressed in later sections.

Taxometric Methods

Meehl recognized the inherent difficulties in detecting taxa with imprecise measures, and the resulting need for a novel approach to resolving the latent, or unobserved structure of psychopathology. To address the issue, he embarked on what became a 30-year effort to develop new methods to test his typological theory of schizophrenia (Meehl, 1962, 1989, 1990). Although portions of his theory have since been disproved, which is sometimes used to argue against a threshold model of schizophrenia (Widiger, 2001), genetic risk for schizophrenia (i.e., schizotypy) has repeatedly emerged as a latent typology (Blanchard et al., 2000; Erlenmeyer-Kimling, Golden, & Cornblatt, 1989; Golden & Meehl, 1979; Horan, Blanchard, Gangestad,&Kwapil, 2004; Korfine&Lenzenweger, 1995; Lenzenweger, 1999; Lenzenweger & Korfine, 1992, 1995; Tyrka, Cannon, et al., 1995; Tyrka, Haslam, & Cannon, 1995).

In the sections to follow, I describe 3 of Meehl’s 13 taxometric procedures and provide some example analyses with simulated data. Even though the data are simulated for clarity of presentation, I use the example of endogenous depression to illustrate several points. As the provided examples imply, taxometric methods can be used for both exploratory and confirmatory purposes. In exploratory contexts, taxometric methods can be used to identify variables that distinguish or fail to distinguish groups of individuals from one another. In confirmatory contexts, individuals can be sorted into hypothesized subgroups, and taxometric methods can be used to corroborate or refute the proposed typology.

Maximum Slope (MAXSLOPE)

Although MAXSLOPE (Grove, 2004, 2005; Grove & Meehl, 1993) has rarely been used in published taxometric analyses, I present it first because it provides some fairly straightforward insights into the conceptual bases of other taxometric procedures (see also Beauchaine, 2003; Beauchaine & Marsh, 2006). When using MAXSLOPE, pairs of putative group indicators are plotted against one another, and a smoothed regression line is fitted to the scatterplot. In contrast to a strictly linear regression approach, smoothing allows the slope of the regression line, which indicates the strength of association between the two variables, to vary nonlinearly along the range of x. If a taxon is present and the effect size separating the two groups is adequate for both variables, then a nonlinearity (increase or decrease) in the regression slope is observed, which is maximized near the level of indicator x that best differentiates between groups. In other words, the correspondence between x and y, represented by the steepness of the regression slope, is greatest near the point along x that optimizes diagnostic accuracy. When there is no taxon present, or when indicators are characterized by inadequate effect sizes, no nonlinearity is observed in the regression slope, which instead is constant across the entire range of x.

Consider the example of melancholic depression. Melancholia has long been recognized in the adult psychopathology literature as a more severe form of mood disorder with an especially insidious course. Those who suffer from melancholia, which has been linked specifically to biological vulnerability to mood disturbance (see, e.g., Shannon, Beauchaine, Brenner, Neuhaus, & Gatzke-Kopp, 2007), typically exhibit a distinct quality of anhedonia that includes failure to derive pleasure from all or nearly all activities and a lack of appetitive responding to usually pleasurable stimuli (American Psychiatric Association, 2000). Symptoms include depression that is worse in the morning, early morning awakening, psychomotor retardation, weight loss, and inappropriate guilt. Melancholic depression has been identified in children as young as preschool age (Luby, Mrakotsky, Heffelfinger, Brown, & Spitznagel, 2004) and confers especially high risk for suicide among adults (e.g., Carroll, Greden, & Feinberg, 1980; Coryell & Schlesser, 2001). As just noted, melancholia has emerged as a discrete form of depression in taxometric studies with both adolescents and adults (e.g., Ambrosini et al., 2002; Beach & Amir, 2003).

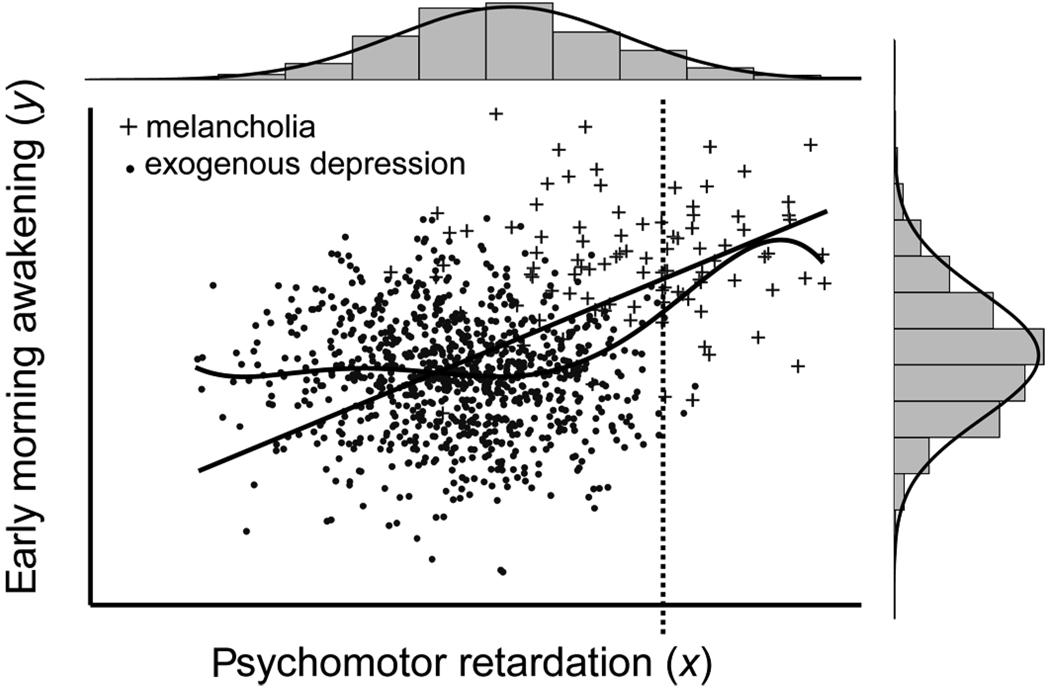
Figure 2 depicts a scatterplot of two symptoms of melancholia, psychomotor retardation (x) and early morning awakening (y). When the symptoms of two groups of depressed patients—one with melancholia and the other with nonmelancholic (exogenous) depression—are mixed in the same scatterplot, increased severity on both symptoms among those with melancholia induces an upward inflection in the smoothed regression function, as indicated by an increase in the regression slope. Such an inflection is suggestive of discrete subgroups embedded within the mixed distribution. Statistical bases of this effect are presented in Appendix A.

Figure 2.

Example of MAXSLOPE using a hypothetical bivariate distribution of exogenous depressives (n = 900) and melancholic depressives (n =100) who are separated by effect sizes of d =2.0 on both psychomotor retardation (x) and early morning awakening (y). The slope of the smoothed regression line is relatively flat within groups but increases near the point along x that best differentiates between exogenous and melancholic depression. This point is referred to as the hitmax value, indicated by the vertical dashed line. Compare this with a strictly linear regression analysis, which yields the straight solid line. Note again that the univariate distributions of variables, depicted above the figure for psychomotor retardation (x) and to the right of the figure for early morning awakening (y), appear to be unimodal despite the admixture of two discrete groups. Adapted from Beauchaine and Marsh (2006)

Maximum Covariance (MAXCOV)

Conceptually related to MAXSLOPE, MAX-COV (Meehl, 1973; Meehl & Yonce, 1996; Waller & Meehl, 1998) is the first to be developed, most commonly used, and most extensively studied taxometric procedure (Haslam & Kim, 2002). Using the MAXCOV procedure, one evaluates the correspondence (covariance) between two variables across the entire range of a third variable. Because it is not intuitively obvious how this practice might distinguish typologies from continua, MAXCOV is best explained by way of example. The top panel of Figure 3 illustrates the MAXCOV procedure with the same data used in the MAXSLOPE example just presented (psychomotor retardation and early morning awakening), with the addition of a third variable, weight loss (z). Here, the covariance of psychomotor retardation (x) and early morning awakening (y) is computed across the entire range of weight loss (z), within 16 successive intervals.

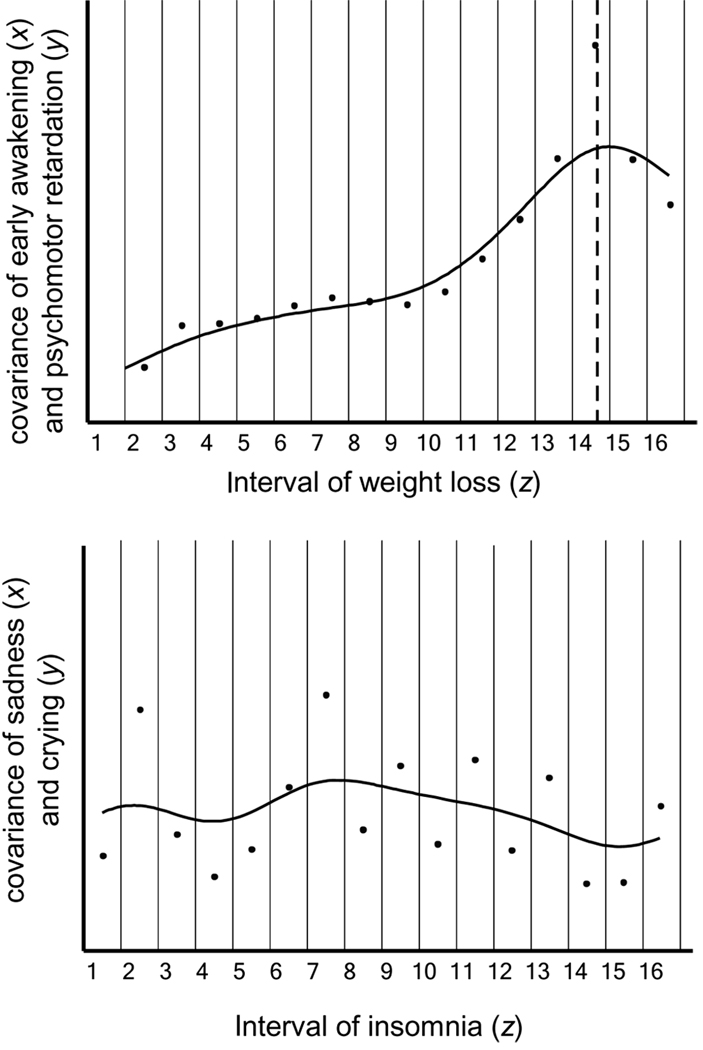
Figure 3.

Examples of MAXCOV with taxonic data, as in the case of melancholia (top panel) and nontaxonic data, as in the case of exogenous depression (bottom panel). The top panel includes analyses with two groups of n=900 (exogenous depression) and n=100 (melancholia) and an effect size of d=2.0. The bottom panel includes analyses using continuous normal distributions of n =1,000. In the case of melancholia (top), the covariance between early morning awakening (x) and psychomotor retardation (y), calculated within 16 adjacent intervals of weight loss (z), is maximized at the amount of weight loss (z) that best differentiates between groups, referred to as the hitmax value (dashed line). In the nontaxonic case (bottom), the covariance values of sadness (x) and crying (y) fluctuate unsystematically across levels of insomnia (z). These variables do not differentiate melancholia from endogenous depression. Adapted from Beauchaine and Marsh (2006)

As the top panel of Figure 3 illustrates, if a taxon is present and the effect size separating the two groups is adequate for all three variables, then a substantial peak is observed in the covariance function, indicating the value of weight loss (z) that best differentiates between groups. All trivariate combinations of variables are subjected to MAXCOV, and the consistency of results is evaluated (see the next example). When there is no taxon present, or when one or more indicators are characterized by inadequate effect sizes, no peak is observed in the covariance function, as depicted in the bottom panel of Figure 3. The location of the MAXCOV peak changes with differing taxon base rates (i.e., proportions of taxon members to nontaxon members). With a base rate of .50, for example, MAXCOV functions peak near the mode of the cut variable (z). As the base rate decreases, the peak shifts toward higher z values. At very low base rates, a rise in the covariance function (rather than a peak) occurs at the right end of the plot. Distinguishing between a taxon-generated rise to the right and an upward inflection caused by some kind of measurement-induced nonlinearity can at times be difficult, which is why “consistency tests” are very important (see next). Statistical details regarding MAXCOV appear in Appendix A.

Mean Above Minus Below a Cut (MAMBAC)

MAMBAC (Meehl, 1995a; Meehl & Yonce, 1994) is the second most commonly used taxometric procedure (Haslam & Kim, 2002). As with MAXSLOPE, MAMBAC operates on variable pairs. As depicted in left panel of Figure 4, the x variable (psychomotor retardation) is first sorted, which also partially sorts the y variable (early morning awakening), provided that the two variables are correlated, a necessary but insufficient condition for a latent taxon to be identified (see Meehl & Yonce, 1996). Next, a sliding “cut” is moved along x (psychomotor retardation), step by step, and the mean of y (early morning awakening) is calculated both above and below this cut. At each increasing value of psychomotor retardation, the mean of early morning awakening above the cut is subtracted from the mean of early morning awakening below the cut, and the resulting values are plotted.

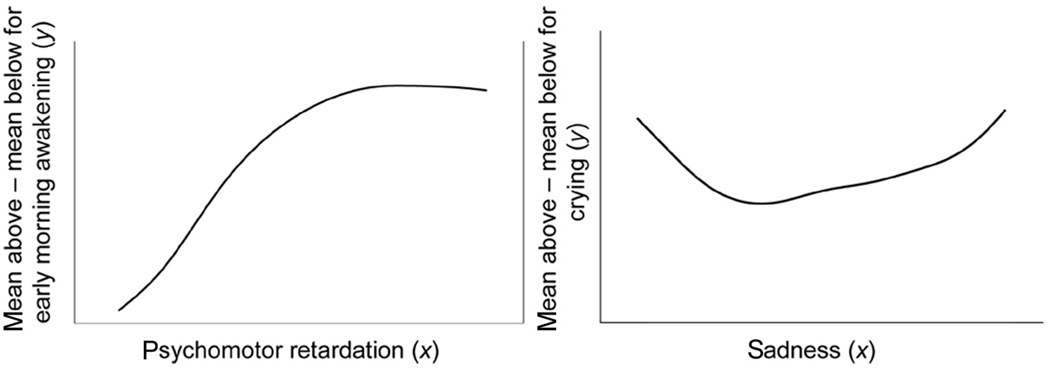
Figure 4.

Examples of MAMBAC using taxonic data, as in the case of melancholia (left) and nontaxonic data, as in the case of exogenous depression (right). The left panel includes smoothed MAMBAC plots from data composing two groups of n = 900 (exogenous depressives) and n = 100 (melancholic depressives) and an effect size of d = 2.0. The right panel includes analyses using continuous normal distributions of n= 1,000. In the taxonic case (left), the MAMBAC function for y (early morning awakening) is maximized near the point along x (psychomotor retardation) that best differentiates between groups. In the non-taxonic case (right), the MAMBAC function of y (crying) is dish shaped along x (sadness)

If a taxon is present and the effect size separating the two groups is adequate for both variables, then a peak is produced in the MAMBAC function. When there is no taxon, or when one or both indicators are of insufficient effect size, no peak is observed in the MAMBAC function, which is instead flatter and often dish shaped. This is depicted in the right panel of True Figure 4, using the same example of exogenous depression outlined earlier. MAMBAC is seldom used by itself in a taxometric analysis. Rather, it is used in conjunction with other methods, as illustrated next. A figure describing MAMBAC appears in Appendix A.

Other Taxometric Procedures

Several other taxometric procedures are becoming more popular, most notably maximum Eigenvalue (MAXEIG) and latent mode (L-Mode) analyses. These procedures operate on multiple variables, which can be an advantage or disadvantage, depending on the validity of variables. When all variables are valid indicators of taxon group membership, MAXEIG may be more powerful than alternatives (Waller & Meehl, 1998). However, when even a subgroup of indicators is imprecise (see next), taxa may go undetected, resulting in false negative outcomes (Beauchaine & Marsh, 2006). Because of space constraints and the complexity of the MAXEIG and L-Mode procedures, they are not described further. Interested readers are referred to Waller and Meehl (1998).

An Example Taxometric Analysis

Step 1: Selecting Indicators

The first step in conducting a taxometric analysis is to select discriminating and reliable variables that are measured with minimal error, which includes several important considerations. As with any statistical procedure, using unreliable and/or invalid indicators of the trait being studied can result in either a false positive error in which a spurious taxon is detected or a false negative error in which a valid taxon goes undetected (Meehl, 1995a).³ Although much greater attention has been paid to the possibility of false positives in taxometrics research, false negatives may be equally or more likely (Beauchaine & Marsh, 2006). I consider each of these in turn next.

False positive errors

Numerous authors have warned against identifying spurious groups when performing taxometric analyses (e.g., J. Ruscio & Ruscio, 2000, 2004a; J. Ruscio & Ruscio, & Keane, 2004; Widiger, 2001). Often referred to as pseudotaxonicity (Brown, 2001; Meehl, 1996), such errors arise from two primary sources. One of these is inappropriate sampling (Grove & Tellegen, 1991). In several studies in which taxometric methods have been used, clinical samples were recruited, and their psychopathology scores were mixed with those collected from normal controls. Based on positive results in subsequent taxometric analyses, evidence for typological distinctions has been maintained.

For example, two taxometric studies have appeared in which evidence for discrete subtypes of eating disorders has been claimed. In each case, symptoms of patients with anorexia, bulimia, and/or binge eating disorder were combined with symptoms of normal controls, and taxometric analyses were performed (Gleaves, Lowe, Green, Cororve, & Williams, 2000; Williamson et al., 2002). Yet conducting such analyses with samples who are recruited for bimodality is tautological. Provided that the measures used are valid, such an analysis should produce a positive result every time. Accordingly, proper sampling for testing taxonic hypotheses requires that participants be recruited representatively across all symptom levels. When representative sampling is used, no evidence for latent taxonic structure in eating disorders is found (Tylka & Subich, 2003).

A second source of pseudotaxonicity derives from the type of data that are subjected to analysis. In a recent study in which we manipulated raters’ beliefs about graduate school performance as dimensional (students’ abilities vary across a wide range) versus categorical (students tend to struggle or excel), we demonstrated that dichotomous distributions can be imparted into observers’ Likert ratings of that construct (Beauchaine & Waters, 2003). This result is consistent with a more general finding that attitudes and beliefs are particularly susceptible to categorical thought processes in which humans implicitly dichotomize continua and classify their observations based on preexisting opinions (Cantor & Genero, 1986; Cantor & Mischel, 1979, Malt, 1993; Rosch & Lloyd, 1978; Semin & Rosch, 1981; Simon, Pham, Le, & Holyoak, 2001).

Such findings, combined with the problems just noted regarding the inherent low measurement precision of Likert ratings, suggest that (a) caution should be applied in interpreting latent taxonic structure that emerges from strictly rating scale data, and (b) more careful planning of measures should precede data collection. Based on these findings and others, we have suggested that variables be selected from multiple levels of analysis, including biological markers that are often measured with less error than Likert scales and are usually not subject to rater biases. For example, the schizotypy taxon has been verified using objective measures including sustained visual attention, neuromotor performance, and cognitive functioning (e.g., Erlenmeyer-Kimling et al., 1989). The taxon can therefore not be attributed to any of the several sources of error specific to rating scale measures. Although we are not suggesting that Likert data be avoided entirely, such measures should be combined with other types of data. To date, most taxometric studies have been conducted exclusively with rating scales (see Beauchaine & Marsh, 2006).

False negative errors

Although numerous admonitions have appeared in the literature regarding false positives in taxometrics research (Beauchaine & Waters, 2003; Miller, 1996; A. Ruscio & Ruscio, 2002; J. Ruscio & Ruscio, 2004a; Widiger, 2001), few have considered the possibility of false negatives. This is problematic for several reasons. First, because measurement imprecision is a hallmark of most psychological data, as previously outlined, taxometric investigations are often hamstrung by inadequate effect sizes, resulting in low power (see Figure 1). Numerous Monte Carlo studies have revealed that taxometric methods cannot uncover latent taxa when the effect size separating the taxon group mean from the nontaxon group mean is much below d = 1.2 (Beauchaine & Beauchaine, 2002; Meehl, 1995a). It is important to note that an effect size of 1.2 is double the average effect size observed in psychological research (Cohen, 1988), which again underscores the need to select precise measures.

For example, if a latent taxon is separated from the nontaxon group by d = 1.00 on all indicators, the taxon is likely to go undetected, despite the fact that this is a large effect size in psychological research. To conclude that the analyzed construct is distributed continuously would therefore constitute a false negative finding. Nevertheless, such conclusions have become quite common in taxometrics research. As we have noted elsewhere (Beauchaine, 2003; Beauchaine & Marsh, 2006; Waters & Beauchaine, 2003), taxometric procedures search for latent subgroups within a multivariate distribution. When no subgroups are found, there are many possible reasons (e.g., inadequate power, invalid indicators), only one of which is continuous latent structure.

To offer an imperfect analogy, the effective null hypothesis is that the analyzed construct is continuous in nature, and the effective alternative hypothesis is that it is categorical. From a philosophy of science standpoint, this parallels null hypothesis significance testing: When the effect size separating the null distribution (nontaxon group) from the alternative distribution (taxon group) is insufficient, real effects will go undetected. Concluding that a negative result from a taxometric analysis suggests a continuous distribution is therefore equivalent to proving the null; it is always possible (even if unlikely) that more precise indicators would reveal a latent taxon.

Intercorrelations among variables

For a variable to be considered as a candidate indicator of a taxon, it must be correlated with all other variables in the analysis. Intuition regarding why this is the case can be gleaned by examining Figure 2, which depicts a MAXSLOPE graph of psychomotor retardation (x) and early morning awakening (y). In this example, a correlation between psychomotor retardation and early morning awakening is observed solely as a result of mixing two discrete groups (within each group, the correlation between psychomotor retardation and early morning awakening is zero). According to the general covariance mixture theorem presented in Appendix A, intercorrelations between variables must be observed to infer taxonic structure. Even though variables can be correlated in the absence of discrete subgroups, subgroups cannot be detected in the absence of variable intercorrelations. This axiom has been largely ignored by psychopathology researchers to date, most of whom have subjected all symptoms and markers available to taxometric analysis.

Although no single lower limit for the required correlation among variables can be offered, Meehl and Yonce (1996, p. 1147) summarized expected correlations for different base rates, effect sizes, and within-group correlations. Those who wish to perform taxometric analyses are encouraged to examine this table, as the covariation induced in an overall sample by mixing discrete groups forms the basis of all taxometric (and other latent class analysis) procedures, as summarized in Appendix B. It should therefore be required that correlation matrices be reported in all taxometrics studies.

Step 2: Bootstrapping the Indicator Pool

Given that there is a taxon, even when great care is taken toward selecting valid and correlated variables based on sound theory, some variables are always more efficient at distinguishing between the taxon group and the nontaxon group, for at least two reasons. First, taxometrics is a psychometric bootstrapping endeavor aimed at uncovering discrete latent (unobserved) structure by examining empirical relations among imperfect and oftentimes imprecise measures (Meehl, 1995a). In psychopathology research, there are almost never gold standards for confirming the validity of symptoms as markers of a discrete latent trait. If there were such gold standards, then there would be no need to conduct the analyses. In other words, there is no way of knowing a priori which indicators will mark a taxon, if one is present. Because we seek to identify taxa that cannot be observed directly, the utility of an indicator can only be assessed based on its performance with other candidate variables. In this context, if a variable performs poorly, it should be eliminated from the indicator pool in a preliminary screening. Otherwise, using it in taxometric analyses will result in a false negative outcome (Beauchaine & Marsh, 2006).

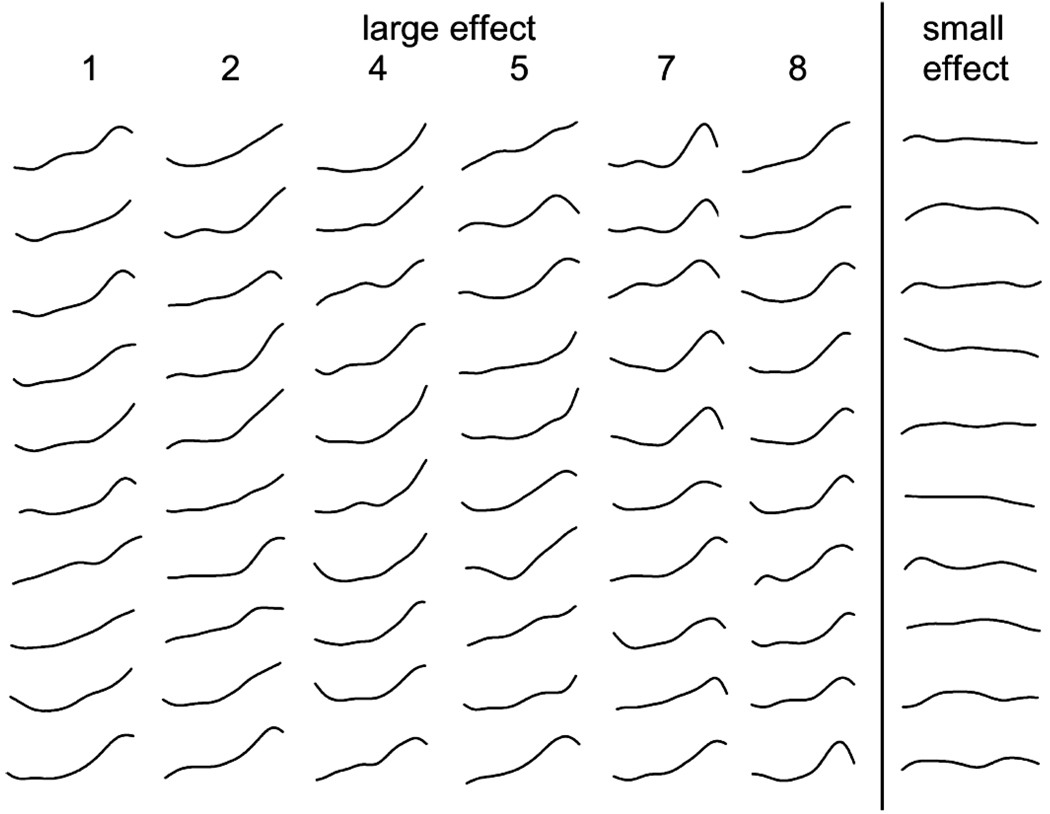
Consider a case in which eight carefully chosen putative indicators are available for analysis, six of which are characterized by large effects (d = 2.0), and two of which are characterized by small effects by taxometrics standards (d = 0.8). For purposes of this example, I created such a dataset containing 50 taxon group members and 450 nontaxon group members, for a taxon base rate of 50/50 + 450 = :10. As proposed by Meehl (1995a, 1999) and implemented by Waller, Putnam, and Carlson (1996), the first step in winnowing the initial indicator pool is to subject all pairwise combinations of variables to MAMBAC analysis. Plots from these analyses can then be arranged in matrix fashion and examined for evidence of taxonic structure (see Beauchaine & Waters, 2003).

Eight indicators produce $2\left(\begin{array}{c}k\\ 2\end{array}\right)=2\left(\begin{array}{c}6\\ 2\end{array}\right)=56$ combinations of variables for analysis. Each of these MAMBAC plots is presented in Figure 5. Plots for Variables 3 and 6, which are indicated in rectangled columns, are those characterized by the smaller effect size of d = 0.8. Because this effect size is inadequate for taxon detection using MAMBAC, the plots are not right-peaked as expected for a low base rate taxon. In contrast, all other plots in which variables of large effect size (d = 2.0) are paired produce right-end peaks, correctly indicating the low base rate taxon. Interestingly, flatter MAMBAC plots are observed when the smaller effect size indicators are used as the output variable to compute the MAMBAC function (columns 3 and 6) than when they are used as the sort variable (rows 3 and 6). Nevertheless, arranging all pairwise MAMBAC plots in matrix fashion makes it quite clear which variables are characterized by a sufficient effect size for continued analysis using MAXCOV or another taxometric procedure. In the example presented here, Variables 3 and 6 should be removed from the variable pool before further analyses are conducted. Note that if none of the variable combinations yielded consistently peaked MAMBAC plots, there would be no need to conduct further analyses.

Figure 5.

Pairwise matrix of MAMBAC plots for the eight variables described in text. For each plot, the sort variable is represented in rows and the output variable on which the MAMBAC functions were calculated is represented in columns. Variables 1, 2, 4, 5, 7, and 8 represent a taxon separated from the nontaxon group by an effect size of d = 2.0. In contrast, the effect size for Variables 3 and 6 is 0.8. Because this effect size is inadequate for taxometric analyses, the MAMBAC functions in columns 3 and 6 do not suggest a latent taxon. These variables should be removed from subsequent analyses, as detailed in text. Note that x and y axis scaling was held constant across plots

Winnowing the indicator pool in this fashion is extremely important because subsequent analyses using methods such as MAXCOV, MAXEIG, and L-Mode, which operate on more than two variables at a time (see next), are ineffective at detecting latent taxa when even a minority of variables of insufficient effect size are used (see Beauchaine & Marsh, 2006, p. 948). Thus, if one skips this step and fails to eliminate nondiscriminating variables, the chances of a false negative finding are greatly inflated, a point that has been underappreciated by many who have conducted taxometric analyses. Note that I am not suggesting that researchers cast a broad net and subject all available variables to this winnowing procedure. Rather, the procedure should be used only after careful selection of a theoretically plausible indicator pool.

Although I demonstrate this in the following section, the winnowing process requires additional discussion given that it has been criticized as a means of stacking the deck in favor of finding latent typologies (Widiger, 2001). Much of Widiger’s concern emerges from the observation that attitudes are susceptible to well documented cognitive biases that can result in artificially dichotomous judgments about external events, as noted above. Therefore, taxometric analyses using rating scales could reflect the cognitive sets of raters rather than a true taxon. Yet when carefully selected variables are chosen from multiple levels of analysis as suggested previously, and when several taxometric analyses consistently produce similar latent parameter estimates (e.g., base rates, means), the false positive rate is exceedingly low. As we and others have noted elsewhere (e.g., Beauchaine & Marsh, 2006; Jevons, 1958; Meehl, 1995a; Salmon, 1984, 1989; Whewell, 1966), the prior probability of several objective indicators drawn from multiple levels of analysis converging on consistent baserate, hitmax, taxon group mean, and nontaxon group mean estimates across different taxometric procedures approaches zero if there is no taxon present.⁴

Furthermore, winnowing indicators is not unlike the classical psychometric approach to scale construction in which less valid items are removed from an initial pool based on low α coefficients, which indicate poor internal consistency (see Nunnally & Bernstein, 1994). Few if any would advocate keeping such items for assessment of continuously distributed traits, which are typically evaluated using such scales. Taxometric procedures are no different; the integrity of the analysis depends on the validity of each variable used.

Unfortunately, the authors of many taxometric analyses conducted to date have subjected all possible variables to analysis without applying a winnowing procedure, thereby reducing power to detect taxa substantially. The problem with this approach is best illustrated by research examining the latent structure of depression. As outlined previously, there is a long history in the mood disorder literature in which a distinction has been made between endogenous (melancholic) and exogenous (nonmelancholic) subtypes of depression (e.g., Harrington, Rutter, & Fombonne, 1996). Cases of the former are considered to be influenced more by heritable biological predispositions (e.g., glucocorticoid receptor polymorphisms that result in hypothalamic-pituitary-adrenal axis hyperactivity; Ruiz et al., 2001), whereas cases of the latter are considered more likely to be precipitated by adverse environmental events. Melancholic depression is characterized by vegetative symptoms including psychomotor retardation, agitation, sleep disturbance, loss of weight, loss of appetite, and diminished libido. These symptoms appear to mark disturbances in homeostatic regulation, whereas other symptoms of depression, including mood disturbance and feelings of hopelessness, reflect distress, which is not specific to any particular subtype.

Taxometric analyses of melancholic depressive symptoms have repeatedly suggested a discrete subtype of mood disorder among both adolescents and adults (Ambrosini et al., 2002; Beach & Amir, 2003; Grove et al., 1987; Haslam & Beck, 1994). In contrast, taxometric analyses that include all symptoms of depression have not (Beach & Amir, 2003; Haslam & Beck, 1994; A. Ruscio & Ruscio, 2002; J. Ruscio & Ruscio, 2000). Thus, when symptoms are subjected to taxometric analysis without winnowing the indicator pool, the endogenous depression taxon goes undetected. This may have important implications for identifying suicide risk among those with certain melancholic symptoms (see Coryell & Schlesser, 2001).

Other researchers have also subjected DSM symptom lists of different disorders to taxometric analysis, without any screening process. Yet as I and colleagues have argued elsewhere (Beauchaine, 2003; Beauchaine & Marsh, 2006), taxa are more likely to be identified by subsets of symptoms that specify more homogenous groups than most DSM syndromes identify. Resolving symptom subsets that identify latent taxa will require an empirical approach to indicator selection that eliminates invalid indicators, much like empirical approaches to scale construction, as noted previously.

Step 3: Consistency Tests

To protect against false positive findings, Meehl (1995a, 1999) strongly advocated the use of multiple consistency tests, which refers to replication of latent distributional parameters (means, base rates, etc.) using alternative taxometric procedures. The assumptions here are that (a) a true latent taxon should be detectable using multiple taxometric methods, and (b) agreement should be observed in estimates of distributional characteristics, both within and across taxometric methods. For the example at hand, I present MAXCOV analyses of the data that were winnowed from eight indicators to six in Step 2. Following this, I demonstrate the effect of performing such analyses without eliminating variables of insufficient effect size.

Because MAXCOV operates on variable triads rather than variable pairs, there are i × (i – 1)!/ (i – 3)!2! = 6 × (120/6 × 2) = 60 combinations available for analysis given six variables. All MAXCOV plots from the winnowed data set appear in the left portion of Figure 6. Recall that each of these variables is characterized by an effect size of d = 2.0. Without exception, all of the MAXCOV plots rise steeply from left to right, with several exhibiting a right-end cusp. This shape is prototypical for low base rate taxa (see Meehl, 1995a; Meehl & Yonce, 1996). Moreover, base rate estimates across MAXCOV runs are highly consistent, with a mean of 0.107, a range of 0.07 to 0.18, and a standard deviation of 0.025. Thus, across analyses the MAXCOV-estimated base rate was impressively close to the true base rate of 0.10. The small standard deviation indicates that most of the base rate estimates were very close to the true taxon base rate.

Figure 6.

Smoothed MAXCOV plots for all combinations of the six variables selected for further taxometric analysis by MAMBAC (left of solid line). Input variables are listed across the top row, with all output variable pair combinations appearing down columns. The effect size for each variable is d = 2.0. Note the consistency of the right-end peaks, indicating the low base rate taxon. For comparison purposes, MAXCOV plots with one of the small effect size (d= 0.8) variables as input are also presented (right of solid line). Note that the plots are much flatter, with no consistent peak, indicating that the taxon went undetected. Both x- and y-axis scaling are identical across plots

For comparison purposes, I also include 10 MAXCOV plots in which one of the small effect size (d = 0.8) variables that was winnowed out by MAMBAC is used as the input variable. These plots appear on the right side of Figure 6. In these analyses and others that included the low effect size variables, base rate estimates across MAXCOV runs were highly inconsistent, with a mean of 0.655, a range of 0.25 to 0.90, and a standard deviation of 0.217. Thus, the standard deviation of base rate estimates was nearly 10 times as large when small effect size indicators were included, and the MAXCOV-estimated base rate was far from the true taxon base rate.

The consistency of base rate estimates for taxonic data forms the basis of the fit index for taxonic structure (FITS), a statistic ranging from 0.0 to 1.0 (with 1.0 indicating perfect fit) that we have proposed as an aid in evaluating taxonic hypotheses (Beauchaine & Beauchaine, 2007). The FITS is described in Appendix C.

Although for illustrative purposes I have emphasized agreement of base rate estimates as a consistency check, many additional tests have been suggested. Because of space constraints, I cannot review all of them here. Yet it is important to note that consistency tests are central to the taxometric method (see Meehl, 1995a), and most taxometric analyses include evaluation of several such tests, a number of which are listed in Appendix D.

Step 4: Assigning Observations to the Taxon Group and Nontaxon Group

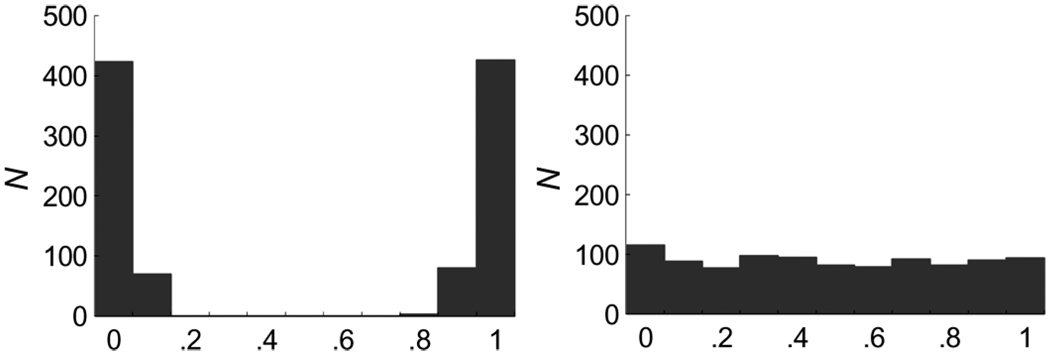
Following a positive result, the next step in a taxometric analysis is to assign individuals to the taxon and nontaxon groups. As outlined in Appendix A, this is accomplished using a derivation of Bayes’ Theorem (Meehl, 1973, Waller & Meehl, 1998). Assigned probabilities of taxon group membership provide an additional check of the taxonic hypothesis. Given discrete latent distributions and sufficient effect sizes among variables, Bayesian-estimated probabilities of taxon group membership aggregate near the limits of the [0,1] probability interval (Waller & Meehl, 1998). In other words, if there is a taxon, Bayes’ Theorem should estimate the probability of taxon group membership for each individual as being close to either 0 (a nonmember) or 1 (a member). In contrast, dimensional data yield probability estimates that are distributed more evenly between 0 and 1, as there is no taxon group with which to belong. This is demonstrated in Figure 7, where histograms of Bayesian-estimated probabilities of taxon group membership for discrete and continuous distributions are presented.

Figure 7.

Histograms of Bayesian-estimated taxon group membership probabilities for two discrete distributions of n = 500 (left), and one continuous distribution of n = 1,000 (right). In the taxonic case, the effect size was d =2.0 Note. From “A Comparison of Maximum Covariance and K-Means Cluster Analysis in Classifying Cases Into Known Taxon Groups,” by T. P. Beauchaine and R. J. Beauchaine, III, 2002,Psychological Methods, 7, p. 249. Copyright 2002 by the American Psychological Association. Reprinted with permission

After individuals are assigned to groups, additional analyses can be conducted to determine whether the groups differ on theoretically important external variables. For example, in their taxometric analysis of infant reactivity among 599 four-month-olds, Woodward et al. (2000) found that infants who were classified into the high-reactive taxon group, which comprised 10% of the sample, exhibited elevated scores on measures of behavioral inhibition 4 years later. Given established relations between behavioral inhibition and risk for internalizing psychopathology, these results demonstrate the predictive validity of the taxonic distinction across an impressive time period, with potential implications for early identification of risk for anxiety and depression. Indeed, among adults, Kotov et al. (2005) found an anxiety taxon with a nearly identical base rate as that observed for behavioral inhibition in infancy. This may suggest continuity in the latent structure of risk for anxiety, a possibility that should be addressed in future research.

Step 5: Interpretation

Confirmatory results

As with any statistical procedure, the final step in a taxometric analysis involves interpretation. Given a positive outcome, the onus is on the researcher to elaborate on the potential implications of his or her findings. These implications are likely to differ depending on the nature of the question being pursued. For example, consistent findings of a melancholic depression subtype, which is characterized by greater long term morbidity and mortality than exogenous depression, has clear implications for assessment and diagnosis (Ambrosini et al., 2002; Beach & Amir, 2003; Grove et al., 1987; Haslam & Beck, 1994). Indeed, Coryell and Schlesser (2001) reported a tenfold increase in suicide risk at 15-year follow up among depressed patients with hypothalamic-pituitary-adrenal (HPA)-axis hyperactivity—a biological marker of endogenous depression—compared with equivalently depressed controls with normal HPA-axis functioning.

In this case, knowledge of endogenous symptoms has clear implications for the urgency of treatment, and for long-term course. This suggests that modifications to our diagnostic criteria should be considered that encourage more thorough assessment of endogenous symptoms for those who present with depression (Beauchaine & Marsh, 2006). As noted earlier, evidence suggests that the distinction between endogenous and exogenous depression is valid among preschoolers (Luby et al., 2003; Luby et al., 2004), which may have additional implications for prevention. Next I provide an example in which taxometrics can already inform prevention efforts.

In certain high-risk research, taxometric analyses can be used to identify symptom cutoffs for children who are particularly vulnerable to severely debilitating psychiatric disorders, facilitating both prevention and early intervention. For example, by performing taxometric analyses on sustained visual attention, neuromotor performance, and intelligence measures, Erlenmeyer-Kimling et al. (1989) identified a schizotypy taxon group among the 7- to 12-year-old offspring of parents with schizophrenia. Although only 5% in the general population exhibit signs of schizotypy (Blanchard et al., 2000; Golden & Meehl, 1979; Korfine & Lenzenweger, 1995; Lenzenweger, 1999; Lenzenweger & Korfine, 1992), 47% of children with an afflicted parent belonged to the taxon group, compared with only 4% of controls. Furthermore, 43% of the schizotypy group were either hospitalized or received significant treatment 15 years later. Similar findings were reported by Tyrka, Cannon, et al. (1995), who identified a schizotypy taxon group among the 10- to 19-year-old offspring of mothers with schizophrenia. The taxon base rate (48%) was nearly identical to that reported by Erlenmeyer-Kimling et al. Moreover, 40% of taxon group members were diagnosed with a schizophrenia spectrum disorder 24 to 27 years later.

These findings have direct implications for prevention. Enrolling all children of parents with schizophrenia into prevention programs is extremely inefficient because only 10 to 15% will go on to develop a spectrum disorder (see Cornblatt, Obuchowski, Roberts, Pollack, & Erlenmeyer-Kimling, 1999). Yet in the studies just summarized, taxon group members exhibited almost four times this level of risk. More efficient detection of genetic risk makes prevention much more plausible (Cornblatt, 2001; Cornblatt, Lencz, & Kane, 2001). Furthermore, recent evidence suggests considerable effectiveness for prevention programs that are designed specifically to attenuate risk for future psychosis (e.g., McGorry et al., 2002). Thus, results from taxometric analyses can and should be used to identify clinical cutoffs for children at especially high risk for schizophrenia spectrum disorders. More recent work with more precise measures suggests that future studies may provide for even more precise identification of risk (e.g., Cornblatt & Malhotra, 2001; Glahn et al., 2003; Ross, 2003). The implications of premorbid identification of risk for schizophrenia are difficult to overstate given clear links between early intervention and improved long-term course (see Cornblatt, 2001; Cornblatt et al., 1999).

Null results

Although we have already commented at length on the likelihood of obtaining false negative findings in taxometrics research, some additional discussion is warranted. Even though the probability of such errors is reduced by subjecting all putative indicators to the winnowing procedure previously outlined, one should still be cautious in interpreting null findings as strong evidence for continuous latent structure. It is always possible that more precise indicators will reveal a latent taxon in future studies, especially if the null outcome is derived from rating scale data, as in most taxometrics research conducted to date. For this reason in particular, researchers should exercise prudence in interpreting null findings and offer recommendations for future research that can address the latent structure of the construct under consideration with greater measurement precision.

Relatedly, researchers should also extend their putative indicator lists beyond DSM-IV criteria to include biological markers of latent traits, which are by nature more precise than rating scale data (Beauchaine, 2003). Although behavioral indicators may be fully valid markers of a particular trait (e.g., anhedonia as a symptom of depression), they are difficult to measure without error, which hamstrings taxometric procedures, as previously outlined. Thus, putting taxonic hypotheses to strong tests requires that indicator selection be considered carefully. To date, most taxometrics studies have been performed on large datasets of convenience with strictly Likert-type measures.

Additional Considerations

Researchers interested in the operating characteristics of taxometric procedures have examined the performance of MAMBAC, MAXCOV, and other methods under a number of conditions that could either adversely affect taxon detection or induce spurious taxa into continuously distributed traits. These include situations in which (a) within-group (nuisance) correlations among indicators are high, violating the local independence assumption (Beauchaine & Beauchaine, 2002; Meehl, 1995b); (b) skewed indicators are used (Cleland & Haslam, 1996; Haslam & Cleland, 1996); (c) dichotomous items serve as variables (Golden, 1982, 1991); (d) effect sizes among indicators vary (Haslam & Cleland, 2002); (e) base rates are exceedingly low (Beauchaine & Beauchaine, 2002); (f) sample sizes are relatively small (Beauchaine & Beauchaine, 2002; Meehl, 1995a); and (g) numbers of indicators are varied (Beauchaine & Beauchaine, 2002). Although space limitations preclude me from reviewing the results of these studies comprehensively, several issues stand out as particularly important to mention.

Sample Size

Monte Carlo studies have indicated that the minimum sample size for conducting MAMBAC and MAXCOV analyses is about 200 with highly valid indicators (e.g., Beauchaine & Beauchaine, 2002; Meehl, 1995a; Meehl & Yonce, 1994).

However, given the problems noted earlier with ensuring measurement precision, which directly impacts validity, sample sizes exceeding 300 are preferred. This eliminates many data sets from consideration for taxometric analysis. However, preliminary evidence suggests that smaller samples might be accommodated by MAXEIG (Waller & Meehl, 1998). Unfortunately, the operating characteristics of MAXEIG are understudied compared with those of MAMBAC and MAXCOV. Until more is known about the performance of MAXEIG with smaller samples, Meehl’s (1995a) recommendation of a minimal sample size of 300 should be followed.

Skew

Among data characteristics known to affect the performance of taxometric methods, skew has probably received the most attention (e.g., Beach & Amir, 2003; Marcus, John, & Edens, 2004; J. Ruscio & Ruscio, 2004a, 2004b; J. Ruscio et al., 2004). Although preliminary reports suggested that both MAMBAC and MAXCOV are effective when used with moderately skewed indicators (Cleland & Haslam, 1996; Haslam & Cleland, 1996), others have noted a tendency for both methods to produce right-peaked plots that are suggestive of low base rate taxa when continuously distributed indicators are highly skewed (J. Ruscio & Ruscio, 2004a; J. Ruscio et al., 2004).

To deal with this problem, Ruscio and Ruscio (A. Ruscio & Ruscio, 2002; J. Ruscio & Ruscio, 2004a) advanced a technique in which both latent dimensional and latent taxonic data sets are simulated to match observed data parameters. All three data sets (observed, simulated dimensional, simulated taxonic) are then subjected to taxometric analysis, and conclusions are reached regarding the latent structure of the observed data based on whether results obtained from those data are more similar to results obtained from the simulated dimensional or the simulated taxonic analyses. Unfortunately, a recent and extensive Monte Carlo simulation (Beach, Amir, & Bau, 2005) revealed that this method often yields false negative findings when the taxon base rate is low and skew is high— precisely the conditions for which the technique was supposed to provide clarification. Thus, a solution to the skew problem remains elusive. Nevertheless, data from our lab indicate that taxometric methods are capable of resolving latent taxonic structure without false positives when skew values are as high as 2.0 (Beauchaine & Beauchaine, 2007).

It is important to note that skew is always induced when a low base rate taxon is embedded in the tail of a normal distribution of scores. It is therefore ill-advised to remove putative indicators from taxometric analyses based solely on skew, particularly if a low base rate taxon is suspected. Doing so will eliminate valid indicators. Also of note, the variables used in the example analyses presented earlier had an average skew value of 0.33, well within acceptable limits for taxometric analyses and most other statistical procedures.

Number of Indicators

As the example analyses presented earlier indicate, taxometric procedures can be executed with only two vaiables. Yet there are no published studies that have included so few. Data from our lab suggest that power to detect latent taxa increases with more variables, asymptoting at about seven to eight (Beauchaine & Beauchaine, 2002). Accordingly, we have recommended that taxometric investigations be conducted with at least five or six indicators (Beauchaine & Marsh, 2006). Given that some putative indicators will almost certainly be winnowed out of most data sets (see previously), researchers should include as many variables as possible when planning a taxometric study. Furthermore, as with psychometric scale construction, indicator redundancy, or the use of several variables that mark the same latent construct, is not only acceptable, it is preferred. Ideally, multiple redundant indicators will be available across alternative levels of analysis, including behavioral, observational, and biological.

Replication

Although I have presented a number of strategies aimed at ensuing the integrity of taxometric analyses, firm conclusions regarding discrete latent structure for a disorder can only be reached through replication. Single studies are always subject to sample-specific variation in symptoms that may be attributable to chance. Accordingly, confirmation of taxonic outcomes should be obtained across multiple studies before drawing inferences about the latent structure of a disorder or about appropriate diagnostic thresholds (Beauchaine & Marsh, 2006). As outlined previously, psychiatric conditions that have been confirmed as taxonic across multiple studies and labs include schizotypy (Blanchard et al., 2000; Erlenmeyer-Kimling et al., 1989; Golden & Meehl, 1979; Horan et al., 2004; Korfine & Lenzenweger, 1995; Lenzenweger, 1999; Lenzenweger & Korfine, 1992, 1995; Tyrka, Cannon, et al., 1995; Tyrka, Haslam, & Cannon, 1995) and endogenous depression (Ambrosini et al., 2002; Beach & Amir, 2003; Grove et al., 1987; Haslam & Beck, 1994). Other disorders and high risk traits for which some replication exists include anxiety (e.g., Kotov et al., 2005; Woodward et al., 2000), and severe antisocial behavior (e.g., Harris et al., 1994; Skilling et al., 2001).

A second strategy that we have advocated is replication within a study using alternative classification methods (Beauchaine & Marsh, 2006). Although this is no substitute for replication across studies, confirming one’s result with both taxometric procedures and latent class analysis (see next), for example, may provide for increased confidence in a given outcome. Recently, we uncovered evidence for discrete subgroups of children with autism spectrum disorders based on cognitive performance measures using MAMBAC, MAXCOV, and latent class analysis (Munson et al., 2007). Although findings indicated a taxon of high functioning individuals, replication by other labs will provide us with much greater confidence in this inference.

Alternative Approaches

As alluded to earlier, taxometric methods are not the only approach to resolving discrete latent structure. Other techniques designed to address similar questions include cluster analysis, latent class analysis, latent profile analysis, finite mixture analysis, growth mixture modeling, and information-theoretic alternatives (see, e.g., Aldenderfer & Blashfield, 1984; Blashfield & Aldenderfer, 1988; Everitt, 2001; Gibson, 1959; Krueger, Markon, et al., 2005; Lazarsfeld & Henry, 1968; McLachlan & Peel, 2000; Muthén, 2001; Muthén & Shedden, 1999; Nagin, 1999). Reviewing the operating characteristics, advantages, and disadvantages of these techniques would require a full-length text. Thus, I provide only the briefest description of their performance vis-a`-vis taxometrics.

Cluster Analysis

As I have discussed in detail elsewhere (Beauchaine, 2003; Beauchaine & Beauchaine, 2002; Beauchaine & Marsh, 2006), cluster analysis may have heuristic utility in some contexts, but it is quite limited as a means of identifying discrete taxa, because most clustering algorithms always partition datasets into subgroups, yet currently available methods for determining the correct number of clusters are only effective when symptom overlap is absent or minimal (see Grove, 1991; Milligan & Cooper, 1985; Tonidandel & Overall, 2004). As discussed extensively in preceding sections, this set of circumstances is highly unusual in psychological research. Furthermore, cluster analysis cannot determine whether a discrete model better captures the latent structure of data than a dimensional model (see Beauchaine, 2003; Beauchaine & Marsh, 2006, for expanded discussions).

Mixture Modeling

Mixture modeling refers to a number of related methods that search for homogenous subgroups within large samples (McLachlan & Basford, 1988). Such methods include latent class analysis (e.g., Lazarsfeld & Henry, 1968), which was designed for use with dichotomous and/or Likert data; latent profile analysis and finite mixture analysis (Gibson, 1959; Lazarsfeld & Henry, 1968; McLachlan & Peel, 2000), which identify latent classes within continuous data; and growth mixture modeling (Muthén, 2001; Muthén & Shedden, 1999; Nagin, 1999; Nagin & Tremblay, 2001), which identifies groups from latent growth trajectories in symptoms (or other variables) collected across multiple longitudinal time points.

Among these methods, growth mixture modeling in particular has enjoyed burgeoning popularity in the developmental psychopathology literature in recent years given its capacity to accommodate longitudinal data (e.g., Nagin & Tremblay, 1999; Schaeffer et al., 2006; Shaw, Gilliom, Ingoldsby, & Nagin, 2003). Although I cannot review the extensive technical bases of growth mixture modeling and related techniques given space limitations, it should be noted that despite their current popularity, these methods are often structure imposing. In other words, they typically converge on a best-fitting solution that includes multiple (n > 1) groups—even when the underlying data are continuous.⁵ Thus, when latent subgroups are identified, it is not possible to determine whether the groups are truly discrete. This limitation applies to both traditional approaches to mixture analysis (Klein & Riso, 1993; McLachlan & Peel, 2000) and to newer growth mixture modeling techniques.

Furthermore, Bauer and Curran (2003a, 2003b, 2004) have shown that growth mixture models are prone to identifying spurious latent classes when only one group is contained within a population. As with cluster analysis, this does not necessarily undermine the heuristic utility of the technique (Cudeck & Henly, 2003). However, it does limit conclusions that might be drawn from mixture models regarding proper placement of diagnostic boundaries. Nevertheless, this set of techniques does offer an approach for subdividing populations into more than two groups—which cannot be accomplished with current instantiations of taxometric methods.⁶ In one of his later writings, Meehl (1999) did advance a modified taxometric technique referred to as TAXSCAN for identifying multiple taxa. However, the operating characteristics of the technique have yet to be explored, and no empirical applications have appeared in the literature to date.

Concluding Remarks

Questions concerning the latent structure of psychopathology have a direct bearing on our ability to understand, accurately diagnose, and effectively treat debilitating conditions. Although discretely distributed disorders are likely to be rare, it is important that we identify those that are taxonic given implications for early detection of vulnerability and prevention of morbidity and mortality. In this article, I have provided examples from the literature in which proper identification of discretely distributed traits has already advanced our understanding of the latent structure of psychopathology, as in the case of endogenous depression, and our ability to identify at risk children premorbidly, as in the case of schizotypy. I have also provided example analyses using simulated data that I hope make taxometric procedures more accessible to those who have not used the methods previously. Readers who are interested in more detailed accounts are referred to the reference list for original sources. When used appropriately, taxometric procedures provide a valuable tool for advancing clinical science. Although they have been used sparingly to date with nonadult samples, future taxometric studies with children and adolescents could answer very important questions about the emergence and basic structure of sychopathology.

Appendix A

This appendix outlines some of the mathematical underpinnings of the taxometric procedures described conceptually in text. My intent is not to offer comprehensive accounts of these procedures. Rather, I provide only as much detail as necessary for interested readers to appreciate the basis of each procedure. Those who seek expanded discussions are encouraged to obtain the original sources cited herein.

MAXSLOPE

MAXSLOPE is based on the assumption that a nonlinearity (increase or decrease) in the regression slope, representing the correspondence between x and y, is imparted entirely by mixing two discrete groups. Within each group, the correlation between x and y is assumed to be 0. This is referred to as local independence in the latent class analysis literature. The relation between x and y can be expressed by the following equations (Grove & Meehl, 1993):

$$\text{convariance}(x,y)={\sigma }_{xy}=Q{\sigma }_{cxy}+P{\sigma }_{txy}+\mathrm{}PQ{\mathrm{\Delta }}_x{\mathrm{\Delta }}_y$$ (1)

$$\text{variance}(x)={\sigma }_x^2=Q{\sigma }_{cx}^2+P{\sigma }_{tx}^2+PQ{\mathrm{\Delta }}_x^2$$ (2)

$$\text{variance}(y)={\sigma }_y^2=Q{\sigma }_{cy}^2+P{\sigma }_{ty}^2+PQ{\mathrm{\Delta }}_y^2$$ (3)

where

• σ_cxy represents the covariance of x and y in the nontaxon group,

• σ_txy represents the covariance of x and y in the taxon group,

• ${\sigma }_{cx}^2$ and ${\sigma }_{ix}^2$ are the variances of x in the nontaxon and taxon groups, respectively,

• ${\sigma }_{cy}^2$ and ${\sigma }_{ty}^2$ are the variances of y in the nontaxon and taxon groups, respectively,

• P is the baserate of the taxon in the population, and Q = 1 – P.

In early instantiations of the MAXSLOPE procedure (Grove & Meehl, 1993), the point along x that best differentiates between the taxon and nontaxon groups (the hitmax value) was estimated by identifying the maximum slope of the smoothed regression function, which corresponds to the largest observed first derivative (dy/dx). Newer instantiations of MAXSLOPE include a more precise method of identifying the hitmax value. Because this newer procedure extends beyond the scope of this article, interested readers are referred to Grove (2004, 2005) for further details.

MAXCOV

MAXCOV capitalizes on differences in within-groups versus between-groups covariances toward detecting discrete latent classes. Given adequate effect sizes separating the taxon and nontaxon groups, moderate within-groups correlations, and two valid indicators of taxon group membership, x and y, the between-groups covariance will exceed the within-groups covariances, as outlined in the general covariance mixture theorem (Meehl, 1995a, p. 271; Meehl & Yonce, 1996, p. 1097):

$$\begin{array}{ll}\text{cov}(xy)=& p{(\text{cov})}_t(xy)+q{(\text{cov})}_c(xy)\\ & +pq({\overline{x}}_t-{\overline{x}}_c)({\overline{y}}_t-{\overline{y}}_c)\end{array}$$ (4)

where cov(xy) represents the covariance of variables x and y, p represents the proportion of taxon group members in the mixed sample, q represents the proportion of nontaxon group members in the mixed sample, x̄_i represents the mean of variable x in group i, ȳ_i represents the mean of variable y in group i, and c and t represent the nontaxon group and taxon group, respectively.

MAXCOV (and other taxometric procedures) can be used to estimate several parameters describing the taxon and the nontaxon distributions. These include the hitmax value, the taxon base rate, the sample sizes of the taxon and nontaxon groups, and the false positive and false negative rates of group assignments. MAXCOV can also be used to assign probabilities of taxon group membership to individuals using a derivation of Bayes’ theorem, described next (Waller & Meehl, 1998, p. 29). From these Bayesian estimated probabilities, individuals can then be sorted into groups, which may correspond to psychiatric classes, high risk status, and so on, depending on the nature of the sample and the question being posed. With three variables (the simplest case), Bayesian estimated probabilities are given by the following formula:

$$\text{Pr}(t|x^{+}{y}^{-}{z}^{+})=\frac{P{p}_{tx}{q}_{ty}{p}_{tz}}{P{p}_{tx}{q}_{ty}{p}_{tz}+Q{p}_{cx}{q}_{cy}{p}_{cz}}$$ (5)

where Pr(t|x⁺y⁻z⁺) represents the probability of taxon group membership given scores above the hitmax value on x and z, and below the hitmax value on y, P represents the taxon base rate, Q represents the nontaxon base rate, p_tx represents the true positive rate for variable x (see below), p_cx represents the false positive rate for variable x as derived from the MAXCOV analysis, q_tx equals 1 – p_tx, and q_cx equals 1 – p_cx. Within each interval, true positives are estimated by taking the positive root of the quadratic equation, and true negatives are estimated by taking the negative root (Beauchaine & Beauchaine, 2002, p. 249; Meehl & Yonce, 1996, pp. 1120–1121):

$$p_{xi}=\frac{({\overline{y}}_t-{\overline{y}}_c)({\overline{z}}_t-{\overline{z}}_c)\pm \sqrt{\begin{array}{l}{(({\overline{y}}_t-{\overline{y}}_c)({\overline{z}}_t-{\overline{z}}_c))}^2\\ -4({\overline{y}}_t-{\overline{y}}_c)({\overline{z}}_t-{\overline{z}}_c){\text{cov}}_{yzi}\end{array}}}{2({\overline{y}}_t-{\overline{y}}_c)({\overline{z}}_t-{\overline{z}}_c)}$$ (6)

where p_xi represents the true positive rate of taxon group members identified within interval i of variable x, and cov_yzi represents the covariance of variables y and z within the same interval of variable x. Estimates are summed across intervals to yield samplewide true positive and false positive rates.

It should be noted that regardless of the method used to determine the most efficient cut point for separating taxon and nontaxon group members, assigning individuals to groups can never be accomplished with perfect accuracy when the distributions overlap. This is always the case, regardless of the method used to resolve latent structure. Nevertheless, specifying the most accurate cut point is exceedingly important because it minimizes misclassifications, including both false positives and false negatives.

MAMBAC

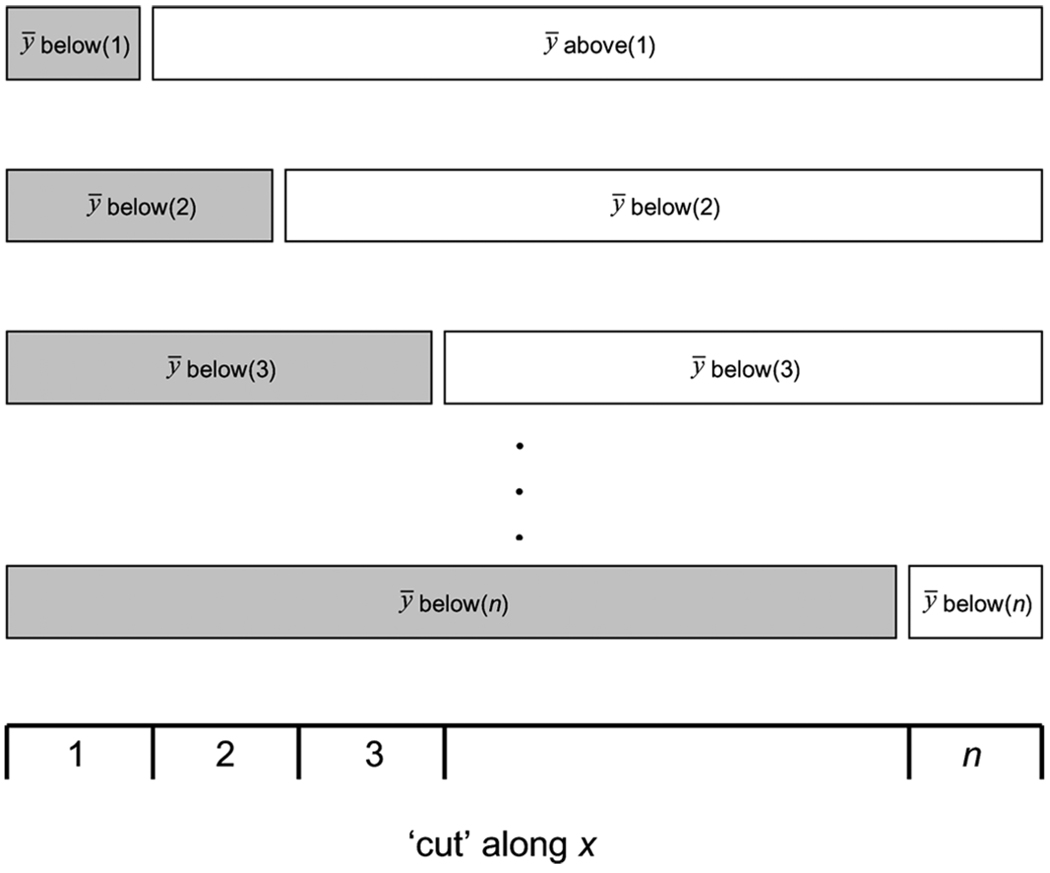
Because MAMBAC is based on simple subtraction, it requires no formulae to be described. As outlined by Meehl and Yonce (1994, p. 1069), the procedure is summarized in Figure A1.

Figure A1.

Pictorial depiction of the MAMBAC procedure. For each increasing value of x, the mean of y both above and below that value of x is computed. Each mean above is then subtracted from the corresponding mean below. This process is repeated until no values of x remain, and the results are plotted. Adapted from Meehl and Yonce (1994)

Appendix B

For two standardized variables that are both valid indicators of the same latent taxon, the observed correlation in the mixed group is given by the following equation (Meehl & Yonce, 1996, p. 1146):

$$r_{mixed}=\frac{\mathrm{cov}(xy)}{\sqrt{{\mathrm{var}}_x{\mathrm{var}}_y}}$$ (7)

Here it is important to distinguish between within-group covariance and between-groups covariance. As the labels imply, within-group covariance refers to the correlation between variables within the taxon and nontaxon groups, often referred to in the literature as nuisance covariance. In contrast, between-groups covariance is imparted by mixing discrete groups and is therefore the covariance of interest when conducting a taxometric analysis. As mentioned previously, an assumption of both taxometrics and latent class analysis is that nuisance covariance is zero (local independence). In practice, however, taxometric methods can be used effectively with nuisance correlations up to about .30, provided that the correlation in the mixed sample exceeds the within group correlations (Beauchaine & Beauchaine, 2002; Meehl, 1995b).

Appendix C

The fit index for taxonic structure (FITS) ranges from 0.0 to 1.0, with the latter value indicating perfect agreement of base rate estimates across analyses. The FITS is given by the following equation:

$$\text{FITS}=1-2\times \sqrt{\frac{{\displaystyle {\sum }_j{(b{r}_j-\overline{br})}^2}}{(N-1)}}$$ (8)

where br_j = the estimated base rate from variable combination j, br̅ is the mean of baserate estimates across all variable combinations, and N = the number of variable combinations available for analysis. Readers will note that the value within the radicand of this equation is simply the standard deviation of base rate estimates. For this example, MAXCOV analyses in which the small effect size variables were winnowed out yielded a FITS value of 0.95, which is strongly indicative of a latent taxon. In contrast, the analyses including the small effect size indicators yielded a FITS value of 0.56, which is not suggestive of a latent taxon. In a large Monte Carlo study (Beauchaine & Beauchaine, 2007), FITS values below .65 were never observed for taxonic data when valid indicators were used. Once again, this illustrates the importance of using carefully selected indicators that are subjected to an empirical winnowing procedure.

Appendix D

In addition to the consistency of base rate estimates within and across taxometric procedures as a consistency test, a number of additional tests have been used and/or suggested. These include but are not limited to the following:

1. The consistency of estimated taxon group means (μ_tx, μ_ty, μ_tz … μ_tn) and nontaxon group means (μ_cx, μ_cy, μ_cz … μ_cn) for each variable;

2. The consistency of estimated taxon group variances $({\sigma }_{t_X}^2,{\sigma }_{t_Y}^2,{\sigma }_{t_Z}^2\dots {\sigma }_{t_n}^2)$ and nontaxon group variances $({\sigma }_{c_X}^2,{\sigma }_{c_Y}^2,{\sigma }_{c_Z}^2\dots {\sigma }_{c_n}^2)$ for each variable;

3. The consistency of estimated taxon group nuisance correlations (r_tXY, r_tXZ, r_tYZ … r_tmn) and nontaxon group nuisance correlations (r_cXY, r_cXZ, r_cYZ … r_cmn) for each variable;

4. Correlations among Bayesian-estimated probabilities of taxon group membership across different procedures (high correlations indicate agreement across methods);

5. Grove’s (2006) disattenuated kappa (k) coefficient test. This involves (a) estimating the sensitivity and specificity of Bayesian-estimated group assignments of observations to taxon versus nontaxon groups and (b) substituting these values into the disattenuation formula for Cohen’s (1960) kappa. Disattenuated k approaches 1.0 if the different procedures are identifying the same taxon.

6. Evaluating histograms of Bayesian-estimated taxon group membership probabilities for a U-shape, which is indicative of consistent classification into the taxon and nontaxon groups (see Figure 7).