A Hierarchy of Homodesmotic Reactions for Thermochemistry

Abstract

Chemical equations that balance bond types and atom hybridization to different degrees are often used in computational thermochemistry, for example, to increase accuracy when lower levels of theory are employed. We expose the widespread confusion over such classes of equations and demonstrate that the two most widely used definitions of “homodesmotic” reactions are not equivalent. New definitions are introduced and a consistent hierarchy of reaction classes (RC1 – RC5) for hydrocarbons is constructed: isogyric (RC1) ⊇ isodesmic (RC2) ⊇ hypohomodesmotic (RC3) ⊇ homodesmotic (RC4) ⊇ hyperhomodesmotic (RC5). Each of these successively conserves larger molecular fragments. The concept of isodesmic bond separation reactions is generalized to all classes in this hierarchy, providing a unique sectioning of a given molecule for each reaction type. Several ab initio and density functional methods are applied to the bond separation reactions of 38 hydrocarbons containing five or six carbon atoms. RC4 and RC5 reactions provide bond separation enthalpies with errors consistently less than 0.4 kcal mol⁻¹ across a wide range of theoretical levels, performing significantly better than the other reaction types and far superior to atomization routes. Our recommended bond separation reactions were demonstrated by determining the enthalpies of formation (at 298 K) of 1,3,5-hexatriyne (163.7 ± 0.4 kcal mol⁻¹), 1,3,5,7-octatetrayne (217.6 ± 0.6 kcal mol⁻¹), the larger polyynes C₁₀H₂ through C₂₆H₂, and an infinite acetylenic carbon chain.

I. Introduction

In 1970, Pople and co-workers introduced “isodesmic” reactions in order to predict thermochemistry at low levels of electronic structure theory.^1–3 Such transformations balance the number of bonds of each type (e.g., C–C single, double, and triple). At that time the only generally feasible ab initio computations were Hartree-Fock applications with small basis sets. Zero-point and thermal energies were not available, as vibrational frequencies could not be computed. Since then, other types of chemical equations have been constructed to improve the accuracy of thermochemical computations. A widely used class of balanced reactions is designated “homodesmotic”.^4–6 Unfortunately, the two common definitions of this term are not consistent, and their misuse is common in the literature. Because basic chemical concepts surrender much of their utility when applied inconsistently, uniform definitions of reaction classes are essential.

The various types of balanced reactions are intertwined with group additivity schemes for hydrocarbon thermochemistry.^7–13 In the extensive group increment scheme developed and refined by Benson,^10,11 enthalpies of formation (or other thermodynamic quantities) are approximated by summing contributions from “groups.” These groups, like C, CH, CH₂ and CH₃ for hydrocarbons, consist of a polyvalent atom and selected neighboring atoms, and account for the surrounding environment.¹¹ While the groups utilized in such additivity schemes are not generally the same as those preserved in balanced reactions, both underlying philosophies build on the additivity of energetic interactions in what are regarded as “non-strained” hydrocarbons.¹⁴

In contrast to using error-canceling transformations for predicting thermochemistry,³ much recent work^15–20 seeks to compute enthalpies of formation to “subchemical accuracy” (near 0.1 kcal mol⁻¹) directly. This approach favors the use of atomization reactions in order to minimize the reference set for which enthalpies of formation (${\mathrm{\Delta }}_f{H}_T^{\circ }$) must be known very precisely. However, atomization schemes demand rigorous accounting of the homolytic cleavage of all bonds simultaneously, a notorious problem requiring exceptionally high levels of theory. To approach subchemical accuracy in this manner generally requires complete basis set extrapolations of high-order coupled cluster theory with at least a perturbative correction for quadruple excitations [CCSDT(Q)] and auxiliary terms for core correlation, post-Born-Oppenheimer effects, special relativity, and the anharmonicity of zero-point vibrations. Moreover, even at such high levels of theory, errors are proportional to system size; hence, subchemical accuracy is not achievable for larger molecules via current atomization schemes. This realization has recently led the developers of the HEAT (High-accuracy Extrapolated Ab initio Thermochemistry) protocol to consider balanced reaction schemes for determining enthalpies of formation.²⁰

The present paper is concerned with the construction of a consistent hierarchy of chemical equations, from isogyric to hyperhomodesmotic, and with the performance in computing thermochemical quantities at each level. A third concern is not investigated here, namely the quantification of many virtual (not directly measurable) chemical concepts such as π-conjugation, hyperconjugation, ring strain, and aromaticity. Quantifying these effects depends critically on the scheme for partitioning the total molecular energy, as well as the choice of reference compounds and of defining equations. Basing analyses of these virtual concepts on different types of reactions can yield disturbing, seemingly inconsistent results.²¹ We reserve further investigation of this issue for subsequent research.

II. Existing Homodesmotic Definitions

The current hierarchy of reaction types preserves energetic interactions in reactants and products to varying extents. Isogyric reactions³ are those in which the total number of electron pairs is conserved. For hydrocarbons, the subset of isogyric reactions in which the number of C–C bonds of a given formal type (single, double, and triple) is conserved was defined as isodesmic (from Greek, desmos = bond) by Pople and co-workers^1–3 in 1970. Isodesmic transformations include “bond separation reactions”, a term for reactions in which each bond between non-hydrogen atoms is separated into the simplest two-heavy-atom fragments with the same formal bond types.³ For example, the isodesmic bond-separation reaction for 3-methyl-1-butene is given by eq (1), where one C–C double bond and three C–C single bonds are on each side.

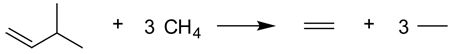(1)

Homodesmotic reactions (with “equal bonds”) were first constructed by George, Trachtman, Bock, and Brett (GTBB)⁴ to provide a greater balance of bond types than isodesmic transformations. The initial definition (HD1) of homodesmotic reactions set forth the following criteria: (a) equal numbers of carbon atoms in their various states of hybridization in reactants and products, and (b) a matching of carbon-hydrogen bonds in terms of the number of hydrogen atoms joined to individual carbon atoms in reactants and products. To clarify this concept, the simplest isogyric, isodesmic, and homodesmotic reactions for the decomposition of butane are:

(2)

(3)

(4)

In a largely overlooked Note added in proof, GTBB⁴ pointed out that HD1 is not applicable to systems containing combinations of sp, sp², and sp³ atoms, promising²² a refined definition in a subsequent (though unspecified) paper. The following year, the same authors⁵ presented homodesmotic reactions as a means of evaluating ring strain in cyclic hydrocarbons. They retained HD1 and went on to assert that this definition “implies that there are equal numbers of each type of C–C bond (sp³–sp³, sp²–sp³, etc.) and that the various types of C–H bonds (H–C_sp³, H–C_sp², etc.) are matched as closely as possible.” In light of the earlier Note Added in Proof,⁴ the word “implies” was probably intended only for the specific hydrocarbon reactions under investigation. This alternative description of homodesmotic transformations was refined in a subsequent publication by George and co-workers⁶ to yield new defining conditions (HD2) for a homodesmotic reaction: (a) equal numbers of each type of carbon-carbon bond [C_sp³–C_sp³, C_sp²–C_sp³, C_sp²–C_sp², C_sp²=C_sp² etc.] in reactants and products, and (b) equal numbers of each type of carbon atom (sp³, sp², sp) with zero, one, two, and three hydrogens attached in reactants and products.

Unfortunately, definitions HD1 and HD2 have been mistakenly perceived as equivalent for general hydrocarbon reactions. IUPAC officially sanctions HD1.²³ A simple transformation proving that HD1 does not imply HD2 is

(5)

In this equation, the C_sp²–C_sp², C_sp³–C_sp³ and C_sp²–C_sp³ single bonds are unbalanced. The literature is peppered with examples^24–44 of “homodesmotic” reactions that satisfy HD1 but not HD2. For instance, Stahl and co-workers³⁸ employed equation (6) to assess the aromatic stabilization of naphthalene. This reaction does not meet the HD2 requirements, since there are eight sp²–sp² single bonds, four sp²–sp³ single bonds, and two sp³–sp³ single bonds in the reactants but nine, two, and three in the products, respectively.

(6)

A litany of reaction classes has followed the homodesmotic concept: hyperhomodesmotic,⁴⁵ semihomodesmotic,⁴⁶ quasihomodesmotic,^47,48 homomolecular homodesmotic,⁴⁹ isogeitonic (from Greek geitonas = neighbor),⁵⁰ isoplesiotic (from Greek plesios = near to, close to),⁵¹ homoplesiotic,⁵¹ and s-homodesmotic,^52–54 among others. These reactions balance the types of bonds and hybridization of constituent atoms to various extents. The idea of homodesmotic reactions has also been extended by many to non-hydrocarbons, although inconsistencies in such efforts have been noted previously.⁵⁵

Illustrating the confusion over reaction classes, many chemical transformations claimed to be homodesmotic satisfy neither HD1 nor HD2, but instead are merely isodesmic^56–62 or even isogyric.^63,64 For example, reaction (7) has been used⁶¹ to compute enthalpies of formation of diacetylene-expanded polyhedranes, but this transformation is only isodesmic, satisfying neither HD1 nor HD2, because the number of −CH, −CH₃ and CH₄ components is not balanced.

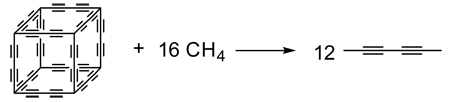(7)

Befuddlement also results from the widespread use of the term “homodesmic” in place of “homodesmotic”. This abbreviation, which was first proposed by Schulman and Disch (see footnote 4 of ref 65), has caused unintended confusion. The term “homodesmic” is already used in crystallography⁶⁶ to refer to materials with identical interactions between constituent atoms, and its use in the context of computational thermochemistry should be avoided. Similarly, the term “homoisodesmic” has appeared in the literature as a pseudonym for homodesmotic.^67–69 We recommend that the original term (“homodesmotic”) be employed uniformly.

While the misinterpreted statement⁵ that definition HD1 implies HD2 is not true for general hydrocarbon transformations, the converse does hold, namely, a reaction satisfying HD2 will necessarily satisfy HD1, because the second criterion of HD2 clearly encompasses both criteria for HD1. In brief, the requirements of HD2 are more stringent than HD1, and HD2 reactions constitute a subset of HD1 reactions.

In 1983, Hess and Schaad⁴⁵ recognized that some key interactions would be unbalanced in homodesmotic equations based on definition HD1. In response, Hess and Schaad apologetically defined⁴⁵ hyperhomodesmotic reactions as those in which eight carbon-carbon bond types (H₂C=CH, HC=CH, H₂C=C, HC=C, C=C, HC–CH, HC–C, and C–C) are conserved,⁷⁰ constituting a further refinement of homodesmotic reactions. However, only conjugated polyenes were considered (in which case HD1 and HD2 are equivalent). To generalize the original hyperhomodesmotic concept, eight additional types of carbon-carbon bonds must be introduced (H₃C-CH₂, H₃C-CH, H₂C-CH₂, H₃C-C, H₂C-CH, H₂C-C, HC≡C, and C≡C), giving a total of 16 bond types to be conserved. Unfortunately, such hyperhomodesmotic transformations are only subsets of HD1, but not HD2, homodesmotic reactions. To demonstrate this flaw, equation (8) satisfies the generalized hyperhomodesmotic conditions but is not homodesmotic under definition HD2, due to the imbalance of sp²–sp², sp³–sp³, and sp²–sp³ C–C bonds.

(8)

III. A New Hierarchy of Homodesmotic Reactions

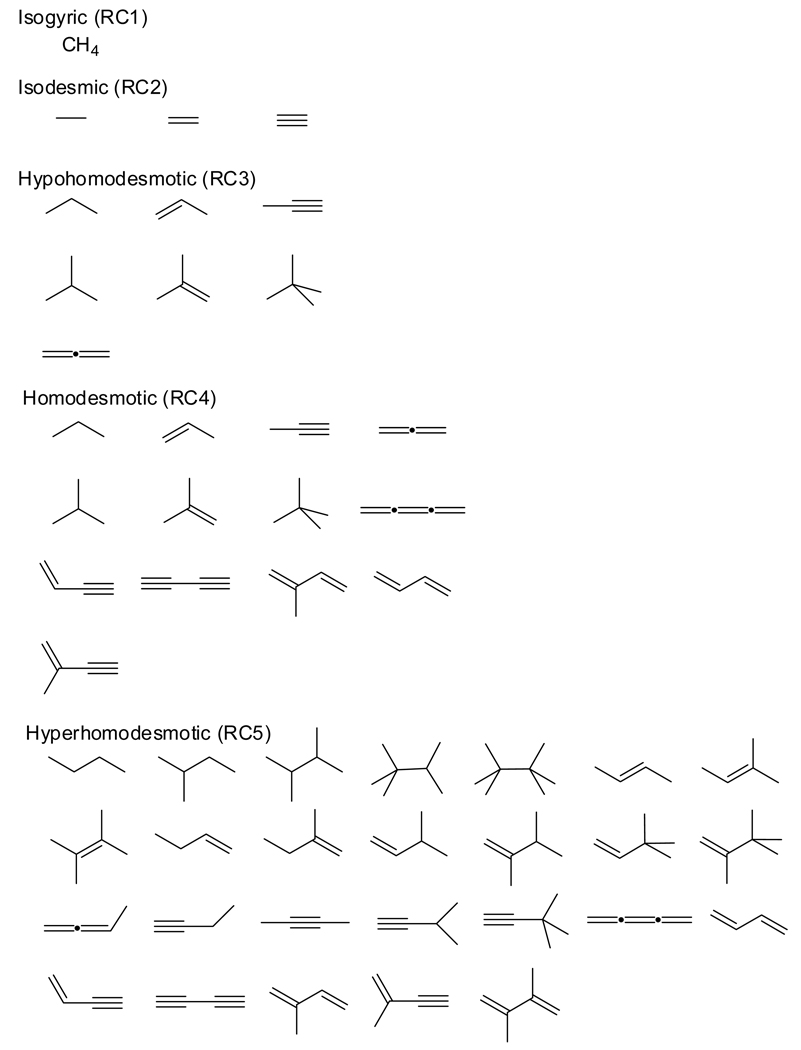
To construct an unambiguous hierarchy of reaction classes (RC1 – RC5), we first redefine a hyperhomodesmotic reaction (RC5) as one containing:

1. equal numbers of carbon-carbon bond types [H₃C–CH₂, H₃C–CH, H₂C–CH₂, H₃C–C, H₂C–CH, H₂C–C, HC–CH, HC–C, C–C, H₂C=CH, HC=CH, H₂C=C, HC=C, C=C, HC≡C, and C≡C] in reactants and products, and

2. equal numbers of each type of carbon atom (sp³, sp², sp) with zero, one, two, and three hydrogens attached in reactants and products.

It is clear that such hyperhomodesmotic reactions are a subset of HD2 reactions, which in turn are a subset of HD1 transformations. We recommend that reactions satisfying only HD1 be called hypohomodesmotic, reserving the term homodesmotic for HD2 reactions. This nomenclature establishes an appealing hierarchy of reaction types, with each group constituting a subset of the preceding one: isogyric (RC1) ⊇ isodesmic (RC2) ⊇ hypohomodesmotic (RC3) ⊇ homodesmotic (RC4) ⊇ hyperhomodesmotic (RC5). Extending the hierarchy past RC4 may have limited use for chemical interpretation but often has substantial merits in thermochemical computations, as shown below. For clarity, our new canonical definitions of homodesmotic and hypohomodesmotic reactions, applicable to closed-shell hydrocarbons,⁷¹ have the following criteria.

Homodesmotic reactions (RC4):

1. equal numbers of each type of carbon-carbon bond [C_sp³–C_sp³, C_sp³–C_sp², C_sp³–C_sp, C_sp²–C_sp², C_sp²–C_sp, C_sp–C_sp, C_sp²=C_sp², C_sp²=C_sp, C_sp=C_sp, C_sp≡C_sp] in reactants and products, and

2. equal numbers of each type of carbon atom (sp³, sp², sp) with zero, one, two, and three hydrogens attached in reactants and products.

Hypohomodesmotic reactions (RC3):

1. equal numbers of carbon atoms in their various states of hybridization in reactants and products, and

2. equal numbers of carbon atoms (regardless of hybridization state) with zero, one, two, and three hydrogens attached in reactants and products.

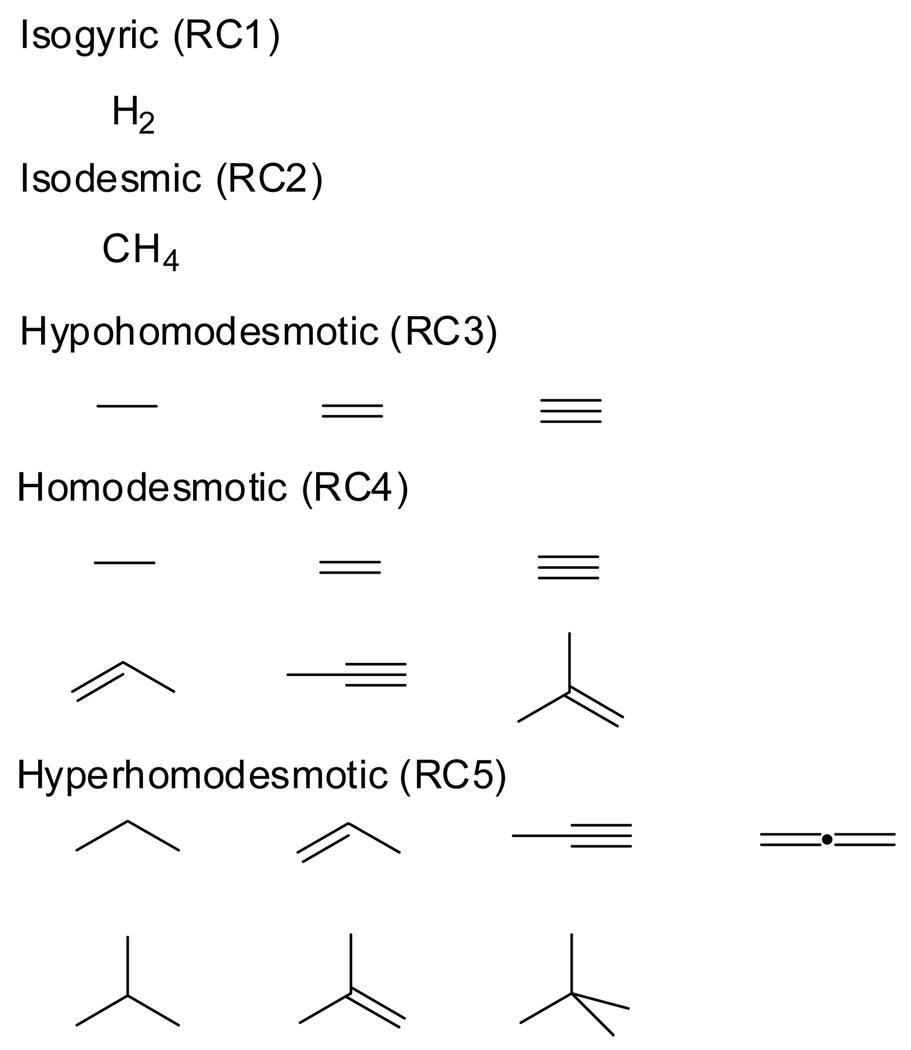
An often touted advantage of isodesmic bond separation reactions³ is that they are uniquely defined, unlike general isodesmic and homodesmotic transformations, of which limitless examples can be written involving a given molecule. However, the concept of isodesmic bond separation reactions can be generalized to our entire homodesmotic hierarchy. First, we define elemental products for each reaction type as the hydrocarbons that cannot be broken down further while maintaining the constraints of the given reaction type. The elemental products for each type of reaction in the homodesmotic hierarchy are compiled in Chart 1. Similarly, for each reaction type there are characteristic elemental reactants, as given in Chart 2. For a closed-shell hydrocarbon, the generalized bond separation reaction of each type is the uniquely defined transformation in which the target compound is sectioned into the elemental products via reactions with the elemental reactants. To illustrate this concept, the hierarchy of bond separation reactions for 2-methylhexa-1,3-diene-5-yne is given in reactions (9) – (13). In each case the bonds are maximally separated within the constraints of the reaction type.

(9)

(10)

(11)

(12)

(13)

Chart 1.

Elemental products.

Chart 2.

Elemental reactants.

Vianello, Liebman, and Maksić⁴⁷ introduced the term “quasihomodesmotic” in 2004 to describe equations such as (14), in which the number of carbon atoms in each hybridization state is conserved, but not the number of σ-bonds between carbons of a given hybridization. In this context, quasihomodesmotic reactions appear to be the same as our newly coined term hypohomodesmotic. More recently, Barić and Maksić⁷² recycled the term “quasihomodesmotic” to describe reactions of highly strained alkanes, such as reaction (15). In this case the hybridization imbalance arises from a more subtle source: the strain in cubane engenders additional p-character in the C-C bonds and hence an effective mismatch in the number of sp³ carbons. Such quasihomodesmotic transformations are intermediate between hypohomodesmotic and homodesmotic reactions. We suggest that the later meaning⁷² of quasihomodesmotic reactions be maintained, using the term hypohomodesmotic to describe imbalances as in equation (14).

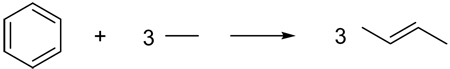(14)

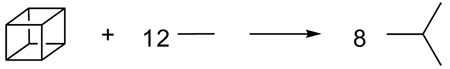(15)

Zhao and Gimarc⁵³ introduced “s-homodesmotic reactions” in 1993 as a succession of isogyric (s = −1), isodesmic (s = 0), homodesmotic (s = 1), and hyperhomodesmotic (s = 2) reactions. General reactions were initially defined for the decomposition of cyclic oxygen species and later extended to nitrogen rings and eventually cyclic alkanes (see ref 73). Reaction (16) is the corresponding decomposition scheme for linear alkanes. The s-homodesmotic construction is of limited utility because it cannot be straightforwardly extended to polyenes, or hydrocarbons in general.

(16)

Our proposed reaction hierarchy can be categorized as n-homodesmotic reactions, where n is the length of the main chain of the elemental products (Chart 1). Specifically, isogyric, isodesmic, hypohomodesmotic, and hyperhomodesmotic reactions are n-homodesmotic reactions with n = 1, 2, 3, and 4, respectively. Extension to n = 5, 6, … is possible to provide an ever increasing balance of bonding environments when sectioning larger hydrocarbons. Homodesmotic reactions must be considered a special case, since the elemental products include all possible acyclic hydrocarbons of main chain length three, plus six conjugated species of main chain length four. Homodesmotic reactions are the only reactions in the hierarchy for which the sets of elemental reactants and products are not mutually exclusive, as propene, propyne, and 2-methylpropene are both homodesmotic elemental reactants and products.

IV. Schemes for Computational Thermochemistry

The hierarchy of bond separation reactions proposed here provides a means of computing highly accurate (gas-phase) enthalpies of formation of general hydrocarbons. The requirement is that reliable reference ${\mathrm{\Delta }}_f{H}_T^{\circ }$ values must be established for all elemental reactants and products involved in the bond separation reaction of the target compound. The chosen bond separation reaction should be at a sufficiently high rung in the homodesmotic hierarchy to ensure adequate balance of errors. The target enthalpy of formation is then simply derived from the corresponding bond separation reaction enthalpy, which can be computed accurately from lower levels of theory as the homodesmotic hierarchy is traversed and error-balancing is successively improved. Pinpointing reference enthalpies for all compounds in Chart 1 and Chart 2 is a lofty but yet unrealized goal, demanding a confluence of the best experimental measurements with the most rigorous ab initio computations. The experimental determination of enthalpies for larger molecules is complicated by the existence of multiple conformers with non-negligible Boltzmann populations. Nonetheless, the database of reference compounds is steadily growing, as exemplified by the recent theoretical determinations of ${\mathrm{\Delta }}_f{H}_0^{\circ }$ for allene,⁷⁴ propyne,⁷⁴ 1,3-butadiene,⁷⁵ vinylacetylene,⁷⁵ and diacetylene,⁷⁶ for which the associated uncertainties are all less than 0.3 kcal mol⁻¹. For allene, propyne, and 1,3-butadiene, precise experimental values were found to match the theoretical determinations within 0.3 kcal mol⁻¹, whereas the experimental enthalpies for vinylacetylene and diacetylene were far less accurate.

We now assess the position in the homodesmotic hierarchy necessary to achieve subchemical accuracy (ca. 0.1 kcal mol⁻¹) as a function of level of electronic structure theory. While valuable previous work^77,78 has found that homodesmotic reaction schemes yield more accurate enthalpies of formation than atomization reactions, we now have a logically consistent methodology to extend these concepts to new limits.

V. Theoretical Methods

For a collection of generalized bond separation reactions of hydrocarbons, as well as a series of hypohomodesmotic prototypes, benchmark reaction enthalpies were computed by the rigorous focal point approach (FPA),^{74,75,79–82} which systematically extrapolates high-level energies to the ab initio limit. Experimental reaction enthalpies of comparable accuracy were not available in most cases. Optimized geometric structures and (unscaled) harmonic zero-point vibrational energies (ZPVEs) were taken from B3LYP density functional⁸³ computations with the 6-31G(d) basis set.⁸⁴ In the focal point analyses, Hartree-Fock (HF) energies computed with a series of correlation-consistent basis sets cc-pVXZ (X = T, Q, 5)⁸⁵ were extrapolated to the complete basis set (CBS) limit using an exponential form.⁸⁶ Likewise, correlation energies from second-order Møller-Plesset perturbation theory (MP2) were evaluated with the cc-pVXZ (X = Q, 5) basis sets and extrapolated with a standard two-parameter X⁻³ asymptotic formula.⁸⁷ Higher-order electron correlation was accounted for by coupled cluster theory including single and double excitations (CCSD)^88–90 with a perturbative treatment of connected triple excitations [CCSD(T)].^91,92 Coupled-cluster computations with the cc-pVTZ basis set were conjoined with the extrapolated MP2 results to approximate CBS CCSD(T) reaction energies. The carbon 1s core electrons were frozen in the focal point analyses; however, core correlation corrections were subsequently appended, as determined from MP2 computations with the cc-pCVTZ basis set.⁹³ As a check, all reaction energies were also computed using the popular G3 (ref ⁹⁴) and CBSQB3 (refs ^95,96) composite approaches. The FPA, G3, and CBS-QB3 results were in full accord, and comparison of them is included in Supporting Information (SI).

To investigate the performance of commonly used theoretical procedures for our error-canceling reactions, the associated enthalpy changes were computed via the B3LYP, M05-2X,⁹⁷ M06, and M06-2X^98,99 density functional approaches applied with the 6-31G(d) basis, as well as the HF, MP2, and CCSD(T) wave function methods utilizing the cc-pVTZ set. To further assess errors arising at lower levels of theory, the benchmark FPA reaction enthalpies at 0 K were partitioned into several terms:

• ε_basis(HF) = HF/CBS − HF/cc-pVDZ

• ε_basis(MP2) = MP2/CBS − MP2/cc-pVDZ

• Δ_corr = CCSD(T)/cc-pVTZ − HF/cc-pVTZ

• ε_corr = CCSD(T)/cc-pVTZ − MP2/cc-pVTZ

• Δ_(T) = CCSD(T)/cc-pVTZ − CCSD/cc-pVTZ

• Δ_core = MP2(all-electron)/cc-pCVTZ − MP2(frozen-core)/cc-pCVTZ

• Δ_ZPVE = ZPVE(products) − ZPVE(reactants)

The ε_basis(HF) and ε_basis(MP2) terms quantify errors in reaction energies from truncating the basis set to double-ζ plus polarization quality; Δ_corr estimates the total electron correlation contribution to the reaction enthalpy, whereas ε_corr is the error made by evaluating correlation effects only at the MP2 level; Δ_(T) measures the importance of higher-order excitations; and Δ_core and Δ_ZPVE are the core correlation and harmonic ZPVE contributions, respectively. Together, these quantities characterize the main computational demands for the accurate determination of a given reaction energy. We are not interested here in analyzing smaller errors from sources such as relativity, the Born-Oppenheimer approximation, and ZPVE anharmonicity,¹⁰⁰ which are accounted for in thermochemical work of the highest accuracy.^{15–18,20,79–81,101}

For comparison with error-balanced reactions, atomization energies were also computed. For the atomic C(³P) fragments, all wave function computations were based on restricted open-shell Hartree-Fock (ROHF) reference determinants, whereas spin-unrestricted density functional methods were employed. In particular, we elected to use the RHF-UCCSD and RHF-UCCSD(T) approaches^102,103 for coupled cluster computations and Z-averaged perturbation theory (ZAPT)^104,105 for second-order correlation treatments. Spin-orbit effects were accounted for by appending a correction of −0.09 kcal mol⁻¹ to the total energy of C(³P).

The Gaussian03 package¹⁰⁶ was employed for the B3LYP, G3, and CBS-QB3 computations. The MP2, CCSD, and CCSD(T) jobs were executed with MOLPRO2006,¹⁰⁷ while MPQC 2.1¹⁰⁸ was utilized for ZAPT2 energies. The M05-2X, M06, and M06-2X density functional results were obtained from NWChem 5.0.^109,110 Absolute total energies and Cartesian coordinates for all computations are tabulated in SI.

VI. Hypohomodesmotic Reaction Prototypes

For reactions involving closed-shell hydrocarbons, a distinction between hypohomodesmotic (RC3) and homodesmotic (RC4) reactions arises in any transformation where C_A–C_A and C_B–C_C bonds are replaced with C_A–C_B and C_A–C_C bonds (A ≠ B,C), where A, B, and C denote the hybridization state (sp³, sp², or sp). Reactions of this kind are embodied in the prototypes (17) – (23), which are representative of the myriad examples of hypohomodesmotic reactions in the literature.^24–44,111

(17)

(18)

(19)

(20)

(21)

(22)

(23)

Conjugative and hyperconjugative interactions are clearly not balanced in these RC3 reactions, unlike the RC4 and RC5 cases. For example, equation (17) juxtaposes the π-conjugation between the two double bonds in butadiene with twice the hyperconjugation in propene. The effects of such imbalances on the computed reaction energies of (17)–(23) are shown in Table 1. The basis set requirements for these reactions are all rather modest, as the differences between cc-pVDZ and extrapolated CBS results (Δ_basis) are less than 0.7 kcal mol⁻¹ both at the HF and MP2 levels. However, the electron correlation contributions to the reaction energies are considerably larger. For equation (18), equation (21), and equation (23), Δ_corr is 3.61, 2.54, and 2.42 kcal mol⁻¹, respectively, and in the first two cases the higher-order correlation effect [Δ_(T)] is greater than 1.1 kcal mol⁻¹. The ε_corr data for (17)–( 23) show that relying on the MP2/cc-pVTZ method engenders reaction energy errors between 0.03 and 1.25 kcal mol⁻¹ relative to CCSD(T)/cc-pVTZ. Core correlation effects are miniscule for these reactions (|Δ_corr| ≤ 0.06 kcal mol⁻¹).

Table 1.

Energetic analysis (in kcal mol⁻¹) of prototypical hypohomodesmotic reactions.^a

Hypohomodesmotic Equation	EFPA	ΔZPVE	Δcorr	Δ(T)	εbasis(HF)	εbasis(MP2)	εcorr	Δcore
17	2.96	−0.33	0.55	0.43	−0.22	−0.35	−0.40	−0.01
18	−1.88	−1.19	3.61	1.16	−0.66	−0.65	−1.25	−0.02
19	−0.18	−0.38	1.19	0.50	−0.40	−0.58	−0.37	−0.03
20	3.14	−0.05	−0.64	−0.07	0.18	0.24	−0.03	0.02
21	1.10	−0.56	2.54	1.11	−0.02	−0.39	−0.25	−0.06
22	1.44	−0.77	1.77	0.59	−0.08	0.16	−0.90	0.03
23	−1.70	0.81	2.42	0.66	−0.26	−0.07	−0.87	0.01
Abs. Mean	1.77	0.58	1.82	0.64	0.26	0.35	0.58	0.02

^aE_FPA is the high-level focal point reaction energy at 0 K. The other symbols are defined in the text. All energies are evaluated at B3LYP/6-31G(d) optimized geometries.

The performance of commonly employed levels of theory for the hypohomodesmotic prototypes is documented in Table 2. The largest errors occur for equation (18), for which CCSD(T)/cc-pVTZ is the only method predicting the reaction energy to better than 1 kcal mol⁻¹. Equation (18) is unbalanced because the π-conjugation in diacetylene is not present in either of the product molecules, and the hyperconjugation in propyne is not compensated in either of the reactant species. On the other hand, both types of conjugation are largely balanced in equation (20), and not surprisingly all methods in Table 2 give its reaction energy to better than 0.6 kcal mol⁻¹. Nevertheless, the errors for the meta-GGA functionals (M05-2X, M06, M06-2X) do not always parallel the number of unbalanced interactions, although these DFT methods are overall more accurate than B3LYP. This observation is consistent with recent findings¹¹² that reaction energy errors for M05-2X are less systematic than those from B3LYP and other functionals.

Table 2.

Performance of commonly used theoretical methods for reaction energies of hypohomodesmotic prototypes.^a

Hypohomodesmotic Equation	HF/cc-pVTZ	B3LYP/6-31G(d)	M05-2X/6-31G(d)	M06/6-31G(d)	M06-2X/6-31G(d)	MP2/cc-pVTZ	CCSD(T)/cc-pVTZ
17	+0.37	−1.38	−0.56	−0.76	−0.42	−0.58	−0.18
18	+2.91	−4.15	−1.39	−2.71	−1.49	−1.94	−0.69
19	+0.79	−1.93	−0.76	−0.98	−0.73	−0.77	−0.40
20	−0.42	+0.55	+0.20	+0.22	+0.30	+0.20	+0.23
21	+2.13	−2.22	−0.63	−1.73	−0.76	−1.16	−0.29
22	+1.71	−1.67	−0.43	−1.51	−0.45	−0.97	−0.07
23	+2.31	−0.14	+1.45	+0.70	+1.39	−0.47	−0.23
Abs. Mean	1.52	1.72	0.77	1.23	0.79	0.87	0.30

^aErrors are given in kcal mol⁻¹ relative to FPA benchmarks (E_FPA, Table 1); B3LYP/6-31G(d) optimized geometries were employed throughout.

VII. Bond Separation Reactions

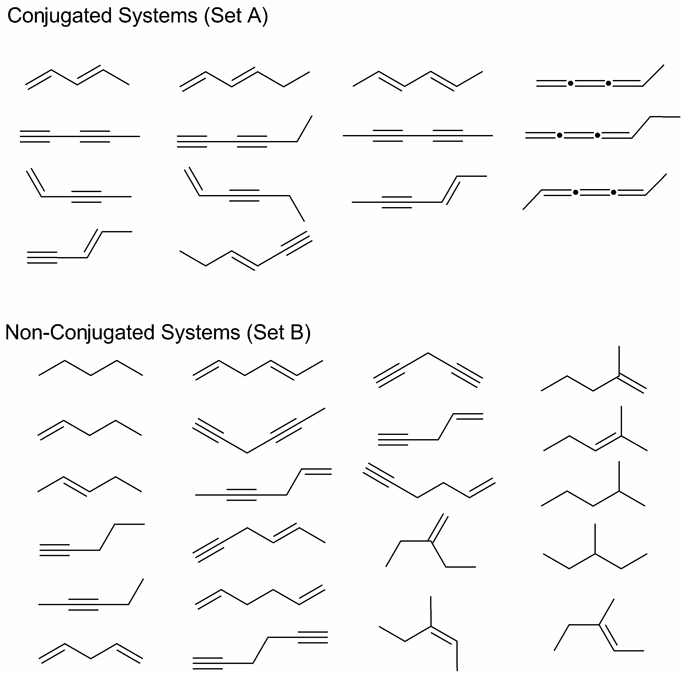
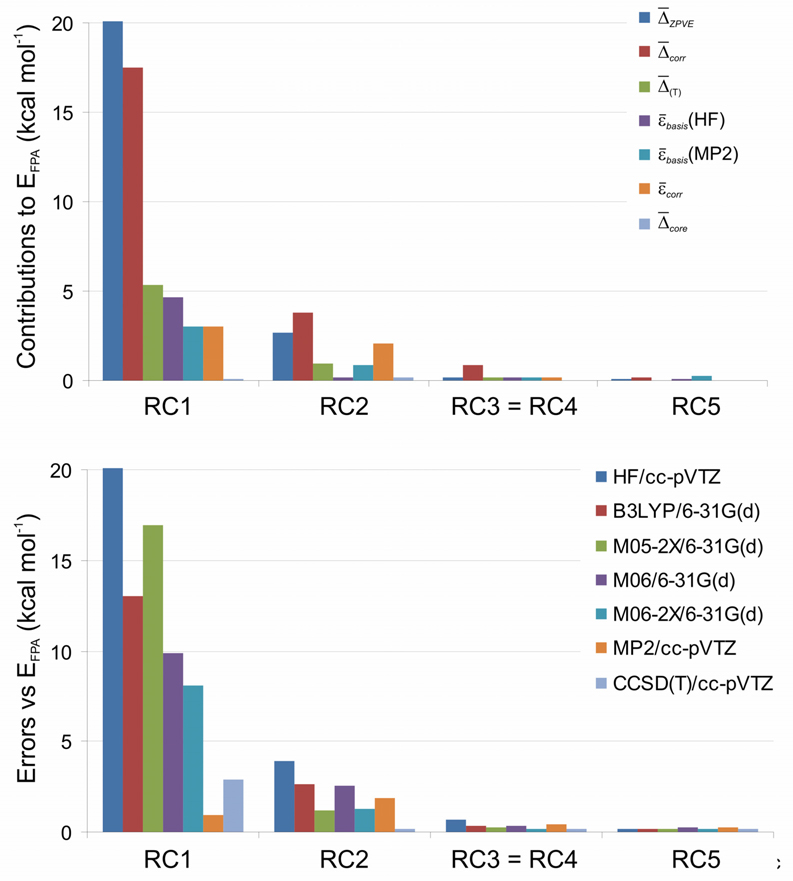
For each reaction type, we have computationally assessed the generalized bond separation reactions for the collection of 36 hydrocarbons shown in Chart 3. The collection is divided into two sets: (A) conjugated systems containing the diene, diyne, enyne, and cumulene functionalities exhibited in the hypohomodesmotic prototype reactions (17) – (23), and (B) nonconjugated compounds, for which there is no distinction between the homodesmotic (RC4) and hypohomodesmotic (RC3) classes. In Table 3, the enthalpy changes of the bond separation reactions of each type are dissected into the ε_basis, Δ_corr, ε_corr, Δ_(T), Δ_core, and Δ_ZPVE terms defined above. For brevity, the only quantities given are mean absolute values over the hydrocarbon sets; details for individual reactions are provided in SI. Table 4 lists mean absolute errors (relative to our FPA benchmarks) in the bond separation reaction energies predicted at commonly used levels of theory. For comparison, results are also given in both tables for atomization reactions (RC0), which could be considered the very bottom of the homodesmotic hierarchy. For visual emphasis, the data in Table 3 and Table 4 are plotted in Fig. 1 and Fig. 2.

Chart 3.

Acyclic hydrocarbons selected for investigation of bond separation reactions.

Table 3.

Energetic analysis (mean absolute quantities in kcal mol⁻¹) of bond separation reaction types for various hydrocarbon classes.^a

Reaction Classb	EFPAc	Δ̅ZPVE	Δ̅corr	Δ̅(T)	ε̅basic(HF)	ε̅basic(MP2)	ε̅corr	Δ̅core
Conjugated hydrocarbons (Set A)
RC0	1273.35	68.03	292.83	21.78	22.16	95.56	32.13	4.34
RC1	148.88	43.43	18.15	6.99	6.97	4.35	3.37	0.06
RC2	19.33	2.32	4.21	1.58	0.62	0.48	3.35	0.32
RC3	1.28	0.38	2.32	0.91	0.48	0.66	0.86	0.03
RC4	0.53	0.29	0.46	0.16	0.15	0.16	0.32	0.01
RC5	1.03	0.18	0.16	0.07	0.10	0.10	0.30	0.02
Non-conjugated hydrocarbons (Set B)
RC0	1423.33	84.72	319.89	20.09	22.28	102.12	26.22	4.28
RC1	114.96	33.82	17.49	5.33	4.66	3.01	2.98	0.06
RC2	16.11	2.71	3.77	0.96	0.14	0.87	2.03	0.20
RC3 = RC4	1.33	0.16	0.83	0.20	0.14	0.18	0.21	0.01
RC5	0.58	0.09	0.19	0.03	0.06	0.24	0.03	0.00
Cyclopentadiene and 1,3-cyclohexadiene (Set C)
RC0	1262.54	67.68	286.97	21.21	19.79	91.97	31.68	4.20
RC1	118.43	40.63	20.49	6.80	5.09	3.42	3.40	0.02
RC2	24.58	5.79	5.48	1.81	0.06	1.73	4.33	0.32
RC3	1.38	1.84	0.49	0.55	0.23	0.20	1.46	0.00
RC4	4.33	2.17	0.28	0.12	0.45	0.30	1.06	0.01
RC5	4.45	1.37	1.20	0.11	0.92	0.76	1.10	0.01

^aSymbols as defined in text; All energies evaluated at B3LYP/6-31G(d) optimized geometries. Details for each reaction are provided in Supporting Information.

^bAbbreviations: RC0 = atomization, RC1 = isogyric, RC2 = isodesmic, RC3 = hypohomodesmotic, RC4 = homodesmotic, RC5 = hyperhomodesmotic.

^cZPVE corrected energy. ZPVE from unscaled B3LYP/6-31G(d) harmonic vibrational frequencies.

Table 4.

Performance of commonly theoretical methods for the energetics (mean absolute errors in kcal mol⁻¹) of bond separation reactions.^a

Reaction Classb	HF/cc-pVTZ	B3LYP/6-31G(d)	M05-2X/6-31G(d)	M06/6-31G(d)	M06-2X/6-31G(d)	MP2/cc-pVTZ	CCSD(T)/cc-pVTZ
Conjugated hydrocarbons (Set A)
RC0	327.93	7.03	8.88	2.09	1.96	6.15	35.10
RC1	21.08	9.87	21.53	10.27	10.51	1.91	2.93
RC2	3.96	7.06	3.71	8.31	4.47	3.59	0.31
RC3	1.77	1.75	0.91	1.25	0.98	1.41	0.55
RC4	0.29	0.24	0.24	0.40	0.22	0.49	0.17
RC5	0.18	0.11	0.18	0.32	0.19	0.43	0.14
Non-conjugated hydrocarbons (Set B)
RC0	356.89	10.62	9.75	3.84	3.18	12.12	37.00
RC1	20.34	13.02	16.93	9.83	8.06	0.94	2.85
RC2	3.92	2.67	1.18	2.51	1.30	1.88	0.16
RC3 = RC4	0.67	0.38	0.21	0.34	0.18	0.40	0.19
RC5	0.14	0.14	0.18	0.28	0.21	0.22	0.19
Cyclopentadiene and 1,3-cyclohexadiene (Set C)
RC0	321.94	10.72	6.36	3.32	2.17	3.29	34.97
RC1	24.20	13.51	18.94	12.37	10.69	0.34	3.71
RC2	6.07	0.14	0.19	1.56	0.58	3.74	0.59
RC3	0.46	0.37	0.70	1.16	1.40	1.48	0.13
RC4	0.41	1.45	1.26	1.92	1.82	0.90	0.15
RC5	0.85	1.15	1.44	2.09	2.16	0.75	0.35

^aErrors relative to FPA benchmarks in Table 3. All energies were evaluated at B3LYP/6-31G(d) optimized geometries. Details for each reaction are provided in Supporting Information.

^bAbbreviations: RC0 = atomization, RC1 = isogyric, RC2 = isodesmic, RC3 = hypohomodesmotic, RC4 = homodesmotic, RC5 = hyperhomodesmotic.

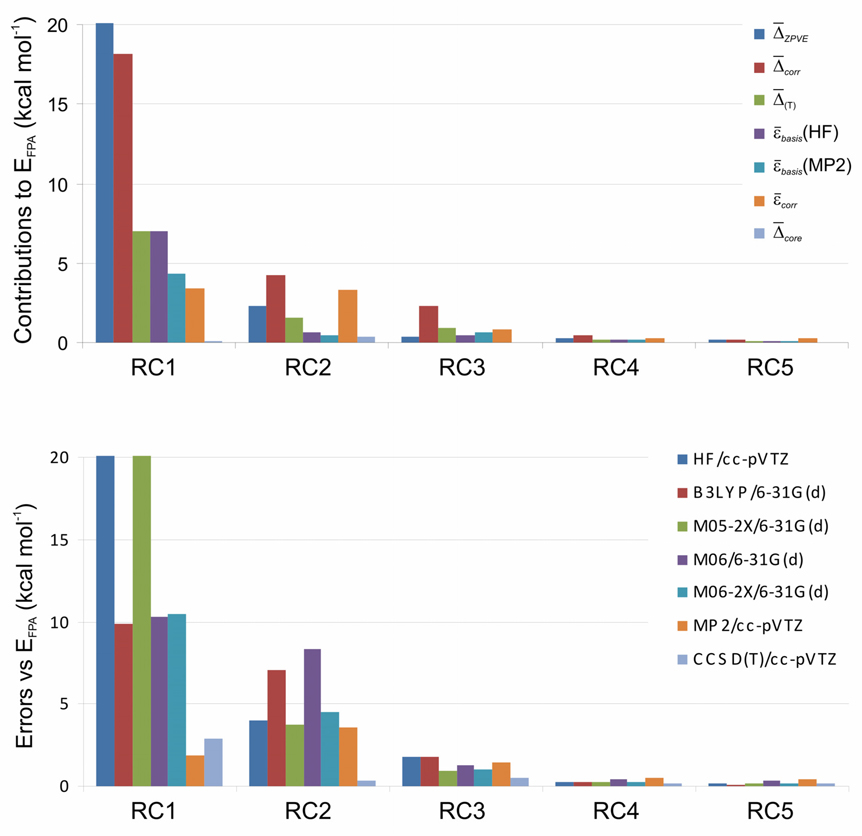
Figure 1.

Analysis of bond separation reaction energies for the conjugated systems (Set A) in Chart 3: upper panel, FPA energy decomposition; lower panel, performance of commonly used theoretical methods. Abbreviations: RC1 = isogyric, RC2 = isodesmic, RC3 = hypohomodesmotic, RC4 = homodesmotic, RC5 = hyperhomodesmotic.

Figure 2.

Analysis of bond separation reaction energies for the non-conjugated systems (Set B) in Chart 3: upper panel, FPA energy decomposition; lower panel, performance of commonly used theoretical methods. Abbreviations: RC1 = isogyric, RC2 = isodesmic, RC3 = hypohomodesmotic, RC4 = homodesmotic, RC5 = hyperhomodesmotic

The most prominent result is that the bond separation reaction energies (E_FPA) decrease dramatically and uniformly as the reaction hierarchy is traversed, and the various energetic components and errors at each level of theory largely follow this trend. For example, within Set B hyperhomodesmotic (RC5) balancing decreases the atomization (RC0), isogyric (RC1), and isodesmic (RC2) mean reaction energies by factors of 2500, 198, and 28, respectively, and the corresponding reductions in ε_basis(MP2) are almost as large. The bar diagrams in Fig. 1 and Fig. 2 vividly show how effective the homodesmotic hierarchy is in balancing electronic effects and canceling errors in computational thermochemistry. There are some cautionary exceptions to the general trends; notably, the homodesmotic mean E_FPA is a little smaller than the corresponding hyperhomodesmotic value within Set A, and the DFT methods perform better for atomization than isogyric reactions.

Another key conclusion is that the distinction among the isodesmic (RC2), hypohomodesmotic (RC3), and homodesmotic (RC4) reaction classes has considerable energetic consequences for conjugated hydrocarbons (Set A). The top panel of Fig. 1 reveals that basis set incompleteness errors and electron correlation are substantial components for RC2 and RC3 reactions but only a few tenths of a kcal mol⁻¹ for RC4 bond separations. The large isodesmic ε_corr = 3.35 kcal mol⁻¹ in Set A casts doubt on common assumptions¹¹³ that these reactions sufficiently balance errors in computed reaction energies. In contrast, RC5 reactions offer a nearly complete cancellation of errors, as highlighted by ε_basis(HF) = 0.10, ε_basis(MP2) = 0.10, Δ_corr = 0.16, and Δ_(T) = 0.07 kcal mol⁻¹ for Set A.

The lower panels of Figs. 4 and 5 demonstrate that for Sets A and B drastically different levels of theory give essentially indistinguishable results at or beyond the homodesmotic rung of the hierarchy. Accordingly, the small-basis density functional method B3LYP/6-31G(d) delivers homodesmotic reaction energies with mean absolute errors of only 0.24 and 0.38 kcal mol⁻¹, respectively, for Sets A and B; in addition, the new meta-GGA functionals considered here (M05-2X, M06, M06-2X) perform about as well as B3LYP in this assessment. The most promising result is that the use of hyperhomodesmotic (RC5) bond separation reactions allows 0.2 ± 0.1 kcal mol⁻¹ mean thermochemical accuracy to be achieved with all density functionals tested here, for both conjugated and non-conjugated hydrocarbons. In stark contrast, for the isodesmic, isogyric, and atomization reactions, the B3LYP/6-31G(d) mean errors are all above 7 kcal mol⁻¹. The new meta-GGAs generally outperform B3LYP for these less refined reaction classes. However, some notable failures are observed – for example, in Set A the mean absolute errors in the M05-2X isogyric and M06 isodesmic cases exceed 21 and 8 kcal mol⁻¹, respectively.

An ancillary benefit of our hierarchy is that the zero-point vibrational contribution (Δ_ZPVE) drops precipitously in going from RC0 to RC5 reactions, due to successively better vibrational mode balancing. While Δ_ZPVE for the atomization processes rivals the energy of a strong chemical bond, this effect is less than 0.2 kcal mol⁻¹ for the hyperhomodesmotic reactions of both Sets A and B. For RC3 through RC5, Δ_ZPVE is small enough to warrant its evaluation from vibrational frequencies at a modest level of theory without inclusion of any anharmonicity effects.

In a similar manner, the effects of core electron correlation are eliminated by homodesmotic thermochemical routes. As shown in Table 3, for atomization reactions the inclusion of some correction for core correlation is mandatory to achieve even modest accuracy. Once the RC5 class is reached in the hierarchy, Δ_core is less than 0.1 kcal mol⁻¹.

Finally, to examine the influence of ring strain on error cancellation, we consider the bond separation reactions of cyclopentadiene and cyclohexa-1,3-diene (Set C). Data averaged over the two reactions are provided in Table 3 and Table 4; details for the individual reactions are given in SI For our cyclic test compounds, the various contributions (Table 3) to the reaction energy once again exhibit excellent successive reductions in going from RC0 to RC3 reactions. In the RC3 case, Δ̅_corr, Δ̅_(T), ε̅_basic(HF), and ε̅_basic(MP2) are significantly smaller for the rings of Set C than for the conjugated chains of Set A, although Δ̅_ZPVE and ε̅_corr are larger for Set C. However, unlike both acyclic Sets A and B, the RC4 and RC5 reactions for Set C fail to deliver further reductions in the terms comprising the reaction energy decompositions and in some cases provide poorer balancing than the RC3 transformations. Most notably, Δ̅_corr, ε̅_basic(HF), and ε̅_basic(MP2) for Set C remain in the 0.7–1.2 kcal mol⁻¹ range even at the RC5 tier. Likewise, in Table 4 the RC4 and RC5 reaction energy errors for the density functional methods lie between 1.2 and 2.2 kcal mol⁻¹ for Set C, showing diminished performance relative to the corresponding levels of the homodesmotic hierarchy for Sets A and B, as well as the RC3 results of Set C.

In brief, the energetic effects and electronic structure errors in the bond separation reactions of cyclopentadiene and cyclohexa-1,3-diene are not generally balanced beyond about 1 kcal mol⁻¹ in the last two tiers (RC4 and RC5) of the homodesmotic hierarchy, presumably as a consequence of ring strain. The difference between the RC3 and RC4 reactions for these systems is the preservation of the 1,3-diene unit in the latter reaction type. The diminished balancing in the RC4 and RC5 reactions in Set C thus appears to arise from dissimilarities between the strained cis-1,3-diene moiety in the cyclic systems and the unstrained trans-1,3-butadiene elemental product. These effects are similar to the features underlying the “quasihomodesmotic reactions” of Barić and Maksić,⁷² in which ring and cage strain causes deviations from ideal hybridization. The addition of strained reference species to the list of elemental products may be a simple means of extending the exceptional balance observed here for acyclic compounds also to rings and cages. Regardless, RC3, RC4, and RC5 reactions provide far greater error cancellation than RC1 and RC2 reactions even for the strained molecules tested here, and reliable reaction enthalpies can be obtained for these hydrocarbons even with modest levels of theory.

VIII. Application to Polyynes

Polyynes (C_2nH₂) are ubiquitous in modern chemistry.¹¹⁴ They are potential carriers of the diffuse interstellar bands,^115,116 as well as models of carbyne,¹¹⁷ the long-sought sp-hybridized carbon allotrope.^{114,118–120} Polyynes exhibit unique electronic and nonlinear optical properties, and are used extensively in the development of nanodevices.^121,122 Naturally occurring derivatives of polyynes (e.g., caryoynencins) have even demonstrated potent antimicrobial activity.^123,124 Polyynes have been detected in meteorites,¹²⁵ in the atmospheres of Titan^126–128 and Saturn,¹²⁹ are key intermediates in combustion and soot formation,^130–133 and are possible synthetic precursors to fullerenes.^134,135

Despite the prevalence of these species, there is a dearth of reliable thermochemical data, with published enthalpies of formation of modestly sized polyynes (C_2nH₂, n ≤ 10) spanning over 50 kcal mol⁻¹ for some species.^136–140 Experimental determinations are plagued by the kinetic instabilities of polyynes under laboratory conditions. The computational determination of accurate enthalpies of formation of polyynes, which are too large for the application of the most rigorous ab initio methods, is hampered by systematic errors in DFT energies for acetylenic systems.³⁹ In our investigations, the polyacetylenic systems in Set A of Chart 3 consistently yielded the largest errors at all levels of the homodesmotic hierarchy (see SI Tables S1, S2, S4, S6, S8, and S9), and thus they pose a particular challenge to computational thermochemistry. Simmonett, Schaefer, and Allen⁷⁶ recently reported a high-accuracy enthalpy of formation for the simplest polyyne, diacetylene. This reference enthalpy of formation, combined with Δ_fH^∘ (acetylene) from the Active Thermochemical Tables (ATcT),^141–144 enables the determination of accurate enthalpies of larger polyynes through homodesmotic bond separation reactions.

For a general polyyne the homodesmotic (RC4) bond separation equation is

(24)

As an application of the thermochemical procedures advocated in this paper, we have computed benchmark enthalpies of formation for n = 1 and 2 (1,3,5-hexatriyne and 1,3,5,7-octatetrayne, respectively) within the focal point approach,^{74,75,79–82} including extrapolation of CCSD(T) correlation energies and higher-order CCSDT(Q) computations.^145,146 These two species then serve as reference compounds for the determination of accurate enthalpies of formation for larger polyynes via DFT methods. Single-point energies were computed at geometries optimized with CCSD(T)¹⁴⁷ paired with the TZ(2d1f,2p1d) basis set.^75,148 A correction for core-correlation effects was determined as the difference between all-electron and frozen-core CCSD(T)/cc-pCVTZ energies.⁹³ Harmonic ZPVE corrections were derived from CCSD(T)/ANO4321 vibrational frequencies.^149,150

Valence focal point analyses for homodesmotic equation (24) (n = 1 and 2) are laid out in Table 5. Analogous tables are included in SI (see Table S27) for the corresponding isodesmic (RC2) bond separations:

(25)

In accord with our observations in Section VII, the homodesmotic bond separation reaction energies converge more rapidly with respect to one-particle basis set completeness and inclusion of electron correlation than their isodesmic counterparts. By combining the extrapolated valence energies for homodesmotic reaction (24) with corrections for core-correlation effects and harmonic ZPVEs, we arrive at 0 K reaction enthalpies of 1.42 kcal mol⁻¹ and 3.30 kcal mol⁻¹ for hexatriyne and octatetrayne, respectively. To account for higher-order correlation effects, CCSDT(Q)/cc-pVDZ reaction energies were computed. In each case, the CCSDT(Q)/cc-pVDZ correction was less than 0.1 kcal mol⁻¹, indicating that the CCSD(T) results are well-converged towards the full CI limit.

Table 5.

Incremental valence focal point table (kcal mol⁻¹) for the homodesmotic (RC4) bond separation reactions of 1,3,5-hexatriyne and 1,3,5,7-octatetrayne.^a,^b

Basis Set	ΔEe[RHF]	+δ[MP2]	+δ[CCSD]	+δ[CCSD(T)]	ΔEe[CCSD(T)]
cc-pVDZ	0.57	+1.67	−1.35	+0.43	[+1.32]
cc-pVTZ	0.39	+2.08	−1.42	+0.45	[+1.50]
cc-pVQZ	0.33	+1.9	−1.42	+0.44	[+1.26]
cc-pV5Z	0.35	+1.86	[−1.44]	[+0.44]	[+1.19]
CBS Limit	[+0.37]	[+1.83]	[−1.47]	[+0.44]	[+1.16]
ΔEFPA = ΔEe[CCSD(T)] + δ[CCSDT(Q)/cc-pVDZ] + ΔE(core) + ΔE(ZPVE)
= 1.16 + 0.03 + 0.02 + 0.21 = 1.42 kcal mol−1
${\mathrm{\Delta }}_f{H}_0^{\circ }$ (C6H2=162.7 ± 0.4 kcal mol−1; ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C6H2=163.7 ± 0.4 kcal mol−1
cc-pVDZ	1.12	+4.17	−3.31	+1.05	[+3.03]
cc-pVTZ	0.74	+4.88	−3.43	+1.09	[+3.29]
cc-pVQZ	0.65	+4.60	−3.43	+1.08	[+2.90]
cc-pV5Z	0.68 +4.53	[−3.46]	[+1.07]	[+2.83]
CBS Limit	[+0.71]	[+4.46]	[−3.50]	[+1.07]	[+2.74]
ΔEFPA = ΔEe[CCSD(T)] + δ[CCSDT(Q)/cc-pVDZ] + ΔE(core) + ΔE(ZPVE)
= 2.74 + 0.06 + 0.04 + 0.46 = 3.30 kcal mol−1
${\mathrm{\Delta }}_f{H}_0^{\circ }$ (C8H2=215.6 ± 0.6 kcal mol−1; ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C6H2=217.6 ± 0.6 kcal mol−1
Fit	a+be−cx	a+bX−3	a+bX−3	a+bX−3
Points (X=)	3,4,5	4,5	3,4	3,4

^aThe symbol δ denotes the increment in the energy difference (ΔE_e) with respect to the previous level of theory. Bracketed numbers are the result of basis set extrapolations (using the fits denoted in the table), while unbracketed numbers were explicitly computed. All energies evaluated at frozen-core CCSD(T)/TZ(2d1f,2p1d) optimized geometries.

^bReference enthalpies of formation (kcal mol⁻¹) were as follows: ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (acetylene) = 54.69 ± 0.07 (ref ¹⁶); ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (acetylene) = 54.52 ± 0.07 (refs ¹⁶ and ¹⁶⁵); ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (diacetylene) = 109.4 ± 0.3 (ref ⁷⁶); ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (diacetylene) = 109.7 ± 0.3 (ref ⁷⁶)

Combining the FPA bond separation enthalpies with ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (acetylene) = 54.69 ± 0.07 kcal mol⁻¹ (ref ¹⁶) and ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (diacetylene) = 109.4 ± 0.3 kcal mol⁻¹ (ref ⁷⁶), we arrive at ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (C₆H₂) = 162.7 ± 0.4 kcal mol⁻¹ and ${\mathrm{\Delta }}_f{H}_0^{\circ }$ (C₈H₂) = 215.6 ± 0.6 kcal mol⁻¹. The quoted uncertainties in these numbers represent 95% confidence intervals. With thermal corrections from standard rigid-rotor/harmonic-oscillator expressions, we obtain ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C₆H₂) = 163.7 ± 0.4 kcal mol⁻¹ and ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C₈H₂) = 217.6 ± 0.6 kcal mol⁻¹. Despite the slower convergence of the isodesmic bond separation reaction energies, the corresponding FPA enthalpies of formation are similar (see SI Table S27), albeit with considerably higher uncertainties.

Sorkhabi and co-workers¹³⁷ presented 0 K enthalpies of formation for 1,3,5-hexatriyne based on B3LYP/6-311+G(d,p) and the G2 model chemistry applied to an isogyric reaction involving H₂ and acetylene. The G2 datum (161 kcal mol⁻¹) is significantly lower than the present 0 K value of 162.7 kcal mol⁻¹, while B3LYP overshoots by about 7 kcal mol⁻¹. That same work¹³⁷ contained an experimentally-derived upper limit on the enthalpy of formation of hexatriyne of 160 ± 4 kcal mol⁻¹, which is consistent with our recommended value. Rogers and co-workers¹⁴⁰ utilized G3(MP2) theory paired with atomization energies to derive 298 K enthalpies of formation for 1,3,5-hexatriyne and 1,3,5,7-octatetrayne of 163.4 and 217.5 kcal mol⁻¹, respectively, which are in good agreement with our results. Rodriguez et al.¹³⁸ presented atomization-energy-derived enthalpies of formation for C_2nH₂ up to n = 40. The G3 model chemistry was employed for C₄H₂ through C₁₀H₂, B3LYP/6-31G(d) for C₄H₂ through C₁₂H₂, and PM3 for the remaining polyynes. For C₆H₂ and C₈H₂, the G3-predicted 298 K enthalpies of formation (164.8 and 219.1 kcal mol⁻¹, respectively) are 1 kcal mol⁻¹ higher than the present benchmark results. Apparently, in this context the more economical G3(MP2) approach outperforms the original G3 method. The B3LYP/6-31G(d) enthalpies of formation exceed the present homodesmotic results by over 10 kcal mol⁻¹, while PM3 underestimates our recommended values by a similar amount. Zahradník and Šroubková¹³⁹ published 298 K values of 164.9 and 216.9 kcal mol⁻¹ for hexatriyne and octatetrayne, respectively, computed at the B3LYP/cc-pVTZ level of theory. The B3P86 functional paired with the cc-pVTZ basis set predicted an enthalpy of formation for hexatriyne more than 30 kcal mol⁻¹ below the presently recommended value.

Enthalpies of formation per carbon atom for hexatriyne and octatetrayne derived from B3LYP, M05-2X, M06-2X, and M06 computations are listed in Table 6, all evaluated at B3LYP/6-31G(d) optimized geometries. For all four DFT functionals, homodesmotic bond separation reactions yield enthalpies of formation in good agreement with the reference focal point values, with errors of at most 1.5 kcal mol⁻¹ (B3LYP for octatetrayne), in contrast to atomization routes.¹³⁸ The meta-GGA functional M06 performs best giving ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C₆H₂) = 6(27.29) = 163.7 kcal mol⁻¹ and ${\mathrm{\Delta }}_f{H}_{298}^{\circ }$ (C₈H₂) = 8(27.21) = 217.7 kcal mol⁻¹, which reproduces the focal point benchmark enthalpies of formation within 0.1 kcal mol⁻¹.

Table 6.

Enthalpies of formation [$\frac{1}{2n+4}{\mathrm{\Delta }}_f{H}_{298}^{\circ }$ in kcal/(mol carbon atoms)] for C₆H₂ through C₂₄H₂, predicted using various DFT functionals. Rigorous focal point results (FPA) are included for comparison.^a

C2n+4H2	B3LYP	M05-2X	M06-2X	M06	FPA	$\frac{1}{2}{[{\mathrm{\Delta }}_f{H}_{298}^{\circ }({\mathrm{C}}_{\mathrm{m}+2}{\mathrm{H}}_2)-{\mathrm{\Delta }}_f{H}_{298}^{\circ }({\mathrm{C}}_{\mathrm{m}}{\mathrm{H}}_2)]}^2$ b
C6H2	27.21	27.34	27.34	27.29	27.28
C8H2	27.04	27.30	27.30	27.21	27.20
C10H2	26.82	26.84	26.84	26.82		26.16
C12H2	26.72	26.74	26.75	26.71		26.19
C14H2	26.63	26.68	26.69	26.64		26.06
C16H2	26.56	26.62	26.63	26.57		26.11
C18H2	26.49	26.59	26.60	26.52		26.01
C20H2	26.44	26.54	26.56	26.47		26.07
C22H2	26.40	26.52	26.53	26.43		25.99
C24H2	26.36	26.48	26.50	26.39		26.06
C26H2	26.33	26.47	26.48	26.37

^aValues for C₆H₂ and C₈H₂ were derived from eq (24), while eq (26) was used for the larger polyynes. All DFT energies were evaluated at B3LYP/6-31G(d) geometries using the 6-31G(d) basis set.

^bBased on M06/6-31G(d) results. Asymptotic limit: 25.97 ± 0.05 kcal/(mol carbon atoms). See SI Figure S1 and S2.

Computed enthalpies of formation per carbon atom for larger polyynes (C₁₀H₂ – C₂₆H₂), are also provided in Table 6. From the valence focal point tables for C₆H₂ and C₈H₂ (Table 5), it is clear that the increments for each level of theory are systematic, with each δ value for C₈H₂ equaling roughly twice the corresponding value for C₆H₂. Thus, enthalpies were computed using our new reference values for C₆H₂ and C₈H₂ via highly balanced eq (26), designed to cancel the remaining systematic errors revealed by the focal point analysis. Eq (26) is an 8-homodesmotic reaction in the parlance of Section III.

(26)

This scheme leads to a very consistent set of predicted enthalpies of formation from all four DFT functionals; the enthalpies of formation for C₂₆H₂ span just over 0.1 kcal/(mol per carbon atoms). Based on the agreement with the FPA results for C₆H₂ and C₈H₂, the final recommended enthalpies of formation for C₁₀H₂ through C₂₄H₂ are from M06/6-31+G(d). Utilization of an equation similar to (26) but employing only C₄H₂ and C₆H₂ yielded less consistent results.

The enthalpy of formation of the gaseous carbyne allotrope can be gleaned from the thermodynamic data for the polyynes listed in Table 6 by extrapolating to the limit of an infinite acetylenic chain. The enthalpic cost of removing an acetylenic unit from a given polyyne can be accurately evaluated using DFT by means of the balanced reaction

(27)

This is simply the difference between eq (26) for C_2n+4H₂ and C_2n+2H₂. Differences between successive enthalpies of formation are given in Table 6, based on the M06/6-31G(d) data. Simple bond additivity arguments suggest the following asymptotic forms for large numbers of carbons (m):

$${\mathrm{\Delta }}_f{H}^{\circ }({\mathrm{C}}_{m+2}{\mathrm{H}}_2)-{\mathrm{\Delta }}_f{H}^{\circ }({\mathrm{C}}_m{\mathrm{H}}_2)=2{\mathrm{\Delta }}_f{H}^{\circ }(\text{carbyne})+\frac{B}{m^2}+\frac{C}{m^3}+\dots$$ (28)

and

$$\frac{{\mathrm{\Delta }}_f{H}^{\circ }({\mathrm{C}}_m{\mathrm{H}}_2)}{m}={\mathrm{\Delta }}_f{H}^{\circ }(\text{carbyne})+\frac{B\prime }{m}+\frac{C\prime }{m^2}+\dots$$ (29)

where Δ^fH^∘ (carbyne) is the target enthalpy per carbon atom of an infinite acetylenic carbon chain, and B, C, B′, and C′ are adjustable parameters. The M06/6-31G(d) data in Table 6 yield Δ^fH^∘ (carbyne) = 25.97 ± 0.05 kcal/(mol carbon atoms) regardless of whether eq (28) is fit for m = 2n+2 with odd and even values of n separately (SI Figure S1) or eq (29) is fit for all even m (SI Figure S2). Including possible uncertainties in the reference enthalpies for C₆H₂ and C₈H₂, we arrive at a final prediction of Δ^fH^∘ (carbyne) = 26.0 ± 0.2 kcal/(mol carbon atoms). Baughman, Eckhardt, and Kertesz¹⁵¹ arrived at an enthalpy of formation for carbyne of 25.4 kcal/(mol carbon atoms) based on the difference in enthalpies of formation of 2-butyne and 2,3-hexadiyne. Cataldo¹⁵² derived a much lower value of 23.3 kcal/(mol carbon atoms) based on a group increment scheme.¹⁵³ Most recently, Rodriguez et al.¹³⁸ computed quite different values of [24.3, 24.9, and 23.6 kcal/(mol carbon atoms)] based on [G3 theory, B3LYP/6-31G(d), and PM3] combined with the finite cluster method of Cioslowski.¹⁵⁴

IX. Summary and Prospectus

In this paper we have advanced a consistent hierarchy of hydrocarbon reaction classes (RC1 – RC5) as a rigorous sequence of subsets satisfying an ever more stringent balance of chemical bonding environments: isogyric (RC1) ⊇ isodesmic (RC2) ⊇ hypohomodesmotic (RC3) ⊇ homodesmotic (RC4) ⊇ hyperhomodesmotic (RC5). The need for such a canonical hierarchy is demonstrated by the nonequivalence of the two definitions of homodesmotic reactions prevailing in the literature, as well as widespread confusion over hydrocarbon reaction classes. We have also extended the concept of isodesmic bond separation reactions throughout the homodesmotic hierarchy. Within each class, a generalized bond separation reaction provides a unique sectioning of a target hydrocarbon into well-defined elemental products via reactions with elemental reactants. The set of elemental products for each reaction class is composed of those hydrocarbons that cannot be broken down further while maintaining the balance of bonding environments required by the the class definition. We specify the complete sets of elemental products and reactants for each class in Chart 1 and Chart 2. The generalized bond separation reactions can be conveniently categorized as n-homodesmotic ( n = 1, 2, 3, and 4) transformations, where n is the length of the main chain of the elemental products, and this principle can be used to systematically extend the hierarchy past the hyperhomodesmotic tier if necessary.

Our extensive computations, including high-level focal-point benchmarks, on the bond separation reactions of a large set of C₅- and C₆-hydrocarbons (Chart 3) demonstrate the effectiveness of the homodesmotic hierarchy in balancing energetic effects and canceling electronic structure errors. Figure 1 and Figure 2 provide a vivid, visual synopsis of our computational results. For reactions of unstrained carbon chains, hyperhomodesmotic (RC5) balancing reduces the basis set and electron correlation errors of simple Hartree-Fock/double-ζ-plus-polarization computations to mere tenths of a kcal mol⁻¹ and also cancels zero-point vibrational effects to a similar extent. Similarly, the RC5 construction allows the B3LYP, M05-2X, M06, and M06-2X density functionals employed with the modest 6-31G(d) basis set to predict bond separation reaction energies of acyclic hydrocarbons to 0.1–0.3 kcal mol⁻¹. Homodesmotic reactions (RC4) perform almost as well for hydrocarbon chains as their more complicated RC5 counterparts, and both of these balancing schemes are clearly superior to RC1, RC2, and RC3 reactions. Therefore, homodesmotic transformations may be preferred for practical thermochemical computations, given the small number and size of the elemental reactants and products for this reaction class.

Recent investigations of failures of density functional methods for larger hydrocarbons^{112,113,155–157} show that seemingly small errors can rapidly become significant with increasing system size. The proper use of error-canceling reactions in the prediction of thermochemical quantities will minimize the accumulation of such errors. Moreover, when striving for high accuracy, maximizing error cancellation is vital in systems with more than four heavy atoms, for which very high accuracy methods are currently not feasible.^15–18,20 Even for the most rigorous theoretical methods,^15–18,20 systematic errors arise in the computation of atomization energies due to grossly unbalanced interactions in reactants and products. These atomization energy errors, even if small for systems with two and three heavy atoms, will grow unacceptably large as one considers more chemically relevant systems. In contrast to atomization approaches, generalized bond separation reactions constitute a well-defined and highly effective scheme for computing accurate enthalpies of formation for large hydrocarbons, provided that accurate reference enthalpies are known for the elementary reactants and products. Pinpointing ${\mathrm{\Delta }}_f{H}_T^{\circ }$ values for all species in Chart 1 and Chart 2 thus gains renewed importance and provides key targets for new ab initio studies at the highest levels. While the paucity of reliable experimental thermochemical data for these elemental compounds is severe, electronic structure theory has matured to a point that accurately computing the necessary enthalpies of formation is feasible.

As an application of the recommended procedures, accurate enthalpies of formation for a series of polyynes have been predicted. Benchmark values of 163.7 ± 0.4 and 217.6 ± 0.6 kcal mol⁻¹ were first derived for C₆H₂ and C₈H₂ by application of the focal point approach to homodesmotic bond separation reactions. These new reference species were then utilized to derive enthalpies of formation for C₁₀H₂ through C₂₆H₂ using M06/6-31G(d). Finally, a new enthalpy of formation for gaseous carbyne of 26.0 ± 0.2 kcal/(mol carbon atoms) was derived based on the convergence of the enthalpic cost of extending these polyyne chains by a single acetylenic unit.

The homodesmotic hierarchy set forth here directly applies only to closed-shell hydrocarbons and thus does not provide a universal thermochemical scheme. However, extensions of our refined definitions to more diverse systems can be readily envisioned. For hydrocarbon radicals, Suresh and Koga⁵⁹ have given examples of putative homodesmotic reactions, without providing explicit criteria for the reaction type. From our perspective, a viable general procedure for hydrocarbon radicals would first construct the (hyper)homodesmotic bond separation reaction for the parent compound that arises by quenching the radical site(s) with hydrogen atoms. Hydrogen atoms would subsequently be removed from both sides of the balanced equation, to regenerate the target radical as a reactant and to create the most structurally similar radical(s) from the elemental products. The enthalpy of formation of the hydrocarbon radical could then be computed using only modest levels of theory, if accurate C-H bond dissociation energies [D₀(C-H)] were known for the reference species in Chart 1 and Chart 2. Establishing the necessary database of D₀(C-H) values is an arduous task but is certainly within reach of state-of-the-art ab initio methods.

For cyclic hydrocarbons, our preliminary work indicates that ring strain diminishes the error cancellation afforded by homodesmotic (RC4) and hyperhomodesmotic (RC5) reactions. In practice, ring strain problems in thermochemical computations may be evidenced by a lack of convergence of reaction enthalpies either across the homodesmotic hierarchy for a fixed level of theory or across levels of theory for a given reaction class. The addition of selectively strained reference structures to the set of elemental reactants and products may rectify such problems. For example, in the bond separation reactions of cyclopentadiene and cyclohexa-1,3-diene, the trans-1,3-butadiene elemental product could be replaced by a cis-1,3-butadiene fragment in which the backbone bond angles are constrained to mimic the environment of the five- and sixmembered rings of the reactants. In this case the energy difference between the cis- and trans-1,3-butadiene structures would be computed at higher levels of theory than employed for the bond separation reactions. A general study on how to best modify the homodesmotic hierarchy to balance ring and cage strain is clearly warranted.

Finally, it should be emphasized that the principles discussed here are not restricted to hydrocarbons and may be generally applied to compounds in which the formal bond types and hybridizations of the constituent atoms are unambiguous. For example, a consistent homodesmotic hierarchy and computational thermochemistry scheme might be constructed for organic systems that contain N, O, P, and S atoms. Numerous papers have already applied homodesmotic concepts to non-hydrocarbons, as illustrated in representative studies.^{31,52–54,158–164} However, the development of a systematic hierarchy of reaction classes and elemental products for general systems is still needed. The primary challenge for such extensions is the growth in the number of formal bond types and fragments involved in the definitions of the reaction classes, as well as the sets of elemental reactants and products for which accurate enthalpies of formation are required.

Supplementary Material

SI. Supporting Information Available.

Complete citations for refs ^{106, 107}, and ¹¹⁰; reaction energies for each species for each reaction type; comparison of FPA, G3, and CBS-QB3 results; absolute energies; and optimized Cartesian coordinates.