Abstract
Sympathetic nervous flow to the vasculature plays a critical role in control of regional blood flow; however, traditional processing methods of multifiber recordings cannot reliably discriminate physiologically irrelevant information from actual nerve activity, and alternative wavelet methods suffer from subjectivity and lack of a well-specified model. We propose an algorithm that allows objective threshold selection under general assumptions regarding the sparsity and statistical structure of the neural signal and noise. Our study shows that the conditional expectation of the actual nerve signal can be estimated and used to maximize the signal-to-noise ratio (SNR). We evaluated the algorithm’s performance on artificial datasets and on actual multifiber recordings (44 datasets from 22 subjects, and 1 set from a rat). On artificial datasets, the algorithm identified 70% and 80% of the spikes at −3.5 and 0.5 dB SNR with a good match between the actual and estimated spike count (R2 = 0.719, p < 0.001). On actual recordings, the overall improvement in performance compared to that of a traditional processing method was significant (t = 3.88; p = 0.0002). Our results show the applicability of this algorithm to multifiber recordings not only in humans, but also in other species.
Keywords: Index Terms, Denoising, human, mixture modeling, spike detection, sympathetic nerve activity
I. Introduction
Sympathetic nervous outflow to the vasculature is critical to control of regional blood flow, and hence, systemic vascular resistance [1]. Dysregulation of sympathetic control has been implicated in pathological conditions, such as hypertension [2], [3], sleep apnea [3], heart failure [4]–[6], and the metabolic syndrome [7]. Therefore, quantification of sympathetic activity is an important focus of cardiovascular research.
Typically, at least in humans, it is only possible to observe multifiber sympathetic activity that is corrupted by various artifacts and embedded in high levels of background noise. Traditional processing of human sympathetic nerve recordings involves three stages: bandpass filtering, full-wave rectification, and integration with a slow time constant (~100 ms) [8]. These stages were originally meant to minimize the effect of artifacts and broadband background noise by averaging them out, and to provide a simple binary measure to indicate nerve firing during a given cardiac cycle [9]. However, bandpass filtering removes the low-frequency content of the signal that may be physiologically relevant [10], [11], rectification may yield artificial amplification of the filtered recording [12], and integration averages sympathetic activity over time, effectively diluting the information contained in the nerve signal. Thus, bandpass filtering and rectification may yield inaccuracies due to signal distortion [9], [13] and simple integration implicitly assigns greater importance to larger amplitude firings more proximal to the electrode. As a result, sparse large-amplitude firings can create the same integrated activity as frequent small-amplitude firings. This may be a serious limitation; relative distance from the electrode has no significance to the physiologic meaning of a nerve firing whereas the relative rate of firing is critically important to the underlying neurophysiology.
In the past, quantification of sympathetic activity from the integrated neurogram has relied upon manual identification of firing bursts. This manual identification of putative sympathetic bursts requires expert skill and tedious effort. Several automated techniques have been explored to lessen the time and effort required for analysis, to minimize the effect of background noise, and to provide a more objective approach. For example, Birkett et al. [14] proposed signal averaging that thresholded the integrated neurogram and coupled it to R-waves of the electrocardiogram; Celka et al. [15] suggested a gamma-distribution model for burst identification; and, Hamner and Taylor [16] derived a method based on morphological characteristics of the integrated neurogram. Although sympathetic bursts identified via these methods may correspond to those identified by a trained observer, none of these methods overcome the limitations inherent in the filtered, rectified, and integrated neurogram.
To avoid problems associated with integration, wavelet-decomposition methods have recently become popular to denoise recorded sympathetic activity and improve quantification [17]–[19]. However, the main drawback of wavelet decomposition methods is that they typically deploy a multiscale analysis based on a particular “mother wavelet” (i.e., the wavelet basis). This may have mathematical utility, but the wavelet is selected a priori, typically via visual judgment, and is not objectively derived from an actual action potential waveform. As a consequence, any signal derived from wavelet analysis is likely to be distorted. Indeed, Zhang et al. [20] reported considerable reduction in spike detection for an artificial signal when a wavelet basis slightly different from the original is used, despite a favorably high signal-to-noise ratio (SNR) (15 dB). In addition, wavelet decomposition methods lack a well-specified theory to select the various wavelet thresholds. This results in the common (mis)use of the so-called “universal threshold,” first proposed by Donoho and Johnstone [21]. The universal threshold is defined as and depends explicitly on the sample size n. Thus, a large sample size gives a very conservative threshold for noise suppression and commonly leads to under-fitting [22]. Therefore, many researchers have proposed more objective methods to obtain a threshold, including minimization of the false discovery rate [23], Bayesian methods [24], [25], and kurtosis of the wavelet coefficients [26].
Although thresholding is a natural approach to discriminate a signal from background noise, the appropriate threshold must be selected to maximize correct detection and minimize false detection and produce an unbiased estimate of the true signal density. The primary aim of this paper was to derive a generic, fully automated technique for restoring raw, multifiber nerve signals that are buried in high levels of noise and other artifacts. We propose an algorithm for threshold selection via general assumptions for the sparsity and statistical structure of the signal and the background noise. We show the following. 1) The conditional expectation that data points correspond to the actual nerve signal can be estimated from the observed recording. 2) The estimated conditional expectation is optimal in the least-squares sense. 3) This information can be used to attenuate background noise, approximately maximizing SNR. The proposed algorithm minimizes signal degradation and is sensitive to different firing modes of multifiber signals. Thus, it avoids problems associated with simple filtering and integration. Furthermore, it is objective and data-driven, avoiding problems associated with current wavelet-based algorithms. A detailed specification of the general problem to which our algorithm applies is described in Section II.
Our algorithm moves forward in independent, explicit steps that are ordered to take advantage of the different statistical properties of artifacts, background noise, and the actual nerve signal in the recorded raw signal. We first remove line noise and movement artifacts from the recording (Section III). We then take advantage of the characteristic cardiac rhytmicity of sympathetic firing to identify action potential candidates and establish a mean action potential template (Section IV-A). This step also facilitates identification of noise spikes. The action potential template in conjunction with the statistical properties of background noise and nerve activity is then used to identify actual spikes and background noise (Section IV). This leaves a clean representation of nerve activity in the form of a spike train. We summarize the performance of the algorithm on artificial datasets, and compare its performance with that of popular wavelet restoration methods in Section V. We also present results with actual sympathetic nerve recordings, and compare the performance of the algorithm to that of a commonly used alternative in Section VI. We provide conclusion remarks in Section VII.
II. Problem Specification and Notation
The algorithm does not identify different action potential waveforms and does not pertain to spike sorting in general. Rather, it attempts to restore the spike train embedded in high levels of noise. However, individual action potentials (with minimal noise) could be obtained from the restored spike train and classified via various approaches (e.g., principal components analysis). We cast the algorithm as a restoration method for human muscle sympathetic recordings. While the complexity of our multistep algorithm precludes definition of an explicit objective function, choice of our parameters is guided by two separate constraints. First, we attempt to minimize the sum of misclassification rates of signal and noise. This minimization effectively penalizes the misclassification error on the relatively sparse neural activity. Second, the parameters are optimized so that the estimated nerve activity is unbiased within a physiological range. We apply an efficient, robust mixture separation algorithm to remove background noise from the recording. As such, the algorithm described here is also applicable to the general problem of sparse time-series restoration, and can be easily adopted for a broader range of problems. In particular, it can be applied to any multifiber recording with a sufficiently high sampling rate (≥1000 Hz) under the following assumptions. We assume that the observed raw, unfiltered, multifiber recording (ot) takes the form of action potentials (kj St−j), embedded in noise (εt)
| (1) |
where k is an underlying common action potential template, M is the duration of the action potential waveform (typically few milliseconds), and
| (2) |
is a sparse, “locally” stationary spike train with an approximately flat spectrum. δ(·) denotes the Kronecker delta function, and N is its temporal length. In (1), εt = αt + nt is a locally stationary noise source that also includes artifacts αt with (at least partially) predictable time-domain and/or spectral properties. Artifacts may include movement artifacts mt and 60-Hz line noise qt that are independent, i.e., αt = mt + qt. Variable nt denotes broadband, white or slightly colored, background noise that we model as a pointwise independent Gaussian white noise 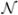 (μ,σ), whose parameters may change slowly over relatively broad intervals. The problem is the estimation of the spike train St from the observed recording ot. We define the power spectrum of the recorded raw signal as Λ(Ω) = |λo (Ω)|, where Ω = [ω1, …, ωN ],
, ψ(n) = cov ot−n, ot), and assume that the movement artifacts in the raw signal, if any, can have relatively slow onset and offset, i.e.,
. The properties of Λ(Ω) and mt that allow the removal of artifacts from the recording with minimal error are summarized next in Section III. Throughout the paper, we use “spike train” to indicate a train of Kronecker delta’s that mark each nerve firing [i.e., St in (2) for each t], “action potential” to indicate the membrane potential waveform [kj in (1)], and “action potential train” to indicate the train of membrane potential waveforms associated with the spike train [i.e., kj St−j in (1) for each t]. Each individual step of the algorithm to recover St is schematized in Fig. 1 and explained next. Under our statistical model (Section IV-C), we define the SNR as
(μ,σ), whose parameters may change slowly over relatively broad intervals. The problem is the estimation of the spike train St from the observed recording ot. We define the power spectrum of the recorded raw signal as Λ(Ω) = |λo (Ω)|, where Ω = [ω1, …, ωN ],
, ψ(n) = cov ot−n, ot), and assume that the movement artifacts in the raw signal, if any, can have relatively slow onset and offset, i.e.,
. The properties of Λ(Ω) and mt that allow the removal of artifacts from the recording with minimal error are summarized next in Section III. Throughout the paper, we use “spike train” to indicate a train of Kronecker delta’s that mark each nerve firing [i.e., St in (2) for each t], “action potential” to indicate the membrane potential waveform [kj in (1)], and “action potential train” to indicate the train of membrane potential waveforms associated with the spike train [i.e., kj St−j in (1) for each t]. Each individual step of the algorithm to recover St is schematized in Fig. 1 and explained next. Under our statistical model (Section IV-C), we define the SNR as
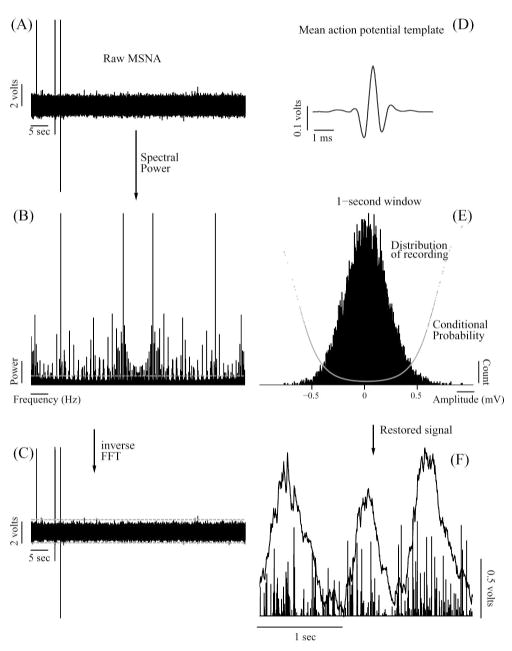
Fig. 1.
Illustration of the proposed technique for processing multifiber nerve activity. (A) Raw recording. (B) Power spectrum of the recording. Dashed horizontal line marks the threshold for removing the line noise, estimated as described in the text. (C) Removal of movement artifacts and other aberrant activity in time domain. Dashed horizontal lines show 1st and 99th quantiles of the recording. (D). Mean action potential template extracted from the recording shown in (C). (E) Representative example of the distribution of recording [shown in (C)] within a 1 s window following the deconvolution with the mean action potential template shown in (D). Also shown in (E), superimposed on the distribution, is the conditional probability for each data point as estimated by the algorithm. (F) Exemplary spike train (shown as bars) obtained by the proposed technique, and corresponding integrated neurogram obtained by traditional processing (bandpass filtering and integration). Note in (F) that two similar bursts in the integrated neurogram (1st and 3rd) can be brought about by different spiking patterns. See Sections II–IV for details.
| (3) |
where l is the range of the estimated or constructed (described in Section V) nerve signal (in millivolts), and σ is the standard deviation of the background noise.
III. Separation of Artifacts From Multifiber Recordings
Two types of artifact common to raw multifiber recordings are 60-Hz line noise (due to alternating current) and movement artifacts. The former is common in most electrophysiological recordings due to electrical equipment. Movement artifacts are common to multifiber muscle sympathetic nerve recordings and caused by voluntary or involuntary contractions of muscles during the recording session. Both artifacts have well-defined characteristics in the frequency and time domains, and should be removed prior to statistical signal denoising as their effects can be substantial.
A. 60-Hz Line Noise
Multifiber nerve recordings can be corrupted by large amounts of periodic sinusoidal oscillations at multiples of the 60-Hz line frequency [27]. The typical way to remove line noise is by notch filtering [28]. The linear method we describe next removes line noise relatively quickly while minimally disturbing the spectrum of the signal. Line noise (qt, Section II) has a characteristic signature in the power spectrum as large-amplitude overshoots with very narrow-band power. Spectral power of these overshoots follows a gamma distribution (partly due to nonnegativity of the power), in contrast to the remaining spectral power that tends to be uniformly distributed [see Fig. 1(B)]. Thus, the spectral power of the whole recording can be approximated as a mixture of gamma and uniform distributions in the frequency domain.
The probability density function of the gamma distribution in the spectral domain, for ω1, …, ωN, can be written as
| (4) |
where Γ(·) is the gamma function, Λ (ωi) is the spectral density of the recording defined in Section II, and α and β are the parameters to be estimated. The task is to fit a mixture of gamma and uniform distributions to the power spectrum using maximum likelihood. We deploy the expectation–maximization algorithm [29] to maximize the log-likelihood with respect to the distribution parameters. Let u = max(Λ (ωi)) be the range of the uniform distribution component and π the probability of gamma distribution component of the mixture, and define the responsibility [30] γi for the ith frequency band as
| (5) |
The log-likelihood of the mixture distribution is given by
| (6) |
Let
Setting the derivatives of (6) with respect to π, α and β to zero and solving for the parameters yields
| (7) |
| (8) |
| (9) |
where Ψ (a; b) is the bth derivative of the logarithm of the gamma function. Equation (8) can be solved quickly by Newton’s method, as the left-hand side is monotonic. The parameter estimates (π̂, α̂, and β̂) and responsibilities (γi) are calculated from (5) and (7)–(9) recursively. After convergence, spectral power Λ(Ω) is thresholded where γi = 0.5 [dashed horizontal line in Fig. 1(B)]. The threshold γi = 0.5 removes the gamma-distributed component up to its 95%th quantile from the mixture distribution. The frequency domain representation of the resulting signal, Λ′(Ω), is obtained by taking the magnitude of the power spectrum and retaining the original phase of the signal so that . This procedure effectively removes line noise artifact (qt, defined in Section II) from the raw multifiber recording. For the remainder of the paper, “recording” refers to raw multifiber recording after removal of 60-Hz line noise (i.e., we replace ).
B. Movement Artifacts
Movement artifacts ( ; Section II) manifest themselves in sympathetic nerve recordings as relatively large pulses, and occur randomly due to voluntary or involuntary subject movements during the recording session. Their relatively large amplitude (Mk ≫ std(ot)) can be considered as their signature in the time domain, and can be successfully identified in the histogram of the whole raw recording as “outliers” (provided these artifacts occur infrequently). The Johnson–Nyquist amplifier noise present in the observed signal [31] ensures the normality of the recording centered around zero. Thus, these outliers can be easily removed by clipping with the cutoff points at the 1st and 99th quantiles of the normal distribution fit to the recording in the time domain [see Fig. 1(C)]. However, this step can be skipped if the raw multifiber recording is deemed to be free of such movement artifacts. While clipping to remove outliers is a standard approach [32], [33], this is the first time where a data-driven threshold is selected for sympathetic nerve recordings.
These two steps yield a recording that is essentially free of line noise and movement artifacts, two pervasive problems with raw, multifiber recordings.
IV. Separation of the Actual Nerve Signal From Background Noise
Making an objective choice for the appropriate threshold to discriminate background noise from the actual nerve signal poses the primary obstacle. A standard approach to this problem is matched-filtering, which maximizes the overall analog SNR. However, if the background noise is white, matched-filtering will blur the actual signal even though optimal SNR may be achieved. Thus, a matched-filter approach would make the detection more difficult. Our algorithm is similar to the Bayesian schema that Johnstone and Silverman [34] proposed for restoring sparse signals embedded in background noise. However, it is computationally more tractable, and is considerably faster. Our algorithm requires that the successive points of the signal be roughly independent. This independence is not satisfied in raw recordings due to the action potential waveforms, but can be approximately achieved by deconvolving the signal with a mean action potential template extracted from the data. This deconvolution maximally concentrates the actual signal (see next). Therefore, it leads to the approximate independence of the data points and considerably increases SNR of the recording (see Section IV-B), facilitating spike detection. Furthermore, if the noise covariance is close to the autocorrelation function of the actual signal, a perfect deconvolution of the signal would be the matched filter up to a constant. Thus, our algorithm may work best in the case where signal and noise spectrum overlap, a situation regarded as extremely difficult. Therefore, we first identify a subset of likely action potentials by taking advantage of the synchronization of sympathetic nerve activity to the cardiac cycle (however, see Section IV-D). We then construct a mean action potential template and deconvolve the recording with this template to reduce the signal spread and to increase the SNR (Section IV-B). Lastly, we identify the points in the recording that correspond to actual nerve activity, based on the a posteriori conditional expectation of each point in the recording (Section IV-C).
A. Spike Template Extraction
After removing artifacts, the recording takes the form
| (10) |
where k is an underlying common action potential template, nt is a Gaussian random process whose power spectrum is approximately flat with nt ~ 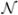 (μ, σ), and St is a spike train of varying amplitude, defined in (2). We assume that nt and k have differing power spectra. We also assume that the shape of a subset of action potentials in our model is roughly similar, and that some fraction of the action potentials is considerably larger in peak amplitude than the noise source, and therefore, can be directly extracted from the recording. We also assume that the spike train St is relatively sparse so that spikes can be accurately extracted.
(μ, σ), and St is a spike train of varying amplitude, defined in (2). We assume that nt and k have differing power spectra. We also assume that the shape of a subset of action potentials in our model is roughly similar, and that some fraction of the action potentials is considerably larger in peak amplitude than the noise source, and therefore, can be directly extracted from the recording. We also assume that the spike train St is relatively sparse so that spikes can be accurately extracted.
In the case of human mucle sympathetic activity, bursts of sympathetic activity occur in phase with the cardiac cycle [35], and thus, these bursts can be extracted from the integrated signal by windowing the waveform in the frequency range of the heart rate. This procedure can be qualitatively described as maximizing the match of sympathetic nerve bursts and the pressure waveform at the diastolic phase of the cardiac cycle. To extract the beat-to-beat bursts, the range of heart rate is obtained from R-to-R intervals of the ECG. A Chebyshev fourth order bandpass filter is constructed based on this passband and applied to the integrated neurogram. Bursts that exceed 2.5 standard deviations of the whole neurogram are considered to have the highest probability of containing action potentials. For the recording, all peaks located within the window of identified bursts are selected for template extraction. A Blackman window of M/2 = 17 in half-length (i.e., ±1.7 ms at a 10-KHz sampling rate) is used to capture the beginning and end of the action potential with the peak centered in the window. This window length should be sufficient since the human single sympathetic nerve action potential spans about 3 ms [36]. All candidate action potentials are then aligned to have their peak in the center of the window.
The candidate action potentials extracted by the earlier procedure contain actual action potentials, as well as noise spikes. The latter can be identified as waveforms with only a few nonzero points since neural spikes are known to have a temporal length of at least a millisecond [37]. That is, noise spikes will have a waveform significantly narrower compared to real action potentials. Thus, these can be identified in the pairwise K × K correlation matrix of action potential candidates with ρ> 0.99 (due to dominance of zero elements). Remaining candidates are considered to be a subset of true action potential waveforms present in the recording, and averaged together to obtain a preliminary mean action potential template (denoted as k̂) that serves as an example of neural impulse response [see Fig. 2(A)]. Note that although this procedure is similar to so-called amplitude-detection algorithms for spike detection, our restoration algorithm relies on these candidate action potentials only to ensure the approximate independence of the points in the transformed recording and enhance SNR.
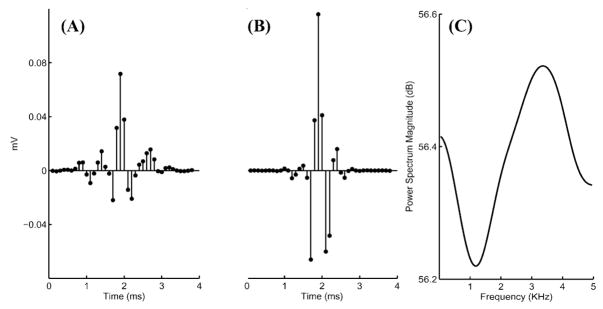
Fig. 2.
(A) Representative example of mean action potential template (neural impulse response k̂). (B) Point spread function of deconvolution of the mean action potential template shown in (A). (C) Power spectrum magnitude of the inverse mean action potential template (k̂−1).
B. Deconvolution
As mentioned earlier, the desired signal St is an unknown train of spikes with varying amplitude. However, we can only observe ot, that is, the spike train convolved with its neural impulse response (i.e., action potential) and corrupted by additive noise. Once we obtain a recording free of observed artifacts (Section III), we deconvolve the recording with the estimated neural impulse response (i.e., the mean action potential template, Section IV-A) so as to obtain an estimate of the spike train corrupted by noise. We minimize the difference between nerve recording (ot) and a theoretical action potential train based on the mean action potential template obtained in the previous step ( ). More specifically, we minimize the objective function
| (11) |
with gradient descent, where ot is defined by (10). This optimization ideally yields ℐ, which is a spike train S corrupted by noise that is approximately independent of the signal [compare with (10)]:
| (12) |
This implies that the spread of the signal has been reduced and the SNR is increased. Thus, this procedure greatly facilitates the recognition of the spike train.
Fig. 2(B) shows the point spread function of the deconvolution of the true signal with the mean action potential template shown in Fig. 2(A). The deconvolution SNR is 9.34 dB suggesting a considerable improvement following deconvolution by the mean action potential template. The point spread function [Fig. 2(B)] gives an upper bound of how much the deconvolution operation concentrates the recording, and the associated SNR indicates the extent of improvement of our result by deconvolution. To further investigate the SNR gain achieved by deconvolution, we constructed 1-s-long artificial signals with −3.4 dB SNR, (i.e., with expected correct classification rate of ~70%; Θ = (w, μ, σ, l) = (0.98, 0, 0.408, 1.0); a detailed description of artificial data construction is provided in Section V), convolved the signal with a mean action potential template obtained from an actual recording, and applied our algorithm separately with and without the deconvolution steps. The estimated SNR of the deconvolved signal was −0.04 ± 0.27 dB (N = 10), whereas that of the signal without deconvolution was −6.69 ± 1.04 dB. This suggests an average gain in SNR of 6.64 ± 0.96 dB with deconvolution. Therefore, even though minimization of (11) is not optimal since not all action potentials have the same morphology, SNR gain achieved by suboptimal deconvolution greatly facilitates the detection of actual nerve signal in the next step.
C. Modeling the Spike Train in Noise
The last step of the algorithm works on segments of data, rather than the whole dataset to handle slowly varying nonstationarity. This approach assumes that the deconvolved recording O = ℐ is locally stationary and is a mixture of a noise source and a spike train (12). The noise is assumed to be present for all data segments and follows an unknown Gaussian distribution, the parameters of which are to be estimated. It is also assumed that each arbitrary segment of data contains an independent, nonzero spike of voltage magnitude L with an a priori probability of p. Thus, the probability distribution of the recording consists of a purely Gaussian distribution (background noise; ξ in (13) next), and a uniform distribution convolved with a Gaussian one [the spike train; (χ[−L, L ]/2L) * ξ in (13) next]. The latter component approximates the Laplace distribution [34], but is computationally more tractable. In addition, our approach exploits the sparsity of the actual nerve signal relative to the sampling rate. Under these assumptions, we show next that one can separate the actual signal from noise using a modified version of the thresholding procedure proposed by Johnstone and Silverman [34].
For a given data segment (of length B), we assume that the probability distribution of the amplitudes (of both noise and actual nerve signal) in the deconvolved recording takes the form
| (13) |
where ξ ~ 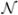 (μ, σ) denotes the background noise, w is the mixture probability, and
(μ, σ) denotes the background noise, w is the mixture probability, and
| (14) |
denotes the amplitude (in millivolts) distribution of the actual nerve signal over the range L = l/2. We assume that the probability distribution p(o|w, μ, σ) of each segment is independent of the rest, and we maximize the log-likelihood of the mixture given in (13)
| (15) |
using the EM algorithm, where Θ = (w, μ, σ). Next, we estimate the conditional a posteriori expectation E(O|w, μ, σ) of the actual nerve signal amplitude for each point in the segment given the estimated parameters that maximize the likelihood (15). If the actual nerve signal S is absent, its expected value is 0, and it is present with probability P (S|O, μ, σ, L) given by
| (16) |
| (17) |
| (18) |
where Φ(·) denotes the cumulative normal distribution. Thus, if the actual signal is present, then its conditional expectation is
| (19) |
From (16)–(19), E(O|w, μ, σ) is equal to P (S|O, μ, σ, L) E′(S|O, μ, σ, L).
Replacing each data point with its corresponding conditional expectation E(O|w, μ, σ) effectively attenuates noise (i.e., points with near-zero conditional probability) and retains the actual nerve signal (i.e., points with conditional probability close to 1) [Fig. 1(E)], thereby enhancing the SNR. As a last step, we choose a soft threshold for our estimated signal amplitude such that the number of spikes observed is within one standard deviation of the spiking rate for the entire segment (i.e., B × w). This is achieved by setting the threshold to σ which is the estimated standard deviation of the Gaussian of the mixture distribution. Note, in (12), that the deconvolved signal contains an additional term k̂−1 * 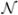 , which remains after the spike train S is produced. Since the shape of k is approximately bandpass [see Fig. 2(A)], k̂−1 is an approximate notch filter [Fig. 2(C)], and thus, k̂−1 *
, which remains after the spike train S is produced. Since the shape of k is approximately bandpass [see Fig. 2(A)], k̂−1 is an approximate notch filter [Fig. 2(C)], and thus, k̂−1 * 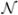 is an approximately notch-filtered noise source. In particular, there may be a significant amount of low amplitude, high-frequency noise remaining in the the denoised signal. The soft threshold at σ = 1 removes this portion of the noise. The thresholded signal is then full-wave rectified to obtain a restored estimate of the underlying spike train [Fig. 1(F)]. Finally, multifiber nerve activity is quantified as the number of spikes per second (or per heart beat, in Section VI). The algorithm is custom written using Matlab (version 2007a with optimization and statistic toolboxes, Mathworks, Natick, MA), and the source code is available from corresponding author upon request. Complete multistep processing of the nerve recordings that are sampled at 10 KHz and 5-min long takes on average ~720 s on a Pentium Centrino 2.00-GHz dual-core personal computer with 2 GB RAM.
is an approximately notch-filtered noise source. In particular, there may be a significant amount of low amplitude, high-frequency noise remaining in the the denoised signal. The soft threshold at σ = 1 removes this portion of the noise. The thresholded signal is then full-wave rectified to obtain a restored estimate of the underlying spike train [Fig. 1(F)]. Finally, multifiber nerve activity is quantified as the number of spikes per second (or per heart beat, in Section VI). The algorithm is custom written using Matlab (version 2007a with optimization and statistic toolboxes, Mathworks, Natick, MA), and the source code is available from corresponding author upon request. Complete multistep processing of the nerve recordings that are sampled at 10 KHz and 5-min long takes on average ~720 s on a Pentium Centrino 2.00-GHz dual-core personal computer with 2 GB RAM.
D. Remarks
What we have described in Section IV-A to extract a mean action potential template is based on the a priori knowledge that bursts of human mucle sympathetic nerve activity occur in synchrony with the cardiac cycle. Therefore, it specifically applies to the problem of sympathetic nerve activity detection, and different problems may require utilization of relevant a priori knowledge. Note also that the action potential template is constructed by averaging only a subset of action potentials, and as such, it does not represent all action potentials in the signal. Therefore, this step should be considered only as an intermediate step to increase SNR of the recording and facilitate detection of actual spikes and background noise in the recording (Section IV-C). Indeed, we showed in Section IV-B that this procedure successfully achieves its aim. In particular, the algorithm represents a method for denoising low-SNR multifiber recordings and does not pertain to spike sorting or differentiation of spike morphologies. However, robust denoising is a prerequisite for spike sorting. Once the multifiber recording is restored, the obtained spike train [St in (10)] can then be used to extract action potential waveforms [kj in (10) for each t] from the recording [ot in (10)], and these action potential waveforms can be classified using techniques readily available in the pertinent literature.
In Section IV-C, the mixture parameter w can be considered as the a priori estimate of the probability that there will be a spike in one sampling interval, and B × w gives the spiking rate for the segment length B. L is the estimated half-length of the actual nerve signal amplitude distribution and μ and σ are the estimated mean and standard deviation of the noise distribution.
Note the implicit assumption that there is no more than one action potential in a single sampling interval. The error rate for this assumption should depend on the sampling rate. It is a reasonable assumption for sufficiently high sampling rates since one sampling interval would be 0.1 ms for a 10-KHz sampling rate. However, this assumption effectively limits the applicability of the proposed algorithm to sampling rates greater than 1 KHz (or higher, if the SNR is not sufficiently high to avoid overlap between the action potentials and noise).
Lastly, note the assumption that the deconvolved signal (12) is “locally stationary.” That is, the fitted parameters of our data μ, σ, L, and w can change slowly on the time scale of the recording. Coefficients of variation (cv) of the parameters estimated from actual recordings (Section VI) showed that this assumption holds in general (cvμ = 1.1 ± 1.7, cvσ = 0.3 ± 1.2, cvL = 0.8 ± 0.7, and cvw = 0.02 ± 0.01), but with considerable variation across datasets (evidenced by relatively high standard deviations in cv values). Accordingly, as is commonly done in speech analysis [38], we estimate our parameters on a segment-by-segment basis.
V. Performance of the Algorithm
To validate the proposed technique, we produced 5-min-long, 10-KHz artificial datasets with various SNR (from −11.5 to 11.5 dB). The artificial nerve signal was sampled from a homogeneous Poisson distribution with 200 spikes per second on average (w = 0.98, and spike amplitude l depending on the SNR). Each spike in the artificial series was then randomly replaced by actual action potential waveforms obtained from a recording. The series were then contaminated with additive noise sampled from a normal distribution with mean μ = 0 and variance σ2 = 1 so as to obtain an artificial nerve signal. These datasets were used to determine the accuracy of our technique in detecting the actual spike train at varying levels of the SNR. We also analyzed these artificial datasets via the modified wavelet method described in Diedrich et al. [18] who showed better performance than regular wavelet and discriminator methods. We used Symlet 7 as the wavelet-type (Daubechies 4, another commonly used wavelet, did not change the results), and used parameters reported as optimal in the original paper (wavelet v coefficient threshold , where k = 0.8 and σ is estimated from Q–Q plot, wavelet decomposition level of 5, and hard thresholding). Receiver–operator characteristic curves (ROC) depicting the tradeoff between cumulative false and cumulative correct detection rates [39] assessed the accuracy of both methods for spike detection. The area under the ROC was used to determine overall the correct performance.
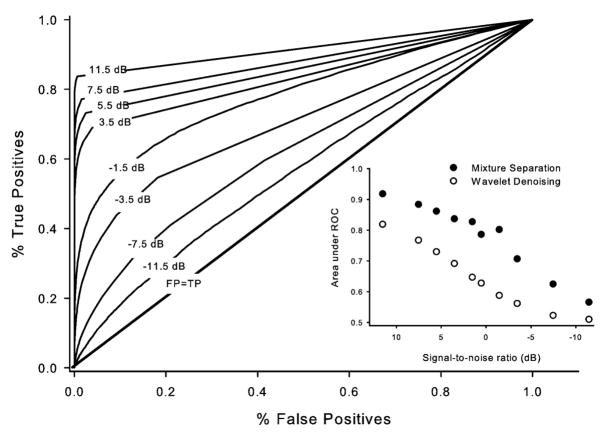
Our algorithm classified 56% (as determined by the area under the ROC, Fig. 3) of the signal correctly even at −11.5 dB SNR, and the performance quickly reached 70% at −3.5 dB, and 80% at 0.5 dB SNR. Change in the classification error rate as a function of the SNR is shown in Fig. 3 inset for our mixture separation algorithm (filled circles) and the modified wavelet method described in [18] (open circles). Note the rather dramatic improvement in performance of our algorithm from about −7 to 3 dB. Furthermore, our mixture separation algorithm’s classification rate is superior compared to that of the modified wavelet method for each SNR tested. Note that this is a rather conservative test of the performance since the noise component used to contaminate the artificial signal has a different spectrum compared to that of the signal. If, in fact, the noise had the same spectra as the signal, the algorithm would yield better results (see Section IV).
Fig. 3.
ROC of restored artificial recordings with noise levels ranging from −11.5 to 11.5 dB. The diagonal line shows the identity signifying random chance level (i.e., percentage of the false positives is equal to percentage of the true positives). Inset shows the change in the area under the ROC as a function of the SNR.
In general, the reported lower limit of SNR for successful detection of sympathetic nerve activity with alternative methods appears to be in the range of 4–10 dB. Zhang et al. [20] reported a significant reduction in the fraction of correctly detected spikes even at 10 dB SNR using a wavelet noise reduction approach; Nenadic and Burdick [17] employed a continuous wavelet transform and observed a considerable decline in their algorithm’s performance at 5.4 dB; Diedrich et al. [18] reported an SNR of around 4.0 dB as the limit for their modified wavelet denoising method; and Brychta et al. [26] reported ~4.7 dB (3:1) as the lower limit for reliable application of their kurtosis-based wavelet denoising method. Diedrich et al. [18] also reported that a SNR roughly below 4.8 dB results in the true positive detections that are equal to the false positive detections (i.e., the area under the ROC approaches 0.5) for amplitude discrimination methods. Using a nonlinear energy operator, Kim and Kim [40] and Choi et al. [41] reported an 80% correct detection at 1.25 dB. In contrast, application of our technique on artificial signals showed that it correctly classifies more than 70% of the spikes buried in −3.5 dB of noise and 80% at 0.5 dB. This is a remarkable improvement over the reported lower bounds for successful spike detection using wavelet methods and amplitude discrimination methods.
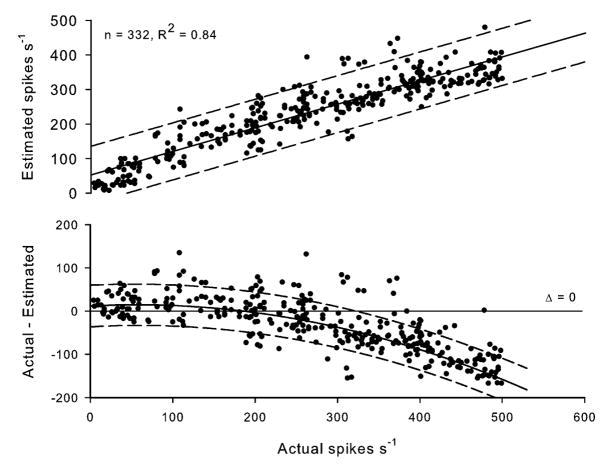
Next, we constructed another ~330-s-long artificial dataset, as described earlier, but fixed the SNR at 1.5 dB (l = 1.2, μ = 0, and σ = 0.275) and varied the average number of spikes per second from 5 to 500 (i.e., w ∈ [0.95, 0.9995]). This artificial recording was used to determine accuracy and bias of the measure obtained by our algorithm (the number of spikes per second) at varying levels of multifiber nerve activity. The match between the actual and estimated spike count was good (R2 = 0.719, p < 0.001; Fig. 4, upper panel), but a bias was evident in the algorithm (Fig. 4, lower panel). Our algorithm tended to overestimate the number of spikes if the actual number is above 335 (Fig. 4). Within this range, however, the bias between actual and estimated number of spikes was close to zero. This may mean that there is little effect of the bias within the range of sympathetic firing in humans which can be estimated to be 50–350 per second on average [42], [43]. We discuss possible reasons for this bias in Section VII.
Fig. 4.
Linear match between actual and estimated number of spikes per second (from an artificial recording with an SNR of 1.5 dB; upper panel) and the bias of the quantification as a function of actual number of spikes per second (lower panel). Dashed curves show 95% confidence intervals.
VI. Application of the Algorithm on Sympathetic Nerve Recordings
In addition to artificial datasets, we quantified actual recordings of human muscle sympathetic activity using the proposed algorithm (expressed as the number of spikes per heart beat). The traditional method for quantification of sympathetic activity is the area of sympathetic bursts identified from a filtered, integrated neurogram by a trained observer [8]. Sympathetic bursts identified from the integrated neurogram via Hamner and Taylor’s approach have been shown to closely relate to those identified by a trained observer [16]. Hence, we compared the performance of our algorithm to that of the automated method previously outlined by Hamner and Taylor [16] that provides a measure of sympathetic nerve activity expressed as integrated burst area per heart beat.
We determined the linear relation of both measures (beat-by-beat spike counts and beat-by-beat burst area) to diastolic blood pressure in 44 datasets. This allowed us to examine whether the proposed algorithm, which should retain more information about sympathetic nerve firing, improves the accuracy of this relation over the traditional method. We used postganglionic multifiber muscle sympathetic activity recorded from 44 datasets obtained following bolus injection of 100 μg of sodium nitroprusside in 22 subjects (7 females). Sodium nitroprus-side decreases blood pressure and reduces baroreflex-mediated sympatho-inhibition, resulting in greater muscle sympathetic nervous activity as a function of decreasing pressure. The subjects were between 21 and 63 years of age (mean 44.1 ± 17.6), were healthy nonsmokers, were not on any medications, and were supine during data collection. Multifiber postganglionic muscle sympathetic nerve activity was obtained from a nerve fascicle of either the right or left peroneal nerve with a tungsten microelectrode in the manner as developed by Vallbo and Hagbarth [8]. Sympathetic nerve activity was recorded at 10 KHz, amplified 70 000- to 100 000-fold, and stored for offline analysis.
The linear relation between sympathetic activity and diastolic blood pressure was assessed by Pearson’s product-moment correlation (r), and the difference in correlation coefficients obtained using both measures of sympathetic activity (beat-by-beat spike counts and beat-by-beat burst area) was tested using paired t-test and Wilcoxon rank test. For the latter, an r-to-z transform [44] was applied to r values between diastolic blood pressure and sympathetic activity. All values below are reported as mean ±SD.
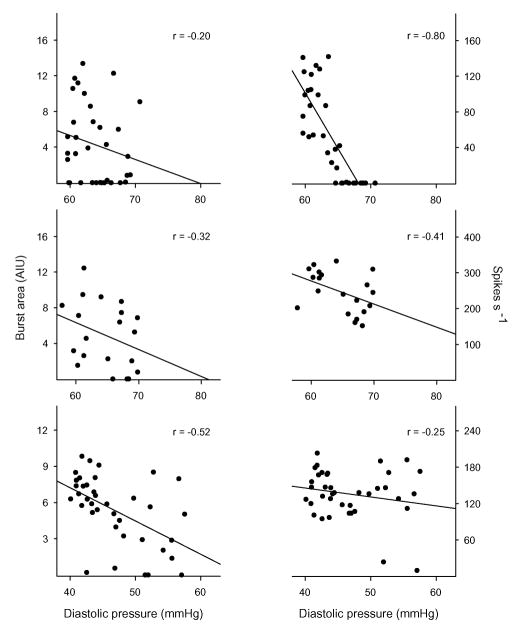
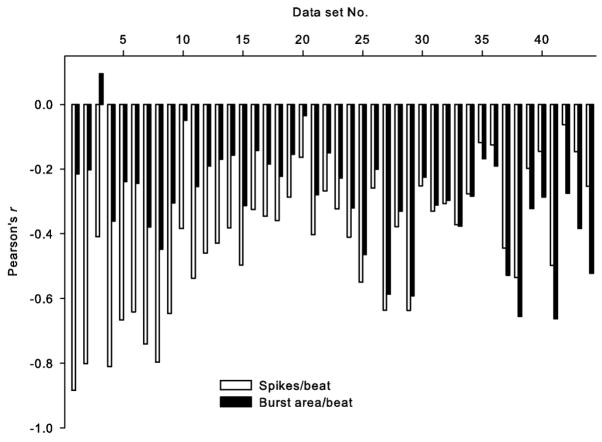
The estimated SNR of the 44 datasets was −2.21 ± 2.37 (range: [−5.24, 2.90]) dB. Thus, we can expect correct detection of spikes from the whole multifiber recording to average at least 73% (69%–82%, Fig. 3 inset).1 Three representative examples of the relation between falling diastolic pressure and increasing sympathetic activity estimated using both measures, spikes per beat and burst area per beat, are shown in Fig. 5. These examples represent cases where: 1) our technique greatly improved the estimated relation [improvement in r-value (Δr = |rspikes − rburst area |): 0.60, upper panel]; 2) the estimated relation differed only insignificantly (Δr = 0.09, middle panel); and 3) traditional processing yielded a better estimate than our technique (Δr = −0.27, lower panel). Fig. 6 shows the Pearson’s product moment correlations between diastolic pressure and both measures of sympathetic activity for all datasets. The estimated linear relation between sympathetic activity and diastolic pressure is improved in 32 out of 44 datasets (by 98 ± 178%; N = 32). Datasets on which traditional processing outperformed our measure (by 34 ± 23%; N = 12) were mostly the ones with relatively high SNR (mean 2.5 ± 2.0 dB). The overall improvement in performance (N = 44) with our technique was statistically significant (paired t-test, t = 3.88; p = 0.0002). The mean difference between two measures in terms of their relation to diastolic blood pressure was and cannot be attributed to pure chance (Wilcoxon paired signed rank test, W = 209; p = 0.0003). There was only a weak correlation between the r-values obtained by both measures (R2 = 0.089, F1,42 = 4.07, and p = 0.0502). However, this weak correlation is expected because differences in the firing patterns (e.g., multiple small-amplitude firings versus sparse large-amplitude firings) are not reflected in the integrated neurogram. In two of the datasets (43 and 44, both from the same subject), a possible effect of strong nonstationarity of noise was observed, i.e., a reduced window size (0.5 s) improved the estimated linear relation between sympathetic activity (spikes/beat) and diastolic blood pressure. The traditional measure (beat-by-beat burst area) nevertheless outperformed the measure obtained by our algorithm on these datasets (see Fig. 6). Reanalysis of the other datasets with reduced window size changed the results only negligibly, suggesting that the observed nonstationarity in these two cases was unusual.
Fig. 5.
Representative scatter plots of diastolic blood pressure versus estimated sympathetic activity as quantified as burst area per beat (left panels) and number of spikes per beat (right panels) for three datasets. Examples shown in the figure correspond to cases where our technique estimated the linear relation between diastolic blood pressure and sympathetic activity better than (upper panels), similar to (middle panels), and worse than (lower panels) traditional processing. Solid lines in each panel show the linear regression line between blood pressure and sympathetic activity.
Fig. 6.
Pearson’s product moment correlation (r) between diastolic blood pressure using both measures of sympathetic activity (number of spikes per beat versus burst area per beat). Pairwise r-values are rank ordered following the improvement achieved by our technique (spike counts) over traditional measure (burst area). Last two datasets (43 and 44) were processed using a 0.5-s window.
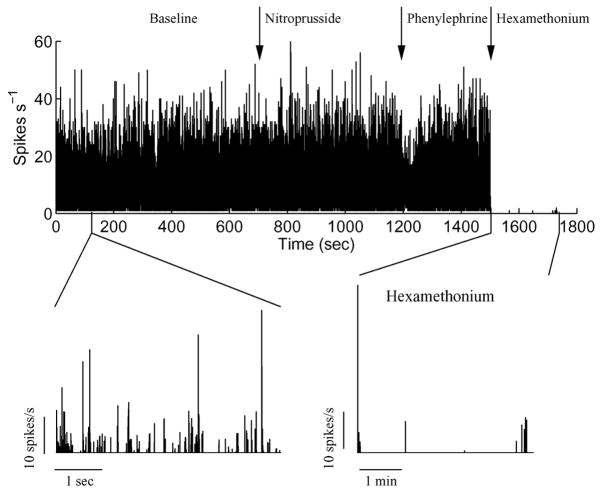
In addition to human sympathetic nerve recordings, we applied our algorithm to renal sympathetic nerve recordings obtained from a freely moving rat under baseline conditions, and following a sequence of bolus nitroprusside (100 μg/kg, reduces baroreflex-mediated sympatho-inhibition), phenylephrine (50 μg/kg, increases baroreflex-mediated sympatho-inhibition), and hexamethonium (30 mg/kg, complete blockade of efferent sympathetic activity) application. Data were recorded using bipolar stainless steel electrodes (OD ~0.1 mm; Telemetry Research, New Zealand) at 1000 Hz. Despite the relatively low sampling rate, high SNR of the recordings ensured successful detection of the nerve activity (see remarks in Section IV-D). Fig. 7 shows the renal sympathetic activity quantified by our algorithm. Note, in particular, in Fig. 7 that following hexamethonium application, our algorithm does indeed reveal that there is no sympathetic activity during this period, further supporting the physiological utility of our approach. Together, these results show the applicability of our algorithm not only in humans, but also in other species, and to multifiber recordings from different nerves (renal and muscle sympathetic recordings).
Fig. 7.
Representative example of the restored renal sympathetic activity (spikes per second) recorded from a rat under baseline condition and following bolus injection of nitroprusside, phenylephrine, and hexamethonium.
VII. Conclusion
We have described a novel algorithm for restoration of multifiber nerve signal buried in high levels of background noise. The main assumption of our algorithm is sparsity of the nerve signal (though there is no strict definition of sparsity in a statistical sense). We observed that our method tends to overestimate the number of spikes, as the rate increases above ~400 spikes per second. This is likely to be related to the observation of Johnstone and Silverman [34] who also reported an overestimation when sparsity is reduced (i.e., increased signal density). They showed this overestimation is due to the algorithm’s threshold becoming more lenient with increased signal density. However, at least in humans, this assumption does not pose a major limitation given the expected number of spikes per beat under normal conditions [13], [43]. Another limitation is the requirement of the relatively high sampling rate for the recording. To accurately determine action potential waveforms, the sampling rate should be sufficiently high. Given that a human single sympathetic nerve action potential spans about 2–3 ms [36], our approach should be used with caution with signals sampled at less than 3 KHz. Note that these two major limitations are related. “Sparsity” is relative to the sampling rate; thus, one can avoid the overestimation of actual firing by increasing the sampling rate as long as action potentials do not overlap considerably.
The results on artificial datasets (Section V) show that our algorithm provides an accurate measure of the nerve signal. Improvement in the accuracy of the linear relation between sympathetic activity to dynamic blood pressure changes (Section VI) further suggests that our algorithm provides a better quantification of the sympathetic signal compared to traditional processing (i.e., filtering and rectification). This improvement is due to the ability of our algorithm to minimize signal degradation and retain more information about nerve firing. Additional advantages of our algorithm are its capability to detect nerve signals in multifiber recordings heavily contaminated with background noise and its capacity to allow estimation of unique characteristics of the noise and signal components.
Even though we cast the algorithm as a restoration method of human muscle sympathetic recordings, it is rather generic in the sense that it can be applied to any recording with a sufficiently high sampling rate (e.g., ≥3000 Hz). The bulk of electrophysiological work in neurophysiology involves the use of intracellular recordings to study cortical sensory processes [45]–[47]. Intra-cellular recordings have the advantage of allowing unambiguous recordings from a single cell. However, multiple adjacent neurons are typically studied by multielectrode techniques or using electrodes with multiple pickup points to record from multiple neurons simultaneously. Examples include the cases where population coding and rate coding is important, such as motor neuron populations [48], and neural control in the cardiovascular system [49]. To enhance the SNR and to facilitate spike sorting, some studies proposed methods for denoising multifiber recordings using the actual noise waveforms recorded from nearby electrodes (e.g., [50]). Even though such methods may be optimal to capture the statistical properties of actual noise source, utilization of additional electrodes that are sufficiently close to the recording electrode may or may not be feasible. Access to sufficiently robust restoration algorithms allows quantification of multifiber responses as well as spiking patterns with a simple gross extracellular electrode. The current study provides a first instalment of one such algorithm. Indeed, our results showed the applicability of our algorithm to different species (rat and human), and to multifiber recordings from different nerves (renal and muscle sympathetic nerves), provided that the major assumptions of the model are met.
Acknowledgments
This research was supported by the National Institutes of Health (NIH) under Grant 5R21HL081693-01 and Grant 5R01AG014376-10.
Biographies
 Can Ozan Tan received the B.S and M.S degrees in biology from Middle East Technical University, Ankara, Turkey, in 2000 and 2002, respectively, and the Ph.D degree in cognitive and neural systems from the Graduate School, Boston University, Boston, MA, in 2007.
Can Ozan Tan received the B.S and M.S degrees in biology from Middle East Technical University, Ankara, Turkey, in 2000 and 2002, respectively, and the Ph.D degree in cognitive and neural systems from the Graduate School, Boston University, Boston, MA, in 2007.
His current research interests include computational neuroscience, cardiovascular physiology, signal processing, and stochastic modeling. He is currently a Postdoctoral Fellow in the Department of Physical Medicine and Rehabilitation, Harvard Medical School, and Cardiovascular Research Laboratory Spaulding Rehabilitation Hospital, Boston.
 J. Andrew Taylor received the M.S degree in exercise sciences from the University of Arizona, Tucson, in 1987, and the Ph.D. degree in physiology from the University of Arizona, Tucson, in 1990.
J. Andrew Taylor received the M.S degree in exercise sciences from the University of Arizona, Tucson, in 1987, and the Ph.D. degree in physiology from the University of Arizona, Tucson, in 1990.
He worked as a Postdoctoral Researcher at Duke University Medical Center, Durham, NC, and the Medical College of Virginia, Richmond. In 1995, he became an Assistant Professor of Medicine in Harvard Medical School with an appointment in the Division of Gerontology at Beth Israel Deaconess Medical Center. Until 2004, he was also the Director of the Laboratories for Cardiovascular Research at the Hebrew Rehabilitation Center for Aged. In 2004, Dr. Taylor joined the Department of Physical Medicine & Rehabilitation at Harvard Medical School as an Associate Professor. He also established the Cardiovascular Research Laboratory at Spaulding Rehabilitation Hospital, and subsequently, obtained an appointment in the Division of Cardiology at Massachusetts General Hospital. His current research interests include baroreflex control of cardiovascular autonomic outflow, mechanisms of cardiovascular variabilities, effects of chronic and acute stressors on the cardiovascular system, and cardiovascular autonomic physiology in aging and disease.
 Albert S. H. Ler received the B.S. degree in psychology from the University of Toronto, Toronto, ON, Canada, in 1995, the M.S degree in psychology from McMaster University, Hamilton, ON, in 1998, and the Ph.D degree in cognitive and neural systems from Boston University, Boston, MA, in 2007.
Albert S. H. Ler received the B.S. degree in psychology from the University of Toronto, Toronto, ON, Canada, in 1995, the M.S degree in psychology from McMaster University, Hamilton, ON, in 1998, and the Ph.D degree in cognitive and neural systems from Boston University, Boston, MA, in 2007.
His current research interests include experimental and computational neuroscience, signal processing, statistics, and machine learning. He has previously studied functional brain imaging and processing of cardiovascular signals. He is currently a Research Scientist studying neurological diseases using electroencephalography.
 Michael A. Cohen received the B.S degree in pure mathematics from Massachusetts Institute of Technology (MIT), Cambridge, in 1969, and the Ph.D. degree in experimental psychology from Harvard University, Cambridge, in 1977.
Michael A. Cohen received the B.S degree in pure mathematics from Massachusetts Institute of Technology (MIT), Cambridge, in 1969, and the Ph.D. degree in experimental psychology from Harvard University, Cambridge, in 1977.
After a Postdoctoral Fellowship at New York University, he came to the Center for Adaptive Systems at Boston University, where he worked first as a Post-doc, and then as a Professor, while serving as the Computer Systems Administrator. He has authored or coauthored more than 50 papers in fields as diverse as applied algebra, ordinary differential equations, child language, cardiovascular physiology, and applied physiology. His current research interests include stochastic modeling, signal processing, cardiovascular physiology, and dynamical systems.
Footnotes
References
- 1.Wray DW, Donato AJ, Nishiyama SK, Richardson RS. Acute sympathetic vasoconstriction at rest and during dynamic exercise in cyclists and sedentary humans. J Appl Physiol. 2007 Feb;102(2):704–712. doi: 10.1152/japplphysiol.00984.2006. [DOI] [PubMed] [Google Scholar]
- 2.Esler M. The sympathetic system and hypertension. Amer J Hypertens. 2000;13(6):99S–105S. doi: 10.1016/s0895-7061(00)00225-9. [DOI] [PubMed] [Google Scholar]
- 3.Usui K, Bradley TD, Spaak J, Ryan CM, Kubo T, Kaneko Y, Floras JS. Inhibition of awake sympathetic nerve activity of heart failure patients with obstructive sleep apnea by nocturnal continuous positive airway pressure. J Amer Coll Cardiol. 2005;45(12):2008–2011. doi: 10.1016/j.jacc.2004.12.080. [DOI] [PubMed] [Google Scholar]
- 4.Floras JS. Sympathetic activation in human heart failure: Diverse mechanisms, therapeutic opportunities. Acta Physiol Scand. 2003;177(3):391–398. doi: 10.1046/j.1365-201X.2003.01087.x. [DOI] [PubMed] [Google Scholar]
- 5.Esler M, Kaye D. Increased sympathetic nervous system activity and its therapeutic reduction in arterial hypertension, portal hypertension and heart failure. J Auton Nerv Syst. 1998;72(2–3):210–219. doi: 10.1016/s0165-1838(98)00107-6. [DOI] [PubMed] [Google Scholar]
- 6.Esler M, Kaye D. Sympathetic nervous system activation in essential hypertension, cardiac failure and psychosomatic heart disease. J Cardiovasc Pharmacol. 2000;35(7):S1–S7. doi: 10.1097/00005344-200000004-00001. [DOI] [PubMed] [Google Scholar]
- 7.Fagius J. Sympathetic nerve activity in metabolic control–Some basic concepts. Acta Physiol Scand. 2003;177(3):337–343. doi: 10.1046/j.1365-201X.2003.01086.x. [DOI] [PubMed] [Google Scholar]
- 8.Hagbarth KE, Vallbo AB. Mechanoreceptor activity recorded percutaneously with semi-microelectrodes in human peripheral nerves. Acta Physiol Scand. 1967;69(1):121–122. doi: 10.1111/j.1748-1716.1967.tb03498.x. [DOI] [PubMed] [Google Scholar]
- 9.Vallbo AB, Hagbarth KE, Wallin BG. Microneurography: How the technique developed and its role in the investigation of the sympathetic nervous system. J Appl Physiol. 2004;96(4):1262–1269. doi: 10.1152/japplphysiol.00470.2003. [DOI] [PubMed] [Google Scholar]
- 10.Stauss HM, Persson PB, Johnson AK, Kregel KC. Frequency-response characteristics of autonomic nervous system function in conscious rats. Amer J Physiol. 1997;273(2):H786–H95. doi: 10.1152/ajpheart.1997.273.2.H786. [DOI] [PubMed] [Google Scholar]
- 11.Brink EE, Mackel RG. Time course of action potentials recorded from single human afferents. Brain. 1993;116:415–432. doi: 10.1093/brain/116.2.415. [DOI] [PubMed] [Google Scholar]
- 12.Abuelma’atti MT. Nonlinear distortion of an fm signal by half-wave linear rectification. Appl Math Comput. 1999 Mar;99(1):47–59. [Google Scholar]
- 13.Macefield VG, Elam M, Wallin BG. Firing properties of single postganglionic sympathetic neurones recorded in awake human subjects. Auton Neurosci. 2002;95(12):146–159. doi: 10.1016/s1566-0702(01)00389-7. [DOI] [PubMed] [Google Scholar]
- 14.Birkett CL, Ray CA, Anderson EA, Rea RF. A signal-averaging technique for the analysis of human muscle sympathetic nerve activity. J Appl Physiol. 1992;73(1):376–381. doi: 10.1152/jappl.1992.73.1.376. [DOI] [PubMed] [Google Scholar]
- 15.Celka P, Vetter R, Vesin JM, Pruvot E, Scherrer U. Exponential-type distribution of human muscle sympathetic nerve activity results in an automatic quantification method. Comput Biol Med. 1998;28(6):627–637. doi: 10.1016/s0010-4825(98)00014-6. [DOI] [PubMed] [Google Scholar]
- 16.Hamner JW, Taylor JA. Automated quantification of sympathetic beat-by-beat activity, independent of signal quality. J Appl Physiol. 2001;91(3):1199–1206. doi: 10.1152/jappl.2001.91.3.1199. [DOI] [PubMed] [Google Scholar]
- 17.Nenadic Z, Burdick JW. Spike detection using the continuous wavelet transform. IEEE Trans Biomed Eng. 2005 Jan;52(1):74–87. doi: 10.1109/TBME.2004.839800. [DOI] [PubMed] [Google Scholar]
- 18.Diedrich A, Charoensuk W, Brychta RJ, Ertl AC, Shiavi R. Analysis of raw microneurographic recordings based on wavelet denoising technique and classification algorithm: Wavelet analysis in microneurography. IEEE Trans Biomed Eng. 2003 Jan;50(1):41–50. doi: 10.1109/TBME.2002.807323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brychta RJ, Shiavi R, Robertson D, Diedrich A. Spike detection in human muscle sympathetic nerve activity using the kurtosis of stationary wavelet transform coefficients. J Neurosci Methods. 2007;160(2):359–367. doi: 10.1016/j.jneumeth.2006.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang Q, Liu Y, Brown L, Shoemaker JK. Challenges and opportunities in processing muscle sympathetic nerve activity with wavelet denoising techniques: Detecting single action potentials in multiunit sympathetic nerve recordings in humans. Auton Neurosci. 2007;134(1–2):92–105. doi: 10.1016/j.autneu.2007.02.007. [DOI] [PubMed] [Google Scholar]
- 21.Donoho DL, Johnstone JI. Ideal spatial adaptation by wavelet shrinkage. Biometrika. 1994 Sep;81(3):425–455. [Google Scholar]
- 22.Vidakovic B. Statistical Modeling by Wavelets. New York: Wiley; 1999. [Google Scholar]
- 23.Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. J Amer Stat Assoc. 1995;90(432):1200–1224. [Google Scholar]
- 24.Vidakovic B. Nonlinear wavelet shrinkage with bayes rules and bayes factors. J Amer Stat Assoc. 1998;93(441):173–179. [Google Scholar]
- 25.Johnstone IM, Silverman BW. Needles and straw in haystacks: Empirical bayes estimates of possibly sparse sequences. Ann Stat. 2004;32(4):1594–1649. [Google Scholar]
- 26.Brychta RJ, Tuntrakool S, Appalsamy M, Keller NR, Robertson D, Shiavi RG, Diedrich A. Wavelet methods for spike detection in mouse renal sympathetic nerve activity. IEEE Trans Biomed Eng. 2007 Jan;54(1):82–93. doi: 10.1109/TBME.2006.883830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Redman-White W, Duffee R, Bramwell S, Rijns H, James S, Tijou J, van der Weide G. A robust analog interface system for submicron cmos video dsp. Proc. 23rd Eur. Solid-State Circuits Conf. (ESSCIRC 1997) ser; Southampton, UK: IEEE; 1998. pp. 1076–1081. [Google Scholar]
- 28.Hamilton PS. A comparison of adaptive and nonadaptive filters for reduction of power line interference in the ECG. IEEE Trans Biomed Eng. 1996 Jan;43(1):105–109. doi: 10.1109/10.477707. [DOI] [PubMed] [Google Scholar]
- 29.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the em. J Roy Stat Soc B. 1977;39(1):1–38. [Google Scholar]
- 30.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer-Verlag; 2001. [Google Scholar]
- 31.Nyquist H. Thermal agitation of electric charge in conductors. Phys Rev. 1928 Jul;32(1):110–113. [Google Scholar]
- 32.Bagnall A, Janacek G. Machine Learning. New York: Springer-Verlag; 2005. [Google Scholar]
- 33.Granger CWJ, Orr D. “Infinite variance” and research strategy in time series analysis. J Amer Stat Assoc. 1972 Jun;67(338):275–285. [Google Scholar]
- 34.Johnstone IM, Silverman BW. Needles and straw in haystacks: Empirical Bayes estimates of possibly sparse sequences. Ann Stat. 2004;32(4):1594–1649. [Google Scholar]
- 35.Xie A, Skatrud JB, Puleo DS, Morgan BJ. Arousal from sleep shortens sympathetic burst latency in humans. J Physiol. 1999 Mar;515(2):621–628. doi: 10.1111/j.1469-7793.1999.621ac.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Murai H, Takata S, Maruyama M, Nakano M, Kobayashi D, Otowa K, Takamura M, Yuasa T, Sakagami S, Kaneko S. The activity of a single muscle sympathetic vasoconstrictor nerve unit is affected by physiological stress in humans. Amer J Physiol—Heart C. 2006 Feb;290(2):H853–H860. doi: 10.1152/ajpheart.00184.2005. [DOI] [PubMed] [Google Scholar]
- 37.Macefield VG, Elam M. Comparison of the firing patterns of human postganglionic sympathetic neurones and spinal alpha motoneurones during brief bursts. Exp Physiol. 2004 Jan;89(1):82–88. doi: 10.1113/expphysiol.2003.002637. [DOI] [PubMed] [Google Scholar]
- 38.Rabiner LR, Juang BH. Fundamentals of Speech Recognition. Englewood Cliffs, NJ: Prentice-Hall; 1993. [Google Scholar]
- 39.Green DM, Swets JA. Signal Detection Theory in Psychophysics. New York: Wiley; 1966. [Google Scholar]
- 40.Kim KH, Kim SJ. Neural spike sorting under nearly 0-dB signal-to-noise ratio using nonlinear energy operator and artificial neural-network classifier. IEEE Trans Biomed Eng. 2000 Oct;47(10):1406–1411. doi: 10.1109/10.871415. [DOI] [PubMed] [Google Scholar]
- 41.Choi JH, Jung HK, Kim T. A new action potential detector using the MTEO and its effects on spike sorting systems at low signal-to-noise ratios. IEEE Trans Biomed Eng. 2006 Apr;53(4):738–746. doi: 10.1109/TBME.2006.870239. [DOI] [PubMed] [Google Scholar]
- 42.Macefield VG, Wallin BG. Firing properties of single vasoconstrictor neurones in human subjects with high levels of muscle sympathetic activity. J Physiol. 1999;516:293–301. doi: 10.1111/j.1469-7793.1999.293aa.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Saxod R, Torch S, Vila A, Laurent A, Stoebner P. The density of myelinated fibres is related to the fascicle diameter in human superficial peroneal nerve. Statistical study of 41 normal samples. J Neurol Sci. 1985;71(1):49–64. doi: 10.1016/0022-510x(85)90036-x. [DOI] [PubMed] [Google Scholar]
- 44.Fisher RA. Statistical Methods for Research Workers. Edinburgh, U.K: Oliver & Boyd; 1958. [Google Scholar]
- 45.Kaada BR. Electrical activity of the brain. Annu Rev Physiol. 1953;15:39–62. doi: 10.1146/annurev.ph.15.030153.000351. [DOI] [PubMed] [Google Scholar]
- 46.Li CL, Ortiz-Galvin A, Chou SN, Howard SY. Cortical intra-cellular potentials in response to stimulation to lateral geniculate body. J Neurophysiol. 1960;23:592–601. doi: 10.1152/jn.1960.23.6.592. [DOI] [PubMed] [Google Scholar]
- 47.Rodieck RW, Kiang NY, Gerstein GL. Some quantitative methods for the study of spontaneous activity of single neurons. Biophys J. 1962;2:351–368. doi: 10.1016/s0006-3495(62)86860-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Haugland M, Sinkjaer T. Cutaneous whole nerve recordings used for correction of footdrop inhemiplegic man. IEEE Trans Rehabil Eng. 1995 Dec;3(4):307–317. [Google Scholar]
- 49.Morillo CA, Eckberg DL, Ellenbogen KA, Beightol LA, Hoag JB, Tahvanainen KU, Kuusela TA, Diedrich AM. Vagal and sympathetic mechanisms in patients with orthostatic vasovagal syncope. Circulation. 1997;96(8):2509–2513. doi: 10.1161/01.cir.96.8.2509. [DOI] [PubMed] [Google Scholar]
- 50.Musial PG, Baker SN, Gerstein GL, King EA, Keating JG. Signal-to-noise ratio improvement in multiple electrode recording. J Neurosci Methods. 2002;115(1):29–43. doi: 10.1016/s0165-0270(01)00516-7. [DOI] [PubMed] [Google Scholar]