Abstract
Continuous arterial spin labeling (CASL) MRI was combined with multivariate analysis for detection of an Alzheimer's Disease (AD) related cerebral blood flow (CBF) covariance pattern. Whole brain resting CBF maps were obtained using spin echo, echo planar imaging (SE-EPI) CASL in patients with mild AD (n=12, age = 70.7± 8.7, 7 males, modified Mini-Mental State Examination (mMMS) = 38.7/57 ± 11.1) and age-matched healthy controls (HC) (n = 20; age = 72.1 ± 6.5, 8 males). A covariance pattern for which the mean expression was significantly higher (p < 0.0005) in AD than HC was identified containing Posterior Cingulate, Superior Temporal, Parahippocampal, and Fusiform gyri, as well as Thalamus, Insula, and Hippocampus. The results from this analysis were supplemented with those from the more standard, ROI and voxelwise, univariate techniques. All ROIs (17/hemisphere) showed significant decrease in CBF in AD [p < 0.001 for all ROIs, αcorrected = 0.05]. The area under the ROC curve for discriminating AD vs. HC was 0.97 and 0.94 for covariance pattern and gray matter ROI, respectively. Fewer areas of depressed CBF in AD were detected using voxelwise analysis [corrected, p < 0.05]. These areas were: Superior Temporal, Cingulate, Middle Temporal, Fusiform gyri, as well as Inferior Parietal Lobule and Precuneus. When tested on extensive split-half analysis to map out the replicability of both multivariate and univariate approaches, the expression of the pattern from multivariate analysis was superior to that of the univariate.
Keywords: AD, CASL, CBF, covariance pattern, multivariate analysis, perfusion
INTRODUCTION
Cerebral blood flow (CBF) is commonly accepted as a physiological correlate of normal brain metabolism and a biomarker of several brain pathologies (Gonzalez et al. 1995). Perfusion imaging techniques such as H2O15 positron emission tomography (PET), single-photon emission computed tomography (SPECT), dynamic contrast enhanced (DCE) MRI and arterial spin labeling (ASL) MRI have proven indispensable tools in studying brain pathologies such as Alzheimer's Disease (AD) (Alsop et al. 2000; Du et al. 2006; Herholz et al. 2002; Johnson et al. 1998; Scarmeas et al. 2004; Silverman et al. 2001). Most AD imaging studies have relied on PET and SPECT and have shown a marked decrease in metabolism and/or regional blood flow in the AD population (Herholz et al. 2002; Johnson et al. 1998; Scarmeas et al. 2004; Silverman et al. 2001). Results from several ASL studies have shown good agreement across techniques (Alsop et al. 2000; Du et al. 2006; Johnson et al. 2005; Sandson et al. 1996). Regardless of the particular imaging technique employed, the general conclusion from these studies is that a quantitative measurement of CBF has the potential of being the imperative biomarker for early detection and diagnosis of AD.
ASL offers several practical and scientific advantages over the other techniques: 1) it is amenable to safe and economical repeated measurements because it uses arterial blood water as an endogenous tracer thus avoiding the need for injection of expensive and potentially harmful tracers required in PET, SPECT, or DCE MRI; 2) it provides CBF quantification without arterial blood sampling, which can be extremely uncomfortable for subjects but necessary for quantitative PET; 3) it can be acquired in the same session with structural and other MR images; 4) ASL CBF measurements are stable across sessions, making this technique ideal for tracking CBF changes over time due to recovery or therapeutic intervention (Floyd et al. 2003; Parkes et al. 2004).
ASL techniques have been used in a variety of applications in both disease and normal brain function (Alsop and Detre 1998; Golay et al. 2004). Based on differences in the way the arterial water is labeled, ASL methods are generally classified as continuous ASL (CASL) or pulsed ASL (PASL). Compared to PASL, CASL has been shown to have higher SNR and offers whole brain coverage via multi-slice acquisition (Wang et al. 2002).
ASL has already been used in studies of AD (Alsop et al. 2000; Du et al. 2006; Johnson et al. 2005; Sandson et al. 1996). The importance of these studies has been two-fold. First, they have served as validation of ASL in studying AD by showing good agreement with hexamethylpropyleneamine (HMPAO) SPECT (El Fakhri et al. 2004; Johnson et al. 1998). Second, the overlap in regions of hypoperfusion obtained with ASL with those of decreased metabolism detected with FDG PET supports the hypothesis of a direct coupling between these two effects in AD (Herholz et al. 2002).
Only one of the aforementioned ASL studies used CASL (Alsop et al. 2000) and found areas of significant CBF depression in Temporal, Parietal, Frontal, and Posterior Cingulate cortices in AD group as compared to healthy controls. The other three studies have reported data from PASL, which, in addition to lower SNR, has the disadvantage of being restricted only to a slab commonly placed in the superior cerebral cortex thus excluding major portions of the Temporal and Inferior Frontal lobes (Du et al. 2006; Johnson et al. 2005; Sandson et al. 1996). Furthermore, a non-quantitative version of PASL was used and therefore only relative measurements (in percent change) of CBF were reported. In all these studies univariate statistical analysis was employed for the between group comparisons.
One of the goals of this paper is to show the feasibility of combining CASL with multivariate analysis for detection of an AD-related CBF covariance pattern that contrasts AD patients and healthy controls at baseline. Multivariate approaches evaluate correlation/covariance of CBF measurement across brain regions, rather than proceeding on a region-by-region (or voxel-by-voxel) basis. Thus, their results can be more easily interpreted as a functional signature of neural networks (Habeck et al. 2005).
However, due to higher computational and conceptual complexity as well as the absence of an easy-to-use software package, multivariate techniques have rarely been applied in clinical imaging.
A study by Scarmeas et al. applied covariance analysis to non-quantitative H2O15 PET data and found a pattern whose mean expression was higher in AD than controls (Scarmeas et al. 2004). When prospectively applied to a sample of minimally to mildly cognitively impaired (MCI) subjects, the expression of the AD-related pattern was predictive of cognitive performance at baseline as well as of the subsequent decline; subjects who had higher baseline expression of the AD-related pattern showed lower cognitive performance and declined faster (Scarmeas et al. 2004).
Our study is the first to combine multivariate analysis with CASL imaging to investigate its utility for differential diagnosis of AD. Furthermore, we compare the sensitivity of diagnosis of the multivariate technique with that obtained using the more standard ROI- or voxel-based univariate analyses.
METHODS
Subjects
Resting CBF maps were obtained using CASL images from 12 subjects (age 70.7 ± 8.7 years, 7 males) diagnosed with mild AD using NINCDS-ADRDA criteria (McKhann et al. 1984) and 20 age-matched healthy controls (HC) (age 72.4 ± 6.5 years, 8 males).
AD and HC subjects were recruited from outpatients who were presented to the Alzheimer's Disease Research Center at Columbia University. AD patients met DSM-III-R criteria for dementia and NINCDS-ADRDA criteria for probable AD (McKhann et al. 1984) and underwent a thorough diagnostic evaluation including neurological examination, neuropsychological testing, functional evaluation, and rating of basic and instrumental activities of daily living (Benton and Hamsher 1976; Buschke and Fuld 1974; Stern 1987; Wechsler 2001). Other causes of dementia were excluded with appropriate laboratory tests. Based on a comprehensive review of all available information, a consensus diagnostic conference of neurologists, psychiatrists and neuropsychologists determined the diagnosis of AD, and finalized a Clinical Dementia Rating (CDR) (Hughes et al. 1982). Only AD patients rated as CDR = 1 were used in this study. CASL MRI results did not play any role in the diagnostic process.
Potential healthy elderly controls were recruited from family members and advertisement. They were carefully screened with medical, neurological, psychiatric and neuropsychological evaluations to exclude those with dementia or cognitive impairment (Nelson and O'Connell 1978; Stern 1987; Wechsler 1981; Wechsler 2001), as well as other neurological, psychiatric or severe medical disorders. Subjects with space occupying lesions or vascular disease were excluded. White matter hyperintensities were permitted but any clinical evidence (symptoms or signs) of stroke or MRI evidence of cortical or lacunar infarcts constituted exclusion criteria.
All subjects received the modified mMMS as a global rating of cognitive function. This is a 57-point modification of the original MMSE (Folstein et al. 1975) that includes the addition of digit span forward and backward (Wechsler 1981) two additional calculation items, recall of the current and 4 previous presidents of the country, confrontation naming of 10 items from the Boston Naming Test (Kaplan et al. 1983), one additional sentence to repeat, and a different copy task including 2 figures.
All subjects provided written consent as approved by the Columbia University Medical Center Institutional Review Board.
MRI acquisition
SE-EPI CASL images were acquired on a 1.5 T Philips Intera scanner using the manufacturer's head transmit-receive coil with: labeling duration = 2000 ms, post-labeling delay (PLD) = 800 ms, TE/TR = 35 ms/5000 ms, flip angle = 90°, acquisition matrix 64 × 58, FOV = 220 × 193 mm2, slice thickness = 7.5 mm/1.5 mm gap, number of trans-axial slices = 15. Slices were acquired in ascending mode (i.e., inferior-to-superior) with slice acquisition time = 64 ms. Total number of CBF images per subject was 30.
To check for the effect of transit time in the CBF measurement, in 6 AD patients, two sets of CASL CBF images were acquired: one with moderate PLD of 0.8 s and one with longer PLD of 1.0 s.
To induce the flow-driven adiabatic inversion (labeling) of the water spins, a “block-shaped” RF pulse 2000 ms long and 35 mG amplitude in the presence of a z-gradient 0.25 G/cm was applied prior to acquisition of each labeled image (Alsop and Detre 1996). To correct for off-resonance saturation effects, an amplitude-modulated (sinusoidal, 250 Hz) RF pulse of the same power and gradient were applied prior the acquisition of each control image (Alsop and Detre 1996). The frequency offset of the RF pulses was set to position the labeling plane 40 mm inferior to the lower edge of the imaging volume.
To spatially normalize images into standard space, a high resolution, T1-weighted, 3D spoiled gradient image was acquired in each subject with: TE/TR = 3 ms/34 ms, flip angle = 45°, acquisition matrix = 256 × 256 × 124, voxel size = 0.94 × 0.94 × 1.29 mm3.
The scanning session started with the rapid (35 sec) acquisition of a T1-weighted image to determine patient position. Subjects were instructed to relax and minimize motion during the scan. Foam padding was inserted around the sides of the head and the forehead to minimize patient motion.
MRI data pre-processing
All image pre-processing was implemented using SPM99 software (Wellcome Department of Cognitive Neurology) and code written in MATLAB (Mathworks, Natick MA). For each subject, images were preprocessed as follows: (i) all control and labeled EPI images were realigned to the first acquired using SPM's automated realignment algorithm. (ii) The T1-weighted structural image and the first acquired EPI image were co-registered using the mutual information co-registration algorithm in SPM99. (iii) The structural image was then used to determine parameters (7 × 8 × 7 non-linear basis functions) for transformation into Talairach standard space defined by the Montreal Neurologic Institute (MNI) template brain supplied with SPM99. (iv) This transformation was then applied to the all the EPI images, which were re-sliced using sinc-interpolation to 2 mm × 2 mm × 2 mm. (v) SPM99 was used to segment the structural images into gray matter (GM), white matter (WM), and cerebral spinal fluid (CSF) posterior probability maps needed for masking and computation of CBF.
Computation of CBF
The spatially normalized control/label pairs were used to calculate percent change maps, which were subsequently used to compute CBF using the two-compartment formula derived by Alsop & Detre and later modified by Wang et al. (Alsop and Detre 1996; Wang et al. 2002). The following parameter values were used: longitudinal relaxation, (T1) of blood = 1400 ms; blood/tissue water partition = 0.9 mL/g; transit time = 1300 ms; labeling duration = 2000 ms; tissue T1 in absence of RF = 1150 ms and 800 ms for GM and WM, respectively; T1 in presence of RF = 750 ms and 530 ms for GM and WM, respectively (Alsop and Detre 1996); PLD adjusted to account for the slice acquisition time, PLDs = (acquisition slice -1)·(64 ms) + 800 ms; labeling efficiency for CASL at 1.5T on Philips Intera = 0.70 (Werner et al. 2005).
For each subject, GM, WM, and CSF posterior probability images were obtained using SPM99 and subject's SPGR. For each voxel, computation of CBF was weighted by the tissue type posterior probability.
To get rid of any signal from scalp and non-brain tissue, a mask including only voxels with SE-EPI intensity > 0.80 was obtained and used to yield an average CBF image for each subject prior to any statistical analysis.
For the voxelwise analysis (in both multi- and univariate versions), CBF images were spatially smoothed with a 6 mm kernel. No smoothing was done for the ROI analysis.
Covariance analysis
To identify CBF network-correlates of early dementia, we employed an analysis technique that originated from the Scaled Subprofile Model (SSM), a covariance-analysis method (Moeller et al. 1987) that has been used previously in resting imaging studies of normal aging and a variety of neurological diseases (Hutchinson et al. 2000; Moeller et al. 1999; Nakamura et al. 2001). We summarize the steps of this algorithm in detail; no room has been left for arbitrary decisions on the part of the analyst:
Zero-meaned average CASL CBF images from all subjects from both groups were simultaneously included in a single Principal Components Analysis, which captures the major sources of between- and within-groups variation, producing a series of principal components (PCs). Voxels participating in each PC may have either a positive or a negative loading. Voxels with positive loadings can be conceived as exhibiting concomitant increased flow and those with negative loadings can be conceived as exhibiting concomitant decreased flow.
The expression of each PC for each subject was quantified by a subject scaling factor (SSF). A higher SSF value indicates more prominent concomitantly increased flow of the voxels with positive loadings and more prominent concomitantly decreased flow of the voxels with negative loadings. In other words, the SSF expresses the degree of subject's expression of the fixed PC.
To identify a covariance pattern that best discriminates AD patients from controls, each subject's SSFs of the specified PCs derived from step 1 together with a spatially uniform image representing the average CBF (since absolute quantification is provided with CASL) was entered into a linear regression model as the independent variable. Group membership (AD vs. HC) was the dependent variable. This regression resulted in a linear combination of the first PCs and the uniform image that best discriminated the 2 groups. This linear combination of the PCs can itself be conceived of as signifying a `pattern' or `network'. The area under the ROC-curve (AUC) was used to determine how many PCs out of the first 6 should be included in the regression. The 4 PCs and the spatially uniform average CBF image were included in the analysis since they achieved the largest AUC value of 0.96.
Estimation of robustness of regional weights in covariance pattern
CASL CBF patterns resulting from multivariate analysis assign different weights to all voxels included in the analysis, depending on the salience of their covariance contribution. Positive voxel weights indicate a positive correlation between the subject's expression value and the associated regional ASL signal; negative weights indicate a negative correlation. This means that as the expression of a pattern increases, ASL signal in the positively weighted regions increases as well, while ASL signal in the negatively weighted regions decreases. The absolute magnitude of a regional weight determines the slope of this change: for instance, a region whose weight is twice as large as that of another also changes its ASL signal twice as steeply. Whether a voxel weight is reliably different from zero is assessed by a bootstrap estimation procedure (Efron and Tibshirani 1994). This entails repeating the derivation of the covariance patterns (regardless of whether cross-sectional or longitudinal) many times on the resampled subject-data to approximate the variability of the regional weights with their standard deviation (s.d.) incurred through the resampling process. Denoting the point estimate of a voxel weight as w, and the standard deviation resulting from the bootstrap-resampling procedure as sw, we can calculate a rough z-statistic according to z = w/sw. Sufficiently small variability of a voxel weight around its point estimate results in a large magnitude of z and indicates a reliable contribution to the covariance pattern. Under the assumptions of a standard-normal distribution for z, z ~ N(0,1), choosing a threshold of |z|>3.09 results in a one-tailed p-level that is smaller than 0.001.
Non-parametric test of the null-hypothesis using method of permutations
To avoid having to rely on parametric distribution theory and its associated simplifying assumptions, we performed a permutation test. We resampled the data from both groups, HC and AD, and recomputed the complete analysis stream for 10,000 iterations, each time breaking the group-subject assignment, while keeping the group strengths, 12 and 20, the same. The PCA step is invariant with respect to this resampling operation, but the discriminant analysis will give different results. We computed the null-hypothesis histogram, using the t-statistic derived from the pattern expressions in both groups. The p-level is read off as the fraction of permutations that gave rise to a bigger value of the test statistic than the point estimate. We performed this test both on the group-contrast t-value and AUC of the AD-pattern expression.
To check for the presence of a gender effect, a two-tailed t-test was run between SSF scores and gender across both groups and within each group, AD and HC. For the AD group alone and the (AD + HC) group, a simple regression analysis was run between mMMS scores and the covariance pattern expression.
ROI analysis
17 ROIs per hemisphere (34 total) in MNI space were selected from wfu_pickatlas in 3-dimensional mode (Maldjian et al. 2004). These ROIs comprise major cortical and subcortical regions associated with AD (Alsop et al. 2000; Du et al. 2006; Scarmeas et al. 2004). The ROIs selected were Right and Left: Cingulate Gyrus, Cuneus, Fusiform Gyrus, Inferior Frontal Gyrus, Inferior Parietal Lobule, Insula, Lingual Gyrus, Middle Frontal Gyrus, Parahippocampal Gyrus, Parietal Lobe, Posterior Cingulate, Precentral Gyrus, Precuneus, Pulvinar, Superior Occipital Gyrus, Supramarginal Gyrus, Temporal Lobe.
ROI analysis was done by conjoining a given ROI with subject's GM posterior probability mask including only voxels that satisfied P[GM] > 0.80. The smallest ROI analyzed was the Right Superior Occipital Gyrus with 107 ± 36 and 148 ± 34 voxels (1 voxel=2×2×2 mm3) for AD and HC, respectively. The Right Temporal Lobe was the largest ROI with 6352 ± 893 and 7459 ± 700 voxels in AD and HC, respectively.
The between-group (AD vs. HC) comparison was done via a one-tailed t-test where false positive rate was controlled at αcorrected=0.05 via Bonferroni correction for multiple comparisons (17 comparisons/hemisphere).
To check the effect of gender, a t-test was run on the average GM CBF values separately computed for males and females in each group. A t-test was also run to check for any significant difference in CBF between right and left hemispheres in both groups.
For the most superior ROI (Precentral Gyrus) a t-test was run to check for a difference in the mean CBF values obtained with two different PLDs, (0.8s and 1.0s). This ROI was selected as the one theoretically expected to be most affected by an insufficiently long PLD value.
Voxelwise analysis
Whole brain voxelwise t-statistic for between-group comparison was computed using SPM99's fixed effect model with multiple comparisons correcting for the entire volume. Only voxels contained in the conjunction of all individual SE-EPI masks were analyzed. SPM99 assigned a t-value to each voxel in the brain and examined the t-map for voxels that exceeded a height threshold [t = 5.7; corrected p < 0.05].
Using SPM99, a simple regression analysis was done to check for the existence of an effect of gender as well as of a relationship between mMMS scores and voxelwise CBF values from both groups, (AD + HC), as well for the within AD group alone.
For both expression of covariance pattern and selected ROI/voxel values, ROC curves were computed to determine threshold values that produced optimal sensitivity and specificity as well as the area under the curve (AUC).
RESULTS
Demographics
Table 1 summarizes gender, age, education, and mMMS scores of the two groups. Only mMMS scores were significantly different between the groups [P = 0.001]. The mean mMMS score in the AD group corresponds to a MMSE (Folstein et al. 1975) of ~22/30 and is consistent with mild dementia. The lowest mMMS score for HC was 47 corresponding to a MMSE of 25.
Table 1.
Demographic, clinical and neuropsychological data for the all subjects. Mean values and standard deviations are reported. P values are calculated with two-tailed t-test. mMMS: modified Mini Mental Status examination
| HC N = 20 | AD N = 12 | P | |
|---|---|---|---|
| Gender, male (%) | 8 (40%) | 7 (58 %) | 0.73 |
| Age years, mean ± sd | 72.1 ± 6.5 | 70.7 ± 8.7 | 0.78 |
| Education years, mean ± sd | 15.8 ± 2.3 | 14.5 ± 3.8 | 0.23 |
| mMMS, mean ± sd | 53.5 ± 2.8* | 38.7 ± 11.1 | 0.001 |
mMMS was available for 19 /20 controls.
Global CASL CBF estimates
For a qualitative assessment of CASL CBF images and their difference between the two groups, average CBF maps for HC and AD are shown in Fig. 1, 1st and 2nd row, respectively. Slices were chosen to represent lower, middle, and upper brain. An overall (HC-AD) difference can be detected visually and is shown in the 3rd row of Fig. 1. Note that the few areas with a negative difference (in blue/green) are mainly in the ventricles where mostly noise and no CBF signal is expected.
Fig. 1.
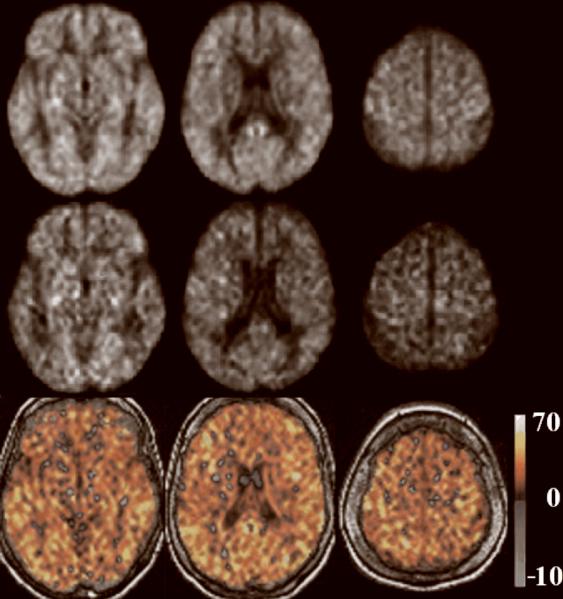
Group average CASL CBF images for HC and AD are shown in the 1st and 2nd row, respectively, at three axial locations from lower, middle, and upper brain. Corresponding difference images (HC-AD) are shown in the 3rd row. Units in the color bar are in [mL/100g•min].
Global GM CBF was significantly lower in AD compared to HC with mean values of 36.1 ± 7.8 ml/100g•min and 62.4 ± 13 ml/100g•min for each group, respectively, [t = 6.05, P < 0.0001]. There was no effect of gender in the GM CBF for either group: [t = -0.8, P = 0.23] and [t = 0.21, P = 0.41] for AD and HC, respectively.
Multivariate analysis
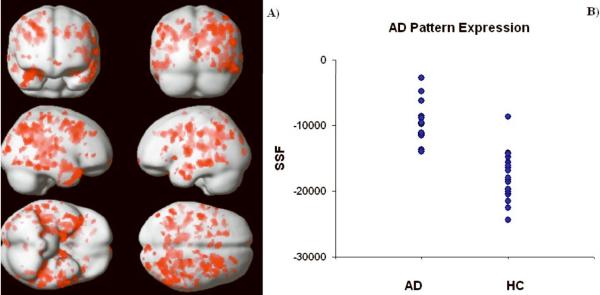
We obtained an AD-related covariance pattern (Fig. 2A) whose subject expression achieves significant separation between AD and HC groups (parametric p < 0.0005). The permutation test for the group discrimination achieved by the covariance pattern also yielded highly significant results, for both T-statistic and AUC: p(AUC) = 0.0002, p(T) = 0.0001. The areas showing concomitant decreased flow in the AD subjects are shown in Table 2. No areas of positive loadings (i.e., with concomitant increased flow in AD subjects) were found. Subject expression of the discriminant pattern is shown in Fig. 2B. One can appreciate the very small overlap between the two groups and the potential it holds for diagnostic purposes. The ROC curve showed that for an SSF cutoff of -14100, the covariance pattern was 100% sensitive and 95% specific; AUC was 0.96. Except for one control (79 yo, female, mMMS = 53) who was misidentified as AD, all other subjects' group identities were correctly assigned.
Fig. 2.
A) areas with robust negative loadings (i.e., concomitant decreased flow in AD relative to HC) as ascertained by the bootstrap procedure. Most areas are located around the Parahippocampal Gyrus in the Medial Temporal and Occipital Lobes; Thalamus was identified by our analysis as well. No areas of positive loadings (i.e., concomitant increased flow for AD subjects) were found. B) Subject expression of the discriminant pattern for both AD and HC groups. One can appreciate the very small overlap between the two groups.
Table 2.
Areas of the AD-related covariance pattern with significant (P<0.02) negative loadings (Highlighted rows show areas that were also identified in voxelwise analysis)
| MNI coordinates [X, Y, Z] | Location | Brodmann Area |
|---|---|---|
| [38, -36, -15] | Fusiform Gyms | 20 |
| [-40, -58, -30] | Fusiform Gyrus | 37 |
| [34, -22, -17] | Hippocampus | - |
| [-30, -34, -22] | Parahipocampal gyrus | 36 |
| [26, -31, -4] | Parahipocampal gyrus | 19 |
| [14, -54, 18] | Posterior Cingulate | 31 |
| [-16, -57, 17] | Posterior Cingulate | - |
| [46, -42, 19] | Superior Temporal Gyrus | 13 |
| [-44, -21, -2] | Superior Temporal Gyrus | 22 |
| [-38, 0, -3] | Insula | 13 |
| [46, -76, -1] | Inferior Occipital Gyrus | 18 |
| [-34, -80, -5] | Inferior Occipital Gyrus | 18 |
| [-6, -75, 24] | Cuneus | 18 |
| [12, -76, -14] | Lingual Gyrus | 18 |
| [-32, -60, -5] | Lingual Gyrus | - |
No significant correlation between the covariance pattern and mMMS scores was found. Also, no effect of gender was detected in either group; [P =0.83] and [P=0.08] for AD and HC, respectively.
ROI analysis
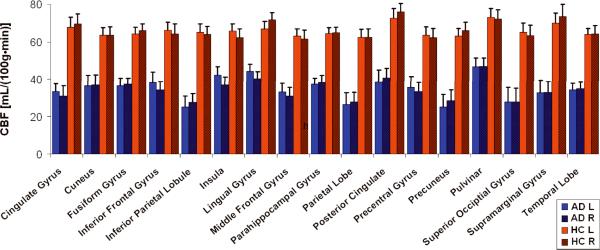
Fig. 3 shows CASL CBF mean values of each ROI in AD patients (in blue) and HC (in red). The largest decrease in CBF, 28.3 [mL/(100g•min)], was found in the Right Supramarginal Gyrus; the smallest, 12.7 [mL/(100g•min)], in the Right Parahipocampal Gyrus (Fig. 3).
Fig. 3.
Plot of CBF values [mL/100g*min] vs. ROI for AD patients (red, n = 12) and HC (blue, n = 20). Left (solid) and right (striped) hemispheres are shown separately. Error bars represent ± 1 SE across subjects in each group.
All ROIs showed a significant CBF decrease in AD patients compared to HC, [αcorrected = 0.05, P < 0.0001]. There was no significant difference between the left and right hemispheres for any of the ROIs in either group [paired t test, P > 0.98 for all ROIs].
Area under the ROC curve for GM and Temporal Lobe Left were 0.94 and 0.93, respectively. Temporal Lobe Left was selected as the ROI with the highest t-value [t = 5.9] while GM ROI was selected to assess the power of global CBF changes in discriminating ADs from HCs. The ROC curve for the global GM ROI was used to determine the CBF cutoff for optimum sensitivity and specificity. For a CBF cut-off of 46 [mL/(100gr•min)] a 100% sensitivity and 85% specificity was achieved. When the specificity value was increased to 95% to match that of the covariance analysis, the sensitivity decreased to 58% and the CBF cut-off to 35 [mL/(100gr•min)]. In this case, in addition to the control subject who was also misidentified by the covariance analysis, 5 additional AD patients (mean age = 76.8 ± 2.1, mean mMMS = 41.4 ± 12.1, 2 males) were misdiagnosed as controls.
To check whether the observed difference in mean CBF values could be at least partially explained by the difference in the arterial transit time between the two groups, CBF images acquired with PLD = 0.8 s were compared with those acquired with longer PLD = 1.0 s in 6 AD subjects. The rationale was that if the PLD of 0.8 s was not sufficiently long for our ascending acquisition, an underestimation of CBF (due to the saturation of labeled spins destined for the upper slices) would be expected in the superior regions of the brain compared to images acquired with longer PLD = 1.0s. A two-tailed t-test showed no significant difference in Precentral Gyrus (our most superior ROI) mean CBF acquired with two different PLD values [t = 2.2, P = 0.58].
The only ROI for which there was a significant positive correlation in AD between mMMS scores and CBF was Supramarginal Gyrus with [R2 = 0.33, P=0.05].
Voxel-wise analysis
Fig. 4 shows the SPM {T} map for the (HC-AD) contrast, [thresholded t = 5.73, corrected p < 0.05] overlaid on a surface rendering of the brain (Fig. 4A) and in a 3D view overlaid on the SPGR of one of the HC subjects (Fig. 4B). Areas that showed a significant CBF decrease in AD vs. HC are listed in Table 3.
Fig. 4.
Voxelwise SPM{T}map for the (HC - AD) contrast [corrected, p < 0.05] overlaid on: A) surface rendering of the brain, B) 3D sections of the SPGR of one of the HC subjects.
Table 3.
Areas showing significant decrease in CBF (AD vs. HC) from voxelwise analysis [corrected, p < 0.05]. (Highlighted rows show areas that were also identified with multivariate analysis)
| MNI coordinates [X, Y, Z] | Location | Brodmann Area |
|---|---|---|
| [-55, -47, 41] | Inferior Parietal Lobule | 40 |
| [44, -44, 19] | Superior Temporal Gyrus | 13 |
| [0, -43, 33] | Cingulate Gyrus | 31 |
| [-61, -20, -7] | Middle Temporal Gyrus | 21 |
| [38, -24, -21] | Fusiform Gyrus | 20 |
| [-30, -44, 46] | Precuneus | 7 |
For the AD group, the regression analysis yielded areas with significant correlation [t > 5.7, uncorrected p < 0.001] between CASL CBF and mMMS scores in Parahippocampal Gyrus (BA 28, 30) and Middle Temporal Gyrus (BA 8, 21). There was no voxelwise effect of gender in neither of the groups.
Supplementary split-half analysis comparing voxelwise univariate and multivariate results
One criterion for the evaluation of the relative efficacies of univariate and multivariate approaches is how well their respective findings generalize beyond a particular data set to any other independently acquired data. To this end, we performed an extensive split-half analysis: we arbitrarily split both the AD and HC groups in half and re-derived the AD-related covariance in one half and then forward applied the result to the other half. We performed such split-half analyses 10,000 times and recorded the group-contrast t-statistic and AUC for the derivation sample, but computed it in the replication sample also, i.e., in the AD and HC subjects that were left out of the analysis. Although the group strengths for replication and derivation samples are now quite low (6 AD and 10 HC), this demonstration nevertheless gives a sense of the robustness of the covariance approach.
To afford a comparison with univariate techniques, we also recorded the voxel with the highest t-value for the AD-HC contrast in the derivation sample and computed AUC in that sample. The prospective check was then simple: we computed t-contrast and AUC for the same voxel, but in the replication sample.
For simple graphical depiction that enables a quick comparison we plotted histograms of the following ratios for both univariate and multivariate analysis (Fig. 5).
AUC-ratio = AUC (replication sample)/AUC (derivation sample)
t-ratio = t-statistic (replication sample)/t-statistic (derivation sample).
Fig. 5.

Ratios of t-statistic (left column) and AUC (right column), plotted for both univariate (top row) and multivariate approaches (bottom row). Ratios were defined as the value obtained for the replication sample divided by the value obtained for the derivation sample. Ratios approaching or surpassing unity indicate good replicability.
Good relative replicability implies ratios approaching and possibly surpassing unity. From Fig.5, one can unequivocally discern that the multivariate method is superior in terms of replicability.
This is true not only in relative, but also in absolute terms as shown in Table 4, where listed are the mean ± s.d. of t-statistic and AUC values in derivation and replication samples for both approaches.
Table 4.
List of mean ± s.d. of t-statistic and AUC values for derivation and replication samples from both univariate and multivariate voxelwise analysis.
| Derivation samples | Replication samples | |
|---|---|---|
| Univariate T | 9.8064 ± 1.7214 | 2.1174 ± 0.9351 |
| Multivariate T | 5.8350 ± 1.4653 | 4.0799 ± 1.0297 |
| Univariate AUC | 0.9558 ± 0.0092 | 0.7624 ± 0.0983 |
| Multivariate AUC | 0.9395 ± 0.0185 | 0.8991 ± 0.0482 |
The univariate approach results in superior values for the derivation samples, but this cannot be reproduced in the replication samples. Although the univariate T-contrasts are higher than the multivariate ones in the derivation samples, the discriminability as measured by the AUC value is not much different. However, the multivariate approach, while yielding more modest values in the derivation sample, holds up much better in absolute terms in the replication samples.
DISCUSSION
This study is the first to report on whole-brain CASL CBF measurements in AD and the establishment of an AD-related CBF covariance pattern that contrasts AD and controls at baseline. This covariance pattern identified by the multivariate analysis showed very robust group difference in its subject expression. This held not only for the t-test of group mean differences, but on a subject-by-subject basis, as evidenced by the ROC characteristics of the discrimination (AUC = 0.97) misdiagnosing as AD only one out of 20 healthy controls (a 79 year old, female, mMMS=53). Interestingly, females in the HC group seemed to have a non-significantly higher covariance pattern expression than males, i.e., showing more `AD-like' behavior. This was not true for the AD group where the effect of gender was highly non-significant.
The global GM ROI analysis was also highly discriminatory of the disease-control status, having, however, a somewhat lower specificity than the multivariate analysis (0.85 vs. 0.95) for a 100% sensitivity. In addition to the one healthy control subject misdiagnosed by the covariance analysis, the GM ROI analysis misdiagnosed 2 additional controls (both females, ages 76 and 70 years with mMMS scores of 56 and 54, respectively). Furthermore, when the specificity was increased to match that of the covariance analysis, the sensitivity of global GM ROI dropped to 58%.
The definition of ROIs can be quite arbitrary across studies and tends to vary both in size and tissue content. This makes the generalization of the results across studies quite difficult. For example, in the CASL study by Alsop et al. (Alsop et al. 2000) the ROIs selected were whole lobe regions from which 6 out of 8 reached significance only at uncorrected level (p < 0.01). In that study, the ROIs were hand drawn potentially including both GM and WM tissue types. In 17 our study, the ROIs were individually defined for each subject using a publicly available atlas and including only voxels with a posterior probability of being GM > 0.8.
In general, multivariate analysis might have increased sensitivity compared to univariate analysis even when the disease-related changes in CBF originate in clearly circumscribed foci and spread spatially during the disease course (Scarmeas et al. 2004). Multivariate analysis can detect these subtle, but robust, changes while univariate analysis might suffer from overly stringent false-positive corrections that tend to "correct away" the true effects (as evidenced by the results of our voxelwise analysis.) The areas pinpointed in the AD-related pattern were mainly located in the mediotemporal lobe and have face validity in terms of AD pathophysiology (Hoffman et al. 2000), but did not reach significance in the univariate voxel-by-voxel analysis.
Critical to our study would be to compare the predictive utility of the AD-related covariance pattern (obtained through multivariate analysis) with the between groups mean CBF difference (based on ROI analysis) when applied to the MCI subjects who have not yet reached the full AD diagnosis. For the multivariate analysis, the expression levels of any AD-related covariance pattern should hold similar predictive powers as our group found with H2O15 PET studies (Scarmeas et al. 2004) where the forward application of the identified covariance pattern to a population with mild to minimal cognitive impairment but no dementia discriminated subjects into those with higher and lower cognitive and functional performance, and predicted differential rates of decline in subsequent follow-up. In contrast to the CASL data presented here, the PET study (Scarmeas et al. 2004) showed no significant differences between groups for the univariate analysis at both ROI and voxel-wise level. This could be explained by the lack of absolute quantification of the PET data and the need for normalization, which could add to the noise in the data.
One of the advantages of CASL MRI is that it offers a direct and absolute quantification of CBF without the need for injection of expensive and potentially harmful exogenous tracers. One of the confounds, however, of the CASL measurement is transit time, namely, the time it takes labeled water to reach the tissue in a given voxel. If the average transit time for one group is lower than that of the other, then a difference in CBF will be detected which cannot be unambiguously attributed to an absolute difference in CBF. To make CASL less sensitive to transit time, Alsop et al. (Alsop and Detre 1996) introduced a delay (PLD) between the end of the labeling pulse and start of the image acquisition. This delay allows more time for blood to arrive and exchange with the tissue. In the presence of vascular disease a longer PLD would be preferable because transit time could potentially be longer (Alsop and Detre 1996); the trade off, however, is a decrease in SNR due to T1 relaxation.
In this study, we focused our analysis in the GM where most of the dementia-related changes are expected to occur (Scarmeas et al. 2004). Although we did not explicitly measure the transit time difference between the groups, we conjecture that the transit times were not significantly different based on the following: 1) There was no significant difference in CASL CBF values acquired with two different PLDs indicating that the shorter PLD we chose for this study was optimum. 2) From the acquisition standpoint, we opted for longer labeling duration (2.0s) and a moderate length PLD (0.8s) bringing the total time range from 2.8 s for the most inferior slice to 3.7 s for the most superior. 3) Our analysis was based on GM tissue for which the CASL measurement is less sensitive to transit time (Alsop and Detre 1996) because of the similarity in T1 between blood and GM, ~1.4 s and ~1.2 s, respectively (Alsop and Detre 1996). 4) It is still not clear whether AD is (at least partially) a vascular disease. We screened AD patients for cerebrovascular disease with careful neurological history and examination. Subjects with history of clinical stroke or imaging evidence of cortical or lacunar infarcts were excluded. Thus, at least clinically, AD patients were not expected to have longer transit time than the controls. However, the transit time could still be a confound in our findings. White matter abnormalities, which to a certain degree are considered a correlate of subclinical microvessel disease, are more common in AD as compared to healthy (Barber et al. 1999). Their presence, even if not yet visible, would potentially increase the transit times. If the goal is to estimate the absolute depression of CBF in AD, the transit time constitutes a confound as the measured decreased would be inflated by a transit time difference. However, if one wants a method that simply distinguishes the two groups at early stages of AD, the effect of transit times would be of little relevance.
In the study by Alsop et al. (Alsop et al. 2000), the CASL implementation was similar to ours but only univariate analysis was applied. The mean GM CBF for AD group in our study is similar to that of Alsop et al., 36 vs. 34 [mL/(100g•min)], respectively. In contrast, for our HC group, the mean GM CBF observed was higher, 62 vs. 38 [mL/(100g•min)]. One of the explanations for this discrepancy could be that we only analyzed voxels with high posterior probability of being GM while in the Alsop et al. study each ROI was hand-drawn from an atlas and therefore could have potentially included WM, which is known to have lower CBF than GM (Alsop and Detre 1996). However, a direct comparison between the two studies is not trivial as in addition to WM inclusion, there are several other differences: First, Alsop et al. study provided only partial coverage of the brain; ours is a whole brain coverage, which ensures that valid data are obtained from all the subjects but can consequently include more noise in the upper slices. Second, in that study it is not clear whether the slice acquisition time was accounted for in the PLD values used for CBF computation. We correct for slice acquisition time, which ensures that our ROI CBF values are independent of the slice number in the acquisition order. Third, in our ROI analysis we did not perform any spatial smoothing whereas CBF images were smoothed with a 12 mm kernel prior to ROI analysis in Alsop et al. study. Another advantage of our CASL implementation was that it was based on SE EPI, which allowed for investigation of areas such as inferior region of the frontal lobe and part of the temporal lobe superior to mastoid sinuses that were lacking in the Alsop et al. study due to susceptibility effects in gradient echo EPI. In general, however, the data from the two studies are in good agreement with each other indicating a promising trend toward using CASL as a tool for detection of CBF abnormalities associated with AD.
Although a direct comparison with PASL studies is not straightforward, it is worth mentioning that Du et al. (Du et al. 2006) showed good specificity and sensitivity in separating ADs from controls using PASL. Furthermore, this group addressed the issue of the partial volume effect by calculating the ASL signal in each voxel based on posterior probability maps and assuming, from PET data, that WM CBF is 40% lower that GM (Du et al. 2006). Our analysis was similar in that we too calculated CBF based on posterior probability masks but circumvented the issue of partial voluming effect by analyzing only voxels with P[GM] > 0.8 rather than making assumptions about WM CBF. In general, due to sensitivity of CASL to transit time effect in WM, any inclusion of this tissue type in CBF computations would lead to an overestimation of CBF (Wang et al. 2003).
Technical advancements in MRI combined with the application of more powerful statistical analysis tools will most likely increase the sensitivity of ASL in detecting CBF changes for early detection, diagnosis, and monitoring of diseases. Theoretically, ASL signal is expected to increase with Bo due to two main factors: an inherent increase in MR SNR with Bo, and a longer longitudinal relaxation time of labeled arterial water (Wang et al. 2002). Wang et al. have provided a theoretical framework for the dependence of ASL signal with Bo (Wang et al. 2002). They found that in the absence of T2* effect (appropriate for SE-EPI), CASL SNR is expected to increase ~ 3 times at 3 T compared to 1.5 T (Wang et al. 2002). Furthermore, using gradient echo EPI, Wang et al. have reported that compared to a standard volume coil, an 8-channel array coil with (2-fold) and without acceleration provided a 45% and 56% decrease in intrasubject standard deviation, respectively (Wang et al. 2005).
In conclusion, we have shown the utility of combining CASL perfusion MRI with multivariate and univariate statistical procedures to characterize the baseline CBF differences between AD and HC. Furthermore, we have identified an AD-related covariance pattern that we think holds greater promise in early detection of the disease and prediction of conversion to AD the MCI than the more standard univariate methods.
ACKNOWLEDGEMENTS
This study was supported in part by the Alzheimer's Association grant IIRG-04-1353 and the National Institutes of Health grant RO1 AG26158. We thank Mathew Tabert, Ph.D., for his contribution in recruiting subjects and Hamed Mojahed, M.Sc., for his help with data acquisition. We are grateful to Xavier Golay, Ph.D, and Eric Zarahn, Ph.D., for their invaluable expertise.
REFERENCES
- Alsop DC, Detre JA. Reduced transit-time sensitivity in noninvasive magnetic resonance imaging of human cerebral blood flow. J Cereb Blood Flow Metab. 1996;16:1236–1249. doi: 10.1097/00004647-199611000-00019. [DOI] [PubMed] [Google Scholar]
- Alsop DC, Detre JA. Multisection cerebral blood flow MR imaging with continuous arterial spin labeling. Radiology. 1998;208:410–416. doi: 10.1148/radiology.208.2.9680569. [DOI] [PubMed] [Google Scholar]
- Alsop DC, Detre JA, Grossman M. Assessment of cerebral blood flow in Alzheimer's disease by spin-labeled magnetic resonance imaging. Ann Neurol. 2000;47:93–100. [PubMed] [Google Scholar]
- Barber R, Scheltens P, Gholkar A, Ballard C, McKeith I, Ince P, Perry R, O'Brien J. White matter lesions on magnetic resonance imaging in dementia with Lewy bodies, Alzheimer's disease, vascular dementia, and normal aging. J Neurol Neurosurg Psychiatry. 1999;67:66–72. doi: 10.1136/jnnp.67.1.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benton A, Hamsher A. Multiligual Aphasia Examination. University of Iowa; Iowa City: 1976. [Google Scholar]
- Buschke H, Fuld PA. Evaluating storage, retention, and retrieval in disordered memory and learning. Neurology. 1974;24:1019–1025. doi: 10.1212/wnl.24.11.1019. [DOI] [PubMed] [Google Scholar]
- Du AT, Jahng GH, Hayasaka S, Kramer JH, Rosen HJ, Gorno-Tempini ML, Rankin KP, Miller BL, Weiner MW, Schuff N. Hypoperfusion in frontotemporal dementia and Alzheimer disease by arterial spin labeling MRI. Neurology. 2006;67:1215–1220. doi: 10.1212/01.wnl.0000238163.71349.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. CRC Press, LLC; New York: 1994. [Google Scholar]
- El Fakhri G, Kijewski MF, Albert MS, Johnson KA, Moore SC. Quantitative SPECT leads to improved performance in discrimination tasks related to prodromal Alzheimer's disease. J Nucl Med. 2004;45:2026–2031. [PubMed] [Google Scholar]
- Floyd TF, Ratcliffe SJ, Wang J, Resch B, Detre JA. Precision of the CASL-perfusion MRI technique for the measurement of cerebral blood flow in whole brain and vascular territories. J Magn Reson Imaging. 2003;18:649–655. doi: 10.1002/jmri.10416. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. "Mini-mental state". A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Golay X, Hendrikse J, Lim TC. Perfusion imaging using arterial spin labeling. Top Magn Reson Imaging. 2004;15:10–27. doi: 10.1097/00002142-200402000-00003. [DOI] [PubMed] [Google Scholar]
- Gonzalez RG, Fischman AJ, Guimaraes AR, Carr CA, Stern CE, Halpern EF, Growdon JH, Rosen BR. Functional MR in the evaluation of dementia: correlation of abnormal dynamic cerebral blood volume measurements with changes in cerebral metabolism on positron emission tomography with fludeoxyglucose F 18. AJNR Am J Neuroradiol. 1995;16:1763–1770. [PMC free article] [PubMed] [Google Scholar]
- Habeck C, Krakauer JW, Ghez C, Sackeim HA, Eidelberg D, Stern Y, Moeller JR. A new approach to spatial covariance modeling of functional brain imaging data: ordinal trend analysis. Neural Comput. 2005;17:1602–1645. doi: 10.1162/0899766053723023. [DOI] [PubMed] [Google Scholar]
- Herholz K, Schopphoff H, Schmidt M, Mielke R, Eschner W, Scheidhauer K, Schicha H, Heiss WD, Ebmeier K. Direct comparison of spatially normalized PET and SPECT scans in Alzheimer's disease. J Nucl Med. 2002;43:21–26. [PubMed] [Google Scholar]
- Hoffman JM, Welsh-Bohmer KA, Hanson M, Crain B, Hulette C, Earl N, Coleman RE. FDG PET imaging in patients with pathologically verified dementia. J Nucl Med. 2000;41:1920–1928. [PubMed] [Google Scholar]
- Hughes CP, Berg L, Danziger WL, Coben LA, Martin RL. A new clinical scale for the staging of dementia. Br J Psychiatry. 1982;140:566–572. doi: 10.1192/bjp.140.6.566. [DOI] [PubMed] [Google Scholar]
- Hutchinson M, Nakamura T, Moeller JR, Antonini A, Belakhlef A, Dhawan V, Eidelberg D. The metabolic topography of essential blepharospasm: a focal dystonia with general implications. Neurology. 2000;55:673–677. doi: 10.1212/wnl.55.5.673. [DOI] [PubMed] [Google Scholar]
- Johnson KA, Jones K, Holman BL, Becker JA, Spiers PA, Satlin A, Albert MS. Preclinical prediction of Alzheimer's disease using SPECT. Neurology. 1998;50:1563–1571. doi: 10.1212/wnl.50.6.1563. [DOI] [PubMed] [Google Scholar]
- Johnson NA, Jahng GH, Weiner MW, Miller BL, Chui HC, Jagust WJ, Gorno-Tempini ML, Schuff N. Pattern of cerebral hypoperfusion in Alzheimer disease and mild cognitive impairment measured with arterial spin-labeling MR imaging: initial experience. Radiology. 2005;234:851–859. doi: 10.1148/radiol.2343040197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan E, Goodglass H, Weintraub S. Boston Naming Test. Lea &Febiger; Philadelphia: 1983. [Google Scholar]
- Maldjian JA, Laurienti PJ, Burdette JH. Precentral gyrus discrepancy in electronic versions of the Talairach atlas. Neuroimage. 2004;21:450–455. doi: 10.1016/j.neuroimage.2003.09.032. [DOI] [PubMed] [Google Scholar]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM. Clinical diagnosis of Alzheimer's disease: report of the NINCDS-ADRDA Work Group under the auspices of Department of Health and Human Services Task Force on Alzheimer's Disease. Neurology. 1984;34:939–944. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]
- Moeller JR, Nakamura T, Mentis MJ, Dhawan V, Spetsieres P, Antonini A, Missimer J, Leenders KL, Eidelberg D. Reproducibility of regional metabolic covariance patterns: comparison of four populations. J Nucl Med. 1999;40:1264–1269. [PubMed] [Google Scholar]
- Moeller JR, Strother SC, Sidtis JJ, Rottenberg DA. Scaled subprofile model: a statistical approach to the analysis of functional patterns in positron emission tomographic data. J Cereb Blood Flow Metab. 1987;7:649–658. doi: 10.1038/jcbfm.1987.118. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Ghilardi MF, Mentis M, Dhawan V, Fukuda M, Hacking A, Moeller JR, Ghez C, Eidelberg D. Functional networks in motor sequence learning: abnormal topographies in Parkinson's disease. Hum Brain Mapp. 2001;12:42–60. doi: 10.1002/1097-0193(200101)12:1<42::AID-HBM40>3.0.CO;2-D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson HE, O'Connell A. Dementia: the estimation of premorbid intelligence levels using the New Adult Reading Test. Cortex. 1978;14:234–244. doi: 10.1016/s0010-9452(78)80049-5. [DOI] [PubMed] [Google Scholar]
- Parkes LM, Rashid W, Chard DT, Tofts PS. Normal cerebral perfusion measurements using arterial spin labeling: reproducibility, stability, and age and gender effects. Magn Reson Med. 2004;51:736–743. doi: 10.1002/mrm.20023. [DOI] [PubMed] [Google Scholar]
- Sandson TA, O'Connor M, Sperling RA, Edelman RR, Warach S. Noninvasive perfusion MRI in Alzheimer's disease: a preliminary report. Neurology. 1996;47:1339–1342. doi: 10.1212/wnl.47.5.1339. [DOI] [PubMed] [Google Scholar]
- Scarmeas N, Habeck CG, Zarahn E, Anderson KE, Park A, Hilton J, Pelton GH, Tabert MH, Honig LS, Moeller JR, Devanand DP, Stern Y. Covariance PET patterns in early Alzheimer's disease and subjects with cognitive impairment but no dementia: utility in group discrimination and correlations with functional performance. Neuroimage. 2004;23:35–45. doi: 10.1016/j.neuroimage.2004.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverman DH, Small GW, Chang CY, Lu CS, Kung De Aburto MA, Chen W, Czernin J, Rapoport SI, Pietrini P, Alexander GE, Schapiro MB, Jagust WJ, Hoffman JM, Welsh-Bohmer KA, Alavi A, Clark CM, Salmon E, de Leon MJ, Mielke R, Cummings JL, Kowell AP, Gambhir SS, Hoh CK, Phelps ME. Positron emission tomography in evaluation of dementia: Regional brain metabolism and long-term outcome. Jama. 2001;286:2120–2127. doi: 10.1001/jama.286.17.2120. [DOI] [PubMed] [Google Scholar]
- Stern Y, Sano M, Paulson J, Mayeux R. Modified mini-mental state examination: validity and reliability. Neurology. 1987;37:179. [Google Scholar]
- Wang J, Alsop DC, Li L, Listerud J, Gonzalez-At JB, Schnall MD, Detre JA. Comparison of quantitative perfusion imaging using arterial spin labeling at 1.5 and 4.0 Tesla. Magn Reson Med. 2002;48:242–254. doi: 10.1002/mrm.10211. [DOI] [PubMed] [Google Scholar]
- Wang J, Alsop DC, Song HK, Maldjian JA, Tang K, Salvucci AE, Detre JA. Arterial transit time imaging with flow encoding arterial spin tagging (FEAST) Magn Reson Med. 2003;50:599–607. doi: 10.1002/mrm.10559. [DOI] [PubMed] [Google Scholar]
- Wang Z, Wang J, Connick TJ, Wetmore GS, Detre JA. Continuous ASL (CASL) perfusion MRI with an array coil and parallel imaging at 3T. Magn Reson Med. 2005;54:732–737. doi: 10.1002/mrm.20574. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Wechler Adult Intelligence Scale Revised. The Psychological Corp; New York: 1981. [Google Scholar]
- Wechsler D. Wechler Test of Adult Reading. The Psychological Corporation; San Antonio, Texas: 2001. [Google Scholar]
- Werner R, Norris DG, Alfke K, Mehdorn HM, Jansen O. Improving the amplitude-modulated control experiment for multislice continuous arterial spin labeling. Magn Reson Med. 2005;53:1096–1102. doi: 10.1002/mrm.20443. [DOI] [PubMed] [Google Scholar]