Dynamics of tRNA at Different Levels of Hydration

Abstract

The influence of hydration on the nanosecond timescale dynamics of tRNA is investigated using neutron scattering spectroscopy. Unlike protein dynamics, the dynamics of tRNA is not affected by methyl group rotation. This allows for a simpler analysis of the influence of hydration on the conformational motions in RNA. We find that hydration affects the dynamics of tRNA significantly more than that of lysozyme. Both the characteristic length scale and the timescale of the conformational motions in tRNA depend strongly on hydration. Even the characteristic temperature of the so-called “dynamical transition” appears to be hydration-dependent in tRNA. The amplitude of the conformational motions in fully hydrated tRNA is almost twice as large as in hydrated lysozyme. We ascribe these differences to a more open and flexible structure of hydrated RNA, and to a larger fraction and different nature of hydrophilic sites. The latter leads to a higher density of water that makes the biomolecule more flexible. All-atom molecular-dynamics simulations are used to show that the extent of hydration is greater in tRNA than in lysozyme. We propose that water acts as a “lubricant” in facilitating enhanced motion in solvated RNA molecules.

Introduction

Water plays a crucial role in the structure, dynamics, and function of biological macromolecules (1–9). Dehydration of DNA results in a conformational change from a native B-form to a particular A-form (8,9). Similarly, dehydration strongly suppresses protein dynamics and enzymatic activity, which are accelerated dramatically upon an increase in hydration level (1–7). Although hydration and its role in protein dynamics and activity have been studied extensively, much less is known about the influence of hydration on the dynamics of RNA (10). For example, it is not known how similar the hydration dependence of the dynamics of RNA is to that of globular proteins, or whether the difference in the chemical structure of nucleic acids compared to amino acids plays an important role.

Quasi-elastic neutron scattering (QENS) spectroscopy has been used to study the internal dynamics of biological macromolecules (1–7,10–12) because it measures the characteristic time and length scales of molecular motions directly. Hydrogen atoms provide the main contribution to the neutron scattering spectra because of their incoherent scattering cross section that is ∼40 times larger than that of a deuterium atom. Because the H-atoms are distributed homogeneously in biological macromolecules, the motions of the H-atoms reflect the global motions of the molecule.

QENS studies on proteins, DNA, and RNA have demonstrated significant activation of local motions upon hydration (1–7,10–12). A sharp rise in the mean-squared atomic displacement (〈r²〉) with temperature above ∼200–230 K (the so-called “dynamical transition temperature,” T_D) has been observed only in hydrated biomolecules with a sufficient hydration level and is absent in dry molecules. It is commonly believed that the molecular motions responsible for the dynamical transition are a consequence of structural relaxation arising from transitions between different conformational substates (2,4,13), and may closely regulate biochemical activity (14–17), although some studies have suggested otherwise (18–20).

It has been extensively reported that the dynamical transition of biomolecules is strongly coupled to the onset of translational motions of hydration water (21–23). However, there is an active discussion about the origin of the dynamical transition and whether it has biological significance (24–33). It is currently believed that the T_D is not a direct consequence of any biological transition intrinsic to the biomolecule, but a result of the coupling of the dynamical crossover of water to the dynamics of the biomolecule (24–27) or a simple structural relaxation of the biomolecule that enters the time window of the spectrometer (18,28,30–34). Despite the controversy, the term “dynamical transition” is still used here.

Recent studies of the dynamics of protein lysozyme at different hydration levels demonstrated that conformational motions are strongly suppressed at h below 0.2 (h is the hydration level in g of water per 1 g protein) and then rise sharply with an increase in h from ∼0.2 up to ∼0.5 at T_D (3). The dynamical behavior correlates well with the hydration dependence of the protein enzymatic activity (1,3). However, no detailed studies on the influence of hydration on RNA dynamics have been published so far. We only know that the dynamics of dry and hydrated RNA differ strongly (10).

Here we present detailed QENS studies of the influence of hydration on the dynamics of tRNA in comparison to the dynamics of lysozyme. It is found that the hydration level affects the dynamics of tRNA much more strongly than it does the dynamics of lysozyme. In particular, a clear hydration dependence of T_D is observed for tRNA, whereas T_D is almost independent of hydration for lysozyme. In addition, the relaxation rate and amplitude of the atomic motions in tRNA increase significantly with hydration. Moreover, the average amplitude of intramolecular motions in hydrated tRNA is much larger than in hydrated lysozyme. The results demonstrate a clear difference in the dynamics of tRNA and lysozyme that reflects the difference in their chemical structures.

Materials and Methods

Samples for neutron scattering measurements

Wheat-germ tRNA from Sigma-Aldrich, St. Louis, MO (R7876) was purified with phenol and chloroform. After its dialysis and lyophilization, all exchangeable H-atoms were replaced with D-atoms in 10 mM deuterated Na-cacodylate and 10 mM MgCl₂ (10). The tRNA was hydrated using isopiestic conditions at 100% relative humidity in a desiccator with 99.9% D₂O. Different incubation times provided varying hydration levels (0.20, 0.35, 0.50, and 0.65 h, determined by thermogravimetric analysis).

Neutron scattering measurements

Neutron scattering measurements were performed on the high-flux backscattering spectrometer (HFBS) at the National Institute of Standards and Technology (NIST) Center for Neutron Research (energy resolution ∼0.8 μeV, ∼0.24 GHz, ∼1 ns). Elastic scans were performed from 300 K to 10 K with a cooling rate of 0.7 K/min to estimate 〈r²〉. The QENS spectra were acquired in the energy range of ±17 μeV (∼ ±4 GHz, ∼40 ps) with energy resolution of ∼0.8 μeV. Therefore, QENS spectra monitored the timescale from 1 ns to 40 ps. The accessible range of the scattering wave vector, Q, was 0.25 Å⁻¹ < Q < 1.75 Å⁻¹. The multiple-scattering contribution was negligible since the total neutron scattering from the samples was chosen to be <∼10%.

Simulations of the hydration layer of tRNA and lysozyme

The sole purpose of the simulations was to analyze the hydration shell around the biomolecules. The first hydration layer on the surface of tRNA and lysozyme was reconstructed and quantified by means of molecular-dynamics (MD) simulations. Protein Data Bank (PDB) structures 1EHZ and 2VB1 were used as starting structures for simulations of tRNA and lysozyme, respectively. Modified tRNA residues were modeled as standard residues, and Mn²⁺ ions were replaced with Mg²⁺ ions in the simulation. The structure of lysozyme was resolved at high resolution, and for many residues the PDB entry contained two sets of coordinates. Two structures of lysozyme were simulated: one including rotameric states with higher occupancies, and one including rotameric states with lower occupancies.

The program CHARMM (35) was used for the system setup and subsequent MD runs in conjunction with the CHARMM force field, version 27 (36). The starting structures were briefly minimized and embedded in a preequilibrated water box that enveloped the biomolecule by more than 10 Å, and all overlapping water molecules were removed. The systems were neutralized by placing ions at random locations but not closer than 6 Å to the biomolecule; 57 Na⁺ ions were added to the tRNA system, and six Na⁺ ions and 14 Cl⁻ ions were added to the lysozyme system. The tRNA system was subjected to minimizations under tetragonal symmetry, and the lysozyme system was minimized under rhombic dodecahedral symmetry.

The systems were heated in steps of 2 K, starting from a temperature of 100 K, until 300 K was reached. Then, equilibration in an NPT ensemble was performed for 100 ps. Finally, one 100 ps trajectory, also in an NPT ensemble, was generated. The particle mesh Ewald method was used to describe electrostatic interactions. A more detailed description of the methods and parameters used for MD runs can be found elsewhere (37). For each of the simulated systems, five heating, equilibration, and dynamics runs were performed, with five different seed numbers for the random number generator used to assign initial velocities.

Results

Mean-squared displacements and dynamic structure factor

Because three-quarters of the nonexchangeable H-atoms are distributed on the sugar riboses and the rest are distributed on the bases, the H-atom motions mostly reflect the dynamics of the RNA main chain. We analyzed and compared neutron scattering data obtained here for tRNA with earlier neutron scattering data for lysozyme (10). The mean-squared displacement of H-atoms, 〈r²(T)〉, was estimated from the measured total elastic scattering intensity using a Gaussian approximation (38):

$$\langle r^2\left(T\right)\rangle =-3Q^{-2}\text{In}[I_{el}(Q,T)/I_{el}(Q,10k)]\text{.}$$ (1)

Here I_el(Q,10K) is the elastic intensity at T = 10 K, at which almost all motions are suppressed. The Gaussian approximation works well at a low scattering wave vector, Q; therefore, only data in the Q-range from 0.35 Å⁻¹ to 1.00 Å⁻¹ were used to estimate 〈r²〉. Fig. 1 shows 〈r²〉 of tRNA and lysozyme at different levels of hydration. The 〈r²(T)〉 is an integrated quantity that includes contributions from vibrations, rotations, and conformational and translational motions on a timescale faster than ∼1 ns (defined by the spectrometer resolution).

Figure 1.

Mean-squared atomic displacement, 〈r²〉, as a function of temperature for (A) tRNA and (B) protein lysozyme (data from Roh et al. (3,39)) at different levels of hydration. The accurate 〈r²〉 of biomolecules hydrated more than 0.70 h for tRNA and 0.50 h for lysozyme was not obtained due to crystallization of bulk D₂O (3,39). Insets show the additional hydration-induced contribution to the mean-squared displacements = 〈r²〉_Add = 〈r²〉 − 〈r²〉_Dry.

Dry tRNA and lysozyme exhibit a smooth increase in 〈r²〉 with temperature. However, 〈r²〉 at T = 300 K is significantly larger in dry protein than in dry RNA (Fig. 1). The difference has been ascribed to the contribution of the methyl group rotation, which is significant in proteins (∼25% of nonexchangeable H-atoms in proteins are on methyl groups) but is negligible in tRNA (∼3%) (3,10,39). Both molecules show weak changes in 〈r²〉 with levels of hydration at h ≤ 0.2 and sharp variations at higher h (Fig. 1). There are, however, three major differences between tRNA and lysozyme in the hydration dependence of = 〈r²〉:

• 1.Hydration up to h ∼ 0.65 can be achieved in tRNA without crystallization of water, whereas for lysozyme crystallization of water is observed at h ∼ 0.50 as a sharp irregular behavior of 〈r²〉 (3,39).
• 2.The difference between hydrated and dry systems in the amplitude of the H-atom motion is significantly larger in tRNA compared to lysozyme: 〈r²〉_Add = 〈r²〉_Wet − 〈r²〉_Dry (Fig. 1, insets).
• 3.Although the dynamical transition temperature, T_D (defined as the temperature at which the sharp increase in 〈r²〉 is observed), exhibits strong hydration dependence in tRNA, it is largely unchanged in lysozyme.

Fig. 2 shows the dynamic structure factor, S(Q,v), of RNA at T = 300 K at different hydration levels. The spectral shape is essentially Q-independent (Fig. 3), so the spectra were summed over all Q to obtain better statistics. No significant quasielastic intensity is observed in the spectrum of the dry RNA, whereas a strong QENS contribution (ascribed primarily to the methyl group dynamics) is usually observed in spectra of dry proteins (3,39). Strong QENS intensity appears in RNA at h ∼ 0.20, which is consistent with the rise in 〈r²〉. The QENS intensity increases significantly with hydration at h > 0.2. This behavior is similar to previous results for proteins (3,39).

Figure 2.

Dynamic structure factor, S(Q,v), of RNA at T = 300 K and different levels of hydration. The spectra are summed up over all measured Q.

Figure 3.

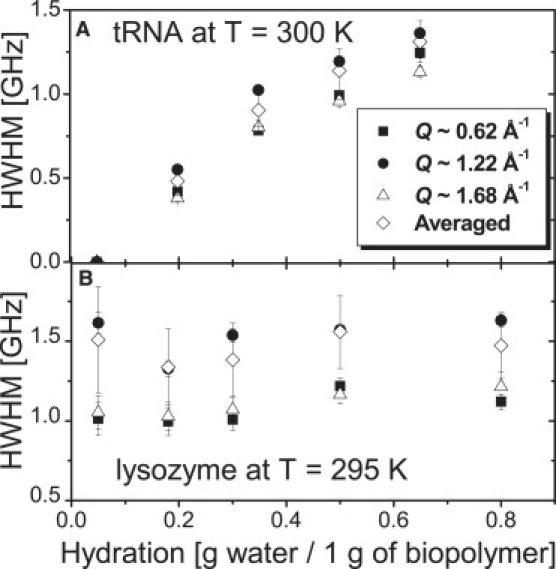
Hydration dependence of the halfwidth at half-maximum, Γ, obtained from the fit of the QENS spectra by a single Lorentzian function at different Q values: (A) tRNA at T = 300 K and (B) lysozyme at T = 295 K.

Estimate of the number of water molecules at different hydration levels

MD was used to estimate the number of hydration waters around lysozyme and tRNA. MD simulations are the most widely used technique for computational modeling of macromolecular dynamics. With careful application, longer simulations than ours can provide useful information about the dynamics and hydration of RNA (40–42). We emphasize, however, that the dynamics of tRNA or the details of the hydration pattern of tRNA are not the goal of our short MD study. Its focus is an estimate of the number of water molecules at different hydration levels that can be compared with experimental data.

The first hydration layer is completed when the whole surface area is covered by water molecules. In simulations, the number of water molecules in the first hydration shell was determined using the criterion that the water oxygen atoms were within 3.5 Å of nonhydrogen atoms of the tRNA. The results (Fig. 4, A1 and A2), which represent averages over all MD runs and 10 snapshots for each of the runs, show that 820 ± 13 and 340 ± 11 water molecules complete the first hydration layer (∼3.5 Å) of tRNA and lysozyme, respectively. The corresponding hydration levels are 0.61 h and 0.42 h. Thus tRNA has ∼45% more water molecules in the first hydration shell (per gram of dry biomolecule) than lysozyme.

Figure 4.

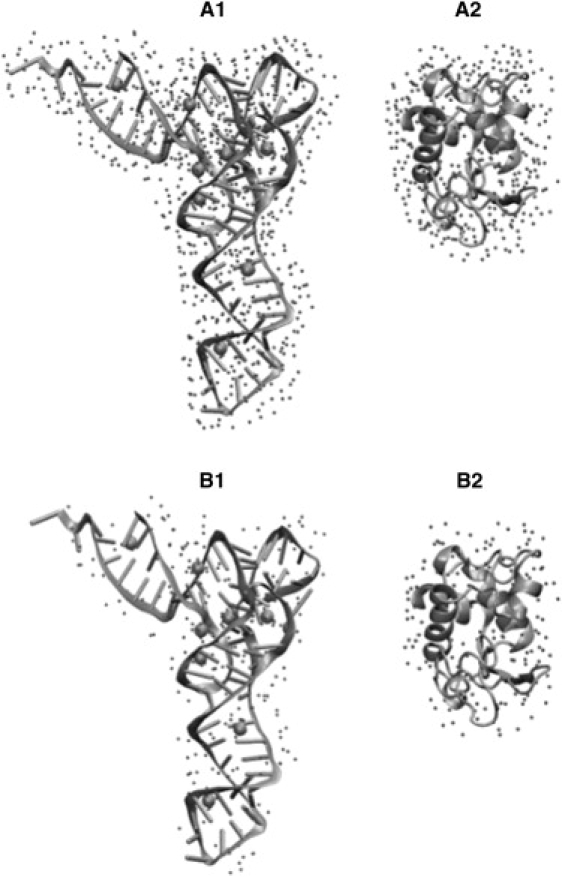
Snapshots from MD simulations of tRNA and lysozyme. Water molecules (small spheres) in the first hydration layer (within 3.5 Å of the surface of the biomolecule) are shown for tRNA in A1 and for lysozyme in A2. Water molecules that approximate the hydration level h = 0.2 in MD simulations are shown for tRNA in B1 and for lysozyme in B2.

From the numbers calculated above for the first hydration shell, the number of water molecules surrounding tRNA and lysozyme at the hydration level h = 0.2 can be estimated as 269 and 162, respectively. Analysis of the MD simulations shows that the average number of water oxygen atoms within 2.74 Å of nonhydrogen atoms of tRNA is 265. For lysozyme, on average 156 water oxygen atoms can be found within 2.9 Å of the biomolecule. The locations of water oxygen atoms within these cutoffs (2.74 Å from tRNA, and 2.9 Å from lysozyme) reveal that at hydration level h = 0.2 water molecules are distributed more inhomogeneously around tRNA than around lysozyme (Fig. 4 B). For tRNA, water molecules cluster around Mg²⁺ ions and regions of strong negative electrostatic potential near the junction between the D and T loops (Fig. 4 B1).

Hydration layers from MD simulations based on the distance-dependent cutoff displayed in Fig. 4 may not correspond precisely to the hydration of the semidry sample. Furthermore, the tRNA sample contains a larger number of Mg²⁺ ions than the simulations. This may result in additional asymmetries in hydration patterns of tRNA, since the simulations suggest that water molecules prefer to cluster around Mg²⁺ ions at low hydration levels. What is important is that our simulations predict a much less uniform distribution of hydration waters around tRNA compared to lysozyme.

Discussion

Because of its molecular structure and negative charge, tRNA is predicted to have a more extended network of hydration water on its surface than lysozyme (Fig. 4). Based on the smooth increase in = 〈r²〉 (Fig. 1), we did not observe any signs of water crystallization in hydrated tRNA even at h ∼ 0.65, whereas crystallization was observed in lysozyme at h ∼ 0.50 (3,39). tRNA absorbs and binds more water molecules than lysozyme (first hydration layer: 0.61 h for tRNA and 0.42 h for lysozyme) because it has a larger hydrophilic surface area and a more open structure in comparison to lysozyme.

Previous computational studies estimated the total solvent-accessible surface area (SASA) of tRNA and lysozyme using the static loci of each atom in tRNA (43) or lysozyme (44) that makes van der Waal's contact with solvent. The total SASAs of tRNA and lysozyme are ∼13,400 Ų and ∼6,000 Ų, respectively. Based on the total surface area, the specific SASAs of tRNA and lysozyme are N_A0.56 Ų/g and N_A0.42 Ų/g, respectively (N_A is the Avogadro number). This means that tRNA is 33% more open to the solvent than lysozyme. The bases, sugars, and phosphates have a similar solvent-accessible area in the 3D structure of RNA, including major and minor grooves (45,46).

Using the SASA, the numbers of hydrating water molecules in unit surface volume for tRNA and lysozyme are estimated to be 0.018/ų and 0.016/ų, respectively. This suggests that tRNA has ∼13% more hydrophilic sites than lysozyme. Previous calculations of the SASA (43,44) indicated that the surface fractions of hydrophilic sites of tRNA and lysozyme are 67% (43) and 59% (44) of the total SASA, respectively. Therefore, the surface of tRNA is 14% more hydrophilic than that of lysozyme, consistent with our simulation results.

Although tRNA needs more water to form its first hydration shell, the amplitude of the hydration-induced additional motions is larger in tRNA than in lysozyme even at the same hydration level. For example, tRNA and lysozyme at h ∼ 0.35 exhibit 〈r²〉_Add = 0.8 and 0.55 Ų, respectively (Fig. 1, insets). 〈r²〉_Add is 1.8 times larger in tRNA than in lysozyme, at hydration levels close to their first hydration shells (∼0.65 h and ∼0.45 h).

The larger scale of the motions in RNA implies that hydrated RNA is more flexible than hydrated protein. The higher flexibility in hydrated RNA may originate from 1), a more flexible hydrated phosphate backbone compared to the amide backbone in protein, especially in nonhelical sites (47,48); 2), the 33% more open structure of native tRNA with major and minor grooves compared to the globular structure of protein with a hydrophobic core; and 3), the 14% higher surface fraction of hydrophilic sites in the tRNA chain that can interact with water molecules.

The more open structure and higher surface fraction of hydrophilic sites allow more water molecules to be placed on the tRNA surface and provide a 45% larger number density of hydrating water for tRNA than for lysozyme. It was reported that a higher density of hydration water in the first hydration layer leads to more fluidic behavior due to H-bond fluctuations with neighboring water molecules or polar atoms of tRNA (24,27).

An interesting observation is the significant shift of T_D in tRNA with hydration (Fig. 1 A, inset). T_D ∼ 240 K is observed for RNA at h ∼ 0.2. An increase in hydration up to h ∼ 0.35 and h ∼ 0.5 shifts T_D down to 230 K and 220 K, respectively. This result suggests that the additional hydration-induced motions in tRNA slow down significantly under dehydration. In contrast, T_D in lysozyme is almost constant with hydration at h ≥ 0.2 and is difficult to observe at h < 0.2 (Fig. 1 B, inset). Therefore, it is obvious that only hydrated biomolecules at h ≥ 0.2, where the H-bonds form a network, exhibit the dynamical transition (1,3,39). We conclude that 0.2 h is the threshold hydration level below which the structural relaxation of the biopolymer is strongly suppressed.

The origin of the dynamical transition of hydrated biomolecules is still unclear. Plausible scenarios include a glass transition that is induced either by increasing the free volume by water or by coupling the dynamical crossover of water with the dynamics of biomolecules (24–27). Alternatively, it may be simply a structural relaxation in hydrated biopolymers that enters the time window of the spectrometer employed for observation (18,28,30–34). Indeed, a recent comparison of neutron scattering and dielectric relaxation data in hydrated lysozyme identified the protein structural relaxation and followed its behavior across the dynamic transition (28,34). This relaxation process exhibits a smooth, slightly non-Arrhenius temperature dependence and approaches the neutron spectrometer resolution window at T∼T_D, causing the observed sharp rise in 〈r²〉. A similar analysis for tRNA would help to unravel the origin of the dynamic transition and its dependence on hydration level in this biomolecule.

A hydration-assisted relaxation process is clearly visible as the strong QENS contribution in the spectra of tRNA (Fig. 2). Analysis of the dynamic structure factor can help unravel the microscopic details of the motions underlying this relaxation process. The absence of any significant QENS intensity in dry tRNA provides significant advantage in analysis of the spectra of the relaxation process that appears in hydrated tRNA (in contrast to proteins, where a correction for the methyl group contribution is required (3,39)).

The dynamic structure factor of RNA (Fig. 2) can be written as

$$S(Q,v)=DW\left(Q\right)[EISF\left(Q\right)+S_{\text{Add}}(Q,v)]\otimes R\left(v\right)\text{.}$$ (2)

Here, DW(Q) is the Debye-Waller factor that takes into account the vibrational amplitude of the atoms; EISF(Q) is the elastic incoherent structure factor, defined as the ratio of elastic scattering intensity to the total (elastic plus quasielastic) scattering intensity; and R(v) is the spectrometer resolution function. We used S(Q,v) of tRNA at h ∼ 0.50 measured at T = 10 K as the resolution function. The S_Add(Q,v) of hydrated tRNA represents the quasielastic scattering contribution due to additional hydration-induced relaxation motions, whereas S_Add(Q,v) of hydrated protein includes the dynamics of methyl group H-atoms that is insensitive to hydration as well as hydration-induced dynamics (see Roh et al. (3) for a detailed analysis of S(Q,v) of dry and hydrated proteins).

The S(Q,v) at each Q was fit to Eq. 2 assuming a single Lorentzian spectral shape for S_Add(Q,v). We emphasize that a single Lorentzian fit is not a good approximation for the stretched relaxation spectra usually observed in biological macromolecules. However, it provides important qualitative information for analysis of the relaxation process.

Fig. 3 shows the half width at half-maximum (Γ) of S_Add(Q,v) obtained from the fit of the QENS spectra. The value of Γ for RNA increases significantly with hydration (Fig. 3 A), in contrast to the behavior observed for lysozyme (Fig. 3 B). Γ exhibits no significant Q dependence at any hydration level of the protein (Fig. 3 B), indicating that this process is localized. In the case of lysozyme, methyl group dynamics contribute together with the additional hydration-induced motions to the QENS spectra (Fig. 3 B) (3,39). As a result, Γ remains large even in the spectra of dry protein because the methyl group dynamics is essentially independent of hydration (3,39).

The observed strong dependence of Γ on hydration of RNA suggests that the structural relaxation process accelerates with an increase in accessible water molecules. This result is consistent with the significant downshift of RNA's T_D with increase in h (Fig. 1 A, inset). Both suggest that the addition of hydration water lowers the activation energy barrier for the structural relaxation in RNA.

Of interest, the Γ of 0.5 h tRNA (∼1.15 GHz, ∼140 ps) is fairly similar to the translational relaxation time (∼150 ps) of hydrating water at ∼0.5 h on RNA reported in a previous study (27) that employed the same neutron scattering spectrometer (NG2, NIST). Besides, the relaxation time of hydrated lysozyme after the correction of methyl group rotation lies in the time range close to the translational motions of hydrating water (∼20–50 ps) (3,24,34). This implies that the dynamics of fully hydrated tRNA is more strongly coupled to the dynamics of hydration water without being disturbed by methyl group rotation, unlike protein lysozyme (21–24).

Analysis of the EISF(Q) provides information on the geometry of the relaxation process and the mobile fraction of H-atoms involved. The EISF(Q) is proportional to the probability that the H-atoms do not move to a distance larger than the length scale R ∼ 2π/Q during the time defined by the spectrometer resolution function (∼1 ns for HFBS used in our experiment). The value of EISF(Q) was obtained from fits of the spectra for tRNA to Eq. 2 (Fig. 5). The EISF(Q) for lysozyme was previously reported (3,39). It shows very peculiar behavior at all hydration levels: it decays rapidly at low Q < 0.6–0.8 Å⁻¹ and then is essentially independent of Q (Fig. 5). This behavior can be described by the model of free diffusion in a sphere (49):

$$EISF\left(Q\right)=1-p_{\text{mobile}}+p_{\text{mobile}}{\left[\frac{3j_1\left(Qa\right)}{Qa}\right]}^2\text{.}$$ (3)

Here, p_mobile represents the mobile fraction of H-atoms involved in the relaxation process existing in the energy window between ∼1 μeV (∼0.24 GH, ∼1 ns) and ∼17 μeV (∼4 GHz, ∼40 ps). The parameter a is a radius of the sphere in which the H-atoms diffuse, and j₁ is the Bessel function. Analysis of the EISF(Q) in Fig. 6 shows that both p_mobile and the length scale of the motions a for the tRNA increase with hydration. The hydration dependence of p_mobile and a for lysozyme was reported in previous studies (3,39), which showed that only p_mobile increases with hydration.

Figure 5.

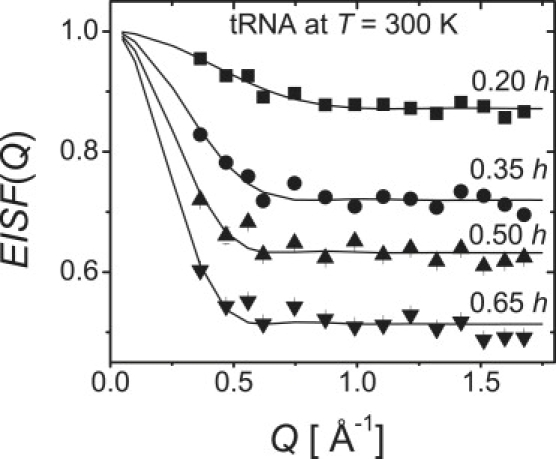
EISF(Q) of tRNA (symbols) at T = 300 K and its fit to the model of diffusion in a sphere.

Figure 6.

Mobile fraction and length scale of the relaxation motion of tRNA obtained from the fit of EISF(Q) at T = 300 K to the model of diffusion in a sphere (Fig. 5).

It is a striking observation that the length scale of the relaxation process in tRNA at 0.65 h is ∼7 Å (Fig. 6). This is twice as large as the value reported for lysozyme ∼3.0 Å at the same hydration level (3,39), which is consistent with the larger 〈r²〉 of hydrated RNA in comparison to 〈r²〉 of hydrated protein (Fig. 1). This result implies that a higher level of hydration allows tRNA to explore a larger dynamic landscape on the same timescale because of its higher chain flexibility. This is comparable with the relaxation rate of the motions promoted by hydration in tRNA (Fig. 3).

A comparison of the dynamics of tRNA with the dynamics of lysozyme shows two qualitative differences in their hydration dependence that underscore their structural differences. All proteins have methyl groups that act as internal plasticizers, leading to local rotational motions for the protein structure and dynamics. This results in the dry state of protein being more flexible than RNA. The difference is clearly shown in the measured = 〈r²〉 for tRNA and lysozyme in the dry state (Fig. 1). However, with hydration, tRNA becomes more flexible than lysozyme. This difference and the observed stronger hydration dependence of the dynamics of tRNA may be related to their difference in biological functions, as has been suggested in the case of lysozyme (3,39).

The difference between tRNA and lysozyme in the length scale of motions observed in experiments is also observed in MD simulations. Root mean-square fluctuations (RMSFs) around the average structure were calculated during the 100 ps long MD runs for all nonhydrogen atoms of tRNA and lysozyme. The RMSFs are averages over all performed MD runs. A large number of uncertainties in the simulations (insufficient equilibration and data collection times, uncertainties in force fields, and locations of ions), as well as a lack of one-to-one correspondence between simulations of fully solvated biomolecules and semidry samples, preclude us from making a direct link between the computations and experiments. Nonetheless, the RMSFs reveal that the most mobile residues of tRNA are located in the regions of the acceptor stem, the anticodon arm, and also include a few unpaired bases. These results are in qualitative agreement with a previous MD study of tRNA (50). The RMSFs of lysozyme show that residues that have the largest motilities on this timescale are located mostly in loops, at edges of secondary structure elements, and at the C-terminus. The total RMSFs are 1.1 Å and 0.8 Å for tRNA and lysozyme, respectively. The total root mean-square deviation (RMSD) values from the initial structure were calculated in a similar fashion and are 3.1 Å and 1.7 Å for tRNA and lysozyme, respectively.

A recent MD simulation and NMR studies showed that the bulges or helix junctions in HIV transactivation response (TAR) RNA undergoes large hinge motions on nanosecond timescales (51,52). Therefore, the large motions (on a scale of ∼7 Å; Fig. 6) observed in the fully hydrated tRNA at h > 0.65 (first hydration shell) probably originate from the global motions of intersecondary structures centered on nonhelix sites between which no tertiary interactions exist, for example, between the acceptor stem and the TψC loop stem, or between the anticodon stem and the D loop stem. More open and flexible structure and larger fraction of hydrophilic sites that interact with hydration water probably undergo relatively large amplitude motion (in comparison to lysozyme).

Conclusions

Our study provides insight into the effect of different levels of hydrating water on the dynamics of chemically and structurally different biological macromolecules. The analysis of the neutron scattering data reveals that the dynamics of tRNA varies much more strongly with hydration than the dynamics of protein lysozyme. In particular, increased hydration of tRNA leads to a shift of the observed T_D and a corresponding decrease of the structural relaxation time. This result clearly indicates that the energy barrier for structural relaxation in tRNA decreases with an increase in hydration. The characteristic length scale of the relaxation motion in tRNA is almost twice as large as in lysozyme. The more hydrophilic and more open structure of RNA (in comparison to lysozyme) apparently results in the larger amplitude of hydration-induced structural relaxation in this biomolecule. This study on the dynamics of RNA and protein with various hydration levels demonstrates that biomolecules with different chemical structures exhibit significantly different dynamic responses to the hydration water. Therefore, the dynamics of biomolecules should not be described simply as being universally driven by the dynamics of solvent alone. Rather, the structures of the biomolecules and their interaction with the hydration solvent determine their dynamics.