Osmotic Transport across Cell Membranes in Nondilute Solutions: A New Nondilute Solute Transport Equation

Abstract

The fundamental physical mechanisms of water and solute transport across cell membranes have long been studied in the field of cell membrane biophysics. Cryobiology is a discipline that requires an understanding of osmotic transport across cell membranes under nondilute solution conditions, yet many of the currently-used transport formalisms make limiting dilute solution assumptions. While dilute solution assumptions are often appropriate under physiological conditions, they are rarely appropriate in cryobiology. The first objective of this article is to review commonly-used transport equations, and the explicit and implicit assumptions made when using the two-parameter and the Kedem-Katchalsky formalisms. The second objective of this article is to describe a set of transport equations that do not make the previous dilute solution or near-equilibrium assumptions. Specifically, a new nondilute solute transport equation is presented. Such nondilute equations are applicable to many fields including cryobiology where dilute solution conditions are not often met. An illustrative example is provided. Utilizing suitable transport equations that fit for two permeability coefficients, fits were as good as with the previous three-parameter model (which includes the reflection coefficient, σ). There is less unexpected concentration dependence with the nondilute transport equations, suggesting that some of the unexpected concentration dependence of permeability is due to the use of inappropriate transport equations.

Introduction

The fundamental physical mechanisms of water and solute transport across cell membranes have long been studied in the field of cell membrane biophysics (1,2). All living cells are enclosed by a plasma membrane that separates the intracellular solution from its extracellular environment. Molecules must cross the phospholipid bilayer of cell membranes to enter or leave the cell. The lipid portion of the membrane is almost always fluid at physiological temperatures. For a molecule to cross the cell membrane, it must enter the lipid region (which is hydrophobic), cross it, and leave the other side of the membrane (3). Since the early 1930s, there have been numerous articles published on the mechanisms of water and solute movement across cell membranes (1,4–10). Water can cross the cell membrane by diffusion through the lipid bilayer when a concentration gradient is present, but some cells exhibit a more rapid transmembrane water transport through specialized protein water channels known as aquaporins (10–12).

Cryobiology is a discipline in which it is important to have an understanding of osmotic transport across cell membranes under nondilute solution conditions. The rate of osmotic transport is critical to cryopreservation protocols. For cells in suspension, when freezing is initiated, ice forms initially outside of the cells, concentrating the solutes in the remaining liquid of the extracellular solution. As a result, water leaves the cell by exosmosis until osmotic equilibrium is reached. If exosmosis is slow compared to the cooling rate, remaining intracellular water will be sufficiently supercooled to freeze, which is normally lethal. On the other hand, if exosmosis is rapid compared with the cooling rate, cells are exposed to increasingly concentrated conditions at relatively high temperatures that are also lethal. To modulate cell responses to cooling, cryoprotectants are normally used. In general, the cell will respond osmotically to both the addition and removal of cryoprotectants as well as to changes occurring during freezing. As a result, an understanding of osmotic transport across cell membranes is important in predicting successful outcomes from cryopreservation protocols. The water (solvent) and cryoprotectant (solute) permeability parameters are used to calculate cellular osmotic responses during the addition and removal of cryoprotectants, and osmotic responses during cooling to and warming from low temperatures (13–15). The permeability parameters may also be used to determine whether solute and water movement occurs through channels or by solubility-diffusion through the lipid bilayer (4,12,16,17).

Many of the transport formalisms currently used make limiting dilute-solution assumptions. While dilute solution assumptions are often appropriate under physiological conditions, they are rarely appropriate in cryobiology where cryoprotectants are often used at high concentrations and the presence of extracellular ice further concentrates the solutions. The first objective of this article is to present a detailed look at the current status of osmotic transport and to point out the explicit and implicit assumptions in commonly-used transport equations. The second objective of the article is to present a set of nondilute transport equations, including a new solute transport equation. An example of how to use the new transport equations with human corneal epithelial cell data is provided.

Osmolality as a Function of Concentration

There are several different ways to express the concentration including molarity (C), osmolarity (π(C)), molality (m), and osmolality (π(m)). The molarity is defined as the number of moles of solute per liter of solution. Since the molarity depends on solution volume, there is a temperature dependence. The osmolarity is defined as the number of moles of solute, per liter of solution, of an ideal, dilute solute that would be needed to produce the same osmotic activity as a particular concentration of a nondilute solute. Like the molarity, the osmolarity is temperature-dependent. A measure of concentration that is as easy to use as the molarity is the molality. The molality is defined as the number of moles of solute per kilogram of solvent. As it is directly related to a weight-per-unit-weight expression of concentration, the molality value of a solution does not change with variations in temperature or pressure. Similar to osmolarity, the osmolality is defined as the number of moles of an ideal, dilute solute, per kg of solvent, which would be needed to produce the same osmotic activity as a particular concentration of a nondilute solute.

There are a number of mathematical relationships in the literature to describe osmolality as a function of concentration. The osmotic virial equation, first proposed by McMillan and Mayer in 1945 (18), is one of the most widely-used thermodynamic equations of state. The osmotic virial equation for a solution containing a single solute, i, describes the osmolality, π, as a polynomial in molality of the solute, m_i,

$$\pi =m_{\mathrm{i}}+B_{\mathrm{i}}{m}_{\mathrm{i}}^2+C_{\mathrm{i}}{m}_{\mathrm{i}}^3+\dots \text{.}$$ (1)

Values for the osmotic viral coefficients, B_i and C_i, can be determined experimentally (19). For many simple solutes, the osmotic virial equation can usually be truncated to include only second-order terms, but the third-order terms are needed for macromolecules (19).

When determining the osmolality of a multisolute solution, it is often assumed that the contribution of each solute to the overall osmolality of the solution is additive (14,20). Elliott et al. (19) recently pointed out that summing the osmolalities for individual solutes in a multisolute solution does not account for the interactions between solutes. Accounting for the solute-solute interactions is necessary in nondilute solutions. Consider a form of the osmotic virial equation (truncated to second-order) that extends to a ternary solution, with two solutes, i and j:

$$\pi =m_{\mathrm{i}}+m_{\mathrm{j}}+B_{\mathrm{i}}^{}{m}_{\mathrm{i}}^2+B_{\mathrm{j}}^{}{m}_{\mathrm{j}}^2+2B_{\text{ij}}^{}{m}_{\mathrm{i}}{m}_{\mathrm{j}}\text{.}$$ (2)

The cross-coefficient, B_ij, accounts for interactions between solutes i and j. To determine the cross-coefficient, most approaches require measurements of the ternary system and the coefficient is found by regressing ternary data, similar to the method used to determine the second virial coefficients from measurements of binary solutions (21). Elliott et al. (19) derived and proposed a simple arithmetic mixing rule to predict for the cross-coefficient in the absence of multisolute data. For a nondilute solution of two solutes, the osmolality is expressed as (19)

$$\pi =m_{\mathrm{i}}+m_{\mathrm{j}}+B_{\mathrm{i}}^{}{m}_{\mathrm{i}}^2+B_{\mathrm{j}}^{}{m}_{\mathrm{j}}^2+\left(B_{\mathrm{i}}^{}+B_{\mathrm{j}}^{}\right)m_{\mathrm{i}}{m}_{\mathrm{j}}\text{.}$$ (3)

Equations 1–3 are easily applied to solutes that dissociate, i.e., salts like KCl or NaCl, by replacing m by Km, where K is a dissociation constant for which we also fit. This form of the osmotic virial equation is a very good approximation for the biological salts of interest (19).

The osmotic virial equation is just one of many approaches for determining the osmolalities of a nondilute solution. For example, the myriad of nondilute equations incorporating activity coefficients could alternatively have been used (22). The advantage of the osmotic virial formulation given by Eq. 3 is that it can predict the osmolalities of ternary and higher order solutions without requiring ternary measurements a priori to fit for coefficients. Although summing the osmolalities of individual solutes in a multisolute solution does not accurately account for interactions between solutes, it nevertheless leads to predictions of solute osmolalities that are accurate to a few percent in some cases (23,24). In addition, in the cases where ternary measurements have been made, accurate empirical equations can be developed for some solutes that could also have been used in place of Eq. 3 (25,26). However, the error can be large in some cases, depending on the cryoprotectant used (i.e., dimethyl sulfoxide). In some cases, the addition of osmolalities is not accurate within a few percent and the error due to summing osmolalities is larger (19).

Theories of Osmotic Transport

Jacobs and Stewart

In 1932, Jacobs and Stewart (1) quantitatively measured cell membrane permeability. A mathematical analysis based on Fick's Law of Diffusion was developed to describe the volume of a cell exposed to a solution containing a permeating solute by making five simplifying assumptions:

• 1.The concentration in the extracellular solution remained constant during the course of the experiment.
• 2.Diffusion across the cell membrane was slower than in the body of the solution or the interior of the cell so that the only gradient that needed consideration was that across the membrane.
• 3.The concentration gradient across the cell membrane may be expressed as $\frac{C^{\mathrm{o}}-C^{\mathrm{i}}}{l}$, where C^o is the concentration outside, Cⁱ is the concentration inside the cell, and l is the thickness of the membrane.
• 4.The thickness of the membrane remained constant during the course of the experiment.
• 5.The osmotic pressure for a given substance may be taken as directly proportional to its concentration.

Based on these assumptions, they developed two coupled differential equations to describe the simultaneous transport of water and a permeable solute,

$$\frac{d{V}_{\mathrm{w}}}{dt}=k_{1}A\left(\frac{\tilde{S}+C_{\mathrm{o}}{V}_{\mathrm{o}}}{V}-C_{\mathrm{s}}-C_{\mathrm{n}}\right),$$ (4)

where $\frac{d{V}_{\mathrm{w}}}{dt}$ is the rate of change in cell water volume (V_w) with time (t), k₁ is the water permeability constant, A is the cell surface area, $\tilde{S}$ is the amount of internal permeating solute, C_o is the initial internal concentration of nonpermeating solutes, V_o is the initial volume of water in the cell, C_s is the external concentration of the permeating solute, and C_n is the external concentration of nonpermeating solute,

$$\frac{d\tilde{S}}{dt}=k_{2}A\left(C_{\tilde{\mathrm{s}}}-\frac{\tilde{S}}{V}\right),$$ (5)

where $\frac{d\tilde{S}}{dt}$ is the rate of change in the amount of internal permeating solute $\left(\tilde{S}\right)$ with time and k₂ is the solute permeability constant. In both of the equations, Jacobs and Stewart stated that the concentrations are taken to be osmolar (1,2), indicating that the expression for concentration should be in units of osmolarity, but used molarity in that study. They also recognized (1) that they were making the limiting assumption that the osmotic pressures of the solutions were linearly related to the concentration. Hence, they developed a set of equations in which a dilute solution assumption was made.

Modern two-parameter formalism

The two parameter (2-P) formalism, developed from the work of Jacobs and Stewart (1,2), is commonly used today to describe cellular osmotic responses in the presence and absence of a permeable solute,

$$\frac{d{V}_{\mathrm{w}}}{dt}=-L_{\mathrm{p}}ART\left({\pi }^{\mathrm{e}}-{\pi }^{\mathrm{i}}\right),$$ (6)

where L_p (μm³/μm²/min/atm) is the membrane hydraulic conductivity and is a measure of the rate of water movement across the cell membrane, R is the universal gas constant, T is absolute temperature, π^e is the extracellular solution osmolarity, and πⁱ is the intracellular solution osmolarity. To describe the solute flux, the following equation is sometimes used in the literature (27–29):

$$\frac{d{N}_{\mathrm{s}}}{dt}=P_{\mathrm{s}}A\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\text{.}$$ (7)

Here $\frac{d{N}_{\mathrm{s}}}{dt}$ is the rate of change in the intracellular number of permeating solute molecules with time, P_s (cm/s) is the solute permeability and is a measure of the rate of solute permeability across the cell membrane, $C_{\mathrm{s}}^{\mathrm{e}}$ is the extracellular solute molarity, and $C_{\mathrm{s}}^{\mathrm{i}}$ is the intracellular solute molarity. To convert from a solute flux to a volume flux, we can multiply by the partial molar volume of the solute, v_s, as

$$\frac{d{V}_{\mathrm{s}}}{dt}=v_{\mathrm{s}}\frac{d{N}_{\mathrm{s}}}{dt}=v_{\mathrm{s}}{P}_{\mathrm{s}}A\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\text{.}$$ (8)

These equations are coupled by the definition of the intracellular molarity (14):

$$\left(C^{\mathrm{i}}=C_{\mathrm{n}}^{\mathrm{i}}+C_{\mathrm{s}}^{\mathrm{i}}\right)\text{.}$$

Note that for a dilute solution, πⁱ = mⁱ = Cⁱ (where again it is understood that for salts, m should be replaced by Km).

In attempting to generalize Eq. 5 from dilute solutions to more general solutions, it has been common to use molality or osmolality as a proxy for solute activity. The osmolarity represents the water activity. As a result, Eq. 4 is correctly generalized to Eq. 6 for nondilute solutions by using osmolarity rather than molarity as the concentration units. In contradiction to the body of literature existing (14,30), it is not thermodynamically correct to generalize Eqs. 5 and 7 to a nondilute form in an analogous manner (by replacing molarity with osmolarity), since it is the solute chemical potential difference that is the driving force and osmolarity is related to the chemical potential of water in the presence of solute. As long ago as 1976, it was pointed out that the correct driving force for the solute was activity of the solute (31); however, this is not always put into practice. Equation 5 was developed based on Fick's Law—an ideal, dilute equation stating that solute flux is proportional to the gradient in solute concentration.

For the concentration appearing in the parentheses of Eq. 6 osmolarity is often used interchangeably with osmolality. For the hydraulic conductivity in Eq. 6 to have units of (μm³/μm²/min/atm), the concentration must be in terms of osmolarity (or molarity). To convert between the two expressions of concentration, one must use the value for the density of water. For a dilute solution, the molarity is proportional to the molality with the proportionality being the water density. The density of water is equal to 1 g/cm³ at 4°C and 1 atm of pressure. This may be why, in biological literature, osmolality and osmolarity are often used interchangeably. However, this is strictly only true for a dilute solution at 4°C at 1 atm. Furthermore, because the solute volume is included in the denominator of molarity, but not the solute weight in the denominator of molality, molarities and molalities (and likewise osmolarities and osmolalities) differ appreciably when the solute makes up a significant portion of the solution. Thus, even if willing to neglect the temperature affect on osmolarity, while either osmolarity or osmolality could be used when fitting Eq. 6, care should be exercised when using coefficients fit in one set of units to make predictions from the other units in highly concentrated solutions.

In their work, Jacobs and Stewart (1,2) did indicate that the expression for concentration should have units of osmolar, but it appears that they were actually using molar, not osmolar, concentrations. In using molar concentration instead of osmolar, an implicit dilute solution assumption is being made. Equation 6 developed by Jacobs and Stewart could be extended to include nondilute solutions if the expression for concentration used is actually osmolarity. In the literature it is often assumed that if the 2-P model is being used, there are no dilute solution restrictions on the equations (14), and that the equations are a good approximation for molar solute concentrations up to a few molar when osmolality and molality are used in the water and solute flux equations.

Staverman

Most natural processes, such as diffusion and permeation, are irreversible (3). Much of our understanding of transport phenomena is based on linear irreversible thermodynamics, and cell volume change due to solute and solvent flow across cell membranes is an example of such a phenomenon. In 1951–1952, Staverman approached the problem of osmotic transport across cell membranes by using the linear theory of irreversible thermodynamics (32,33), which was formalized most notably by Onsager in 1931 (34,35). Staverman examined permeability in leaky membranes (i.e., those permeable to solutes). The leakage of a membrane was described by a reflection coefficient, $\tilde{\sigma }$, ranging from 0 for a completely permeable membrane (unselective membrane) to 1 for a semipermeable membrane (permeable to the solvent only and impermeable to the solute molecules). A value of $\tilde{\sigma }$ = 1 indicated that 100% of the solutes get reflected back from the membrane. The reflection coefficient is concentration-dependent and describes the selectivity of the membrane to a specific solute (32) so the value of $\tilde{\sigma }$ is determined by both the properties of the membrane and the permeable solute. Staverman specified that these conditions were for a dilute system with a single permeating solute and were inappropriate to use for concentrated or multicomponent systems, but could be generalized to cover systems for which linear flux equations were applicable (32,36).

Kedem and Katchalsky

In 1958, Kedem and Katchalsky modified and extended the work of previous authors also using Onsager's irreversible thermodynamics approach (37). The theory is based on the premise that for a system sufficiently close to equilibrium, any flux (such as heat flux or mass flux) is linearly proportional to a driving force (or a gradient in an intensive property such as pressure or concentration). Kedem and Katchalsky developed a formalism to describe osmotic transport across a cell membrane when water and solute transport across a membrane are coupled, usually through cotransport in a common channel. As a result, the water and solute interact and the degree of interaction between the solvent and solute was characterized by a reflection coefficient, σ. However, the equations developed were general enough to be applied empirically to a number of transport situations in the presence or absence of cotransport channels. In the Kedem-Katchalsky (K-K) equations, three parameters are used to characterize the membrane permeability: the water permeability (hydraulic conductivity, L_p); the solute mobility $\left(\tilde{\omega }\right)$; and the reflection coefficient (σ). The solute mobility may be expressed as a solute permeability, $P_{\mathrm{s}}=\tilde{\omega }RT$, where R is the universal gas constant and T is absolute temperature.

Assuming dilute solutions and near-equilibrium conditions, Kedem and Katchalsky developed transport equations by considering mass transport across a cell membrane. The rate of total volume change of the cell was described by (37)

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=-L_{\mathrm{p}}ART\left\{\left(C_{\mathrm{n}}^{\mathrm{e}}-C_{\mathrm{n}}^{\mathrm{i}}\right)+\sigma \left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\right\},$$ (9)

where L_p is the membrane hydraulic conductivity, A is the surface area of the cell, R is the universal gas constant, and T is absolute temperature. The value C is the molarity with the superscripts denoting the internal cell solution (i) and the solution external to the cell (e) and the subscripts denoting the nonpermeating solutes (n) and the permeating solutes (s). Although they used Staverman's concept of a reflection coefficient, Kedem and Katchalsky used a reflection coefficient σ, that has a different physical meaning than the reflection coefficient $\tilde{\sigma }$ used by Staverman.

The equation to describe the change in intracellular, permeating solute is given as

$$\frac{d{N}_{\mathrm{s}}}{dt}=\left(1-\sigma \right)\left(\frac{1}{2}\right)\left(C_{\mathrm{s}}^{\mathrm{e}}+C_{\mathrm{s}}^{\mathrm{i}}\right)\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}+P_{\mathrm{s}}A\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right),$$ (10)

where N_s is the number of moles of solute in the cell and P_s is the membrane solute permeability.

The value σ is constrained by the condition

$$0\le \sigma \le 1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{RT{L}_{\mathrm{p}}}\text{.}$$ (11)

Kedem and Katchalsky assumed that the solute and solvent transport were physically coupled (37) and that the degree of interaction was characterized by the reflection coefficient. They assumed that solvent and solute interacted with each other, and that the extent of the interaction in the passage through the membrane depended on the nature of the system. Systems in which the solvent and solute followed different paths through the membrane had the lowest degree of interaction, such as aqueous solutions of lipid-soluble substances passing through a mosaic membrane. The highest degree of interaction of solvent and solute occurs in free aqueous diffusion, such as in coarse capillary membranes (37).

Kleinhans

In 1998, Kleinhans pointed out that the K-K formalism and σ were often unnecessary and demonstrated that the 2-P formalism worked just as well as the K-K formalism and essentially gave the same results for a number of different transport situations in which a common channel for solute and solvent was not present. Using simulations, he demonstrated this to be true for a number of circumstances including 1), bilayer transport in which the solute and water diffuse across the bilayer; 2), transport in which water only moves through a selective channel and the solute diffuses across the bilayer; and 3), transport in which the water and solute use separate channels. Kleinhans noted that the 2-P model and the K-K model deviated from each other at high concentrations, but that there were no practical differences between the two models up to solute concentrations of several molar (14).

The Reflection Coefficients σ and $\tilde{\sigma }$

It has been recognized by many in the literature that there are often many interpretational problems with the reflection coefficient when using the K-K equations (14,22,38–40) and the validity and necessity of σ has been questioned (22,41). The K-K equations were designed to deal with cotransport across cell membranes. In deriving the limits for σ, Kedem and Katchalsky used the solute driving force, which was based on the chemical potential of the solute. In deriving the solute driving force equations, both a near equilibrium and a dilute solution assumption were made. The limits of σ for the K-K equations are based on a hydrodynamic interaction. When water and solute move across the membrane using independent pathways, this is the noninteracting case and σ = $1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{RT{L}_{\mathrm{p}}}$. In this case, σ is completely dependent on the values of L_p and P_s and is, therefore, not an independent parameter. For situations where solute and solvent move through a common channel, there is a greater possibility of a hydrodynamic interaction in the membrane. For this interacting case, $\sigma <1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{RT{L}_{\mathrm{p}}}$, and in this situation, σ is an independent parameter, which depends on the strength of the flux interaction (37). In the literature it is often thought that the limits of σ for the K-K equation are the same as those of $\tilde{\sigma }$ in Staverman's original equations. As pointed out by Kleinhans as well (14), people often mistakenly believe that a σ < 1 means that there is a solute-solvent interaction (42), which is not true. In Kleinhans' article, he discusses the issue and misconceptions that are often present when people assume a value of σ = 1. Let us first recall that a σ = 1 means that there is 100% reflection of the solute back from the membrane (no solute permeability, i.e., P_s = 0). If we substitute σ = 1 into the K-K equations, then Eq. 9 takes the form

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=-L_{\mathrm{p}}ART\left(C^{\mathrm{e}}-C^{\mathrm{i}}\right)\text{.}$$ (12)

Kleinhans points out that it is often thought that substituting σ = 1 into the K-K equation, Eq. 12, leads to an equation that looks like the 2-P formalism (Eq. 6). Recall that the 2-P equation in terms of molarity had the form

$$\frac{d{V}_{\mathrm{w}}}{dt}=-L_{\mathrm{p}}ART\left(C^{\mathrm{e}}-C^{\mathrm{i}}\right)\text{.}$$ (13)

Kleinhans argues that when comparing Eq. 13 with Eq. 12, we can see that the 2-P equation accounts for only the water volume flux, whereas Eq. 12 is total volume flux of both the solute and the solvent, so the two equations are not the same.

As Kleinhans discusses, if σ = 1 is substituted into the K-K solute flux equation Eq. 10, it reduces to

$$\frac{d{N}_{\mathrm{s}}}{dt}=P_{\mathrm{s}}A\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right),$$ (14)

which is identical to the 2-P solute flux equation, Eq. 7,

$$\frac{d{N}_{\mathrm{s}}}{dt}=P_{\mathrm{s}}A\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\text{.}$$ (15)

He argues that when σ = 1, there should be no solute flux present and this is part of the confusion when using σ and the K-K equations. This, compounded with the fact that people often use the incorrect limits for σ when using the K-K equations, leads to much confusion. However, it is important to note that by Staverman's definition, σ = 1 means that there is 100% reflection of the solute back from the membrane and no solute permeability (P_s = 0). If P_s = 0, it means that $\frac{d{V}_{\mathrm{s}}}{dt}=0$. As a result, there is no problem when comparing Eq. 6 with Eq. 12. So even though Kleinhans argues that the two equations look different, they are in fact the same, since by definition σ = 1 means that $\frac{d{V}_{\mathrm{s}}}{dt}=0$. Kleinhans argued that when σ = 1, there should be no solute flux present, but says when substituting σ = 1 into the K-K solute flux equation we get Eq. 14. However, again there is no problem with this because when σ = 1, P_s = 0, $\frac{d{N}_{\mathrm{s}}}{dt}=0$, and Eq. 14 is correct. In the literature when using the K-K equations and solving for L_p, P_s, and σ, people often end up with a value of σ = 1 (43) even when P_s ≠ 0. However, in doing this they are violating the conditions of the K-K equations because σ cannot equal 1 if P_s ≠ 0.

In the literature, the 2-P model is often preferred over the K-K model because of the fewer parameters required to describe the osmotic response of cells. People have noted that despite the fact that the K-K model accurately describes cell volume data, the model lacks the capability to detect changes in σ and that it is often phenomenologically inconsistent with application for high permeability solutes (44). It has also been pointed out that the interpretational value of σ to identify the transport pathway can be problematic (5).

Comparing the 2-P and the K-K equations

To look at the total solute and solvent volume flux using the 2-P equations, we add together the water volume flux given in Eq. 6 in terms of molarity, with the solute volume flux given in Eq. 8 and use the definition of the extracellular solution molarity $\left(C^{\mathrm{e}}=C_{\mathrm{n}}^{\mathrm{e}}+C_{\mathrm{s}}^{\mathrm{e}}\right)$ and the intracellular solution molarity $\left(C^{\mathrm{i}}=C_{\mathrm{n}}^{\mathrm{i}}+C_{\mathrm{s}}^{\mathrm{i}}\right)$ to get the following:

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=\frac{d{V}_{\mathrm{w}}}{dt}+\frac{d{V}_{\mathrm{s}}}{dt}=-L_{\mathrm{p}}ART\left\{\left(C_{\mathrm{n}}^{\mathrm{e}}-C_{\mathrm{n}}^{\mathrm{i}}\right)+\left(1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{L_{\mathrm{p}}RT}\right)\left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\right\}\text{.}$$ (16)

We can compare the total volume flux obtained from the 2-P equations with the total volume flux of the K-K equations as given in Eq. 9:

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=-L_{\mathrm{p}}ART\left\{\left(C_{\mathrm{n}}^{\mathrm{e}}-C_{\mathrm{n}}^{\mathrm{i}}\right)+\sigma \left(C_{\mathrm{s}}^{\mathrm{e}}-C_{\mathrm{s}}^{\mathrm{i}}\right)\right\}\text{.}$$ (17)

Note that the two equations look identical except there is a σ in Eq. 9 and in the 2-P equation, Eq. 16, there is instead the expression $\left(1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{L_{\mathrm{p}}RT}\right)$, which is the upper limit of σ in the K-K equations. The upper limit of σ (the noninteracting case) occurs in the situation when water and solute move across the membrane using independent pathways. Therefore, for situations when there is no interaction between the water and solute, the 2-P and the K-K total volume flux equations are identically the same. Kleinhans demonstrated, using simulations, that when cotransporting channels are absent, the 2-P and the K-K equations essentially give the same result. In the literature people have even stated that the 2-P model is more consistent than the K-K model for the assumption of independent pathways, which assumes that water and solute use different pathways to permeate the cell membrane (45). However, the two formalisms arrive at the same equation for the total volume flux in the noninteracting case. People often use the K-K equations with the noninteracting case (42,46). In 1994, Du et al. (22) reported on permeability of human spermatozoa to glycerol using the 2-P model and the noninteracting case of the K-K model. They found that the two models gave essentially identical results. We can understand now that this is because the total volume flux equations are the same. An article in 2003 by Xu et al. (29) reported measurements of chondrocyte membrane permeability to a number of cryoprotectants and compared them using the 2-P model and the K-K model. Examination of their graphs of normalized volume change during dimethyl sulfoxide addition in that study indicates that the 2-P model and the K-K model gave identical results. We calculated the noninteracting value of σ—i.e., $\left(1-\frac{P_{\mathrm{s}}{v}_{\mathrm{s}}}{L_{\mathrm{p}}RT}\right)$ —for that system, and found it resulted in a value of σ = 0.918. The value of σ reported in their article when fitting the K-K equation was 0.91 ± 0.09, again demonstrating that the 2-P and K-K models give identical results for σ in the noninteracting case.

Kleinhans noted that the 2-P model and the K-K model deviated from each other at high concentrations, but there were no practical differences between the two models up to solute concentrations of several molar (14). It is possible then that the fitting of σ is simply adjusting for nondilute behavior, since in both equations a dilute solution assumption is being made. In the literature, it has been reported that there is no pattern that emerges to define how the solute concentration effects membrane permeability characteristics (46,47), and at times researchers found solute inhibition of L_p (46). In some reports, the hydraulic conductivity decreases in the presence of increased solute concentrations (48); in other reports, exposing cells to a permeable solute increases the hydraulic conductivity (49). It is possible that some proportion of these reported variations of the hydraulic conductivity are a result of dilute solution expressions being used in the transport equations and may not appear if nondilute transport equations were utilized. It has been shown in the literature that different values for the hydraulic conductivity and the solute permeability are obtained depending on the set of transport equations used (42,43). This may be problematic when comparing transport results or utilizing the transport values obtained from different research groups to determine optimal cryopreservation protocols.

The confusion of using a reflection coefficient as well as the dilute solution assumptions currently made in the commonly used transport formalisms suggest a need for new nondilute transport equations.

Nondilute solvent transport equations

Consider a cell immersed in a hypertonic or hypotonic solution that undergoes osmotic shrinkage or swelling (Fig. 1), where the intracellular solution contains molecules of water, denoted by $N_1^{\mathrm{i}}$, a permeating solute such as a permeating cryoprotectant like dimethyl sulfoxide (DMSO), denoted as $N_2^{\mathrm{i}}$, and a nonpermeating intracellular solute such as KCl, denoted by $N_3^{\mathrm{i}}$. Assume that the extracellular environment contains molecules of water, $N_1^{\mathrm{e}}$, the permeating solute, $N_2^{\mathrm{e}}$, and a nonpermeating extracellular solute such as NaCl, denoted by $N_4^{\mathrm{e}}$.

Figure 1.

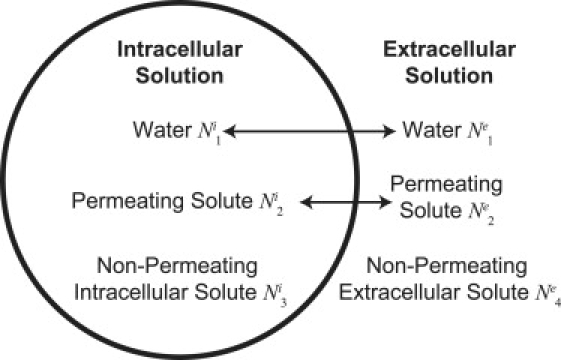
A system of water, a permeating solute, an intracellular nonpermeating solute, and an extracellular nonpermeating solute.

For the solvent transport equation, the change in the number of water molecules with time will be proportional to a water permeability coefficient denoted by $\tilde{L}$, the cell surface area, A, and the difference between the chemical potentials of the water outside $\left({\mu }_{\mathrm{w}}^{\mathrm{e}}\right)$ and inside $\left({\mu }_{\mathrm{w}}^{\mathrm{i}}\right)$ the cell:

$$\frac{d{N}_{\mathrm{w}}^{\mathrm{i}}}{dt}=\tilde{L}A\left({\mu }_{\mathrm{w}}^{\mathrm{e}}-{\mu }_{\mathrm{w}}^{\mathrm{i}}\right)\text{.}$$ (18)

The chemical potential is the thermodynamic property of a solution that drives passive mass transport across a cell membrane. The chemical potential of the water can be derived from solution theory. As an example, a particular form of the osmotic viral equation can be used. The derivation of such a chemical potential of the water has been described elsewhere (19). Briefly, assuming a regular solution, the Gibbs free energy may be written as

$$G\left(T,P,N_1,N_2,N_3\right)=N_1{\mu }_1^{\ast }\left(T,P\right)+N_2\psi \left(T,P\right)+N_3\varphi \left(T,P\right)+N_{1}RT\text{ln}\left(\frac{N_1}{N_1+N_2+N_3}\right)+N_{2}RT\text{ln}\left(\frac{N_2}{N_1+N_2+N_3}\right)+N_{3}RT\text{ln}\left(\frac{N_3}{N_1+N_2+N_3}\right)+\frac{{\omega }_{12}{N}_1{N}_2}{\left(N_1+N_2+N_3\right)}+\frac{{\omega }_{13}{N}_1{N}_3}{\left(N_1+N_2+N_3\right)}+\frac{{\omega }_{23}{N}_2{N}_3}{\left(N_1+N_2+N_3\right)},$$ (19)

where subscript 1 refers to the solvent, ${\mu }_1^{\ast }$ is the chemical potential of the pure solvent, ψ is a function of temperature and pressure related to the standard state (infinite dilution) of the solute denoted by subscript 2, and ϕ is another function of temperature and pressure. The ω_ij values are the interchange energies of species i with species j. To arrive at a theory that does not require ternary data or solute-solute molecular interaction information to obtain values of parameters, the last term of Eq. 19 must be neglected. This will be a good assumption when ω₂₃N₂N₃ << ω₁₂N₁N₂ or ω₁₃N₁N₃. If the interchange energies are similar, this will be a good assumption if N₂ << N₁ or N₃ << N₁. Such an assumption in the Gibbs free energy can be thought of as a semidilute solution assumption, since it still allows second-order terms in the chemical potentials but does not introduce any adjustable parameters in the mixing of second-order terms.

The chemical potential of the solvent, μ₁, can then be found by differentiation:

$${\mu }_1={\mu }_{\mathrm{w}}={\left(\frac{\partial G}{\partial N_1}\right)}_{\text{T},\mathrm{P},{\mathrm{N}}_2,{\mathrm{N}}_3}\text{.}$$ (20)

The natural logarithms can be expanded and terms to second-order can be kept. By simplifying and using the following definitions,

$$B_2^{+}=\frac{1}{2}-\frac{{\omega }_{12}}{RT},$$ (21)

$$B_3^{+}=\frac{1}{2}-\frac{{\omega }_{13}}{RT},$$ (22)

the chemical potential of the water inside the cell in terms of the mole fraction, x, is

$${\mu }_{\mathrm{w}}^{\mathrm{i}}={\mu }_{\mathrm{w}}^{\ast }-RT\left(x_2^{\mathrm{i}}+x_3^{\mathrm{i}}\right)-B_2^{+}RT{\left(x_2^{\mathrm{i}}\right)}^2-B_3^{+}RT{\left(x_3^{\mathrm{i}}\right)}^2-\left(B_2^{+}+B_3^{+}\right)RT{x}_2^{\mathrm{i}}{x}_3^{\mathrm{i}},$$ (23)

where ${\mu }_{\mathrm{w}}^{\ast }$ is the chemical potential of pure water, R is the universal gas constant, T is the temperature, $x_2^{\mathrm{i}}$ is the mole fraction of the intracellular permeating solute, and $x_3^{\mathrm{i}}$ is the mole fraction of the intracellular nonpermeating solute. $B_3^{+}$ is the second osmotic virial coefficients in terms of mole fraction for the nonpermeating intracellular solute.

The chemical potential of the water outside the cell in terms of the mole fraction is given as

$${\mu }_{\mathrm{w}}^{\mathrm{e}}={\mu }_{\mathrm{w}}^{\ast }-RT\left(x_2^{\mathrm{e}}+x_4^{\mathrm{e}}\right)-B_2^{+}RT{\left(x_2^e\right)}^2-B_4^{+}RT{\left(x_4^{\mathrm{e}}\right)}^2-\left(B_2^{+}+B_4^{+}\right)RT{x}_2^{\mathrm{e}}{x}_4^{\mathrm{e}},$$ (24)

where $x_2^{\mathrm{e}}$ is the mole fraction of the extracellular permeating solute, and $x_4^{\mathrm{e}}$ is the mole fraction of the extracellular nonpermeating solute. $B_2^{+}$ and $B_4^{+}$ are the second osmotic virial coefficients in terms of mole fraction for the permeating solute and the nonpermeating extracellular solute, respectively.

Substituting Eqs. 23 and 24 into Eq. 18 yields the expression

$$\frac{d{N}_{\mathrm{w}}^{\mathrm{i}}}{dt}=-\tilde{L}ART\left[\begin{array}{l}\left(x_2^{\mathrm{e}}+x_4^{\mathrm{e}}\right)+B_2^{+}{\left(x_2^{\mathrm{e}}\right)}^2+B_4^{+}{\left(x_4^{\mathrm{e}}\right)}^2+\left(B_2^{+}+B_4^{+}\right)x_2^{\mathrm{e}}{x}_4^{\mathrm{e}}-\\ \left(x_2^{\mathrm{i}}+x_3^{\mathrm{i}}\right)-B_2^{+}{\left(x_2^{\mathrm{i}}\right)}^2-B_3^{+}{\left(x_3^{\mathrm{i}}\right)}^2-\left(B_2^{+}+B_3^{+}\right)x_2^{\mathrm{i}}{x}_3^{\mathrm{i}}\end{array}\right]\text{.}$$ (25)

Equation 25 represents the nondilute solvent transport equation without any dilute solution or near equilibrium assumptions. To write the dilute solution expression for Eq. 25, we would neglect the second-order terms in the equation to yield

$$\frac{d{N}_{\mathrm{w}}^{\mathrm{i}}}{dt}=-\tilde{L}ART\left[\left(x_2^{\mathrm{e}}+x_4^{\mathrm{e}}\right)-\left(x_2^{\mathrm{i}}+x_3^{\mathrm{i}}\right)\right]\text{.}$$ (26)

This equation is identical to the modern-day two-parameter formalism, but is written in terms of mole fraction. It is important to note that Eq. 25 is equivalent to Eq. 6 but with a specific expression for osmolality, π. Therefore, the literature is correct in using Eq. 6 for nondilute solutions.

Nondilute solute transport equations

In the literature, many of the nondilute adjustments to the transport equations correct the solvent transport equations but not the solute transport equations. In the solute transport equations currently utilized in the literature, either a dilute solution assumption or near-equilibrium assumption or both assumptions are made. Unlike the solvent transport equations, the solute transport equations cannot be extended to nondilute situations by simply replacing molality with osmolality. To derive a new set of solute transport equations, we will again consider an example situation of a cell that is immersed in a hypertonic or hypotonic solution and undergoes osmotic shrinkage or swelling (Fig. 1).

For the solute transport equations, the change in the number of solute molecules as a function of time will be proportional to a solute permeability coefficient denoted by $\tilde{P}$; the cell surface area, A; and the difference in the chemical potential of the permeating solute outside $\left({\mu }_{\mathrm{s}}^{\mathrm{e}}\right)$ and inside $\left({\mu }_{\mathrm{s}}^{\mathrm{i}}\right)$, the cell given by Eq. 27,

$$\frac{d{N}_{\mathrm{s}}^{\mathrm{i}}}{dt}=\tilde{P}A\left({\mu }_{\mathrm{s}}^{\mathrm{e}}-{\mu }_{\mathrm{s}}^{\mathrm{i}}\right)\text{.}$$ (27)

The chemical potential of the solute in terms of the mole fraction, x, can be derived from solution theory. As an example, consider a regular solution (Eq. 19). In an analogous manner to the solvent chemical potential, the chemical potential of the solute, μ₂, can be found by differentiating Eq. 19,

$${\mu }_2={\mu }_{\mathrm{s}}={\left(\frac{\partial G}{\partial N_2}\right)}_{\text{T},\mathrm{P},{\mathrm{N}}_1,{\mathrm{N}}_3}\text{.}$$ (28)

With the same assumptions as described previously for Eq. 20, the chemical potential of the permeating solute inside the cell in terms of the mole fraction is given as

$${\mu }_2^{\mathrm{i}}={\psi }_2+RT\text{ln}\left(x_2^{\mathrm{i}}\right)+RT\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)\left(1-x_2^i\right)-RT\left(\frac{1}{2}-B_3^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)x_3^{\mathrm{i}},$$ (29)

where the function ${\psi }_2$ is related to the standard state for the permeating solute (usually taken to be infinite dilution). Similarly, the chemical potential of the permeating solute outside the cell in terms of the mole fractions is

$${\mu }_2^{\mathrm{e}}={\psi }_2+RT\text{ln}\left(x_2^{\mathrm{e}}\right)+RT\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^e-x_4^e\right)\left(1-x_2^e\right)-RT\left(\frac{1}{2}-B_4^{+}\right)\left(1-x_2^{\mathrm{e}}-x_4^{\mathrm{e}}\right)x_4^{\mathrm{e}}\text{.}$$ (30)

Although there are many other thermodynamic approaches to finding chemical potential for the solute (such as those based on solute activity), we note that it is important to choose a thermodynamically consistent form of the solute chemical potential. Equations 23 and 29, and similarly, Eqs. 24 and 30, satisfy the Gibbs-Duhem equation to second-order (i.e., Eqs. 29 and 30 are the thermodynamically consistent solute chemical potentials that should be used if the osmotic virial equation has been chosen for the solvent).

Substituting Eqs. 29 and 30 into Eq. 27 yields the expression

$$\frac{d{N}_{\mathrm{s}}^{\mathrm{i}}}{dt}=\tilde{P}ART\left[\begin{array}{l}\text{ln}\left(x_2^{\mathrm{e}}\right)+\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^{\mathrm{e}}-x_4^{\mathrm{e}}\right)\left(1-x_2^{\mathrm{e}}\right)-\left(\frac{1}{2}-B_4^{+}\right)\left(1-x_2^{\mathrm{e}}-x_4^{\mathrm{e}}\right)x_4^{\mathrm{e}}\\ -\text{ln}\left(x_2^{\mathrm{i}}\right)-\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)\left(1-x_2^{\mathrm{i}}\right)+\left(\frac{1}{2}-B_3^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)x_3^{\mathrm{i}}\end{array}\right]\text{.}$$ (31)

Equation 31 is a new nondilute solute transport equation without dilute solution assumptions applicable to regular, semidilute solutions. To write the dilute solution expression for Eq. 31, the higher order terms in the equation would be neglected to yield

$$\frac{d{N}_{\mathrm{s}}^{\mathrm{i}}}{dt}=\tilde{P}ART\left[\text{ln}\frac{\left(x_2^{\mathrm{e}}\right)}{\left(x_2^{\mathrm{i}}\right)}\right]\text{.}$$ (32)

Equation 31 is very different from the one used in the modern-day two-parameter formalism, which is written as a simple difference in concentration. Equation 32 is similar to the modern-day two-parameter formalism. Kedem and Katchalsky (37) also arrived at this expression, but then made a near equilibrium assumption, in addition to the nondilute assumption (50). Linearizing the logarithms in Eq. 32 yields

$$\begin{array}{l}\frac{d{N}_{\mathrm{s}}^{\mathrm{i}}}{dt}=\tilde{P}ART\left(\frac{c_{\mathrm{s}}^{\mathrm{o}}-c_{\mathrm{s}}^{\mathrm{i}}}{c_{\text{average}}}\right),\\ \text{where}{c}_{\text{average}}=\frac{c_{\mathrm{s}}^{\mathrm{o}}+c_{\mathrm{s}}^{\mathrm{i}}}{2}\text{.}\end{array}$$ (33)

Comparing Eq. 33 with Eq. 7, a relationship between the solute permeability P_s (μm/min) and solute permeability coefficient $\tilde{P}$ (mol²/(min·atm·μm⁵), which have different units, can be obtained as

$$P_{\mathrm{s}}=\frac{\tilde{P}RT}{c_{\text{average}}}\text{.}$$ (34)

New total volume change transport equations

The total volume flux is the sum of the water and solute fluxes. The total cell-volume change as a function of time may therefore be written as

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=v_{\mathrm{w}}\frac{d{N}_{\mathrm{w}}}{dt}+v_{\mathrm{s}}\frac{d{N}_{\mathrm{s}}}{dt}\text{.}$$ (35)

Substituting Eqs. 25 and 31 into Eq. 35 yields the expression

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=-v_{\mathrm{w}}\tilde{L}ART\left[\begin{array}{l}\left(x_2^{\mathrm{e}}+x_4^{\mathrm{e}}\right)+B_2^{+}{\left(x_2^{\mathrm{e}}\right)}^2+B_4^{+}{\left(x_4^{\mathrm{e}}\right)}^2+\left(B_2^{+}+B_4^{+}\right)x_2^{\mathrm{e}}{x}_4^{\mathrm{e}}\\ -\left(x_2^{\mathrm{i}}+x_3^{\mathrm{i}}\right)-B_2^{+}{\left(x_2^{\mathrm{i}}\right)}^2-B_3^{+}{\left(x_3^{\mathrm{i}}\right)}^2-\left(B_2^{+}+B_3^{+}\right)x_2^{\mathrm{i}}{x}_3^{\mathrm{i}}\end{array}\right]+v_{\mathrm{s}}\tilde{P}ART\left[\begin{array}{l}\text{ln}\left(x_2^{\mathrm{e}}\right)+\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^{\mathrm{e}}-x_4^{\mathrm{e}}\right)\left(1-x_2^{\mathrm{e}}\right)-\left(\frac{1}{2}-B_4^{+}\right)\left(1-x_2^{\mathrm{e}}-x_4^{\mathrm{e}}\right)x_4^{\mathrm{e}}\\ -\text{ln}\left(x_2^{\mathrm{i}}\right)-\left(\frac{1}{2}-B_2^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)\left(1-x_2^{\mathrm{i}}\right)+\left(\frac{1}{2}-B_3^{+}\right)\left(1-x_2^{\mathrm{i}}-x_3^{\mathrm{i}}\right)x_3^{\mathrm{i}}\end{array}\right]\text{.}$$ (36)

The total cell volume, V_C, is given as

$$V_{\mathrm{C}}=V_{\mathrm{w}}+V_{\mathrm{s}}+V_{\mathrm{b}},$$ (37)

where V_w is the volume of water, V_s is the total solute volume (permeating and nonpermeating solutes), and V_b is the osmotically inactive volume.

Equation 36 represents the complete nondilute transport equation (for semidilute regular solutions assumptions). In this equation there are no near-equilibrium or dilute solution assumptions made. If we were to write the dilute solution expression, we would again neglect any second-order terms and Eq. 36 would take the form

$$\frac{d{V}_{\mathrm{w}+\mathrm{s}}}{dt}=-v_{\mathrm{w}}\tilde{L}ART\left[\left(x_2^{\mathrm{e}}+x_4^{\mathrm{e}}\right)-\left(x_2^{\mathrm{i}}+x_3^{\mathrm{i}}\right)\right]+v_{\mathrm{s}}\tilde{P}ART\left[\text{ln}\frac{\left(x_2^{\mathrm{e}}\right)}{\left(x_2^{\mathrm{i}}\right)}\right]\text{.}$$ (38)

Comparing To Data and Goodness of Fit

To examine the effects of using our new transport equation, Eq. 36, compared to traditional transport formalisms, we reanalyzed data for human corneal epithelial cells exposed to various concentrations of DMSO (0.5 M, 1 M, and 2 M) at 13°C (51). The solutions had measured osmolalities of 631, 1227, and 2589 mOsm/kg, respectively. The data had been obtained and previously analyzed using a three-parameter formalism and fitting for L_p, P_s, and σ (51,52). Cell volume measurements for the human corneal epithelial cells were reanalyzed using our new transport equation, Eq. 36.

The values for the osmotic virial coefficients, B and B⁺, for different solutes were calculated by fitting the osmolality of various solutions to a single solute osmotic viral equation truncated at the quadratic term as given in Eq. 39 (in terms of molality) and in Eq. 40 (in terms of mole fraction),

$$\pi =m_{\mathrm{i}}+B_{\mathrm{i}}^{}{m}_{\mathrm{i}}^2,$$ (39)

$$\begin{array}{l}\pi x_1=\tilde{A}\left(x_{\mathrm{i}}+B_{\mathrm{i}}^{+}{x}_{\mathrm{i}}^2\right)\\ \tilde{A}=\frac{1}{M{W}_{\text{solvent}}}=55.49\text{mole/kg}\end{array}\text{.}$$ (40)

The value $\tilde{A}$ is used to convert between units of molality and mole fraction. The osmolality as a function of concentration for different solutes was obtained from various freezing point depression data in the literature (19) in terms of either mole fraction or molarity. The freezing point depression was converted to osmolality using the equation

$$FPD=1.86\pi x_1,$$ (41)

where FPD is the freezing point depression, 1.86 is the molal freezing point depression constant for water (53), and x₁ is the mole fraction of water.

For solutes that dissociate, such as salts like KCl or NaCl, the concentration unit (molality) in Eq. 39 or (mole fraction) in Eq. 40 needs to be multiplied by a dissociation constant that is also fit for (19). The value of the dissociation constant depends on the units of concentration used. For solutes that do not dissociate, such as DSMO, glycerol, or propylene glycol, the dissociation constant is simply equal to 1. A list of the osmotic virial coefficients for various solutes of interest are given in Table 1.

Table 1.

Virial coefficient values B and B⁺ for various solutes

Solute	B+ (for virial expansion in mol fraction)	B [molal−1] (for virial expansion in molal)
Dimethyl sulfoxide (DMSO)	4.716	0.0843
Glycerol	2.950	0.0259
Propylene glycol (PG)	3.415	0.0399
Potassium chloride (KCl)	−0.057	0.0000
(dissociation constant)	(1.79)	(1.74)
Sodium chloride (NaCl)	2.759	0.0299
(dissociation constant)	(1.68)	(1.70)

The human corneal epithelial cell volume data on exposure to different concentrations of DMSO were fit to our new transport equations using Mathematica 5.1 (Wolfram Research, Champaign, IL). The parameters used in the program are given in Table 2.

Table 2.

Epithelial cell parameters

Parameter	Value	Symbol
Isotonic cell volume	3626 μm3	iVto
Osmotically inactive fraction	0.41	vb
Temperature	13°C (286 K)	T
Universal gas constant	8.206 × 1013μm3 × atm/mol × K	R
Partial molar volume of water	18.02 × 1013μm3/mol	${\overline{v}}_{\mathrm{w}}$
Partial molar volume of DMSO	71.33 × 1012μm3/mol	${\overline{v}}_{\mathrm{s}}$
Second osmotic virial coefficient for DMSO (in terms of mole fraction)	4.716	$B_2^{+}$
Second osmotic virial coefficient for KCl (in terms of mole fraction)	−0.057	$B_3^{+}$
(dissociation constant)	(1.79)
Second osmotic virial coefficient for NaCl (in terms of mole fraction)	2.759	$B_4^{+}$
(dissociation constant)	(1.68)
Initial intracellular salt (KCl) mole fraction (0.172 molal = 0.300 osmoles)	0.003	$x_3^{\mathrm{i}}$ initial
Initial intracellular solute (DMSO) mole fraction	0.000	$x_2^{\mathrm{i}}$ initial
For 0.5 M DMSO
Extracellular salt (NaCl) mole fraction (0.175 molal = 0.300 osmoles)	0.003	$x_4^{\mathrm{e}}$
Extracellular solute (DMSO) mole fraction (0.5 molal = 0.631 osmoles)	0.011	$x_2^{\mathrm{e}}$
For 1 M DMSO
Extracellular salt (NaCl) mole fraction 0.175 molal = 0.300 osmoles	0.003	$x_4^{\mathrm{e}}$
Extracellular solute (DMSO) mole fraction 1 molal = 1.227 osmoles	0.022	$x_2^{\mathrm{e}}$
For 2 M DMSO
Extracellular salt (NaCl) mole fraction0.175 molal = 0.300 osmoles	0.003	$x_4^{\mathrm{e}}$
Extracellular solute (DMSO) mole fraction 2 molal = 2.589 osmoles	0.044	$x_2^{\mathrm{e}}$

Results

The result for one data-set fit with the new transport equation for 2-molal DMSO is shown in Fig. 2. The new transport equations similarly fit all the other data sets as well. Tables 3–5 show a summary of the values obtained for the three-parameter fit of the data as well as the values for the permeability coefficients of the new transport equations. For almost all the comparisons, the relative sum of square errors (SSE) was very similar for the two methods of fitting the data. The units for $\tilde{L}$ and $\tilde{P}$ are in mol²/min×atm×μm⁵, while the units for L_p are in μm³/μm²/min/atm and the units for P_s are in μm/min.

Figure 2.

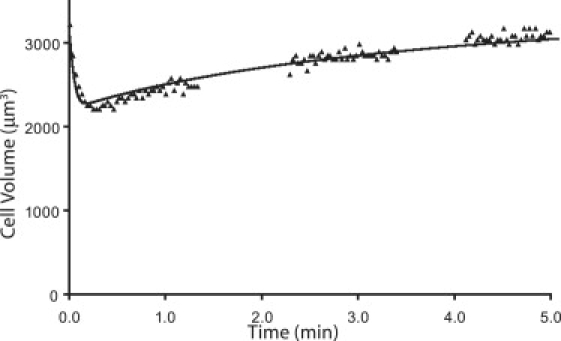
Volume change of human corneal epithelial cells on addition of 2 molal DMSO. The data was fit using Eq. 36.

Table 3.

Permeability parameters obtained from 0.5 molal DMSO data fit with the new transport equations and the three-parameter equations (n = 9)

	$\tilde{L}$ × 10−28 mol2/ (min×atm×μm5)	$\tilde{P}$ × 10−31 mol2/ (min×atm×μm5)	SSE	Lp (μm3/μm2/ min/atm)	Ps (μm/min)	σ	SSE
Avg ± SD	3.85 ± 0.26	0.571 ± 0.07	0.025 ± 0.01	0.220 ± 0.05	2.162 ± 0.61	0.456 ± 0.13	0.024 ± 0.01

Table 4.

Permeability parameters obtained from 1.0 molal DMSO data fit with the new transport equations and the three-parameter equations (n = 9)

	$\tilde{L}$ × 10−28 mol2/ (min×atm×μm5)	$\tilde{P}$ × 10−31 mol2/ (min×atm×μm5)	SSE	Lp (μm3/μm2/ min/atm)	Ps (μm/min)	σ	SSE
Avg ± SD	5.64 ± 0.83	1.69 ± 0.14	0.040 ± 0.03	0.325 ± 0.12	2.941 ± 1.24	0.376 ± 0.15	0.046 ± 0.02

Table 5.

Permeability parameters obtained from 2.0 molal DMSO data fit with the new transport equations and the three-parameter equations (n = 9)

	$\tilde{L}$ × 10−28 mol2/ (min×atm×μm5)	$\tilde{P}$ × 10−31 mol2/ (min×atm×μm5)	SSE	Lp (μm3/μm2/ min/atm)	Ps (μm/min)	σ	SSE
Avg ± SD	5.05 ± 0.82	4.13 ± 0.29	0.071 ± 0.02	0.206 ± 0.03	5.306 ± 0.96	0.495 ± 0.12	0.081 ± 0.03

Discussion

Despite the fact that for almost all the runs, the relative sum of square errors was very similar for the two methods of fitting the data, it is important to note that the new transport equations fit for only two parameters instead of three and can be extended to data at high concentrations.

It is possible then that the fitting of σ in the three parameter formalism is simply adjusting for nondilute behavior. In the literature it has been reported that no pattern emerges to describe how the solute concentration affects membrane permeability characteristics, and some researchers have reported solute inhibition of L_p (46). Some studies have reported a decrease in the hydraulic conductivity in the presence of increased solute concentrations (48), while other studies report an increase (49). It is possible that these reported variations of the hydraulic conductivity are a result of dilute solution expressions being used in the transport equations and may not appear if nondilute transport equations were utilized.

When comparing the solute transport flux equation in Eq. 7 with the new dilute solute transport equation in Eq. 33, we see that there is a difference in the concentration dependence of the permeability coefficients. Equation 34 gives a relationship between the solute permeability P_s and the solute permeability coefficient $\tilde{P}$. When the $\tilde{P}$ values are divided by concentration, there should not be any further concentration dependence. On analyzing the data for fit with the new transport equations, there appeared to be an obvious concentration dependence of $\tilde{P}$ —as the concentration of DMSO increased, the value for $\tilde{P}$ also increased. $\tilde{L}$ did not appear to have the same strong concentration dependence. To compare the concentration relationships for P_s and for $\tilde{P}$, we can compare the standard deviation of the average values as shown in Table 6.

Table 6.

Concentration relationship comparisons for P_s and $\tilde{P}$

Molal concentration	Ps	$\left(\frac{\tilde{P}}{\mathit{molar}\mathit{concentration}}\right)$ × 10−31
0.5	2.16 ± 0.61	1.14 ± 0.07
1.0	2.94 ± 1.24	1.69 ± 0.14
2.0	5.31 ± 0.96	2.07 ± 0.29
Average value	3.47	1.63
Standard deviation in values	1.65 (48% of the average value)	0.46 (28% of the average value)

From Table 6, we see that there is a larger unexpected deviation with concentration of the P_s values as compared to the $\tilde{P}$ values. The prior analysis of the data for the human corneal epithelial cells (51) assumed that there was no concentration dependence of the permeability parameters. However, the data for the epithelial cells exposed to various concentrations of DMSO (0.5 M, 1 M, and 2 M) at 13°C showed that there was a statistical difference in the solute permeability coefficients at the higher 2-molal concentration. The reason cited for this was the possible linearity in the three-parameter transport equations utilized.

Conclusions

The main objective of this article was to provide a better understanding of osmotic transport. A detailed look into the current status of osmotic transport in the literature was provided. The assumptions made when using the two-parameter formalism and the Kedem-Katchalsky formalism were examined. In the literature, osmolarity and osmolality are used interchangeably; however, they are only equal for dilute solutions at 4°C. It was demonstrated that despite what is often stated in the literature, using either the 2-P or the K-K equations results in dilute solution assumptions being made, specifically in the solute transport equations wherein molarity cannot simply be replaced with osmolarity. For situations where there was no interaction between water and solute, it was shown that the 2-P and the K-K total volume flux equations are formally equivalent. Kleinhans noted that the 2-P formalism and the K-K formalism deviated from each other at high concentrations, but there were no practical differences between the two models up to solute concentrations of several molar. The 2-P model uses only two parameters while the K-K model uses three parameters. It is possible that adjusting σ accommodates for nondilute behavior, since in both the 2-P and K-K equations a dilute solution assumption is made. This again highlighted the importance of developing nondilute transport equations.

In this article, we have derived a complete set of transport equations, which includes a new nondilute solute transport equation that does not make the previous dilute solution or near-equilibrium assumptions, and can now be applied to regular, semidilute solutions. The particular form of the solute chemical potential used in the transport equation is thermodynamically consistent with the osmotic virial equation (to second-order) and thus should be valid when the osmotic virial equation is valid. This is applicable to many fields including cryobiology where dilute solution conditions are not often met, since concentrated solutions are used over large temperature ranges. The nondilute transport equations will be of particular importance when trying to predict cell behavior when modeling the freezing process and predicting cryopreservation protocols. The modeling of cell response during cryopreservation protocols involves concentrations up to 10+ molar in the regime where nondilute transport equations are essential. Utilizing our new transport equations that fit for two permeability coefficients, the fits were as good as with the previous three-parameter model and did not use σ. There is less unexpected concentration dependence with the new transport equations, suggesting that some of the unexpected concentration dependence of permeability (>40%) is due to the use of inappropriate transport equations.