Abstract
Transmembrane signaling implies that peripheral protein binding to one leaflet be detected by the opposite leaflet. Therefore, protein recruitment into preexisting cholesterol and sphingolipid rich platforms may be required. However, no clear molecular picture has evolved about how these rafts in both leaflets are connected. By using planar lipid bilayers, we show that the peripheral binding of a charged molecule (poly-lysine, PLL) is detected at the other side of the bilayer without involvement of raft lipids. The diffusion coefficient, DP, of PLL differed by a factor of √2 when PLL absorbed to one or to both leaflets of planar membranes. Fluorescence correlation spectroscopy showed that the changes of the lipid diffusion coefficient, DM, were even more pronounced. Although DM remained larger than DP on PLL binding to the first membrane leaflet, DM dropped to DP on PLL binding to both leaflets, which indicated that the lipids sandwiched between two PLL molecules had formed a nanodomain. Due to its small area of ∼20 nm2 membrane electrostriction or leaflet interaction at bilayer midplane can only make a small contribution to interleaflet coupling. The tendency of the system to maximize the area where the membrane is free to undulate seems to be more important. As a spot with increased bending stiffness, the PLL bound patch in one leaflet attracts a stiffening additive on the other leaflet. That is to say, instead of suppressing undulations in two spots, two opposing PLL molecules migrate along a membrane at matching positions and suppress these undulations in a single spot. The gain in undulation energy is larger than the energy required for the alignment of two small PLL domains in opposite leafs and their coordinated diffusion. We propose that this type of mechanical interaction between two membrane separated ligands generally contributes to transmembrane signaling.
Introduction
In morphologically polarized cells, lipids and lipid-anchored proteins are differentially presented on the apical and basolateral membranes. The cytoplasmic cell-sorting machinery can obviously recognize these molecules, even though they are on the inner surface of trafficking vesicles (1). Long- and short-range ordering of lipids and proteins in the lateral dimension play a crucial role in this process (2). Small, heterogeneous, highly dynamic, sterol- and sphingolipid-enriched domains are formed, called membrane rafts (3). Any coupling between rafts in opposing biological membranes involves domains that differ in size and stability in the inner and outer monolayers (4). Lipid recruitment into so-called lipid shells surrounding integral proteins (5) may contribute to interleaflet coupling. Several protein-independent coupling mechanisms were also proposed like interdigitation of acyl chains (6), and high frequency interchange of cholesterol between leafs (7). However, interdigitation is so weak that it seems unable to affect translational diffusion of lipids in liquid crystalline bilayers (8). Moreover, interdigitation of lipids whose two chains have significantly different lengths appears to be obliterated by the presence of cholesterol (9). Cholesterol flow from the leaflet of higher concentration to the second leaflet may provide an explanation, as the accompanying change in packing density will lead to a larger lateral pressure in the second leaflet and a lower pressure in the first leaflet. As a result, phase shifts may occur in both leafs. But if the chemical potentials of cholesterol in the two leaflets are identical, the molecular coupling mechanism is not so clear (10). Moreover, interleaflet coupling seems to be possible even in the absence of rafts. For example, cholesterol-free domains in model membranes also appear to be coupled (11,12).
It was proposed recently that acyl chains of the ordered and disordered membrane layers interact at the midplane of the bilayer via overhang, i.e., the contact of two different liquids at the midplane of a bilayer incurs a free energy penalty over the state without overhang. The associated interfacial energy that scales with the contact area was assumed to be large enough to not only bring preexisting domains of the two leafs into alignment, but also to perturb the compositions of those domains and to change the equilibrium phase behavior of the system (10). The theory is supported by the observation that lipid mixtures can be tuned to induce or suppress macroscopic domains across leaflets of unsupported asymmetric bilayers (13). However, experimental evidence is missing to confirm that midplane interaction energy is physiologically relevant for the much smaller domains often found in biological membranes. Furthermore, the midplane coupling does not provide a clear molecular picture of how the attachment of peripheral proteins to one leaflet is sensed at the opposite leaflet, i.e., how transmembrane signaling may occur in this case. Although protein or peptide binding is likely to expel interfacial water and ions and may, thus, increase lipid ordering (14), little is known about the resulting midplane tension. For midplane tension to occur, we have to hypothesize that the order parameter of the acyl chains in the middle of the bilayer increases as is the case in the presence of cholesterol and sphingomyelin.
More compelling is the hypothesis that transmembrane signal transduction is a direct result of electrostatic interactions. As a starting point, the electrostatic attraction between highly charged proteinaceous residues and lipids recruits acidic lipids into nanodomains in the leaflet adjacent to the peripheral protein (15). However, a mechanistic explanation of how the matching nanodomain is formed in the opposing monolayer is not available. Direct electrostatic interactions across charged bilayers were ruled out between peripheral proteins under physiological salt concentrations (16). The large drop in the dielectric constant across a lipid bilayer diminishes the electrostatic coupling between charged leaflets or charged macro ions adsorbed to them.
We test three additional concepts; one attributes an increase in membrane tension to the electric field imposed by a peripheral protein, the second is based on an increase in tension generated by membrane curvature, and the third considers the suppression of membrane undulations by ligand binding.
Materials and Methods
Lipid bilayers
Both dry and solvent-containing horizontal model membranes were formed from diphytanoyl phosphatidylcholine and diphytanoyl phosphatidylserine (DPhPS) (Avanti Polar Lipids, Alabaster, AL). Solvent-containing membranes (17) were spread from a lipid solution in n-decane across a circular aperture (40–150 μm) in a polytetrafluoroethylene (PTFE) septum, which separated two aqueous phases of a PTFE chamber. Membrane thinning was observed optically and electrically, via the determination of membrane capacitance. Therefore, chlorinated silver electrodes were immersed into the buffer solutions. A sine input wave was generated by a function generator (model 33120A; Agilent, Santa Clara, CA). The output signal was amplified by a current to voltage converter (model VA-10; NPI, Tamm, Germany) and recorded by an oscilloscope (model TDS 210; Tektronix, Beaverton, OR). The specific capacitance of the solvent-free and the dry membranes was equal to (0.85 ± 0.06) μF/cm2 and (0.5 ± 0.05) μF/cm2, respectively.
The so-called dry membranes were folded from lipid monolayers that were spread on top of the aqueous solutions (18). Therefore, the aperture (diameter of 40–150 μm) of the PTFE septum dividing both solutions was immersed below the air-water interface so that both monolayers combined spontaneously (19). All PTFE septa were pretreated with a hexadecane/hexane mixture at the volume ratio of 1:199.
Fluorescence correlation spectroscopy
To visualize lipid diffusion, the membranes contained 0.01 weight % of rhodamine labeled phosphatidylethanolamine (RhPE, Avanti Polar Lipids). Polymer diffusion was monitored by adding a rhodamine label to PLL (PLL-Rh, synthesized by Dr. N. S. Melik-Nubarov, Moscow State University, by conjugation of TRITS with PLL, molecular weight, 3000, ∼5% of lysine residues were labeled with rhodamine). Unlabeled PLL was added in 60-fold excess. For calibration experiments the dye Rhodamine 6G (Invitrogen, San Diego, CA) was used.
We used fluorescence correlation spectroscopy (FCS) to determine the two dimensional diffusion coefficients, DP and DM, of PLL and domains of membrane lipids, respectively (11). In brief, the average residence time τD of single fluorescent molecules in the focus area (radius ω ≈ 0.16 μm) was derived from the autocorrelation function G(τ) of the fluorescence temporal signal. An additional micromanipulator (model PatchMan NP2, Eppendorf, Hamburg, Germany) was attached to the LSM 510 META ConfoCor 3 (Carl Zeiss Jena, Jena, Germany). A water drop formed the connection between the objective of the microscope and the coverslip, which provided the bottom of the measurement chamber. The lower Teflon-chamber was placed on the stage of the microscope whereas the upper chamber was fixed on the PatchMan to position the membrane exactly in the focus.
DM and DP were determined as ω2/4τD with an absolute accuracy of ∼20% (20). For the scope of the current work, only relative changes of DM and DP are important, and these were determined with much higher precision.
Results
DM, of labeled lipids (RhPE, 0.01 weight %) was equal to 8.1 ± 0.4 μm2/s (Fig. 1 A). It was the same whether the free standing planar bilayers were folded (18) from diphytanoyl phosphatidyl serine (DPhPS) monolayers on top of the aqueous solutions or painted (17) using DPhPS dissolved in decane (Table 1). The increased compressibility probably compensates for the increase in thickness of the painted membranes. DM in giant vesicles is similar (20).
Figure 1.
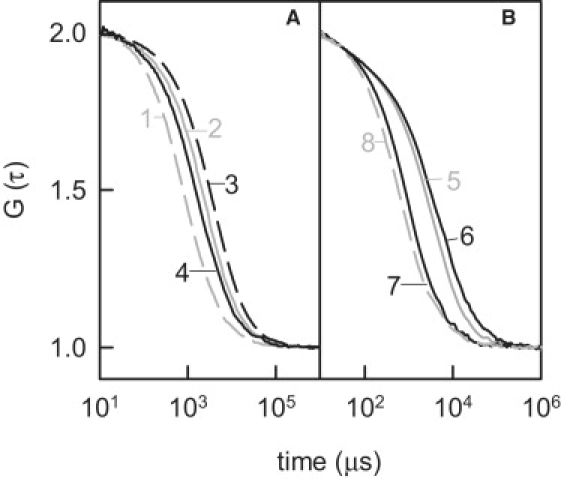
Two-dimensional (A) lipid and (B) polymer diffusion. Free standing planar bilayers were folded from DPhPS monolayers or painted using DPhPS dissolved in decane (B). Unilateral addition of 1.4 μM PLL (N = 126) increased τD of dioleoyl-rhodamine-phosphatidyl-ethanolamine (Rh-PE, 0.01%) from 762 ± 38 (1) to 1469 ± 73 μs (4). Bilateral addition increased τD to 3188 ± 159 μs (3). PLL with N = 20 (2) had a smaller effect (1996 ± 100 μs). τD of poly-lysine (N = 126, 5% of PLL were labeled with rhodamine) was, respectively, equal to 2688 ± 134 (5) and 4071 ± 204 μs (6) on unilateral and bilateral additions. Going from 0.025 to 1 M KCl (7) decreased τD to 828 ± 41 μs. Substitution of DPhPS for neutral phosphatidyl choline showed τD =584 ± 29 μs in case of bilateral presence of PLL in 25 mM KCl (8). The buffer was 10 mM HEPES and 0.1 mM EDTA (pH 7.0).
Table 1.
Effect of PLL length on the residence time τD of Rh-PE
| Number | N | τD (μs) | DM (μm2/s) | |
|---|---|---|---|---|
| 1 | Control | 0 | 777 ± 39 | 8.1 ± 0.4 |
| 2 | L-lysine | 1 | 735 ± 37 | 8.5 ± 0.4 |
| 3 | Pentalysine | 5 | 1176 ± 59 | 5.4 ± 0.3 |
| 4 | PLL | 20 | 1870 ± 94 | 3.4 ± 0.2 |
| 5 | PLL (unilateral) | 126 | 1763 ± 88 | 3.6 ± 0.2 |
| 6 | +PLL (bilateral) | 126 | 3576 ± 179 | 1.8 ± 0.1 |
| 7 | +1 M KCl | 126 | 1278 ± 64 | 4.9 ± 0.2 |
Except number 5, PLL was present in both compartments. Numbers 5–7 denote subsequent additions. The conditions were as noted in Fig. 1.
PLL, poly-lysine; τD, residence time in the focus; Rh-PE, rhodamine labeled phosphatidylethanolamine; N, number of lysine units; DM, lipid diffusion coefficient.
Adsorbing to the lipid bilayer, PLL induces domain formation when the lipid is below its phase transition temperature (21,22) and increases acyl chain order above the phase transition temperature (14). In both cases, a decrease in DM is expected. Accordingly, addition of PLL to both sides of the membrane resulted in a decrease of DM (Fig. 1). The electrostatic nature of PLL binding was shown i), by the recovery of the fast diffusion coefficients of lipid monomers, DM,1 after shielding of surface potential, or ii), by short τD of PLL when charged lipids were substituted for neutral lipids (Fig. 1 B).
A charge stoichiometry of two lysine residues per charged lipid was reported for small lysine peptides (23). This stoichiometry results from geometric requirements as the distance between individual phospholipid headgroups is ∼8 Å whereas, even for a fully extended peptide chain, the distance between adjacent residues is only 3.8 Å. Consequently, the radius RD of the area in which DM decreases should match the radius of the interacting PLL. That is, DM is anticipated to depend on PLL size according to (24):
| (1) |
where μm, h, and λ respectively denote membrane viscosity, bilayer thickness, and correlation length. By simplifying Eq. 1, we determined RD from measurements of τD:
| (2) |
where RL = 5 Å and τM,1 are the radius of a lipid molecule and its residence time in the focus, respectively. This approach implies that λ is invariant and that those molecules spanning only one or both leaflets have equal mobility. The latter assumption contrasts with multi-bilayer experiments suggesting a one-third smaller diffusion coefficient DL for membrane spanning molecules (25), but is justified by more recent experiments (24). For monomeric lysine, DM was expected to be the same as in control experiments carried out in its absence. In line with these anticipations, our FCS measurements showed that DM was equal to DM,1. In contrast, pentalysine may bind two or three lipids at once. The resulting RD of ∼7–8 Å should lead to DM = 0.6 DM,1, which was observed experimentally (Table 1). For the PLL N = 20, the measured residence time corresponds to an RD of 13 Å. This value coincides with the predicted radius (Eq. 1) if it is assumed that every second lysine residue interacts with a lipid molecule. For the larger PLL with N = 126 the extended surface configuration is very unlikely, and thus, a binding stoichiometry of 4.6 lysine residues per lipid has to be assumed (23). According to Eq. 1 this would correspond to a RD of 25 Å that is only slightly larger than the measured value of 21–23 Å. The small discrepancy may originate from the fact that for RD > 20Å the Saffman-Delbrück equation should be used (24).
The observed effect of PLL molecules on DM suggests that PLL molecules are so tightly bound to the lipids that both species (PLL and lipids) have the same diffusion coefficient. But in a contrasting report, peptide and lipid diffusion coefficients were found to be independent of each other. Small charged peptides, which were added to giant vesicles, “skated” over the lipids (26). There were two main differences between these vesicle experiments and our planar experiment: i), the sidedness of peptide addition, and ii), the peptide concentration. Although present on both sides in our experiments, the peptides adsorbed to only one leaflet in the vesicle experiments. Therefore, we hypothesized that DP depended on the sidedness of PLL addition. Measurements of the residence time of labeled PLL molecules confirmed the prediction (Fig. 1, Table 1). When bound to one leaf, DP was equal to 2.3 μm2/s. Thus, its value was √2 larger than DP (1.5 μm2/s) observed after PLL (PLL with N = 126) binding to both leafs. It should be noted that both values were measured at saturating PLL concentrations, whereas peptide skating along vesicles was measured at low concentrations (26). Because FCS is a single molecule technique, the amount of unlabeled PLL exceeded the amount of labeled polymer.
In our experiments both DP and DM (not shown) decreased with increasing PLL concentrations. A similar concentration dependence has been observed before in case of nucleic acid adsorption to positively charged membranes. It was explained by the observation that the concentration increase results in the transformation of the extended polymer conformation into a condensed conformation (27). This transformation, in turn, was accompanied by an increase in surface charge density and stronger binding to the lipid. The polymer diffusion coefficient scaled with the square root of molecular weight (27). Consequently, the √2 fold decline in DP observed for bilateral addition indicates coordinated PLL migration along opposing leafs. Under these conditions, i.e., when bound in saturating concentrations to both leafs, we observed DM ≈ DP that indicates the formation of stable nanodomains that extend over both leaflets.
Discussion
We have shown that two PLL molecules may migrate along opposing leafs like one molecule with doubled molecular mass. Once two PLL attached domains are aligned with each other, the exchange of lipids from inside this PLL sandwich with lipids outside the cluster is delayed so that the velocities of lipid and PLL diffusion match each other. The proof of these criteria indicates that interleaflet domain coupling takes place.
The loss in entropy that accompanies the coupled PLL diffusion somehow has to be compensated. Most compelling is the hypothesis that electrostatic interactions provide the gain in energy. However, direct electrostatic interactions across charged bilayers were ruled out between peripheral proteins under physiological salt concentrations (16). The large drop in the dielectric constant across a lipid bilayer diminishes the electrostatic coupling between charged leaflets or charged macro ions adsorbed to them. Nevertheless, the electrostatic attraction between highly charged proteinaceous residues and lipids recruits acidic lipids into nanodomains in the leaflet adjacent to the peripheral protein (15). Assuming that only every second lysine residue binds to a lipid molecule (21), we arrive at a density of one positive charge per lipid molecule in the PLL facing lipid and one negative charge per lipid in the opposing leaflet (DPhPS). According to the Gouy Chapman theory, this charge density gives rise to a surface potential, Ψ, of about +150 mV and −150 mV for the two interfaces in 25 mM KCl, respectively. The resulting difference in surface potentials, ΔΨ = 300 mV, gives rise to an electrostriction of the bilayer (Fig. 2 A). If the membrane remains flat during thinning, such that there is no increase in free energy from bending, then the isothermal work is equal to the change in Helmholtz free energy of compression (28):
| (3) |
where ɛ0 is the permittivity and ɛ is the relative dielectric constant for the membrane. A, he, and Δh are, respectively, the thinned area of the membrane, the dielectric (hydrocarbon) thickness and the decrease in total bilayer thickness. For he = 3 nm, ɛ = 2.3, Δh = 0.2 nm, and A = 20 nm2, we calculate a ΔF of ∼4 × 10−22 J. ΔF is, thus, an order of magnitude smaller than the thermal energy. Consequently, its release cannot account for interleaflet coupling. We conclude that electrostriction does not provide enough interaction energy to dominate thermal noise. Depending on membrane potential, it may gain physiological importance for larger domains.
Figure 2.
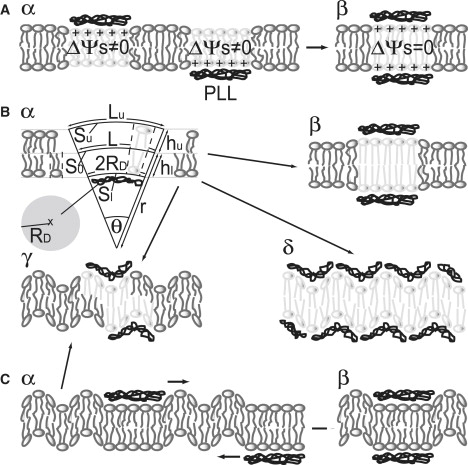
Mechanisms of domain formation. (A) Electrostriction. (α) Adsorption of a positively charged PLL molecule to only one leaflet generates a local asymmetry of membrane surface potential. The resulting difference in membrane surface potential Δψ gives rise to electrostriction. (β) The mechanical stress is released on registration of the two PLL bound spots. Due to the small spot size the Helmholtz free energy of compression is too small to dominate thermal noise. (B) Stretching of bent lipids. (α) Electrostatic binding of a charged peptide (PLL) to the lipid bilayer induces membrane bending. In its condensed configuration the peptide has a disk-like shape with radius RD. On binding, PLL reduces the distance between the lipid headgroups in an area Sl. The cross-sectional area S0 of the respective lipids at the midplain remains unchanged. As a result, the bilayer is bent with a negative curvature of radius r. hu and hl denote the thicknesses of the upper and lower leaflets. If the lipids in the two leafs do not slip relative to each other, the membrane patch in the upper leaf is expanded to Su. The cross sections of Su and S0 are indicated as Lu and L, respectively. (β) Complete registration of two spots releases the energy required for dilatation of the upper layer Ed. However, binding of a second PLL to the positively curved zone right opposite from first one is particularly unfavorable. (γ) The second PLL will be attracted to a position right beside the footprint of the first PLL bound to the other leaflet. (δ) In this case more than two PLLs are involved, forming interlaced arrays on the two leaflets. The large screening (Debye) length of 1.9 nm leads to electrostatic repulsion and restricts the number of PLL molecules to one per domain and leaflet. However, the large penalty for stretching the lipids in the upper leaf (resulting from the nonslip assumption) cannot be explained by bilayer midplane coupling. (C) Undulations. (α) The membrane undulates so that a spot of increased bending stiffness on one side should suppress undulations and (β) thus attract a stiffening additive on the other leaflet. (γ) If it is assumed that PLL induces membrane bending complete registration does not occur. The second PLL will be attracted to a position right beside the footprint of the first PLL bound to the other leaflet. Nevertheless, the gain in undulation energy is large enough to dominate thermal noise.
So far we have assumed that the membrane stays flat during binding of peripheral molecules. This assumption is in contrast with previous reports about membrane curvature induced by PLL (21,29,30). On binding, PLL immobilizes water molecules in the restricted volume between the bilayer surface and the bound PLL (14). As a result the distance between the lipid headgroups decreases and, due to the invariance of membrane volume, the thickness of the bilayer increases (<10%). However, the ordering PLL effect (14) is unlikely to extend to the midplane of the bilayer, so that the cross-sectional area of the acyl chains at the midplain remains unchanged. As a result, the cylindrical lipids transform into cone-shaped molecules that, in turn, give rise to negative bilayer curvature with radius r (Fig. 2 B).
Whereas the former leaf bends spontaneously, the disordered leaf is forced to bend. Assuming that the area occupied by the polymer is equal to the curved area of lower membrane surface Sl, we denote the unconstrained surface at the midplane with S0 and the upper surface with Su. r is determined by Sl and S0 because all surface normal vectors meet at the central angle θ (Fig. 2). Assuming that the bilayer is incompressible, the change in monolayer thickness (Δhl) induced by PLL binding transforms into an area change according to:
| (4) |
For Δhl = 0.15 nm and RD = 2.5 nm, S0 is calculated to be equal 22 nm2. The equation for a circle sector:
| (5) |
returns r = 29 nm, where L = 5.3 nm denotes the diameter of S0. Similarly, the diameter of the upper leaf LU is calculated to be 5.6 nm assuming that it is hu = 1.38 nm thick. The bending energy Eb of the upper layer is estimated according to:
| (6) |
where κb is the bending rigidity of the disordered leaf. The much smaller Gaussian rigidity is neglected. For model bilayers from dimyristoyl phosphatidylcholine, dioleoylphosphatidylcholine, or stearyl-oleyl phosphatidylcholine κb is equal to 18 (31), 21 (32), or 23 kT (33). Assuming that our diphytanoylphosphtatidyl choline membrane adopts an intermediate value of about κb ∼20 kT, we arrive at Eb ∼0.3 kT. Consequently, the release of bending energy cannot account for domain formation.
However, if we assume that the upper and lower layers cannot slip relative to each other, a change is introduced into the area per lipid molecule in both layers. The energy required for dilatation of the upper layer is calculated according to:
| (7) |
Assuming that the compression modulus KA is 0.19 J/m2 (33), we arrive at Ed ∼2 × 10−19 J, which is ∼50 times kT. With ∼167 kT the binding free energy of PLL is adequate to drive this deformation. The value was estimated from the observation that in 100 mM KCl every second basic residue of a short peptide binds to lipids contributing thereby ∼2 kcal/mol (34). Accordingly, we arrive at ∼6 kT per binding lysine residue in 25 mM KCl. With respect to the altered stoichiometry of 4.6 lysine residues per lipid (23), the binding free energy of one PLL molecule is calculated to exceed Ed threefold.
Bending does not occur if two peripherally bound PLL molecules are aligned, i.e., if the lipid bilayer is sandwiched between two PLL molecules. Such an alignment would result in the loss of entropy of migration. Because the accompanying gain in Ed would be much larger, alignment would be energetically favorable. However, a complete alignment is very unlikely to occur. Because PLL binding induces negative curvature, binding of a second PLL to the positively curved zone right opposite from a previously bound one should be particularly unfavorable and avoided. Given that the positive curved zone of the trans leaflet is surrounded by a ring of negative curvature, the second PLL will be attracted to a position right beside the “footprint” of the PLL bound to the other leaflet. If the screening (Debye) length of our medium was <1.9 nm, more than two PLLs could be involved, forming interlaced arrays on the two leaflets. Although electrostatic repulsion restricts the number of PLL molecules to one per domain and leaflet, the partial release of Ed remains large enough to drive domain formation.
The above calculation implies a nonslip condition to both leaflets in the bent region. The lack of slippage may be due to the invariance of the cross-sectional areas of the lipids in the midplane of the membrane. Recent theoretical work has identified that the match of the areal densities at membrane midplane is energetically favorable, and that spatial area changes in one leaflet are predicted to result in variations of the areal density in the other leaflet (35). In line with these considerations, midplane tension was postulated to be the main player in coupling ordered domains in two opposing leaflets (10). For the quantitative assessment of its energetic contribution, their interfacial line tension was used as an indicator. On average, the interfacial line tension of an ordered domain is ∼1–3.5 pN (36). Along with chain-chain interactions, headgroup interactions and elastic mechanical deformations also contribute to the interfacial line tension. Elastic deformations are required to prevent the partial exposure of the acyl chains to water that otherwise would be an immediate consequence of the ordered phase being ∼10% thicker than the surrounding disordered region. They are calculated to account for 1–2 pN (37,38). Because contributions from deformations are missing at the midplane, and assuming that the interaction between the acyl chains along the fatty acids is not much different from the interactions at the midplane (10), the midplane tension is unlikely to exceed 1.5 pN. Taking into account that the contact area between ordered and disordered phases extends over the whole thickness of the lipid monolayer, i.e., over 2.5 nm, we arrive at a two dimensional tension of ∼0.6 pN/nm that at the midplane corresponds to a free energy per unit area of 0.15 kT/nm2. Considering the area of the PLL molecules involved leads to the conclusion that the energy of midplane coupling is much smaller than Ed. Consequently, midplane tension cannot account for the lack of slippage between both leaflets.
In the absence of the large penalty for stretching the bent lipids, we are left with the rather small contribution from midplane coupling. If two PLL bound membrane spots register in opposing leaflets, these contributions would add to ∼3 kT. Even if we assume that registration is incomplete due to membrane bending, this state would be significantly populated in a statistical ensemble. However, it should be pointed out that this estimate is very rough and that relatively small changes in the underlying assumptions could affect it very strongly.
Yet another explanation alternative to midplane coupling may be provided if membrane undulations are considered. A spot of increased bending stiffness on one membrane leaflet should suppress undulations and thus attract a stiffening additive on the other leaflet. Alignment of the two spots in opposing leafs results in an incremental area A = 20 nm2 that is free to undulate. The gain in free undulation energy Eu can be assessed if Eu is assumed to be equal to the energy required to inhibit these shape fluctuations by increasing membrane tension. For cholesterol free membranes, it was shown that reduction of membrane undulations accounts for ∼3% of area increase, whereas the area increase at higher tension is due to a direct expansion in area per molecule (33):
| (8) |
Being equal to ∼28 kT, Eu is certainly large enough to drive domain formation. This conclusion holds also if we assume that registration is only 20% complete due to membrane bending, i.e., if due to the positive curvature in the first leaflet, the PLL at the second leaflet will not adopt a matching position but will be attracted to a position right beside the footprint of the first PLL (compare Fig. 2 C).
The gain in Eu may not only drive the formation of a PLL-bilayer-PLL sandwich but may also give rise to interleaflet coupling if the negatively charged lipids are substituted for negatively charged peptides of equal length. In case of negatively charged gramicidin derivatives, sandwich formation should lead to a stabilization of the conductive dimer. This is exactly what has been observed in the experiment (39).
In contrast, the coupling mechanism observed for polymers on supported bilayers is expected to be different. As these bilayers are not free to undulate, midplane coupling or electrostriction should work. Consequently, the amount of lipid molecules involved has to be >50. In line with these arguments, a slow mode of diffusion was observed for polymers covering ∼80 lipids on a solid supported bilayer (40).
We now conclude that the attraction between two spots of increased bending stiffness on both sides of the bilayer may serve as the driving force for interleaflet coupling as it maximizes the free undulation energy. It is the most important factor in maintaining small nanodomains. When size increases, midplane surface tension and electrostriction may become increasingly important.
Acknowledgments
We thank Nikolay Melik-Nubarov (Moscow State University) for synthesizing Rh-PLL, Sandro Keller (FMP, Berlin) for critically reading the manuscript, Sergey Akimov and Yuri Chizmadzhev for critical discussions, and Quentina Beatty for editorial help.
This work was supported by the Austrian Science Fund (W1201-N13), the Russian Foundation of Basic Research (060490595BNTS), and the Austrian Academic Exchange Service.
References
- 1.Rodriguez-Boulan E., Nelson W.J. Morphogenesis of the polarized epithelial cell phenotype. Science. 1989;245:718–725. doi: 10.1126/science.2672330. [DOI] [PubMed] [Google Scholar]
- 2.Simons K., Ikonen E. Functional rafts in cell membranes. Nature. 1997;387:569–572. doi: 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- 3.Pike L.J. Rafts defined: a report on the Keystone Symposium on Lipid Rafts and Cell Function. J. Lipid Res. 2006;47:1597–1598. doi: 10.1194/jlr.E600002-JLR200. [DOI] [PubMed] [Google Scholar]
- 4.Devaux P.F., Morris R. Transmembrane asymmetry and lateral domains in biological membranes. Traffic. 2004;5:241–246. doi: 10.1111/j.1600-0854.2004.0170.x. [DOI] [PubMed] [Google Scholar]
- 5.Anderson R.G., Jacobson K. A role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science. 2002;296:1821–1825. doi: 10.1126/science.1068886. [DOI] [PubMed] [Google Scholar]
- 6.Rietveld A., Simons K. The differential miscibility of lipids as the basis for the formation of functional membrane rafts. Biochim. Biophys. Acta. 1998;1376:467–479. doi: 10.1016/s0304-4157(98)00019-7. [DOI] [PubMed] [Google Scholar]
- 7.Hildenbrand M.F., Bayerl T.M. Differences in the modulation of collective membrane motions by ergosterol, lanosterol, and cholesterol: a dynamic light scattering study. Biophys. J. 2005;88:3360–3367. doi: 10.1529/biophysj.104.050112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schram V., Thompson T.E. Interdigitation does not affect translational diffusion of lipids in liquid crystalline bilayers. Biophys. J. 1995;69:2517–2520. doi: 10.1016/S0006-3495(95)80122-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McIntosh T.J., Simon S.A., Needham D., Huang C.H. Structure and cohesive properties of sphingomyelin/cholesterol bilayers. Biochemistry. 1992;31:2012–2020. doi: 10.1021/bi00122a017. [DOI] [PubMed] [Google Scholar]
- 10.Collins M.D. Interleaflet coupling mechanisms in bilayers of lipids and cholesterol. Biophys. J. 2008;94:L32–L34. doi: 10.1529/biophysj.107.124362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Korlach J., Schwille P., Webb W.W., Feigenson G.W. Characterization of lipid bilayer phases by confocal microscopy and fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA. 1999;96:8461–8466. doi: 10.1073/pnas.96.15.8461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dietrich C., Bagatolli L.A., Volovyk Z.N., Thompson N.L., Levi M. Lipid rafts reconstituted in model membranes. Biophys. J. 2001;80:1417–1428. doi: 10.1016/S0006-3495(01)76114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Collins M.D., Keller S.L. Tuning lipid mixtures to induce or suppress domain formation across leaflets of unsupported asymmetric bilayers. Proc. Natl. Acad. Sci. USA. 2008;105:124–128. doi: 10.1073/pnas.0702970105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schwieger C., Blume A. Interaction of poly(L-lysines) with negatively charged membranes: an FT-IR and DSC study. Eur. Biophys. J. 2006;36:437–450. doi: 10.1007/s00249-006-0080-8. [DOI] [PubMed] [Google Scholar]
- 15.McLaughlin S., Murray D. Plasma membrane phosphoinositide organization by protein electrostatics. Nature. 2005;438:605–611. doi: 10.1038/nature04398. [DOI] [PubMed] [Google Scholar]
- 16.Wagner A.J., May S. Electrostatic interactions across a charged lipid bilayer. Eur. Biophys. J. 2007;36:293–303. doi: 10.1007/s00249-006-0089-z. [DOI] [PubMed] [Google Scholar]
- 17.Mueller P., Rudin D.O., Tien H.T., Wescott W.C. Methods for the formation of single bimolecular lipid membranes in aqueous solution. J. Phys. Chem. 1963;67:534–535. [Google Scholar]
- 18.Montal M., Mueller P. Formation of bimolecular membranes from lipid monolayers and a study of their electrical properties. Proc. Natl. Acad. Sci. USA. 1972;69:3561–3566. doi: 10.1073/pnas.69.12.3561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Serowy S., Saparov S.M., Antonenko Y.N., Kozlovsky W., Hagen V. Structural proton diffusion along lipid bilayers. Biophys. J. 2003;84:1031–1037. doi: 10.1016/S0006-3495(03)74919-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Przybylo M., Sykora J., Humpolickova J., Benda A., Zan A. Lipid diffusion in giant unilamellar vesicles is more than 2 times faster than in supported phospholipid bilayers under identical conditions. Langmuir. 2006;22:9096–9099. doi: 10.1021/la061934p. [DOI] [PubMed] [Google Scholar]
- 21.Hartmann W., Galla H.J. Binding of polylysine to charged bilayer membranes: molecular organization of a lipid-peptide complex. Biochim. Biophys. Acta. 1978;509:474–490. doi: 10.1016/0005-2736(78)90241-9. [DOI] [PubMed] [Google Scholar]
- 22.de Kruijff B., Rietveld A., Telders N., Vaandrager B. Molecular aspects of the bilayer stabilization induced by poly(L-lysines) of varying size in cardiolipin liposomes. Biochim. Biophys. Acta. 1985;820:295–304. doi: 10.1016/0005-2736(85)90124-5. [DOI] [PubMed] [Google Scholar]
- 23.Kleinschmidt J.H., Marsh D. Spin-label electron spin resonance studies on the interactions of lysine peptides with phospholipid membranes. Biophys. J. 1997;73:2546–2555. doi: 10.1016/S0006-3495(97)78283-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gambin Y., Lopez-Esparza R., Reffay M., Sierecki E., Gov N.S. Lateral mobility of proteins in liquid membranes revisited. Proc. Natl. Acad. Sci. USA. 2006;103:2098–2102. doi: 10.1073/pnas.0511026103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vaz W.L., Hallmann D., Clegg R.M., Gambacorta A., De R.M. A comparison of the translational diffusion of a normal and a membrane-spanning lipid in L alpha phase 1-palmitoyl-2-oleoylphosphatidylcholine bilayers. Eur. Biophys. J. 1985;12:19–24. doi: 10.1007/BF00254091. [DOI] [PubMed] [Google Scholar]
- 26.Golebiewska U., Gambhir A., Hangyas-Mihalyne G., Zaitseva I., Radler J. Membrane-bound basic peptides sequester multivalent (PIP2), but not monovalent (PS), acidic lipids. Biophys. J. 2006;91:588–599. doi: 10.1529/biophysj.106.081562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Maier B., Radler J.O. Conformation and self-diffusion of single DNA molecules confined to two dimensions. Phys. Rev. Lett. 1999;82:1911–1914. [Google Scholar]
- 28.Needham D., Hochmuth R.M. Electro-mechanical permeabilization of lipid vesicles. Role of membrane tension and compressibility. Biophys. J. 1989;55:1001–1009. doi: 10.1016/S0006-3495(89)82898-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Epand R.M., Lim W. Mechanism of liposome destabilization by polycationic amino acids. Biosci. Rep. 1995;15:151–160. doi: 10.1007/BF01207455. [DOI] [PubMed] [Google Scholar]
- 30.Dolowy K. Effect of interfacial tension and curvature of charged lipid bilayer-polylysine complexes. J. Electroanal. Chem. 1979;104:305–307. [Google Scholar]
- 31.Mutz M., Helfrich W. Bending rigidities of some biological model membranes as obtained from the Fourier-analysis of contour sections. J. Phys. 1990;51:991–1002. [Google Scholar]
- 32.Rawicz W., Olbrich K.C., McIntosh T., Needham D., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Evans E., Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- 34.Ben-Tal N., Honig B., Peitzsch R.M., Denisov G.A., McLaughlin S. Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results. Biophys. J. 1996;71:561–575. doi: 10.1016/S0006-3495(96)79280-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Allender D.W., Schick M. Phase separation in bilayer lipid membranes: effects on the inner leaf due to coupling to the outer leaf. Biophys. J. 2006;91:2928–2935. doi: 10.1529/biophysj.106.086868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tian A., Johnson C., Wang W., Baumgart T. Line tension at fluid membrane domain boundaries measured by micropipette aspiration. Phys. Rev. Lett. 2007;98:208102. doi: 10.1103/PhysRevLett.98.208102. [DOI] [PubMed] [Google Scholar]
- 37.Akimov S.A., Kuzmin P.I., Zimmerberg J., Cohen F.S., Chizmadzhev Y.A. An elastic theory for line tension at a boundary separating two lipid monolayer regions of different thickness. J. Electroanal. Chem. 2004;564:13–18. [Google Scholar]
- 38.Kuzmin P.I., Akimov S.A., Chizmadzhev Y.A., Zimmerberg J., Cohen F.S. Line tension and interaction energies of membrane rafts calculated from lipid splay and tilt. Biophys. J. 2005;88:1120–1133. doi: 10.1529/biophysj.104.048223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krylov A.V., Kotova E.A., Yaroslavov A.A., Antonenko Y.N. Stabilization of O-pyromellitylgramicidin channels in bilayer lipid membranes through electrostatic interaction with polylysines of different chain lengths. Biochim. Biophys. Acta. 2000;1509:373–384. doi: 10.1016/s0005-2736(00)00320-5. [DOI] [PubMed] [Google Scholar]
- 40.Zhang L., Granick S. Slaved diffusion in phospholipid bilayers. Proc. Natl. Acad. Sci. USA. 2005;102:9118–9121. doi: 10.1073/pnas.0502723102. [DOI] [PMC free article] [PubMed] [Google Scholar]


