Mechanism and Energetics of Charybdotoxin Unbinding from a Potassium Channel from Molecular Dynamics Simulations

Abstract

Ion channel-toxin complexes are ideal systems for computational studies of protein-ligand interactions, because, in most cases, the channel axis provides a natural reaction coordinate for unbinding of a ligand and a wealth of physiological data is available to check the computational results. We use a recently determined structure of a potassium channel-charybdotoxin complex in molecular dynamics simulations to investigate the mechanism and energetics of unbinding. Pairs of residues on the channel protein and charybdotoxin that are involved in the binding are identified, and their behavior is traced during umbrella-sampling simulations as charybdotoxin is moved away from the binding site. The potential of mean force for the unbinding of charybdotoxin is constructed from the umbrella sampling simulations using the weighted histogram analysis method, and barriers observed are correlated with specific breaking of interactions and influx of water molecules into the binding site. Charybdotoxin is found to undergo conformational changes as a result of the reaction coordinate choice—a nontrivial decision for larger ligands—which we explore in detail, and for which we propose solutions. Agreement between the calculated and the experimental binding energies is obtained once the energetic consequences of these conformational changes are included in the calculations.

Introduction

Accurate description of protein-ligand interactions is one of the central problems in molecular biology. A variety of experimental methods are employed for this purpose, e.g., structures of bound complexes are determined from x-ray diffraction and NMR, binding energies from rate constants, and specific pairs of residues involved in binding from site-directed mutagenesis studies (1). While a fairly complete characterization of the bound complex can be obtained from experimental studies, interesting questions about the intermediate states in binding and a comprehensive account of the binding process itself are not usually accessible to experiments. Such questions can be naturally addressed using simulation methods, which have become feasible during the last decade thanks to the rapid growth in computational power.

Several methods are available for computational studies of protein-ligand interactions, ranging from the simplest docking methods (2,3) to Brownian dynamics (4) and the more sophisticated molecular dynamics (MD) simulations (5–7). The aim of the docking methods is to predict the binding configurations and energies of large number of ligands for a given receptor with minimal computational effort. This makes them very fast but also limits their accuracy (8). An accurate and detailed description of the binding/unbinding processes requires explicit representation of water molecules, which is possible only in MD simulations. Unfortunately predicting the binding configuration for a protein-ligand complex from MD simulations is a very slow process, so it can be reliably applied to those few cases where the complex structure has already been determined from experiments (9–17). For the majority of cases lacking a complex structure, one can use a docking method to generate initial binding positions, which are subsequently refined in MD simulations (18–22). While this is a promising method and it has been gaining in popularity, its accuracy in predicting the binding configurations is yet to be established.

Ion channel-toxin complexes offer some unique advantages for studying the protein-ligand unbinding problem: Firstly, protein interactions in solution do not necessarily yield obvious reaction coordinates for the unbinding of a ligand, whereas it is naturally defined by the pore axis in most cation channels. Secondly, toxins have long been used in many physiological and pharmacological studies of ion channels (23–25). The general pharmacophore for potassium channels is well established, namely, there is a functional dyad of a pore-plugging lysine and an associated aromatic residue, which are surrounded by a basic ring of residues (26). Thus, there is a large amount of literature on the binding properties of toxins including site-directed mutagenesis studies, which can be used to check the accuracy of the computational results. Finally, there is a growing appreciation of toxins as potential drug leads, targeting ion channels because of their high affinity and selectivity for specific ion channels (27). A molecular-level understanding of how toxins interact with ion channels, therefore, would be of great interest in such pharmacological applications.

Until the recent publication of a KcsA channel surrogate in complex with charybdotoxin (ChTX) (28), there were no structures of ion channel-toxin complexes that would enable a computational study of their binding. Yu et al. (28) combined the known structures of KcsA (Protein Data Bank (PDB) ID: 1BL8) and ChTX (PDB ID: 2CRD), and determined the complex structure using nuclear-Overhauser-effect constraints. Because the KcsA channel does not bind ChTX strongly, mutations in the pore mouth of KcsA are made to mimic the Shaker sequence, which binds ChTX with high affinity (28). Charybdotoxin is a well-known blocker of potassium channels and has been used in many experimental studies to probe their pore structure (29,30), before the first crystal structure of the KcsA channel became available (31).

Our aim in this study is to get a comprehensive physical picture for the unbinding process including the mechanism and free energy of unbinding. Umbrella sampling MD simulations (32) provide the most suitable approach for this purpose, as one can analyze individual umbrella windows to get a detailed account of the changes occurring in the ion channel-toxin system during the unbinding process. The potential of the mean force (PMF) of the toxin along the reaction coordinate can be obtained from the sampling of the toxin coordinates via the weighted histogram analysis method (33), and the binding constant (and hence the binding energy) can be estimated from the integral of the PMF. Analysis of the distances between the interacting pairs and the number of water molecules in the channel-toxin interface provide complementary information that help to interpret the PMF results.

Previously umbrella sampling MD simulations have been used mainly in constructing the PMF of ions in ion channels to study their permeation and binding properties (34–38). Its extension to more complex ligands is quite recent, and there are only a few examples so far. For example, Woo and Roux studied binding of the phosphotyrosine peptide pYEEI to the Src homology-2 domain of human Lck (13), and Lee and Olson studied binding of the compounds BUQ and FK506 to the FK506 binding protein (14). We note that these ligands are relatively small molecules, e.g., pYEEI is a four-residue peptide with 44 heavy atoms, and BUQ and FK506 are compounds with six and 57 heavy atoms, respectively. In comparison, ChTX is a 37-residue peptide with 296 heavy atoms, and its structure contains an α-helix and a three-stranded β-sheet. Thus, this study takes the complexity of ligands to a higher level where ligand flexibility and proper sampling of the toxin coordinates are likely to be important issues. To address them we pay special attention to the convergence of the PMF results and the conformational changes that occur in ChTX during umbrella sampling simulations.

Methods

Model system and MD simulations

The NMR structure of ChTX (39) is taken from the Protein Data Bank (PDB) database (PDB ID: 2CRD). The structure is shown in Fig. 1 from two different perspectives to indicate the important motives involved in its rigidity and binding. As indicated in Fig. 1 A, it has three disulfide bonds between the α-helix and three-stranded β-sheet, which confer upon it a relatively rigid structure. The charged side chains on ChTX—four lysine, three arginine, and one glutamate—are indicated in Fig. 1 B. This gives ChTX a net charge of +5e, as the N-terminal residue is the neutral pyroglutamic acid (PCA) residue while the C-terminal has charge −e. For purposes of comparison with the structure in complex, the NMR structure of ChTX is equilibrated in a box of water with five Cl⁻ ions.

Figure 1.

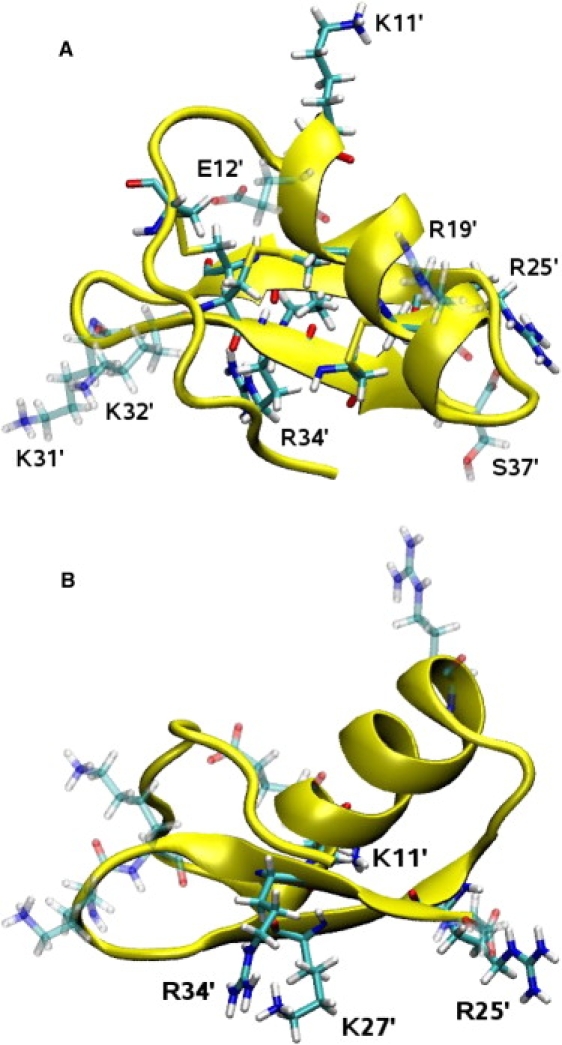
NMR structure of ChTX from two different perspectives. (A) View from the top, as it is docked in the KcsA channel. The three disulfide bonds that confer some rigidity to ChTX are clearly visible (indicated by yellow). (B) Side view, where the arginine and lysine residues involved in the binding are indicated. Visual figures in this article have been rendered using Tachyon (Tachyon Software, Denver, CO) within the VMD environment.

The coordinates of the KcsA channel surrogate in complex with ChTX (28) are taken from the PDB database (PDB ID: 2A9H). A snapshot of the complex structure obtained after equilibration is shown in Fig. 2. We note in particular K27′, whose side chain inserts into the filter and strongly interacts with the carbonyl oxygens of Y78 (toxin residues are distinguished using a prime). Other significant couplings include K11′-D64(B), R25′-D64(C), and R34′-D80(D). The surrogate KcsA structure has three mutations in the outer pore mouth region (Q58A, T61S, and R64D), which ensure binding of ChTX with high affinity. Further three mutations in the inner helix (F103Y, T107F, and L110V) are performed to mimic the cavity structure of the hERG channel, which are not relevant for this study of the outer surface.

Figure 2.

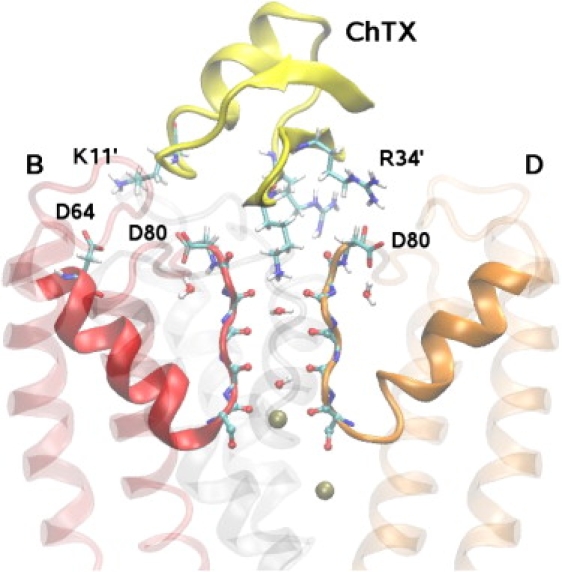
Side view of ChTX in complex with a KcsA potassium channel surrogate. ChTX backbone is shown in yellow and the side chains of K11′, K27′, R25′, and R34′ residues involved in the binding are explicitly shown. Two of the four monomers in KcsA (B and D) are shown clearly. The monomer A is removed and C is shown as a shadow for clarity. The carbonyl groups in the filter and the side chains of D80 and D64 residues are explicitly indicated. The water molecules in the filter and two K⁺ ions (one at the S4 binding site and one in the cavity) are also shown.

The simulation system is constructed using the VMD software (40). The complex structure is embedded in a lipid bilayer consisting of 112 1-palmitoyl-2-oleoyl-phosphatidylethanolamine molecules and solvated with 13,239 water molecules and 15 K⁺ and 20 Cl⁻ ions. The KcsA surrogate has no net charge, thus overall the system is charge-neutral. Two of the K⁺ ions are initially placed in the cavity and at the S3 binding site of KcsA, as observed in the crystal structure (41). After equilibration, the K⁺ ion at S3 is observed to move to S4, presumably induced by the presence of the K27′ side chain in the filter. We have also experimented with putting a third K⁺ ion at the S1 site and found that the K27′ side chain bent away from the filter and assumed a completely different conformer. Therefore, in the rest of the MD simulations, a third K⁺ ion is not placed at the S1 binding site.

Molecular dynamics simulations are carried out using the version (2.6) of the NAMD code (42) with the CHARMM22 force field (43) and the TIP3 model for water molecules. Recently introduced CMAP dihedral correction terms are included in the force field (44). CHARMM22 provides a complete set of parameters for all the atoms in the system except for the PCA residue, which forms the N-terminal of ChTX in the NMR structure of the complex. To parameterize PCA, its coordinates are taken from the complex and modified to form the free reduced form. These coordinates are then subjected to QM-level refinement using Gaussian03 (45) and MP-2 level theory. The accuracy of the result is verified by comparing the structure to x-ray structural data (46), and correlating predicted peaks of its IR/Raman spectrum with experimental results (47). We have taken the final parameters from the average bonds and angles of the molecule. Analogous molecules in the CHARMM22 force field are used as a template to construct the dihedral angles and the bond constants.

We perform MD simulations using an NpT ensemble with periodic boundary conditions. Pressure is kept at 1 atm and temperature at 300 K using the Langevin pressure (48) and temperature coupling with damping coefficients of 5 ps⁻¹. We use a switching distance of 10–13.5 Å for the Lennard-Jones interactions, and compute electrostatic interactions with the particle-mesh Ewald algorithm. A timestep of 2 fs has been employed in all MD simulations, writing out trajectory data at either 1-ps or 5-ps intervals. In umbrella sampling simulations, the z component of the center of mass of ChTX is collected at every timestep. We use units of kT for the PMF, which can be converted to kcal/mol using 1 kcal/mol = 1.7 kT.

The system is equilibrated in two stages. First, the coordinates of the KcsA channel-ChTX complex are fixed and the system is equilibrated with 1 atm pressure coupling until the correct water and lipid densities are obtained. In the second stage, the x and y dimensions of the simulation box are fixed at 76 and 72 Å, respectively, and pressure coupling is applied in the z direction (average z dimension is 105 Å). The restraints on first the ChTX atoms and then the KcsA atoms are relaxed in MD simulations lasting 2 ns. A small restraint of 0.1 kcal/mol/Ų is retained on the backbone atoms of KcsA to preserve the structural integrity of the channel during the long umbrella sampling simulations. The final system is further equilibrated for 1.5 ns without any restraints on the ChTX atoms to check its stability and characterize the main interactions involved in the binding.

Umbrella sampling and PMF

Umbrella windows at 0.5 Å intervals are generated along the channel axis (z axis) using steered MD simulations. A harmonic force with k = 20 kcal/mol/Ų is applied to the center of mass (COM) of the ChTX backbone, which is pulled at a constant speed of 5 Å/ns over 0.5 Å. After each pulling step, ChTX is equilibrated at the window position by applying a harmonic restraint of 20 kcal/mol/Ų to its center of mass for 200 ps to relax the effect of steering on the environment. Initially a total of 31 windows are generated over 15 Å. Due to a local potential barrier, insufficient overlap occurs between the adjoining window samples at 34.5 Å. To improve sampling at this position, an extra window is included in the middle of the two windows, increasing the number of windows to 32. At each window, the system is subjected to 3.4 ns of umbrella sampling MD simulations with the same force constant of 20 kcal/mol/Ų. The center-of-mass coordinates of ChTX collected during the umbrella sampling simulations are used in constructing its PMF via the weighted histogram analysis method (33). Convergence of the PMF is the main criterion in choosing the length of the umbrella sampling simulations.

To ensure that the PMF is not affected by sampling problems in other windows, we have performed a second set of umbrella sampling simulations by doubling the number of windows in the first 5 Å, where the PMF rises most steeply. Extra windows are created in the middle of the original ones using the same protocol as above. A total of 41 windows are generated in this way. At each extra window the system is subjected to 3.4 ns of umbrella sampling simulations in conformity with the first set.

To investigate the effect of the harmonic force constant on the PMF, we have performed a third set of umbrella sampling simulations using a force constant of 40 kcal/mol/Ų. The reason for using a larger force constant is that the center of mass of ChTX is found to be displaced from the umbrella window position up to 2 Å near the binding site, which indicates that the umbrella force is much weaker compared to the attractive forces between the channel and ChTX. We have generated the windows for the third set from those of the first set by increasing the force constant from 20 to 40 kcal/mol/Ų in 20 steps in 200-ps MD simulations. For each window, data are collected for 2.4 ns. A shorter time is sufficient in this case because the PMF is found to converge much faster when a larger force constant is used.

The binding constant of ChTX with the KcsA channel can be estimated from the integral of the PMF, W(z)

$$K_{\text{eq}}=\pi R^2{\int }_{z_1}^{z_2}{e}^{-W\left(z\right)/kT}dz,$$ (1)

where R is an effective radius for ChTX, which is found to be ∼10 Å. The integration limits are chosen such that z₁ is in the binding pocket and z₂ is in the bulk region where W vanishes. Adequate choices determined from the PMF are z₁ = 30 Å and z₂ = 46 Å. The absolute binding free energy of ChTX is determined from the binding constant using ΔG_b = −kT ln [K_eqC^o], where C^o is the standard concentration of 1 M/L.

Change in the configurational free energy of ChTX is estimated using Jarzynski's equation (49) in steered MD simulations (50,51). The system is driven from an initial state to a final one by applying a stiff harmonic force to the chosen distance constraint (k = 20 kcal/mol/Ų), which is pulled along the reaction coordinate at a constant velocity of v = 5 Å/ns. For each steered MD simulation (indexed by i), the work function W_i(z) is calculated from the integral of the force on the spring as a function of the path. The free energy change is determined from the ensemble average of the work done for several paths (49) as

$$e^{-\Delta G/kT}=\langle e^{-W_{\text{i}}/kT}\rangle \text{.}$$ (2)

The orientation of ChTX, and how it changes during the umbrella sampling simulations, is an important consideration. We use the dipole moment of ChTX for this purpose because physically it is the most relevant quantity for depicting its orientation. The dipole moment is calculated with respect to the center of mass of ChTX using

$$\mathbf{D}=\sum _{\text{i}}{q}_{\text{i}}{\mathbf{r}}_{\text{i}},$$ (3)

where the index i runs over all the atoms in ChTX with nonzero partial charges q_i, whose distance from the center of mass is r_i. Because the monopole charge interactions dominate the binding, the magnitude of the dipole moment is not directly relevant, but its direction and fluctuations in its direction provide valuable information.

Results and Discussion

Characterization of the KcsA channel-charybdotoxin complex

The KcsA channel-ChTX complex has a very stable structure. To demonstrate this point, we analyze the trajectory data obtained from MD simulations of the complex, the KcsA channel alone and ChTX in bulk water. In the top panel of Fig. 3, we show the root mean-square deviation (RMSD) of the toxin backbone with respect to the NMR structure in three cases: in bulk water, in complex with KcsA, and in the last umbrella sampling window where the PMF vanishes. The average RMSD values for the three cases are 1.70 ± 0.14, 1.76 ± 0.19, and 2.51 ± 0.15 Å, respectively. It is clear from the comparison of the results for the first two cases that ChTX does not undergo any significant configurational changes upon unbinding from the KcsA channel. Implications of the third case will be discussed after presenting the PMF results. A similar comparison is presented for the KcsA channel showing the effect of ChTX binding (bottom panel in Fig. 3). Only the surface residues of KcsA (i.e., 49–64 in S5-Pore helix and 78–87 in Filter-S6) are included in the RMSD calculations. The average RMSD value in the ChTX-free case is 1.21 ± 0.03, which decreases to 0.93 ± 0.07 when blocked. Thus binding of ChTX reduces the fluctuations of the surface residues, in conformity with the observations made in Yu et al. (28).

Figure 3.

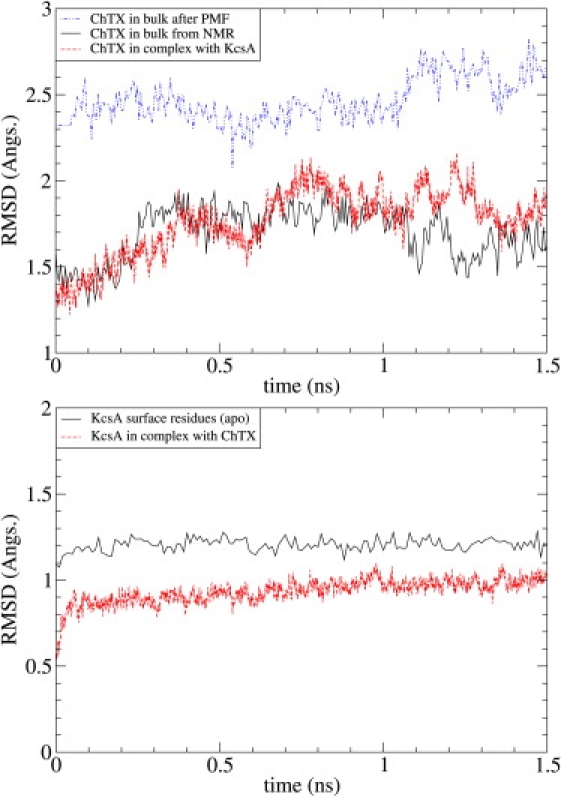
The RMSD of ChTX in bulk water, in complex with the KcsA channel, and in the last umbrella sampling window (top). The NMR structure 2CRD1 is used as the reference state. RMSD of the surface residues of KcsA (i.e., 49–64 in S5-P and 78–87 in F-S6) with and without ChTX bound (bottom). The NMR structure of the complex 2A9H is used as the reference state.

MD simulations at the binding site reveal that the KcsA channel-ChTX complex is primarily characterized by charge interactions, with secondary contributions from aromatic and aromatic-sulfur interactions. An illustration of the binding mode is shown in Fig. 2, while a comprehensive list showing the average distances between the heavy-atom pairs involved in binding is given in Table 1. Three of the four monomers of KcsA have significant involvement in the complex formation by providing charge contacts with the basic ring surrounding the pore-plugging K27′. These contacts secure ChTX into place with KcsA, in a mode similar to other members of the α-KTX family (29,52).

Table 1.

List of interacting residues in the ChTX-KcsA complex, and their average distances

ChTX	KcsA	Avg. dist.
K11′	D64(B)	5.7 ± 0.8
K11′	D80(B)	7.6 ± 1.1
R25′	D64(C)	3.3 ± 0.5
R25′	D80(C)	3.7 ± 0.5
K27′	Y78(A)	2.8 ± 0.1
K27′	Y78(B)	2.9 ± 0.2
K27′	Y78(C)	3.1 ± 0.4
K27′	Y78(D)	2.9 ± 0.2
M29′	Y82(A)	4.8 ± 0.7
R34′	D80(D)	3.1 ± 0.7
Y36′	Y82(D)	5.4 ± 0.4

Distances between charged residues are given by N-O separation, whereas, for the aromatic and aromatic-sulfur interaction, the closest carbon atom in the ring is chosen to be the candidate.

To give a better idea about the nature of the charged interactions, we show pair-distance histograms for several aforementioned pairs in Fig. 4. The K27′-Y78 pairs shown in the top panel are the most significant ones. This histogram shows that the K27′ nitrogen remains at about equal distance from the carbonyl oxygens of the four Y78 residues. The sharpness of the distributions indicate that the side chain of K27′ is firmly bound to the Y78 carbonyls and completely blocks the channel while in that position. A similarly sharp distribution is found for the R34′-D80(D) pair. To understand the trailing distances in the histogram we have looked at the time series of this distance, which shows that the D80 side chain is initially oriented sideways and forms a link with R34′ after a few hundred ps. However, once the link is formed, the N-O pair remains in that configuration for the rest of the simulation.

Figure 4.

Distributions of the distances between the strongly interacting pairs in the KcsA channel-ChTX complex. The K27′-Y78 histogram shows the N-O distances for each of the four monomers denoted by A–D. Three H atoms in the amide group make hydrogen bonds with the carbonyls of A, B, and D, while that of C is left free. The elongated tail in the R34′-D80 plot stems from equilibration—this interaction is established shortly after system equilibration and remains associated for the rest of the simulation.

The R25′ residue faces the C-monomer and interacts with the side chains of both D64(C) and D80(C). As seen in the histograms, the pair distributions are quite similar, with D64(C) being slightly more preferred compared to D80(C). As the R25′ side chain fluctuates between the two binding sites, the distributions are much wider compared to those of K27′ and R34′. The K11′ residue faces the B-monomer and can similarly interact with the side chains of D64(B) and D80(B). The histograms show that D64(B) is closer to K11′. However, both the average distance and the width of the distribution are significantly larger compared to the other three cases, indicating a weaker coupling between K11′-D64(B). Nevertheless, as will be shown later, K11′ does play an important role at the intermediate stages of unbinding.

M29′ and Y36′ both make contacts with the Y82 residues around the pore, and also stabilize the binding conformation. The larger average distances recorded (∼5 Å) are typical of aromatic-aromatic and aromatic-sulfur interactions, caused by the ring orbitals and larger van der Waals radii. Although the aromatic contacts are not as significant as the charge contacts, there is evidence pointing to their importance in binding, both by mutational analysis and computational simulation, e.g., (22,28,52).

PMF of charybdotoxin

A crucial issue in the PMF calculations, especially for a large peptide such as ChTX, is the convergence of the results. To demonstrate the convergence of the PMF, we discard the first 0.2 ns of the 3.4-ns MD data collected from the umbrella sampling simulations with k = 20 kcal/mol/Ų, and divide the rest of the 3.2-ns data into eight equal parts. A separate PMF is constructed from each set of data, which are numbered from one to eight, sequentially. As shown in Fig. 5, the PMFs systematically come down for the first four sets and then fluctuate around a baseline. This indicates that the system has not been properly equilibrated in the first three sets. Therefore they are excluded in favor of the remaining five sets (i.e., the last 2 ns of the MD data) when constructing the final PMF (indicated by the thick black line in Fig. 5). A similar convergence study is performed for each PMF presented in the article.

Figure 5.

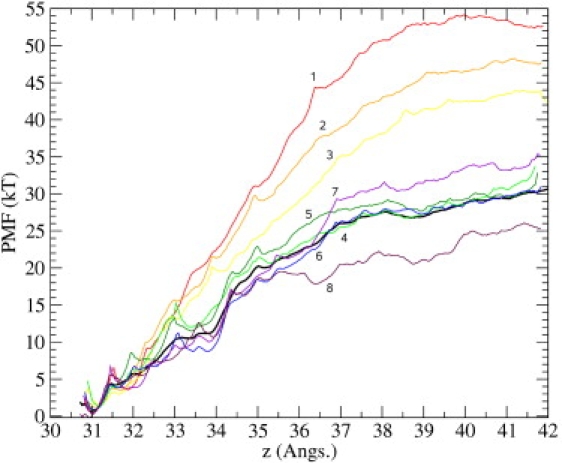
Convergence study of the PMF. Data from the first 11 Å is used as a guide to check for sufficient convergence. Here, vertical axis refers to the estimated PMF, and horizontal axis, z, refers to the COM position of the ChTX backbone heavy-atoms, with z = 0 defined as the center of the simulation box (this convention holds throughout the article). The binding site is located at z ∼ 31 Å measured along the channel axis. The last 3.2 ns of the MD data is divided into eight equal parts and a PMF is constructed from each set. The PMFs are sequentially numbered from 1 to 8, as indicated in the figure.

As already mentioned in Methods, sampling problems can arise between windows where the PMF steeply rises. This has necessitated the inclusion of an extra window at 34.5 Å, where the sampling density drops significantly (see the inset later in Fig. 7). To check whether this extra window is sufficient, and more generally to investigate the sensitivity of the PMF calculations to the density of umbrella windows, we have added a second set of umbrella sampling simulations with windows at 0.25 Å intervals in the first 5 Å of the PMF. The resulting PMF (solid line) is compared to the original one (dashed line) in Fig. 6. The new PMF is ∼1 kT deeper than the original one, which is likely to have originated from a slightly better definition of a small pocket at 32 Å. Because the difference is within the accuracy of the free energy calculations and the inclusion of the extra windows do not change the overall shape of the PMF, we conclude the number of windows used in the first set is adequate and the extra windows are not required.

Figure 7.

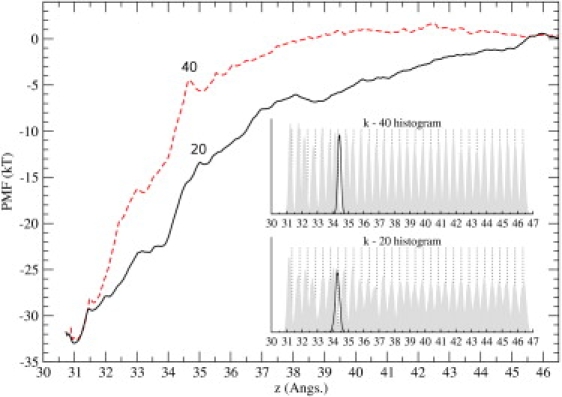
Comparison of the PMFs obtained from the umbrella sampling simulations using the force constants of 20 kcal/mol/Ų (solid line) and 40 kcal/mol/Ų (dashed line). The same routine employed in the construction of the k-20 PMF has been used for the k-40 PMF. (Inset) Distribution of the ChTX-COM as overlapping histograms along the reaction coordinate. For each window, we display the actual distribution of the ChTX-COM (shaded histogram) and its constraint coordinate (dotted line, usually to the right). (Solid curve) Distribution for the extra window (to cover the poorly sampled region, see Methods).

Figure 6.

Effect of increasing the number of windows on the PMF. The density data used in Fig. 5 are augmented by including extra windows at 0.25 Å intervals, up to z ∼ 36 Å as shown by the dotted lines. The window number and positions are indicated in the figure. The resulting PMF (solid line), is compared to the first one obtained using 0.5 Å intervals (dashed line).

The final issue to be considered is the effect of the force constant used in the umbrella sampling simulations on the PMF. A third set of umbrella sampling simulations with a force constant of 40 kcal/mol/Ų is performed for this purpose. Study of the convergence of the PMF results, similar to that in Fig. 5, shows that convergence is obtained after the first 0.4 ns. The PMF constructed from the remaining 2 ns of MD data is shown Fig. 7 (dashed line) together with the first PMF obtained using k = 20 kcal/mol/Ų (solid line). Distributions of the z coordinates of ChTX sampled during the MD simulations are shown in the inset for both cases. There is a very good agreement between the two PMFs regarding the depth of the binding pocket, which is pleasing because the binding constant and energy are essentially determined by the well depth. The marked difference in distance dependence of the PMFs is caused by the softer umbrella potential allowing the strongly interacting pairs in the KcsA-ChTX complex to remain in contact for longer separation distances. However, this has a completely negligible effect on the observables as the calculated binding energies in Table 2 demonstrate. The absolute value of the binding energy is 0.5 kT larger in the softer PMF (k = 20 kcal/mol/Ų) compared to the harder one. However, comparison of the well depths shows that 0.4 kT of this amount actually comes from the slightly lower minimum in the softer PMF. Thus only 0.1 kT in the binding energy difference can be attributed to the differences in the shapes of the PMFs, which is much smaller than the accuracy of the PMF calculations.

Table 2.

The dissociation constant, K_D = 1/K_eq, and the absolute binding free energy ΔG_b obtained from the two PMFs with k = 20 and 40 kcal/mol/Ų

k	Predicted KD (pM)	ΔGb	ΔGwell
20	0.28	−28.9	−33.0
40	0.44	−28.4	−32.6

The well depths from the PMFs are also listed in the last column. All energies are in units of kT. The experimental dissociation constant is 900 nM (28), which corresponds to a binding free energy of −14 kT.

While the foregoing discussion has established that a fairly unique value for the binding energy can be obtained from the PMF calculations, the predicted value is much larger than the experimental result. To understand the reason for this discrepancy and see how it can be corrected, we analyze the trajectory data in the umbrella windows. This will also allow us to gain a more comprehensive picture of the unbinding process.

Analysis of umbrella windows

Comparison of the ChTX structure taken from the last umbrella window with that of NMR shows that it has undergone a configurational change during the umbrella sampling simulations (Fig. 8). Specifically, the L20′ residue at the C-terminal end of the helix breaks its H-bond with its natural partner V16′ and forms an H-bond instead with the first residue of the N-terminal. This explains the distortion of ChTX and its increased RMSD in the last umbrella window versus bulk and complex conditions (Fig. 3). A plot of the average RMSD of ChTX as a function of its center of mass (not shown) reveals that even larger configurational changes occur between z = 31 and z = 35 Å, where the PMF rises very steeply. In the k-20 PMF, the average RMSD rises to a maximum of 3.3 Å at z = 32.6 Å—caused by the opening of the N-terminal. It then drops to 2.5 Å at z = 35 Å, and remains constant thereafter. Inspecting the toxin backbone at these windows, we find that the maximum arises from the detachment of the N-terminal from its pocket and general bending of the α-helix—which settles into the alternate conformer shown in Fig. 8 from z = 35 Å onwards.

Figure 8.

Comparison of the NMR structure of ChTX (light shaded) with that obtained from the last umbrella window (dark shaded). The side chains of the residues Z1′, V16′, and L20′ are explicitly shown. K27′ (in licorice representation) is also displayed to give a sense of orientation. (Dashed lines) The V16′-L20′ hydrogen bond in the last turn of the α-helix, which is broken by tidal forces during pulling.

A similar picture is obtained for the k-40 PMF except that the maximum value of the RMSD is even higher (4.2 Å), associated with a more exaggerated distortion of the toxin. Once ChTX is dissociated, it assumes a configuration similar to that shown in Fig. 8, regardless of the force constant used. The stability of the final ChTX structure after the umbrella sampling simulations has been verified by subjecting it to bulk simulations for several nanoseconds, where no change in the pattern is observed.

The configurational changes in ChTX are caused by tidal forces during the steered component of the simulation. As the toxin is moved away from KcsA, the strong coupling between pairs of interfacial residues (Table 1) causes the center of mass of ChTX to move 1–2 Å from the umbrella position toward KcsA, resulting in a large umbrella force acting on all the residues in the opposite direction. The N-terminal and helical region containing L20′ are furthest away from KcsA and are largely neutral—thus they are the weakest links in the peptide chain and the tidal forces are strong enough to induce the configurational changes discussed above. We note that ChTX is otherwise held together by three disulfide bonds, which prevents the possibility of major unfolding. The differences between the two PMFs in Fig. 7 is partly explained by the fact that the tidal forces are larger in the k-40 case, which leads to larger transient changes in ChTX.

To get a more complete picture of the processes occurring during unbinding, we consider the average distances of strongly interacting pairs and discuss how they change with the position of ChTX (Fig. 9). We consider the same pairs as in Fig. 4, except we show the K27′-Y78 distance for only one monomer but include instead the distance of K27′ from G79(A) and D80(D). This is because unlike other residues K27′ changes partners during the pulling, making contacts with all three residues in sequence. The most important observation in Fig. 9 concerns the pair distances between z = 31 and z = 35 Å. Except for K11′ in the last panel (which is weakly coupled), all three strongly coupled ChTX side chains are seen to retain their contact distances, or at least move much less compared to ChTX itself. Thus the steep rise in the k-20 PMF between z = 31 and z = 35 Å (Fig. 7) is not caused by the breaking of the pairs but mainly results form the work done by the umbrella forces while inducing conformational changes in ChTX. Breaking of the pairs occurs between z = 35 and z = 38 Å, which gives rise to a more mild increase in that region's PMF. Results obtained from the k-40 umbrella sampling simulations are qualitatively similar, other than the observation that interaction pairs are broken in earlier windows, contributing to the steeper rise of the k-40 PMF compared to the k-20 PMF. These observations suggest that the more rapid convergence of the k-40 PMF to bulk values is due to the faster occurrence of all changes.

Figure 9.

Average distances of interacting pairs in the KcsA channel and ChTX, plotted as a function of the reaction coordinate z. Additional pair distances are included in the K27′ plot to show its sequential transfer along the channel backbone. The trajectory data are from the k-20 umbrella sampling simulations. Error bars indicate one standard deviation.

Another important observation in Fig. 9 is that several interaction pairs exhibit very large jumps in distances that cannot be explained by conformational changes in side chains alone, and in some cases pair distances decrease despite the monotonic increase in ChTX-channel distance. This is only possible if ChTX rotates around its center of mass to maximize the charge interactions. To demonstrate this point, we consider the orientation of ChTX as defined by its dipole vector (Fig. 10). In the complex, the dipole vector of ChTX makes a 40° angle with the −z axis. Significant changes occurring in the pair distances at ∼z = 35 Å (e.g., breaking of the R34′-D80(D) pair and establishment of K27′-D80(D) and K11′-D80(B) pairs) are associated with the rotation of the dipole vector by 40° away from the channel axis. Another large tumbling of ChTX occurs at ∼z = 39–40 Å, where the dipole moment points almost in the direction of the channel axis. From Fig. 8 this is seen to be associated with the breaking of K11′-D80(B) and limited reassertion of R34′-D80(D). The polar graph of the dipole moment (Fig. 10, inset) gives an alternate summary of the rotational motion. ChTX dipole moment gradually swings away from the channel axis to optimize its decreasing charge interactions (A-B). Once all the strong charge interactions have been dissipated, the dipole vector aligns with the channel axis (C). Moving further away, it assumes a random orientation as indicated by the increasing fluctuations in its orientation (D).

Figure 10.

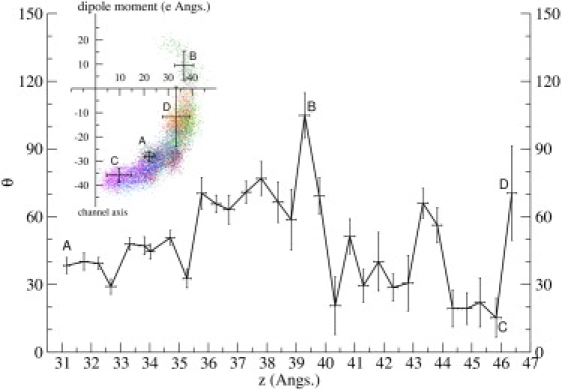
Orientation and fluctuations of the dipole moment of ChTX plotted as a function of the reaction coordinate z. The angle θ is defined between the dipole moment and the −z axis (toward the channel). (Inset) Polar graph of the dipole moment sampled from all the k-20 umbrella windows, where individual data points are plotted as a vector with angle θ from the channel axis and radius equal to its dipole magnitude. Error bars indicate one standard deviation.

Binding of ChTX to the KcsA channel requires dehydration of the residues along their interfaces. Thus, another interesting quantity to look at is the number of water molecules in the interface, and how it changes with the distance of ChTX from the channel. To this end, we have calculated the average number of water molecules between the channel and the toxin and within 5 Å of the channel axis for each window (Fig. 11) (note that using a larger radius gives essentially similar results but with larger fluctuations). Though one might expect the number of water molecules to increase steadily as ChTX moves away, the changing orientation of ChTX may delay entry or expel some of the incoming solvent. This can be seen by correlating the local minima in dipole orientation with decreases in water volume—each time the dipole moment swings toward the channel axis, the water number drops. That is, the maximal hydration of the interfacial residues requires the dipole moment of ChTX orienting away from the axis.

Figure 11.

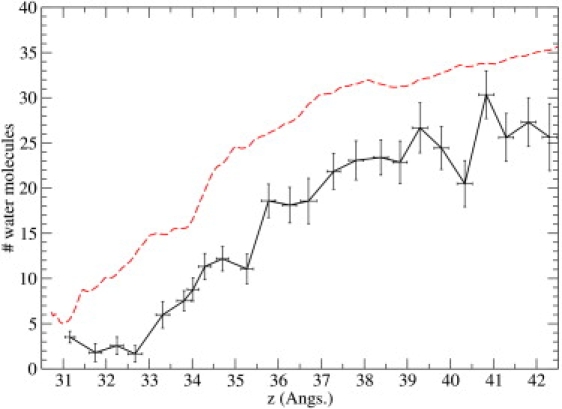
Number of water molecules in the KcsA channel-ChTX interface plotted as a function of the reaction coordinate z. (Dashed line) Relevant PMF values, purely for comparison purposes. Trajectory data are derived from the k-20 umbrella sampling simulations.

Combining all the analysis performed so far, we can propose a plausible picture for the binding process. Initially ChTX approaches the channel under the influence of attractive Coulomb forces with its positively-charged side facing the channel (z = 46–40 Å). The first contact is established at z ∼40 Å, most likely between K11′ and one of the D80’s, which requires a substantial rotation of ChTX. This contact is retained from z = 40–36 Å, as more primary contacts between R25′-D80 and K27′-D80 are established. The most critical stage in the binding occurs at z ∼35 Å, when the dipole moment swings toward the channel axis, expelling a large number of waters from the interface and establishing the correct key contacts between the toxin and channel, e.g., K27′ hops along the backbone carbonyls to its pore-plugging position. This swing is likely to be controlled by the association of R25′ and R34′, via their strong interactions with aspartates. After that point, the orientation of ChTX is fairly well established, and all that is left to form the complex is for the side chains to move into optimal positions and expel some more water to make contacts among the hydrophobic residues.

In making the above inferences on binding, we have assumed that the PMF gives the reversible work done on the ligand regardless of whether it is pulled in to or out of the binding site. Apart from the matching of the initial and final configurations in the two processes, which is further discussed below, validity of this assumption relies on sufficient sampling of the configurational space during the MD simulations. Adequacy of the orientational sampling can be surmised from Fig. 10, which gives the average orientation of ChTX and its fluctuations at each window position. The local potential energy in the θ direction is approximately given by U(θ) = 0.5(θ/σ)² kT, where σ denotes the fluctuations in θ. From Fig. 10, σ ≈ 10° or less for most windows in the binding region. Because ChTX is quite rigid and the long-range Coulomb forces dominate the interaction, we expect this estimate to remain valid beyond its immediate range. To give an example, the energetic cost of ChTX swinging θ = 45° away from its minimum energy position is ∼10 kT, and from Boltzmann factor the probability of this happening is very small (∼10⁻⁵). A completely flipped orientation of ChTX will have a higher energy, hence its probability is even smaller. These estimates indicate that orientation of ChTX is rather well determined by the strong Coulomb interactions, and the present nanosecond MD simulations should be adequate for sampling the orientation of ChTX.

Trapping of water in the interface during binding is another possibility that could distinguish it from the unbinding process. However, as shown in Fig. 11, water numbers in the interface exhibit substantial fluctuations even at the binding position. That is, water can freely access the interface at all window positions, and there should be no problem with its equilibration, regardless of whether the ligand is pulled in or out. While these arguments lend strong support for the reversibility of the unbinding process, for the ultimate proof one needs to construct several PMFs for the binding of ChTX starting from random orientations in bulk, and show that they are similar to the one obtained from the unbinding of ChTX.

The observation that ChTX takes a distinct path along the rotational space raises some interesting questions on applying rotational constraints on the overall toxin structure to reduce sampling space. We have shown here that as strongly coupled pairs break sequentially, the remaining interactions will actively rotate the toxin so as to optimize contacts. These findings suggest that rotation of toxin ligands is essential to the kinetics of binding/unbinding. Thus, artificially limiting the rotational space will also remove information about the dynamics—as the toxin can no longer traverse the optimal path on the underlying potential energy surface.

Change in the configurational free energy

The binding energy calculated from the PMF includes the work done on ChTX to induce the configurational change indicated in Fig. 8. We need to subtract this work from the calculated binding energy to get a more accurate value that can be compared to experiments. To estimate the free energy associated with the configurational change, we apply Jarzynski's equation to work functions obtained from steered MD simulations. For this purpose, we perform 10 steered MD simulations driving the NMR structure of ChTX to the structure obtained after the umbrella sampling simulations. This is achieved by pulling the H-bond between the L16′ and V20′ residues apart by constraining the center of mass distance between the respective backbones. To prevent work being done on other parts of the toxin (e.g., due to drift or rotation), a single center-of-mass constraint is applied to the rest of the toxin, except to the residues in between L16′ and V20′, which have significant participation in the deformation.

The work functions computed from individual steered MD simulations and the resulting free energy profile obtained from the work functions using Jarzynski's equation are shown in Fig. 12. From the free energy profile, we find that the energetic cost of the deformation is ∼15.5 kT. The computed value for ΔG_b (from Table 2) is then reduced to −13 kT, which is in good agreement with the experimental value of −14 kT. Of course, it is possible that sampling errors in the calculation of the PMF and the configurational free energy have cancelled each other, yielding a rather good value for the binding energy. While the umbrella sampling simulations account for all the degrees of freedom available to the toxin, how well they are sampled depends on the simulation time. Here we have checked the convergence of the PMF at the nanosecond timescale. If there are significant contributions to the PMF from slower degrees of freedom, it will obviously have an impact on the PMF. The configurational free energy change is less likely to suffer from such sampling problems because it is dominated by the short-distance covalent interactions, which assures a faster convergence (50,51). It is worthwhile to emphasize that regardless of the accuracy of the binding energy, the general picture of the toxin unbinding from a channel obtained here is likely to remain valid. The configurational changes in ChTX occur on the opposite end and do not have any influence on the interacting pairs on the channel-side of ChTX.

Figure 12.

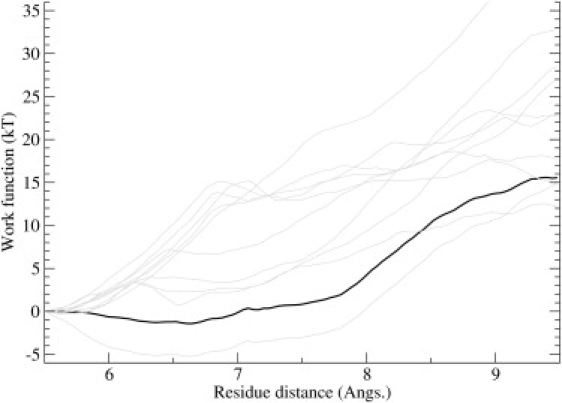
PMF estimate for the conversion of the ChTX structure from the NMR conformer to the distorted conformer. The horizontal axis refers to the COM distance between V16′ backbone and L20′ backbone. Individual work functions are shown in shading, while the PMF obtained from Jarzynski's equation is shown in solid representation.

Concluding Remarks

In this study, we have presented a comprehensive analysis of the unbinding process of ChTX from a modified KcsA, a novel channel-toxin structure. This process is primarily characterized by the sequential breaking of contacts among the charged pairs on KcsA and ChTX—an observation that can be generalized to other similar channel-toxin complexes, especially among the α-KTX family of scorpion toxins. The choice of the backbone center of mass as the reaction coordinate is shown to be useful in determining the binding energy, despite an artificial introduction of tidal forces on the toxin. Although it may be possible to avoid such artifacts by excluding nonessential residues from the reaction coordinate, the same choice may also affect rotational motions that occur during unbinding. An alternative method less likely to interfere with the unbinding process is to put extra distance constraints on those parts of the toxin that suffer most from tidal forces—provided, of course, that these distances remain the same in the complex and the bulk forms of the ligand. Considering that ChTX is a relatively rigid peptide thanks to the disulfide bonds, it is likely that similar problems will be encountered in binding/unbinding studies of other peptide ligands. Thus clarification of this issue will be important for application of the umbrella sampling simulations to other protein-ligand systems.

The size of the ligand in this study also raise issues on the balance between binding energy prediction and computational costs. During this study, we had to amend the protocols to adequately sample the reaction coordinate. It is also possible to utilize alternative methodologies, e.g., adaptive biasing force calculations, to achieve the same objective. Comparing the efficiency of these methods at this scale of complexity will be an interesting next step for future studies.