Sorting of Lipids and Proteins in Membrane Curvature Gradients

Abstract

The sorting of lipids and proteins in cellular trafficking pathways is a process of central importance in maintaining compartmentalization in eukaryotic cells. However, the mechanisms behind these sorting phenomena are currently far from being understood. Among several mechanistic suggestions, membrane curvature has been invoked as a means to segregate lipids and proteins in cellular sorting centers. To assess this hypothesis, we investigate the sorting of lipid analog dye trace components between highly curved tubular membranes and essentially flat membranes of giant unilamellar vesicles. Our experimental findings indicate that intracellular lipid sorting, contrary to frequent assumptions, is unlikely to occur by lipids fitting into membrane regions of appropriate curvature. This observation is explained in the framework of statistical mechanical lattice models that show that entropy, rather than curvature energy, dominates lipid distribution in the absence of strongly preferential lateral intermolecular interactions. Combined with previous findings of curvature induced phase segregation, we conclude that lipid cooperativity is required to enable efficient sorting. In contrast to lipid analog dyes, the peripheral membrane binding protein Cholera toxin subunit B is effectively curvature-sorted. The sorting of Cholera toxin subunit B is rationalized by statistical models. We discuss the implications of our findings for intracellular sorting mechanisms.

Introduction

The sorting of both lipids and proteins in trafficking pathways lies at the heart of cellular organelle homeostasis. Most membrane-bound molecules do not require specific signals to effectively recycle to the cell surface (1). However, the significantly different protein and lipid composition of various cellular membranes (2) requires sorting in cellular trafficking centers, such as the trans-Golgi network, the plasma membrane, endosomes and the endocytic recycling compartment. Precisely how sorting occurs for components that lack proteinaceous recognition sequences remains largely unknown (3–6).

Direct evidence for nonhomogenous intracellular lipid distributions and cellular lipid sorting can be obtained from microscopy imaging of fluorescent lipids (7,8) or lipid-like fluorophores (8–10). By alternative methods, the unconventional lipid lysobisphosphatidic acid has been shown to be enriched in endosomes of highly curved multivesicular morphology. Lipid lysobisphosphatidic acid is assumed to be crucial for regulating the membrane geometry of this organelle (11,12). A coupling of membrane curvature to the translocation of cellular lipids has been invoked to explain changes in lipid distributions associated with fusion pore formation (13).

In addition to vesicular transport intermediates, the intracellular sorting of lipids and proteins crucially involves tubular membranes (4,6). These are essential components of both secretory and endocytic pathways. Tubular membranes are morphological features characteristic of the trans-Golgi network, as well as sorting endosomes (6). Furthermore, the endocytic recycling compartment is essentially a collection of tubular membranes with diameters ∼60 nm that are associated with microtubules (6). The endoplasmic reticulum also shows regions of interconnected tubular membranes (14). Cellular membrane tubes have received significantly increased attention recently, in part due to the discovery of tubular intercellular connections (“tunneling nanotubes”) (15). Furthermore, intracellular membrane tubes have come to a forefront since biophysical mechanisms and the proteins that are involved in shaping these membranes are beginning to be identified (16,17).

Lipid membrane tubes were first investigated by biophysicists in 1973 (18). Since then, the quantitative understanding of tube mechanics, in particular, has been advanced both by experimental (19–22) and theoretical (23–29) analyses, and also through simulations (30). Most of these studies have focused on single-component membranes. Recently, however, membrane tubes consisting of lipid mixtures with the propensity for fluid-fluid phase separation have been approached experimentally (31,32) and theoretically (33), and mechanical consequences of lipid/protein interactions in membrane tubes are beginning to be addressed (16,34).

The research described in this study is motivated in part by seminal findings from Mukherjee et al. (35). To investigate sorting of lipids in live cells, the authors incubated CHO cells with three different fluorescent dyes from the dialkylindocarbocyanine (DiI) series. It was found that those dyes, which all had the same headgroup but different lipid chain regions, were internalized equivalently. However, shortly after uptake, a dye with long and saturated chains (DiIC₁₆(3)) was sorted away from both a short saturated chain lipid analog dye (DiIC₁₂(3)) and an unsaturated chain dye (FAST DiI) (35).

Essentially two (nonmutually exclusive) hypotheses were put forward to explain the underlying sorting mechanisms. One of them assumed that lipids laterally partition between membrane domains that vary in phase state (and degree of fluidity) (35). The second hypothesis was based on the molecular shape of these lipids (35). This latter explanation has been invoked frequently (6,36–38), and is the focus of this study.

There is evidence for lipid sorting from a biophysical perspective, obtained from self-assembled lipid model membranes of giant unilamellar vesicles (GUVs) with fluid-fluid phase coexistence, namely of the liquid ordered (L_o) and liquid disordered (L_d) phases. In ternary mixtures consisting of egg sphingomyelin, dioleoylphosphatidylcholine, and cholesterol, phase segregation in membranes with curvature gradients was seen to lead to curvature-dependent segregation of fluid domains, in starfish vesicles and connected strings of membrane beads (32). Similar curvature sorting was also observed in membrane tubes pulled from giant vesicles, where L_d phase markers were shown to enrich in nanoscale tubes, relative to giant vesicle membranes with essentially negligible curvature (31). These sorting phenomena in domain-forming membranes are likely to result from the differing bending stiffnesses of L_o and L_d domains (32,39,40).

An additional means of sorting established by model membrane research is through differential partitioning of lipids among membrane domains. The partitioning of numerous membrane fluorophores and proteins among L_o and L_d domains has been investigated (41,42). The biological relevance of phase partitioning associated with fluid phase coexistence is currently a matter of intense biophysical interest (43,44).

The goal of this study is a quantitative analysis of the extent to which individual lipids can be sorted among laterally connected high curvature (tubular), and small curvature (vesicular) membranes. We show that a stepwise elongation of tethers pulled via a microbead from pipette-aspirated giant vesicles allows measurement of membrane tube diameters. We find in all cases that simple quadratic continuum theory describes tether mechanics. We examine the curvature partitioning of lipid-like fluorophores by measuring tether fluorescence intensity as a function of tether radius. We proceed with a measurement of lateral distributions of the protein Cholera toxin subunit B (CTB) in response to changing membrane curvature. CTB curvature partitioning is of interest due to the fact that it is a tool used widely to study trafficking and cellular function (45,46). A paradigm emerging from our work is that individual lipids (as opposed to lipid domains) are not effectively curvature-sorted by membrane curvature differences of magnitudes found in intracellular membranes, and even down to an extremely small tube curvature radius of ∼10 nm. For membranes that show cooperative demixing effects, however, it has been shown previously that curvature amplifies demixing (31). Finally, peripheral membrane proteins can segregate significantly between membrane regions of different curvature.

Materials and Methods

Materials

Palmitoyloleoylphosphatidylcholine (POPC), distearoylphosphatidylethanolamine-N-[Biotinyl(Polyethylene Glycol)2000] (DSPE-Bio-PEG2000), and ganglioside GM1 were obtained from Avanti Polar Lipids (Alabaster, AL). Fatty-acid free bovine serum albumin (BSA) was from Sigma Chemical (St. Louis, MO). CTB-Alexa Fluor 488 (A488), CTB-A555, C18:2-1,1′-dilinoleyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (FAST DiI), C12:0-DiI (DiIC₁₂(3)), C16:0-DiI (DiIC₁₆(3)), 3,3′-dihexadecyloxacarbocyanine perchlorate (DiOC₁₆(3)), Texas Red-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine triethylammonium salt (TR-DHPE) and N-4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-s-indacene-3-propionyl (BODIPY)-DHPE were purchased from Invitrogen (Carlsbad, CA).

Preparation of GUVs

GUVs were prepared by electroformation as described (47). Briefly, we spread 50 μL lipid solution (POPC 1 mM in chloroform, 1–3 mol % GM1, 0.3 mol % TR-DHPE, or 0.1 mol % BODIPY-DHPE) on the surface of ITO glass slides (Delta Technologies, Stillwater, MN), at 60°C. The slides were subsequently evacuated for at least 2 h. Two slides were then combined with a silicone spacer (Grace Bio-Labs, Bend, OR) to enclose 100 mM sucrose solution, and incubated at 60°C in the presence of an AC field (2 V/mm, 5 Hz) for 2 h. After GUV formation, we added 1% v/v CTB stock solution (0.1 mg/mL in phosphate buffered saline [PBS]) to GUVs containing GM1. DiI dyes were complexed with BSA for outer leaflet labeling as described (35).

Preparation of micropipettes

Micropipettes (World Precision Instruments, Sarasota, FL) were fabricated with a pipette puller, and the tips were clipped using a microforge. The inner diameters of the micropipettes were ∼3 μm. To prevent irreversible membrane/pipette adhesion, micropipette tips were incubated with 0.05% fatty-acid-free BSA dissolved in PBS using a MICROFIL needle (WPI), and the pipettes were then filled with a 120 mM sucrose solution.

Formation of solid supported membranes

Supported bilayers were formed on glass surfaces by vesicle fusion. Small unilamellar vesicles (SUV) were prepared by first depositing 500 μL of a 1mg/mL lipid solution in chloroform on the wall of a 50 mL round bottom flask. The flask was evacuated for at least 2 h. PBS (1 mL) was added to the flask, which was vortexed until all lipid was suspended. The lipid dispersion was extruded 21 times through polycarbonate filters with 50 nm pores mounted in a mini-extruder (Avestin, Ottawa, Canada).

Glass substrates were washed with detergent, rinsed excessively with DI water, and then dried under air. The substrates were subsequently plasma cleaned. SUV solution (100 μL) was deposited on the glass surfaces, followed by incubation for 5 min. Surfaces were then rinsed with PBS. For membranes to be incubated with CTB, 1 μL of 0.2 mg/mL CTB solution in PBS was added after rinsing, and the supported membranes were then incubated for another 5 min before rinsing a second time.

Chamber preparation and tether pulling

GUV dispersions were diluted 1:10 in 120 mM sucrose solution. Diluted GUV dispersion (80 μL) and 0.5 μL streptavidin coated polystyrene bead solution (Polysciences, Warrington, PA; diameter ∼6 μm) were injected into a measurement chamber constructed from microscope slides and coverslips that allowed access by two micropipettes oriented at an angle of 90° (Fig. 1 b). Additionally, 1 μL 10× PBS had to be added to the measurement chamber as, in its absence, beads would not robustly bind to vesicular membranes. Micropipettes were operated by a motorized manipulator system (Luigs and Neumann, Ratingen, Germany). A vesicle was pipette-aspirated with an initially small suction pressure (5–12 Pa), while a second pipette held a bead with aspiration pressure of ∼60 Pa (Fig. 1, a and b). The aspiration pressure was controlled by adjusting the water level of a reservoir connected to the micropipettes, and was measured via a pressure transducer with a DP-28 diaphragm (Validyne Engineering, Los Angeles, CA). The bead was slowly moved toward the aspirated vesicle until contact, and was then moved away from the vesicle to pull an initial membrane tube of ∼5 μm in length.

Figure 1.

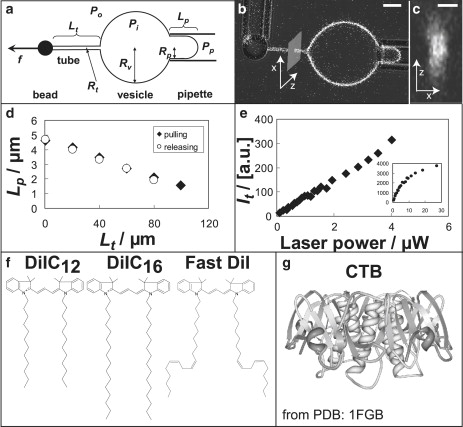
(a) Schematic configuration of a vesicle aspiration and tube pulling experiment, where P_i, P_o, and P_p are the pressures inside vesicle, outside vesicle and in the micropipette, respectively; R_t, R_v, and R_p are the radius of tube, vesicle, and pipette, respectively; L_t and L_p are the lengths of tube and vesicle projection in pipette, respectively; f indicates pulling force. (b) Combined transmitted light/confocal fluorescence microscopy image of aspirated vesicle and membrane tether that is pulled by means of a bead. Scale bar = 5 μm. (c) Cross section image of a membrane tether obtained by confocal line scan as indicated by the gray area in panel b. Scale bar = 1 μm. (d) Stepwise pulling and releasing demonstration of tether radius measurements. Tether radius is 44 nm. (e) Tether fluorescence intensity recorded under varying laser power. Tether radius = 22 nm. (f) Molecular structures of DiI derivatives. (g) Molecular structure of CTB (obtained from PDB: 1FGB), lipid-binding sites are at the bottom. A negative spontaneous curvature is suggested.

Tether radius measurement

We obtained tether radii from stepwise horizontal elongation of the membrane tube at constant lateral membrane tension (adjusted by the pipette aspiration pressure) by moving the pipette-aspirated bead with a micromanipulator (48), and concomitantly determining the associated change in the length of the pipette-aspirated vesicle projection (Fig. 1, a and d). A similar method was used by Bo and Waugh (20). where tethers were elongated vertically by means of a freely suspended membrane-attached bead that exerted a constant pulling force. Even earlier measurements extended the tube in a continuous dynamic fashion, which allowed researchers to also measure membrane viscosity (19).

To measure tether radius, the tether was typically elongated in five steps (each of 20 μm) to a maximum length of 105 μm and was then released to the beginning position using the same step distance (Fig. 1 d). For the lowest pressures, the number of steps occasionally had to be decreased because of insufficient excess area available for tube extension in the pipette-aspirated vesicle projection (see below). The tether length range was chosen based on the following considerations. At constant lateral membrane tension, tube elongation occurs at constant pulling force (28,29,49), provided the following conditions are met. First, the tether has to be long enough to have overcome a force barrier for tube formation (49,50). This initial elongation step associated with variable pulling force is expected to cover a range of <50 times the tether radius R_t (29) and is below our initial pulling length of 5 μm. Second, the pipette-aspirated projection of the vesicle used for tube pulling has to be long enough to provide enough excess membrane area (relative to the area for a spherical vesicle) over the entire tether elongation experiment (50). This requirement is met if, for the longest tether length, the projection within the pipette still consists of a cylindrical element terminated by a spherical cap (with inner pipette radius R_p; Fig. 1 a). Only in that case is the lateral membrane tension Σ related by the following formula (51) to the pipette aspiration pressure ΔP = P_o − P_p, where P_o and P_p are the hydrostatic pressures outside and inside the pipette:

$$\Sigma =\mathrm{\Delta }P\frac{R_{\text{p}}}{2\left(1-R_{\text{p}}/R_{\text{v}}\right)},$$ (1)

where R_v is the vesicle radius. We used Eq. 1 to compute lateral membrane tension. Third, for long tethers pulled from the vesicle, the resulting area difference between outer and inner membrane leaflet in tubes with high curvature will measurably influence force equilibria (22,24,27). This effect can be neglected for tethers with lengths in the range of and below 100 μm (20,22,27). Finally, sticking of the membranes to the pipette walls has to be avoided. All of the above mentioned complications would lead to deviations from a linear relationship (see below) between projection length and tether length change, as well as to unreliable bending stiffness values, as deduced from the relationship $k_{\text{c}}=2\Sigma R_{\text{t}}^{\text{2}}$ (29). Experiments with such outcomes were not considered further. A successful tube pulling experiment is shown in Fig. 1 d that indicates clearly a linear relationship between tether length L_t and projection length L_p. Also indicated in Fig. 1d is the required condition of reversibility comparing tube elongation and release cycles.

After each pulling step, the length of the vesicle projection L_p within the micropipette was determined by image analysis. Tether radii were determined based on these tether and projection length pairs. Following Hochmuth et al. (19,23), the tether radius is proportional to the ratio of projection length change (ΔL_p) and tether length change (ΔL_t), i.e., the slope in Fig. 1 d. The radius can be derived from this slope and the pipette radius R_p, as well as vesicle radius R_v (Fig. 1 a):

$$R_{\text{t}}=-\frac{\mathrm{\Delta }{L}_{\text{p}}}{\mathrm{\Delta }{L}_{\text{t}}}\left(1-\frac{R_{\text{p}}}{R_{\text{v}}}\right)R_{\text{p}}\text{.}$$ (2)

This relationship results from conservation of membrane area and constant vesicle volume (23) over the time course of the experiment. Linearity and reversibility in Fig. 1 d indicate that those conditions are met. We estimate the error in pipette radius measurements by confocal microscopy imaging to be ∼10%. By means of the partial derivative method, we obtained errors in tube radius and bending stiffness on the order of 20% and 50%, respectively.

Tether fluorescence intensity measurement

To investigate curvature sorting, we related the change in the fluorescence intensity to the change in tube diameter and probe concentration in the tubular membrane. The tether fluorescence measurements are shown in Fig. 1, b and c. The fluorescence intensity of the tether was recorded after the pulling steps to measure the tether radius. A z-scan across the tether cross section was taken at a step width of 0.15 μm to yield a total depth of 6 μm. The resulting cross-sectional intensity profile was background-corrected, and intensity was measured in an elliptical region of interest defined by the point spread function of the microscope with image processing software FLUOVIEW (Olympus, Center Valley, PA). After each intensity measurement the pipette suction pressure was changed, resulting in a different tube radius, and we repeated measurements until the tether ruptured or detached from the pulling bead.

We chose our laser power range by means of the following method. To test the reliability of the intensity recording and analysis approach, we measured intensities of a tether with fixed radius at varying laser powers. At laser powers below ∼4 μW (measured at the objective back-aperture), a linear relationship between tether intensity and laser power was observed (Fig. 1 e), whereas at larger laser power, the curve deviates from the linear trend (Fig. 1 e, inset). The linear range below 4 μW laser power was subsequently used to reliably measure tether intensity.

For normalization of the tether fluorescence intensity, we determined vesicle fluorescence intensity from the average of five randomly chosen circular regions of interest with equal area on the membrane contour of the equatorial plane.

Imaging

Vesicles were imaged by fluorescence confocal microscopy (FV300 scanning system integrated with a motorized inverted microscope IX81; Olympus, Center Valley, PA), using a 60×, 1.2 NA water immersion lens with coverslip correction collar (Olympus). Image analysis was carried out using IMAGEJ (National Institutes of Health, Bethesda, MD).

Diffusion measurements via fluorescence recovery after photobleaching

For fluorescence recovery after photobleaching (FRAP) measurements on the membrane tube, a tether of length 19 μm was pulled from the vesicle and the entire tether was bleached via full power illumination with a 488 nm laser. Pre- and postbleach intensities were measured using excitation with attenuated laser (0.1%–0.3% of full power) at 488 nm. For diffusion measurements in supported bilayers, a circular area with a diameter of 3–14 μm was bleached by simultaneous full intensity illumination with 488 nm and 405 nm lasers of our confocal microscope setup. Fluorescence recovery was imaged with attenuated excitation intensity (0.1%–0.3%) of the 488 nm laser. Photobleaching recovery data were analyzed according to Soumpasis (52).

Results

One of the main objectives of this study was to establish the partitioning of DiI dye derivatives between connected membranes with a steep curvature gradient. DiI probes are amphiphilic molecules with a headgroup composed of an indocarbocyanine ring system and two hydrophobic alkyl chains (Fig. 1 f). We tested three DiI derivatives: DiIC₁₆(3), DiIC₁₂(3), and FAST DiI. These dyes differ in their alkyl chains, but have identical headgroups. They have been suggested to segregate differentially among membranes with differing phase state or curvatures (35).

Fig. 2 shows results of DiI dyes symmetrically (Fig. 2, first column) and asymmetrically (Fig. 2, second column) incorporated in trace amounts into quasi single-component (POPC) membranes. Symmetric labeling was achieved by addition of fluorophores to lipid solutions before vesicle swelling. In tubular membranes, the outer and inner leaflets have mean curvature with opposing signs. Consequently, in membranes labeled both in outer and inner leaflets, lateral partitioning of molecules in curvature gradients could compensate each other such that the measured tube fluorescence intensity remains constant. We therefore labeled vesicles asymmetrically (in outer leaflets only) by forming GUVs in the absence of fluorophore and subsequent addition to the GUV dispersion of a DiI/BSA complex solution (35) (5% v/v; see Materials and Methods). Tether radii were determined as explained in the methods section, by stepwise elongation (relaxation) of the tether and measurement of the resulting decrease (increase) of the vesicle projection within the aspiration pipette.

Figure 2.

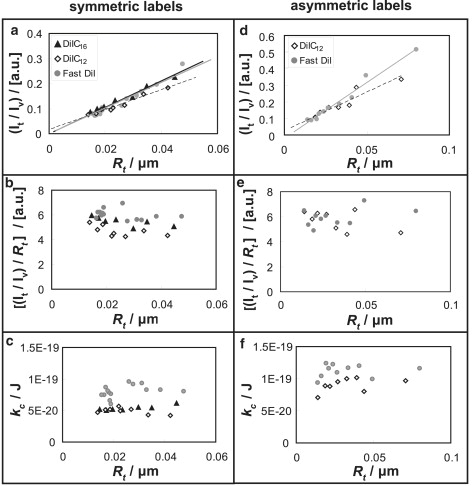
Partitioning of DiI derivatives in POPC membrane tethers. (a–c) Plots of double leaflet labeled DiI dyes from the same experiments with shared figure legend shown in a. (d–f) Plots of outer leaflet labeled DiI dyes from the same experiments with shared legend shown in d. (a, b, d, and e) Relationship of DiI dye intensities in tethers and tether radius. (a and d) Tether intensities normalized with respect to the intensities of vesicles from which tethers were pulled. Black solid lines, gray solid lines, and black dashed lines are the trend lines of DiIC₁₆, FAST DiI, and DiIC₁₂ data points, respectively. (b and e) Tether intensity to vesicle intensity ratios of panels a and b respectively scaled with respect to corresponding membrane curvature plotted versus tether radius. (c and f) Bending stiffness at varying tether radius.

Fig. 2, a and d, indicate linear dependency of fluorescence intensity on the tube radius extrapolating approximately to the origin of the graphs. As we discuss below, if fluorophores were measurably curvature sorted, we would expect a vertical translation of the linear relationships in Fig. 2, a and d along the ordinate. Fluorophore enrichment in high curvature membrane tubes would lead to an upward shift, and vice versa for fluorophores that are depleted from high curvature membranes. To quantify the relationship of intensity and radius, we fitted linear equations to these intensity curves. The intercept of the intensity plot linear fit is used to determine the partitioning of fluorescent molecules. For example the intercept of the Fast DiI curve in Fig. 2 d is −0.022 ± 0.015 (n = 4). The uncertainty of intercept (obtained from the least squares fitting uncertainty) within one data set is consistently smaller than that between different data sets and has been neglected. For Fast DiI outer leaflet labeling, the intercept is −0.014 ± 0.039 (n = 4). Because the intercept value is small and the uncertainty is large, displacements in the case of DiI dyes in POPC bilayers are not detected with sufficient accuracy. Absence of such displacements (Fig. 2, a and d) suggests inefficient curvature sorting of lipid-like fluorophores as we quantitatively examine below. For Fig. 2, a and d, variable slopes are apparent comparing different fluorophores. Repeated experiments for tubes pulled from different vesicles containing the same fluorophore indicated (data not shown) that slopes did not depend on fluorophore type but on conditions such as the vesicle radius and the exact location of the region used to determine vesicle fluorescence intensity. These conditions varied slightly among experiments, explaining the different slopes in Fig. 2, a and d. To amplify potential deviations from linearity for small tether radius, we scaled the tube fluorescence intensity ratios in Fig. 2, a and d, by the inverse of the tube radius (Fig. 2, b and e). Both figures indicate that the ratio of fluorescence intensity to tube radius is independent of tube curvature. We thus conclude that curvature-induced sorting is not detectable in either leaflet of a high curvature membrane tube attached to a GUV with small curvature.

The accuracy of the indirect determination of tether radius by tube elongation for quasi-single component (POPC) membranes can be evaluated through computation of the tether bending stiffness k_c. These k_c values are related to lateral membrane tension Σ and the tube radius R_t via $k_{\text{c}}=2\Sigma R_{\text{t}}^{\text{2}}$. Every measured tube radius therefore yields a bending stiffness; examples are displayed in Fig. 2, c and f. We determined a stiffness mean value of 9.2 × 10⁻²⁰ J with a standard deviation of 3.0 × 10⁻²⁰ J for tubes from 22 POPC vesicles with different labels. These values are in the range of published numbers (53,54). We did not observe statistically significant differences in bending stiffness comparing symmetric labeling and outer leaflet DiI dye labeling. Furthermore, we did not observe bending stiffness to depend on tether radius for single component membranes (Fig. 2, c and f), in agreement with earlier observations (20,21), and with recent molecular dynamics simulations of tethers with radius that approached bilayer thickness (30). This indicates that the bending energy is a simple quadratic function of tube radius for single component membranes over the entire range of our measurements.

In membranes of ternary lipid mixtures with composition near a liquid ordered mixing/demixing phase boundary, we have measured a significant decrease of bending stiffness with increasing curvature (not shown). Those results, obtained with the same method as described above, will be published in a forthcoming contribution.

We caution that our fluorescence intensity analysis is based on assuming a negligible dependence of lipid fluorophore quantum yield on membrane curvature. Because we used headgroup-labeled lipids in all cases, however, we do not expect the environment of our fluorophores to significantly change with membrane curvature. Furthermore, it could be the case that the membrane affinity of our probes is curvature-dependent, which would interfere with our partitioning analysis. Generally, the half-time for desorption of double-chain lipids is on the order of days (3), but could increase with membrane curvature. Indeed, an important mechanism of intracellular lipid sorting is based on monomeric lipid transport that involves desorption facilitated by lipid-transfer proteins (3). Our observation of linear fluorescence intensity / tube radius relationships in our system indicates that in the absence of such proteins potentially curvature-dependent monomeric desorption of double-chained lipids is not likely to be an important sorting mechanism.

In addition to lipid curvature partitioning we investigated the curvature-dependent lateral segregation of a large membrane-bound fluorescently labeled protein Cholera toxin subunit B (structure shown in Fig. 1 g). Fluorescent CTB is a tool used commonly to investigate intracellular trafficking. However, the mechanisms that underlie its sorting into retrograde pathways are far from being understood (45,46). This protein peripherally binds to five GM1 lipids per molecule. To mimic intracellular membrane trafficking, we ideally would examine CTB curvature sorting on the inner membrane leaflet of GUVs. Due to the associated delivery problem, however, we labeled vesicles with CTB bound on the outer leaflet. To investigate protein curvature partitioning, both CTB fluorescence intensity and tether radius were measured. In the experiment depicted in Fig. 3, a and b, vesicles were incubated with CTB before tether formation. Fig. 3 a shows CTB-A488 fluorescence in the green channel, and the red channel refers to the lipid fluorophore TR-DHPE. From the image overlay in Fig. 3 a it is thus observed that the tether shows predominantly red (TR-DHPE) color whereas the vesicle exhibits more green. This suggests that CTB is segregated from the high curvature tubular membrane to the lower curvature vesicle membrane. To ensure that the depletion of CTB fluorescence on the membrane tube is not specific to the particular choice of fluorescence dyes, we used an opposite color pair in the form of CTB-A555 and BODIPY-DHPE (Fig. 3 b). In agreement with the observations of Fig. 3 a, more lipid fluorescence (BODIPY-DHPE, green) is seen in the high curvature tether compared to the low curvature vesicle.

Figure 3.

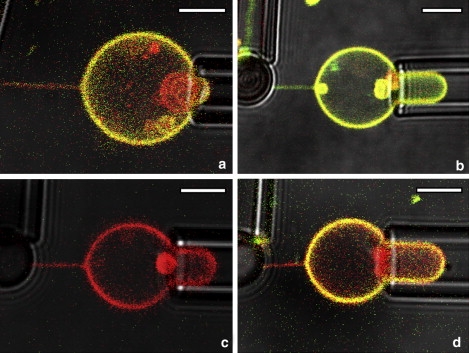
Combined images of red, green and transmitted light channels of POPC (1% GM1) tethers and vesicles coated with CTB. (a) Lipid membrane labeled symmetrically (i.e., in both leaflets) with TR-DHPE, whereas CTB-A488 was added before tether formed; R_t = 63 nm. (b) Membrane symmetrically labeled with BODIPY-DHPE. CTB-A555 was added before tether formed; R_t = 66 nm. (c and d) Membrane symmetrically labeled with TR-DHPE; R_t = 50 nm, images taken before (c) and 18 min after (d) CTB-A488 was added. Scale bar = 5 μm.

The results summarized in Fig. 3, a and b, indicate curvature sorting of CTB. This sorting effect might be explained by the following three hypotheses. First, when a tether is pulled from a vesicle, most of the CTB molecules could remain on the vesicle membrane due to a barrier to CTB transport presented by the tether neck. Second, the membrane affinity of CTB may be a function of membrane tube radius, with high curvature promoting dissociation of CTB from the tether membrane into solution. Third, CTB could dynamically partition laterally between vesicle and tube membrane, with a lateral partition coefficient depending on tube curvature.

To address the first hypothesis, we added CTB to the solution containing TR-DHPE labeled vesicles only after a tether was pulled and tested the binding preference of CTB to high curvature (tube) or low curvature (vesicle) membranes. Fig. 3 c shows the tether and vesicle before CTB addition, and Fig. 3 d displays the same tether after CTB had been added. Clearly CTB fluorescence is almost absent in the tether because mostly red lipid dye fluorescence is found in the tube whereas the vesicle shows yellow color due to simultaneous red and green (CTB) fluorescence (Fig. 3 d). Thus, even if a CTB diffusion barrier were to exist at the vesicle neck, CTB molecules incubated with a vesicle-attached membrane tether system preferentially are observed to bind from solution to the low curvature vesicular membranes. All experiments in Fig. 3 indicate qualitatively that CTB is measurably curvature sorted.

We proceed with a quantitative investigation of curvature-dependent partitioning of CTB. Fig. 4, a and b, indicate decreasing CTB to lipid dye intensity ratio as the tether radius is decreased. As tether radius is reduced, the total amount of any tether component in a given cylindrical tube element of length ΔL will decrease. In the absence of curvature sorting, this decrease should be equivalent for all components, and thus the fluorescence intensity ratio of two different membrane components should be independent of tether radius. However, Fig. 4, a and d, suggest that the CTB concentration decreases significantly faster than that of the lipid dyes as the curvature increases. To further evaluate this possibility, we plotted the tube intensities (relative to vesicle intensities) of CTB and lipid dyes versus tether radius separately in Fig. 4, b and e, and found approximately linear fluorescence/radius relationships for both TR-DHPE and CTB. The essential difference, however, is that the TR-DHPE curve tends toward the origin as in the case of the lipid-like DiI dyes examined above, whereas the CTB curve does not. Instead, it lies significantly below the TR-DHPE curve and the CTB intensity becomes immeasurably small long before the minimal tube radius is achieved (as indicated by tube rupture). The finding of negligible curvature sorting of TR-DHPE and BODIPY-DHPE is further emphasized in the curvature-scaled plots of Fig. 4, c and f, respectively. Fig. 4 thus depicts quantitatively the curvature preference of CTB already qualitatively observed in Fig. 3, and confirms absence of curvature sorting for lipid-analog dyes.

Figure 4.

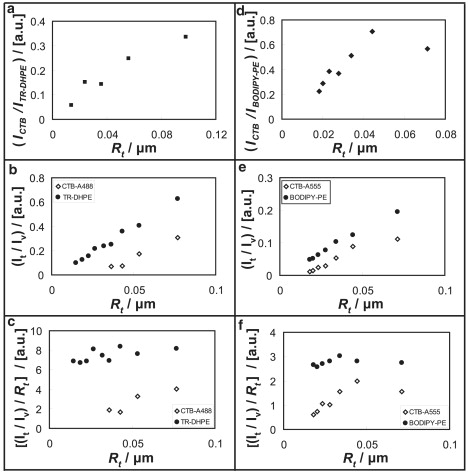
(a and d) POPC tether membrane fluorescence intensity ratios of (a) CTB-A488 to TR-DHPE and (d) CTB-A555 to BODIPY-DHPE (BODIPY-PE) versus tether radius plots of tethers containing (a) 1% GM1 and (d) 3% GM1. (b and e) Normalized tether intensity ratios with respect to vesicle intensities of (b) CTB-A488 and TR-DHPE and (e) CTB-A555 and BODIPY-DHPE at varying tether radius of POPC membranes with 1% GM1 (b) and 3% GM1 (e). (c and f) Same data sets as panels b and e, respectively; curvature-scaled tether intensities plotted with respect to tether radius. (a–c) Tether radius was measured from stepwise elongation and releasing as described in Materials and Methods. (d–f) Approximate tether radius calculated from membrane tension by assuming k_c = 8 × 10⁻²⁰ J.

To exclude potential double labeling artifacts such as fluorescence resonance energy transfer, we tested a vesicle labeled with fluorescent CTB only (no lipid fluorophore). The CTB measurements in Fig. 5 show the same curvature trend as observed in Fig. 4, b and e; the fluorescence intensity as a function of tube radius does not pass through the origin (Fig. 5 a). We furthermore ensured that our CTB experiments were carried out under the condition of mechanical and thermodynamic equilibrium, i.e., in the absence of hysteresis and time-dependent phenomena. These conditions are confirmed by the complete reversibility of tube CTB fluorescence intensity shown in Fig. 5 a.

Figure 5.

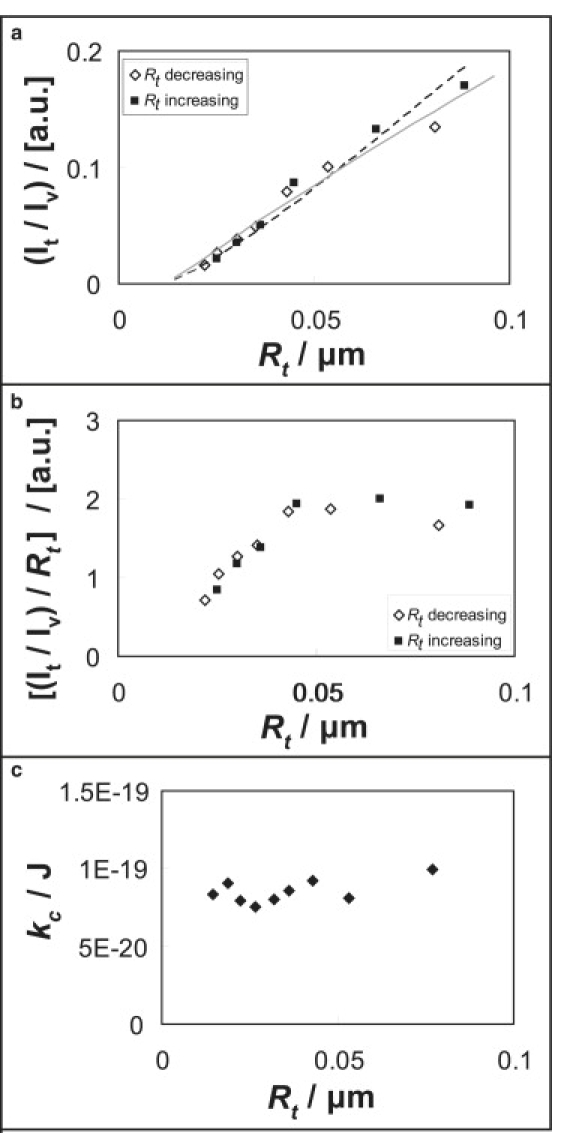
(a and b) Reversibility test of tether intensity at varying tether radius of POPC (2% GM1) membrane labeled only with CTB-A488. Tether intensity is normalized with respect to vesicle intensity. The dashed line refers to the fitting of data points using the spontaneous curvature sorting model, and the gray solid line to fitting with the bending stiffness sorting model. (b) Same data as in panel a additionally scaled with membrane curvature. (c) Bending stiffness versus tether radius of POPC (1% GM1) membrane labeled with both CTB-A488 and TR-DHPE. Note that these bending stiffness values refer to the data set of the first column in Fig. 4.

Furthermore, intensity ratios scaled by tube radius decrease with increasing curvature (Fig. 5 b), which means that CTB is sorted away from high positive curvature. As shown in Fig. 5 c, from tether radius measurements we obtain a constant membrane tube bending stiffness, confirming that changing molar ratios of CTB/lipid do not measurably influence tether bending stiffness, as the tube radius decreases in quasi-single component membranes.

Finally, we compared diffusivities of lipid fluorophores and CTB on membrane tethers, as well as on supported bilayers by FRAP measurements. Fig. 6 depicts the FRAP curves of CTB (Fig. 6 a) and DiOC₁₆(3) (Fig. 6 b) on POPC membrane tethers at the same radius and tether length (whole tether is bleached), in which CTB shows a longer (by ∼2 times) half-recovery time (t_1/2 = 46.7 ± 8.5 s, n = 6) compared to DiOC₁₆(3) (t_1/2 = 21.6 ± 3.8 s, n = 5). The fast lateral diffusion of membrane fluorophores in the pulled tether shown in Fig. 6 indicates that the tether neck under no condition in our experiment functioned as a measurable diffusion barrier. This contributes to the reversibility of our measurements shown in Fig. 5 a. FRAP with the same labeled molecules was also carried out on supported POPC bilayers for comparison to the tube diffusivities. We measured the diffusion coefficients of CTB and DiOC₁₆(3) on supported bilayer as 0.35 ± 0.09 μm²/s (n = 8) and 2.7 ± 0.5 μm²/s (n = 6), respectively.

Figure 6.

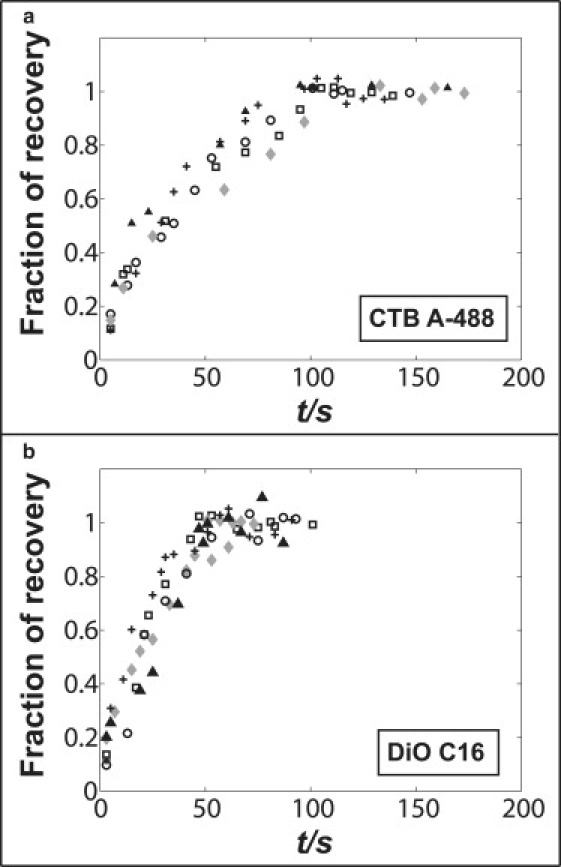
Fluorescence recovery after photobleaching data comparing (a) CTB-A488 and (b) DiOC₁₆(3) on membrane tethers with similar radius ∼65 nm and tether length 19 μm. Whole tethers are bleached in this experiment. Each panel contains five data sets shown with different symbols. CTB is observed to diffuse more slowly compared to DiO on membrane tubes. See the main text for a comparison to diffusion measurements in planar membranes.

From this comparison, we see that CTB diffuses nearly eight times slower than DiOC₁₆(3) on supported bilayers, but only two times slower on membrane tethers. Assuming that there is no difference in the CTB membrane binding mode comparing tether and supported bilayer, the ratio of its diffusivity to that of the lipid dye is expected to be similar both on tethers and on supported membranes. A hypothesis for explaining this difference is that CTB might be more crowded on flat bilayers (55) compared to tethers. The clustering of CTB on planar supported membranes could slow its diffusion compared to monomeric CTB molecules, which may be more prominent on highly curved membrane tethers compared to flat membranes. A curvature-dependence of diffusion coefficients has been suggested (56), and could be addressed by the investigation of diffusion as a function of membrane tube radius in future studies.

Discussion

By our methodology, lipid-like DiI dyes, as well as the labeled lipids TR-DHPE and BODIPY-DHPE, are not detectably sorted in POPC membranes with cylindrical curvature down to cylinder radius of ∼10 nm. In contrast, the peripherally membrane-associating protein CTB was effectively curvature sorted.

The problem of interleaflet lipid sorting in cylindrically shaped bilayer membranes was addressed recently by coarse grained molecular dynamics simulations (57). They were based on a model consisting of a bilayer composed of lipids that were represented by three beads with differing sizes, arranged to form cone or inverted-cone shaped molecules. Those lipids were allowed to flip without restriction among leaflets to minimize curvature energy. Preferential lateral interactions, associated with non-ideal mixing and phase separation, however, were excluded. In accordance with our observations, membrane curvature was not found by those investigators to be an efficient driving force for individual lipid sorting (57).

A simple lattice model (57–60) shows that favorable energetic (curvature energy) contributions to free energy changes associated with sorting of individual lipids are insufficient to overcome the entropic penalty of sorting. More complex free energy models further underline that sorting is amplified near phase transitions and particularly mixing/demixing critical points (61,62). In the following, we develop a model considering individual molecule curvature sorting based on spontaneous curvature in membrane tubes attached to vesicles. Lateral partition coefficients between large and small curvature membrane regions as a function of lipid shape and membrane curvature are obtained based on equal chemical potentials in tube and vesicle. Free energies for tether F_t (29) and for vesicle F_v are:

$$F_{\text{t}}=U_{\text{t}}-T{S}_{\text{t}}-fL,$$ (3)

and

$$F_{\text{v}}=U_{\text{v}}-T{S}_{\text{v}},$$ (4)

respectively, where U_t, T, and S_t, are internal energy, temperature, and entropy, respectively of the tube. The last term arises from the pulling force f, acting on the membrane tether of length L. This free energy expression neglects the normal pressure difference across the membrane, which is an approximation that is appropriate for thin tethers (26). We consider membranes consisting of two types of molecules α and β with differing spontaneous curvature of values C_j for molecules j and same molecular cross-section area a. The weighted average spontaneous curvature is C_s = (C_αN_α + C_βN_β)/N (63), N is the total number of molecules.

We obtained partition coefficients as (for details see Appendix A)

$$K_{\text{o}}=\exp \left(\frac{k_{\text{c}}{a}_{\text{j}}C{C}_{\text{j}}}{k_{\text{B}}T}\right)=\frac{{\varphi }_{\text{jot}}}{{\varphi }_{\text{jov}}}{K}_{\text{i}}=\exp \left(-\frac{k_{\text{c}}{a}_{\text{j}}C{C}_{\text{j}}}{k_{\text{B}}T}\right)=\frac{{\varphi }_{\text{jit}}}{{\varphi }_{\text{jiv}}}\text{.}$$ (5)

where k_c is the bending stiffness, C = 1/R_t is the tube curvature, a_j is the molecular area, ϕ are the mole fractions of molecules in tube and vesicle in each leaflet, e.g., in outer leaflet ϕ_jot = N_jot/N_ot.

Essentially equivalent expressions have previously been derived for interleaflet partitioning in a lipid tube (57). The time scale of DiI dyes' flip-flop has been analyzed by fluorescence quenching in large unilamellar vesicles and was found to be negligible over at least 4 h at temperatures between 4 and 37°C (64). Measurements in black lipid membranes, however, have suggested higher flip-flop rates (65), and it is also possible that flip-flop rates increase in tubular membranes with high curvature (66). Regardless of whether curvature sorting would occur in our system primarily by lateral partitioning or by interleaflet flipping, we did not detect curvature sorting for the lipid dyes used in this study.

The model reproduces the expectation that molecules are laterally sorted oppositely in the inner and the outer leaflet. Furthermore, from Eq. 5, cone-shaped lipids (C_j < 0), are depleted in the outer tube leaflet relative to the vesicle, whereas inverted cone-shaped lipids are enriched. Note that this lattice model neglects the geometric requirement that the total lipid amount in the inner tube leaflet be smaller compared to the outer leaflet.

The molecular structures of the DiI dyes used in this study suggest an inverted-cone shape for DiIC₁₆(3) and DiIC₁₂(3) (35), and a cylindrical or cone shape for FAST DiI (35). Measurements of the spontaneous curvature of these dyes are not available; however, the probe DiIC₁₈(3) was observed to lower the transition temperature for formation of an inverted hexagonal phase (67), indicating an inverted cone shape for that molecule.

In Fig. 7 a, we plot theoretical fluorescence intensity ratios in the outer tether leaflet (in arbitrary units) computed from the following equation:

$$\frac{I_{\text{ot}}}{I_{\text{ov}}}=\varepsilon R_{\text{t}}{K}_{\text{o}}=\varepsilon R_{\text{t}}\exp \left(\frac{k_{\text{c}}{a}_{\text{j}}{C}_{\text{j}}}{k_{\text{B}}T{R}_{\text{t}}}\right),$$ (6)

where ɛ is an unknown parameter that depends on laser beam waist, imaging methods, and other factors. Two lipids with extreme spontaneous curvature (68): diacylglycerol (DAG), a cone-shaped lipid with negative spontaneous curvature C_DAG = −1/1.01 nm⁻¹, and lysophosphatidic acid (LPA), an inverted-cone-shaped lipid with positive spontaneous curvature C_LPA = 1/2 nm⁻¹ are used for illustration purposes. Also considered is dioleoylphosphatidylethanolamine (DOPE), a phospholipid with rather strong cone shape: C_DOPE = −1/3 nm⁻¹ (68). The fluorescence intensity ratio that is expected for cylindrically shaped lipids (C_j = 0, K = 1) is shown in Fig. 7 a as a solid line. Nonzero spontaneous curvature primarily displaces the intensity ratio versus tube radius plots along the ordinate, whereas the slope remains constant at R_t larger than ∼8 nm (Fig. 7 a). This can be understood from expanding Eq. 6 to yield for the intensity ratios I_jot/I_jov the simplified relation

$$\frac{I_{\text{jot}}}{I_{\text{jov}}}=\varepsilon R_{\text{t}}+\varepsilon \frac{k_{\text{c}}{a}_{\text{j}}}{k_{\text{B}}T}{C}_{\text{j}}\text{.}$$ (7)

Equation 7 is linear in the tube radius R_t and causes the intercept to be proportional to the spontaneous curvature. This form explains the shift along the ordinate in Fig. 7. However, such a simplification is only suitable for the case where K is close to unity. Therefore, in the case of CTB, for which K is significantly less than unity, we cannot expand the exponential in Eq. 6 to obtain a suitable linear form.

Figure 7.

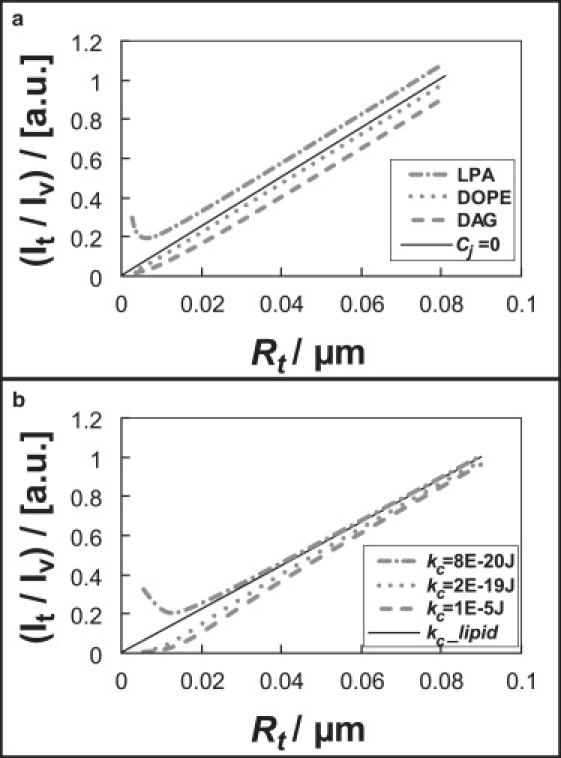
(a) Relative theoretical outer leaflet tether fluorescence intensity as a function of tether radius calculated from spontaneous curvature sorting model, for two extreme spontaneous lipid curvatures (DAG and LPA), or moderate spontaneous curvature (DOPE), as well as a cylindrical (i.e., zero spontaneous curvature) lipid (solid line). Tether intensity is calculated from Eq. 6 (a = 0.5 nm², T = 295 K). Note that the presence of spontaneous curvature primarily shifts the curves along the ordinate (see Eq. 7). (b) Theoretical tether fluorescence intensity plots calculated from bending stiffness model. Different bending stiffness is applied as legend shows. Tether intensity is calculated based on $I\propto R_{\text{t}}\frac{{\varphi }_{\alpha \text{ot}}}{{\varphi }_{\alpha \text{ov}}},$ in which the molar ratios were obtained from Eq. 8 (a = 25 nm², T = 295 K).

Fig. 7 a shows that DOPE partitioning would be experimentally indistinguishable from the case of cylindrically shaped lipids, given the degree of uncertainty of our experimental data (see Figs. 2 and 4). The simple model underlying the graph shown in Fig. 7 a therefore is in accordance with our DiI dye curvature partitioning measurements that indicate absence of detectable curvature sorting, considering that their spontaneous curvature is expected to be significantly smaller compared to DAG or LPA.

From our simple model, spontaneous curvatures of labeled membrane components can be determined. As we discussed in the results section, based on the small intercept and large uncertainty of linear fitting for DiIC₁₂ and Fast DiI, significant curvature sorting of DiI dyes does not occur. The spontaneous curvatures of DiI dyes therefore cannot be determined accurately. For example, fitting experimental intensity ratios to Eq. 7 (a_DiI = 0.64 nm² (69), T = 295 K, k_c = 9.2 × 10⁻²⁰ J), we calculated spontaneous curvatures of DiIC12 and Fast DiI as C_DiIC12 = 0.32 ± 0.47 nm⁻¹ (n = 4) and C_{Fast DiI} = −0.11 ± 0.41 nm⁻¹ (n = 4).

However, for CTB, whose intensity curve shows a large displacement from the simple proportional relationship, we are able to determine a spontaneous curvature of the membrane patch covered by CTB. Experimental CTB intensity profiles were fitted to Eq. 6 (a_CTB = 25 nm² (55), T = 295 K, k_c = 9.2 × 10⁻²⁰ J). A representative fit is shown in Fig. 5 a (dashed line). We obtained C_CTB = −0.055 ± 0.012 nm⁻¹ (n = 8).

In addition to our spontaneous curvature sorting model, we developed an alternative theoretical model for CTB curvature partitioning based on bending stiffness differences. In this model, we assume that membrane patches coated by molecules added in trace amount have a bending stiffness k_α different from the bulk lipid k_β. The weighted average bending stiffness is $k_{\text{c}}=\frac{A{k}_{\alpha }{k}_{\beta }}{k_{\beta }{a}_{\alpha }{N}_{\alpha }+k_{\alpha }{a}_{\beta }{N}_{\beta }}$(63). The free energies for tether and vesicle are equivalent to those of Eqs. 3 and 4. We obtain the partition coefficient for both leaflets as (for details see Appendix B):

$$K=\exp (\frac{k_{\beta }^{2}a{C}^2}{2k_{\text{B}}T}(\frac{1}{k_{\alpha }}-\frac{1}{k_{\beta }}))=\frac{{\varphi }_{\alpha \text{t}}}{{\varphi }_{\alpha \text{v}}},$$ (8)

where a is the molecular area of the protein adsorbed to the membrane.

From Eq. 8, theoretical fluorophore intensity ratios obtained from our bending stiffness model are plotted in Fig. 7 b. The graph indicates that the sorting efficiency does not sensitively depend on specific stiffness values if the bending stiffness of the trace component is significantly larger than that of the lipid membrane. For instance, the plots for k_α = 5 × 10⁻¹⁹ J and k_α = 10⁻⁵ J essentially overlap each other (not shown). Consequently, fitting experimental CTB intensity data to the theoretical curve (T = 295 K) gives widely spread CTB bending stiffness values from k_c(CTB) = 10⁻⁵ J to k_c(CTB) = 10⁻¹⁹ J (n = 8). A representative fitting result is shown in Fig. 5 a (gray solid line).

Despite the fact that both models fit well to the experimental data, the fitting quality from the spontaneous curvature model is slightly better than that from the bending stiffness model (eight data sets). Further evidence for the spontaneous curvature model can be obtained from a quantitative comparison of the data shown in Fig. 5 c, to our sorting models. Fig. 5 c indicates that the bending stiffness of a membrane covered by CTB (with a coverage area fraction of ∼20%) does not measurably depend on tube radius. In the context of sorting by bending stiffness, this suggests that this observation implies a contribution by cholera toxin to the overall membrane bending stiffness too small to allow for the efficient sorting shown in Figs. 4, b and e, and 5 a. This comparison solidifies our hypothesis of CTB sorting by spontaneous curvature. Moreover, induction of spontaneous curvature by CTB binding to membranes does not seem to be unreasonable as we have previously described inward invagination of cholera toxin domains on GUVs (42). Furthermore, it has been reported that the related protein Shiga Toxin induces tubular membrane invaginations (70).

We have shown that the CTB/GM1 complex is effectively curvature-sorted. However, we have not yet addressed the curvature partitioning of GM1 itself. This could be achieved by means of GM1 variants labeled with fluorophores in the headgroup region. Based on the partitioning results for the three DiI dyes, as well as the fluorescent lipids TR-DHPE and BODIPY-DHPE, we do not expect GM1 to be curvature sorted in the absence of CTB, unless GM1 by itself significantly clusters, which currently is a matter of debate (55,71,72). Recent evidence indicates that clustered GM1, however, inhibits Cholera toxin binding (72). We therefore regard it as unlikely that curvature sorting of clustered GM1 underlies the sorting of fluorescent CTB that we describe here.

Conclusions

The main conclusion from our investigation is that individual lipids, in contrast to the peripherally binding protein CTB, do not sense curvature effectively enough to be significantly sorted by their shape. This experimental observation is in accordance with molecular dynamics simulations (57), as well as a simple analytical model for lateral curvature sorting developed here, which is in the spirit of those developed by Cooke and Deserno (57), Iglic et al. (58), and Kralj-Iglic et al. (59).

Although the absence of effective lipid sorting by molecular shape is shown, non-ideal mixing lipids display significant curvature sorting, as has been shown clearly in previous model membrane research (31,32,73). In a situation where lipids non-ideally mix to form extended regions with differing bending stiffness (32,39), or differing spontaneous curvature (61,62), curvature energy effectively contributes to lipid sorting. Theory predicts that this effect becomes amplified close to a phase boundary and particularly a critical mixing/demixing point (61). If lateral segregation into membrane domains is an important mechanism for sorting of lipids and proteins in cells, then an essential question is whether segregation is present before budding of transport vesicles in intracellular sorting centers, or if segregation occurs during vesicle budding (3). It is conceivable that membrane curvature may trigger lateral phase segregation (74) in membranes with compositions near a phase boundary (31,75).

Whereas we did not observe lipids to be individually sorted, the protein CTB showed more effective segregation. Two statistical mechanical sorting models were developed. Comparison of the two models and our data suggests sorting of CTB by spontaneous curvature. Preferential interactions of proteins with lipids could cause lipid sorting as a secondary effect to protein sorting in live cells. The area of lipid and protein trafficking is one where understanding of fundamental mechanisms remains missing (3), and we expect model membrane biophysics to be an important contributor in solving some of the essential questions.

Appendix A

Curvature sorting based on spontaneous curvature:

For the outer leaflet of the tether, we have the internal energy:

$$U_{\text{ot}}=\frac{1}{2}{k}_{\text{c}}{(C-C_{\text{st}})}^2{A}_{\text{t}}+{\Sigma }_{\text{t}}{A}_{\text{t}}\text{.}$$ (A1)

The entropy is defined by the following expression:

$$S_{\text{ot}}=-k_{\text{B}}(N_{\alpha \text{ot}}\ln \frac{N_{\alpha \text{ot}}}{N_{\text{ot}}}+N_{\beta \text{ot}}\ln \frac{N_{\beta \text{ot}}}{N_{\text{ot}}})\text{.}$$ (A2)

From Eqs. A1–A3, chemical potentials of molecule α in outer leaflet of the tether are obtained

$${\mu }_{\alpha \text{ot}}={\left(\frac{\partial F_{\text{ot}}}{\partial N_{\alpha \text{ot}}}\right)}_{N_{\beta \text{ot}}}=k_{\text{c}}a\left(C-C_{\text{st}}\right)\left(-{\varphi }_{\beta \text{ot}}{C}_{\alpha }+{\varphi }_{\beta \text{ot}}{C}_{\beta }\right)+k_{\text{B}}T\ln {\varphi }_{\alpha \text{ot}}\text{.}$$ (A3)

The mechanical balance equations resulting from partial derivatives with respect to variables describing the tether geometry, are identical to those of single component tethers (27,29). It can be shown for multicomponent membranes that in the absence of line tension both vesicle and tether are under the same lateral (mean) tension, Σ. Similarly, chemical potentials in the outer leaflet of the vesicle are calculated from Eq. 4. From equal chemical potentials of molecule α (β) on tether and vesicle, it follows that:

$$k_{\text{c}}a(C-C_{\text{st}}+C_{\text{sv}})(C_{\beta }-C_{\alpha })=k_{\text{B}}T\ln \frac{{\varphi }_{\alpha \text{ov}}}{{\varphi }_{\alpha \text{ot}}}+k_{\text{B}}T\ln \frac{{\varphi }_{\beta \text{ot}}}{{\varphi }_{\beta \text{ov}}}\text{.}$$ (A4)

For curvature-partitioning molecules present in trace amounts, we approximate Eq. A4 by considering C_sv = C_st. In addition, ϕ_αov is close to 0, and we set C_β = 0. Equation A4 thus simplifies to Eq. 5.

Appendix B

Curvature sorting based on bending stiffness differences:

The internal energy of the tether is a function of the overall bending stiffness k_ct:

$$U_{\text{t}}=\frac{1}{2}{k}_{\text{ct}}{C}^2{A}_{\text{t}}+{\Sigma }_{\text{t}}{A}_{\text{t}}\text{.}$$ (B1)

The whole membrane is considered to be composed of membrane patches with protein molecular area a. Thus k_ct is simplified as $k_{\text{ct}}=\frac{N_{\text{t}}{k}_{\alpha }{k}_{\beta }}{k_{\beta }{N}_{\alpha \text{ot}}+k_{\alpha }{N}_{\beta \text{ot}}}\text{.}$ From Eqs. B1, A2, and 3, the chemical potential of membrane patch α covered with protein on the tether is obtained

$${\mu }_{\alpha \text{t}}={\left(\frac{\partial F_{\text{t}}}{\partial N_{\alpha \text{t}}}\right)}_{N_{\beta \text{t}}}=\frac{1}{2}{k}_{\text{ct}}a{C}^2\left(1-\frac{k_{\text{ct}}}{k_{\alpha }}\right)+k_{\text{B}}T\ln {\varphi }_{\alpha \text{t}}\text{.}$$ (B2)

Similarly, chemical potentials on the vesicle are obtained from Eq. 4. At chemical equilibrium, we find:

$$\frac{1}{2}a{C}^2{k}_{\text{ct}}^2(\frac{1}{k_{\beta }}-\frac{1}{k_{\alpha }})=k_{\text{B}}T\ln \frac{{\varphi }_{\alpha \text{v}}}{{\varphi }_{\alpha \text{t}}}+k_{\text{B}}T\ln \frac{{\varphi }_{\beta \text{t}}}{{\varphi }_{\beta \text{v}}}\text{.}$$ (B3)

We consider ϕ_αv close to 0, and assume that k_α and k_β are of the same order of magnitude. Under those conditions, Eq. B3 simplifies to Eq. 8.

Enthalpic contributions leading to lipid phase separation can be accounted for by adding i), an interaction term; and ii), a line tension term to the free energy functional, causing a modification of the chemical balance equations and adding a jump in in-plane tension and transverse shear to the mechanical balance equations.