Recoil after Severing Reveals Stress Fiber Contraction Mechanisms

Abstract

Stress fibers are cellular contractile actomyosin machines central to wound healing, shear stress response, and other processes. Contraction mechanisms have been difficult to establish because stress fibers in cultured cells typically exert isometric tension and present little kinetic activity. In a recent study, living cell stress fibers were severed with laser nanoscissors and recoiled several μm over ∼5 s. We developed a quantitative model of stress fibers based on known components and available structural information suggesting periodic sarcomeric organization similar to striated muscle. The model was applied to the severing assay and compared to the observed recoil. We conclude that the sarcomere force-length relation is similar to that of muscle with two distinct regions on the ascending limb and that substantial external drag forces act on the recoiling fiber corresponding to effective cytosolic viscosity ∼10⁴ times that of water. This may originate from both nonspecific and specific interactions. The model predicts highly nonuniform contraction with caps of collapsed sarcomeres growing at the severed ends. A directly measurable signature of external drag is that cap length and recoil distance increase at intermediate times as t^1/2. The severing data is consistent with this prediction.

Introduction

In many processes, cells assemble force-producing contractile machines from myosin motor proteins, actin filaments, and other structural and regulatory components. Examples include the muscle myofibril whose contraction pumps the heart or moves limbs, the contractile ring that pinches the cell into two daughters during cytokinesis, and the stress fiber (SF). SFs are tension-generating actomyosin bundles terminating at one or both ends in transmembrane focal adhesions (FAs) anchored to the extracellular matrix (ECM) (see Fig. 1). By coupling to the ECM and exerting force, they enable cells to mechanically influence their environment and sense its mechanical properties. SFs contribute to adhesion of vascular endothelial cells to the basal lamina (1), generate contraction in myofibroblasts which provokes tissue reorganization during wound healing (2), and may assist cells in migration (3).

Figure 1.

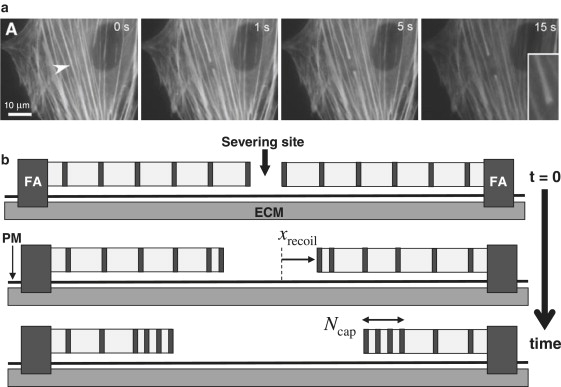
Recoil of severed stress fibers (SFs). (a) Kumar et al. tracked EYFP-actin SF recoil after severing with a femtosecond laser nanoscissor (9). (Arrowhead) Incision position. (b) Severed SF schematic. Regions of myosin (dark) alternate with α-actinin (light). Each fiber end connects to a focal adhesion (FA) anchored to the extracellular matrix (ECM) through the plasma membrane (PM). Our model predicts that sarcomeres near the severed end contract first, resulting in a growing cap of N_cap collapsed sarcomeres.

What are the working parts of SFs and how do they coordinate to generate force? SFs are similar in some respects to the thoroughly studied myofibrils of striated muscle (4). A myofibril is built from many contractile repeat units (i.e., sarcomeres) arranged in series, each comprising an array of parallel bipolar myosin aggregates (i.e., thick filaments) interdigitated with two oppositely oriented actin filament arrays, one on either side. Sarcomeres contract when thick filament myosins pull inward on the actin arrays whose pointed ends lie in the central myosin zone. The actin barbed ends and the actin cross-linker α-actinin reside at the sarcomere boundaries (i.e., Z disks) which are connected to the thick filament centers by the giant spring-like protein titin.

SFs in stationary cells appear to be organized in a sarcomeric myofibril-like fashion. Along the fiber axis, zones of α-actinin alternate with zones of nonmuscle myosin II (5) and actin polarity alternates periodically (3). Moreover, a nonmuscle isoform of titin, c-titin, localizes periodically to SFs (6). Thus, it is natural to ask whether the operating principles are similar to those of myofibrils. Striated muscle sarcomere kinetics depends on two fundamental relations: the isometric sarcomere force-length relation (7) (see Fig. 2) and the force-velocity relation giving myosin-generated force versus sarcomere contraction velocity (8). The analogous relations for SFs, if they exist, are unknown.

Figure 2.

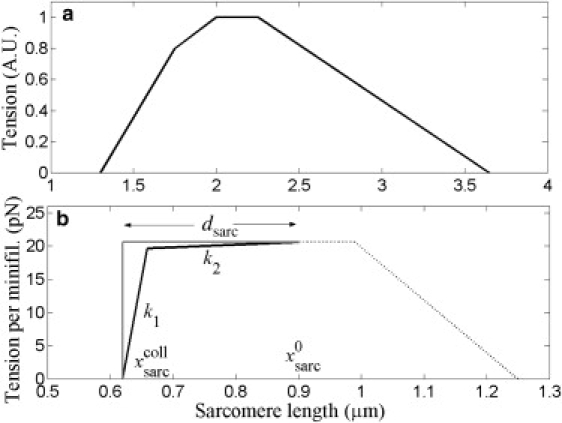
Force-length relations. (a) Striated muscle sarcomere force-length relation measured by Gordon et al. (7). The ascending limb spans lengths ∼1.3–2 μm. (b) Proposed SF force-length relation: a shallow, tensile leg with elastic constant k₂ = 4 pN/μm and a steep, compressive leg with elastic constant k₁ = 500 pN/μm intersect at length $x_{\text{sarc}}^{\ast }$ = [f_s + k₁($x_{\text{sarc}}^0$ – d_sarc)](k₁ – k₂)⁻¹ ≈ 0.66 μm. At the minimum length x_sarc^coll = $x_{\text{sarc}}^0$ − d_sarc ≈ 0.62 μm (collapsed sarcomere) the elastic resistance stalls the myosin. Hard core limit in gray.

Establishing a representative model of SFs is challenging because in stationary cultured cells they normally exert isometric tension with little kinetic activity that could reveal contraction mechanisms. Laser ablation is a powerful method that can reveal otherwise hidden internal forces in such situations. Recently Kumar et al. severed single SFs in living endothelial cells using femtosecond laser ablation and measured rapid fiber recoil (∼1 μm/s) over ∼5 s (see Fig. 1) (9). Although contractility of isolated SFs was previously demonstrated (10), the quantitative nature of the in vivo data of Kumar et al. (9) provides the opportunity for quantitative modeling of SF mechanisms. We will argue that because such large velocities are realized, recoil kinetics reveal information not only about the internal fiber machinery but also about its coupling to the cellular environment.

Several models of SFs have been developed. In the tensegrity model of Luo et al. (11), tension from viscoelastic cables is resisted by elastic struts under compression. This is a general framework successfully reproducing observed recoil kinetics and other features such as widening of the severed ends (9). However, the model's relationship to the measured sarcomeric organization and actin filament polarity distribution of SFs is not direct. Other models aimed to explain the relaxation kinetics after chemical stimulation observed by Peterson et al. (5). In Stachowiak and O'Shaughnessy (12), the role of actin turnover in SF relaxation was investigated, whereas in Besser and Schwarz (13), a feedback loop between FA-based signaling and fiber contraction was proposed.

Here we develop a systematic quantitative model of the SF machine based on known components and existing experimental findings. The model consists of a balance of forces in a sarcomeric organization:

• 1.Contractile forces, exerted by nonmuscle myosin II, characterized by a force-velocity relation.
• 2.Elastic forces, characterized by a force-length relation that we infer from experimental data.
• 3.Viscous forces, both internal and external to the SF.

Applied to the kinetics revealed by the fiber-severing assay, the model predicts an SF force-length relation similar to that of muscle. We find the internal viscosity is relatively small but substantial external drag forces act on the retracting fiber, corresponding to an effective cytosolic viscosity ∼10⁴ times that of water. In addition to nonspecific interactions, this may reflect specific interactions with cytoskeletal or membrane proteins. Thus, the severed SF can be viewed as a natural internal probe of the cell's effective viscosity.

Stress Fiber Forces

Contractile force

SF contraction depends on nonmuscle myosin II motor proteins (9,10), which aggregate into ∼0.3-μm-long bipolar minifilaments, each containing 10–30 molecules (14,15). Both minifilament formation and force generation are promoted by phosphorylation of the myosin regulatory light chain (16), which is regulated by both myosin light chain kinase (MLCK) and Rho-kinase (ROCK) (17). In a sarcomeric arrangement, motor activity is characterized by a force-velocity relation by analogy with striated muscle (8). Although this relation has not been measured for nonmuscle myosin II, several principal features can be estimated (see Table 1):

• 1.From gliding assays, the maximum rate at which bipolar minifilaments can contract a sarcomere (at zero load) is $v_{\text{myo}}^0\approx 0.6\mu \mathrm{m}/\mathrm{s}$ (18).
• 2.The stall force of a minifilament (at zero velocity) is estimated to be f_s ≈ 17 pN, using measurements of muscle myosin II since nonmuscle myosin II forces have not been directly measured to the best of our knowledge.
• 3.The slope of the force-velocity relation at stall, ν_myo.

Table 1.

Parameter values

Symbol	Meaning	Value
$x_{\text{sarc}}^0$	Initial sarcomere length	0.9 μm∗
Ntot	Number of sarcomeres	12†
dsarc	Sarcomere collapse distance	0.28 μm†
fs	Minifilament stall force	17 pN‡
vmyo0	No-load myosin velocity	0.6 μm/s§
νmyo	Force-velocity relation slope	28 pN·s/μm¶
k1	Compressive elasticity	500 pN/μm‖
k2	Tensile elasticity	4 pN/μm∗∗
νext	External drag coefficient	5.3 pN·s/μm††
νint	Internal drag coefficient	5.0 pN·s/μm††
nmini	Minifilaments per sarcomere	50‡‡
w	SF diameter	0.5 μm§§

^∗From Sanger et al. (32).

^†Images from Kumar et al. indicate relative shortening ∼1/3 after severing; total recoil distance was ∼3.35 μm (9). Thus, N_tot ≈ 12 sarcomeres each shrank by d_sarc ≈ 0.28 μm.

^‡Assumes 10 myosins on each side of a minifilament (15) each with the muscle myosin stall force, 1.7 pN (33).

^§Bipolar minifilaments can contract actin at twice the velocity measured in gliding assays (18).

^¶For linear force-velocity relation ν_myo = f_s/$v_{\text{myo}}^0$.

^‖Value for steep region in striated muscle relation (7).

^∗∗From muscle titin (20).

^††Fit to experimental data.

^‡‡Assumes two actin filaments per minifilament (34) and 100 actin filaments in parallel, consistent with electron micrographs showing SFs ∼10 filaments across (3).

^§§From Kumar et al. (9).

Elastic forces: force-length relation

The striated muscle force-length relation is well established (7) and is typically represented as isometric tension versus sarcomere length as in Fig. 2 a. On the ascending limb, tension decreases with decreasing sarcomere length where actin pointed ends first overlap in the myosin region. Tension decreases more rapidly in the steepest portion at the onset of compressive stresses when thick filaments are forced against Z disks (7,19). Although the SF force-length relation has not been directly measured in living cells, two experiments suggest a similar form with two distinct regions on the ascending limb (see Fig. 2 b): Experiment 1. Peterson et al. (5) treated fibroblasts with the phosphatase inhibitor calyculin A, inducing small spatial variations in myosin phosphorylation level about the mean value along SFs. This caused peripheral (central) sarcomeres to contract (expand). Now a sarcomere whose myosin stall force is δ f_s per minifilament above the mean will contract distance Δx ≈ δ f_s/k where k is the SF force constant per minifilament. In Stachowiak and O'Shaughnessy (12), it was estimated δ f_s = 0.06f_s for those sarcomeres which contracted by amount Δx = 0.3 μm (5), implying k ≈ 3.4 pN/μm. This is a small value, close to that of muscle titin (20). Experiment 2. Other evidence suggests that a much larger value onsets at smaller lengths: sarcomeres shrank an estimated amount d_sarc ≈ 0.28 μm after severing (9) (see Table 1), reaching a collapsed state where enough compressive force developed to balance the tensile myosin stall force. The force constant required to stall myosin after a contraction of d_sarc is ≫3.4 pN/μm.

Thus, taken together, Experiments 1 and 2 suggest a force-length relation with two distinct portions in its ascending limb as in Fig. 2 b. One portion reflects tensile forces, perhaps from c-titin, which are much smaller than the myosin contractile forces (elastic constant k₂); the other reflects strong compressive forces at short sarcomere lengths (elastic constant k₁). The latter stalls contraction after severing at sarcomere length $x_{\text{sarc}}^{\text{coll}}=x_{\text{sarc}}^0-d_{\text{sarc}},$ where $x_{\text{sarc}}^0$ is the initial sarcomere length.

Viscous forces

Two classes of viscous drag forces may be present. Internal drag depends on the sarcomere contraction velocity whereas external drag depends on the relative velocity between the SF and its surroundings. We will find that the existing experimental data cannot be explained without invoking external viscous forces.

Model and Parameters

The model

In this section, a model is built incorporating the forces discussed in the previous section. The model, depicted in Fig. 3, describes one of the two SF pieces after severing, comprising N_tot sarcomeres in series. The severed end is free (n = 1), whereas the other end is anchored to an FA (n = N_tot). Fiber kinetics results from the balance of contractile, elastic, and viscous forces acting on each sarcomere of length x_sarc and contraction velocity v_sarc.

Figure 3.

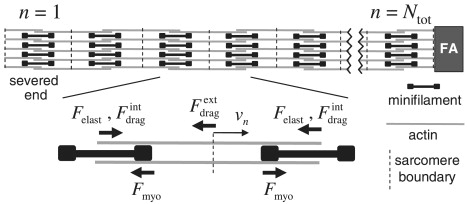
The model. External drag acts on bipolar actin bundle n, proportional to its velocity v_n. Other forces are internal drag, elastic, and myosin forces from sarcomeres to its left and right (see Eq. 1).

The contractile myosin force in each sarcomere obeys force-velocity relation F_myo(v_sarc) per minifilament. Since this has not been measured for SFs, we consider two forms:

• 1.Linear, F_myo = f_s − ν_myov_sarc.
• 2.The well-known hyperbolic Hill relation for muscle (8), $F_{\text{myo}}/f_{\mathrm{s}}=\alpha {\left(v_{\text{sarc}}/v_{\text{myo}}^0+\beta \right)}^{-1}$ – β, where α and β are dimensionless parameters.

In each sarcomere, the elastic force per minifilament at longer sarcomere lengths is F_elast(x_sarc) = k₂x_sarc, which reflects weak tensile force, possibly from titin. Below a threshold sarcomere length $x_{\text{sarc}}^{\ast }$ strong compressive forces onset, $F_{\text{elast}}\left(x_{\text{sarc}}\right)=k_1\left(x_{\text{sarc}}-x_{\text{sarc}}^{\text{coll}}\right)-f_s,$ which balance the stall force at the collapsed sarcomere length $x_{\text{sarc}}^{\text{coll}}$. Thus the maximum possible sarcomere shrinkage is $d_{\text{sarc}}\equiv x_{\text{sarc}}^0-x_{\text{sarc}}^{\text{coll}}$. The elastic force is presented in Fig. 2 b as an isometric force-length relation (summed with the myosin contribution) to aid comparison with the analogous relation for muscle of Fig. 2 a.

The internal and external drag forces per minifilament are determined by the corresponding friction coefficients ν_int and ν_ext: $F_{\text{drag}}^{\text{int}}\left(v_{\text{sarc}}\right)={\nu }_{\text{int}}{v}_{\text{sarc}}$ and $F_{\text{drag}}^{\text{ext}}$(v) = ν_extv, where v is actin velocity relative to the cytoplasm.

It is convenient to apply the force balance to the n^th bipolar actin bundle at x_n moving with velocity v_n, pulled by two minifilaments to either side (see Fig. 3). Thus, sarcomere n has length x_sarc = x_n+1 − x_n and contraction velocity v_sarc = v_n − v_n+1. The force balance reads

$$\begin{array}{c}{F}_{\text{drag}}^{\text{ext}}\left(v_{\mathrm{n}}\right)=-F_{\text{myo}}\left(v_{n-1}-v_n\right)+F_{\text{myo}}\left(v_{\mathrm{n}}-v_{\mathrm{n}-1}\right)+F_{\text{drag}}^{\text{int}}\left(v_{\mathrm{n}-1}-v_{\mathrm{n}}\right)-F_{\text{drag}}^{\text{int}}\left(v_{\mathrm{n}}-v_{\mathrm{n}+1}\right)-F_{\text{elast}}\left(x_{\mathrm{n}}-x_{\mathrm{n}-1}\right)+F_{\text{elast}}\left(x_{\mathrm{n}+1}-x_{\mathrm{n}}\right)\end{array}\text{.}$$ (1)

The severed-end boundary condition (n = 1) is $F_{\text{drag}}^{\text{ext}}$(v) = F_myo(v_sarc) + F_elast(x_sarc) − $F_{\text{drag}}^{\text{int}}$(v_sarc), since internal forces act on one side of the bundle only, whereas v = 0 at the fixed adhesion (n = N_tot + 1). Thus, we neglect possible alterations in severed-end sarcomere properties due to laser ablation; for example, the widening of severed ends observed by Kumar et al. (9).

Since v_n ≡ dx_n/dt, Eq. 1 is a closed system solvable for the time-dependent velocities and locations of all actin bundles (and hence sarcomeres).

Parameters

The parameter values used in our model are listed in Table 1. Since SF elastic constants have not been directly measured, we use the muscle value in the steep region (k₁) and the value for muscle titin in the shallow region (k₂). Note that the internal and external drag coefficients are key SF parameters that are not known. A major objective of this work is to use our model to infer their values using the measured post-severing recoil data.

Dynamics of the collapsed cap

As will become clear, Eq. 1 reveals a sequential collapse of sarcomeres propagating inward from the free severed end. After severing, the end sarcomere finds itself in an extraordinarily asymmetrical situation: myosin pulling forces on one side are unopposed by myosins on the other (severed) side. The large imbalance is resisted by weak drag forces only. Thus, the end sarcomere swiftly contracts to its minimum length. This collapsed sarcomere is inactive, its myosin contractility exactly negated by elastic resistance. Hence, the second sarcomere finds itself in the same asymmetrical situation and subsequently collapses, and so on: a collapse front propagates inward, leaving in its wake a growing cap of N_cap collapsed sarcomeres at the severed end (see Fig. 1 b and Movie S1 in the Supporting Material).

What equations govern the cap growth in time, N_cap(t)? Cap dynamics are most clearly phrased in the hard-core model, defined as

• 1.In the force-length relation, k₁ → ∞ and k₂ → 0, excellent approximations since there is one very shallow and one very steep region (Fig. 2 b).
• 2.The continuous limit is taken ($v_{\mathrm{n}+1}-v_{\mathrm{n}}\to \partial v/\partial n$, etc.), which accurately describes many-sarcomere behavior.
• 3.A linear force-velocity relation is assumed.

Equation 1 then simplifies to (see Appendix A for derivation)

$$\begin{array}{l}v={\xi }^2\frac{{\partial }^{2}v}{\partial n^2},{\xi }^2=\frac{{\nu }_{\text{myo}}+{\nu }_{\text{int}}}{{\nu }_{\text{ext}}}\left(N_{\text{cap}}\le n\le N_{\text{tot}}\right),\end{array}$$ (2)

where the velocity penetration depth ξ plays a crucial role in the severed fiber's evolution. The first N_cap sarcomeres are collapsed (1 ≤ n < N_cap) whereas this equation describes the uncollapsed portion of the fiber. It is to be solved for the fiber velocity profile v(n) subject to boundary condition v = ξ²(v_sarc⁰ + ∂v/∂n)/N_cap at the collapse front n = N_cap, where v_sarc⁰ ≡ ${\tilde{f}}_{\mathrm{s}}$/(ν_myo + ν_int) and ${\tilde{f}}_{\mathrm{s}}$ is the effective stall force at t = 0 including the elastic contribution (see Appendix A). In Appendix B, we show that the collapsed cap length N_cap and sarcomere length profile x_sarc obey the equations

$$\begin{array}{l}\frac{d{N}_{\text{cap}}}{dt}={\theta }^{-1}{v}_{\text{sarc}}\left(N_{\text{cap}}\right),\\ \frac{\partial x_{\text{sarc}}}{\partial N_{\text{cap}}}=-\theta \frac{v_{\text{sarc}}\left(n\right)}{v_{\text{sarc}}\left(N_{\text{cap}}\right)},\\ \theta \equiv \frac{\partial x_{\text{sarc}}}{\partial n}{|}_{\mathrm{n}=N_{\text{cap}}}\text{.}\end{array}$$ (3)

Solutions of Model Equations

For a given cap length N_cap, Eq. 2 is solved for the SF velocity profile v(n). This gives the severed-end recoil velocity v_recoil = v(N_cap) and the sarcomere contraction velocity profile v_sarc = −∂v/∂n:

$$\begin{array}{l}{v}_{\text{recoil}}=\frac{\xi v_{\text{sarc}}^0}{1+N_{\text{cap}}/\xi },\\ v_{\text{sarc}}\left(n\right)=\frac{v_{\text{sarc}}^0}{1+N_{\text{cap}}/\xi }{e}^{-\left(n-N_{\text{cap}}\right)/\xi }\\ \left(n\ge N_{\text{cap}}\right)\text{.}\end{array}$$ (4)

Short time recoil

Immediately after severing (N_cap = 1), the first sarcomere contracts with velocity $v_{\text{sarc}}^0$/(1 + 1/ξ) (Eq. 4) and collapses in time τ_coll = τ_coll⁰(1 + 1/ξ) where ${\tau }_{\text{coll}}^0$ = d_sarc/$v_{\text{sarc}}^0$ and $v_{\text{sarc}}^0$ are, respectively, the collapse time and velocity in the absence of external drag (ξ → ∞). From Eq. 4, the length profile at the instant of the first sarcomere collapse is x_sarc(n) = $x_{\text{sarc}}^0$ − d_sarce^{−(n−1)/ξ}.

Steady state

Equation 3 is solved for the sarcomere length profile as a function of cap length in Appendix B. After the first collapse (t = τ_coll), a steady-state profile is established relative to the moving collapse front at n = N_cap:

$$x_{\text{sarc}}\left(n\right)=x_{\text{sarc}}^0-d_{\text{sarc}}{e}^{-\left(\mathrm{n}-N_{\text{cap}}\right)/\xi }\left(t>{\tau }_{\text{coll}},n\ge N_{\text{cap}}\right)\text{.}$$ (5)

Note this matches the profile at the instant of the first collapse. With θ = d_sarc/ξ, Eq. 3 is then solved for cap length as a function of time

$$N_{\text{cap}}\left(t\right)=\xi \left[{\left(2t/{\tau }_{\text{coll}}^0-C\right)}^{1/2}-1\right]\left(t>{\tau }_{\text{coll}}\right),$$ (6)

where C = 1 − ξ⁻² was determined by the initial condition N_cap = 1 at t = τ_coll.

Initially, the severed end recoils at constant velocity (Eq. 4 with N_cap = 1). Using N_cap(t) from Eq. 6 in Eq. 4 gives the recoil velocity at later times when the steady-state sarcomere profile is established. Thus

$$x_{\text{recoil}}\left(t\right)=\{\begin{array}{ll}\xi v_{\text{sarc}}^{0}t/\left(1+1/\xi \right)\hfill & \left(t<{\tau }_{\text{coll}}\right)\hfill \\ d_{\text{sarc}}\xi {\left(2t/{\tau }_{\text{coll}}^0-C\right)}^{1/2}\hfill & \left(t>{\tau }_{\text{coll}}\right)\hfill \end{array}\text{.}$$ (7)

These results apply until all sarcomeres have collapsed and the SF has length N_tot$x_{\text{sarc}}^{\text{coll}}$. This occurs after time T_coll ≈ (τ_coll⁰/2)(N_tot/ξ)², obtained by setting N_cap = N_tot + 1 in Eq. 6.

Comparison of Model Results to Experimental Recoil Profile

In the experiments of Kumar et al. (9) (Fig. 1), severed end displacement x_recoil(t) was followed in time. The measured recoil is plotted in Fig. 4 together with the hard core model predictions, Eq. 7 (dashed line), using Table 1 parameter values. Also shown are numerical solutions to the exact discrete model equations (Eq. 1), using both the linear (thick solid line) and Hill (dotted line) force-velocity relations. We fitted the numerical solutions to the experimental data (9) using only the drag force coefficients as fitting parameters. For internal drag, the best fit values ν_int = 5.0 pN·s/μm (linear) and ν_int = 0 (Hill) were considerably less than the effective drag due to myosin, ν_myo = 28 pN·s/μm. Best fit external drag coefficients were ν_ext = 5.3 pN·s/μm (linear) and ν_ext = 4.3 pN·s/μm (Hill).

Figure 4.

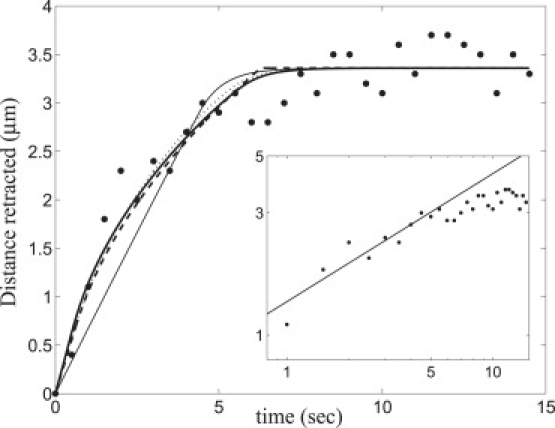
Recoil kinetics: model predictions compared to experimental results. (Solid circles) Experimental data from Kumar et al. (9). (Thick solid line) Numerical solution of Eq.1 using the linear force-velocity relation with best-fit values ν_ext = 5.3 pN·s/μm and ν_int = 5 pN·s/μm. (Dotted line) Numerical solution using the Hill force-velocity relation with best- fit values ν_ext = 4.3 pN·s/μm and ν_int = 0. All other parameters as in Table 1. (Dashed line) Hard core model, Eq. 7, truncated at x_recoil = N_totd_sarc. (Thin solid line) Recoil curve with ν_ext = 0, fit for best corresponding internal drag, ν_int = 338 pN·s/μm. (Inset) Log-log plot showing experimental recoil distance (9) (solid circles) and predicted t^1/2 law (solid line).

The results in Fig. 4 demonstrate the following:

• 1.With the parameters of Table 1, model predictions are in excellent agreement with experiment.
• 2.Results for the hard core and exact discrete models are almost indistinguishable, showing that the continuous limit and hard core approximation to the force-length relation accurately describe SF severing.
• 3.Linear and nonlinear force-velocity relations yield similar results, both indicating myosin dominates internal dissipation. Thus, hereafter we consider only the linear force-velocity relation.

An important prediction of the hard-core model is that for intermediate times (before complete SF collapse), severed end displacement follows a one-half power law, x_recoil ∼ t^1/2 (see Eq. 7 for $t\gg {\tau }_{\text{coll}}^0$). The measured recoil profile is in rather close agreement with this prediction (Fig. 4, inset). In the next section, we will show this power law results directly from external drag.

External Drag Results in Nonuniform Sarcomere Length Profile and Collapsed Cap

The state of the severed SF at any instant is specified by the lengths of all sarcomeres. Model predictions were presented in Solutions of Model Equations. Using Table 1 parameter values, their main features can be summarized as

• 1.Immediately after severing, the sarcomere at the severed end contracts at rate v_sarc = 0.45 μm/s and collapses after τ_coll ≈ 0.62 s.
• 2.Thereafter a cap of N_cap(t) collapsed sarcomeres grows at the severed end as successive sarcomeres collapse (Fig. 5 and Movie S1). The cap growth law predicted by the hard-core model (Eq. 6) agrees closely with that of the exact discrete model (Fig. 5, inset).
• 3.After collapse of the first sarcomere, noncollapsed sarcomeres attain a steady-state exponential length profile of width ξ ≈ 2.5 (Eq. 5). This is evident in Fig. 6, where a collapsed cap grows, ahead of which only ∼ξ sarcomeres have significantly contracted at any instant. Continuous hard-core and discrete model profiles are in good agreement.
• 4.Complete fiber collapse occurs after T_coll ≈ 5.2 s (cap engulfs entire fiber).
• 5.Before total fiber collapse, cap growth follows a one-half power law, N_cap ∼ t^1/2.

Figure 5.

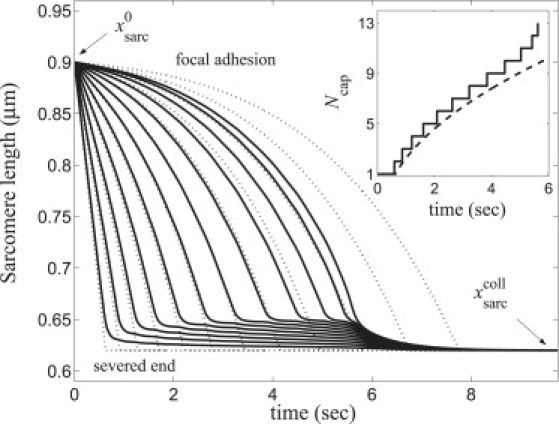
Sequential sarcomere collapse. Numerical (solid lines, Eq. 1) and hard core model (dotted lines, Eq. 4) solutions for sarcomere length evolution using parameters from Table 1. (Inset) Numerical (solid line, Eq. 1) and hard core model (dashed line, Eq. 6) solutions for collapsed cap growth. For numerical solution, a sarcomere was defined as collapsed when x_sarc < $x_{\text{sarc}}^{\ast }$.

Figure 6.

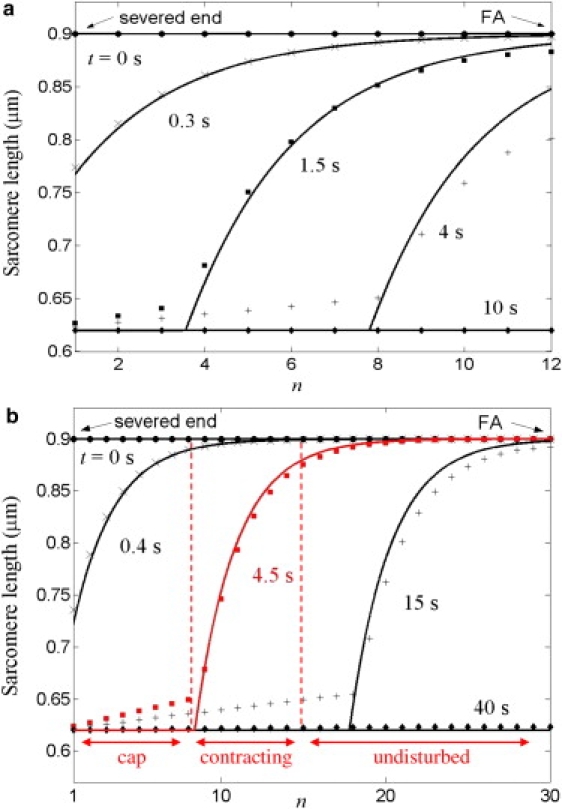
Evolution of sarcomere length profile according to numerical solutions (Eq. 1, symbols) and hard core model (Eq. 5, solid lines) for fibers of N_tot = 12 (a) and N_tot = 30 (b) sarcomeres. Other parameters from Table 1. Three regions of differing sarcomere contractile activity are indicated for the N_tot = 30 fiber 4.5 s after severing (red).

In summary, the severed SF comprises three zones (see Fig. 6): a collapsed portion near the severed end; a contracting zone of ∼ξ partially collapsed sarcomeres; and an undisturbed portion near the adhesion. The origin of this highly nonuniform profile is drag force exerted on the recoiling fiber by its surroundings, which causes nonuniform sarcomere contraction velocities (Eq. 4). Were drag force absent, every sarcomere would experience the same forces: the myosin contractile force f_s would be resisted only by internal friction (ν_int + ν_myo)$v_{\text{sarc}}^0$, where the effective myosin drag coefficient ν_myo is the slope of the myosin force-velocity relation. Equating forces, all sarcomeres would contract with the same velocity v_sarc⁰ ≈ f_s/(ν_myo + ν_int) and collapse in the same time τ_coll⁰ = d_sarc/$v_{\text{sarc}}^0$. The sarcomere profile would be uniform at all times. We find this zero external drag scenario is inconsistent with the measured recoil profile: setting ν_ext = 0, the model predicts almost constant recoil velocity (see Fig. 4, thin solid line) in clear contradiction to the pronounced curvature of the observed profile.

Effect of external drag: scaling arguments

How does external drag modify the drag-free scenario? What is the origin of the predicted t^1/2 laws for recoil and cap length at intermediate times (Eqs. 7 and 6)? Consider the following simple scaling arguments. Central to the discussion is the velocity penetration length ξ (Eq. 4), the width of the contracting zone: only these ∼ξ sarcomeres have substantial contraction velocity v_sarc. Note that the larger the external drag, the smaller this penetration depth.

• 1.Early transient. Consider the sarcomere at the severed end. Immediately after severing, it feels the forces discussed previously, but now an additional external drag ν_extv resists contraction. Its velocity relative to the surroundings is v ≈ ξ v_sarc since ∼ξ sarcomeres are contracting. Balancing forces now gives contraction velocity v_sarc = $v_{\text{sarc}}^0$/(1 + 1/ξ) and collapse time τ_coll = ${\tau }_{\text{coll}}^0$(1 + 1/ξ). External drag prolongs collapse by the factor 1 + 1/ξ ≈ 1.4.
• 2.Steady state. At large times, resistance to contraction of the first uncollapsed sarcomere is dominated by the large drag force ≈ N_cap ν_extv_recoil acting on the cap moving with velocity v_recoil = dx_recoil/dt. Note its total drag is proportional to cap size N_cap. Equating this to the myosin contraction force f_s yields v_recoil ≈ $v_{\text{sarc}}^0$ξ²/N_cap. Now the cap growth rate dN_cap/dt ≈ v_sarc/δx_sarc is proportional to v_sarc ≈ v_recoil/ξ, the sarcomere shrinkage rate in the contracting zone across which velocity falls to zero from the value v_recoil at the cap. Here δx_sarc ≈ d_sarc/ξ is the length of the first uncollapsed sarcomere relative to the collapsed length (the remaining slack). Across the contracting zone, the slack changes from zero at the cap to d_sarc at the edge of the unaffected zone. Hence, the cap dynamics are dN_cap/dt ≈ ξ²/(${\tau }_{\text{coll}}^0$N_cap) with solution

$$N_{\text{cap}}=\xi {\left(2t/{\tau }_{\text{coll}}^0\right)}^{1/2},x_{\text{recoil}}=N_{\text{cap}}{d}_{\text{sarc}}\left(t\gg {\tau }_{\text{coll}}^0\right)\text{.}$$ (8)

These are precisely the results predicted by the hard core model for large times (Eqs. 6 and 7). The arguments reveal that for such times the experimentally observed recoil distance is simply the total cap length. Thus, recoil distance and cap size are fundamentally related. The experimental data are consistent with this t^1/2 recoil law (Fig. 4, inset).

External Drag Prolongs Relaxation of Force on Focal Adhesions

FAs play important roles in a cell's mechanical communication with its environment and can respond to applied force (21,22). Immediately after severing, the tension vanishes at the severed SF ends and thus the force exerted by the severed fiber on its anchoring FAs will eventually decay to zero. We used our model to calculate this decay (see Fig. 7). The predicted decay time equals the end recoil relaxation time (T_coll ≈ 5.2 s) since the total external drag on the retracting fiber is communicated to the FA. Finite decay time of FA force is entirely due to external drag: without drag, decay would be instantaneous, since the vanishing tension is the same throughout the fiber.

Figure 7.

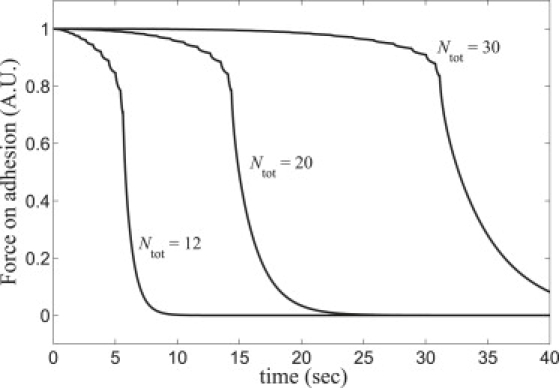
Force exerted by a severed SF on its anchoring FA for fibers of three lengths as indicated. All other parameters from Table 1. Force profiles are numerical solutions of Eq. 1 for force exerted on the actin bundle connected to the adhesion (n = N_tot + 1). Note that the total force on the FA may have contributions from other attached SFs.

Kumar et al. used traction force microscopy to measure total cellular traction reduction after severing a SF. This includes contributions from all FAs (9). Although FAs were not visualized and single FA forces not measured, consistent with our model's predictions, substrate relaxation near the intact SF end (where an adhesion is expected to reside) appeared to occur on a timescale similar to that of fiber recoil.

Discussion

We developed a model of SFs starting from the experimentally established organization of actin, myosin, and other components. The model was applied to fiber kinetics after severing. Comparing model predictions to a recent experimental severing study enabled us to test contraction mechanisms and to quantitatively infer fundamental SF properties.

Force-length relation

As for muscle, a fundamental property is the single sarcomere force-length relation. We find the profile is similar to that of muscle (Fig. 2 a) in that there are two distinct regions on the ascending limb (Fig. 2 b): 1. Shallow region. At normal operating lengths, resistance to length change is weak. The long sarcomere relaxation times observed in Peterson et al. (5) imply a small force constant similar to that of muscle titin (20), k₂ = 4.0 pN/μm per minifilament. This suggests the shallow region originates in tensile stress due to c-titin (6), consistent with evidence of elastic contribution to SF stress (23,24), although apparently inconsistent with other observations (9). This remains an important question to resolve by future experiment. 2. Steep region. In the severing experiments of Kumar et al. (9), after sarcomeres contracted, total estimated distance d_sarc = 0.28 μm compressive elastic forces suddenly built up and stalled the myosin contractile force, f_s = 17 pN per minifilament. We found the corresponding force constant at these small lengths is much greater than in the shallow region, and we used the value from muscle, k₁ = 500 pN/μm. These forces presumably originate from interference of overlapping actin filaments within myosin regions and from myosin-myosin interference between adjacent sarcomeres. Note the steep ascending region in muscle (Fig. 2 a) likely also has its origin in compressive elastic forces (7).

Current experiment is not consistent with a simple constant-slope relation. Severing experiments dictate that the single force constant value would be k ≈ f_s/d_sarc ≈ 60 pN/μm per minifilament. Although this model can fit the severing data well (it is mathematically equivalent to a viscoelastic cable (9)), it cannot explain the slow relaxation seen in Peterson et al. (5).

Assuming each sarcomere contains n_mini = 50 minifilaments in parallel and is w = 0.5 μm wide (see Table 1), the total sarcomere force constant is n_minik₂ = 200 pN/μm at normal operating lengths. This implies an effective modulus ∼10³ pN/μm², considerably less than the value ∼10⁵-10⁶ pN/μm² reported by Deguchi et al. for isolated SFs (24). The mechanical properties of these latter SFs may have been altered by isolation and the absence of ATP. Future mechanical studies in living cells may resolve this discrepancy.

External drag force

We find substantial external drag forces must be invoked to explain the curvature in the experimental recoil profile (see Fig. 4). Our model leads to drag coefficient ν_ext ≈ 5.3 pN·s/μm per minifilament. Now the total drag coefficient of a cylindrical sarcomere of length $x_{\text{sarc}}^0$ = 0.9 μm in a medium with viscosity η_cyt is n_mini ν_ext = 2πη_cyt $x_{\text{sarc}}^0$/(ln $x_{\text{sarc}}^0$/w + 0.25) (25). Our model then implies effective cytosolic viscosity η_cyt ≈ 39 Pa·s, or ∼10⁴ times the viscosity of water. Thus, severed fiber recoil kinetics contain information about how the SF interacts with its surroundings in the cell. Indeed, the recoiling SF is an internal probe of effective cellular viscosity. Our result is similar in magnitude to that from the microrheological study of fibroblasts by Tseng et al., who measured an effective cytosolic viscosity of 10 Pa·s at frequency 0.16 s⁻¹ (26). Other studies of macrophages have reported apparent viscosities in the range 10²−10³ Pa·s (27,28). Variations in reported values are expected, since viscosity depends on the time- and length-scale probed, reflecting structural heterogeneity and the complex nonlinear viscoelastic response of living cells.

The effective cytosolic viscous drag may originate not only from nonspecific interactions with the cytosol but also from breaking of dynamic cross links between the SF and its surroundings. ECM proteins are concentrated along SFs, indicating possible interactions between SFs and transmembrane proteins (29), and electron microscopy reveals connections between SFs and the surrounding cytoskeleton (30). Indeed, buckled SFs exhibit 2 μm wavelength undulations, possibly suggesting lateral connections (23).

Internal drag force

From the model, we conclude that most internal dissipation is due to myosin: fitting to the experimental recoil data, we found internal drag coefficient ν_int = 5.0 pN·s/μm, smaller than the myosin force-velocity slope at stall, ν_myo, which represents an effective myosin internal drag coefficient. The nonmyosin component may derive from friction between overlapping F-actin in the myosin zones at sarcomere centers or displacement of dynamic α-actinin cross links by myosin which, unlike striated muscle, must accompany sarcomere shrinkage. Another possibility, investigated in Stachowiak and O'Shaughnessy (12), is that when sarcomeres change length, actin filaments adjust via polymerization or depolymerization. Applying this framework to severing kinetics, filaments would shrink during recoil (as in contractile ring constriction) and ν_int would represent an effective polymerization-derived value (12). Following a perturbation, the model of Stachowiak and O'Shaughnessy (12) identified an additional early transient with a smaller ν_int value; this picture could thus explain curvature in the end recoil profile, and would then lead to an external drag coefficient smaller than the value implied by the present model assuming fixed actin lengths. Future severing experiments studying SFs of different lengths can distinguish between these two pictures, since the two models predict very different length-dependencies.

Effect of myosin inhibition

Kumar et al. severed SFs after reducing myosin phosphorylation levels by treatment with inhibitors of the kinases ROCK and MLCK (9). Recoil was diminished by 60% 17 s after severing (ROCK inhibition) and by 92% 8.5 s after severing (MLCK inhibition). To model these experiments, we set myosin stall force to zero (f_s = 0). We found recoil rate was retarded, with 60% recoil loss after 8.5 s and 34% loss after 17 s, but the eventual total recoil distance was virtually unchanged due to weak passive elastic forces (see Fig. S1). This agrees with previous studies indicating a passive elastic contribution to contraction in the absence of ATP (24). However, the predicted recoil rate exceeds that measured by Kumar et al. (9), which may be explained by disruption of stress fiber structure due to compromised minifilament formation when myosin phosphorylation is inhibited (16). It would be interesting to sever SFs treated with blebbistatin, which inhibits myosin force-generation but not phosphorylation (31).

Relaxation of cellular traction

Our model predicts that after severing, the force exerted by the severed SF on its adhesion decays to zero over the recoil timescale, T_coll = 5.2 s (Fig. 7). Using traction force microscopy, Kumar et al. measured a loss of >50% of the cell's total traction over 30 s after severing a single SF (9). This large drop suggests tension loss in one fiber precipitates on longer timescales tension loss elsewhere in the cytoskeletal network by physical or biochemical mechanisms beyond the scope of our single SF model. Over yet longer timescales of minutes, loss of force applied on FAs causes FA disassembly (21,22) by increasing the off-rate of a mechanosensitive component (22).

Experimentally testable predictions

The model makes numerous quantitative predictions that can be tested by future experiments:

• 1.Sarcomere length profiles. External drag leads to dramatically inhomogeneous SF collapse kinetics after severing, since contraction of a given sarcomere is opposed by the net drag on the entire fiber section between it and the severed end. Thus, more interior sarcomeres contract more slowly. We predict a sarcomere profile with three zones (see Fig. 6) including a cap of collapsed sarcomeres at the severed end. The predicted sarcomere length profiles (Eq. 5 and Fig. 6) could be directly measured by labeling a periodic SF component (e.g., myosin II or α-actinin).
• 2.Fiber length dependence. We compared our model to a single experimental recoil profile for a severed fiber containing N_tot = 12 sarcomeres. Experiments following severed SFs of different lengths could test our prediction that total fiber collapse time-scales as $N_{\text{tot}}^2$, another consequence of external drag. Were external drag absent, collapse time would be independent of fiber length.
• 3.Sarcomere length dependence. Assuming a sarcomere's external drag coefficient is proportional to its length (for example, there may be a constant number of connections with the surroundings per unit length), our model predicts that SFs with initially longer sarcomeres recoil more slowly and total collapse time-scales linearly with sarcomere length, T_coll ∼ $x_{\text{sarc}}^0$ (see Fig. S2).
• 4.End recoil and collapsed cap: power law time dependencies. We predict that end recoil distance and collapsed cap length grow as power laws in time: x_recoil ∼ N_cap ∼ t^1/2 (see Eq. 8), consistent with current end recoil data (Fig. 4, inset). Severing longer SFs, where the power law window is larger, would more stringently test the end recoil law.
• 5.Forces on focal adhesions. The predicted adhesion force decay after severing (Fig. 7) could be directly measured using techniques measuring forces on FAs (21). For FAs attached to just a single SF, we predict the decay time increases with SF length as ∼$N_{\text{tot}}^2$. This may also describe the short time decay for adhesions attached to multiple SFs.
• 6.Modifying fiber-cell coupling. An interesting possibility is to sever SFs in cells where candidate linker proteins between SFs and their surroundings are interfered with. In our model this would modify the external drag coefficient ν_ext. Comparing with model predictions may thus help identify such proteins.

Appendix A: Equation for Velocity Profile

The hard core model assumes a linear myosin force-velocity relation and approximates the shallow (steep) portion of the force-length relation (Fig. 2 b), as flat (infinitely steep). Thus contraction is stalled in collapsed sarcomeres (n < N_cap), whereas for active sarcomeres, $F_{\text{elast}}\left(x_{\text{sarc}}\right)\to 0$. The myosin force terms are expressed as F_myo(v_sarc) = ${\tilde{f}}_s$ − ν_myov_sarc, where ${\tilde{f}}_s$ = f_s + k₂$x_{\text{sarc}}^0$ is the effective stall force including the elastic contribution at the initial sarcomere length (see Fig. 2 b). Thus, the fiber dynamics (Eq. 1) for active sarcomeres (n ≥ N_cap) simplify to

$${\nu }_{\text{ext}}{v}_{\mathrm{n}}=\left({\nu }_{\text{myo}}+{\nu }_{\text{int}}\right)\left(v_{\mathrm{n}-1}-v_{\mathrm{n}}\right)-\left({\nu }_{\text{myo}}+{\nu }_{\text{int}}\right)\left(v_{\mathrm{n}}-v_{\mathrm{n}+1}\right)\text{.}$$

Note the slope of the force-velocity relation ν_myo emerges as a contribution to the total internal drag coefficient. The continuous limit then yields Eq. 2. Strictly, this limit is valid provided ξ ≫ 1. In practice, we find even for our best-fit value ξ ≈ 2.5, it provides an excellent approximation.

Appendix B: Equations and Solutions for Sarcomere Profile and Collapsed Cap Length

It is convenient to express the sarcomere lengths as functions of N_cap in favor of time, $x_{\text{sarc}}\left(n,t\right)\to x_{\text{sarc}}\left(n,N_{\text{cap}}\right)$ (time-dependence is recovered later using the cap solution N_cap(t)). Then the sarcomere shrinkage velocity can be written v_sarc(n) = −(∂x_sarc/∂N_cap)(dN_cap/dt). Meanwhile, in the continuous limit, the cap growth rate is the product of the sarcomere contraction velocity and length gradient at the cap front, dN_cap/dt = θ⁻¹v_sarc(N_cap), where $\theta \equiv \partial x_{\text{sarc}}/\partial n{|}_{n=N_{\text{cap}}}$. These expressions give the cap and sarcomere dynamics (Eq. 3).

Using the explicit solution for the sarcomere velocity profile (Eq. 4) and changing variables $x_{\text{sarc}}\left(n,N_{\text{cap}}\right)\to {\tilde{x}}_{\text{sarc}}\left(w,N_{\text{cap}}\right)$, where w = n − N_cap is the sarcomere location relative to the collapsed cap, the sarcomere length dynamics in Eq. 3 become

$$\frac{\partial {\tilde{x}}_{\text{sarc}}}{\partial w}-\frac{\partial {\tilde{x}}_{\text{sarc}}}{\partial N_{\text{cap}}}=e^{-\mathrm{w}/\xi }\frac{\partial {\tilde{x}}_{\text{sarc}}}{\partial w}{|}_{\mathrm{w}=0}\text{.}$$

The boundary conditions are

• 1.The sarcomere at the cap boundary (w = 0) is collapsed, x_sarc = $x_{\text{sarc}}^{\text{coll}}$ ≡ $x_{\text{sarc}}^0$ − d_sarc;

and

• 2.Far from the severed end, sarcomeres are undisturbed, x_sarc = $x_{\text{sarc}}^0$ for w → ∞.

The steady state solution, ∂${\tilde{x}}_{\text{sarc}}$/∂N_cap = 0, is the exponential profile of Eq. 5. The profile, depending only on w, has constant shape and propagates inward at the same speed as the collapsed cap front.

Supporting Material

One movie and two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00913-8.