Hydration and Hydrodynamic Interactions of Lysozyme: Effects of Chaotropic versus Kosmotropic Ions

Abstract

Using static and dynamic light scattering we have investigated the effects of either strongly chaotropic, nearly neutral or strongly kosmotropic salt ions on the hydration shell and the mutual hydrodynamic interactions of the protein lysozyme under conditions supportive of protein crystallization. After accounting for the effects of protein interaction and for changes in solution viscosity on protein diffusivity, protein hydrodynamic radii were determined with ±0.25 Å resolution. No changes to the extent of lysozyme hydration were discernible for all salt-types, at any salt concentration and for temperatures between 15–40°C. Combining static with dynamic light scattering, we also investigated salt-induced changes to the hydrodynamic protein interactions. With increased salt concentration, hydrodynamic interactions changed from attractive to repulsive, i.e., in exact opposition to salt-induced changes in direct protein interactions. This anti-correlation was independent of solution temperature or salt identity. Although salt-specific effects on direct protein interactions were prominent, neither protein hydration nor solvent-mediated hydrodynamic interactions displayed any obvious salt-specific effects. We infer that the protein hydration shell is more resistant than bulk water to changes in its local structure by either chaotropic or kosmotropic ions.

Introduction

Water molecules bound to the surface and incorporated into the core of protein molecules are considered to play a critical role in regulating the biological functions of proteins and their phase separation behavior (1,2). Yet the structure and dynamics of hydration water remain the topic of ongoing experimental and theoretical research efforts (3). Neutron scattering and x-ray diffraction from protein crystals indicate that water density near the surface is increased by ∼10%–15% beyond the bulk density (4), with similar results obtained from molecular dynamics simulations (5). NMR, time-resolved fluorescence, and dielectric relaxation spectroscopy have all been used to probe relaxation of water on subnanosecond timescales, showing an overall retardation of the rotational relaxation dynamics of water molecules near protein surfaces (6–8). Similarly, the ability of salt ions to either disrupt or enhance hydrogen bonding networks is well established (9,10). Salt ions are categorized as either water-structure makers (kosmotropic) or breakers (chaotropic). The efficacy of specific salt ions at enhancing or disrupting local water structure is similar in many different systems. This rank ordering of salt ions was established originally by Hofmeister's studies of salt-specific effects on protein precipitation (11). However, just as the case of water at interfaces itself, no universally accepted model has been put forth to explain the mechanisms mediating the salt-specific effects of the Hofmeister series.

We investigated whether addition of either chaotropic or kosmotropic salt ions at concentrations up to 1 M would alter lysozyme hydration or the hydrodynamic interaction among the lysozyme molecules. Lysozyme is a small globular protein frequently used in studies of protein hydration (6–8) and protein diffusion (12,13). Although salt-specific effects on direct protein-protein interactions have been studied repeatedly (12–14), much less is known about salt-specific effects on hydrodynamic interactions and protein hydration. We used five different salts (MgCl₂, CsCl, NaCl, NaI, and NaHPO₄) to investigate ion-specific effects on hydration or hydrodynamic interactions. These salts are composed of ions varying from strongly kosmotropic (PO₄³⁻, Mg²⁺) to strongly chaotropic (Cs⁻, I⁻), contained at least one negative and positive ion among either chaotropic or kosmotropic salts and allowed us to keep either the co-ion (Na⁺) or counterion (Cl⁻) to the positively charged lysozyme molecule constant. The overall goal was to gain insights into the effects of chaotropic or kosmotropic ions on the hydration layer around lysozyme, and on solvent-mediated hydrodynamic interactions among multiple lysozyme molecules. Both questions can be addressed simultaneously by measuring static and dynamic light scattering from lysozyme in salt-water solutions.

Materials and Methods

Chemicals

Dialyzed, 2× recrystallized and lyophilized lysozyme stock (catalog No. 2933; Worthington Biochemicals, Lakewood, NJ) was used for all experiments. We have shown previously that Worthington stock material was least likely to be contaminated by preexisting submicron lysozyme clusters that interfere with light scattering and/or nucleation studies (15). All other chemicals were obtained from Fisher Scientific (Rockford, IL) and were reagent grade or better.

Preparation of lysozyme solutions

Lyophilized lysozyme was dissolved directly into 25 mM sodium acetate/ acetic acid (NaAc) buffer at pH = 4.5. Stock solutions for MgCl₂, NaCl, NaH₂PO₄, and CsCl were prepared by dissolving each into the same 25 mM NaAc buffer at pH = 4.5 at a final salt concentration of 2 M. To avoid complex formation, NaI stock solutions had to be prepared fresh on the day of the experiment and the highest stock concentration used was 0.2 M. The pH of all stock solutions was re-adjusted after the addition of salt, if necessary. Lysozyme solutions for light scattering measurements were prepared by 1:1 mixing of lysozyme/buffer with salt/buffer stock solutions, each at twice their final concentrations. Before mixing, lysozyme solutions were filtered through 20 nm pore size Anotop syringe filters. Salt solutions were filtered through 220 nm syringe filters. At the higher salt concentrations (≥600 mM), lysozyme solutions become supersaturated at or below room temperature and can form crystals. Therefore, after mixing, lysozyme solutions were heated to 45°C to reduce the risk of inducing crystal seeds. Solutions were then transferred to glass cuvettes and placed into the thermostated holder of the light scattering unit. Actual lysozyme concentrations of solutions were determined from ultraviolet absorption measured at λ = 280 nm using α₂₈₀ = 2.64 mL/(mg cm) (16).

Static and dynamic light scattering measurements

Both static (SLS) and dynamic (DLS) light scattering measurements were carried out using a Zetasizer Nano S (Malvern Instruments, Worcestershire, UK) with a 3 mW He-Ne laser at λ = 633 nm. The unit collects back-scattered light at an angle of θ = 173°. Sample temperature during measurements was controlled to within ±0.1°C by the built-in Peltier element. Scattering intensities and autocorrelation functions were determined from the average of five correlation functions, with a typical acquisition time of 60 s per correlation function. Scattering intensities for SLS analysis were derived from the average count rate of the samples and were calibrated against toluene, using the Rayleigh ratio of R_T = 13.52 × 10⁻⁶ cm⁻¹ quoted by the manufacturer. For DLS measurements, any correlation functions with polydispersity values >0.08 were rejected. For the three salts (MgCl₂, NaCl, CsCl) for which temperature-dependent viscosity data were available, light scattering measurements were carried out at six different temperatures starting from 40°C down to 15°C in steps of 5°C. After each temperature step, solutions were allowed to equilibrate thermally for 5 min.

Growth of macroscopic crystals

Macroscopic lysozyme crystals were grown using 20 mg/mL lysozyme at pH = 4.5 and MgCl₂, NaCl, and CsCl at concentrations of 0.625 M or 1 M. Solutions were placed in sealed crystallization wells and incubated overnight (16 h) at 4°C.

DLS analysis

The autocorrelation function of scattered light measured in DLS yield the decay rates Γ of local concentration fluctuations for macromolecules in solution (17–19). For data analysis, the experimentally measured (and normalized) autocorrelation function of intensity fluctuations g₂(τ) is first converted into the field autocorrelation function g₁(τ) via the Siegert relation (18,20)

$$g_1\left(\tau \right)=\surd \left[g_2\left(\tau \right)-1\right]\text{.}$$ (1)

For the essentially homogeneous distributions of monomeric protein molecules we are concerned with, the field correlation function g₁(τ) will decay with a single rate

$$\Gamma =D_{\mathrm{m}}{q}^2,$$ (2)

where D_m is the mutual diffusion coefficient and q is the magnitude of the scattering wave vector given by

$$q=\left(4\pi n_0/{\lambda }_0\right)\text{sin}\left(\mathrm{\theta }/2\right)\text{.}$$ (3)

Here, n₀ is the solution's refractive index, λ₀ is the wavelength of the incident laser in air and θ is the in-plane angle at which the scattered light is detected. Because all measurements are carried out at finite protein concentrations (>3–5 mg/mL), both direct (e.g., electrostatic, dipole-dipole, van der Waals, hydrophobic interactions) and solvent-mediated hydrodynamic interactions among the protein molecules will alter the decay rates compared to purely thermally driven concentration fluctuations (13,21,22). These interaction effects on mutual protein diffusivity D_m vary both with salt concentration and salt identity (12,13). At moderate protein concentrations, contributions from interactions to mutual diffusivity increase in direct proportion to the protein concentration. To this approximation, the corresponding mutual diffusion coefficient D_m is related to the single particle diffusivity D₀ via

$$D_{\mathrm{m}}=D_0\left[1+k_{\mathrm{D}}\varphi \right]=D_0\left[1+\left(k_{\mathrm{S}}+k_{\mathrm{H}}\right)\varphi \right],$$ (4)

where k_D = k_S + k_H is the sum of the direct and hydrodynamic protein interactions k_S and k_H, ϕ is the protein volume fraction and D₀ is the single-particle diffusivity of the protein given by the Stokes-Einstein relation

$$D_0=k_{\mathrm{B}}T/\left(6\pi \eta R_{\mathrm{H}}\right)\text{.}$$ (5)

In the Stokes-Einstein formula, k_B is the Boltzmann constant, T the absolute temperature, η = η (Cs,T) the (salt- and temperature-dependent) solution viscosity, and R_H is the hydrodynamic protein radius. Measuring the protein dependence of the mutual diffusion coefficient D_m, while simultaneously accounting for the contributions from direct protein interactions k_S and changes in solution viscosity η (Cs,T), we can derive values for both the hydrodynamic radius R_H and the hydrodynamic interaction parameter k_H of the protein. Values for the direct protein interaction parameter k_S can be obtained independently from measurements of the static light scattering intensity versus protein and salt concentration.

SLS analysis

SLS measures the Rayleigh ratio R_θ, i.e., the excess scattering due to protein concentration fluctuations per unit volume, at a given observation angle θ, and normalized by the incident intensity. In practice, R_θ is obtained by comparison against a standard of known scattering cross section (in our case, toluene):

$$R_{\theta }=\left[\left(I_{\text{tot}}-I_{\text{sol}}\right)/I_{\text{tol}}\right]{\left[n/n_{\text{tol}}\right]}^2{R}_{\theta ,\text{tol}},$$ (6)

where I_tot, I_sol, and I_tol are the measured scattering intensity of the protein solution, the salt/buffer background and of the toluene standard, respectively. R_θ,tol is the Rayleigh ratio for toluene at λ = 633 nm and the ratio n/n_tol accounts for the difference in scattering volume imaged onto the detector due to the refractive index differences between the aqueous solvent and toluene. For our setup, the manufacturer quotes a Rayleigh ratio of R_tol = 13.52 × 10⁻⁶ cm⁻¹. For interacting particles, this normalized Rayleigh ratio R_θ is related to the properties of the protein solution via

$$K{C}_{\mathrm{p}}/R_{\mathrm{\theta }}=M^{-1}\left[1+k_{\mathrm{s}}\varphi \right],$$ (7)

where M is the molecular weight of the protein, C_p is the protein concentration (in mg/mL), k_s is the direct interaction parameter, and ϕ = ν C_p is the protein volume fraction. The constant K in Eq. 7 is given by

$$K=\left(2{\pi }^2{n}_0^2/N_{\mathrm{A}}{\lambda }_0^4\right){\left(d{n}_0/d{C}_{\mathrm{p}}\right)}^2,$$ (8)

where n₀ is the refractive index of the solvent, N_A Avogadro's number, λ₀ the wavelength of incident light, and (dn/dC_p)_λ = 0.185 is the refractive index increment with lysozyme concentration at λ = 633 nm (23). For our setup, the inverse scattering wavenumber q⁻¹ ≈ 38 nm and the hydrodynamic radius of lysozyme is R_H = 1.9 nm. Because R_H q ≪ 1, lysozyme is a Rayleigh scatterer thereby eliminating the need for scattering intensity measurements at multiple angles θ. The molecular weight of lysozyme obtained from Eq. 7 using the above calibration constants was 14.3 ± 0.5 kD which remains within 4% of the formula weight of 14.3 kD for lysozyme (24). Multiplying with 1/2 ν/M converts the direct interaction parameter k_s into the commonly quoted second virial coefficient B₂₂. For lysozyme, ν = 0.703 mL/g.

Results

The overall goal of this study were twofold: to ascertain whether strong chaotropic or kosmotropic ions alter the extent of hydration around individual lysozyme molecules; and to determine whether and how chaotropic or kosmotropic ions selectively alter the water-mediated hydrodynamic interactions among lysozyme molecules. Using measurements of lysozyme diffusion, we tracked changes to the hydrodynamic radius of lysozyme and to its hydrodynamic interactions in the presence of various chaotropic or kosmotropic salt ions.

Salt-specific changes to water viscosity

The selection of salts used for this study was driven by several considerations. First, we used salts for which reliable viscosity data versus salt concentration and, preferentially, versus solution temperature were available. These data are critical both for careful determinations of the hydrodynamic radius of lysozyme (Eq. 5) and for quantifying the chaotropic/kosmotropic character of the ions that make up the salts. We chose the following five salts for our study: MgCl₂, NaCl, CsCl, NaH₂PO₄, and NaI. This way we either kept the anion (Cl⁻) or cation (Na⁺) of the salts constant, while selecting corresponding cations/anions ranging from strong kosmotropic to strong chaotropic (see Table 2). Na⁺ and Cl⁻ themselves are weakly kosmotropic and chaotropic, respectively. Published values for salt-induced changes to the viscosity of water at 25°C for each salt are summarized in Fig. 1. Because experimental data points are sparse, we used Kaminsky's extension to the empirical Jones-Dole equation (25),

$$\eta \left(C_{\mathrm{s}}\right)={\eta }_0\left(1+K_1\surd C_{\mathrm{s}}+K_2{C}_{\mathrm{s}}+K_3{C}_{\mathrm{s}}^2\right)\text{,}$$ (9)

to derive viscosity values for the specific salt concentrations used in our experiments. Here η₀(T) is the water viscosity at a given solution temperature and K₁ through K₃ are empirical fitting coefficients. The square-root coefficient K₁ accounts for the effects of salt screening, and is negligible expect at very low salt concentrations. The linear K₂-term, when measured for multiple combinations of ions, is equivalent to the Jones-Dole B coefficient that quantifies whether water viscosity increases (kosmotropic ion) or decreases (chaotropic ion) with ion concentration.

Table 2.

Jones-Dole viscosity B coefficients for the salt ions in this study

Ion	Jones-Dole B-coefficient
PO43−	0.590
Mg2+	0.385
Na+	0.086
Cl−	−0.007
Cs+	−0.045
I−	−0.068

Positive B coefficients indicate kosmotropic and negative coefficients chaotropic ions. Data adapted from Table 1 in Collins (39).

Figure 1.

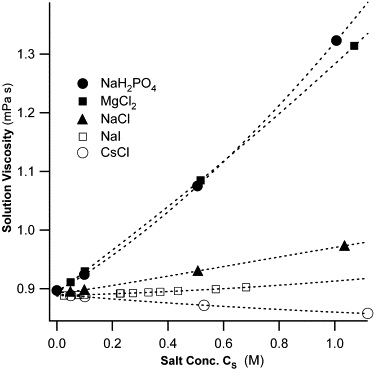
Salt-induced changes in water viscosity. Plot of the viscosity of salt/water solutions at T = 25°C as function of dissolved salt concentration. The slope of the initial increase (NaH₂PO₄, MgCl₂, NaCl) or decrease (NaI, CsCl) is indicative of the predominant kosmotropic (solid symbols) or chaotropic (open symbols) character of the cation/anion combination for a given salt. Symbols represent measured viscosity values for NaH₂PO₄, MgCl₂, NaCl, NaI, and CsCl (42), whereas the dotted lines represent fits through the viscosity data using the Kaminsky equation (25). Extrapolated viscosity values were used for all salt concentrations for which measured viscosities were unavailable. Fitting parameters for all solution temperatures are summarized in Table 1.

The resulting fits of Eq. 9 through the experimental viscosity data for T = 25°C are displayed as dashed curves in Fig. 1. Fitting coefficients for each salt, and at all temperatures for which data were available, are summarized in Table 1. The Jones-Dole B coefficients for the salt ions in this study are quoted in Table 2.

Table 1.

Summary of fitting parameters for water-salt viscosities using the Kaminsky equation

Salt	Temperature (°C)	K1 [mM]−1/2 (× 10−4)	K2 [mM]−1 (× 10−5)	K3 [mM]−2 (× 10−8)
NaCl	15	−6.20	9.22	−0.27
	20	−8.47	10.96	−0.563
	25	−7.11	11.39	−0.651
	30	−3.54	10.60	−0.266
	35	−5.49	11.89	−0.549
MgCl2	15	8.82	34.02	6.66
	20	8.80	33.96	6.22
	25	8.87	35.34	6.09
	30	7.29	36.46	5.64
	35	9.07	36.13	5.91
CsCl	15	−2.11	−7.33	1.96
	20	−12.72	−1.14	−0.028
	25	3.56	−6.10	1.73
	30	8.49	−7.05	2.36
	35	7.91	−5.77	2.15
NaH2PO4	25	−5.36	34.17	14.62
NaI	25	1.27	0.86	1.57

Measuring protein hydration and hydrodynamic protein interactions

Combining SLS and DLS, we determined salt-specific effects on lysozyme hydration and on the mutual hydrodynamic interactions among the lysozyme molecules. As detailed in Materials and Methods, the diffusive behavior of macromolecules in solution is altered by the presence of direct and solvent mediated hydrodynamic interactions. These interaction effects on mutual protein diffusivities D_m are significant and depend both on salt concentration and salt identity (12,13,21). For moderate protein concentrations, direct and hydrodynamic interaction increase linearly with protein concentration (Eq. 4). Depending on the dominance of net attractive or repulsive interactions, the protein's mutual diffusivity D_m can be either higher (net repulsion) or lower (net attraction) than the corresponding single-particle diffusivity (Eq. 5). By measuring the protein dependence of the mutual diffusion coefficient D_m(C_Lys), while accounting for the contributions from direct protein interactions k_S and changes in solution viscosity η(C_s,T), we can derive values for both the single-molecule hydrodynamic radius R_H and the mutual hydrodynamic interaction parameter k_H. Values for the direct protein interaction parameter k_S are determined independently from the protein-dependence of the static light scattering intensity (Eq. 7).

Direct and hydrodynamic interactions of lysozyme in solution

The top row in Fig. 2 summarizes the changes in SLS with lysozyme concentration C_Lys at T = 25°C, for a series of increasing salt concentrations and for three (MgCl₂, NaCl, and CsCl) of the five salts considered in our study. Scattering intensities are displayed as normalized Debye ratios KC_Lys/R_θ (Eq. 7). Debye plots provide a particularly straightforward interpretation of SLS data: the y-intercept of the KC_Lys/R_θ versus C_Lys data is the inverse of the protein's molecular weight M, whereas the sign of their slope indicates whether proteins experience net repulsive (positive slope) or attractive (negative slope) interactions at the given solution conditions (14,26). The change from positive to negative slopes with increasing salt concentration results from the transition of charge-mediated protein-protein repulsion at low salt concentration to attraction due to short-range protein interactions (van der Waals, hydrophobic, etc.). Several previous studies have matched the transition from repulsive to attractive interactions using colloidal DLVO theory (12,13,22). Although successful for any given salt, DLVO theory can not account for the ion-specific differences in protein interactions at identical ionic strengths (i.e. effective charge screening).

Figure 2.

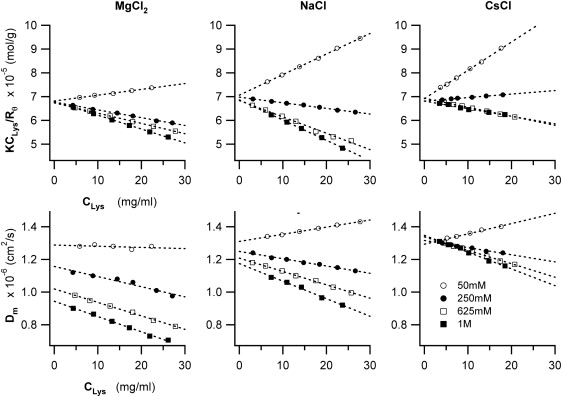
Salt-specific effects on Debye ratios KC_Lys/R and mutual diffusivities D_m of lysozyme. Plot of (top row) the Debye ratios KC_Lys/R and (bottom row) mutual diffusivities D_m of lysozyme as function of lysozyme concentration C_Lys, in the presence of MgCl₂, NaCl, or CsCl, at increasing concentrations (○, 50 mM; •, 250 mM; □, 625 mM; and ■, 1 M). The y axis intercepts of the Debye plots yields the inverse of the molecular weight M of lysozyme, whereas the sign of the slope indicates whether interactions among the lysozyme molecules are either net repulsive (positive slope) or attractive (negative slope). For the plots of mutual diffusivities, the y axis intercepts yield the free particle diffusivity D₀ at the given solution viscosity, whereas the slope indicates the magnitude and sign of the combined effects of direct and hydrodynamic interactions on mutual lysozyme diffusion. All measurements shown were taken at T = 25°C.

The bottom row of Fig. 2 displays the changes in the mutual diffusion constant D_m of lysozyme under the same conditions used for the SLS measurements in the top row. For all DLS data in Fig. 2 the measured size polydispersity δ was <0.08, indicating that changes in D_m are not contaminated by aggregate formation in solution. Any measurements at high salt concentrations suggesting potential aggregate/cluster formation (high polydispersity, temporal drifts in scattering intensity, or D_m) were excluded from the analysis. The presence of positive slopes in both DLS and SLS data, together with the strictly linear behavior of both data sets with protein concentration are further indicators that potential contributions due to protein aggregation are negligible (27).

The plots of mutual diffusivity D_m versus lysozyme concentration are very similar in appearance to the Debye plots in the top row. Mutual lysozyme diffusivities D_m vary linearly with lysozyme concentration, with the slopes changing from positive to negative values as salt concentration increases. As indicated in Eq. 4, the slopes of D_m versus C_Lys results from the superposition of both direct and hydrodynamic interactions effects on protein diffusion. Subtracting the k_s values obtained with SLS, therefore, we determined the magnitude of the hydrodynamic interaction parameter k_H for solution-mediated interactions among the lysozyme molecules. Using this approach enabled us to determine whether the presence of chaotropic versus kosmotropic ions—similar to the well-established effects on direct protein interactions—can induce salt-specific changes in either protein hydration or in the solution-mediated hydrodynamic protein interactions.

Effects of chaotropic versus kosmotropic ions on lysozyme hydration

Based on the significant influence of salt ions on water structure, it seems natural to wonder whether chaotropic or kosmotropic ions can alter the extent of the ordered water layer around proteins. Using DLS, we determined whether different salts lead to discernible swelling or contraction in lysozyme's hydration layer. We can obtain the single-particle diffusivity D₀ of lysozyme by extrapolating the mutual diffusivity D_m to its y axis intercept at C_Lys = 0. Using the Stokes-Einstein relation (see Eq. 5), the radius of hydrated lysozyme can be obtained from the single-particle diffusivity D₀ (Fig. 2) and values of the solution viscosity η(C_s,T). Fig. 3 A displays the resulting values for lysozyme's hydrodynamic radius for each of the five salts. These data are notable in several ways. First of all, when accounting for salt- and temperature-dependent solution viscosity and for protein interaction effects on diffusivity, the hydration radii of lysozyme under any conditions are within ±0.25 Å of one another. These differences are well below the thickness for a single monolayer of water extending ∼2.6–2.8 Å (28). Hence, our experimental resolution permits us to resolve changes down to 1/10 the thickness of a single water layer.

Figure 3.

Effects of chaotropic and kosmotropic salt ions on lysozyme hydration. (A) Mean hydrodynamic radius R_H of lysozyme in the presence of various salts with predominately chaotropic or kosmotropic salt ions. R_H values were derived from the measured free particle diffusivity D₀ (see Fig. 1) and corrected for the salt- and temperature-dependent changes in water viscosity (see Fig. 2 and Table 1). R_H values for different concentrations of the same salt were averaged because they displayed no discernible systematic variations (B). For comparison, the thickness of a monolayer of water is ∼0.26–0.28 nm. (B) Hydrodynamic radius R_H of lysozyme in the presence of MgCl₂ at different solution temperatures T, and for MgCl₂ concentrations ranging from 50 mM to 1 M. The lack of any systematic variation with temperature or salt concentration is representative for our measurements with any salts, and at all salt concentrations and solution temperatures.

Equally remarkable, while the effects of chaotropic versus kosmotropic salt ions on the bulk structure of water are significant, there is no discernible swelling or disruption of the lysozyme hydration layer due to the presence of either kosmotropic or chaotropic ions. This remains true up to salt concentrations of 1 M and over the entire range of temperatures in our experiments. This is shown in Fig. 3 B for the case of MgCl₂, which is representative for the behavior of all the other salts. These results imply that the overall extent of lysozyme's hydration layer is very stable. The question remained whether the net charge of the protein itself might determine whether chaotropic/kosmotropic ions can disrupt the protein hydration layer. It has been shown before that the Hofmeister series for the solubility of lysozyme was inverted (29), presumably due to the net lysozyme charge of +10 at pH = 4.5 (30,31). According to Debye-Hückel theory, the concentration of cations near the positively protein surface will be reduced from their bulk concentrations (32). To investigate this possibility, we included NaH₂PO₄ and NaI in our measurements, salts with either a highly chaotropic (I⁻) or kosmotropic (PO₄³⁻) co-ion. Yet, neither of these two negative ions altered the hydrodynamic radius of lysozyme (Fig. 3 A).

It is well known that water becomes progressively disordered with increasing temperature (2). We therefore determined whether there were temperature-dependent variations in the hydrodynamic radius of lysozyme in the presence of chaotropic versus kosmotropic ions. Fig. 3 B shows the results of a typical measurement with MgCl₂ over the temperature range of 15–35°C. The range of temperature values was limited due to problems with bubble formation (high T) and the onset of phase separation (low T). Within these limitations there are, again, no indications for any salt-specific effects on protein hydration with solution temperature. The lack of any discernible effects on the hydrodynamic radius of lysozyme with salt concentration or salt type indicates that there is also no salt-induced swelling of the protein itself. In fact, all the observed changes to D₀ (see C_Lys = 0 intercepts in Fig. 2 B) were fully accounted for by the variation of the bulk viscosity η(C_s,T) with salt type, salt concentration, and solution temperature.

Salt-specific effects on direct and hydrodynamic protein interactions

To convert the slopes of our static and dynamic light scattering data (Fig. 2, A and B) into direct and hydrodynamic interaction parameters (see Eqs. 4 and 7), we use the value ν = 0.703 mL/g for the specific volume of lysozyme (16). Fig. 4 displays the resulting values for the direct and hydrodynamic interaction parameters k_S and k_H, as function of solution temperature and salt concentration. The systematic variations become more apparent when displayed against solution temperature (shown here for MgCl₂, NaCl, and CsCl, and for increasing salt concentrations). At the lowest salt concentrations (50 mM), the direct protein interactions parameter k_S remains positive at all temperatures. For the same salt concentration, repulsive protein interactions are more prominent in the 1:1 salt solutions (NaCl, CsCl) than the 2:1 MgCl₂ solutions. Both observations are consistent with the Debye theory of diffusive charge screening. At low salt concentrations, protein interactions will be dominated by protein-protein charge repulsion, with the 2:1 salt MgCl₂ more effective than NaCl and CsCl in screening out this charge repulsion (see e.g., Hunter (32)).

Figure 4.

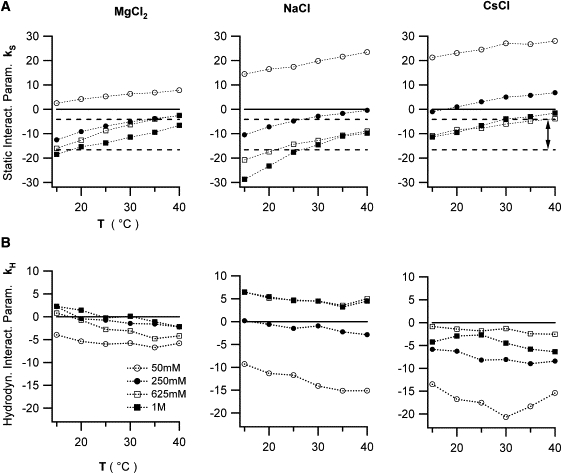
Dependence of direct and hydrodynamic interaction parameters on salt type, salt concentration, and solution temperature. Plot of the net strength of (top row) direct lysozyme interactions k_S and (bottom row) corresponding hydrodynamic interactions k_H = k_D − k_S as a function of solution temperature T, and for four different salt concentration C_s. Data are shown for (left column) MgCl₂, (middle column) NaCl, and (right column) CsCl. k_S and k_D are derived from the slopes of the SLS and DLS data, respectively. The band of negative k_s values indicated by the two horizontal dashed lines in the top row is considered favorable for protein crystal growth (26).

With increasing salt concentration charge repulsion progressively diminished and net protein repulsion (positive k_S) turns into net attraction (negative k_S). Although the salt-induced decrease in net repulsion, at least qualitatively, follows the logic expected for salt screening of protein charges, salt-specific effects rapidly emerge even at moderate salt concentrations. In particular, NaCl ≥250 mM is significantly more effective in promoting attractive lysozyme interactions than either MgCl₂ or CsCl. Several recent theoretical studies have incorporated specific ion-protein interactions (in particular dispersion forces) to account for such salt-specific effects (33–35).

The dotted lines in Fig. 4 A indicate the range of interaction parameters k_S (or, equivalently, second virial coefficients B₂₂) considered favorable for protein crystal growth (26). As shown in Fig. 5, we were able to obtain lysozyme crystals with all three salts when incubating solutions at low temperature and at sufficiently high salt concentrations to reach the “crystallization band” in Fig. 4 A. Lysozyme solutions incubated with 1 M NaCl yielded larger numbers of smaller crystals, consistent with the enhanced attraction among lysozyme monomers and, therefore, the increased supersaturation of the solutions under otherwise identical growth conditions.

Figure 5.

Protein crystals grown with lysozyme in the presence of chaotropic versus kosmotropic salts. Microscope images of tetragonal lysozyme crystals grown with (left column) 625 mM or (right column) 1 M of (top row) MgCl₂, (middle row) NaCl, or (bottom row) CsCl. All solutions contained 20 mg/mL of lysozyme in 25 mM NaAc buffer (pH = 4.5) and were incubated overnight (16 h) at 4°C. The lysozyme crystals grown at [NaCl] = 1 M show a mixture of tetragonal crystals and (sea urchin like) spheres of needle crystals. The latter are most likely orthorhombic crystals.

Discussion

Lysozyme's hydrodynamic radius of (1.89 ± 0.025) nm remained unaltered by the presence of salts containing either strong chaotropic or kosmotropic ions. This remained true up to salt concentrations of 1 M (NaH₂PO₄, MgCl₂, NaCl, CsCl) or up to the onset of lysozyme precipitation (NaI). Previous measurements had noted the lack of changes in lysozyme hydration in the presence of NaCl up to 0.4 M or sodium acetate up to 2.5 M (13) and MgCl₂ up to 1 M (12). Our measurements extend these observations to a series of salts with either predominately chaotropic or kosmotropic character and put a much tighter limit (0.25 Å or <1/10th of a monolayer of water) on residual changes that might evade detection. The data also indicate that it did not matter whether the chaotropic or kosmotropic ion carried the same (Mg²⁺, Cs⁺, Na⁺) or opposite charge (PO₄³⁻, Cl⁻, I⁻) as the net charge of lysozyme. Hence, the elevation (negative ions) or depression (positive ions) of local salt concentrations in the double layer near the positively charge lysozyme surface did not alter these results. There are indications that several of the ions in our study can adsorb onto lysozyme's surface (36). Yet again, we find no evidence that specific ion adsorption alters overall protein hydration. Variations in solution temperature did not produce any discernible changes in lysozyme hydration in the presence of various salts, either.

The lack of any discernible changes in lysozyme hydration by either chaotropic or kosmotropic salts seem surprising given the pronounced salt-specific effects on viscous dissipation in bulk water (see Fig. 1). Apparently, neither chaotropic nor kosmotropic ions are able to alter the extent of the hydration layer around lysozyme. This could imply that the protein surface residues and surface structure are much more effective at ordering water than either chaotropic or kosmotropic ions. Alternatively, ion-specific effects onto surface water might only change the fast relaxation dynamics of water occurring at or below picoseconds, much faster than the microsecond relaxation times probed in translational diffusion of lysozyme. This later viewpoint seems somewhat difficult to reconcile with the obvious salt-specific effects on bulk water viscosity that do need to be accounted for. Hence, specific effects on water relaxation even at a much faster timescale should translate into changes in viscosity near the protein's surface (37).

We prefer the interpretation that neither chaotropic nor kosmotropic ions will significantly perturb the structure and dynamics of surface water, but that ion-specific effects are dominated by direct interactions with the protein (38). This is supported by the clear ion-specific effects on direct protein-protein interactions obtained with static light scattering (Fig. 2 A). However even there, the ordering of specific ion effects on attractive lysozyme interactions (Na⁺ > Mg²⁺ > Cs⁺) is at odds with considerations of either charge screening (MgCl₂ > NaCl, CsCl) or the typical order of these cations within the Hofmeister series (Mg²⁺ > Na⁺ > Cs⁺) (39). It is hard to imagine that the twofold higher bulk concentrations of (weakly) chaotropic Cl⁻ ions in MgCl₂ versus NaCl solutions should be able to compensate for the strong kosmotropic character of Mg²⁺ compared to the moderately kosmotropic Na⁺ ions. This implies that there are other ion-specific effects on protein interactions beyond the scope of the Hofmeister series.

As with protein hydration, there are no indications that hydrodynamic protein interactions are directly altered by ion-specific effects. However, hydrodynamic interactions are strongly anticorrelated with direct protein interactions thereby coupling them indirectly to salt-specific effects on direct protein interactions. With increasing salt concentration, hydrodynamic interactions transition from net attraction to repulsion whereas direct protein interactions move in the opposite direction (Fig. 4). We have noted previously that trend in lysozyme solutions at fixed temperature for both NaCl and sodium acetate (13). This anticorrelation is not dependent on any specific salt ion and persists as a function of temperature. Experiments on hydrodynamic interactions with pairs of colloidal spheres can provide guidance in the interpretation of such coupling (40,41). Specifically, direct attractive interactions are likely to bias diffusion in favor of colinear motion toward one another. Hydrodynamic momentum transfer will oppose such motion, resulting in enhanced hydrodynamic repulsion. Similarly, with proteins experiencing net repulsion, the direct interaction will tend to push other proteins out of the way, thereby decreasing solution-mediated momentum transfer when compared to noninteracting particles. Hence, enhanced attraction or repulsion among the lysozyme molecules would be accompanied by corresponding increases or decreases in hydrodynamic interactions, as observed in our experiments.