Stiffness Tomography by Atomic Force Microscopy

Abstract

The atomic force microscope is a convenient tool to probe living samples at the nanometric scale. Among its numerous capabilities, the instrument can be operated as a nano-indenter to gather information about the mechanical properties of the sample. In this operating mode, the deformation of the cantilever is displayed as a function of the indentation depth of the tip into the sample. Fitting this curve with different theoretical models permits us to estimate the Young's modulus of the sample at the indentation spot. We describe what to our knowledge is a new technique to process these curves to distinguish structures of different stiffness buried into the bulk of the sample. The working principle of this new imaging technique has been verified by finite element models and successfully applied to living cells.

Introduction

The atomic force microscope (AFM) was designed primarily to provide high resolution images of the surface of nonconductive samples, and consists of a very sharp tip mounted at the end of a cantilever that scans the surface of the sample. The minute deflections of the cantilever during the scanning procedure are recorded by a computer, which reconstructs the 3D topography of the scanned area on its screen. Soon after its invention, the AFM was also used to measure the mechanical properties of a sample with a nanometric resolution (1–4). These measurements are accomplished by using the AFM as a nano-indenter and by monitoring the cantilever deflection during the process. The curve displaying the force applied as a function of the tip indentation is referred to as a force-indentation (FI) curve. The shape of this curve permits estimating Young's modulus, in that some parameters such as the shape of the tip and the Poisson's ratio of the sample are known (Fig. 1). See Kasas and Dietler (5) for a review on the use of AFM to probe nanomechanical properties.

Figure 1.

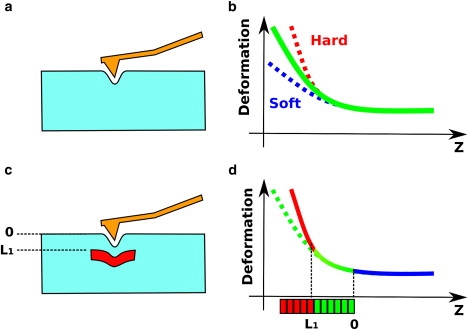
FD curves are recorded by indenting (pushing) the tip of the AFM into the sample (a) and by plotting the deformation of the cantilever as a function of the height (b). A hard sample produces a steeper curve (b, dashed red line) than a softer one (b, dashed blue line). In the case where the sample contains harder inclusions (c, red rectangle) located at the L1 level, the FD curve follows the same path as in a (d, green line) initially, but starts to adopt a steeper path just before reaching the L1 level (d, red line). The dashed green line represents the path the curve should follow in the absence of inclusions. By dividing the curve in small segments and by analyzing their individual slope one can detect the presence of the inclusion (d, red and green horizontal bar).

FI curves have been used to examine mechanical properties of bone tissue (1), cartilage (6), platelets (7), synaptic vesicles (8), and different types of living cells (2,9,10). In all these studies, cells were considered as homogeneous objects and the FI curves were fitted to the so-called Hertz model that assumes a homogeneous isotropic infinite sample.

In this study, we consider the indented substrate as a composite structure, which contains “inclusions” that change the FI curve shape in a deterministic way. In a simplified view, if we consider an infinite homogeneous and soft sample, a FI curve recorded on it will have a shape that can be fitted well with the Hertz function (Fig. 1 b). However, if a harder material is included in the bulk of this sample, the recorded FI curve will deviate from the curve recorded on the sample without inclusion at a distance that reflects the depth of the inclusion (Fig. 1, c and d). The validity of this concept has been shown recently on living cells (11). To obtain information about the mechanical characteristics and the depth of the inclusion we systematically divide the FI curve in segments and apply the Hertz model on each of them. This procedure shows stiffness differences along the indentation path. This method, when applied to a force volume scan, i.e., an image in which every pixel consists in a FI curve, gives information about the surface topography and the interior mechanical properties of the sample. We therefore decided to call this imaging mode a “stiffness tomography” of the sample. The postprocessing of the force volume scans was done with software that was used for a previous study on the mechanical properties of the cell membrane (12).

Materials and Methods

Cell culture and AFM experiments

293T cells were grown in a humidified incubator at 37°C and 5% CO₂ in full medium of D-MEM (Invitrogen 41966, Paisley, UK) with 10% fetal calf serum and 1% penicillin. A 10-μM solution of Cytochalasin B was prepared and introduced into the incubation-chamber using a homemade setup to yield a final concentration of 5 μM.

Hippocampal neurones derived from rat embryos were prepared and cultured as described previously (13). The cells were plated in petri dishes at a numerical density of 2500/cm² and were maintained in K5 medium [128 mM NaCl, 5 mM KCl, 2.7 mM CaCl₂, 1 mM MgCl₂, 10 mM glucose, 20 mM HEPES (pH 7.4)] at ambient temperature. Each experiment was initiated 15 min after inserting the petri dish into the AFM. This delay was required for the thermal equilibration of the cantilever.

All experiments were carried out at ambient temperature using a commercial stand-alone AFM (Bioscope; Veeco Instruments, Santa Barbara, CA) that was combined with an inverted optical microscope (Axiovert 200; Zeiss, Jena, Germany). We used standard triangular silicon nitride cantilevers from Veeco (DNP) with a nominal spring constant of 0.06 N/m and a nominal tip radius of curvature of 20 nm. The cantilever spring constant was measured by using the Nanoscope 4.43 software calibration tool. The AFM was operated in the force-volume mode at a force distance curve acquisition frequency of 7 Hz.

Data postprocessing

The data were postprocessed using our software written in MATLAB (The MathWorks, Natick, MA), running under a GNU/Linux environment. In the first step, we compute the FI curve: a reference force distance (FD) curve recorded on a stiff substrate (the petri dish) is subtracted from a FD curve recorded on the soft sample. The obtained curve referred to as a FI curve is than sliced to equal segments of a predefined depth. Every segment is than fitted with the Hertz model to calculate its Young modulus. Finally, the Young's moduli segments are used to build the 3D matrix that constitute the stiffness tomography data set. A more detailed description of the postprocessing is available in the Supporting Material.

Results

Verification of the concept by finite elements simulation

To verify the concept of stiffness tomography, we modeled a virtual AFM and a sample containing various inclusions. For this purpose we used a commercially available finite elements program (ANSYS 9.0, Canonsburg, PA). The simulated sample was made of a homogeneous material with stiff inclusions (Fig. 2, a and c). The dots above the sample indicate the positions where the indentation was simulated. The Young's modulus of the red inclusions was set three times higher than the modulus of the bulk (in blue) of the sample. The FI curves obtained during the simulated indentation were analyzed by our method using homemade software.

Figure 2.

Simulation of the indentation process by using the finite elements method. The sample contains inclusions (a) colored in red that have a Young's modulus tree times higher than the bulk of the sample colored in blue. The AFM tip and the spots where indentation was simulated are also represented in blue. During the indentation process the sample deforms as depicted in b. The displacement magnitude is displayed in false colors according to the color bar. (c) The stiffness tomography analysis results. The false colors represent the stiffness in arbitrary units according to the color bar. (d and f) Shows similar simulation using three times stiffer and three times softer platforms with their resulting stiffness tomography in e and g, respectively. The same data scale is used between e and g. One can notice that the stiffness difference appear less contrasted in the case of soft platforms. Arrows in g points to stiffness differences induced by the presence of soft platforms.

The resulting stiffness tomography image for the simulated materials is depicted in Fig. 2, c and e. The y axis has been expanded slightly to show the small rectangles representing the single positions where the stiffness analysis has been carried out. The color of each rectangle corresponds to the Young's modulus calculated by fitting the corresponding FI curve segment with the Hertz model. The stiff red columns (Fig. 2 c) and platforms (Fig. 2 e) that are located under the surface of the sample show clearly on the tomography image. The stiffness tomography of the platforms shows stiffness shadow under the stiff material. To verify if the method detects soft inclusions, we simulated platforms with lower Young's modulus than the surrounding material (Fig. 2 f). The resulting stiffness tomography image shown in Fig. 2 g also shows the softer platforms (Fig. 2, black arrows). The data scale was set to be equal to the previous simulations. These simulations show that the FI curves fragmentation method efficiently detects inclusions embedded into the sample.

Stiffness tomography shows material inside living cells

In a next step we applied the stiffness tomography imaging technique to living cells by using the force volume mode of the AFM. In this mode, the microscope recorded successive FD curves on a scanning area of 2 × 2 μm containing 32 × 32 (1024) FD curves. Each FD curve was sampled with 256 points. The AFM files were always processed with the same home made software as above and each FI curves was divided in segments of 10-nm depth.

Fig. 3, a–d, depicts stiffness tomography slices recorded on four different living neurons. The red regions indicate the presence of hard structures buried into the cytoplasm of the cell. We believe these structures correspond to the cortical actin cytoskeleton that is known to lie under the cellular membrane. Moreover, softer materials can be seen under stiff structures. A possible interpretation is that the hard, superficial material slips or breaks as the tip penetrates the cell.

Figure 3.

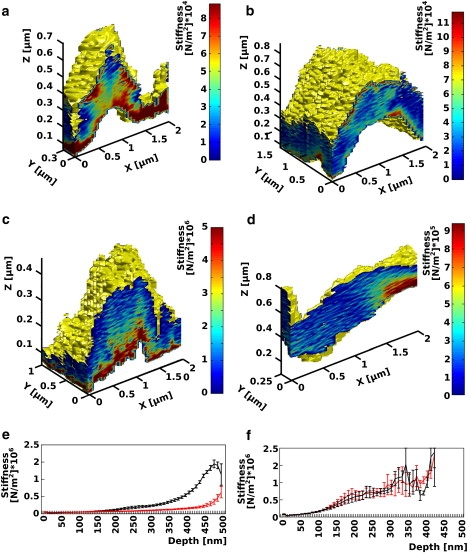
(a–d) Stiffness tomography images obtained on living neurons. The stiffness, calculated according to the Hertz model, is coded in false colors. Due to the lack of a more accurate model, only color differences are relevant. One can notice the presence of “red” harder inclusions underneath the membrane. The yellow color of the surface of the cells is arbitrary and do not correspond to any stiffness value. The graphs e and f represent the average stiffness of fibroblast as a function of the depth underneath the cell membrane. (e, black curve) Stiffness before the injection of cytochalasin. (e, red curve) Corresponds to the stiffness after the injection. One can notice that in average the cortical part of the cell located under 180 nm became softer after the cytochalasin injection (p < 0.05, two-tailed t-test). (f) The same experiment carried out by injecting the imaging buffer instead of cytochalasin.

Stiffness tomography shows actin cytoskeleton depolymerization

To confirm the hypothesis that the stiff structures corresponds to the cortical actin cytoskeleton, we compared the stiffness of living human fibroblasts (293T cells) before and after the injection of cytochalasin B, a chemical that is known to depolymerize the actin cytoskeleton. To monitor the depolymerization process, we calculated the Young's modulus of each segment as a function of its depth under the membrane. The values of all the segments located at the same depth were averaged for all the data set. Fig. 3 e depicts the Young's modulus change of the average cell, as a function of the depth under the membrane, before (Fig. 3, black curve), and after (Fig. 3, red curve) the injection of cytochalasin. The black curve represents the average of four force volume files recorded between 20 and 5 min before the injection of cytochalasin. The red curve represents the average of six force volume files recorded between 30 and 55 min after the injection of cytochalasin. The two curves show the development of a very clear softening starting at a depth of ∼180 nm under the membrane in the cell after the arrival of actin depolymerizing agent (p < 0.05, two-tailed t-test). The control experiment (Fig. 3 f) shows no differences on the stiffness tomography before and after buffer injection (p > 0.05, two-tailed t-test).

Discussion

We developed what to our knowledge is a new imaging mode called stiffness tomography (14) that permits us to image stiffness differences inside a soft sample. The validity of the concept has been successfully tested by finite elements modeling as well as on living cells. The finite element model shows that stiff column-like structures gives higher contrast than soft platforms. In this version, the FI curves segments are fitted with the Hertz model. We are aware that it is only a convenient approximation and at this stage no absolute Young's value can be extracted from the images. The FI curves reflect a highly complex and nonlinear phenomenon and the mathematical model we are using is only an approximation. However, despite this simplistic approach, with the finite elements simulations and the application on living cells, we have shown that stiffness tomography can highlight structures located underneath the surface of the sample, a domain up to now invisible to the AFM.

This method can be applied to other samples such as thin membranes or polymers. Because the method does not require any additional hardware it can be implemented easily on any AFM or indentometer by adding an additional step to the data postprocessing chain.

Supporting Material

Data postprocessing, three figures, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00971-0.