Roles of Boundary Conditions in DNA Simulations: Analysis of Ion Distributions with the Finite-Difference Poisson-Boltzmann Method

Abstract

The wide use of lattice-sum strategies in biomolecular simulations has raised many questions on potential artifacts in these strategies. One interesting question is the artifacts in the counterion distributions of highly charged systems. As one would anticipate, Coulombic interactions under the periodic boundary condition may deviate noticeably from those under the free boundary condition in the highly charged systems, significantly influencing their counterion distributions. On the other hand, the electrostatic screening due to water molecules and mobile ions may effectively damp the possible periodic distortions in Coulombic interactions. Therefore, the magnitude of periodicity-induced artifacts in counterion distributions is not straightforward to dissect without detailed analyses. In this study, we have developed a hybrid explicit counterion/implicit salt representation of mobile ions to address this question. We have chosen a well-studied DNA for easy validation of the minimal hybrid ion representation. Our detailed analysis of continuum ion distributions, explicit ion distributions, radial counterion distribution functions, and sequence-dependent counterion distributions, however, indicates that periodicity artifacts are not apparent at the surface of the tested DNA. Nevertheless, influence of boundary conditions does show up starting at the second solvation shell and becomes apparent at the cell boundary.

Introduction

Molecular dynamics (MD) simulations are widely applied to the studies of chemical and physical properties of biomolecules. Although the simulation techniques are successful in describing the biomolecular systems, many issues remain to be addressed, especially on the approximations introduced for efficient computation of long-range Coulombic interactions. Two major approaches have been developed to approximate long-range Coulombic interactions. The cutoff-based methods (1), in which the Coulombic interactions beyond a predefined cutoff distance are truncated or modified, were widely employed in the early days of MD simulations. Although the cutoff-based methods reduce the computation complexity from quadratic scaling to linear scaling with respect to the atom number, the methods introduce many artifacts in the simulations of liquids (1), solvated ions (2,3), ion pairs (4), and biomolecules (5,6). Indeed, the truncation approximation is possibly obsolete when rigorous treatments of long-range interactions are required. The second group of methods can be loosely termed as the lattice-sum methods, such as the Ewald summation method (7), the particle-particle-particle-mesh method (8), and the particle-mesh Ewald (PME) method (9). In contrast to the cutoff-based methods, the lattice-sum methods permit exact calculation of Coulomb interactions under the periodic boundary condition (PBC). Although their numerical accuracy is in fact limited in simulations (10), stable trajectories of biomolecules are often obtained for systems where cutoff-based methods fail to maintain (6,11). Due to the simulation robustness, the lattice-sum methods are now mainstream tools for biomolecular simulations. However, the PBC approximation may still lead to artifacts in simulations. Indeed PBC artifacts in the calculation of the free energies of ionic hydration were identified more than a decade ago (11). Similar artifacts were also observed in the calculation of potentials of mean forces of ion-ion separation processes (12). Obviously, the PBC artifacts need to be analyzed more quantitatively for the simulation community to employ this general approach with higher confidence.

Historically, the challenge in the PBC artifact analysis lies in the fact that adequate sampling of solvent molecules and counterions is extremely time-consuming. This is especially true for the reference system treated by the free boundary condition (a.k.a., the nonperiodic boundary condition (NPBC)), the sampling of which is an almost unachievable task. Thanks to recent developments, sampling of solvent molecules in such analysis can be replaced by implicit solvation treatment. Thereby, a direct comparison is computationally feasible between the results expected for otherwise identical simulation setups but under different boundary conditions (PBC and NPBC). Along this line, a series of studies were conducted by Hünenberger and co-workers (13–18). These studies resulted in many interesting insights on possible PBC artifacts; for instance, a nonnegligible energetic bias (17), low dielectric permittivity, and other periodicity-induced artifacts (13,14), all of which can be more prominent with the decrease of box sizes and/or with the increase of solute charges. Moreover, based on these analyses, a modified lattice-sum algorithm was proposed to alleviate periodicity-induced artifacts (16).

Despite the successful analyses of the solvation aspect of PBC-induced artifacts, which are noted above, the periodicity-induced effect on the counterion distributions is still not clear (17). Since counterions play an important role in the simulations of biomolecules, especially in highly charged nucleic acids, typical MD simulations require the inclusion of both explicit water molecules and explicit counterions. As one would anticipate, Coulombic interactions under PBC may deviate more noticeably from those under NPBC in highly charged systems; and the use of PBC may significantly influence their counterion distributions. Therefore, analysis of the counterion aspect of PBC-induced artifacts should be of importance as well. In this study, we would like to address this question by comparably mapping the counterion distribution around a double-strand DNA with a canonical sequence with both periodic and nonperiodic boundary conditions.

To achieve an efficient and accurate analysis on the periodicity-induced artifacts on the counterion distribution of the DNA, we designed a unique hybrid representation of the system with an explicit representation of both the solute atoms and the counterions and an implicit representation of solvent and bulk salt. The electrostatic interactions of the hybrid system can be readily modeled within the Poisson-Boltzmann (PB) framework. Under this design, the highly charged solute is neutralized, so that the more efficient linear PB treatment of electrostatics can be utilized with reasonable accuracy. Furthermore, a robust numerical linear PB algorithm (19,20) is used to compute electrostatic interactions at every Monte Carlo sampling step. To enhance explicit counterion sampling, we utilized an advanced Monte Carlo sampling method—a variant Hamiltonian replica exchange method (VHREM) that was designed for systems with both the requirements of energy-barrier-crossing sampling and diffusion sampling (21). Note that our Monte Carlo simulation in the hybrid representation is different from most previous Monte Carlo simulations of explicit ions (22), in which typical electrostatic treatments were based on either straight Coulombic law in the dielectric of 80 or the distance-dependent dielectric.

Methods

Hybrid ion representation

In this study, we developed a minimal hybrid representation of the solvated nucleic acid system for efficient and accurate analysis of the counterion distribution. First, the nucleic acid is represented in the all-atom detail, although all atoms are fixed throughout a simulation trajectory as in previous analyses of counterion distributions, since the focus is on mobile ions in such analyses (22). Second, all solvent molecules are represented as a continuum. Finally, the ions are represented in two different ways:

• 1.The counterions that are needed to neutralize the nucleic acid are explicitly represented and sampled.
• 2.The rest of the ions that are needed to maintain a bulk salt concentration are implicitly represented.

If the solvated nucleic acid is without any ion, the total electrostatic interactions of the system can be modeled with the Poisson's equation in classical electrostatics, given that:

• 1.The charges are located on all atomic centers of the nucleic acid; and
• 2.The dielectric constant is set to be 1 within the nucleic acid and the dielectric constant is set to be 80 outside the nucleic acid.

The solute and solvent interface is usually defined as the solvent-excluded surface or the molecular surface. Thus, we have

$$\nabla \cdot \varepsilon \nabla \varphi =-4\pi {\rho }_0,$$ (1)

where ɛ is the dielectric constant, ϕ is the electrostatic potential, and ρ₀ is the solute charge density.

When explicit counterions are used, they can be treated as part of the solute, i.e., we simply solve the Poisson's equation with both the nucleic acid atoms and all counterions present. However, when the implicit salt ions are used, they are modeled as continuum in a mean-field manner. The implicit ion densities are assumed to follow the Boltzmann distribution. Thus, the Poisson-Boltzmann's equation is used to model the total electrostatic interactions of the solvated system,

$$\nabla \cdot \varepsilon \nabla \varphi =-4\pi {\rho }_0-4\pi \sum _{\mathrm{i}}e{z}_{\mathrm{i}}{c}_{\mathrm{i}}\lambda \text{exp}\left(-e{z}_{\mathrm{i}}\varphi /k_{\mathrm{B}}T\right),$$ (2)

where e is the unit charge, z_i is the valence of ion type i, c_i is the number density of ion type i, λ is the Stern layer masking function, k_B is the Boltzmann constant, and T is the absolute temperature. For a solution with symmetric 1:1 salt, Eq. 2 is usually written as

$$\nabla \cdot \varepsilon \nabla \varphi =-4\pi {\rho }_0+\frac{{\kappa }^2}{C}\lambda \sinh \left(C\varphi \right),$$ (3)

where ${\kappa }^2=\frac{8\pi e^{2}I}{k_{\mathrm{B}}T}$ and $C=\frac{ez}{k_{\mathrm{B}}T}$. Here I represents the ionic strength of the bulk solution and I = z²c. If the electrostatic potential is weak and the ionic strength is low, Eq. 3 can be simplified to a linear form to improve computation efficiency (23):

$$\nabla \cdot \varepsilon \nabla \varphi =-4\pi {\rho }_0+{\kappa }^2\varphi \text{.}$$ (4)

The electrostatic free energy of the nonlinear Poisson-Boltzmann equation can be written as (24,25)

$$G=\int \left[{\rho }_0\varphi -\frac{\varepsilon }{2}{\left(\nabla \varphi \right)}^2-{\kappa }^2\left(\cosh \varphi -1\right)\lambda \right]dv\text{.}$$ (5)

For sufficiently small ϕ, we can derive the linearized form of the free energy by using the approximation of cosh ϕ ∼ 1 + ϕ²/2. Additional simplification can be achieved by using the Gauss law on the second term of Eq. 5,

$$-\int \frac{\varepsilon }{2}{\left(\nabla \varphi \right)}^{2}dv=\int \frac{\varphi }{2}\nabla \cdot \varepsilon \nabla \varphi dv\text{.}$$ (6)

Finally, application of the linear Poisson-Boltzmann equation yields the following well-known free energy for the linear Poisson-Boltzmann equation,

$$G=\frac{1}{2}\int {\rho }_0\varphi dv\text{.}$$ (7)

Finite-difference Poisson-Boltzmann method

In typical finite-difference Poisson-Boltzmann (FDPB) calculations, the solution system is discretized with a cubic lattice, i.e., electrostatic potentials, charges, and mobile ion concentrations are all defined on grid points, whereas the dielectric constants are defined on grid edges. Thus, FDPB usually consists of the following steps:

• Step 1.

  All atomic charges are mapped to the nearest finite-difference grid points.

• Step 2.

  The molecular surface is generated as the boundary between high-dielectric (i.e., water) and low-dielectric (i.e., biomolecule) volumes. Further, the dielectric boundary has to be mapped on the finite-difference grid.

• Step 3.

  Boundary conditions, i.e., electrostatic potentials on the external surfaces of the finite-difference grid are assigned.

• Step 4.

  These steps allow the partial differential equation to be converted into a linear or nonlinear system and solved (20,26).

• Step 5.

  Once the system is solved, the solution is used to compute the electrostatic energies and forces.

NPBC and PBC in FDPB

In this study, NPBC was implemented in FDPB with the facility of electrostatic focusing for efficiency. In the electrostatic focusing treatment, both a coarse grid and a fine grid were used in each FDPB calculation. Here the coarse-grid calculation was solved only to obtain the boundary potential for the fine-grid calculation. Specifically, the space boundary potentials for the fine grid were computed using the trilinear interpolation technique from the coarse grid. Note that electrostatic focusing or the double grid run is an approximation to the single fine grid run even with the same boundary condition. We analyzed the error introduced by electrostatic focusing with the initial solute structure as a test case. We found that the energy difference between the single grid run and the double grid run is <0.01 kcal/mol, a relative error of 10⁻⁷. Another source of potential error in NPBC lies in the use of the Debye-Hückel potential of a spherical solute for the coarse-grid boundary potential. The Debye-Hückel boundary potential is only a good assumption when the finite-difference boundary grid is far away from the solute. We have estimated the error of the approximation in the tested solute by using successively larger grids, i.e., with the grid dimension two, four, six, and eight times larger than the solute dimension. We found that the energy difference is <0.01 kcal/mol when the grid dimension is changed from two to eight times larger than the solute dimension. This corresponds to a relative error of 10⁻⁷. Thus, we have set the dimension of the coarse grid to be roughly twice that of the solute to secure good free-space boundary potential for NPBC.

To realize PBC in FDPB, we adopted a straightforward strategy for the purpose of minimizing changes in the existing FDPB solvers. Given that FDPB potentials and charges are defined from grid 1 to n along any dimension, periodicity implies that grid −n to 0 and grid n+1 to n+2n are both the exact images to grid 1 to n. Besides setting up FDPB charge and dielectric constant in the boundary region following the periodicity convention, the FDPB equation should be solved by setting the boundary potentials as follows. Since the potential at grid 0 is used for the boundary condition for grid 1, and the potential for grid n+1 is used as boundary condition for grid n, we simply copied the potential at grid n to grid 0, and copied the potential at grid 1 to grid n+1. The initially unknown boundary potentials can be set up as guessed values, or set up as zero. Subsequent FDPB runs would allow us to obtain the potential from grid 1 to n according to the initial boundary potential values. The new potentials at grid 1 and n were then used as new boundary potentials at n+1 and 0, respectively, to start the next FDPB run. Repeat of these steps would achieve a self-consistency between the boundary potential and the potential on grids 1 to n. The pseudo code is shown below:

• Step 1.

  Set up initial boundary condition, i.e., ϕ(0) = 0 and ϕ((n+1) = 0.

• Step 2.

  Do FDPB iteration.

• Step 3.

  If convergence is reached (i.e., the boundary potential no longer changes), exit.

• Step 4.

  Copy the potential of grid 1 to grid n+1; copy the potential of grid n to grid 0; update boundary condition, go to Step 2.

The PBC/FDPB implementation was validated by two charges in a dipolar arrangement and four charges in a quadrupolar arrangement in vacuum. It can be seen from Table 1 that PBC/FDPB energies are very close to those of Ewald and PME. Three methods, including Ewald (27), PME (28), and PBC/FDPB, were used to compute the electrostatic energies of the two test cases. The box size is 20 Å × 20 Å × 20 Å. The unit charges are placed in the x-y plane and the distance between any two charges is 10 Å in the x and y direction.

Table 1.

Electrostatic energies (kcal/mol) under the periodic boundary condition by three different methods

Computational method	Dipolar	Quadrupolar
Ewald summation	−45.5138	−107.1771
PME	−45.4893	−107.1358
FDPB	−45.5228	−107.2291

Monte Carlo simulation of counterions

Monte Carlo (MC) has been proven to be a successful method in the studies of counterion distributions of nucleic acids. Previous simulation findings were found in good agreement with the counterion condensation theory and experiment (22,29,30). To enhance sampling of explicit counterions, a revised strategy based on the general Hamiltonian replica exchange method (HREM), termed VHREM, was used in this study (21). The VHREM method was designed to improve the diffusion sampling of counterions by targeting each individual counterion in turn (21). This is different from a general HREM implementation (31–36), which would target all counterions simultaneously. The general HREM is apparently straightforward to implement, but the diffusion sampling can still be very challenging when the number of degrees of freedom subject to treatment is large (31,36). This is similar to the limitation in temperature replica exchange methods (31,36), which activate all degrees of freedom at higher temperatures, resulting in reduced sampling efficiency in interested degrees of freedom.

In VHREM, in addition to one replica at the targeted state, which is described by the original energy potential U₀, we designed N replicas at scaled states. Each of these scaled states has a unique portion of energy potential, corresponding to one specific ion, scaled by a scaling parameter λ. The scaled potential is

$$U_{\mathrm{i}}=\lambda U_{\mathrm{s}}^{\mathrm{i}}+U_{\mathrm{e}}^{\mathrm{i}},i=0,1,\dots ,N,$$ (8)

where $U_{\mathrm{s}}^{\mathrm{i}}$ represents the energy potential corresponding to the ith ion and $U_{\mathrm{e}}^{\mathrm{i}}$ stands for the rest of the energy terms in the original energy function $U_0\left(U_{\mathrm{s}}^{\mathrm{i}}+U_{\mathrm{e}}^{\mathrm{i}}=U_0\text{for all}i\right)$. Specifically to realize the energy scaling in FDPB, the charge of ion i in replica i is scaled by λ before calling FDPB to obtain the electrostatic energy.

If there are N ions in the simulated systems, we need to set up N + 1 replicas: one replica at the target state and N replica at scaled states. Each pair of neighboring replicas acted by the potentials of U_j and U_k are scheduled for structure exchanges based on canonical replica exchange acceptance probability relationship,

$$w\left(C^{\text{old}}\to C^{\text{new}}\right)=\min \left(1,\exp \left\{-\beta \left[\left(U_{\mathrm{k},\mathrm{j}}+U_{\mathrm{j},\mathrm{k}}\right)-\left(U_{\mathrm{k},\mathrm{k}}+U_{\mathrm{j},\mathrm{j}}\right)\right]\right\}\right),$$ (9)

where U_x,y represents the energy calculated with the energy function of U_x, but on the structure of the replica acted by the potential U_y. After each trial replica exchange, the sequence of all the scaled state replicas is reshuffled to guarantee thorough structural exchanges between the target state replica and all the scaled state replicas. The neighboring replicas in the replica exchange are determined for exchange according to the topology shown in Fig. 1 of Min et al. (21). In this study, 23 replicas on 23 CPUs were employed in each VHREM/MC simulation. These 23 replicas include the target state replica and 22 scaled states replicas corresponding to 22 counterions, respectively. The MC move step was set to 0.25 Å to yield an acceptance ratio of 65%. The scaled parameter λ in VHREM was set as 0.7 to achieve a replica exchange ratio of ∼55%.

Figure 1.

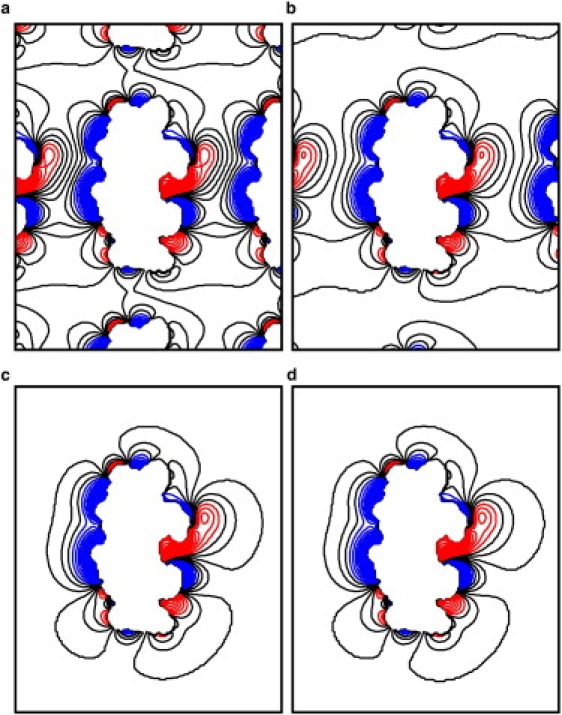
Continuum ion distributions in the x-z plane for 1BNA. Contours are plotted from 75 mM negative charge (red) to 150 mM positive charge (blue) with an interval of 5.625 mM. The five counters from −13.125 mM to +15 mM are colored black. (a–c) PBC simulations in the small, medium, and large boxes, respectively. (d) NPBC simulation.

In PBC simulations, if a counterion moves out of the box from one side, it moves into the box from the other side. In NPBC simulations, the centers of mass of counterions are confined within the same ion-accessible volume in the PBC simulations. The reflective boundary condition was used to prevent counterions from diffusing away from the simulation box. Specifically, if a counterion reaches the boundary, it can move to any direction except crossing the boundary.

To accelerate FDPB calculations, the DNA was fixed throughout the simulations and only counterions were allowed to move. This fact is exploited to save the CPU times of certain portions of a FDPB calculation. For example, the charge and dielectric grids of the DNA alone were first computed before the start of the simulations and saved. The complete charge and dielectric grids of the DNA and counterions were then updated at every step with the actual positions and radii of counterions.

We carried out 40 independent simulations in both PBC and NPBC, respectively. These independent simulations were started with different random seeds but from the same initial conformation. Each single simulation was run for 470,000 steps per replica. Structures were saved every 100 steps for analysis. Convergence of the simulations was monitored by analyzing the running average energies of all 40 simulations. The running average energies show that at least 200,000 steps per simulation are needed for equilibrium in both the PBC and NPBC simulations. Nevertheless, the first 270,000 steps were discarded to secure good equilibration in both sets of simulations, and the remaining 200,000 steps per simulation were used and referred to as the production trajectory.

Computation details

All simulations were performed with a revised AMBER 10 suite of programs and the ff94 atomic charges for DNA and counterions (37). In both PBC and NPBC simulations, the explicit sodium ions are treated as hard spheres with their radii set as the cavity radius of the sodium ion (38). The radii of DNA atoms were previously optimized against TIP3P solvation free energy simulations (38). The solvent dielectric constant is 80, whereas the solute dielectric constant is 1.

The dielectric interface between the solute and solvent regions was defined by the solvent-excluded molecular surface, obtained with a solvent probe radius 0.6 Å (38). Note that the unconventionally small probe radius was optimized based on our quantitative comparative analyses of FDPB versus the TIP3P explicit solvent model (38). In Tan et al. (38) and subsequent analysis (X. Ye, J. Wang, C. Tan, and R. Luo, unpublished), we found that the electrostatic solvation energies of small molecules are not very sensitive to the different probe sizes. However, the electrostatic potentials of mean force of hydrogen-bonded or salt-bridge dimers are quite sensitive to the probe radius used and a solvent probe radius of 0.6 Å can best reproduce the TIP3P solvent among the tested values (X. Ye, J. Wang, C. Tan, and R. Luo, unpublished). Our subsequent analysis of ion pairs on peptides and proteins also indicates that the probe radius of 0.6 Å can best reproduce the TIP3P solvent. Indeed, unconventionally small probe radii, as small as zero (i.e., van der Waals surface), were also used in previous studies and were found to yield good agreement with experiment (39,40). It should be pointed out that a small probe might cause numerical difficulties in loosely packed biomolecules. These contradicting observations apparently result from the limitation of hard-sphere models used in dielectric assignment in the PB theory. These observations also support the arguments for more physical treatment of dielectrics for biomolecules. Since our interests are in the mobile ions in this study and our fixed DNA structure does not contains any artificial water-accessible pockets even with the small water probe, the use of the optimized probe radius is a clearly a better choice to reproduce the TIP3P electrostatic potentials of mean force.

The continuum salt is a 1:1 electrolyte of 150 mM behaving according to the linear PB equation. The temperature is 300 K. The ion exclusion layer is 2.0 Å away from the DNA/explicit counterions surface. For NPBC/FDPB, one coarse grid and one fine grid were used. The coarse-grid dimension is 82 Å × 86 Å × 116 Å with a spacing of 2 Å and the fine-grid dimension is 42 Å × 44 Å × 59 Å with a spacing of 0.5 Å. For PBC/FDPB, only a single fine grid of 0.5 Å was used, and the grid dimension is the same as the fine grid in NPBC/FDPB. The convergence criterion was set to be 10⁻⁵. Other details can be found elsewhere (19,20).

The initial structure was taken from the classical Drew-Dickerson dodecamer B-DNA structure (PDB id: 1BNA). Twenty-two Na⁺ ions were added to neutralize the system. Thus, the simulation system consists of DNA and 22 explicit Na⁺ counterions in the implicit water and 150 mM continuum salt in a rectangular cell. The initial 22 sodium coordinates were determined by successive positioning of each counterion at the lowest electrostatic potential site from linear PB runs with NPBC/FDPB. Note that addition of a neutralizing number of counterions alone approximates the screening effects of counterions in a qualitative manner. However, it does not correspond to a particular ionic strength. The final ionic strength also depends on the size of the simulation box. This will be discussed below.

Counterion occupancy was analyzed with the method of Ponomarev et al. (41). Specifically, explicit counterion occupancy for each atom was first calculated with a cutoff distance of 5 Å. The explicit counterion occupancy of each nucleotide was then computed by summing the occupancies of all atoms of the nucleotide. The continuum counterion occupancies were computed similarly, through volume integration. The summation of explicit ion and implicit ion was reported as the ion occupancy for a given nucleotide. In this work, each ion was assigned to one and only one nucleotide of the DNA.

Results and Discussions

Continuum ion distribution

The periodic artifacts on ion distributions were first analyzed by studying the effect of box size in PBC from the continuum point of view. In this analysis, different box sizes centered on the DNA were used in FDPB calculations to probe the effect of box size. Here, the small box is merely large enough to solvate the DNA by a layer of water of ∼4 Å (box size 34 Å × 36 Å × 51 Å). The medium-size box and the large box solvate the DNA by a layer of water of ∼10 Å (box size 42 Å × 44 Å × 59 Å) and 15 Å (box size 52 Å × 54 Å × 69 Å), respectively. Specifically the medium box size was chosen to be similar to the typical box size chosen by most workers in MD simulations with PME.

The PBC ion distributions from the different boxes are shown in Fig. 1. The NPBC ion distribution is also shown for comparison. The figure shows two-dimensional ion concentration contours in the x-z plan. Note that the z axis is chosen to be the DNA helical axis in this study. Contours are shown at intervals of 5.625 mM from 75 mM negative charge to 150 mM positive charge. For the small simulation box, it is apparent that the PBC ion distribution is similar to the NPBC ion distribution near the surface of the DNA (Fig. 1 a). However, their difference becomes obvious in regions away from the DNA (Fig. 1 a). In the medium box shown in Fig. 1 b, almost no difference can be seen near the DNA surface; in the region away from the DNA, some deviations can be identified, but not as obvious as that in the small box. In the large box shown in Fig. 1 c, no visible difference can be seen throughout the simulation box when compared with the NPBC ion distribution. To rule out likely artifacts in arbitrary choice of the plan perpendicular to the helix of DNA, the continuum ion distributions in the y-z plane were also compared for the commonly used medium box (Fig. 2). It can be seen that the visible difference is only located near the box boundary region as in the x-z plane. Finally, it should be pointed that the effect of box size is small for the NPBC ion distribution. Indeed, we tested the effect by doubling and quadrupling the box size and found no noticeable differences in continuum ion distributions in NPBC. This shows that the medium box chosen here is large enough for NPBC calculations. These observations are also in qualitative agreement with previous studies of proteins: it was reported that the periodicity-induced artifacts may be enhanced when the solute size is nonnegligible, when compared to the size of the simulation box (14).

Figure 2.

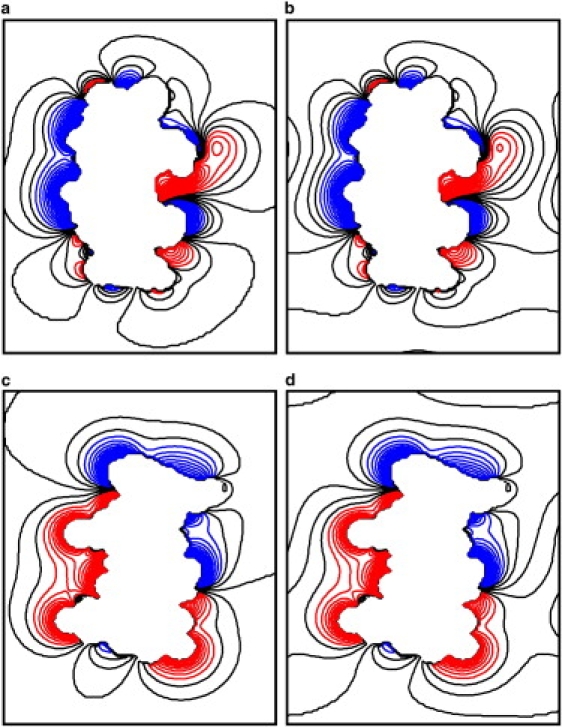
Continuum ion distributions in the x-z and y-z planes for the medium-sized box. (a) NPBC, x-z plane; (b) PBC, x-z plane; (c) NPBC, y-z plane; (d) PBC, y-z plane. See Fig. 1 for more details.

Explicit counterion distribution

A visual representation of the spatial distribution of the 22 explicit counterions is shown in Fig. 3. Note that all simulations were conducted with the medium-sized box discussed above. The most frequently visited positions by explicit counterions were chosen through 10 lowest energy configurations. As shown in Fig. 3, the density of clustered spheres, each of which represents an individual counterion, can be used to estimate the local concentration of explicit counterions. The explicit counterions, as expected, preferentially visit the vicinity of, but are not necessarily directly bound to, the double helix. This does not imply that these explicit counterions spend most of the time bound to the surface of the DNA, and this indeed is not the case. The detailed analysis of counterion occupancy is described below. Nevertheless, these lowest-energy snapshots show that explicit counterion distributions are very similar between NPBC and PBC at least when the medium box is used.

Figure 3.

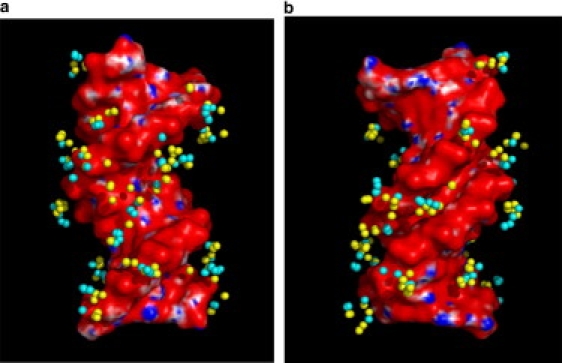
Superposition of 10 lowest energy snapshots from the MC simulations. (a) Major groove; (b) minor groove. Ions in PBC simulations are colored yellow, and those in NPBC simulations are colored blue.

Radial distribution of total counterion and Manning radius

Given the above analyses of continuum and explicit ion distributions, we went ahead to quantify the total counterion distributions in PBC and NPBC simulations. Here, the total counterion concentration is the sum of both explicit and implicit cations from the hybrid ion representation. Fig. 4 shows the total counterion distributions as a function of distance from the DNA helical axis. The figure shows that counterion densities in both PBC and NPBC are as high as 1.5 M in region 6–12 Å from the helix axis (Fig. 4, upper panel). This region happens to fall in the major and minor grooves where the counterions frequently visit as shown above. Note that the shape of the distribution function is similar to that observed in full explicit ion simulations with the Poisson's equation (42). Since the simulation box in this study is smaller, the highest density observed is expected to be higher. Both simulations also show that the concentration of counterions near the surface of DNA (∼10 Å from the helix axis) is >1 M, consistent with previous theoretical nonlinear PB studies (43). Finally, if the total volume is used (Fig. 4, lower panel), the peak of distribution function is narrowed and centered in the region 11–13 Å and the highest density is also reduced from 1.5 M to 1.25 M.

Figure 4.

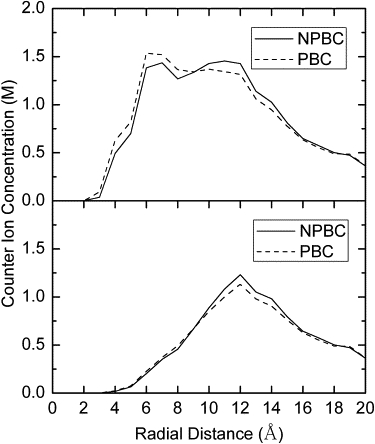
Counterion radial distribution functions. Radial distance measured from the average helical axis. The upper panel is computed with ion accessible volume and lower panel is computed with the total volume.

An interesting common observation from both the PBC and NPBC simulations is the rather high counterion density, approaching 500 mM, near the box boundary. This is very different from the bulk value as set to be 150 mM, indicating the artificially high density is not due to the use of PBC, but mostly due to the use of rather small simulation box. It is likely that the high counterion concentration might cause energetic artifacts and subsequent dynamic artifacts when the DNA is fully mobile during simulations.

One commonly used measure of total counterion distributions in DNA is the radius within which the Manning fraction of the net DNA charge is neutralized. For B-DNA, it is 76% (43). The Manning radius is 17.75 Å in NPBC, and it is 18.00 Å in PBC. This is quite close to those reported in a previous nonlinear PB study, 17 Å for a salt concentration of 250 mM (29). In our work, the ionic strength is set as 150 mM, so that the Manning radius should be somewhat larger, as predicted from the trend of Manning radius versus ionic strength, i.e., the Manning radius increases as the ionic strength decreases. Here we also tested the linear PB theory without any explicit counterions to calculate the Manning radius. We found that it is much larger, at ∼25 Å. It is apparent that the linear PB alone without neutralizing counterions is insufficient in modeling highly charged systems (23).

Sequence dependence of total counterion distribution

The sequence dependence of total counterion distributions in both PBC and NPBC simulations were also analyzed and shown in Fig. 5. Consistent with above analyses, the difference between PBC and NPBC is not obvious; but at least the peaks and troughs from both boundary conditions are at the same locations. The calculated occupancies of counterions within the major/minor grooves are clearly sensitive to sequence, as pointed out previously (23). In the major groove, the preferred sites for counterions are at basepairs A5:T20 to T8:A17; on average, 0.4–0.5 counterions per pair are bound to these nucleotides. The preferred sites in the minor groove are at basepairs G4:C21 and C9:G16, with, on average, 0.5 counterions per basepair bound to them. These findings are also consistent with the previous reports in explicit ion/explicit solvent simulations (21,41), further validating the minimal hybrid ion approach in our analysis of counterion distributions.

Figure 5.

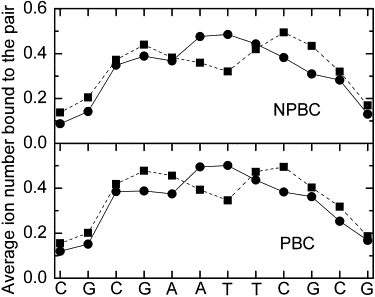
Counterion occupancies as a function of sequence. Minor and major groove occupancies are shown as square and cycle, respectively.

Further considerations

Effects of solute charge and structure on counterion distribution

It is important to note that the above comparisons are made for a particular nucleic acid, 1BNA. The short and rigid DNA is a relatively homogeneously charged and highly asymmetrical biomolecule. It is likely that the effects of PBC would be more prominent if a solute with asymmetrical charge distribution or a geometrically asymmetrical solute were considered. To assess the generality of above comparisons, we analyzed the continuum ion distributions for two more systems. The first one is an asymmetrical nucleic acid, 310D, a t-RNA. The second one is a DNA-binding protein, 1TSR B chain, with a large dipole moment of (−96.9 eÅ, 6.6 eÅ, −44.7 eÅ). Fig. S1 and Fig. S2 in the Supporting Material show the continuum ion distributions of the 310D and 1TSR, respectively. As in the analysis for 1BNA (Fig. 1), the continuum ion distribution in NPBC is compared with those in PBC with different box dimensions. These comparisons show that the continuum salt distributions in the medium box between PBC and NPBC are qualitatively similar near the solute surface, although differences are noticeable at second solvation shell, consistent to the findings for 1BNA in Fig. 1.

Linear approximation in the hybrid ion representation

It is well known that electrostatic energy and its salt dependence are strongly affected by accounting for nonlinearity in highly charged systems. An interesting question to ask is whether the nonlinearity is still prominent when enough counterions are used to neutralize the system, or whether a linearized PB treatment is enough when the minimal hybrid ion representation is used. Using 1TSR and 1BNA as the test cases, our comparative analysis shows that the potential in the nonlinear FDPB is ∼10% less than that in the linear FDPB in the cell boundary region. Nearby the solute surface, the continuum ion density by the nonlinear PB is higher than that by linear PB due to the nonlinear effect (Fig. S3). Nevertheless, the qualitative comparison of PBC and NPBC in Fig. 1, Fig. S1, and Fig. S2 still holds when the nonlinear PB is used.

To further assess the approximations introduced by using the linear FDPB instead of nonlinear FDPB in the electrostatic energies, we studied the correlation between two sets of 28 relative electrostatic energies of eight snapshots roughly evenly, covering the sampled electrostatic free energy values in one MC trajectory. Although the two sets of absolute electrostatic energies are clearly different, the two set of relative energies (these relative energies were actually used in a MC simulation) are highly correlated with each other with a correlation coefficient of 0.9994, a linear regression slope of 1.02, and a root-mean square relative deviation of 2.8%, as shown in Fig. S4. Note also that our current implementation of the nonlinear FDPB is ∼10 times slower that of the linear FDPB. Balancing both accuracy and efficiency, we believe the linear FDPB is a reasonable initial choice for the minimal hybrid ion treatment in DNA simulations.

Conclusions

The wide use of lattice-sum strategies in biomolecular simulations brought up a series of questions regarding artifacts in periodic simulations. One remaining question is the artifacts in the counterion distributions in periodic simulations. As one would anticipate, Coulombic interactions under PBC may deviate more noticeably from those under NPBC especially in highly charged systems; and the use of PBC may significantly influence the counterion distributions in such systems. However, the electrostatic screening due to the high-dielectric constant of water and ion-ion screening might significantly damp the charge-charge interactions. Therefore, the magnitude of PBC-induced artifacts in counterion distributions is not straightforward to dissect without detailed analysis. In this study, we have addressed this question by comparably mapping the counterion distributions around a double-strand DNA with a canonical sequence from simulations with both boundary conditions.

The PBC artifacts on ion distributions were first analyzed from the continuum point of view. Our analysis, however, shows that the ion distributions near the DNA surface are quite similar between PBC and NPBC calculations. Nevertheless, their difference becomes obvious in regions further away from the DNA. As expected, the difference in ion distributions becomes smaller when the simulation cell in PBC is larger. These observations are in qualitative agreement with previous studies in the context of proteins, i.e., the PBC artifacts may be enhanced when the solute size is comparable to the simulation cell. The effect of boundary conditions upon ion distribution was then analyzed by studying the spatial distribution of the explicit counterions. Consistent with the observations in the continuum ion analysis, explicit counterion distributions are very similar between NPBC and PBC when a typical-sized simulation cell is used.

The analysis of total counterion distributions in PBC and NPBC simulations shows that counterion densities in both PBC and NPBC are as high as 1.5 M in region 6–12 Å from the helical axis. This region happens to fall in the major and minor grooves where the counterions frequently visit. The distribution functions are similar to that observed in full explicit ion simulations with the Poisson's equation. Both simulations show that the concentration of counterions near the DNA surface can be as high as 1 M, which is consistent with previous nonlinear PB studies. An interesting common observation from both the PBC and NPBC simulations is the rather high counterion density, approaching 500 mM, near the box boundary. This is very different from the bulk value that is set to be 150 mM, indicating the artificially high density is not due to the use of PBC, but mostly due to the use of a rather small simulation box. The analysis of the Manning radius shows a consistent picture with highly similar radii from the NPBC and PBC simulations, 17.75 Å vs. 18.00 Å. The sequence dependences of counterion distributions were also analyzed and the difference between PBC and NPBC is not obvious.

In summary, our comparative analyses with the minimal hybrid ion treatment of mobile ions show that periodicity artifacts are small in the ion distributions of the tested DNA. This is especially so near the solute surface, although the difference in distributions is visible starting from the second solvation shell. Interestingly, a rather high counterion density that is noticeably different from bulk concentration was observed near the simulation cell boundary, regardless of the boundary conditions used. This indicates that the artificially high density is mostly due to the use of the rather small simulation cell that is typical in periodic simulations.

Due to the limited computational resources, the bulk of our comparable analyses is only for a particular nucleic acid, 1BNA, with a rather symmetrical charge distribution. Thus, these conclusions do not exclude the presence of periodicity-induced artifacts of counterion distributions in other untested biomolecular systems. To assess the generality of the above comparisons, we analyzed the continuum ion distributions for two more biomolecules: a t-RNA with an asymmetrical geometry and a DNA-binding protein with a large dipole moment. The two additional comparisons of the continuum ion distributions show that the findings obtained for 1BNA are still relevant at least for the continuum ion distributions. Another limitation of our analyses lies in the use of linear FDPB calculations for computational efficiency. To estimate the potential influence from the linearization approximation, we further compared the continuum ion distributions between PBC and NPBC with nonlinear FDPB calculations. The additional comparisons show that the conclusions drawn from the linear FDPB calculations are qualitatively consistent with those obtained from nonlinear FDPB calculations, as far as the continuum ion distributions are concerned.

Supporting Material

Four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00973-4.