Abstract
To provide theoretical guidance for the design and in vitro cultivation of bioartificial tissues, we have developed a multiscale computational model that can describe the complex interplay between cell population and mass transport dynamics that governs the growth of tissues in three-dimensional scaffolds. The model has three components: a transient partial differential equation for the simultaneous diffusion and consumption of a limiting nutrient; a cellular automaton describing cell migration, proliferation, and collision; and equations that quantify how the varying nutrient concentration modulates cell division and migration. The hybrid discrete-continuous model was parallelized and solved on a distributed-memory multicomputer to study how transport limitations affect tissue regeneration rates under conditions encountered in typical bioreactors. Simulation results show that the severity of transport limitations can be estimated by the magnitude of two dimensionless groups: the Thiele modulus and the Biot number. Key parameters including the initial seeding mode, cell migration speed, and the hydrodynamic conditions in the bioreactor are shown to affect not only the overall rate, but also the pattern of tissue growth. This study lays the groundwork for more comprehensive models that can handle mixed cell cultures, multiple nutrients and growth factors, and other cellular processes, such as cell death.
Introduction
Tissue engineering combines our knowledge in medicine, cell biology, materials science, and bioreactor engineering to develop bioartificial tissues in vitro or to induce tissue remodeling in vivo to replace, repair, or enhance the function of a particular tissue or organ (1,2). To cultivate bioartificial tissues in vitro, the appropriate type(s) of cells may first be seeded into a highly porous scaffold made from natural materials such as fibrin, collagen, and chitosan (3–6), biocompatible synthetic polymers such as polylactic acid, polyglycolic acid, poly-lactic-glycolic acid, and poly(propylene fumarate-co-ethylene glycol) (7–12), or a combination of natural and synthetic fibers (13–16). The cell-scaffold construct is then cultured in bioreactors where conditions (temperature, pH, nutrient concentration, etc.) are maintained at levels suitable for cell migration, proliferation, and, possibly, differentiation until the tissue is ready for implantation. There are many obstacles to overcome before clinically useful bioartificial tissues can be readily made in laboratories (17). In particular, the identification of the optimal conditions for in vitro or in vivo cultivation of bioartificial tissues requires a better understanding of the complex interactions between fundamental intracellular processes and the constantly changing extracellular environment.
In an earlier publication (18), we demonstrated that cell population dynamics can play an important role in determining the growth rates of developing tissues. Specifically, our simulation results revealed that the speed and persistence of cell locomotion modulate the rates of tissue regeneration by overcoming the adverse effects of contact inhibition, a process that characterizes the proliferation of anchorage-dependent mammalian cells cultured on flat surfaces or three-dimensional (3D) scaffolds (19–29). We have also found that the magnitude of this modulation strongly depends on the spatial distribution of seed cells and the geometry of the scaffold, a conclusion that may have significant implications for the design of experiments that test the efficacy of biomimetical surface modifications designed to enhance cell migration speeds.
However, tissue growth is also affected by the availability of nutrients and growth factors (GFs). As cells proliferate in the scaffold interior, the total demand for nutrients and GFs increases and may outstrip the ability of the system to transport these compounds from the culture media to the scaffold interior. Such mass transport limitations decrease the availability of nutrients and GFs in the scaffold and limit the viable size of bioartificial constructs. Several studies have shown that the formation of engineered tissues in bioreactors is limited to a thin peripheral layer (less than a few hundred microns deep) surrounding a relatively cell-free scaffold interior (30–33). Mass transport limitations become even more severe for tissues that normally have high metabolic demands. Only very thin peripheral layers ranging from 50 to 180 μm have been reported for engineered cardiac tissues when passive diffusion was the only mass transport mode inside the scaffolds (32,34).
Several recent studies have focused on the development of theoretical models that can predict the steady-state distribution of key nutrients (such as oxygen and glucose) inside bioartificial tissues (35–40). Although they provide valuable insights into the interplay between transport and consumption of nutrients in tissues, such models cannot elucidate the dynamic process of tissue development inside biomaterial scaffolds.
Galban and Locke (41) proposed a dynamic model for the in vitro growth of cartilage tissues based on species continuity equations and the volume averaging method. The volume averaging method, however, removes the spatial dependence from the diffusion-reaction equations for nutrients, thus ignoring the spatial heterogeneity that is a very important characteristic of bioartificial tissue growth. Also, proliferation is the only cellular function considered in the Galban and Locke model, although it has been shown that low-passage, primary chondrocytes not only migrate in some biomaterial scaffolds, but also form aggregates from cell-cell collisions (42–45). More recently, Chung and co-workers (46) developed a similar volume-averaging model with cell migration added as another important cellular function. By describing cell migration as a diffusion-like process, this model requires an estimation of the key motility parameter, the cell “diffusion” coefficient, from population measurements and the solution of an inverse problem for each system studied. This continuous approach does not allow us to study how tissue growth is affected by important single-cell properties (like migration speed and persistence) that can be measured directly (18). Nor does it allow the incorporation of more complicated cell behavior such as cell-cell collision (18). Similar limitations can be found in another recent continuous model (47).
A more promising alternative for tissue-growth modeling is the hybrid discrete-continuous (HDC) approach. In HDC models, cells are simulated explicitly with a discrete, stochastic component, the cellular automaton (CA), whereas processes such as diffusion and consumption of nutrients are described with a continuous, deterministic component usually based on partial differential equations (PDEs). Such hybrid models have been used to solve two-dimensional (2D) problems involving the aggregation and self-organization of the cellular slime mold Dictyostelium discoideum (48–50) and the interactions between extracellular matrix and fibroblasts (51). More recently, the HDC approach has been used effectively for modeling tumor development. Chaplain used 2D and 3D models to describe angiogenesis and tumor growth (52), Patel and co-workers used a 2D model to study acidosis (53), and Jiang and co-workers employed a 3D model to investigate avascular tumor growth (54). The CA component of these models only considered proliferation, adhesion, and viability of individual cells. The migration of individual tumor cells was incorporated in a recent 2D model developed by Anderson and co-workers to study tumor morphology and phenotypic evolution (55).
This study presents what we believe is a novel dynamic HDC model that describes tissue growth under conditions leading to significant mass transport limitations. The discrete component of our model considers an asynchronous population of cells that migrate, collide, and proliferate to build a tissue inside a 3D scaffold. Between divisions, all cells execute persistent random walks and cell-cell collisions are handled as discrete events. The diffusion and consumption of a limiting nutrient is modeled by a time-dependent PDE with boundary conditions imposed by the bioreactor used to culture the engineered tissue. Finally, the division times and migration speeds of individual cells are dynamically modulated by the changing nutrient concentrations in their extracellular environment. Our main objective is to accurately characterize the dynamics of tissue growth in the regime of significant transport limitations and to identify the key system parameters that affect the structure and growth rate of the developing tissue. To meet the significant computational requirements of this model, the HDC algorithm has been parallelized for execution on distributed-memory multicomputers.
Model Formulation
The configuration of the tissue engineering bioreactor and the culturing conditions can vary widely. One example is the system described in Fig. 1, where several scaffolds seeded with a single type of cell are fixed on needles and cultured in a well-stirred bioreactor. This is the so-called “dynamic” tissue culture method that has been shown to promote both cell proliferation and extracellular matrix component deposition in bioartificial tissues (56–58). However, our model can handle other reactor configurations by changing the boundary conditions of the diffusion-reaction problem defined later in this section.
Figure 1.
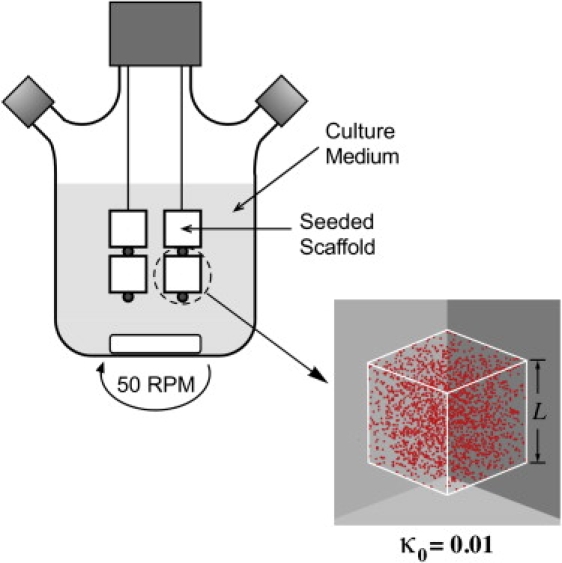
Seeded bioartificial tissue constructs cultured in a well-stirred bioreactor.
We assume that cells can be seeded in two modes: the “uniform” mode, in which seed cells distribute uniformly throughout the scaffold (Fig. 2 A); and the “surface” mode, in which seed cells are placed in a thin layer next to the scaffold surface (Fig. 2 B). It is possible to achieve the uniform initial distribution of cells with dynamic seeding methods, in which mixing or stirring is employed to promote the penetration of cells into the scaffold interior (32,59). The seeding density, κ0, is in the range 0.367–1.33% (cell volume fraction) for various combinations of cell type and scaffold material (31,60–65). When cells are seeded by simply immersing an empty scaffold into a static cell solution for a certain period of time, the spatial distribution of seed cells can often be described by the surface mode. This is also likely the case when the scaffold is big or its pore structure is too tortuous for cells to penetrate deeply.
Figure 2.
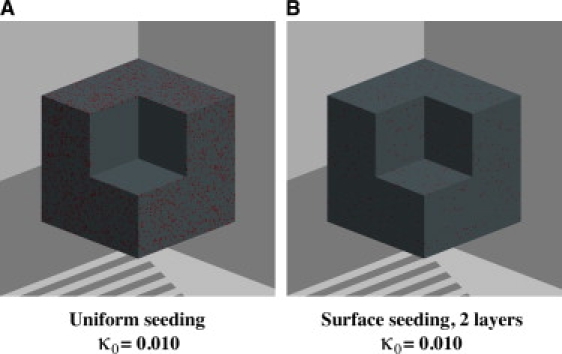
Initial spatial distribution of seed cells. (A) “Uniform” seeding mode. (B) “Surface” seeding mode.
Discrete model for cell population dynamics
Our CA model for cell population dynamics has been described in detail before (18). Briefly, we first assume that the scaffold provides a uniform structure that allows cells to move freely in all directions while going through their division cycles. We also assume that the degradation of scaffold material does not affect tissue growth. The behavior of individual cells and cell-cell interaction are then simulated with a cellular automaton consisting of a 3D array with cubic computational sites (66,67). Each site in the cellular array can exist at one of a finite number of states at each time interval. That is, a site may be empty, and thus available for a cell to move/divide into, or occupied by a cell that is at a certain phase of its mitotic cycle and is either moving in a certain direction or stationary. The state of each site can be initialized and tracked individually. Every site is “connected” to six neighbors (von Neumann neighborhood) and its state evolves at discrete time steps through interactions with these neighbors (18,68). These interactions are governed by a set of “rules” that simulate cell migration and proliferation, as well as cell-cell collisions. Other cellular activities, such as differentiation, are currently not considered, but can be easily incorporated when necessary.
In accordance with experimental observations, we assume that cells migrate by executing persistent random walks (69–71). That is, each cell moves with speed S in one direction for a certain length of time (quantified by a persistence time tp) before turning to another direction to continue its migration. In a uniform environment, the direction after each turn is randomly selected. However, cell movement can be biased in our model to simulate chemotaxis or haptotaxis. This can be achieved by appropriately changing the transition probabilities (that is, the probabilities with which a cell will change its direction of movement from one to another) to favor cell motility along directions dictated by environmental cues such as chemoattractant concentration gradients or substrate surface patterns (see Cheng et al. (18) for more details). If the cell does not collide with another cell, this persistent random movement continues until the end of the cell's current division cycle, upon which the cell will stop and divide into two daughter cells. Cell division is asynchronous in our model, and the distribution of cell division time, td, is a measurable characteristic of each cell phenotype. Immediately after the division, the two daughter cells assume their own persistent random walk in two randomly selected directions. If one cell collides with another, both cells pause for a given period of time—the pausing time, tc—before moving away from each other (72,73). A detailed description of this process is available in Cheng et al. (18). The values of S, tp, td, and tc are characteristic of each cell type and can be measured directly through time-lapse observation of cell migration (74–76).
Diffusion-reaction problem for nutrient mass transport dynamics
Experiments have shown that concentration gradients of both glucose and oxygen, two key nutrients for cellular function, exist in bioartificial scaffolds and affect tissue growth (36,77,78). In this study, to demonstrate the importance of mass transport dynamics, we assume that glucose is the single limiting nutrient. More than one nutrient can be similarly modeled by introducing additional PDEs.
Let us now consider a tissue growing in a cubic scaffold of size L. In the absence of forced convection (i.e., flow or perfusion of media through the scaffold), the spatiotemporal evolution of the nutrient concentration C(x,y,z,t) can be described by the PDE
| (1) |
where Ω denotes the cubic scaffold, De is the effective diffusion coefficient, ρcell is the local cell density, R(ρcell, C) is the cell uptake rate, S(ρcell, C) is the rate of secretion by the cells, and D(C) is the rate of natural degradation. To integrate Eq. 1, we must define the initial condition,
| (2) |
where C0(x,y,z) is a known concentration profile with boundary conditions that depend on the bioreactor configuration. For the bioreactor depicted in Fig. 1, the appropriate boundary condition is
| (3) |
where ∂Ω refers to the surface of the scaffold and denotes the derivative with respect to the normal to the scaffold surface, kg is the mass transport coefficient in the medium-scaffold interface, and Cb is the nutrient concentration in the bulk of the medium.
The effective diffusivity in Eqs. 1 and 3 obviously depends on local cell density. Let De,s and De,t denote its value in tissue-free and tissue-filled regions respectively. For the diffusivity between an empty element in the cellular array and an occupied element, the averaging method used is
For small nutrient molecules, such as glucose, that pass directly across the cell membrane, the kinetics of uptake and metabolism generally follow a Michaelis-Menten type dependence (79). The reaction term R(ρcell, C) in Eq. 1 thus takes the form
| (4) |
where Vmax is the maximum cell-uptake rate and Km is the saturation constant. Both Vmax and Km can be measured experimentally (80). The secretion term S(ρcell, C) is zero, since the cells do not produce glucose. The natural degradation term, D(C), is ignored because it is insignificant compared to diffusion and cell uptake.
Substituting the terms from Eq. 4 in Eq. 1, we obtain the diffusion-reaction PDE for glucose:
| (5) |
Since this continuous PDE must be coupled to our discrete CA model, the cell density, ρcell, is a discontinuous function that is nonzero only in elements occupied by cells. Thus, , where
In other words, the migrating and proliferating cells act as moving sinks for our diffusion-reaction PDE. We can now put Eq. 5 in dimensionless form by introducing the dimensionless variables
where C∗ and are appropriate reference values for the concentration and effective diffusivity, respectively. The dimensionless form of Eq. 5 is then
| (6) |
In a similar way, if we let , , , and , we obtain the dimensionless forms of the initial and boundary conditions:
| (7) |
| (8) |
The extent of mass transport limitations can be evaluated (81,82) by the magnitude of two dimensionless numbers generated in the nondimensionalization process: 1), the Thiele modulus, , which indicates the relative magnitude of the nutrient uptake rate over the nutrient diffusion rate; and 2), the Biot number, , which indicates the relative magnitude of the external nutrient transport rate (from the media to the surface of the scaffold) over the nutrient diffusion rate in the interior of the scaffold.
Modulation of cellular functions
Experiments have shown that both cell division time, td, and cell migration speed, S, are affected significantly by glucose concentration (83–85). Therefore, cell proliferation and migration must be modulated by the extracellular glucose concentration, which is computed by solving the boundary value problem defined by Eqs. 6–8 at each time step of the simulation.
Previous studies have shown that the dependence of the doubling rate, rg, on extracellular nutrient concentration can be described with a Monod-type expression:
| (9) |
where is the maximum cell population doubling rate and K is a saturation constant. Reported values of K for a line of human lung fibroblasts are 2.7 × 10−5 M for glucose and 1.1 × 10−5 M for glutamine (80). This study will use the following values we determined experimentally (86) for human dermal fibroblasts: rg,max = 2.03 doublings/day and K = 6.022 × 10−4 M.
Our model modulates cell proliferation by introducing a special “countdown” division counter for every cell (86). If the nutrient concentration were at all times the same at every location visited by the migrating cell, the division counter would be decremented by a fixed amount at every time step. In our simulations, however, every cell may move through regions with varying glucose concentrations and its division time will depend on the trajectory followed. Therefore, the division counter is decremented at each time step by a variable amount that depends on the nutrient concentration, C, in the site occupied by the cell.
The energy required to maintain cell migration is provided from either glycolysis or oxidative phosphorylation. An earlier study from our lab reported that the speed of cell migration decreased significantly when cells were moved from glucose-containing to glucose-free medium (85). However, the quantitative relation between glucose concentration, C, and cell migration speed, S, was not elucidated. Our model assumes that the speed of migration is modulated by the glucose concentration, C, according to the formula
| (10) |
where Clow is the threshold glucose concentration below which cell migration stops, and Chigh is the critical glucose concentration above which cells migrate at the maximum speed, Smax.
Implementation of parallel algorithm
The boundary value problem, defined by Eqs. 6–8, is discretized over the cellular array with the seven-point finite difference method (see our previous study (86) for details) and an implicit-explicit time integration scheme (87). The resulting sparse linear system is then solved with a Preconditioned General Minimum Residual solver from the PDE toolkit PETSc (88). We have checked the correctness of our PDE solving method by comparing the numerical solution to the analytical solution for a diffusion-reaction problem that assumes uniform and constant cell density, a linear cell uptake term, and a Dirichlet boundary condition on all surfaces of the cube. The analytical solution of this problem can be obtained with finite Fourier trans form (86). The relative error of our numerical solution is ∼0.1% for dξ = 0.01, dτ = 1.0 × 10−4, and ϕ2 = 1.0 × 10−2.
The flow chart in Fig. 3 presents the integration of the three components of our HDC model. First, the seed cells are distributed according to one of the two seeding modes described at the beginning of the Model Formulation section. Next, the PETSc objects needed for solving the diffusion-reaction PDE are defined and initialized. The CA iterations are then started. Because the CA time step (typically ∼0.1 h) is usually too big for the PDE solver, the diffusion-reaction PDE is integrated using a smaller time step (∼0.002 h) within each CA step to maintain both stability and accuracy of the solver. When the PDE loop is completed, the computed concentrations are imported into the subsequent CA routines to modulate cell proliferation, migration, and collision. The next CA iteration then starts with an updated cellular array. The simulation continues until all CA iterations are completed (see our previous study (86) for additional details).
Figure 3.
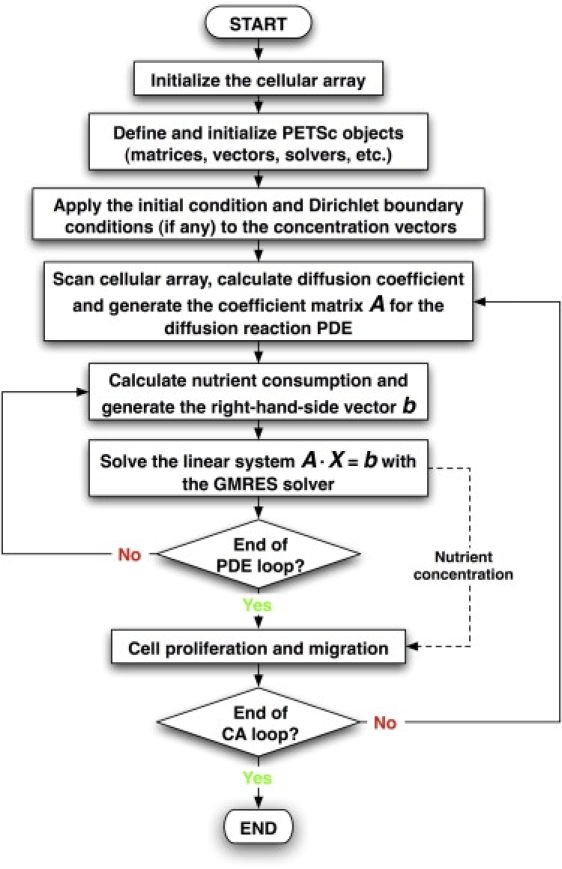
Main flow chart of the hybrid model.
The algorithm described above is both memory- and computation-intensive, because it requires large 3D arrays to accommodate the cell population (one cell per element) and small time steps to accurately solve the diffusion-reaction PDE. Therefore, we have parallelized it using the Message Passing Interface (89), so that the simulations can run on parallel computer clusters. This not only reduces the CPU time, but also enables us to solve problems of larger, and therefore more realistic, size. Our simulations were carried out on a Linux cluster (Evolocity High-Performance Cluster, Linux Networx, Bluffdale, UT) with one master node and 41 slave nodes. Each node has two 1.7-GHz Pentium 4 Xeon processors and 2 GB of DDR memory. The nodes are connected using Myrinet, a switched 1.2 GB/s network. The CPU time required to run a simulation depends on many conditions, especially the size of the tissue, the nutrient diffusivity, and the number of nodes used. A typical simulation like the one whose model parameters are shown in Table 1 takes ∼4000 s on 10 nodes.
Table 1.
Base-case model parameters
| Parameter | Physical meaning | Value |
|---|---|---|
| Parameters for cells | ||
| d (μm) | Average cell diameter | 20 |
| td (h) | Minimum cell division time | 12 |
| Smax (μm/h) | Maximum cell migration speed | 20 |
| tp (h) | Cell migration persistence time | 0.8 |
| tc (h) | Pausing time after cell-cell collision | 1.4 |
| Seeding mode | Uniform | |
| Parameters for the diffusion-reaction PDE | ||
| De,, (m2/s) | Nutrient diffusivity in tissue-free scaffold | 2.7 × 10−10 |
| De,, (m2/s) | Nutrient diffusivity in tissue-filled scaffold | 7.0 × 10−11 |
| Vmax (mol/cell·h) | Maximum nutrient uptake rate by cells | 3.31 × 10−13 |
| Km (mole/m3) | Saturation constant for nutrient uptake | 2.4 |
| K (mole/m3) | Saturation constant in Monod kinetics | 6.022 × 10−2 |
| Clow (mole/m3) | Nutrient concentration below which cell migration stops | 0.0 |
| Chigh (mole/m3) | Nutrient concentration above which cells migrate at Smax | 5.0 |
| Cb (mole/m3) | Nutrient concentration in the bulk of the medium | 5.0 |
| C0 (mole/m3) | Initial nutrient concentration in the scaffold | 0.0 |
| kg (m/s) | Mass transfer coefficient for mixed boundary condition | 1.0 × 10−10 |
| L (m) | Side length of the cubic scaffold | 0.002 |
Results and Discussion
We now present simulation results from a series of parametric studies to explore the interplay of cell population and mass transport dynamics that governs the growth of 3D bioartificial tissues. Tissue growth was quantified by computing the volume fraction, κ (t), of the computational domain (i.e., scaffold) occupied by cells after each iteration:
Note that the volume fraction (or tissue growth curve), κ (t), is essentially the ratio of the integral of γ (x,y,z,t) over the volume of the scaffold at time t over the total scaffold volume V = L3. For our simulations, we will assume that the initial cell volume fraction in the scaffold is κ0 = 0.01 and that the cell-scaffold constructs will be cultured for 10 days. Other key model parameters for the base case are shown in Table 1. The parameters De,n and kg of the boundary condition given by Eq. 3 can be modified to reflect the configuration of the bioreactor and the tissue culture method. To simplify the analysis, we first assume that the tissue culture medium is well mixed and, therefore, that kg >> De,n. Equation 8 then reduces to the Dirichlet boundary condition u = ub on ∂Ω, which will be used throughout this section unless specified otherwise.
Effect of mass transport limitations
With the previous assumptions, we can use the bulk concentration, Cb, as our reference concentration and De,t as our reference diffusion coefficient. Then, the Thiele modulus becomes:
| (11) |
Note that the Thiele modulus defined by Eq. 11 corresponds to confluence conditions when the scaffold is completely filled with cells and transport limitations are most severe. If we further assume that the simulation starts from the moment the seeded scaffolds are immersed into the medium (i.e., there is no nutrient in the scaffold interior), the initial and boundary conditions become
| (12) |
| (13) |
| (14) |
where again Ωand ∂Ω refer to the cubic scaffold and the six faces of the scaffold, respectively. The boundary value problem defined by Eqs. 12–14 is a transient diffusion-reaction problem. The fact that the cell distribution function, γ, varies with time and spatial location makes our problem significantly more complicated than the classical isothermal diffusion-reaction problem that has been extensively studied in the chemical engineering literature (81,82). Still, the results of these earlier studies allow us to predict the conditions that will cause severe nutrient transport limitations inside the scaffold:
-
1.
Large scaffold (tissue) size, L;
-
2.
High final cell density, , and high values of the nutrient consumption rate, Vmax;
-
3.
Low nutrient diffusivity, De,s; and
-
4.
Low nutrient concentration on the scaffold surface, Cb.
Quantitative prediction of tissue growth under such conditions is computationally challenging due to the temporal and spatial variations of the cell distribution function γ that lead to a complex interplay of nutrient transport and cell population dynamics. However, our HDC model is uniquely equipped to handle the complexities of this system.
Table 1 presents the values of the model parameters for our base case. In this case, the Thiele modulus of Eq. 11 has a value of ϕ = 11.5 ≡ ϕ∗. Note that ϕ increases if we increase the size of the scaffold, L, and the value of uptake rate, Vmax(that is, make the cells more metabolically active), and decrease the glucose diffusivity, De,s, or the value of the glucose concentration, Cb, at the surface of the scaffold.
Fig. 4 presents the tissue growth curves, κ (t), for a wide range of values for the Thiele modulus. We observe first that the tissue growth curves for ϕ = 0.1 ϕ∗ and ϕ = ϕ∗ are almost identical. However, Fig. 5 reveals significant differences in the spatiotemporal evolution of the nutrient concentration profiles between these two cases. When ϕ = 0.1 ϕ∗, the nutrient uptake rate and the mass transport rate are closely matched. As a result, the nutrient quickly diffuses into the scaffold and its concentration remains almost constant even as the scaffold is filled with cells (see Fig. 5, A–D). When ϕ increases to ϕ∗, the nutrient transport rate becomes significantly slower than the nutrient uptake rate, and sharp concentration gradients develop in the scaffold interior (Fig. 5, E–H). Since our current model does not consider cell death due to nutrient depletion, cells do not become apoptotic/necrotic even when nutrient concentration drops very low, which is why the tissue growth curves for ϕ = 0.1 ϕ∗ and ϕ = ϕ∗ are almost identical, even though the nutrient concentrations in the scaffold interior drop to very low values in the latter case (compare concentrations in Fig. 5, G and H, to those in Fig. 5, C and D).
Figure 4.
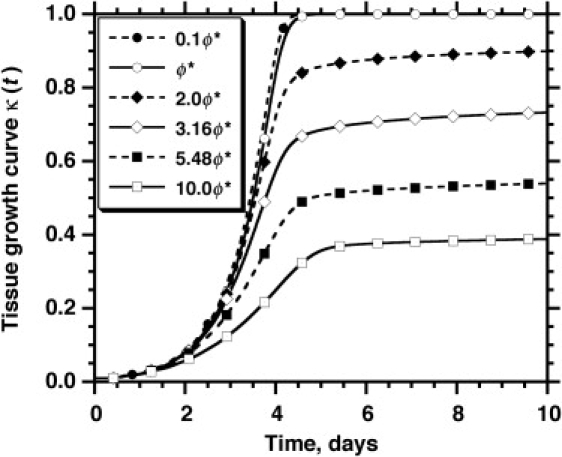
Effect of the Thiele modulus, , on the tissue growth curve. The legend lists the value of ϕ for each run, with ϕ∗ = 11.46 corresponding to the base case whose model parameters are listed in Table 1.
Figure 5.

Temporal evolution of spatial cell distributions and nutrient (glucose) concentrations for three runs with the same initial cell configuration but different values of the Thiele modulus. The top half of each image pair shows the cells (gray dots in print or red dots online) located on a horizontal section plane through the center of the cubic scaffold, and the bottom half depicts the dimensionless nutrient concentration, u(ξ,ψ,ζ,τ), according to the scale shown by the color bar located at the bottom of the figure. Note that u varies from 0 to 1 as the nutrient concentration, C(x, y, z, t), varies from 0 to Cb. This applies to all subsequent figures containing similar surface plots of the dimensionless nutrient concentration. (A–D) ϕ = 0.1ϕ∗. (E–H) ϕ = ϕ∗. (I–L) ϕ = 10.0ϕ∗.
This tissue structure changes drastically as we further increase the Thiele modulus to ϕ = 10.0 ϕ∗ (Fig. 5, I–L). In this case, severe mass transport limitations create a very sharp nutrient concentration gradient in the scaffold soon after the simulation starts. As a result, only a thin layer of cells is able to form just below the surface of the scaffold. This enhances even more the “bottleneck effect” of diffusional limitations, leaving the majority of the scaffold interior with near-zero nutrient concentration and essentially stopping tissue growth after κ(t) reaches 0.4 (Fig. 4). We should note here that the dense peripheral tissue layer shown in Fig. 5 L has a thickness of ∼100 μm. This is similar to what has been observed when bioartificial tissues with high metabolic demand (e.g., cardiac tissues) are cultured in bioreactors under conditions similar to those assumed in our simulation (32–34,90,91).
Effect of seeding mode
The initial distribution of cells is an important parameter because it affects the evolution of the concentration field from the beginning of the simulation, which in turn modulates tissue growth. Simulation results for the uniform and surface seeding modes are shown in Fig. 6. All the other parameters for these two runs are the same as in Table 1. The surface seeding mode gives slightly higher cell volume coverage at the early stages of the simulation, since in this case all the cells are located in the peripheral zone, where the nutrient concentration is almost equal to the surface value. The volume coverage for the surface seeding mode, however, is surpassed by the uniform seeding mode at t = 3.1 days (κ(t) ≈ 0.3065). By t = 5.0 days, the growth curve for the uniform seeding mode has reached complete coverage, whereas the curve for the surface mode lags behind and even at 10 days has not reached complete coverage. The values of κfinal at 10 days are rather close: 1.00 for the uniform seeding mode versus 0.96 for the surface seeding mode.
Figure 6.
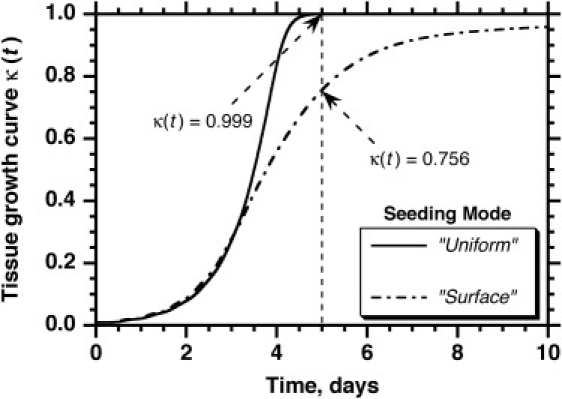
Effect of initial seeding mode on the tissue growth curve. All other parameters are the same as in Table 1.
These results can be explained by comparing the time series of images showing the spatial cell distributions and glucose concentrations for the uniform seeding mode (Fig. 5, E–H) and surface seeding mode (Fig. 7, A–D). The two time series reveal significant differences in tissue growth dynamics. When the cells are seeded uniformly, cell proliferation can take place throughout the scaffold at all stages of the process. The uniform dispersion of cells in the scaffold (Fig. 5, E and F) minimizes the adverse effects of contact inhibition on cell proliferation rates, as we established in an earlier publication (18). With the surface seeding mode, however, growth begins from the peripheral layer next to the scaffold surface and the tissue expands as a diffuse front of cells moving toward the center of the scaffold (Fig. 7, A–D). Between 2.5 and 5 days, a confluent layer of cells forms next to the surface of the scaffold. This leads to severe contact inhibition effects, since only the cells located in the proliferating front continue to divide. The fraction of nonproliferating cells increases as the thickness of the confluent layer increases (Fig. 7 C), and the overall tissue growth rate slows down with time (Fig. 6). Note that even though the average glucose concentration at t = 5 days is higher for the surface seeding mode (Fig. 7 C) than for the uniform seeding mode (Fig. 5 G), we have faster tissue growth (κ ≈ 0.999 at t = 5 days) when we start with uniform seeding than when we start with surface seeding (κ ≈ 0.756 at t = 5 days). This is because the high glucose concentration available in the scaffold interior cannot be fully exploited in the surface seeding mode since the cell front has not yet reached the center of the scaffold.
Figure 7.
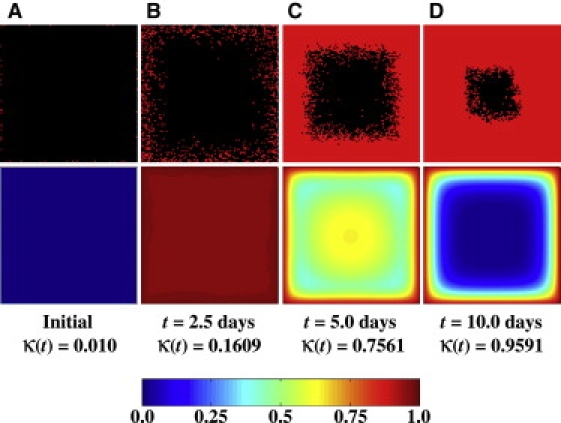
Temporal evolution of spatial cell distribution and glucose concentration for a run with surface seeding mode and ϕ = ϕ∗. Each pair of images depicts the location of cells and the nutrient concentration on a horizontal section plane through the center of the scaffold. All other parameters are the same as in Table 1. Compare with Fig. 5, E–H, which shows results from a run with uniform seeding mode and the same model parameters.
Our simulation results on the effect of seeding mode are supported by experimental studies in which a more uniform initial distribution of cells, achieved by applying either a lower-than-atmospheric pressure (92,93) or cyclic compression-force-induced suction (94) during seeding, has been shown to significantly promote the growth of bioartificial tissues.
Effect of cell migration speed
Cell migration speed, S, varies widely among different cell types. Reported values from 2D migration studies range from S = 30 μm/h for human microvascular endothelial cells (95,96), bovine pulmonary artery endothelial cells (73), and smooth muscle cells (96,97) to S = 600 μm/h for rabbit neutrophils (98). Recent 3D studies reported speeds of 8–15 μm/h for adenocarcinoma and prostate cancer cell lines in collagen (71) and 20–40 μm/h for melanoma cells migrating in collagen matrices modified with RGD peptides (69). We are interested in cell migration speed because if its effect on tissue growth is known, we can modulate S to promote tissue growth by varying the concentrations of growth factor in the media (74,99–101) or by biomimetically modifying the scaffold material (102,103).
Fig. 8 shows the results from four simulations with two migration speeds (20 μm/h and 1 μm/h) and two seeding modes, uniform and surface. All other parameters are the same as in Table 1. For the runs that started with the uniform seeding mode, the results show that the cell migration speed has a minimal effect on the tissue growth curves. However, higher migration speeds result in significantly faster tissue growth when we start with the surface seeding mode. Fig. 9, A–D, presents the time series of images with the spatial cell distributions and glucose concentrations for the uniform seeding mode and S = 1 μm/h, and Fig. 5, E–H, presents the corresponding results for S = 20 μm/h. The time series for the surface seeding mode is shown in Figs. 9, E–H, and 7, A–D, respectively.
Figure 8.
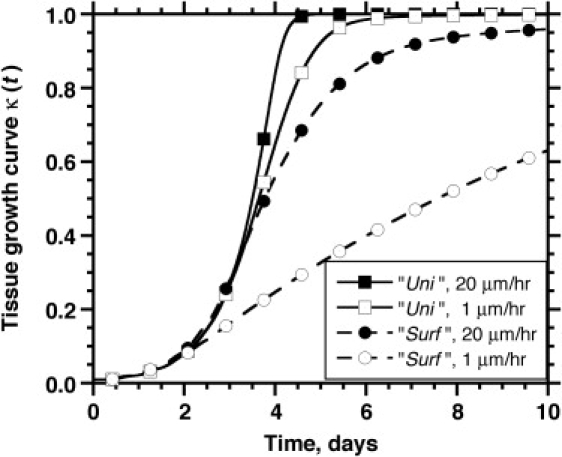
Combined effect of initial seeding mode and cell migration speed on tissue growth rates. The legend shows the seeding mode and the cell migration speed. All other parameters are the same as in Table 1.
Figure 9.
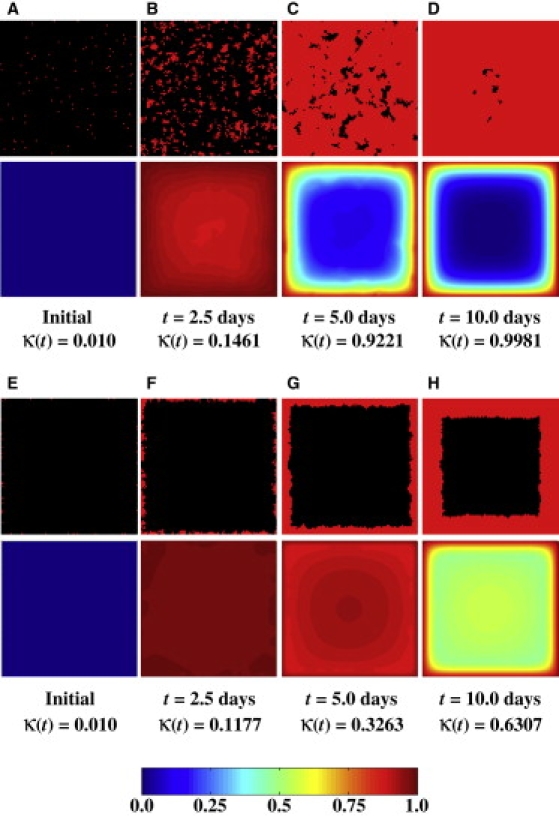
Temporal evolution of cell distribution and nutrient (glucose) concentration for two runs at S = 1 μm/h and different seeding modes. All other parameters are the same as in Table 1. Each pair of images depicts the location of cells (top half) and the nutrient concentration (bottom half) on a horizontal section plane through the center of the scaffold. (A–D) Uniform seeding mode. (E–H) Surface seeding mode.
For the uniform seeding mode, clumps of cells form after only a few divisions when S = 1 μm/h (Fig. 9 B). Because of contact inhibition, only the cells located on the surface of these clumps can divide, and thus, the tissue grows more slowly than when S = 20 μm/h. The latter speed is high enough to produce a much more uniform distribution of cells at 2.5 days (Fig. 5 F). However, the contact inhibition effects are not strong enough even at S = 1 μm/h to drastically delay tissue growth rates.
The effect of cell migration speed is much more significant in the surface seeding mode. When S = 1 μm/h, a peripheral layer of densely packed tissue develops next to the scaffold surface (Fig. 9, E–H). Since only the cells on the “tortuous” inner surface of this layer can proliferate, contact inhibition effects dominate from the early stages of this run, and tissue growth is significantly delayed. By t = 10 days, the tissue growth curve is still far from its plateau phase. When S = 20 μm/h, however, a wide and diffuse front of proliferating cells forms and moves toward the interior of the scaffold (see Fig. 7, B and C). This migration-driven dispersion delays the onset of contact inhibition effects until the diffuse front reaches the center of the scaffold and the cell density there reaches high levels. As a result, a significantly larger fraction of cells can divide when the speed of migration is 20 μm/h and the tissue growth rate is significantly enhanced.
Effect of boundary conditions
Although we have so far presented results from runs with Dirichlet boundary conditions, our simulator can solve the diffusion-reaction problem for other boundary conditions corresponding to different bioreactor configurations or tissue culture methods. In simple static culturing systems, for example, seeded scaffolds are often placed at the bottom of a petri dish or some other tissue culture plate. As a result, there will be no flux of nutrients through the bottom surface of the scaffold. This situation can be handled by applying a Neumann boundary condition at the bottom face of the scaffold with Dirichlet conditions on the five other faces:
| (15) |
Fig. 10, A–G, presents results from a run with ϕ = 5.48ϕ∗ = 62.8 and a Dirichlet boundary condition on all six faces (A–D) (Eq. 14), and another run with the same initial spatial distributions of seed cells and the same value of ϕ, but with a Neumann boundary condition on the bottom face and a Dirichlet boundary condition on the other five faces of the scaffold (E–G) (Eq. 15). Although both boundary conditions give similar growth curves (κfinal is 0.5392 for the full Dirichlet boundary condition and 0.4798 for the Dirichlet-Neumann condition), we observe a significant difference in the structure of the final tissues. Because of the lack of incoming nutrients, no dense peripheral tissue layer forms at the bottom of the scaffold (Fig. 10 H).
Figure 10.
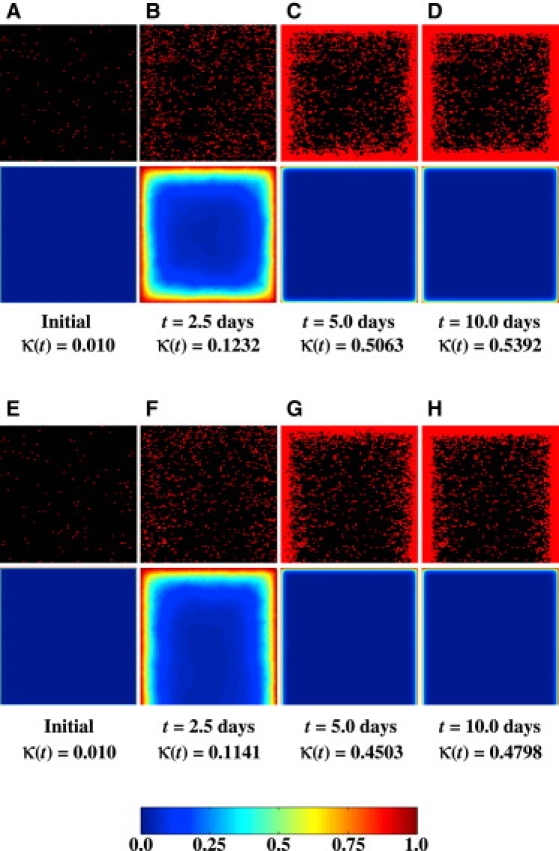
Temporal evolution of cell distributions and nutrient (glucose) concentrations for two runs with ϕ = 5.48ϕ∗ and the same initial cell configuration but different boundary conditions. All other parameters are the same as in Table 1. Each pair of images depicts the location of cells (top half) and the nutrient concentration (bottom half) on a vertical section plane through the center of the scaffold. (A–D) The Dirichlet boundary condition is applied to all six surfaces of the scaffold. (E–H) A Neumann boundary condition is applied to the bottom surface, with Dirichlet boundary conditions on the other five surfaces.
If the tissue culture medium in the bioreactor is not vigorously stirred, external mass transport rates (from the medium to the scaffold surface) may become comparable to internal transport rates. Then, we can no longer apply Dirichlet boundary conditions to the surfaces of the scaffold. Instead, we need to apply the following mixed boundary condition:
| (16) |
where the dimensionless Biot number Bi, as mentioned earlier, provides a measure of the relative magnitude of the external and internal resistances to mass transport. Fig. 11 shows the effect of Bi on tissue growth. Large values of the Biot number (achieved, for example, by vigorously stirring the tissue culture medium) clearly promote tissue growth, but this beneficial effect gradually diminishes.
Figure 11.
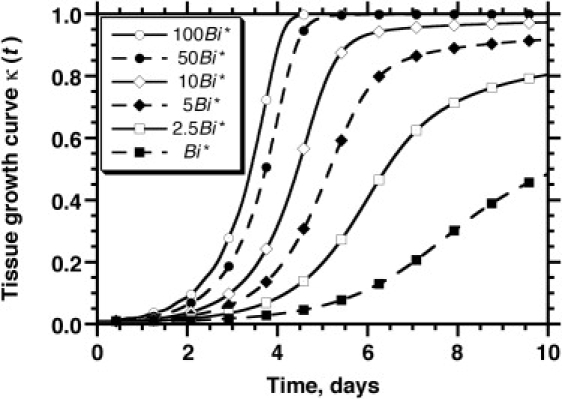
The effect of the Biot number, , on tissue growth rates. The mixed boundary condition is applied on all surfaces and the mass transfer coefficient, kg, is varied to affect the value of Bi. Its base case value, Bi∗ = 7.41 × 10−4, corresponds to the parameters shown in Table 1.
Conclusions
To establish a framework for simulating in vitro growth of 3D bioartificial tissues under realistic conditions, we have developed a high-performance, hybrid discrete-continuous model that has three major components: 1), a cellular automaton simulating individual cell activities and cell-cell interactions; 2), a transient PDE describing the diffusion and consumption of a limiting nutrient; and 3), equations describing how single-cell behavior is modulated by the local concentrations of the nutrient. These model components are integrated to describe in detail the intricate interplay between cell population and mass transport dynamics with parameters that can be measured directly through experiments. The hybrid nature of our model also makes it highly adaptable for simulating complicated system configurations involving, for example, mixed cell cultures and cell differentiation.
The dimensionless Thiele modulus and Biot number identify the major parameters affecting the severity of nutrient transport limitations in the tissue culture system. We have also seen that transport limitations affect both the overall tissue growth rate and the final spatial distributions of cells inside the scaffold. When the Thiele modulus is large, the nutrient consumption rates are much faster than the corresponding mass transport rates and sharp concentration gradients develop in the scaffold interior. Tissue growth stops in the nutrient-deficient interior of the scaffold and a dense, thin layer of cells forms just below the surface of the scaffold. The thickness of the dense peripheral tissue layer predicted by our model has values similar to those observed when bioartificial tissues with high metabolic demand are cultured in bioreactors.
Cell migration is also shown to be very important for tissue growth due to its effect on reducing contact inhibition and alleviating the bottleneck effect on nutrient transport. High cell migration speed is more beneficial if cells are initially seeded close to the scaffold surface rather than uniformly distributed throughout the entire scaffold. Our simulations offer interesting insights into the interplay between cell population and mass transport dynamics that leads to these phenomena. We also demonstrate our model's ability to simulate various boundary conditions corresponding to different bioreactor configurations. Thus, the conclusions drawn from our simulations provide much needed theoretical guidance for tissue engineers in their design of scaffold biomaterials, cell seeding methods, bioreactor configurations, and tissue culture medium formula.
The simulations discussed in this study were based on the assumption that cell proliferation does not stop until the nutrient concentration drops to zero. However, our model can easily handle cases where both migration and proliferation stop when the nutrient concentration drops below certain critical levels. Simulation results (not shown here) indicate that the setting of nonzero concentration thresholds for proliferation will have minimal effects on tissue growth in the absence of significant transport limitations. As expected, these effects become more pronounced with the onset of severe nutrient transport limitations.
The hybrid modeling approach described in this study can form the framework for the development of a comprehensive model that incorporates many more realistic features. For example, it has been found that coculture of multiple cell types is necessary for enhanced organ-specific cellular functions (104,105), the formation of vascular network (106–108), and cell differentiation (109–111) in biomaterial scaffolds. Other processes that can be easily incorporated into our model include scaffold heterogeneities, convection of medium through the scaffold when the tissue is cultured in perfused bioreactors (33,112–114), natural cell death (apoptosis), and cell death caused by nutrient depletion (necrosis). In the case of cell death due to nutrient depletion, for example, one would expect the development of necrotic regions in the scaffold interior for large values of the Thiele modulus instead of the sparsely populated inner cores observed, for example, in Fig. 5, K and L. Of course, experiments must be performed to measure the parameters related to the regulatory mechanism for cell death, including the critical nutrient concentration below which cells become quiescent, the reduced nutrient consumption rate of quiescent cells, the duration of the quiescent state of cells before they commit to necrosis, and the time it takes for necrotic cells to decompose and make their position available for other cells. Work to extend the model to systems with heterogeneous cell populations and cell death is already underway in our lab.
Acknowledgments
This work was supported in part by grants from the National Institutes of Health (R01-DE13031), the National Science Foundation (CNS-0116289), and the Texas Advanced Research Program (003652-0360).
Footnotes
Gang Cheng's present address is Steele Laboratory of Tumor Biology, Department of Radiation Oncology, Massachusetts General Hospital and Harvard Medical School, Boston, MA 02114.
References
- 1.Langer R., Vacanti J.P. Tissue engineering. Science. 1993;260:920–926. doi: 10.1126/science.8493529. [DOI] [PubMed] [Google Scholar]
- 2.Mooney D.J., Mikos A.G. Growing new organs. Sci. Am. 1999;280:60–65. doi: 10.1038/scientificamerican0499-60. [DOI] [PubMed] [Google Scholar]
- 3.Wu X., Black L., Santacana-Laffitte G., Patrick C.W. Preparation and assessment of glutaraldehyde-crosslinked collagen-chitosan hydrogels for adipose tissue engineering. J. Biomed. Mater. Res. A. 2006;81:59–65. doi: 10.1002/jbm.a.31003. [DOI] [PubMed] [Google Scholar]
- 4.Dang J.M., Leong K.W. Natural polymers for gene delivery and tissue engineering. Adv. Drug Deliv. Rev. 2006;58:487–499. doi: 10.1016/j.addr.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 5.Helm C.L., Zisch A., Swartz M.A. Engineered blood and lymphatic capillaries in 3-D VEGF-fibrin-collagen matrices with interstitial flow. Biotechnol. Bioeng. 2007;96:167–176. doi: 10.1002/bit.21185. [DOI] [PubMed] [Google Scholar]
- 6.Eyrich D., Brandl F., Appel B., Wiese H., Maier G. Long-term stable fibrin gels for cartilage engineering. Biomaterials. 2007;28:55–65. doi: 10.1016/j.biomaterials.2006.08.027. [DOI] [PubMed] [Google Scholar]
- 7.Cao D., Liu W., Wei X., Xu F., Cui L. In vitro tendon engineering with avian tenocytes and polyglycolic acids: a preliminary report. Tissue Eng. 2006;12:1369–1377. doi: 10.1089/ten.2006.12.1369. [DOI] [PubMed] [Google Scholar]
- 8.Fisher J.P., Jo S., Mikos A.G., Reddi A.H. Thermoreversible hydrogel scaffolds for articular cartilage engineering. J. Biomed. Mater. Res. 2004;71A:268–274. doi: 10.1002/jbm.a.30148. [DOI] [PubMed] [Google Scholar]
- 9.Georgiou G., Mathieu L., Pioletti D.P., Bourban P.E., Manson J.A. Polylactic acid-phosphate glass composite foams as scaffolds for bone tissue engineering. J. Biomed. Mater. Res. B Appl. Biomater. 2006;80:322–331. doi: 10.1002/jbm.b.30600. [DOI] [PubMed] [Google Scholar]
- 10.Sedrakyan S., Zhou Z.Y., Perin L., Leach K., Mooney D. Tissue engineering of a small hand phalanx with a porously casted polylactic acid-polyglycolic acid copolymer. Tissue Eng. 2006;12:2675–2683. doi: 10.1089/ten.2006.12.2675. [DOI] [PubMed] [Google Scholar]
- 11.Shin H., Temenoff J.S., Bowden G.C., Zygourakis K., Farach-Carson M.C. Osteogenic differentiation of rat bone marrow stromal cells cultured on Arg-Gly-Asp modified hydrogels without dexamethasone and β-glycerol phosphate. Biomaterials. 2005;26:3645–3654. doi: 10.1016/j.biomaterials.2004.09.050. [DOI] [PubMed] [Google Scholar]
- 12.Xin X., Hussain M., Mao J.J. Continuing differentiation of human mesenchymal stem cells and induced chondrogenic and osteogenic lineages in electrospun PLGA nanofiber scaffold. Biomaterials. 2007;28:316–325. doi: 10.1016/j.biomaterials.2006.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fujita M., Kinoshita Y., Sato E., Maeda H., Ozono S. Proliferation and differentiation of rat bone marrow stromal cells on poly(glycolic acid)-collagen sponge. Tissue Eng. 2005;11:1346–1355. doi: 10.1089/ten.2005.11.1346. [DOI] [PubMed] [Google Scholar]
- 14.Hiraoka Y., Kimura Y., Ueda H., Tabata Y. Fabrication and biocompatibility of collagen sponge reinforced with poly(glycolic acid) fiber. Tissue Eng. 2003;9:1101–1112. doi: 10.1089/10763270360728017. [DOI] [PubMed] [Google Scholar]
- 15.Ito T., Nakamura T., Takagi T., Toba T., Hagiwara A. Biodegradation of polyglycolic acid-collagen composite tubes for nerve guide in the peritoneal cavity. ASAIO J. 2003;49:417–421. [PubMed] [Google Scholar]
- 16.Hosseinkhani H., Azzam T., Kobayashi H., Hiraoka Y., Shimokawa H. Combination of 3D tissue engineered scaffold and non-viral gene carrier enhance in vitro DNA expression of mesenchymal stem cells. Biomaterials. 2006;23:4269–4278. doi: 10.1016/j.biomaterials.2006.02.033. [DOI] [PubMed] [Google Scholar]
- 17.McIntire L.V. World technology panel report on tissue engineering. Ann. Biomed. Eng. 2002;30:1216–1220. doi: 10.1114/1.1531632. [DOI] [PubMed] [Google Scholar]
- 18.Cheng G., Youssef B.B., Markenscoff P., Zygourakis K. Cell population dynamics modulate the rates of tissue growth processes. Biophys. J. 2006;90:713–724. doi: 10.1529/biophysj.105.063701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Levine E.M., Jeng D.Y., Chang Y. Contact inhibition, polyribosomes, and cell surface membranes in cultured mammalian cells. J. Cell. Physiol. 1974;84:349–364. doi: 10.1002/jcp.1040840304. [DOI] [PubMed] [Google Scholar]
- 20.Schmialek P., Geyer A., Miosga V., Nündel M., Zapf B. The kinetics of contact inhibition in mammalian cells. Cell Tissue Kinet. 1977;10:195–202. doi: 10.1111/j.1365-2184.1977.tb00144.x. [DOI] [PubMed] [Google Scholar]
- 21.Folkman J., Moscona A. Role of cell shape in growth control. Nature. 1978;273:345–349. doi: 10.1038/273345a0. [DOI] [PubMed] [Google Scholar]
- 22.Gotlieb A.I., Spector W., Wong M.K.K., Lancey C. In vitro reendothelialization: microfilament bundle reorganization in migrating porcine endothelial cells. Arteriosclerosis. 1984;4:91–96. doi: 10.1161/01.atv.4.2.91. [DOI] [PubMed] [Google Scholar]
- 23.Aoki J., Umeda M., Takio K., Titani K., Utsumi H. Neural cell adhesion molecule mediates contact-dependent inhibition of growth of near-diploid mouse fibroblast cell line m5S/1M. J. Cell Biol. 1991;115:1751–1761. doi: 10.1083/jcb.115.6.1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Takahashi K., Suzuki K. Density-dependent inhibition of growth involves prevention of EGF receptor activation by E-cadherin-mediated cell-cell adhesion. Exp. Cell Res. 1996;226:214–222. doi: 10.1006/excr.1996.0221. [DOI] [PubMed] [Google Scholar]
- 25.Kandikonda S., Oda D., Niederman R., Sorkin B.C. Cadherin-mediated adhesion is required for normal growth regulation of human gingival epithelial cells. Cell Adhes. Commun. 1996;4:13–24. doi: 10.3109/15419069609010760. [DOI] [PubMed] [Google Scholar]
- 26.Risbud M.V., Karamuk E., Moser R., Mayer J. Hydrogel-coated textile scaffolds as three-dimensional growth support for human umbilical vein endothelial cells (HUVECs): possibilities as coculture system in liver tissue engineering. Cell Transplant. 2002;11:369–377. [PubMed] [Google Scholar]
- 27.Misago N., Toda S., Sugihara H., Kohda H., Narisawa Y. Proliferation and differentiation of organoid hair follicle cells co-cultured with fat cells in collagen gel matrix culture. Br. J. Dermatol. 1998;139:40–48. doi: 10.1046/j.1365-2133.1998.02312.x. [DOI] [PubMed] [Google Scholar]
- 28.Shigematsu M., Watanabe H., Sugihara H. Proliferation and differentiation of unilocular fat cells in the bone marrow. Cell Struct. Funct. 1999;24:89–100. doi: 10.1247/csf.24.89. [DOI] [PubMed] [Google Scholar]
- 29.Nehls V., Herrmann R., Hühnken M., Palmetshofer A. Contact-dependent inhibition of angiogenesis by cardiac fibroblasts in three-dimensional fibrin gels in vitro: implications for microvascular network remodeling and coronary collateral formation. Cell Tissue Res. 1998;293:479–488. doi: 10.1007/s004410051140. [DOI] [PubMed] [Google Scholar]
- 30.Sikavitsas V.I., Bancroft G.N., Mikos A.G. Formation of three-dimensional cell/polymer constructs for bone tissue engineering in a spinner flask and a rotating wall vessel bioreactor. J. Biomed. Mater. Res. 2002;62:136–148. doi: 10.1002/jbm.10150. [DOI] [PubMed] [Google Scholar]
- 31.Kim B.S., Andrew J.P., Thomas J.K., Mooney D.J. Optimizing seeding and culture methods to engineer smooth muscle tissue on biodegradable polymer matrices. Biotechnol. Bioeng. 1998;57:46–54. [PubMed] [Google Scholar]
- 32.Carrier R.L., Papadaki M., Rupnick M., Schoen F.J., Bursac N. Cardiac tissue engineering: cell seeding, cultivation parameters, and tissue construct characterization. Biotechnol. Bioeng. 1999;64:580–589. doi: 10.1002/(sici)1097-0290(19990905)64:5<580::aid-bit8>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 33.Carrier R.L., Rupnick M., Langer R., Schoen F.J., Freed L.E. Perfusion improves tissue architecture of engineered cardiac muscle. Tissue Eng. 2002;8:175–188. doi: 10.1089/107632702753724950. [DOI] [PubMed] [Google Scholar]
- 34.Bursac N., Papadaki M., Cohen R.J., Schoen F.J., Eisenberg S.R. Cardiac muscle tissue engineering: toward an in vitro model for electrophysiological studies. Am. J. Physiol. 1999;277:H433–H444. doi: 10.1152/ajpheart.1999.277.2.H433. [DOI] [PubMed] [Google Scholar]
- 35.Williams K.A., Saini S., Wick T.M. Computational fluid dynamics modeling of steady-state momentum and mass transport in a bioreactor for cartilage tissue engineering. Biotechnol. Prog. 2002;18:951–963. doi: 10.1021/bp020087n. [DOI] [PubMed] [Google Scholar]
- 36.Botchwey E.A., Dupree M.A., Pollack S.R., Levine E.M., Laurencin C.T. Tissue engineered bone: measurement of nutrient transport in three-dimensional matrices. J. Biomed. Mater. Res. A. 2003;67:357–367. doi: 10.1002/jbm.a.10111. [DOI] [PubMed] [Google Scholar]
- 37.McClelland R.E., MacDonald J.M., Coger R.N. Modeling O2 transport within engineered hepatic devices. Biotechnol. Bioeng. 2003;82:12–27. doi: 10.1002/bit.10531. [DOI] [PubMed] [Google Scholar]
- 38.Malda J., Rouwkema J., Martens D.E., Le Comte E.P., Kooy F.K. Oxygen gradients in tissue-engineered PEGT/PBT cartilaginous constructs: measurement and modeling. Biotechnol. Bioeng. 2004;86:9–18. doi: 10.1002/bit.20038. [DOI] [PubMed] [Google Scholar]
- 39.Radisic M., Deen W., Langer R., Vunjak-Novakovic G. Mathematical model of oxygen distribution in engineered cardiac tissue with parallel channel array perfused with culture medium containing oxygen carriers. Am. J. Physiol. Heart Circ. Physiol. 2005;288:H1278–H1289. doi: 10.1152/ajpheart.00787.2004. [DOI] [PubMed] [Google Scholar]
- 40.Radisic M., Malda J., Epping E., Geng W., Langer R. Oxygen gradients correlate with cell density and cell viability in engineered cardiac tissue. Biotechnol. Bioeng. 2006;93:332–343. doi: 10.1002/bit.20722. [DOI] [PubMed] [Google Scholar]
- 41.Galban C.J., Locke B.R. Analysis of cell growth kinetics and substrate diffusion in a polymer scaffold. Biotechnol. Bioeng. 1999;65:121–132. doi: 10.1002/(sici)1097-0290(19991020)65:2<121::aid-bit1>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 42.Chang C., Lauffenburger D.A., Morales T.I. Motile chondrocytes from newborn calf: migration properties and synthesis of collagen II. Osteoarthritis Cartilage. 2003;11:603–612. doi: 10.1016/s1063-4584(03)00087-6. [DOI] [PubMed] [Google Scholar]
- 43.Hamilton D.W., Riehle M.O., Monaghan W., Curtis A.S. Articular chondrocyte passage number: influence on adhesion, migration, cytoskeletal organisation and phenotype in response to nano- and micro-metric topography. Cell Biol. Int. 2005;29:408–421. doi: 10.1016/j.cellbi.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 44.Hamilton D.W., Riehle M.O., Monaghan W., Curtis A.S. Chondrocyte aggregation on micrometric surface topography: a time-lapse study. Tissue Eng. 2006;12:189–199. doi: 10.1089/ten.2006.12.189. [DOI] [PubMed] [Google Scholar]
- 45.Hamilton D.W., Riehle M.O., Rappuoli R., Monaghan W., Barbucci R. The response of primary articular chondrocytes to micrometric surface topography and sulphated hyaluronic acid-based matrices. Cell Biol. Int. 2005;29:605–615. doi: 10.1016/j.cellbi.2005.03.013. [DOI] [PubMed] [Google Scholar]
- 46.Chung C.A., Yang C.W., Chen C.W. Analysis of cell growth and diffusion in a scaffold for cartilage tissue engineering. Biotechnol. Bioeng. 2006;94:1138–1146. doi: 10.1002/bit.20944. [DOI] [PubMed] [Google Scholar]
- 47.Pisu M., Lai N., Concas A., Cao G. A novel simulation model for engineered cartilage growth in static systems. Tissue Eng. 2006;12:2311–2320. doi: 10.1089/ten.2006.12.2311. [DOI] [PubMed] [Google Scholar]
- 48.Hogeweg P. Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation. J. Theor. Biol. 2000;203:317–333. doi: 10.1006/jtbi.2000.1087. [DOI] [PubMed] [Google Scholar]
- 49.Marée A.F., Hogeweg P. How amoeboids self-organize into a fruiting body: multicellular coordination in Dictyostelium discoideum. Proc. Natl. Acad. Sci. USA. 2001;98:3879–3883. doi: 10.1073/pnas.061535198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Palsson E., Othmer H.G. A model for individual and collective cell movement in Dictyostelium discoideum. Proc. Natl. Acad. Sci. USA. 2000;97:10448–10453. doi: 10.1073/pnas.97.19.10448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dallon J.C., Sherratt J.A., Maini P.K. Mathematical modelling of extracellular matrix dynamics using discrete cells: fiber orientation and tissue regeneration. J. Theor. Biol. 1999;199:449–471. doi: 10.1006/jtbi.1999.0971. [DOI] [PubMed] [Google Scholar]
- 52.Chaplain M.A. Mathematical modelling of angiogenesis. J. Neurooncol. 2000;50:37–51. doi: 10.1023/a:1006446020377. [DOI] [PubMed] [Google Scholar]
- 53.Patel A.A., Gawlinski E.T., Lemieux S.K., Gatenby R.A. A cellular automaton model of early tumor growth and invasion. J. Theor. Biol. 2001;213:315–331. doi: 10.1006/jtbi.2001.2385. [DOI] [PubMed] [Google Scholar]
- 54.Jiang Y., Pjesivac-Grbovic J., Cantrell C., Freyer J.P. A multiscale model for avascular tumor growth. Biophys. J. 2005;89:3884–3894. doi: 10.1529/biophysj.105.060640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Anderson A.R., Weaver A.M., Cummings P.T., Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- 56.Neves A.A., Medcalf N., Brindle K.M. Influence of stirring-induced mixing on cell proliferation and extracellular matrix deposition in meniscal cartilage constructs based on polyethylene terephthalate scaffolds. Biomaterials. 2005;26:4828–4836. doi: 10.1016/j.biomaterials.2004.12.002. [DOI] [PubMed] [Google Scholar]
- 57.Shangkai C., Naohide T., Koji Y., Yasuji H., Masaaki N. Transplantation of allogeneic chondrocytes cultured in fibroin sponge and stirring chamber to promote cartilage regeneration. Tissue Eng. 2006;13:483–492. doi: 10.1089/ten.2006.0181. [DOI] [PubMed] [Google Scholar]
- 58.Wang H.J., Bertrand-de Haas M., van Blitterswijk C.A., Lamme E.N. Engineering of a dermal equivalent: seeding and culturing fibroblasts in PEGT/PBT copolymer scaffolds. Tissue Eng. 2003;9:909–917. doi: 10.1089/107632703322495556. [DOI] [PubMed] [Google Scholar]
- 59.Vunjak-Novakovic G., Obradovic B., Martin I., Bursac P.M., Langer R. Dynamic cell seeding of polymer scaffolds for cartilage tissue engineering. Biotechnol. Prog. 1998;14:193–202. doi: 10.1021/bp970120j. [DOI] [PubMed] [Google Scholar]
- 60.Dar A., Shachar M., Leor J., Cohen S. Optimization of cardiac cell seeding and distribution in 3D porous alginate scaffolds. Biotechnol. Bioeng. 2002;80:305–312. doi: 10.1002/bit.10372. [DOI] [PubMed] [Google Scholar]
- 61.Dvir-Ginzberg M., Gamlieli-Bonshtein I., Agbaria R., Cohen S. Liver tissue engineering within alginate scaffolds: effects of cell-seeding density on hepatocyte viability, morphology, and function. Tissue Eng. 2003;9:757–766. doi: 10.1089/107632703768247430. [DOI] [PubMed] [Google Scholar]
- 62.Holy C.E., Shoichet M.S., Davies J.E. Engineering three-dimensional bone tissue in vitro using biodegradable scaffolds: investigating initial cell-seeding density and culture period. J. Biomed. Mater. Res. 2000;51:376–382. doi: 10.1002/1097-4636(20000905)51:3<376::aid-jbm11>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 63.Mauck R.L., Wang C.C., Oswald E.S., Ateshian G.A., Hung C.T. The role of cell seeding density and nutrient supply for articular cartilage tissue engineering with deformational loading. Osteoarthritis Cartilage. 2003;11:879–890. doi: 10.1016/j.joca.2003.08.006. [DOI] [PubMed] [Google Scholar]
- 64.Saini S., Wick T.M. Concentric cylinder bioreactor for production of tissue engineered cartilage: effect of seeding density and hydrodynamic loading on construct development. Biotechnol. Prog. 2003;19:510–521. doi: 10.1021/bp0256519. [DOI] [PubMed] [Google Scholar]
- 65.Wiedmann-Al-Ahmad M., Gutwald R., Lauer G., Hübner U., Schmelzeisen R. How to optimize seeding and culturing of human osteoblast-like cells on various biomaterials. Biomaterials. 2002;23:3319–3328. doi: 10.1016/s0142-9612(02)00019-4. [DOI] [PubMed] [Google Scholar]
- 66.Tchuente M. Computation on automata networks. In: Fogelman-Soulie F., Robert Y., Tchuente M., editors. Automata Networks in Computer Science. Theory and Applications. Princeton University Press; Princeton, NJ: 1987. [Google Scholar]
- 67.Toffoli T., Margolus N. MIT Press; Cambridge, MA: 1987. Cellular Automata Machines. A New Environment for Modeling. [Google Scholar]
- 68.Youssef B.B., Cheng G., Zygourakis K., Markenscoff P. Parallel implementation of a cellular automaton modeling the growth of three-dimensional tissues. Int. J. High Perform. Comput. Appl. 2007;21:196–209. [Google Scholar]
- 69.Burgess B.T., Myles J.L., Dickinson R.B. Quantitative analysis of adhesion-mediated cell migration in three-dimensional gels of RGD-grafted collagen. Ann. Biomed. Eng. 2000;28:110–118. doi: 10.1114/1.259. [DOI] [PubMed] [Google Scholar]
- 70.Shields E.D., Noble P.B. Methodology for detection of heterogeneity of cell locomotory phenotypes in three-dimensional gels. Exp. Cell Biol. 1987;55:250–256. doi: 10.1159/000163423. [DOI] [PubMed] [Google Scholar]
- 71.Weidt C., Niggemann B., Hatzmann W., Zänker K.S., Dittmar T. Differential effects of culture conditions on the migration pattern of stromal cell-derived factor-stimulated hematopoietic stem cells. Stem Cells. 2004;22:890–896. doi: 10.1634/stemcells.22-6-890. [DOI] [PubMed] [Google Scholar]
- 72.Lee Y., Kouvroukoglou S., McIntire L.V., Zygourakis K. A cellular automaton model for the proliferation of migrating contact-inhibited cells. Biophys. J. 1995;69:1284–1298. doi: 10.1016/S0006-3495(95)79996-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lee Y., Markenscoff P., McIntire L.V., Zygourakis K. Characterization of endothelial cell locomotion using a Markov chain model. Biochem. Cell Biol. 1996;73:461–472. doi: 10.1139/o95-052. [DOI] [PubMed] [Google Scholar]
- 74.Cheng G., Zygourakis K. Cell migration. In: Bronzino J.D., editor. Tissue Engineering and Artificial Organs (Biomedical Engineering Handbook) CRC Press; Boca Raton, FL: 2006. pp. 21–31. [Google Scholar]
- 75.Bergman A.J., Zygourakis K. Migration of lymphocytes on fibronectin-coated surfaces: temporal evolution of migratory parameters. Biomaterials. 1999;20:2235–2244. doi: 10.1016/s0142-9612(99)00154-4. [DOI] [PubMed] [Google Scholar]
- 76.Lee, Y. 1994. Computer-assisted analysis of endothelial cell migration and proliferation. Ph.D. thesis. Rice University, Houston, TX.
- 77.Obradovic B., Carrier R.L., Vunjak-Novakovic G., Freed L.E. Gas exchange is essential for bioreactor cultivation of tissue engineered cartilage. Biotechnol. Bioeng. 1999;63:197–205. doi: 10.1002/(sici)1097-0290(19990420)63:2<197::aid-bit8>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 78.Malda J., Martens D.E., Tramper J., van Blitterswijk C.A., Riesle J. Cartilage tissue engineering: controversy in the effect of oxygen. Crit. Rev. Biotechnol. 2003;23:175–194. [PubMed] [Google Scholar]
- 79.Murray J.D. Springer-Verlag; New York: 1989. Mathematical Biology. [Google Scholar]
- 80.McKeehan W.L., McKeehan K.A. Extracellular regulation of fibroblast multiplication: a direct kinetic approach to analysis of role of low molecular weight nutrients and serum growth factors. J. Supramol. Struct. Cell. Biochem. 1981;15:83–110. doi: 10.1002/jsscb.1981.380150109. [DOI] [PubMed] [Google Scholar]
- 81.Aris R. Clarendon Press; Oxford, UK: 1975. The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts: Questions of Uniqueness, Stability and Transient Behaviour. [Google Scholar]
- 82.Aris R. Clarendon Press; Oxford, UK: 1975. The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts: The Theory of the Steady State. [Google Scholar]
- 83.Cedrola S., Cardani R., La Porta C.A. Effect of glucose stress conditions in BL6T murine melanoma cells. Melanoma Res. 2004;14:345–351. doi: 10.1097/00008390-200410000-00003. [DOI] [PubMed] [Google Scholar]
- 84.Hwang S.O., Lee G.M. Nutrient deprivation induces autophagy as well as apoptosis in Chinese hamster ovary cell culture. Biotechnol. Bioeng. 2008;99:678–685. doi: 10.1002/bit.21589. [DOI] [PubMed] [Google Scholar]
- 85.Kouvroukoglou S., Lakkis C.L., Wallace J.D., Zygourakis K., Epner D.E. Bioenergetics of rat prostate cancer cell migration. Prostate. 1998;34:137–144. doi: 10.1002/(sici)1097-0045(19980201)34:2<137::aid-pros9>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 86.Cheng, G.2005. Hybrid computational modeling of cell population and mass transfer dynamics in tissue growth processes. PhD thesis. Rice University, Houston, TX.
- 87.Ruuth S.J. Implicit-explicit methods for reaction-diffusion problems in pattern formation. J. Math. Biol. 1995;34:148–176. [Google Scholar]
- 88.Balay S., Gropp W.D., McInnes L.C., Smith B.F. Efficient management of parallelism in object oriented numerical software libraries. In: Arge E., Bruaset A.M., Langtangen H.P., editors. Modern Software Tools in Scientific Computing. Birkhauser Press; Basel, Switzerland: 1997. pp. 163–202. [Google Scholar]
- 89.Hempel R., Walker D.W. The emergence of the MPI message passing standard for parallel computing. Comput. Stand. Interfaces. 1999;21:51–62. [Google Scholar]
- 90.Akins R.E., Boyce R.A., Madonna M.L., Schroedl N.A., Gonda S.R. Cardiac organogenesis in vitro: reestablishment of three-dimensional tissue architecture by dissociated neonatal rat ventricular cells. Tissue Eng. 1999;5:103–118. doi: 10.1089/ten.1999.5.103. [DOI] [PubMed] [Google Scholar]
- 91.Papadaki M., Bursac N., Langer R., Merok J., Vunjak-Novakovic G. Tissue engineering of functional cardiac muscle: molecular, structural, and electrophysiological studies. Am. J. Physiol. Heart Circ. Physiol. 2001;280:H168–H178. doi: 10.1152/ajpheart.2001.280.1.H168. [DOI] [PubMed] [Google Scholar]
- 92.Solchaga L.A., Tognana E., Penick K., Baskaran H., Goldberg V.M. A rapid seeding technique for the assembly of large cell/scaffold composite constructs. Tissue Eng. 2006;12:1851–1863. doi: 10.1089/ten.2006.12.1851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Wang J., Asou Y., Sekiya I., Sotome S., Orii H. Enhancement of tissue engineered bone formation by a low pressure system improving cell seeding and medium perfusion into a porous scaffold. Biomaterials. 2006;27:2738–2746. doi: 10.1016/j.biomaterials.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 94.Xie J., Jung Y., Kim S.H., Kim Y.H., Matsuda T. New technique of seeding chondrocytes into microporous poly(L-lactide-co-ɛ-caprolactone) sponge by cyclic compression force-induced suction. Tissue Eng. 2006;12:1811–1820. doi: 10.1089/ten.2006.12.1811. [DOI] [PubMed] [Google Scholar]
- 95.Rupnick M.A., Stokes C.L., Williams S.K., Lauffenburger D.A. Quantitative analysis of random motility of human microvessel endothelial cells using a linear under-agarose assay. Lab. Invest. 1988;59:363–372. [PubMed] [Google Scholar]
- 96.Stokes C.L., Lauffenburger D.A., William S.K. Migration of individual microvessel endothelial cells: stochastic model and parameter measurement. J. Cell Sci. 1991;99:419–430. doi: 10.1242/jcs.99.2.419. [DOI] [PubMed] [Google Scholar]
- 97.DiMilla P., Stone J., Quinn J., Albelda S., Lauffenburger D.A. Maximal migration of smooth muscle cells on fibronectin and collagen-IV occurs at an intermediate attachment strength. J. Cell Biol. 1993;122:729–737. doi: 10.1083/jcb.122.3.729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Zigmond S.H., Klausner R., Tranquillo R.T., Lauffenburger D.A. Analysis of the requirements for time-averaging of receport occupancy for gradient detection by polymorphonuclear leukocytes. In: Czech M., Kahn C.R., editors. Membrane Receptors and Cellular Regulation. Alan R. Liss; New York: 1985. pp. 347–356. [Google Scholar]
- 99.Barrandon Y., Green H. Cell migration is essential for sustained growth of keratinocyte colonies: the roles of transforming growth factor-α and epidermal growth factor. Cell. 1987;50:1131–1137. doi: 10.1016/0092-8674(87)90179-6. [DOI] [PubMed] [Google Scholar]
- 100.Barrandon Y., Green H. Three clonal types of keratinocyte with different capacities for multiplication. Proc. Natl. Acad. Sci. USA. 1987;84:2302–2306. doi: 10.1073/pnas.84.8.2302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Sato Y., Rifkin D.B. Autocrine activities of basic fibroblast growth factor: regulation of endothelial cell movement, plasminogen activator synthesis, and DNA synthesis. J. Cell Biol. 1988;107:1199–1205. doi: 10.1083/jcb.107.3.1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Shin H., Jo S., Mikos A.G. Biomimetic materials for tissue engineering. Biomaterials. 2003;24:4353–4364. doi: 10.1016/s0142-9612(03)00339-9. [DOI] [PubMed] [Google Scholar]
- 103.Shin H., Zygourakis K., Farach-Carson M.C., Yaszemski M.J., Mikos A.G. Attachment, proliferation, and migration of marrow stromal osteoblasts cultured on biomimetic hydrogels modified with an osteopontin-derived peptide. Biomaterials. 2004;25:895–906. doi: 10.1016/s0142-9612(03)00602-1. [DOI] [PubMed] [Google Scholar]
- 104.Poll D.V., Sokmensuer C., Ahmad N., Tilles A.W., Berthiaume F. Elevated hepatocyte-specific functions in fetal rat hepatocytes co-cultured with adult rat hepatocytes. Tissue Eng. 2006;12:2965–2973. doi: 10.1089/ten.2006.12.2965. [DOI] [PubMed] [Google Scholar]
- 105.Seo S.J., Kim I.Y., Choi Y.J., Akaike T., Cho C.S. Enhanced liver functions of hepatocytes cocultured with NIH 3T3 in the alginate/galactosylated chitosan scaffold. Biomaterials. 2006;27:1487–1495. doi: 10.1016/j.biomaterials.2005.09.018. [DOI] [PubMed] [Google Scholar]
- 106.Koike N., Fukumura D., Gralla O., Au P., Schechner J.S. Tissue engineering: creation of long-lasting blood vessels. Nature. 2004;428:138–139. doi: 10.1038/428138a. [DOI] [PubMed] [Google Scholar]
- 107.Levenberg S., Rouwkema J., Macdonald M., Garfein E.S., Kohane D.S. Engineering vascularized skeletal muscle tissue. Nat. Biotechnol. 2005;23:879–884. doi: 10.1038/nbt1109. [DOI] [PubMed] [Google Scholar]
- 108.Rouwkema J., de Boer J., Van Blitterswijk C.A. Endothelial cells assemble into a 3-dimensional prevascular network in a bone tissue engineering construct. Tissue Eng. 2006;12:2685–2693. doi: 10.1089/ten.2006.12.2685. [DOI] [PubMed] [Google Scholar]
- 109.Choong C.S., Hutmacher D.W., Triffitt J.T. Co-culture of bone marrow fibroblasts and endothelial cells on modified polycaprolactone substrates for enhanced potentials in bone tissue engineering. Tissue Eng. 2006;12:2521–2531. doi: 10.1089/ten.2006.12.2521. [DOI] [PubMed] [Google Scholar]
- 110.Kobayashi K., Nomoto Y., Suzuki T., Tada Y., Miyake M. Effect of fibroblasts on tracheal epithelial regeneration in vitro. Tissue Eng. 2006;12:2619–2628. doi: 10.1089/ten.2006.12.2619. [DOI] [PubMed] [Google Scholar]
- 111.Niemeyer P., Kornacker M., Mehlhorn A., Seckinger A., Vohrer J. Comparison of immunological properties of bone marrow stromal cells and adipose tissue-derived stem cells before and after osteogenic differentiation in vitro. Tissue Eng. 2006;13:111–121. doi: 10.1089/ten.2006.0114. [DOI] [PubMed] [Google Scholar]
- 112.Pazzano D., Mercier K.A., Moran J.M., Fong S.S., DiBiasio D.D. Comparison of chondrogensis in static and perfused bioreactor culture. Biotechnol. Prog. 2000;16:893–896. doi: 10.1021/bp000082v. [DOI] [PubMed] [Google Scholar]
- 113.Bancroft G.N., Sikavitsas V.I., Mikos A.G. Design of a flow perfusion bioreactor system for bone tissue-engineering applications. Tissue Eng. 2003;9:549–554. doi: 10.1089/107632703322066723. [DOI] [PubMed] [Google Scholar]
- 114.Radisic M., Yang L., Boublik J., Cohen R.J., Langer R. Medium perfusion enables engineering of compact and contractile cardiac tissue. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H507–H516. doi: 10.1152/ajpheart.00171.2003. [DOI] [PubMed] [Google Scholar]


