Secondary Structure Propensities in Peptide Folding Simulations: A Systematic Comparison of Molecular Mechanics Interaction Schemes

Abstract

We present a systematic study directed toward the secondary structure propensity and sampling behavior in peptide folding simulations with eight different molecular dynamics force-field variants in explicit solvent. We report on the combinational result of force field, water model, and electrostatic interaction schemes and compare to available experimental characterization of five studied model peptides in terms of reproduced structure and dynamics. The total simulation time exceeded 18 μs and included simulations that started from both folded and extended conformations. Despite remaining sampling issues, a number of distinct trends in the folding behavior of the peptides emerged. Pronounced differences in the propensity of finding prominent secondary structure motifs in the different applied force fields suggest that problems point in particular to the balance of the relative stabilities of helical and extended conformations.

Introduction

Molecular dynamics (MD) simulations are routinely utilized to study the folding dynamics of peptides and small proteins as well as biomolecular aggregation. The critical constituents of such molecular mechanics studies are the validity of the underlying physical models together with the assumptions of classical dynamics and a sufficient sampling of the conformational space. To verify and validate simulation results, a careful comparison of the simulation outcome directly to experimental data is mandatory (e.g., obtained by nuclear magnetic resonance (NMR), circular dichroism (CD), or infrared spectroscopy (1)).

Comprehensive reports on applications and improvements, and the remaining challenges of empirical force-field-based simulation methods, the choice of water model, and electrostatic interaction schemes to study biomolecular systems, have been discussed in the literature (2–7).

Within the framework of MD force fields, particular importance is directed toward the consistent and proper parameterization of the atomistic interactions, with the functional formulation of the bonded and nonbonded forces often similar among nonpolarizable MD schemes. The latest efforts to improve the accuracy of the popular and commonly used force fields AMBER (8,9), CHARMM (10), GROMOS96 (11), and OPLS (12) mainly focused on refining parameters for the torsional potentials of the protein backbone to balance the conformational equilibrium between extended and helical structures.

A recent comparative study using selected variants of the AMBER, CHARMM, GROMOS96, and OPLS force fields reported on converging results for folded proteins between the different compared models. It was suggested that there is an apparent consensus view of protein dynamics (13). In that study, simulations of relatively short lengths were performed and the natively folded state was used as starting point, possibly biasing the results (13).

For folding simulations, such a systematic test has not been carried out so far, although with growing computer power several approaches toward the in silico folding problem for peptides and small proteins, both using an implicit or explicit representation of the solvent environment, have been presented (14–20). Given an efficient sampling of conformational space and access to sufficient simulation timescales, one should expect to sample conformational ensembles close to the natively most populated states in solution, even when starting from peptide conformations away from the native structure. Hence, the application of biomolecular simulations offers the unique opportunity to study and predict complex processes in detail that underlie the protein folding thermodynamics and kinetics: for instance, the early events of peptide and protein folding, marked by established and stabilized secondary structure motifs (21).

A realistic preferential formation and representation of secondary structure is therefore a critical prerequisite for the successful study of in silico folding and aggregation. Thus, the question of overall peptide folding representation in different force fields prompted us to investigate the folding behavior and secondary structure formation at the microsecond timescale of a number of prototypic peptides in different MD force fields.

Here, we present the results of peptide folding and secondary structure formation for five model peptides (two β-hairpins, two α-helical peptides, and the Trp-cage) in five state-of-the-art force fields and different schemes for calculating electrostatic interactions. Extensive MD simulations in explicit water, starting from both extended and prefolded structures are presented that address the folding thermodynamics and sampling characteristics of the different interaction schemes.

Methods

Model peptides

We performed MD simulations of five isolated peptides, which adopt different well-defined, stable secondary or tertiary structures in solution (Table 1). We considered the chosen peptides as minimalistic model systems to probe the different force fields for either α-helical or β-sheet folding propensity. See the Supporting Material for details.

Table 1.

Experimental characterization of the model peptides

Peptide	Secondary structure (experimental conditions)	Experimental technique	Reference
Chignolin	β-Hairpin: 60% (300 K, pH 5.5)	CD and NMR	(22)
Mbh12	β-Hairpin: 66 ± 4% (278 K, pH 5)	CD and NMR	(23)
Trp-cage	α-Helix: 30% (300 K, pH 7)	CD and NMR	(24)
Fs21	α-Helix: 90% (Fs-NH2, 273 K, pH 7)	CD	(25)
	α-Helix: 55% (278 K)	Raman	(26,27)
	α-Helix: 50% (MABA-Fs-NH2, 300 K, pH 7)	CD	(28)
	Helical: 68% (300 K, pH 7)	AGADIR prediction algorithm	(21)
Agd1	Helical: 50% (300 K, pH 7)	AGADIR prediction algorithm	(21)

Setup and simulation procedure

The simulations were categorized according to the name of the peptide and the starting model. An overview of the simulated peptide systems is given in Table 2.

Table 2.

Summary of performed simulations with the respective number of residues (N_res) and the expected net charge in water at neutral pH (N_cha) for each model peptide

Peptide	Sequence (Nres/Ncha)	Simulation name	PDB #	Starting structure	Simulation length [ns]
Chignolin	NH3+-GYDPETGTWG-CO2−	CHI	(PDB: 1uao)	Extended	8 × 250
	(10/2−)	CHI.REF		β-Hairpin	8 × 250
Mbh12	NH3+-RGKWTYNGITYEGR-CO2−	MBH	(PDB: 1k43)	Extended	8 × 250
	(14/2+)	MBH.REF		β-Hairpin	8 × 250
Trp-cage (Tc5b)	NH3+-NLYIQWLKDGGPSSGRPPPS-CO2−	TC5B.REF	(PDB: 1l2y)	α-Helix/turn	8 × 250
	(20/1−)				8 × 3 × 30
Fs21	Ace-A5[AAARA]3A-NME	FS21		Extended	8 × 250
	(21/3+)	FS21.REF		α-Helix	8 × 250
Agd1 (de novo)	Ace-EVLMKVLMEIYLK-NH2	AGD1		Extended	8 × 250
	(13/0)	AGD1.REF		α-Helix	8 × 250

To overcome limited sampling and possible bias imposed by the starting structure, each peptide was simulated starting from both a folded and an unfolded (extended) conformation. The initially extended structures were obtained by constructing the respective peptide chain with PyMOL (29) by imposing an all-trans geometry to every backbone dihedral. The folded conformations were either obtained from the Protein Data Bank (i.e., PDB; first model of the respective NMR-ensembles) 1uao (Chignolin), 1k43 (Mbh12), 1l2y (Tc5b), or, in case of the helical peptides (Fs₂₁, Agd1), by building an α-helical conformation. The Fs₂₁ and Agd1 peptides were capped with acetyl groups at the N-terminus. To cap the C-terminal site, N-methyl- and amino groups were used, respectively. The terminal residues of the Chignolin and Mbh12 peptides were considered charged. The protonation state of the peptides was according to the one in solution at pH 7; counterions (Na⁺, Cl⁻) were added to adjust for excess charges.

The MD simulations of the respective peptide monomers and subsequent analysis were carried out using the GROMACS software package (version 3.3.1) (30–32). Each of the production runs after equilibration was 250-ns long. In case of the Tc5b peptide, three additional 30-ns runs per force field were carried out.

We focused on the comparison of force-field variants as implemented in the GROMACS simulation software suite: GROMOS96 43A1 (33,34), GROMOS96 53A6 (11,35), OPLS-AA/L (12,36), AMBER03 (ff03) (8), and AMBER99SB (ff99SB) (9,37). The input parameters were chosen according to the original publications of the developers to ensure a systematic comparison between the tested force fields. Table S1 summarizes the cutoff distances for the nonbonded interactions that were used with the different force fields, respectively.

All simulations were carried out with electrostatic schemes as originally used for force-field development. In addition, the particle mesh Ewald (PME) (38) method was used for comparison, as it is nowadays common practice to apply PME in conjunction with force fields like OPLS and GROMOS96 (G96), which were originally designed using cutoff and reaction-field (RF) (39), respectively.

In our study, the electrostatic interactions with PME were calculated with a grid spacing of 0.12 nm. The relative tolerance at the cutoff was set at 10⁻⁶, and electrostatic interactions for a distance smaller than the real space cutoff were calculated explicitly. For the calculations with reaction-field (G96 force fields), the relative dielectric permittivity outside the cutoff sphere was set to ɛ = 54 (SPC water) (40).

To set up the simulation system, each peptide was placed in a periodic truncated octahedral box solvated with explicit water. The distance between solute and box was chosen to be at least 1.5 nm on all sides. The SPC water model (41) was used for the simulations with the G96 43A1/53A6 force fields; the TIP4P solvent model (42) was applied when using the OPLS-AA/L force field, and TIP3P was applied (43) for AMBER03 and AMBER99SB. The system was subsequently energy-minimized using steepest descent. Initial velocities were taken from a Maxwell distribution at 300 K. Rigid bond constraints were chosen, providing a reasonable representation of the covalent bond geometry of the studied timescales (44). All protein bonds were constrained with the SHAKE algorithm (45) for simulations with G96 43A1/53A6 and OPLS-AA/L, and LINCS (46) when using AMBER03 and AMBER99SB. An integration time step of 2 fs was chosen. Water was constrained using SETTLE (47). Neighbor lists for nonbonded interactions were updated every five steps for the G96 and OPLS, and every 10 steps for simulations with the AMBER force fields. Berendsen coupling algorithms (48) were applied to the simulation system. The temperature was kept constant by weakly (τ = 0.1 ps) coupling the system to a temperature bath of 300 K. Likewise, the pressure was kept constant by coupling the system to a pressure bath of 1 bar (τ = 1 ps).

Analysis

For assessment of secondary structure type and content, the DSSP definition introduced by Kabsch and Sander (49) was used. The data was averaged over both simulations starting from the extended and the reference structure. The first 10% of the 250-ns and the first 50% for the 30-ns runs of each trajectory were omitted to reduce the bias of the respective starting model.

Nuclear Overhauser enhancement

The nuclear Overhauser enhancement (NOE) distance restraint sets for Chignolin, Mbh12, and Tc5b (available from the PDB) were used to calculate ensemble sum-averaged violations (r⁻⁶) of NOE distances in the MD ensembles. The violations were calculated based on a set of 250 conformations (one snapshot per ns) taken from each trajectory, respectively. To account for the different representations of the peptides in the used force fields, each of the 250 representative structures was converted to a OPLS topology with the pdb2gmx program before analysis, adding explicit proton positions to aliphatic carbon atoms.

Principal component analysis

The principal component analysis (PCA) (50) was carried out over the combined trajectories starting from different initial structures (extended and reference) for each peptide in each force-field test setting. The covariance matrix of atomic displacement was calculated and diagonalized for the coordinates of main-chain and C_β atoms. All structures were superimposed to the respective reference conformation before analysis.

Results

Structural properties

The conformations sampled during the simulations were compared to experimental data from CD and NMR measurements.

Root mean-square deviation

We performed an analysis of the root mean-square deviations (RMSD) for the peptides with experimentally determined native state (Chignolin, Mbh12, and Tc5b). Fig. 1 shows the RMSD for the main-chain and C_β atom coordinates of these three peptides to the respective NMR reference structure as function of simulation time. A low RMSD (<0.2 nm) denotes a conformational state that is close to the one observed in the experiment. Averaged RMSDs for each simulation are summarized in Table S2.

Figure 1.

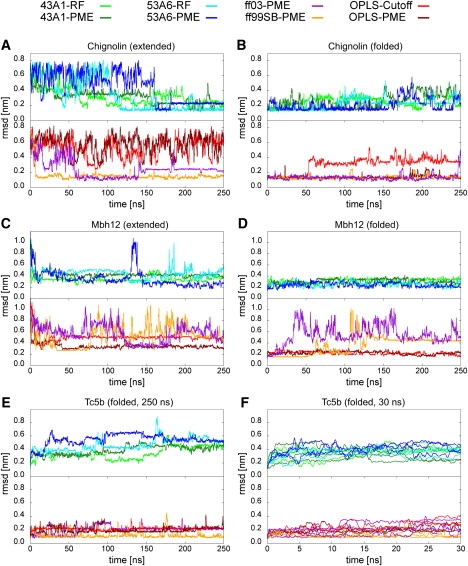
RMSD of the main-chain and C_β atoms with respect to the NMR reference structure as function of the simulation time for Chignolin, Mbh12, and Tc5b. RMSD curves for the simulations CHI (A), CHI.REF (B), MBH (C), MBH.REF (D), TC5B.REF −250 ns (E), and TC5B.REF −30 ns (F) were smoothed.

We will first focus on the RMSDs for the β-hairpin-peptides (Chignolin, Mbh12). For the simulations starting from the folded reference state of Chignolin (CHI.REF), we found only small structural deviations over the total range of simulation time in most of the different force fields, indicating a stable fold.

Particularly low deviations from the reference structure are found with ff99SB, OPLS-PME for the CHI.REF simulations. The hairpin structure is partly lost for the simulations with ff03, 43A1 as well as OPLS-Cutoff. Different results were obtained for the simulations started from an extended peptide chain (CHI). The Chignolin peptide is folded to a structure very close to the experimentally determined one, for example with ff99SB and ff03, respectively (Fig. 1, A and B). A high structural stability from the prefolded state and fast sampling toward the reference therefore led to the overall smallest RMSDs in both AMBER force fields, irrespective of the initial configuration. In addition, the correct folded state was adopted in all G96 simulations (Fig. 1, A and B). The OPLS force fields with either PME or cutoff, however, did not sample the folded configuration within 250 ns. This is in contrast to the result that the hairpin structure was found to be stable for the combination of OPLS and PME.

A different scenario arises from the simulations starting from the extended chain of the Mbh12 peptide (MBH). Hairpin formation took place rather fast in all studied G96 and OPLS force-field variants. The peptide conformations were also stable from the reference structure for these force fields. The MBH simulations in both AMBER force fields, however, did not sample stable hairpin structures, and the folded state was only transiently visited. Instead, partly α-helical conformations were sampled, which resulted in large RMSDs. Interestingly, this was also observed in the simulations starting from the NMR reference structure. The hairpin peptide did not unfold in any of the other MBH.REF simulations (Fig. 1, C and D).

The Tc5b simulations were started only from the reference NMR structure in the different force-field variants. In addition to one simulation of 250 ns, three independent runs of 30 ns were conducted to check for statistical significance of our results (Fig. 1, E and F). Reproducible low RMSDs of ∼0.12 nm were found for the structural ensembles sampled in the ff99SB force field. In contrast, large RMSDs were observed in the simulations using the G96 force fields. Furthermore, substantial unfolding events occurred already within the first 30 ns in most of the G96 trajectories (Fig. 1 F).

Nuclear Overhauser enhancement

An additional structural comparison to experimental data for both β-hairpin peptides and the Trp-cage can be drawn based on NOEs between proton pairs or groups of protons obtained from NMR experiments. Measured NOEs are usually translated into proton-proton distance ranges. Exceeding the upper limit of such a distance range was counted as NOE violation. For the studied peptides, the set of NOE restraints included short-range restraints between atoms on neighboring residues and intraresidual atoms, medium- and long-range restraints (see the Supporting Material). We determined the violations as an ensemble averaged sum. Results are shown in Table 3. As a consequence of slow or incomplete sampling toward the native structure, in general we found a larger total violation for the simulated ensembles starting from the extended conformations as compared to the simulations starting from the prefolded state.

Table 3.

Sum of NOE distance violations as ensemble average over 250 structures

System	Sum of NOE violations [nm]
	CHI	CHI.REF	MBH	MBH.REF	TC5B.REF
ff03-PME	0.99	0.72	7.83	3.87	3.10
ff99SB-PME	0.66	0.64	7.61	1.17	1.95
43A1-RF	1.30	1.17	3.04	1.16	6.09
43A1-PME	0.83	0.59	9.19	1.05	4.54
53A6-RF	0.98	0.72	7.09	0.83	7.25
53A6-PME	2.69	0.67	1.22	0.87	10.03
OPLS-Cutoff	5.32	1.34	10.27	1.11	3.21
OPLS-PME	12.04	0.61	5.29	0.95	2.73

From the calculated interproton distances, we observed marginal deviations from the experimental structures for all hairpin peptides with the 53A6-PME and the 43A1-RF force-field variants, irrespective of the peptide's starting conformation. Except for 53A6-PME, all force fields showed rather large structural deviations for the Mbh12 peptide when starting from the extended state. The partially helical Trp-cage, however, is not represented correctly in any of the G96 force fields; the 53A6 versions, especially, yielded large NOE violations. The ff99SB force field showed fewest violations of distance restraints for the Trp-cage simulations with an ensemble sum-average of <2 nm, corresponding to a stable fold over the simulated 250 ns (Table 3).

This is in line with low values of summed NOE violations found with ff99SB and OPLS-PME, and to some extent with ff03, for both hairpin and helical peptides, in trajectories starting from the NMR reference structure (Table 3).

Secondary structure propensity

We calculated the average populations of various secondary structure elements as listed for the individual simulations in Tables 4 and 5. Each listed fraction represents a mean over 450 ns for the peptides Chignolin, Mbh12, Fs₂₁, Agd1, and 270 ns for the Tc5b in each specified force-field configuration, respectively. The development of the secondary structure content and representative snapshots for all simulations as a function of the simulation time are shown in Fig. S1–S10.

Table 4.

Averaged secondary structure content from DSSP analysis for the hairpin peptides

System	α-Helix		310-Helix		β-Sheet		β-Bridge		Turn
	CHI	MBH	CHI	MBH	CHI	MBH	CHI	MBH	CHI	MBH
ff03-PME	0.0	5.6	0.2	3.7	23.0	0.8	5.3	0.5	33.4	12.6
ff99SB-PME	0.0	0.4	0.1	0.9	26.2	16.9	5.9	1.3	37.1	14.5
43A1-RF	0.4	0.0	0.1	0.2	10.8	27.2	7.0	2.6	18.0	4.8
43A1-PME	0.1	0.0	0.3	0.1	8.8	45.9	0.3	2.1	22.6	10.1
53A6-RF	0.1	0.0	0.1	0.1	19.6	37.6	4.7	2.0	25.7	8.1
53A6-PME	0.0	0.0	0.2	0.0	15.5	34.3	4.6	2.0	24.7	5.1
OPLS-Cutoff	0.0	0.0	1.9	0.0	1.7	27.0	2.1	1.4	15.8	14.0
OPLS-PME	0.0	0.0	0.0	0.0	11.6	32.3	3.6	3.0	18.6	5.7

Table 5.

Averaged secondary structure content from DSSP analysis for the helical peptides

System	α-Helix			310-Helix			π-Helix			β-Sheet/ β-Bridge			Turn
	TC5B	FS21	AGD1	TC5B	FS21	AGD1	TC5B	FS21	AGD1	TC5B	FS21	AGD1	TC5B	FS21	AGD1
ff03-PME	33.8	74.4	32.5	15.0	0.8	9.2	0.0	0.0	0.0	0.0	0.0	0.0	9.9	4.7	14.0
ff99SB-PME	34.2	0.6	5.7	15.1	2.5	6.8	0.0	0.0	0.0	0.0	8.7	0.2	10.4	8.1	10.4
43A1-RF	26.8	7.8	25.7	0.4	0.6	0.0	0.2	0.3	20.0	3.1	14.2	3.6	15.6	10.0	8.4
43A1-PME	25.9	16.8	3.6	0.1	0.3	0.1	0.0	0.0	25.8	3.5	16.6	2.9	9.8	7.7	12.6
53A6-RF	7.1	0.3	2.7	0.3	0.1	0.1	0.1	0.0	1.8	5.4	18.4	3.5	5.3	5.4	7.8
53A6-PME	3.6	0.1	0.3	0.0	0.0	0.0	0.5	0.0	0.1	9.7	36.3	16.1	4.3	5.2	3.2
OPLS-Cutoff	22.5	14.5	14.0	1.2	4.5	4.6	0.0	0.0	0.1	0.2	3.4	0.0	17.9	13.3	18.7
OPLS-PME	20.7	13.4	2.7	1.7	3.2	4.3	0.0	0.1	0.0	0.2	4.3	6.4	19.9	12.6	11.9

The highest fractional population of turn and β-sheet conformations were found in the simulations of the hairpin peptides with ff99SB, ff03 for Chignolin and with 43A1-PME, both 53A6 sets, and OPLS-PME for Mbh12 (Table 4). These results are compatible with stable hairpin-structures, as found in solution. A significantly low presence of extended β-structures is observed in the conformational ensembles produced by OPLS used with cutoff for the Chignolin peptide. The same is true for the simulations of Mbh12 with ff03. Moreover, in ff03 a notable extent of α- and 3₁₀-helix structures was sampled instead, which was not found for the other hairpin peptides and appears to be in contrast to the experimental observations.

The secondary structure analysis of the helical peptides yielded a picture with larger differences between the occupied populations (Table 5).

Several differences in the secondary structure content for Tc5b (Trp-cage) were observed in the various tested force fields. The highest helical propensity was obtained with ff99SB and ff03. Both force fields yield the same percentage of α- and 3₁₀-helix, preserving the content of the reference state. In contrast, the 43A1 and OPLS force fields sampled no or only very few 3₁₀-helix structures, but maintained α-helical structures. A low occurrence of helical content is found with the 53A6 force-field variants, which also sampled the overall highest amount of β-structures for the Trp-cage among all tested force fields.

We identified the content of α-helical conformations in the simulations as a function of time (Fig. 2) to better assess the representation of the mainly helical peptides, which were also simulated from the extended conformation (Fs₂₁ and Agd1).

Figure 2.

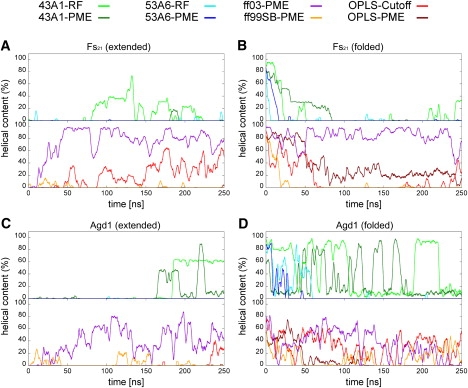
Percentage of α-helical segments present in the trajectories of Fs₂₁ and Agd1 peptides as function of simulation time. Helical content curves for the simulations FS21 (A), FS21.REF (B), AGD1 (C), and AGD1.REF (D) were smoothed.

In the respective combinations of force-field and electrostatic scheme we observed a distinct trend with a marked difference between the two different initial conformations for the Fs₂₁ peptide (Fig. 2, A and B). Starting from the completely α-helical reference state of Fs_21, the helix content in all systems, except for the simulations with ff03 and OPLS-PME, vanished rapidly (Fig. 2 A). Moreover, the helical content was found to be substantially higher with ff03 than in any of the other force fields. The Fs₂₁ peptide did not visit any helical conformation with ff99SB, but instead sampled coil structures. The simulations with 43A1 showed a tendency to nonlocal β-bridge/sheet contacts between the terminal sites of the peptide. The preference of coil and extended structures over helical ones was less pronounced when the reaction-field approach for electrostatics was used. Most notable for the simulations of Fs₂₁ is an observed loss or complete absence of helical content in most of the G96 simulations. Particularly low fractions of α-helix and a preferential conversion to extended conformations were found when using the 53A6 force field, regardless of the applied model for electrostatic treatment and starting structure. In fact, β-sheet was the predominant secondary structure for the Fs₂₁ peptide with 53A6-PME. Here, the whole peptide was readily folded into stable hairpinlike structures.

Starting from the extended conformation, the formation of an α-helix took place only in the simulations with the ff03, OPLS-Cutoff, and transiently with the 43A1-RF force field (Fig. 2 B). Sampling from the extended peptide chain did not converge within 250 ns with OPLS-PME.

The comparison to the experimental findings (Table 1) indicate that, for the conditions used in our simulations close to the melting temperature of the Fs₂₁ peptide at ∼300 K, neither a high helicity, as found with ff03, nor the completely extended structures sampled with the G96 force fields, are reasonable. Instead, a helical content of ∼50% would be consistent with the available CD data, therefore suggesting that only the FS21.REF simulation with OPLS and PME is reasonably well in line with the helical content found in the experiment.

The relative preference toward a certain secondary structure element is less distinct for the Agd1 peptide in the different force fields, although the overall trends are similar to the results obtained for Fs₂₁ (Fig. 2, C and D). Helix formation proceeded fast with ff03, while no helix formation and fast unfolding of the helix were observed with the 53A6 force field. The setup with 43A1 preserved the most helical content starting from the reference state of the Agd1 peptide. In addition, a significant amount of π-helix is observed, especially in combination with PME, which was not observed in simulations with other force fields or any of the other peptides. The repeated interconversion of α- to the π-helix can be seen as oscillation in the helical content plot (Fig. 2 D).

The helical content predicted with AGADIR for Agd1 (50% at 300 K) matched best with the ff03 and 43A1 simulations, while it was lower with all other remaining force fields.

In general, for simulations where force fields with different methods for the electrostatic interactions are used, distinct variations are observed. Particularly, the balance between the sampling of α-helix and β-sheet is affected. As can be seen from the analysis, the OPLS force field populates more sheet and less helix in all simulations with PME than with a simple cutoff for the electrostatics. For the 53A6 force field, the relative populations of α-helix and β-sheet are similarly affected. The differences are less distinct and systematic for the 43A1 model.

To further assess these differences we performed a dihedral analysis, obtaining a more direct view on the adopted local backbone conformations (Fig. S12, Fig. S13, and Fig. S14). The results highlight the preferential and relative sampling of extended versus helical structures for the model peptides, particularly for the simulations carried out with the G96 53A6 force field.

Sampling Properties

Principal component analysis

The conformational space explored by the peptides in each simulation was quantified using PCA (see Methods).

Figs. 3 and 4 show the projections of the trajectories onto the plane spanned by the first two common eigenvectors obtained from the PCA for the two hairpin peptides, respectively. The covered area in the projections represents the sampled conformational space in the given force field and with respect to the reference structure. Each point is a low-dimensional representation of a conformation sampled in the trajectory.

Figure 3.

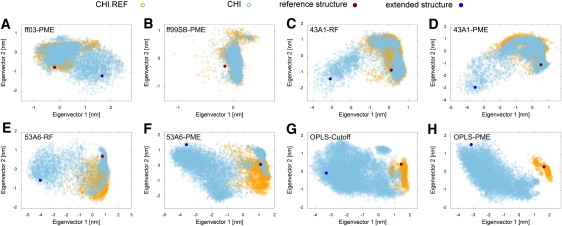
Comparison of the conformational space sampled in the simulations of the Chignolin peptide with ff03 (A), ff99SB (B), 43A1-RF (C), 43A1-PME (D), 53A6-RF (E), 53A6-PME (F), OPLS-Cutoff (G), and OPLS-PME (H). The individual trajectories were projected onto the first two common eigenvectors obtained from the PCA of the combined simulation runs for each force field, respectively. The location of the NMR reference structure and the completely extended starting conformation is indicated by a dot. Snapshots from each trajectory are shown with open circles.

Figure 4.

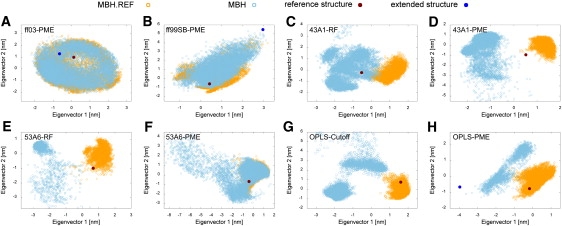
Conformational space sampled in the simulations of the Mbh12 peptide. Projections of the NMR reference structure, extended starting conformation, and snapshots from each trajectory are denoted according to Fig. 3.

The PCA projections of the Chignolin peptide simulations with the different force fields shown in Fig. 3 exhibit mostly overlaying phase space regions close to the reference structure. This denotes that the folded state was successfully found from the extended structure. Starting from the prefolded hairpin structure of Chignolin, mostly conformations close to the reference structure were sampled, compatible with a stable hairpin in solution. Interestingly, irrespective of the initial structure, almost the same conformational space is sampled by the ff99SB force field, indicative of a converged ensemble. Both independent trajectories (CHI and CHI.REF) cover the same area in the projection close to the NMR reference state (Fig. 3 B). For ff03, 43A1-RF, and 43A1-PME we found strongly overlapping areas in the projections of the simulations, irrespective of the starting conformations (Fig. 3, A, C, and D). The 53A6 force-field variants also found stable structures of the Chignolin peptide, sampling regions close to the reference (Fig. 3, E and F). In particular, the conformational space around the NMR reference was sampled exhaustively with 53A6-PME for both initial conditions, corresponding to the lowest averaged RMSDs and sum-averaged NOE distance violations among all tested force fields (Fig. 3 F). The overall trends of the conformational sampling in the simulations of Chignolin with OPLS-PME (Fig. 3 H) and OPLS-Cutoff (Fig. 3 G) are similar. The simulation ensembles, when started from the extended hairpin peptide (CHI), do not contain defined structures close to the reference state. A broad area corresponding to predominantly unfolded conformations was sampled with only few structures approaching the reference state. The explored conformational space in the CHI.REF simulations, however, was only very small and close to the reference. This substantial difference in the extent of visited phase space results in well-separated regions for the simulations with the different initial structures, especially with OPLS-PME (Fig. 3 H).

The PCA of the trajectories for Mbh12 yielded a less uniform picture concerning the sampling behavior of different force fields. For ff03, both trajectories of the hairpin peptide sampled the same regions of conformational space in the PCA projection, as seen before in the case of Chignolin. Most of the structures did not match with the NMR reference (Fig. 4 A). This is in line with the observation that the Mbh12 hairpin was least stable in ff03 among all force fields. Fig. 4 B shows an overlay of sampled phase space for both production runs with ff99SB, with structural ensembles close to the reference. A refolding event of the hairpin during the MBH.REF simulation resulted in a stable off-register structure, which is observed as a strongly sampled substate. As shown in Fig. 4 F, the simulations of Mbh12 carried out with 53A6-PME yielded nearly identical conformational ensembles in the projection, extensively populating conformations close to the NMR reference state.

In contrast, the sampled conformational space in the MBH and MBH.REF trajectories are separated for all other force fields. The 43A1-RF simulation starting from the extended peptide chain populated several substates in the PCA projection en route to hairpin formation (Fig. 4 C). We found markedly separated areas when comparing this projection to the one obtained from the 43A1-PME trajectories (Fig. 4 D). The projected simulation ensemble of Mbh12 with 53A6-RF was, contrary to one obtained with 53A6-PME, separated. The explored conformational space in the MBH simulation with the 53A6-RF force field appears very small and dense (Fig. 4 E).

The projections of the OPLS trajectories resemble the ones of the Chignolin peptide. The simulations from the extended chain (MBH) sampled mainly two states, which are separated in conformational space from the reference. Starting from the hairpin (MBH.REF), mostly folded conformations were gauged during the simulation as shown in Fig. 4, G and H.

Pronounced differences in conformational space sampling could also be found among the probed force fields for the simulations of the Trp-cage. The PCA projections are shown in Fig. S15.

Discussion

As seen from the NOE and PCA analysis, most of the simulations starting from the extended and folded structure showed differences in the sampled conformational ensembles indicating incomplete convergence. The only exceptions are the simulations with both tested AMBER force fields, in which the conformational space was quickly explored and did not critically depend on the initial structure.

The ff03 force field compared favorably to available experimental data in most of the simulations carried out. The only exceptions are a particularly high percentage of helical content for the polyalanine peptide Fs₂₁ and the unfolding of the Mbh12 hairpin, indicating a slight preference of helix over extended β-sheet conformations with ff03. This is in line with the results from Hornak et al. (9) for trialanine peptides and is known from previous AMBER force fields (52,53).

A fast sampling toward the reference state of the Chignolin peptide and particularly low RMSDs for the Trp-cage were found for the ff99SB force field. The analysis of secondary structure content and the low interproton distance violations suggest that the simulations with ff99SB agree well to available experimental data. The content of α-helix for the mainly helical peptides (Fs₂₁, Agd1) was likely underestimated.

The GROMOS96 force fields revealed an underestimation of propensity for sampling α-helical conformations in the simulations. While the results for the 43A1 version were well balanced for most of the model peptides, a significant disparity was the considerable amount of π-helix, which was not found in the other force fields. Different methods for electrostatics (RF, PME) in conjunction with the 43A1 force field were found to have little effect on the folding characteristics of the model peptides. The simulations using PME showed a slightly better structural representation, but sampling might be more efficient with the reaction-field approach (54). With the 53A6 force-field variants, β-sheet formation was most abundant and persistent when comparing the results from all simulations. The structural representation of the hairpin peptides was in very close agreement with NOE data. Preformed α-helical conformations were, however, least stable with 53A6 in all helical model peptides. Moreover, using PME appears to favor extended conformations even more. In accordance with our results, reproducible unfolding of α-helical peptides was reported recently by Cao et al. in a study presenting refined terms of conformational backbone description for 53A6 (55). Another study also found reduced structural variety and less covered phase space in the simulations with 53A6 compared to earlier GROMOS96 variants, which was suggested to be due to the increased partial charges on the backbone carbonyls and amides (11,56). The peptide torsion angle potentials used within the GROMOS 53A6 force field are currently being revised (B. Zagrovic, Split Mediterranean Institute for Life Sciences, and A. E. Mark, Molecular Dynamics Group, School of Molecular and Microbial Sciences, University of Queensland, personal communication, 2009).

The combination of OPLS force field and PME for electrostatics provided superior results compared to the OPLS with a straight cutoff, and most of the other force field models, when representing the folded state. However, the chosen initial conformations affected the sampled structural ensembles considerably. A dependence on the initial conditions, especially for the OPLS force field, was apparent, suggesting slower conformational sampling than observed in the other studied force fields. The sampling differences between the different force fields indicate a different roughness of the respective energy landscapes, affecting the convergence of the simulations.

For the helical peptides, we found least overall concurrent sampled secondary structure with the different force fields as the helical systems were simulated near their melting temperature. In this regime, small shifts in the free energy involve large changes in the population of folded and unfolded conformations, and thus slightly different melting temperatures in the different force fields might contribute to the found pronounced differences in sampled helical propensity among the simulations.

In the large set of simulations presented here, the CHARMM force field was not included, as it is still lacking a validated port for the GROMACS software package. Assessing the performance of the CHARMM force field in the context of the discussed simulation results would be an interesting aspect to address in future studies.

Conclusion

Peptide folding with MD simulations is inherently dependent on the accuracy of the applied force field. The observed similarities between different force fields support the consensus view of biomolecular dynamics (13), but remaining differences emphasize the importance of continuous force-field development and refinement.

The folding behavior of various peptide sequences in different MD force fields revealed significant and systematic differences in the stability and formation propensity of dominant secondary structure elements. Our observations suggest that, in particular, the relative stabilities of helical and extended conformations depend on a subtle balance of force-field parameters. In addition, we found indications for different sampling characteristics of the respective force fields, affecting both the kinetics and convergence of the simulations.

It is likely that the discussed deviations in the structural representations are less critical in protein simulations, when starting from the folded native state. However, a significant bias for peptide and protein simulations on long timescales is expected (20). This also indicates the relevance for simulations of folding intermediates, natively unfolded proteins, and studies on peptide aggregation.

Concerning the treatment of electrostatics, it is nowadays common practice to apply PME for biomolecular simulations. However, care is required when employing PME in conjunction with force fields and water models which were originally developed using cutoff or reaction-field (OPLS, GROMOS96) (2). In terms of secondary structure propensities, the peptides studied here revealed a tendency toward sampling β-hairpin structures when employing PME combined with the OPLS and GROMOS96 force fields.

In summary, for folding studies, a force-field bias cannot be excluded, and from the current perspective there is no single best-fit solution for peptide folding simulations with today's nonpolarizable force fields. We suggest a multiple force-field or consensus approach, if computationally feasible to simulate, using more than one suitable force field to address the particular question at hand, and whenever possible, to compare the simulation results to direct experimental data.

Supporting Material

Two tables and 15 figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00980-1.