Alternating-Site Mechanism of Kinesin-1 Characterized by Single-Molecule FRET Using Fluorescent ATP Analogues

Abstract

Kinesin-1 motor proteins move along microtubules in repetitive steps of 8 nm at the expense of ATP. To determine nucleotide dwell times during these processive runs, we used a Förster resonance energy transfer method at the single-molecule level that detects nucleotide binding to kinesin motor heads. We show that the fluorescent ATP analog used produces processive motility with kinetic parameters altered <2.5-fold compared with normal ATP. Using our confocal fluorescence kinesin motility assay, we obtained fluorescence intensity time traces that we then analyzed using autocorrelation techniques, yielding a time resolution of ∼1 ms for the intensity fluctuations due to fluorescent nucleotide binding and release. To compare these experimental autocorrelation curves with kinetic models, we used Monte-Carlo simulations. We find that the experimental data can only be described satisfactorily on the basis of models assuming an alternating-site mechanism, thus supporting the view that kinesin's two motor domains hydrolyze ATP and step in a sequential way.

Introduction

Kinesin-1 (formerly conventional kinesin) is a molecular motor that moves along microtubules at the expense of ATP. Its mechanism has been studied extensively and many of its features are well understood (1). However, kinetic and laser trapping experiments suggest an incredibly fast rate from the prestep to poststep position in an 8 nm distance of >1000–2000 s⁻¹, which is hard to reconcile with kinetic and structural models (2,3). Several studies suggest that kinesin can adopt a conformation in which it “waits” for a fresh ATP molecule that triggers the subsequent, extremely fast step. In this “ATP waiting state”, the tightly microtubule-bound head is nucleotide-free and the other one contains ADP. Kinesin's conformation in this ATP waiting state is still controversial, but several structural and kinetic studies are consistent with the view that the ADP-containing, weakly microtubule-bound motor head lags behind the firmly attached, nucleotide-free head (4–10). Alternatively, it has been suggested that the ADP-containing head may wait in a “parked” position close to the tightly bound head and without contact to the microtubule (11). To approach this problem and to understand the entrance into and exit from the waiting state (regardless of its structure), accurate knowledge about the nucleotide binding times and rates is crucial. This issue has been addressed extensively in kinetic studies that elucidated the microtubule-dependent ATPase cycle of Kinesin-1 and gave rise to the so-called “alternating-site catalysis” model proposed in early studies (12–14). It turned out, however, that the interpretation of these “classical” experiments is not easy because the observed signals result from convoluted events of two interdependent kinesin heads. The two heads of kinesin undergo the same kinetic cycle but are shifted in phase. Moreover, it is not clear whether the experimental entry point into the kinetic cycle always reflects the kinetics during processive movement. For some purposes, for example, ADP release experiments are initiated by mixing free kinesin with microtubules. Under these conditions, one head binds to microtubules and loses ADP, but it is not clear whether this initial microtubule-binding event is fully equivalent to microtubule binding during processive movement.

To circumvent these problems, we used a microscopy assay that allows the observation of nucleotide turnover by single kinesin motors moving processively along microtubules. To detect nucleotide binding to kinesin, we used Förster resonance energy transfer (FRET) between the motor head and nucleotide (Fig. 1). To obtain the time resolution required (∼1 ms), we used our recently developed kinesin motility assay based on single-motor confocal fluorescence microscopy (15). Our approach reveals key features of kinesin's chemomechanical cycle.

Figure 1.

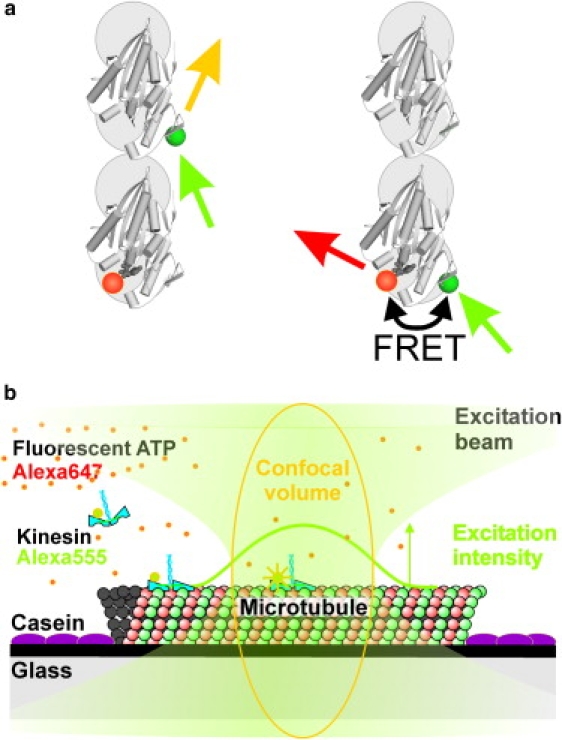
Schematic representation of the experimental setup. (a) Molecular model of FRET between S43C-labeled kinesin and fluorescent nucleotide. Two microtubule-bound motor domains (PDB: 2KIN (27)), one of which is labeled by Alexa Fluor 555 (green dots), are depicted from the top (+ end upward). The acceptor-labeled nucleotide (orange dots) is bound to the rearward head. Negligible FRET efficiencies are expected in the situation shown on the left, where fluorescent nucleotide is bound to the leading head. The close proximity of S43C to the nucleotide-binding pocket gives rise to efficient FRET when Alexa Fluor 555 label and fluorescent ATP are at the same motor domain (right). (b) Schematic representation of the single-motor FRET assay based on confocal fluorescence microscopy. A microtubule is attached to a glass surface using charge interactions. The surface is blocked for nonspecific interactions with casein. The confocal spot of a fluorescence microscope is positioned on the microtubule. Alexa Fluor 555-labeled kinesins walk through the excitation spot and either emit or transfer the excitation to Alexa Fluor 647-labeled ATP bound to the motor. The fluorescence of both Alexa Fluor 555 and 647 is collected and detected.

Materials and Methods

Construction, purification, and labeling of Kinesin-1

The Kinesin-1 used in this study was a 391 amino acids long version of human ubiquitous kinesin (KIF5B) with a reduced number of cysteine residues (16). Its gene was cloned into a bacterial pET17 expression vector by polymerase chain reaction. Residue S43 was chosen as a labeling target on the basis of the crystal structure (PDB accession codes 1BG2 and 3KIN). This residue is solvent-exposed and does not appear to be functionally important. The distances from the Cα atom of residue 43 to the 2′OH of ADP in 3KIN is ∼25–30 Å (intrahead distances in head A and B). The codon for S43 was replaced with a cysteine codon using the QuikChange protocol (Stratagene, La Jolla, CA). Protein was expressed in Escherichia coli BL21(RIL) and purified by phosphocellulose and Q-sepharose chromatography in 25 mM Pipes · NaOH, pH 7.2, 2 mM MgCl₂, and 1 mM EGTA. Kinesin was eluted in the same buffer with increasing NaCl concentrations.

The protein was labeled with Alexa Fluor 555 maleimide (Invitrogen, Carlsbad, CA). To that end, protein was incubated on ice with a fourfold stoichiometric excess of dye for 45 min. The reaction was stopped with 2 mM DTT, and excess dye was removed by microtubule affinity. For this, kinesin was incubated with an excess of microtubules and 1 mM AMP-PNP (adenosine 5′-(β,γ-imido)triphosphate) for 30 min at room temperature, followed by 10 min of centrifugation at 80,000 rpm over a 40% (w/v) sucrose cushion in a Beckman (Fullerton, CA) Optima TLA 100 rotor. The pellet was thoroughly washed and suspended in buffer containing 1 mM ATP. For fluorimetric FRET assays, the release was induced by 1 mM Alexa Fluor 647 ATP (Alexa Fluor 647 2′-(or-3′)-O-(N-2-aminoethyl)urethane), hexa(triethylammonium)) (A22362; Invitrogen, Carlsbad, CA). To wash out excess fluorescent ATP, the solution was successively concentrated and diluted three times in an Amicon Ultra4 centrifuge bottle. The labeling stoichiometry was assessed by comparing the absorption at 280 nm and the wavelength of maximal dye absorption. The stoichiometry was comparable in different preparations with ∼1 fluorophore per kinesin dimer.

Bulk fluorescence spectra were measured in an Aminco Bowman AB1 spectrophotometer in PEM80 buffer (80 mM Pipes · KOH, pH 6.8, 5 mM MgCl₂, 0.5 mM EGTA, 20 μM taxol).

Sample preparation for confocal fluorescence assays

Microtubule seeds were polymerized by mixing 7.5 μM unlabeled tubulin, 2.5 μM TMR-labeled tubulin, and 0.2 mM GMPCPP (Guanosine-5′[(α,β)-methyleno]triphosphate; Jena Bioscience, Jena, Germany) for 15 min at 36°C. Afterward they were stabilized with PEM80 buffer (80 mM Pipes · KOH pH 6.8, 1 mM EGTA, 2 mM MgCl₂) containing 10 μM taxol. Microtubules were diluted and injected into the sample chamber and incubated for 10 min. Casein (sodium salt, from bovine milk; Sigma-Aldrich, St. Louis, MO) at 0.4 mg/mL in PEM80 was flushed into the chamber and allowed to incubate for 10 min. The chamber was rinsed with 10 μL PEM12 buffer (identical to PEM80 but with 12 mM Pipes · KOH). After these steps, the mix with kinesin motors was flushed into the chamber and the sample was sealed with vacuum grease. The mix consisted of PEM12 buffer containing kinesin, 2 mM MgCl₂, 5 mM TROLOX (Sigma-Aldrich, St. Louis, MO), an oxygen scavenger system (20 μg/mL glucose-oxidase, 35 μg/mL catalase, and 25 mM glucose) (15,17), an ATP regeneration system (10 mM phosphocreatine and 50 μg/mL creatine kinase), and fluorescent ATP and/or regular ATP (disodium salt, A-2383; Sigma-Aldrich). The use of DTT instead of TROLOX did not result in good motility.

Sample chambers were prepared as described before (15). Coverslips and slides were cleaned by incubation for 10 min in a plasma cleaner (Harrick Plasma, Ithaca, NY).

Confocal fluorescence microscope

The experimental setup used to measure donor fluorescence alone was exactly as described previously (15). For simultaneous donor and acceptor measurements, the detection path was altered. The emitted fluorescence first passed a 550DCLP dichroic long-pass mirror, and was then split into donor and acceptor channels by a second dichroic mirror 645DCXR. Finally, the emission beams passed band-pass filters before detection (filters HQ575/50 or HQ675/50; all dichroic mirrors and filters from Chroma, Rockingham, VT). Two separate avalanche photo diodes (SPQM-AQR-14; PerkinElmer, Vaudreuil, Canada) were used to count single photons in the donor and acceptor channels. Photon arrival times were detected with 12.5 ns time resolution using a counter board (6602; National Instruments, Austin, TX) and stored on a computer using custom-built LabVIEW software (LabVIEW 7.1; National Instruments, Austin, TX).

Calculation and analysis of the intensity autocorrelation

To detect single-molecule motility events, photon arrival times in the donor channel were binned in 20-ms time slices and analyzed visually. Only traces with a Gaussian shape, an amplitude corresponding to one donor fluorophore, and a width corresponding to the expected velocity were used for autocorrelation. The intensity autocorrelation, G, was calculated from the discrete intensity time traces, x(kΔt), Δt = 1 ms, using the following equation (discrete form of (18)):

$$G(n\Delta t)=\sum _{k=0}^{2N-2}x{(k\Delta t)}_{}x(n\Delta t+k\Delta t),$$ (1)

where N denotes the total number of bins that describe the signal. Equation 1 describes an autocorrelation that is not normalized and decays to zero for large time lags (from now on, nΔt is approximated as being a continuous time lag, τ). The correlations obtained by Eq. 1 were fitted with

$$G\left(\tau \right)={\left(1+\frac{\tau }{T_T}\right)}^{-1}\exp \left(-\frac{{\tau }^2}{\alpha T_{\text{step}}^2}\right)\left(1+A\exp \left(-\frac{\tau }{T_{\text{FRET}}}\right)\right),$$ (2)

which contains two contributions. The last term describes the intensity fluctuations due to FRET (with decay time T_FRET and amplitude A) (19). The first two terms describe the transit through the confocal spot, consisting of a Gaussian term (where α is a factor describing the width of our confocal volume, and T_step is the average step time) and a term containing the apparent diffusional contribution due to the stochastic nature of stepping (described by T_T) (15).

Monte Carlo modeling of the autocorrelations

To understand which chemomechanical models, kinetics, and fluorescence intensities may underlie the observed autocorrelation curves, we performed Monte Carlo simulations. The simulations and their analyses were performed using LabVIEW. First, we chose a kinetic scheme that could describe our data, consisting of the interconversion rates between the states and the fluorescence intensities of all the states. Initially, a circular four-state model without back reactions was used. From such a kinetic scheme, we randomly generated a series of dwell times in the states. On the basis of this and the intensities of the different states, we calculated intensity time traces that were subsequently transformed by autocorrelation and fitted with a single exponential.

Results

Fluorescent ATP binds, hydrolyzes, and produces movement

To measure the kinetic characteristics of ATP turnover during processive motility, we considered a FRET-based assay to detect motor-bound nucleotide (Fig. 1). To assess the feasibility of this approach, we characterized the binding of fluorescent ATP (ATP-Alexa Fluor 647, acceptor) to labeled kinesin (hKinS43C-Alexa Fluor 555, donor) by bulk fluorescence spectroscopy (Fig. 2). Alexa Fluor 555-labeled kinesin that was purified in the presence of ATP-Alexa Fluor 647 and therefore did not contain regular ATP was incubated with microtubules and additional fluorescent ATP. The fluorescence intensity was higher in the spectral range of acceptor emission (∼670 nm) than in that of the donor (560 nm). After the fluorescent nucleotide was chased with a large excess of regular, unlabeled ATP, the acceptor intensity decreased substantially and the donor intensity increased (Fig. 2 a, open circles). These observations show that ATP-Alexa Fluor 647 or its hydrolysis product, ADP-Alexa Fluor 647, binds to the motor domain of labeled Kinesin-1 and causes FRET.

Figure 2.

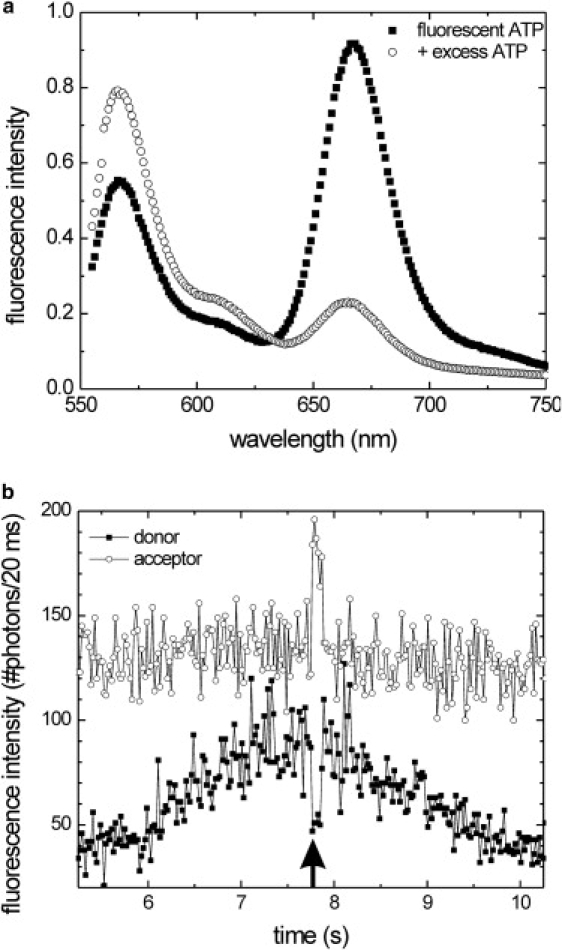
Properties of the fluorescent kinesin-ATP complex. (a) Emission spectra of Alexa Fluor 647-ATP: black squares show the emission spectrum of Alexa Fluor 647-ATP bound to Alexa Fluor 555-labeled kinesin (∼20 nM kinesin with an approximately equimolar amount of fluorescent ATP (see Materials and Methods); λ_excitation = 535 nm). The open circles represent the same sample after the addition of 1 mM of regular ATP. The drop of the acceptor emission (∼670 nm) and the rise of the donor emission (∼560 nm) after the ATP chase indicate resonance transfer between Alexa Fluor 647-ATP and Alexa Fluor 555-labeled kinesin. (b) Simultaneously collected fluorescence intensity time traces of both the donor (black squares) and the acceptor channel (open circles) of a donor-labeled kinesin moving through a confocal spot in the presence of 5 μM regular ATP and 0.5 μM fluorescent ATP. A dip in the donor signal (black arrow) is accompanied by a peak in the acceptor intensity, indicating that in this short time interval a fluorescent ATP was bound to the labeled motor domain.

To determine whether the fluorescent ATP analog is able to drive motility, we measured FRET signals at the single-molecule level using the confocal fluorescence kinesin motility assay we recently developed (15). In this approach, the focus of the excitation laser is positioned on a microtubule (Fig. 1 b). Photons emitted by individual, labeled fluorescent kinesin motors moving along the microtubule are collected, separated into two spectral channels, and counted by an avalanche photodiode. For further analysis, photon arrival times are recorded and binned in appropriate time slots. Time traces generated on the basis of these data typically show a Gaussian intensity profile, from which the motor's velocity (proportional to the width of the Gaussian curve) and the labeling stoichiometry (proportional to the amplitude) can be determined (Figs. 2 and 3) (15)). Using the Alexa Fluor 555-labeled kinesin mutants described above in the presence of 5 μM regular and 0.5 μM fluorescent ATP, we observed time traces with this characteristic shape. The acceptor intensity was roughly constant in time and rather high, due to direct excitation of acceptor molecules free in solution. Once in a while, the donor intensity showed short dips accompanied by concurrent short jumps in acceptor intensity (Fig. 2 b). These events show clear characteristics of FRET and can be attributed to binding of acceptor-labeled ATP to the motor.

Figure 3.

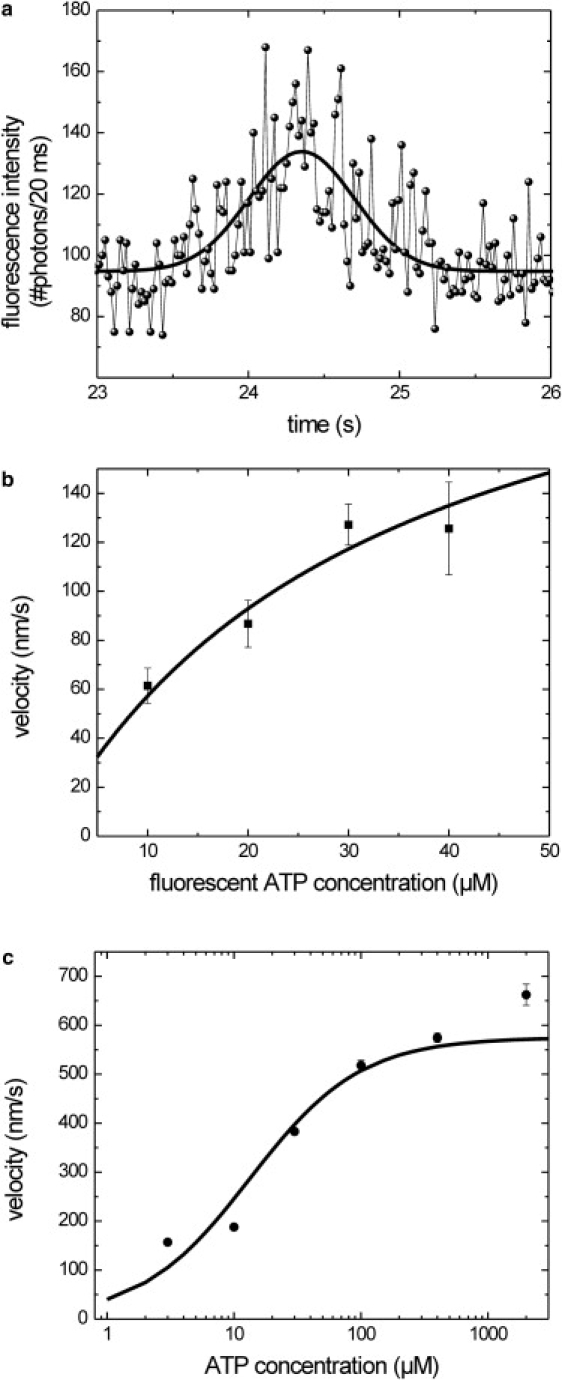
ATP and fluorescent ATP dependence of kinesin's velocity. (a) Donor fluorescence intensity trace of single-labeled kinesin in the presence of 40 μM fluorescent ATP. The solid black line represents a Gaussian fit with a width of 700 ± 70 ms (v = 170 nm/s). The relatively high background signal is due to acceptor fluorescence excited at the donor excitation wavelength. (b and c) Average velocities (mean ± SE) of kinesin at different concentrations of fluorescent ATP (b) or ATP (c), as determined from time traces such as those shown in a. Lines represent weighted Michaelis-Menten fits to the data $\left(\nu ={\nu }_{\max }\left[ATP\right]/\left(K_M+\left[ATP\right]\right)\right)\text{.}$

To test whether fluorescent ATP not only binds to the motor, but is also able to fuel processive movement, we measured the motility of single Kinesin-1 motors in the presence of fluorescent ATP only. At 40 μM fluorescent ATP, we obtained Gaussian-shaped intensity time traces with a width of 0.80 ± 0.12 s (mean ± standard error (SE)), N = 8, Fig. 3 a; additional traces are shown in Fig. S1 of the Supporting Material). This indicates that Kinesin-1 moved processively with a velocity of 126 ± 19 nm/s under these conditions. Since the kinesin used for these experiments was purified in the presence of fluorescent ATP, we can rule out the possibility that trace amounts of unlabeled ATP caused movement. To determine how the kinetics of Kinesin-1 motility were altered by the substrate fluorescent ATP, we measured the motor's velocity at different fluorescent ATP concentrations and fitted the data with the Michaelis-Menten equation (Fig. 3 b). Data could be obtained only in a limited range of concentrations: below ∼10 μM the number of events was very low, and above 40 μM the background fluorescence due to directly excited fluorescent ATP was too high to discern single-motor events. A weighted fit of the data set yielded a maximum velocity, v_max, of 247 ± 99 nm/s and a Michaelis constant, K_m, of 32 ± 22 μM. For comparison, when normal ATP was used, v_max was 575 ± 9 nm/s and K_m was 13.4 ± 0.6 μM (Fig. 3 c). These results show that Alexa Fluor 647 ATP can fuel Kinesin-1's processive motion and is a suitable substrate analog, but it alters the motor's kinetic parameters.

The kinetics of fluorescent nucleotide turnover measured on single motors

Next, we set out to determine the kinetics of nucleotide binding and release during processive Kinesin-1 movement. To that end, we further analyzed fluorescence time traces obtained from single motors in the presence of fluorescent ATP using the confocal fluorescence assay described previously (15). Although under the conditions of these experiments (10–40 μM fluorescent ATP) the background intensity caused by direct excitation of fluorescent ATP in solution was too high to discern signals of ATP bound to motors in the acceptor channel, the donor fluorescence intensity of labeled motors could be reliably determined (Fig. 3 a). Because of the nature of resonance transfer, changes in the donor intensity alone are enough to determine the FRET properties of the nucleotide-bound state if other sources of intensity fluctuations can be excluded (see below). The fluorescence intensity time traces (Fig. 3 a) do not show clear dips that can unambiguously be attributed to the binding and release of single fluorescent ATP or ADP (as in Fig. 2 b). This is to be expected since binding and release of fluorescent nucleotides are taking place continuously on a timescale of tens of milliseconds, leading to the observed large and apparently random intensity fluctuations (compare the amplitude of the fluctuations in Fig. 3 a with that in Fig. 2 b). To determine the timescale of these fluctuations, we analyzed the donor fluorescence intensity time traces of individual motors by autocorrelation, an approach similar to fluorescence correlation spectroscopy (18). The autocorrelation of intensity time traces spanned almost four orders of magnitude in time (from 1 ms to 6 s) and revealed two phases (Fig. 4, a and b). The slower phase corresponds to the time it takes a motor to pass the confocal spot (15). The faster phase (on a timescale of tens of milliseconds) reflects donor intensity fluctuations due to FRET caused by the binding and release of acceptor-labeled nucleotide. In support of this interpretation, a fast component of ∼10 ms was absent when no fluorescent ATP was present (Fig. 4 c). To obtain quantitative information on the intensity fluctuations, we fitted the autocorrelations using Eq. 2 and obtained values for the amplitude (A) and decay time (T_FRET) of the FRET component. At 40 μM fluorescent ATP, we derived a T_FRET of 18 ± 5 ms and at 20 μM fluorescent ATP, a T_FRET of 57 ms. We generally observed increasing decay times with lowered ATP concentrations (Fig. 5 b).

Figure 4.

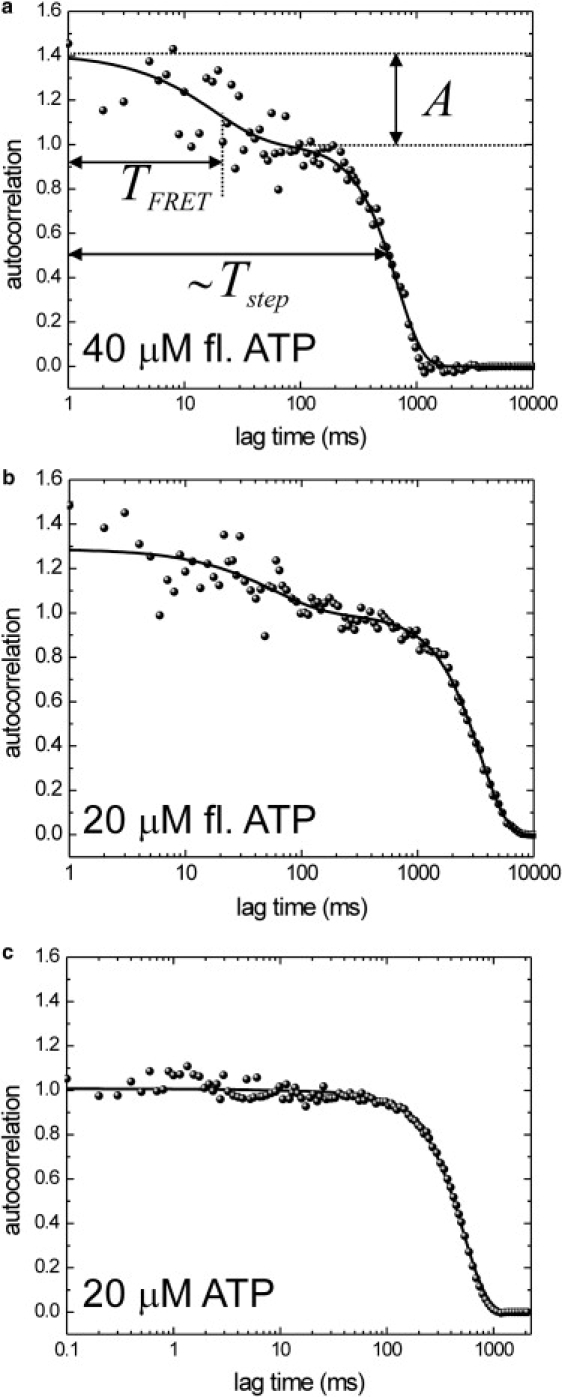
(a) Autocorrelation of the intensity signal represented in Fig. 3 a (40 μM fluorescent ATP). The slower (timescale ∼1 s), Gaussian decay of the autocorrelation reflects the transit time of the kinesin through the confocal spot, and its width is proportional to the velocity and stepping rate. An additional decay of the autocorrelation is observed on a timescale of ∼10 ms. It is due to intensity changes caused by repetitive binding and release of fluorescent ATP. The black curve is a fit of Eq. 2, with A = 0.4 and T_FRET = 18 ± 5 ms. (b) Autocorrelation of the fluorescence intensity of a kinesin in the presence of 20 μM fluorescent ATP. The slower rate occurs at a longer timescale, reflecting the lower velocity at this lower fluorescent ATP concentration. In addition, the decay time of the fast FRET component has increased. The solid black curve represents a fit of Eq. 2, with A = 0.29 and T_FRET = 57 ms. (c) Intensity autocorrelation of the fluorescence intensity from a single kinesin motor in the presence of regular ATP only. In contrast to a and b, no decay of the autocorrelation can be discerned on a ∼10 ms timescale, and the slower decay is much faster (∼400 ms).

Figure 5.

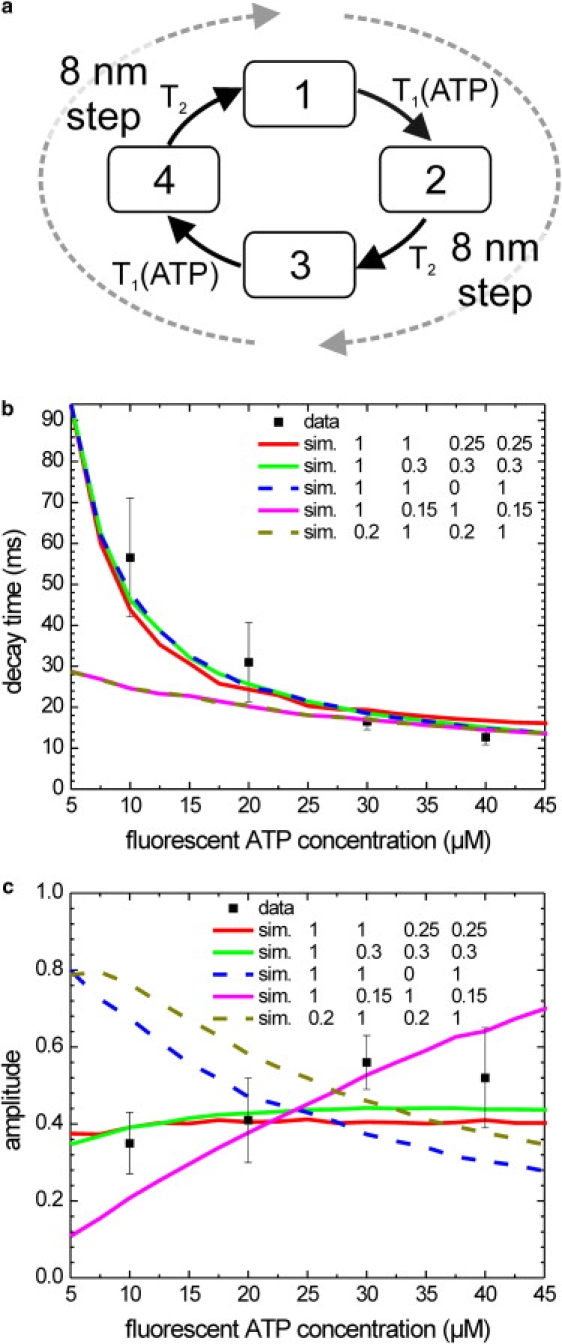
Experimental and simulated decay times and amplitudes of the autocorrelations of donor intensity time traces at different fluorescent ATP concentrations. (a) Schematic representation of the four-state model used for the simulations. Each state has its own intensity, due to differences in FRET efficiency. One full cycle consists of two 8 nm steps and two nucleotide turnovers. Both steps/turnovers are built up of the same transitions, characterized by lifetimes T₁ and T₂. Only T₁ depends on the concentration of fluorescent ATP. (b) Average (mean ± SE) decay times obtained from exponential fits to the experimental (solid squares with error bars) and simulated autocorrelations of the donor fluorescence intensity (colored lines). For all simulations the v_max and K_m values obtained from the fit of Fig. 3b were used to determine T₁ and T₂. Shown are simulations calculated according to the four-state model shown in panel a, with intensities for the respective states as indicated. (c) Average (mean ± SE) amplitude obtained from exponential fits to the experimental (solid squares with error bars) and simulated autocorrelations of the donor fluorescence intensity (colored lines).

To understand this increase and its implications for kinesin's chemomechanical cycle, one must compare the experimental autocorrelations with autocorrelations calculated from kinetic models. To determine the type of model required to describe our data, one must carefully consider the experimental setup. The S43C kinesin construct we used was labeled only at one of its two motor domains. Hence, the symmetry between both motor domains was broken, requiring inspection of a double-cycle for modeling. Furthermore, the fluorescence donor on the motor domain's residue S43C was very close to the nucleotide (2.5–3 nm; cf. PDB entries 2KIN, 2BG1, or 1MKJ), making it very likely that FRET between the Alexa Fluor 555 donor dye and the Alexa Fluor 647-ATP (or ADP) acceptor dye bound to the same motor head was very efficient. In addition, donor quenching could also occur due to interhead FRET because resonance energy transfer is efficient below distances of ∼5 nm, and structural models predict distances in that range during the ATP waiting state. Finally, our experiments were performed at fluorescent ATP concentrations close to K_m,_ATP, implying that more than one kinetic step was rate-limiting (at least one ATP-dependent and one ATP-independent transition). Together, these considerations suggest that the minimal scheme describing our FRET data has to comprise at least four states with potentially different FRET efficiencies and, consequently, intensities (head A ATP-bound, head B ATP-bound, head A in ATP waiting state, and head B in ATP waiting state; Fig. 5 a). We devised a model in which these four states are connected in a unidirectional cyclic scheme, with rate constants that are equal between the two halves of the scheme, each representing a single 8 nm step. The two rates of a single 8 nm step were chosen such that they obeyed Michaelis-Menten kinetics. We assumed that the lifetime of one of the states (T₂) was independent of ATP concentration and set it to d/v_max (with d the step size, 8 nm). We furthermore assumed that the other lifetime reflects the effective time of ATP binding and set it equal to $K_{m}d/\left({\nu }_{\max }\left[ATP\right]\right)$. The only parameters that were varied were the relative intensities of the four states. We supposed that the dominating factor in the intensity is FRET within a single motor domain between donor and acceptor-labeled nucleotide, and limited the number of free parameters by only considering in total two different intensities for all the states. To compare this model with our data, we constructed intensity time traces using Monte Carlo simulations and different realizations of the model. Next, we calculated the autocorrelation of these traces and fitted them with a single exponential decay. The resulting amplitudes and decay times were compared with those obtained from the experimental autocorrelation traces (Fig. 5, b and c). The low-intensity values of each simulation were optimized for best comparison with the experimental amplitudes (changing these intensities did not influence the decay times). Good descriptions of the data with this four-state model could only be obtained when just one of the ATP-dependent states had a lower intensity as a result of FRET with fluorescent nucleotide, in addition to one or both of the ATP-independent states. In these cases, we found that a FRET efficiency of 0.25 ± 0.05 is required, consistent with the small distance between donor and acceptor when fluorescent nucleotide is bound to the labeled motor domain. Of note, simulations using intensities that were identical for both halves of the cycle did not correspond well to the data. Such simulations could correspond to single-site catalysis (only one of the motor domains, the labeled one, is turning over ATP) or independent-site catalysis (both motor domains hydrolyze ATP independently of each other and only the labeled one shows fluctuations in fluorescence intensity). Our data, which directly probe binding and release of nucleotides to an individual motor domain, thus are inconsistent with kinetic models based on single-site or independent-site catalysis. A kinetic scheme with both motor domains hydrolyzing ATP in sequence can describe the data well.

To further test whether the models proposed describe kinesin's properties appropriately, we performed similar FRET experiments using donor-labeled kinesin and acceptor-labeled ATP (20 μM) in the presence of varying amounts of normal ATP (0, 5, 10, 20, and 30 μM). We recorded donor intensity time traces, calculated their autocorrelations, and fitted the autocorrelations. The decay times and amplitudes obtained in this way are represented in Fig. 6 (note that at 30 μM ATP, the fluorescent ATP concentration was 30 μM, instead of 20 μM used for the other data points). The decay times appear to decrease slightly with increasing ATP concentration, whereas a drop of the amplitude is more pronounced. To understand which kinetic cycles could cause such signals, we again used Monte Carlo simulations. For the case of mixtures of fluorescent and normal ATP, we expanded the four-state model used above by eight additional states and 12 additional transitions (Fig. 6 a). This increase in complexity arises because each ATP-dependent step can lead to either a nucleotide-bound state or an Alexa Fluor 647 nucleotide-bound state. In our model, we used the Michaelis-Menten parameters to assign a transition probability from the nucleotide-free binding site to either ATP or Alexa Fluor-ATP bound states. The intensities of the states were taken to be the same as in the four-state model for the corresponding states. The new states with normal nucleotide bound were set to an intensity of one, since FRET cannot occur. The autocorrelations of the simulated time traces were fitted with a single exponential decay and compared with experimental data (Fig. 6, b and c). Fig. 5, b and c, shows two simulations corresponding to the ones that described the fluorescent ATP data best, in addition to the model that could represent independent or single-site catalysis. As for the four-state model, the independent- and single-site models poorly described the data, in particular the decrease of the autocorrelation amplitude at increasing ATP concentrations. This aspect of the data was described better by both of the other models, in particular the one in which only one fluorescent ATP-dependent state and one fluorescent ATP-independent state showed FRET. Of interest, in all of the simulations we tried using this model (as well as when we changed the Michaelis-Menten parameters within reasonable limits), we observed an increase of decay times with ATP concentration, saturating at roughly half the step time. None yielded the slight decrease of the decay time at higher ATP concentrations that we experimentally observed, which may suggest that the implicit assumption made in the modeling—that the kinetic rates of transitions on one motor domain are independent of the nature of the substrate bound to the other one—is not absolutely correct. The decrease may be explained by the observation that v_max of fluorescent ATP bound to one motor domain is higher when ATP binds to the other motor domain. Despite these minor deviations from the simple stochastic models used, our experimental results can only be explained well by using a model that assumes alternating-site catalysis, at least under limiting ATP conditions.

Figure 6.

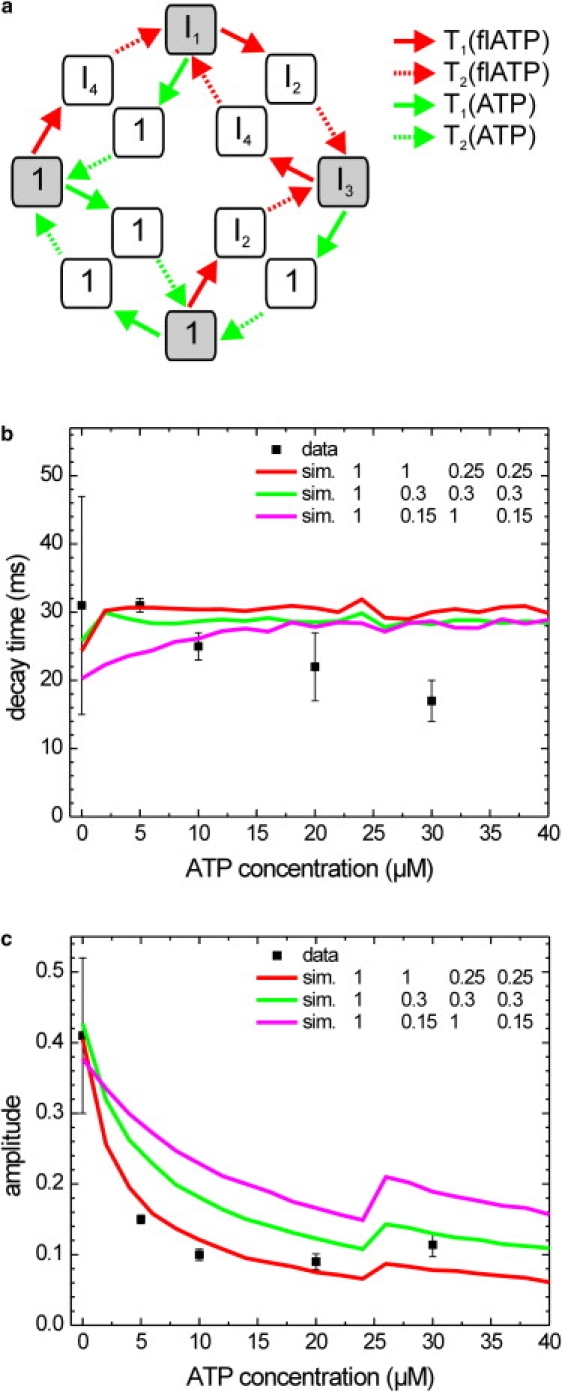
Experimental and simulated decay times and amplitudes of the autocorrelations of donor intensity time traces obtained with mixtures of fluorescent and normal ATP. (a) Schematic representation of the 12-state model used for the simulations. The model is an extension of the one presented in Fig. 5 and it incorporates all the possible conformations and transitions of a single-labeled construct with two types of substrate. The intensities of the states corresponding to those in the four-state model are indicated; the additional states have normal nucleotide bound and consequently intensity 1. Four transition rates are considered, as indicated. T₁ for fluorescent ATP depends on the fluorescent ATP concentration, T₁ for ATP depends on the ATP concentration, and both are calculated using the respective Michaelis-Menten parameters. Both T₂ values are independent of the nucleotide concentrations and are obtained from v_max of the respective nucleotide. The four states on the corners (shaded gray) represent ATP waiting states and act as branching points where a fluorescent or normal ATP can bind. (b) Average (mean ± SE) decay times obtained from exponential fits to the experimental (solid squares with error bars) and simulated autocorrelations of the donor fluorescence intensity (colored lines). For the simulations, a 12-state model was used, corresponding to the model used in Fig. 5a, with additional branching to states with normal nucleotide bound. The three simulations shown correspond to those with the same labeling and color in Fig. 5 (the intensities of other states, with ATP bound, were set to one). (c) Average (mean ± SE) amplitudes obtained from exponential fits to the experimental (solid squares with error bars) and simulated (colored lines) autocorrelations of the donor fluorescence intensity. The discontinuity at 25 μM ATP is caused by the abrupt increase of the fluorescent ATP concentration from 20 to 30 μM, for better comparison with the data.

Discussion

In this study we investigated Kinesin-1's kinetic cycle (in particular, so-called alternating-site catalysis) by means of single-molecule fluorescence techniques on a timescale of milliseconds. To date, the ATP turnover has not been resolved to such a high resolution in single-molecule assays (8). Furthermore, our approach allows, for the first time to our knowledge, measurement of nucleotide-binding rates in the course of processive kinesin runs. To that end, we used FRET between donor-labeled kinesin and acceptor-labeled ATP, which allowed for the detection of single-nucleotide-binding events. Our experiments show that Kinesin-1 moves processively at the expense of Alexa Fluor 647 ATP with a kinetic cycle that appears qualitatively unaltered compared to that of the natural substrate.

We analyzed the single-molecule donor fluorescence intensity time traces obtained from single kinesins walking through the confocal spot with a temporal resolution not achieved previously. This method is technically challenging due to the limited number of photons that can be collected during one run, and the resulting limited statistics. Consequently, some of the kinetic parameters that can be deduced from these data in theory are not available in practice. For example, the rate of detected photons was too low and as a consequence the shot noise too high to allow direct discrimination of transitions between states of high (fluorescent nucleotide bound to the labeled motor domain) and low (no fluorescent nucleotide bound) FRET in the single-motor fluorescence traces. We therefore transformed the primary data by autocorrelation, allowing the analysis of intensity fluctuations over almost four orders of magnitude in time (1 ms to 10 s). Autocorrelation curves, however, average out part of the direct information on the underlying transition rates, intensities, and FRET efficiencies (20). To find out which kinetic models can underlie the observed autocorrelations, different probable models need to be solved, transformed into intensity autocorrelations, and compared with the experimental data. We chose to perform Monte Carlo simulations, to fit both experimental and simulated autocorrelations with single-exponential decays, and to compare the resulting amplitudes and decay times. Using this analysis, we could well describe our data using models consisting of four states. We tried more-complex models, and in some cases these models gave matching curve fits, but our data did not provide an experimental basis for more-complex models and the additional free parameters associated with them.

We were able to test several models that differ substantially in the connection between nucleotide turnovers in both motor domains. What we observed is that models that are based on only one motor domain hydrolyzing ATP, or on both domains hydrolyzing ATP independently, poorly describe the fluorescent ATP concentration dependence of the experimental fluorescence intensity autocorrelations (Figs. 5 and 6). In the two models that describe the data satisfactorily, ATP turnover takes place sequentially in each of the two motor domains. A chemomechanical scheme consistent with these two kinetic models is represented in Fig. 7. In the first state, both motor domains are bound to subsequent binding sites on the microtubule. Fluorescent ATP is bound to the trailing, unlabeled motor domain. In this configuration, the donor and acceptor are more than 8 nm apart, and thus the FRET efficiency is expected to be <6% (assuming a Förster radius of 5.1 nm for this dye pair (Invitrogen/Molecular Probes) and fast rotation of the probes). The lifetime of this state is independent of the fluorescent ATP concentration, and in our model is determined by the maximal turnover rate at saturating substrate concentrations. In the next state, the fluorescent ATP on the unlabeled motor domain is hydrolyzed and this motor domain could release from the microtubule into a tethered state (8,11). In this state, the donor and acceptor could be close enough for FRET to occur as in the “1 0.3 0.3 0.3” model (green line in Fig. 5, b and c); however, it is more likely that FRET in this state is low or zero, since the “1 1 0.25 0.25” model (red line) describes the fluorescent ATP data as well (Fig. 5, b and c), but is better at describing the mixture data (Fig. 6, b and c). This state lives as long as the fluorescent nucleotide binds to the labeled head, a lifetime that depends on the concentration of the nucleotide. After fluorescent ATP binding, the motor is in a state equivalent to the first, with both motor domains microtubule-bound. Now, however, the labeled motor domain is fluorescent nucleotide-bound and is trailing. Since the nucleotide-binding pocket is very close to the 43 residue to which the donor label is attached, efficient FRET can be expected, as was observed. This state lives as long as the first state, independently of the fluorescent ATP concentration. In the final, fourth state (equivalent to the second one), the fluorescent ATP has been hydrolyzed, but the product (fluorescent) ADP is still bound and close to the donor, such that efficient FRET can take place, as was observed. After binding of fluorescent ATP (with a concentration-dependent rate), the motor is back in state 1 and a new cycle commences. In the minimal model presented here, important nuances are left out. For example, it is well established that the chemomechanical cycle of Kinesin-1 consists of at least two ATP-independent kinetic events (21), and it would be very likely that nucleotide binding to one motor domain and release from the other are two different processes. These important aspects could in principle be taken into account by considering more-complex models. We noticed, however, that the autocorrelations hardly changed when we added an additional ATP-independent state, with or without FRET (data not shown; compare with Block et al. (21)). Furthermore, as indicated above, our data did not provide a solid basis to determine the additional parameters required for such models.

Figure 7.

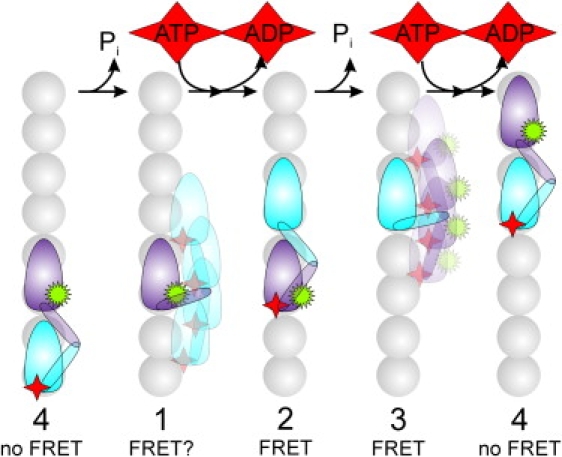
Structural model of the proposed four-state model of two sequential kinesin steps. The reaction sequence shown is consistent with the kinetic model that fitted the autocorrelation curves best. It includes two ATP concentration-dependent transitions, leading to high FRET in one case and low FRET efficiency in the other case. We depicted the state in which a motor domain waits for ATP to bind as a tethered state. Our data and modeling do not provide conclusive evidence as to whether this state, in the case of fluorescent nucleotide bound to the unlabeled head, shows FRET or not. The donor label attached to one of the motor domains is depicted as a green 16-pointed star; the acceptor is labeled nucleotide as a red, four-pointed star.

Apart from these conclusions regarding the general mechanism, we observed that the size of key kinetic parameters of Kinesin-1 was clearly affected by the use of Alexa Fluor-ATP. Both the maximum velocity and the Michaelis constant were reduced to ∼40% of normal, and it is likely that both substrate binding and catalysis were affected. Given the additional size of the labeled nucleotide (the weight is about four times that of ATP), one can imagine that its binding properties are altered compared to its natural counterpart because of steric effects or additional charged and hydrophobic interactions. This could alter the kinetics of initial nucleotide binding and the fast conformational change that disables ATP release after binding of regular ATP (22,23), as well as decrease the stabilization of the transition state of γ-phosphate bond breaking.

To conclude, we have shown that Alexa Fluor 647 ATP is a valid substrate for Kinesin-1. We determined the kinetics of binding and release of individual motor domains in walking kinesin using a FRET-based assay, with a donor fluorophore on one of kinesin's motor domains and Alexa Fluor 647 ATP as the acceptor. By comparing the donor fluorescence intensity autocorrelations with curves obtained from stochastic models, we find that they are only consistent with models in which each motor domain hydrolyzes ATP in turn (13), consistent with current models for kinesin's hand-over-hand mechanism (24–26).

Supporting Material

One figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00843-1.