Slowing Down Downhill Folding: A Three-Probe Study

Abstract

The mutant Tyr²²Trp/Glu³³Tyr/Gly⁴⁶Ala/Gly⁴⁸Ala of λ repressor fragment ${\lambda }_{6-85}^{}$ was previously assigned as an incipient downhill folder. We slow down its folding in a cryogenic water-ethylene-glycol solvent (−18 to −28°C). The refolding kinetics are probed by small-angle x-ray scattering, circular dichroism, and fluorescence to measure the radius of gyration, the average secondary structure content, and the native packing around the single tryptophan residue. The main resolved kinetic phase of the mutant is probe independent and faster than the main phase observed for the pseudo-wild-type. Excess helical structure formed early on by the mutant may reduce the formation of turns and prevent the formation of compact misfolded states, speeding up the overall folding process. Extrapolation of our main cryogenic folding phase and previous T-jump measurements to 37°C yields nearly the same refolding rate as extrapolated by Oas and co-workers from NMR line-shape data. Taken together, all the data consistently indicate a folding speed limit of ∼4.5 μs for this fast folder.

Introduction

The energy-landscape theory of protein folding states that folding barriers are small and that multiple paths to the native state exist (1–5). Experiments may nonetheless show only a single pathway, because populations are very sensitive to the free-energy profile along each path (6). For an activated reaction with two pathways,

$$\frac{\text{Population taking path}1}{\text{Population taking path}2}\approx e^{-\Delta \Delta G_{12}/RT}\text{.}$$ (1)

$\Delta \Delta G_{12}$ is the difference between the highest free energies along path 1 and path 2, the gas constant R, and the temperature T. A free-energy difference of just 3 RT between two pathways makes the higher free-energy path nearly invisible to experiment, although parallel pathways are occasionally close enough in free energy that both populations can be measured simultaneously (7). By perturbing the sequence or solution environment of a protein, different pathways, ranging from downhill folding to folding via long-lived intermediates, can be revealed (8).

Downhill folding is the “speed limit” achieved by proteins when all the barriers along at least one path approach the thermal energy RT (5,9). Signatures of downhill folding have been observed experimentally by biasing the free-energy surface toward the native state. Biasing is achieved by adjusting the temperature, sequence, or solvent composition. In steady-state measurements, one looks for probe-dependent melting points, assuming the protein still folds downhill near the middle of the unfolding transition (10,11). In kinetic measurements, one looks for a transition from simple to complex back to simple kinetics, as a thermally activated reaction switches to a diffusive reaction when the protein is stabilized (6,12).

λ repressor (13,14) is a typical example of a small protein that can approach the downhill speed limit. Its 6–85 fragment was the first submillisecond two-state folder characterized by dynamic NMR studies (15–17). We later tuned mutants of this protein to cover all folding scenarios from folding via intermediates (18) to two-state folding (19), incipient downhill folding (19,20) (barrier <3 kT), and complete downhill folding (20,21) (barrier <1 kT). In particular, the alanine-rich mutant ${\lambda }^{\ast }\text{YA}$ has been characterized previously by NMR and fluorescence studies (20,22,23). Its maximum folding rate was estimated to be ∼4.5 μs)⁻¹ at 37°C, based on extrapolating either NMR data in 37°C urea solution, or denaturant-free T-jump data taken at 61.5–73.2°C (22,23).

Our goal in this study was to use cryogenic (−18 to −28°C) and high-viscosity (ethylene glycol) solvent conditions to slow down the refolding kinetics of ${\lambda }^{\ast }\text{YA}$. We used stopped-flow mixing to measure the kinetics. The questions were: Do all three data sets (NMR, T-jump, and cryogenic stopped flow) extrapolate to the same limiting rate? Are the cryogenic folding kinetics of ${\lambda }^{\ast }\text{YA}$ more concerted or less concerted than those of the pseudo-wild-type ${\lambda }_{6-85}^{\ast }$? What structural path does the fast mutant take under cryogenic conditions?

To answer these questions, we characterized the refolding process by three probes. Small-angle x-ray scattering (SAXS) was used to extract the radius of gyration, indicating the degree of collapse during folding. Circular dichroism (CD) detected average secondary-structure content, in particular, helical content at 222 nm, given the helical nature of λ repressor proteins. Fluorescence excited at 295 nm detects mainly the local solvation environment around tryptophan 22, the only tryptophan residue. We compared the fast-mutant data with multiprobe data previously published for the slower-folding pseudo-wild-type ${\lambda }_{6-85}^{\ast }$. The pseudo-wild-type contains the same tryptophan, but fewer alanines than ${\lambda }^{\ast }\text{YA}$ (18). Like the wild-type, the fast-folding mutant shows three distinct phases, one submillisecond, one ∼100 ms, and one ∼0.7 s. Unlike the wild-type, the mutant yields the same timescale of 100 ms for the main resolved phase using all three probes. The mutant kinetics are more concerted, and it has a smoother free-energy landscape than the wild-type under cryogenic conditions.

From a structural point of view, our results in this particular case are compatible with the classic framework model, wherein secondary structure forms rapidly, followed by collapse. Many proteins, even those containing β-sheets, form an excess of nonnative secondary structure early on during folding (24–27). Such nonnative helical structure could actually help accelerate folding by preventing the formation of compact misfolded states early on in the folding process.

The framework mechanism is not unique. Nonspecific collapse before secondary structure formation has also been observed (28). Protein free-energy landscapes are sufficiently smooth (5,29) to support several different paths at low free energy. Because of the exponential sensitivity of Eq. 1, most of the population may go through a single path, but others are available to take over if changing solvent conditions or mutations block the predominant path. The robustness conferred by multiple available folding paths may be one of the underlying physical reasons that evolution selected proteins as the main carriers of phenotype: nucleic acids tend to have much more rugged free-energy landscapes.

Methods

Protein mutant and pseudo-wild-type

λ repressor fragment 6–85 derives from a DNA-binding phage regulatory protein (30,31). The pseudo-wild-type ${\lambda }_{6-85}^{\ast }$ (molecular mass ∼9160 Da) contains five α-helices and a Tyr²²Trp mutation to enable fluorescence detection (17). We made the mutant ${\lambda }^{\ast }\text{YA}$ = ${\lambda }_{6-85}^{\ast }$ Q³³Y/G⁴⁶A/G⁴⁸A (Fig. 1, inset) by site-directed mutagenesis (Quickchange kit; Stratagene, La Jolla, CA), starting with a wild-type plasmid donated by Terry Oas. Genes were overexpressed and purified as described in detail in Dumont et al. (18). The histidine tag was removed by thrombin cleavage, and purity was confirmed by matrix-assisted laser desorption ionization mass spectrometry and sodium dodecyl sulfate polyacrylamide gel electrophoresis.

Figure 1.

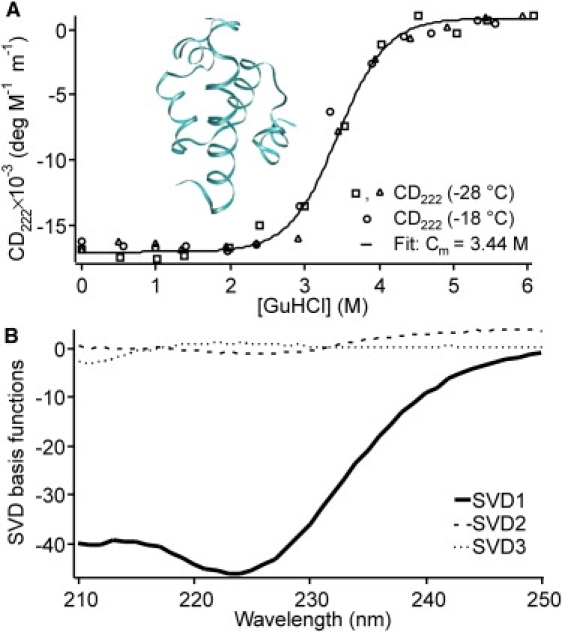
Steady-state CD data at −28 ± 0.2°C in 45% ethylene glycol 50 mM phosphate buffer. (A) Guanidine hydrochloride titration detected by CD. The midpoint of 3.44 M agrees within measurement uncertainty with the fluorescence from Yang and Gruebele (20) (C_m = 3.27 M), indicating that ${\lambda }^{\ast }\text{YA}$ has been tuned to two-state folding by addition of the denaturant. (Inset) X-ray crystal structure of ${\lambda }^{\ast }\text{YA}$ from F. Liu, Y. Gao, and M. Gruebele, unpublished, visualized using VMD software (54). (B) Basis functions from SVD of the CD spectra from 0–6 M guanidine hydrochloride at −28°C. Only one major component contributes near the denaturation midpoint.

Cryogenic solvent conditions

The proteins were suspended in a 45%:55% by volume ethylene glycol:water buffer containing 50 mM phosphate at pH 7, similar to our previous cryogenic experiments (18,25). The viscosity η of the aqueous solvent depends on the mole fraction χ of ethylene glycol (χ = 0.21 in our buffer) and temperature as (18)

$$\eta (T,\chi )=(0.004757+0.047\chi )\{1+(221+573\chi ){\text{e}}^{-0.048\text{T}/°\text{C}}+(154-69\chi ){\text{e}}^{-0.01\text{T}/°\text{C}}\}\text{.}$$ (2)

In stopped-flow refolding studies, a calibrated 5-M guanidine hydrochloride buffer was used (32,33). Low-temperature measurements were carried out at −28 ± 0.2°C, −24 ± 0.2°C, and −18 ± 0.2°C to gauge the effect of temperature on folding kinetics. The cell was insulated with a cork/foam envelope and cooled by an ethylene glycol/water bath (ULT-80DD recirculator; Neslab, Newington, NH).

Stopped-flow setup

Nearly identical stopped-flow mixers made by UNISOKU were used in Japan (CD and fluorescence) and in the United States (SAXS). The cryogenic stopped-flow mixers are custom instruments built to operate at high viscosity and low temperature. For all protein refolding measurements, denatured protein in 5 M guanidinium buffer was mixed down to a 0.7 M final guanidinium concentration. For all three probes, a cell 1 mm in path length with 50-μm sapphire windows was used. The dead time for the stopped flow was calibrated to be <6 ms in 45% ethylene glycol at −28°C, the most viscous solvent condition we used. The fast reduction of 2,6-dichlorophenol sodium by ascorbic acid at pH 4 was used as the calibration reaction (18).

Fluorescence and CD

Fluorescence and CD were detected using the same instrument multiple times. The averaged data were normalized to yield fluorescence intensity with ∼±1.5% root mean-square noise, and molar ellipticity with ∼±1000 deg M⁻¹ m⁻¹ accuracy. Fluorescence was excited at 295 nm, and integrated from 325 to 500 nm to avoid the buffer Raman peak. CD data were collected between 210 and 250 nm, limited at short wavelengths by guanidine hydrochloride buffer absorption. Three types of experiment were carried out: steady-state measurements at the initial and final conditions of the stopped-flow measurements; guanidine hydrochloride titrations; and stopped-flow refolding kinetics from 5 to 0.7 M guanidinium at −18°C, −24°C, and −28°C. Steady-state final conditions were obtained 5–20 min after the end of a kinetic trace. Final protein concentration in the fluorescence and CD experiments ranged from 30 to 50 μM. Steady-state CD data were analyzed by singular value decomposition (SVD) (34) to determine how many significant components existed in the spectra near the midpoint of the melting transition.

Small angle x-ray scattering

SAXS data for the ${\lambda }^{\ast }\text{YA}$ mutant were collected at the BioCAT 18 undulator beamline (Advanced Photon Source at Argonne National Laboratory, Argonne, IL) (35). The 1.0-Å-wavelength x-ray beam was collimated to 300 × 130 μm² at the sample.

One characteristic of downhill folders such as ${\lambda }^{\ast }\text{YA}$ is that they aggregate more easily than the wild-type (19), so the final protein concentration in our SAXS experiments was limited to ≤200 μM, less than half the concentration used in our previous experiments on the wild-type (18). In addition, we conducted a detailed SAXS aggregation study of ${\lambda }^{\ast }\text{YA}$ and determined the effective intermolecular potential of ${\lambda }^{\ast }\text{YA}$ (36). The results of this study also show that aggregation is minimal at 200 μM protein concentration and −28°C. The radius of gyration was obtained via

$$I\left(Q\right)\sim e^{-R_g^2{Q}^2/3}\text{.}$$ (3)

The upper cutoff of the scattering angle was defined by the Guinier criterion Q_maxR_g given in Fig. 2 A (37). The lower cutoff, Q² ≈ 0.001, was caused by scatter from the metal target that blocked the x-ray beam from impinging on the center of the CCD camera. For consistency, all data were fitted over the same range of Q² = 0.002–0.008 Å⁻².

Figure 2.

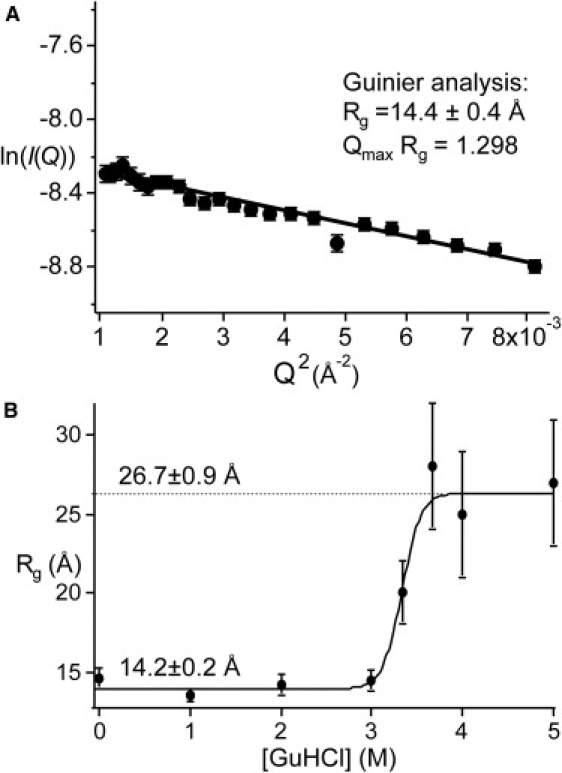
Steady-state SAXS data for ${\lambda }^{\ast }\text{YA}$. (A) Guinier plots of folded protein in 0.7 M guanidine hydrochloride, 45% ethylene glycol buffer at −28 ± 0.2°C. The range of the straight-line Guinier fit is limited by target scatter at small Q, and pseudo-wild-type-spherical protein shape at large Q. (B) Guanidinium melt of ${\lambda }^{\ast }\text{YA}$ detected by SAXS. The midpoint of 3.40 ± 0.25 agrees with both the CD and fluorescence data within experimental uncertainty, indicating that ${\lambda }^{\ast }\text{YA}$ has been tuned to two-state folding by addition of the denaturant. All fitting errors are 1-SD confidence intervals.

Three types of measurement were carried out. First, steady-state measurements at 0.7 M and 5 M guanidine hydrochloride concentration at −18°C to −28°C were used to characterize the endpoints. Then, a guanidine hydrochloride titration was used to determine the midpoint denaturant concentration, C_m. Finally, two types of kinetics measurements were carried out. For steady state and some of the kinetics experiments, the scattering intensity was detected with an Aviex CCD camera with an active area of ∼160 × 80 mm² (2084 × 1042 pixels), described in an earlier study (36). With this detector, each kinetic data point requires a separate stopped-flow data acquisition. In addition, the BioCAT 18 beamline recently acquired a Pilatus CCD detector capable of streak mode. In streak mode, a single stopped-flow dilution is followed by multiple data collections at 45 (20), 100 (50), 200 (100), 400/500 (100), 750 (200), 1000 (200), 1500 (200), and 3000 (500) ms, where the numbers in parentheses (ms) indicate the time window around the center value. Radiation-damage experiments showed that windows >2 s could not be used without distorting the R_g, so the cumulative exposure was kept below that value. A 0.7-M guanidine hydrochloride buffer reference was collected and subtracted from the sample intensity for both kinetic and steady-state experiments. The details of the raw data processing (including angular averaging of the scatter and removal of artifacts from crystallinity in the sapphire windows) are described elsewhere (18,38,39).

Rate coefficient comparison

The extrapolation of the 37°C NMR data to 0 M urea is described in detail in the original study (16), and in personal communications (T. Oas, Duke University, personal communication, 2000). To briefly summarize, the NMR data used a linear free-energy dependence on denaturant concentration to extrapolate the free energy to 0 M urea. Burton et al. (16) analyzed a data series spanning 2–5 M urea that allowed denatured and folded peaks to be observed simultaneously in the histidine proton spectrum. The protein was an apparent two-state folder under those conditions, so they used a two-state analysis of the line shape to extract the activated relaxation rate $k_{\text{a}}=k_{\text{folding}}+k_{\text{unfolding}}$. At 37°C, the native state is much more stable than the unfolded state, so $k_{\text{folding}}\gg k_{\text{unfolding}}$ and $k_{\text{a}}\approx k_{\text{folding}}$.

The temperature-jump data was recorded from 61.5 ± 1°C to 73.2 ± 1°C (19). The observed kinetic relaxation consisted of two phases. The slower, 20-μs phase was fitted to an activated rate coefficient k_a and assigned to folding over a low activation barrier (19). The faster, sub-5-μs phase was fitted to a molecular rate coefficient, k_m, and assigned to diffusional dynamics of a large activated population that was observable because of the very low activation barrier. This approach has been validated by Langevin dynamics simulations that do not a priori separate the molecular and activated phases (8,40). As discussed in Yang and Gruebele (20), when the protein is near the thermal denaturation midpoint, the activated k_a phase is at its largest. When the temperature is lowered toward room temperature to stabilize the protein, the diffusive k_m phase becomes dominant. Thus, at the optimal temperature, where the protein reaches its “speed limit” (9), one expects it to fold with a rate close to k_m (19). If a temperature is reached at which the k_m phase is present exclusively, the protein folds completely downhill. This limit was not quite reached by ${\lambda }^{\ast }\text{YA}$ in the studies by Yang and Gruebele (19,20).

For comparison with the data presented in this study, we plotted measured relaxation rates, not folding rates. This avoids the two-state assumption. However, for the NMR and stopped-flow data, the observed rates correspond essentially to refolding rates, and for the T-jump data, they are within a factor of 2 of the folding rates obtained by an assumption of two states. Rate coefficients were obtained by nonlinear-least-squares fits to multiexponential functions, and errors shown are the mean ± 1 SD.

Results

Steady-state SAXS and CD signals

Fig. 2 A shows a Guinier plot for the folded state, at −28°C and 0.7 M guanidine hydrochloride (the final condition for the lowest-temperature refolding experiments). As seen in Fig. 2 B, the radius of gyration of ${\lambda }^{\ast }\text{YA}$ is independent of denaturant concentration below 3 M guanidine hydrochloride. The resulting R_g = 14.2 ± 0.2 Å is in agreement with the value of 14 ± 1 Å obtained previously for the pseudo-wild-type. Both values include scattering of the solvation shell. Using the program CRYSOL (41) to subtract the effective contribution of the solvation shell yields 11 ± 1 Å for ${\lambda }^{\ast }\text{YA}$. This smaller value agrees, within measurement uncertainty, with the radius of gyration obtained for the bare protein from the x-ray crystal structure of ${\lambda }^{\ast }\text{YA}$ represented by the ribbon plot in Fig. 1 A.

The guanidinium-denatured R_g = 26.7 ± 0.9 Å is somewhat larger than the value of 23 Å observed previously for ${\lambda }_{6-85}^{\ast }$. Using the scaling for a self-avoiding random coil, $R_{\text{g}}\sim {\left(\text{residues}\right)}^{0.6}$, proposed by Kohn et al. (42) yields R_g = 26 Å, in perfect agreement with experiment. The ${\lambda }^{\ast }\text{YA}$ mutant is thus closer to the ideal random coil value than the pseudo-wild-type ${\lambda }_{6-85}^{\ast }$, for which we determined above that R_g ≈ 23 Å.

A random-coil radius of gyration should not be taken to guarantee that the denatured state of ${\lambda }^{\ast }\text{YA}$ at −18 to −28°C is a random coil. We previously demonstrated that the wild-type λ-repressor fragment in high-temperature guanidine hydrochloride solution contains residual structure, which can be approximated by extended (β-sheet-like) structure on a length scale less than three to five residues, and random jointed structure at over three to five residues (43). However, our denatured CD spectra at −28°C closely resemble the SVD2 and SVD3 functions shown in Fig. 1 B (34), so there appears to be little extended structure at low temperature in 6 M guanidine solution.

At 0 M guanidine hydrochloride, the CD spectrum of ${\lambda }^{\ast }\text{YA}$ closely resembles the SVD1 function in Fig. 1 B, with α-helical peaks at 210 and 223 nm. The native steady-state value at 222 nm is −16,500 ± 300 deg M⁻¹ m⁻¹. This is significantly larger than the −14,000 value obtained previously for ${\lambda }_{6-85}^{\ast }$. Based on molecular dynamics simulations (44), the difference is most likely due to additional structure in helix 5 of the mutant.

Unfolding titrations

SVD of the ${\lambda }^{\ast }\text{YA}$ spectra from 210 to 250 nm as a function of guanidinium concentration yields a sigmoidal transition with one dominant singular value. (Compare SVD 1 with SVD 2 or SVD 3 in Fig. 1 B.) (34). The denaturation thus corresponds to a loss of CD intensity without a change in spectral shape, as expected for two-state unfolding if the denatured state has negligible spectral intensity between 210 and 250 nm. The same denaturation midpoint of C_m = 3.44 ± 0.20 M is also obtained by plotting the data at 222 nm (Fig. 1 A). The fit in Fig. 1 A is to the two-state linear free-energy relationship (45)

$$\Delta G=m(\left[\text{GuHCl}\right]-C_{\text{m}})\text{.}$$ (4)

The midpoint of the unfolding transition is the same, within measurement uncertainty, as the one obtained for ${\lambda }^{\ast }\text{YA}$ at high temperature (23). It appears that stabilization by the cryogenic solvent offsets destabilization by cold denaturation.

Denaturation detected by SAXS yields C_m = 3.4 ± 0.3 M (Fig. 2 B), in agreement with the CD titration. This agreement is a further indication of apparent two-state behavior near the denaturation midpoint. The cooperativity (slope near the midpoint) in Fig. 2 B may be somewhat higher than that in Fig. 1 A, but the measurement uncertainty does not allow a significant difference to be determined between the CD and the SAXS data.

Refolding kinetics

All three probes have a main resolved phase of ∼100 ms at −28°C. Fig. 3 shows the stopped-flow refolding kinetics of ${\lambda }^{\ast }\text{YA}$ monitored by tryptophan fluorescence, CD at 222 nm, and small-angle x-ray scattering. An unresolved jump in the fluorescence intensity at time zero is most likely due to changes in tryptophan solvent exposure after the switch in solvent condition. The CD spectrum has a large unresolved phase corresponding to a −3000 deg M⁻¹ m⁻¹ overshoot of helical structure relative to the native state. All three probes also show evidence of a slower phase ranging from 0.5 to 1 s. The slow phase is sufficiently small that we could not reliably determine whether its time constant significantly differs among probes.

Figure 3.

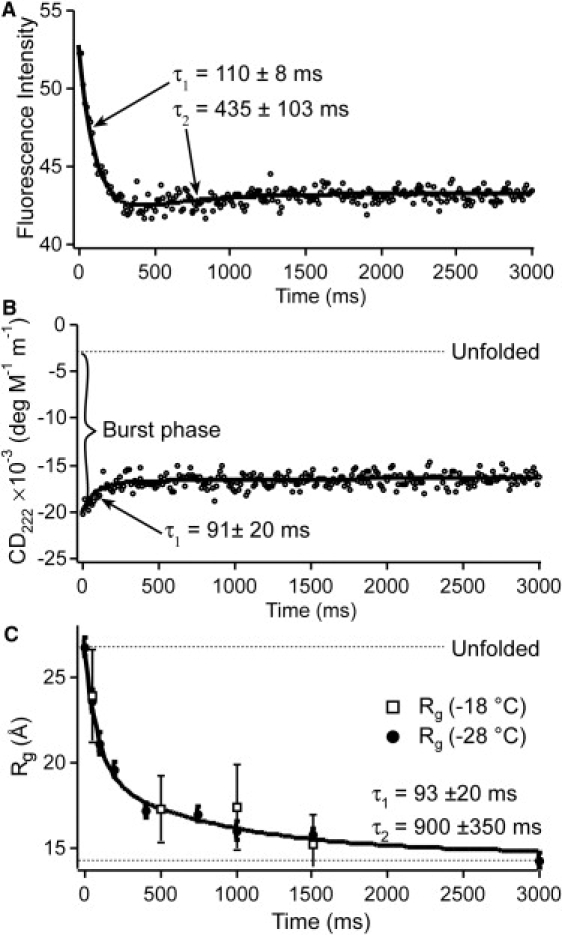
Refolding kinetics of ${\lambda }^{\ast }\text{YA}$ upon dilution from 5 to 0.7 M guanidine hydrochloride by cryogenic stopped flow. (A) Fluorescence detection at −28°C shows a major phase of ∼0.1 s and a minor inverted slow phase. (B) [θ]₂₂₂ detected by circular dichroism at −28°C shows an unresolved burst phase, and an ∼0.1-s recovery to native secondary structure. There may be a very small slower phase also. (C) The radius of gyration detected by SAXS at −28°C shows a major phase of ∼0.1 s and a smaller slow phase. All fitting errors are 1-SD confidence intervals.

The radius of gyration smoothly decays from 26.7 Å to 14 Å in Fig. 3 C. The observed SAXS kinetics at −28°C can be fitted within the signal/noise ratio only by a double-exponential decay, with rate coefficients shown in Fig. 3 C. At −24°C and −18°C, R_g obeys the same trend as at −28°C, but due to increased aggregation of the protein at higher temperatures, R_g could not be determined as reliably (see error bars in Fig. 3 C).

The fluorescence-detected kinetics produced the best signal/noise ratio and allowed us to determine the temperature dependence of the main phase (Fig. 4 A). The rate speeds up by about a factor of 5 for every 10°C higher temperature. The observed rates are measured under strongly refolding conditions (0.7 M guanidine hydrochloride (Fig. 1 A)), so they correspond approximately to folding rates. Folding of ${\lambda }^{\ast }\text{YA}$ is thus an activated process in ethylene glycol/water buffer at low temperature. In addition to changes in the main-phase rate, the amplitude of the slow phase switches from negative to positive as the temperature is increased from −28 to −18°C.

Figure 4.

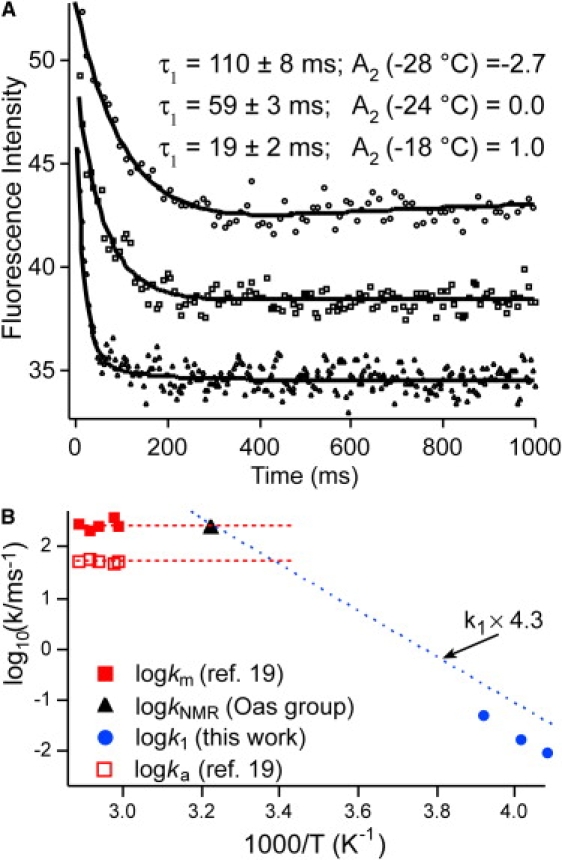
Refolding kinetics observed for ${\lambda }^{\ast }\text{YA}$ by fluorescence. (A) When the temperature is raised, the fast phase speeds up and the slow phase is no longer inverted. (B) Arrhenius plot of the main kinetic phase described in this article (solid circles). A linear free-energy extrapolation, viscosity-corrected from ethylene glycol solvent to water, is shown as a dotted line. Previously measured aqueous T-jump data are shown as squares (solid, molecular-rate coefficient, k_m; open, activated-rate coefficient, k_a, from Yang and Gruebele (23)). The dashed lines indicate the k_m and k_a brackets. The black triangle is the rate coefficient extrapolated from denaturant NMR experiments at 37°C by Myers and Oas ((55) and personal communication (T. Oas, Duke University, 2000)). All three data sets are consistent with a speed limit of ∼(4.5 μs)⁻¹ for ${\lambda }^{\ast }\text{YA}$ at ∼40°C.

Discussion

Refolding of the ${\lambda }^{\ast }\text{YA}$ mutant differs from the slower ${\lambda }_{6-85}^{\ast }$ in one important aspect. The pseudo-wild-type we studied previously (18) has different rates for the main phase observed by CD and SAXS: (29 ms)⁻¹ and (330 ms)⁻¹ at −28°C, a factor of 10 difference between rapid secondary-structure formation and much slower acquisition of native compactness. In contrast, the main resolved refolding phase of ${\lambda }^{\ast }\text{YA}$ has the same timescale within measurement uncertainty using all three probes monitored here (Fig. 3), indicating that collapse, nativelike secondary-structure formation, and nativelike tryptophan packing are more concerted in the stable mutant.

Is the temperature dependence of the main observed phase consistent with other measurements of ${\lambda }^{\ast }\text{YA}$ kinetics? Two other sets of data exist in the literature: NMR line-shape analysis at 37°C revealed fast folding by extrapolation from denaturant solution (22). T-jump relaxation kinetics were subsequently studied at higher temperature (23). Fig. 4 compares the three sets of rate coefficients, which were obtained as described in detail in the Methods section and are summarized here. The T-jump data yielded an activated rate coefficient, k_a (open squares), and the faster molecular rate coefficient, k_m, assigned to the folding “speed limit” of ${\lambda }^{\ast }\text{YA}$ (solid squares; see Methods). As indicated by the dashed lines, the speed limit and activated rate obtained from T-jumps bracket the rate coefficient inferred from NMR data. It has been shown that as the temperature is lowered, the molecular phase amplitude increases, so a single-exponential fit of T-jump data eventually converges to k_m, not k_a (6,20). In a similar way, a two-state analysis of the NMR data could also lead to a rate dominated by k_m, which might explain why the NMR extrapolation is at the upper end of the bracket set by T-jump relaxation data. The dotted line is a simple Arrhenius fit to our low-temperature data (circles), but shifted upward to correct for having a viscosity a factor of 4.3 lower in aqueous buffer than in ethylene glycol buffer (Eq. 2). This simple extrapolation is also consistent with the T-jump speed limit and with the NMR data (k_NMR = (4.5 μs)⁻¹ at 37°C). Of course, such a simple linear extrapolation is expected to break down as the protein reaches the speed limit. Instead, the dotted line should split into an activated (k_a) and a molecular (k_m) branch.

The speed limit expected for ${\lambda }^{\ast }\text{YA}$ based on agreement of three extrapolations is nearly as fast as the fastest-folding λ-repressor mutant observed directly: Y²²W/Q³³H/G⁴⁶A/G⁴⁸A had an observed rate coefficient of (2.3 μs)⁻¹ at 44°C. In both cases, the activation barrier, ΔG^† = kTln(k_m/k_f), approaches 1 kT as the optimal folding temperature is reached (19). The agreement also validates the interpretation of k_m as the “molecular rate” coefficient for diffusion on a rough free-energy surface once the dominant activation barrier has been removed.

The low-temperature main phase, even after viscosity adjustment, is much slower than the T-jump or NMR data. This observation resolves a puzzle from a Yang and Gruebele study (23): ${\lambda }^{\ast }\text{YA}$ was the only mutant whose folding rate did not eventually decline as the temperature was lowered. We see here that the rate eventually decreases, but at a much lower temperature than for other λ-repressor variants. The decreasing rate is due to a combination of increased solvent viscosity and the onset of cold denaturation destabilizing the native state and leading back to activated folding.

At low temperature, folding is clearly slow enough to be activated. The main refolding phases obtained here by three different probes have identical rate coefficients within measurement uncertainty, indicating that ${\lambda }^{\ast }\text{YA}$ is closer to the two-state limit than is the pseudo-wild-type ${\lambda }_{6-85}^{\ast }$. Nonetheless, ${\lambda }^{\ast }\text{YA}$ is not quite a two-state folder. In addition to rapid secondary-structure formation seen by CD, fluorescence- and SAXS-detected kinetics show evidence of a slower phase that comes after the main phase. The relaxation time constant of this phase, between 440 and 900 ms at −28°C (Fig. 3), is closer to the collapse time reported for the pseudo-wild-type (18).

Two mechanisms could produce such a slow phase. In the first mechanism, the unfolded state is kinetically partitioned, and a small fraction of the population folds via a slower pathway. In the second mechanism, an intermediate forms that has nativelike secondary structure, but only near-native tryptophan fluorescence and R_g. We prefer the second scenario in this case. The first scenario would require one of the unfolded states to have higher fluorescence intensity than the native state, and the other to have very similar intensity. This seems unlikely unless a very specific quenching interaction exists in the second unfolded state. The intermediate scenario requires a compact intermediate to have a temperature-dependent fluorescence slightly different from that of the native state, which is more likely. The intermediate could be a trap, or on-pathway.

We now postulate that high temperature and cryogenic conditions decrease the native bias and/or increase the roughness of the free-energy landscape compared to the optimal folding conditions in aqueous solvent at ∼40°C. This assumption is justified by the existing kinetic data in Fig. 4.

Using this postulate, all the differences between the fast-folding ${\lambda }^{\ast }\text{YA}$ mutant and the slower, pseudo-wild-type ${\lambda }_{6-85}^{\ast }$ can be rationalized in terms of the one-dimensional free-energy cartoons in Fig. 5. These cartoons show what happens to the free-energy surface when its roughness or bias toward the native state are changed. The ${\lambda }^{\ast }\text{YA}$ free-energy surface at low native bias is modeled by the free-energy surface computed by Pogorelov and Schulten (46) for that mutant. The ${\lambda }_{6-85}^{\ast }$ surface is modeled by increasing the roughness of the ${\lambda }^{\ast }\text{YA}$ surface. The shift from cryogenic high-viscosity solvent (lower native bias) to aqueous solvent below the melting transition (higher native bias) is modeled by a tilt of the free-energy surfaces toward the native state (Fig. 5, right columns).

Figure 5.

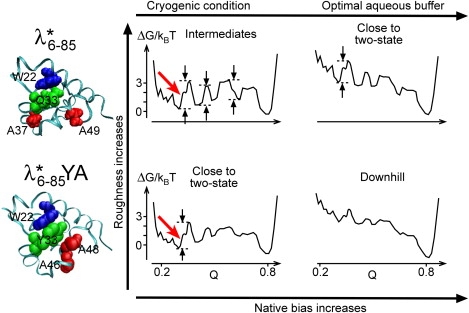
Free energy cartoons indicating the difference between pseudo-wild-type ${\lambda }_{6-85}^{\ast }$ (upper) and fast-folding mutant ${\lambda }^{\ast }\text{YA}$ (lower). Q is the fraction of native contacts. The free-energy surface at the lower left is modeled after Pogorelov and Luthey Schulten for ${\lambda }^{\ast }\text{YA}$ (46). The other surfaces are derived from it by increasing roughness or native bias. Less roughness on the free-energy surface of ${\lambda }^{\ast }\text{YA}$ means that it remains closer to the two-state limit at low temperature (at least the main phases are identical by all probe techniques), whereas ${\lambda }_{6-85}^{\ast }$ folds through several distinct intermediates. The thick gray (red in print) arrows indicate that both proteins form extensive secondary structure before any barrier crossing occurs.

At low native bias, the more rugged ${\lambda }_{6-85}^{\ast }$ surface features several local minima that allow intermediates to accumulate. This explains the multiple timescales for CD and SAXS observed under cryogenic conditions in a previous study (18). At higher native bias, the ${\lambda }_{6-85}^{\ast }$ surface has an early barrier followed by low-barrier intermediates between the transition state and native state, as envisioned by Englander and co-workers (47). This explains the apparent two-state kinetics observed in aqueous solution by Ghaemagammi et al. (17) and Yang and Gruebele (23).

At low native bias, the less rugged ${\lambda }^{\ast }\text{YA}$ surface features an early transition state and smaller local minima. This explains why folding of ${\lambda }^{\ast }\text{YA}$ is more concerted than folding of ${\lambda }_{6-85}^{\ast }$ in the cryogenic experiments, although it is not quite in the two-state limit. Fast secondary-structure formation is illustrated by a heavy red arrow in Fig. 5, indicating that excess secondary structure accumulates before the main barrier is crossed. At higher native bias, the ${\lambda }^{\ast }\text{YA}$ surface approaches downhill folding, in agreement with the nearly identical speed limit extrapolated from NMR, T-jump, and stopped-flow experiments.

The example of ${\lambda }^{\ast }\text{YA}$ illustrates that very fast folding is compatible with classic structural scenarios for folding. The negative overshoot of the CD signal at 220 nm (Fig. 3 B) shows that excess secondary structure forms rapidly and then rearranges to the native secondary structure as collapse to a compact structure occurs. ${\lambda }^{\ast }\text{YA}$ cryogenically slowed down thus folds by the framework structural hypothesis (48,49). Excess secondary structure may retard loop formation, preventing the protein from getting trapped in compact misfolded states, and thus speed up the folding process. Indeed, Oas and co-workers have seen evidence for accumulation of a slow folding intermediate in wild-type ${\lambda }_{6-85}^{\ast }$ (22), whereas we see such evidence for ${\lambda }^{\ast }\text{YA}$ only under cryogenic conditions.

λ-repressor fragment proves that a given protein fold can support many alternative folding mechanisms, conferring robustness to the folding process as protein sequences evolve to adapt to their environment. Such folding mechanisms reported in the literature include downhill folding (20,21), incipient downhill folding (19,21), two-state folding (15–17,19,21,50), secondary-structure formation followed by slow collapse (this article), and multiple intermediate folding mechanisms (18) for λ repressor fragment. The λ-repressor fold can form by many mechanisms. Rapid collapse, collapse concomitant with secondary-structure formation, and slow collapse have all been reported for other proteins also (e.g., (51–53)). These observations, taken together, emphasize what is expressed in Eq. 1: The energy landscape supports multiple paths to the folded state, but the exponential sensitivity of the protein population to the free energy may strongly emphasize one of these paths in ensemble experiments. It will clearly be worthwhile to extend the throughput and speed of single-molecule experiments so that the more rarely visited higher-free-energy paths can be monitored independently of the most probable path.