Mechanisms of β-Adrenergic Modulation of I_Ks in the Guinea-Pig Ventricle: Insights from Experimental and Model-Based Analysis

Abstract

Detailed understanding of I_Ks gating complexity may provide clues regarding the mechanisms of repolarization instability and the resulting arrhythmias. We developed and tested a kinetic model to interpret physiologically relevant I_Ks properties, including pause-dependence and modulation by β-adrenergic receptors (β-AR). I_Ks gating was evaluated in guinea-pig ventricular myocytes at 36°C in control and during β-AR stimulation (0.1 μmol/L isoprenaline (ISO)). We tested voltage dependence of steady-state conductance (Gss), voltage dependence of activation and deactivation time constants (τ_act, τ_deact), and pause-dependence of τ_act during repetitive activations (τ_react). The I_Ks model was developed from the Silva and Rudy formulation. Parameters were optimized on control and ISO experimental data, respectively. ISO strongly increased Gss and its voltage dependence, changed the voltage dependence of τ_act and τ_deact, and modified the pause-dependence of τ_react. A single set of model parameters reproduced all experimental data in control. Modification of only three transition rates led to a second set of parameters suitable to fit all ISO data. Channel unitary conductance and density were unchanged in the model, thus implying increased open probability as the mechanism of ISO-induced Gss enhancement. The new I_Ks model was applied to analyze ISO effect on repolarization rate-dependence. I_Ks kinetics and its β-AR modulation were entirely reproduced by a single Markov chain of transitions (for each channel monomer). Model-based analysis suggests that complete opening of I_Ks channels within a physiological range of potentials requires concomitant β-AR stimulation. Transient redistribution of state occupancy, in addition to direct modulation of transition rates, may underlie β-AR modulation of I_Ks time dependence.

Introduction

The delayed rectifier potassium current (I_K) accounts for the majority of repolarizing current during the action potential plateau, and its time dependence contributes to the rate-dependent shortening of action potential duration (APD). The slowly activating component of I_K, referred to as I_Ks, is strongly upregulated by phosphorylation through protein kinase A (PKA) (1–3), thus balancing the increase in inward current elicited by β-adrenergic stimulation of I_CaL. The I_Ks channel is constituted by four KCNQ1 proteins, which can form functional homomeric potassium channels, plus an uncertain (probably two) number of KCNE1 β-subunits (4,5). Loss of function of I_Ks due to KCNQ1 mutations in humans is associated with QT prolongation and a high incidence of Torsade de Pointes (TdP) ventricular tachycardia (LQT1 syndrome) (6,7). In LQT1 patients, TdP typically ensues during physical or emotional stress, conditions that involve high levels of β-adrenergic stimulation (7). Taken together, the β-adrenergic modulation of I_Ks and the arrhythmic consequences of LQT1 mutations strongly suggest a role of I_Ks in the complex pattern of current changes required to maintain repolarization stability during sympathetic activation. Because of channel kinetic properties, current amplitude during repolarization is rate-dependent. Thus, in vivo, sympathetic activation modulates repolarization currents by the concurrence of direct action on adrenergic receptors and heart-rate changes. We have shown that these two factors interact in a complex way and that their match may be crucial for repolarization stability (8). Rate-dependent increase in I_Ks has been generally attributed to incomplete channel deactivation during short diastolic intervals, causing rate-dependent accumulation of channels in the open state. However, this should only affect the magnitude of “instantaneous” I_Ks appearing during the action potential upstroke, a view disputed by our observation that the “time-dependent component” of I_Ks onset is mainly enhanced by fast pacing (8,9). This was tentatively interpreted as rate-dependent accumulation of channels in a nonconductive state from which activation may occur rapidly (9). This interpretation has been elegantly formalized by Silva and Rudy (10) in a numerical model of I_Ks. This model accurately reproduced the features of I_Ks rate-dependence observed under basal conditions in experiments on guinea pig myocytes.

The purpose of this work was to test whether the complex interaction between direct and rate-dependent effects of β-adrenergic modulations of I_Ks could be interpreted within the framework of the same kinetic model. To this aim, I_Ks kinetics and its adrenergic and rate-dependent modulations were evaluated in guinea-pig ventricular myocytes and subsequently used as the reference for identification of the model parameters.

The results obtained extend the applicability of the model structure proposed by Silva and Rudy (10) to a broad range of complex conditions and provide insights on the molecular mechanisms potentially accounting for direct and rate-dependent adrenergic modulation of I_Ks.

Materials and Methods

The presented investigation conforms to the Guide to the Care and Use of Laboratory Animals published by the U.S. National Institutes of Health (NIH publication No. 85-23, revised 1996) and endorsed by the University of Milan.§

Myocyte studies

Ventricular myocytes from Hartley guinea pigs were used within 12 h from isolation. Whole-cell I_Ks measurements were performed at 36°C in the presence of I_CaL, I_NCX, and I_Kr blockade. I_Ks identity was verified at the end of each experiment by checking complete elimination of time-dependent outward current upon specific I_Ks blockade. Information on myocyte isolation procedure, experimental solutions, and channel blockers is provided in the Supporting Material (section 1.2).

The voltage dependencies of steady-state activation, activation kinetics, and deactivation kinetics were evaluated by voltage step protocols described in the Supporting Material (section 1.2). Steady-state activation data were fitted by the Boltzmann function, from which midactivation potential (V_0.5), inverse slope factor (1/S), and asymptotic current amplitude (I_max) were estimated. I_Ks kinetics during activation was quantified by biexponential fitting of current onset during the depolarizing steps; to exclude the activation delay, the initial 2% of the time course was not considered. The faster exponential component was used to quantify the kinetics of I_Ks onset (τ_act). Pause-dependence of I_Ks onset kinetics was analyzed by a two-step protocol, as we have described in a previous study (8). Briefly, two activating steps (S1 and S2) were separated by a variable pause. I_Ks onset during S2 included an instantaneous component, followed by a time-dependent one; the time-dependent component, referred to as “reactivation”, was fitted and its time constant (τ_react) was estimated as for activation (11). Dependency of τ_react on the S1–S2 interval, referred to as “restitution”, was quantified by monoexponential fitting to yield the restitution time constant (τ_rest). The same criteria for quantification of I_Ks kinetics were applied for experimental and model results.

Each experimental protocol was performed in control conditions and in the presence of 0.1 μmol/L of isoprenaline (ISO), a concentration one log unit above the half-maximal effective concentration (12.9 nM) (12)). Control and ISO measurements were performed within the same myocyte, thus allowing for internal comparison.

Statistical analysis

Experimental data are presented as mean ± standard error (SE). Differences in experimental activation, deactivation and reactivation data sets between control and ISO were tested by two-way ANOVA for paired measurements (SAS/LAB software); difference was defined by significance of F statistics for either the treatment factor, or the treatment by voltage interaction. Curve fitting was performed by the least-square method (Origin Microcal 7.0); goodness of fitting was tested by the chi-square test on correlation coefficients (R). Differences between parameter means were tested by Student's t-test for paired measurements, and with post-hoc analysis (SAS/LAB software) in the case of multiple comparisons. Sample size for each protocol is reported in the respective figure legend.

In the analysis of myocyte experiments, curve fitting was performed on data from individual cells and results are reported as the mean ± SE of parameter estimates; in this case, differences between curves were tested by comparing parameter populations. To obtain a reference for model optimization, curves fitted on averaged myocyte data points were also obtained. Parameters from “average” experimental curves (reported without SE) were used only to provide a quantitative comparison with model-generated curves. Parameters obtained by fitting an average curve may differ slightly from the mean of individual cell parameters.

Computational analysis

The Markov model structure (Fig. S1) implemented in this study was derived by Silva and Rudy (10). It describes the properties of I_Ks, including all of its KCNQ1 and KCNE1 subunits, by means of 15 closed states to account for four independent voltage sensors, each undergoing two conformational changes before channel opening. The group of closed states representing channels for which the first transition has been completed by only part of the four voltage sensors is called “Zone 2”. The group of closed states representing channels in which the first transition has been completed by all four voltage sensors is called “Zone 1”. There are two open states. The whole-cell I_Ks current is given by:

$$I_{\text{Ks}}=G_{\text{Ks}}\times P_{\text{O}}\times \left(V-E_{\text{Ks}}\right),\text{where}{G}_{\text{Ks}}=\sigma \times g_{\text{Ks}}\text{.}$$ (1)

The variable P_o represents the sum of the probabilities of occurrence in the open states, V is the membrane potential, and E_Ks is the K⁺ reversal potential. G_Ks is the maximum membrane conductance obtained as the product of channel density (σ) and the unitary channel conductance (g_Ks). E_Ks was set to −72.4 mV, as measured in preliminary experiments (8). G_Ks was set to 12 nS and remained unchanged under ISO stimulation. G_Ks dependence on changes in cytosolic Ca²⁺ was neglected, because ISO modulation of I_Ks gating was analyzed under conditions ruling out its contribution (with both I_CaL and I_NCX blocked).

The expressions describing transition rates between channel states and their parameters are reported in Tables S1 and S2. Parameter identification was based on model optimization versus experimental data, as described in the Supporting Material (section 1.3). MATLAB 7 and Simulink (The MathWorks, Natick, MA) were used for all the numerical computations.

Implementation of previous Hodgkin-Huxley-type models

To test whether alternative models could reproduce specific I_Ks features such as pause-dependence (also referred to as “restitution”) of reactivation rate, we implemented the formulations proposed by Terrenoire et al. (13) and by Imredy et al. (12), respectively. The two models were applied (with their original parameter values) to compute I_Ks and its modulation by ISO in the S1–S2 protocol. This section, presented in detail in the Supporting Material (section 2.2), is summarized here.

Action potential simulations

The effect of 100 nM ISO was simulated by modulation of I_Ks (according to presented results), I_CaL (scaled by a factor of 1.5), and rate of Ca²⁺ uptake by the sarco/endoplasmic reticulum Ca²⁺-ATPase (SERCA) flux scaled by a factor of 1.5. Changes in conductances other than I_Ks were required, because I_CaL directly contributes to APD and SERCA flux can indirectly affect the Na⁺/Ca²⁺ exchanger current. In the case of I_CaL, simple scaling is an approximation of PKA-dependent modulation, which also involves shifts in activation and inactivation voltage dependency (14), but may be adequate for our purposes.

Results

I_Ks properties in myocytes under control conditions

Voltage dependence of I_Ks gating properties measured from myocytes in control is illustrated by open symbols in Figs. 1 and 2; sample current records are shown in Fig. S2. Boltzmann fitting of steady-state activation curves of individual cells yielded V_0.5 = 26.6 ± 2.5 mV, 1/S = 12.0 ± 0.7 mV, and I_max= 197 ± 26 pA. However, even at the most positive potential tested, steady-state current failed to show clear-cut saturation in most of the experiments; thus, the parameters estimated by Boltzmann fitting should be interpreted with caution and are reported here only for comparison with previous work.

Figure 1.

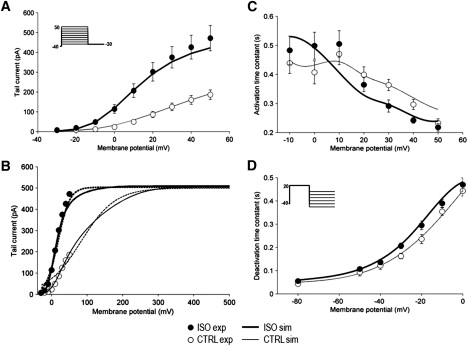
ISO effect on voltage dependence of I_Ks gating. Experimental data (mean ± SE) shown by symbols (control: open symbols; ISO: solid symbols); model simulations by lines (control: thin lines; ISO: thick lines). (A) Steady-state activation (n = 15). (B) Extension of steady-state activation simulations over a wider range of potentials (experimental data points as in A superimposed for comparison); dotted lines represent Boltzmann fitting of simulated data. (C) Activation kinetics (n = 15); (D) Deactivation kinetics (n = 16). Voltage protocols in inset.

Figure 2.

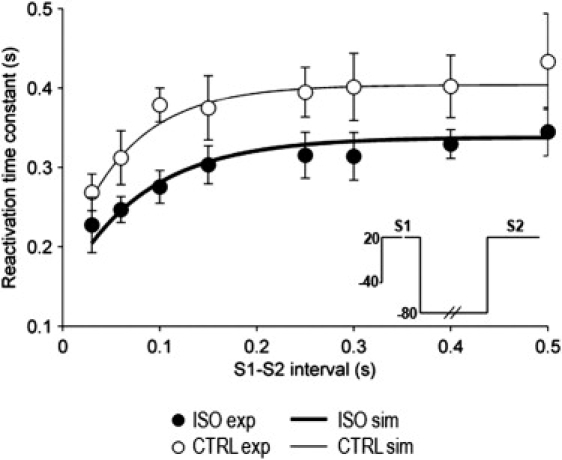
ISO effect on I_Ks reactivation kinetics and its pause-dependence (restitution, n = 5). Reactivation time constants (τ_react) are plotted versus S1–S2 intervals. Meaning of symbols and lines as in Fig. 1. Experimental data points from Rocchetti et al. (8).

The time constant of the fast component of I_Ks activation (τ_act, Fig. 1 C) remained unchanged between 0 and 10 mV and decreased between 10 and 50 mV. Deactivation time constant (τ_deact, Fig. 1 D) decreased monotonically with membrane hyperpolarization. At 0 mV, deactivation rate did not differ significantly from activation rate (τ_deact = 443 ± 22 ms; τ_act = 407 ± 39 ms, NS).

The reactivation of I_Ks, analyzed by the S1–S2 protocol, was composed of a time-independent (instantaneous) component and a time-dependent one (Fig. S2 C). As the S1–S2 interval was shortened, the instantaneous component of I_Ks activation during S2 increased, with a time course reflecting channel deactivation at –80 mV. The time constant (τ_react) of the time-dependent component increased as S1–S2 was prolonged. The dependency of τ_react on S1–S2 (Fig. 2) was fitted by a single exponential, with a time constant (τ_rest) of 68.5 ms and an asymptotic value of τ_react of 411 ms. Because reactivation after a sufficiently long S1–S2 interval is equivalent to activation from resting conditions, the asymptote of τ_react was similar to that ofτ_act at the same membrane potential (20 mV, τ_act = 399 ms).

Model identification under control conditions

As described in the Supporting Material (section 1.3), the Markov model (Fig. S1) was optimized to reproduce all the experimental results in control by a single set of parameters. Model simulations of gating voltage dependence in control are shown in Figs. 1 and 2 by thin lines (symbols omitted for clarity); simulations of sample I_Ks records are shown in Fig. S2. Within the voltage range tested experimentally (≤50 mV), the simulated steady-state activation curve visually overlapped the data (Fig. 1 A); indeed, Boltzmann fitting of simulated points (R² > 0.99) yielded parameters similar to those obtained by fitting mean experimental values (V_0.5 = 25.6 vs. 25.6 mV, inverse slope factor = 14.6 vs. 13.0 mV, and asymptote = 231 vs. 215 pA.). However, extension of simulations to potentials beyond 50 mV showed a further increase in steady-state current, which achieved a saturation value (I_max) of 509 pA at much more positive potentials (Fig. 1 B). Interestingly, the Boltzmann function could not be adequately fitted to the extended activation curve predicted by the model (Fig. 1 B), even if no constraint was put on parameter estimation.

Simulated voltage dependence of τ_act was consistent with that of experimental data (Fig. 1 C), even if τ_act was overestimated at 50 mV. Voltage dependence of τ_deact was accurately reproduced by simulations over the wide range of membrane potentials tested (Fig. 1 D).

As shown in Fig. 2, I_Ks reactivation and its restitution were also well predicted by the model; exponential fitting of simulated restitution (R > 0.93) yielded a τ_rest of 62.9 ms and an asymptotic τ_react of 406 ms, with both values similar to those measured in myocytes (68.5 ms and 411 ms, respectively).

To summarize, except for minor quantitative inaccuracy in the prediction of activation rate, the model reproduced I_Ks gating features examined by all of the protocols. Such a stringent validation confirms the adequacy of the I_Ks model structure proposed by Silva and Rudy (10).

I_Ks properties in myocytes during β-adrenergic stimulation

Voltage dependency of I_Ks gating properties measured from myocytes during exposure to ISO is illustrated by solid symbols in Figs. 1 and 2; sample current records are shown in Fig. S2. β-receptor stimulation by ISO markedly increased I_Ks amplitude (Fig. 1 A), with smaller but significant effects on its kinetics (Fig. 1, C and D).

Boltzmann fitting of steady-state activation curves of individual cells yielded a V_0.5 of 15.7 ± 1.9 mV, a 1/S of 11.9 ± 0.6 mV, and an I_max of 464 ± 62 pA. A significant difference was found for I_max (266 ± 34% of control; p < 0.05; Fig. 1 A) and V_0.5 (Δ = −10 ± 2.2 mV; p < 0.05) between ISO and control. However, as in control conditions, also in the presence of ISO, steady-state current failed to show clear-cut saturation.

The voltage dependence of activation time constant (τ_act, Fig. 1 C) was slightly rotated clockwise by ISO, thus resulting in a slowing of activation between 0 and 10 mV and acceleration between 10 and 50 mV (p < 0.05 for voltage by treatment interaction in ANOVA).

Deactivation was slowed by ISO (Fig. 1 D, p < 0.05 for treatment in ANOVA). In particular, τ_deact was increased by a maximum of 59 ms at −20 mV (p < 0.05); at diastolic potential (−80 mV), τ_deact was 43 ± 2.5 ms in control and 55 ± 2.9 ms with ISO (NS).

Exponential fitting of the restitution of τ_react (Fig. 2) yielded an asymptotic τ_react of 339 ± 8 ms (p < 0.05 versus control) and a τ_rest of 132 ± 30 ms (192% of control; p < 0.05). Thus, ISO significantly accelerated reactivation at all S1–S2 intervals (p < 0.05 for treatment in ANOVA) and slowed the restitution process, thereby extending its influence to a wider range of diastolic intervals.

I_Ks model identification during β-adrenergic stimulation

ISO effects detected in myocytes were reproduced, within the same model structure used in control, by adjusting the parameters governing the transitions between channel states (Fig. 3). The G_max parameter (see Eq. 1) was deliberately kept constant to test the hypothesis that its change is theoretically unnecessary to account for I_Ks response to ISO. The ground for such a hypothesis is discussed in the detail in the Supporting Material (section 3.2).

Figure 3.

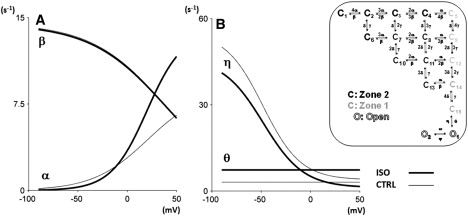
Changes in the voltage dependence of model transition rates (see schematic on the right) required to model ISO effects. (A) Zone 2 forward (α) and backward (β) transition rates. (B) Opening (θ) and closing (η) transition rates. Thin lines for control conditions; thick lines for ISO. Transitions rates unaffected by ISO not shown for simplicity.

Simulations of gating voltage dependence in ISO are shown in Figs. 1 and 2 by thick lines (symbols omitted for clarity); simulations of sample I_Ks records are shown in Fig. S2. Boltzmann fitting of the simulated steady-state activation curves during ISO yielded a V_0.5 of 10.3 mV (−15.3 mV versus control), 1/S of 12.1 mV (−2.5 mv versus control), and an I_max of 436 pA (188% of control). These parameters should be compared with those obtained by fitting mean experimental values, which estimated (R² > 0.99) a V_0.5 of 14.2 mV (−11.4 mV versus control), a 1/S of 11.9 (−1.1 mV versus control), and an I_max of 484.1 pA (225% of control). Thus, when analyzed by Boltzman fit over the physiological range of potentials, modeled and experimental data consistently indicated that ISO increased I_max and shifted V_0.5, without changing 1/S. However, when simulations were extended to potentials beyond 50 mV, the same I_max value was achieved in ISO and control (509 pA, Fig. 1 B), ISO markedly increased the steepness of the activation curve (i.e., substantially reduced 1/S), and its Boltzmann fitting, although not yet optimal, was considerably improved compared with that obtained in control (Fig. 1 B).

In the voltage dependence of τ_act (Fig. 1 C), the crossover between control and ISO curves was reproduced by simulation; however, it occurred at a slightly more negative potential than that occurring in experiments. On the other hand, the voltage dependency of τ_deact was also well reproduced by the model in quantitative terms (Fig. 1 D). The model also succeeded in reproducing the complex effect of ISO on I_Ks reactivation rate and on its restitution process (Fig. 2). Exponential fitting of simulated τ_react restitution curves yielded an asymptotic τ_react of 338 ms (83% of control) and a τ_rest of 107 ms (169% of control). Whereas estimates of ISO-induced changes were qualitatively correct, the increase in τ_rest was slightly underestimated by the model (169% vs. 192%).

Overall, the model was able to qualitatively reproduce all ISO effects, with minor quantitative differences. We then proceeded to identify which transitions in the kinetic scheme (Fig. S1) were crucial in modeling ISO effects.

Model-based analysis β-adrenergic modulation of channel kinetics

As illustrated in Fig. 3, model optimization to reproduce ISO effects resulted in modification of only few among the transition rates of the Markov model, namely α, θ, and η. For each channel monomer, the changes resulted in facilitation of the transition between the first and the second closed state (α increased for V > −20 mV, β minimally affected) and of the final opening transition (θ increased, η decreased). The second voltage-dependent transition (rates γ and δ) and the transition between the two open states (rates ψ and ω), were not modified in reproducing ISO effects.

ISO effects on I_Ks were first analyzed in steady-state conditions by observing the distribution of state occupancy at different voltage levels (Fig. 4). At resting potential (−80 mV, Fig. 4 A), channels almost exclusively resided in Zone 2, and, up to −40 mV (not shown), ISO minimally affected the occupancy distribution. Upon small depolarization beyond threshold (e.g., 0 mV, Fig. 4 B), ISO increased open-state occupancy at the expense of Zone 2 occupancy, with Zone 1 remaining almost unchanged. At mid-activation potential (20 mV, Fig. 4 C), ISO induced a strong shift from all closed states toward the open ones. For depolarization to 50 mV (Fig. 4 D) in control conditions, the occupancy of closed states (mainly Zone 1) was still substantial (0.6). This situation was dramatically changed by ISO, which caused almost complete channel opening.

Figure 4.

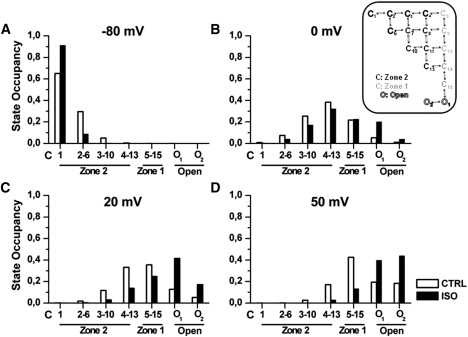
Steady-state distribution of model states occupancy at selected potentials. (A) −80 mV = diastolic. (B) 0 mV. (C) +20 mV ≅ 50% activation. (D) +50 mV ≅ 95% activation in control (open bars) and in ISO (solid bars). States (see schematic on the right) are represented on the abscissa from those farther (Zone 2) to those closer (Zone 1) to channel opening (open). State occupancy is defined as (n of channels in a state)/(total n of channels).

The effect of ISO on the dynamic evolution of state occupancies is analyzed in Figs. 5–8. To this end, simulations were run for conditions maximizing differences between control and ISO (activation V_test = 30 mV; deactivation V_test = −20 mV: reactivation S1–S2 interval = 100 and 500 ms).

Figure 5.

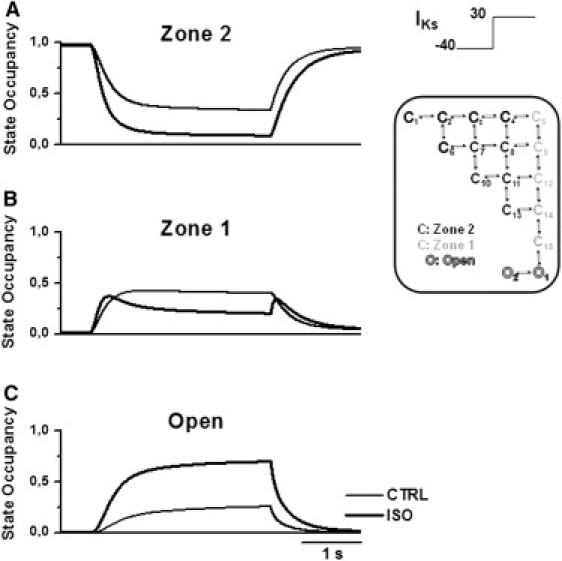
Model analysis of I_Ks activation course during a V-step protocol (inset) in control (thin lines) and in ISO (thick lines). (A) Zone 2 occupancy. (B) Zone 1 occupancy. (C) Open-state occupancy.

Figure 6.

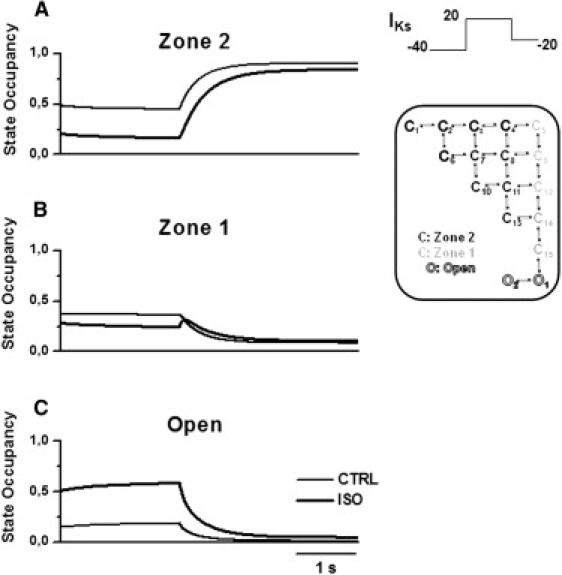
Model analysis of I_Ks deactivation course during a V-step protocol (inset) in control (thin lines) and in ISO (thick lines). Panels as in Fig. 5.

Figure 7.

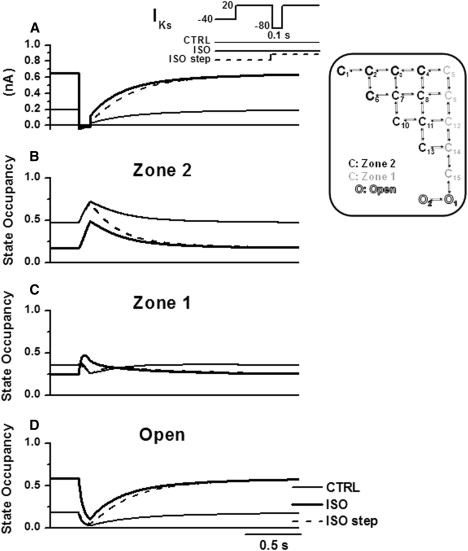
Model analysis of I_Ks reactivation at a short S1–S2 interval (100 ms) in control (thin line) and in ISO (thick line). Voltage protocols in inset. The dashed line shows the effect of ISO applied after S1 (“ISO step” in inset). (A) Current (I_Ks). (B) Zone 2 occupancy. (C) Zone 1 occupancy. (D) Open-state occupancy.

Figure 8.

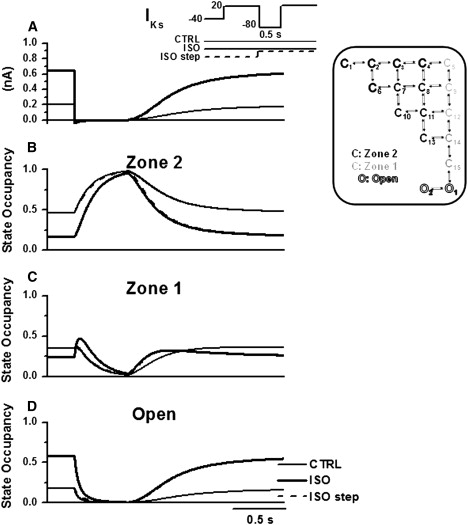
Model analysis of I_Ks reactivation at a long S1–S2 interval (500 ms). Protocol and legends as in Fig. 7.

During activation (Fig. 5), ISO increased the amount and the velocity of channels exiting Zone 2, thus promoting transient accumulation of channels in Zone 1 (Fig. 5 B). Furthermore, ISO facilitated the opening transition (Fig. 5 C). The two effects cooperated in accelerating I_Ks onset during activation and led to the opening of the majority of channels. Indeed, after 3 s at 30 mV, 70% of channels opened with ISO compared with 26% in control (Fig. 5 C).

ISO-induced slowing of I_Ks deactivation was analyzed by simulating repolarization to −20 mV from steady-state activation at 20 mV (Fig. 6). In control conditions, repolarization caused channels to move rapidly from open states, through Zone 1, to Zone 2 (Fig. 6). In the presence of ISO, the flow of channels from open states with increased occupancy met the bottleneck generated by the slow Zone 1–Zone 2 transition. This factor led to a transient accumulation of channels in Zone 1 (Fig. 6 B), which was a hindrance to the transition of channels from the open to a nonconductive state. Thus, albeit directly slowed by ISO (smaller η; see Fig. 3), the closing transition may not represent the only rate-limiting factor for deactivation in this scheme.

I_Ks pause-dependence (representative of rate-dependence) and its modulation by ISO were analyzed by comparing effects on reactivation at short (100 ms, Fig. 7) and long (500 ms, Fig. 8) S1–S2 intervals. During the S1–S2 interval, channels migrate from the open states to Zone 1 and Zone 2, sequentially. As suggested by Silva and Rudy (10), with shorter S1–S2 intervals reactivation during S2 was faster because of incomplete return to Zone 2 (cf. Fig. 7 B with Fig. 8 B); this decreased the proportion of channels requiring two transitions before opening. ISO enhanced the rate-dependence of I_Ks instantaneous component and of reactivation rate, respectively, by different mechanisms. The former effect was very small and occurred because of slight deactivation slowing at −80 mV, which prolonged persistence in the open state at short S1–S2 intervals (Figs. 7 D and 8 D). In myocytes ISO mainly affected reactivation rate in two ways: it decreased the steady-state value of τ_react and slowed the time course by which the steady-state was achieved (increased τ_rest). Steady-state reactivation is in fact equivalent to activation; thus, ISO effects on steady-state τ_react and on τ_act (at 20 mV) were unsurprisingly similar and were explained by the same mechanism (see above). A more complex mechanism accounted for the rate-dependent effect of ISO on τ_react. Fig. 7 C shows that, in the presence of ISO (thick line), Zone 1 occupancy during the S1–S2 interval transiently increased above the value achieved during S1. This increased the proportion of channels available for direct opening during S2. In turn, the ISO-induced increase in Zone 1 occupancy during the S1–S2 interval was the consequence of the large increase in open-state occupancy during S1 (Fig. 7 D, thick line). This interpretation was tested in the model by introducing ISO-induced gating changes only at the beginning of the S1–S2 interval. Under this condition (Figs. 7 and 8, dashed line), probability of open-state occupancy was not increased during S1, no Zone 1 channel accumulation occurred during the S1–S2 interval (in Fig. 7 C, dashed line initially overlaps with control line), and reactivation during S2 was slower than that achieved when ISO was applied throughout the entire protocol (Fig. 7 A, cf. dashed and thick lines). The dashed-line reactivation was still faster than the control one (Fig. 7 A, thin line) because of pause-independent (i.e., steady-state) ISO effect on τ_react. The difference in reactivation rate between the thick and dashed lines in Fig. 7 A represents the pause-dependent component of ISO effect, which accounts for the slowing in the restitution process. Indeed, Fig. 8 C shows that, at long S1–S2 intervals, ISO-induced channel accumulation in Zone 1 dissipates before reaching S2, thus leading the thick and dashed lines to overlap during reactivation (Fig. 8 A).

Comparison with reactivation kinetics in Hodgkin-Huxley-type models

A comparison of I_Ks reactivation between the presented and HH-type models is shown in Fig. S3. The model by Terrenoire et al. (13) included three independent but identical gates. Some pause-dependence of reactivation rates could be generated by such formulation, but it did not reproduce experimental observations, because the time range of restitution was too narrow and insensitive to ISO. This is because pause-dependence of reactivation rate required diastolic deactivation to be incomplete at the time of S2; therefore, modulation of residual activation was constrained by the small effect of ISO on τ_deact at −80 mV (Fig. 1 D). This explains why, although Terrenoire's formulation may in principle accommodate restituition of reactivation rates, it cannot reproduce experimental observations (Fig. S4).

Imredy's formulation (12) failed to reproduce reactivation pause-dependence (Fig. S4). In this model, gating was simulated by the product of two gating components with independent and strongly different kinetics. Reactivation pause-dependence could not be reproduced at all because of the specific formulation of the gating components. Even if pause-dependence of reactivation rate could be reproduced in this model, it would still rely on incomplete diastolic deactivation.

In summary, depending on the specific formulation, Hodgkin-Huxley (H-H)-type models may incorporate pause-dependence of reactivation rate in principle; nevertheless, they cannot reproduce experimental data in terms of magnitude and response to ISO. This is mainly because, in H-H models, pause-dependence of reactivation rate depends uniquely on incomplete diastolic deactivation (i.e., gating variables > 0 at the onset of S2), which strictly constrains the model output. This is not the case for Markov models, in which redistribution between sequential closed states can contribute to explain the phenomenon. The results obtained with Terrenoire's and Imredy's models are illustrated and discussed in further detail in the Supporting Material (section 2.2).

Action potential simulations

In guinea-pig myocytes, ISO causes counterclockwise rotation of the relationship between APD and stimulation cycle length (CL) (8), with convergence of control and ISO relationships at a CL of 0.15 s. To test the performance of modeled I_Ks in simulating such an effect, we incorporated the presented I_Ks formulation in an action potential model (10,15). Under control conditions, the model generated an APD/CL relationship comparable to that observed in guinea pig myocytes, and incorporation of ISO-induced changes reproduced its counterclockwise rotation (Fig. S5). The model-generated control and ISO relationship converged at a CL of 0.7 s, which was significantly longer than the CL observed experimentally. ISO modulation of APD reflected the balance between the opposite effects of I_CaL and I_NCX enhancement on one side and I_Ks enhancement on the other. The CL at which opposite contributions balance each other is highly sensitive to their relative magnitudes and rate-dependence. Therefore, modulation of I_CaL and SERCA other than arbitrary scaling may be required to achieve quantitatively accurate simulation of ISO effects.

β-adrenergic stimulation was then reproduced in the presence of a 50% reduction in I_Ks maximal conductance (Fig. S5). In this case, counterclockwise rotation was accompanied by an upward shift of the whole APD/CL relationship and, at CL ≥ 1.5 s, repolarization failed. The effect of such partial I_Ks reduction was large compared with that of repolarization abnormalities in human long QT syndromes with almost complete loss of I_Ks function (16). Such a difference may reflect the larger role of I_Ks in guinea-pig repolarization, for which the action potential model was developed.

Discussion

The presented experimental results extensively describe I_Ks gating properties in guinea-pig myocytes and their modulation by ISO. In model simulations all baseline I_Ks features could be reproduced by a single set of kinetic parameters and ISO-induced effects were reproduced, within the same model structure, by changes in the parameters governing selected transitions. Analysis of the model adjustments necessary to reproduce ISO effects leads to several “inferential” conclusions on the modulation of I_Ks gating by β-AR stimulation.

I_Ks properties in myocytes

PKA-dependent modulation of I_Ks gating properties were previously described in heterologously expressed human channels and native guinea-pig myocytes (13,17). The purpose of our experiments was to fully characterize gating of native I_Ks and its β-adrenergic modulation under strictly uniform conditions, as necessary in developing and testing a comprehensive model with quantitative accuracy.

A feature of I_Ks consistently observed in this and in many other studies (3,18,19) is failure of its steady-state activation to saturate within the range of potentials that can be tested experimentally in myocytes (<50–60 mV), and up to 120 mV in heterologous KvLQT1/IsK (20). In the absence of clear-cut saturation, I_max estimation by Boltzmann fitting is arbitrary; regardless, adrenergic modulation of I_Ks activation is routinely analyzed in terms of changes in parameters estimated from Boltzmann fitting. When such an approach was applied to the data, ISO effect on steady-state activation consisted of a large increase in I_max and a smaller negative shift of V_0.5, which is in line with previous findings. Extension of steady-state activation analysis to a wider range of potentials by model simulations suggests that this approach might be misleading (see section on model-based analysis of adrenergic modulation, below). Thus, ISO-induced changes in Boltzmann parameters should not be interpreted mechanistically.

ISO increased activation rate and slightly slowed deactivation rate. ISO-induced changes in I_Ks dependency on interpulse interval included an increase of reactivation rates and a slowing of their restitution. Consistent with the nonsignificant effect of ISO on I_Ks deactivation rate at −80 mV (Δτ_deact = +12 ms at −80 mV), pause-dependence of I_Ks instantaneous component was almost unaffected. Faster reactivation may partly reflect ISO-induced acceleration of activation rate; however, at short S1–S2 intervals, reactivation (in S2) was accelerated more than activation (in S1), and the restitution course was also affected.

This complex pattern of changes provides highly stringent conditions for testing any kinetic scheme; thus, the performance of the relatively simple model applied in this work was almost surprising. In light of this, the gating mechanisms suggested by model simulations, albeit theoretical, deserve to be considered in detail.

Mathematical model of I_Ks

To encompass the wide spectrum of I_Ks properties tested in the presented study, we adopted a Markov-type model structure, previously demonstrated by Silva and Rudy (10) to adequately reproduce I_Ks complex features under baseline conditions. Several features of our control data were not correctly reproduced using the parameters published by Silva and Rudy (10), which resulted in excessive maximal conductance, slow deactivation rates (especially for Vm > −50 mV), and unsatisfactory fitting of the pause-dependence of reactivation rates (restitution). This may result from quantitative differences between the presented results and those of Lu et al. (21), used as a reference for parameter optimization by Silva and Rudy (10).

The single set of parameters identified by the optimization procedure was adequate to reproduce all I_Ks features observed under baseline conditions. The voltage dependence of steady-state activation predicted by the model could not be fitted by a Boltzmann function, even if no constraint was put on its parameters. This observation can be interpreted in terms of channel kinetics. Indeed, because a Boltzmann function describes a single transition between closed and open states, it may not be adequate to model multiple sequential transitions over the whole range of activation voltages. In terms of I_Ks dynamic behavior, the presented results lead to the relevant conclusion that interpretation of pause-dependence of reactivation rates can be effectively explained by redistribution of channels to states nearer to the open one within a single chain of Markov states (i.e., no requirement of transition between different gating modes). A more detailed discussion of I_Ks gating features relevant to its modeling is also provided in the Supporting Material (section 3.1).

Modeling of β-adrenergic I_Ks modulation has been previously addressed by H-H-type formulations, in which I_Ks kinetics were represented by the product of multiple (2 (12,22) or 3 (13) identical (13,22) or nonidentical (12)) gating variables, as required to reproduce the initial lag in current activation. However, it was unclear to what extent these models could reproduce the complex pause-dependence of I_Ks reactivation rate, a feature observed for both heterologously expressed human channels (11) and native ones (9) and modulated by β-adrenergic receptors (8). This issue was addressed by implementing previous H-H-type models and applying them to the presented experimental data. This analysis showed that, although H-H models can in principle reproduce pause dependence of reactivation rate, failure to consider sequential (not independent) transitions between closed states strictly constrains their output, thus making it unsuitable to match experimental observations. The presence of sequential transitions for the activation of each independent KCNQ1 subunit, such as those implemented in the presented model, are suggested by experimental evidence (23). The presented results support the concept that sequential gating may be necessary to account for I_Ks kinetic behavior and its modulation.

Model-based analysis of I_Ksβ-adrenergic modulation

According to Boltzmann analysis, the most prominent effect of ISO consists in a large increase in I_max (Fig. 1 A). In previous models (13,22), such an increase was reproduced by an increment in the term G_Ks of Eq. 1, which implies an increase in g_Ks, in channel density (σ), or both.

To our best knowledge, modulation of g_Ks by protein phosphorylation has been described exclusively in nonvoltage-gated channels (gap-junctions, AMPA-R, RyR) (24–26), whereas the possibility of ISO-induced changes in g_Ks has not been experimentally tested because of difficulties in recording I_Ks single-channel currents. On the other hand, modulation of σ might occur with a time course roughly compatible with the response of I_Ks amplitude to ISO (27), but it would not account for changes in the voltage dependence of current kinetics (for detailed discussion see the Supporting Material, section 3.2). These considerations motivate the interest in testing the unitary interpretation that all ISO effects on I_Ks may be mediated by changes in channel P_o.

Model fitting to data points under control conditions identified a set of gating parameters that estimated an open probability of 0.4 at 50 mV, the most positive potential experimentally tested; maximal conductance was achieved only at potentials exceeding the physiological range. According to this interpretation, the apparent ISO-induced increase in I_max was instead a simple increased P_o within the range of potentials tested, and may reflect enhanced sensitivity of the activation gating to membrane depolarization. In this context, I_Ks “reserve” available to recruitment through receptor stimulation would amount to 60% of the total channel population and correspond to the fraction of channels still residing in Zones 2 and 1 during depolarization at 50 mV (Fig. 4). The magnitude of available reserve identified by our results is far larger than that predicted by the original Silva and Rudy model (10). Indeed, simulations carried out with their parameters (not shown) resulted in more than 90% of channels being open upon depolarization at 50 mV under baseline conditions. This implies that a biologically implausible increase in G_Ks would still be required in the original model formulation to account for the large effect of ISO on maximal steady-state current. Nevertheless, such a limitation was overcome in the presented study by acting exclusively on transition rates, thus proving that the Silva and Rudy kinetic scheme (10) can accommodate a wider range of observations. Interestingly, the Boltzmann function fitted the predicted activation curve much better in ISO than in control (Fig. 1 B). This may result from an apparent lumping of sequential closed-state transitions, resulting from the steeper voltage dependence of their rates (α-parameter, Fig. 3 A).

The effects of ISO on the complex time-dependent behavior of I_Ks were also well reproduced by the model. The opening transition rate was directly modulated by ISO; however, a relevant feature underlying ISO effects on current time course after membrane potential changes was transient “accumulation” of channels in states near to the open one (Zone 1). By analogy with the concentration of reactants in a chemical reaction, such an accumulation contributes to determine the flow of channels between states. Transient changes in occupancy are, in turn, the consequence of modulation of transition rates. However, the latter may be far more complex than is direct modulation of channel opening; indeed, a change in occupancy may reflect the net balance between effects on multiple transitions, including those between nonconductive states. In terms of channel structure, this implies that stabilization at diastolic potential of a conformation corresponding to an intermediate closed state might paradoxically increase the kinetics of current onset during activation.

Study limitations

The guinea pig was chosen as the animal model for this analysis because it has a robust I_Ks expression even under baseline conditions; moreover, the original model formulation was developed for this species. However, important differences in I_Ks expression level and kinetics exist between the guinea pig and larger mammals (dog and man) (3,28,29); therefore, these observations may not directly extrapolate to those species.

Parameter optimization was performed on several mutually independent I_Ks properties; this should minimize the number of suitable parameters combinations. Still, the procedure of nonlinear optimization does not guarantee uniqueness of the identified parameters in generating a set of current properties. Thus, interpretation of ISO effects, as is always the case for modeling studies, is subject to uncertainty. Moreover, in terms of mechanistic interpretation, modeling only proves that a given degree of complexity can reproduce the observed behavior, but it does not rule out more complex mechanisms.

Because we focused this study on β-adrenergic modulation of I_Ks gating, results on action potential simulations should only be considered as preliminary. Indeed, a more accurate modeling of β-AR modulation of cellular targets other than I_Ks would be necessary to predict in quantitative terms the impact of I_Ks modulation on whole-cell electrophysiological function.

Conclusions

The presented results show that the full complexity of I_Ks kinetics and of its β-AR modulation can be accounted for by the relatively simple kinetic scheme proposed by Silva and Rudy (10). Because the study was performed on native I_Ks, the modeled behavior is the one resulting from all channel α- and β-subunits considered as a functional unit. Model analysis of ISO effects provides a novel putative interpretation of agonist-induced changes in maximal channel conductance and highlights the importance of redistribution of state occupancy in determining I_Ks time dependence.