Abstract
We present a model that provides a mechanistic understanding of the processes that govern the formation of the earliest integrin adhesions ex novo from an approximately planar plasma membrane. Using an analytic analysis of the free energy of a dynamically deformable membrane containing freely diffusing receptors molecules and long repeller molecules that inhibit integrins from binding with ligands on the extracellular matrix, we predict that a coalescence of polymerizing actin filaments can deform the membrane toward the extracellular matrix and facilitate integrin binding. Monte Carlo simulations of this system show that thermally induced membrane fluctuations can either zip-up and increase the radius of a nucleated adhesion or unzip and shrink an adhesion, but the fluctuations cannot bend the ventral membrane to nucleate an adhesion. To distinguish this integrin adhesion from more mature adhesions, we refer to this early adhesion as a nouveau adhesion.
Introduction
Adhesion to an extracellular matrix, an essential process in mammalian cellular locomotion, requires interaction between adhesion receptors and their ligands. Unfortunately, a mechanistic understanding of the processes that govern the formation of integrin adhesions ex novo from an essentially planar plasma membrane (i.e., the “big bang” of adhesion formation) has previously been elusive. After binding to an extracellular ligand, integrin receptors facilitate both the transmission of mechanical force to cytoskeletal actin filaments and the assembly of an array of cytoskeletal, scaffolding, and signaling proteins that form a plaque on the cytoplasmic face (1,2). Integrin adhesion sites, which include focal complexes, focal adhesions, fibrillar adhesions, and podosomes, are uniquely distinguished by morphology, composition, and functional dynamics (3–5). These features, however, can change with time; e.g., a short-lived, small focal complex will either remodel to become a larger focal adhesion or it will vanish (3,6).
In this article, we model the mechanisms that lead to the birth of an adhesion site and predict the characteristics of the earliest adhesion. To distinguish this integrin adhesion from more mature adhesions, we refer to this as a nouveau adhesion. Unlike other types of integrin adhesions, a nouveau adhesion is not initially anchored to the cytoskeleton by protein interactions on the cytoplasmic face, but it could mature by recruiting adaptor proteins.
In our model, a nouveau adhesion precedes the currently recognized early adhesions: the preadhesion complex (7), an initial adhesion (1,6,8), or a nascent adhesion (9). Although more complex than a nouveau adhesion, these early integrin adhesion sites are molecularly simple integrin adhesions, compared with the general integrin adhesome network that consists of 156 adhesion related molecules with 690 interactions and numerous constituents (5). Just as the transformation of a preadhesion to a focal complex is marked by increased strengthening of the adhesion complex and a concomitant increase in molecular complexity (1,6–9), our model predicts that a nouveau adhesion could grow into a larger adhesion.
Among the hierarchical processes that form an integrin adhesion, integrin activation is a necessary condition before the binding between integrin's extracellular domain and a protein ligand (10). Activation increases the affinity for ligands by rapidly and reversibly exposing ligand-induced binding site epitopes in integrin extracellular domains; however, many activated integrins are not ligated and it has been conjectured that ligation without binding is a priming mechanism, enabling the cell to sample the extracellular matrix before binding (11). Although integrin activation is a necessary condition for ligand binding, it is not a sufficient condition because the stalks of the conformationally activated heterodimer have relatively short projections from the plasma membrane into the extracellular space and longer molecules on the crowded membrane surface sterically inhibit the extended integrins from binding to their ligands (2,10,12–15). Therefore, the ligand-binding domain needs to be displaced so that it can reach a ligand on the extracellular matrix (ECM). We present a model that predicts that polymerizing actin filaments locally deform the membrane and translate integrin's extracellular binding domain toward the ECM.
Data acquired from interference reflection microscopy and electron microscopy experiments indicate that local membrane deformation is associated with adhesion and that the plasma membrane at an integrin adhesion appears to be closer to the substrate than adjacent regions (a distance of ∼30 nm) (9,16). Therefore, these data suggest that activated integrins bind to ligands on the ECM in regions of membrane that have bent toward the substrate. Many published models of integrin adhesions, however, present schematic pictures of a globally flat membrane that contains transmembrane integrin segments spanning the lipid bilayer (17,18). Instead, we envision the formation of an integrin adhesion as a process that begins with local membrane bending, a redistribution of long molecules from the site that culminates with integrin aggregation.
Our model, which emphasizes the mechanisms responsible for the earliest events in adhesion formation before the myriad of proteins assemble on the cytoplasmic face to form the plaque, extends the thermodynamic principles delineated by Bell et al. (19) to an analysis of the free energy landscape of a system of freely diffusing receptors and repeller molecules and a dynamically deformable membrane. As the membrane approaches the ECM, receptors can diffuse into the displaced region and can bind to ligands. Our model predicts the nucleation, growth, disassembly, and merging of nouveau adhesions.
Components of the System and the Model
We envision a nouveau adhesion nucleated ex novo from an approximately planar membrane under the lamellipodium. The membrane is sandwiched between an actin network on the cytoplasmic face and compressible repeller molecules on the ventral surface side (Fig. 1). Initially, the membrane rests above a rigid substrate; the receptor and repeller molecules are homogeneously distributed, and they freely diffuse laterally on the cell membrane. A cylindrically symmetric nouveau adhesion begins when polymerizing actin filaments in denser regions of the actin network provide a protrusion force to bend the membrane to form a focal plate and the homogeneously distributed ligated receptors begin to aggregate within the base of the focal plate; although the polymerizing actin network is predominately responsible for the progression of the leading edge of the lamellipodium (20), this network is polymerizing in all three dimensions (21), and actin filaments can push the membrane toward the substrate.
Figure 1.
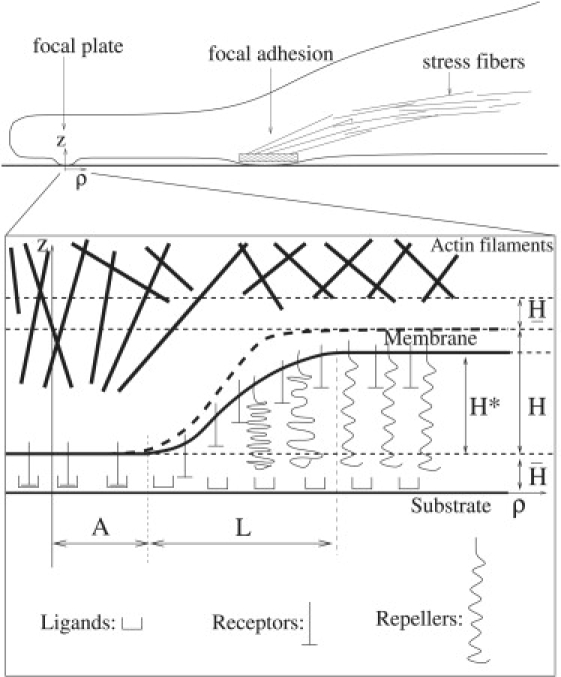
The components of a focal plate showing a membrane constrained between an actin network on the cytoplasmic face and a layer of freely diffusing repellers that extend toward the substrate. Formation of a nouveau adhesion requires membrane bending and the subsequent exclusion of repeller molecules from the plate region. Cylindrical symmetry is assumed for an analytic analysis of the system and the total number of each type of molecule is assumed to be preserved before and after the nouveau focal plate formation. The profile for compressible repellers pictured by a solid line, which equilibrates at + H∗. When the repellers become incompressible, H∗ → H.
The base of the focal plate has radius A and the membrane smoothly deforms from a height above the substrate in the base region, until it reaches the planar membrane at a height (Fig. 1, solid line). Because we treat the repeller molecules as compressible springs (see Compression Energy of Repellers), the equilibrium height, , will generally differ from the relaxation height of the repellers, (Fig. 1, dashed line); if the repeller molecules are incompressible, then H∗ = H.
To account for the existence of many focal plates, we initially model a cell with N identical nouveau focal plates on its ventral surface. We consider the growth of the N focal plates with large center-to-center separations such that they are isolated. In Monte Carlo Simulations of the System, we exploit Monte Carlo (MC) simulations, which relax the constraint on cylindrical symmetry and include an analysis of nonidentical and interacting focal plates.
Before the formation of the nouveau adhesion, the surface density of active receptors on the plasma membrane is assumed to be d0. The density of bound receptors at the base of a focal plate is referenced with respect to this initial density as βd0; this density is assumed to equal the density of ligands on the substrate. The density of repellers before the nouveau adhesion begins to form is αd0. The entire cell has surface area S = 4πR2 (although it is not necessarily spherical in shape). Therefore, the total number of free receptors is d0S and the total number of the repellers is αd0S. Both α and β are dimensionless parameters. The total number of repellers and the total number of receptors (bound plus free) are conserved.
As the nouveau adhesion grows, the number of bound receptors that aggregate on the base increases and the number of freely diffusing receptors decreases. The total number of bound receptors becomes βd0NπA2 and the number of free receptors then decreases to d0S-βd0NπA2 such that the sum of free and bound receptors equals the total number of receptors. Similarly, as the membrane bends toward the substrate, the density profile of the compressible repellers, which have one end anchored on the membrane, changes. As will be shown, this density profile varies continuously from zero within the base of the focal plate to a uniform distribution at the outer region of the plate. The change in the membrane geometry and the subsequent reorganization of the repeller and receptor molecules alters the membrane elastic energy and the entropy of the system.
Formation Energy of Nouveau Adhesions
Deformation of the membrane and the subsequent compression of repeller molecules and aggregation and binding of receptor molecules to form a nouveau adhesion requires energy. We separately compute
-
1.
The energy required to compress the repeller molecules.
-
2.
The change in the entropic component of the free energy caused by variations in the densities of repeller and receptor molecules.
-
3.
The change in total energy caused by receptor-ligand binding.
-
4.
Membrane elastic energy.
-
5.
The loss of fluctuation entropy caused by the rigid substrate and actin network, i.e., the Helfrich repulsion due to hard-wall interactions.
Compression energy of repellers
As the membrane bends toward the substrate, the repeller molecules may be compressed. The energy required to compress a repeller molecule, which has one end anchored in the membrane, can be determined by assuming that the compression is governed by the potential (22–24)
| (1) |
where h(ρ) is the spatially varying height of the repeller molecule on the membrane at radial position ρ, is the relaxation height of the molecule, and Ω is the spring constant (Fig. 1). Because the repeller molecules are confined between the membrane and substrate, we assume that the change in the free energy in the azimuthal direction is principally associated with the elastic compression energy of the molecule. For a repeller molecule at thermal equilibrium, the probability that a repeller is compressed to a height h(ρ) (governed by the Boltzmann distribution (25)) is given by e−v/kT where k is the Boltzmann constant and T is the temperature. Therefore, the spatial varying density of repellers drep = αd0e−v/kT. Correspondingly, the compression energy per unit area can be expressed as
| (2) |
In the Appendix, we introduce an alternative model that assumes that the repeller molecules are rigid.
Free energy of repellers and receptors
In our model, the cell's plasma membrane and repeller and receptor molecules are in equilibrium with their environment. We separately determine the free energy associated with each type of molecule in our system: F1 for the repellers that diffuse freely outside the plate; F2 for active receptors, which freely diffuse outside the base region; and F3 for the bound receptors inside the base. We treat molecules, which freely diffuse on the membrane as a two-dimensional (2D) ideal gas (26). The relative free energy change per molecule is given by kT ln(d/dini), where dini and d are the surface densities before and after adhesion formation, respectively (19,27,28). For example, as the nouveau adhesion forms, the area initially occupied by repeller molecules, 4πR2, decreases. Therefore, the free energy with respect to the initial area can be determined as F1 = 4πR2αd0 , where Q = is the partition function and 4πR2αd0 is the total number of repellers. Hence, the three free energies for N focal plates, measured in units of kT, can be expressed as
| (3) |
| (4) |
| (5) |
Binding energy
Upon binding, there is an additional change in the total energy, NUbound, caused by the attraction energy of the bound receptor-ligand pairs such that it is equal to the number of bound pairs times the energy per bond, which is given by
| (6) |
where ɛ stands for the absolute interaction energy per bond, in units of kT. In general, ɛ ranges between 5 and 15 kT, depending upon the type of the molecule (29,30).
Although ɛ represents the adhesion energy, the definition of ɛ could be expanded to account for an effective total attraction energy per bond, which arises from attractive forces associated with the receptor-ligand bonds and effective repulsion forces due to molecules that can be trapped between the membrane and the substrate in the base region; adhesion may occur only if the attractive forces dominate.
Membrane bending energy
The energy, Em, required to bend an essentially bare, flat membrane may be determined by modeling the membrane as a 2D elastic surface with bending modulus κ and a constant surface tension γ. The energy associated with membrane deformation can be written in accordance with the Helfrich integral in radial coordinates under the small deformation approximation as (31)
| (7) |
where the domain of the integral is the entire membrane and em is the membrane elastic energy density as given by Eq. 8 and under the assumption that the spontaneous membrane curvature is zero:
| (8) |
As shown in Fig. 1, the membrane height, h(ρ), is measured with respect to the substrate. At the base of the plate, the membrane is constrained and the boundary conditions become h(A) = and h′(A) = 0. The membrane then relaxes to its essentially flat profile with an equilibrium height, , at a large radial distance from the center of the plate, ρ = ρmax. In Analysis and Results, we compute the membrane shape that minimizes the total energy of the system.
Helfrich repulsion
Because the cell's plasma membrane is in thermal contact with its environment, the membrane height undergoes random displacements. As the membrane approaches the rigid substrate near the adhesion, these out-of-plane fluctuations repel the membrane and it loses entropy compared with the free membrane. It has been shown that the subsequent loss of fluctuation entropy imparts an effective repulsion to the membrane and, for a tensionless membrane, the Helfrich repulsion varies inversely with the square of the distance of the membrane from the hard wall (22,32,33). However, for a membrane under tension, both the strength and range of this effective repulsion are considerably reduced (34). Accordingly, because most cells exhibit a nonzero membrane tension (35), we model the effect of the Helfrich repulsion using a potential that decays exponentially with the mean separation.
We include the effect of two repulsive Helfrich potentials, which arise from the interaction of the planar membrane with the actin network and the repulsion from the rigid substrate at the base of the focal plate. As shown in Fig. 1, the actin network is located at above the substrate. The repulsion energy per unit area from the actin network, vrepact, and substrate, vrepsub, may be written as (34)
| (9) |
| (10) |
where c0 = 0.085γkT/κ and
Total energy of the nouveau adhesions
Collecting the individual energy contributions from the five subsections above, we will analyze the total energy landscape to predict the nucleation, growth, disassembly, and merging of nouveau adhesions. Using Eqs. 2–6 and 8–10, the total energy of N identical, noninteracting focal plates may be written as
| (11) |
Because the terms in Eq. 11, except F2, F3 and Ubound, depend upon the shape of the membrane, it is first necessary to determine h(ρ) and then compute the total energy. All the terms that depend upon h(ρ) may be brought into the integrand by expansion of the logarithmic term of the free energy F1 in Eq. 3 as ; this approximation is accurate under the assumption that the total effective surface area of the bound receptors is less than the total surface area of the cell. After applying the same approximation to the free energy F2 (Eq. 4), the total energy per plate (in units of kT), E ≡ Etot/N, becomes
| (12) |
The limits of the integral extend from the base of the plate, A, to a distance, ρ = ρmax, where the membrane has relaxed to its essentially flat profile with an equilibrium height, . In the following section, we investigate the shape of the membrane and the properties of the energy landscape.
Analysis and Results
Although there are many permissible membrane shapes that are consistent with the boundary conditions in Membrane Bending Energy, i.e., and h′(A) = 0, we seek a membrane profile, h(ρ), that minimizes the energy, E, in Eq. 12. To find the axially symmetric membrane shape, we applied a simulated annealing method (36,37). This approach implements a discrete profile hi = h(iΔρ) between ρ = A and ρ = ρmax. Far from the base of the plate, namely at ρmax, it is not necessary to constrain both the slope and the height of the membrane because our computational method automatically allows the membrane to relax to its essentially flat profile with an equilibrium height above the substrate at ρmax. We determine the distance ρ = ρmax and the membrane shape using an iterative process that continually increases ρmax until the discrete profiles, associated with the minimum energy, converge to a uniform profile.
Membrane profile and repeller density distribution
To run the simulated annealing, we used A = 150 nm, α = 16, β = 11, = 10 nm, nm, and Ha = 45 nm, and the remaining parameters are provided in Table 1. For compressible repellers, we used an estimate of Ω assuming that a 1 kT thermal fluctuation can compress the repellers by ≈25%; from Eq. 2, Ω ≈ 0.01 kT/nm2.
Table 1.
The list of parameters and variables used in the formulas; values for all constant parameters are presented
| d0 = 100/μm2, initial density of free active receptors (19,57,58). |
| αd0 Initial density of repellers. |
| βd0 Density of bound receptors, density of ligands. |
| 4πR2 Surface area of the cell, R = 15 μm. |
| N Number of nouveau adhesions. |
| A Base radius of the plates. |
| H = 30 nm, height of the plates above the base line (14,15). |
| κ = 30 kT, bending modulus of the membrane (59,60). |
| γ = 0.01 kT/nm2, surface tension of the membrane (60). |
| ɛ = 5 kT, energy per single ligand-receptor bond (29,30). |
Fig. 2 shows both the membrane shape, h(ρ), and normalized repeller density profile, drep/αd0, obtained with two separate values for the repeller spring constant that represent either compressible (Ω = 0.01 kT/nm2) or incompressible repellers (Ω = ∞). Regardless of the value of Ω, the density of repellers is essentially zero inside the focal plate, i.e., ρ ≤ A. If the repellers are incompressible, then the density of repellers will be zero (solid lines) whenever the membrane height is lower than the length of the repellers, ; in this case, the density becomes a step function of ρ.
Figure 2.
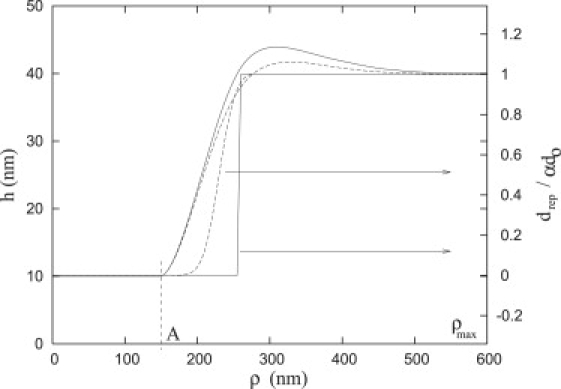
The shape, h, and normalized repeller density, drep/αd0, profiles for the case where Ω = 0.01 kT/nm2 and for the incompressible repeller case (dashed and solid lines, respectively). The minimization of the energy and the corresponding shape is computed by simulated annealing method. The whole list of parameters chosen is A = 150 nm, κ = 30 kT, γ = 0.01 kT/nm2, α = 16, β = 11, d0 = 100 μm−2, ɛ = 5 kT, Ha = 45 nm, and = 10 nm.
For incompressible repellers, the equilibrium membrane height, H∗, and the repeller height, H, are equal. For compressible repellers, the entropic repulsion caused by the interaction of the membrane with the actin network pushes the membrane down toward the substrate and H∗ < H. It is possible to determine the membrane height, H∗, by setting the partial derivative of the integrand (with respect to h) in Eq. 12 to zero and solving for h; because the membrane elastic energy vanishes, the solution can be obtained from a zero order transcendental equation. Our numerical results demonstrate that |H∗ − H| < 1 nm.
Conversely, if the repellers are compressible (dashed lines, Fig. 2), they can enter a region where the membrane height is ; however, when , the repeller density becomes essentially uniform (i.e., drep/αd0 = 1, Fig. 2). For convenience, the radial distance from the center of the plate, A, to the position where the membrane height equals may be defined as the width of the focal plate, L, such that . Therefore, a focal plate can be characterized by a base radius, A, and outer radius A + L. For the data in Fig. 2, we have A = 150 nm and L = 110 nm for Ω = 0.01 kT/nm2 and for incompressible repellers, L = 105 nm. The distance L is essentially independent of the base radius, A (data not shown), but it depends upon several parameters including the density of repellers. With the increasing density of repellers, α, the width of the profile gets narrower for both compressible and incompressible repellers (Fig. 3, dashed and solid lines). Furthermore, in Critical Radius, we will examine the functional dependence of L upon α. In the Appendix, we examine the significance of the width, L, when the repellers are modeled as incompressible.
Figure 3.
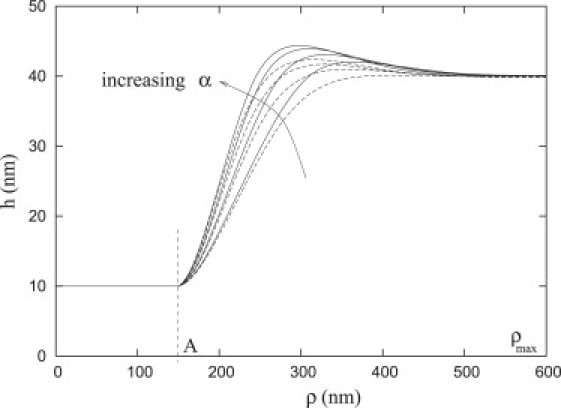
Membrane shape profiles with increasing α (i.e., 4, 9, 16, and 25) for compressible (Ω = 0.01 kT/nm2) and incompressible repellers (dashed and solid lines, respectively). As α increases, the plate-width decreases.
Critical radius
A focal plate begins to form when the membrane bends and the repeller molecules are forced out of the base region. This deformation of the membrane and the subsequent aggregation and binding of receptor molecules to form a nouveau adhesion requires energy. Fig. 4 shows the total energy per plate (Eq. 12) for four values of the repeller density, α (= 4, 9, 16, 25), as a function of the base radius of the plate with A < 500 nm (dashed parabolic curves with circles) and the contribution of the membrane energy, Em, of a single plate (N = 1) to the total energy (dashed straight lines with circles). The plots of an analytic expression, Eq. 13, that approximates the total energy are also shown (solid lines). In Maximum Adhesion Size, we will examine the energy landscape for values of A larger than 500 nm.
Figure 4.
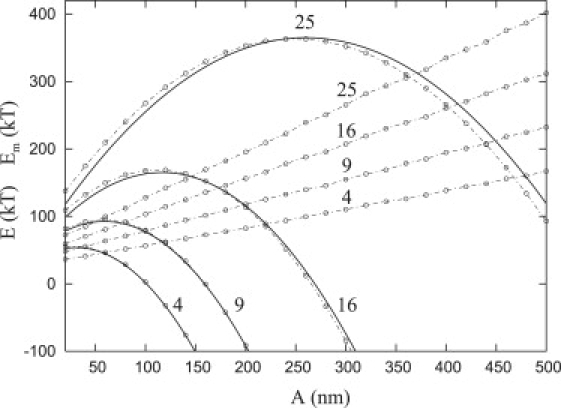
Total energy per plate, E, (dashed parabolas with circles) with an analytical approximation (solid parabolas) and the membrane energy, Em, (dashed straight lines with circles) versus the base radius of the focal plate, A. Each curve represents the total energy per plate with α = 4, 9, 16, and 25, and β = 11.
Fig. 4 demonstrates that the total energy required to form an adhesion increases as the density of repellers increases and that beyond a certain radius, less energy is required to form a large adhesion rather than a smaller adhesion. For example, for α = 16, ∼150 kT is required to form an adhesion with base radius A = 100 nm, whereas <100 kT is required to form an adhesion with A = 250 nm. Therefore, the maximum point on the upside-down parabolic shape of the total energy (Fig. 4) implies that there is an energy barrier governing the formation of an adhesion and that there is a critical radius, Ac, for the growth of the focal plate. If a focal plate is formed with a base radius A > Ac, then it will be energetically favorable for the plate to continue to form more integrin bonds and the plate will reach a larger radius. Conversely, if the plate has a radius less than Ac (A < Ac), then the plate will dissolve unless it is constrained to its initial radius (i.e., by actin filaments). We examine these consequences in greater detail in Monte Carlo Simulations of the System.
Although we can investigate the variation of Ac with the parameters α and β numerically, it would be preferable to find an analytical expression that relates these variables. Because the critical radius can be determined by maximizing E with respect to A, i.e., ∂E/∂A = 0, we need an expression for E as an explicit function of A. As derived in the Appendix, we can approximate the total energy per plate for compressible repellers as
| (13) |
where the values of c1 and c2 can be determined from a linear fit to the membrane energy (Fig. 4) and L may be determined from the repeller density and shape profile as in Membrane Profile and Repeller Density Distribution. Therefore, the critical radius may be determined from Eq. 13:
| (14) |
From the data in Fig. 4, the values for c2 and L, as a function of α, were determined to be c2 ≈ 0.17 + 0.02 α and L ≈ 370 α−0.4. Inserting these values in Eq. 13, this approximation may be compared with E given by Eq. 12; Fig. 4 (solid and dashed parabolas, respectively) shows good agreement.
In addition to numerical estimates of c1 and c2, we are able to derive approximate analytical expressions for these variables. As shown in the Appendix, we introduce a simpler alternative model for the repeller molecules that assumes that the repellers are rigid and diffuse on a membrane constrained by four strict boundary conditions. From Eqs. 27 and 28, we have
| (15) |
| (16) |
where τ is given by
| (17) |
with . Using these values, we now have an analytical formula for Ac for rigid repellers:
| (18) |
From either Eqs. 14 or 18 and Fig. 5, the critical radius increases with increasing α and decreases with increasing β. Furthermore, these variations do not differ significantly between compressible and rigid repellers (dashed and solid lines, respectively).
Figure 5.
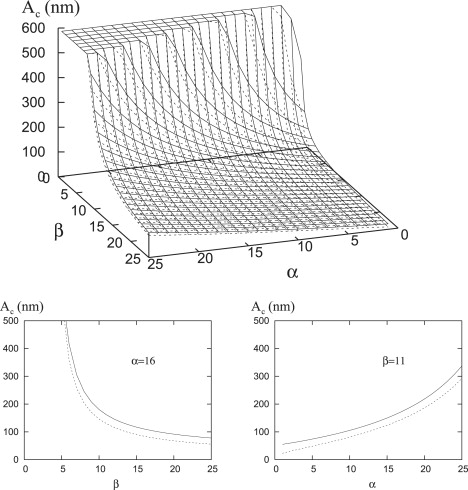
Plots of the critical radius, Ac, from Eqs. 14 and 18 as function of α and β for both rigid and compressible repellers (solid and dashed lines, respectively). All values with Ac > 600 nm are shown as = 600 nm. In the rigid repeller case, the line tension is obtained from Eq. 17 and L ≈ 120 nm. In the compressible repeller case, c2 and the width L are obtained by the numerical fits, c2 = 0.17 + 0.02 α and L = 370 α−0.4.
The sensitivity of the critical radius to changes in the spring constant, Ω, which is not evident in either Eqs. 14 or 18, may be determined numerically by analyzing the variation of the total energy landscape with respect to Ω. Fig. 6 demonstrates that the value of Ac is rather insensitive to changes in Ω and that Ac for compressible repellers (dashed circles) is quite close to the value of Ac(≈140 nm) for rigid repellers (solid line).
Figure 6.
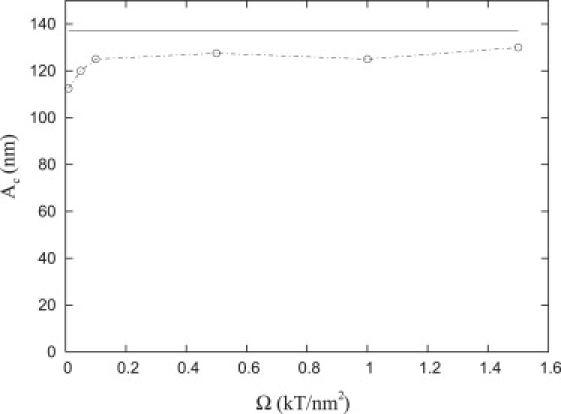
Critical radius, Ac, as a function of Ω for α = 16 and β = 11 for compressible (dashed line with circles) and incompressible repellers, Ω → ∞ (solid line).
Maximum adhesion size
In Critical Radius, an examination of the energy landscape for small values of A provided insight into the formation of nouveau adhesions; an adhesion with a radius larger than the critical radius should continue to grow because it is energetically favorable. Ultimately, however, the radius of an adhesion is limited by the total number of available receptors because the cell provides a large, but finite, pool of integrins. Therefore, the maximum possible value of A can be determined from the conservation of the number of receptors as NπA2βd0 = 4πR2d0 which gives for the maximum radius, , and for the maximum area of the plate.
To examine the energy landscape for large A, we begin by reexamining Eq. 11, but unlike the development in Total Energy of the Nouveau Adhesions, we will now use the logarithmic forms of the free energies F1 and F2 (Eqs. 3 and 4) so that we can capture the behavior for both small and large values of the plate radius, A. Consequently, the free energies now depend nonlinearly upon the number of focal plates, N, and the energy per plate, E = Etot/N, depends not only upon the density of repellers and receptors, but also upon the number of focal plates.
In the Appendix, we develop an analytical expression that describes the total energy as a function of A and N (Eq. 29). Fig. 7 shows the resultant energy profiles per plate for N = 1, 10, 20, and 30 with α = 16, β = 11 and L ≈ 120 nm. For small values of A, all the energy paths essentially follow the same profile where the maximum along this energy path (see Fig. 7 and the inset) defines the critical radius, Ac (see Critical Radius). It may be observed that the radius of the focal plates is indeed ultimately limited by , but before this maximum radius is reached, there is an energy minimum along each of these energy profiles. Therefore, there is an attraction to this energy minimum and this effectively restricts the radius of the plates to a value <. Our numerical results show that these minima are near for a range of different values of α and β so that the maximum size of the focal plates is ≈.
Figure 7.
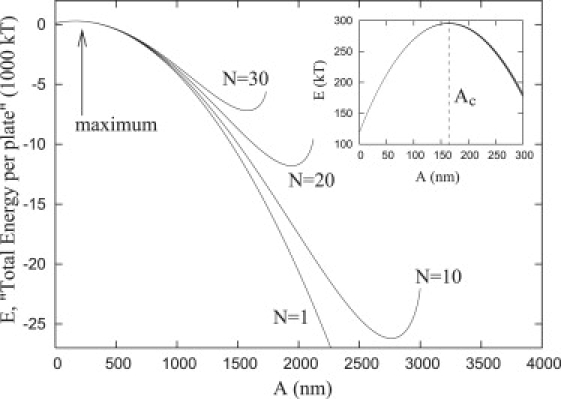
Minimum energy paths for N = 1, 10, 20, and 30 obtained with the simplified model developed in the Appendix. For low values of A, all three curves approximately overlap. (Inset) Blowup of region around the critical radius, i.e., the maximum point of the energy landscape.
Actin filaments nucleate nouveau adhesions
Nucleation of nouveau adhesions requires a significant change in the total free energy: depending upon the values of α and β, ∼300 kT is required to create an adhesion with a minimum radius A ≈ Ac (Fig. 7, inset). Indeed, the minimum change in free energy required to nucleate a single focal plate (N = 1) with an infinitesimal base radius, A → 0, can be determined from Eq. 30 (Appendix); assuming a repeller density 9 < α < 25, we have 90 kT < E < 140 kT. Indeed, it is likely that an adhesion may have a small initial radius, A0. Fig. 8 shows the required nucleation energies obtained via simulated annealing as a function of α for nucleation sizes of A0 = 10 nm and A0 = 50 nm, assuming both rigid and compressible repellers.
Figure 8.
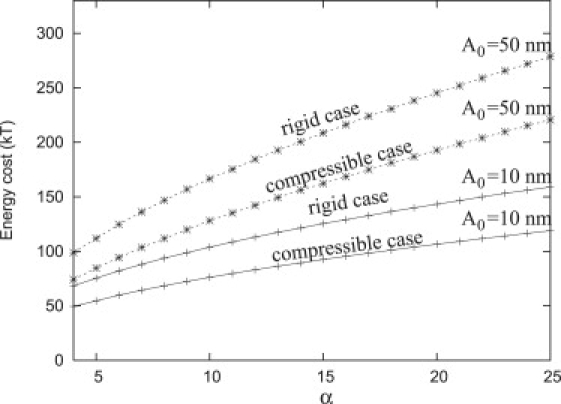
Energy to form a plate as a function of α for two different values of the initial base radius, A0 (= 10 nm and 50 nm) for either rigid or compressible repellers (dashed-star and solid-cross, respectively).
Because all the energies are much larger than kT and the system obeys Boltzmann statistics, we can conclude that the probability of generating nouveau adhesions solely by thermally induced deformations is extremely small. Therefore, an additional energy source must be required to bend the membrane and balance the lateral inward pressure of the repellers. The most likely mechanism is polymerization of actin filaments. Polymerization of actin generates an effective force that depends upon the ratio of the concentration of free actin monomers in the cytoplasm, [Act], to the critical concentration for polymerization, [Actc], such that the addition of each monomer drops the free energy (25) by . Therefore the effective force, f, along the direction of polymerization produced by each filament is
| (19) |
where δ = 2.8 nm is the increment of length upon the addition of one monomer. For values 2 μM < [Act] < 10 μM and [Actc] = 0.12 μM, the effective force is 1 kT/nm < f < 1.5 kT/nm, or 4 pN < f < 6 pN.
Nucleation of a nouveau adhesion ex novo requires deformation of the membrane by H = 30 nm to form a focal plate. Therefore, the associated protrusion energy per actin filament is ∼30 kT < w = Hf < 40 kT. The minimum number of actin filaments to nucleate an infinitesimal adhesion (A → 0) may be determined by dividing the minimum energy cost by the protrusion energy per filament, yielding 3–5 actin filaments. To form a finite-sized nouveau adhesion at the critical radius, Ac, requires an energy of ≈300 kT to be supplied by actin filaments (as shown in Fig. 7); therefore, at least eight filaments are required for [Act] = 10 μM. The number of actin filaments increases as the concentration of actin monomers decreases; for example, with [Act] = 1 μM, 13 filaments are required.
Monte Carlo Simulations of the System
The analytical work presented in previous sections was subject to the geometric assumption that the plates are cylindrically symmetric. To expand our analysis into more realistic cases, we have implemented a Monte Carlo (MC) simulation of the system without imposing any sort of symmetry. Therefore, MC simulations can account for the formation of several nonidentical focal plates and thermal effects, which are the main source of random fluctuations and symmetry breaking. Although thermal fluctuations are not capable of generating nouveau adhesions ex novo, MC simulations demonstrate that these fluctuations can significantly contribute to the growth and disassembly of nouveau adhesions.
In MC simulations, the membrane height at each discrete lattice point, h(xi, yi), is described by the local displacements from a planar reference surface (at the base of the plate) represented on a square grid, 100 × 100 points, with a lattice constant Δ; in our simulations, a value of Δ = 10 nm reproduces the results from analytical calculations (data not shown). At each lattice point, the Helfrich energy is computed by using discrete derivatives (38,39) and the change in the total free energy is computed for each MC step in accordance with the Metropolis algorithm (40) by making trial displacements from a uniform probability distribution with range [−δh, δh], where δh = 1 nm.
In these simulations, we place ligands on a gridded substrate with a separation distance, s, equal to an integer multiple of Δ. When any point on the membrane is close enough to the substrate, h(xi, yi) < ξ, the energy of the system drops by ɛ to mimic binding of receptors with ligands. We assume that the effective interaction between receptors and their ligands takes place over a distance ξ = 2 nm. These bonds may be formed and broken if thermal fluctuations provide enough energy to move a bound lattice point into or out of this attractive well. Additionally, we have assumed that the actin network behaves as a hard wall, which constrains the membrane height at the distance z = H + 5 nm. Similarly, the membrane height cannot drop below z = 0. The effective force caused by the polymerizing actin network can be included in the simulation by adding an auxiliary potential function V= to the total energy where is the effective protrusive force which only has nonzero value if the position, (xi, yi), is within the base of a focal plate.
Free energy of rigid repellers and receptors is computed in these simulations by calculating the available surface area occupied by the repellers and receptors. The total surface area that repellers may occupy is determined by counting the number of points with membrane height <H–ξ′ and multiplying by the area of this membrane patch, Δ2. This approach models the steric exclusion of repeller molecules. Analogously, the available surface area for freely diffusing receptors can be computed by counting the total number of membrane points that have a height >ξ. The parameter ξ′ allows a degree of flexibility to adjust the average membrane height to the value of H; in our simulations, ξ′ = 2 nm.
For compressible repellers, the compression energy and the free energy were directly applied by using Eq. 2 and the logarithmic expansion of Eq. 3, respectively, in the MC energy kernel without introducing the parameter ξ′.
Starting from a planar geometry, once the MC simulations have achieved thermal equilibrium, we turn on the auxiliary potential, V, inside a circular region so that the membrane adheres to the substrate with an initial radius A0. Fig. 9 shows a snapshot of the membrane before and after application of the auxiliary potential. In some simulations, the auxiliary potential remains constant; however, in other simulations we remove the auxiliary potential to simulate a dissolving actin network.
Figure 9.
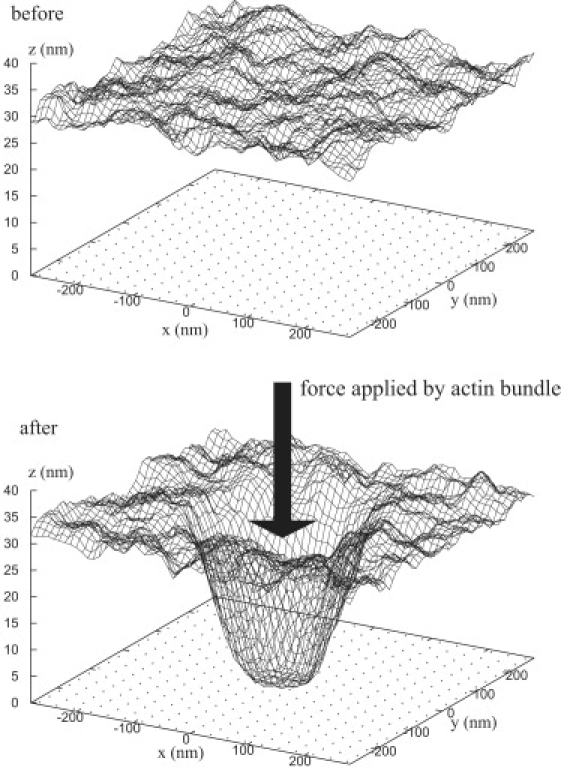
Effect of thermal fluctuations and force on a discrete, initially planar membrane. After application of a pushing force (from an actin bundle), the membrane bends by an amount that depends upon both the magnitude of the force and the energy landscape of the system of repellers and receptors molecules and the elasticity of the membrane. The membrane height at each lattice point is shown with respect to the base of the focal plate.
A MC simulation of a system consisting solely of membrane and repellers, but not ligands and receptors yields the shape of a nouveau adhesion that agrees with our numerical prediction. Because of thermal fluctuations, the membrane can assume many different shapes (realizations) within the range allowed by the constraints (i.e., using the assumed boundary conditions for the membrane and hard wall effect from the substrate and the actin network). Fig. 10 shows the MC simulation of the membrane profile for rigid repellers with an initial radius A0 = 90 nm and a repeller density α = 16. Because of the absence of ligands and receptors, the adhesion can neither enlarge nor dissolve. One realization is shown as a dotted line. The average shape as determined from 500 independent realizations is shown (solid line) with the standard deviation from this mean shape (error bars).
Figure 10.
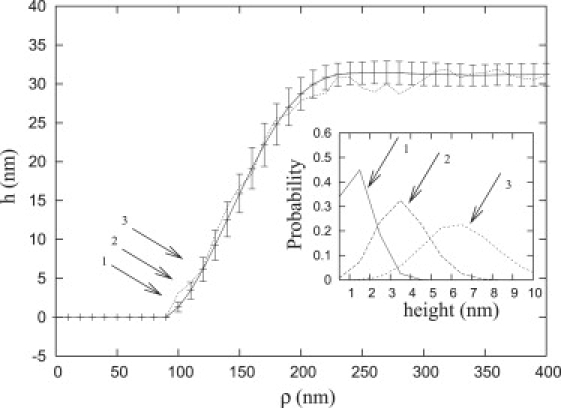
Effect of thermal fluctuations on the profile of a focal plate (N = 1). After nucleating the adhesion, further growth or disassembly of the plate is prevented by setting the attractive potential between ligands and receptors to zero, otherwise. The solid line and the error bars are the shape averaged over 500 realizations and their standard deviations at each point, respectively. The dotted line is one sample profile chosen from different realizations. (Inset) Height distribution of the three grid points closest to the base boundary.
Consistent with previous numerical estimates, the average profile has a width, L ≈ 110 nm. Although each point on the base of the plate is bound, immediately outside the base the membrane height can fluctuate. Fig. 10 (inset) shows the distribution of the membrane heights at the first three grid points outside the base (points 1, 2, 3). Points on the membrane that are laterally separated from the edge of the base within ≈25 nm have significant probability of reaching a height within 2 nm of the base, and at these points, a receptor may bind to a ligand. In the next subsection, we explore the consequences of these thermal fluctuations in more detail.
Growth and disassembly of nouveau adhesions
Although thermal fluctuations are not large enough to nucleate a focal plate ex novo from a planar membrane, our MC simulations demonstrate that after the formation of a focal plate, thermally induced membrane deformations can move a point on the membrane outside the base closer to the substrate so that a receptor may bind to a ligand. Therefore, this mechanism works like a zipper such that thermally induced membrane deformations may zip-up and increase the radius of an adhesion or unzip and dissolve a nouveau adhesion.
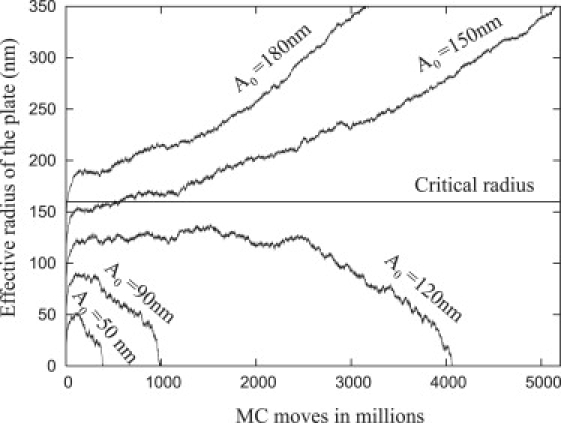
Fig. 11 shows the effective radius of the plate as a function of MC moves obtained from a simulation of the entire system nucleated with plates of five different initial base radii (A0 = 50 nm, 90 nm, 120 nm, 150 nm, and 180 nm) with α = 16, β = 11, and Ac = 160 nm. A constant auxiliary potential, V, simulates a fixed nucleating actin network for the entire run. Because the MC simulation removes the cylindrical symmetry constraint, we defined the effective radius of the plate as the radius of a circle with equivalent area to the base of the simulated plate.
Figure 11.
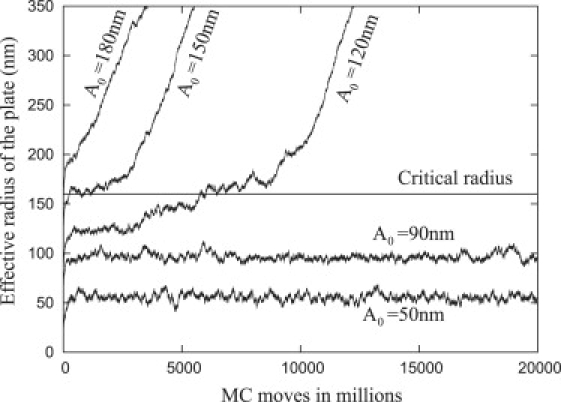
Monte Carlo simulation showing the effect of thermal fluctuations on the growth of the adhesion (effective radius of the focal plate as function of MC moves) for various initial radii (A0). The critical radius was obtained from the analytic formula as Ac = 160 nm, β = 11, and α = 16. The effective radius is defined as the radius of a circle with equivalent area to the base of the simulated plate.
If the initial radius, A0, is greater than the critical radius, Ac, then the nouveau adhesion grows quickly; however, if the initial radius is significantly below Ac (i.e., A0 = 90 nm and A0 = 50 nm with Ac = 160 nm), then the radius does not increase even for long simulation times (greater than 50 thousand-million MC steps). When the initial radius is slightly smaller than Ac (A0 = 120 nm and A0 = 150 nm), the radius of the focal plate can also increase, but the plates with small initial base radii require more time until they begin to increase because the energy barrier increases with decreasing A0. From Fig. 7 (inset), the free energy difference is ≈30 kT when A0 = 120 nm and decreases to ≈5 kT when A0 = 150 nm. Therefore, the existence of the energy barrier practically prevents adhesions from growing unless they are nucleated with a large enough initial radius. Once A ≈ Ac, the plates grow at approximately the same rate.
In analogy with Fig. 11, Fig. 12 shows the effective radius of the plate as a function of MC moves when the repellers are modeled as compressible (Ω = 0.01 kT/nm2) with four different values for the initial base radii (A0 = 50 nm, 100 nm, 150 nm, and 200 nm) with α = 16, β = 11, and Ac = 120 nm. In comparison with the data in Fig. 11, the compressibility of the repellers does not change the character of the growth of the plate and the previous conclusions remain valid. Indeed, although the value of Ω affects the size of the critical radius, the general characteristics of the following MC simulations were observed to be relatively insensitive to the value of Ω; therefore, we only present the results of the subsequent MC simulations for rigid repellers.
Figure 12.
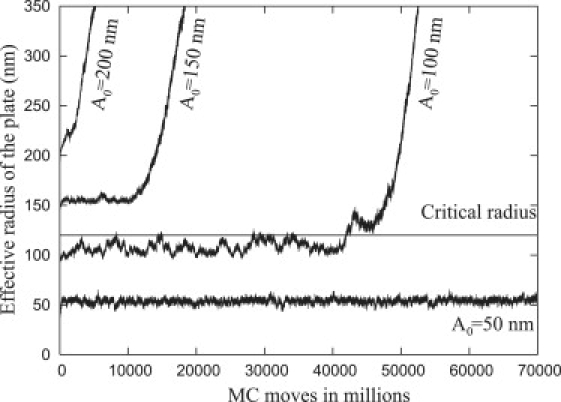
Monte Carlo simulation showing the effect of thermal fluctuations on the growth of the adhesion with compressible repellers (Ω = 0.01 kT/nm2) for various initial radii (A0). The critical radius was obtained from the analytic formula as Ac = 120 nm, β = 11, and α = 16.
In the previous simulations, the pushing force of actin filaments was held constant over the base of radius A0. To explore the full effect of thermal fluctuations, however, after the formation of the base, we turned off the auxiliary function. In these simulations (Fig. 13), the formation and relaxation of the nucleation sites was achieved after 100 million MC moves and then, at this time point, the pushing force per filament, , was set to zero to mimic the dissociation of the actin network. As shown in Fig. 13, only those nouveau adhesions that are close to or larger than the critical radius continue to grow after the removal of the nucleating actin bundle. This result is consistent with the analytical analysis of the energy landscape as presented in the previous sections. Removing the effect of the actin bundle eliminates the constraint on the radius. Therefore, if A0 < Ac, then the free energy will decrease as A decreases and the plate will dissolve. Conversely, if A0 > Ac, then the free energy will decrease as A increases and the plate will grow.
Figure 13.
Monte Carlo simulation showing the effect of thermal fluctuations on the growth and disassembly of an adhesion as a function of the initial radius (A0). Same values as Fig. 11, except that after 100,000,000 MC moves, the effect of the actin network has been removed. The simulated disassociation of the actin network allows focal plates below the critical size to dissolve, but focal plates above the critical radius continue to grow.
Effects of ligand density on nouveau adhesions
Using MC simulations, we are able to predict the effect of varying the ligand density on the growth of an adhesion. To simulate substrates (ECM) with different uniform ligand densities, we chose ligand separations, s = 10 nm, 20 nm, 30 nm, and 40 nm, where the relation between s and β is given by . Fig. 14 shows the growth of the plates at four different ligand densities (β = 100, 25, 11, and 6) as a function of MC moves. Because all of the nucleation sites began with initial radii A0 that are slightly above the corresponding critical radius, growth of each of these adhesions is energetically favorable. It may be observed from these data, however, that with increasing s (decreasing β), the growth speeds (i.e., the slopes of the effective radius as a function of MC moves) decreases. If the separation becomes large enough (s = 40 nm), growth of the plate is halted completely (the slope stays zero for a long time of simulation run).
Figure 14.
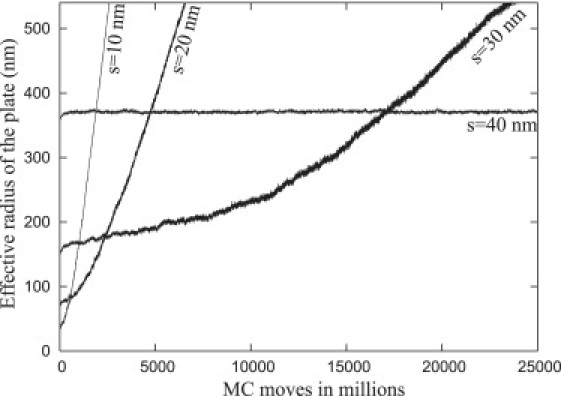
The growth pattern of plates with α = 16 and different values of ligand separations s = 10 nm, 20 nm, 30 nm, and 40 nm, which corresponds to β = 100, 25, 11, and 6, respectively. All the plates start with an initial radius that is larger than the relevant critical radius. Note that the growth speeds drop drastically for larger separations of ligands and for s = 40 nm, the plate does not grow.
Because growth of a focal plate requires sequential receptor-ligand binding as the boundary of the base of the focal plate spreads, the probability of a binding event decreases as the proximity of a ligand to a receptor increases. Although thermally driven membrane fluctuations provide the main mechanism that governs the probability that a membrane point will visit the substrate, points on the membrane at larger radial distances from the base of the plate have lower probability of being in close contact with the substrate, because a binding event requires the existence of ligands as the receptor approaches the ECM. As the density of ligands decreases, the average radial distance of a ligand to the boundary of the base of the focal plate increases and points on the membrane at large radial distances have extremely low probability of reaching the substrate, so the receptor-ligand binding rate approaches zero. Therefore, growth will not occur even though the energy of the entire system will decrease.
Merging of neighboring plates
Using MC simulations, it is also possible to investigate the interactions of neighboring nouveau adhesions. If two focal plates are close to one another, then they may exhibit different growth patterns as compared with an isolated nouveau adhesion. Under certain conditions, adhesions with initial radii, A0, that are <Ac may merge and form an adhesion with an effective radius comparable to Ac. If the two adhesions are too close, however, the radius of the combined adhesions may be too small to support growth. Conversely, if they are too far apart, neither adhesion will grow. Specifically, when the outer plate radius of a single adhesion, A0 + L, is larger than half of the center-to-center distance, D, between the adhesions, i.e., D < 2(A0 + L), the two nucleation sites can merge and form a bigger adhesion with an inner radius of ∼D/2 + A0, otherwise the two nucleation sites never affect each other. If two adhesions merge such that the average radius of the resultant adhesion is larger than the critical radius, i.e., D/2 + A0 > Ac, it is possible to observe spontaneous growth.
Fig. 15 shows the merging of two neighboring focal plates with A0 = 50 nm for three different D values both schematically and as a quantitative plot. Because the critical radius is Ac = 160 nm, neither adhesion may grow. If the plates are too close to each other, D = 140 nm, the effective radius of the larger plate is still too small to overcome the energy barrier required for additional growth. For the case D = 425 nm, the two plates are too far apart and they cannot merge. At the appropriate distance of D = 280 nm, however, the two plates can merge and form a larger size plate with an effective radius that is comparable to the critical radius. Therefore, depending upon the separation distance, multiple small nucleation sites (with radii smaller than the critical radius) may form bigger composite focal plates that can overcome the energy barrier and grow.
Figure 15.
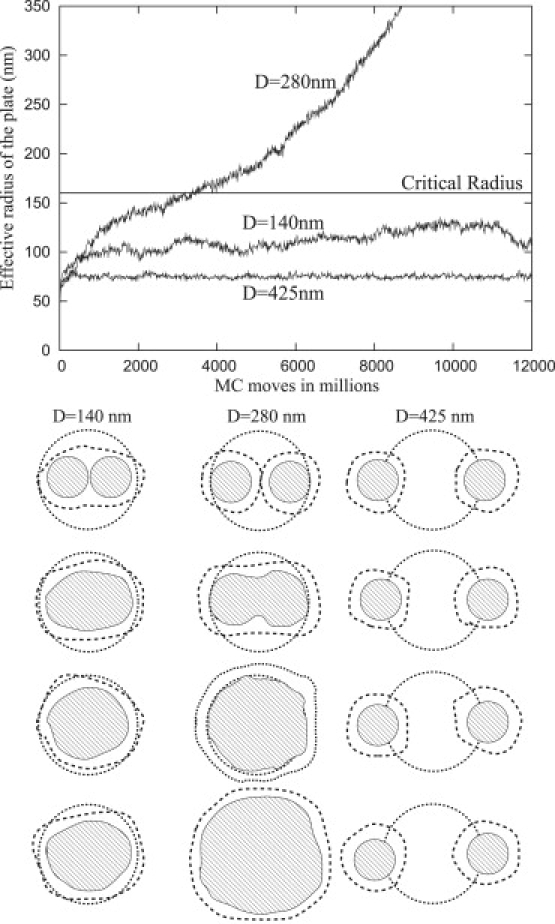
Upper graph shows the growth rates for different center-to-center distances, D, of two nucleation sites with A0 = 50 nm initial radii. The sequence of pictures are the schematic representations of the upper plot. Growth happens only if and merging occurs only if as predicted by the analytic theory.
Discussion
We have presented a model that predicts the nucleation of an integrin adhesion ex novo from a planar membrane. The model presents a framework in which to understand the mechanisms responsible for the growth of integrin adhesions and explains how some adhesions can ultimately vanish. We postulate that freely diffusing, long repeller molecules on the plasma membrane prevent integrin receptors from binding to their ligands. This is consistent with the known diversity of membrane-associated molecules; compared with these molecules, integrin receptors have relatively short extracellular extensions (15,41).
The existence of repellers prevents cells from randomly sticking to the extracellular matrix and our model predicts that actin polymerization at the leading edge enables cells to form adhesions where they are required. This prediction is consistent with experiments that show that initial adhesions generally form under the lamellipodia (12,42). Recent evidence also suggests that the location of the earliest adhesions is correlated with a high concentration of actin-barbed ends (11); this experimental article provides the methodology for examining the importance of actin activity.
Actin filaments play an important role in our model because an analysis of the free energy of our system indicates that thermal fluctuations of the lipid bilayer are not large enough to nucleate an adhesion ex novo. The nucleation and growth of an early adhesion requires an applied force that can bend the membrane and enable the initial binding between integrins and its ligand on the ECM. We postulate that a small group of polymerizing actin filaments locally bends the membrane. Our analysis provides an estimate for the number of actin filaments that would be required to deform the membrane and nucleate an adhesion.
We envision a scenario for adhesion site formation that begins with the polymerizing dendritic actin network. The polymerizing actin network is primarily responsible for the progression of the leading edge of the lamellipodium (20). Because this network is polymerizing in all three dimensions (21), however, actin filaments also push the membrane toward the substrate. The majority of polymerizing actin filaments tips that reach the membrane on the ventral surface are randomly distributed and maintain the planar membrane shape. It is likely that the coalescence of several filaments may occur. These densely packed regions of actin filament could deform the membrane toward the substrate by an actin ratcheting mechanism that would subsequently establish the first integrin-ligand bonds. In a future work, we intend to implement simulations of a three-dimensional actin filament network (see Fig. 9 in (21)) to determine the probability of nucleating adhesion and their subsequent distribution on the ventral surface, by the coalescence of actin filaments.
If the size of a nucleated adhesion is larger than a critical size (i.e., critical radius), it will be energetically favorable for this adhesion to grow until all the available integrins bind to their ligands. Under this scenario, actin filaments are only required to nucleate the adhesion to its initial size, but further growth does not require the additional coalescence of actin filaments because thermally induced membrane deformations may zip-up and increase the radius of an adhesion (Figs. 10–12). Conversely, if actin filaments nucleate an adhesion smaller than the critical radius and the filaments subsequently depolymerize, then it is probable that thermal fluctuations can break integrin bonds and the adhesion will disassemble (Fig. 13). It is also possible that neighboring small adhesions may merge to form a composite focal plate with radius larger than Ac (Fig. 15). Additionally, the probability of ligation depends upon the density of ligands; as the ligand density decreases, growth and merging of adjacent adhesions will decrease and ultimately will cease (Fig. 14).
Once these nouveau adhesions form and grow, they could mature into focal complexes by recruiting adaptor proteins from the cytoplasm (7). Actin bundles, which contain filamentous actins (F-actin), could then connect the adhesion site to the network inside the cell. Subsequently, the adhesion sites could trigger signaling pathways that promote actin polymerization and acto-myosin contractility (43). Once stress fibers form, contractile forces will either strengthen the focal contacts or result in detachment and dissociation (1,8,44–46). Because of the lateral forces exerted on the adhesions, they can grow anisotropically (1,17). The density of ligands on the ECM ultimately governs the number of small adhesions that may mature into focal adhesions because as the density of ligands on the ECM decreases, the critical radius increases and as a result, fewer adhesions will have an opportunity to mature. Sensitivity to ligand density has been observed experimentally (47) and it has been shown that below a critical ligand density, integrin adhesions can form, but they fail to mature into stable focal adhesions.
In Maximum Adhesion Size, we have derived formulas for the adhesion's maximum radius and area that depend upon both integrin density and the total number of adhesions. From the data in Fig. 7, the maximum radius is of approximately microns. Observations of cellular adhesions indicate spikelike shapes 3–10 μm long and 1–2 μm wide (48). As a comparison, our model predicts that if 30 adhesions were formed on the ventral surface of a cell, they would each have adhesion areas of ≈8 μm2. Therefore, our estimate is in reasonable agreement with observed sizes, especially considering the wide variability of the parameters and the simplicity of our model.
Although our model predicts a variety of mechanisms that govern the early phase of integrin adhesion, the model does not include dynamical events such as the association and the dissociation rates of receptor-ligand bonds or the diffusion dynamics of either repellers or receptors. We could expand this model by including Langevin dynamics and specifically incorporating chemical reaction rates (49) or other convenient simulation techniques (50). In our MC simulations, a linear relation can be stated between the real time parameter and MC moves (39,51), but it is not trivial to equate MC moves to real time because the transverse diffusion constant of the membrane patches simulated in the program is generally not known. Hence, we have chosen instead to represent our time axis as MC moves. The uncertainty in the dynamical information does not alter the validity of our energetical arguments, however, and our MC simulations should be considered as an average behavior of the system, rather than an exact picture that represents the temporal evolution of integrin adhesion on an absolute timescale.
Alternatively, we can estimate the conversion from our MC moves to time as (39,51), where η is the viscosity of the medium surrounding the membrane, NMC is the total number of MC lattice points (104 in our simulations), and the other parameters are defined in the text. It has been observed that the cytoplasm exhibits regions with different viscosity, ranging from 5 Pa to 400 Pa (52,53). Therefore, using the lower viscosity value, we estimate that dt ≈ 3 s for one billion MC moves. From the data in Fig. 14, with a ligand spacing, s = 20 nm, an adhesion will grow at the rate of ≈30 nm/s; if the adhesion were to continue to grow at this rate, ∼100 s would be required to reach a radius of 3 μm. Although it is problematic to compare this estimate to published measurements because of the large variation in several parameters such as ligand and repeller densities, our velocity estimate is nevertheless in good agreement with a recent measurement of the rate of contact growth ≈50 nm/s (see Fig. 1 in (53)).
Our model makes several predictions concerning the mechanisms that govern the formation and dynamics of adhesion growth. Although challenging, it should be possible to confirm some of these predictions experimentally. For example, in analogy with the experimental methods presented in Pierres et al. (53), we have constructed an interference microscope to measure the membrane topography and we are investigating the nucleation, dissolution, and merging of integrin adhesions at the ventral surface of cells on glass substrates. Using fluorescence correlation microscopy, it should be possible to measure the dynamics of integrin aggregation. Because our model predicts a critical radius of nouveau adhesions below the diffraction limit, it will be difficult to observe the dynamics directly with conventional microscopy. In addition to experiments on cells (11), experiments using vesicles decorated with receptor and/or repeller molecules could be conducted (30,34,41,54,55). Although vesicle experiments do not address the essential role that our model attributes to the actin network, a recent series of experiments using giant unilamellar vesicles with mobile receptors supports our prediction that thermal fluctuations can zip-up an adhesion that has an initial radius close to or above a critical radius (55).
Conclusions
Our model presents a mechanistic understanding of the interplay among the actin network, the membrane, and receptor-ligand interactions. Only a few actin filaments are required to bend the membrane and nucleate a nouveau adhesion by initiating the binding of a few integrins. Thermal fluctuations could subsequently lead to the growth or dissociation of integrin adhesions, but these fluctuations are too small to nucleate an adhesion ex novo.
Acknowledgments
We thank the reviewers for introducing several ideas that have considerably strengthened this manuscript. B.O. thanks the Institute for Pure and Applied Mathematics at the University of California Los Angeles for the program “Cells and Materials: at the interface between Mathematics, Biology and Engineering”. Several discussions with program participants have been quite helpful. B.O. wishes to acknowledge helpful conversations with participants at two workshops organized by the Aspen Center for Physics: “Cytoskeletal Assembly and Cellular Motility” and “Decision Making in Cells”.
This work was supported by a grant from the National Institutes of Health (No. R01GM076293 to B.O.).
Appendix
Energy landscape for rigid repellers
In Compression Energy of Repellers, we modeled the repellers as compressible with spring constant Ω. We now introduce a simplified model based upon treating the repellers as rigid molecules associated with a membrane that is constrained by four strict boundary conditions. As before, we envision a nouveau adhesion nucleated ex novo from an approximately planar membrane under the lamellipodium. With rigid repellers, the membrane rests at a distance above a rigid substrate, sandwiched between the actin network on the cytoplasmic face and repeller molecules, of length H, on the ventral surface side. The base of a focal plate has radius A, but when the repellers are rigid, we assume that the membrane smoothly deforms over a length scale L, from a height above the substrate in the base region, until it reaches the planar membrane at the outer radius of the plate (ρ = A + L) with height . Therefore, we assume that the membrane profile, h = h(ρ), is subject to the boundary conditions
| (20) |
In the main body of the article, the width of the plate evolved naturally as result of the application of the simulated annealing method. Note that, with the simplified model, we must treat the plate width as an external parameter. This width must be determined as the value L that minimizes the total energy, i.e., from the solution of . As before, the width of the focal plate, L, is a useful parameter because it provides a simple geometric framework that aids in interpreting the results. For example, the free energy associated with repellers given by Eq. 3 has a simple expression when the repellers are rigid because as the initial area occupied by repeller molecules, 4πR2, changes with adhesion growth, the repeller molecules become excluded from the focal plate and the area available to the molecules then becomes = 4πR2 − Nπ(A + L)2. Multiplying the free energy per molecule with the total number of repeller molecules, 4πR2αd0, yields (in units of kT)
| (21) |
We can now use the width of the plate, L, and Eq. 21 to derive an expression for the total energy. As before, we will assume that the Helfrich repulsion terms associated with the substrate and the actin network do not significantly contribute to the energy landscape so that their contribution may be ignored. Because the compression energy becomes zero for rigid repellers, the total energy for rigid repellers may be written from Eq. 11, as
| (22) |
where em represents the membrane elastic energy density as defined before (Eq. 8). Inserting Eqs. 4–6 and Eq. 21 into Eq. 22, the total energy of N focal plates can be written as
| (23) |
The five terms in Eq. 23 represent
-
1.
Membrane elastic energy.
-
2.
Free energy of repellers excluded from ρ < A + L.
-
3.
Free energy of receptors excluded from the base, i.e., ρ < A.
-
4.
Free energy of bound receptors.
-
5.
Binding energy of ligand-receptor pairs.
Inserting Eq. 8 into the integral term in Eq. 23, the membrane energy becomes
| (24) |
The shape profile of the membrane, h = h(ρ), may be determined by using the four boundary conditions in Eq. 20 via the corresponding Euler-Lagrange equation (56), obtained by functional minimization of Eq. 24,
| (25) |
where and in radial coordinates, .
Although there is a solution for Eq. 25, it does not have a simple analytic form (it is a fourth-order differential equation with solution in terms of modified Bessel functions of the first and second kind (56)). However, it is simple to convert this equation into a set of four first-order differential equations that can be solved numerically to high accuracy by standard iteration algorithms such as Runge-Kutta and using a Newton-Raphson minimization algorithm to match the end points of the trajectory with the boundary conditions.
After computing the energy of the membrane, the total energy of the system can be determined from Eq. 23 using known values for the relevant parameters. Fig. 16 shows a portion of the total energy landscape when 20 focal plates (N = 20) have formed and α = 16 and β = 11. The total energy landscape per focal plate, shown as a function of the plate radius, A, and width, L, indicates that a saddle point is located at the top of an energy barrier, which runs parallel to the A axis and an energy well, which runs parallel to the L axis. As shown in Fig. 7 (inset), the energy barrier determines the critical radius, Ac. Because the bottom of the energy well does not vary appreciably with A, the plate width is essentially constant; this conclusion is valid over the entire range of A, (data not shown).
Figure 16.
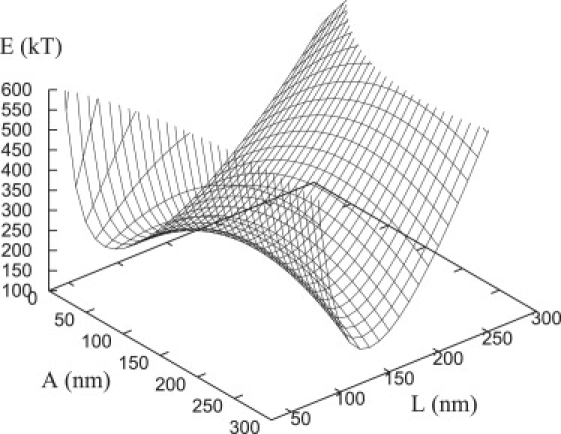
Portion of the total energy landscape (per adhesion) as a function of the plate radius (A) and the width (L). The membrane energy obtained via the numerical method as described in the text. Parameters chosen: α = 16, β = 11, and N = 20.
To find the plate width precisely, we note that only the free energy of repellers, F1, and the bending energy of the membrane, Em, depend upon L. Therefore, from Eq. 23, . We solve the equation numerically to find L. The value of L was determined as 110 nm < L < 160 nm with 9 < α < 25.
Analytical approximation to the membrane elastic energy
We seek a simple analytical solution to the membrane energy to gain greater insight into the sensitivity of the membrane energy to variations of the parameters A and L. For large values of the radial axis, ρ, the Euler-Lagrange equation for the shape function of the 2D plate system asymptotically reduces to its one-dimensional counterpart,
with solution
| (26) |
where the four unknown coefficients, the ci values, can be found from four boundary conditions (Eq. 20). By using this asymptotic approximation and omitting terms of ∼1/ρ, the energy integral reduces to a simple analytical expression
| (27) |
where
| (28) |
This formula suggests a simple physical model such that a closed curve has a constant line tension τ on a 2D planar surface and a topological constant Lπτ. Therefore, for fixed L, the membrane elastic energy might be expressed as (Lπ + C)τ on a smooth, closed deformed curve where C is the circumference.
In Fig. 17 A, we show the percentage deviation (as a function of A and L) of the asymptotic approximation for the membrane elastic energy (Eq. 27) from its exact solution (i.e., the energy derived from the shape functions of the full numeric solution of Eq. 25). For a range of plate widths between 30 nm and 300 nm, all the errors are <12% in absolute values; as expected, the larger the value of A, the better the approximation because the exact solution approaches its asymptotic limit when A gets bigger.
Figure 17.
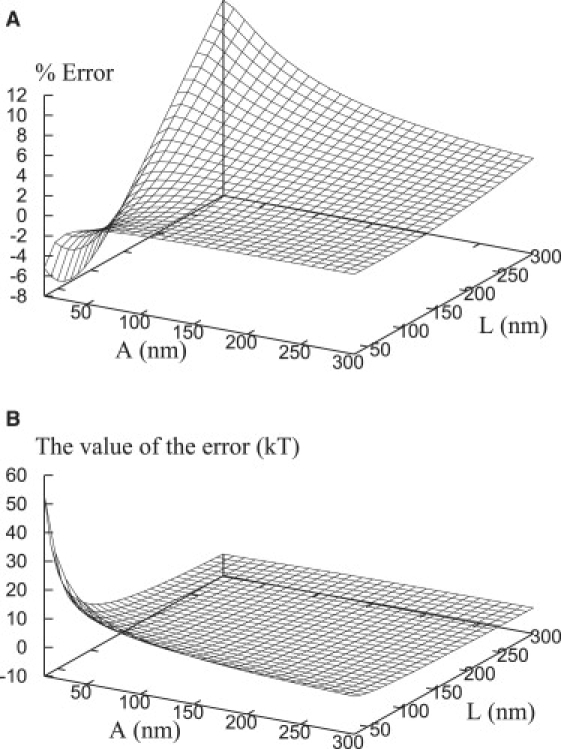
(A) Percentage deviation of the analytical formula for energies given by the asymptotic approximation (i.e., Eq. 27) with respect to the energies (Eq. 24) obtained via the exact numerical solution of Eq. 25. (B) The difference between exact and approximate solutions. Parameters used in both panels A and B: H = 30 nm, κ = 30 kT, and γ = 0.01 kT/nm2.
We have also shown that the difference between the exact and approximate values of the energy decreases as A and L increases (see Fig. 17 B). Note that the deviations are approximately a couple of kT (<5) for the majority of the points, and only some points near the origin show relatively high deviations, although never larger than 60 kT. According to our MC simulations, thermal fluctuations are of ∼100 kT for the whole system that has been chosen (500-nm × 500-nm membrane patch including the boundaries), so that the values of the errors are of the order of the thermal effects. This further validates our approximate formula equation (Eq. 27). The error decreases even further along the minimum paths. These numerical results show that the asymptotic formulas are good approximations for the shape and the deformation energy of the focal plate membrane for rigid repellers.
Analytical approximation to the energy landscape
Because we now have a simple analytical expression that describes the linear dependence of the membrane energy (Eq. 27) upon A, we can insert this expression into Eq. 23, and the total energy becomes
| (29) |
To find an analytical expression for the critical radius, we can further approximate the total energy, Eq. 29, by taking the first-order terms in the expansion of the logarithmic terms. Therefore, the total energy per plate when the repellers are rigid and the membrane is subject to strict boundary conditions becomes
| (30) |
For an infinitely large reservoir of receptors and repellers, i.e., R → ∞ in Eq. 29, Eq. 30 represents the energy per plate exactly. In this instance, the energy landscape does not depend upon either the size of the cell or the number of focal plates.
The transition from compressible repellers to rigid repellers
In this article, we have presented two models for the repeller molecules:
-
1.
Compressible repellers associated with a membrane that relaxes to an essentially flat profile at a large radial distance from the base of the focal plate and
-
2.
Rigid repeller molecules associated with a membrane that is constrained by strict boundary conditions (i.e., a simplified model).
We now demonstrate explicitly the link between the compressible and rigid repeller models.
Returning to the compressible repeller model and using the logarithmic expansions for Eqs. 3 and 4, we minimize the total energy Eq. 12 to find the energy landscape that governs the initial growth of a focal plate. In particular, as in Membrane Profile and Repeller Density Distribution, we use the simulated annealing method to minimize the energy with respect to h to obtain the shape profile. The terms in the energy that depend upon h are contained in the integral
| (31) |
To investigate this model as the repellers become rigid, we seek to minimize Eq. 31 in the limit Ω → ∞. Using Eq. 1, the limit of the sum of the second and third term in Eq. 31 as Ω → ∞ becomes
Therefore, Eq. 31 simplifies to
| (32) |
where
It is now possible to perform the minimization numerically and obtain the membrane shape and density profile.
The resultant shape and density profiles indicate a plate with width L and size A + L (solid line, Fig. 18), i.e., the density profile is zero, where ρ < A + L and constant when ρ > A + L. Therefore, the repellers are excluded from a circular region of area π(A + L)2 and the density is a step-function of ρ. For comparison, we also show the membrane shape determined with the simplified model; by definition, the repeller density is also a step function of ρ, but now the width is Lsimplifiedmodel. It may be observed that the simplified repeller model with strict boundary conditions effectively dampens the membrane profile obtained for the compressible repellers with relaxed boundary conditions; however, the width of the plate is approximately the same with both models, L = 105 nm and L = 120 nm, the simulated annealing model and the simplified model, respectively.
Figure 18.
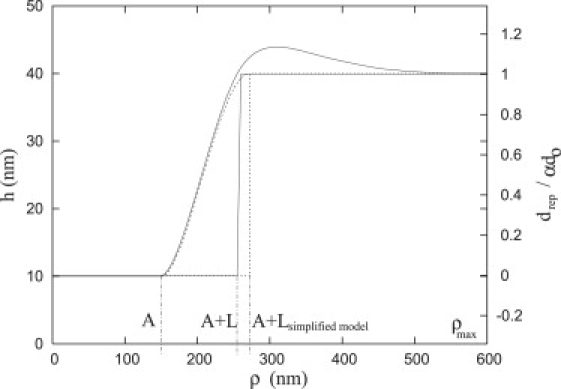
Shape (solid line, over damped curve) and density (solid line, step function of ρ) profiles of rigid repeller from simulated annealing minimization. Note that there are no repellers in the region where ρ < A + L. To simplify the model, we span the membrane between A and A + Lsimplified model and applied the boundary conditions listed in Eq. 20. (Dotted line) Shape of the membrane given by this simplified model after the minimization.
We now compare the energy landscapes obtained with the two models. As Fig. 19 demonstrates, the minimized total energy per plate, obtained with the simulated annealing method with α = 16, for Ω = 0.01 kT/nm2 and Ω = ∞ (solid and dashed parabolas, respectively) is in close agreement with the approximate analytic approximation for the simplified model, Eq. 30 (dotted parabola). We also show the corresponding membrane energy (dashed and solid straight lines) for compressible repellers with Ω = ∞ and Ω = 0.01 kT/nm2 and rigid repellers with strict boundary conditions (i.e., the simplified model), respectively (dotted straight lines). Therefore, in general and as a numerical fit, we can represent the membrane energy as c1 + c2A. For the simplified repeller model, c1 = τLπ and c2 = τ2π. Hence analogous to Eq. 30, it is possible to find an analytical formula for the compressible repeller case. This may be accomplished by
-
1.
Expressing the membrane energy as c1 + c2A.
-
2.
Approximating the density of compressible repellers to that of rigid repellers.
-
3.
Omitting the Helfrich repulsion.
Figure 19.
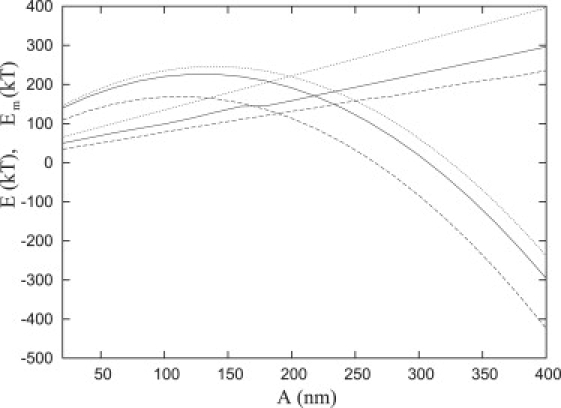
Energy landscape obtained with two models for the repeller molecules. Total energy per plate, E, and membrane energy, Em, calculated via the simulated annealing method applied to compressible repellers (dashed parabolas and solid straight lines, respectively) and from the simplified model for rigid repellers (dotted parabolas and straight lines, respectively). For compressible repellers, two values of Ω are presented (Ω = 0.01 kT/nm2 and Ω = ∞ (dashed and solid, respectively).
The approximate energy per plate for compressible repellers becomes
| (33) |
After obtaining the values of c1 and c2 from a fit to the membrane energy, this approximation (Eq. 33) is plotted together with the exact numeric results (i.e. Fig. 4 in Critical Radius) and we conclude the approximation is valid.
References
- 1.Shemesh T., Geiger B., Bershadsky A.D., Kozlov M.M. Focal adhesions as mechanosensors: a physical mechanism. Proc. Natl. Acad. Sci. USA. 2005;102:12383–12388. doi: 10.1073/pnas.0500254102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Evans E.A., Calderwood D. Forces and bond dynamics in cell adhesion. Science. 2007;316:1148–1153. doi: 10.1126/science.1137592. [DOI] [PubMed] [Google Scholar]
- 3.Zaidel-Bar R., Milo R., Kam Z., Geiger B. A paxillin tyrosine phosphorylation switch regulates the assembly and form of cell-matrix adhesions. J. Cell Sci. 2007;120:137–148. doi: 10.1242/jcs.03314. [DOI] [PubMed] [Google Scholar]
- 4.Webb D., Brown C., Horwitz A. Illuminating adhesion complexes in migrating cells: moving toward a bright future. Curr. Opin. Cell Biol. 2003;15:614–620. doi: 10.1016/s0955-0674(03)00105-4. [DOI] [PubMed] [Google Scholar]
- 5.Zaidel-Bar R., Itzkovitz S., Ma'ayan A., Iyengar R., Geiger B. Functional atlas of the integrin adhesome. Nat. Cell Biol. 2007;9:858–867. doi: 10.1038/ncb0807-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Galbraith C., Yamada K., Sheetz M. The relationship between force and focal complex development. J. Cell Biol. 2002;159:695–705. doi: 10.1083/jcb.200204153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cluzel C., Saltel F., Lussi J., Paulhe F., Imhof B.A. The mechanisms and dynamics of αVβ3 integrin clustering in living cells. J. Cell Biol. 2005;171:383–392. doi: 10.1083/jcb.200503017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bruinsma R. Theory of force regulation by nascent adhesion sites. Biophys. J. 2005;89:87–94. doi: 10.1529/biophysj.104.048280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Beningo K., Dembo M., Kaverina I., Small J., Wang Y. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 2001;153:881–888. doi: 10.1083/jcb.153.4.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hynes R. Changing partners. Science. 2003;300:755–756. doi: 10.1126/science.1084854. [DOI] [PubMed] [Google Scholar]
- 11.Galbraith C.G., Yamada K.M., Galbraith J.A. Polymerizing actin fibers position integrins primed to probe for adhesion sites. Science. 2007;315:992–995. doi: 10.1126/science.1137904. [DOI] [PubMed] [Google Scholar]
- 12.Zaidel-Bar R., Ballestrem C., Kam Z., Geiger B. Early molecular events in the assembly of matrix adhesions at the leading edge of migrating cells. J. Cell Sci. 2003;116:4605–4613. doi: 10.1242/jcs.00792. [DOI] [PubMed] [Google Scholar]
- 13.Cohen M., Joester D., Geiger B., Addadi L. Spatial and temporal sequence of events in cell adhesion: from molecular recognition to focal adhesion assembly. ChemBioChem. 2004;5:1393–1399. doi: 10.1002/cbic.200400162. [DOI] [PubMed] [Google Scholar]
- 14.Erlandsen S., Greet Bittermann A., White J., Leith A., Marko M. High-resolution CryoFESEM of individual cell adhesion molecules (CAMs) in the glycocalyx of human platelets: detection of P-selectin (CD62P), GPI-IX complex (CD42a/CD42bα,bβ), and integrin GPIIbIIIa (CD41/CD61) by immunogold labeling and stereo imaging. J. Histochem. Cytochem. 2001;49:809–820. doi: 10.1177/002215540104900702. [DOI] [PubMed] [Google Scholar]
- 15.Sackmann E., Bruinsma R.F. Cell adhesion as wetting transition? ChemPhysChem. 2002;3:262–269. doi: 10.1002/1439-7641(20020315)3:3<262::AID-CPHC262>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 16.Chen W., Singer S.J. Immunoelectron microscopic studies of the sites of cell—substratum and cell-cell contacts in cultured fibroblasts. J. Cell Biol. 1982;95:205–222. doi: 10.1083/jcb.95.1.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Satyajit K., Hanson D.A., Schlaepfer D.D. Focal adhesion kinase: in command and control of cell motility. Nat. Rev. Mol. Cell Biol. 2005;6:56–68. doi: 10.1038/nrm1549. [DOI] [PubMed] [Google Scholar]
- 19.Bell G.I., Dembo M., Bongrand P. Cell adhesion: competition between nonspecific repulsion and specific bonding. Biophys. J. 1984;45:1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Prass M., Jacobson K., Mogilner A., Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J. Cell Biol. 2006;174:767–772. doi: 10.1083/jcb.200601159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Atilgan E., Wirtz D., Sun S.X. Morphology of the lamellipodium and the organization of actin associated proteins at the leading edge of crawling cells. Biophys. J. 2006;89:3589–3602. doi: 10.1529/biophysj.105.065383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Safran S.A. Addison-Wesley; Reading, MA: 1994. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. [Google Scholar]
- 23.Milner S.T., Witten T.A., Cates M.E. Theory of the grafted polymer brush. Macromolecules. 1988;21:2610–2619. [Google Scholar]
- 24.Milner S.T. Polymer brushes. Science. 1991;251:905–914. doi: 10.1126/science.251.4996.905. [DOI] [PubMed] [Google Scholar]
- 25.Howard J. Sinauer; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 26.Gao H., Shi W., Freund L.B. Mechanics of receptor-mediated endocytosis. Proc. Natl. Acad. Sci. USA. 2005;102:9469–9474. doi: 10.1073/pnas.0503879102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shenoy V.B., Freund L.B. Growth and shape stability of a bilayer membrane adhesion complex in the diffusion-mediated regime. Proc. Natl. Acad. Sci. USA. 2005;102:3213–3218. doi: 10.1073/pnas.0500368102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Torney D.C., Dembo M., Bell G.I. Thermodynamics of cell adhesion. II: Freely mobile repellers. Biophys. J. 1986;49:501–507. doi: 10.1016/S0006-3495(86)83660-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zuckerman D., Bruinsma R. Statistical mechanics of membrane adhesion by reversible molecular bonds. Phys. Rev. Lett. 1995;74:3900–3903. doi: 10.1103/PhysRevLett.74.3900. [DOI] [PubMed] [Google Scholar]
- 30.Zuckerman D., Bruinsma R. Vesicle-vesicle adhesion by mobile lock-and-key molecules: Debye-Hückel theory and Monte Carlo simulation. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1998;57:964–977. [Google Scholar]
- 31.Torney D.C., Dembo M., Bell G.I., Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. [C] 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 32.Bar-Ziv R., Menes R., Moses E., Safran S.A. Local unbinding of pinched membranes. Phys. Rev. Lett. 1995;75:3356–3359. doi: 10.1103/PhysRevLett.75.3356. [DOI] [PubMed] [Google Scholar]
- 33.Menes R., Safran S.A. Nonlinear response of membranes to pinning sites. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1997;56:1891–1899. [Google Scholar]
- 34.Rädler J.O., Feder T.J., Strey H.H., Sackmann E. Fluctuation analysis of tension-controlled undulation forces between giant vesicles and solid substrates. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1995;51:4526–4536. doi: 10.1103/physreve.51.4526. [DOI] [PubMed] [Google Scholar]
- 35.Gov N.S., Gopinathan A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 37.Press W., Teukolsky S., Vetterling W., Flannery B. 2nd Ed. Cambridge University Press; New York: 1988. Numerical Recipes in C: The Art of Scientific Computing. [Google Scholar]
- 38.Weikl T.R., Andelmann D., Komura S., Lipowsky R. Adhesion of membranes with competing specific and generic interactions. Eur. Phys. J. E. 2002;8:59–66. doi: 10.1140/epje/i2002-10008-2. [DOI] [PubMed] [Google Scholar]
- 39.Rozycki R., Lipowsky R., Wekl T.R. Adhesion of membranes with stickers. Phys. Rev. Lett. 2006;96:048101–048104. doi: 10.1103/PhysRevLett.96.048101. [DOI] [PubMed] [Google Scholar]
- 40.Metropolis N., Rosenbluth A., Rosenbluth M., Teller A., Teller E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 41.Boulbitch A., Guttenberg Z., Sackmann E. Kinetics of membrane adhesion mediated by ligand-receptor interaction studied with a biomimetic system. Biophys. J. 2001;81:2743–2751. doi: 10.1016/S0006-3495(01)75917-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ballestrem C., Hinz B., Imhof B.A., Wehrle-Haller B. Marching at the front and dragging behind: differential αVβ3-integrin turnover regulates focal adhesion behavior. J. Cell Biol. 2001;155:1319–1332. doi: 10.1083/jcb.200107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wehrle-Haller B., Imhof B.A. The inner lives of focal adhesions. Trends Cell Biol. 2002;12:382–389. doi: 10.1016/s0962-8924(02)02321-8. [DOI] [PubMed] [Google Scholar]
- 44.Schwarz U., Erdmann T., Bischof I.B. Focal adhesions as mechanosensors: the two-spring model. Biosystems. 2006;83:225–232. doi: 10.1016/j.biosystems.2005.05.019. [DOI] [PubMed] [Google Scholar]
- 45.Erdmann T., Schwarz U.S. Bistability of cell-matrix adhesions resulting from nonlinear receptor-ligand dynamics. Biophys. J. Biophys. Lett. 2006;91:L60–L62. doi: 10.1529/biophysj.106.090209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nicolas A., Safran S.A. Limitation of cell adhesion by elasticity of the extracellular matrix. Biophys. J. 2006;91:61–73. doi: 10.1529/biophysj.105.077115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cavalcanti-Adam E., Volberg T., Micoulet A., Kessler H., Geiger B. Cell spreading and focal adhesion dynamics are regulated by spacing of integrin ligands. Biophys. J. 2007;92:2964–2974. doi: 10.1529/biophysj.106.089730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bershadsky A.D., Ballestrem C., Carramusa L., Zilberman Y., Gilquin B. Assembly and mechanosensory function of focal adhesions: experiments and models. Eur. J. Cell Biol. 2006;85:165–173. doi: 10.1016/j.ejcb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- 49.Frenkel D., Smith B. 2nd Ed. Academic Press; London: 2005. Understanding Molecular Simulation. [Google Scholar]
- 50.Atligan E., Wirtz D., Sun S.X. Mechanics and dynamics of actin-driven thin membrane protrusions. Biophys. J. 2005;90:65–76. doi: 10.1529/biophysj.105.071480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rozycki B., Weikl T.R., Lipowsky R. Adhesion of membranes via switchable molecules. Phys. Rev. E. 2006;73 doi: 10.1103/PhysRevE.73.061908. 061908–14. [DOI] [PubMed] [Google Scholar]
- 52.Feneberg W., Westphal M., Sackmann E. Dictyostelium cells' cytoplasm as an active viscoplastic body. Eur. Biophys. J. 2001;30:284–294. doi: 10.1007/s002490100135. [DOI] [PubMed] [Google Scholar]
- 53.Pierres A., Benoliel A.-M., Touchard D., Bongrand P. How cells tiptoe on adhesive surfaces before sticking. Biophys. J. 2008;94:4114–4122. doi: 10.1529/biophysj.107.125278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Limozin L., Sengupta K. Modulation of vesicle adhesion and spreading kinetics by hyaluronan cushions. Biophys. J. 2007;93:3300–3313. doi: 10.1529/biophysj.107.105544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Smith A.-S., Sengupta K., Goennenwein S., Seifert U., Sackmann E. Force-induced growth of adhesion domains is controlled by receptor mobility. Proc. Natl. Acad. Sci. USA. 2008;105:6906–6911. doi: 10.1073/pnas.0801706105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Norouzi D., Muller M.M., Deserno M. How to determine the local elastic properties of the lipid bilayer membranes from atomic force microscopy measurements: a theoretical analysis. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:61914–061926. doi: 10.1103/PhysRevE.74.061914. [DOI] [PubMed] [Google Scholar]
- 57.Ward M.D., Hammer D.A. Focal contact assembly through cytoskeletal polymerization: steady state analysis. J. Math. Biol. 1994;32:677–704. doi: 10.1007/BF00163022. [DOI] [PubMed] [Google Scholar]
- 58.Darrell J.I., Hue K., Mayes A.M., Griffith L.G. Simulations of cell-surface integrin binding to nanoscale-clustered adhesion ligands. Biophys. J. 2002;82:120–132. doi: 10.1016/S0006-3495(02)75379-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Evans E., Rawicz W. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 1990;64:2094–2097. doi: 10.1103/PhysRevLett.64.2094. [DOI] [PubMed] [Google Scholar]
- 60.Dai J., Sheetz M.P. Membrane tether formation from blebbing cells. Biophys. J. 1999;77:3363–3370. doi: 10.1016/S0006-3495(99)77168-7. [DOI] [PMC free article] [PubMed] [Google Scholar]


