Single-Channel Current Through Nicotinic Receptor Produced by Closure of Binding Site C-Loop

Abstract

We investigated the initial coupling of agonist binding to channel gating of the nicotinic acetylcholine receptor using targeted molecular-dynamics (TMD) simulation. After TMD simulation to accelerate closure of the C-loops at the agonist binding sites, the region of the pore that passes through the cell membrane expands. To determine whether the structural changes in the pore result in ion conduction, we used a coarse-grained ion conduction simulator, Biology Boltzmann transport Monte Carlo, and applied it to two structural frames taken before and after TMD simulation. The structural model before TMD simulation represents the channel in the proposed “resting” state, whereas the model after TMD simulation represents the channel in the proposed “active” state. Under external voltage biases, the channel in the “active” state was permeable to cations. Our simulated ion conductance approaches that obtained experimentally and recapitulates several functional properties characteristic of the nicotinic acetylcholine receptor. Thus, closure of the C-loop triggers a structural change in the channel sufficient to account for the open channel current. This approach of applying Biology Boltzmann transport Monte Carlo simulation can be used to further investigate the binding to gating transduction mechanism and the structural bases for ion selection and translocation.

Introduction

Channel-forming proteins provide low-energy pathways for ions and water to cross the otherwise impermeable cell membrane and are essential to all life forms. The nicotinic acetylcholine receptor (nAChR) at the motor endplate is a prototypical channel-forming protein within a large family of neurotransmitter-activated ion channels that mediates rapid synaptic transmission. Despite decades of research, the mechanism by which neurotransmitter binding triggers channel gating remains elusive due to the lack of experimental approaches to monitor the protein and ions in real time and at atomic resolution. A general view of the channel gating mechanism is that agonist binding to the extracellular binding sites triggers a structural change in the channel.

Recent advances in structural determination of the nAChR and homologous proteins have contributed to steady progress in elucidating the gating mechanism. First, x-ray crystal structures of acetylcholine binding protein (AChBP), a homolog of the nAChR extracellular domain, provided a detailed picture of how an agonist binds to the receptor: a peripheral loop, called the C-loop, closes when agonist occupies the binding site (1–7). Second, a cryo-electron microscopic (cryo-EM) structure of the Torpedo nAChR was solved at a resolution of 4 Å and represents a nearly complete model of the nAChR (8). This structure is considered to be a model of the closed state because agonist was not present during the EM sampling. Recently, x-ray structures of related prokaryotic proton-activated channels were solved. The channel from the bacterium Erwinia chrysanthemi (ELIC) was solved in the inactive state and exhibited a narrow hydrophobic constriction at the upper half of the channel (9), whereas the channel from the cyanobacterium Gloebacter violaceus (GLIC) was solved in the apparently open state and showed widening in the upper half of the channel (10,11).

Although these solved structures provide invaluable information, they do not include thermodynamic fluctuations vital to protein function, such as the structural motion that transmits agonist binding to the channel. By using computational molecular-dynamics (MD) simulations, we can gain insight into the atomistic motion underlying this transduction process. In a previous study (12), we used targeted MD (TMD) simulations to apply force to close the C-loop at the binding sites to mimic the effect of agonist binding, and found that the structural rearrangement led to pore widening. The question remained, however, whether these structural changes result in an ion-conductive pore.

MD simulations of ion transport through the nAChR channel have been attempted since publication of the cryo-EM Torpedo structure. With only the transmembrane domains embedded in a bilayer-mimetic slab, potential of mean force calculations revealed an energy barrier of 9 kcal/mol midway through the bilayer, suggesting that the channel was closed to ion translocation (13). With the transmembrane domains embedded in an explicit bilayer, MD simulations showed that water molecules evacuated the narrowest constriction of the pore and ion translocation did not occur. However, when the narrow constriction was manually widened by 1.5 Å, water and ions entered the channel and the resulting ion transport rate approached that expected from the single-channel current amplitude (14). The inherent limitations of these studies include an incomplete structure of the nAChR and the absence of a transmembrane potential.

We previously applied all-atom MD simulation to a homology model of the human muscle nAChR in an explicit bilayer with an applied transmembrane potential (15). Single cations passed through the channel but paused at each of a series negatively charged rings along the translocation pathway. One of these rings, at a position equivalent to αAsp⁹⁷ in the extracellular vestibule, was recently shown to affect unitary current amplitude, indicating that it functions as a cation-selective filter (16).

The major challenge of MD simulations is the computational cost, which still prohibits simulation of biological processes such as the electrical current through ion channels (17). Ion translocation is a rare event, demanding simulations that last several microseconds (18), but it is also essential to account for short-range interactions between atoms, which can be very strong and occur on the femtosecond timescale. Although MD simulations can provide essential information on protein dynamics and mechanisms of ion conduction, the computational cost is still very high even on massively parallel supercomputers.

Coarse-grained particle approaches such as Monte Carlo (MC) or Brownian dynamics (BD) can extend simulation times beyond those achievable by MD simulations while retaining some atomistic representation (19–21). In such coarse-grained approaches, ions are modeled as discrete particles with finite size, whereas the rest of the system (protein, water, and membrane) is treated as continuum media with a given electrical permittivity. BD simulations, in particular, are being increasingly applied to obtain macroscopic information with respect to channel conductance and ion selectivity (22–24). However, representing ion-water interactions with a single frictional coefficient and a random stochastic force may be an oversimplification in narrow regions of the channel where complicated ion scattering events could occur (21). Biology Boltzmann transport Monte Carlo (BioMOCA) is an alternative coarse-grained method for simulating ion translocation through channels. It was developed based on the Boltzmann Transport Monte Carlo (BTMC) methodology, which was used for several decades to simulate charge transport in solid state and plasma devices. In this study, we applied BioMOCA simulation and combined it with TMD simulations to determine whether closure of the nAChR C-loop is sufficient to produce a conducting channel.

Materials and Methods

Homology modeling

Two homology models of the human muscle nAChR were constructed using the comparative protein structural modeling program Modeller v8.0 (25). The first model was constructed based on the cryo-EM structure of the Torpedo nAChR (PDB code: 2BG9). Details of the modeling procedure employed for construction of the first model have been described previously (15). The second model was constructed based on a hybrid model consisting of the x-ray structure of AChBP (PDB code: 1UV6) as the extracellular domain and the cryo-EM Torpedo structure (PDB code: 2BG9). Construction of the second model involved two steps. First, a homology model of the extracellular domain of the human nAChR was built from the AChBP structure in an agonist-bound conformation. Then the full receptor was modeled by simultaneously using the newly built extracellular domain and the Torpedo receptor structures as templates. Because the agonist binding domain template already had the same sequence as that of the target, the corresponding coordinates were directly transferred to the final model. As a result of this two-step procedure, the two templates were joined by implicitly satisfying geometrical constraints, thereby avoiding errors from manually overlaying the two domains. All the obtained models were evaluated with PROCHECK and Prosa 2003.

MD simulations

The control MD simulations were carried out with the first nAChR model embedded in a fully hydrated palmitoyl-2-oleoyl-sn-glycerol-phosphatidylcholine (POPC) bilayer (120 Å × 120 Å) using the membrane subroutine included in the VMD script library. Lipids within 0.8 Å of the protein were removed. The total number of lipids was 298, with 141 on the extracellular side and 157 on the intracellular side. Next, the membrane-protein complex was solvated in TIP3P water using the solvate subroutine. Ions were added to neutralize the net charge of the protein using the autoionize subroutine, and amounted to 84 sodium and 26 chloride atoms, achieving a salt concentration of 100 mM. The resulting system comprises 247,568 atoms, which includes 1886 protein residues and 59,080 TIP3P water molecules.

We used the highly scalable MD simulation program NAMD (26) and the CHARMM27 force field (27). Once the protein ensemble was built, the following four rounds of equilibrations were completed: 1), 2000 steps of energy minimization for the nonbackbone atoms; 2), five cycles of a 500-step energy minimization with decreasing position restraints on the protein α-C atoms; 3), a gradual increase in the temperature from 50 K to 310 K in 10,000 steps of constant volume (NVT ensemble) simulation with restraints (with a force constant of 3 kcal.mol⁻¹.Å⁻²) applied to the protein α-C atoms; and 4), a 2 ns constant surface area ensemble MD equilibration with decreasing positional restraints on the α-C atoms. A short cutoff of 9 Å was used for nonbonded interactions, and long-range electrostatic interactions were treated using the particle mesh Ewald method (28). Langevin dynamics and a Langevin piston algorithm were used to maintain the temperature at 310 K and a pressure of 1 atm. The r-RESPA multiple time step method (29) was employed with a 2 fs time step for bonded atoms, a 2 fs step for short-range nonbonded atoms, and a 4 fs step for long-range electrostatic forces. The bonds between hydrogen and heavy atoms were constrained with the SHAKE algorithm.

Targeted MD simulations

The procedure for the TMD simulation was described in detail in our previous article (12). One difference between that study and the one presented here was in the choice of sites to which force was applied. Instead of applying force to the entire C-loop, here we selected five residues at each of the two agonist binding sites. These five residues are key determinants of acetylcholine binding and include four residues from the principal face (Tyr⁹³, Trp¹⁴⁹, Tyr¹⁹⁰, and Tyr¹⁹⁸) and one from the complementary face (Trp⁵⁵). They also form an “aromatic box” around the bound agonist (Fig. 1). Application of force to these five key residues mimics the effect of agonist binding and also reduces the computational cost. During the TMD simulation, the root mean-square deviation (RMSD) of the five resides at each binding site was calculated every 2 ps based on the starting structure and the target structure of the second homology model, and was used in an energy term: V = 0.5 ^∗ k ^∗ (RMSD(t) − RMSD₀(t))², where the RMSD(t) term represents the simulation structure at time t relative to the prescribed target structure, the RMSD₀(t) term represents the prescribed target RMSD value at time t, and the force constant k equals 20 kcal · mol⁻¹ · Å⁻². The calculations were performed independently for the two binding sites, under the assumption of independent agonist binding. The RMSDs of the two binding sites decreased independently from the initial values of 6–7 Å to 1 Å within the first 4 ns, and remained at 1 Å for the rest of simulation time. The total TMD simulation took 20 ns.

Figure 1.

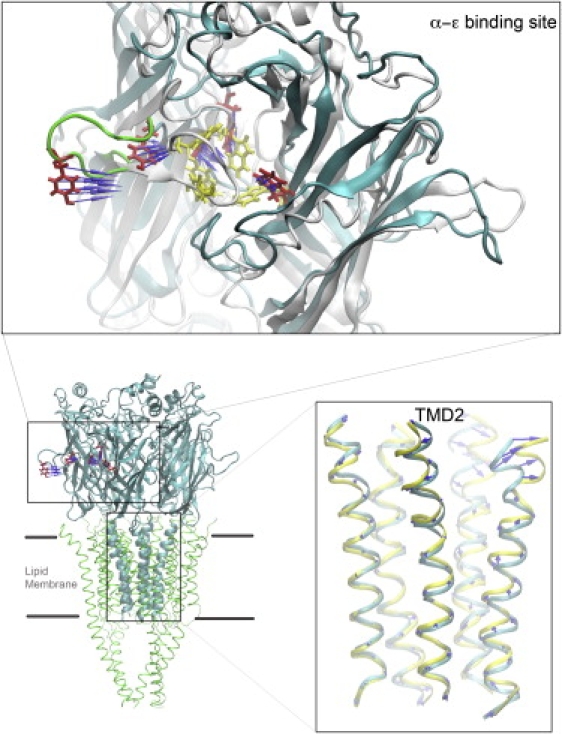
TMD simulation. The lower-left panel shows the entire nAChR, with the cell membrane indicated by dark lines. The top panel shows one of the two agonist binding sites (α−ɛ site). The C-loop is represented as a green tube. The selected key residues are in red in the pre-TMD structure (cyan backbone), and in yellow in the post-TMD structure (white backbone). Blue arrows indicate forces applied to the side-chain atoms of the selected key residues. The lower-right panel shows structural models of the pre- and post-TMD simulation in the region of the channel, and, for clarity, displays only the five α-helices of the second transmembrane domain. The pre-TMD structure is in cyan and the post-TMD structure is in yellow.

BioMOCA

BioMOCA was developed at the University of Illinois at Urbana-Champaign to simulate ion transport in electrolyte environments of ion channels or nano-pores embedded in membranes (21). It is based on two methodologies: BTMC (30) and particle-particle-particle-mesh (P³M) (31). BTMC uses an MC method to solve the Boltzmann equation and has been used for several decades to study charge transport in solid state and plasma devices. The P³M methodology splits the electrostatic forces into short- and long-range components. To reduce the computational cost, the protein, membrane, and water are treated as continuum media with assigned permittivity. Ions are the only particles explicitly represented; they move according to Newtonian physics, and are overdamped by frequent scattering events with water molecules. The electrostatic potential is computed at regular time intervals by solving the Poisson equation:

$$\nabla \cdot \left(\varepsilon \left(r\right)\nabla \Phi (r,t)\right)=-\left({\rho }_{\text{ions}}(r,t)+{\rho }_{\text{perm}}\left(r\right)\right),$$ (1)

where ρ_ions(r,t) and ρ_perm(r) are the charge densities of ions and permanent charges on the protein, respectively; ɛ(r) is the local dielectric constant or permittivity; and ϕ(r,t) is the local electrostatic potential. Solving this equation provides a self-consistent way to include an applied voltage bias and the effects of image charges induced at dielectric boundaries.

The ion and partial charges on protein residues are assigned to a finite rectangular grid using the cloud-in-cell (CIC) scheme (31). Solving the Poisson equation on the grid is based on the particle-mesh part of the P³M scheme. However, the use of a grid leads to an unavoidable truncation of the short-range component of electrostatic force, which can be corrected by computing the short-range charge-charge interactions. The Lennard-Jones potential was employed to prevent superposition of ions.

Dielectric coefficient

Assigning appropriate values for the dielectric permittivity of the protein, membrane, and aqueous regions is of great importance. The dielectric coefficient determines the strength of the interactions between charged particles, and also the dielectric boundary forces on ions approaching two regions of different permittivity. However, the task of assigning specific permittivity is problematic and not straightforward at nanometer scales. The protein or membrane environment could respond to an external field in a number of ways (21). The issue of protein dielectric coefficients is addressed elsewhere (32,33). Also, water molecules inside ion channels could be very ordered due to the tapered shape of the pore, which is often lined with highly charged residues or contains hydrogen bonds between water molecules and the protein (34). As a result, the dielectric constant of water inside ion channels could be lower than the value under bulk conditions. For the simulations presented here, we adopted the same dielectric constant for all of the aqueous regions to reduce the computational cost required to account for a gradually changing water permittivity from bulk-like baths to the channel. However, we used 60 and 80 separately as the dielectric constants of water to assess the effects of parameter choices on the conclusion.

Ion-water interactions

BioMOCA is a reduced-particle approach that replaces explicit water molecules with a continuum background and handles the ion-water interactions using the BTMC method. Ion trajectories are randomly interrupted by scattering events that account for the ions' diffusive motion in water (21). Between these scattering events, ions follow Newtonian physics. The free flight times T_f are generated statistically from the total scattering rate according to

$$-\ln \left(r\right)={\int }_0^{T_f}\lambda \left(\overrightarrow{p}\left(t\right)\right)dt,$$ (2)

where r is a random number uniformly distributed on the unit interval, and λ, a function of momentum, is the total scattering rate for all collision mechanisms. Although BioMOCA is equipped to handle multiple scattering processes, for this work we used bulk diffusion coefficients inside the pore region.

Ion-protein interaction

The available high-resolution x-ray structures provide information about the type and location of all atoms in the protein. BioMOCA uses this information in the Position-Charge-Radius (PQR) format to map the protein system onto a rectangular grid and partition the simulation domain into continuous regions based on the Adaptive Poisson Boltzmann Solver (APBS) scheme (35). Ions are deemed to have access to protein and lipid regions. If any point within the finite size of an ionic sphere crosses the protein or membrane boundary, a collision is assumed and the ion is reflected diffusively (21).

The detailed procedures for BioMOCA simulations have been described elsewhere (36). In brief, we obtained the receptor's static structural models by extracting snapshots of the structural coordinates before and after the TMD simulation, and added the charge and radius of each atom using the CHARMM force field and a pH of 7.4. The resulting files were then uploaded to a web-based BioMOCA suite (http://nanoHub.org) for ion-conduction simulations. In detail, the nAChR models were separately embedded in a rectangular box with dimensions of 70 Å × 70 Å × 150 Å and grid spacing of 1.5 Å, and then wrapped with a 33-Å-thick layer of simplified lipid membrane with a 13-Å-radius hole to surround the protein's transmembrane domains. The dielectric constants of protein and lipid were set to 5 and 2, respectively. The dielectric constant of water was set to 80 or 60 as indicated. Each simulation was carried out using a single Intel Xeon processor at 3.0 GHz and achieved a computing speed of 6 ns/day. To examine current-voltage relationships, we subjected each simulation to external voltage biases of −200, −100, 0, +100, and +200 mV. To examine the effect of divalent cations, we applied each simulation in two solution settings. Without divalent cations, the intracellular solution contained (mM) Na⁺, 5; Cl⁻, 145; K⁺,140; and the extracellular solution contained (mM) Na⁺, 140; Cl⁻, 145; K⁺, 5. With divalent cations, the intracellular solution contained (mM) Na⁺,10; Cl⁻, 76; K⁺, 100; Ca²⁺, 0; Mg²⁺, 3; and the extracellular solution contained (mM) Na⁺, 140; Cl⁻,100; K⁺, 5; Ca²⁺, 2; Mg²⁺, 1. All MD simulations were carried out with the use of an in-house-built supercomputing cluster in the Receptor Biology Laboratory at Mayo Clinic Rochester, and additional computing resources from the Minnesota Supercomputing Institute.

Single-channel recordings

Single-channel recordings were obtained in the cell-attached patch configuration at 22°C. Human wild-type nAChR subunit cDNAs were transfected into the 293 HEK cell line using calcium phosphate precipitation. Cells were used for measurements 1 or 2 days after transfection. The bath and pipette solutions contained (mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, 10 HEPES, pH 7.4. Patch pipettes were pulled from 7052 capillary tubes (Garner Glass, Clavemount, CA) and coated with Sylgard (Dow Corning, Midland, MI). Single-channel currents were recorded using Acquire software (Bruxton) and an Axopatch 200B patch-clamp amplifier (Molecular Devices, Sunnvate, CA), digitized at 2 μs intervals with a PCI-6111E fast data acquisition board (National Instruments, Austin TX), and analyzed using TAC software (Bruxton, Seattle, WA) at a final bandwidth of 10 kHz. The single-channel amplitudes were determined by fitting a Gaussian function to all-point histograms generated from the digitized current traces. In most cases, two Gaussian distributions were needed to describe the all-point histogram from each recording; one Gaussian corresponded to the closed channel current level, and the other corresponded to the open channel current level. The difference between the mean values of the two distributions yielded the single-channel current amplitude.

Results and Discussion

TMD simulations

To assess the extent to which the agonist bound conformation changes the structure of the channel, we mimicked agonist binding using TMD simulation. The top panel of Fig. 1 illustrates one of the two agonist binding sites; the selected key residues are colored red in the simulated structure (cyan) and yellow in the target structure (white), and the backbone of the C-loop is represented as a green tube. Blue arrows indicate the direction of the forces applied to the side chain atoms of the selected key residues. The lower-right panel shows the changes of the channel before and after TMD simulation, and displays only the five α-helices of the second transmembrane domain with the pre-TMD structure in cyan and the post-TMD structure in yellow. The lower-left panel shows the entire nAChR, with the dark lines indicating the cell membrane. After forcing the C-loop to close via TMD simulation, we detected structural changes in the channel.

The HOLE program (37) was used to measure the pore radius along the channel axis in the region of the cell membrane. The pore radius is plotted as mirror images to represent an idealized channel. In Fig. 2 A, the solid line represents the channel of the pre-TMD model, and the dashed line represents that of the post-TMD model. A comparison of the solid and dashed lines reveals that at the upper half of the channel, the channel radius of the post-TMD model is greater than that of the pre-TMD model. The two models are similar at the lower half of the channel, but the post-TMD model has a smaller radius at both the middle and the intracellular end of the channel. A third, dotted line represents the channel radius from the recently solved GLIC structure in an apparently open conformation (PDB code: 3EAM), showing that the radius of the upper half of the channel in the GLIC structure approaches that observed in our post-TMD structure. The overall changes indicate that closure of the C-loops at the two binding sites generates a funnel shape in the upper half of the nAChR channel, corresponding to an outward tilting motion of the second transmembrane domain suggested by previous MD simulations (12), patch-clamp recordings (38,39) and comparison of ELIC and GLIC x-ray structures (9–11).

Figure 2.

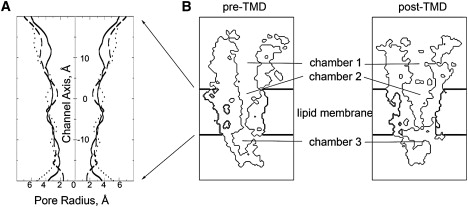
Comparison of the pre- and post-TMD models. Panel A plots the pore radii of the two models, as measured by the HOLE program. The solid line represents the pore radius of the pre-TMD model, and the dashed line corresponds to the post-TMD model. The dotted line is the pore radius of the bacterial channel GLIC. Panel B shows cross sections of the two models displayed with the protein surfaces outlined in black thin lines and the virtual membrane indicated by thick lines.

To illustrate structural differences between the pre- and post-TMD models, we display cross sections of the two models, with the surface of the protein outlined in black thin lines and the virtual membrane indicated by thick lines (Fig. 2 B). For ease of presentation, we divide the ion translocation pathway into three separate chambers, from extracellular to intracellular: chamber 1 is the extracellular vestibule, chamber 2 is the upper half of the channel, and chamber 3 is the intracellular vestibule. The region at the lower half of the channel connecting chambers 2 and 3 is the narrowest constriction. To our surprise, the main difference between the two structural models is not at the narrowest constriction, where changes might be expected, but in chamber 2, which is considerably wider in the post-TMD model than in the pre-TMD model.

Ion conduction simulations

To determine whether the observed changes in the pore structure correspond to an open channel capable of conducting cations, we subjected both the pre- and post-TMD models to BioMOCA simulations with 80 as the dielectric constant of water. We included explicit ions in the virtual solutions and applied external voltage biases to investigate current-voltage relationships. We also tested the effects of divalent cations. The simulated channel conductance of the post-TMD model is similar to that determined experimentally. In addition, our simulation results are consistent with several functional properties characteristic of the nAChR, including charge selectivity, inward current rectification, and screening by divalent cations. We will describe these results further in the following sections.

Charge selectivity

With a solution containing only Na⁺, K⁺ and Cl⁻ ions, we found that oppositely charged ions exhibited distinguishable distributions inside the channel for both the pre- and post-TMD structures. To illustrate the different charge distributions, we plotted the time-averaged ion density in a plane passing through the channel axis. In both pre- and post-TMD structures (Fig. 3, left and right), cations achieved high concentrations in chambers 1 and 3, as indicated by the predominantly red color, but chamber 2 in the post-TMD model had a higher cation concentration than that of the pre-TMD model. The distributions of cation density are consistent with our previous all-atom MD simulations showing that cations paused for extended periods at each of a series of rings of negatively charged residues along the ion translocation pathway (15). By contrast, anion density remained low in both the pre- and post-TMD models. Considering that the nAChR is a cation-selective channel, it is not surprising to observe high concentrations of cations at both ends of the channel where negatively charged residues are enriched. However, a gap between chambers 2 and 3 in cation distribution is observed in both models, suggesting that cations cannot easily pass through the narrowest constriction under normal ionic conditions without a transmembrane potential. In fact, our previous all-atom MD simulations showed that cations can pass through the channel under external voltage biases (15).

Figure 3.

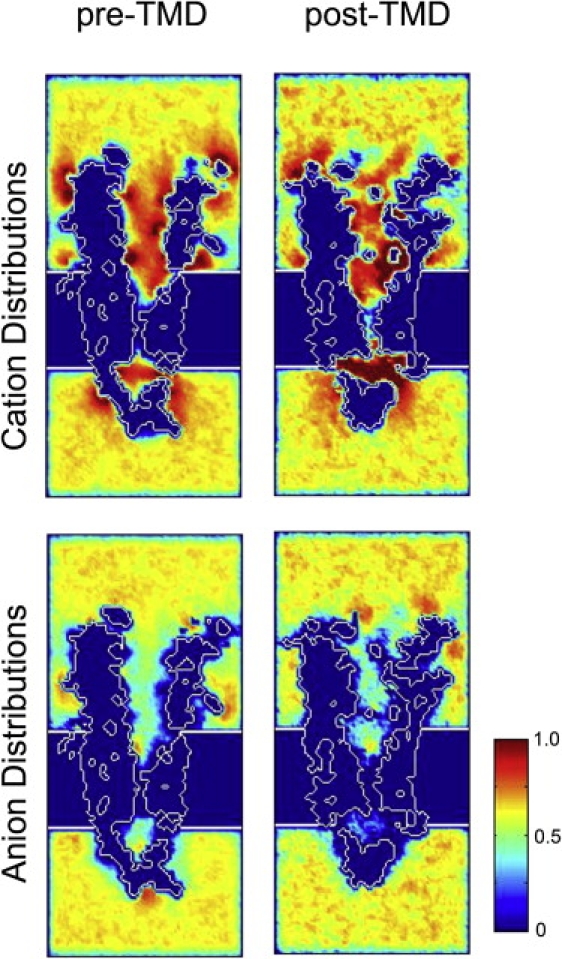
Time-averaged ion distributions. In both pre-TMD (left) and post-TMD (right) models, cations achieved high concentrations in chambers 1 and 3 (see Fig. 2), but in the post-TMD model chamber 2 has a higher cation concentration than in the pre-TMD model. By contrast, anion density remains low in both the pre- and post-TMD models.

Current-voltage relationship

To examine current-voltage relationships for the pre- and post-TMD models, we added external voltage biases, with depolarized potentials of +100 mV and +200 mV, and hyperpolarized potentials of −100 mV and −200 mV. Comparisons between the two models are shown with the corresponding time-averaged electrostatic potentials and cation/anion distributions (Fig. 4). The top row shows electrostatic potential distributions for each simulation in which the reference potential in the extracellular compartment is set to zero. The net transmembrane voltage can be seen by comparing the colors in the extra- and intracellular compartments. The second and third rows display the density distributions of cations and anions, respectively. Of particular interest, in the cation distributions of the post-TMD model, the gap between chambers 2 and 3 disappeared when a hyperpolarized potential was applied, suggesting that ion conduction occurred.

Figure 4.

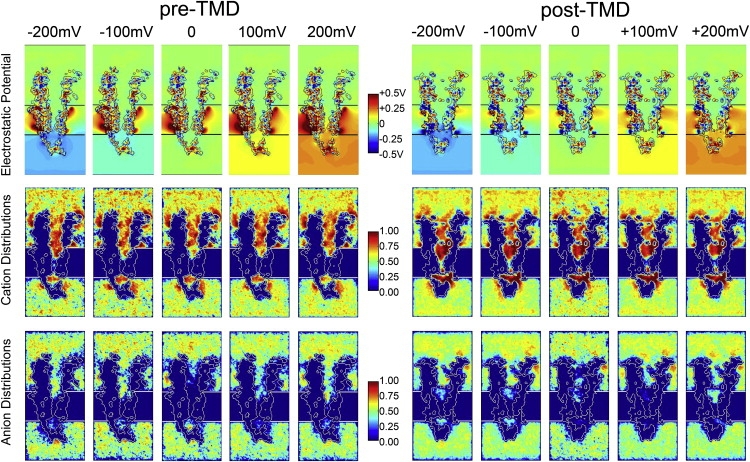
Effects of transmembrane voltage. The top row shows electrostatic potentials for each simulation computed using BioMOCA. The net transmembrane voltage difference is shown by the difference in color between extra- and intracellular compartments. The second and third rows show density distributions of cations and anions, respectively. Note that in the post-TMD simulation, cation density increases in the narrow region of the channel.

The overall results are compiled in the upper half of Table 1, which contains observed translocation events for Na⁺, K⁺, and Cl⁻ (here “−” indicates inward ion movement (from extracellular to intracellular), and “+” indicates outward ion movement). For the pre-TMD structure, ion translocation is infrequent and corresponds to a small net current (1–2 pA). For the post-TMD structure, however, ion translocation increases and corresponds to a much larger current (2–14 pA, depending on the applied potential).

Table 1.

Results of 500 ns BioMOCA simulation without divalent cations

Model	DE	Pre-TMD					Post-TMD
Voltage/mV	80	−200	−100	0	+100	+200	−200	−100	0	+100	+200
Na+	80	−6	—	—	—	—	−42	−13	—	—	+2
Cl−	80	—	—	—	−2	−1	—	—	—	—	—
K+	80	—	—	—	+2	+2	−1	0	+1	+7	+19
Current/pA	80	−1.92	0	0	1.28	0.96	−13.67	−4.13	0.32	2.22	6.73
Na+	60	−2	−1	—	—	—	−30	−8	—	−1	+3
Cl−	60	—	−1	—	—	−2	—	—	—	—	—
K+	60	—	—	—	—	+2	0	−1	−1	+7	+17
Current/pA	60	−0.74	0	0	0	1.28	−9.60	−2.88	−0.32	1.92	6.41

Numbers of observed translocation events are listed for each ion (Na⁺, K⁺, and Cl⁻); here “−” indicates inward ion movement (from extracellular to intracellular), and “+” indicates outward movement. Currents were calculated from the net charge transferred divided by the simulation time.

DE, delectric constant of water.

To examine the effects of the choice of dielectric constant on the results, we performed additional BioMOCA simulations using 60 as the dielectric constant of water (Table 1, lower half). For the pre-TMD structure at negative potentials, the lower dielectric constant gives rise to much smaller net currents. At positive potential, the net currents for both the pre- and post-TMD structures are similar for both 60 and 80. Moreover, the current amplitude for the pre-TMD structure remains much lower than that for the post-TMD structure. A significant difference still remains in the net current between the pre- and post-TMD structures. In subsequent computations, we used 80 as the dielectric constant of water.

Fig. 5 plots current amplitude versus voltage for the post-TMD simulations (open squares). The current-voltage relationship is linear in both inward and outward directions. A bend is observed near the reversal potential at ∼0 mV, so we fitted two straight lines to the data corresponding to negative and positive potentials; at negative potentials the slope conductance is 69 pS, whereas at positive potentials the slope conductance is 32 pS. The reduced conductance at positive potentials, known as inward current rectification, was previously reported from single-channel recordings of currents through nAChRs (40–42).

Figure 5.

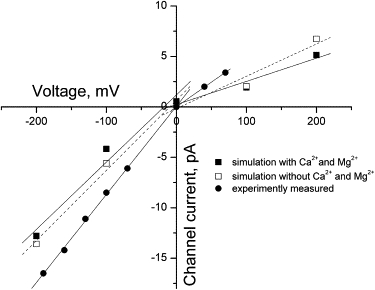
Current-voltage relationships. Experimentally measured single-channel current amplitudes (solid circles) are plotted against membrane potential. Simulated single-channel current amplitudes are taken from Table 1, without divalent cations (open squares), and Table 2, with divalent cations (solid squares). Straight lines are fitted to the data at positive and negative membrane potentials. The slope of each line gives the unitary conductance for each condition (see text).

To directly compare the simulation results with data obtained experimentally, we used the patch-clamp to determine the single-channel current amplitude for the wild-type human nAChR expressed in the 293 HEK cell line (see Materials and Methods). The measured channel conductance is 84 pS at negative potentials and 40 pS at positive potentials (Fig. 5, solid circles). Thus, the simulated single-channel conductances at negative and positive potentials are ∼80% of those measured experimentally. However, the ratio of inward to outward conductance is the same for both simulation and experiment.

Effects of divalent cations

Divalent cations such as Ca²⁺ and Mg²⁺ reduce the single-channel conductance (40,43,44), presumably because they interact more strongly than monovalent cations with the negative electrostatic field in the channel vestibule. To examine whether such a screening effect by divalent cations can be detected in BioMOCA simulations, we included Ca²⁺ and Mg²⁺ ions in both the extra- and intracellular solutions (see Materials and Methods). With Ca²⁺ and Mg²⁺ included, the slope conductance is reduced to 61 pS at negative potentials and 28 pS at positive potentials, both of which are ∼12% less than observed without divalent cations (Table 2; Fig. 5, solid squares).

Table 2.

Results of 500 ns BioMOCA simulation with divalent cations included in the solution (see Materials and Methods)

Model	DE	Pre-TMD					Post-TMD
Voltage/mV	80	−200	−100	0	+100	+200	−200	−100	0	+100	+200
Na+	80	−4	−4	—	—	+1	−41	−8	−2	+2	+6
Cl−	80	+1	—	—	−3	−1	—	—	—	—	—
K+	80	—	—	—	—	+1	−2	—	—	+4	+10
Current/pA	80	−1.60	−1.28	0	0.96	0.96	−13.7	−2.6	−0.64	1.92	5.13

Numbers of observed translocation events are listed for each ion (Na⁺, K⁺ and Cl⁻); here “−” indicates inward ion movement (from extracellular to intracellular), and “+” indicates outward movement. Currents were calculated from the net charge transferred divided by the simulation time. Translocation of divalent cations was not observed.

DE, delectric constant of water.

These simulations recapitulated several properties characteristic of the nAChR: cation selectivity, single-channel current amplitude, inward current rectification, and screening by divalent cations. Furthermore, the simulated single-channel conductance was similar to that obtained experimentally. The success of the simulation results may be partly fortuitous because several factors could impact the simulations, including the missing part of the intracellular domain, imperfect methodology used in TMD simulation, simplifications inherent to BioMOCA simulations, and the use of static rather than dynamic structures. These factors are discussed below.

First, the cryo-EM structural determination of the Torpedo nAChR could not resolve a major portion of the cytoplasmic domain, which contains residues that contribute to channel conductance (42,45,46). Furthermore, in the prokaryotic proton activated channel, with 20% homology to the nAChR and without an intracellular domain, the measured channel conductance is only 8 pS (47). On the other hand, detection of small numbers of cations and anions in the pre-TMD model highlights a potential limitation of the Torpedo nAChR structure used as a template for homology modeling in this work, namely, the functional state of the cryo-EM Torpedo structure. There are two possible explanations for the low but detectable ion translocation in the pre-TMD model: the receptor's resting state may not be absolutely closed to ions, or the cryo-EM structure may not precisely depict the resting state. We are unable to distinguish between these possibilities on the basis of our findings. Nevertheless, anion translocation was not detected in the post-TMD model, further implying that the open-like structural model is reliable.

Second, the accelerated method of TMD simulation may not be an ideal way to generate an open-state structural model. Force was applied to the C-loop to mimic the effect of agonist binding. Without knowledge of the AChR structure in the open state, the possibility remains that the post-TMD structure could be intermediate between the closed and open states. Indeed, the upper half of the channel of the post-TMD model is slightly narrower than that of the GLIC structure in the apparent open state (Fig. 2 A). That may explain why the simulated single-channel conductance is smaller than observed experimentally. Nevertheless, the TMD simulation provides a plausible hypothesis for the conformational change that underlies transduction of agonist binding into channel opening.

Third, the BioMOCA simulations were applied to static protein structures. Because the receptor protein is not a rigid body but undergoes dynamic motions essential to its function, slight structural differences from different frames of the TMD simulation snapshot may affect the outcome of the simulated single-channel conductance. To overcome this limitation in future work, we can apply BioMOCA to multiple structural frames and obtain an average single-channel current amplitude. The latest software development achieved at the University of Illinois at Urbana-Champaign increases the speed of BioMOCA simulations by 8 to 20 times, which will enable application of BioMOCA to large-scale studies of ion channels.

Finally, the dielectric constant of water inside an ion channel could be much lower than the value under bulk conditions. Using a lower dielectric constant for water could make two contributions to charge transport: the dielectric boundary force and charge-charge interactions. First, when the difference in permittivity between the bulk and protein is reduced, the dielectric boundary force barrier is reduced. However, a drop in this barrier does not necessarily translate to more ion translocation. Second, when ions are less shielded by water, Coulombic forces become stronger, enhancing charge-charge interactions between ions, or between ions in narrow regions of the channel and permanent charges on channel lumen.

In summary, closure of the C-loop at the nAChR binding sites triggers conformational changes of the channel that produce a single-channel conductance similar to that determined experimentally. This combination of all-atom TMD simulation with coarse-grained BioMOCA simulation has potential applications in computational studies of other ion channels, such as GLIC in an apparent open state. As we seek to understand the structure of the biologically active state, it will be essential to determine whether candidate structures conduct cations at the appropriate rate. By using BioMOCA to simulate ion translocation rate and ion selectivity, we can guide future investigations of how agonist binding triggers channel opening. Also, our previous studies predicted that negatively charged residues in the extracellular vestibule contribute to cation selectivity (15). By using BioMOCA simulation combined with virtual side-chain mutations, we can further examine how the structure of the ion translocation pathway impacts channel conductance and selectivity.