Abstract
The mitogen-activated protein kinase cascade is a conserved signal transduction pathway found in organisms of complexity spanning from yeast to humans. In many mammalian tissue types, this pathway can correctly transduce signals from different extracellular messengers, leading to specific and often mutually exclusive cellular responses. The transduced signal is tuned by a complicated set of positive and negative feedback control mechanisms and fed into a downstream gene expression network. This network, based on the immediate early gene system, has two possible, mutually exclusive outcomes. Using a mathematical model, we study how different stimuli lead to different temporal signal structure. Further, we investigate how each of the feedback controls contributes to the overall specificity of the gene expression output, and hypothesize that the complicated nature of the mammalian mitogen-activated protein kinase pathway results in a system able to robustly identify and transduce the proper signal without investing in two completely separate signal cascades. Finally, we quantify the role of the RKIP protein in shaping the signal, and propose a novel mechanism of its involvement in cancer metastasis.
Introduction
One of the most fascinating questions in cellular biology is how a signal transduction network with one or more shared components can accurately transmit multiple independent signals from the cell surface to their proper targets (nucleus, vacuoles, cytoskeletal junctions, etc.). Often, the subcellular localization of the signal target is the same, but the distinct signals elicit very different outcomes. The best studied of this phenomenon is the PC-12 model system (1–3). PC-12 cells are rat-derived neural progenitor cells that can be induced to proliferate upon epidermal growth factor (EGF) stimulation, or to differentiate upon neural growth factor (NGF) stimulation (3). In both cases, the signal is transduced through the mitogen-activated protein kinase cascade (MAPK) of Raf, Mek, and Erk (4,5). While some of the biological details about how this pathway works and how it evolved are still unclear, a general scheme for pathway specificity has been uncovered. When stimulated with EGF, PC-12 cells exhibit a transient spike in Raf, Mek, and Erk activity, which quickly dies out back to background levels. Induction with NGF causes a transient spike similar in magnitude and duration, but in contrast to EGF stimulation, the spike decays only partway, leading to a long-term, stable level of Erk activity many hours after the initial stimulus pulse (3,5). In the presence of an NGF signal, there is a positive feedback force acting from Erk to Raf, stabilizing Raf in its active confirmation (2,3,6). This feedback mechanism is suppressed under EGF signaling. The key mediator of this suppression was identified as RKIP, a known inhibitor of Raf kinase activity (3,6,7). This protein appears to not only competitively block Raf's ability to activate Mek, but also through steric or other forces block Erk's ability to phosphorylate Raf. The working hypothesis is that a secondary signaling pathway is activated upon NGF stimulation, leading to a deactivation of RKIP and hence, enhancement of the positive feedback loop. Several hypotheses concerning the next step of the process, how the immediate early genes (IEG) respond to transient and sustained Erk activity, have also been proposed (8); however, the details of gene expression in response to the IEG activity are not known.
We hypothesize that signal transduction networks are optimized to maintain the specificity of a given signal input in a robust manner. An abstract definition of specificity is given in Komarova et al. (9) to be the ratio of the correct output to the spurious output of a signaling network relative to a given input stimulus. This definition was then applied to several simple network architectures involving multiple inputs and outputs but at least one shared component can be tuned to generate specificity under general conditions on the network connection strengths and the character of the input stimuli. Later work applied these abstractions to networks involving scaffolding and cross-network inhibition (10). These definitions have also been used to analyze the yeast pheromone and stress response pathways (11). In this work, we extend this concept of specificity to include robustness, which we define as a network's ability to properly interpret a wide range of signal input profiles into the proper temporal output.
There is growing interest in investigating more complex mammalian signal transduction pathways using theoretical and computational approaches. The classic Raf-Mek-Erk MAPK cascade has drawn much interest, especially concerning receptor activation (12,13), internalization (14), and cross-interactivity with other networks (15,16). These computationally intensive models have been shown to be robust in their parameterization (17,18). RKIP has been incorporated into several basic MAPK models with the goal of better quantifying difficult-to-measure in vivo interaction parameters (13,19). The MAPK/RKIP system has also been modeled from a stochastic process algebra perspective; however, the biological consequences of the model were not greatly explored (20). Work of a more theoretical nature has focused on ideas of specificity within pathways with shared components. The work of Behar et al. (21) demonstrated the concept of kinetic insulation, based on adaptive feedback mechanisms (22), in which two sets of enzymatic reactions upstream of a single shared component interpret a signal for transduction by transforming that signal into a specific temporal and kinetic profile. Ueda and Shibata investigated a simple stochastic model of the chemotactic sensing mechanism of Dictyostelium to quantify the roles of different sources of noise in signaling processes, and to uncover regimes of optimal signal/noise transduction (23).
In this work, we formulate and investigate a mathematical model of both the major proteins involved in the MAPK cascade (Raf, Mek, Erk, and RKIP) and the downstream gene expression network that the cascade activates. We explore how the output of the MAPK cascade ensures specificity of the IEG network in a robust manner. This expression network is represented by the canonical IEG protein Fos and the two potential cell fate programs it can activate, proliferation and differentiation. We hypothesize a simple network architecture in which the differentiation program can inhibit the proliferation program and show that under proper stimulation input, based on biological observations, this network is specific for both outputs.
We further explore how RKIP controls the long-term dynamics of MAPK activity and demonstrate how each of the control mechanisms contributes toward the specificity of the network. These numerical experiments generate predictions that can be translated into experimental studies. Our results indicate that this network is designed to prevent fluctuations in the temporal nature of the input signal from spuriously activating the improper pathway without the need to invest in two separate pathways. We also discuss this hypothesis in the context of dysfunction of the control mechanisms brought on by mutation and its consequences for aberrant signal pathway behavior.
Model Formulation
MAPK cascade
The classic mammalian MAPK cascade involves a signal transduced from a cell membrane receptor, such as a receptor tyrosine kinase, to a membrane-associated intermediate, and on to a series of protein kinases (24,25). These kinases act in a sequential manner, each one activated by the kinase directly upstream of itself and in turn activating the next. The canonical pathway involves three kinases, Raf, Mek, and Erk (see Fig. 1). We base this model on the work summarized in Santos et al. (3). Raf is activated by the small GTPase Ras upon proper upstream stimulation. Raf phosphorylates Mek, which then phosphorylates Erk, which upon translocation into the nucleus activates a number of transcription factors important in IEG expression. Each enzyme is inactivated by ubiquitous phosphatases found throughout the cytoplasm. While the general orientation and flow of signal information through this pathway has been well established, recent work has also illustrated several important feedback control mechanisms in this pathway. Firstly, active Erk has an inhibitory effect on the signaling scaffold built around the original receptor tyrosine kinase, and thus will attenuate signal flowing from the extracellular space even if the extracellular messenger remains for a protracted period. Secondly, under certain stimuli, Erk shows a stabilizing effect on Raf activity. This stabilizing effect is neutralized by the presence of a known inhibitor of Raf, RKIP; the hypothesis therefore is that particular signaling events lead to a decrease in RKIP levels or activity, thus enhancing the feedback stabilization of Raf activity by Erk.
Figure 1.
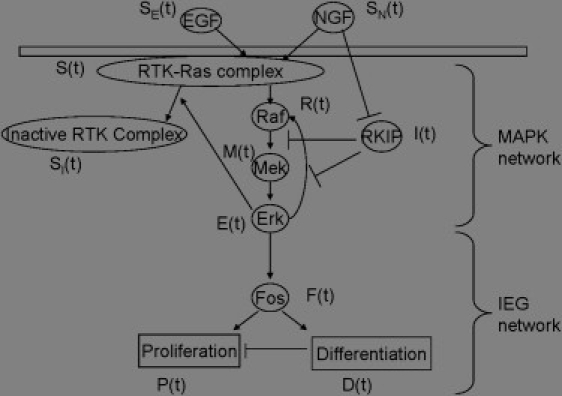
Schematic diagram of the MAPK cascade and IEG expression network.
To model this pathway, we make the following assumptions. Firstly, we assume Michaelis-Menten enzyme kinetics govern flow of signal information down the pathway, as well as any inhibitory mechanisms which block the flow of signal. We also assume there are finite concentrations of total Raf, Mek, and Erk available for activation, and so the pathway is limited in its ability to continuously amplify a signal. We also assume there is a finite amount of upstream transduction machinery with a single limiting member. We list each of the state variables for this system in Table 1.
Table 1.
State variables for the MAPK-IEG network model
| Component | Variable |
|---|---|
| Active receptor complex | S(t) |
| Disabled receptor complex | SI(t) |
| Active Raf fraction | R(t) |
| Active Mek fraction | M(t) |
| Active Erk fraction | E(t) |
| RKIP protein level | I(t) |
| c-Fos protein level | F(t) |
| Proliferation program level | P(t) |
| Differentiation program level | D(t) |
Extracellular signal is input into the system in the form of time-dependent functions SE(t) and SN(t). These functions represent the extracellular concentrations of EGF (SE(t)) and NGF (SN(t)) in the PC12 system (3). The only functional difference between them is that the SN(t) signal involves the secondary signaling mechanism, which inactivates the RKIP inhibitor (see Fig. 1). Both signal inputs activate upstream signaling machinery at the same rate, dependent upon the amount of inactive but competent transducer available (Eq. 1 below). Active transducer S(t) in turn activates Raf (R(t), Eq. 3) and decays back into inactive but available transducer via a first-order process. S(t) can also be inactivated by the presence of active Erk (E(t)); however, this inactivation event renders it into a form, SI(t), incompetent to become active again for a period of time longer than the signal events under consideration (Eq. 2). Active Raf converts inactive Mek (M(t), Eq. 4) into its active form, and likewise Mek converts inactive Erk to its active form (Eq. 5).
Finally, we assume the presence of an inhibitory molecule, I(t), taken to be RKIP or an associated protein (Eq. 6). This protein interferes with the pathway at two points. Firstly, it blocks Raf from activating inactive Mek. Secondly, it sequesters active Raf and thus prevents active Erk from stabilizing it (6,7). These effects, while dependent upon the same physical binding event, are separable from a modeling perspective. Based on recent studies (3), this protein can be inactivated by stimulation by NGF, one of the two principal input mechanisms in the system (represented here by SN(t)). As in receptor resensitization after inactivation, we do not consider new inhibitor synthesis, as this will occur on a timescale longer than those under study.
The full system of equations governing the dynamics of the MAPK cascade is
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
The model is nondimensional, with each variable describing the fraction of each enzyme in the signal cascade that is active, and with time normalized to the rate of signal input into the system. Following with the Michaelis-Menten kinetics assumption, the action of the inhibitor will modify the Michaelis-Menten rate equation with the form . We nondimensionalize the inhibitor concentration by its binding affinity, which leads to the functional terms (1 + I)KR and (1 + I)KM seen in Eqs. 3 and 4, respectively. Parameters and their values are listed in Table 2.
Table 2.
Parameters for the MAPK network model
| Parameter | Role | Value | Reference |
|---|---|---|---|
| ds | Upstream signal inactivation rate | 2 | Estimate |
| ɛ | Erk-mediated upstream attenuation factor | 1 | Estimate |
| ks | Receptor-mediated Raf activation rate | 1 | (14) |
| kR | Erk-mediated Raf activation rate | 1.5 | (14) |
| kM | Raf-mediated Mek activation rate | 2.9 | (14) |
| kE | Mek-mediated Erk activation rate | 5.7 | (14) |
| KR | Michaelis-Menten constant for Erk-Raf interaction | 1.5 | (14,28) |
| KM | Michaelis-Menten constant for Raf-Mek interaction | 0.01 | (14) |
| KE | Michaelis-Menten constant for Mek-Erk interaction | 0.05 | (14) |
| dR | Raf inactivation rate | 1 | Estimated from Schoeberl et al. (14) |
| dM | Mek inactivation rate | 2 | Estimated from Schoeberl et al. (14) |
| dE | Erk inactivation rate | 2 | Estimated from Schoeberl et al. (14) |
References are provided for parameters when available; otherwise parameters are marked as estimates. Representative values used in simulations are provided as well.
IEG expression network
The second module consists of the gene expression cassettes induced by the transient and long-term activity of the MAPK cascade (see Fig. 1, lower portion). The principle gene product under consideration is c-Fos (F(t), Eq. 7), a member of the IEG family of transcription factors. These genes are quickly induced by Erk activity. Once translated, the proteins typically have a very short half-life, and their levels quickly fall back to background. However, in the presence of sustained Erk activity, IEG gene products become stable, leading to long-term transcription activation activity and a secondary set of gene products being induced. This secondary set of genes activates a separate cell fate program, suppressing the activity of the first program. We take as our model system the PC-12 neuronal differentiation model, and therefore the competing outcomes are proliferation (P(t), Eq. 8) and differentiation (D(t), Eq. 9). We assume F(t) is induced linearly by active E(t) and decays via a first-order process; likewise, the cell fate products are induced linearly via F(t) and decay with first-order kinetics. In addition, we assume that the activity of the differentiation program, D(t), is able to suppress the activity of the proliferation program. This assumption is based on the mechanisms of cell-cycle arrest in differentiation found in the literature (26,27) while maintaining the idea that P and D are the net activities of the respective programs, and not any one representative effector. If we assume E(t) follows the dynamics described above, then the model for the second module is
| (7) |
| (8) |
| (9) |
Parameters for this module are listed in Table 3.
Table 3.
Estimated parameters for the IEG network model
| Parameter | Role | Estimated value |
|---|---|---|
| kF | Erk-mediated Fos production rate | 1 |
| dF | Fos inactivation rate | 1.5 |
| kP | Fos-mediated proliferation induction rate | 10 |
| dP | Proliferation program inactivation rate | 1 |
| kD | Fos-mediated differentiation induction rate | 0.04 |
| dD | Differentiation program inactivation rate | 0.01 |
| δ | D-mediated P inhibition factor | 10 |
Specificity
We define specificity as in the literature (9,10), in which the specificity of a pathway relative to a given input is the total amount of proper pathway output divided by the spurious pathway output. We introduce the notation that PE(t) is the amount of proliferation product at time t in response to the SE(t) signal; likewise, PN(t) is the amount of proliferation product in response to the SN(t) signal. Then the specificity of the pathway in response to an EGF stimulus is
| (10) |
while in the presence of NGF, the specificity is
| (11) |
We will also use the idea of mutual specificity in analyzing this pathway. Mutual specificity of degree k is defined as the regime of possible architectures (inputs and connection strengths) in which all possible outputs of a pathway with shared components demonstrate specificity >k (9).
Simulations
All simulations were performed in MATLAB R14 (The MathWorks, Natick, MA) using the ODE15s integrator. Simulations were computed to Tf = 100 min post signal input time. For the given input signal,
with some value of signal strength S0 and duration T0, then the specificity SP is
and likewise for a SN(t) input. Specificities (Figs. 2, 4, and 8–10) were computed numerically by integrating the complete time series solutions according to the definitions in Bardwell et al. (10) using the MATLAB quadl function. For Fig. 5, T1 is measured as the width of the primary peak at half-height above the long-term steady-state value of F. In Fig. 6, F1 is computed as the average value of the F signal up to the computed T1 point. And, in Fig. 7, F2 is the steady-state height of the F signal past the peak (be it zero or nonzero). T2 is the difference between the duration of the input signal and T1.
Figure 2.
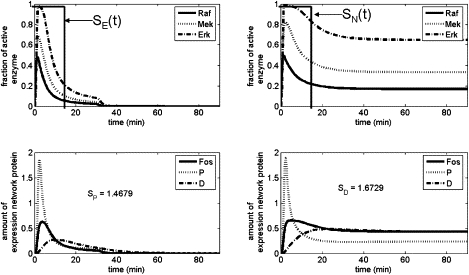
Representative simulations of the MAPK model (top row) and IEG network (bottom row) with SE(t) (left) or SN(t) (right) stimulation input. Computed specificity (Eqs. 10 and 11) of each IEG network output is included. Both input pulses are of magnitude 1 and duration 15 min.
Figure 4.
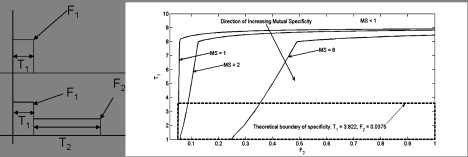
Comparison between numerically determined specificity and the strict analytic bound for various initial pulse durations and pulse amplitude ratios. (Left) An idealized schematic representation of the two observed temporal profiles of c-Fos. The upper plot shows c-Fos dynamics under a typical EGF input signal, in which the protein is quickly induced and then quickly falls back to baseline; whereas the lower plot shows c-Fos dynamics after a typical NGF signal, in which the protein is quickly induced and then falls to a long-term intermediate level before returning to baseline. (Right) Contours of network specificity levels subject to the constraint that mutual specificity is >1 are plotted, along with the region determined by conditions 12 and 13. Parameters as listed in Table 3.
Figure 8.
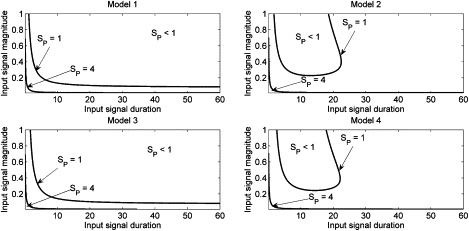
Specificity of the model networks in response to the SE(t) input signal. Parameters as in Tables 2 and 3, except as noted in Table 4.
Figure 9.
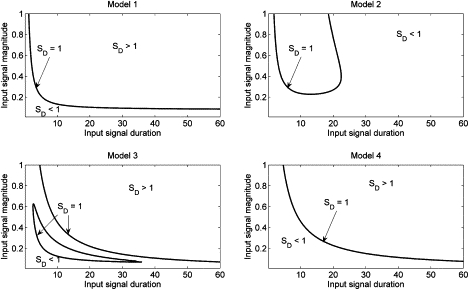
Specificity of the model networks in response to the SN(t) input signal. Parameters as in Tables 2 and 3, except as noted in Table 4.
Figure 10.
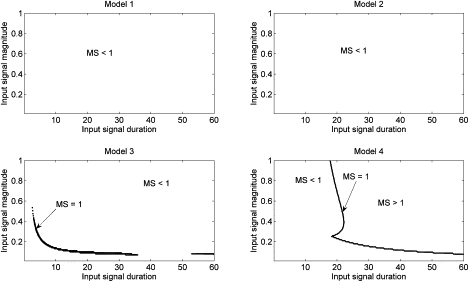
Network specificity in regions of mutual specificity for IEG output of MAPK pathways. Parameters as in Tables 2 and 3, except as noted in Table 4.
Figure 5.
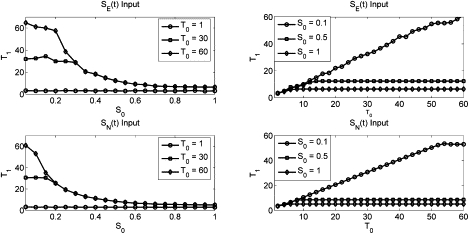
T1 duration as computed from the MAPK model as a function of input signal strength for specified signal durations (T0) (left column) or of input signal duration for specified signal strengths (S0) (right column) of SE (top row) or SN (bottom row) input.
Figure 6.
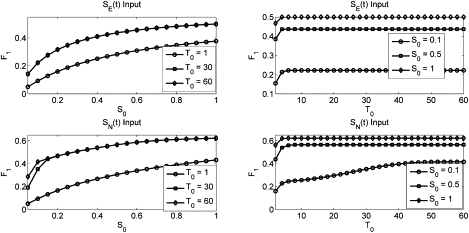
F1 magnitude as computed from the MAPK model as a function of input signal strength for specified signal durations (T0) (left column) or of input signal duration for specified signal strengths (S0) (right column) of SE (top row) or SN (bottom row) input.
Figure 7.
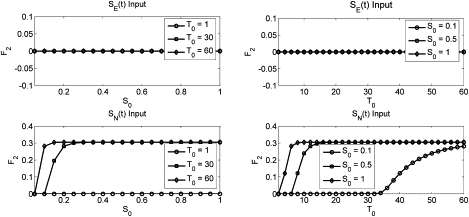
F2 magnitude as computed from the MAPK model as a function of input signal strength for specified signal durations (T0) (left column) or of input signal duration for specified signal strengths (S0) (right column) of SE (top row) or SN (bottom row) input.
The MAPK cascade
The temporal signal structure
Representative simulations of the complete model, Eqs. 1–9, are shown in Fig. 2 for SE(t) and SN(t) input, along with plots of the resulting P(t) and D(t) production and the computed specificity for each case. All simulations were performed using the ODE15s solver routine from MATLAB.
As is observed experimentally, upon SE(t) stimulation there is a transient rise in MAPK activity levels, which then decay back to background levels. This transient spike induces sharp production of the P(t) genetic program and only lesser amounts of the D(t) program, leading to specificity favoring the former. In the case of SN(t) induction, the transient spike is still observed; however, it decays only partially and settles instead into a long-term sustained activity level. This long-term activity is successful in switching the specificity of the downstream expression network to favor the D(t) product.
The twofold role of RKIP in shaping the output signal
We first study numerically how changes in the inhibitor level affects the long-term dynamics of the Erk signal. We adjust the model slightly by treating the inhibitor as a constant and perform a bifurcation analysis (i.e., we remove Eq. 6 from the system and instead treat I(t) ≡ i). The results of this analysis are shown in Fig. 3. Since there are, in principle, two mechanisms of control, even though they are linked by a single binding event, we investigate the effects each one has independent of the other on the system, and then we combine them. As seen in Fig. 3, the RKIP effect of sequestration of Raf is far more important from the standpoint of long-term Erk signal suppression than interruption of the signal flow from Raf to Mek. Moreover, combining the two mechanisms leads to only a very modest improvement in signal suppression. Thus, we hypothesize that the two-phase nature of the system evolved around the steric inhibitory effects the large molecule inhibitor RKIP has on Raf kinase, and that direct Raf-to-Mek signal interruption by RKIP is important in other contexts.
Figure 3.
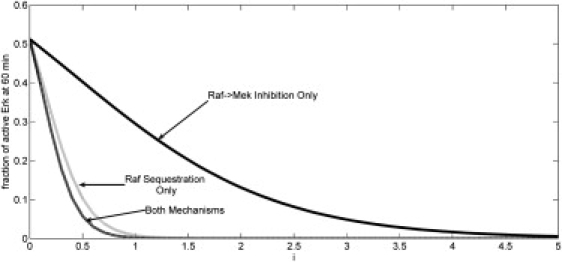
Steady-state magnitude of E(t) as a function of inhibitor (i) level. Plots represent a purely forward inhibitory role, a purely feedback sequestration role, or both mechanisms (as marked).
We can gain insight into the cause of the disparity between these two control mechanisms by studying the steady-state equations for the MAPK pathway. Since there are no control mechanisms acting directly upon Erk, we make the same approximation as before (the linear approximation to Michaelis-Menten kinetics and the quasi-steady state assumption), and thus, have nonlinear steady-state equations for Raf and Mek only,
These equations seem, at first glance, nearly symmetric, and thus, one might expect each of the two control points to exert equal influence on the pathway outcome. However, the symmetry is broken by the nondimensional parameters KR and KM. While each enzyme in question, Erk and Raf, have similar affinities for their targets, the large disparity in expression number between the substrates implies KR >> KM. In particular, it has been observed that the kinetic parameter values for Raf, Mek, and Erk are nearly the same (28). On the other hand, the abundance of the Raf protein is much lower relative to that of Mek and Erk (14). Therefore, the value for the scaled parameter KR is much higher relative to the others. Thus, a similar amount of inhibitor will be able to change the dynamics of the Raf stabilization reaction to a much greater extent than the Mek activation reaction. This leads us to the hypothesis that RKIP's role in the modulation of Erk's long-term dynamics evolved separately from its role as a direct inhibitor of Raf activity.
IEG network driven by the MAPK pathway
Specificity in the IEG network
We begin by analyzing the potential specificity mechanisms of the gene expression network relative to the temporal activation profiles observed in the in vitro experiments. A network with a similar basic architecture was analyzed previously (10). It was found that mutual specificity could be attained when the stimuli were simple square pulses whose durations were longer than the timescale of inactivation for each network member. This assumption allowed the authors to make a quasi-steady-state approximation on the levels of active network elements and derive specificity criteria based on the model parameters. We now extend this analysis to consider a biphasic input pulse similar to that produced by the upstream MAPK cascade.
The gene network receives two distinct input signals: a transient spike that decays quickly to zero, induced by EGF; and a similar transient spike that decays quickly to a nonzero, long-term active state, induced by NGF. These signal inputs can be represented qualitatively by a combination of square-wave pulses. Both situations involve a pulse of amplitude F1 and duration T1. In the EGF case, this is the only signal input into the expression network. However, in the NGF case, there is an additional square-wave pulse of amplitude F2, which terminates at time T2. We make the restrictions that F1 > F2 and T2 – T1 > T1; that is, the first signal pulse is strong, but of much shorter duration, than the second (see Fig. 4, left panel).
It is not possible to compute the integrals in the definition of specificity analytically for the equations given for the IEG network. However, we can compute bounds that can be useful for defining regimes in which specificity for both pathways is possible. We first consider the specificity of the EGF signal (Eq. 10). For a given square-wave input pulse, we can directly compute from Eq. 9 that . Since F1 > 0 only when t < T1, the maximum value for D(t) is . Substituting this value into Eq. 8 in place of the D(t) nonlinearity yields a linear equation. We can then compute the total amounts of each network output and determine the specificity to be
Rearranging this condition under the goal of specificity >1 yields
| (12) |
We perform a similar analysis in the context of the two-step signal, to yield the following condition for specificity (Eq. 11):
This condition is cumbersome, but under the assumptions that T2 >> T1 and F1 = 1 (that is, we normalize the first signal pulse), it reduces to
which we can rearrange to yield a condition to provide specificity >1:
| (13) |
We can combine Eqs. 12 and 13 into a single compatibility condition for mutual specificity for both pathways under both input regimes:
| (14) |
Thus, we obtain an upper bound for the duration of the initial, high intensity pulse as a function of the lifetime of the D class gene products and the ratio of the amplitudes between the initial and long-term signal inputs. Also note that if F2 = 0, mutual specificity is impossible; this is very reasonable, as the D program is designed to gain specificity only in the presence of the second pulse.
Since these bounds were derived by making stricter assumptions than necessary, we compare the analytic condition required for mutual specificity to a numerical experiment in which the first pulse time, T1, and ratio of second to first pulse amplitude, , are varied for fixed values of δ, dD, and . These results are summarized in Fig. 4. In this figure, we present a contour plot of the network specificity, S = SPSN, in regimes of mutual specificity, SP > 1 and SN > 1. In regimes without mutual specificity, we set network specificity to 0 for contrast. We also plot the theoretical bounds for T1 and F2 determined under the strict assumptions discussed in the preceding section.
As seen in Fig. 4, the system exhibits mutual specificity in a regime bounded above by T1 ∼10 for a wide range of . The analytic bound on F2 is very accurate, whereas the bound for T1 is much stronger than necessary, which is to be expected given the assumptions made to compute it. However, the results clearly indicate the need to bound the duration of the high intensity pulse so that specificity may be achieved. We also observe how T1 and F2 relate in providing for mutual specificity for P(t) and D(t) output. We see that, up to a threshold for T1, mutual specificity for a system with fixed T1 can be increased by increasing F2 (which provides more input strength into the D program). Conversely, for a system with fixed F2, mutual specificity can be increased by decreasing T1 (which more clearly delineates the separation between P and D).
Given these conditions, we can now return to the model of the MAPK pathway, and investigate how the complex connections affect the key parameters, which themselves determine specificity. We consider the full model introduced above, and perform numerical experiments to study why such a complex interweaving of control systems may be necessary by removing key feedback control loops and assessing their impact.
The role of input signal strength and duration in shaping c-Fos dynamics
Equation 14 shows how the magnitude and duration of the two input pulses into the IEG expression network effect the mutual specificity of the network output. We next explore how factors that are controllable in the in vitro laboratory experiments, namely the strength and duration of exposure to the extracellular messengers, affect the signal inputs into the gene expression system. We measure the magnitude of the transient and long-term F(t) signals, and compute the duration of the F1 phase as the width of the transient peak at half-height above the steady-state F(t) magnitude. (We experimented with different methods to obtain F1 and T1 and found no qualitative differences in the results. F1 can also be computed by taking it to be the maximum value of the initial F signal peak, and then T1 by approximating the area under the F peak as a rectangle with height F1 and width T1. These results were virtually identical to those given in the text.)
We first study the impact of extracellular signal strength and duration on the duration of the initial c-Fos expression pulse, T1. The results of this experiment are found in Fig. 5. The simulation demonstrates that the system's intrinsic shutdown mechanism, presumed to be caused by the negative feedback loop from Erk to the receptor complex, is strongly dependent upon the magnitude of the incoming signal, and that a threshold amount of stimulus must be exerted to activate it. Further, there is little distinction between the two input stimuli, implying the duration of the initial IEG expression burst is independent of which receptor has been activated.
The magnitude of the Fos transient under both SE(t) and SN(t) stimulation is shown in Fig. 6. This response is surprisingly insensitive to input duration, suggesting the upstream machinery becomes quickly saturated upon stimulation. The system also displays saturation kinetics as a function of input magnitude. We note that the SN(t) signal allows for a steeper climb to threshold as a function of input magnitude than the SE(t) input, and the steepness is itself time-dependent. This is likely due to the slow degradation of RKIP caused by the SN(t), but not SE(t), signal.
As shown in Fig. 7, no combinations of input signal duration or strength allow the SE(t) signal to generate a long-term Fos signal, in accordance with experiments. Moreover, even at high input strengths, there is a minimum signal time necessary for the SN(t) input to generate a long-term Fos response. This correlates very well with the observation that, in PC-12 cells, the NGF-specific signal profile can be disrupted by interfering with its receptor, but only up to a critical time point; after this time, the NGF signal pattern is established and further loss of the receptor or extracellular signal does not collapse the internal response.
Robustness of the MAPK-IEG network
We next explore the relative contributions to mutual specificity each feedback control mechanism provides to each input signal. We investigate three possible modifications to the MAPK model, by removing the positive feedback loop from E to R (kR = 0), removing the negative feedback loop from E to S (ɛ = 0), or both. We summarize the characteristics of these four models in Table 4.
Table 4.
Listing of alternate models to the system of Eqs. 1–9
We numerically simulated each of these four possibilities over a wide range of extracellular messenger stimulation strengths and times, to assess regimes of input signal in which each achieves both maximum individual specificity as well as maximum mutual specificity for the network. Since both stimuli activate the same pathway, we seek to measure what role, if any, the dynamic nature of the stimulus input has in determining the pathway output. Pathways in which the temporal nature of the stimulus (i.e., signal strength and magnitude) can itself strongly determine the outcome without regard to the identity of the stimulus will be very sensitive to fluctuations in the extracellular messenger. Individual output specificities for each model network are shown in Figs. 8 and 9 for the SE(t) and SN(t) inputs, respectively.
Fig. 8 clearly demonstrates that the Erk-to-Raf positive feedback plays no role in properly interpreting the SE(t) signal (compare models 2 and 4). However, loss of the Erk to S negative feedback (models 1 and 3) severely limits the ability of the system to transduce a wide range of SE(t) stimuli. Loss of this mechanism leads to a decrease in specificity during long duration stimulation for all but very weak signal stimuli, which implies a spurious long-term Erk signal is being generated and thus, forcing the IEG network toward the differentiation output.
As seen in Fig. 9, all models also show a lower bound for input duration necessary for proper signal integration, in accordance with the biological literature. Loss of the Erk-mediated receptor attenuation mechanism (models 1 and 3, respectively) both enhances the specificity of the SN(t) input and allows for a broader range of properly interpreted input signals. However, comparisons between Figs. 8 and 9 for models 1–3 show minimal regions of overlap between their respective areas of high specificity for each signal input.
The results for model 1 also confirm the analysis performed earlier on a network with the same architecture as the IEG system here (10). In their steady-state analysis, the authors found mutual specificity could be attained in this system only if two different types of input stimuli were considered: one long but weak, the other strong but short. Since the MAPK network presented here without any feedback mechanisms (i.e., model 1) merely serves as an amplifier that responds to each input source equally, we expect specificity to depend entirely on the temporal nature of the input signal, and for mutual specificity, to a single type of input from both sources (same strength, same duration) to be incapable of ever providing mutual specificity.
This result is more apparent in an analysis of the total network specificity, shown in Fig. 10. Here too we plot the specificity of the full MAPK-IEG network only in regions of mutual specificity. The role of the feedback mechanisms is striking. The systems with no positive feedback (models 1 and 2) show no mutual specificity at all, while model 3 shows an extremely small regime of mutual specificity. Conversely, the full MAPK model gives mutual specificity >1 over a vast range of possible input strengths and durations. It indicates a minimum signal strength and duration necessary for both pathways to be specific, in accordance with the F1 and T1 studies presented above. Thus, we hypothesize that the feedback control mechanisms allow the system to properly interpret the nature of the input signal by greatly reducing the impact any fluctuations in signal delivery may have on the downstream pathways, without the need to maintain two completely separate pathways. Mutual specificity implies that there is a regime of input signal dynamics for which the proper signal is transmitted without excess spurious output. Thus, the mechanisms ensure that a long EGF signal that acts like an NGF signal does not induce an NGF response; only the character of the signal (EGF versus NGF) is important.
Fig. 10 shows the boundaries for mutual specificity for signal inputs of identical dynamics (i.e., strength and duration) but different nature (i.e., EGF versus NGF). Our hypothesis is in part that the various feedback mechanisms could at least partially insulate the system from temporal variations in the original input signal. Comparing the lower-left and upper-right panels of Figs. 8 and 9 show this is the case: in the presence of a fully functional feedback system, the P program gains specificity even under protracted signal inputs at the cost of specificity for the D program only over a small regime of short signal input. Taken together, these simulations show that the feedback system provides a measure of insensitivity to dynamics of the input signal.
While Fig. 10 demonstrates how loss of any of the control mechanism completely ablates specificity in the system, it is also important to note that the data in Fig. 4 coupled with Figs. 5–7 clearly demonstrate that the system has higher specificity. Fig. 5 shows the how the mutual specificity of the IEG system depends on the temporal structure of its input (via c-Fos), and yields a large regime of mutual specificity of ∼6 or greater; while Figs. 5–7 demonstrate how input into the MAPK system determine the structure of the c-Fos response. In general, mutual specificity is increased with longer input pulses, which allows the D(t) program to more clearly distinguish itself from the P(t) program.
Discussion
The central questions in qualitatively analyzing the mammalian MAPK cascade are how the cell maintains the integrity of the pathway when it is used in transducing very different signals, and how differences in activity states of the pathway in response to different stimuli can lead to very different genetic responses. In this work, we have shown how a single pathway with one auxiliary protein, which is differentially controlled based on signal inputs, can lead to two very different cell fates by driving a relatively simple gene expression network. The signal network is designed to provide robust interpretation of the extracellular signal into one of two distinct temporal profiles independent of the temporal profile of the input signal itself. The expression network is tuned to these profiles so that upon the eventual termination of the signal, the proper product is dominant.
Theoretical and empirical connections
The results presented here lend themselves quite naturally to experimental exploration. Firstly, we have hypothesized that the purpose of the joint network is to insulate the genetic response from fluctuations in the input signals to the greatest extent possible. The temporal profiles of the Fos signal are quite stable over a wide range of extracellular stimuli (Figs. 5–7). Each of the features of this profile, namely the length and magnitude of the initial transient as well as the magnitude of the long-term signal, can be measured in vitro under varied stimulation scenarios. Also, specific intervention in the feedback control loops, for example via point mutation ablation of the Erk-mediated receptor complex inactivation, can be used to confirm or refute the hypotheses generated by the reduced models (e.g., Fig. 8), and show how loss of these control mechanisms leads to changes in the joint network specificities.
This analysis also lends insight into how changes in the members of this pathway may lead to aberrant signal processing. As seen in Fig. 3, a mutation leading to either a loss of expression or a truncation of the inhibitor protein, so that it is only competent to perform the direct Raf inhibitory effects (but not the sequestration effects), would render the cell incapable of properly transducing a signal to generate a transient Erk activity spike but no long-term activity. This phenomenon also has implications in the development of small molecule inhibitors of Raf activity (29). Fig. 3 demonstrates that a small molecule inhibitor, which blocks only Raf activity, will not fully rescue the loss of RKIP activity.
The metastatic site selection hypothesis
While in the model system of this work, the PC-12 system, loss of RKIP activity leads to a loss of proliferative potential, in other cell systems long-term Erk activity is a driving force for proliferation, in which the transient spike leads to a nonproliferative state (8). Thus, such an occurrence would have the potential to drive cells into an unnatural proliferative state by transforming a nonmitogenic signal into a mitogenic one. It is well established that the MAPK pathway itself plays a prominent role in many forms of cancer (29,30). Loss of RKIP activity itself has been identified as a marker of malignancy in hepatocellular carcinoma, via aberrant signal processing through the IGF-1/MAPK system. Furthermore, it has been observed that RKIP is a suppressor of metastasis in several tumor types (31,32); however, the mechanism underlying this observation is unknown. Conversely, recent work has indicated a direct, positive role for RKIP in upregulation of migration in MDCK cells (33,34).
The results presented here offer a novel hypothesis for yet another mechanism by which RKIP might affect metastasis. The predicted misinterpretation of extracellular signals (Figs. 8 and 9 and (3)) to a loss of RKIP activity might indicate that cells with ablated RKIP activity have more potential regions in which they can successfully colonize and form secondary tumors. Factors native to those regions, which might be suppressive to cells with active RKIP, may now induce permissive signals due to aberrant signal transduction. This suggests that RKIP-deficient strains will undergo positive selection in tissue regions rich with cytokines and other factors which trigger an abnormal proliferative signal, whereas strains with full, normal RKIP find those same regions as unsupportive of colonization. We summarize this metastatic site selection hypothesis in Fig. 11.
Figure 11.
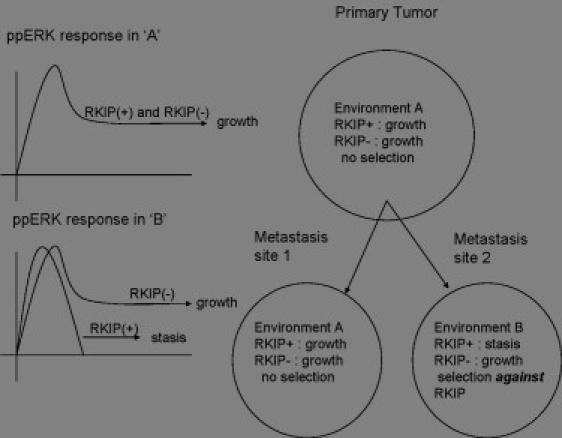
Schematic representation of the metastasis site selection hypothesis, in which strains bearing a loss of RKIP activity have preferential site selection and competitive exclusion advantages over strains still containing RKIP.
This hypothesis is testable. The factors native to the known preferential metastatic targets of RKIP positive and RKIP negative tumor strains can be examined. In the RKIP negative strains, any receptor-cytokine pairing capable of activating the MAPK pathway would lead to a sustained ERK, pro-growth signal. However, in the RKIP positive cells, only those receptors that also activate the secondary pathway (such as the SN(t) signal in Fig. 1) would lead to a sustained ERK signal, and thus we would expect to observe enrichment of those receptors at the metastatic site.
Further on, it would be interesting to investigate the selective environment of the primary tumor sites. Are there selective pressures for or against the expression of RKIP? Or is it a neutral trait in the primary tumor? In the latter case, the following simple calculation is possible (see (35,36)). If the mutation rate by which RKIP negative mutants are created is given by u, and N is the size of the primary tumor, then (in the absence of deaths in the colony of cells), the fraction of mutant cells in the tumor is given roughly by u log N. It follows that if the mutation rate is ∼10−7 RKIP mutations per cell division, then the fraction of mutants in a tumor of size N = 108 is ∼1.8 × 10−6. This means that only a negligible fraction of cells contains mutations in the RKIP gene, and given that the process of metastases is extremely inefficient (see (37)), such cells would hardly make a difference in creating new colonies. Also, this estimate is at odds with experimental data suggesting that the level of RKIP expression is low even at the primary tumor locations (38). There are two ways to resolve this inconsistency:
-
1
RKIP mutants have a selective advantage at the primary site.
-
2
The mutation rate is higher than the basic rate quoted above, as a result of genetic instability.
There is evidence that both chromosomal instability (39) and microsatellite instability (40) are observed in hepatocellular carcinomas, and that they are correlated with metastases (41). Thus, an experimental test of hypothesis 1, directly above, would greatly aid in our understanding of the internal dynamics of RKIP mutants at the primary site.
Presently we are developing a stochastic model of mutant generation that will take in the information on the mutation rate and selective pressures inside the tumor. The goal is to create a theoretical method to evaluate the probability distribution for the number of mutants in a colony of a given size, in a system where the mutations confer a selective advantage. We are also working on developing tools to answer the following question: how early does the tumor adaptation have to start to make metastases possible at later stages?
Conclusion
We have generated a mathematical model of the MAPK-IEG network system in the context of the PC-12 proliferation/differentiation model. While the feedback mechanisms modeled in this article are well established in recent experimental results (3), our goal in this work was to explore how these regulatory mechanisms effect the specificity of the pathway. Further, we investigated how the theoretical foundations of specificity could be used to explain the effects of malfunctions in these mechanisms, and understand how they lead to the results that are observed in experiments. The combined pathway, which contains both MAPK and IEG networks, has never been considered. Since the entire core pathway is shared in this system, and the only difference lies in the auxiliary feedback mechanisms, this is a new class of pathway in which the concepts of specificity have been applied. Our analysis further demonstrates how specificity can be useful in generating hypotheses concerning broader consequences from the localized failures in a particular segment of a network. In particular, we present a hypothesis about the role of RKIP in metastatic site selection.
Acknowledgments
This work was supported by the National Institutes of Health/National Science Foundation joint initiative on Mathematical Biology through National Institutes of Health grant No. GM75309 and National Institutes of Health/National Institute of General Medical Sciences grant No. 1P50GM076516-01A1. N.L.K. gratefully acknowledges the support of the Sloan Fellowship.
References
- 1.Noordman Y.E., Jansen P.A., Hendriks W.J. Tyrosine-specific MAPK phosphatases and the control of ERK signaling in PC12 cells. J. Mol. Signal. 2006:1–14. doi: 10.1186/1750-2187-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.D'Alessio A., Cerchia L., Amelio I., Incoronato M., Condorelli G. Shp2 in PC12 cells: NGF versus EGF signaling. Cell. Signal. 2007;19:1193–1200. doi: 10.1016/j.cellsig.2006.12.011. [DOI] [PubMed] [Google Scholar]
- 3.Santos S.D., Verveer P.J., Bastiaens P.I. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
- 4.O'Neill E., Kolch W. Conferring specificity on the ubiquitous Raf/MEK signaling pathway. Br. J. Cancer. 2004;90:283–288. doi: 10.1038/sj.bjc.6601488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sun P., Watanabe H., Takano K., Yokoyama T., Fujisawa J. Sustained activation of M-Ras induced by nerve growth factor is essential for neuronal differentiation of PC12 cells. Genes Cells. 2006;11:1097–1113. doi: 10.1111/j.1365-2443.2006.01002.x. [DOI] [PubMed] [Google Scholar]
- 6.Hagan S., Garcia R., Dhillon A., Kolch W. Raf kinase inhibitor protein regulation of Raf and MAPK signaling. Methods Enzymol. 2005;407:248–259. doi: 10.1016/S0076-6879(05)07021-7. [DOI] [PubMed] [Google Scholar]
- 7.Rath O., Park S., Tang H.H., Banfield M.J., Brady R.L. The RKIP (Raf-1 kinase inhibitor protein) conserved pocket binds to the phosphorylated N-region of Raf-1 and inhibits the Raf-1-mediated activated phosphorylation of MEK. Cell. Signal. 2008;20:935–941. doi: 10.1016/j.cellsig.2008.01.012. [DOI] [PubMed] [Google Scholar]
- 8.Murphy L.O., Smith S., Chen R.H., Fingar D.C., Blenis J. Molecular interpretation of ERK signal duration by immediate early gene products. Nat. Cell Biol. 2002;4:556–564. doi: 10.1038/ncb822. [DOI] [PubMed] [Google Scholar]
- 9.Komarova N.L., Zou X., Nie Q., Bardwell L. A theoretical framework for specificity in cell signaling. Mol. Sys. Biol. 2005;1 doi: 10.1038/msb4100031. 2005.0023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bardwell L., Zou X., Nie Q., Komarova N.L. Mathematical models of specificity in cell signaling. Biophys. J. 2007;92:3425–3441. doi: 10.1529/biophysj.106.090084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zou X., Peng T., Pan Z. Modeling specificity in the yeast MAPK signaling networks. J. Theor. Biol. 2008;250:139–155. doi: 10.1016/j.jtbi.2007.09.024. [DOI] [PubMed] [Google Scholar]
- 12.Haugh J.M. A unified model for signal transduction reactions in cellular membranes. Biophys. J. 2002;82:591–604. doi: 10.1016/S0006-3495(02)75424-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Orton R.J., Sturm O.E., Vyshemirsky V., Calder M., Gilbert D.R. Computational modeling of the receptor-tyrosine-kinase-activated MAPK pathway. Biochem. J. 2005;392:249–261. doi: 10.1042/BJ20050908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schoeberl B., Eichler-Jonsson C., Gilles E.D., Muller G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat. Biotechnol. 2002;20:370–375. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- 15.Kim D., Rath O., Kolch W., Cho K.H. A hidden oncogenic positive feedback loop caused by crosstalk between Wnt and ERK pathways. Oncogene. 2007;26:4571–4579. doi: 10.1038/sj.onc.1210230. [DOI] [PubMed] [Google Scholar]
- 16.Suresh B.C.V., Babar S., Song E.J., Yoo Y.S. Kinetic analysis of the MAPK and PI3K/Akt signaling pathways. Mol. Cells. 2008;25:397–406. [PubMed] [Google Scholar]
- 17.Mayawala K., Gelmi C.A., Edwards J.S. MAPK cascade possesses decoupled controllability of signal amplification and duration. Biophys. J. 2004;87:L01–L02. doi: 10.1529/biophysj.104.051888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sasagawa S., Ozaki Y., Fujita K., Kuroda S. Prediction and validation of the distinct dynamics of transient and sustained ERK activation. Nat. Cell Biol. 2005;7:365–373. doi: 10.1038/ncb1233. [DOI] [PubMed] [Google Scholar]
- 19.Kolch W., Calder M., Gilbert D. When kinases meet mathematics: the systems biology of MAPK signaling. FEBS Lett. 2005;579:1891–1895. doi: 10.1016/j.febslet.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 20.Calder M., Gilmore S., Hillston J. Modeling the influence of RKIP on the ERK signaling pathway using the stochastic process algebra PEPA. Lecture Notes Computer Sci. 2006;4230:1–23. [Google Scholar]
- 21.Behar M., Dohlman H.G., Elston T.C. Kinetic insulation as an effective mechanism for achieving pathway specificity in intracellular signaling networks. Proc. Natl. Acad. Sci. USA. 2007;104:16146–16151. doi: 10.1073/pnas.0703894104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Behar M., Hao N., Dohlman H.G., Elston T.C. Mathematical and computational analysis of adaptation via feedback inhibition in signal transduction pathways. Biophys. J. 2007;93:806–821. doi: 10.1529/biophysj.107.107516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ueda M., Shibata T. Stochastic signal processing and transduction in chemotactic response of eukaryotic cells. Biophys. J. 2007;93:11–20. doi: 10.1529/biophysj.106.100263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hanahan D., Weinberg R.A. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- 25.Kolch W. Coordinating ERK/MAPK signaling through scaffolds and inhibitors. Nat. Rev. Mol. Cell Biol. 2005;6:827–837. doi: 10.1038/nrm1743. [DOI] [PubMed] [Google Scholar]
- 26.Hughes A., Gollapudi L., Sladek T., Neet K. Mediation of nerve growth factor-driven cell cycle arrest in PC12 cells by p53. J. Biol. Chem. 2000;275:37829–37837. doi: 10.1074/jbc.M003146200. [DOI] [PubMed] [Google Scholar]
- 27.Pumiglia K., Decker S. Cell cycle arrest mediated by the MEK/mitogen-activated protein kinase pathway. Proc. Natl. Acad. Sci. USA. 1997;94:448–452. doi: 10.1073/pnas.94.2.448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee D., Zimmer R., Lee S., Park S. Colored Petri net modeling and simulation of signal transduction pathways. Metab. Eng. 2006;8:112–122. doi: 10.1016/j.ymben.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 29.Roberts P.J., Der C.J. Targeting the Raf-MEK-ERK mitogen-activated protein kinase cascade for the treatment of cancer. Oncogene. 2007;26:3291–3310. doi: 10.1038/sj.onc.1210422. [DOI] [PubMed] [Google Scholar]
- 30.Dhillon A.S., Hagan S., Rath O., Kolch W. MAP kinase signaling pathways in cancer. Oncogene. 2007;26:3279–3290. doi: 10.1038/sj.onc.1210421. [DOI] [PubMed] [Google Scholar]
- 31.Al-Mulla F., Hagan S., Al-Ali W., Jacob S.P., Behbehani A.I. Raf kinase inhibitor protein: mechanism of loss of expression and association with genomic instability. J. Clin. Pathol. 2008;61:524–529. doi: 10.1136/jcp.2007.046987. [DOI] [PubMed] [Google Scholar]
- 32.Al-Mulla F., Hagan S., Behbehani A.I., Bitar M.S., George S.S. Raf kinase inhibitor protein expression in a survival analysis of colorectal cancer patients. J. Clin. Oncol. 2006;24:5672–5679. doi: 10.1200/JCO.2006.07.5499. [DOI] [PubMed] [Google Scholar]
- 33.Henry K.T.M., Montesano R., Zhu S., Beshir A.B., Tang H.H. Raf kinase inhibitor protein positively regulates cell-substratum adhesion while negatively regulating cell-cell adhesion. J. Cell. Biochem. 2008;103:972–985. doi: 10.1002/jcb.21470. [DOI] [PubMed] [Google Scholar]
- 34.Lee H.C., Tian B., Sedivy J.M., Wands J.R., Kim M. Loss of Raf kinase inhibitor protein promotes cell proliferation and migration of human hepatoma cells. Gastroenterology. 2006;131:1208–1217. doi: 10.1053/j.gastro.2006.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Angerer W. An explicit representation of the Luria-Delbrück distribution. J. Math. Biol. 2001;42:145–174. doi: 10.1007/s002850000053. [DOI] [PubMed] [Google Scholar]
- 36.Komarova N., Wu L., Baldi P. The fixed-size Luria-Delbrück model with a nonzero death rate. Math. Biosci. 2007;210:253–290. doi: 10.1016/j.mbs.2007.04.007. [DOI] [PubMed] [Google Scholar]
- 37.Welch D. Do we need to redefine a cancer metastasis and staging definitions? Breast Dis. 2006;26:3–12. doi: 10.3233/bd-2007-26102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Minoo P., Zlobec I., Baker K., Terracciano L., Jass J. Loss of Raf-1 kinase inhibitor protein expression is associated with tumor progression and metastasis in colorectal cancer. Am. J. Clin. Pathol. 2007;127:820–827. doi: 10.1309/5D7MM22DAVGDT1R8. [DOI] [PubMed] [Google Scholar]
- 39.Nakajima T., Moriguchi M., Mitsumoto Y., Sekoguchi S., Nishikawa T. Centrosome aberration accompanied with p53 mutation can induce genetic instability in hepatocellular carcinoma. Mod. Pathol. 2004;17:722–727. doi: 10.1038/modpathol.3800115. [DOI] [PubMed] [Google Scholar]
- 40.Salvucci M., Lemoine A., Saffroy R., Azoulay D., Lepère B. Microsatellite instability in European hepatocellular carcinoma. Oncogene. 1999;18:181–187. doi: 10.1038/sj.onc.1202279. [DOI] [PubMed] [Google Scholar]
- 41.Zhang S., Cong W., Xian Z., Dong H., Wu M. Genomic instability in hepatocellular carcinoma revealed by using the random amplified polymorphic DNA method. J. Cancer Res. Clin. Oncol. 2004;130:757–761. doi: 10.1007/s00432-004-0613-4. [DOI] [PubMed] [Google Scholar]


