Reaction Dynamics of Halorhodopsin Studied by Time-Resolved Diffusion

Abstract

Reaction dynamics of a chloride ion pump protein, halorhodopsin (HR), from Natronomonas pharaonis (N. pharaonis) (NpHR) was studied by the pulsed-laser-induced transient grating (TG) method. A detailed investigation of the TG signal revealed that there is a spectrally silent diffusion process besides the absorption-observable reaction dynamics. We interpreted these dynamics in terms of release, diffusion, and uptake of the Cl⁻ ion. From a quantitative global analysis of the signals at various grating wavenumbers, it was concluded that the release of the Cl⁻ ion is associated with the L2 → (L2 (or N) ⇆ O) process, and uptake of Cl⁻ occurs with the (L2 (or N) ⇆ O) → NpHR′ process. The diffusion coefficient of NpHR solubilized in a detergent did not change during the cyclic reaction. This result contrasts the behavior of many photosensor proteins and implies that the change in the H-bond network from intra- to intermolecular is not significant for the activity of this protein pump.

Introduction

Halobacteria, such as Halobacterium salinarum (H. salinarum) and Natronomonas pharaonis (N. pharaonis), have rhodopsin-like photoreceptors (Type 1 rhodopsins), which have a bound chromophore, all-trans retinal, in the hydrophobic pocket. This pocket is surrounded by seven transmembrane α-helices. Halorhodopsin (HR) is one of these archaeal rhodopsins, and it functions transporting chloride ions (Cl⁻) from the periplasmic side to the cytoplasmic side using absorbed photon energy (1–4). Because structural information, including that on analogous rhodopsins from haloarchaea (e.g., bacteriorhodopsin (BR)), is available and the reaction can be triggered by light, the archaeal rhodopsins are considered to be ideal systems to study the relationship between protein structures and reaction dynamics. However, compared with extensive studies on the light-driven proton pump BR, knowledge on the reaction kinetics and ion pumping dynamics of HR is limited.

The chromophore of HR is an all-trans retinal, and it is isomerized to a 13-cis form by absorbing a photon (5). This isomerization of the chromophore triggers a series of reactions of the protein. The sequential reactions involve several short-lived intermediates, and the initial state is ultimately recovered within a second (photocycle) (5–8). During this photocycle, Cl⁻ is transported from the periplasmic side to the cytoplasmic side of the cell. The Cl⁻ transport mechanism has attracted significant attention, and a variety of research efforts (e.g., Cl⁻ binding assay combined with mutagenesis, UV-Vis, and/or infrared absorption detection or circular dichroism detection) have been conducted to identify interacting amino-acid residues and intermediates that are associated with the binding of the Cl⁻ (6). Spectroscopic techniques combined with pulsed-laser excitation have been mainly employed to study the reaction dynamics; in particular, a flash-photolysis method has identified several reaction intermediates and the kinetics of the HR photocycle. The absorption spectra of these intermediates are similar to those observed for the BR photocycle, and the intermediates have been named K, L, and O in the order of the appearance during the photocycle (5,9). The release and uptake of Cl⁻ should occur in particular intermediates during the photocycle. Although flash-photolysis is powerful, this method cannot directly observe the movement of Cl⁻. To overcome this limitation, nonspectroscopic methods such as photovoltage measurements have been used to detect the movement by, e.g., a transmembrane voltage change (10,11). However, because the voltage changes simultaneously originate from various factors other than solely ion movements (e.g., charged group reorientations), it is difficult to identify the signal due to the Cl⁻ transport process. Hence, the assignment of the signal is invariably ambiguous, and there remain controversial points on the dynamics of the Cl⁻.

A difficulty of the reaction kinetics on HR is that, although the reaction can be triggered by pulsed-laser light, the spatial movement of Cl⁻ cannot be monitored by the absorption change. In fact, there are few techniques available to trace the spatial movement of atoms in the time domain. Recently, a new method has been developed to monitor spectrally silent dynamics in the time domain; time-resolved volume change and diffusion measurements based on the pulsed- laser induced transient grating (TG) technique (12,13). This TG method is sensitive to changes in the refractive index and has been applied to photoreactions of many photosensor proteins. Many conformational changes that could not be detected by absorption changes have been successfully revealed using the TG method (14–23).

In this study, we applied this TG method to characterize the reaction dynamics of the ion pump protein, HR from N. pharaonis (NpHR). As a comparison, the reaction kinetics by the absorption detection method were also measured. There are two central aims in this research. First, it is important to examine if there is any spectrally silent reaction dynamics related with protein conformational change far from the chromophore and/or Cl⁻ movement during the photocycle reaction. If Cl⁻ movement can be detected, it would be a direct method for studying the kinetics. Second, previous TG studies revealed that most of the photosensor proteins exhibit so-called diffusion-sensitive conformational changes (17,18,20–22,24,25). These changes were interpreted as changes in the H-bond network between the proteins and water molecules or changes in the oligomeric states. During the reaction of HR, it was suggested that Cl⁻ movement is associated with H-bond changes (7,26). It will be interesting to observe whether such H-bond changes are so extensive to induce a measurable change in the diffusion coefficient. For comparison with the dynamics of NpHR, we also measured the reaction of its T218V mutant (T218V). Thr218 is considered to be a Cl⁻ interacting site in the cytoplasmic channel (7,27). The O intermediate has been reported to not accumulate for this mutant. Therefore, the role of the O intermediate in the reaction scheme is expected to be revealed by using this mutant.

Material and Methods

Protein expression and purification of NpHR

The construction of the expression plasmids for C-terminal His-tagged wild-type NpHR and T218V mutants was reported previously (7). The protein expression of the recombinant NpHR in Escherichia coli (E. coli) (strain BL21 (DE3)) and purification procedures were described earlier (28). Fractions of the target proteins separated by Ni-NTA-agarose (Qiagen, Hilden, Germany) were collected by elution with buffer A [50 mM Tris-HCl (pH 7.0), 300 mM NaCl, 0.1% n-dodecyl-β -D-maltopyranoside (DDM) (Dojindo Lab, Kumamoto, Japan)]. Each sample was concentrated, if required. The protein concentration was estimated using an absorption coefficient ɛ₅₇₈ of 54,000 M⁻¹cm⁻¹ at 578 nm (29). To remove imidazole and adjust the NaCl concentration, the NpHR solution was desalted on ice by passing it over a PD-10 column (Amersham Biosciences, Uppsala, Sweden) in 10 mM MOPS buffer (pH 7.0) containing 0.1% DDM. Two different concentrations of NaCl (0.3 and 4 M) were used for the wild-type NpHR sample.

Transient absorption measurement

The experimental setup for the transient absorption (TA) measurements was similar to previous reports (19,20). Briefly, a pulsed-laser beam from a dye laser (λ = 560 nm, repetition rate = 0.5 Hz, Sirah, Newport Corp. Spectra-Physics Division, Mountain View, CA) pumped by the second harmonic light from a Nd:YAG laser (λ = 532 nm, Quantum-Ray Model GCR-170-10, Newport Corp. Spectra-Physics Division) was used for excitation light of the sample solution. For recording time evolutions of absorption changes at particular probe wavelengths after excitation, beams from He-Ne lasers (λ = 594, 612, and 633 nm) were introduced to the sample from the same side as the pump light with a small crossing angle. The probe beams were guided to a monochrometer to remove the scattering light of the pump beam. Their intensity changes were monitored by a photomultiplier tube and a digital oscilloscope (Tektronix TDS-520, Beaverton, OR), and the signal was transferred to a computer for analysis.

Transient grating measurement

The experimental setup for the TG measurements was similar to that previously reported (12–14,19,20). The same pump beam as the TA measurements was used for excitation of the sample solution. The laser pulse was split into two by a beam splitter and then crossed inside the sample cell. A continuous wave laser light from a diode laser (λ = 840 nm) was used for the probe light. A part of the probe beam diffracted by the grating was detected by a photomultiplier tube, and the temporal profile was recorded by a digital oscilloscope (Tektronix TDS-520, Beaverton, OR). To prevent the scattering of the probe light by the sample solution, we removed any dust by centrifugation at 1000 x g, and the sample solution was filtered by a cellulose acetate membrane filter (Cosmospin Filter G (pore size = 0.2 μm), Nacalai Tesque, Kyoto, Japan). The sample solution was placed in a quartz cell (optical path length = 2 mm) at 25°C. Usually, 100 signals were averaged to improve the signal/noise ratio. The repetition rate of the pump beam was 0.5 Hz to avoid multiexcitation of the sample. The grating wavenumber q at each experimental setup was determined from the decay rate of the thermal-grating signal of a calorimetric reference (Evans Blue) solved in the same buffer, which quickly releases the excitation photon energy (30).

Results and Discussion

Reaction dynamics monitored by TA

Before describing the study by the TG method, the reaction kinetics of NpHR by the TA method under the same conditions used for the TG analysis is reported. The time profiles of the TA signals of NpHR at a Cl⁻ concentration of 300 mM and at probe wavelengths of 594, 612, and 633 nm are depicted in Fig. 1 a. We performed a global analysis of these signals and found that the signals were well reproduced by the sum of six exponential functions:

$$I_{\text{TA}}\left(t\right)={\text{a}}_{\text{1}}\exp (-k_{1}t)+{\text{a}}_{\text{2}}\exp (-k_{2}t)+{\text{a}}_{\text{3}}\exp (-k_{3}t)+{\text{a}}_{\text{4}}\exp (-k_{4}t)+{\text{a}}_{\text{5}}\exp (-k_{5}t)+{\text{a}}_{\text{6}}\exp (-k_{6}t),$$ (1)

where k₁ > k₂ > k₃ > k₄ > k₅ > k₆. The fitting was always satisfactory, and the fittings with different initial values always converged to the same values. The time constants are listed in Table 1. Previously, Sato et al. (7) reported flash-photolysis measurements after 10 μs of photoexcitation and observed three reaction processes, which have been assigned to the decays of L1 (220 μs), L2 (680 μs), and a mixture of L2 and O (L2 ⇆ O) (750 μs) intermediates at a Cl⁻ concentration of 1 M. Hasegawa et al. (8) reported the photocycle under various Cl⁻ concentrations and analyzed the signals by a scheme of L1 (240 μs) → L2 (650 μs) → (N ⇆ O) (1.7 ms), where (N ⇆ O) represents the equilibrium mixture of N and O intermediates at a Cl⁻ concentration of 200 mM. We also observed similar time constants: k₂⁻¹ = 290 μs, k₃⁻¹ = 520 μs, and k₄⁻¹ = 1.4 ms (Table 1). On the basis of the previous assignments, these phases were attributed to the decays of L1, L2, and L2 (or N) ⇆ O intermediates, respectively. Additionally, we observed a fast decay in the submicrosecond timescale range (k₁⁻¹ = 550 ns). This decay was assigned to K → L1 (9,31). At a long timescale (i.e., after 10 ms), two additional components were observed, k₅⁻¹ = 17 ms and k₆⁻¹ = 370 ms. Compared with the other decays, the absorption changes of these components were relatively weak. This indicates that the reaction intermediates related to these processes have very similar absorption spectra to the initial NpHR state. Therefore, we will call these intermediates NpHR′ and NpHR″. Similar identifications of the intermediates, which have similar spectra to the unphotolyzed state, were reported using TA measurements with probe wavelengths in the visible region (9). Therefore, our assignment of the signal at >10 ms is considered to be appropriate, and the signal does not originate due to other possibilities (e.g., branching reversible reactions or impurities). Since the residuals of the fitting did not improve by adding more exponential terms, there is no significant reaction process other than those listed in Table 1. Hence, we observed the processes of K → L1 → L2 → (L2 (or N) ⇆ O) → NpHR′ → NpHR″ → NpHR by the TA method.

Figure 1.

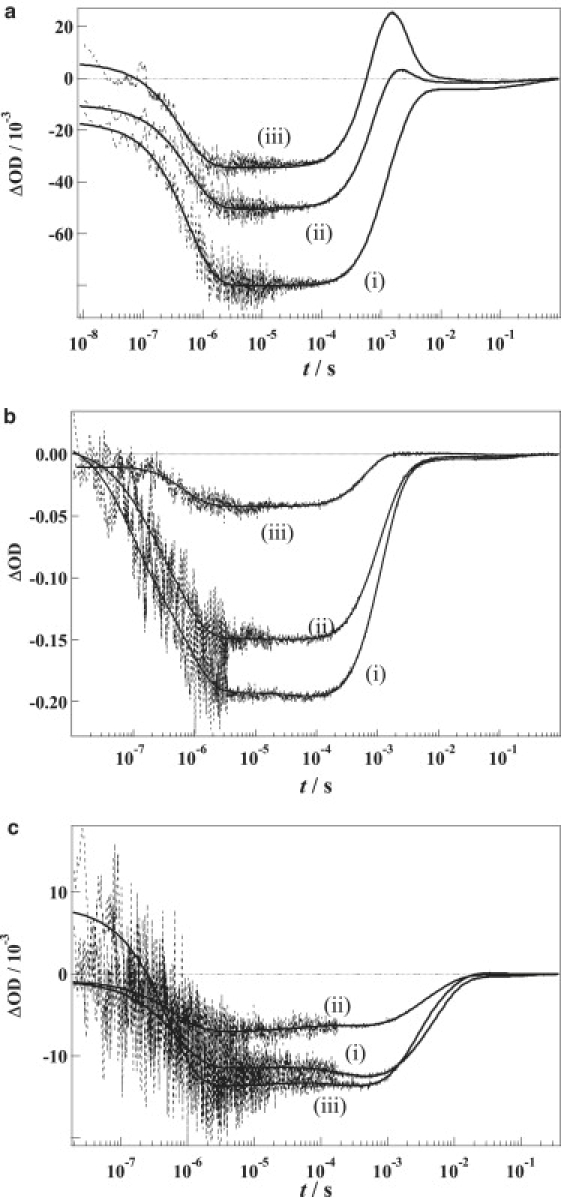
(a) Time profiles of the absorption change (dotted lines) of wild-type NpHR at [Cl⁻] = 300 mM at probe wavelengths of (i) 594 nm, (ii) 612 nm, and (iii) 633 nm. The best-global-fitted curves by Eq. 1 are shown by the solid lines. (b) Time profiles of the absorption change (dotted lines) of wild-type NpHR at [Cl⁻] = 4 M. The probe wavelengths are the same as those of (a). The best-global-fitted curves by Eq. 1 plus two additional exponential components are shown by the solid lines. (c) Time profiles of absorption change of T218V at [Cl⁻] = 300 mM and the same probe wavelengths. The best-fitted curves by Eq. 1 plus one exponential term are shown by the solid lines.

Table 1.

Time constants of exponential components used to reproduce the transient absorption signals of wild-type NpHR and the T218V mutant

	k0−1/ns	k1−1/ns	k2−1/μs	k3−1/μs	k4−1/ms	k5−1/ms	k6−1/ms	k7−1/ms
WT 300 mM chloride	N	550 ± 80	290 ± 80	560 ± 60	1.4 ± 0.1	17 ± 5	370 ± 30	N
WT 4 M chloride	120 ± 30	600 ± 180	200 ± 40	500 ± 300	1.0 ± 0.2	3.7 ± 0.7	100 ± 80	120 ± 90
T218V 300 mM chloride	N	640 ± 110	41 ± 25	620 ± 40	1.25 ± 0.05	5.23 ± 0.05	31 ± 5	88 ± 9

N, not observed; WT, wild-type.

The number of intermediates and their decay rate constants determined by our TA measurements were highly consistent with the results reported by Chizhov and Engelhard (9). They reported the rate of K → L1, L1 → L2 (noted as L → (L ⇆ O) in their study), L2 → (L2 (or N) ⇆ O), (L2 (or N) ⇆ O) → NpHR′, and NpHR′ → NpHR as 400 ns, 250 μs, 450 μs, 1.5 ms, and 20 ms, respectively. These values are essentially identical to the results presented herein. Although they observed an additional 50 μs component between L1 and L2 and did not discover NpHR″, both of these absorption changes are relatively weak, and we conclude that there is no significant difference between the two models. Váró et al. (32) modeled the photocycle by using several reversible steps. In this study, the reported kinetics of NpHR are similar to our results (they reported K → L, N → O, O → NpHR′ and NpHR′ → NpHR with time constants of 1.5 μs, 480 μs, 3 ms, and 29 ms, respectively). These consistencies with previous studies support the accuracy of the fitting routine used.

Fig. 1 b shows the TA signals of NpHR at [Cl⁻] = 4 M. The TA signals were reproduced by the sum of eight exponentials. The lifetimes of these exponentials are listed in Table 1. The majority of the time constants were similar to those reported at [Cl⁻] = 300 mM; however, two additional components at the higher Cl⁻ concentration were observed. One component (120 ns) was faster than K → L (we termed this component as k₀). It is interesting to observe the effect of the Cl⁻ concentration on the fast timescale. The second additional component was observed in the millisecond timescale range (1/k = 3.7 ms). This component has a relatively weak amplitude, but it was reproducible. Before the appearance of this component, the major absorption change decayed. Because the origin of these components is unclear and it is not the focus of this study to identify these intermediates, the origin will be investigated in future research efforts.

The most prominent difference of the TA signal between [Cl⁻] = 4 M and [Cl⁻] = 300 mM is the disappearance of O. The enhanced absorption observed in the millisecond timescale at 633 nm (Fig. 1 a (iii)) at [Cl⁻] = 300 mM corresponds to the accumulation of the red-shifted O intermediate. This signal has completely disappeared at [Cl⁻] = 4 M. This indicates that the O species does not accumulate to a significant concentration at the higher Cl⁻ concentration. A similar finding was reported in previous studies and it was explained by the equilibrium shift of (L2 (or N) ⇆ O) to L2 (or N) (8,9).

The TA signals of T218V at [Cl⁻] = 300 mM are shown in Fig. 1 c. Although the profiles were similar to those of NpHR, some differences were clearly visible. The recovery of the bleached signal at 594 nm, which corresponds to the decay of L2 observed in the submillisecond timescale for NpHR, was much slower than that of NpHR. Additionally, the enhanced absorption at the 633 nm probe wavelength observed for NpHR at a 300 mM chloride concentration had disappeared in the signal of T218V (Fig. 1 c (iii)). As we mentioned above, because this absorption originates from the red-shifted O, this indicates that the O intermediate does not accumulate during the T218V photocycle. These characteristics are consistent with the results previously presented (7). We could not reproduce the TA signals of T218V by a sum of six exponential functions but had to use a sum of seven exponential functions by adding a₇exp(-k₇t) to Eq. 1 for the analysis of T218V. The residuals of the fitting did not improve by adding more exponential terms. The time constants of each component are listed in Table 1. On the basis of the previous report (7), the rate constants of k₁–k₇ were attributed to a series of transitions involving K → L1 → L2 → L3 → L4 → NpHR′ → NpHR″ → T218V.

Reaction dynamics of NpHR monitored by the TG method

The TG signals of NpHR at [Cl⁻] = 300 mM are shown in Fig. 2 a. In principle, the TG signal is proportional to the square of the amplitude of the spatially modulated refractive index change (12–14,33). Under the experimental conditions presented here, the refractive index change should primarily arise from the thermal energy released from the excited molecules (δn_th; thermal grating), and the creation (or depletion) of chemical species by the photoreaction (δn_spe; species grating) (15,17–19,34). The species grating consists of the following two contributions: change in the absorption spectrum (δn_pop; population grating) and the change in the molecular volume (δn_vol; volume grating). The species-grating signal is created by the refractive index changes due to the reactant (δn_R) and product (δn_P). Hence, the observed TG signal is expressed by

$$I_{\text{TG}}\left(t\right)=\alpha {\{\delta n_{\text{th}}\left(t\right)+\delta n_{\text{P}}\left(t\right)-\delta n_{\text{R}}\left(t\right)\}}^2,$$ (2)

where α is a constant, and the signs of both δn_P and δn_R are positive. The decay of the thermal-grating term is determined by the thermal diffusivity (D_th) and the grating wavenumber q², and it is written as δn_thexp(−D_thq²t). The temporal profile of δn_R(t) is determined by the protein diffusion of the reactant so that it should be δn_Rexp(−D_Rq²t), whereby D_R is the diffusion coefficient of the reactant. The temporal profile of the species grating due to the intermediate and the product δn_P(t) is governed by the chemical reaction kinetics and the diffusion process. Generally, the rate constant of this term is given by D_Pq²+k, whereby D_P is the diffusion coefficient of the intermediate (or product) and k is the reaction rate (33). If D_Pq² is much smaller than k, the rate constant of δn_P(t) is almost the same as that of the reaction kinetics.

Figure 2.

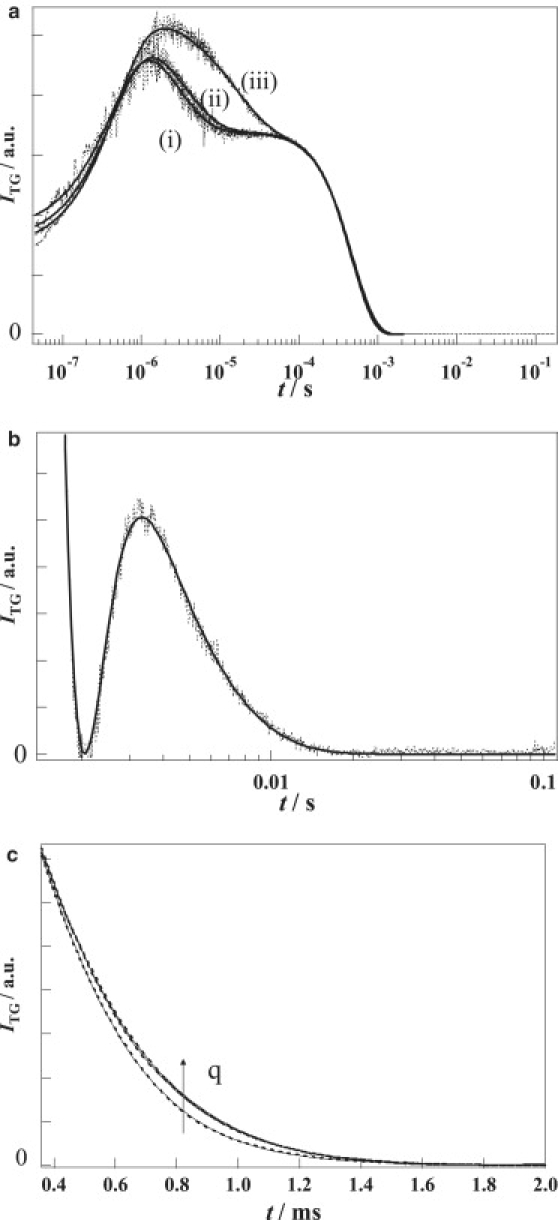
(a) Typical TG signals (dotted lines) of NpHR at [Cl⁻] = 300 mM at q² = (i) 2.54 × 10¹² m⁻², (ii) 1.91 × 10¹² m⁻², and (iii) 4.17 × 10¹¹ m⁻². The best-fitted curve by Eq. 4 is shown by the solid lines. (b) Amplified TG signal (dotted lines) on a long timescale at q² = 2.54 × 10¹² m⁻². The best-fitted curve by Eq. 4 is shown by the solid line. D_P was determined from the decay rate of this part of the curve. (c) The amplified signal (dotted lines) in 0.4–1.5 ms range at various q of NpHR. q²-values were 3.80 × 10¹¹ m⁻², 1.91 × 10¹² m⁻², and 2.54 × 10¹² m⁻². It should be noted that the signals appear to decay slower at increasing q². The best-fitted curve using Eq. 4 is shown by the solid lines.

The observed TG signal of NpHR was fitted by a sum of exponential functions. One of the rate constants agreed with the decay rate of the thermal-grating component observed from the calorimetric reference sample. As such, this component was assigned to the thermal-grating signal (δn_thexp(−D_thq²t)). Including this term and based on the reaction kinetics from the TA measurements (Eq. 1), we found that the observed TG signal was roughly reproduced by a function of

$$I_{\text{TG}}\left(t\right)=\alpha {\{\delta n_1\exp (-k{\prime }_{1}t)+\delta n_{\text{th}}\exp (-D_{\text{th}}{q}^{2}t)+\delta n_2\exp (-k{\prime }_{2}t)+\delta n_3\exp (-k{\prime }_{3}t)+\delta n_4\exp (-k{\prime }_{4}t)+\delta n_5\exp (-k{\prime }_{5}t)\}}^2,$$ (3)

where k′₁ > k′₂ > k′₃ > k′₄ > k′₅. The sign of the refractive index change of the thermal-grating component is negative (δn_th < 0) at the temperature used in the experiment. For explaining the observed signal, the signs of δn for the other terms were determined to be δn₁ > 0, δn₂ > 0, δn₃ < 0, δn₄ > 0, and δn₅ < 0. There is no ambiguity in these signs, because the signal calculated with different signs could not reproduce the observed signal at all. The rate constants k′₁, k′₂, k′₃, and k′₄ were roughly independent of q²-values and close to the rate constants of k₁, k₂, k₃, and k₄, as determined from the TA method. Hence, these TG dynamics essentially represent the dynamics detected by the TA signal, and the diffusion contribution (D_Pq²) is negligibly small compared with the reaction rate constants, k₁, k₂, k₃, and k₄ (i.e., D_Pq² << k₄).

The intensities of the TG signals drastically decreased after 1 ms, whereby NpHR′ and NpHR″ were predominant, and these components were ∼1/2000 of the signal before 1 ms (Fig. 2 b). The weakness of the signal is due to the weak population grating terms of NpHR′ and NpHR″, i.e., similar absorption spectra to the initial state. The signal was found to be in the long time region with the smallest rate constant k′₅ dependent on the q²-value. The signal was much larger than k₅ from the TA measurement. The q² dependence and larger rate constant can be explained by the contribution of the protein diffusion, i.e., k′₅ should be given by D_Pq² + k₅ and D_Pq² is no longer negligible compared with k₅. Using the rate constants of k′₅ from the TG signal and k₅ from the TA signal, D_P was determined to be 4.4 ± 0.3 × 10⁻¹¹ m²/s.

The phase of k₆ observed in the TA signal (Eq. 1) did not appear in the TG signal (Eq. 3), because the protein diffusion process smeared out the grating profile completely with the rate constant of D_Pq² before the phase of k₆ (i.e., D_Pq² >> k₆).

Although the above equation roughly reproduced the TG signal, a closer examination of the signal fitting revealed that the best-fitted curve by Eq. 3 was inadequate. The most serious discrepancy between the observed signal and the fitted curve was manifested in the q² dependence of the decay part in the 10⁻⁴ to 10⁻³ s time region. The signal in this range was amplified and is shown in Fig. 2 c. As described above, in general, each TG signal component should decay with the sum of a rate constant of the reaction (k) and the diffusion (Dq²). Therefore, the decay rates of all TG components should be slower by decreasing q². Surprisingly, however, the signals in this time region appeared to decay “faster” with decreasing q² (Fig. 2 c). This opposes the normal behavior predicted from the principles of the TG method, and this behavior cannot be explained by Eq. 3. (Although this anomalous q²-dependence appears minor in the signal, this represents an extraordinary and significant feature when comparing the signal with “normal signals” such as those measured at the higher Cl⁻ concentration and/or T218V as described later.)

What is the origin of such unexpected behavior? Only one possible explanation can explain this observation: this decay component is not a single phase but contains a second component, which is superimposed. For example, let us consider the following case. If a decay component having a form of δn_Xexp(−D_Xq²t) (δn_X and D_X are the refractive index and the diffusion coefficients of the unknown species) is superimposed with a δn₃exp(−k′₃t) term and q² is small enough to satisfy D_Xq² < k₃, the decay appears faster due to the cancellation at the long time range (Fig. 3). When q² increases, the cancellation takes place in a faster time range such that the decay looks “slower” (Fig. 3).

Figure 3.

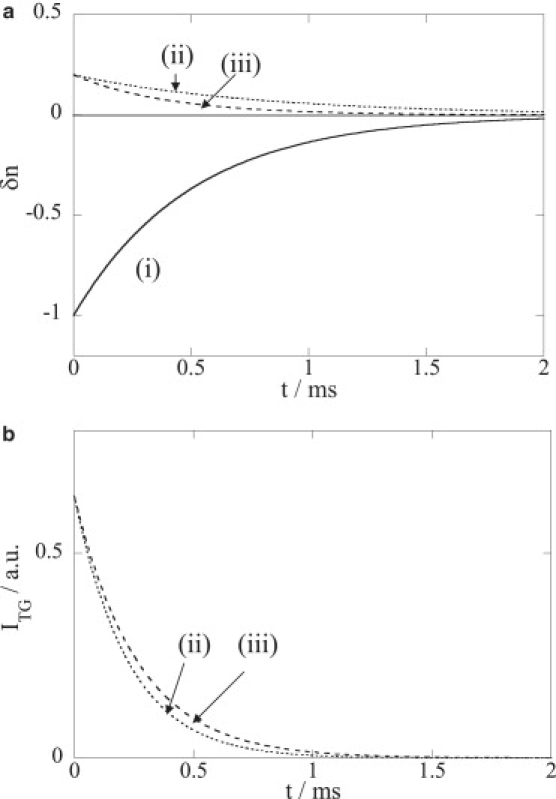
Simulated curves to explain the observed anomalous q² dependence of NpHR. (a) The curve of (i) simulates the δn₃exp(−k′₃t) term of Eq. 3; (ii) (dotted line) and (iii) (broken line) are calculated curves by −0.2δn₃exp(−k_Xt), where (ii) k_X⁻¹ = 0.7 ms,and (iii) k_X⁻¹ = 0.4 ms as representative curves at smaller and larger q², respectively. (b) Calculated TG signals by taking the sum of (i) and (ii) (dotted line), and (i) and (iii) (broken line).

For explaining the apparent “faster” decay at smaller q² by the above model, there are two necessary conditions: the rate constant of this component should depend on q², and the sign of this component should be opposite to the main component in this time range, i.e., δn₃. The first condition indicates that this phase has to be a diffusion process. Interestingly, the decay due to protein diffusion appeared in the 10 ms time range (Fig. 2 b) at these q²-values. Hence, regardless of the species contributing to this phase, the diffusion coefficient of this species should be at least 10 times larger than D of the protein. This order estimation suggested that the species should be a much smaller size when compared with the protein. Compared with the sign of δn₃ < 0, the above second condition implies that the additional phase should possess a positive δn. This indicates that this component should be a photoinduced species (cf., Eq. 2), i.e., an intermediate or a product. Consequently, we may speculate that the photoinduced product having a smaller size than the protein is Cl⁻.

Considering the role of the Cl⁻ pump of HR, there must be Cl⁻ release and uptake processes. Furthermore, it is important to note that the diffusion signal of Cl⁻ appears only when Cl⁻ is present outside of HR, i.e., only when Cl⁻ release is faster than Cl⁻ uptake. The TG signal was calculated based on a model that includes the Cl⁻ release and uptake processes during the photocycle with rate constants of k_out and k_in, respectively. The TG signal taking into account the contribution of the Cl⁻ release, diffusion, and uptake is expressed as:

$$I_{TG}\left(t\right)=\alpha [\sum _{i=1}^5\left\{\delta n_i\exp \left(-k_{i}t\right)\right\}+\delta n_{C{l}^{-}}\{\frac{k_{out}^2}{\left(k_{out}-k_{in}\right)\left(D_{C{l}^{-}}{q}^2-k_{out}\right)}\exp \left(-k_{in}t\right)-\frac{k_{in}{k}_{out}}{\left(k_{out}-k_{in}\right)\left(D_{C{l}^{-}}{q}^2-k_{in}\right)}\exp \left(-k_{out}t\right)+{\left(\frac{k_{out}^2}{\left(k_{in}-k_{out}\right)\left(D_{C{l}^{-}}{q}^2-k_{out}\right)}-\frac{k_{out}{k}_{in}}{\left(k_{in}-k_{out}\right)\left(D_{C{l}^{-}}{q}^2-k_{in}\right)}\right)\exp \left(-D_{C{l}^{-}}{q}^{2}t\right)\}]}^2,$$ (4)

where δn_i and k_i (i = 1–5) are the refractive index change accompanying the production of i-th intermediate of NpHR and its decay rate, respectively. The first term of the right-hand side of Eq. 4 represents the contribution of NpHR. Other terms represent the refractive index changes due to the presence of Cl⁻, and δn_Cl− is the refractive index change of Cl⁻. We analyzed the TG signal by assuming that k_out and k_in are represented by k_i (i = 1–5). The rate constants of k_out and k_in could not be k_i. However, if we did not use this assumption, it was difficult to determine the parameters without fitting ambiguities. Hence, we used this assumption. However, considering that D of Cl⁻ from the fitting agreed quite well with the literature value (vide infra), we consider that this assumption was not inappropriate. Even if the rate is not exactly the same as k_i, the rate should be reasonably close to it. Because the diffusion signal appeared in a range of 10⁻⁴–10⁻³ s, it is reasonable to consider that Cl⁻ is released by the k₂ or k₃ process. We fitted the observed signal with different sets of the rate constants for k_out and k_in, and found that the residuals of the fitting reached a minimum when we used k_out = k₃ (L2 → (L2 (or N) ⇆ O) process) and k_in = k₄ ((L2 (or N) ⇆ O) → NpHR′ process).

At the same time, we were able to determine D of Cl⁻ (D_Cl−) by the curve fitting of the TG signals with Eq. 4 and obtained D_Cl⁻ = 1.63 ± 0.01 × 10⁻⁹ m²/s. This D_Cl⁻ agrees quite well with a reported value D_Cl⁻ = 1.6 × 10⁻⁹ m²/s (35). This agreement supports the above analysis.

Previously, Shibata et al. (36) reported that Glu234 is deprotonated on L2. One may consider that the observed fast diffusion species could be H₃O⁺ released by this process. However, D of the proton (D_H3O⁺) is much larger than other ionic species. In our solvent, D_H3O⁺ was reported to be 2.3 × 10⁻⁹ m²/s (35), and it is significantly larger than the reported D_Cl⁻. Therefore, the fast diffusing species observed by the TG is not H₃O⁺. We concluded that Cl⁻ release and uptake in solution at room temperature occurs during the processes of L2 → (L2 (or N) ⇆ O) and (L2 (or N) ⇆ O) → NpHR′, respectively. We believe this is the first direct observation of the Cl⁻ movement by the time-resolved diffusion method. (A similar experiment using various anion species (e.g., Br⁻, I⁻, NO₃⁻) might further support the above assignment. However, when the anions are changed, the photocycle of NpHR, the number of intermediates, and the decay rates of the intermediates should change (37–39), and the assignment may not be simple. We will investigate this point in the future.)

Váró et al. (32) concluded that in NpHR, the N-decay (O formation) and O decay (NpHR′ formation) accompanied the Cl⁻ release and uptake, respectively. This conclusion does not necessarily contradict Váró et al. (5), because the forward and backward reaction rates of the equilibrium between L2 (or N) and O are much faster than the L2 decay (k₃). Moreover, as the decay of (L2 (or N) ⇆ O) is a slower process, the Cl⁻ release from the N to the O intermediate may be observed as the L2-decay. The O intermediate is considered to be a Cl⁻ free form or the intermediate in which Cl⁻ is located far from the Schiff base (28,40). Hasegawa et al. (8) observed that the N and O equilibrium was shifted to N with an increase in the Cl⁻ concentration. This observation supports the concept that Cl⁻ release occurs during the O formation. Furthermore, Muneyuki et al. (10) previously studied the Cl⁻ movement by photovoltage measurements and also reported that Cl⁻ is released on N → O, and uptake occurs on O → NpHR. However, another group employing a photovoltage method suggested that the O intermediate does not participate in Cl⁻ transport (41). One of the origins of these discrepancies could be due to the fact that the photovoltage measurement detects voltage change not only attributable to the release and uptake of Cl⁻ and the protein, but also to other dynamics, e.g., intraprotein movements of ions and/or charged groups reorientations. This ambiguity makes the assignment of the signal difficult. In contrast, the assignment of the TG signal is possible by the characteristic diffusion coefficient. In conclusion, Cl⁻ is released just before the generation of O and rebinds to NpHR associated with the O decay. This model is consistent with previous studies.

Reaction dynamics of NpHR at a higher Cl⁻ concentration

Fig. 4, a and b depict the TG signal of NpHR at [Cl⁻] = 4 M. The apparent signals were similar to those at [Cl⁻] = 300 mM. These signals were analyzed by the sum of seven exponentials, and the rate constants were fixed to the ones of the first six components of the TA signal and the thermal diffusion. The most notable difference of the signal from that at [Cl⁻] = 300 mM is the q² dependence in submilli- to millisecond timescale (Fig. 4 b). In contrast to the signal at [Cl⁻] = 300 mM, the TG signal decayed faster with increasing q²-values. This q² dependence is “normal” and is an expected feature arising from the contribution due to protein diffusion. By considering the protein diffusion of D_P = (5.0 ± 0.2) × 10⁻¹¹ m²/s (i.e., without the contribution of Cl⁻ diffusion), the TG signals at various q² were consistently reproduced. This result clearly indicates that the Cl⁻ diffusion signal vanished at [Cl⁻] = 4 M and implies that the Cl⁻ transport activity of NpHR is weaker at the higher Cl⁻ concentration.

Figure 4.

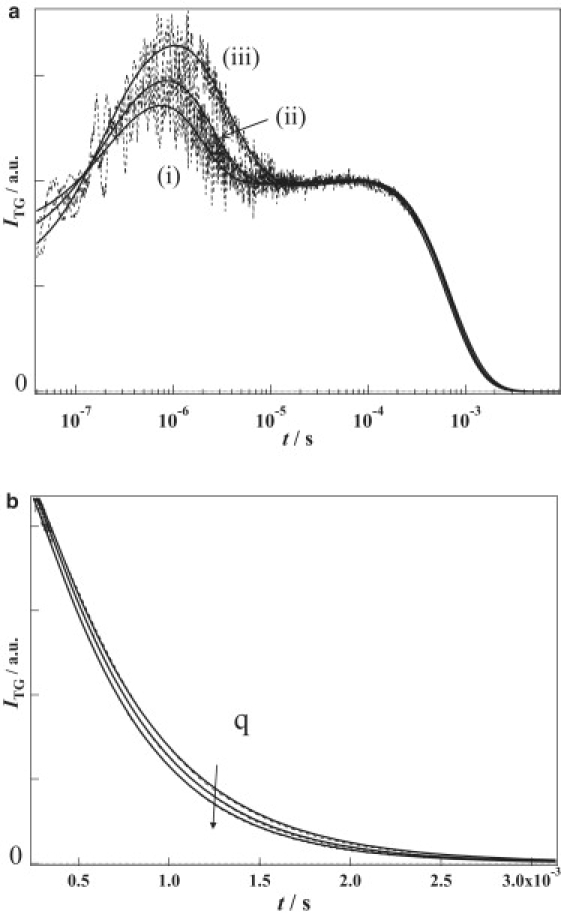
(a) Typical TG signals (dotted lines) of NpHR at 4 M chloride at q² = (i) 6.49 × 10¹² m⁻², (ii) 3.86 × 10¹² m⁻², and (iii) 1.98 × 10¹² m⁻². The best-fitted curves by Eq. 3 plus an additional one component are shown by the solid lines. (b) The amplified TG signals shown in (b) (dotted lines) in 0.4–3.1 ms range at various q of NpHR.

This phenomenon is consistent with the conclusions drawn from TA measurements in previous studies (8,9,42). Hasegawa et al. (8) reported that O is in fast equilibrium with unknown species X (probably N), which holds Cl⁻ within the protein, and a higher Cl⁻ concentration causes X to dominant in this equilibrium. Chizhov and Engelhard (9) also reported that the fast equilibrium is associated with a lower affinity chloride ion-binding site (K_d ≈ 1.1 M), and some studies also claimed that NpHR has such a lower affinity site (8,42,43). Our findings indicate that this lower binding site does not participate in the transport of Cl⁻ during the NpHR photocycle.

Reaction dynamics of T218V monitored by the TG method

Fig. 5 a shows the TG signals of T218V measured under the same condition as NpHR. The signals of T218V were reproduced by a sum of eight exponentials as follows:

$$I_{\text{TG}}\left(t\right)=\alpha {\{\delta n_1^{\prime }\exp (-k_1^{″}t)+\delta n_{\text{th}}\exp (-D_{\text{th}}{q}^{2}t)+\delta n_2^{\prime }\exp (-k_2^{″}t)+\delta n_3^{\prime }\exp (-k_3^{″}t)+\delta n_4^{\prime }\exp (-k_4^{″}t)+\delta n_5^{\prime }\exp (-k_5^{″}t)+\delta n_6^{\prime }\exp (-k_6^{″}t)+\delta n_7^{\prime }\exp (-k_7^{″}t)\}}^2\text{.}$$ (5)

Figure 5.

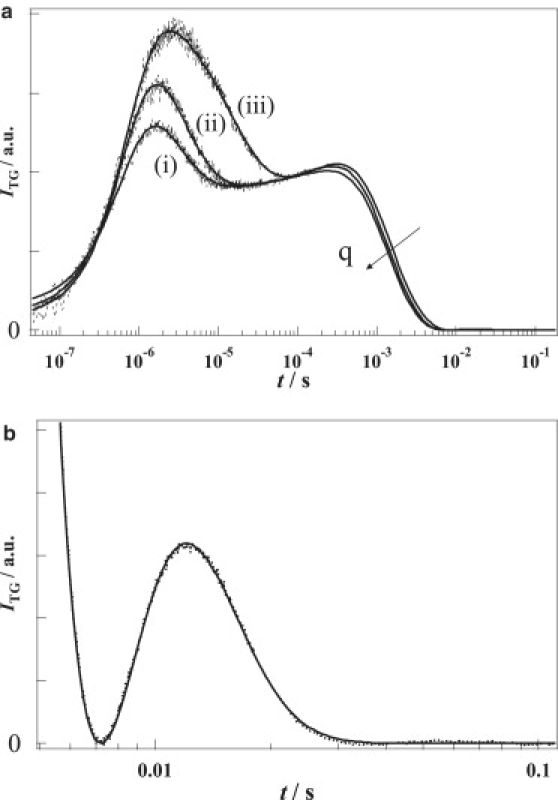
(a) Typical TG signals (dotted lines) of T218V at [Cl⁻] = 300 mM, q² = (i) 2.40 × 10¹² m⁻², (ii) 1.87 × 10¹² m⁻², and (iii) 4.20 × 10¹¹ m⁻². Solid lines are the best-fitted curves using Eq. 5. (b) The longer time part of the signal shown in (a) at 2.40 × 10¹² m⁻².

Six of the rate components, k″_i (i = 1–6) were almost independent of q², and they agreed with the reaction rate constants of k_i (i = 1–6) from the TA signals. Conversely, the smallest rate constant k″₇ decreased with decreasing q². This q² dependence indicates that the decay due to diffusion is not negligible for this process (Fig. 5 b). From the reaction rate constant of k₇ by the TA measurement and k″₇ (=D_Pq² + k₇), D of T218V was determined to be D_P = 4.8 ± 0.1 × 10⁻¹¹ m²/s.

It is noteworthy that the TG signals at various q² were reproduced quite well by Eq. 5; that is, the decay in a time range of 10⁻⁴–10⁻³ s became slower with decreasing q². This is normal behavior for the TG signal and completely different from the behavior of NpHR. This observation indicates that the diffusion signal of Cl⁻ is not observed in this case. We consider that there are two possible reasons for accounting for the weak signal of Cl⁻. First, if we assume that Cl⁻ release occurs on the O formation process in a similar manner to the wild-type protein, the formation of O (or the decay of L2) for T218V (31 ms) is too slow compared with the diffusion rate of Cl⁻ (D_Cl⁻q² = 0.23–1.3 ms). Hence, the released Cl⁻ should diffuse before the accumulation of Cl⁻ is large enough to cause a detectable refractive index change. Second, because the L2 decay of T218V is a rate-limiting process, the O intermediate does not accumulate in this photocycle. This indicates that the Cl⁻ rebinding rate is faster than the release rate. These two factors make the TG observation of the Cl⁻ diffusion signal difficult. Indeed, when we simulated the TG signal including the contribution of Cl⁻ with the rate constants for T218V, the signal was almost identical to the signal calculated without the Cl⁻ contribution. Hence, the absence of the Cl⁻ signal for T218V is consistent with the finding from NpHR. On the other hand, if we assume that the Cl⁻ was released on a much faster process, such as k₃ or k₄, the Cl⁻ signal should be observed. Hence, we consider that the release of Cl⁻ occurs on the O formation process. This is similar to the wild-type situation.

A recent study on the x-ray crystallographic structure of the L1 intermediate of T203V mutant (equivalent to T218V of NpHR) of HR from H. salinarum (HsHR) showed that the L1 intermediate still contains Cl⁻ in the protein structure, and the release of Cl⁻should take place at a later process (43). This observation is consistent with our findings.

Diffusion coefficient

The diffusion coefficients of NpHR (32 kDa) at [Cl⁻] = 300 mM and 4 M, and T218V at [Cl⁻] = 300 mM were determined to be 4.4, 5.0, and 4.8 × 10⁻¹¹ m²/s, respectively. A small difference in D depending on the Cl⁻ concentration and the mutation is difficult to explain. This could be due to a small conformational difference attributable to the different environment or the charge effect around the protein. However, it is more important to note that these values are much smaller than diffusion values of proteins with similar molecular mass (e.g., cytochrome peroxidase: 35 kDa, D = 9.4 × 10⁻¹¹ m²/s; luciferase: 35 kDa, D = 8 × 10⁻¹¹ m²/s), but close to D-values of proteins with much larger molecular mass (e.g., plasminogen: 89–94 kDa, D = 5 × 10⁻¹¹ m²/s; myeloperoxidase: 150 kDa, D = 4.8 × 10⁻¹¹ m²/s; L-lysin-2-monooxygenase: 190 kDa, D = 4.8 × 10⁻¹¹ m²/s) (44,45). The small D could be due to the effect of the surfactant molecules around the proteins. There has been no detailed investigation on the relationship between D and the protein-surfactant complex. However, D of octopus rhodopsin was determined to be 6.0 × 10⁻¹¹ m²/s (46), which is larger than the D of NpHRs. Furthermore, it was shown that the effect of the detergent molecules on D was insignificant in that report. If this observation applies to the case presented here, the small D may suggest that NpHR solubilized in the detergent forms exists as a larger species, such as a homooligomer consisting of 3–6 molecules. Previously, the crystal structure of HsHR was reported, and it showed that HsHR forms a homotrimer arrangement with threefold symmetry (27). Moreover, BR also forms a trimer in the crystal and the cell membrane of archea (47). Recently, Sasaki et al. (48) observed the trimer of NpHR solubilized by DDM by column chromatography and cross-linking experiments. The conditions used in that report are identical to those used in this study. Our measured small D does not contradict these previous reports.

It is also noteworthy that only one diffusion component of the protein was observed. This observation shows that D of NpHR does not change during the reactions (i.e., D_P = D_R). Previously, pressure-dependent experiments showed that the protein volume of NpHR decreased 60–80 cm³/mol on N, O, and NpHR′ states (32). However, this volume change is much smaller than the whole protein volume (∼26,000 cm³/mol) (49,50), and it is hard to consider that this induces notable D-value changes. In fact, if we use the Stokes-Einstein equation, we expected D to change <0.1%. Therefore, the change in D caused by the volume contraction of the protein is negligible. Photoreactions of many sensory proteins including a visual rhodopsin from octopus have been studied by the TG method, and it was found that most of these proteins showed large D changes during the reactions (15–23,46). The D change is an indication of a change in intermolecular interactions. For example, when the hydrogen-bond network changes from an intramolecular type to an intermolecular one between the protein and water by, e.g., unfolding of the secondary structure, the intermolecular interaction, i.e., friction for the translational motion, increases such that D decreases. Therefore, a change in D is clear evidence for showing an increase in protein-water intermolecular interactions or interprotein interactions accompanying the conformational change. We think that large conformational changes affecting intermolecular interactions are essential to biological function of signaling proteins. For example, in the case of the D75N mutant of N. pharaonis sensory rhodopsin II (NpSRII), one of the signal transferring archaeal rhodopsins, the diffusion coefficient changed only when in complex with the transducer protein, which transfers the signal to the following cytoplasmic Che proteins. However, the D did not change in the photocycle of NpSRII alone (19,20).

In NpSRII, cytoplastic opening and/or tilting of helix F (51), which may change the hydrogen-bond network between the protein and water molecules was suggested. For the release of Cl⁻ bound to NpHR, it was also suggested that changes in the hydration state of Cl⁻ could be one of the driving forces of Cl⁻ movement (7). Hence, it is not surprising if these changes induce D-change. However, D-change was not observed for these proteins. Hence, although hydrogen-bonding changes could be important as a driving force for the movement of Cl⁻, we have to consider that the changes in H-bonding are not extensive and therefore do not lead to measurable changes in D but could be local structural changes. We consider that large conformational changes, which are necessary for achieving light sensing, are not required for the ion pumping.

Enthalpy change

Finally, the enthalpy change of the first intermediate of NpHR is briefly discussed. The amplitude of the thermal-grating signal represents the thermal energy released from the photoexcited protein (12,14,15,19,23). Under the experimental condition of Fig. 2, the amplitude is proportional to the difference of the energy between the photoexcitation photon and the enthalpy of L1. Therefore, the enthalpy of the L1 can be determined from δn_th and the photon energy by using the relationship of

$$\frac{\delta n_{th}\left(sample\right)}{\delta n_{th}\left(reference\right)}=1-\frac{\Phi \Delta H}{h\upsilon },$$ (6)

where δn_th(sample), δn_th(reference), Φ, ΔH, and hν are the amplitudes of the thermal-grating components of NpHR, the calorimetric reference sample, the reaction yield to create L1, and the enthalpy difference between L1 and the initial state and photon energy, respectively. Previously, Losi et al. (31) reported the value of the reaction yield of the generation of L1 as Φ = 0.52. By using this value, we determined the enthalpy difference of L1 as ΔH = 149 ± 37 kJ/mol.

This value is much larger than the previously reported value (27 ± 11 kJ/mol) determined by the photoacoustic method (31). A possible origin of the difference may be due to the difference between the buffers used. In this study, a Tris-HCl buffer was used, whereas a phosphate buffer was used in the previous study. The ΔH of the K intermediate was shown to depend on the buffer. Here, it was shown that the ΔH was 30 kJ/mol larger when using a Tris-HCl buffer compared with the results obtained using a phosphate buffer (31). Therefore, ΔH of L1 could be larger due to a similar buffer effect. Losi et al. (31) interpreted this ΔH dependence on the solvent type as “an enthalpy-structural volume change compensation”, which is associated by the breaking and formation of hydrogen bonds. This would be examined by performing TG measurements in various buffers and detergents. Furthermore, for calculation of ΔH from the photoacoustic signal, it is necessary to assume that ΔH is temperature independent. However, it was shown previously that ΔH is temperature dependent for several protein reactions such as PYP and AppA (23,52). As such this temperature independence assumption is not always correct. This temperature dependency of ΔH can also be a cause for the ΔH difference.

Previously, ΔH of the L intermediate of NpSRII without the transducer protein was measured by the TG method and reported to be 169 kJ/mol. This value is large yet similar to the value calculated for L1 of NpHR. NpSRII without the transducer protein is reported to act as a transmembrane proton pumping protein (53,54). As such, the function of NpSRII becomes similar to NpHR. The archaeal rhodopsins use the majority of the absorbed photon energy to transport ions across the cell membrane.

Conclusion

We investigated the photoreaction of NpHR by the TG method in the time domain. The TG signal was primarily explained by the reaction dynamics that were detected by the absorption change. This fact indicates that the protein structure of NpHR is rather rigid, and any conformational change results in the absorption change. However, a detailed examination showed that there is a spectrally silent diffusion process of Cl⁻. The rates of releasing Cl⁻ and uptake of the ion were determined from the q²-dependence of the signal. We believe this is the first direct observation of the release of Cl⁻ and uptake of the ion by a spectroscopic method in the time domain without using any mutants or concentration-dependent study of Cl⁻. The diffusion coefficient of the protein does not change during the photoreaction. This result indicates that the hydrogen-bond network of the protein is not significantly rearranged between inter- and intramolecular interactions. The enthalpy change of the first intermediate of NpHR was determined. It was found that the value (149 kJ/mol) is quite large, and the archaeal rhodopsins use the majority of the absorbed photon energy to transport ions across the cell membrane.