A Free-Energy Approach for All-Atom Protein Simulation

Abstract

All-atom free-energy methods offer a promising alternative to kinetic molecular mechanics simulations of protein folding and association. Here we report an accurate, transferable all-atom biophysical force field (PFF02) that stabilizes the native conformation of a wide range of proteins as the global optimum of the free-energy landscape. For 32 proteins of the ROSETTA decoy set and six proteins that we have previously folded with PFF01, we find near-native conformations with an average backbone RMSD of 2.14 Å to the native conformation and an average Z-score of −3.46 to the corresponding decoy set. We used nonequilibrium sampling techniques starting from completely extended conformations to exhaustively sample the energy surface of three nonhomologous hairpin-peptides, a three-stranded β-sheet, the all-helical 40 amino-acid HIV accessory protein, and a zinc-finger ββα motif, and find near-native conformations for the minimal energy for each protein. Using a massively parallel evolutionary algorithm, we also obtain a near-native low-energy conformation for the 54 amino-acid engrailed homeodomain. Our force field thus stabilized near-native conformations for a total of 20 proteins of all structure classes with an average RMSD of only 3.06 Å to their respective experimental conformations.

Introduction

Methods for de novo protein folding and tertiary structure prediction require accurate, transferable potentials (1). Molecular-mechanics force fields based on physical interactions promise the greatest degree of transferability and predictive value. However, presently such force fields play only a marginal role in protein structure prediction assessments, which are dominated instead by template-based methods and knowledge-based scoring functions (2,3). This is due in part to the computational cost of physics-based models, but also to the lack of transferability of the available potentials. For medium-sized proteins, de novo folding studies starting from the unfolded ensemble mostly use coarse-grained (4) or knowledge-based potentials (5,6) to overcome the timescale gap between the individual simulation step and the experimental folding time. Kinetic simulations using molecular mechanics force fields have, however, demonstrated their accuracy for a number of small proteins and peptides (7,8).

The inherent difficulty to develop transferable, physics-based potentials arises from the long timescales that must be sampled to directly parameterize and validate a force field for a family of proteins. Force fields parameterized for small molecules with a much wider range of physico-chemical characteristics are often difficult to transfer to larger biomolecular systems (7) and may have a secondary structure bias (9–11). There is a complex interplay of many interactions (electrostatic interactions in a nontrivial dielectric environment; hydrogen bonding and solvation effects) that all cooperate to stabilize one native conformation among a multitude of competitors.

Here we pursue an alternate, free-energy approach to protein simulation, which can be applied to structure prediction and folding. This approach permits a rational, decoy-based development of an all-atom force field, itself based on models of the most important biophysical interactions for family of medium-size proteins (12). It is based on the thermodynamic hypothesis (13), which stipulates that many proteins in their native conformation are in thermodynamic equilibrium with their environment. Based on this paradigm, the native conformation of a protein corresponds to the global optimum of its free-energy surface (14,15) in a suitable biophysical model. Such a model must parameterize the internal free energy of a particular backbone conformation, including side-chain and solvent entropy, and thus permits the direct comparison of the internal free energy of different backbone conformations (decoys). Comparing the energies of large libraries of decoys (16) with the energy of the native conformation then helps to select force-field parameters that stabilize the native conformations of many proteins as the optimum of the force field.

A variety of methods can be used with such force fields to describe protein thermodynamics (17), to analyze the protein-free energy landscape (14) and the folding kinetics (18,19). Many recent investigations have shown that implicit solvent force fields can describe the folding process in agreement with experimental investigations (20,21). The development of universal force fields that can treat a wide variety of proteins remains a significant challenge (20). In this study, we take one important further step toward the rational and systematic development of a universal free-energy force field that can fold α-helical, β-sheet, and mixed secondary structure proteins. We also demonstrate that free-energy-based simulation methods are capable to fold medium-sized proteins using distributed computing strategies. We use nonequilibrium sampling methods, such as the basin-hopping method (22) or its generalizations (23,24), to exhaustively sample the protein energy landscape starting with completely unfolded conformation. In all cases reported here, near-native conformations are uniquely identified as the lowest energy conformation of the population.

In the first part of this investigation we show that a small correction to PFF01 (25) permits us to treat three nonhomologous β-hairpins with 14–17 amino acids to 2.5–3.8 Å backbone root mean-square deviation of the respective native conformations. This advance would be worth little if the modified force field, PFF02, would destabilize the helical proteins we have previously investigated. In the second part of this investigation, using extensive decoy sets (25–32), we demonstrate that the new force field stabilizes near-native conformations of all proteins that we have previously folded. In addition, we show that PFF02 stabilizes near-native conformations of 32 proteins of the ROSETTA decoy set, excluding those that are stabilized by external ligands. With an average Z-score of −3.46, PFF02 has a higher selectivity than other scoring functions. In a third part of this investigation, we use nonequilibrium sampling techniques for four structurally different proteins starting from completely unfolded conformations. For all proteins investigated—the 40-amino-acid all-helix HIV accessory protein, the 20-amino-acid three-strand all-β peptide (33–35), the 29-amino-acid zinc-finger protein of ββα structure (36), and the 54 amino-acid engrailed homeodomain (37)—we find near-native conformations with the lowest energy.

Methods

With this study, we extend our efforts to develop a method that exploits Anfinsen's thermodynamic hypothesis (13) to model large-scale structural changes of proteins in a free-energy approach (12). In this approach, each protein backbone conformation is assigned an internal free-energy, obtained by integrating the solvent degrees of freedom, such that the relative occupation probability of two states i and j with free-energies E_i, E_j, respectively, is given by

$$\frac{p_{\text{i}}}{p_{\text{j}}}=\exp \left(-\beta \left(E_{\text{i}}-E_{\text{j}}\right)\right)\text{.}$$

The advantage of this approach is that it decouples the sampling of the conformational space from the computation of relative free-energies of conformations. We can therefore use any sampling technique, including nonequilibrium methods (38–43), to generate a protein conformational ensemble—as long as the low-energy region of the free-energy surface, including the native conformation, is fully reproduced. Nonequilibrium sampling methods, e.g., Monte Carlo, comprise a move-generation step and an acceptance criterion. In the following, we only use move-generation methods that gradually deform the conformation by small changes of the dihedral angles of the protein, thus generating a nearly continuous protein trajectory. To accelerate the sampling of the conformational space, we use a simulated annealing protocol (44) that starts at a high temperature to generate a new conformation based on the last accepted conformation. At the end of this move-generation step, we use an acceptance criterion (see below) (45) to either accept or discard the generated move (22). To clearly differentiate low-lying metastable conformations, a low final temperature in the annealing simulations is essential. Entropic effects differentiating such metastable conformations must thus be incorporated into the effective potential for the microstate.

Force field

A free-energy force field approximates the internal free energy (47) of the peptide/protein and must therefore account for differential solvation effects among protein microstates in the folded, the partially folded, and the unfolded ensemble. Entropic contributions to the hydrophobic effect, i.e., changes in the solvent entropy upon exposure of the aliphatic groups of the protein, are described in an implicit solvation model. In addition, the electrostatic model must be adapted to account for the nontrivial screening of electrostatic interactions by the solvent (48).

We extend the all-atom free-energy protein force field (PFF01) (12,25) by adding terms that differentiate between the backbone dipole alignments found in different secondary structure elements (49) and a Ramachandran potential for backbone dihedral angles:

$$V=V_{\text{PFF01}}+{\lambda }_{\text{bb}}{V}_{\text{bb}}+{\lambda }_{\text{tor}}{V}_{\text{tor}}\text{.}$$ (1)

The additional electrostatic interaction V_bb was proposed in Avbelj and Moult (49) to differentiate different types of secondary structure. The torsional potential is given as

$$V_{\text{tor}}=\sum _{\text{i}}\text{exp}(-{\gamma }_{\varphi }{\left({\varphi }_{\text{i}}-{\varphi }_0\right)}^2-{\gamma }_{\psi }{\left({\psi }_{\text{i}}-{\psi }_0\right)}^2),$$ (2)

and was chosen to provide an additional stabilization of the region in the Ramachandran plot that corresponds to β-sheet formation. The values ϕ_i,ψ_i designate the backbone dihedral angles of amino acid i. We used ϕ₀ = −110°, ψ₀ = 130° and γ_ϕ = 5 × 10⁻³ deg⁻², γ_ψ = 1.25 × 10⁻³ deg⁻² irrespective of any amino-acid propensities; i.e., these values were used for all amino acids (except proline). The prefactors λ_tor, λ_bb control the relative weight of the correction terms; in PFF02 they are chosen as λ_tor = −0.6 kcal/mol and λ_bb = 1.0. The full force-field parameterization is provided as Supporting Material.

Simulation protocols

Basin hopping

We use an adapted version of the basin-hopping technique (22,50–52), which simplifies the original potential energy surface by replacing the energy of each conformation with the energy of a nearby local minimum. In contrast to earlier work (53), we use a simulated annealing (SA) process (44) for the minimization step. Within each SA simulation, new configurations are accepted according to the Metropolis criterion. The temperature is decreased geometrically from its starting (chosen randomly from exponential range of temperatures) to the final value (2 K). The number of steps in the cycle N increased with the square-root of the cycle number m (N = 10,000 × $\sqrt{m}$). In the folding simulations, a new conformation at the end of one annealing cycle is accepted if its energy difference to the current configuration was no higher than a given threshold energy ɛ_T (55). We used ɛ_T = 1 kcal/mol for the β-hairpins and ɛ_T = 3 kcal/mol for all larger proteins.

Evolutionary algorithm

We have generalized the basin-hopping method to a population of size N (here N = 64), which is iteratively improved by P concurrent dynamical processes (we used P = 512) (23,43). The whole population is guided toward the optimum of the free-energy surface with a simple evolutionary strategy. This strategy must balance energy improvement and diversity of the population. Conformations are drawn from the population and subjected to an annealing cycle. At the end of each cycle, the resulting conformation is either integrated into the active population or discarded maintaining diversity and achieving lower average energy of the population. Similar strategies were explored in simulations of the 23 amino-acid BBA5 protein (57) and 40 amino-acid HIV accessory protein (24,52). This algorithm was implemented on a distributed master-client model in which idle clients request a task from the master. The master maintains and updates the population of active conformations of the population and distributes the work to the clients.

Results and Discussion

β-sheet peptides

PFF01 (12) was specifically parameterized for helical proteins and has shown difficulties with β-hairpins, which is the starting point of this investigation. We have attempted to fold three nonhomologous hairpin peptides with PFF01 and selected the highly structured 14-amino-acid synthetic peptide (PDB code: 1K43), the 17-amino-acid N-terminal mutant peptide of ubiquitin (PDB code: 1E0Q), and the 17-amino-acid hairpin of the wild-type barnase (residues 85–102, PDB code: 1A2P) as representative examples for small, stable β-sheet peptides easily amenable to our simulation approach. For each protein we performed 10 independent basin-hopping simulations (22,43) starting from completely unfolded conformations. In all simulations, we find no near-native conformations in the resulting low-energy ensemble generated by the accepted conformations of the basin-hopping trajectories (see Fig. 1).

Figure 1.

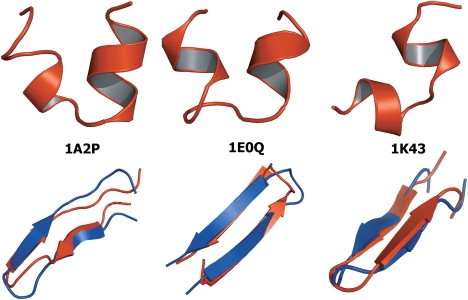
The top row shows the misfolded structures of 1A2P, 1E0Q, and 1K43 in PFF01. The bottom row shows the overlay of the folded (red on the web and upper curve in print) and the experimental (blue on the web and dark color in print) conformations of the same peptides in PFF02.

Several studies have attributed the difference in electrostatic stabilization of β-sheet secondary structure over helical conformations to differences in the alignment of the backbone dipoles in both types of conformations (48,58). We have therefore investigated the local correction to the backbone electrostatics (V_bb, see Methods) proposed in Avbelj and Moult (49) as a possible source of overstabilization of helical content in PFF01. This correction can be interpreted as a modification of the short-range dielectric constant/polarizability of the participating groups and is easily incorporated in the model. Using this correction to PFF01 alone (λ_tor, see Methods), we repeated the folding simulations for several increasing values of λ_bb. For λ_bb > 0.8, 1K43 folds into a near-native conformation with a backbone root mean-square deviation (bRMSD) of 2.8 Å, but five of 10 simulations result in helical conformations with energy differences that are only 0.5–1.2 kcal/mol higher than their misfolded competitors. The bRMSD of the lowest energy structure of the other two peptides remains at 7.14 Å and 5.12 Å for 1E0Q and 1A2P, respectively. Many conformations with backbone hydrogen-bonding characteristic of a β-sheet topology emerge, but these conformations are still energetically higher than the helical conformation. The energetic difference between the misfolded helical structures and the near-native hairpin conformations is significantly reduced in comparison to PFF01, but the local correction alone appears insufficient to fold the proteins into β-sheet structures. We have therefore investigated the effect of an additional backbone torsional potential (V_tor, see Methods), which can contribute to a differentiation between various secondary structure classes. In accordance with the prior development of this approach, this term should contain no amino-acid specific correction and thus uses only the average values of β-sheet dihedral angles as a reference point. Again, we conducted 10 independent basin-hopping simulations for increasing values of λ_tor (see Methods).

For λ_tor > 0.25 kcal/mol, λ_bb = 1 simulations for all three peptides converged to conformations close to their respective native conformations (see Fig. 1). The bRMSDs of the lowest energy structures to the native conformations were 2.67 Å, 3.47 Å, and 2.53 Å for 1K43, 1E0Q, and 1A2P, respectively. The overlay of the experimental structure with the lowest energy conformation found in the simulations is shown in the bottom panel of Fig. 1. We also find that 2 of 3, 4 of 4, and 4 of 4 native backbone hydrogen bonds are correctly reproduced for 1A2P, 1K43, and 1E0Q, respectively. The size of the correction for β-hairpin stabilization is small, favoring β-sheet conformations over helices by ∼0.3 kcal/mol per amino acid, where such a difference occurs. By varying the prefactors, we find only a small window in which both α-helical and β-sheet secondary structure is stabilized.

Force-field validation

The modified force field is thus a good candidate to stabilize the native conformation of a larger family of proteins (in comparison to PFF01) as its global optimum. To validate the force field we have 1), checked the stability of the helical proteins we have investigated before; and 2), investigated decoy sets for a set of larger proteins that cannot be readily folded with the available computational resources.

Helical proteins

We must insure that the additional terms introduced above do not destabilize helical proteins. A stringent test is provided by the decoy sets of the folding studies of the helical proteins folded with PFF01. Such a test only validates the relative stability of the native conformation with respect to the decoy set; only de novo simulations (as reported below) can determine global stability. We have therefore collected all conformations generated in previous folding simulations and ranked them in the new force field. According to the thermodynamic hypothesis, the near-native conformations should have lower energies than nonnative decoy conformations. Using data from previous investigations we compiled decoy sets for the engrailed homeodomain (∼900 decoys), the Trp-cage protein (∼1200 decoys), 2A3D (∼1000 decoys), the villin headpiece (∼4000 decoys), and the bacterial ribosomal protein (∼1000 decoys). These decoys sample the native ensemble as well as many competing low-energy metastable states. Since many conformations lie just a few kcal/mol in (free) energy above the native conformation in PFF01, testing the force field against these decoy sets is a strong test for the selectivity of PFF02.

We find that PFF02 stabilizes near-native conformations of all investigated proteins against the decoy sets. The bRMSD of the lowest energy conformation deviates by 2.33 Å, 2.42 Å, 2.68 Å, 4.59 Å, and 3.76 Å from the native conformation for the Trp-cage protein (1L2Y), engrailed homeodomain protein (1ENH), 2A3D (a designed three-helical bundle), the villin headpiece (1VII), and the bacterial ribosomal protein L20 (1GYZ), respectively. It is encouraging that the native conformation of the bacterial ribosomal protein L20 is stabilized despite the fact that it has a long loop region (Gly²⁷-Leu³⁵). The overlays of the native conformation with the lowest energy conformation for the villin headpiece, the engrailed homeodomain protein, and the bacterial ribosomal protein L20, are shown in the top panel of Fig. 2. The bottom panel shows energy versus bRMSD plots for the respective proteins.

Figure 2.

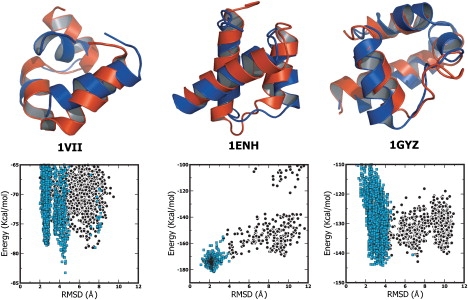
(Top panel) Overlay of the best energy decoys selected by PFF02 from the decoy sets generated in earlier folding studies (red) and the experimental (blue) conformations of the villin headpiece (1VII, 36 amino acids), the engrailed homeodomain (1ENH, 57 amino acids), and the bacterial ribosomal protein L20 (1GYZ, 60 amino acids). (Bottom panel) Energy versus bRMSD for the decoys sets of the three proteins. The black points indicate decoys generated starting from random conformations, while the cyan points indicate decoys generated starting from the folded conformation.

Rosetta decoy sets

The all-atom ROSETTA decoy sets (59) were specifically designed for the evaluation of force fields and scoring functions. They provide a set of ∼2000 conformations for a large, structurally diverse family of proteins ranging from 30–85 amino acids in size. The ROSETTA scoring function, as well as individual components of standard molecular-mechanics force fields (Lennard-Jones interactions, electrostatics, etc.), fail to differentiate native from near-native decoys in these datasets. Several knowledge-based scoring functions, such as RAPDF (60) or DFIRE (61), in contrast, perform very well. The use of these decoy sets is thus a challenging test for the selectivity of scoring functions for protein structure prediction. In this investigation, we excluded proteins that are stabilized by transition metal clusters or other ligands, as such interactions are not implemented in this force field.

The Z-score (the difference between energies of near-native decoys to the mean energy of the decoy set in units of its standard deviation) gives a quantitative measure of the selectivity of the force field. We generated near-native conformations for 32 proteins of the latest ROSETTA decoy library, which generally deviate, at most, 4 Å from the experimental conformation. Exceptions are 1AM3 and 1UTG, where deviations of 4.05 Å and 5.4 Å, respectively, are observed (top panel of Fig. 3, Table 1 for all data). These deviations arise because both proteins are dimeric in their biological conformation, but included in isolation in the decoy set.

Figure 3.

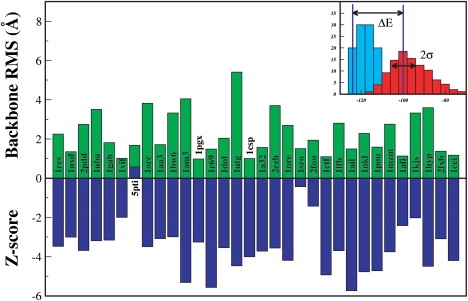
Z-Scores (inset) measure the energetic difference of near-native conformations to the average energy of the decoy set in units of its standard deviation. The vertical axis arranges the ROSETTA decoy sets in order of increasing size. The upper-horizontal axis gives the bRMSD of the lowest energy decoy to native for the lowest energy decoy in the decoy set; obviously this approach can select only among the decoys in the database. The lower-half of the main figure shows the Z-scores of the native ensemble for decoy sets (more negative is better).

Table 1.

Z-scores and lowest energy bRMSD values for the 32 proteins of the ROSETTA decoy set studied in PFF02

PDB ID	Z-Score	RMSD (Å)	PDB ID	Z-Score	RMSD (Å)
1a32	3.72	1.57	1nre	4.19	2.69
1aa3	3.08	1.71	1orc	3.49	3.82
1afi	2.41	1.13	1pgx	3.26	0.98
1ail	5.73	1.49	1pou	4.72	1.58
1am3	5.32	4.05	1r69	5.57	1.48
1bw6	2.98	3.32	1res	3.47	2.25
1cei	4.19	1.17	1sro	0.43	1.51
1csp	4.01	1.00	1uba	3.19	3.96
1ctf	4.93	1.10	1utg	4.47	5.41
1dol	3.54	2.04	1uxd	3.00	1.35
1gab	3.16	1.81	1vif	2.00	1.01
1hyp	4.49	3.59	2ezh	3.56	3.70
1kjs	2.02	3.32	2fow	1.43	1.94
1lfb	3.69	2.80	2fxb	3.09	1.37
1mzm	3.75	2.75	2pdd	3.69	2.74
1nkl	4.77	2.28	5pti	0.58	1.68

To arrive at a meaningful comparison of the energies, we relaxed the ∼2000 decoys for each of the proteins in the decoy library in PFF02 (one simulated annealing simulation, 50,000 steps, geometrically cooling from T = 200 K to T = 3 K). This procedure maps each decoy to a local minimum of the force field; the average change in bRMSD between the starting and relaxed conformation is <0.2 Å.

For all proteins, PFF02, with the exception of 1UTG, selects near-native decoys with a bRMSD of <4 Å as the lowest energy structure (see Fig. 3). The average deviation between the experimental and near-native conformation in the force field for the set of 32 proteins was 2.14 Å. Fig. 3 also indicates that there is little correlation between the size of the protein and the accuracy with which the local minimum of the force field agrees with the experimental conformation. Of the resulting Z-scores (lower panel of Fig. 3), 29 of 32 are <−2, indicating a good selectivity of the force field for these proteins. The average score of −3.46 is lower than the Z-scores computed for previously reported scoring functions for the same decoy sets. Only for 5PTI do we find a positive Z-score, indicating that the near-native conformation is near the mean energy of the decoy set. This is explained by the fact that 5PTI has long unstructured regions stabilized by two disulfide bridges, which are not accounted for in this force field. Since the ROSETTA decoys were specifically generated to span a wide range of conformations for each protein, these data indicate that PFF02 stabilizes near-native conformations of a large family of small- and medium-size proteins of all secondary structure classes.

Sampling the energy landscape

Simulations starting from completely extended structures offer the most stringent validation of the free-energy methodology. In the following we report simulations for four proteins with completely different secondary structure: For the 40 amino-acid three-helix bundle HIV accessory protein (1F4I), the 20-amino-acid three-stranded GSGS peptide, and a 29-amino-acid ββα zinc finger protein (1RIK), we generated 20 independent trajectories with the basin-hopping method (see Methods). For the larger 54-amino-acid engrailed homeodomain protein (1ENH), we used a massively distributed computational architecture to demonstrate convergence to a near-native conformation from completely unfolded conformations in ∼24 h. Each simulation started from a completely unfolded conformation with a bRMSD of 37 Å (1F4I), 10 Å (GSGS), 23 Å (1RIK), and 53 Å (1ENH) for the four proteins, respectively. The results of these simulations are summarized in Fig. 4.

Figure 4.

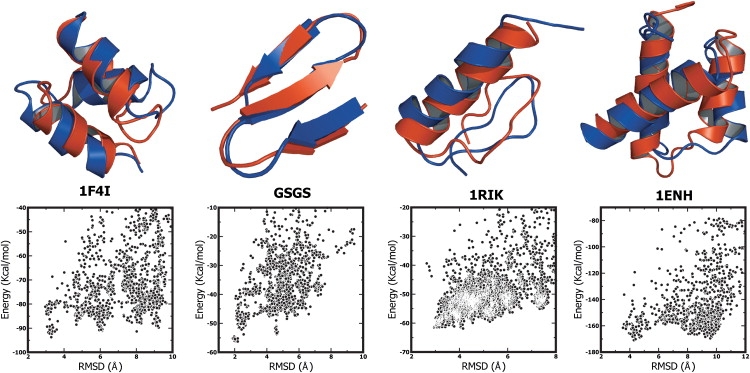
(Top row) Overlay of the lowest-energy (red) and the experimental (blue) conformations of the HIV accessory protein, the GSGS peptide the zinc-finger protein 1RIK, and the engrailed homeodomain protein 1ENH. (Bottom row) Energy versus bRMSD for all accepted conformations generated in the simulations. These plots indicate the existence of a single stable native minimum for all three peptides. For the three-helix bundle, there is one metastable conformation with a bRMSD of ∼6 Å; for the β-sheet protein, one conformation at 4.3 Å. The ββα zinc finger protein has a single folding funnel that is broader than for the other two systems. The engrailed homeodomain protein has a metastable conformation at ∼10 Å.

Three-helix bundle

For the HIV accessory protein (Fig. 4 a), the lowest energy structure (overall bRMSD 3.29 Å) shows a perfect alignment of all secondary structure elements and only small deviations in the loops connecting the defined secondary structure elements. The second helix (Glu¹⁶ to Phe²⁴) of the lowest-energy structure of the HIV accessory protein occurs at the same position of the amino-acid sequence as in the native conformation but has a slightly different tertiary alignment with the other helices, because of the succeeding loop (Ala²⁵ to Glu³⁰) folds in a different direction. Considered independently, the helical segments (Lys³ to Leu¹²; Glu¹⁶ to Phe²⁴; and Asn³¹ to Ser³⁹) deviate only by 0.36 Å, 1.11 Å, and 0.53 Å from their native conformation, respectively. The overlay illustrates that helices H1 and H3 align very well, while the alignment of H2 with either of the other two helices is less pronounced, presumably because of the variation in the turn region. This is also illustrated in the C_β-C_β distance difference map in Fig. 5 a. The bottom row of Fig. 4 demonstrates the reproducible and predictive folding of the protein: There is a well-defined single low-energy ensemble with bRMSD 3.29 Å and two sets of metastable conformations with a bRMSD of ∼6 Å and 8 Å to the native conformation. These conformations have an energy difference of 2.6 kcal/mol and 2.4 kcal/mol, respectively, to the native conformation. Interestingly, these conformations have nearly the same secondary structure, but a different tertiary arrangement than the native conformation (mirror image problem), indicating that PFF02 is capable of selecting the right tertiary arrangement.

Figure 5.

(a–d) C_β-C_β distance difference maps of the lowest energy conformation for the HIV accessory protein (1F4I), GSGS peptide, zinc finger protein (1RIK), and Engrailed Homeodomain protein (1ENH). A pixel in row i and column j of the grayscale distance map indicates the difference in the C_β-C_β distances of the native and the folded structures. Solid (shaded) squares indicate that the C_β-C_β distances of the native and other structure differ by <3.0 (6.0) Å, respectively. Open squares indicate larger deviations.

Three-stranded β-sheet

We have performed 20 independent basin-hopping simulations on the 20-amino-acid GSGS peptide, which was extensively investigated with phenomenological and all-atom molecular dynamics studies (33). We find that three of the four lowest energy trajectories converge to near-native conformations with a bRMSD to the native conformation of 2.19, 2.26, and 2.67 Å, respectively. The lowest-energy conformation of the GSGS peptide (Fig. 4 b, overall RMSD 2.19 Å) shows a perfect alignment of the three secondary structure elements and only small deviations in the loops connecting the defined secondary structure elements.

Aligned independently, the β-sheet the regions from Thr¹ to Asn⁵, Thr⁸ to Asn¹³, and Thr¹⁶ to Tyr¹⁹ agree to within 0.50 Å, 0.55 Å, and 0.55 Å with the experimental conformation. The C_β-C_β distance difference map shown in Fig. 5 b for the GSGS peptide indicates perfect alignment to within experimental resolution. The energy versus bRMSD map (bottom row of Fig. 4) demonstrates that a near-native conformations is lowest, but indicates a secondary metastable minimum at 4.6 Å bRMSD with an energy difference of 2.6 kcal/mol. The associated conformation also corresponds to an all-β structure with different hydrogen-bond pairings.

ββα protein

Zinc fingers number among the most abundant proteins in eukaryotic genomes, and occur in many DNA binding domains and transcription factors (62). They function in DNA recognition, RNA packaging, transcriptional activation protein folding, and assembly and apoptosis. Many zinc fingers contain a Cys₂His₂ binding motif that coordinates the Zn-ion in a ββα-framework (63). Because of their many functions, much effort has been directed toward the engineering of novel Cys₂His₂ zinc fingers (64). Their minimal ββα motif makes such proteins excellent test cases to study mixed secondary structure proteins. Here we investigated 1RIK, a 29-amino-acid zinc finger protein, as a representative member of this class. As the bottom panel of Fig. 4 indicates, there is a single, relatively broad funnel of conformations that all have the native α-helical and sheetlike segments. The minimum of the energy corresponds to a conformation with 4.15 Å bRMSD to the experimental conformation (see overlay), which agrees in the helical section (Arg¹⁴-Asn²⁷) to within 0.88 Å of the native conformation. The overlay of the lowest energy conformation with the experimental conformation is shown in Fig. 4 c and the respective C_β-C_β distance difference map is shown in Fig. 5 c. Both turns connecting the helical with the first sheetlike segments and the two sheet regions are predicted correctly. There is a large set of conformations with even smaller bRMSD and nearly the same energy, which all have the same secondary structure but differ in their alignment of the helix and the β-sheet regions. In the absence of the stabilizing ion, the crucial enthalpy contribution stabilizing one single conformation from this ensemble is missing in PFF02, which explains the occurrence of this relatively broad isoenergetic family of conformations.

Engrailed homeodomain

The engrailed homeodomain has served as a model system in a large number of experimental (37,65) and theoretical studies of protein folding, but was never previously folded in a biophysical all-atom force field. Here we performed 20 cycles of the evolutionary algorithm (1.5 × 10⁹ energy evaluations in 566 CPU days on 512 3 GHz off-the-shelf processors; see Methods) starting from a single unfolded conformation (bRMSD 53 Å). The energy versus backbone RMSD plot (bottom panel of Fig. 4 d) falls into two broad low-energy ensembles that are separated by 1.4 kcal/mol in energy. The metastable state has the same fraction of helical content as in the native state and all three helices are correctly predicted including the N-terminal unstructured loop. Completely different tertiary arrangement of the helices is responsible for the high bRMSD of this state. Note that the evolutionary algorithm does not sample conformations according to their thermodynamic probabilities, but is a nonequilibrium multiconfigurational approach. The number of times a particular conformation is visited in the simulation is thus not indicative of its thermodynamic population, which is solely determined by the energy difference to the native (lowest energy) conformation.

The good agreement of the experimental and the lowest-energy simulated conformation is illustrated in the top panel of Fig. 4 d. Considering the whole molecule, the lowest energy conformation had a bRMSD of 4.28 Å to the native conformation, which underestimates the performance of PFF02, because the amino acids (Arg¹-Ser⁷) are unstructured in the experimental ensemble. Excluding this region, the best energy conformation has a bRMSD of 3.45 Å to the native conformation, while the individual helices (H1, Ser⁸-Glu²⁰; H2, Glu²⁶-Leu³⁶; and H3, Glu⁴⁰-Lys⁵³) have a bRMSD of 0.35, 0.30, and 0.44 Å to their experimental counterparts, respectively. This is also illustrated in the C_β-C_β distance difference map in Fig. 5 d.

The convergence of the energy as a function of the total number of simulated annealing cycles is shown in Fig. 6. The best energy converges quickly to a near-optimal value with the total number of simulated annealing cycles. The average energy trails the best energy with a finite energy difference, which will remain indefinitely by construction, because the algorithm is designed to balance diversity and energy convergence. The convergence of the RMSD with the number of cycles indicates a rapid collapse into a preformed ensemble that slowly settles into the native and nonnative populations. The convergence to the native conformation is driven by helix formation and hydrophobic packing, as illustrated in Fig. 7. The lowest energy structure attains its energy optimum by combining maximal energetic contributions from backbone hydrogen bonding with almost complete solvent exclusion of the hydrophobic residues Phe⁶, Phe¹⁸, Phe⁴⁷, Leu¹¹, Leu¹⁴, Leu²⁴, Leu³², Leu³⁶, Leu³⁸, and Ile⁴³. In agreement with the experimental observation, the figure illustrates the large flexibility of the protein in the first eight amino acids of the N-terminal region The gradual convergence into the native conformation is illustrated in Fig. 8, where we show the structural elements of the six lowest-energy conformations, which share nearly the same secondary structure.

Figure 6.

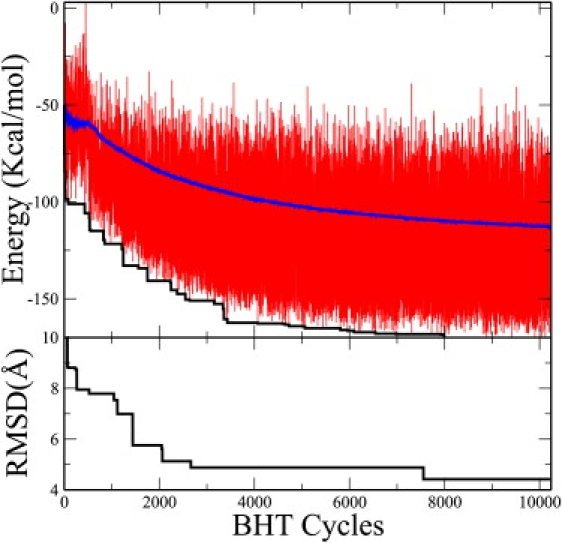
Simulations of 1ENH using the evolutionary algorithm. (Top panel) Instantaneous (red on the web and light color in print), average (blue on the web and the upper curve in print), and lowest (black) energy of the conformations that are returned asynchronously from the client nodes to the master. (Bottom panel) The RMSD of the conformation with the lowest energy in the population, indicating convergence of the simulation.

Figure 7.

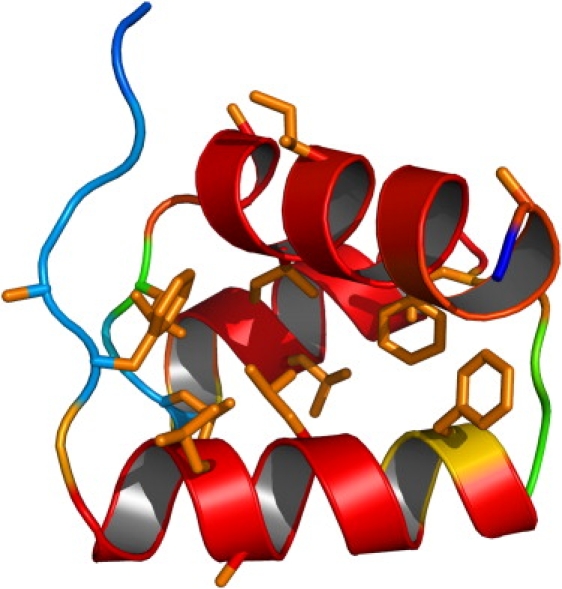
Color-coded helix content illustrated on the native conformation for 1ENH (web only: red, high helix content; yellow, intermediate; blue, low) averaged over all conformations of the final ensemble. The hydrophobic side chains are shown in orange on web.

Figure 8.

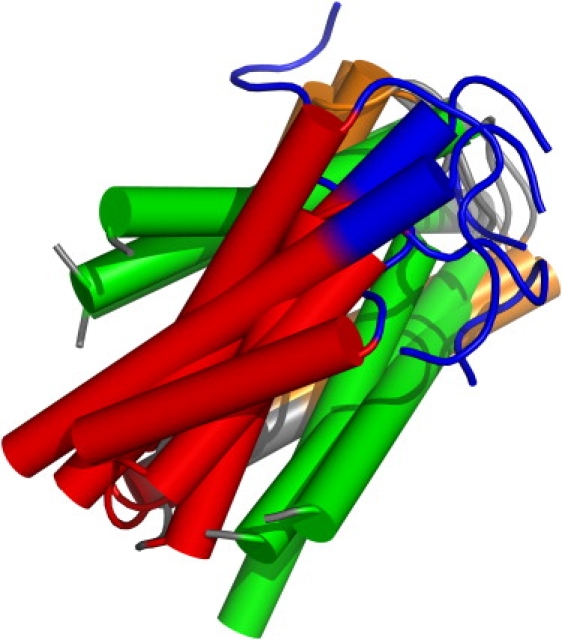
Overlay (top left) of the six low-energy conformations of the final ensemble for 1ENH (web-only: blue, unstructured region; red, H1; green, H2; and orange, H3, as defined in the text). It can be seen that the lowest-energy conformations from the ensemble have the same secondary structure.

Discussion

The free-energy methodology offers a complementary approach to explore large-scale protein structural changes at the all-atom level. Its great advantage lies in the fact that nonequilibrium simulation methods can be used to generate the complete low-energy structural ensemble without recourse to the detailed kinetics of the folding process. Such methods are orders-of-magnitude faster than the kinetic simulations, but unfortunately discard the information on the short-term kinetics of the folding process. The results of this study demonstrate the existence of a transferable free-energy force field based on physical interactions that stabilizes the native conformations of a variety of proteins as the respective global optimum of their free-energy landscapes. Our decoy-based studies demonstrate a high selectivity of the force field with respect to challenging decoys sets for a large, structurally diverse family of proteins. The results obtained in the free-modeling section of the competitive assessment of protein structure prediction (CASP7) (http://www.predictioncenter.org/, group P033) (66) suggest that this result holds beyond the 45 proteins investigated here.

Combined with complementary results from other investigations, in particular regarding kinetic and thermodynamic stability, these data demonstrate a wide applicability of the PFF02 force field. Using a variety of different simulation techniques, we have found near-native lowest energy conformations for 20 proteins with this approach (67) with an average RMSD of only 3.06 Å to the respective native conformation, as summarized in Table 2. The decoy-based, force-field development approach (20) used here is rational, systematic, and extensive. The development of PFF02 is thus an important step toward the development of universal free-energy-based simulation methodology for protein simulation. Because free-energy estimates for near-native conformations are computationally inexpensive, the free-energy approach can more easily differentiate between force field and sampling failures than can kinetic techniques (68).

Table 2.

List of proteins stabilized by PFF02 in simulations starting from completely extended conformations

	PDB ID	#AA	Topology	RMSD(Å)	Structure Overlay
Helical	1L2Y	20	α	3.11
	1RIJ	23	α	4.36
	1WQE	23	αα	2.33
	1F4I	40	ααα	3.29
	1ENH	54	ααα	3.40
	1EDK	56	ααα	4.05
Sheet	1LE0	12	ββ	1.50
	1LE1	12	ββ	1.96
	2EVQ	12	ββ	2.62
	1J4M	14	ββ	2.46
	1K43	14	ββ	2.67
	1NIZ	14	ββ	2.04
	1PG1	16	ββ	1.67
	1U6U	17	ββ	4.57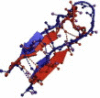
	1E0Q	17	ββ	3.47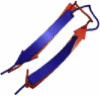
	1A2P	17	ββ	2.53
	GSGS	20	βββ	2.19
Mixed	1T8J	23	ββα	4.69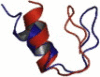
	1RIK	29	ββα	4.15
	1BHI	29	αββ	4.11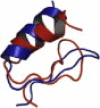

Overlays of lowest energy conformation (red on the web and light color in print) show the structural agreement with the native conformation (blue on the web and dark color in print).

With PFF02 in hand, it is possible to develop more efficient folding methods, particularly for the reconstruction of folding dynamics and the transition state ensemble. Promising candidates for such methods exist based on Monte Carlo simulation (5,6,69) and network models (18,19,70). The development of a transferable all-atom force field thus opens many new opportunities to study protein folding, aggregation, and structure prediction.

The physical origin of the correction terms in PFF02, particularly of the torsional potential, also needs further investigation. Torsional terms are used in several existing protein-force fields, but the complex interplay of different terms to stabilize one type of secondary structure over the other is not easy to resolve into unique contributions. This is partly because each of these terms is only an approximation of the physical reality of the underlying interactions. Free-energy force fields approximate the internal free-energy of the peptide, but cannot directly account for backbone conformational entropy, because only a single backbone conformation is considered, thus differential entropic contributions between different secondary structure conformations may play a role in addition to terms also encountered in force fields for the internal energy of the protein (e.g., quantum effects for dihedral bonding not accounted for by the steric interactions of the peptide backbone). Several studies have investigated the impact of dynamic flexibility on backbone propensity of α-helix and β-sheet proteins, suggesting a larger flexibility of β-sheet conformations (71–74), but these findings are not undisputed. Further complementary studies are thus required to help us better understand the torsional correction term.

Conclusions

We developed an atomistic free-energy force field for proteins based on the biophysical interactions governing protein conformational changes. Using this approach, we have been able to demonstrate for a wide variety of proteins, with all types of secondary structure, that near-native conformations are lowest in energy. For a total of 20 proteins, ranging 12–56 amino acids in size, the lowest energy conformations differ by an average RMSD of 3.06 Å to their native conformations. However, it should be noted that the efficiency of this simulation approach is rooted in the neglect of the details of the short-time kinetics of the underlying biophysical process and the crossing of kinetic barriers is accelerated in nonequilibrium simulation methods. Further studies must demonstrate the thermodynamic stability of the proteins. In addition, it is important to develop methods that can recover detailed kinetic information based on the conformational ensembles generated in the free-energy approach (8,19,70).