Stiffening Effect of Cholesterol on Disordered Lipid Phases: A Combined Neutron Spin Echo + Dynamic Light Scattering Analysis of the Bending Elasticity of Large Unilamellar Vesicles

Abstract

In this study, the center-of-mass diffusion and shape fluctuations of large unilamellar 1-palmitoyl-2-oleyl-sn-glycero-phosphatidylcholine vesicles prepared by extrusion are studied by means of neutron spin echo in combination with dynamic light scattering. The intermediate scattering functions were measured for several different values of the momentum transfer, q, and for different cholesterol contents in the membrane. The combined analysis of neutron spin echo and dynamic light scattering data allows calculation of the bending elastic constant, κ, of the vesicle bilayer. A stiffening effect monitored as an increase of κ with increasing cholesterol molar ratio is demonstrated by these measurements.

Introduction

Cholesterol is an essential lipid component of eukaryotic cell membranes assumed to control the fluidity and the packing state of the bilayer (1–3). The relative content of cholesterol under in vivo conditions is variable, depending on the type of the membrane: up to 50 mol % is present in the plasmatic membrane, but highly curved structures such as the inner mitochondrial membrane or the endoplasmatic reticulum contain <5 mol % (4,5). Lipids do not mix uniformly in membranes but separate into different lipid phases depending on the differential pair-interaction energies between the various components (6,7). Lipids in the ordered phase usually occur as microdomains, referred to as lipid rafts. These are enriched in saturated sphingolipids and cholesterol and are believed to be involved in the regulation of membrane protein interaction and activity (8). Unsaturated phospholipids usually blend with variable proportions of cholesterol to form the continuous fluid matrix of the lipid bilayer. The two main effects of increasing cholesterol in disordered lipid phases are 1), an increase of the orientational order of the unsaturated hydrocarbon chains; and 2), a decrease of the free volume available. These two effects combined result in a structural condensation (9,10) and a decrease in molecular mobility (1) within the lipid membrane. Consequently, cholesterol is expected to induce profound changes of the thermodynamic and mechanical properties of the bilayer. In particular, fluidity and flexibility might be modified by cholesterol, thus controlling not only molecular transport, but also the mechanical and conformational states of lipids and proteins in the bilayer. Flexibility of the bilayer is a major issue in crucial functional aspects such as the precise folding of transmembrane proteins depending on their local mechanical interplay with the surrounding lipids (11,12), the macroscopic shape of the cell in relation to the interaction of the membrane with the cytoskeleton (13), and the ability of cell envelopes to accommodate shape to external flows (14).

The mechanical characterization of model membranes has only become available since the pioneering work of Luzatti and co-workers on the structure of the lamellar phases of phospholipids (15–17). Afterward, high-flux x-ray and neutron sources became powerful tools for studying not only structure but dynamics. Although thermal fluctuations present a challenge for obtaining accurate structural data via diffraction experiments (18), they are crucial in quasielastic scattering experiments, where they are necessary for exciting the linear mechanical response (19). Scattering and line-shape analysis indeed have been revealed as powerful tools for gaining access to the mechanical coefficients of bulk lamellar phases, particularly the bending (κ) and compression (B) moduli (20,21). However, powder averaging, inherent to diffuse scattering from unoriented lamellar domains, leads to a smearing out of the signal and subsequent loss of information. The use of highly oriented bilayers stacked over planar solid supports enhances monocrystal signals, which then provide structural information in the two relevant directions, out-of-plane (q_z) and in-plane (q_in) (22–25). Alternatively, unilamellar lipid vesicles provide an adequate system for arranging a single bilayer in a stable configuration (26). In particular, large unilamellar vesicles (LUVs), as prepared by the extrusion method (27), are frequently used as models of lipid membranes (13,26). In this work, we are concerned with the effect of increasing cholesterol concentration on the bending flexibility of lipid bilayers in the fluid state, so we have used the monounsaturated phospholipid 1-palmitoyl-2-oleyl-sn-glycero-phosphatidylcholine (POPC; T_m ∼ 3°C), one of the most abundant phospholipids in natural membranes. POPC is indeed the major component of the continuous lipid phase and is essential in maintaining its fluidity.

Most quasielastic scattering experiments deal with the study of thermal shape fluctuations of floppy microemulsion droplets (κ ∼ k_BT) (28–32), however, to our knowledge, no success has been achieved on nanometer-sized lipid vesicles, which are substantially stiffer (κ >> k_BT). The classical alternative has been to observe the curvature undulations of giant unilamellar vesicles (GUVs) directly by optical video-microscopy techniques (33–36). Two different techniques are productively exploited in determination of the bending modulus of GUVs: micropipette aspiration (34) and flickering spectroscopy (37). The application of these techniques is limited by the possibility of obtaining unilamellar vesicles by the electroformation method (38). However, this electroswelling method fails with certain lipid mixtures, being indeed quite inefficient in the presence of relatively low salt or proteins. This is why we propose LUVs as a versatile model for measuring mechanical properties of single bilayers by scattering methods. Neutron spin echo (NSE) provides the adequate q-range to quantitatively probe fast dynamics over small lengths typical of these nanometer-sized vesicles. Therefore, an approach based on NSE experiments performed on diluted LUV dispersions might be rather advantageous for studying membrane mechanics. First and foremost, NSE probes the dynamics of isolated single bilayers. As an added convenience, very small amounts of lipid (only a few milligrams/sample) are required. Second, the technique is noninvasive. And third, NSE provides an ensemble average over a large population of vesicles. Compared to GUVs, for which micropipette and flickering techniques are performed on individual vesicles, the statistics must be made, in practice, over a much smaller population. In the case of pure lipids, this results in a relative narrow distribution of the parameters, but much wider distributions, related to the compositional heterogeneity intrinsic to the GUV formation method, are observed in more complex mixtures. Extruded LUVs are comparatively much more monodisperse than GUVs not only with respect to size but also in chemical composition.

NSE is adequate for studying the relaxation dynamics of the curvature undulations in the regime of high wave vectors, where fluctuations are short compared to vesicle dimensions (qR >> 1, where q is the fluctuation wave vector and R the vesicle radius). Larger fluctuations appear mixed together with translational effects. Dynamic light scattering (DLS) is mainly used to characterize the vesicles with respect to their size and polydispersity but no internal motions are resolved in this case (39–42). To our knowledge, only a very limited number of works investigate thermal shape fluctuations of vesicles with DLS. Brocca et al. (43,44) have proposed the use of ultraviolet-laser radiation for extending the DLS operative range to larger q values, and hence, faster relaxations corresponding to deformation modes can be detected eventually in relatively small vesicles. From this approach, a second, faster relaxation was resolved in the light-scattering correlation functions, which was attributed to global vesicle shape deformations. Alternatively, we propose a combined NSE + DLS methodology to gain insight into the dynamics of the shape fluctuations of LUVs based on POPC. We will determine the effect of increasing cholesterol content on the bending elasticity of the fluid POPC bilayers. In the next section, we describe the theory necessary to discuss shape fluctuations as bending modes of an elastic membrane.

Theory

The dynamics of the curvature undulations of elastic membranes is usually described by the Helfrich hamiltonian (45). Within this continuum mechanical theory, Milner and Safran (MS) have described the fluctuation dynamics of microemulsion droplets and vesicles (46). In brief, the MS theory couples the normal bending modes of the flexible shell-like membrane with the viscous friction exerted by the suspending viscous medium. When the dynamical equations are solved in view of the fluctuation-dissipation theorem, the autocorrelation function for the amplitude of the bending fluctuations is obtained as a single exponential decay (46),

$$g_{\text{bend}}^{\left(\text{MS}\right)}\left(t\right)\sim \exp \left(-{\Gamma }_{\text{MS}}t\right),$$ (1)

with a relaxation rate of

$${\Gamma }_{\text{MS}}=\frac{\mathit{\kappa }}{4\mathit{\eta }}{q}^3,$$ (2)

where η is the effective viscosity of the fluid medium and κ the bending modulus of the bilayer.

This result assigns faster relaxation to stiffer bilayers. The ∼q³ power law has been experimentally observed with good accuracy in soft sponge and lamellar phases (19). When applied to vesicles, the MS approach leads to a qualitatively reasonable interpretation of the experimental findings, but fails to give realistic values for the bending elastic constant, κ. For lipid bilayers, κ should be of the order of a few k_BT; however, significantly higher values are obtained when the experimental relaxation times are discussed in view of the MS theory (47). Furthermore, the relaxation profiles obtained from sponge and lamellar phases and from vesicle suspensions do not accurately follow the single-exponential behavior of Eq. 2 (48,49). Adequate descriptions of the experimental data are only achieved when a stretched exponential profile is used, g(t) ∼ exp(−Γt)^β; the stretching exponent β ∼ 0.7 usually holds for systems made of slightly curved bilayers (48,49).

These apparent contradictions have been recently resolved by Zilman and Granek (ZG) by considering the coupling of the collective bending modes of motion with the local diffusive motions of the lipid molecules (50,51). The key idea of the ZG theory is that a stiffer membrane is less efficient in exploring volume, so that longer times are actually required for an empty solvent blob to be filled up by membrane material. Consequently, two competitive effects are present in rigid membranes at increasing stiffness: 1), regular increase of the relaxation rate of the shape fluctuations (∼κq³, as in the MS theory); and 2), decrease of the average amplitude of the undulation modes 〈u²〉 ∼ k_BT/κq⁴. For rigid membranes (κ >> k_BT), the ZG theory predicts an anomalous subdiffusive relaxation for the bending motion of the membrane, which is described by a stretched exponential decay:

$$g_{\text{bend}}^{\left(\text{ZG}\right)}\left(t\right)\sim \exp {\left(-{\Gamma }_{\text{ZG}}t\right)}^{2/3},$$ (3)

with a relaxation rate of

$${\Gamma }_{\text{ZG}}=0.025{\mathit{\gamma }}_q{\left(\frac{k_{\text{B}}T}{\mathit{\kappa }}\right)}^{1/2}\left(\frac{k_{\text{B}}T}{\mathit{\eta }}\right)q^3,$$ (4)

where the factor γ_q is a weak, monotonous function of κ defined as

$${\mathit{\gamma }}_q=1-\frac{3}{4\mathit{\pi }}\left(\frac{k_{\text{B}}T}{\mathit{\kappa }}\right)\ln \left(qh\right),$$ (5)

which takes values close to unity for large undulations in rigid membranes (in the limit qh << 1 of wavelengths larger compared to membrane thickness, h, and if κ > k_BT, then γ_q ≈ 1).

The stretching exponent predicted by the ZG theory (β = 2/3) is close to the experimental value (β ∼ 0.7), e.g., found in a variety of lamellar phases (48,49). The main result of the ZG theory is that relaxation rates of the shape fluctuations vary as Γ_ZG ∼ κ^−1/2q³, recovering the q³ dependence, in agreement with experiments. Furthermore, the Γ_ZG ∼ κ^−1/2 dependence, which predicts that relaxation rates will decrease with increasing κ, is also consistent with experiments (52,53). The purpose of this work is to apply the ZG theory to quantitatively study elastic properties of vesicle lipid bilayers.

Methods

Scattering methods provide a powerful tool to probe experimentally the relaxation dynamics of thermal fluctuations (54). For dilute dispersions of vesicles, two principal types of motion are expected to be observable, depending on the scrutinized q-range (q = (4π/λ) sin(θ/2) is the magnitude of the scattering vector): the center-of-mass translational diffusion of the vesicle as a whole, and, at shorter times (higher q), the shape deformation modes of the bilayer. This means that the scattering function should contain at least two contributions, g_q(t) ≈ g_T(t) + g_bend(t).

DLS spans a q-window adequate to study the translation dynamics of large unillamelar vesicles in solution (40,41). Most DLS studies deal with the determination of particle-size distributions. In these measurements the intensity of light scattered from a diffusing particle is detected and the autocorrelation function calculated. For near-monodisperse vesicles undergoing Brownian motion, the translational autocorrelation function g_T(t) decays exponentially, as follows:

$$g_{\text{T}}\left(t\right)\sim \exp \left(-{\Gamma }_{\text{T}}t\right),$$ (6)

with a decay rate governed by the translational diffusion coefficient of the vesicle (D_T).

$${\Gamma }_{\text{T}}\left(q\right)=D_{\text{T}}{q}^2\text{.}$$ (7)

For dilute dispersions, diffusional translation is essentially governed by Stokes friction, thus D_T is determined by the hydrodynamic radius of the vesicle, R_h, through the Stokes-Einstein relationship

$$D_{\text{T}}=\frac{k_{\text{B}}T}{6\mathit{\pi \eta }{R}_{\text{h}}},$$ (8)

where k_B is Boltzmann's constant and η the bulk viscosity of the medium.

For small LUVs, DLS usually probes the window qR_h < 1. Thus, this experimental technique usually fails to resolve faster internal motions as those corresponding to bending modes. By analogy to classical studies of bending fluctuations of microemulsion droplets (30,55,56), we propose NSE as the adequate technique for probing undulation fluctuations of nanometer-sized LUVs. In the range of wave vectors qR_h > 1 > qh, NSE gains access to the intermediate relaxation function that accounts for undulation fluctuations, g_bend(t); thus, these dynamical measurements offer a very stringent method for studying the bending motion of the vesicles. However, because of the translational drift of the vesicle, the relaxation function is not fully decayed, so an accurate analysis requires that the terminal translational component, g_T(t), independently determined in DLS experiments, was accounted for at longer times.

Dynamic light scattering

DLS experiments have been performed using a multiangle light scattering device (ALV, Langen, Germany) using a diode-pumped Nd-YAG solid-state laser as a monochromatic light source (λ = 532 nm; output power regulated at 150 mW). The samples were placed in a thermostated matching bath. The fluid used to match the refractive index of the sample cell was decaline. The temperature of the bath is kept constant and measured by a Pt-100 sensor with a precision of ±0.1°. Measurements were performed at scattering angles ranging from 30° to 120°, at constant temperature (22.0°C) and vesicle concentration (0.1 mg/mL). The intensity correlation function g⁽²⁾(q,t) is generated using an ALV-5000E autocorrelator. This function is related to the field autocorrelation function g⁽¹⁾(q,t) through the Siegert relation,

$$g^{\left(2\right)}(q,t)=1+C|g^{\left(1\right)}(q,t){|}^2\text{.}$$ (9)

The field autocorrelation function is analyzed by CONTIN, an algorithm based on the inverse Laplace transform (57,58). Within experimental precision, identical results are obtained by REPES (59). No assumption need be made about either the number of relaxation processes or the distribution shape using these methods.

Neutron spin echo

The reported NSE experiments were done on the IN15 instrument at the Institut Laue-Langevin (Grenoble, France) (60). This instrument provides the longest Fourier times,currently available for NSE instruments. The samples are poured into quartz cells (1 mm thick, Hellma, Mullheim, Germany). The instrument was equipped with a thermostated holder for these cells and all measurements were done at a temperature of 22°C. A Fourier time range up to 170 ns was explored at different q-values from 0.119 nm^-1 to 1.102 nm^-1. To achieve this, measurements had to be performed at wavelengths of λ = 12 Å and 15 Å. The wavelength distribution in both cases had a full width at half-maximum of Δλ/λ = 0.15.

Experimental intermediate scattering function

For an elastic shell undergoing Brownian fluctuations, two relevant contributions might be considered in the intermediate scattering function, the bare diffusional translation and the bending undulation modes, which are internal motions coupled to translation (46,50,56):

$$S(q,t)/S(q,0)=g_{\text{T}}\left(t\right)\left[A_q+\left(1-A_q\right)g_{\text{bend}}\left(t\right)\right]\text{.}$$ (10)

This function should fit both NSE and DLS data. Since both DLS and NSE lead to normalized functions, both components sum up to unity, i.e., 0 < A_q < 1. For long times, the normalized intermediate scattering function decays completely, i.e., S(q,t)/S(q,0) ∼ 0 at t >> Γ_T⁻¹ (>Γ_bend⁻¹). Although Brownian translational motion is always present in the relaxation function, local bending modes only contribute above a lower cut-off of q ≥ q₀, defined by a fundamental oscillation q₀; for a sphere of radius R, q₀ = 2π/(2πR) = 1/R; higher fluctuation modes correspond to discrete spherical harmonics with wave vector q_l ∼ l/R, with l = 1, 2, 3…). In this study, the vesicles prepared are ∼100 nm in size (q₀ ∼ 10⁻² nm⁻¹); thus, DLS measurements are adequate for probing the center-of-mass translation but also potentially efficient in detecting bending undulations (the typical q_DLS range is (0.8–3.0)10⁻² nm⁻¹, so qR ≈ 1). Conversely, translational motion is nonrelaxed at the q-window probed in NSE experiments (q_NSE range of (0.1−1) nm⁻¹, with q >> q₀ and qR >> 1). In the NSE window, small-wavelength membrane-shape fluctuations might be clearly observable (q_l ∼ l/R, thus, l >> 1). Indeed, the submicrosecond dynamics probed by NSE corresponds to undulation motions of the vesicle that are much faster than its bare diffusional translation (i.e., Γ_bend ∼ t_NSE⁻¹ >> Γ_T), consequently, both motions, translation and shape undulations, can be considered essentially decoupled at the NSE window. Assuming the validity of the ZG approach in describing the local undulation dynamics of the bilayer of lipid vesicles, g_bend(t) ∼ exp(−Γ_ZGt)^2/3, Eq. 10 is written as S(q,t)/S(q,0) = exp(−Γ_Tt)[A_q + (1−A_q) exp(−Γ_ZGt)^2/3]. This expression might provide an adequate model for describing the NSE scattering functions and is similar to approaches used previously to describe microemulsion systems (28,30,55,56). However, no stable fits are achieved in this case when the three adjustable parameters (A, Γ_T, and Γ_ZG) are left to vary. Two a priori conditions must be imposed to get nonbiased fits: 1), the translational relaxation rate is fixed at the value deduced from the DLS data, i.e., Γ_T(q) = Dq²; and 2), the translational motion is considered essentially nonrelaxed at the NSE window, i.e., exp(−Dq²t) ≈ 1 − o(Dq²t). This last is strictly true only at q << (1/Dt_NSE)^1/2. Under these conditions, Eq. 10 can be approximated as a linear combination of two independent relaxation modes:

$$S(q,t)/S(q,0)\approx A_q\exp \left(-{\Gamma }_{\text{T}}t\right)+\left(1-A_q\right)\exp {\left(-{\Gamma }_{\text{ZG}}t\right)}^{2/3}\text{.}$$ (11)

This approximated expression has been successfully used for fitting our experimental NSE relaxation curves. Predictions from the exact relaxation curve in Eq. 10 differ by <1%, well below the experimental uncertainty (typically 3%) In practice, the use of Eq. 11 has been restricted to q ≤ 0.4 nm⁻¹ for fitting purposes. Since NSE probes times t_NSE ≈ 170 ns, the approximated function in Eq. 11 is reasonably close to the exact expression in the considered q-range (for vesicles of radius ∼100 nm, D ≈ 10⁻¹² m²/s, one gets (1/Dt_NSE)^1/2 ≈ 2 nm⁻¹).

Sample preparation

POPC was obtained from Avanti Polar Lipids (Alabaster, AL) at 99% purity and cholesterol from Sigma (St. Louis, MO). Lipids were stored at −20°C and used as received without further purification. Deuterated water (Sigma) was used as solvent for both the NSE and DLS experiments (η = 1.2010 MPa s at 22°C). LUVs were prepared by the extrusion method using a commercial miniextruder (Avanti Polar Lipids). To avoid possible differences between DLS and NSE experiments, we always used D₂O as the aqueous solvent. To prepare vesicles, the blend of POPC and cholesterol is first dissolved in a chloroform/methanol mixture (2:1). Later, the solvent is slowly removed by evaporation in a dry nitrogen stream, yielding a homogenous lipid film consisting of multiple lamellae. The lipid film is then hydrated by pouring the aqueous phase. During the hydration phase (1 h), the dispersion is frequently vortexed and maintained above the melting temperature of the lipid mixture (T_m ∼ 3°C in this case). Then, this lipid suspension is extruded through a polycarbonate filtering membrane (Whatman, Florham Park, NJ) with a defined pore size (100 nm), producing unillamelar vesicles with a diameter near the pore size. Extrusion is performed at a temperature well above T_m. Ten extrusion cycles ensure a homogeneous dispersion of LUVs with a constant size and low polydispersity (61–63). The dispersion was then filtered through a 0.2-μm teflon filter and poured into quartz tubes.

Results

DLS experiments: diffusional translation and vesicle radius

We have performed DLS experiments on aqueous dispersions of LUVs made of POPC and of POPC mixed with different amounts of cholesterol up to a maximum content of 50 mol %. These dispersions are quite diluted (typically 1 mg/mL lipid), so no interaction effects between vesicles are expected. Indeed, identical results are found independently of the lipid concentration in the range 0.1–2 mg/mL (data not shown). Fig. 1 shows typical intensity autocorrelation functions (g⁽²⁾(t)) measured for vesicle suspensions (POPC + 50 mol % cholesterol) at four different scattering angles. In all cases, CONTIN reveals monomodal relaxation and the curves can be also described by second-order cumulant functions, as expected from the low size polydispersity intrinsic to the extrusion method (62,63). The distribution of the relaxation times, as calculated by CONTIN, is indeed found to be rather narrow at low q values (<1/R), as expected for monodisperse systems (Fig. 1, inset). These distributions become slightly broader as q increases, which could be attributed either to size polydispersity arising from small vesicles or lipid aggregates or to the progressive contribution of undulation modes at q >> q₀ (1/R) (64). It is worth noting that small spontaneous vesicles are not stable with respect to the larger extruded LUVs (they imply higher curvatures), so effective polydispersity induced by shape fluctuations seems a more plausible scenario for explaining the broader distributions observed at high q values.

Figure 1.

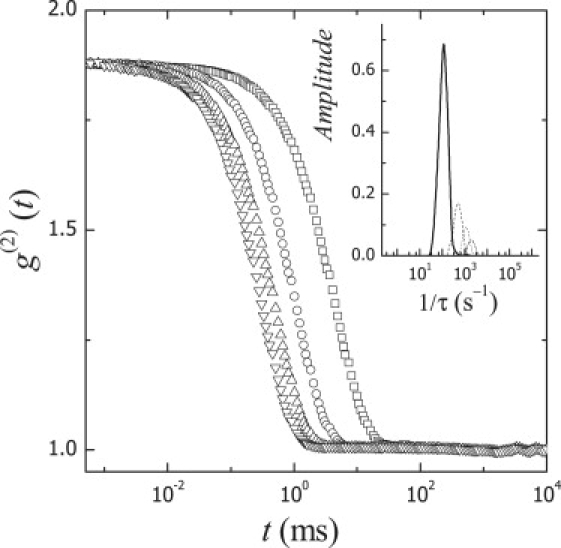
Experimental DLS intensity autocorrelation functions g⁽²⁾(t) for vesicles based on POPC + 20% cholesterol at different scattering wave vectors (q = 0.0081 nm⁻¹ (○), 0.0157 nm⁻¹ (□), 0.0222 nm⁻¹ (△), and 0.0272 nm⁻¹ (▽)). (Inset) Distributions of relaxation rates calculated by CONTIN.

In the DLS window, the center-of-mass diffusional translation is expected to be dominant; to verify their diffusive character, the relaxation rates have been plotted in Fig. 2 as a function of q².

Figure 2.

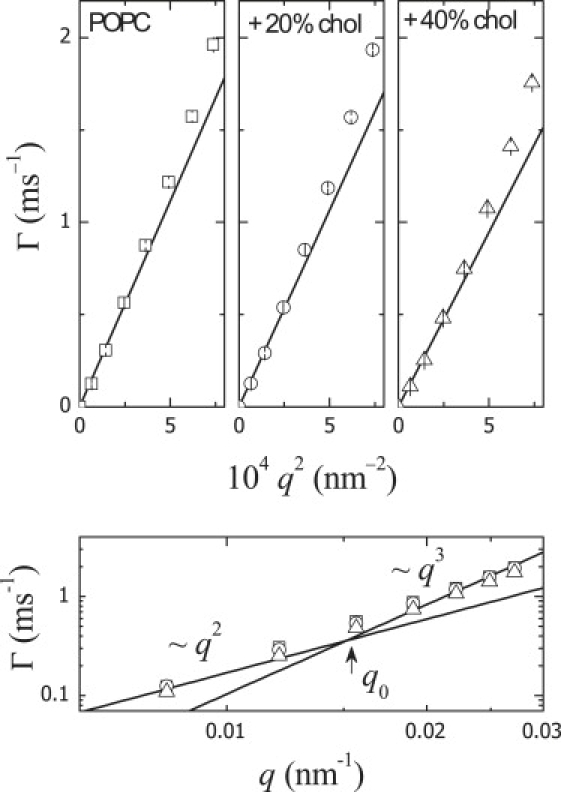
Typical plot of Γ_T versus q² of the translation relaxation frequencies obtained from CONTIN analysis of the DLS autocorrelation functions.

As expected, the experimental relaxation rates follow a linear dependence with a zero intercept. Similar behavior was found for the other studied systems. However, weak deviations from a limiting-q² behavior, probably arising from nonresolvable contributions from the bending fluctuations, are systematically detected at q > q₀. This effect is clearly visible in the log-log plot (Fig. 2, lower panel), where a renormalization from the ∼q² behavior to an ∼q³ dependence, characteristic of the relaxation of bending fluctuations, is observed at q > q₀. The relaxation times of the bending fluctuations are, in this regime, probably similar to the diffusional translation times, and deconvolution algorithms are thus unable to discriminate between the modes, yielding an average relaxation frequency. Brocca et al. (43,44) have discriminated the two modes by measuring the correlation function extended up to higher q (at the ultraviolet wavelengths), where both motions (translation and bending fluctuations) are expected to relax at a very different timescale.

Therefore, using Eq. 7, the bare diffusion coefficient for translational motion can be calculated from the limiting slopes in Fig. 2 (upper panel). In practice, this implies fits to five points with just one adjustable parameter, D₀. Vesicle sizes can be then easily calculated from the Stokes-Einstein equation (Eq. 8); the hydrodynamic radius, R_h = k_BT/6πηD₀. The fitted values of the limiting slope, D₀, and the calculated hydrodynamic radii are collected in Table 1 for the different cholesterol contents studied. These results will be later used when analyzing the NSE scattering functions in terms of Eq. 11.

Table 1.

Translational diffusion coefficient D₀ and hydrodynamic radii of extruded LUVs at different cholesterol contents

xchol (mol %)	D0 1012 (m2/s)	Rh (nm)
0	2.23 ± 0.06	81 ± 2
10	2.21 ± 0.07	81 ± 2
20	2.13 ± 0.05	84 ± 2
40	1.89 ± 0.06	95 ± 3
50	1.75 ± 0.08	102 ± 5

In all cases vesicle sizes are obtained higher than the nominal radius (R₀ = 50 nm) expected from the extruder pore size (100 nm, diameter). Part of the difference can be attributed to the hydration shell of the vesicles (50,51). In addition, the vesicles deform during extrusion and therefore larger LUV's can flow trough nominally smaller pores. However, in both experiments we are dealing with the translational motion of the “effective hydrodynamic sphere”; hence, NSE and DLS should probe the same kind of motion.

Fig. 3 shows the normalized intermediate NSE relaxation functions S(q,t)/ S(q,0) obtained at different scattering wave vectors for suspensions of POPC vesicles at different cholesterol contents.

Figure 3.

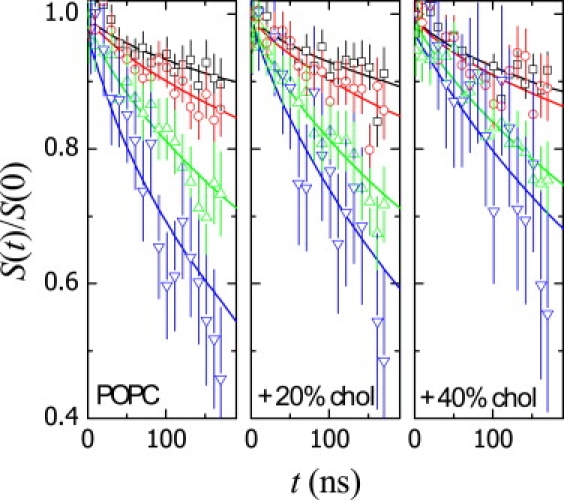
Intermediate NSE relaxation functions for vesicle dispersions at different cholesterol contents from experiments at different wave vectors (q = 0.12 nm⁻¹ (□), 0.43 nm⁻¹ (○), 0.70 nm⁻¹ (△), and 0.97 nm⁻¹ (▽)). The presence of increasing cholesterol leads to longer relaxation times and, hence, slower relaxation rates. The straight lines represent the best fits to Eq. 11 (see text for details).

These relaxation curves correspond to high-order membrane fluctuations shorter than the vesicle perimeter (qR >>1) but large enough compared to molecular dimensions. In this regime, bending modes are expected to be separated from the translational terminal contribution that is present at very long times. Also in this regime, center-of-mass translation can be considered essentially nonrelaxed; even at the higher q values, the translational relaxation time, τ_T ∼ Γ_T⁻¹ (1/D_Tq²) ∼ 50 μs, is already quite a bit longer than the NSE experimental time. In other words, the considered vesicle shape fluctuations occur at a timescale such that the vesicle does not translate so far.

Consequently, shape deformation can be considered the main scattering contribution in the NSE data. Translation need be considered only as a terminal contribution leading to incomplete decay in the NSE time window. Under these conditions, Eq. 11 can be reasonably used to interpret the experimental data in Fig. 3. The straight lines represent the best fits of Eq. 11 to the experimental data, the fitting parameters being the amplitude, A, and the relaxation frequency, Γ_ZG, of the fluctuation modes. The translational frequencies have been fixed at Γ_T = D₀q² on the basis of the translational diffusion coefficients from the DLS experiments (data from Table 1). A model based on a single-exponential decay for the shape fluctuations (as predicted by the MS theory (Eq. 1)) is unable to fit these experimental data.

For the sake of comparison, the intermediate scattering functions for POPC and a mixture of POPC with 50 mol % cholesterol obtained at the same q are shown in Fig. 4. Based on this comparison, it appears evident that the insertion of cholesterol in the bilayer leads to longer relaxation times, hence to smaller relaxation rates of the undulation bending modes. Because of the unequivocal condensation caused by cholesterol in disordered phases of phospholipids (65), a certain stiffening, measurable as an increase in κ, might be expected at increasing cholesterol content. This scenario is qualitatively compatible with expectations from the ZG theory (stiffer membranes engender slower modes, Γ_ZG ∼ 1/κ^1/2), but it is in absolute disagreement with the MS description (Γ_MS ∼ κ).

Figure 4.

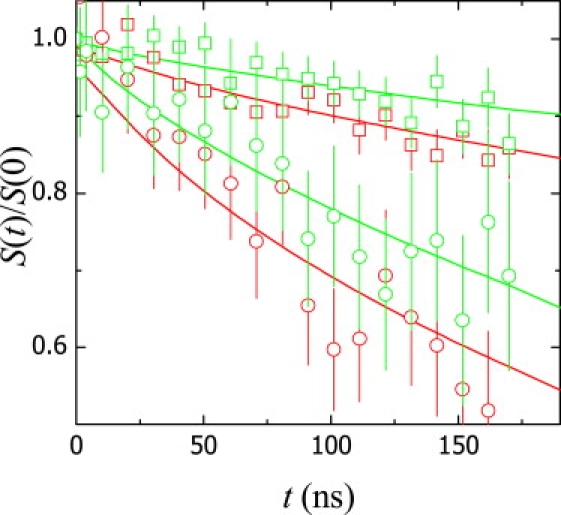
Influence of cholesterol on NSE intermediate scattering functions in pure POPC vesicles (red symbols) and POPC vesicles with 50 mol % added cholesterol (green symbols). For simplicity only two different wave vectors are plotted: q = 0.12 nm⁻¹ (squares) and q = 0.97 nm⁻¹ (circles). The presence of cholesterol leads to longer relaxation times and, hence, slower relaxation rates. The straight lines represent the best fits to Eq. 11.

Discussion

The NSE relaxation functions contain dynamical information occurring at times <100 ns, corresponding to short-range, high-order membrane fluctuations (at the NSE window qR >> 1; the probed undulations, q_l = l/R, correspond hence to harmonics l ∼5–50). In this regime, the mode wavelength is much smaller than the vesicle perimeter (λ = 2π/q = 2πR/l), and bending modes thus can be described as motions of locally flat bilayers at the continuous q-regime intrinsic to the ZG theory. We have plotted in Fig. 5 the relaxation frequencies of the fast mode of the NSE relaxation functions of Fig. 4. The data are represented as a function of q³. Linear plots are achieved, as expected for bending modes. Similar plots are obtained for all cases considered in this study.

Figure 5.

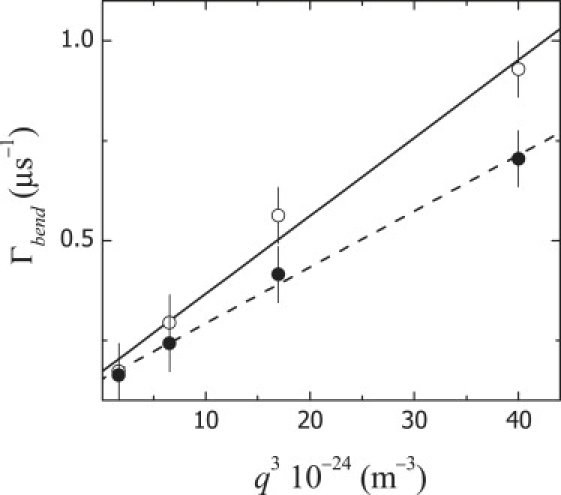
ZG plot of the relaxation rates of the fluctuation mode for POPC (○) and POPC + 50 mol % cholesterol (•). According to ZG theory, the Γ versus q³ plot should be linear and the bending rigidity, κ, can be calculated from the slope (see Eq. 4).

The experimental relaxation rates can be easily rationalized in view of the ZG theory (see Eqs. 3–5). For the cases studied, the limit γ_q ∼ 1 is reasonably accomplished (typically, bilayer thickness of h ≤ 3 nm and κ > k_BT); thus, in the ZG approach, κ can be easily calculated from the slope of the Γ-q³ plots.

Fig. 6 shows the values of the bending elasticity calculated from the analog plot to Fig. 5 for every sample with different cholesterol content. Although no large changes (within experimental uncertainty) are observed up to 20% cholesterol, upon increasing cholesterol, a meaningful increase of κ is clearly observable. The trend displayed by the data in Fig. 6 is comparable to that reported in similar lipid systems by Evans and Rawicz from micropipette experiments performed on larger GUVs (33), and by Pan et al. from x-ray scattering experiments on orientated bilayers stacked on silicon wafers (66). Henriksen et al. (47) took advantage of flickering spectroscopy to measure the bilayer bending elasticity in GUVs of the latter system. In the experiments of Henriksen and co-workers, the autocorrelation function of the shape fluctuations is directly computed from the dynamic evolution of the bending fluctuations recorded by videomicroscopy. These authors used the MS theory to interpret the relaxation times of the autocorrelation functions, obtaining much higher values of κ than those reported here or those from static micropipette (33) or x-ray (66) experiments. We have alternatively used the MS relations (Eqs. 1 and 2) to compute κ from relaxation times inferred by NSE. As in the work of Henriksen et al., unrealistic values of the bending modulus are obtained when NSE relaxation times are discussed in view of the MS approach. The cholesterol-free sample is the control in this study. The bending elasticity calculated for POPC bilayers, κ = (19 ± 2)k_BT at 22°C, is in good quantitative agreement with values reported from micropipette experiments in GUVs (67) and more recently by Kucerka et al. from x-ray experiments (68). This value corresponds to a fluid lipid bilayer that is relatively flexible upon bending. In contrast, lipids at nonfluid states, for instance, DPPC at room temperature, assemble much stiffer bilayers, κ ∼ 200k_BT (69). On the other side, experiments at the highest cholesterol content indicate a meaningful stiffening; κ = (37 ± 2)k_BT at 50 mol % cholesterol, which is the maximum cholesterol at which stable bilayers form (2). This value of κ corresponds to a rather stiff bilayer as compared to that made of pure POPC (70).

Figure 6.

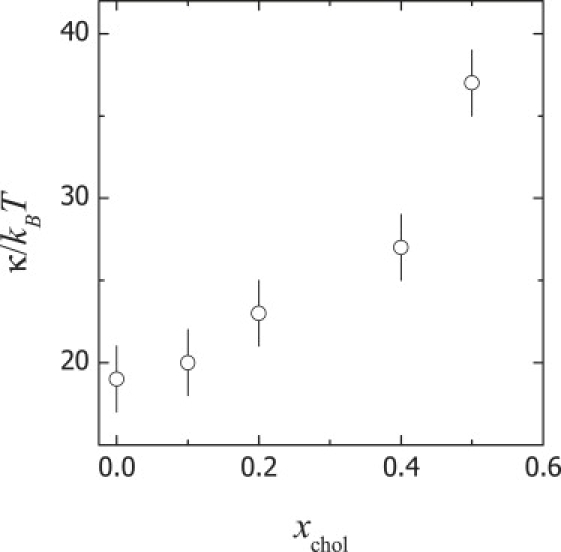
Bending rigidity, κ, of POPC vesicles at increasing cholesterol content. x_chol, cholesterol molar fraction.

The reported increase of κ at increasing cholesterol content is compatible with the well-known structural condensation caused by cholesterol on the disordered phases of fluid phospholipids (1–3). This condensing effect is assumed to underlie cohesive interactions driven by hydrogen bonding (55). Doping phospholipids with small amounts of cholesterol causes a relatively high degree of structural condensation, but strong collective effects, such as the mechanical stiffening observed here, are only expected at higher concentrations (2). At a 30% molar in cholesterol, 2:1 complexes are formed (71), and each monolayer then organizes as a triangular network at the level of the phospholipid polar heads, with one small cholesterol molecule at the center of the cell unit. In these data, net mechanical stiffening is detected just at this range of lipid composition, thus suggesting the forcefulness of hydrogen bonding to assemble a dynamical network with enhanced mechanical properties.

Conclusions

The bending elastic properties of lipid membranes with cholesterol are still not fully understood. In this article, we present a novel experimental approach based on a study of the dynamics of bilayer fluctuations using NSE combined with DLS. The data can be analyzed with the Zilman-Granek model for membrane undulations using a combination of simple diffusional dynamics to account for vesicle translation. This approach allows us to determine the bending elasticity, κ, for POPC vesicles containing different amounts of cholesterol. Realistic values of κ in the range 19–37 k_BT are obtained, depending on cholesterol content. The observed stiffening effect of cholesterol on POPC bilayers is compatible with structural condensation caused by hydrogen-bonding complexes between the phospholipids and cholesterol.