Amyloid Protofibrils of Lysozyme Nucleate and Grow Via Oligomer Fusion

Abstract

The mechanisms linking deposits of insoluble amyloid fibrils to the debilitating neuronal cell death characteristic of neurodegenerative diseases remain enigmatic. Recent findings implicate transiently formed intermediates of mature amyloid fibrils as the principal toxic agent. Hence, determining which intermediate aggregates represent on-pathway precursors or off-pathway side branches is critical for understanding amyloid self-assembly, and for devising therapeutic approaches targeting relevant toxic species. We examined amyloid fibril self-assembly in acidic solutions, using the model protein hen egg-white lysozyme. Combining in situ dynamic light scattering with calibrated atomic-force microscopy, we monitored the nucleation and growth kinetics of multiple transient aggregate species, and characterized both their morphologies and physical dimensions. Upon incubation at elevated temperatures, uniformly sized oligomers formed at a constant rate. After a lag period of several hours, protofibrils spontaneously nucleated. The nucleation kinetics of protofibrils and the tight match of their widths and heights with those of oligomers imply that protofibrils both nucleated and grew via oligomer fusion. After reaching several hundred nanometers in length, protofibrils assembled into mature fibrils. Overall, the amyloid fibril assembly of lysozyme followed a strict hierarchical aggregation pathway, with amyloid monomers, oligomers, and protofibrils forming on-pathway intermediates for assembly into successively more complex structures.

Introduction

Alzheimer's disease and Parkinson's disease are familiar representatives of a category of human disorders called amyloidoses. Amyloidoses are characterized by the deposition of protein plaques in the extracellular (and sometimes intracellular) matrix, and extensive tissue damage in the immediate vicinity of these plaques (1,2). The protein fibrils forming the scaffold for these extracellular deposits share a common cross-β-sheet architecture (3,4) that has little correlation with the native structure of the various proteins or proteolytic fragments that form these protein fibrils. Recent studies implicated intermediate aggregates formed during the assembly of mature fibrils, and not the prominent protein plaques, as the molecular species mediating cellular toxicity in amyloidoses (5,6). Understanding the process of amyloid self-assembly into mature fibrils with a shared quaternary structure represents a basic challenge in protein science, and is critical for unraveling the causes of cell death associated with amyloidoses.

Several distinct aggregate species were clearly identified as intermediates during amyloid fibril growth, including small oligomeric species, protofibrils, and mature fibrils (7). The latter represent the basic building block of large polymer bundles forming protein plaques (7,8). One contentious and actively pursued topic in amyloid fibril growth concerns whether transient aggregates such as oligomers and protofibrils represent essential on-pathway precursors toward mature fibril assembly (9,10) or off-pathway alternatives to mature fibrils (11), or whether multiple competing aggregation pathways (12,13) converge in the shared structure of mature fibrils. Part of the difficulty in answering these questions is intrinsic to the very nature of intermediate aggregates: they represent metastable and transient states that are in dynamic exchanges with their monomeric background (14). These difficulties are aggravated by the sensitivity of aggregates sizes and morphologies to subtle manipulations in solution conditions or sample preparations (15,16). As a result, the noninvasive and quantitative characterization of the intrinsic growth kinetics, sizes, and morphologies of different soluble amyloid intermediates represents an important step toward unraveling the elusive relationship between different types of intermediate aggregates and their role in amyloid fibril self-assembly.

We combined in situ dynamic light scattering (DLS) with offline atomic-force microscopy (AFM) for investigating the amyloid fibrillogenesis of hen egg-white lysozyme (HEWL). Lysozyme is a small globular enzyme, and is often used as a model system for studying amyloid fibril formation (17–19). Variants of human lysozyme were also implicated in occurrences of hereditary systemic amyloidosis (20). Upon incubation in acid solutions below pH 4 and at elevated temperatures, native HEWL will grow amyloid fibrils (21). A commercial lysozyme stock can be prepared that is essentially devoid of any preassembled aggregates that can interfere with intrinsic nucleation and growth behavior (22). Therefore, HEWL represents an attractive and biomedically relevant model system for characterizing intermediate amyloid species, and for investigating their aggregation pathways (17).

We place strong emphasis on tight, quantitative correlations between the results obtained with DLS and AFM measurements. DLS distinguishes itself from alternative characterization techniques because it is essentially noninvasive, is highly sensitive to aggregate formation, and provides an in situ readout of particle distributions and growth kinetics (23). These significant advantages of DLS are mitigated by its limited ability to resolve aggregates whose hydrodynamic radii R_h differ by less than a factor of 2 or 3. AFM, in contrast, provides direct images of aggregate morphology and quantitative measurements of aggregate heights. Using AFM, however, can be problematic because deposition on various surfaces has the potential to alter the very aggregate structures one is trying to characterize (16). In addition, measurements of lateral (in-plane) aggregate dimensions are less common because of the dilation of lateral aggregate dimension by the finite-sized scanning tip.

To address these shortcomings, we calibrated AFM scanning tips, obtaining not just images of aggregate morphologies but quantitative measures of vertical and lateral aggregate dimensions. Some of the simpler aggregate geometries characterized using AFM were compared with the in situ diffusion and growth behavior observed using DLS. As a result, we were able to make specific statements regarding the geometries, physical dimensions, assembly pathways, and nucleation and growth kinetics of lysozyme oligomers and protofibrils during amyloid fibril growth.

Materials and Methods

Protein and chemicals

For all experiments, 2× recrystallized, dialyzed, and lyophilized lysozyme from Worthington Biochemicals (Lakewood, NJ) was used. All other chemicals were from Fisher Scientific (Pittsburgh, PA), and were reagent grade or better. We used 18 MW distilled water (Barnstead E-pure, Dubuque, IA) throughout.

Preparation of HEWL amyloid fibrils

Solutions of lysozyme (17 mg/mL) at pH 2.0 with 175 mM NaCl were prepared by dissolving lyophilized lysozyme in distilled water at twice its final concentration, and mixing it 1:1 with a NaCl/water solution, also at twice its final concentration. Before mixing, lysozyme solutions were warmed to 45°C to remove any preformed clusters. All samples were centrifuged at 9500 × g for 5 min, and filtered consecutively through a 220-nm and a 20-nm pore-size syringe filter. Solution pH was readjusted to pH 2.0 with 1 N HCl. Lysozyme concentrations in solution were determined from ultraviolet absorption measured at λ = 280 nm (α₂₈₀ = 2.64 mL mg⁻¹ cm⁻¹) (24). Lysozyme solutions incubated for 4–5 days at 50°C started to form a soft gel. Fibers taken from the gelled-out samples induced a red shift in the absorption spectrum of Congo red, a feature diagnostic for the formation of mature amyloid fibrils. Samples analyzed before ∼3 days of incubation all showed a much weaker spectral shift, identical in magnitude to the nonspecific shift induced by lysozyme monomers (data not shown).

DLS during amyloid aggregation

DLS measurements were performed with a Zetasizer Nano S (Malvern Instruments, Worchestershire, UK) containing a 3-mW He-Ne laser (λ = 633 nm) and with built-in temperature control for sample cuvettes. After thermal equilibration of the samples (typically < 5 min), autocorrelation functions were collected every 10 min, using acquisition times of 60 s. Autocorrelation functions were converted into particle-size distributions, using the “narrow modes” algorithm provided with the Zetasizer Nano S. Particle-size distributions obtained from alternative inversion algorithms yielded comparable results.

AFM of amyloid aggregates

Amyloid samples were imaged with an MFP-3D atomic-force microscope (Asylum Research, Santa Barbara, CA) using NSC36/NoAl (Mikromasch, San Jose, CA) or PFP-FMR-50 (Nanosensor, Neuchatel, Switzerland) silicon tips with nominal tip radii of 10 nm and 7 nm, respectively. The cantilever was driven at 60–70 kHz in alternating current mode and a scan rate of 0.5 Hz, acquiring images at a 1024 × 1024-pixel resolution. Raw image data were corrected for image bow and slope.

During DLS measurements of amyloid fibrillogenesis, 10-μL aliquots of solution were taken from the DLS cuvette for subsequent AFM imaging. Aliquots were diluted 100-fold with 175 mM NaCl/pH 2.0 salt solutions. Typically, 75 μL of solution were deposited on freshly cleaved mica for 5 min, rinsed with deionized water, and dried with dry nitrogen. Images of monomers required significantly longer deposition periods (≥15 min), apparently because their surface affinity and/or deposition kinetics onto mica are significantly lower than those of higher-order aggregates. These differences presumably account for the apparent lack of monomers and/or oligomers after protofibril formation. Images of amyloid aggregates were acquired in air. Using DLS, we confirmed that cooling the lysozyme samples from 50°C to room temperature essentially arrested aggregation (data not shown). Hence, AFM images faithfully represented the aggregate distribution at the time of aliquot collection.

AFM tip calibration and correction for tip dilation

The AFM tip radii were determined by imaging 5-nm gold colloid standards (catalogue No. GC5; BBI International, Cardiff, UK). Poly-d-lysine (1%) was deposited onto freshly cleaved mica for 10 s, rinsed with deionized water, and dried with nitrogen. The gold colloids were diluted 1:20 with deionized water and deposited for 1 min, rinsed with deionized water, and dried with nitrogen. As indicated in Fig. 1, the apparent width W_app of an incompressible object imaged with an AFM tip is considerably larger than its physical width W. Apparent width W_app and height for a given gold colloid were determined from individual scan lines across the maximal height of a given gold colloid. Following Taatjes et al. (25), the apparent width W_app and height of a sphere were used to obtain the radius R_t of the scanning tip. Assessed according to measured heights, the radii of individual gold colloids will vary slightly. Therefore, we determined the radius R_t using a series of gold colloids. This approach yielded reproducible and self-consistent values for R_t. Repeating tip calibrations during extended imaging sessions on mica substrates indicated that tip radii remained unaltered.

Figure 1.

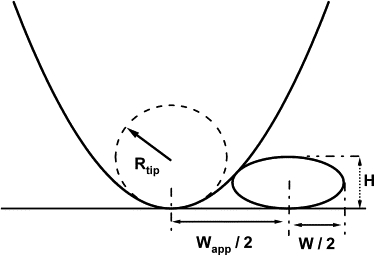
Dilation of lateral particle dimension during AFM imaging. Finite size of AFM scanning tips (shown here as parabola) increases apparent width W_app of particles well beyond their actual width W. For an ellipse, W can be derived using the measured height H and W_app of the particle and the tip radius R_t (25).

To correct for the dilation in apparent particle width induced by scanning tips (Fig. 1), line profiles of apparent particle width versus height were taken across the center of a given particle. The direction for these line profiles was typically chosen as perpendicular to the scanning direction of the AFM tip during image acquisition. The shape of profiles was highly symmetric around the peak height, suggesting that mechanical tip distortions were small. Assuming that aggregates had ellipsoidal cross sections, and using the AFM tip radius determined during tip calibration, the actual particle width was calculated (25).

Prediction of hydrodynamic radii from AFM particle dimensions

Particle dimensions for lysozyme monomers and oligomers were extracted from AFM line scans. The formula of Perrin (26) predicts the hydrodynamic radius for a sphere diffusing at the same rate. For an oblate ellipsoid with major axis a and minor axis b, the hydrodynamic radius is given by Perrin (26) as:

$$R_{\mathrm{h}}=bx/{\tan }^{-1}\left(x\right),\text{where}x\equiv {\left[{\left(a/b\right)}^2-1\right]}^{1/2}\text{.}$$ (1)

Similarly, the straight protofibrils present shortly after nucleation were approximated as cylindrical rods. The effective hydrodynamic radius for a cylinder of length L and diameter d is given by

$$R_{\mathrm{h}}=L/2\left[{\left(1-x^2\right)}^{1/2}/\ln \left((1+{\left(1-x^2\right)}^{1/2})/x\right)\right],\text{where}x\equiv d/L\left[1+0.37\left(L-d\right)/L\right]\text{.}$$ (2)

Results

In situ DLS measurements of aggregate distributions and growth kinetics

DLS is a minimally invasive technique for detecting and characterizing submicron aggregates in situ, and with high temporal resolution. These are distinct advantages when trying to resolve the growth kinetics of multiple aggregate species that are in dynamic equilibrium with one another. Fig. 2 A shows the temporal evolution of the field correlation functions g₁(τ) of light scattered during the fibril formation of HEWL at pH 2.0 over a period of 4 days. After a nearly single-exponential decay of g₁(τ) for DLS measurements during the initial 10 h of incubation, g₁(τ) suddenly developed a prominent shoulder. This shoulder indicates the formation of a second population of larger aggregates, characterized by slower diffusion coefficients. The increasing amplitude of this shoulder and its steadily decreasing decay rate suggest that both the sizes and numbers of these larger aggregates are increasing in time.

Figure 2.

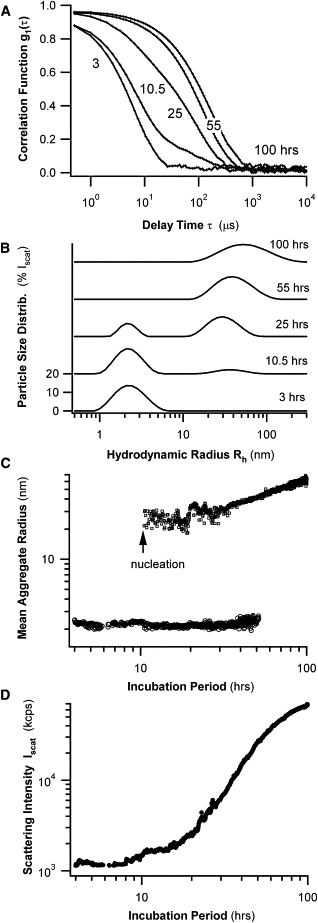
Kinetics of fibril formation by HEWL, monitored in situ with DLS. (A) Temporal evolution of field autocorrelation functions g₁(τ) of light scattered from HEWL solutions during amyloid fibrillogenesis at pH 2.0 and T = 50°C. After a latency period of ∼10 h, a prominent shoulder of slower decay rates emerges in correlation functions. (B) Semilog plot of PSDs derived from correlation functions in A. Initially, the PSD has a single, narrow, “small-aggregate” peak. After a lag period of several hours, a second “large-aggregate” peak emerges and starts to dominate PSDs. (C) Log-log plot of center position of two aggregate peaks in B as a function of incubation period. Note nucleation and gradual growth of larger aggregate peak. (D) Log-log plot of changes in static scattering intensity I_scat versus incubation period. Intensity values were corrected for changes in laser attenuation used to avoid detector saturation.

Particle size distributions (PSDs) were derived from the measured correlation function by analyzing their underlying distribution of decay rates (detailed in Materials and Methods). The PSDs thus obtained contained, at most, two aggregate peaks with well-separated hydrodynamic radii, which we refer to as “small-aggregate” and “large-aggregate” peaks (Fig. 2 B). During initial stages of incubation, the small-aggregate peak, with a distribution centered near a hydrodynamic radius R_h of 2 nm, was dominant. The larger-aggregate species emerged after a sample-specific latency period of several hours, with its initial R_h ∼25 nm. After the appearance of the large-aggregate peak, the small-aggregate peak began to fade slowly. Fig. 2 C shows the temporal evolution of the mean radius for either of these two aggregate populations. The mean radius of the small-aggregate peak appears to be essentially stationary (but see Results for comparisons of DLS with AFM data), whereas larger aggregates increase their mean radius slowly but steadily over the course of 2 days. Fig. 2 D displays the corresponding changes in static scattering intensity as a function of time. The nucleation event of the large-aggregate peak seen in Fig. 2 C leads to an accelerating growth in scattering intensity. At the end of the 4-day period, the total scattering intensity has increased nearly 100-fold above its value at the beginning of the experiment. This latter observation has two implications. First, one must be careful interpreting the apparent “loss” of small aggregates from the particle-size distribution observed after ∼2 days of incubation (Fig. 2, B and C). This loss is attributable, at least in part, to the rapid rise in scattering signal from the larger aggregates, which overwhelms residual scattering contributions from smaller aggregates. Second, the nearly 100-fold increase in scattering intensity (Fig. 2 D) is in marked contrast to the very modest twofold increase in mean hydrodynamic radius of the large-aggregate species over the same 2–3 days (Fig. 2 C). This behavior puts significant constraints on any kinetic model of aggregate growth in this system.

Aside from the expected variations in the latency period of nucleation, all of the above features of DLS data were remarkably reproducible (N_total = 12), indicating that they capture the intrinsic behavior of lysozyme amyloid growth in acidic solutions. The observed evolution of PSDs and corresponding changes in scattering intensity provide detailed information about the kinetics of aggregate nucleation and growth. However, the DLS data also contain several ambiguities that prevented a more detailed analysis. In particular, it was unclear whether either the small-aggregate or large-aggregate peaks in Fig. 2 B were composed of multiple distinct aggregate species not resolved into separate components by DLS. In addition, the identity of intermediate aggregates undergoing nucleation from solution remained uncertain. Finally, no specific information was provided about the morphology of any of the intermediate aggregate species comprising either aggregate peak. To address these shortcomings, we performed offline AFM on samples undergoing fibril formation.

Offline AFM measurements of aggregate morphologies and their dimensions

To correlate AFM data with DLS measurements, lysozyme fibrillogenesis was monitored using DLS while small aliquots were withdrawn for AFM imaging at various times during the incubation period. Before AFM measurements, the radii of all AFM scanning tips were calibrated against colloidal gold standards. As detailed in Materials and Methods, this enabled us to derive not just aggregate height distributions, but also lateral aggregate dimensions.

The AFM images of lysozyme before heating yielded uniform particles well approximated by oblate ellipsoids, with dimensions of 3.0 ± 0.2 nm in height and 3.8 ± 0.8 nm in equatorial width (Fig. 3 A and Table 1). Because their volume of 22.6 nm³ is in close agreement with the volume of 21.2 nm³ for lysozyme monomers in crystals (27), we identified these particles as lysozyme monomers. The aspect ratio of surface-absorbed lysozyme monomers was only slightly different from that of their counterparts in solution (28). After raising sample temperatures to 50°C, solutions contained mixtures of lysozyme monomers and compact elliptical aggregates with narrow size distributions (Fig. 3 B). We refer to these small, compact aggregates as oligomers. Our AFM observations thus imply that the seemingly uniform small-aggregate peak observed with DLS was indeed composed of lysozyme monomers, combined with an increasing number of oligomers that formed upon sample heating. Oligomer dimensions, determined by AFM at different times, remained constant. The ratios of apparent widths versus heights obtained using AFM were not consistent with the assumption of spherical geometries for either oligomers or monomers, but did match those expected for oblate ellipsoids. Based on this ellipsoidal geometry, the volume of oligomers was estimated at 8.1 times that of a lysozyme monomer, suggesting that oligomers are composed of eight monomers.

Figure 3.

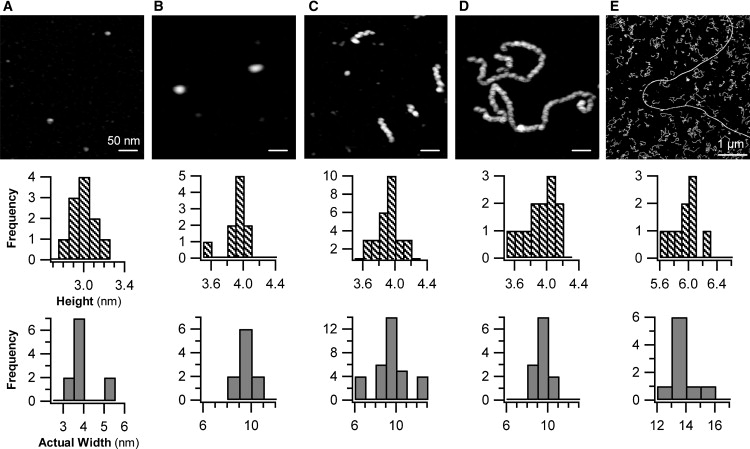
AFM images of intermediate amyloid aggregates formed by lysozyme. Evolution of aggregate morphologies for lysozyme amyloid growth at pH 2.0 and T = 50°C. (A) Before heating (T = 20°C), a uniform population of HEWL monomers is present. (B) AFM images of HEWL samples after 3 h of incubation at 50°C predominately yield oligomers. (C) AFM image of protofibrils appearing ∼10 h, i.e., shortly after nucleation event seen in DLS. (D) AFM image of protofibrils after 25 h of incubation. (E) AFM image of long, straight fibrils formed after ∼100 h of incubation, against a background of protofibrils (note change in scale-bar dimension). Below each image is the distribution of aggregate heights and lateral aggregate widths (the latter corrected for AFM tip distortions). Apparent difference in oligomer size in B versus protofibril width in C highlights effect of AFM scanning tips (16 nm in A and B versus 12.5 nm in C–E) on lateral aggregate dimensions. Tip-corrected aggregate dimensions are identical (see Fig. 5 and Table 1).

Table 1.

Heights and actual widths of amyloid aggregates

Sample	Height (nm)	Actual width (nm)
Monomer (0 h)	3.0 ± 0.2	3.8 ± 0.8
Oligomer (3 h)	3.9 ± 0.1	9.5 ± 1.0
Protofibril (10.5 h)	3.9 ± 0.3	9.5 ± 1.7
Protofibril (55 h)	3.9 ± 0.2	9.6 ± 1.0
Mature Fibril (100 h)	6.0 ± 0.2	13.9 ± 1.0

Averages of heights and actual widths for various intermediate aggregates formed during HEWL fibrillogenesis were obtained using AFM.

The prominent nucleation of larger aggregates detected by DLS (Fig. 2 C) coincides with the appearance of short, cylindrical polymers in AFM images (Fig. 3 C). We identify this polymeric species as protofibrils, consistent with previous AFM assignments of intermediate aggregate morphologies observed with beta-amyloid (Aβ)1-40 (29). During the 2–3-day growth period after nucleation, the contour length of protofibrils increases significantly (Fig. 3 D). The increase in protofibril contour length goes hand-in-hand with a significant increase in the curvature of protofibril strands. This transition from straight to highly curved morphologies is particularly apparent when comparing late-stage protofibril shapes (Fig. 3, D and E) with the short, straight protofibrils present shortly after nucleation (Fig. 3 C).

The AFM images of protofibrils reveal several intriguing features. First of all, protofibrils have noticeable and rather regular height undulations. In principle, this variegated appearance is compatible with the presumption that any polymeric precursor of mature fibrils already displays the helical twists known to exist in mature fibrils (3). However, our calibrated AFM measurements of aggregate dimensions indicate that protofibril heights and width are identical to those of oligomers seen before protofibril nucleation (Table 1 and Fig. 4). Fig. 5 gives a comparison of the three-dimensional profile of an oligomer versus the corresponding appearance of a short protofibril, both visualized with AFM using identical scanning tips. The height undulations (Fig. 5 B), combined with the tight agreement of the protofibril cross section with the overall height and width of oligomers (Figs. 4 and 5), indicate that protofibrils are composed of oligomers. The appearance of well-distinguished “blobs” with dimensions very close to those of oligomers suggests how oligomers coalesce to form protofibrils: oligomers fuse along their high-curvature perimeter, forming strings of aggregates similar to hockey pucks lining up edge to edge on a flat surface.

Figure 4.

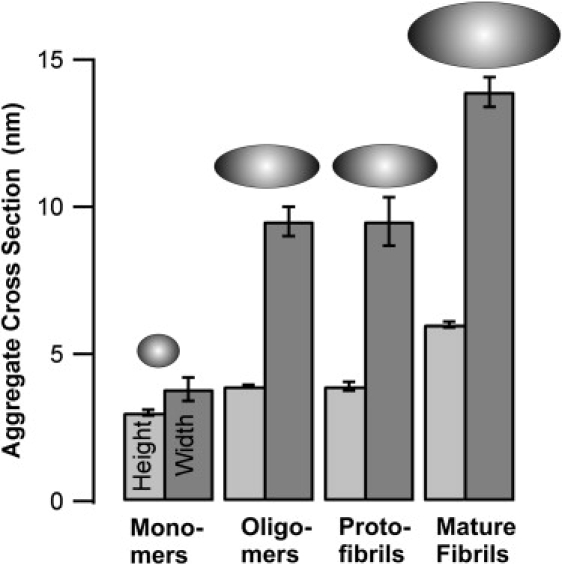
Dimensions of intermediate amyloid aggregates. Summary of heights and widths of lysozyme monomers, oligomers, protofibrils, and mature fibrils obtained from AFM images after tip correction. Ellipses are scale representations of measured cross sections.

Figure 5.

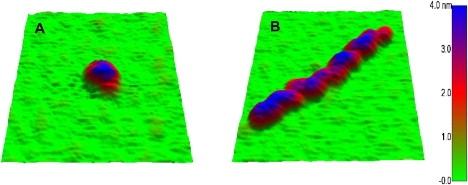
AFM surface topography of oligomers and protofibrils. (A) AFM topography of a HEWL oligomer after 3 h of incubation at 50°C. (B) AFM topography of HEWL protofibrils shortly after nucleation event. Both images were collected with same scanning tip, but aggregate dimensions were not corrected for dilation in x-y plane. Images are 125 nm on a side.

During the late stages of our experiments, a second, distinct population of fibers emerged. These mature fibrils are much longer and stiffer than those of the shorter protofibrils (Fig. 3 E). A direct comparison of mature fibril cross sections with those of protofibrils (Fig. 4) indicates that the former are ∼1.5 times as high and wide as protofibrils. Both the radius of curvature of mature fibrils and their overall length are dramatically increased over those of protofibrils (Fig. 3 E). This dramatic increase in persistence length indicates that mature fibrils are mechanically much stiffer than protofibrils. Although we did not analyze this feature quantitatively, it is again in good qualitative agreement with AFM images of Aβ1-40 protofibrils versus mature fibrils (e.g., Fig. 1 in Koo et al. (29)). Distributions of aggregate heights and actual widths (corrected for AFM tip dilation) of all intermediate amyloid aggregates are summarized in Fig. 4 and Table 1.

Quantitative comparison of DLS with AFM aggregate dimension

As alluded to in the Introduction, any offline analysis of intermediate amyloid aggregates carries the potential risk of disrupting some of the aggregate features it is intended to characterize. With AFM, the morphology of amyloid aggregates can depend on the properties of the substrate used for deposition or growth (16). It is also not obvious whether the sizes and shapes of amyloid aggregates in solution should match those that were dried and deposited on mica substrates. We therefore tested whether aggregate shapes and sizes obtained from offline AFM scans with calibrated tip sizes matched corresponding hydrodynamic radii obtained from in situ DLS. For comparisons of particle dimension we chose monomers, oligomers, and early-stage protofibrils. Monomers and oligomers were suitable, because their shapes can be closely approximated by oblate ellipsoids, and their sizes did not change over time. Similarly, the geometry of early-stage protofibrils (Fig. 3 C) were well represented by cylindrical rods with an initial length of 125 ± 28 nm and a diameter of ∼6 nm. Using Perrin's formulas (see Materials and Methods and Perrin (30) allowed us to calculate the hydrodynamic radius of an equivalent sphere with the same (translational) diffusion constant as an oblate ellipsoid or a long, thin cylinder. Table 2 summarizes these equivalent hydrodynamic radii for lysozyme monomers, oligomers, and initially rod-like protofibrils, as predicted from their dry-aggregate dimensions (AFM) versus measured average hydrodynamic radii (DLS). Given our simplifying assumptions about particle geometry, the neglect of hydration layers, and the potential for particle distortions from AFM tips of surface adhesion, the hydrodynamic radii of monomers and protofibrils predicted from AFM measurements matched surprisingly well with measured DLS radii for either population. The DLS radius for oligomers deserves further comment. The less than twofold difference in hydrodynamic radii for oligomers versus monomers, as predicted by AFM, is below the resolution limit typical for DLS. Hence DLS could not separate the small aggregate peak into its two components. The “oligomer” radius reported in Table 2 is really the average of monomers and oligomers, weighted by their respective scattering intensities. This interpretation is also supported by subtle changes to the shape of the “small-aggregate peak” during the early stages of nucleation (Fig. 6 A). As time passes, the narrow PSD peak progressively broadens with time, because of the formation of an increasing number of oligomers.

Table 2.

Comparison of measured (DLS) and estimated (AFM) hydrodynamic radii of intermediate aggregates

Sample	DLS Rh (nm)	AFM Rh (nm)
Monomer (0 h)	1.9	1.8 ± 0.3
Oligomer (3 h)	2.3∗	3.8 ± 0.4
Protofibril (10.5 h)	21.6	18.2 ± 3.0

DLS R_h (nm), measured hydrodynamic radii for lysoyzme monomers (0 h), weighted averages of monomers and oligomers (3 h), and protofibrils shortly after nucleation (10.5 h). AFM R_h (nm), predicted hydrodynamic radii for lysozyme monomers, oligomers, and protofibrils, based on AFM dimensions.

^∗DLS “oligomer radius” is average of monomers and oligomer radius, weighted by scattering intensity for each species present at 3 h.

Figure 6.

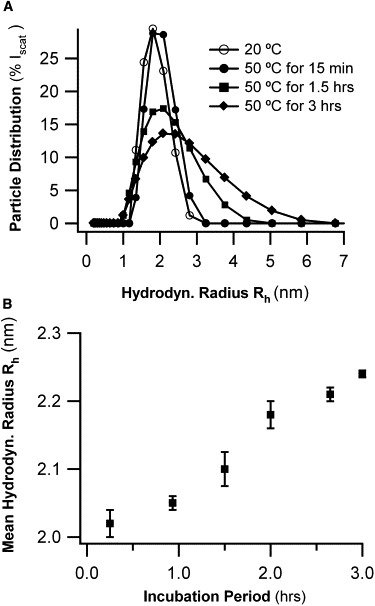
Analysis of oligomer formation in DLS. (A) PSD of “small-aggregate peak” before protofibril nucleation becomes increasingly skewed, with its center position shifting slightly. These changes coincide with growth of uniformly sized oligomers seen in AFM (Fig. 3B). (B) Changes in mean hydrodynamic radius <R_h> obtained from double-exponential fits to DLS autocorrelation functions during initial 3 h of oligomer growth.

The above analysis indicates that, whenever a direct comparison was feasible, the dimensions of intermediate aggregates derived from calibrated AFM measurements were consistent with corresponding in situ measurements obtained with DLS. Hence, we felt assured that conclusions about aggregate morphologies and dimensions derived from offline AFM observations accurately represented the in situ behavior of aggregates during growth in solution. Conversely, we used our a priori knowledge of aggregate morphologies derived from AFM imaging to reduce the ambiguities intrinsic to the inversion of DLS decay rates into particle-size distributions. Specifically, AFM indicates that, before protofibril nucleation, the solutions are mixtures of monomers and oligomers, each with fixed hydrodynamic radii. Therefore, we directly fit the field correlation functions g₁(τ) to double exponentials, with decay rates set to the predetermined monomer and oligomer radii. Residual errors for this double-exponential fit (without adjustable parameters) were significantly reduced over comparable fits to single exponentials with adjustable decay rates. Using this approach, we found that the mean hydrodynamic radius <R_h> increases linearly during the first 3 h of oligomer growth (Fig. 6 B). Thus the rate of oligomer formation during the lag phase is essentially constant.

Discussion

Clearly, lysozyme fibril formation shares many similarities with the aggregation kinetics and aggregate morphologies of the Alzheimer amyloid peptide Aβ1-40. For example, the relative sizes and appearance of lysozyme protofibrils and double-stranded fibrils (Fig. 3 E) closely match AFM images of comparable Aβ1-40 samples (29). Similarly, the reported growth kinetics of protofibrils are highly reminiscent of kinetic data obtained from Aβ1-40 fibrils grown in acidic solutions (31). These similarities support the idea that important aspects of amyloid fibrillogenesis are shared among many different types of amyloid proteins, including the formation of oligomeric species, the formation of both oligomers and protofibrils before the emergence of mature fibrils, and the shared cross-β-sheet structure of mature fibrils (32).

Aside from these similarities, the data indicate that lysozyme offers distinct advantages as a model system for studying critical aspects of amyloid-aggregation kinetics. One such advantage is the control over the rate of aggregation via simple experimental interventions, such as changes in solution pH or temperature. As a result, we were able to retard protofibril nucleation sufficiently to open up an experimental window of several hours for studying the intrinsic growth kinetics of oligomer formation, unobstructed by interference from other aggregate species (Fig. 2 C). Similarly, the separation of early stages of oligomer formation from the nucleation and subsequent growth of protofibrils permitted us to analyze how oligomer formation is coupled to protofibril nucleation and growth. In addition, correlating in situ DLS data with calibrated AFM measurements of aggregate dimension during the same experiment qualitatively improved the range of conclusions that could be derived from these data sets.

Solution morphology and growth kinetics of oligomers

Before protofibril nucleation, AFM images indicate the presence of oligomeric lysozyme aggregates with very narrow size distributions and a volume equivalent to eight monomers. The AFM dimensions of these oligomers (Fig. 4 and Table 1) are consistent with oblate ellipsoids of 3.9-nm height and a 9.5-nm equatorial diameter. The hydrodynamic radius for the equivalent sphere of only 3.8 nm naturally accounts for the difficulties of separating the small-aggregate peak in DLS into separate monomer and oligomer peaks. Using the a priori knowledge of oligomer geometry enabled us to analyze DLS correlation functions as a simple superposition of only two decay components, with decay rates matching those for monomers and oligomers. More importantly, the self-consistency between AFM aggregate dimensions and corresponding bimodal fits to the DLS data indicated that the oligomer shapes and dimensions derived using AFM closely approximated the actual oligomer conformation in solution. The correlation functions before protofibril nucleation also indicated that the average hydrodynamic radius of a small-aggregate peak increases linearly with incubation period (Fig. 6 B). Combined with the constant size of oligomers seen in AFM (Fig. 3 B), this observation indicates that oligomer formation initially proceeds at an essentially constant rate.

Nucleation and growth of protofibrils from oligomers

Aside from opening up a window on the intrinsic growth kinetics of oligomers, the DLS data also clearly resolve a prominent nucleation event (Fig. 2 C). The concurrent emergence of short protofibrils seen in AFM identifies them as the aggregate species undergoing nucleation-limited growth. As indicated in the Introduction, there are conflicting results regarding the nucleation and growth process of protofibrils. The correlated DLS and AFM measurements indicate that lysozyme protofibrils both nucleate and grow from oligomers. Evidence for this conclusion is provided by both the kinetic data on protofibril nucleation from DLS, and by comparisons of protofibril cross sections with oligomer dimensions obtained using AFM. First, the presence of a well-defined nucleation event (DLS) and the identification of the nucleating species as protofibrils (AFM) established that protofibrils undergo nucleation-limited growth. Multiple scenarios have been proposed to explain how protofibril nucleation and growth are linked to amyloid monomers and/or oligomers. It has been suggested that protofibrils grow via monomer addition, with oligomers only acting as (heterogeneous?) nucleation sites lowering the nucleation barrier. The DLS and AFM data on lysozyme indicate, instead, that oligomer formation commences without delay upon heating the solutions (Fig. 6 B), whereas protofibrils nucleation is delayed by several hours. The model of oligomers as nucleation sites, in contrast, implies that protofibril nucleation begins in lock-step with oligomer formation.

Alternately, oligomers and protofibrils might both grow directly from monomers, but along competing aggregation pathways. In this scenario, oligomers would initially grow from monomers. Protofibril formation would be delayed by the need to form a seed. After protofibril nucleation, however, they would start to compete with oligomers for the same pool of monomeric growth units. The kinetic data per se obtained via DLS cannot readily distinguish between the growth of oligomers and protofibrils from monomers along competing pathways versus the on-pathway growth of oligomers leading up to the nucleation and growth of protofibrils. However, the quantitative agreement between the AFM cross sections of protofibrils with the overall dimensions of oligomers (Table 1 and Figs. 4 and 5) strongly argues in favor of oligomers as the basic nucleation and growth unit for protofibrils, and against off-pathway oligomer formation. This further implies that oligomer formation represents the rate-limiting step for the nucleation and growth of protofibrils.

Protofibril elongation and self-assembly into mature fibrils

Closer inspections of AFM images of short protofibrils, i.e., those observed soon after nucleation, suggest how oligomers come together to form protofibrils. Oligomers appear to coalesce into linear aggregates along their highly curved perimeters, reminiscent of hockey pucks lining up along a surface. This model appears rather distinct from predictions of protofibrils with spiral geometries (33) that resemble the helical structures observed for mature fibrils with fully developed cross-β-sheet structures (3,34).

As the overall contour length of protofibrils increases, their morphology changes from short cylindrical rods to curvilinear polymer chains. We presume that this switch in protofibril morphology is a direct consequence of the short persistence length for protofibril polymers. We cannot rule out, however, that the observed changes in the morphology of protofibrils reflect concomitant changes in their internal structure. The transition from initially straight to highly curved protofibril geometries can also account for the apparent discrepancy between the very modest increase in the hydrodynamic radius of protofibrils (Fig. 2 C) versus the rather dramatic increase in scattering intensity (Fig. 2 D) during ∼3.5 days of growth. Because the radius of gyration for random Gaussian coils grows with the square root of the coil's contour length, the hydrodynamic radius would be expected to increases only slowly with the molecular weight of the protofibrils, whereas the scattering intensity would increase with roughly the square of the aggregate's molecular weight.

The short persistence length of protofibrils compared with the stiffness of mature fibrils (Fig. 3 E) further reinforces our assertion that protofibrils do not yet posses the helical cross-β-sheet structure of mature fibrils. Although the increase in diameter of mature fibrils over protofibrils should increase their stiffness, the modest 1.5-times difference in cross sections seems insufficient to account for the dramatic increase in stiffness from protofibrils to mature fibrils. We presume, instead, that the difference in mechanical stiffness arises from the distinct internal organization of protofibrils versus mature fibrils. Macromolecular assemblies with a helical organization, such as mature amyloid fibrils, tend to be mechanically stiff. The large persistence length of double-stranded DNA provides a classical example of this behavior. The long, straight shapes of double-stranded fibrils match the expected relationship between helical structure and mechanical stiffness. Protofibrils, in contrast, seem to lack such mechanical stiffness.

Linear, hierarchical assembly pathway

In summary, under acid growth conditions, lysozyme amyloid growth proceeded along a clearly defined and hierarchical aggregation pathway. Amyloid monomers aggregated into small oligomers of uniform size, without any apparent nucleation barrier. The population of these oligomers increased steadily throughout the lag period before protofibril nucleation. After increasing to some critical threshold concentration, protofibril nucleation commenced. Protofibrils grew as polymeric aggregates of oligomers, with oligomers adding to the ends of protofibrils. The agreement between the heights and widths of protofibrils and oligomers indicates that lysozyme oligomers coalesce along their highly curved perimeter when forming protofibrils. It also indicates that protofibrils do not yet share the helically twisted structure of mature fibrils (4). After reaching a contour length of few hundred nanometers, protofibrils then appeared to self-assemble into much longer and stiffer mature fibrils.

Our results regarding correlated AFM and DLS measurements suggest that lysozyme amyloid fibril formation at acid pH values provides a favorable model system for detailed analyses of the nucleation and growth kinetics of intermediate amyloid aggregates. The well-characterized structure of lysozyme monomers, the ease of controlling aggregation kinetics, the clear separation of oligomer formation from subsequent growth steps, and the ability to perform in situ characterization of aggregation kinetics are advantages that would be difficult to achieve with many other amyloid proteins and peptides. Such control provides significant advantages when trying to unravel the multifaceted interplay between various intermediate aggregates species, how they depend on their internal structure, how they respond to various interventions, and how they relate to cellular toxicity.