Ligand-Dependent Effects on the Conformational Equilibrium of the Na⁺,K⁺-ATPase As Monitored by Voltage Clamp Fluorometry

Abstract

Voltage clamp fluorometry was used to monitor conformational changes associated with electrogenic partial reactions of the Na⁺,K⁺-ATPase after changes in the concentration of internal sodium (Na⁺_i) or external potassium (K⁺_o). To probe the effects of the Na⁺_i concentration on the Na⁺ branch of the Na⁺,K⁺-ATPase, oocytes were depleted of Na⁺_i and then loaded with external sodium (Na⁺_o) using the amiloride-sensitive epithelial sodium channel. The K⁺ branch of the Na⁺,K⁺-ATPase was studied by exposing the oocytes to different K⁺_o concentrations in the presence and absence of Na⁺_o to obtain additional information on the apparent affinity for K⁺_o. Our results demonstrate that lowering the concentration of Na⁺_i or increasing the amount of K⁺_o in the external solution shifts the equilibrium toward E₁/E₁P. Furthermore, the K⁺_o-induced relocation toward E₁ occurs at a much lower K⁺_o concentration when Na⁺_o is absent, indicating a higher apparent affinity. Finally, voltage-dependent steps associated with the K⁺ branch or the Na⁺ branch of the Na⁺,K⁺-ATPase are affected by the K⁺_o concentration or the Na⁺_i concentration, respectively.

Introduction

The Na⁺,K⁺-ATPase is a P-type ATPase that is expressed in almost all animal cells. The enzyme is comprised of a mandatory α/β heterodimer where the α subunit contains the cytoplasmic phosphorylation site at a highly conserved aspartate residue, the cation-binding sites, and the site of action of cardiac glycosides such as ouabain and digoxin (1). The β-subunit is responsible for stabilization, proper trafficking of the holoenzyme to the plasma membrane, and modulation of cation affinities (2). The holoenzyme can also contain an optional third subunit from the FXYD family of proteins, which regulate the cation-binding affinity of the ion pump (3).

The sodium pump maintains a low internal Na⁺ (Na⁺_i) concentration and a high external K⁺ (K⁺_o) concentration against the prevalent ion gradients by utilizing the energy provided by ATP hydrolysis. The reaction cycle is described in terms of the Albers-Post scheme (4) (Fig. 1). Ion transport follows a “ping-pong” mechanism whereby three Na⁺_i and two K⁺_o ions cross the membrane sequentially and in opposite directions. The reaction steps consist of ion binding, ion occlusion (paralleled by phosphorylation or dephosphorylation of the enzyme), conformational transition, deocclusion, and ion release on the opposite side of the membrane. Ion transport is electrogenic, since a net charge is moved across the membrane. In addition, ion transport can be affected by the membrane potential (5). Originally, the definition of electrogenicity referred to the complete pump cycle, and the associated steady-state pump current-voltage (I/V) relationship was shown to be sigmoidal (6). However, several partial reactions of the cycle are electrogenic (7,8). In the absence of K⁺_o, dephosphorylation of E₂P is impaired or slowed from 366 s⁻¹ in the presence of K⁺_o (9), and to 24 s⁻¹ in the absence of K⁺_o (7,10). Under these conditions, the pump is restricted to the Na⁺ translocating branch of the cycle and shuttles in a voltage-dependent manner almost exclusively between the E₁P and E₂P conformations (Na⁺/Na⁺ exchange conditions). In contrast, investigation of the K⁺ branch of the reaction cycle by electrophysiological methods is more difficult due to the complicated redistribution of the reaction intermediates (11).

Figure 1.

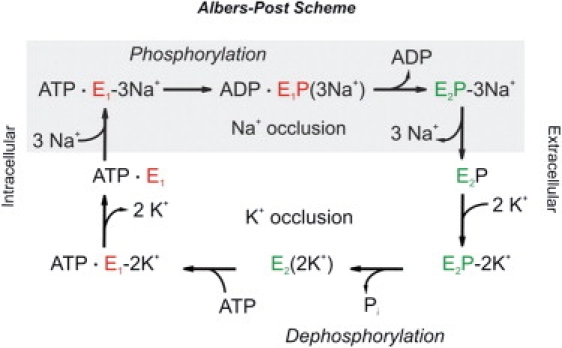
Albers-Post scheme for the Na⁺,K⁺-ATPase reaction cycle. The enzyme can assume two major conformations: E₁, where the ion-binding sites face the cytoplasm; and E₂, where access to the cation-binding sites is from the extracellular space.

Voltage clamp fluorometry (VCF) was previously utilized to monitor the voltage-jump-induced shuttling between the E₁P and E₂P conformations of the sodium pump under Na⁺/Na⁺ exchange conditions by analyzing the fluorescence relaxations of site-specifically labeled tetramethylrhodamine-6-maleimide (TMRM) (12). It was demonstrated that the saturation values of the fluorescence relaxations after labeling of N790C recorded in parallel to electrical measurements show the same voltage-dependent behavior as the transported charge. Therefore, changes in fluorescence intensity document a structural rearrangement during the conformational transition that is linked to charge translocation. Under Na⁺/Na⁺ exchange conditions, the observed fluorescence intensity at selected residues represents a measure of the concentrations of E₁P and E₂P: high fluorescence is an indication of the E₁P state, whereas low fluorescence is indicative of the E₂P state (12). More recent investigations have demonstrated that VCF can also be applied to gain information about the conformational dynamics and structural alignment of the β and γ subunits (13,14).

To investigate certain partial reactions of the Na⁺,K⁺-ATPase, it is necessary to control the concentration of the cytoplasmic pump ligands. An established method to measure and manipulate the concentration of Na⁺_i is to coexpress the epithelial sodium channel (ENaC) with the sodium pump (15). ENaC is involved in the regulation of blood pressure and Na⁺ balance. It is comprised of three subunits (α, β, and γ) that likely form a heterotrimer (16). ENaC is selective for Na⁺ and sensitive to the channel inhibitor amiloride (K_i = 0.1 μM), which blocks the channel from the extracellular side. After Na⁺_i is depleted by incubating oocytes in the absence of extracellular Na⁺ (Na⁺_o), a Na⁺ concentration gradient across the plasma membrane can be used to successively load a cell with Na⁺_o by temporarily removing amiloride from the extracellular solution. Each Na⁺_i concentration can be determined by using the respective reversal potential and the Nernst equation (15).

By combining VCF of the Na⁺,K⁺-ATPase with coexpression of ENaC, we were able to demonstrate that the conformational equilibrium of the Na⁺,K⁺-ATPase is highly sensitive to the concentration of both internal and external cations. In addition, evidence for the existence of an extracellular ion well for K⁺_o and an intracellular ion well for Na⁺_i can be obtained.

Materials and Methods

Expression of the Na⁺,K⁺-ATPase in Xenopus oocytes

Stage V/VI oocytes were isolated by partial ovariectomy of MS222-anesthetized, oocyte-positive Xenopus leavis females and subsequent collagenase treatment. The TMRM-reactive sheep Na⁺,K⁺-ATPase α₁ construct N790C and rat β₁ subunit were prepared as described previously (12). The α₁-subunit cDNA contained no native extracellular exposed cysteines (mutations C911S and C964A) and carried two additional mutations (Q111R and N122D) that confer increased ouabain resistance to selectively inhibit the endogenous oocyte Na⁺,K⁺-ATPase (17). Each oocyte was injected with sheep α₁ (25 ng) and rat β₁ (2.5 ng) subunit cRNA of the Na⁺,K⁺-ATPase. Unless stated otherwise, oocytes were kept at 18°C for 3–5 days in ORI solution (90 mM NaCl, 2 mM KCl, 2 mM CaCl₂, 5 mM MOPS, 100 μg/L gentamycin) to allow for a high level of exogenous Na⁺,K⁺-ATPase expression. Before experiments were conducted, the oocytes were incubated in Na⁺ loading solution (110 mM NaCl, 2.5 mM Na Citrate, 10 mM MOPS/TRIS pH 7.4) for 30–45 min to elevate [Na⁺]_i up to 80 mM, which fully activates the ion pump from the cytoplasmic side (18,19), and then in post-loading solution (10 mM NaCl, 1 mM CaCl₂, 5 mM BaCl₂, 5 mM NiCl₂, 5 mM MOPS/Tris pH 7.4) for 30 min. The latter solution was also used for fluorophore labeling of the oocytes after addition of 5 μM TMRM for 5 min in the dark. Tests for functionality of the TMRM-labeled and unlabeled Na⁺,K⁺-ATPase α₁ constructs were conducted by replacing Na⁺ in the test solution (100 mM NaCl, 5 mM BaCl₂, 5 mM NiCl₂, 5 mM Hepes pH 7.4, 10 μM ouabain) with 90 mM Na⁺ and 10 mM K⁺ in the external solution before and after reaction with TMRM.

Two electrode voltage clamp epifluorescence measurements

A fluorescence microscope (Axioskop 2FS; Carl Zeiss MicroImaging GMBH, Göttingen, Germany) with a 40× water-immersion objective (numerical aperture = 0.8) was equipped with the RC-10 perfusion chamber (Warner Instruments, Hamden, CT). Electrical measurements were performed with a two-electrode voltage clamp amplifier (CA-1B; Dagan, Minneapolis, MN) that was connected via an analog-digital converter (Digidata 1200B; Molecular Devices, Sunnyvale, CA) to a personal computer running pClamp 9 software (Molecular Devices). The intracellular voltage recording and current electrodes were Ag/AgCl electrodes with glass-pipette tips (GB 150-8P; Science Products GmbH, Hofheim, Germany) filled with 3 M KCl, and had a resistance of <1 MΩ. The bath electrodes were low-resistance agar bridges connected to Ag/AgCl electrodes in compartments containing 3 mM KCl. For fluorescence measurements, a 100 W tungsten lamp was used as a light source, combined with a 535DF50 excitation filter, a 565EFLP emission filter, and a 570DRLP dichroic mirror (Omega Optical, Brattleboro, VT). Fluorescence was detected by a PIN-022A photodiode (UDT Instruments, San Diego, CA) and amplified by a patch clamp amplifier (EPC; HEKA Instruments, Port Washington, NY). Fluorescence data were stored and processed using the pClamp9 software. The solution exchange was accomplished with a manually operated perfusion system (ESF Electronic, Göttingen, Germany) supported by a pump for rapid removal of excess fluid. All experiments were performed on the vegetal pole of Xenopus oocytes at 20–22°C in the dark.

Depending on the experimental requirements and the potential range of interest, one of two voltage step protocols was used. One protocol consisted of 14 20-mV steps (600 ms) from 80 mV to −180 mV. The second protocol included 11 30-mV steps (330 ms) from 100 mV to −200 mV. During the protocols, each step-ladder was successively approached from two different holding potentials (HP = −80 mV and HP = 0 mV, respectively). Unless stated otherwise, data were averaged from two consecutive runs, the sampling rate was 25 kHz, and filtering occurred at 2 kHz.

Experiments to assess the influence of the K⁺_o concentration on the conformational equilibrium of the Na⁺,K⁺-ATPase were carried out in a manner similar to that described by Geibel et al. (12). Measurements under Na⁺/Na⁺-exchange conditions were performed in test solution containing 10 μM oubain or, if required, 10 mM ouabain to inhibit the heterologously expressed ion pump. K⁺_o was substituted in equimolar amounts as indicated. Measurements were also conducted in the absence of Na⁺_o (100 mM NMG-Cl, 5 mM BaCl₂, 5 mM NiCl₂, 5 mM Hepes pH 7.4, and 10 μM oubain).

The decrease of the fluorescence signal over time due to bleaching was monitored by means of intermediate recordings under Na⁺/Na⁺-exchange conditions. The first recording in a series of measurements served as a normalization standard for subsequent measurements in solutions of varying composition.

Manipulation and determination of the Na⁺_i concentration

To evaluate the influence of the Na⁺_i concentration on the conformational equilibrium of the Na⁺,K⁺-ATPase, coexpression of the epithelial sodium channel (ENaC) was used to manipulate and quantify [Na⁺]_i (15). This approach allowed [Na⁺]_i to be assessed by determining the reversal potential of the Na⁺ current. At the same time, the specific ENaC blocker amiloride facilitated controlled loading of the oocyte with Na⁺_o.

In coexpression experiments, 8 ng cRNA of the rat ENaC α, β, and γ subunits were coinjected with 17 ng cRNA of the sheep Na⁺,K⁺-ATPase α₁ subunit and 1.7 ng rat β₁ subunit. The cells were then kept at 18°C for 3–5 days in ORI solution, which contained 100 μM amiloride to block ENaC. Depletion of [Na⁺]_i was achieved by incubating the oocytes in Na⁺_i depletion solution (70 mM NMG-Cl, 40 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 5 mM Hepes pH 7.4, 100 μM amiloride) for 1–2 days before measurements were obtained. This solution was also used for fluorophore labeling (5 μM TMRM, 5 min in the dark).

To monitor the stepwise increase of [Na⁺]_i, Na⁺ loading steps using the open ENaC channel were followed by a short voltage step protocol to determine the reversal potential. This was immediately followed by measuring the voltage step-induced fluorescence responses of the Na⁺,K⁺-ATPase-TMRM sensor complex in solution containing 100 μM amiloride. The short step protocol consisted of a step-ladder of seven 20 mV steps (390 ms long) from 100 mV to −20 mV that was approached from a holding potential (HP) of −80 mV, whereas for fluorescence measurements the protocols described above were applied. The procedure was repeated until a [Na⁺]_i of >50 mM was reached. When necessary, inflow of Na⁺_o through the open ENaC channel was significantly increased by applying an HP of −100 mV for 1–2 min. Since determining the reversal potential for Na⁺ in amiloride-free solution required raising the Na⁺_i concentration, it was not possible to determine [Na⁺]_i for the first fluorescence measurement in a series.

The constant increase of [Na⁺]_i from one experiment to the next did not allow for standardized recordings under Na⁺/Na⁺-exchange conditions to correct for bleaching of the fluorophore. Therefore, the decrease in fluorescence intensity over time was compensated for by gradually increasing the illuminated area of the oocyte to maintain a constant fluorescence background. Consequently, changes in the background fluorescence due to a shift in the conformational equilibrium were overlaid by bleaching and could not be quantitated. As a normalization standard, one measurement in the series was chosen that exhibited the largest changes in fluorescence intensity under the prevailing Na⁺/Na⁺-exchange conditions. Usually located at a Na⁺_i concentration of 20–30 mM, this measurement represents saturated Na⁺_i conditions.

The reversal potential for Na⁺ was determined from the intersection of consecutive pairs of I/V curves measured with and without amiloride. This allowed the calculation of [Na⁺]_i with the Nernst equation:

$${\left[{\text{Na}}^{+}\right]}_{\text{i}}={\left[{\text{Na}}^{+}\right]}_{\text{o}}\exp (-FV/RT),$$ (1)

where [Na⁺]_o is 100 mM, F is the Faraday constant, R is the universal gas constant, T is the temperature (in Kelvin), and V is the reversal potential of the amiloride-sensitive current. Since the internal pH of oocytes was previously determined to be 7.3, the effect of a proton gradient can be disregarded in this calculation (20).

By definition, with Eq. 1, ENaC must be opened to determine [Na⁺]_i; therefore, it was not possible to determine [Na⁺]_i in the first fluorescence trace, because ENaC had not yet been opened. However, in a number of experiments it was observed that when [Na⁺]_i was increased, V_0.5 was shifted to more hyperpolarizing potentials in a saturating manner with respect to the Na⁺,K⁺-ATPase. It was therefore possible to elucidate [Na⁺]_i in cases where only V_0.5 was known by approximating the relationship between both parameters using a monoexponential function (pooled data of seven individual experiments). In this protocol, two assumptions were applied: 1), saturating levels of [Na⁺]_i are reached at a concentration of 20 mM with respect to the Na⁺ pump; and 2), as suggested by previous experiments (15), the most thoroughly [Na⁺]-depleted oocytes that showed fluorescence changes (V_0.5 = +91mV) were assigned a [Na⁺]_i of 1 mM.

Data analysis

The relaxation processes were best fit by monoexponential functions that yielded the fluorescence saturation values (ΔF) and the rate constants (reciprocals of time constants, k). The fluorescence saturation values were corrected for bleaching, fit to a Boltzmann distribution, and normalized to the relevant reference measurement under Na⁺/Na⁺-exchange conditions. Original current and fluorescence traces were analyzed in Clampfit 9 and Origin 7.

Results

Effects of Na⁺_i on the conformational equilibrium of the Na⁺, K⁺-ATPase

The recordings in Fig. 2 A depict four sets of voltage step-induced fluorescence responses after progressive increases of [Na⁺]_i. Each set of traces is aligned according to the respective background fluorescence at the HP (−80 mV). However, since no correction for bleaching was possible, the shift from E₁P to E₂P is not quantitative. To isolate the Na⁺ branch of the reaction cycle, the extracellular solution contained 100 mM Na⁺_o (Na⁺/Na⁺-exchange conditions). In several experiments, no fluorescence changes could be observed in Na⁺_i-depleted oocytes (data not shown). After the Na⁺_i concentration ([Na⁺]_i = 1.0 mM) was increased, voltage-dependent changes in fluorescence intensity could be evoked by depolarizing voltage steps. Since depolarization shifts the equilibrium toward E₂P (12), most pump molecules can be expected to reside in E₁P under these conditions. Further raising the Na⁺_i concentration ([Na⁺]_i = 2.1 mM and 6.1 mM) relocates the equilibrium toward E₂P as hyperpolarizing potentials gradually become the primary source for fluorescence changes. At [Na⁺]_i = 13.5 mM, the fluorescence responses are basically identical to those acquired in previous experiments performed at a saturating concentration of Na⁺_i, with most pump molecules residing in the E₂P conformation (12).

Figure 2.

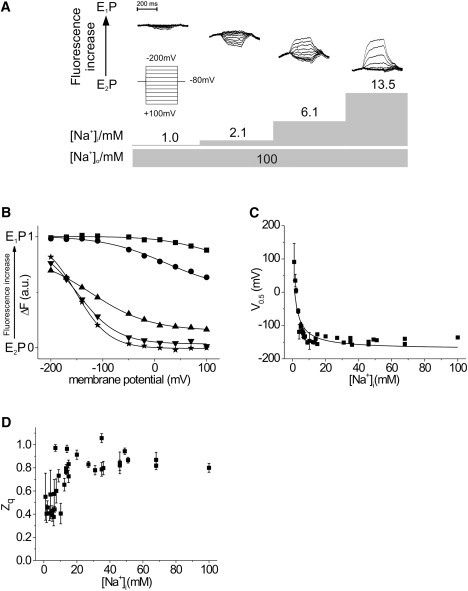
[Na⁺]_i dependence of the conformational equilibrium of the Na⁺,K⁺-ATPase. (A) Voltage step-induced fluorescence traces under Na⁺/Na⁺-exchange conditions at increasing concentrations of Na⁺_i. (B) Voltage dependence of the fluorescence saturation values and the related Boltzmann functions. Voltage steps were performed from an HP of −80 mV in 30 mV steps to the potentials indicated. The experiments were performed at different [Na⁺]_i concentrations of 1.0 mM (squares), 2.1 mM (circles), 6.6 mM (triangles), 12.4 mM (inverted triangles), and 13.5 mM (stars). (C) Midpoint potentials, V_0.5 (± SE), of the Boltzmann functions. To fit the data, the data were inverted and fit with the Hill function. (D) Translocated charge, z_q (± SE), related to the observed conformational change. (C and D) Scatter plots of the data of six cells.

To obtain more detailed information about the conformational equilibrium, the fluorescence saturation values (ΔF) were determined from monoexponential fits to the original voltage step-induced fluorescence relaxations. The ΔF-V data were normalized to the data acquired under Na⁺/Na⁺-exchange conditions at saturating Na⁺_i concentration and fit to a Boltzmann function.

Fig. 2 B shows the effects of different Na⁺_i concentrations on the ΔF-V relationship of the experiment displayed in Fig. 2 A. At low concentrations of Na⁺_i (1.0 mM and 2.1 mM), changes in fluorescence intensity are restricted to depolarizing potentials and only the “upper” section of the sigmoid Boltzmann distribution is visible. This indicates that the majority of the participating ion pumps are in the E₁P conformation. As the concentration of Na⁺_i is increased ([Na⁺]_i = 6.6 mM), the sigmoid shape of the voltage dependence becomes apparent and voltage jumps can shift the equilibrium to both E₁P and E₂P conformations. At higher [Na⁺]_i (13.5 mM), the concentration-dependent relocation of the equilibrium to E₂P progresses to the point where fluorescence signals are primarily evoked by jumps to hyperpolarizing potentials.

Increasing [Na⁺]_i shifts the Boltzmann curves from depolarizing to more hyperpolarizing potentials. This shift can best be analyzed by monitoring changes in the midpoint potential (V_0.5) of the curves (Fig. 2 C). When [Na⁺]_i is ∼1.0 mM, the V_0.5 is 91 ± 56 mV. In contrast, under saturating ion conditions V_0.5 values in the range of −130 mV to −150 mV are observed. The K_0.5 of 2.3 ± 0.4 mM determined for the [Na⁺]_i-dependent shift of the midpoint potential of the ΔF-V data agrees with a previous study in which K_m (3.2 ± 0.4 mM) was calculated from the concentration-dependent increase in translocated charge (Q-V relationship) (21).

From these data, it is also possible to determine the value of z_q, which is the amount of charge translocated per translocating step, as a function of increasing [Na⁺]_i (Fig. 2 D). At low [Na⁺]_i (<10 mM), the amount of [Na⁺]_i is not saturating, and therefore all of the internal Na⁺-binding sites are not occupied. This limits the amount of charge being translocated, since rebinding of Na⁺ is an electrogenic event. In contrast, at saturating [Na⁺]_i (>10 mM), the value of z_q is ∼0.8 and represents the maximal z_q because both internal and external Na⁺-binding sites can be filled.

Effects of K⁺_o on the conformational equilibrium of the Na⁺, K⁺-ATPase in the presence of Na⁺_o

The presence of K⁺_o in a Na⁺_o-containing solution allows for turnover of the pump: three Na⁺_i are pumped out of the cell via the Na⁺ branch, and two K⁺_o are pumped into the cell via the K⁺ branch. The resulting steady-state current is dependent on the membrane voltage (6), which means that one or more steps of the reaction cycle are electrogenic. Transient currents cannot be observed at increased concentrations of K⁺_o (11). Therefore, information on the position of the conformational equilibrium cannot be gained by purely electrical means. However, VCF offers an alternative means to obtain this information by looking directly at the voltage-dependent conformational changes, which provides equivalent information (12,22).

The progressive changes of the voltage step-induced fluorescence relaxations in response to increasing amounts of K⁺ in a Na⁺-containing external solution (turnover conditions) are shown in Fig. 3 A. At each concentration, the sets of fluorescence traces are aligned according to their respective levels of background fluorescence at −80 mV. As stated above, in the absence of K⁺_o (when only the Na⁺ branch is accessible), fluorescence signals are mainly evoked by hyperpolarizing potentials and most pump molecules reside in E₂P. As the concentration of K⁺_o is raised, fluorescence signals are increasingly induced by depolarizing potentials. These data are consistent with the idea that there is a gradual displacement of the conformational equilibrium toward E₁ due to the growing involvement of the K⁺ branch. In the presence of 5 mM K⁺_o, changes in fluorescence intensity are observed only at extreme depolarizing membrane potentials (+80 and +100 mV), whereas in the presence of 10 mM K⁺_o, the shift of the conformational equilibrium progresses to the point where depolarizing voltage jumps of the step protocol are no longer sufficient to evoke changes in fluorescence intensity (Fig. 3 B). In line with the voltage jump data, the background fluorescence increases in a concentration-dependent manner during the experiment, which also indicates the relocation toward E₁ (12).

Figure 3.

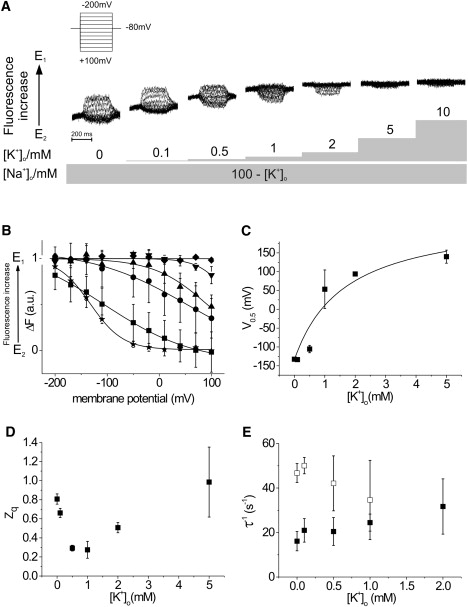
[K⁺]_o dependence of the conformational change and the related charge translocating step(s) of the Na⁺,K⁺-ATPase. (A) Voltage step-induced fluorescence traces at increasing concentrations of K⁺_o in the presence of Na⁺_o. (B) Voltage dependence of the fluorescence saturation values and the related Boltzmann functions. Voltage steps were performed from an HP of −80 mV in 30 mV steps to the potentials indicated. The external solution contained as its main constituent 100 mM Na⁺ (stars), which was successively substituted by 0–10 mM K⁺ (for the sake of clarity, only data acquired in K⁺-free solutions (stars) and at concentrations of 0.5 mM K⁺ (squares), 1 mM K⁺ (circles), 2 mM K⁺ (triangles), 5 mM (inverted triangles), and 10 mM K⁺ (diamonds) are shown here). (C) Midpoint potentials, V_0.5 (± SE), of the Boltzmann functions. The concentration dependence of the V_0.5 values can be approximated by a sigmoidal function. (D) Translocated charge, z_q (± SE), related to the observed conformational change. (E) Apparent rate constants, τ⁻¹ (± SD), of the fluorescence relaxations in response to voltage jumps from an HP of −80 mV to +100 mV (solid squares) and −200 mV (open squares).

The K⁺_o dependence of the ΔF-V curves and their corresponding Boltzmann functions is shown in Fig. 3 B. These results demonstrate that the addition of K⁺_o produces a shift of the ΔF-V curves toward more depolarizing potentials. In addition, at 0.5 mM K⁺_o and 1 mM K⁺_o, the slope of the Boltzmann fit is less steep, which indicates that the voltage dependence is reduced. Extrapolation of the Boltzmann functions at 0.1, 0.5, and 1 mM K⁺_o results in curves that surpass the saturation values of the reference measurement under Na⁺/Na⁺-exchange conditions (up to a maximum of 1.3 times the reference value at 0.5 mM K⁺_o, respectively). The reason for this increase could be the availability of new enzyme conformations, such as E₂P-2K⁺ and E₁-2K⁺, under turnover conditions (see the Albers-Post scheme in Fig. 1) that exhibit different fluorescence intensities.

The K⁺_o dependence of V_0.5 was fitted to a Hill equation (Fig. 3 C). In accordance with previous studies (7,22,23) the Hill coefficient was held at one. A low apparent affinity (K_0.5 = 1.7 ± 1 mM) for K⁺_o in the presence of Na⁺_o can be observed that is compatible with previous results obtained with a comparable reporter construct under similar conditions (K_0.5 = 2.8 ± 0.3 mM (22)).

It is evident that z_q changes as a function of K⁺_o (Fig. 3 D). The value of z_q decreases from 0.81 ± 0.05 under Na⁺/Na⁺ exchange conditions to a value of 0.27 ± 0.09 in the presence of 1 mM K⁺_o (12,24). However, at higher K⁺_o, an increase of z_q is observed. This suggests that at low K⁺_o (0.1–1.0 mM), K⁺_o inhibits Na⁺_o rebinding, and that during hyperpolarization, K⁺_o binding, which has a lower z_q, occurs. Above 1.0 mM K⁺_o, as also demonstrated by the original fluorescence traces (Fig. 3 A), the only changes in fluorescence intensity are observed after depolarizing membrane pulses. Under these conditions, the determination of z_q is derived from intracellular Na⁺ binding and subsequent ion translocation.

The apparent rate constants of the fluorescence relaxations show a different response to depolarizing (+100 mV) and hyperpolarizing (−200 mV) membrane pulses (Fig. 3 E). Upon depolarization, values of ∼20 s⁻¹ up to a K⁺_o concentration of 1 mM can be observed, with a slight acceleration at 2 mM K⁺_o (32 ± 12 s⁻¹). Because of the error in measurements, it is difficult to determine whether the apparent increase in τ⁻¹ when K⁺_o is increased is linear. In contrast, the apparent rate constants upon hyperpolarization are clearly accelerated in the absence of K⁺_o (47 ± 4 s⁻¹) but slow down upon addition of K⁺_o (35 ± 18 s⁻¹ at 1 mM K⁺_o). Hyperpolarization accelerates Na⁺_o rebinding and the transition to E₁P due to the existence of an external access channel for Na⁺ (25). This process seems to become impeded at increasing K⁺_o concentrations. It was not possible to determine the rate constant for the potential jump to −200 mV at higher K⁺_o concentrations due to the shift of the ΔF-V curves.

Effects of K⁺_o on the conformational equilibrium of the Na⁺, K⁺-ATPase in the absence of Na⁺_o

We were next interested in further isolating and examining the K⁺ branch of the reaction cycle by replacing Na⁺_o with NMG⁺_o to eliminate competition between K⁺_o and Na⁺_o for access to the ion-binding sites (Fig. 4 A). In these experiments, substitution of Na⁺_o with NMG⁺_o prevents the E₂P/E₁P transition upon hyperpolarization. In addition, judging from the background fluorescence, NMG⁺ also leads to a slight overall shift of the conformational equilibrium toward E₂P. Therefore, depolarization and hyperpolarization lead to only marginal changes in fluorescence intensity. Upon substitution of NMG⁺_o by K⁺_o, the amplitudes of the fluorescence responses evoked by depolarizing potentials are increased upon addition of micromolar amounts of K⁺_o, which documents a gradual shift of the equilibrium toward E₁. As observed in the presence of Na⁺_o at 10 mM K⁺_o, the shift proceeds to a point where depolarizing voltage jumps no longer evoke changes in fluorescence intensity. This relocation of the equilibrium toward E₁ is also documented by an increase of the background fluorescence. It should be noted that fluorescence responses upon hyperpolarization show a noticeable increase in magnitude in the lower micromolar K⁺_o range. At higher concentrations, however, this effect is completely negated by the shift of the equilibrium toward E₁.

Figure 4.

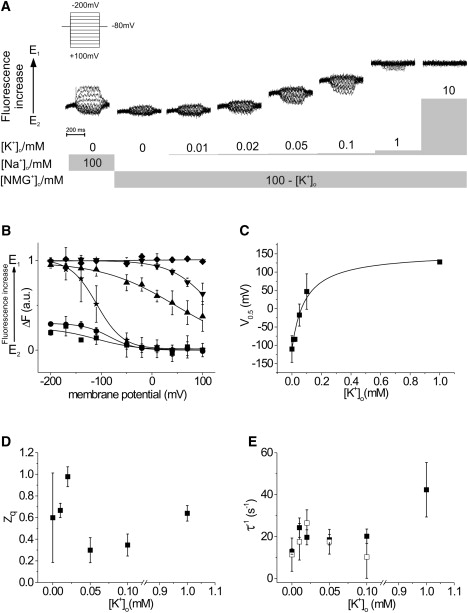
[K⁺]_o Dependence of the conformational change and the related charge translocating step(s) of the Na⁺,K⁺-ATPase. (A) Voltage step-induced fluorescence traces at increasing concentrations of K⁺_o in the absence of Na⁺_o. (B) Voltage dependence of the fluorescence saturation values and the related Boltzmann functions. Voltage steps were performed from an HP of −80 mV in 30 mV steps to the potentials indicated. The external solution contained as its main constituent either 100 mM Na⁺ (stars) or 100 mM NMG⁺ (squares) substituted with 0–10 mM K⁺ (for the sake of clarity, only data acquired in K⁺-free solutions (stars and squares) and at concentrations of 0.02 mM K⁺ (circles), 0.1 mM K⁺ (triangles), 1 mM K⁺ (inverted triangles), and 10 mM K⁺ (diamonds) are shown here). (C) Midpoint potentials, V_0.5 (± SE), of the Boltzmann functions. The concentration dependence of the V_0.5 values can be approximated by a monoexponential function. (D) Translocated charge, z_q (± SE), related to the observed conformational change. (E) Apparent rate constants, τ⁻¹ (± SD), of the fluorescence relaxations in response to voltage jumps from an HP of −80 mV to +100 mV (solid squares) and −200 mV (open squares).

In a subsequent analysis, we were interested in examining the K⁺_o dependence of the ΔF-V curves and the corresponding Boltzmann functions in the absence of Na⁺_o (Fig. 4 B). Reference data were obtained under Na⁺/Na⁺-exchange conditions, but all other data were acquired in Na⁺_o-free NMG⁺_o solutions that contained 0.01–10 mM K⁺_o. With increasing K⁺_o concentration, the Boltzmann distributions are shifted toward more depolarizing potentials. In addition, the shallow slope at [K⁺]_o = 0.1 mM shows that the voltage dependence of the ΔF-V curves changes during the course of these experiments. Again it should be noted that, at low [K⁺]_o, small but significant changes in fluorescence intensity are evoked upon hyperpolarizing potential steps.

For further analysis, the K⁺_o concentration dependence of the midpoint potential, V_0.5, of the Boltzmann functions was plotted (Fig. 4 C). Data were fit to a Hill equation and the Hill coefficient was held at one. A high apparent affinity for K⁺_o in the absence of Na⁺_o can be observed (K_0.5 = 90 ± 20 μM), which is comparable with the findings reported in a similar study on the β subunit of the Na⁺,K⁺-ATPase (K_0.5 = 80 ± 20 μM (22)) and by other laboratories (24,26).

These experiments also facilitated an analysis of the dependence of the K⁺_o concentration on the translocated charge, z_q (Fig. 4 D). In K⁺_o-free solution, it was observed that z_q is 0.60 ± 0.41. This result is difficult to interpret since, at least in the extracellular solution, the only ions in solution that can be transported by the ion pump are protons. Upon addition of small amounts of K⁺_o, z_q increases (up to 0.98 ± 0.10 at 0.02 mM). However, z_q decreases upon further addition of K⁺_o (0.30 ± 0.12 at 0.05 mM K⁺_o), which is reminiscent of the behavior in Na⁺_o-containing solution. This also suggests that at low K⁺_o, K⁺ acts an inhibitor, whereas at high K⁺ the pump follows the K⁺ branch of the Albers-Post scheme. One notable difference is that the inflection point where z_q increases is higher (∼1 mM) in Na⁺-containing solution than in solution that has no extracellular Na⁺ (∼0.05 mM).

As before, two membrane potentials (+100 mV and −200 mV) were selected to display the effect of depolarizing and hyperpolarizing potentials on the apparent rate constants of the original voltage step-induced fluorescence relaxations (Fig. 4 E). Up to a concentration of 0.1 mM K⁺_o, differences between the two membrane potentials are small and the rate constants show values of ∼20 s⁻¹. Consequently, low concentrations of K⁺_o do not influence the apparent rate of the monitored conformational transition at either membrane potential. However, a distinct acceleration (42.3 ± 13.0 s⁻¹) can be observed at 1 mM K⁺_o upon depolarization to 100 mV. No fluorescence signals in response to hyperpolarization could be observed at this K⁺_o concentration, and it was not possible to determine the rate constant of this process.

Discussion

These experiments demonstrate that by combining heterologous expression of the Na⁺, K⁺-ATPase with the ENaC channel in oocytes alongside two electrode voltage clamp and fluorescence measurements, one can examine how internal and external ligands affect the conformational equilibrium of the ion pump. Furthermore, these data can be compared with the crystal structures of both the Na⁺, K⁺-ATPase and the SERCA Ca²⁺-ATPase, as well as a large body of biochemical data, to gain further mechanistic insights into ion transport (27,28).

Effects of low Na⁺_i concentrations on the sodium pump can be monitored by a fluorescent probe in the extracellular loop region

In contrast to previous studies that combined site-specific fluorescence labeling with electrophysiology measurements using preloaded Na⁺ oocytes, our results demonstrate that changes in [Na⁺]_i affect the voltage dependence of the fluorescence relaxations and therefore the position of the conformational equilibrium of the sodium pump (22,29).

We base this conclusion on the observation that at a Na⁺_i concentration of ≥13.5 mM, fluorescence signals are mainly evoked by hyperpolarizing potentials, which promote the E₁P conformation, whereas at low [Na⁺]_i (1.0 mM) changes in fluorescence intensity are limited to depolarizing potentials, which promote E₂P. Furthermore, the V_0.5 of Boltzmann fits to the fluorescence data is significantly shifted to more positive potentials as the Na⁺_i concentration is lowered. Such a shift also indicates a substantial redistribution of the E₁P/E₂P equilibrium toward the E₁P conformation. The ion pump is shifted to E₁P because although there is saturating Na⁺ in the bath solution, which enables the E₂P-to-E₁P transition, the absence of Na⁺ in the cell inhibits Na⁺ binding in the cell and the subsequent E₁P-to-E₂P transition. Therefore, the E₁P conformation accumulates.

Thus, the [Na⁺]_i-dependent change of the voltage step-induced fluorescence signals in Fig. 2 A shows a close resemblance to the [K⁺]_o-dependent change of the fluorescence signals that are visible in Fig. 3 A and were also described previously (12). Both can be interpreted as an incremental shift of the conformational equilibrium from E₂P to E₁P or, in the presence of K⁺, from E₂ to E₁. This suggests that an increase of [K⁺]_o influences the position of the equilibrium in a comparable way as would a decrease of [Na⁺]_i, and that both conditions shift the equilibrium toward E₁P (E₁).

VCF can be used to investigate the conformational states of the K⁺ branch

Under Na⁺/Na⁺-exchange conditions, voltage jumps redistribute the E₁P/E₂P equilibrium in a saturating manner (19). By combining site-specific fluorophore labeling with electrophysiology measurements, we demonstrated that a high fluorescence intensity can be correlated with the E₁P conformation, and a low fluorescence intensity can be correlated with the E₂P conformation (12). Furthermore, N790C appears to be involved in opening and closing of an outward-facing access channel, as elucidated from structural data (27,28). Thus, changes in fluorescence intensity, which are the result of a local environmental change of the fluorophore, are directly related to Na⁺ release/rebinding from the ion pump.

In contrast to Na⁺/Na⁺-exchange conditions, it seems likely that the structural rearrangements that open the external exit pathway for Na⁺ release and close the pathway for K⁺ occlusion in the Na⁺,K⁺-ATPase are related but not identical. Whereas K⁺ ions initiate dephosphorylation and the subsequent closing of the cytoplasmic gate, the phosphoenzyme is required to open the Na⁺ exit pathway (30–32). Thus, the change in fluorescence intensity that follows the conformational transition for K⁺ occlusion will likely differ, and our observation is that the changes in fluorescence intensity that accompany the E₁P/E₂P transition of the Na⁺ branch and those that accompany the E₂/E₁ transition of the K⁺ branch are of different magnitudes. In addition, it has to be considered that in the presence of K⁺ and Na⁺, several different conformations of both branches with different fluorescence intensities contribute to the total fluorescence signal. However, this is probably only true at low K⁺ concentrations. The fact that fluorescence data acquired at high K⁺_o concentrations in the presence or absence of Na⁺ are similar suggests that the observed fluorescence signals can mainly be attributed to conformational changes in the K⁺ branch (Figs. 3, A and B, and 4, A and B).

External Na⁺ and K⁺ influence the conformational equilibrium

In agreement with previous studies in this and other laboratories, the apparent affinity for K⁺_o is higher in solutions that do not contain Na⁺ (22,26). Furthermore, the kinetics of the fluorescence changes also reflects the impact of the ion composition of the external solution on the conformational equilibrium. If Na⁺ is present at low K⁺_o concentrations ([K⁺]_o = 0–0.1 mM), the apparent rate constants of the fluorescence relaxation are accelerated upon hyperpolarization to −200 mV (∼48 s⁻¹), but not upon depolarization to +100 mV (∼19 s⁻¹). Under these conditions, hyperpolarization promotes Na⁺ rebinding and the conformational change to E₁P via the Na⁺ branch due to the existence of an external access channel (25). At higher K⁺_o concentrations, the apparent rate constant upon hyperpolarization decreases until it matches up with the slightly accelerated apparent rate constant for depolarization (∼30 s⁻¹). Na⁺ rebinding is at this point no longer promoted in a specifically voltage-dependent fashion, and the conformational equilibrium is shifted in favor of the K⁺ branch and the E₂/E₁ transition. Correspondingly, experiments in Na⁺-free solution exhibit both hyperpolarizing and depolarizing voltage-step rate constants of ∼19 s⁻¹ in the presence of 0–0.1 mM K⁺ (Fig. 4 E).

Indications that K⁺ translocation is electrogenic and ion binding is promoted via an ion well

In the presence of K⁺_o, the ion pump is driven along the E₂/E₁ conformational transition through the K⁺ branch. Therefore, it can be assumed that the voltage-dependent changes in fluorescence intensity upon hyperpolarization that can be observed up to a K⁺ concentration of 0.1 mM are the result of the electrogenicity of the K⁺ branch (Fig. 4 A). The fluorescence relaxations disappear at higher K⁺ concentrations due to the shift of the ΔF-V curves toward depolarizing potentials (Fig. 4 B). However, this shift shows that the conformational equilibrium, which can be assumed to be mainly set up via the K⁺ branch, depends not only on the membrane potential but also on the K⁺ concentration. In analogy to previous findings for Na⁺ (25), this suggests that K⁺ also binds in an ion well (33).

Generally, K⁺ translocation is not thought to be voltage dependent (34). However, in agreement with our findings, Rakowski and co-workers (24) reported a pump I/V relationship with a negative slope in Na⁺-free solution at subsaturating K⁺ concentrations. The authors proposed that under these conditions hyperpolarization increases the effective K⁺ concentration at the binding sites via an ion well. Yet, the pump operates independently of voltage when the K⁺ concentration has reached saturation.

Indications for the existence of an intracellular ion well for Na⁺

The presence of an internal ion well is in dispute. Some data support the existence of a shallow internal ion well with a dielectric coefficient of ∼0.25 (35,36). In addition, Holmgren and Rakowski (21) investigated the effect of changes in the intracellular Na⁺ concentration on the voltage step-induced transient currents of the Na⁺,K⁺-ATPase. They observed pronounced effects of changes in [Na⁺]_i on the amount of the translocated charge and on the kinetics of the charge translocation, which are in agreement with the fluorescence data of the study presented here. Yet, they did not observe a Na⁺_i-dependent shift of the midpoint potential in the Q-V relationship. As a possible explanation for this, Holmgren and Rakowski proposed that the intracellular ion-binding process is isolated due to the relatively slow occlusion reaction that follows ion binding.

Studies on the N790C-TMRM construct clearly show a shift of the midpoint potential, V_0.5, toward more positive potentials at low Na⁺_i concentrations. Midpoint potentials at saturating [Na⁺]_i (above 20 mM) are in the range of −130 to −150 mV, whereas values up to +100 mV can be measured if [Na⁺]_i is lowered to ∼1 mM. Analogously to the properties of an external ion well (25), this observation suggests the presence of an internal ion well. A fraction of the potential difference between the extra- and intracellular sides of the membrane drops across the length of this narrow access channel and renders the equilibrium dissociation constants of the transported ions at the binding sites voltage-dependent. Consequently, a change of electrical potential has a similar effect as a change of the ion concentration on the occupancy of the ion-binding sites (33). This, in turn, influences the conformational equilibrium, and in an electrophysiological approach a change of the ion concentration will result in a shift of the midpoint potential of the Q-V and ΔF-V relationship, respectively. There is, however, no obvious reason why the shift of V_0.5 would be detectable by fluorescence and not electrically.

In summary, these results show that by introducing the coexpression of the ENaC channel in combination with VCF measurements of the Na⁺, K⁺-ATPase, one can investigate partial reactions of the Na⁺, K⁺-ATPase pump cycle that have low electrogenicity, such as binding of Na⁺_i or K⁺_o, and thus are difficult to study by purely electrophysiological means. These results provide information on the effect of concentration changes of multiple ion pump ligands on the kinetics of the conformational dynamics of the ion pump. To date, our experiments have demonstrated that external Na⁺ and K⁺, as well as internal Na⁺, can be manipulated for VCF investigations of the Na⁺, K⁺-ATPase to investigate changes in the equilibria of the main conformational states as well as the kinetics of ion transport. Our current goal is to combine a ligand-gated ion channel, such as the nicotinic acetylcholine receptor, with the Na⁺, K⁺-ATPase to examine the mechanistic affects of varying K⁺_o and thus gain complete control of cation ligands for electrophysiological studies in intact cells.