Abstract
Coarse-grained elastic network models elucidate the fluctuation dynamics of proteins around their native conformations. Low-frequency collective motions derived by simplified normal mode analysis are usually involved in biological function, and these motions often possess noteworthy symmetries related to the overall shape of the molecule. Here, insights into these motions and their frequencies are sought by considering continuum models with appropriate symmetry and boundary conditions to approximately represent the true atomistic molecular structure. We solve the elastic wave equations analytically for the case of spherical symmetry, yielding a symmetry-based classification of molecular motions together with explicit predictions for their vibrational frequencies. We address the case of icosahedral symmetry as a perturbation to the spherical case. Applications to lumazine synthase, satellite tobacco mosaic virus, and brome mosaic virus show that the spherical elastic model efficiently provides insights on collective motions that are otherwise obtained by detailed elastic network models. A major utility of the continuum models is the possibility of estimating macroscopic material properties such as the Young's modulus or Poisson's ratio for different types of viruses.
Introduction
Recent years have seen growing numbers of studies that resort to normal mode analysis (NMA) as a simple, yet physically meaningful, way of studying the dynamics of proteins under equilibrium conditions (1). NMA has been a method used in computational biology for more than two decades (2–4). Although NMA is much more efficient than methods based on full atomic simulations, it becomes prohibitively expensive as the size of the biomolecular system increases because of the computational cost of energy minimization at the atomic scale, as well as the eigenvalue decomposition of increasingly large Hessian matrices.
Coarse-grained models have been developed to reduce the computational cost, while maintaining structural information. These include: the one-parameter Gaussian network model (5) and anisotropic network model (ANM) (6,7); the rotational translational block (8–10) or block NMA (11); and hierarchical ANM (12) and hierarchical clustering based on Markovian stochastics (13). Such reduced models proved useful for exploring the complex machinery of supramolecular systems such as the ribosomal complex (14,15), GroEL-GroES (16–18), virus capsids (19–21), or large structures determined by cryo-electron microscopy (22–25).
These studies suggest that molecular shape governs dynamics, especially the low frequency dynamics that are the dominant modes of functional reorganization (26). Indeed, one can gain insights into the collective motions relevant to biological function by examining the lowest frequency modes predicted by NMA conducted either at the atomic level, or by using low-resolution models (27–29). These low frequency modes often are highly symmetric (Fig. 1), and exhibit similarities between different biological molecules.
Figure 1.
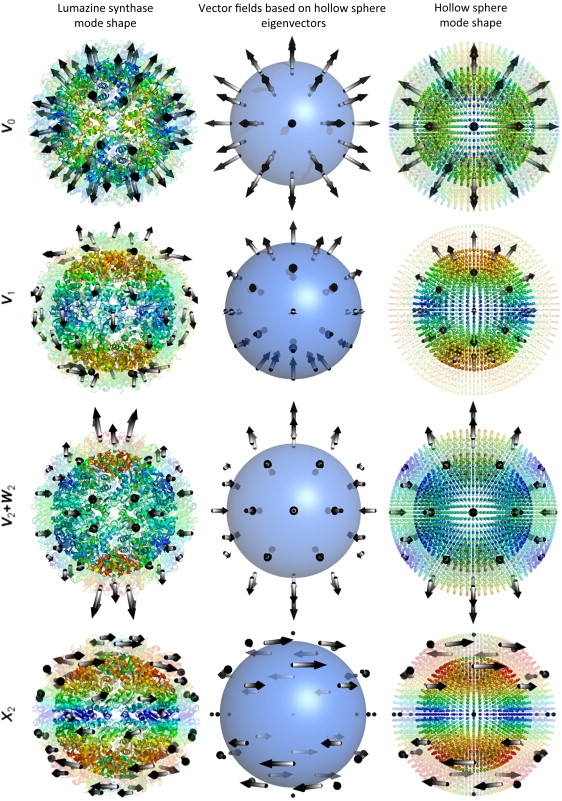
Correspondence between ANM modes and vector spherical harmonics illustrated for lumazine synthase. The diagrams on the left display the structure from PDB file 1NQW (31) color-coded according to the mobilities of residues predicted by the ANM, from blue (small) to red (large). The arrows indicate the directions of collective motions on or above the middle surface, halfway between the inner and outer radii. The interior portion (i.e., inside the middle surface) is shown as opaque, and the exterior portion as transparent. The middle and right columns display the equivalent vector fields and mode shapes generated by the ANM for a hollow sphere with comparable dimensions and packing density. The diagrams on the right column are also colored by the mobilities of the nodes. The labels on the left indicate the vector spherical harmonics corresponding to the displayed modes.
In this study, we explore the utility of carrying coarse-graining to its extreme by substituting continuum models for discretized ones. A major utility of adopting a continuum model is to be able to derive analytic solutions that can assist in assessing the basic aspects of complex processes. Here, a continuous mass density replaces the discrete masses, elastic moduli (Young's modulus and shear modulus) replace the springs linking the masses, and continuum elastic wave equations replace the usual Newton's equations of motion. Although the discrete Newton's equations yield a set of coupled ordinary differential equations that can be solved using matrix diagonalization, the continuum wave equation is a partial differential equation. Provided the material is spatially isotropic and homogeneous, and the boundary conditions not too complicated, the wave equation can be solved analytically.
We solve the continuum elastic wave equations for systems with spherical symmetry, exploiting the symmetry to express our solutions using the natural basis set provided by vector spherical harmonics. We compare the collective dynamics predicted for biomolecular systems using discretized models with the vibrational spectra of solid and hollow spheres (see, for example, Fig. 1). Specifically, the analytical solutions based on the continuum elastic wave equations are compared with those obtained with simple toy models based on the Mackay icosahedron (see Fig. SC1 in Supporting Material) (30) and with naturally occurring supramolecular assemblies: lumazine synthase (LS, Fig. 2) (31), an enzyme responsible for the synthesis of riboflavin (vitamin B2); satellite tobacco mosaic virus (STMV, Fig. 3 and Fig. SD1) (32), one of the smallest viruses known; and triangulation number T = 1 particle of brome mosaic virus (BMV, see Fig. SE1) (33), a virus that infects a type of grass known as Bromus.
Figure 2.
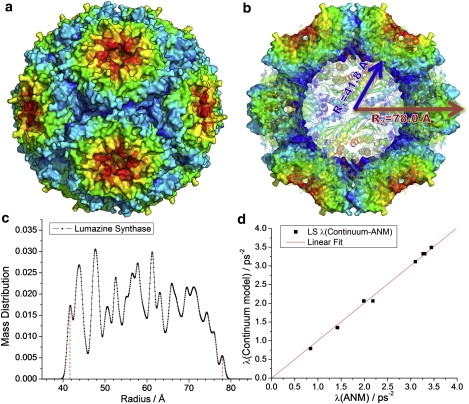
Results for LS. (a) Three-dimensional structure of LS (PDB file: 1NQW (31)), with the surface colored by geometric position to illustrate the icosahedral symmetry. (b) Cross-sectional view of the same structure. (c) Mass distribution as a function of radial position, used as basis for defining the inner and outer radii of the hollow sphere model used in continuum elasticity theory, and (d) comparison of the ANM eigenvalues with those found by the continuum elasticity theory for a hollow sphere with the same dimensions and packing density.
Figure 3.
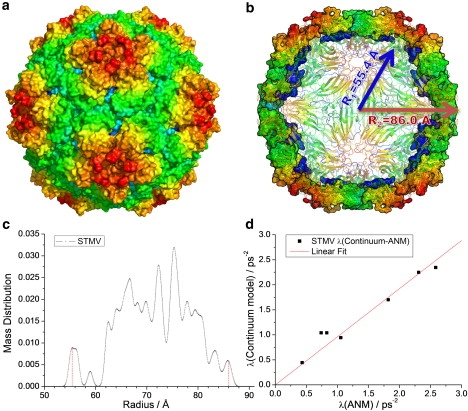
Results for STMV empty capsid. (a) Three-dimensional structure of STMV (PDB file: 1A34 (32), capsid only), with the surface colored by geometric position to illustrate the icosahedral symmetry. (b) Cross-sectional view of the same structure. (c) Mass distribution as a function of radial position, used as basis for defining the inner and outer radii of the hollow sphere model used in continuum elasticity theory, and (d) comparison of the ANM eigenvalues with those found by the continuum elasticity theory for a hollow sphere with the same dimensions and packing density.
The low-lying vibrational frequencies and their associated normal modes closely follow patterns predicted by spherical symmetry and can be reproduced using a small number of parameters defined by elastic theory. Deviations from these predictions can be interpreted as weak perturbations that lower the spherical symmetry to icosahedral symmetry, which is naturally selected by many biological molecules. Comparison of discretized models with continuum elastic theory predictions permit us to assess macroscopic mechanical properties of the examined biomolecular systems, such as their Young's moduli (normalized with respect to the ANM force constants) and Poisson's ratios.
Theory
Anisotropic network model
The basic approach in ANM is to determine the ensemble of normal modes of motion accessible to a given structure under equilibrium conditions, assuming that the close neighborhood of the energy minimum can be approximated by a harmonic potential. Conventional NMA requires energy minimization before eigenvalue decomposition of the 3N × 3N Hessian matrix representative of the second derivatives of the potential with respect to the components of all 3N generalized coordinates that define the structure. In ANM, the nodes of the elastic network are typically defined by the Cα atom coordinates, and the springs are representative of the interresidue interactions within a cutoff distance rc (6,7). The native structure deposited in the Protein Data Bank (PDB) is assumed to be the equilibrium state so that no further energy minimization is required.
In particular, the ijth super-element (3 × 3 matrix) of the Hessian takes the form
| (1) |
which directly follows from the adoption of a harmonic potential with uniform force constant γ,
| (2) |
Here Rij and are the respective instantaneous and equilibrium distances between nodes i and j. Γij is the ijth element of the Kirchhoff matrix Γ of interresidue contacts, set equal to 1 if is smaller than a cutoff distance rc, and zero otherwise (5,7). Xij, Yij, and Zij are the components of the distance vector . The diagonal elements of H are defined as the negative sum of all off-diagonal terms in a given row (or column; H is symmetrical).
The squared frequency and shape of each mode is given by the nonzero eigenvalue (λk) and corresponding eigenvector (v(k)), respectively, of H. We denote the nonzero eigenvalue of H as λk (1 ≤ k ≤ 3N – 6) in ascending order, and the corresponding eigenvector as , where is the three-dimensional displacement vector of residue i induced by mode k. We are interested here in the lowest frequency portion of the mode spectrum, which we obtain by Arnoldi iteration (34,35).
Continuum elastic theory
For an isotropic elastic medium, the equation of motion can be written as a wave equation (36)
| (3) |
where μ is the shear modulus, λ a Lamé coefficient, and ρ the density of the material, whereas u = u(r, t) represents the displacement from equilibrium and ∇ is the gradient operator with respect to the position vector r. Specifying the elastic constants λ and μ is equivalent to specifying the Young's modulus E and Poisson's ratio σ, in particular
| (4) |
The Poisson ratio is defined as the ratio of the strains along the transverse and axial directions in response to an axial stress. In the case of presently considered spherical models, these two respective directions are, for example, the tangential and radial directions.
In a normal mode, the entire medium oscillates at a single temporal frequency ω. The solution then separates into spatial and temporal parts, so that u can be written as
| (5) |
If u0 is divergenceless (i.e., ∇·u0 = 0), then substitution into the wave equation (Eq. 3) yields ∇2u0 + k2u0 = 0, where k = ω/ct is recognized as a transverse wavenumber, and the transverse sound speed is given by
| (6) |
If instead u0 is curl-free (i.e., ∇ × u0 = 0), then substitution yields ∇2u0 + q2u0 = 0, where q = ω/cl is recognized as a longitudinal wavenumber, and the longitudinal sound speed is given by
| (7) |
Notice that the longitudinal and transverse wavenumbers obey the relation
| (8) |
When analyzing problems with spherical symmetry it is advantageous to represent the displacement field u0 in a basis of spherical harmonics and spherical Bessel functions. Solutions to Eq. 3 take the generic form (37–40)
| (9) |
where L = r × ▿ is the angular momentum operator, and
| (10) |
Here Ylm(θ, ϕ) is a spherical harmonic, and jl is the spherical Bessel function of the first kind and is analytic at the spatial coordinate r = 0. Vector fields of these forms, known as vector spherical harmonics, are discussed in greater detail in Appendix SA in Supporting Material. If the sphere is hollow, so that our solution does not include the point r = 0, then we must add to u0 a function of the form
| (11) |
where
| (12) |
Here nl is the spherical Bessel function of the second kind, and is nonanalytic at the origin.
The three terms in Eq. 9 (and also in Eq. 11) have physical interpretations related to sound waves. The first term, as the gradient of a scalar function, is longitudinal in the sense that the direction of the vector u0 is parallel to the direction in which the amplitude varies. The second term is transverse, because it is perpendicular to the first. It is also perpendicular to the radial direction; that is, at every point r, it lies tangent to the sphere of radius r. The third term is also transverse, and is perpendicular to the first two terms.
Discrete allowed wavenumbers are determined by the boundary conditions. For free boundaries, the appropriate condition is vanishing normal component of the stress tensor τ. Elements of τ can be written in term of the elements of strain tensor, uik, which can be derived from the displacement vector, u0 (36), as
| (13) |
where ull is the trace of the strain tenor, and δik is the Kronecker delta. The normal component vanishes if , with the normal to the surface at the boundary. In spherical coordinates, i and k refer to the unit vectors , , or . The appropriate boundary condition for a sphere of radius R is thus (37)
| (14) |
Since i takes on three allowed values (, , and ), Eq. 14 constitutes a set of three linearly independent equations. Similarly, for a hollow sphere we obtain two sets of equations (38),
| (15) |
where R1 and R2 are the inner and outer radii, respectively, yielding a set of six linearly independent equations.
These boundary condition equations are solved using methods of linear algebra as discussed in Appendix SB. Solutions exist only for well-defined quantized values of the wavenumbers q and k, and therefore only for special vibrational frequencies ω = clq = ctk.
Each mode has a degeneracy arising from spherical symmetry. Specifically, the frequency depends on the total angular momentum index l but does not depend on the azimuthal angular momentum index m, which ranges from – l to + l by integers. Therefore, each allowed frequency has degeneracy
| (16) |
Spherical, icosahedral, and tetrahedral symmetry
The solutions to the equation of motion Eq. 3 are constrained by the requirements of spherical symmetry (41,42). Given a solution with a specific vibrational frequency (i.e., a normal mode), any spatial rotation generates a new solution of identical vibrational frequency. The set of all solutions of identical frequency form an invariant set known as an irreducible representation. A linearly independent subset forms a basis of the irreducible representation. The number of elements in the basis is known as the dimension of the irreducible representation, and corresponds to the degeneracy of the vibrational mode.
Spherical harmonics provide basis sets for irreducible representations of the spherical rotation symmetry group SO(3). For a given angular momentum l, the set {Ylm, m = – l, …, + l} constitutes a basis for an Ωl-dimensional irreducible representation. Consequently, any normal mode u0 can be expressed in terms of spherical harmonics multiplying a function of radius r, as in Eqs. 10 and 12, or equivalently using the vector spherical harmonics. Conversely, given a normal mode u0 obtained from the diagonalization of the Hessian matrix, we may identify its angular momentum content by projecting it onto vector spherical harmonics as shown in Appendix SA.
At the atomistic level, biological structures always break spherical symmetry, with icosahedral rotation symmetry being prevalent (43). Owing to the chirality of the protein subunits, we consider only pure rotations, without inversion or reflection (44–46). The symmetry-breaking may be confined to the internal structure, with the external boundaries remaining nearly spherical, as in the case of LS and STMV. In other cases, the external shape may strongly break the spherical symmetry, as in the case of the T = 1 particle of BMV (see Appendix SE). This distinction is illustrated by a toy model we introduce based on the Mackay icosahedron (30). The Mackay icosahedron consists of 20 independent grains of face-centered cubic crystal arranged with special orientations inside an icosahedron (see Fig. SC-1 a). By definition, it exhibits both internal and external icosahedral symmetry. We can utilize this structure to generate a spherical object where the nodes are icosahedrally arranged. To this aim, we project each node along the radial direction, so that they are located at the same radial distance, forming concentric shells (see Fig. SC-1 b). By varying the inner and outer radii, one can obtain corresponding solid or hollow spheres (see Fig. SC-1, c and d). For example, we create an analog of the structure of LS, by setting the inner and outer radii of the hollow sphere in a 2:1 ratio.
Because the symmetry group Y of the icosahedron comprises a finite subset of the full rotational symmetry group of a sphere, the icosahedral symmetry group has finitely many irreducible representations. As listed in Table 1, these are: the one-dimensional unit representation A; two three-dimensional representations F1 and F2; a four-dimensional representation G; and a five-dimensional representation H (42). Since the dimensionality of the irreducible representations determines the degeneracy of each normal mode, we see that the allowed degeneracies of vibrational frequency are 1 (nondegenerate), 3, 4, and 5. No other degeneracies may occur. This pattern of degeneracies differs from the spherical case as given in Eq. 16.
Table 1.
Icosahedral group character table showing angular momenta l and irreducible representations (“irreps”)
| l | irreps | 1C0 | 15C2 | 20C3 | 12C5 | 12C52 |
|---|---|---|---|---|---|---|
| 0 | A | 1 | 1 | 1 | 1 | 1 |
| 1 | F1 | 3 | −1 | 0 | τ | −τ−1 |
| 2 | H | 5 | 1 | −1 | 0 | 0 |
| 3 | F2 | 3 | −1 | 0 | −τ−1 | τ |
| 3 | G | 4 | 0 | 1 | −1 | −1 |
| 4 | G + H | 9 | 1 | 0 | −1 | −1 |
| 5 | F1 + F2 + H | 11 | −1 | −1 | 1 | 1 |
| 6 | A + F1 + G + H | 13 | 1 | 1 | τ | −τ−1 |
Here is the Golden Mean, and Cn indicates an axis of n-fold rotational symmetry.
The subgroup relationship between the icosahedral group and the full rotation group, Y ⊂ SO(3), allows us to relate irreducible representations of Y to the spherical harmonics Ylm. We identify l = 0 with A, l = 1 with F1, and l = 2 with H. For l = 3 and beyond, the spherical harmonics contain multiple irreducible representations of Y, as listed in Table 1. For instance, l = 3 contains both F2 and G. The l = 0 spherical harmonic, Y00, is the unit representation of the spherical symmetry group, whereas the unit representation A of the icosahedral group is contained in l = 0, 6, 10, 12, …. Notice this pattern reproduces the pattern of projections of icosahedrally symmetric structures discussed in Appendix SA.
We will occasionally need to consider a further reduction of symmetry, to that of a tetrahedron with symmetry group (41) T ⊂ Y. The tetrahedral group T has irreducible representations A (dimension 1), E (dimension 2), and F (dimension 3). The allowed degeneracies of vibrational frequencies are thus 1, 2, and 3. Irreducible representations of Y are sometimes reducible as representations of T. We can write A = A, F1 = F, F2 = F, G = A + F, and H = E + F, where the left-hand side of the equation corresponds to icosahedral representations and the right-hand side corresponds to tetrahedral representations.
For a given vibrational mode (i.e., eigenvector of the Hessian H), we can form arbitrary linear combinations of degenerate modes and the result is still a mode (eigenvector) of the same frequency. When considering modes of a given type of vector spherical harmonic, we take linear combinations to make them real rather than complex, and we group them further into combinations corresponding to irreducible representations of the icosahedral and tetrahedral symmetry groups.
Calculational procedures
In the following, we compare the eigenvalue spectra obtained from ANM with the predictions of continuum elastic theory. A priori, we do not know the elastic constants E and σ (or equivalently μ and λ, or sound speeds ct and cl), so we determine these by least-squares fitting to the eigenvalues obtained from ANM. Elastic constants E, λ, and μ have units of Pa (or N/m2), whereas the Poisson's ratio σ is dimensionless. The ANM force constant γ has units of N/m (note the conversion factor 1 N/m = 1.44 kcal/mol × Å2). Eigenvalues λ = ω2 will be quoted in units of (rad/ps)2. Fits of continuum elasticity to ANM eigenvalues yield the relative Young's modulus E/γ, which we quote in units of nm−1. The uncertainty in the relative Young's modulus is also estimated from the linear fit.
To construct the ANM, we take a cutoff distance of rc = 15 Å and we assign an average amino-acid mass of 108 Da to each node (in the case of STMV+RNA, the node mass is 120 Da). Hollow-sphere continuum models are defined in a consistent manner by using the first and last peaks in the mass distribution functions as the inner and outer radii R1 and R2, respectively (Figs. 2 and 3, and Fig. SD1 and Fig. SE1). For the hollow-sphere model representing the LS structure, we take R1 = 41.8 Å and R2 = 78.0 Å. The mass density is obtained from ρ = M/V, where M is the total mass and V the hollow-sphere volume.
Using the solvability conditions (Eq. SB4 and Eq. SB5 in the Appendix SB), we calculate the allowed wavenumbers k and q arising from boundary conditions for a given geometry (Eqs. 14 or 15). Notice that k and q depend on the Poisson's ratio σ but not the Young's modulus E or the density ρ. Then, from the sound speeds (Eqs. 6 and 7), we predict the resonant frequency ω = ctk = clq.
To fit the elastic constants we define a mean-squared difference (MSD) between the ANM and the continuum eigenvalues,
| (17) |
where the sum runs over each distinct eigenvalue λn whose eigenvector v(k) has angular momentum l ≤ 3. For a given σ, the optimal Young's modulus E can be determined analytically by minimizing the MSD (Eq. 17) using the relation
| (18) |
In this manner, we obtain the MSD for arbitrary σ, then select the optimal σ that minimizes the MSD.
Results
Overview
The results obtained for the four biological structures analyzed in this study—LS; STMV empty capsid; STMV containing its genetic material (RNA); and T = 1 particle of BMV—are presented in the respective Figs. 2 and 3, and Fig. SD1 and Fig. SE1. In each case, panel a displays the molecular system color-coded by the geometric position (see below), panel b a cross-sectional view, panel c the mass distribution as a function of radial position, and panel d the comparison of the dispersion of modes predicted by the ANM and the continuum model. A principal result from this study is the identification of the types of modes operating in each system, expressed in terms of their icosahedral and vector spherical representations, as summarized in Table SC1 and Table SC2 for toy models and in Tables 2 and 3 for biological systems (see also Fig. 1). Table 4 summarizes the results, i.e., the Poisson's ratios and effective Young's moduli corresponding to each system (columns 3 and 4), and the correlation between the two sets of data in terms of MSD (Eq. 17) and correlation coefficient (columns 5 and 6). More details for each examined system will be presented below.
Table 2.
ANM eigenvalues and mode types of lumazine synthase
| Mode # | Eigenvalue (ps−2) | Tetrahedral representations | Icosahedral representations | Vector spherical representations |
|---|---|---|---|---|
| 1–2 | 0.83817 | E | H | V2 + W2 |
| 3–5 | 0.84045 | F | ||
| 6–8 | 1.41542 | F | H | X2 |
| 9–10 | 1.42215 | E | ||
| 11–13 | 1.98688 | F | G | V3 + W3 |
| 14 | 1.99022 | A | ||
| 15–17 | 2.18280 | F | F2 | |
| 18 | 3.09788 | A | A | V0 |
| 19–21 | 3.26416 | F | F2 | X3 |
| 22–24 | 3.29502 | F | G | |
| 25 | 3.30125 | A | ||
| 26–28 | 3.44217 | F | F1 | V1 |
Icosahedral symmetry breaking ρ6/ρ0 = 0.0049 and tetrahedral symmetry breaking ρ4/ρ6 = 0.1148.
Table 3.
ANM eigenvalues and mode types of STMV (capsid only)
| Mode # | Eigenvalue (ps−2) | Icosahedral representations | Vector spherical representations |
|---|---|---|---|
| 1–5 | 0.43242 | H | V2 + W2 |
| 6–8 | 0.73901 | F2 | V3 + W3 |
| 9–12 | 0.82876 | G | |
| 13–17 | 1.05426 | H | X2 |
| 18–21 | 1.22444 | G | V4 + W4 |
| 22–26 | 1.46058 | H | |
| 27 | 1.81925 | A | V0 |
| 28–32 | 2.13790 | H | V5 + W5 |
| 33–35 | 2.28670 | F2 | |
| 36–38 | 2.30968 | F1 | V1 |
Icosahedral symmetry breaking ρ6/ρ0 = 0.0066.
Table 4.
The results of fitting the eigenvalues
| Density ρ (kg/m3) | Poisson's ratio σ | Relative Young's modulus E/γ (nm−1) | Mean-squared difference (ps−4) | Fitting correlation | |
|---|---|---|---|---|---|
| Solid sphere | 905.99 | 0.26 | 31.2 ± 0.4 | 0.0136 | 0.9984 |
| Hollow sphere | 941.53 | 0.27 | 32.8 ± 0.7 | 0.0192 | 0.9966 |
| Lumazine synthase | 987.60 | 0.30 | 36.2 ± 0.3 | 0.0040 | 0.9993 |
| STMV | 823.82 | 0.24 | 26.0 ± 1.1 | 0.0317 | 0.9863 |
| STMV+RNA | 981.79 | 0.20 | 28.5 ± 1.7 | 0.0980 | 0.9674 |
| BMV | 561.39 | 0.30 | 6.58 ± 0.2 | 0.0016 | 0.9932 |
Results for toy models
Before we proceed to the results for the four biomolecular systems, we first note that the results for the filled and hollow spheres constructed from the Mackay icosahedron confirm that the mode spectra from ANM and continuum elastic model yield a remarkably high correlation (respective MSD values of 0.0136 ps−4 and 0.0192 ps−4, and correlation coefficients above 0.99; see Fig. SC1 and Table 4) in so far as the distribution of eigenvalues is concerned. The comparison yields Poisson's ratios of σ = 0.26 and 0.27, and relative Young's modulus E/γ = 31.2 ± 0.4 nm−1 and 32.8 ± 0.7 nm−1. As discussed in Spherical, icosahedral, and tetrahedral symmetry, spherical symmetry modes of high angular momentum (e.g., l = 3) split into multiple icosahedral symmetry modes (e.g., F2 and G) with different eigenvalues. For our toy models, the reduction of spherical to icosahedral symmetry is weak, so the eigenvalue splitting is small, as is evident in Table SC1 and Table SC2 (e.g., compare eigenvalues of F2 and G).
Lumazine synthase
LS is a hollow, nearly spherical molecule consisting of 60 identical subunits arranged with icosahedral symmetry. ANM calculations were based on the crystallographic structure resolved in a body-centered cubic lattice with space group I23, deposited in the PDB (47) (ID:1NQW (31)). As a result, the structure exhibits tetrahedral symmetry, which may be viewed as a reduced form of icosahedral symmetry. Accordingly, the degeneracies of the accessible vibrational modes are 1, 2, and 3 (see Table 2). For example, the fivefold degenerate (lowest frequency) mode observed in the case of the solid and hollow spheres is now split into two sets of modes, with degeneracies 2 and 3. Note that the distinction between the frequencies of these two sets of modes appears only at the third significant digits of the corresponding eigenvalues.
The continuum elastic model adopted for LS requires the use of inner and outer radii, which were deduced from the mass distribution calculated as a function of radial distance (Fig. 2 c). The red dotted bars delimit therein the inner and outer radii as R1 = 41.8 Å and R2 = 78.0 Å, respectively. Table 2 lists the representations of the ANM modes in the icosahedral and spherical symmetry groups. For example, the lowest frequency (doubly degenerate) mode (modes 1 and 2) corresponds to the vector spherical harmonics V2 and W2 (see Appendix A), whereas the nondegenerate mode 18 corresponds to V0, as illustrated in Fig. 1. Comparison of the outputs from both methods permit us to evaluate the two macroscopic quantities E/γ = 36.2 ± 0.3 nm−1 and σ = 0.30 (with MSD of 0.0040 ps−4) for the respective relative Young's modulus and Poisson's ratio that best represent the global relaxational behavior of LS.
Virus capsids STMV and BMV
The ANM calculations for STMV were performed using the PDB structure (ID:1A34 (32)). Note that STMV has T = 1, i.e., it is composed of 60 icosahedrally arranged identical subunits. In this case, the reduction of spherical symmetry to icosahedral is slightly stronger (Fig. 3); however, no breaking of icosahedral symmetry due to crystallographic lattice type is evident. The eigenvalues calculated with ANM are listed in Table 3 for the empty capsid and in Table SD1 for the capsid with RNA (see Appendix SD). Taking R1 = 55.4 Å for the empty capsid and R2 = 86.0 Å, we find the eigenvalues match continuum elastic theory with E/γ = 26.0 ± 1.1 nm−1 and Poisson's ratio σ = 0.24 with MSD of 0.0317 ps−4.
Results for the RNA-containing STMV capsid are discussed in Appendix SD, and our study of BMV is presented in Appendix SE.
Discussion
Having compared vibrational modes and eigenvalue spectra from simplified toy models and three different protein assemblies (LS, STMV, and BMV), we note that the global modes in all cases may be expressed as combinations of vector spherical harmonics. These modes, which are likely to be biologically relevant, can be predicted and classified purely on the basis of molecular symmetry, which explains their distinctive shapes, and the strong resemblance between modes of different structures. Given the values of two elastic moduli, we can predict the vibrational frequencies of many low-lying modes. For spherical symmetry, these predictions are highly accurate, and the accuracy remains high even for biological assemblies with icosahedral symmetry.
For example, the lowest frequency mode for all hollow structures turns out to be fivefold degenerate, with vector spherical harmonic type V2 + W2 (icosahedral type H). This mode can be visualized physically as the result of squeezing a sphere radially inwards at the poles, allowing it to bulge outwards at the equator. Such a deformation occurs when a molecule is probed with an atomic-force microscope, and the hollow spheres are quite soft in response to this force (49,50). The applied uniaxial strain of the AFM tip couples to the mode of type H just discussed (superconductivity in the Fullerenes is also related to this mode (51,52)).
To estimate the effective spring constant of this global deformation, we may express the energy as
| (19) |
where M represents the mass of the capsid, aH is the amplitude of deformation in mode H, and PHF is the projection of the applied force F onto the deformation v(H). That is, , where Fi is the force acting on the ith node and v(H) is assumed normalized to 1. The first term in Eq. 19 represents deformation energy, whereas the second represents the work done by the applied force. Minimizing the energy yields the displacement in the direction of the applied force as h = PHaH = F/MλH and an effective spring constant
| (20) |
This estimate is actually an upper bound on keff because other modes can share in the deformation energy if the applied force projects onto them also. The more general result is (42)
| (21) |
where Pk represents the projection onto the eigenvector v(k). Recently, Eyal and Bahar explored the single molecular response of external forces with elastic network models (53).
Next lowest in frequency (for our hollow sphere, LS and BMV) is the fivefold degenerate mode of vector spherical harmonic type X2 and icosahedral type H. This mode can be visualized as the result of twisting the upper and lower hemispheres in opposite directions.
For empty and filled STMV, modes of vector spherical harmonic type V3 + W3 (icosahedral types F2 and G) appear at frequency below X2. These modes are poorly fit by the continuum elastic theory and involve disordered protein chains (and nucleic acids) in the interior of the sphere.
Deformations of vector spherical harmonic type V0 (icosahedral type A) are nondegenerate because they preserve icosahedral symmetry. They correspond to radially directed displacements of angle-independent magnitude—a shrinking or swelling (breathing) of the entire structure. This type of deformation occurs in response to strong internal pressure (such as genome packaging in a bacteriophage) or external pressure (such as osmotic pressure). Such icosahedrally symmetric modes have been chosen to strongly correlate with the structural changes occurring during capsid maturation (21). It is notable that the eigenvalue of this mode is substantially higher than the low frequency modes just discussed, implying relative resistance against these naturally occurring forces. Because of the high symmetry, it is easy to calculate the response of the shell to pressure differentials. For example, the increase in outer radius of a spherical shell, subject to internal pressure p, is (36)
| (22) |
Experimental observation of capsid dimensions in the presence of strong pressure differentials can thus yield information about elastic constants.
For a solid sphere, the relative frequencies of the lowest two mode types are interchanged relative to their order in the hollow sphere. As shown in Table SC1 for the solid sphere, the eigenvalue of the spheroidal squeezing modes V2 + W2 (modes 6–10) become higher than the torsional twisting modes X2 (modes 1–5), reflecting the increased resistance to compression of the material near the center of the sphere. Similarly, in the solid sphere, the spheroidal l = 1 modes (Table SC1, modes 11–13) appear at lower frequency than the l = 3 modes, whereas in the hollow sphere the l = 1 modes (Table SC2, modes 18–20) appear above the frequency of the l = 3 modes. In the solid sphere, these l = 1 modes correspond to an optical phonon in which the heavy interior of the sphere displaces in the opposite direction from the surface. In the hollow sphere (Fig. 1), these modes involve oppositely directed displacements of the poles and equator.
Although neither our ANM method, nor continuum elasticity, can predict either the value of the ANM force constant γ, or the continuum Young's modulus E, our fitting method yields ratios E/γ so that knowledge of one allows prediction of the other. For example, a γ = 0.1 N/m implies a Young's modulus of E = 3.28 GPa for the hollow sphere.
In the absence of experimental knowledge of elastic constants (or, equivalently, sound speeds), we could obtain the elastic constants by fitting to vibrational frequencies calculated on the basis of an intermolecular force field (54). In this case, the continuum theory is no longer needed to predict vibrational frequencies; however, it is still useful for the purpose of classifying the calculated normal modes. Additionally, the elastic constants obtained are needed for other applications of the continuum elastic theory, such as finite element analysis of deformation.
Recently Young's moduli have been obtained from nanoindentation experiments. Bacteriophage ϕ29 has a value of E = 1.8 ± 0.2 GPa (55), which is close to hard plastics and other proteins such as actin, tubulin (56), and lysozyme crystals (57,58). The cowpea chlorotic mottle virus is soft in comparison, with Young's moduli of 140 MPa and 190 MPa for the wild-type and mutants, respectively (49), which are similar in magnitude to soft plastics and Teflon (56). For murine leukemia virus particles, the Young's moduli of immature and mature capsids are 0.23 GPa and 1.03 GPa (50), which are comparable to bacteriophage ϕ29 and microtubules (∼0.8 GPa) (59).
A longitudinal sound speed cl = 1817 m/s was measured by ultrasound in lysozyme single crystals (57). Assuming Poisson's ratio σ = 1/3 yields a predicted transverse sound speed of ct = 915 m/s. Brillouin scattering measurements (60) yielded sound velocities of STMV capsids ranging from cl = 1920 m/s (fully hydrated) to cl = 3350 m/s (fully dehydrated). Assuming σ = 1/3, these sound speeds for STMV imply Young's moduli of 3.7 and 11.2 GPa, respectively.
We note that a generic value for the Gaussian network model force-constant has been deduced by Kundu et al. (61), based on the comparison of predicted residue fluctuations with experimental B-factors. Accordingly, the force constant is given by kBT/γ = 0.87 ± 0.46 Å2, or γ = 0.48 ± 0.35 N/m. Using this value together with the ratio E/γ = 26 nm−1 obtained here for STMV (Table 4), the Young's modulus becomes E = 12 ± 9 GPa, which is comparable to that inferred from Brillouin scattering data.
Note that the Poisson's ratio is unaffected by a scaling of γ, hence our fitting serves as a prediction of the value of σ. Experimentally σ has been hard to obtain for biological molecules, and values around 0.3 have been assumed (55) based on analogy with similar materials. Inspecting Table 4, we see predicted values in the range of 0.2–0.3.
Simple scaling laws follow from the continuum theory. For example, for a set of biomolecular assemblies sharing a common shape and elastic constants but differing in size, our theory predicts the allowed wavenumbers q and k vary as the inverse of the linear dimension. Consequently, the lowest vibrational frequency also varies as the inverse of the linear dimension.
Our analysis so far deals with spherical and icosahedral structures. Similar ideas can be applied to other symmetries. For example, modes in cylindrical molecules should be described as plane waves along the axis of the cylinders, sinusoidal oscillations around the circumference, and cylindrical Bessel functions in the radial direction. Such an analysis has been carried out for cylindrical viruses (62) allowing predictions of Raman vibrational frequencies.
In summary, our method provide a means of identifying and classifying the types of normal modes that arise from the structural symmetry, by expressing them in terms of icosahedral and vector spherical representations. The fitting procedure yields a relationship between the Young's modulus (E), which is a macroscopic elastic constant, and the microscopic force constant (γ) representative of residue-residue interactions. In addition, it yields the optimal Poisson's ratio (σ), which depends only on topological properties of the elastic network.
Our continuum model is restricted to the study of symmetric movements undergone by isotropic materials. Recent molecular simulations of STMV and BMV (63,64) and nanoindentation experiments with viral capsids (65–67) revealed asymmetric fluctuations and inhomogeneities in mechanical properties (68), which are beyond the scope of our theory.
Acknowledgments
We thank S. B. Larson and P. Freddolino for discussions on the genome structure with the STMV capsid.
This research was supported in part by National Science Foundation grant No. DMR-0111198 (to M.W.) and National Institutes of Health grant No. 1 R01 LM007994-06 and 5R01GM086238-02 (to I.B.).
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Supporting Material
References
- 1.Cui Q., Bahar I. Mathematical and Computational Biology Series. Chapman Hall/CRC; Boca Raton, FL: 2006. Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems. [Google Scholar]
- 2.Brooks B., Karplus M. Normal modes for specific motions of macromolecules: application to the hinge-bending mode of lysozyme. Proc. Natl. Acad. Sci. USA. 1985;82:4995–4999. doi: 10.1073/pnas.82.15.4995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Levitt M., Sander C., Stern P.S. Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 1985;181:423–447. doi: 10.1016/0022-2836(85)90230-x. [DOI] [PubMed] [Google Scholar]
- 4.Go N., Noguti T., Nishikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 1983;80:3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bahar I., Atilgan A.R., Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- 6.Doruker P., Atilgan A.R., Bahar I. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to A-amylase inhibitor. Proteins. 2000;40:512–524. [PubMed] [Google Scholar]
- 7.Atilgan A.R., Durell S.R., Jernigan R.L., Demirel M.C., Keskin O. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Durand P., Trinquier G., Sanejouand Y.-H. A new approach for determining low-frequency normal modes in macromolecules. Biopolymers. 1994;34:759–771. [Google Scholar]
- 9.Tama F., Gadea F.X., Marques O., Sanejouand Y.H. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 2000;41:1–7. doi: 10.1002/1097-0134(20001001)41:1<1::aid-prot10>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 10.Li G., Cui Q. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca2+-ATPase. Biophys. J. 2002;83:2457–2474. doi: 10.1016/S0006-3495(02)75257-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li G., Cui Q. Analysis of functional motions in Brownian molecular machines with an efficient block normal mode approach: myosin-II and Ca2+-ATPase. Biophys. J. 2004;86:743–763. doi: 10.1016/S0006-3495(04)74152-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Doruker P., Jernigan R.L., Bahar I. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 2002;23:119–127. doi: 10.1002/jcc.1160. [DOI] [PubMed] [Google Scholar]
- 13.Chennubhotla C., Bahar I. Markov propagation of allosteric effects in biomolecular systems: application to GroEL-GroES. Mol. Syst. Biol. 2006;2:1–13. doi: 10.1038/msb4100075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tama F., Valle M., Frank J., Brooks C.L. Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc. Natl. Acad. Sci. USA. 2003;100:9319–9323. doi: 10.1073/pnas.1632476100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang Y., Rader A.J., Bahar I., Jernigan R.L. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 2004;147:302–314. doi: 10.1016/j.jsb.2004.01.005. [DOI] [PubMed] [Google Scholar]
- 16.Keskin O., Bahar I., Flatow D., Covell D., Jernigan R. Molecular mechanisms of chaperonin GroEL-GroES function. Biochemistry. 2002;41:491–501. doi: 10.1021/bi011393x. [DOI] [PubMed] [Google Scholar]
- 17.Ma J., Sigler P.B., Xu Z., Karplus M. A dynamic model for the allosteric mechanism of GroEL. J. Mol. Biol. 2000;302:303–313. doi: 10.1006/jmbi.2000.4014. [DOI] [PubMed] [Google Scholar]
- 18.Chennubhotla C., Yang Z., Bahar I. Coupling between global dynamics and signal transduction pathways: a mechanism of allostery for chaperonin GroEL. Mol. Biosyst. 2008;4:287–292. doi: 10.1039/b717819k. [DOI] [PubMed] [Google Scholar]
- 19.Rader A.J., Vlad D.H., Bahar I. Maturation dynamics of bacteriophage HK97 capsid. Structure. 2005;13:413–421. doi: 10.1016/j.str.2004.12.015. [DOI] [PubMed] [Google Scholar]
- 20.van Vlijmen H.W., Karplus M. Normal mode calculations of icosahedral viruses with full dihedral flexibility by use of molecular symmetry. J. Mol. Biol. 2005;350:528–542. doi: 10.1016/j.jmb.2005.03.028. [DOI] [PubMed] [Google Scholar]
- 21.Tama F., Brooks C.L. Diversity and identity of mechanical properties of icosahedral viral capsids studied with elastic network normal mode analysis. J. Mol. Biol. 2005;345:299–314. doi: 10.1016/j.jmb.2004.10.054. [DOI] [PubMed] [Google Scholar]
- 22.Ming D., Kong Y., Wakil S.J., Brink J., Ma J. Domain movements in human fatty acid synthase by quantized elastic deformational model. Proc. Natl. Acad. Sci. USA. 2002;99:7895–7899. doi: 10.1073/pnas.112222299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ming D., Kong Y., Lambert M.A., Huang Z., Ma J. How to describe protein motion without amino acid sequence and atomic coordinates. Proc. Natl. Acad. Sci. USA. 2002;99:8620–8625. doi: 10.1073/pnas.082148899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Delarue M., Dumas P. On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proc. Natl. Acad. Sci. USA. 2004;101:6957–6962. doi: 10.1073/pnas.0400301101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hinsen K., Reuter N., Navaza J., Stokes D.L., Lacapère J.-J. Normal mode-based fitting of atomic structure into electron density maps: application to sarcoplasmic reticulum Ca-ATPase. Biophys. J. 2005;88:818–827. doi: 10.1529/biophysj.104.050716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tama F., Brooks C.L. Symmetry, form, and shape: guiding principles for robustness in macromolecular machines. Annu. Rev. Biophys. Biomol. Struct. 2006;35:115–133. doi: 10.1146/annurev.biophys.35.040405.102010. [DOI] [PubMed] [Google Scholar]
- 27.Bahar I., Rader A.J. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 2005;15:586–592. doi: 10.1016/j.sbi.2005.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ma J. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 2005;13:373–380. doi: 10.1016/j.str.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 29.Nicolay S., Sanejouand Y.-H. Functional modes of proteins are among the most robust. Phys. Rev. Lett. 2006;96:078104. doi: 10.1103/PhysRevLett.96.078104. [DOI] [PubMed] [Google Scholar]
- 30.Mackay A.L. A dense non-crystallographic packing of equal spheres. Acta. Crystal. 1962;15:916–918. [Google Scholar]
- 31.Zhang X., Meining W., Cushman M., Haase I., Fischer M. A structure-based model of the reaction catalyzed by lumazine synthase from Aquifex aeolicus. J. Struct. Biol. 2003;328:167–182. doi: 10.1016/s0022-2836(03)00186-4. [DOI] [PubMed] [Google Scholar]
- 32.Larson S.B., Day J., Greenwood A., McPherson A. Refined structure of satellite tobacco mosaic virus at 1.8 Å resolution. J. Mol. Biol. 1998;277:37–59. doi: 10.1006/jmbi.1997.1570. [DOI] [PubMed] [Google Scholar]
- 33.Larson S.B., Lucas R.W., McPherson A. Crystallographic structure of the T=1 particle of brome mosaic virus. J. Mol. Biol. 2005;346:815–831. doi: 10.1016/j.jmb.2004.12.015. [DOI] [PubMed] [Google Scholar]
- 34.Arnoldi W.E. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Math. 1951;9:17–29. [Google Scholar]
- 35.Lehoucq R.B., Sorensen D.C., Yang C. SIAM Publications; Philadelphia, PA: 1998. ARPACK Users' Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. [Google Scholar]
- 36.Landau L.D., Lifshitz E.M. Course of Theoretical Physics, Vol. 7. 3rd Ed. Butterworth-Heinemann; Oxford, UK: 1986. Theory of elasticity. [Google Scholar]
- 37.Lobo J.A. What can we learn about gravitational wave physics with an elastic spherical antenna? Phys. Rev. D. 1995;52:591–604. doi: 10.1103/physrevd.52.591. [DOI] [PubMed] [Google Scholar]
- 38.Coccia E., Fafone V., Frossati G., Lobo J.A., Ortega J.A. Hollow sphere as a detector of gravitational radiation. Phys. Rev. D. 1998;57:2051–2060. [Google Scholar]
- 39.Lamb H. On the vibrations of an elastic sphere. Proc. Lond. Math. Soc. 1981;13:189–212. [Google Scholar]
- 40.Lamb H. On the vibrations of a spherical shell. Proc. Lond. Math. Soc. 1882;14:50–56. [Google Scholar]
- 41.Tinkham M. McGraw Hill; Englewood Cliffs, NJ: 1964. Group Theory and Quantum Mechanics. [Google Scholar]
- 42.Widom M., Lidmar J., Nelson D.R. Soft modes near the buckling transition of icosahedral shells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:031911. doi: 10.1103/PhysRevE.76.031911. [DOI] [PubMed] [Google Scholar]
- 43.Caspar D.L., Klug A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
- 44.Zandi R., Reguera D., Bruinsma R.F., Gelbart W.M., Rudnick J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA. 2004;101:15556–15560. doi: 10.1073/pnas.0405844101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lorman V.L., Rochal S.B. Density-wave theory of the capsid structure of small icosahedral viruses. Phys. Rev. Lett. 2007;98:185502. doi: 10.1103/PhysRevLett.98.185502. [DOI] [PubMed] [Google Scholar]
- 46.Lorman V.L., Rochal S.B. Landau theory of crystallization and the capsid structures of small icosahedral viruses. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;77:224109. [Google Scholar]
- 47.Berman H.M., Westbrook J., Feng Z., Gilliland G., Bhat T.N. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Reference deleted in proof.
- 49.Michel J.P., Ivanovska I.L., Gibbons M.M., Klug W.S., Knobler C.M. Nanoindentation studies of full and empty viral capsids and the effects of capsid protein mutations on elasticity and strength. Proc. Natl. Acad. Sci. USA. 2006;103:6184–6189. doi: 10.1073/pnas.0601744103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kol N., Gladnikoff M., Barlam D., Shneck R.Z., Rein A. Mechanical properties of Murine Leukemia virus particles: effect of maturation. Biophys. J. 2006;91:767–774. doi: 10.1529/biophysj.105.079657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Varma C.M., Zaanen J., Raghavachari K. Superconductivity in the fullerenes. Science. 1991;254:989–992. doi: 10.1126/science.254.5034.989. [DOI] [PubMed] [Google Scholar]
- 52.Jishi R.A., Dresselhaus M.J. Electron-phonon coupling strength and implications for superconductivity in alkali-metal-doped fullerenes. Phys. Rev. B. 1992;45:2597–2600. doi: 10.1103/physrevb.45.2597. [DOI] [PubMed] [Google Scholar]
- 53.Eyal E., Bahar I. Toward a molecular understanding of the anisotropic response of proteins to external forces: insights from elastic network models. Biophys. J. 2008;94:3424–3435. doi: 10.1529/biophysj.107.120733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Dykeman E.C., Sankey O.F. Low frequency mechanical modes of viral capsids: an atomistic approach. Phys. Rev. Lett. 2008;100:028101. doi: 10.1103/PhysRevLett.100.028101. [DOI] [PubMed] [Google Scholar]
- 55.Ivanovska I.L., de Pablo P.J., Ibarra B., Sgalari G., MacKintosh F.C. Bacteriophage capsids: tough nanoshells with complex elastic properties. Proc. Natl. Acad. Sci. USA. 2004;101:7600–7605. doi: 10.1073/pnas.0308198101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Howard J. Sinauer Associates; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 57.Tachibana M., Kojima K., Ikuyama R., Kobayashi Y., Ataka M. Sound velocity and dynamic elastic constants of lysozyme single crystals. Chem. Phys. Lett. 2000;332:259–264. [Google Scholar]
- 58.Koizumi H., Tachibana M., Kojima K. Observation of all the components of elastic constants using tetragonal hen egg-white lysozyme crystals dehydrated at 42 humidity. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:041910. doi: 10.1103/PhysRevE.73.041910. [DOI] [PubMed] [Google Scholar]
- 59.de Pablo P.J., Schaap I.A.T., MacKintosh F.C., Schmidt C.F. Deformation and collapse of microtubules on the nanometer scale. Phys. Rev. Lett. 2003;91:098101. doi: 10.1103/PhysRevLett.91.098101. [DOI] [PubMed] [Google Scholar]
- 60.Stephanidis B., Adichtchev S., Gouet P., McPherson A., Mermet A. Elastic properties of viruses. Biophys. J. 2007;93:1354–1359. doi: 10.1529/biophysj.107.109033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kundu S., Melton J.S., Sorensen D.C., Phillips J., George N. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys. J. 2002;83:723–732. doi: 10.1016/S0006-3495(02)75203-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dykeman E.C., Sankey O.F., Tsen K.T. Raman intensity and spectra predictions for cylindrical viruses. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:011906. doi: 10.1103/PhysRevE.76.011906. [DOI] [PubMed] [Google Scholar]
- 63.Arkhipov A., Freddolino P.L., Schulten K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure. 2006;14:1767–1777. doi: 10.1016/j.str.2006.10.003. [DOI] [PubMed] [Google Scholar]
- 64.Freddolino P.L., Arkhipov A.S., Larson S.B., McPherson A., Schulten K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure. 2006;14:437–449. doi: 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
- 65.Gibbons M.M., Klug W.S. Influence of nonuniform geometry on nanoindentation of viral capsids. Biophys. J. 2008;95:3640–3649. doi: 10.1529/biophysj.108.136176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gibbons M.M., Klug W.S. Nonlinear finite-element analysis of nanoindentation of viral capsids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:031901. doi: 10.1103/PhysRevE.75.031901. [DOI] [PubMed] [Google Scholar]
- 67.Gurin T., Bruinsma R. Theory of conformational transitions of viral shells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:061911. doi: 10.1103/PhysRevE.76.061911. [DOI] [PubMed] [Google Scholar]
- 68.Zandi R., Reguera D. Mechanical properties of viral capsids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:021917. doi: 10.1103/PhysRevE.72.021917. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


