Diffusion and Partitioning of Fluorescent Lipid Probes in Phospholipid Monolayers

Abstract

The pressure-dependent diffusion and partitioning of single lipid fluorophores in DMPC and DPPC monolayers were investigated with the use of a custom-made monolayer trough mounted on a combined fluorescence correlation spectroscopy (FCS) and wide-field microscopy setup. It is shown that lipid diffusion, which is essential for the function of biological membranes, is heavily influenced by the lateral pressure and phase of the lipid structure. Both of these may change dynamically during, e.g., protein adsorption and desorption processes. Using FCS, we measured lipid diffusion coefficients over a wide range of lateral pressures in DMPC monolayers and fitted them to a free-area model as well as the direct experimental observable mean molecular area. FCS measurements on DPPC monolayers were also performed below the onset of the phase transition (Π < 5 mN/m). At higher pressures, FCS was not applicable for measuring diffusion coefficients in DPPC monolayers. Single-molecule fluorescence microscopy and differential scanning calorimetry clearly showed that this was due to heterogeneous partitioning of the lipid fluorophores in condensed phases. The results were compared with dye partitioning in giant lipid vesicles. These findings are significant in relation to the application of lipid fluorophores to study diffusion in both model systems and biological systems.

Introduction

In recent years there has been increasing interest in the role of structural heterogeneities such as lipid rafts, lipid domains, and protein clusters in biological membranes. This has led to a renaissance in investigations of the physical factors that control the organization and dynamics of aggregated lipid structures. One of the essential dynamic processes in biomembranes is lateral diffusion, which is central for bimolecular reactions between different membrane species. The rate of lateral diffusion within the membrane is expected to be highly dependent on the lipid density and the potential of the lipid structure to phase-separate. These properties depend strongly on the thermodynamic variables of the system, such as local concentrations, pH, ionic strength, and lateral pressure. This means that changes in the thermodynamical variables that control the lateral organization of the lipid structure have the potential to control the rate of chemical reactions in the membrane. Changes in lateral organization can even prevent a reaction by causing the reactants to partition in separate lipid domain structures.

In pioneering studies conducted over 30 years ago (1–4), investigators began to study lipid diffusion in biological and model membranes using fluorescence techniques. The experimental data for lipid diffusion in a lipid matrix have generally been shown to fit the free-area model (5–10) quite well. The free-area model is theoretically simple and qualitatively intuitive, but quantitatively it is often criticized for the number of fitting parameters required, which at present seem to vary with the different methods used and systems investigated (11). A further source of confusion in the literature is that experimental data from different studies using FRAP and SPT have produced different numbers for the diffusion coefficient of a lipid probe in a lipid monolayer (6–10). These inconsistencies highlight the necessity of evaluating different model systems to 1), measure the absolute value of diffusion coefficients at different MMAs; and 2), evaluate the obtained data with respect to the free-area model to test whether it has predictive power (11,12). An ideal experimental platform for this purpose is the Langmuir technique (13), in which individual thermodynamic parameters (e.g., composition, pH, salt concentration, temperature, and lateral pressure) can easily be varied over a broad range.

Lipid diffusion has been measured by a variety of fluorescence techniques on different length- and timescales. Since its invention in the mid-1970s, FRAP (14) has been by far the most frequently applied technique (for a recent review, see Sprague and McNally (15)). In FRAP, fluorophores within an area of typically a few micrometers are bleached, and the time until the area is replenished via diffusion of nonbleached fluorophores is measured. Typical recovery times are on the order of seconds. Another fluorescence technique that is becoming increasingly popular is SPT with WFM. SPT is a powerful technique with the potential to reveal a wealth of information. It has been argued that the strong point of SPT is its ability to disclose distributions rather than ensemble properties (16,17). The length scale of SPT is from tens of nanometers to a hundred micrometers, and timescales range from milliseconds to seconds. In practice, however, this range is limited by bleaching effects when small organic fluorophores are used as probes. The drawback of SPT is that it requires extensive data analysis of many individual tracks to obtain reliable statistics (18). FCS offers a compromise between FRAP and SPT. FCS has single-molecule sensitivity, the highest temporal resolution of the three methods, and can readily measure thousands of diffusion events in a matter of seconds, providing reliable diffusion coefficients in short acquisition times (19–23).

As mentioned above, at present the absolute diffusion coefficients of lipid fluorophores in an LE monolayer can not be convincingly determined. For instance, diffusion coefficients measured by SPT (8) are one order of magnitude lower than diffusion coefficients measured by FRAP (6,9,10). For DLPC monolayers at surface pressures of 30 mN/m, they are reported to be 1.5 μm²/s and ∼30 μm²/s, respectively. This indicates that either the diffusion coefficient depends on the length- and timescales of the measurement, which is not expected in a homogeneous lipid environment, or that FRAP measurements tend to overestimate the diffusion coefficients due to surface flow. This can be a serious problem in monolayer studies, especially when the measuring times and length scales are large, as in FRAP. In this regard, FCS has an inherent advantage in that potential surface flow is directly manifested in the correlation profile (24,25). Additionally, since both the length- and timescales of FCS are relatively short compared to SPT and FRAP, the influence of surface flow will be small. FCS is therefore an ideal method for evaluating the diffusion coefficients in expanded lipid films, which can be subject to potentially interfering surface flow. When it comes to reported diffusion coefficients for condensed lipid phases (e.g., LC, gel) the variation is even larger than for expanded phases (e.g., LE, fluid). In condensed phases, reported diffusion coefficients vary by seven orders of magnitude, from 10⁻⁸ to 10⁻¹ μm²/s (26,27). This has been speculated to be due to diffusion confined in “oily streaks” or along line defects in the structure (27).

The goal of this study was to investigate the effect of lateral pressure on the diffusion and partitioning behavior of lipid fluorophores in DMPC and DPPC monolayers at the air-water interface (“Langmuir films”). This was done with the use of an in-house-built fluorescence setup equipped with a monolayer trough custom designed for single-molecule WFM and FCS studies (Fig. 1). FCS is currently considered to be one of the most statistically reliable methods for determining diffusion coefficients. Therefore, the combination of monolayers and the FCS technique is ideal for determining the pressure and area dependence of diffusion coefficients and thereby evaluating the free-area model. The single-molecule imaging capabilities of the setup made it possible to investigate fine structure in the sample. Such fine structure can limit the diffusion to specific regions, causing significant deviations from normal (“free”) diffusion. If diffusion coefficients are evaluated in such systems under the assumption of free diffusion, the diffusion coefficients will naturally be erroneously determined.

Figure 1.

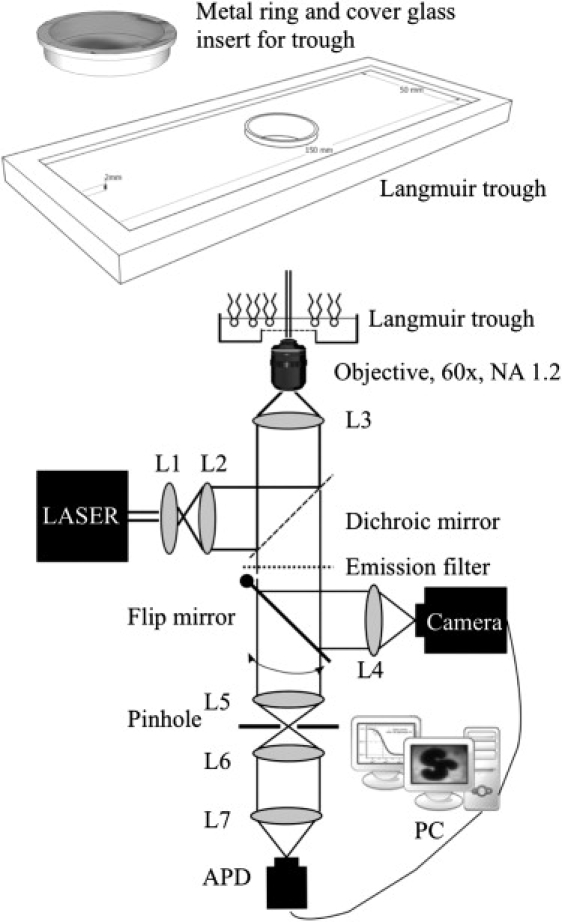
(Top) Schematic of the custom-built monolayer trough. Internal dimensions: 150 × 50 × 2 mm. The central hole has a diameter of 25 mm and is elevated 2 mm over the trough bottom. The observation window, a coverglass No. 00, was glued to a stainless-steel ring that fits exactly into the central hole of the trough. The design allowed extensive cleaning of the coverglass, which was needed to keep the 100 μm aqueous subphase stable above the observation window. (Bottom) Schematic of the in-house-built fluorescence microscopy/spectroscopy setup. L1–L7 are simple achromatic lenses. A flip mirror makes it possible to guide the fluorescence signal either to an EMCCD camera or through a pinhole to the APD. The setup is shown in the WFM configuration. Removal of lens L3 and flipping of the mirror transforms the setup to an FCS configuration.

Theory

In general, 2D diffusion can be described by

$$\langle r^2\rangle =4{Dt}^{\alpha },$$ (1)

where α = 1 if the diffusion is normal (free, unhindered). This is the expected behavior when the lipid matrix is homogeneous. For 0 < α < 1, the diffusion is said to be anomalous. In a system exposed to a constant directed flow (such as surface flow due to convection or directed transport), the diffusion can be described by

$$\langle r^2\rangle =4{Dt}^{\alpha }+{\left(vt\right)}^2,$$ (2)

where v is the constant velocity of the directed flow. In monolayer studies, surface flow due to convection and air can be a problem. However, in FCS, directed flow is easily identified in the autocorrelation profile because it will clearly deviate from that obtained under normal diffusion behavior (24,25).

Free-area model

It has been known for almost 100 years that the viscosity η of a solution varies markedly with an external applied pressure. This was first investigated by Batchinski (28) and later formalized by Doolittle (29), who found that the viscosity of a solution could be well approximated by the excess volume of the solution:

$$\ln \eta =\ln A+B\left(v_0/v_f\right),$$ (3)

where η is the viscosity, A and B are substance-specific constants, v_f is the free volume in 1 g of solution at a given pressure and temperature, and v₀ is the volume of 1 g of the solution at zero Kelvin (extrapolated without phase change). Using this empirical equation, Cohen and Turnbull (30) set up the first free-volume model to describe particle diffusion. Their model was later adapted for the 2D case by Galla et al. (5) and is commonly referred to as the free-area model. In this model, diffusion is a purely statistical process. The essence of the model is that the translational motion of a particle occurs when random density fluctuation creates a particle-free site in the molecular lattice into which a particle can be displaced (5,6,30). The original free-area model operates with few parameters. The molecules (e.g., lipids) are modeled as hard rods with an area a₀, which defines the free area a_f of every lipid:

$$a_f\equiv MMA-a_0,$$ (4)

where MMA is the experimentally determined MMA of the lipid. Typically, a₀ is chosen as the van der Waals area of lipid, a_{0, DMPC} = 42.5 Ų. According to the free-area model, the relationship between the diffusion coefficient D and the free area a_f is given by

$$\ln D=\ln \left(g\cdot l_c\cdot u\right)-\gamma a_c/a_f,$$ (5)

where g is a geometric factor (≈1/4), l_c is the average length of free travel of the particle in the free area, μ is the gas kinetic constant $\left(=\sqrt{2k_{B}T/m}\right)$, γ is a numerical factor correcting for possible overlap of free areas (0.5 < γ < 1), and a_c is the critical area above which translational diffusion becomes possible. Note that a_c and a₀ are not necessarily equal in the free-area model.

For simplicity we abbreviate Eq. 5 to the following form:

$$\ln D=\ln D_{\max }-\beta /a_f,$$ (6)

where D_max = gl_cu, and β = γ × a_c.

Materials and Methods

Chemicals

Lipids were purchased from Avanti Polar Lipids (Birmingham, AL). Fluorescence labels TRITC-DHPE (Cat. No. T 1391), DiI-C₁₈ (DiI-C18(3), Cat. No. D282), DiD-C₁₈ (DiI-C18(5), Cat. No. D7757), and Rhodamine 6G (R6G, Cat. No. R 634) were from Invitrogen (Carlsbad, CA). All solvents were spectroscopic grade from Merck (Darmstadt, DE). In all steps involving water, MilliQ water (>18.0 MΩ/cm @ 25°C) was used.

Langmuir film preparation

An in-house-built Langmuir Teflon trough (150 × 50 mm) with two moveable Delrin barriers was used for the experiments. The unique trough design (cf. Fig. 1) primarily accommodated the short working distance of our 60× water immersion microscope objective (0.2 mm) and facilitated easy removal/exchange of the glass observation window from the trough for extensive cleaning (a full description will be published elsewhere). Electronics and control software was obtained from Kibron (Espoo, SF). The Langmuir trough was mounted on optical table equipment with a piezoelectric nanopositioning Z-system and manual XY positioning.

To reduce surface flow of the monolayer in the observation region, a Teflon ring (ø 15 mm, height 3 mm) with a slit opening (2 mm) was placed on the glass observation window in the trough during experiments. A second coverglass was placed on top of the ring to further reduce air flow. Finally, the entire trough was covered by an acrylic box.

All monolayers were spread from n-hexane/methanol (99.9/0.1 vol %). The lipid/lipid fluorophore ratio was adjusted between 1:50,000 and 1:200,000 (∼10⁻³–10⁻⁵ mol %). The lowest ratio yielded ∼1–2 fluorophores in the FCS focus, yielding maximal amplitudes in the time-ACFs and thus, in principle, the optimal signal/noise ratio due to the strong signal fluctuations (31). The measured diffusion times proved to be independent of the lipid ratio within the concentration range used.

WFM

Images were recorded on an EMCCD camera from Andor (Belfast, Northern Ireland) (IXON EM+, DU897BV, pixel array: 512 × 512, pixel size: 16 μm). Samples for WFM were excited using a 200 mW laser emitting at 532 nm. The final excitation irradiance at the sample plane was adjusted to 0.5–2 kW/cm².

DSC

DSC was performed on multilamellar vesicles using a high-sensitivity differential VP-calorimeter (MicroCal, Northampton, MA) with scan rates of 5°/h. Vesicles containing fluorescence dyes were prepared by mixing the dyes with the lipids in a chloroform/methanol mixture. The samples were dried under a nitrogen flow and subsequently left in a vacuum desiccator. Distilled water was added to the dry lipid mixture and shaken on a vortexer.

Confocal microscopy

Giant lipid vesicles were prepared by electroformation on coverslips coated with indium tin oxide (ITO) and visualized by confocal microscopy. Details are described elswhere (23).

FCS

Samples for FCS were excited with a linearly polarized continuous-wave 532 nm Nd:Yag laser (Laser 2000, Wessling, Germany) with a maximal power of 5 mW. To avoid photobleaching in samples with slow label diffusion (e.g., at high surface pressures), optical filters were used to attenuate the excitation intensity by up to 4000-fold (OD 3.6).

The setup is schematically shown in Fig. 1. A 60× water immersion objective (NA 1.20, UPLAPO; Olympus Denmark, Ballerup, Denmark) and a confocal setup with a pinhole size of 30 μm was used for FCS measurements. The fluorescence signal was detected by a SPCM-AQR-13 APD (Laser Components, Olching, Germany). Timescales were calibrated externally with Rhodamine 6G solutions at 295 K with a known diffusion coefficient of D = 3.0 × 10⁻⁶ cm²/s at 22°C (32). The radius of the observation volume in the XY plane under the applied conditions was r_min = 225 ± 10 nm. The signal from the APD was analyzed using a FLEX5000/fast correlator card (Correlator.com, Bridgewater, NJ). Time-ACF profiles were fitted assuming a Gaussian cross section of the focus, using the correlation function for normal diffusion in a planar system:

$$G\left(\mathit{\tau }\right)=1+\frac{1}{N}\left(\frac{1}{1+\mathit{\tau }/{\mathit{\tau }}_d}\right),$$ (7)

where N is the mean number of fluorophores in the focus, and τ_d is the dwell time of the labeled lipids in the focus (33). Fitting experimental autocorrelation profiles sensitively depends on the assumption of a Gaussian focus (34), with the detection intensity described as a function of the distance from the focus center. This detection probability is a convolution of excitation profiles and pinhole properties (35). In our experiments, the autocorrelation profiles of the pure lipid phases were well described by the ACF in Eq. 7, indicating that the focus profile was close to being Gaussian and that no significant surface flow was present (25).

Z-scan method for determination of diffusion coefficients

All FCS measurements on monolayers presented herein were performed with TRITC-DHPE as the lipid fluorophore at 20 ± 0.5°C and 22 ± 0.5°C. All experiments were repeated at least three times using slightly different compression rates (∼1–2 Ų/lipid/min) and waiting times between measurements without any systematic influence on the measured values. Before time-ACFs were recorded, the monolayers were left to equilibrate at the target pressure for 5–15 min. FCS measurements were initiated with the focus deliberately placed below the air-water interface, and thus with the monolayer slightly out of focus. During the FCS measurements the position of the air-water interface spontaneously moved down along the Z-axis, due to evaporation, bringing the air-water interface first into focus and then out of focus again (with the final focus position above the air-water interface). The rate of evaporation was kept low by keeping a highly humid atmosphere inside the cover box of the monolayer trough. No attempt was made to completely eliminate evaporation, because the spontaneous evaporation provided a functional way for the monolayer to travel slowly and smoothly through the FCS focus. A similar method was previously described and named “time-dependent Z-scan” (36,37).

Diffusion times, τ_d, were in practice recorded at various surface pressures Π. Subsequently, Π was converted to the corresponding MMA by comparison with previously recorded, continuously compressed pressure-area isotherms. This approach was necessary because FCS measurements over a complete range of surface pressures lasted several hours, accompanied by lipid loss over time due to adsorption of lipid to barriers, trough edges, and the PTFE ring used to minimize surface flow (38).

The duration of each FCS trace was set to 10 s with a 2-s pause between each trace. Short trace times were preferred to minimize possible effects from the monolayer movement along the Z axis (i.e., the optical axis). A complete time-dependent Z-scan typically lasted 30 min and resulted in 150 individual FCS traces. The first and last traces were often too far from focus and could not be fitted to the time-ACF. On average, 60 FCS traces, recorded in the vicinity of the optimal optical focus of each Z-scan, were used to determine the diffusion coefficient at a given pressure.

In Fig. 2 (left) two recorded ACFs are shown: one corresponding to an in-focus measurement (diamonds, solid line), and one to an out-of-focus measurement (triangles, dashed line). From the fits to the time-ACFs, the average diffusion time τ_d through the FCS focus volume can be determined as the FWHM, and the average number of molecules N in the focus can be found from the reciprocal value of the amplitude of G(τ) − 1 (cf. Eq. 7). All of the time-ACFs presented herein could be fitted satisfactorily using Eq. 1 with an α value of one. This indicates that diffusion was normal on the length- and timescales of the experimental conditions, and that no significant surface flow was present during the measurements.

Figure 2.

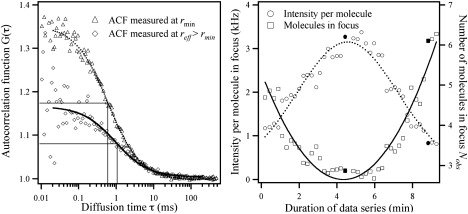
Typical data set from a time-dependent Z-scan recorded on a DMPC monolayer at Π = 26 mN/m. The data points corresponding to the two experimental time-ACF profiles in the left panel are highlighted in the right panel. (Left) Two measured time-ACF curves including the fits used to determine the mean diffusion time through the focus (defined as FWHM). The first time-ACF curve (triangles, full line) was recorded near the optical focus r_min. It therefore measured fluorescence fluctuations from the smallest possible area and the fewest possible number of fluorophores in the focus. This gives a relatively high amplitude of the time-ACF fit, and a relatively short diffusion time through the focus. The other FCS trace (diamonds, dashed line) was recorded out of focus. This resulted in the opposite characteristics. Note the semilogarithmic axes. (Right) The “intensity per molecule in focus” (○) increases over time as the air-water interface position first moves toward the optimal focus (0–4 min) and then decreases as the monolayer moves past the optimal focus (6–8 min). The number of molecules within the focus (N_obs, □) acts in the opposite manner and has minima at the optimal focus (∼4–6 min). The fit to the intensity per molecule is Gaussian, and the fit to the number of molecules in the focus is parabolic (cf. Eq. 11). The fits were not used analytically and only serve as a guide for the eye.

Fig. 2 (right) shows the analyzed result from a typical time-dependent Z-scan. The time needed for the monolayer to move due to evaporation through the observation volume was 10 min in this case (only the time interval providing traces with adequate signal/noise ratio for fitting is shown). At the beginning of the scan, the monolayer is out of focus. This means that the observed area is large, resulting in relatively many lipid fluorophores N residing in the observation area. It also results in the typical, relatively long diffusion time τ_d for a lipid fluorophore. At intermediate times, the monolayer is near the optical focus plane; the observation area is the smallest possible (radius = r_min) and the diffusion time is also at a minimum. At the end of the scan, the monolayer has again moved out of focus. Under ideal conditions (e.g., the monolayer moving through the focus at constant speed), the profile of the intensity per molecule versus time should have a Gaussian profile according to the Gaussian approximation of the FCS beam profile. In addition, the number of molecules in focus versus time profile should be parabolic. This follows from the number of molecules N being proportional to the area A, which is proportional to the radius r squared (N, A ∝ r²). In practice, though, the air-water interface did not move at constant speed during all of the measurements. Therefore, the fitted lines shown in Fig. 2 (right) were not used analytically. Note also that the parabolic fit minima and the Gaussian fit maxima do not correspond to the same measurement (or time). This phenomenon was always observed, and was previously described (36). For the experimentalist working on 2D (flat) samples, it is important to note that apparently one does not obtain the highest intensity per molecule at the beam-waist minimum (36).

The diffusion coefficients were determined from ∼60 measured pairs of values for the diffusion time τ_d and the observed number of fluorophores N_obs in the focus. This approach makes use of measurements made both in and out of focus, which is possible when we know 1), the number of TRITC-DHPE molecules N_min at the optimal focus; and 2), the radius of the optimal focus r_min. The lowest values of N_obs, found near the minima of the parabola in Fig. 2, define N_min. The minimal radius of the focus r_min was found from external calibration using R6G (see above). With this pair of values (r_min; N_min) at hand, the surface density of fluorophores Γ in the monolayer can be expressed as

$$\Gamma =\frac{N}{Area}=\frac{N_{\min }}{\pi \cdot r_{\min }^2}\text{.}$$ (8)

Assuming that the density of fluorophores Γ does not depend on the size of the observed area A_obs, which is fair when the fluorophore is expected to be homogeneously distributed in the lipid structure (this may not be true for highly heterogeneous or compartmentalized biological membranes), we can determine the observed area A_obs of any out-of-focus measurement from the number of molecules N_obs in the area obtained from the time-ACF fit from the following relation:

$$A_{obs}=\frac{N_{obs}}{\Gamma }\text{.}$$ (9)

From this we can find the effective radius of focus r_eff as a function of N_obs:

$$r_{eff}=\sqrt{\frac{N_{obs}}{\Gamma \cdot \pi }}\text{.}$$ (10)

By combining Eqs. 1, 8, and 10, we get

$$D=\frac{r_{eff}^2}{4\cdot \tau }=\frac{r_{\min }^2}{4\cdot \tau }\cdot \frac{N_{obs}}{N_{\min }},$$ (11)

where α in Eq. 1 has been set to unity. Rearranging Eq. 11 gives

$$\tau =\frac{r_{\min }^2}{4\cdot D}\cdot \frac{N_{obs}}{N_{\min }}\text{.}$$ (12)

The corrected diffusion coefficient then becomes readily obtainable by plotting the diffusion time τ_d as function of the ratio N_obs/N_min, where the slope is given by r_min²/4D (cf. Eq. 12). Representative fits for data points obtained at four different pressures are shown in Fig. 3. In principle, this plot also contains information on the size of the FCS focus radius r_min, which makes the external calibration by measuring the diffusion of R6G with the known diffusion coefficient unnecessary (36). We therefore attempted to fit the data with both r_min and D as free parameters, but were unable to do so consistently because the scatter in our data was too large.

Figure 3.

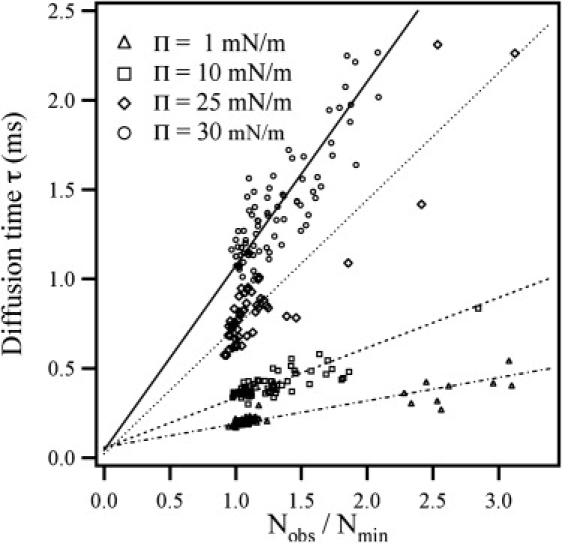
Measured diffusion time τ_d vs. N_obs/N_min for representative data recorded at 22°C. The slope is given by r_min²/4D. All lines pass through the point (0.0 ± 0.1) as predicted by Eq. 11.

Results and Discussion

The pressure versus area compression isotherms of DMPC and DPPC are shown in Fig. 4 (left). The isotherms have characteristics similar to those previously reported (39,40). All of the isotherms show the pressure onset at a mean molecular just below 100 Ų and a gradual increase until the respective phase transition from the LE phase to the LC phase. For DMPC, a narrow transition region is found at a surface pressures Π just above 40 mN/m and an MMA just below 50 Ų. The narrow transition in DMPC isotherms indicates that the system is near the critical temperature T_C, in agreement with previous reported values (39). The position of the phase transition can also be deduced from the plot of compressibility κT versus surface pressure Π in Fig. 4 (right) or from the derivatives of the Π-A isotherm (not shown) (41). The LE-LC phase transition observed in the DPPC isotherm is significantly broader and is found at Π = 5 mN/m in the MMA interval from 56 to 83 Ų.

Figure 4.

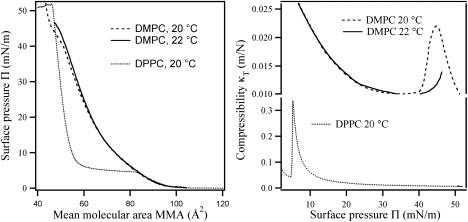
(Left) Pressure-area isotherms of DMPC at 20°C and 22°C, and of DPPC at 20°C (all recorded until monolayer collapse). (Right) Compressibility κ_T versus surface pressure Π. The DMPC compressibility curve at 22°C is incomplete due to monolayer instabilities/collapse observed at temperatures close to the critical temperature T_c (cf. left panel). The profile for compressibility of DPPC shows a narrow peak centered at Π = 8 mN/m, which is more than 10 times higher in magnitude than for DMPC.

FCS measurements were conducted in the pure LE phases of both DMPC and DPPC monolayers. As described above (see Materials and Methods), the diffusion time τ_d of the fluorophores through the confocal volume was determined at different effective foci represented by the ratio N_obs/N_min (cf. Eq. 12). Four representative τ_d vs. N_obs/N_min data sets are shown in Fig. 3. The slope of lines was used to derive the diffusion coefficient of the fluorophore at a given surface pressure Π according to Eq. 12. The plot also reveals that diffusion was normal over the entire range of measured values according to the FCS diffusion law, since all lines pass through the origin (0,0) (42,43).

The experimentally determined diffusion coefficients D in DMPC monolayers are plotted versus surface pressure in Fig. 5. Error bars represent 1 standard deviation (SD) determined from an average of 60 measurements at each surface pressure. Evidently, D decreases monotonically with increasing surface pressure from 120 ± 16 μm²/s at Π = 1 to 6.5 ± 0.8 μm²/s at Π = 40 (20°C). The plots of Π versus D and Π versus MMA are almost exactly superimposable (Fig. 5). With respect to temperature, no significant difference in D is observed for measurements performed at either 20°C or 22°C below surface pressures of 35 mN/m. At pressures above 35 mN/m, D deviates significantly and is smaller at 20°C than at 22°C. In this region the isotherms, and especially the compressibilities of the DMPC monolayers at the two different temperatures, also show distinct differences (Fig. 4, right). At 20°C the compressibility is at a minimum at 35 mN/m, and at 22°C the compressibility is at a minimum at 38 mN/m. These compressibility minima correspond very well to the pressures at which the kinks in the pressure versus diffusion coefficient curves are observed (Fig. 5). It is noteworthy how closely the diffusion coefficients also follow the pressure profile of the isotherms in the region where the free-area model is not expected to be valid, i.e., near the phase transition (Fig. 5, inset).

Figure 5.

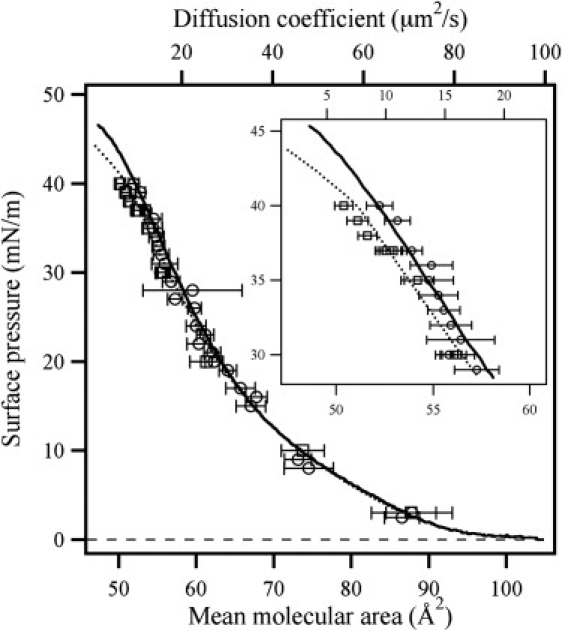
Pressure Π versus diffusion coefficient D (markers) and compression isotherm (Π vs. MMA) for data sets recorded at 20°C (squares and broken line) and 22°C (circles and full line). The plots of Π vs. MMA and Π vs. D follow the exact same trend. It is noteworthy that the slight temperature-induced offset of the Π-A isotherm clearly affects the measured diffusion coefficients at the higher lateral pressures. (Inset) Magnification of data in the pressure range; Π = 28–45 mN/m.

FCS measurements on DPPC monolayers in the LE region yielded diffusion coefficients of D = 50 μm²/s at surface pressures Π = 3 mN/m. This is slightly lower than the measured diffusion coefficient in a DMPC monolayer at the same Π and MMA, and much lower than reported diffusion coefficients in DLPC monolayers at the same pressure (6,9,10). All values are summarized in Table 1. We were unable to obtain FCS measurements in the LE-LC and LC regions of a DPPC monolayer. In the LE-LC region, the spontaneous diffusion of condensed lipid domains into the FCS focus made it impossible to perform complete Z-scans, which typically lasted 30 min. At higher pressures, in the LC region of the DPPC monolayer, the time-ACF could not be fitted satisfactorily with any known fit function. The origin of the problems encountered in the LC region of DPPC will be shown and discussed below in the section Partitioning of fluorophores in condensed phases).

Table 1.

Values extracted from the fit of the measured data to the free-area model; values from previous published studies are given for comparison

Method	Lipid	Temp. (°C)	β (Å2)	Dmax (μm2/s)	D (3 mN/m) (μm2/s)	D (30 mN/m) (μm2/s)	Reference
FCS	DMPC	22	23 ± 0.9	88 ± 5	70	16	—
	DPPC		—	—	50	—
FRAP	DLPC	21–22	25	120	90	26	(6)
	DPPC		—	—	40	(0.02)∗
FRAP	DLPC	22–23	31	180	110	28	(9)
FRAP	DLPC	22–24	23	120	100	35	(10)
SPT	DMPC	24	8	5	4	1.5	(8)

Values from linear fits of lnD vs. 1/a_f plots. The coefficient β (= γ a_c) is given by the slope of the plot in Fig. 6, and D_max is estimated by extrapolation of the straight line to a_f → ∞. D_max is the theoretical maximal diffusion coefficient at infinite dilution without phase change. The values from the studies given for comparison were found by reanalyzing the original data. The diffusion coefficients at the approximate monolayer-bilayer equivalent pressure (∼30 mN/m) are larger by approximately a factor of 5–6 than reported diffusion coefficients for fluid bilayers (see Discussion in text).

^∗Diffusion coefficient measured in the LC phase of a DPPC monolayer.

Correlation between D, MMA, and the free-area model

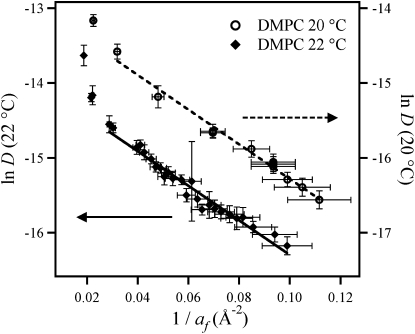
According to the free-area model, a plot of ln D vs. 1/a_f is expected to yield a straight line as long as the system is homogeneous and “far from” phase transitions (44). In the case of DMPC, pronounced pressure-induced phase transitions are found at both low (∼0 mN/m) and high (>35 mN/m) pressures. Obviously, the free-area model must fail in regions where domain formation is expected, e.g., in the G-LE and LE-LC phase transitions. Indeed, only the experimental data points for Π > 3 mN/m (MMA > 87 Ų, 1/a_f ≈ 0.02 Å⁻²) were found to fit on a straight line predicted by the free-area model (Fig. 6). The two most likely reasons for the anomalies seen at MMA > 87 Ų are that 1), the system is near the G-LE phase transition; and 2), the model fails when the MMA becomes twice as large as the hardcore area (a₀ = 42 Ų). Data points below Π = 5 mN/m were therefore omitted from the linear least-square fits and analysis. Note also that the data points in the high-pressure (i.e., low free area) end of the fluid phase appear to lie on the straight line. This is slightly surprising because the free-area model is strictly not valid in this region close to the LE-LC phase transition. A partial explanation for this is that the error in the free area becomes significantly larger as the experimentally determined MMA becomes close to a₀. This is shown clearly by the error bars in Fig. 6, in which the data points have been plotted and fitted to the free-area model in Eq. 6. The linear fits were performed with data points weighed according to their SD, and coefficients from the linear fits are given in Table 1.

Figure 6.

Plots according to the free-area model; lnD vs. 1 / a_f (see text). Error bars on the ordinate axis originate from the SD of the experimentally determined MMA, which was ∼0.5 Ų. The data points and fitted lines from the two different temperatures are virtually superimposable. Axes scaling on the ordinate axes have been shifted by one to visually distinguish the data points from the different temperatures.

A key fitting parameter in the free-area model fits described above is the hard-core (or van der Waals) area a₀ of the lipid. This is typically set to ∼42–43 Ų for phosphocholines (6,8–10,45). This value for the hard-core area seems reasonable because it is slightly below the average lipid area of 48 Ų in a gel phase bilayer (46) in which translational diffusion is still possible, and therefore must include both the hard-core lipid area a₀ as well as the additional free area. This value for a₀ also fits well with the minimum value for the MMA, where continuously compressed monolayers are always seen to collapse (e.g., Fig. 4). For these reasons, a value for a₀ of 42 Ų was chosen for the analysis presented here. This provided a quality-of-the-fit value (Pearson's R) of 0.99 for ln D vs. 1/a_f.

It should be stressed that one can obtain a similar good fit by simply plotting D versus MMA. This is shown in Fig. 7 for the data set recorded at 22°C, and it can be seen that D and MMA are linearly dependent in the region between 50–90 Ų, with slopes of the least-square linear fit being 1.7 s⁻¹ (fit not shown) and 1.8 s⁻¹ for 20°C and 22°C, respectively. Extrapolation of the straight lines to D = 0 yields a value of 47 Ų at both temperatures. This extrapolation neglects the phase change, which would have taken place since the experiments were carried out below the critical temperature T_c. In the nomenclature of the free-area model, this corresponds to the critical area a_c above which lipid translational diffusion becomes possible in a fluid monolayer. A diffusion coefficient corresponding to that of a fluid DMPC bilayer at 25°C (5 × 10⁻⁸ cm²/s) would be obtained at an MMA of 50 Ų according to the extrapolated straight lines. This value is significantly below the typical average area per lipid in a fluid DMPC bilayer (a_bilayer = 61–64 Ų at 40–50°C (46–48)).

Figure 7.

Plot of the measured diffusion coefficient D vs. MMA. Both data sets can be fitted perfectly by a straight line (except for one data point at (MMA, D) (95 Ų, 120 μm²/s), which is excluded from the linear fit).

It is generally assumed that γ, the factor correcting for overlap of free area, is between 0.5 and 1 (30). Using these values, we find from the slopes (β) of the free-area model fits (Fig. 6) a critical area a_c between 24 Ų and 48 Ų at both temperatures. For γ = 0.5, the critical area found from fitting to the free-area model corresponds well to the value determined by plotting D directly versus MMA (a_c ∼47 Ų). The fit coefficients from the free-area model fits from this and previously published studies are given in Table 1. Also given are single data points for the measured diffusion coefficients at a surface pressure of Π = 3 and 30 nM/n for previously published experiments. Values measured in this study are similar to those reported from FRAP measurements (6,9,10), but are one order of magnitude larger than values found by SPT (8). The origin of the discrepancy between FCS/FRAP and SPT cannot be resolved with the available data, but is discussed further below.

The monolayer surface pressure at which monolayers and bilayers should be compared (the so-called monolayer-bilayer equivalent pressure) is often assumed to be in the range of 30–35 mN/m (45,49). At this surface pressure, diffusion coefficients measured by FRAP and FCS in monolayers are higher by a factor of 2 than diffusion coefficients measured in bilayer systems, which are in the range of 3–5 μm²/s irrespective of the method used (FRAP (50), FCS (33), or SPT (23,51,52)). The notion that diffusion occurs more rapidly in monolayers than in bilayers at equivalent lateral pressures seems quite reasonable. For instance, effects such as van der Waals coupling between the acyl chains of the opposing monolayers and interdigitation (sometimes called dynamic interpenetration) are absent in monolayers, and intuitively should result in faster lipid diffusion in monolayers compared to bilayers. Therefore, we find it likely that that the very low diffusion coefficients found in SPT experiments on lipid monolayers (cf. Table 1) have been systematically underestimated.

In the first part of this experimental study, we deliberately changed the surface pressure of the monolayer by applying an external force (by monolayer compression via the trough barriers), and found that the diffusion is highly dependent on the lateral pressure. In biology, for instance, such lateral pressure changes are expected as a consequence of protein adsorption and potential insertion into the biological membrane (53). Heimburg (24) calculated that adsorption of small proteins on a membrane generates a significant increase in lateral surface pressure of the membrane. For a protein covering 15 lipid molecules when adsorbed, the increase in surface pressure is on the order of 10 mN/m when protein coverage reaches 80% of the membrane surface. Such protein adsorption processes play an important role in diverse biological processes, such as pore formation due to adsorption of melitin (53), endocytosis, and inflammation, which involves adsorption of phospholipase A₂ to the membrane (54,55). Lateral pressure changes are also expected to occur in other experimental techniques, although this is rarely mentioned. An example is pipette aspiration experiments, such as patch clamp, in which forces are created that lead to significant changes in MMAs. The amount of deformation can be calculated by comparing the rupture tension of 1,2-dierucoyl-sn-glycero-3-ethylphosphocholine (di22:1-EPC) vesicles, which is 12 mJ/m², and the elastic constant, which is 200 mJ/m². This shows that the average lipid area changes by up to 6% at the rupture point (John H. Ipsen, University of Southern Denmark, personal communication, 2008). Our measurements show that a 6% area change from, e.g., 61 Ų (typical area for a lipid in a fluid-state phospholipid membrane) to 57 Ų, will result in a significant change in the diffusion coefficient of >25% (from 23 μm²/s to 15 μm²/s).

Partitioning of fluorophores in condensed phases

As mentioned above, it was not possible to perform FCS measurements on DPPC monolayers in the coexistence or condensed regions. To investigate the cause of this is in more detail, we directly visualized the DiI-C₁₈-doped DPPC monolayers with WFM.

The WFM images clearly revealed that in the coexistence region of the DPPC monolayer all of the tested fluorophores partitioned exclusively in the LE regions (Fig. 8). None of the fluorophores were able to penetrate into the gel domains, which shows that the condensed domains acted as impermeable (“hard”) obstacles. Very few (far less than 1%) of the fluorophores were observed inside LC domains, and they appeared completely immobile until irreversible photobleaching occurred.

Figure 8.

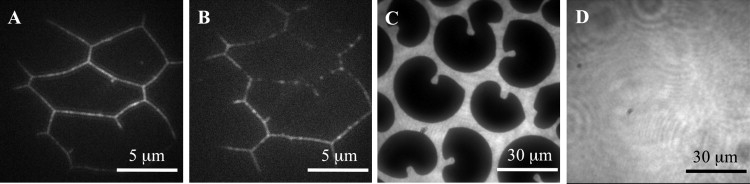
Partitioning of DiI-C₁₈ marker in DPPC monolayers at various stages of compression. (A) Line-shaped liquid defects at grain boundaries formed in the DPPC monolayer as a result of compression into the LC region (see text). (B) Same as A. However, as bleaching of the lipid fluorophores along the grain boundaries progressed, single lipid fluorophores in this region became identifiable, showing high mobility. Diffusion appeared along the boundaries in a 1D fashion. The lipid fluorophore concentration was ∼10⁻⁴ mol %. (C) LE-LC coexistence regime. (D) LE phase.

When the doped monolayers were compressed into the LC condensed region (LC, Π = 25–30 mN/m) line-shaped liquid defects were formed that contained virtually all of the lipid fluorophores (Fig. 8). The fact that one can still find liquid regions at these high pressures is likely a consequence of dye-induced freezing-point depression (Fig. 9, bottom; see Discussion below). By continuously monitoring the slow monolayer compression from the LE-LC region to the LC region, we observed that these liquid line defects were formed along the reminiscent domain boundaries (grain boundaries). Diffusion of the lipid fluorophores in Fig. 8 obviously took place along the line-like defects and was of a 1D rather than 2D nature. Of interest, this effect was not detectable when lipid fluorophore concentrations of 0.1 mol % were used, which is a normal concentration for FRAP studies. Under these conditions, a homogeneously illuminated monolayer was observed at high surface pressures. Although the grain boundaries were not detectable at this fluorophore concentration, it must be assumed that an essential part of the effect seen at low lipid fluorophore concentrations also remains at higher fluorophore concentrations.

Figure 9.

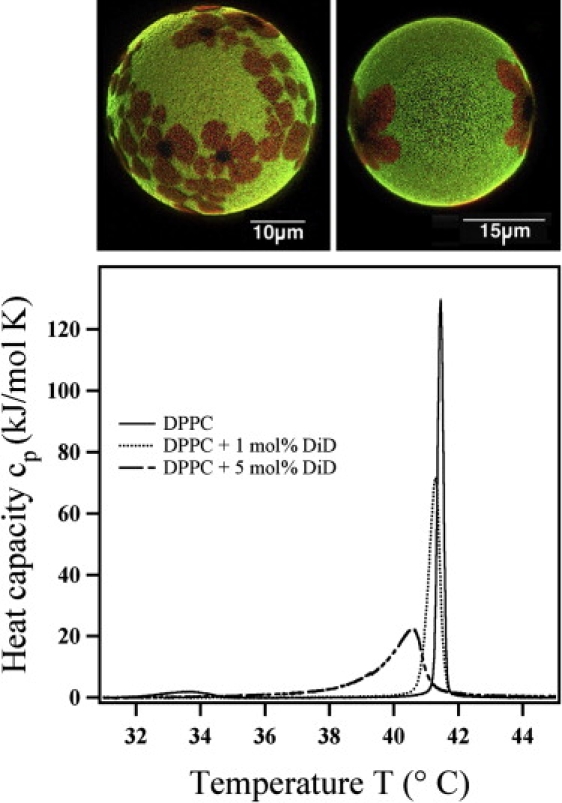
(Top) Fluorescence microscopy mixtures of giant DLPC:DPPC=33:67 vesicles at 27°C. The liquid-disordered phase is labeled with the green BODIPY-C₁₆ marker (light gray shades in print version), and the solid-ordered phase is labeled by a red DiD-C₁₈ marker. DiD-C₁₈ (dark gray shades in print version) is a red color variant of DiI-C₁₈. Although Di markers are often used to label solid-ordered bilayer phases, we find that the markers are progressively squeezed out from the domain solid domain centers. (Bottom) Calorimetric profiles of the DiD-C₁₈ marker in DPPC membranes shows that the profiles are shifted toward lower temperatures, indicating a preference for partitioning in the liquid regions.

We now compare these findings with those made in lipid bilayers. Ivanova et al. (56) showed that a favorable partitioning of small molecules (e.g., fluorescence markers) in one of two coexisting phases of bilayer membranes leads to a shift of melting temperatures due to the differences in mixing free energy. Favorable partitioning in the liquid phase leads to a lowering of the transition temperature, an effect called “melting point depression”. Translated to monolayers, a favorable partitioning in the LE phases would lead to an increase of the pressure of the LC-LE coexistence regime. We did not observe such an effect on pressure in this study. However, this was not surprising given the extremely low fluorophore concentrations used (<10⁻⁴ mol %). We have found that fluorescence markers generally cause a lowering of melting points in both single lipid bilayers and mixtures. The melting point depression caused by DiI-C₁₈ (actually of the red color analog DiD-C₁₈) markers in DPPC membranes is shown in Fig. 9 (bottom). We found the same results for all other fluorescence markers we have investigated, including BODIPY-C₁₆, DiI-C₁₈, DiI-C₁₆, and TRITC-DHPE (data not shown (26,57)). This means that all of these markers dissolve better in liquid phases. This finding is seemingly in conflict with the common practice in fluorescence microscopy to label solid-ordered phases with DiI-C₁₈ or DiI-C₂₀ markers (23,33). Fig. 9 (top) shows two GUVs made of a DLPC:DPPC=33:67 mixture measured at 27°C (the vesicle was prepared as described previously (23)). At this temperature the lipid mixture is in the phase coexistence regime. The two phases were labeled with BODIPY-C₁₆ (liquid, green) and DiI-C₁₈ (solid, red). Similar pictures were obtained by Korlach et al. (33) with a DiI-C₂₀ marker used to label the solid phase. However, close inspection of the GUVs in Fig. 9 shows that in the centers of the domains, dark regions form that do not contain any label. Since this always happens in the domain centers, we suspect that the domains assume a single crystalline order starting from a nucleation point in the domain center. It seems as if the red DiD-C₁₈ markers are kinetically trapped in the solid domains and equilibrium partitioning is only very slowly assumed. This trapping may consist of a local demixing into dye-enriched region between solid domains, as we have described for the monolayer case (Fig. 8). We have in fact found giant vesicles in which all dye (BODIPY-C₁₆ and DiD-C₁₈) was exclusively found in the liquid phases. We suspect that this is the equilibrium case obtained only upon very slow cooling of the vesicles into the phase coexistence regime. Note that compression in our monolayer experiments was always performed very slowly.

The above findings raise important questions concerning diffusion measurements by fluorescence means (FRAP and FCS) in lipid monolayers and bilayers in general. The general assumption that fluorescence dyes mix homogeneously with the host matrix is obviously not always true. In the literature, diffusion coefficients of bilayers in solid phases have been reported that differ by several orders of magnitude, ranging from 2 × 10⁻² μm²/s to 10⁻⁸ μm²/s (6,23). Since it seems that in equilibrium the fluorescence dyes generally do not dissolve in solid phases, the different values for D may just indicate differences in equilibration, and that in fact all these data obtained for condensed regions are incorrect.

Monolayers of DMPC at 20°C do not display obvious phase separation in microscopy, even in the regime of the peak in the compressibility (images not shown). Either domains do not form or they are too small for microscopic resolution (∼0.5 μm). This obviously resulted in an apparently simple diffusion behavior in our experiments. The free-area model approach must fail in the presence of heterogeneities of the order of the microscope focus, where one expects anomalous diffusion (58–60).

Conclusions

Time-dependent Z-scan FCS measurements were used to measure diffusion coefficients of TRITC-DHPE in DMPC and DPPC monolayers at different surface pressures, predominantly in the LE regions. This Z-scan method greatly improved the accuracy in determining diffusion coefficients on 2D samples, where it can be difficult to define the exact location of the beam-waist position relative to the sample.

The trend in measured diffusion coefficient D as a function of MMA was found to closely follow the direct observable surface pressure Π versus MMA. The diffusion coefficient D was also found to be proportional to the MMA in the LE region. Extrapolation of the fit to experimental data yielded a critical area (the MMA at which D = 0) a_c = 47 Ų for both investigated temperatures. The measured diffusion coefficients also fit the free-area model well, and extrapolation of the model fits yielded realistic values of the critical area a_c = 24–48 Ų and a maximal diffusion coefficient D ≈ 85 μm²/s in the LE phase of a DMPC monolayer. The measured diffusion coefficients are slightly below those found by FRAP measurements on DLPC monolayers, and an order of magnitude higher than diffusion coefficients measured in different phospholipid bilayer systems (supported bilayers, stacked bilayers, and GUVs). The difference in diffusion coefficients in relation to lipid bilayers is attributed to a more free diffusion in monolayers. In bilayers, the lipid fluorophore will be hindered by van der Waals coupling to an opposing monolayer, as well as subject to interdigitation.

Since a variety of biological processes are expected to change the lateral pressure in membranes, our findings imply that the diffusion coefficient of membrane components is influenced by these processes. This may have a profound effect on membrane function and the rate of bimolecular reactions in the membrane.

In addition to the FCS measurements, wide-field fluorescence imaging revealed the presence of lipid fluorophores along the reminiscent grain boundaries of condensed lipid regions. This is believed to be the origin of the large spread in reported diffusion coefficients in the literature. The microscopy images also showed that condensed lipid domains act as impermeable (hard) obstacles for fluorophores diffusing in the expanded regions of the monolayer. We compared the monolayer data with findings for giant lipid vesicles. The preferential partitioning of the fluorophores in liquid monolayers is in agreement with melting point depression found in calorimetric data of bilayers containing these dyes. However, this is seemingly in contrast to findings in giant bilayer vesicles, where solid phases are routinely labeled with such markers. We argue that this is an equilibration artifact. After slow annihilation, we found that these markers were excluded from the solid domain, as in the monolayer case. Thus, the wide range of diffusion constants for gel-phase bilayers most likely has the same origin as in monolayers in the LC phase.