Stretching Submicron Biomolecules with Constant-Force Axial Optical Tweezers

Abstract

Optical tweezers have become powerful tools to manipulate biomolecular systems, but are increasingly difficult to use when the size of the molecules is <1 μm. Many important biological structures and processes, however, occur on the submicron length scale. Therefore, we developed and characterized an optical manipulation protocol that makes this length scale accessible by stretching the molecule in the axial direction of the laser beam, thus avoiding limiting artifacts from steric hindrances from the microscope coverslip and other surface effects. The molecule is held under constant mechanical tension by a combination of optical gradient forces and backscattering forces, eliminating the need for electronic feedback. We demonstrate the utility of this method through a measurement of the force-extension relationship of a 1298 bp ds-DNA molecule.

Introduction

Optical tweezers have become an important tool to study the mechanics of biomolecules and biomolecular processes. In a typical experiment, the molecule or molecular system of interest is attached on one end to a microsphere, which serves as a handle of optical manipulation, and on the other end to either a second microsphere or, more often, a solid support such as a microscope coverslip. A laser beam is then used to move the microsphere in the focal plane of the objective, thus applying a force to the molecule. These techniques serve well when it comes to the manipulation of molecules that are several microns in length, but become increasingly difficult when submicron-sized systems are to be studied.

The ability to reliably manipulate shorter molecules is important, however, because molecules that extend freely for microns are scarce in living cells. DNA, for instance, is subject to a number of constraints, which range from packing by histones into chromatin in eukaryotes to attachments to the cytoskeleton and cell wall in prokaryotes. To get closer to this highly constrained in vivo situation, techniques that can look at shorter DNA fragments are required. Another advantage of working with shorter molecules is that the amplitude of the thermal fluctuations of the molecule held under constant tension scales linearly with its length (1). Thus, reducing the length of the molecule makes events of interest, such as stepping of a molecular motor or binding of a protein, easier to observe. Similar considerations have also been applied to magnetic tweezers, and in one study, a reduction of molecular length from 4 kb to 2 kb resulted in a twofold improvement in the signal/noise ratio (2).

Stretching shorter molecules with optical tweezers is technically difficult primarily because when the molecule is attached to the coverslip on one end, the angle between the extended molecule and the coverslip becomes steeper as the molecule gets shorter. This means that the microsphere sees an anisotropic optical potential in which the trap gets softer as the force is no longer applied purely in the focal plane, but is increasingly applied in the axial direction. Thus, applying a well-calibrated force during the stretching protocol is almost impossible. Furthermore, the microspheres used as handles are rarely perfectly round and tend to preferentially align themselves in the anisotropic optical potential and rotate somewhat when pulled. This in turn makes accurate displacement measurements problematic. To overcome these problems, we present a scheme in which the microsphere is no longer moved in the focal plane of the microscope and the molecule is always stretched perpendicular to the coverslip in the axial direction (see Fig. 1). This geometry is reminiscent of magnetic tweezers, but without the complication of uncontrolled torques from having a magnetic center of the microsphere that often does not coincide with the geometric center, which primarily limits how short the molecules in magnetic tweezers can be.

Figure 1.

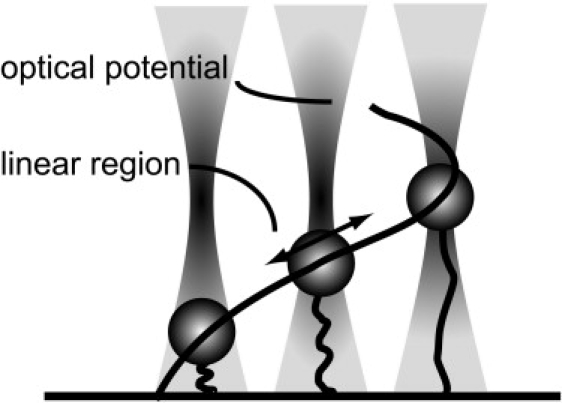
The principle of our constant-force axial trapping scheme. A short DNA molecule is attached to a coverslip and a microsphere and placed in the linear region of the axial optical potential, which is represented by the bold curve. This holds the molecule under constant tension, irrespective of its extension. The figure shows one molecule at three different extensions, with the middle one correctly placed in the linear region, and the other two at the edges where the constant-force approximation begins to break down.

Another important consideration for our scheme is the need to hold the molecule under constant tension, no matter what its extension is, which is required by many experimental protocols. Typical examples are the motion of molecular motors, where the DNA is reeled in (3,4), or the observation of protein binding and unbinding events, where the apparent length of the DNA depends on the binding state (5). Conventionally in optical trapping, the microsphere is held in the parabolic minimum of the optical potential, resulting in an applied force proportional to the displacement of the microsphere from the center of the trap. To obtain a constant force instead, electronic feedback is generally employed. More recently, passive schemes in which linearly shaped optical potentials are used to apply a constant force irrespectively of the extension of the system have been introduced (6,7). Similarly, Greenleaf et al. (8) used the approximately linear region of an optical potential from a Gaussian beam to locally create constant-force conditions. The elimination of the feedback led to an increased bandwidth and decreased measurement noise, enabling them to see motion with single basepair (bp) resolution (9). We apply the same principle to axial optical manipulation and trap the microsphere in the linear region of the combined optical potential from the Gaussian intensity gradient and the backscattering force (Fig. 1).

Materials and Methods

Optical tweezers setup

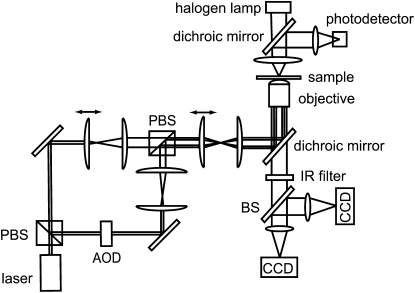
The optical setup of the constant-force axial optical tweezers shown in Fig. 2 is very similar to conventional dual-beam optical tweezers, such as the one described by Meiners and Quake (10). A linearly polarized beam from a 1064-nm Nd:YVO₄ laser (T40-Z-106C; Spectra-Physics, Mountain View, CA) is split into two orthogonally polarized beams of variable intensity. One of these beams is eventually used to manipulate the biomolecule of interest, and the other serves calibration purposes. In this work they will be referred to as the manipulation beam and calibration beam, respectively. To control the intensity of the manipulation beam independently and avoid interference effects between the beams, a computer-controlled acousto-optic deflector (AOD, DTD-274HA6; IntraAction, Bellwood, IL) is inserted into the manipulation beam path. Beam-steering mirrors control independently the direction of both beams, and separate telescopes on motorized translation stages allow us to focus the beams into different focal planes, with different beam sizes, if desired. After the beams are recombined on a second polarizing beam splitter (PBS), a final telescope conditions the beam parameters before an oil immersion microscope objective with a high numerical aperture (PlanApo 60×/1.40 oil; Olympus, Center Valley, PA) focuses the beams into the sample cell. To obtain optimal trapping efficiency with the calibration beam, its beam parameters are chosen such that it overfills the back aperture of the microscope objective 1.5-fold; an overfill factor of 1.2 for the manipulation beam gives a somewhat shallower focus and therefore a larger constant-force region in the optical potential to work with.

Figure 2.

Schematic diagram of the optical tweezers setup. The original laser beam is split by a PBS into two beams, which are independently controlled through movable mirrors, telescopes, and an AOD. The beams are jointly focused into the sample cell through a microscope objective. A photodetector in the back focal plane is used to measure the fluctuations of a trapped microsphere for calibration purposes. Two CCD cameras record brightfield images of the sample. One CCD camera is used to measure the axial position of the trapped microsphere, and the other is used to compensate for drift in real time.

The optical tweezers are integrated into a custom-built brightfield microscope. The sample is mounted on a precision piezo-stage (Nano-LP100; Mad City Labs, Madison, WI) that controls the position of the sample with respect to the objective. A condenser and a halogen lamp are used to provide illumination from the other side of the microscope objective. The brightfield image is separated from the laser trapping beam paths through a dichroic mirror and imaged on two CCD cameras. The digital CCD camera (PL-A741; PixeLINK, Ottawa, Canada) is our main means of acquiring data, and is triggered under computer control to take brightfield videos or images of the sample at a desired sampling rate synchronized with any manipulation protocol. In addition, a secondary CCD camera (WAT-902B; Watec, Orangeburg, NY) is used as a part of a feedback control system that compensates for thermal and mechanical drifts in the microscope. It enables virtually unlimited observation time by automatically adjusting the stage such that a reference microsphere that is stuck to the coverslip always remains in the same position and focus.

In addition, we collect the transmitted and forward-scattered laser light with the illumination condenser and project it onto a photodetector (ET-3020; Electro-Optics Technology, Traverse City, MI) such that the laser spot overfills the active area of the photodetector ∼1.2-fold. This allows a measurement of the displacement of a trapped microsphere in the axial direction from fluctuations in the intensity of this signal, as the spot size at the detector changes with the position of the microsphere (11,12). The signal from the photodetector is filtered by an antialiasing filter with a cutoff frequency of 100 kHz and amplified by a low-noise amplifier (SR560; Stanford Research Systems, Sunnyvale, CA) before it is acquired by a data acquisition card (PCI-6025E; National Instruments, Austin, TX) at a sampling rate of 200 kHz.

Sample preparation

DNA molecules of interest are attached to the coverslip on one end and to a microsphere on the other end with the use of digoxigenin-antibody and biotin-streptavidin chemistry, following protocols similar to those used in previous tethered-particle and optical tweezers experiments (13,14). For our experiments, we used a ds-DNA fragment with a length of 1298 bp, which we obtained by polymerase chain reaction from the pRW490 plasmid of Hsieh et al. (15), using primers with biotin and digoxigenin modifications on the 5′ end.

The sample chamber for the tethered-particle experiments consists of a microscope slide, a coverslip, and a parafilm spacer in between. First, two access holes are drilled into a microscope slide; Tygon tubing is inserted and affixed with epoxy glue. Then the parafilm spacer, with a cutout for the flow channel between the holes, and the coverslip are sandwiched together and baked to create a sealed chamber with a volume of ∼9 μL in the center of the slide.

To attach the DNA and microspheres, the chamber is first filled with a solution containing 20 μg/mL anti-digoxigenin (anti-digoxigenin from sheep; Roche, Indianapolis, IN) in phosphate-buffered saline (137 mM NaCl, 10 mM phosphate, 2.7 mM KCl, pH 7.4) and left to incubate for 20 min at room temperature. Then the excess antidigoxigenin is washed away by 200 μL of potassium Tris Cl (PTC) buffer (20 mM Tris-acetate, pH 8.0, 130 mM KCl, 4 mM MgCl₂, 0.1 mM EDTA, 0.1 mM DTT, 20 μg/mL BSA, 80 μg/mL Heparin). To prevent nonspecific binding, the chamber is washed again with 200 μL of PTC1 buffer (PTC buffer plus 1 mg/mL α-casein) and left to incubate for half an hour. Separately, a 30 μL volume of a DNA-microsphere mixture containing 1 ng/mL of end-labeled DNA and 60 pM of streptavidin-coated polystyrene microspheres (800 nm in diameter; Spherotech, Lake Forest, IL) in PTC1 buffer is spun slowly on a rotating rack at room temperature for half an hour to allow the microspheres to bind to the DNA molecules without sedimentation. Then, the DNA-microsphere mixture is introduced into the prepared chamber and incubated for 5 min. Finally, the chamber is flushed with 500 μL of PTC1 buffer to remove any unbound DNA and microspheres. By using an excess of microspheres, we ensure that virtually each of the remaining tethered microspheres is bound to a single DNA molecule. Before the sample is used, the inlet and outlet tubes of the chamber are sealed to prevent evaporation and fluid flow.

Image analysis

In the constant-force axial optical tweezers setup, the position of a trapped microsphere is measured by analyzing the size of its defocused brightfield image as captured by the CCD camera using procedures similar to those described by Revyakin et al. (16) for magnetic tweezers. To measure the apparent sizes of the images, the geometric pattern matching function in LabVIEW is utilized to find the center of the image of the microsphere first. Then a radial intensity profile is obtained by averaging cross sections of the image over 360° around the center. The peak of the radial profile, which corresponds to the white ring in the brightfield images in Fig. 3, is then fit with a quadratic function, and the distance between this maximum and the center of the image is used as a measure for the apparent size of the image of the microsphere. To obtain a calibration curve, a microsphere that is stuck to the coverslip is initially placed ∼1 μm below the focus of the microscope objective to obtain a clear defocused image. This distance is then gradually increased using the calibrated piezoelectric microscope stage while additional images are acquired. From the analysis of these images, we construct the calibration curve that yields the apparent sizes of the images as a function of the axial positions of the microsphere, as shown in Fig. 3. The statistical error for each data point is 0.0045 pixels or 1.35 nm, as determined from the scatter between measurements in successive video frames. Despite this low noise, multiple calibration runs under nominally identical conditions result in a variation of the slopes of the measured microsphere sizes versus axial positions of as much as 5%. We attribute this systematic uncertainty in our calibration primarily to mechanical drifts in the system. These drifts cannot be compensated for by the autofocus feedback control system detailed below because the drift-induced change in the apparent sizes of the stuck microsphere cannot be measured correctly when the piezo-stage is moved axially during the calibration. In fact, the feedback control system has to be disabled temporarily to avoid interfering with the calibration. Nevertheless, since the calibration of the microsphere size versus axial position can be accomplished in <1 min, the effect of the slow drifts is not significant.

Figure 3.

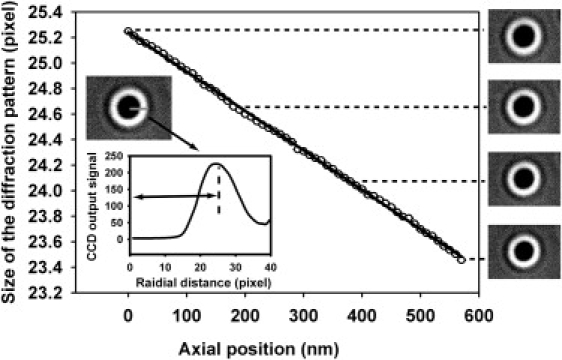
Calibration of the apparent size of defocused images as a function of the axial positions of the microsphere. During the calibration, the microsphere is gradually moved toward the microscope objective by a precision piezo-stage while video images are recorded. The size of the pattern is determined from the radial intensity distribution, as shown in the inset. The result shows that the apparent size of the image decreases linearly with the increasing distance between the microsphere and the objective.

Measuring the axial stiffness of the calibration trap

The purpose of measuring the axial stiffness of the calibration trap is to calibrate the optical force in the linear region of the optical potential created by the manipulation beam. Therefore, we measure the optical potential of the manipulation beam first to identify the axial position of the linear region, which will be detailed later. After the optical potential of the manipulation beam is mapped, the calibration trap is moved to the same height as the linear region of the manipulation beam by moving the telescope lenses, as shown in Fig. 4. Then, the axial stiffness of the calibration trap is measured while the manipulation beam is turned off. For this purpose, a free microsphere is trapped in the calibration trap, whose focus is located 0.98 μm above the coverslip. At this distance, electrostatic interactions with the surface can safely be disregarded, as the Debye screening length under our buffer conditions is ∼0.8 nm. The photodetector for the transmitted laser light is used to record the thermal motion of the microsphere in the axial direction. The autocorrelation of this signal is then computed and fit with a single exponential decay function to obtain the time constant τ_z of the fluctuations (10,17–19). For a typical laser intensity of 48 mW at the back aperture of the microscope objective, we find a time constant of 4.62 ± 0.09 ms. From this time constant and the friction coefficient of the microsphere ζ, the stiffness of the calibration trap is found as k_z = ζ / τ_z. The hydrodynamic friction coefficient of the microsphere is corrected for the proximity of the surface using the expansion by Brenner (20) and Neuman and Block (21):

$$\varsigma =6\pi \eta r\frac{4}{3}\sinh \alpha \sum _{n=1}^{\mathrm{\infty }}\frac{n\left(n+1\right)}{\left(2n-1\right)\left(2n+3\right)}\times \left[\frac{2\sinh \left(2n+1\right)\alpha +\left(2n+1\right)\sinh 2\alpha }{4{\sinh }^2\left(n+1/2\right)\alpha -{\left(2n+1\right)}^2{\sinh }^2\alpha }-1\right],$$ (1)

where

$$\alpha ={\cosh }^{-1}\left(\frac{h}{r}\right)=\ln \left\{\frac{h}{r}+{\left[{\left(\frac{h}{r}\right)}^2-1\right]}^{1/2}\right\},$$

ζ is the friction coefficient, r is the radius of the microsphere, h is the height of the center of the microsphere above a surface, η is the viscosity of the fluid, and 6πηr is the Stokes drag coefficient. Ten terms of Eq. 1 are used to obtain the friction coefficient ζ, given that the sum in Eq. 1 converges quite quickly.

Figure 4.

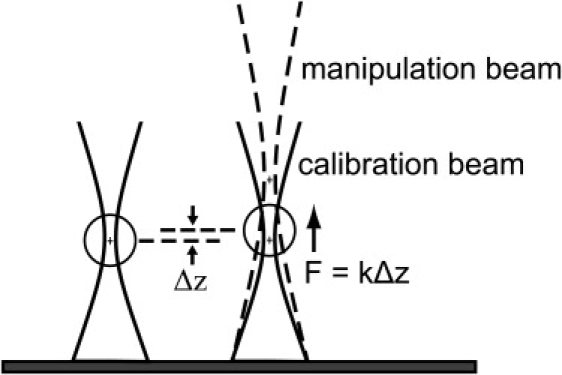
Mapping the optical potential. The manipulation beam (dashed lines) and the calibration beam (solid lines) are aligned laterally but have a different axial focus. First, a microsphere is trapped in the calibration trap of known stiffness k. When the manipulation beam is turned on, it exerts a small incremental force on the microsphere, which results in a displacement Δz. This displacement is measured for varying offsets between the axial foci of the two beams to map the potential of the manipulation beam as a function of axial position.

Under our experimental conditions, Eq. 1 represents a 77.5% correction to the Stokes drag coefficient in free solution, yielding a final value of 1.2 × 10⁻⁸ kg/s for the drag coefficient when the proximity of the surface is taken into account. The stiffness of the calibration trap is then 2.59 pN/μm. The most important uncertainty in this calibration is the aforementioned systematic error in the determination of the axial position of the microsphere, because the correction to the Stokes drag coefficient is not insignificant. The estimated 5% error in the measurement of the axial position results in an error of ∼4% in the calibration of the optical trap stiffness. An additional source of error stems from the temperature dependency of the viscosity of the buffer, which contributes an additional 1–2% to the overall calibration error. Overall, we estimate that we have an error of ∼6% in the calibration of the axial stiffness of the trap. It is worth noting that, when the height of the microsphere h is smaller, the friction coefficient ζ and thus the calculated stiffness k_z, are more sensitive to the change in h because the hydrodynamic proximity of the surface becomes more significant. In other words, it is more accurate to measure the stiffness with the microsphere at a higher position from the coverslip because the measurement is less sensitive to errors in the measurement of the trap height. On the other hand, any stiffness calibration should be made close to where the actual measurement takes place. Otherwise, changes in trap stiffness as a function of distance from the coverslip (12) dominate the overall error. The result of the tradeoff in accuracy is that we calibrate the trap stiffness of the calibration beam and map the optical potential of the manipulation beam 800–1000 nm above the coverslip, which is ∼300 nm higher than the position where tethered DNA molecules are manipulated.

Feedback control system for drift compensation

Like any microscope, our setup is subject to thermal and mechanical drifts that place time limits on precision measurements. To compensate for these drifts, we employ an autofocus feedback mechanism. In addition to the trapped object, we observe another microsphere that is laterally close to the optical trap but stuck to the coverslip by a secondary camera at a frame rate of 30 fps. Axial movement of the stuck microsphere with respect to the focal plane of the objective also reflects the drift experienced by a trapped microsphere with respect to the coverslip. Therefore, we continuously analyze the images captured by the secondary camera with a custom LabVEW program in real time to determine the changes in the apparent sizes of the images, which correspond to the drifts in the axial direction. Based on the magnitude and direction of the drift, a proportional-integral control loop generates an output voltage on the data acquisition card (PCI-6025E; National Instruments, Austin, TX), which in turn controls the position of the piezo-stage to cancel the drift. Therefore, the time of optical trapping is almost unlimited by drifts.

Results and Discussion

The demonstration and characterization of the constant-force optical tweezers consists of two parts: first, we carefully map the optical potential of the manipulation beam with the help of the calibration trap; second, we use the manipulation beam to stretch and hold a 1298 bp DNA fragment under constant tension.

Mapping the optical potential

To map the optical potential of the manipulation beam and calibrate the optical forces it exerts, we trap a free microsphere in the calibration trap. Then the collinearly aligned manipulation beam is turned on, which exerts an additional optical force on the trapped microsphere (19) (see Fig. 4). It is worth noting that for such a calibration measurement, the calibration trap needs to be substantially stronger than the manipulation beam. Typically, we use 48 mW at the back aperture of the objective for the calibration beam and intensities of up to 9 mW for the manipulation beam. The axial displacement of the microsphere in the calibration trap that results from the force exerted by the manipulation beam is measured by video analysis from the defocused brightfield image as described above. Under all circumstances in this study it was <170 nm and well within the range of our calibration.

To map the optical potential along the axis of the manipulation beam, we move one of the telescope lenses such that the focus of the calibration beam moves axially. Since the calibration beam is much stronger than the manipulation beam, the trapped microsphere mostly moves with the axial movement of the calibration beam focus, whereas the manipulation beam adds a small incremental displacement that is proportional to the manipulation force of interest, as shown in Fig. 4. This incremental displacement is determined as a function of axial position from a differential measurement of the microsphere position in the presence and absence of the manipulation beam. The center of the linear region of the manipulation beam is then determined as the position where the displacement is largest. We then move the calibration trap to the same height as the linear region and measure the stiffness of the calibration trap using the autocorrelation method described above. Using this calibration, we obtain the optical force of the manipulation beam as a function of the axial position as shown in Fig. 5 A. This yields the profile of the optical potential of the manipulation beam along the axial direction as shown in Fig. 5 B through integration.

Figure 5.

(A) Optical forces versus axial positions in the region below the laser focus. The solid lines show scaled predictions from the GLMT model. The experimental data show a constant-force region that is ∼330 nm deep, where the variation in force is <10%. The x axis shows the relative axial position with respect to the starting point of the measurement, which is ∼1500 nm blow the laser focus. (B) Optical potentials versus axial positions in the region below the laser focus, as obtained from an integration of the optical force shown in A along the axial direction. The linear region of the optical potential is clearly discernible.

The linear region of the optical potential is clearly discernible. If we define the constant-force region as the region over which the force varies by <10%, we can determine that the constant-force region extends for 330 nm in the axial direction. As expected, this constant-force region is longer than what Greenleaf et al. (8) reported for their lateral optical trap, given that the intensity distribution of a Gaussian beam is shallower in the axial direction than in the lateral direction. These results suggest that the linear region allows us to stretch a DNA molecule with an approximately constant force as long as the length of the DNA molecule changes by ∼1000 bp or less. Given that the change in DNA length upon protein binding is usually smaller, this region is long enough to study the effect of force on the interactions between proteins and DNA. In addition, this useful operating range dovetails nicely with where conventional optical micromanipulation become unusable in the submicron range, and allows the mechanical properties of shorter biomolecules to be studied.

During the course of these experiments, we noted that the exact location of the linear region changed slightly when the distance between the microscope objective and the coverslip is changed (data not shown). Specifically, we found that the linear region moved closer to the objective when the distance between the coverslip and the objective was shorter. This is consistent with reports by Deufel and Wang (12) and Neuman et al. (22), who reported that the laser focus moves closer to the microscope objective when the coverslip is moved toward the objective. The change in the optical potential is due to the spherical aberrations caused by the refractive index mismatch between the coverslip and the buffer solution in the chamber.

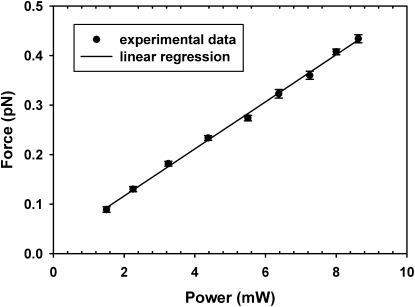
After the optical potential of the manipulation beam is characterized, we establish the relationship between laser power in the manipulation beam and optical force in the linear region, since this is how a varying desired force is applied in biomolecular stretching applications. For this purpose, we position the trapped microsphere at the center of the linear region of the optical potential. We then measure the displacements of the microsphere as a function of laser intensity to obtain the desired force calibration, as shown in Fig. 6. The observed linear relationship between laser power and optical force also confirms that the microsphere is indeed placed in the linear region of the optical potential.

Figure 6.

Optical force calibration. The optical force changes linearly with the laser intensity. The error bars show the mean ± standard error (SE) obtained from 11 independent measurements. For each measurement, 400 image frames were acquired at a frame rate of 100 fps for nine different laser intensities. The bandwidth of the measurements is limited by the thermal fluctuations of the trapped microsphere to ∼0.1 s.

Under these experimental conditions, we estimate that the absolute measurement of the optical force is accurate to within 10%, as systematic errors arise mostly from the measurement of the axial positions and the calibration of the axial stiffness. We note, however, that relative measurements, such as comparisons of the elasticity of two different DNA molecules, can be accomplished with considerably higher accuracy because of the outstanding linearity of the power-force relationship in Fig. 6, as long as the microsphere remains within the linear region of the optical potential. If, on the other hand, the microsphere leaves this linear region due to errors in the initial alignment or exceedingly large changes of the extension of the molecule, errors in excess of the 10% calibration error may result.

To quantitatively model our experiment, we use the generalized Lorenz-Mie theory (GLMT) to solve Maxwell's equations for scattering by particles of arbitrary size (23,24). The force acting on the particle in the axial direction using GLMT is given by (23,24):

$$\begin{array}{l}{F}_Z=\frac{n_m}{c}{I}_m{C}_{pr,z}\\ =\frac{n_m}{c}\frac{2P}{\pi {\varpi }_0^2}{C}_{pr,z},\end{array}$$ (2)

where

$$C_{pr,z}=\frac{{\lambda }^2}{2\pi }\sum _{n=1}^{\mathrm{\infty }}\left\{\begin{array}{l}\frac{2n+1}{n\left(n+1\right)}{\left|g_n\right|}^2\mathrm{Re}\left(a_n+b_n-2a_n{b}_n^{\ast }\right)\\ +\frac{n\left(n+2\right)}{n+1}\mathrm{Re}\left[g_n{g}_{n+1}^{\ast }\left(a_n+b_n+a_{n+1}^{\ast }+b_{n+1}^{\ast }-2a_n{a}_{n+1}^{\ast }-2b_n{b}_{n+1}^{\ast }\right)\right]\end{array}\right\}\text{.}$$

I_m is the intensity at the focus; n_m is the refractive index of the medium; c is the speed of light in vacuum; P is the beam power; ω₀ is the beam waist; C_pr,z is the cross section for radiation pressure; a_n and b_n are Mie coefficients, which are functions of the size and refractive index of the microsphere; and g_n are beam-shape coefficients. To solve Eq. 2, we used the Optical Tweezers Computational Toolbox of Nieminen et al. (25), using P = 0.25 mW; refractive indices of n_m = 1.33 and n_p = 1.59 for the medium and the particle, respectively; and an effective numerical aperture of 1.4. Qualitatively, the results agree with our experiments and show the approximately linear region of the optical potential that we are using for optical force-clamping. Because of uncertainties in some of our parameters, such as the infrared transmission of the microscope objective and the actual laser beam profile, the results of the GLMT calculation were linearly scaled by a factor of 4.0 to fit the experimental data. These fitted force and potential curves are shown together with the experimental data in Fig. 5.

Stretching a short DNA molecule

With the force calibration in hand, we measure the force-extension relationship of a 1298 bp long ds-DNA, as shown in Fig. 7, following in the footsteps of similar experiments for longer molecules with contour lengths of 32.8 μm (26), 1.3 μm (27), and 0.6 μm (28). For this purpose, we position the manipulation beam above a DNA-tethered microsphere such that the microsphere is at the beginning of the linear region of the potential when the DNA is not extended by an external force.

Figure 7.

Force-extension curve of a 1298 bp long ds-DNA molecule and a fit to the WLC model. The error bars show the mean ± SE obtained from four independent measurements. In each measurement, 400 frames were taken at a frame rate of 100 fps for each force point. The entropic force resulting from the volume-exclusion effect is taken into account in the fitted curve as an offset at zero optical force. This zero-force extension of 79.9 nm corresponds to an excluded-volume force of 36.7 fN.

To assure ourselves that we are indeed in the correct position, we adjust the axial position of the coverslip with respect to the objective first and then adjust the axial position of the focus of the manipulation beam, using one of the motorized telescopes until the DNA molecule is within the linear region, which is apparent when the extension of the DNA is least sensitive to the motion of the telescope. With this alignment in place, we determine the relationship between the optical force and the extension of the DNA molecule by varying the intensity of the manipulation beam.

It is important to note that the average extension of the DNA in the absence of any external optical force is not zero. This residual entropic stretching force results from volume-exclusion effects due to the proximity of the DNA and the tethered microsphere to the coverslip, which they cannot penetrate. Theoretical and computational analyses by Segall et al. (29) show that the volume-exclusion effect between the tethered microsphere and the coverslip becomes more significant with increasing excursion number N_R ≡ R / (Ll_p/3)^1/2, which is a function of the radius R of the microsphere, the contour length L of the DNA molecule, and its persistence length l_p. They suggest that under the Gaussian-chain approximation, the effective force resulting from excursions can be estimated by

$$\langle F_{eff}\rangle =\frac{k_{b}T}{{\pi }^{1/2}{\left(L{l}_p/3\right)}^{1/2}}\left(\frac{1-e^{-N_R^2}}{erf\left(N_R\right)}\right),$$ (3)

Since this excluded-volume force is difficult to measure directly with sufficient accuracy, we incorporate the corresponding excluded-volume extension x₀ as an adjustable parameter into fits of the data to the worm-like chain (WLC) model as approximated by Marko and Siggia (30) for an extended polymer. The total force acting on the DNA is thus

$$F_{opt}+F_{WLC}(x_0,l_p,L)=F_{WLC}(x_0+x_{opt},l_p,L),$$ (4)

where F_opt is the optical force exerted by the manipulation beam, x₀ is the extension under zero optical force, and x_opt is the incremental extension of the molecule under optical force. F_WLC (x, l_p, L) is the force of an extended polymer in the WLC model:

$$F_{WLC}=\left(\frac{k_{B}T}{l_p}\right)\left[\frac{1}{4{(1-x/L)}^2}-\frac{1}{4}+\frac{x}{L}\right]\text{.}$$ (5)

Using the crystallographic axial rise of ds-DNA of 0.34 nm/bp, we fix the contour length of our DNA at 441 nm. Leaving the persistence length and the excluded-volume extension as adjustable parameters, we find l_p = 33.9 nm and x₀ = 79.9. The extension of 79.9 nm corresponds to an excluded-volume force of 36.7 fN, compared with 33 fN estimated by Eq. 3. In addition, the persistence length of 33.9 nm is significantly smaller than generally accepted values of ∼50 nm, as determined in several single-molecule experiments (27,30–32).

Fits to an improved WLC model proposed by Bouchiat et al. (32) did not appear to improve the accuracy or change the results of our measurements significantly, because the added higher-order terms decreased the numerical stability of the fitting algorithm significantly. According to Bouchiat et al., the persistence length obtained from the fit to Marko and Siggia's WLC model (30) typically overestimates the persistence length by at most ∼5% for our range of extensions. Given that the uncertainty in our calibration is ∼10%, the error in the persistence length due to the Marko-Siggia approximation is comparatively small.

Seol et al. (28) provide a different explanation for the discrepancy in the persistence length from the literature value. They suggest that when the elasticity of ds-DNA is analyzed within the framework of the WLC model, the effective value for the persistence length is not fully independent of the contour length of the molecule. In fact, they report a reduction of >10% in the persistence length for a molecule with a contour length of <1.3 μm. More specifically, the persistence lengths of their 864-nm, 756-nm, 666-nm, and 632-nm DNA molecules, which are their four shortest DNA molecules, are 44 nm, 43 nm, 42.4 nm, and 42.1 nm, respectively, as estimated from Fig. 9 of Seol et al. (28). They attribute the decrease of the effective persistence length with the contour length of DNA to the lack of considerations of finite chain length, chain-end boundary conditions, and the microsphere rotational fluctuations inherent in optical trapping assays. To describe this finite-length effect, they suggest scaling the persistence length as

$$l_p=\frac{l_{p\mathrm{\infty }}}{1+a{l}_{p\mathrm{\infty }}/L},$$ (6)

with l_p∞ = 51.51 nm and an empirical parameter a = 2.78. For our molecule with a contour length L of 441 nm, which is shorter than those used by Seol et al. (28), Eq. 6 yields an effective persistence length of 38.8 nm, which is close to our experimental result of 33.9 nm, considering that we have a systematic error of ∼5% in the measurement of molecular extensions.

Conclusions

We have demonstrated and characterized a novel protocol for applying optical tweezers to manipulate submicron biomolecules. The attached microsphere is pulled away from the coverslip, reducing unwanted artifacts from steric hindrances and other surface effects. The use of a combination of optical gradient forces and backscattering forces allows the application of a constant optical force that is independent of the extension of the molecule.

We applied this method to measure the force-extension relationship of a 1298 bp ds-DNA molecule, and found that its elastic behavior is well described by the WLC model of Marko and Siggia (30) when excluded-volume effects from the proximity of the coverslip are taken into account and the persistence length is corrected for finite-length effects as proposed by Seol et al. (28).