Coefficients for Active Transport and Thermogenesis of Ca²⁺-ATPase Isoforms

Abstract

Coefficients for active transport of ions and heat in vesicles with Ca²⁺-ATPase from sarcoplasmic reticulum are defined in terms of a newly proposed thermodynamic theory and calculated using experiments reported in the literature. The coefficients characterize in a quantitative manner different performances of the enzyme isoforms. Four enzyme isoforms are examined, namely from white and red muscle tissue, from blood platelets, and from brown adipose mitochondria. The results indicate that the isoforms have a somewhat specialized function. White muscle tissue and brown adipose tissue have the same active transport coefficient ratio, but the activity level of the enzyme in white muscle is higher than in brown adipose tissue. The thermogenesis ratio is high in both white muscle and brown adipose tissue, in agreement with a specific role in nonshivering thermogenesis. Other isoforms do not have this ability to generate heat. A calcium-dependence of the coefficients is found, which can be understood as being in accordance with the role of this ion as a messenger in muscle contraction as well as in thermogenesis. The investigation points to new experiments related to structure as well as to function of the isoforms.

Introduction

The Ca²⁺ transport by the Ca²⁺-ATPase has been studied under numerous conditions since the pioneering work of Hasselbach and co-workers (1,2). A surprising property of the pump, first documented by de Meis and co-workers (3–9), and supported by others (10,11), is its ability to also transport heat. This property opens several new questions on the physiological role of the pump. For instance, does it also have a role in nonshivering thermogenesis, and if so, can we allocate this function to particular isoform(s) of the pump? This question was first raised by De Meis and co-workers. It is an aim of this article to add to this discussion.

There are different isoforms expressed by the pump, often in cells from the same tissue (12,13). The SERCA 1 isoform is mainly expressed in fast-twitch skeletal muscle cells, but is also expressed in brown adipose tissue (BAT). The structure of this isoform is known in amazing detail (14). Cells of red muscles express both SERCA 1 and SERCA 2a isoforms. The SERCA 2b and SERCA 3 isoforms are expressed in cells of nonmuscular tissues such as blood platelets (15). There are two different fractions in sarcoplasmic reticulum: the light fraction, enriched in SERCA 1; and the heavy fraction, which contains both SERCA 1 and the ryanodine channel, a membrane pathway for calcium efflux (12).

Skeletal muscle and BAT are both tissues that produce heat, by so-called nonshivering thermogenesis, when called upon to do so by thermal stresses imposed on the animal from the outside (16). BAT might for instance contribute as much as 60%–70% of the total metabolic heat production in reindeer calves, when summit metabolism is required (17). Some of this heat production is aerobic, caused by the uncoupling protein. However, the abundance of Ca²⁺-ATPase in BAT, may point to a role in heat generation also for this enzyme, in addition to the role played by the uncoupling protein.

The existing isoforms may not have the same role in thermogenesis. Animals that are exposed to cold over a long period will experience that shivering is progressively replaced by nonshivering thermogenesis. At the same time, the amount of SERCA 1 isoform increases (18). It has been observed that the heat released during pump operation varies with the isoform and the solution composition. Furthermore, a positive heat release in the forward mode of operation can be turned into a negative heat effect in the reverse mode of operation (4). The heat transport also seems to be reversible.

By using the theory of mesoscopic nonequilibrium thermodynamics, we have been able to derive equations that describe the active ion transport and the accompanying heat transport in Ca²⁺-ATPase (19,20). The equations describe an activated chemical reaction and activated ion transports. They represent an extension of classical nonequilibrium thermodynamics (21,22). The heat effects that accompany the processes in the enzymatic cycle can thus be given a thermodynamic basis.

Having established a theoretical basis, the next stage is to show the value of the theory at work. This is the aim of this article. We shall apply the theory developed in the previous articles (19,20), to actual cases, and explain how meaningful transport coefficients can be defined and obtained from experiments. We shall continue to look at active transport by the Ca²⁺-ATPase, drawing heavily on the experiments of de Meis and co-workers (3–9). Our aim is to compare the performance of different isoforms during their initial state of operation as a pump, using this theory.

A short description of the system and processes is first given. We summarize the flux-force relations and the assumptions used to derive them (20). Sets of experimental results (3–9) are then used to calculate the fluxes and forces for several isoform experiments, and the transport coefficient are determined and discussed. The results point to a functional specialization among the isoforms.

Vesicles and Coupled Processes

The catalytic cycle of Ca²⁺-ATPase involves at least four different processes of energy conversion: Coupled and uncoupled ATP hydrolysis and coupled and uncoupled calcium efflux. In this context, “coupled” means that the process interacts with at least one other process, whereas “uncoupled” means lack of such interaction. The purpose of this work is to demonstrate a possibility to quantify such interactions.

Experiments on energy conversion in the catalytic cycle have been carried out on vesicles derived from the sarcoplasmic or endoplasmic reticulum of several tissues like rabbit white and red muscle, rat BAT, and human blood platelets (23). The spontaneous process in experiments that start with empty vesicles, is coupled ATP hydrolysis, or active transport.

Calcium transport is a function of the concentration of essential chemical species in the medium where the vesicles are suspended. Free Ca²⁺, ATP, ADP, K⁺, inorganic phosphate (Pi), Mg²⁺, and pH, and functional compounds (thapsigargin, caffeine, ruthenium red, and ATP regenerating compounds) are compounds that affect the transport. It depends also on the SERCA isoform as expressed in various tissues (SERCA 1, SERCA 2a and 2b, SERCA 3) (4,24,25). In this work, we examine the initial state uptake of Ca²⁺, as a function of Ca²⁺-concentration in various isoforms, keeping all other concentrations constant. The transport coefficients derived under these special conditions apply more generally, however.

The driving forces for transport stem from lack of equilibrium in essentially two reactions, to be discussed. In the presence of a significant heat flux, there may in addition be a temperature gradient across the vesicle membrane, see the section on the thermodynamic basis.

The driving force for active transport of Ca²⁺ into vesicles against its chemical potential, derives from the reaction of ATP and water to ADP and Pi:

$$\text{ATP}+{\text{H}}_2\text{O}\leftrightharpoons \text{ADP}+\text{Pi}\text{.}$$ (1)

Component charges are not indicated, as is common when writing biological reactions (26). The Gibbs energy change of the reaction is Δ_rGⁱ, where letter i refers to the phase external to the vesicles (the assay medium). The rate of reaction, r, is given by the rate of formation of ADP.

Water is consumed on the i-side in this reaction. We expect that a possible osmotic difference created by process (1) leads to fast reequilibration of water across the vesicle membrane:

$${\text{H}}_2\text{O}\left(\text{o}\right)\leftrightharpoons {\text{H}}_2\text{O}\left(\text{i}\right)\text{.}$$ (2)

The letter o indicates the vesicle interior, whereas i indicates the phase external to the vesicles. This reaction shall be taken to be at equilibrium.

There are two binding sites for Ca²⁺ in the Ca²⁺-ATPase. The flux of Ca²⁺ divided by r gives the number of Ca²⁺ ions transported per turnover of ATP. This number is characteristic for each SERCA and each experimental situation. A number of 2 has only been measured when the experimental conditions ensure a low calcium concentration on the vesicle inside (27). Evidence has accumulated over the last years that protons move simultaneously in the opposite direction of Ca²⁺ (28–31). According to Obara et al. (28), 2–3 H⁺ are transported per 2 Ca²⁺ across the pump, possibly associated with water equilibration in process (2). The total exchange of ions that accompany ATP hydrolysis must be electroneutral in the absence of respiration (no electric work is done), and protons may also use other paths than that across the enzyme (31). We assume therefore, in agreement with Fibich et al. (32), that the reaction relevant to energy conversion is

$${\text{Ca}}^{2+}\left(\text{i}\right)+{2\text{H}}^{+}\left(\text{o}\right)\leftrightharpoons {\text{Ca}}^{2+}\left(\text{o}\right)+2{\text{H}}^{+}\left(\text{i}\right)\text{.}$$ (3)

The Gibbs energy change of the exchange reaction is Δμ_Ca/2H = μ^o_Ca/2H – μⁱ_Ca/2H, where we have used the abbreviation μ^l_Ca/2H = μ^l_Ca − 2μ_H^l for l = i or o. In experiments, the solutions are always buffered and vesicles are leaky to protons, so the osmotic force has only one contribution from the difference in Ca²⁺ between the vesicle interior and exterior. We can then refer to the osmotic force by the Ca²⁺-gradient only. We shall keep on using Δμ_Ca/2H for the sake of precision. Hydrolysis of ATP without calcium transport has been documented only for the SERCA 1 isoform (33).

ATP-synthesis by calcium transport is referred to as coupled calcium efflux. A passive leak of calcium from the vesicle inside to the assay medium through the Ca²⁺-ATPase, so-called uncoupled calcium efflux, can also take place. The processes (1–3), as well as the accompanying heat production, can be reversed as mentioned already (1,2,34): Hydrolysis of ATP can drive Ca²⁺-uptake, but Ca²⁺-efflux can also drive synthesis of ATP. Likewise, during ATP hydrolysis, there is a positive heat production in an adjacent calorimeter, which is turned negative during synthesis.

Thermodynamic Basis

Practical flux equations

De Meis and co-workers reported sets of simultaneous measurements of the initial rates of the following variables: Ca²⁺-uptake, ATP hydrolysis and calorimetric heat production or absorption (see Table S1 in Supporting Material). In the theoretical analysis of the experimental situation, it was suitable to divide the system into three subsystems plus surroundings (see Fig. S2):

• 1.The solution external to the vesicles indicated by i in Fig. S2. The reactants and products as well as Ca²⁺ change their concentration in this subsystem after a spontaneous process is initiated.
• 2.The vesicle membranes containing all Ca²⁺-ATPases indicated by s. During a steady-state process, there are no material changes in the membrane: Ca²⁺-ion is coming in from the left, but is leaving to the right at the same rate. Reactants are coming in, but are used in the reaction in Eq. 1 and disappear from this subsystem.
• 3.The vesicles interior indicated by o. In this subsystem, Ca²⁺ can accumulate. When the membrane is made leaky to Ca²⁺, the vesicle interior chemical potential is the same as the exterior chemical potential.

The calorimeter represents the surroundings to the total of the three subsystems. It can supply or receive heat to/from the solution in which the vesicles are suspended, as illustrated on the left side of the figure. We define as positive direction of transport, a flux directed into the vesicle membrane. This occurs jointly with r > 0 in the hydrolysis of ATP.

According to the second law of thermodynamics, the entropy production determines the conjugate fluxes and forces. Caplan and Essig (21) gave the entropy production, σ, for an isothermal system with active transport,

$$\sigma =-r\frac{{\Delta }_{\text{r}}{G}^{\text{i}}}{T^{\text{i}}}-J_{\text{Ca}}\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}}{T^{\text{i}}}>0,$$ (4)

where Tⁱσ > 0 is the energy dissipated at Tⁱ in the ATPase, and the external and internal solutions to the vesicles. The driving forces based on σ, are the chemical driving force (minus the Gibbs energy change of the hydrolysis reaction equation (Eq. 1) divided by the temperature, −Δ_rGⁱ/Tⁱ), and the osmotic driving force, (minus the Gibbs energy change of the ion exchange equation (Eq. 2) divided by the temperature, −Δμ_Ca/2H/Tⁱ). The conjugate fluxes are the reaction rate, r, and the net rate of Ca²⁺-uptake, J_Ca.

Because vesicles produce heat (3–9), Kjelstrup and Bedeaux (19,20) added a thermal force and flux to the entropy production, giving

$$\sigma =-r\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{T^{\text{o}}}-J_{\text{Ca}}\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{T^{\text{o}}}+J_{\text{q}}^{\prime \text{i}}(\frac{1}{T^{\text{o}}}-\frac{1}{T^{\text{i}}})>0\text{.}$$ (5)

The driving forces were now the chemical driving force, the osmotic driving force and a thermal driving force, respectively. These forces all referred to the temperature of the vesicle inside, T^o, as a consequence of choosing the heat flux into the membrane, J′_qⁱ, as the heat flux conjugate to the thermal driving force (see (20) for the derivation). The fluxes J′_qⁱ and J_Ca are illustrated in Fig. S2.

The linear flux-force relations that can be derived from Eqs. 4 or 5 directly do not describe activated transports like chemical reactions. This led us to introduce two internal variables, namely the degree of reaction (γ_r) and the degree of Ca²⁺-ion transfer (γ_d) (20). The transport of Ca²⁺ by the Ca²⁺-ATPase takes place on the millisecond scale, with a high activation energy for the overall process (35). The barrier is illustrated in Fig. S1. In such a situation, one must move from a description where the forces are differences between the beginning and the end state, to a mesoscopic description that is continuous. This was done using the coordinates (γ_r, γ_d) (see (20) for detailed explanations, and the Supporting Material for a short one). By integrating over the internal coordinates, Bedeaux and Kjelstrup (20) found the following nonlinear flux-force relations:

$$\begin{array}{c}r=-D_{\text{rr}}\left[1-\exp \left(-\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]+D_{\text{rd}}\left[1-\exp \left(\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]-\frac{D_{\text{rq}}^{\prime }}{R{T}^{\text{i}}}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\\ J_{\text{Ca}}=-D_{\text{dr}}\left[1-\exp \left(-\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]+D_{\text{dd}}\left[1-\exp \left(\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]-\frac{D_{\text{dq}}^{\prime }}{R{T}^{\text{i}}}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\\ J_{\text{q}}^{\prime \text{i}}=-D_{\text{qr}}^{\prime }\left[1-\exp \left(-\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]+D_{\text{qd}}^{\prime }\left[1-\exp \left(\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]-D_{\text{qq}}^{\prime }\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\end{array}\text{.}$$ (6)

The forces were made dimensionless, to enable a comparison of variables. The coefficients D_rr, D_dd, D_rd, and D_dr, have the dimension of the mass flux (nmol/mg min), and the coefficients with a prime obtain the dimension of the heat flux (mJ/mg min). The prime indicates that a coefficient relates to the measurable heat flux.

The coefficients on the diagonal of the matrix are the main coefficients. They refer to: diffusion across the activation barrier for the reaction, D_rr; diffusion for ion exchange, D_dd; and diffusion for heat transport, D′_qq.

The coupling coefficients outside the diagonal are of two types. The coupling coefficients D_rd and D_dr give information on the active transport (the transport of Ca²⁺-ions against their chemical potential (D_rd), or the hydrolysis rate due to a Ca²⁺-gradient (D_dr)), and will be termed the coefficients for active transport.

Of the four remaining coefficients, the first two describe the isothermal heat production by the reaction (D′_qr) and by the ion exchange (D′_qd), and last two describe the reaction rate (D′_rq) and the calcium flux (D′_dq) that are triggered by temperature drops in the system. We shall call them coefficients of thermogenesis, for reasons to be explained below.

The coefficients, according to theory, do not depend on the values of the forces or fluxes (36). They may depend on the state variables, i.e., the concentrations and the temperature. Onsager relations apply in γ-coordinate space, whereas the coefficient set becomes asymmetric after the integration. Bedeaux and Kjelstrup (20) gave the detailed relationships. The coefficients D_ij can be used to characterize the function of the Ca²⁺-ATPase. Though not equal, the coefficients D_ij and D_ji have the same sign.

We show here how these flux equations can be used to determine coefficients for heat and ion transport. We shall see how experimental results found in the literature can be interpreted, and propose experiments to test the theory. We shall see that the coefficients can be used to characterize the isoforms. The near-equilibrium situation and the case of a stoichiometric pump are useful limiting cases that need to be considered first.

Near global equilibrium

Stoichiometric pumps

In the presence of small driving forces, the fluxes (6) reduce to

$$\begin{array}{c}r=-D_{\text{rr}}^0\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-D_{\text{rd}}^0\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-\frac{D_{\text{rq}}^{\prime 0}}{R{T}^{\text{i}}}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\\ J_{\text{Ca}}=-D_{\text{dr}}^0\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-D_{\text{dd}}^0\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-\frac{D_{\text{dq}}^{\prime 0}}{R{T}^{\text{i}}}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\\ J_{\text{q}}^{\prime \text{i}}=-D_{\text{qr}}^{\prime 0}\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-D_{\text{qd}}^{\prime 0}\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}-D_{\text{qq}}^{\prime 0}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\end{array}\text{.}$$ (7)

Superscript 0 is used to denote that the equations apply near global equilibrium. Equation 7 applies when the conditions on the two sides of the membrane are similar, so the coefficients, $D_{\text{ij}}^0$, refer to the average composition and temperature. This coefficient set becomes symmetric (20),

$$D_{\text{ij}}^0=D_{\text{ji}}^0,$$ (8)

for i, j = r, d, q. These coefficient relations may serve as first estimates to coefficients for the nonlinear regime. By disregarding the heat flux and the thermal driving force, one obtains the flux-forces relations given originally by Kedem and Katchalsky (37). In the presence of sugar phosphates, the ATP concentration is low. It may still be sufficient to drive the uptake of calcium ions. The ATP hydrolysis reaction is then close to equilibrium (4,25). This situation might well be described by the expressions in Eq. 7.

When the ratio J_Ca/r equals 2, the pump is said to be stoichiometric. If this flux ratio applies for all driving forces, we can combine the two first terms in the expression for the entropy production from Eq. 5, and obtain one effective driving force for active transport. The following relations apply (21):

$$D_{\text{dd}}{/2=D}_{\text{rd}}\text{and}{D}_{\text{dr}}=2D_{\text{rr}}\text{.}$$ (9)

If this system is nonisothermal, the following relation also applies:

$$D_{\text{dq}}^{\prime }=2D_{\text{rq}}^{\prime }\text{.}$$ (10)

The relations from Eqs. 9 and 10 can be used to give upper boundaries for the coefficients:

$$D_{\text{dd}}\le 4D_{\text{rr}},D_{\text{dr}}\le 2D_{\text{rr}},D_{\text{dq}}^{\prime }\le 2D_{\text{rq}}^{\prime }\text{.}$$ (11)

A flux ratio of 2 has only been observed during the initial few milliseconds of reaction (27).

Transport Coefficients

We show here how all transport coefficients in the expressions in Eq. 6 can be determined. We define first the main coefficients. A definition of the coupling coefficients for active transport and thermogenesis follows. In each case, we show how experiments with vesicles can lead to coefficient values. After a discussion on how to do the experiments, we proceed to use existing data to calculate some of the coefficients.

The coefficient D_rr for diffusion of the reaction across an activation energy barrier

The main coefficient, D_rr, characterizes the transformation of reactants to products over the activation enthalpy barrier, i.e., along the coordinate γ_r in Fig. S1. The definition

$$D_{\text{rr}}=-{\left[\frac{r}{1-\exp \left(-{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)/R{T}^{\text{o}}\right)}\right]}_{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0,\Delta T=0}$$ (12)

shows that the osmotic driving force and the thermal driving force must be zero in the experiment. This condition can apply to experiments with leaky vesicles, but also to initial states of hydrolysis in intact vesicles, before significant ion- or temperature gradients have been built. In both cases, Δμ_Ca/2H(T^o) = 0 and ΔT = 0. The coefficient obtains the same dimension as the reaction rate. A common unit is nmol/mg min.

The upper-left corner in the matrix of fluxes and forces in Eq. 6 represents the law of mass action. To see this, consider a first-order reaction where $\mathrm{A}\rightleftharpoons \mathrm{B}$. From reaction kinetics the reaction rate is r = k_fc_A – k_bc_B, where k_f and k_b are rate constants for the forward and reverse reactions, respectively. The (dimensionless) concentration of each component can be expressed in terms of its activity and chemical potential as c_i/c⁰ = a_i = exp [(μ_i – μ_i⁰)/RT]. The rate is then also equal to r = −k_b exp([μ_B – μ_B⁰]/RT)[1 − exp(Δ_rG/RT)], or

$$r=-r_0[1-\exp \left(-{\Delta }_{\text{r}}{G}^{\text{i}}/RT\right)],$$ (13)

where r₀ is the equilibrium exchange reaction rate. When compared with the upper-left corner of Eq. 6, we have D_rr = r₀.

This insight provides us with two extra ways to determine D_rr. Firstly, we can find r₀ from isotope exchange studies of the reaction at chemical equilibrium in the presence of the enzyme. In that case, when Δ_rGⁱ = 0, we have r_f = r_b = r₀. We can also write

$$r=r_{\text{f}}-r_{\text{b}}=-r_{\text{b}}\left[1-\frac{r_{\text{f}}}{r_{\text{b}}}\right]\text{.}$$ (14)

A comparison with Eq. 13 allows us to make the identification

$$\frac{r_{\text{f}}}{r_{\text{b}}}=\exp \left(-{\Delta }_{\text{r}}{G}^{\text{i}}/RT\right)$$ (15)

and

$$D_{\text{rr}}=r_0=r_{\mathrm{b}}\text{.}$$ (16)

The coefficient has, as follows from the law of mass action, as well as from the nonequilibrium thermodynamics, an Arrhenius-type behavior. Unidirectional rates and rate ratios are frequently measured with good precision. They can therefore be used to give both D_rr and Δ_rGⁱ, as discussed above. Care must be taken to avoid conditions where the osmotic driving force is large.

The coefficient D_dd for exchange of Ca²⁺ across the activation energy barrier

The diffusion coefficient D_dd is defined from the flux equation (second expression in Eq. 6). It describes interdiffusion of Ca²⁺ and 2H⁺ at chemical and thermal equilibrium:

$$D_{\text{dd}}={\left[\frac{J_{\text{Ca}}}{\left[1-\exp \left(\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)/R{T}^{\text{o}}\right)\right]}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta T=0}\text{.}$$ (17)

Efflux must be measured in the absence of chemical and thermal forces. When Δμ_Ca/2H is small, the exponential term can be expanded, and the determination becomes similar to that of a regular diffusion experiment:

$$D_{\text{dd}}=-{\left[\frac{J_{\text{Ca}}R{T}^{\text{o}}}{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta T=0}\text{.}$$ (18)

In the absence of Pi and ADP, there is no ATP hydrolysis or synthesis, and also no heat released or absorbed in the calorimeter (4). Calcium efflux can also be measured under such conditions.

Situations with zero calcium transport are excluded for determination of D_dd. But similar to the situation for D_rr, alternatives exist. We can use the equilibrium exchange rate for Ca²⁺ as an estimate of D_dd. Similar to Eq. 16, the reverse reaction may give an estimate for D_dd, when the chemical force is negligible. Under efflux conditions, the reverse reaction corresponds to the influx:

$$D_{\text{dd}}\approx J_{\mathrm{Ca},\mathrm{b}}\text{.}$$ (19)

Exchange rates for Ca²⁺ were measured by de Meis and co-workers in many experiments (4,6,8,9). These exchange rates were obtained with Δ_rG ≠ 0, however, and do not obey the criteria given by Eq. 18.

The coefficient D_qq for heat transfer across the membrane

The main transport coefficient that belongs to the heat flux is the thermal conductivity

$$D_{\text{qq}}^{\prime }=-{\left[\frac{J_{\text{q}}^{\prime \text{i}}}{\left(1-T^{\text{i}}/T^{\text{o}}\right)}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0}\text{.}$$ (20)

Heat is here transported due to a temperature difference, and not because of active transport, because the chemical and osmotic forces are both zero in the experiment.

The heat flux is measured in J/mg min (one assumes that the surface area of the vesicle is proportional to the amount of enzyme embedded in the membrane). The dimension of D_qq is thus also J/mg min. In reality, heat will leak across the protein but also across other parts of the vesicle membrane. In terms of Fourier's law, we have for a layer of thickness δ,

$${\left[\frac{J_{\text{q}}^{\prime \text{i}}}{\left(T^{\text{o}}-T^{\text{i}}\right)}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0}=-\frac{h}{\delta },$$ (21)

where h is the conductivity of the layer. An estimate for D′_qq can and will therefore be obtained from

$$D_{\text{qq}}^{\prime }=T^{\text{o}}\frac{h}{\delta }\text{.}$$ (22)

Although it is possible to compute the heat flux from experimental data, it may be difficult to measure a temperature difference.

Two coefficients of active transport, D_dr and D_rd

The coefficient D_dr describes Ca²⁺-transport by the chemical driving force and the coefficient D_rd describes chemical reaction by the osmotic driving force. Both coefficients characterize active transport. From the flux equations, we have

$$\begin{array}{l}{\left[\frac{J_{\text{Ca}}}{r}\right]}_{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0,\Delta T=0}=\frac{D_{\text{dr}}}{D_{\text{rr}}}\\ {\left[\frac{r}{J_{\text{Ca}}}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta T=0}=\frac{D_{\text{rd}}}{D_{\text{dd}}}\end{array}\text{.}$$ (23)

The driving force, Δ_rGⁱ(T^o), may change during an uptake experiment. The coefficients D_dr and D_rd may therefore best be determined from the ratio of fluxes in the initial uptake phase, once D_rr and D_dd are known. The two coefficients must be positive to explain active transport (38). Near global equilibrium, the coefficients are the same, because Onsager relations apply. They may not be the same when |ΔGⁱ| << RT^o.

The flux ratio (23a), without conditions Δμ_Ca/2H(T^o) = 0, ΔT = 0, has been called the stoichiometry of the pump. According to de Meis and co-workers (4,5), a ratio equal to 2 can be measured only under special conditions. These are during initial stages of uptake and in the presence of a calcium buffer inside the vesicle, conditions which may obey Δμ_Ca/2H(T^o) = 0. The approximation Δμ_Ca/2H(T^o) = 0 can be good in the start of the uptake experiment. Away from this condition, any value smaller than 2 may be expected.

The coefficient D_dr can also be defined by

$$D_{\text{dr}}=-{\left[\frac{J_{\text{Ca}}}{1-\exp \left(-{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)/R{T}^{\text{o}}\right)}\right]}_{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0,\Delta T=0}\text{.}$$ (24)

The subscripts again mean that the experiment refers to the initial phase of ion uptake, when osmotic or thermal driving forces have not yet formed or are negligible.

Four coefficients of thermogenesis, D′_qr, D′_qd, D′_rq, and D′_dq

Coefficients that describe this heat production under isothermal conditions can now be defined. The origin of the heat production is the chemical or the osmotic force in the system. The coefficients D′_qr and D′_qd describe this heat production.

Additionally, a reaction rate and ion uptake can be triggered by a temperature jumps, via the coefficients D′_rq and D′_dq. The heat flux promoted by D′_qr or D′_qd is reversible, since it flows without a thermal driving force. The heat flux can be reversed by changing the direction of the other forces. This is why we can associate these four phenomena with nonshivering thermogenesis (see the end of this section). A logical name for the coefficients is, therefore, coefficients of thermogenesis.

The first-mentioned thermogenesis coefficients use the heat flux into the membrane from the assay medium in their definition. At isothermal conditions, with a zero osmotic force, but with a nonzero chemical driving force, we have

$$D_{\text{qr}}^{\prime }=-{\left[\frac{J_{\text{q}}^{\prime \text{i}}}{1-\exp \left(-{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)/R{T}^{\text{o}}\right)}\right]}_{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0,\Delta T=0}\text{.}$$ (25)

Similar to the situation for D_dr, the coefficient D′_qr is easiest found from a flux ratio in the initial state. At initial conditions, only the chemical driving force is substantial and

$${\left[\frac{J_{\text{q}}^{\prime \text{i}}}{r}\right]}_{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0,\Delta T=0}=\frac{D_{\text{qr}}^{\prime }}{D_{\text{rr}}}\text{.}$$ (26)

The ratio gives access to D′_qr when D_rr is known. This experiment is often done with a positive r. When the heat flux into the membrane is negative, D′_qr < 0.

The osmotic driving force causes a heat flux into the membrane through a nonzero D′_qd. The isothermal heat flux due to an osmotic force defines the second thermogenesis coefficient:

$$D_{\text{qd}}^{\prime }={\left[\frac{J_{\text{q}}^{\prime \text{i}}}{1-\exp \left(\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)/R{T}^{\text{o}}\right)}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta T=0}\text{.}$$ (27)

Again, subscripts define experimental conditions. An enhanced heat flux was found for white muscle tissue when an ion gradient was allowed to form across the vesicle membrane (8). In the initial phase, the osmotic force is negative. An enhanced negative heat flux means then that D′_qd is negative, in agreement with Eq. 10.

The first expression in Eq. 6 is a relation between the reaction rate and a temperature difference across the membrane. The equation predicts that external cold can generate a finite reaction rate via the coefficient, D′_rq, a phenomenon that also can be associated with thermogenesis. The definition of this coefficient is

$$D_{\text{rq}}^{\prime }=-{\left[\frac{rR{T}^{\text{i}}}{(1-T^{\text{i}}/T^{\text{o}})}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0}\text{.}$$ (28)

A negative value of the coefficient D′_rq, similar to D′_qr, is compatible with r > 0 or hydrolysis. This may fit with a role in thermogenesis. When the temperature is lowered on the outside of the vesicle, (1 − Tⁱ/T°) > 0, and hydrolysis starts. The second expression in Eq. 6 gives a positive Ca²⁺-flux, with this thermal force, and D′_dq < 0:

$$D_{\text{dq}}^{\prime }=-{\left[\frac{J_{\text{Ca}}R{T}^{\text{i}}}{\left(1-T^{\text{i}}/T^{\text{o}}\right)}\right]}_{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)=0,\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)=0}\text{.}$$ (29)

Altogether, this leads to enhanced heat production in the assay medium. Therefore, a cold vesicle exterior leads to Ca²⁺-influx even if the chemical reaction is at equilibrium.

Equations 28 and 29 offer, in principle, a way to determine the coefficients D′_rq and D′_dq. In practice, however, it seems impossible to control the thermal driving force. So, the experiments described by Eqs. 27–29 are difficult.

It is common to measure the heat production at steady state using both intact and leaky vesicles. One steady state is defined by J_Ca = 0. When the vesicles are intact, a gradient in Ca²⁺ will form during hydrolysis and uptake, until the condition of zero net uptake is reached. There is then a balance of chemical, osmotic, and thermal forces, which can be derived from the second flux equation in Eq. 6:

$$0=-D_{\text{dr}}\left[1-\exp \left(-\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]+D_{\text{dd}}\left[1-\exp \left(\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]-\frac{D_{\text{dq}}^{\prime }}{RT}\left(1-\frac{T^{\text{i}}}{T^{\text{o}}}\right)\text{.}$$ (30)

This condition may be useful in finding D′_dq, because the state is well defined. It requires that all other properties are known, however. When sugar phosphates are used as ATP regenerating systems and the reaction Gibbs energy is small (4,25), one may neglect the first term on the right-hand side of Eq. 30.

Results

The results for coefficients D_rr, D_dr, and D′_qr are plotted in Fig. 1 and summarized in Table 1.

Figure 1.

(a) The coefficient D_rr for evolution of the ATP hydrolysis catalyzed by SERCA isoforms, (b) the coefficient D_dr for active transport of calcium, and (c) the coefficient D_qr′ for thermogenesis. The calcium concentration is the initial state of the assay medium. Other conditions for experiments are given in Transport Coefficients and Supporting Material. ○, skeletal white muscle (SERCA 1 isoform); ■, skeletal white muscle heavy fraction; □, brown adipose tissue (BAT) (SERCA 1 isoform); ▴, skeletal red muscle (SERCA 1 and 2a isoform); and ◇ , human blood platelets (SERCA 2b and 3 isoform).

Table 1.

Summary of coefficient determinations

Coefficient for process	Symbol	Basis for determination	Results so far
Progress of ATP hydrolysis	Drr	Eq. 12	Fig. 1a
Active transport	Ddr	Eq. 23	Fig. 1b
Thermogenesis	Dqr	Eq. 26	Fig. 1c
Ca-diffusion	Ddd	Eq. 11	<4 Drr, Fig. 1a
Heat transport	Dqq	Eqs. 21 and 22	15 J mg−1 min−1
Active transport	Drd	Eq. 8: $D_{\text{rd}}^0=D_{\text{dr}}^0$	≈Ddr
Thermogenesis	Drq	Eq. 8: $D_{\text{rq}}^0=D_{\text{qr}}^0$	≈Dqr
Thermogenesis	Ddq	Eq. 8: $D_{\text{dq}}^0=D_{\text{qd}}^0$	≈Dqd

The main coefficients D_rr, D_dd, and D′_qq

The coefficient D_rr (Fig. 1 a) depends on the initial free calcium concentration of the assay medium where the vesicles are suspended. The transport coefficient has a characteristic value and dependence in each tissue. Thus, at low Ca²⁺ concentrations, the coefficient D_rr for SERCA 1 of white muscle is nine times the value for SERCA 1 of BAT, and five times the value for isoforms expressed in red muscle. There is an interesting increase in the value of D_rr for SERCA 1 of white muscle and BAT as Ca²⁺ increases in the medium, but only for this isoform. The largest value by far is obtained with the SERCA heavy fraction from white muscle.

The criterion from Eq. 11, together with results in Fig. 1 a, give the upper boundary for coefficient D_dd (see Table 1). For the SERCA 1 isoform expressed in white muscle, D_dd < 7.6 μmol/mg min, whereas for the SERCA 1 isoform expressed in BAT, it is D_dd < 1.6 μmol mg⁻¹ min⁻¹. Both values refer to the high Ca²⁺ concentration.

The thermal conductivity of lipids is typically h = 0.2 W K⁻¹ m⁻¹ at 35°C (308 K) (39). The thickness of a bilayer membrane is order-of-magnitude δ = 10⁻⁸ m. According to Diamond et al. (40), the vesicle volume can be given per mg protein as 5 μL/mg or 5 × 10⁻¹² m³/mg. This corresponds to the surface 15 × 10⁻⁸ m²/mg. By introducing these relations into Eq. 22, we obtain D′_qq= 15 J mg⁻¹ min⁻¹, as listed in Table 1.

The active transport and thermogenesis coefficients: D_dr, D′_qr

The active transport coefficient D_dr, which has a characteristic value for each tissue, is plotted in Fig. 1 b as a function of the free calcium concentration in the solution. At low Ca²⁺ concentration, the coefficient D_dr for SERCA 1 of white muscle is eight times the value for SERCA 1 of BAT, and six times the value for isoforms expressed in red muscles. Only D_dr from BAT tissue can be said to depend significantly on the initial calcium concentration. The SERCA heavy fraction from white muscle now has a low coefficient value.

The thermogenesis coefficient D′_qr calculated from data in Table S1, and plotted in Fig. 1 c, is a function of calcium concentration in the BAT tissue mainly. The heat released by SERCA 1 isoform expressed in white muscle is three times the amount released by the same isoform expressed in BAT, and ∼30 times the amount released by isoforms expressed in red muscles. The coefficient was negative in all vesicles, apart from those vesicles made from SERCA 1 heavy fraction of white muscle.

Discussion

The coefficients of the different isoforms

A discussion of the results in Fig. 1 and Table 1 is of interest. To further elucidate the differences and similarities of the isoforms, we also report the ratios of the transport coefficients in Figs. 2 and 3.

Figure 2.

The ratio D_dr/D_rr. The calcium concentration is the initial of the assay medium. Other conditions for experiments are given in Transport Coefficients. ○, skeletal white muscle (SERCA 1 isoform); ■, skeletal white muscle heavy fraction; □, brown adipose tissue (BAT) (SERCA 1 isoform); ▴, skeletal red muscle (SERCA 1 and 2a isoform); and ◇ , human blood platelets (SERCA 2b and 3 isoform).

Figure 3.

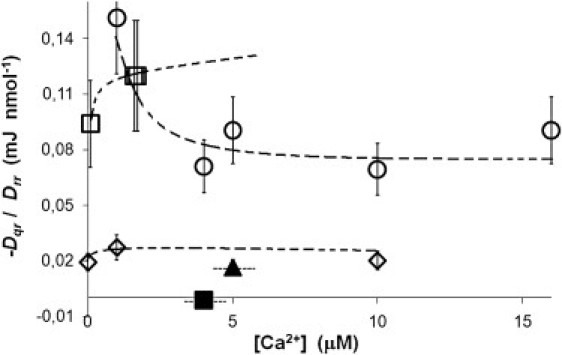
The ratio −D_qr/D_rr. The calcium concentration is the initial of the assay medium. Other conditions for experiments are given in Transport Coefficients. ○, skeletal white muscle (SERCA 1 isoform); ■, skeletal white muscle heavy fraction; □, brown adipose tissue (BAT) (SERCA 1 isoform); ▴, skeletal red muscle (SERCA 1 and 2a isoform); and ◇ , human blood platelets (SERCA 2b and 3 isoform).

All figures show that the kinetic characteristics of each SERCA isoform are different; they are even different for the same isoform expressed in different tissues (compare SERCA 1 results from white muscle and BAT tissue in Fig. 1). There is a marked dependence on the calcium concentration of the coefficients, but mainly for SERCA 1 from white muscle and BAT.

A calcium variation in the coefficients may be connected to a messenger role of Ca²⁺. It is well known that calcium is present in high concentrations in the sarcoplasmic lumen of muscle cells, and that its release into the cytoplasm allows for muscle contraction. At the end of the contraction, the calcium in cytoplasm must be pumped back into the lumen of sarcoplasmic reticulum. For Ca²⁺ to serve as a messenger, say to start or increase the pumping, a calcium concentration dependence as in Fig. 1, a and b, is reasonable. Fig. 1 shows that some of the coefficients D_rr and D_dr are increasing from a low value at low calcium concentration to a constant high level. The increase is most effective for SERCA 1 from white muscle, but is also good for SERCA 1 from BAT.

In white muscle tissue, the free intracellular calcium concentration varies largely with the calcium influx to the cytoplasm (via calcium channels) and the calcium transport out of the cytoplasm (via ATPases in the plasma membrane and the sarcoplasmic reticulum) (41). According to Fig. 1, the calcium transport into SR is enhanced, as the concentration increases, until a certain threshold value is reached.

Fig. 2 elucidates the ratio D_dr/D_rr further. All pumps are far from being stoichiometric. The surprising observation is that the ratio D_dr/D_rr is the same within error limits for white skeletal muscle, BAT, and skeletal red muscle. The mechanism of active transport of Ca²⁺ is clearly more effective in these tissues than in the others, because the highest ratios are observed here. Active transport of Ca²⁺ is, according to these data, not so effective in terms of chemical energy conversion to work in human blood platelets and BAT.

All ratios D_dr/D_rr in Fig. 2 converge to the same limit, a value between 0.20 and 0.25, as the calcium concentration increases, indicating that there is a limiting behavior at high turnover of Ca²⁺. The white muscle heavy fraction, which contains the ryanodine channel, has the lowest efficiency in Fig. 2. The small coefficient D_dr for vesicles from this fraction can reflect that active transport takes place in the presence of an open passive channel.

The coefficient D′_qr is negative in all tissues (Fig. 1 c), except from the tissue in the white muscle heavy fraction. According to Eqs. 11 and 8, D′_qd is then negative as well. There is at present no experimental evidence in favor of that conclusion, because we do not know, for certain, the direction of the osmotic driving force during initial uptake in tight vesicles. However, such evidence is essential for proving the theory, and should be obtained.

According to Suzuki et al. (42), the vesicle membrane may be able to maintain a temperature difference of 1 K during Ca²⁺-uptake. The value calculated for D′_qq (see Table 1) gives a heat flux of 1.4 mJ/mg min for a temperature difference of 1 K across the membrane, a value that is the same order of magnitude as the heat flux J′_qⁱ in Table S1. This means that its estimate in Table 1 may be reasonable.

Fig. 3 brings out the ability to produce heat in the various tissues. The figure shows the ratio D′_qr/D_rr as a function of calcium concentration of the assay medium for the various isoforms. We see that D′_qr/D_rr is high in white muscle and BAT—both are tissues that can be associated with nonshivering thermogenesis and the SERCA 1 isoform. The ratio is low in red muscle and blood platelets. There is no convergence of the lines to a common limit, unlike in Fig. 2. The results point to a role of white muscle SERCA 1 in heat production in small animals and newborns.

We also see that the heat flux generated in white muscle tissue, when the ryanodine channel is open, is nearly zero. This may also point to a role of calcium for dynamic signaling for thermogenesis in cells.

We have proposed that the flux equations presented and used in this work can describe one possible route to nonshivering thermogenesis. Through changes in the chemical driving force or osmotic driving force, a heat flux results, according to

$$J_{\text{q}}^{\prime \text{i}}=-D_{\text{qr}}^{\prime }\left[1-\exp \left(-\frac{{\Delta }_{\text{r}}{G}^{\text{i}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]+D_{\text{qd}}^{\prime }\left[1-\exp \left(\frac{\Delta {\mu }_{\text{Ca}/2\text{H}}\left(T^{\text{o}}\right)}{R{T}^{\text{o}}}\right)\right]\text{.}$$ (31)

Experiments can be performed to test this expression. The production of ATP under conditions that promote a heat flux is central. An exponential dependence of J′_qⁱ on Δ_rGⁱ should be found.

The fact that the SERCA 1 isoform has such different transport coefficients than other isoforms should be further investigated. All such differences should be traceable to structural differences. The function may also depend on the membrane in which they are embedded. SERCA isoforms are identified via their interaction with monoclonal antibodies. This interaction does not reveal structural differences (15), but such differences have been reported (13).

Similar statements to those made here on the relative role of these Ca²⁺-ATPase isoforms have been made by de Meis and co-workers, who, to a large extent, produced the data we used. We have added a quantitative framework to the discussion, and have assigned results to new properties of the system.

A practical set of fluxes and forces

This work is, to our knowledge, a first implementation of a thermodynamic description recently presented (20). We have given a set of flux equations that can be used to describe active transport and heat transport by an ion pump. We have defined transport coefficients and discussed how they can be determined from experiments. One may say that the early attempts by Kedem and Katchalsky (37) to formulate practical equations for membrane phenomena have been generalized in two respects: In the first place, one no longer need to be close to global equilibrium to have a well-defined thermodynamic description; and in the second place, it has become possible to use the temperature as a variable in biological systems.

The description further improves an earlier description (19) using an activated chemical reaction and a nonactivated ion-transport. Caplan and Essig (21) described small deviations around stationary states by linear flux-force relations (so-called proper pathways), but these could not be used in all of the nonlinear regime.

Three assumptions were used in the derivation of the expressions in Eq. 6 (see also (20)), namely those of

• 1.An activated chemical reaction and ion transport
• 2.A relatively fast binding and unbinding of ATP and ADP to the enzyme.
• 3.A membrane temperature T^s(γ_r, γ_d) equal to the temperature T^o of the vesicle interior

Although experimental evidence exists for the first two assumptions (43), the last is not documented. The fact that it is possible to obtain meaningful values of the coefficients may suggest, however, that also this assumption is fair.

The outcome of the analysis, the coefficients, can be used in modeling of biological systems. It helps define hypotheses for cause-effect relationships. It is important to be able to separate causes from effects, and this is what the flux-force relations can do. According to theory, the coefficients do not depend on the driving forces. This means, for instance, that a value found for zero osmotic force also applies when this force is finite. This becomes useful in modeling. Efforts to calculate overall performances of organelles can benefit from such coefficients.

Structural information is now available on the Ca²⁺-ATPase to an amazing detail (14). It is therefore appropriate to ask what a description of fluxes and forces can add to the understanding of the enzyme and why this description is important. We have seen that the different SERCA isoforms have significantly different transport coefficients. This presents a question to structure investigators: Can differences be traced in the enzyme structure or in its near surroundings?

Conclusions

Equations of transport for hydrolysis, ions, and heat by the Ca²⁺-ATPase in sarcoplasmic reticulum have been used to derive transport coefficients for various isoforms, using experimental results reported in the literature (3–9). The data reduction led to values for three transport coefficients, which support the idea of Ca²⁺ as a messenger for muscle contraction and nonshivering thermogenesis in white muscle and BAT.

A theoretical framework was used to give a set of equations, from which several new experiments can be defined. The results of Figs. 1–3 indicate a functional specialization between the various isoforms. Three of the isoforms are efficient ion pumps—namely those in white muscle, red muscle, and human blood platelets. Two tissues have a relatively high ability to release heat when exposed to the cold—white muscle tissue and BAT. We propose that these functional differences, which may be understandable, should be traceable to structural differences of the enzymes.

In addition to such structural investigations, we propose that more experiments be done to set the theory on a firmer basis. For instance, one may measure calcium uptake in presence of sugar phosphates, to test the linear approximation in Eq. 7, and to test the dependence of the heat flux on the exponential relationship in Eq. 31.