The Temperature Dependence of Lipid Membrane Permeability, its Quantized Nature, and the Influence of Anesthetics

Abstract

We investigate the permeability of lipid membranes for fluorescence dyes and ions. We find that permeability reaches a maximum close to the chain melting transition of the membranes. Close to transitions, fluctuations in area and compressibility are high, leading to an increased likelihood of spontaneous lipid pore formation. Fluorescence correlation spectroscopy reveals the permeability for rhodamine dyes across 100-nm vesicles. Using fluorescence correlation spectroscopy, we find that the permeability of vesicle membranes for fluorescence dyes is within error proportional to the excess heat capacity. To estimate defect size we measure the conductance of solvent-free planar lipid bilayer. Microscopically, we show that permeation events appear as quantized current events very similar to those reported for channel proteins. Further, we demonstrate that anesthetics lead to a change in membrane permeability that can be predicted from their effect on heat capacity profiles. Depending on temperature, the permeability can be enhanced or reduced. We demonstrate that anesthetics decrease channel conductance and ultimately lead to blocking of the lipid pores in experiments performed at or above the chain melting transition. Our data suggest that the macroscopic increase in permeability close to transitions and microscopic lipid ion channel formation are the same physical process.

Introduction

Lipid membranes are regarded as insulators that are practically impermeable to ions and larger charged molecules. This is crucial for the Hodgkin-Huxley model for the action potential (1), but also for the interpretation of many microscopic permeation events associated with proteins. Near the melting transition, however, membranes become permeable to water (2), ions (3,4), and even to large molecules. This may be of some relevance since many biological membranes are in fact found close to such a regime (5,6). It has been known since the early 1970s that the permeability of lipid membranes approaches a maximum in the chain-melting regime of lipids in the absence of proteins (7), and this is also likely to be so for biological membranes in the transition regime. The reason for this enhanced permeability is the enhanced area fluctuations that lead to a maximum in the lateral compressibility (8,9). Nagle and Scott (8) proposed that the changes in lateral compressibility lead to a facilitation of pore formation since the increased compressibility lowers the work necessary to create a membrane defect. In the melting transition, one also finds domain formation. Papahadjopoulos et al. (7) suggested in their seminal article that permeation events take place at domain boundaries. This view has also been adopted by Cruzeiro-Hansson and Mouritsen (10) and Corvera et al. (11). At domain boundaries, fluctuations in lipid state are maximal, and this suggests that domain interfaces are especially leaky. However, this view is not identical to that of Nagle and Scott (8) since the overall length of domain interfaces is not identical to large fluctuations. Unfortunately, the overall quality of permeation data for membranes so far has been low. This is partially due to difficulties in maintaining constant temperature during optical experiments. Melting transitions of single lipid LUV display half-widths of −1°. For a quality permeability experiment on such a system, an accuracy of at least 0.1 K is required.

Although the measurements mentioned above refer to ensembles, i.e., dispersions of vesicles, one can also monitor permeability for ions on microscopic scales. This is done either by using black lipid membrane (BLM) spanning a small hole in a Teflon film with a diameter of 50–100 μm (Montal-Müller technique (12)) or in patch-clamp measurements where one uses membrane patches of ∼1 μm². Surprisingly, measurements of the conductance of pure synthetic lipid membranes can display quantized steps very similar to those reported for ion channel proteins. Although there is, to our knowledge, no convincing explanation of why such currents should be quantized, there are several publications documenting such channellike behavior. The first article on this is from Yafuso et al. (13) on oxidized cholesterol films, which appeared two years before the famous article by Neher and Sakmann (14) on quantized currents through the acetylcholine receptor (quantized currents through protein-containing BLMs were actually already shown significantly earlier by (15)). Antonov et al. (3) were the first to show that these lipid membrane conduction events are strongly enhanced in the phase transition regime. Using pure synthetic lipids, they could switch permeation on and off merely by shifting the temperature by a few degrees. This basically rules out the possibility that one is observing proteins or peptide impurities. Kaufmann and Silman (16,17) and Kaufmann et al. (18) showed that the occurrence of such lipid ion channels depends not only on temperature but also on other intensive variables such as lateral tension and pH (i.e., the chemical potential of protons). Along the same lines, Antonov et al. (19) as well as Gögelein and Koepsell (20) showed that channellike events are influenced by calcium concentration (i.e., the chemical potential of calcium). Furthermore, they depend on voltage (21). All of these changes are also known to influence transition temperatures in lipid membranes. Several other publications describe quantized ion currents in pure lipid membranes in the absence of proteins (4,22–24). Despite the putative relevance of such findings that are well documented and which show the coupling to thermodynamical variables convincingly, this phenomenon is not well known to a broad community.

It is well established that anesthetics change the melting behavior of membranes. In particular, they lead to a lowering of the transition temperature (25–27). Thus, it seems obvious to study the effect of anesthetics on permeability. It is an interesting historical note that Charles Ernest Overton, who first demonstrated the general action of anesthetics and its relationship to membrane solubility (Meyer-Overton rule (28)) was also the first to studied the permeability of membranes to anesthetics (60).

In this publication, we compare ensemble permeation experiments on lipid vesicles with ion conductance measurements in planar lipid membranes. We use the fluorescence correlation spectroscopy (FCS) technique to measure the ensemble permeation rate for fluorescent dyes. In particular, we study the influence of temperature and the presence of anesthetics on permeability. Then, we determine the permeability for ions in a BLM setup. Here, we vary temperature, voltage, and anesthetic concentration. The goal is to demonstrate the thermodynamic couplings that lead to changes in permeability. In particular, we show that anesthetics influence the permeability in a manner closely related to their influence on the melting of lipid membranes that can be explained by freezing-point depression.

Materials and Methods

Chemicals

Decane and 1-octanol were purchased from Fluka Chemie (Deisenhofen, Germany); n-hexadecane, chloroform, and methanol were obtained from Merck (Hohenbrunn, Germany); n-pentane was provided by BDH (Poole, UK); and potassium chloride from J.T. Baker (Deventer, Holland). 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dipalmitoyl-sn-glycero-3-phosphoglycerol (DPPG), and 1,2-dioleoyl-sn-glycero-3- phosphocholine (DOPC) were purchased from Avanti Polar Lipids (Birmingham, AL) and used without further purification. Rhodamine 6G and tetramethylrhodamine dextrane were purchased from Invitrogen/Molecular Probes (Carlsbad, CA). For all experiments, MilliQ water (18.1 MΩ; Millipore, Billerica, MA) was used.

Fluorescence correlation spectroscopy

Sample preparation

We prepared unilamellar lipid vesicles (LUV) from DPPC/DPPG = 95:5 mol/mol with an Avestin extruder (Avestin Europe, Mannheim, Germany) using a filter with a pore size of 100-nm diameter. Extrusion was performed in the presence of high concentrations of Rhodamine 6G fluorescence markers (50 μM). Subsequently, remaining free dye was removed on a G50 Sephadex column at temperatures below the melting temperature of the lipids where the membranes are nearly impermeable. We used vesicles made of a DPPC/DPPG = 95:5 mixture. DPPG is negatively charged and was added to prevent the aggregation of vesicles. All experiments were performed in a 200-mM NaCl buffer. At this salt concentration, vesicles do not aggregate but R6G (positively charged) does, nevertheless, not associate with the membranes.

Fluorescence correlation spectrometer

Our inverted microscope setup has been described in detail in Hac et al. (29). We used a linearly polarized continuous wave 532 nm Nd:Yag laser (Laser 2000, Wessling, Germany) with a power of 5 mW. Further, we used a 1.20 NA 60 × water immersion objective (UPLAPO; Olympus, Melville, NY) and a confocal setup with pinhole sizes of 30 μm. The fluorescence signal was detected by a SPCM-AQR-13 avalanche photo diode (Laser Components, Olching, Germany). Timescales were calibrated with a Rhodamine 6G solution at 296 K with a known diffusion coefficient of D = 3 × 10⁻⁶ cm²/s at 22°C. The signal from the APD was analyzed using a FLEX5000/fast correlator card by Correlator.com (Bridgewater, NJ). To adjust temperatures in the FCS experiment, both sample and microscope objective were temperature-controlled using a HAAKE DC30 K20 (Thermo Fisher Scientific, Waltham, MA) waterbath. Additionally, the entire setup was heated by a ventilating radiator so that ambient temperature was close to the experimental temperature at the objective.

Calorimetry

Differential scanning calorimetry experiments were performed on a VP-DSC Calorimeter (MicroCal, Northampton, MA) with a scan rate of 5°C/h. The calorimetric experiment related to the FCS experiment (see Figs. 2 and 3) was performed on the same sample as the one used in the FCS experiments. For the DCS experiments related to the BLM experiments (see Figs. 4 and 5), the lipid samples were prepared by predissolving in chloroform and drying the solvent under vacuum overnight. The dried lipid mixtures were dispersed in MilliQ water to a final concentration of 20 mM. The buffer used was the same as for the BLM experiments. Before filling the calorimeter, the solutions were degassed for 10 min.

Figure 2.

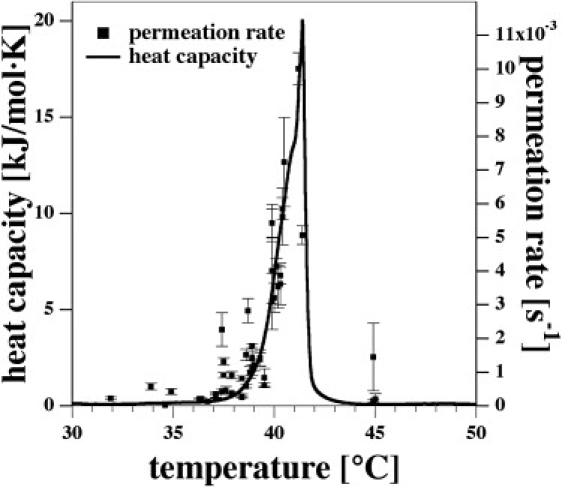
Permeation rate of R6G through DPPC/DPPG (95:5) LUV (200 mM NaCl) as a function of temperature compared with the heat capacity profile of the identical sample. The permeation rate is closely related to the heat capacity as predicted by Eq. 12.

Figure 3.

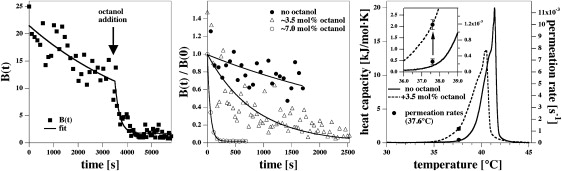
Effect of the anesthetic octanol on the permeation rate. (Left) Permeation of R6G through DPPC/DPPG (95:5) LUV at 37.1°;C after the sudden addition of 1-octanol at the time indicated by the arrow. Permeation increases dramatically. (Center) Permeation in the absence and the presence of 3.5 mol % and 7 mol % octanol in the membrane at 37.6°C. (Right) Heat capacity profiles of the lipid LUV in the absence of octanol (see Fig. 2) and in the presence of 7 mol % octanol. In the presence of octanol, the melting events occur at lower temperature. The solid circles indicate the permeation rates at 37.6°C in the absence of octanol and in the presence of 7 mol % octanol. The increase in permeability caused by octanol correlates nicely with the increase in heat capacity at 37.6°C.

Figure 4.

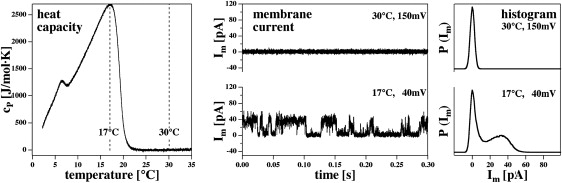
Spontaneous quantized currents through BLMs made of a DOPC/DPPC = 3:1 mixture (150 mM KCl) as a function of temperature. (Left) Heat capacity traces with a heat capacity maximum around 17°C. At 30°C, the sample above the melting regime in its fluid phase. (Center) Current traces at 17°C (40 mV) and 30°C (150 mV). One only finds current steps in the lipid melting regime. (Right) Current histograms for the two temperatures. At 17°C, two maxima in the histogram can be seen.

Figure 5.

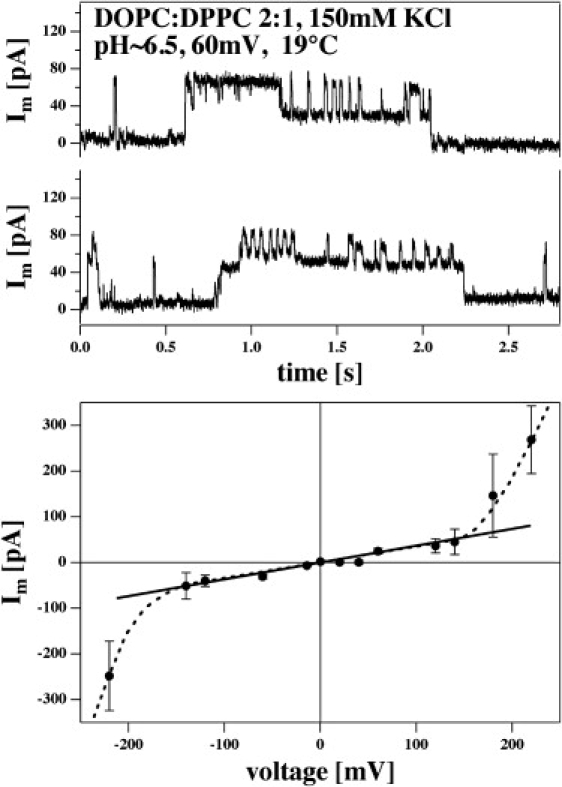
Currents and current-voltage relationship for BLMs made of a DOPC/DPPC = 2:1 mixture (150 mM KCl, 19°C, pH ≈ 6.5). The membrane is in its melting regime (see Fig. 6, left panel). (Top) Current traces at a voltage of 60 mV. One can see up to five current levels with equal distance between adjacent levels. (Bottom) Current-voltage relation for the above membranes. The mean amplitude of current events is shown as a function of voltage. It is linear in the range between −150 mV and +150 mV. If |V| is larger than 150 mV, the relationship is nonlinear due in part to several simultaneous open events in the membrane. A total of 328 current traces of 30 s duration was used for this analysis.

Black lipid membranes

Planar bilayers were formed over a round aperture in a Teflon film of 25-μm thickness, dividing two compartments of a Teflon chamber embedded in a brass block that could be heated by a circulating water bath. The aperture of ≈80 μm radius was punctured by a steel needle (experiments in Figs. 5 and 6) or by an electric spark (see Fig. 4). Lipid mixtures were prepared from chloroform-methanol solutions. The samples were dried under a weak flow of nitrogen gas/air and placed under vacuum overnight to remove the residual solvent. The aperture in the Teflon film was prepainted with 5% hexadecane in pentane. The BLMs were painted with DOPC/DPPC 2:1 lipid solutions in decane/chloroform/methanol 7:2:1 and formed following the method described by Montal and Müller (12). The two compartments of the Teflon block were filled with unbuffered 150-mM KCl (pH 6.5). Lipid solution (25 mg/mL) was spread on the buffer surface in each compartment (∼3 μL on each side). Ag/AgCl electrodes were placed into both compartments of the chamber. After 15–30 min to allow for the evaporation of the solvent, the water level of the compartments was lowered and raised several times until a bilayer was formed over the hole. The formation of BLMs was controlled visually and by capacitance measurements (with triangular 100-mV voltage input pulse). The specific capacitance of the membranes was found to be 0.9–1.2 μF/cm². These values are close to literature values (0.85 μF/cm² for DPPC (30), 0.61 μF/cm² for a DOPC/1,2-dioleoyl-sn-glycero-3-phosphatidylethanolamine (DOPE) = 50:50 mixture (31), and 0.93 μF/cm² for a pure DOPC membrane as deduced from monolayer measurements (32)). Our values have been obtained by dividing the total capacitance (∼80 pF) by the area of the hole as determined under the microscope. Our value for the capacitance serves only as a quality control for bilayer. To measure accurately the capacitance of a planar lipid bilayer, one must carefully vary the parameters during the measurement (for example, the area by bulging). The most critical unknown is the status of the bilayer at the edge. The rim depends on the experimental method, e.g., prepainting, applied volume and solvent, or solvent for the lipid. This rim may cover more than half of the surface of the actual hole. Bulging may push the membrane out of the hole, allowing much larger surfaces (even twice) compared with the hole in the septa. A second contribution is caused by the solvent applied for the prepainting or to solubilize the lipid. Although, in our approach, we used solvent free membranes, there is definitely some solvent associated with the lipid. Revisiting published data revealed values differing by a factor of three. A careful study was done by Dilger and Benz (33). They used solvent containing membranes and varied the solvent systematically. Using hexadecane to solubilize the lipid revealed very thin membranes with a specific capacitance of 0.585 μF/cm². In our case, the membranes are slightly thinner. Further, the capacitance of a membrane should be higher in the lipid-melting transition region, since it is proportional to charge density fluctuations. Those fluctuations should be high in the melting regime, as both area and thickness have maximum fluctuation (9).

Figure 6.

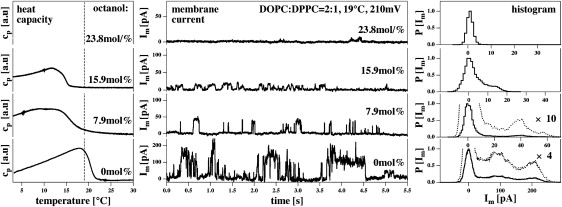
Influence of the anesthetic octanol on membrane currents through BLMs made of a DOPC/DPPC = 2:1 mixture (150 mM KCl, 19°C, pH ≈ 6.5) at a voltage of 210 mV. Shown are four different octanol concentrations, 0 mol % (bottom panels), 7.9 mol % (second from bottom), 15.9 mol % (second from top), and 23.8 mol % (top panels) given as mol % of molecules in the membrane. (Left) Heat capacity traces for three octanol concentrations (trace for 23.8 mol % not shown). Increasing octanol content leads to a shift of the profiles toward lower temperatures. This effect is known as freezing-point depression (27). In the absence of octanol, the experimental temperature is at the c_p-maximum, whereas it is above the c_p-maximum in the presence of octanol. (Center) Representative current traces at the four octanol concentrations. The current amplitudes and the total time in the open state become smaller with increasing octanol concentration. (Right) Current histograms showing several peaks. At higher octanol concentration, the peak positions are at lower voltages. At 23.8 mol %, current events disappear completely. Note the different scales of the current axis in the center and the right panel.

For the experiments with octanol, 15% v/v octanol in methanol solution was prepared and added symmetrically on both sides of the Teflon chamber.

Conductance measurements were performed on an Axopatch 200B amplifier in voltage-clamp mode connected to a DigiData 1200 digitizer (both Molecular Devices, Sunnyvale, CA). Current traces were filtered with 1 kHz low-pass Bessel filter and recorded with Clampex 9.2 software (Axon Instruments, Foster City, CA) on the hard drive of the computer using an AD converter with a time resolution of 0.1 ms. The data was further analyzed with Clampfit 9.2 and low-pass filtered with Bessel (eight-pole) filter at a cutoff frequency of 300 Hz. Temperature was controlled by a HAAKE DC30 K20 (Thermo Fisher Scientific) waterbath and a thermocouple (WSE, Thermocoax, Alpharetta, GA).The BLM experiments in Fig. 4 were performed in the laboratory of M. Winterhalter in Bremen, and the experiments shown in Figs. 5 and 6 were performed using a very similar setup in the laboratory of T. Heimburg in Copenhagen.

The FCS correlation function of vesicles with variable content of fluorescence dyes

The correlation function of a freely diffusing dye in a microscope focus of Gaussian cross section is given by

$$G\left(\tau \right)=\frac{1}{\langle N\rangle }{\left[1+\frac{\tau }{{\tau }_{\text{D}}}\right]}^{-1}{\left[1+{\left(\frac{r_0}{z_0}\right)}^2\frac{\tau }{{\tau }_{\text{D}}}\right]}^{-\frac{1}{2}}\text{.}$$ (1)

If one has several markers of similar brightness, the correlation functions add, and the number of diffusing particles can be deduced from the relative amplitude of the steps in the correlation function. The situation becomes more complicated if different objects with different brightnesses are present or if there is a distribution of brightnesses since the brightness enters the correlation as a square,

$$G\left(\tau \right)=\frac{1}{{\left(\sum _{\text{j}}{B}_{\text{j}}\langle N_{\text{j}}\rangle \right)}^2}{\sum _{\text{i}}{B}_{\text{i}}}^2\langle N_{\text{i}}\rangle {\left[1+\frac{\tau }{{\tau }_{{\text{D}}_{\text{i}}}}\right]}^{-1}{\left[1+{\left(\frac{r_0}{z_0}\right)}^2\frac{\tau }{{\tau }_{{\text{D}}_{\text{i}}}}\right]}^{-\frac{1}{2}},$$ (2)

where the brightness of particle species i is given by B_i = κ_iɛ_iQ_i (34). Here, κ_i is the efficiency of the fluorescence detector, ɛ_i is the molar extinction coefficient of the fluorophore at the wavelength of excitation, and Q_i is the quantum yield of the fluorophore. For fluorophores of equal brightness, the B_i values cancel. In the presence of a single dye species, one obtains Eq. 1.

Permeation through vesicles studied by FCS

In this work, we wish to monitor the permeation of fluorescence markers from the inside of a 100-nm vesicle to the outside. These vesicles are smaller than the microscope focus. Even though all markers have the same brightness in this particular experiment, a vesicle that contains n dye molecules is n times brighter than a single dye molecule (neglecting quenching effects). In particular, vesicles do not all contain precisely the same number of fluorophores. The dye entrapped in vesicles, and that free in solution, is rhodamine 6G. Thus, the difference in brightness between freely diffusing single dye molecules and the vesicles is directly proportional to the number of dye molecules trapped within the vesicle. Therefore, in the following only the number of dye molecules per vesicles will appear. From statistics, one expects a Poisson distribution of the dye content of the vesicles,

$$p\left(B_{\text{i}}\right)\approx \frac{\exp (-\tilde{B}){\tilde{B}}^{\text{i}}}{i!},$$ (3)

where $\tilde{B}$ is the mean number of dyes per vesicle. If one inserts this distribution into Eq. 2, one obtains

$$G\left(\tau \right)=\frac{\langle N_{\text{R}6\text{G}}\rangle }{{\left(\langle N_{\text{R}6\text{G}}\rangle +\tilde{B}\langle N_{\text{V}}\rangle \right)}^2}{\left[1+\frac{\tau }{{\tau }_{\text{R}6\text{G}}}\right]}^{-1}{\left[1+{\left(\frac{r_0}{z_0}\right)}^2\frac{\tau }{{\tau }_{\text{R}6\text{G}}}\right]}^{-\frac{1}{2}}+\frac{{\tilde{B}}^2\langle N_{\text{v}}\rangle \left(1+{\tilde{B}}^{-1}\right)}{{\left(\langle N_{\text{R}6\text{G}}\rangle +\tilde{B}\langle N_{\text{V}}\rangle \right)}^2}{\left[1+\frac{\tau }{{\tau }_{\text{V}}}\right]}^{-1}{\left[1+{\left(\frac{r_0}{z_0}\right)}^2\frac{\tau }{{\tau }_{\text{V}}}\right]}^{-\frac{1}{2}}\text{.}$$ (4)

The detailed derivation can be found in the MSc thesis of A. Blicher (35). This equation contains five unknown parameters that must be determined from experiment. The correlation function yields the two diffusion correlation times τ_R6G and τ_V of rhodamine 6G and the vesicles, respectively. The mean number of free dye molecules in the focus, 〈N_R6G〉, the mean number of vesicles in the focus, 〈N_V〉, and the mean number of dye molecules per vesicle, $\tilde{B}$, can be obtained from the absolute fluorescence intensity of the uncorrelated data, and the magnitude of the two steps in the correlation function (Fig. 1). In a time-dependent experiment, the mean number of dye molecules per vesicle will decrease. The change of $\tilde{B}$ with time is proportional to the permeation rate through the vesicular membrane. The permeation rate is likely to be closely related to the pore formation rate, assuming fast diffusion inside the vesicle and through the pore. However, the vesicles contain a small fraction of negatively charged lipids, whereas the dye itself carries a positive charge. Therefore, there may be a finite influence from dye adsorption to the vesicle walls. We tried to minimize this by adding salt into the buffer.

Figure 1.

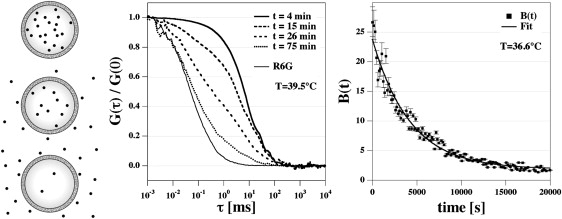
Principle of the measurement of permeation of the fluorescence dye R6G in the FCS experiment. (Left) Schematic drawing. Dye molecules trapped in vesicles smaller then microscopic focus size diffuse with the characteristic time constant of the vesicles. With time, molecules permeate through the vesicle membranes and diffuse with the characteristic time constant of free molecules. (Center) The correlation profiles of this situation show two correlation steps corresponding to free molecules and vesicles. The relative step size changes as a function of time such that the number of free molecules increases and the number trapped in vesicles decreases. Five experiments are shown that were performed after the times indicated. (Right) The mean number of dye molecules per vesicle (calculated from the mean brightness, see text) decreases exponentially with time. Data shown have been recorded on DPPC/DPPG (95:5 mol/mol) LUV in 200 mM NaCl at temperatures of 39.5°C (center panel) and 36.6°C (right panel) below the chain melting transition maximum (see Fig. 2). At 36.6°C, the time constant of permeation is 4200 s. Each data point corresponds to an FCS experiment as shown in the center panel.

Theory

The connection among compressibility, heat capacity, and permeability

The permeability of the membrane is maximal in the transition regime. This phenomenon is related to the well-known phenomenon of the opalescence of fluids close to critical transitions. In this regime, fluctuations in density may approach the length scale of visible light. Einstein (36) calculated the work required to generate density fluctuations on the length scale of light. In particular, he determined the work necessary to change the density of box of size L³ by moving volume into another box of equal dimensions. Close to transitions, this is considerably easier because the volume compressibility becomes high. In fact, one can see the increased fluctuations in liquids close to their transition in optical experiments. The problem of permeability changes and of pore formation is of a similar nature, since it requires moving lipids into another region of the membrane to create a pore. In particular, the likelihood to form pores or holes in the membrane is closely related to fluctuations in density. The problem can now be posed as follows: How much work must be performed to move a lipid from a membrane segment of dimensions L² into another region of similar size?

The work necessary to compress a membrane (i.e., the Helmholtz free energy change) by an area a is a quadratic function of the area that has the form

$$\Delta W\left(a\right)=\frac{1}{2}{K}_{\text{T}}^{\text{A}}{\left(\frac{a}{A_0}\right)}^2{A}_0,$$ (5)

where A₀ is the total area of the membrane, a is the size of a defect, and K_T^A is the isothermal area compression modulus (e.g., (8)). The compressibility of a membrane is given by

$${\kappa }_{\text{T}}^{\text{A}}=-\frac{1}{A_0}{\left(\frac{\partial A}{\partial \Pi }\right)}_{\text{T}}\equiv \frac{1}{K_{\text{T}}^{\text{A}}},$$ (6)

where κ_T^A is the isothermal area compressibility. The compressibility is also proportional to the area fluctuations (9)

$${\kappa }_{\text{T}}^{\text{A}}=\frac{\langle A^2\rangle -{\langle A\rangle }^2}{\langle A\rangle kT},$$ (7)

whereas the heat capacity is proportional to the fluctuations in enthalpy (9):

$$c_{\text{p}}=\frac{\langle H^2\rangle -{\langle H\rangle }^2}{k{T}^2}\text{.}$$ (8)

The empirical finding that, close to transitions, the changes in area and the changes in enthalpy are proportional functions of temperature, i.e., ΔA(T) = γ_AΔH(T) (9,37–39), leads to

$$\Delta {\kappa }_{\text{T}}^{\text{A}}=\frac{{\gamma }_{\text{A}}^{2}T}{A_0}\Delta c_{\text{p}}$$ (9)

or

$${\kappa }_{\text{T}}^{\text{A}}={\kappa }_{\text{T},0}^{\text{A}}+\frac{{\gamma }_{\text{A}}^{2}T}{A_0}\Delta c_{\text{p}}\text{.}$$ (10)

Nagle and Scott (8) assumed that the permeability can be expressed as a series expansion with respect to the area fluctuations that are also proportional to the lateral compressibility. The resulting permeability obtained by Nagle and Scott is

$$P=a_0+a_2{\kappa }_{\text{T}}^{\text{A}}+\text{higher}\text{order}\text{terms,}$$ (11)

where a₀ and a₂ are constants to be determined from experiment. Using Eq. 10 yields

$$P=c_0+c_2\Delta c_{\text{p}},$$ (12)

where c₀ and c₂ are also constants to be determined from experiment. This is a simple expression directly coupled to the calorimetric experiment. In particular, it predicts that the change in permeability is proportional to the excess heat capacity, which is easily measured. This approach relies on area fluctuations and does not involve a molecular model for a pore. In particular, we do not consider a line tension around the pore. The experimental results below will justify this approach.

The results of this section also immediately imply that everything that changes heat capacity profiles will also change the permeability in a coherent and predictable manner. The similarity of this problem to critical opalescence implies that it should be possible to detect the critical nature of pore formation in optical experiments.

Results

We have investigated two different aspects of lipid membrane permeability: the macroscopic permeability of lipid vesicles for fluorescence markers and the permeability of planar lipid membranes for ions. Although in the first setup, one obtains an ensemble average over many permeation events, in the second experiment, the permeation events allow us to draw conclusions regarding the possible size of the defects. In particular, we investigate the correlation with anesthetics. We show that such drugs influence the permeability in a coherent and predictable manner.

Permeability of LUV measured by FCS

Fluorescence correlation spectroscopy is a technique with single molecule resolution in which the diffusion constant and particle concentration can easily be determined on the length scale of the microscope focus. Rhodamine 6G fluorescence dyes were entrapped in lipid vesicles of 100-nm diameter. Both vesicles and dyes are smaller than the microscope focus diameter. However, the diffusion constant of the singular dyes is much higher than that of the much larger vesicles. Although the typical dwell time of a single dye molecule in our FCS setup is ∼100 μs, the dwell time of a fluorescing vesicle is of ∼10 ms. If both single dye molecules and fluorescent vesicles coexist in a solution, the correlation function will show two steps with amplitudes related to the concentrations of dyes in vesicles and free dyes.

Initially, all R6G molecules are trapped in the vesicles. With time, they leak out of the vesicles as shown schematically in Fig. 1 (left). This process can be followed in repeated FCS experiments (Fig. 1, center), and the relative fraction of dye in vesicles and as free molecules can be deduced from the amplitudes of the steps in the correlation function following the procedure given in Eq. 4. As an example, we show the leakage of R6G out of vesicles made of 95 mol % DPPC and 5 mol % DPPG measured at 39.5°C, which is ∼2 K below the heat capacity maximum of the membrane melting profile. Under these conditions, permeation of dyes through the vesicular walls is quite slow. One can see two correlation steps. Although the correlation times remain constant, the relative fraction of slow and fast diffusion species is changing. Fig. 1 (right) shows that the progress of leakage for a sample at 36.6°C (≈5 K below the transition maximum) yields a single exponential decay with a time constant of 4800 s and a permeation rate constant of 2.1×10⁻⁴ s⁻¹.

We recorded the permeation rate constants as a function of temperature and compared them with the heat capacity profile (Fig. 2). It was found that the permeation rate of R6G was, within experimental accuracy, linearly related to the excess heat capacity as predicted by Eq. 12. In the temperature range from 36.5° to 41.4°C, the permeability changed by a factor of 50. Compared with temperatures below the pretransition temperature (<34°C), the change is several orders of magnitude (data not shown). Close to the heat capacity maximum the permeation rate is ∼0.01 s⁻¹, which corresponds to a time constant of 100 s. The dwell time of a vesicle in the microscope focus is ∼10 ms. To obtain a correlation function of reasonable quality, one needs to record a fluorescence noise trace of at least 10 s. Thus, the permeation rate at heat capacity maximum is close to the resolution limit of our method. Only two data points have been measured above the melting regime. These points are difficult to obtain because, during equilibration of the sample to the experimental temperature, it passes through the phase transition regime and most of the dye leaks out before the start of the experiment. The permeation rates for temperatures above 41.4°C given in Fig. 2 represent the single exponential decay of the remaining fluorescence markers (of ∼10% of the original dye concentration). This slow decay is absent in the data at the transition point. We conclude that the permeability returns to values similar to those below the transition range, in agreement with previous studies. A control experiment with tetramethylrhodamine dextrane (MW ≈ 3000 g) at the melting temperature of 41.4°C showed that this large dye remained inside of the vesicles on timescales of several hours (data not shown). This indicates that the vesicles stay intact when passing through the melting regime and do not rupture.

Influence of anesthetics

In 2007, we showed that anesthetics act as freezing-point depressants (27). At critical anesthetic dose (2.6 mol % of anesthetics in the membrane), one obtains a melting point depression of ∼0.6°. Since all anesthetics shift the heat capacity profile by the same known value, one expects a predictable change of anesthetics on permeability. In particular, if one measures permeability below the melting temperature of the vesicles, anesthetics should increase the permeability since the melting events are moved toward experimental temperatures. If one repeats the same experiment above the melting temperature, addition of anesthetics should decrease the permeability since the transition events are moved away from experimental temperatures. This was investigated using the anesthetic 1-octanol. Fig. 3 (right) shows the effect of the addition of 3.5 mol % percent of octanol (calculated from the total octanol content and a lipid/water partition coefficient of 200 (40)) on the heat capacity profile. It shifts by ∼0.9 K to lower temperatures, in agreement with the freezing-point depression relation derived in Heimburg and Jackson (27). Upon addition of octanol to the vesicle dispersion at 37.6°C, the permeation rate increases dramatically (Fig. 3, left; the time of octanol addition is indicated by an arrow). Dye release for different amounts of octanol is shown (Fig. 3, center). The permeation rates are 0.24 × 10⁻³ s⁻¹ in the absence of octanol, 1.19 × 10⁻³ s⁻¹ in the presence of 3.5 mol % octanol, and 19.8 × 10⁻³ s⁻¹ in the presence of 7 mol % octanol. In Fig. 3 (right), the permeation rates with and without octanol are compared with the heat capacity changes. At 37.6°C, the permeability increase caused by octanol is approximately fivefold and matches exactly the change of the excess heat capacity caused by octanol at the same temperature.

Permeation of ions through black lipid membranes

It has been shown previously (3,4) that permeation of ions through BLMs is most prominent in the phase transitions regime. Further, conductance changes occur in quantized steps similar to those reported for channel forming proteins or peptides (3,4,13,16–20). To stay closer to room temperature, we used lipid mixtures in the BLM experiments, which differed from those of the FCS experiments. BLMs below the transition are typically not stable. In Fig. 4, we show data recorded on a DOPC/DPPC = 3:1 (mol/mol) mixture (150 mM KCl, 1 mM Tris, pH 7.4). This mixture displays a broad melting profile with a maximum at 17°C (Fig. 4, left panel). Above 22°C, the mixture is in the fluid phase. We compared current measurements at 17°C and 30°C (Fig. 4, center panel). At 17°C and a transmembrane voltage of 40 mV, one sees discrete current steps with an amplitude of ∼35 pA (see histogram in the right-hand panel) and typical channel open times of several 10 ms. At 30°C, one does not see any current steps even at higher voltages of 150 mV. This supports the notion that the transition is the regime in which such events can be found. Our observation of well-defined conductance steps indicates that this particular lipid composition is able to form well-defined defects even in the absence of peptides or proteins (e.g., (20)).

Fig. 5 (top) shows traces from a DOPC/DPPC = 2:1 (150 mM KCl, 60 mV, pH ≈ 6.5, 19°C). This mixture has a heat capacity maximum close to 19°C. The figure shows that one can find traces with at least four equally spaced conductance steps, probably corresponding to several lipid channels opening simultaneously. Such multiple events seem to be more frequent when one is closer to the transition regime or if the voltage is higher. The bottom panel of Fig. 5 shows a current-voltage relationship for the membranes used in the top panel recorded at 19°C. It represents the average current for all events where I_m is larger than zero. It is linear in the regime between −150mV and +150 mV. If |V| > 150 mV, the overall conductance increases, probably because of a significant contribution of multiple conductance steps induced by higher voltage. Note that the electrostatic potential is an intensive thermodynamic variable that influences the state of the membrane (see Discussion). From the slope in the linear regime, one can calculate a channel conductance of 300 ± 80 pS. Assuming a pore in the lipid membrane filled with electrolyte (4), one calculates a pore radius of ∼0.75 nm, which is practically identical to the diameter of a single lipid. (DPPC has a cross-sectional area of 0.63 nm² in the fluid state (9) corresponding to a diameter of ∼0.8 nm.) This size is similar to the radii reported for protein channels, e.g., 0.45–0.5 nm for the voltage-gated potassium channel K_v1.2 (41) or 0.3 nm for the acetylcholine receptor (42). The fact that lipid ion channels display larger conductance at high voltage could be considered as a voltage-gating. However, it seems likely that this effect reflects, instead, the influence of voltage on the transition.

In the section above on dye permeation through vesicles, it was shown that anesthetics (octanol) influence permeation because of the influence of anesthetics on the heat capacity, and hence on the lateral compressibility. In Fig. 6 (left panel), the heat capacity profiles of DOPC/DPPC = 2:1 membranes are shown in the absence and the presence of 1-octanol. For the DPPC/DPPG = 95:1 membranes in Fig. 3, the melting events are shifted toward lower temperatures. We performed BLM measurements at 19°C, which is close to the transition maximum. Thus, one expects that adding octanol moves the membranes out of their transition regime and according to Eq. 12, the permeability should decrease. That this is in fact the case is shown in Fig. 6 (center and right). At 210 mV, the currents in the absence of octanol show two maxima at ∼100 and 200 pA. In the presence of 7.9 mol % octanol, the current steps range between 20 and 40 pA, whereas in the presence of 15.9 mol % octanol, the current amplitudes are ∼15 pA. At higher octanol concentrations (23.8 mol %), conductance events disappear completely. This reflects the decrease in heat capacity at 19°C induced by increasing octanol concentrations. Visual inspection of the current traces also seems to indicate that the mean open time per channel decreases with increasing octanol content. For each octanol concentration, we recorded ∼50–60 traces of 30 s each that all looked similar to the traces shown in Fig. 6. We performed a statistical analysis of all the traces recorded for each condition, and evaluated the percentage of the total time in which no current events were observed. We found 62% closed time in the absence of octanol, 84% closed time for membrane containing 7.9 mol % octanol, 89% closed time for 15.9 mol% octanol, and 93% closed time for 23.8 mol % octanol. Thus, increasing amounts of octanol decrease the overall probability of the membrane to be found in a conducting state. Visual inspection of the current traces also indicates that the mean open time per channel decreases with increasing octanol content.

Discussion

In this article, we investigated the permeability of lipid membranes for dyes and ions using FCS and BLM measurements. In agreement with earlier studies (3,4,7,11), we found that the permeability for both dyes and ions is maximum in the melting regime of the membranes. The FCS experiments showed that the permeation rate is, within experimental error, proportional to the heat capacity of a DPPC/DPPG = 95:5 membrane. This can be understood by the large fluctuations in area near the transition. This leads to a high compressibility and, consequently, the work required to create a pore by thermal fluctuation is small (see Theory). Several degrees below the transition the membrane was practically impermeable to dyes. Using the BLM technique (12), we measured ion currents through lipid pores. The findings are in agreement with the dye permeation experiments. We showed that one finds quantized currents in the melting regime which are absent at higher temperatures. Because of their similarity with protein channel currents, one can consider these events as lipid ion channels. Wunderlich et al. (43) showed that the mean conductance of a membrane of a lipid mixture indeed correlates well with the heat capacity (in their case of a DC₁₅PC/DOPC mixture). One may compare the permeation rates measured by FCS and the BLM measurements. The surface of the BLM hole with ∼80 μm diameter is ∼1.6 × 10⁵ larger than the surface of a 100-nm vesicle. If the mean frequency of pore creation is between 1/s and 100/s (e.g., traces in Fig. 5), and assuming that the content of the vesicles empties upon one hole formation, one would assume that the time constant of the dye release from the vesicles is of ∼10³–10⁵ s. This is approximately the order of magnitude found in our experiments (where we find between 100 and several 1000 s). This suggests that the permeation process in the BLM and the FCS experiments is the same or very similar. Glaser et al. (44) suggested that, at sufficiently high voltages, stable hydrophilic pores of 0.6–1 nm can exist. This is in agreement with our findings that suggest pore sizes of approximately one lipid cross-section. The ionic radius of K⁺ is 0.138 nm, the radius of Cl^– is 0.181 nm, and the size of the dye molecule is ∼1 nm. In contrast to protein channels, the number of lipid channels is not fixed. They are merely fluctuating defects in membranes, and their occurrence depends on the state of the membrane as controlled by the intensive thermodynamic variables of the system (e.g., temperature, pressure, electrostatic potential, and the chemical potential of the components). We suggest that, if number and lifetime allow it, such lipid pores may fuse to form pores that are big enough to be permeable to large molecules. If one is precisely at the transition, this may already occur at zero or small voltages. It is known that at high voltages one finds the well-documented phenomenon of electroporation (45). At and above 500 mV, long-lived pores can be produced in biological cell membranes. This effect is used to facilitate the transport of drugs into cancer cells (46). Molecular dynamics simulations suggest that stable pores of nm-size can exist after applying transmembrane voltage pulses (47,48). We have shown here that at voltages above 150 mV the current-voltage relationship becomes nonlinear so that currents are much larger. We further showed the existence of pores of a size sufficient to be permeable for small fluorescence dyes. One may well ask if the quantized currents found at lower voltages and electroporation found at high voltages are, in fact, the same phenomenon, with the difference that the pore sizes are larger at high voltage. This matter requires further investigation. In our experiments, the BLMs typically rupture above 300 mV. It should be noted here that one major disadvantage of the BLM technique is that the Teflon hole is prepainted with 5% hexadecane or decane in pentane. Thus, the membranes contain some residual alkanes that may influence the state of the membrane to a degree that may vary between different experiments. It would be of great interest to develop the Montal-Müller technique such that no additional organic solvent is required—or to repeat these studies with the patch-clamp technique, as for example done in Kaufmann et al. (18).

We have shown above that the presence of a melting transition and the accompanying area fluctuations are necessary for permeation effects. Whatever changes the state of the membrane potentially affects the permeability. Here, we studied in particular the effect of anesthetics on the permeation of dyes in FCS and ions in the BLM technique. We found that, in both techniques, the permeability changes in agreement with the changes in heat capacity. The lipid ion channels showed smaller conductances in the presence of anesthetics. In a recent article (27), we investigated the effect of anesthetics on membranes that lower the melting point of membranes. Here, we have shown that, below the melting transition, the presence of anesthetics can increase the permeability because the transition temperature is shifted toward the experimental temperature (Fig. 3). If one is above the transition, the presence of anesthetics lowers the permeability because the transition events are moved further away from experimental conditions (Fig. 6). In Heimburg and Jackson (27), we derived the following equation for the difference in free energy between fluid and gel phase of a membrane

$$\Delta G=\Delta H\left(\frac{T_{\text{m}}-T}{T_{\text{m}}}-\frac{RT}{\Delta H}{x}_{\text{A}}+{\gamma }_{\text{V}}\Delta p\frac{T}{T_{\text{m}}}+f\left({\mu }_{{\text{H}}^{+}}\right)+f\left({\mu }_{{\text{Ca}}^{2+}}\right)+f(\Psi )+\dots \right),$$ (13)

where ΔH is the transition enthalpy, T_m is the melting temperature, x_A is the molar fraction of anesthetics in the membrane, Δp is the hydrostatic pressure, and γ_V is a parameter describing the relation between volume and enthalpy changes (γ_V = 7.8 × 10⁻¹⁰ m²/N). This equation contains one term describing the effect of temperature, a term for the influence of anesthetics and a further term describing the effect of hydrostatic pressure. For each change in an intensive thermodynamic variable, one can add further terms into this equation; for example, for pH, calcium concentration or voltage, denoted here as $f\left({\mu }_{{\text{H}}^{+}}\right)$, $f\left({\mu }_{{\text{Ca}}^{2+}}\right)$, and f(Ψ). We suggested in Heimburg and Jackson (27) that whenever the value of the potential ΔG is the same, the anesthetic action is also the same. Similarly, one can state here that whenever the value of ΔG is the same, one expects the same permeability. Changes in different variables may compensate; for example, the pressure and the anesthetics concentration known as pressure reversal of anesthesia (27). Therefore, it is to be expected that the decrease in permeability observed in our BLM measurements would be compensated by hydrostatic pressure. In biological preparations that are found slightly above the transition of their membranes, one would expect an increase in conductance of lipid ion channels with increased pressure. In this context, it is interesting to note that the acetylcholine receptor displays a dependence on hydrostatic pressure, which becomes apparent at 400 bars (49), corresponding to a shift of the transition temperature of ∼10 Kelvin to higher temperatures (39). This is the approximate difference of the melting temperature of biological membranes and physiological temperature. One would also expect that an increase in voltage would change the state of membranes because each monolayer of the membrane possesses a quite high dipole potential of ∼200–500 mV (e.g., (50)). Antonov et al. (21) showed that increase in voltage increases the chain melting temperature. Here, we found a nonlinear current-voltage relationship (Fig. 5). The increase in conductance at higher voltages observed in our BLM measurements (Fig. 5) is in agreement with Antonov's findings. However, the voltage effect is not well studied. Since the bilayer possesses two monolayers with opposing dipole potentials, the effect of voltage may be different in the two layers. Impurities and proteins (or their chemical potentials) are further intensive variables. We have shown previously that fluctuations in lipid state are especially enhanced at lipid domain boundaries (51) and at protein interfaces (52). This makes domain boundaries and protein-lipid interfaces particularly susceptible for lipid ion channel formation.

Elliott and Haydon (53) found that octanol also increases the tension in the membrane. We find it unlikely that the tension in the fluid membrane itself makes the membrane more permeable other than by its influence on the melting transition. This judgment is based on the coherence of the explanation of permeation events presented in this article. However, we have no independent experimental evidence that rules out the possibility of changes in the membrane tension having some influence on the permeability.

Previously, we have investigated the fluctuation lifetimes of lipid vesicles that are identical to the relaxation timescale after a small perturbation (54,55). We found that relaxation timescales are proportional to the heat capacity. Multilamellar vesicles with very cooperative transitions display relaxation times of up to 30 s at the c_p maximum. Unilamellar vesicles display less cooperative transitions with maximum relaxation times at ∼1–2 s. If calorimetric profiles are broader (and the heat capacity is smaller), one instead expects relaxation times near 10–100 ms. E.g., it has been estimated that the relaxation timescale in the c_p maximum of lung surfactant is ∼100 ms. This timescale is close to what we find here for the channel lifetimes. It has been discussed before that channel lifetimes are in fact longer when the heat capacity is higher (55). This has been shown in BLMs by Wunderlich et al. (43) showing longer mean open times of the lipid channels close to the c_p-maximum of a DC₁₅PC/1,2-dimyristoyl-sn-glycero-3-phosphocholine mixture that correlated with the heat capacity changes. This may explain why Antonov et al. (4) found channel lifetimes on the order of seconds at the c_p maximum of DPPC membranes. As mentioned, this is the relaxation timescale for unilamellar DPPC membranes (55). Overall, the channel lifetimes seem to be related to the fluctuation timescales of lipid membranes.

Finally, it is tempting to compare lipid channels with protein channels. It seems that they display very similar signatures both with respect to conductances and to mean channel open times. This is striking and raises the question of whether the physics behind these events is similar. It is remarkable that Na⁺ channels and the acetylcholine receptor are affected by octanol in a manner similar to our lipid channels (56,57). The same is true for the effect of ethanol that leads to an increase in channel lifetimes (data not shown) and which has also been reported to have a similar affect on the acetylcholine receptor (58,59). In the literature, the effect of anesthetics on ion channels has led to the notion that anesthesia acts via a specific binding mechanism to channel proteins, a view that we have opposed in Heimburg and Jackson (27) on thermodynamic grounds. The similarity between protein channel data and lipid membrane conductance deserves to be investigated in greater detail in future studies. At present, the precise connection between the two phenomena must remain an open question. However, it must be concluded that

• 1.The finding of quantized currents in itself does not prove the activity of a channel protein since lipid membranes show very similar or identical events close to transitions.
• 2.The effect of drugs on the conduction events does not prove drug binding to a protein, because anesthetics can strongly influence conductance events in the complete absence of proteins because of their effect on the thermodynamics of the membrane.

Thus, an analysis of channel proteins exclusively based on conduction events and their alteration by drugs must be considered logically incomplete. To identify the action of a protein, one needs a clearcut criterion that allows discrimination between lipid and protein ion channels. The readers should feel encouraged to develop such criteria, should they exist.

Conclusions

We have shown here that lipid membranes are permeable to dyes and ions if one is close to the chain melting regime. The microscopic permeation for ions has been shown to be quantized with conductances and lifetimes similar to those reported for proteins channels. Membrane permeation can be influenced by changes in intensive thermodynamic variables, particularly temperature, voltage, and chemical potential of anesthetic molecules. Other authors have shown that permeation for ions can be influenced by calcium (20,19), pH changes (16,17), and changes in membrane tension (18). The same will be true for an increase of hydrostatic pressure. Thus, it must be concluded that the overall physics of lipid membrane permeation is straightforward and easily understood as a consequence of lateral area fluctuations. Since all biological membranes possess lipid membranes (and membrane proteins), it cannot be conclusively excluded that some of the quantized current events reported in the literature for proteins are in fact due to lipid channels, especially when considering that biological membranes exist in a state close to their melting transitions (5,6). In a recent article, we proposed that the action potential in nerves is related to the phase transition in biomembranes (27). In particular, we have shown that close to such transition one obtains the possibility of solitary piezoelectric pulses. It is interesting to note that, under exactly these conditions, one finds the quantized ion currents through lipid membranes.