Abstract
Radiofrequency (RF) ablation has become an accepted treatment modality for unresectable tumors. The need for larger ablation zones has resulted in increased RF generator power. Skin burns due to ground pad heating are increasingly limiting further increases in generator power, and thus, ablation zone size. We investigated a method for reducing ground pad heating in which a commercial ground pad is segmented into multiple ground electrodes, with sequential activation of ground electrode subsets. We created finite-element method computer models of a commercial ground pad (14 × 23 cm) and compared normal operation of a standard pad to sequential activation of a segmented pad (two to five separate ground electrode segments). A constant current of 1 A was applied for 12 min in all simulations. Time periods during sequential activation simulations were adjusted to keep the leading edge temperatures at each ground electrode equal. The maximum temperature using standard activation of the commercial pad was 41.7 °C. For sequential activation of a segmented pad, the maximum temperature ranged from 39.3 °C (five segments) to 40.9 °C (two segments). Sequential activation of a segmented ground pad resulted in lower tissue temperatures. This method may reduce the incidence of ground pad burns and enable the use of higher power generators during RF tumor ablation.
Keywords: Cancer, dispersive electrodes, finite-element method (FEM), grounding pads, radiofrequency (RF) ablation (RFA), skin heating, tumor ablation
I. Introduction
Radiofrequency (RF) ablation is increasingly utilized in cases where surgery is not possible as a minimally invasive treatment for kidney, lung, bone, adrenal gland, and both primary and metastatic liver cancer [1]-[6]. In RF ablation, current is delivered via an RF electrode that is inserted into the target tumor percutaneously (i.e., through a small incision in the skin), laparoscopically, or during open surgery. Cell death near the RF electrode results from the conversion of electromagnetic energy to heat by resistive heating. While a threshold value of tissue temperature does not exist due to the time–temperature relationship of tissue damage [7], in general, temperatures above 50−60 °C result in cell necrosis due to protein coagulation [8].
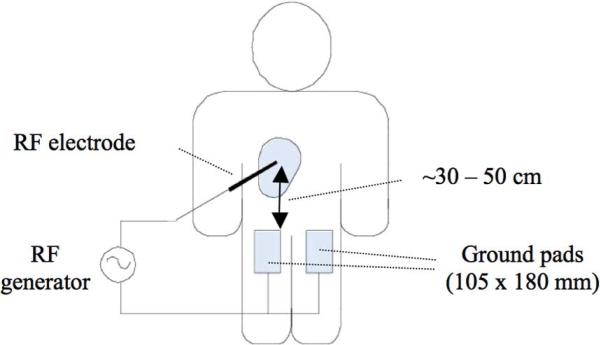
During RF ablation, large dispersive ground electrodes (ground pads) placed on the patient's skin provide a return path for the applied RF current (Fig. 1). Clinical RF ablation procedures currently use multiple ground pads (typically two or four) connected in parallel to the RF power source. Each pad consists of a flexible, thin-layered electrical conductor, usually aluminum, covered by an adhesive polymer gel layer. This adhesive layer increases the area of surface contact between the ground pad and skin, which is especially important in areas with irregular surface contours. RF ablation ground electrodes are different from those used in surgical electrocautery systems, which are typically stainless steel plates. The increased complexity of RF ground electrodes is necessary because RF ablation systems are characterized by greater power deposition (up to 250 W) over a much longer time (up to ∼35 min) than surgical electrocautery.
Fig. 1.
During RF ablation, the RF electrode is inserted into the target tissue, and ground pads are placed on the patient's thighs, equidistant from the RF electrode. If four pads are used, they are placed on top and bottom of each thigh (reproduced with permission from [28]).
Since the introduction of RF ablation for tumor treatment, coagulation zone size has been a major limitation in treatment of large tumors. Initial systems (25 W) created coagulation zones of ∼1.5 cm diameter in liver tissue [9], which was too small to adequately treat even the smallest tumors with a single application, especially since a ∼1 cm margin of ablated normal tissue around each tumor is desired to prevent recurrence [10]. The need for multiple probe placements and power applications resulted in long procedural times and reduced efficacy. Recent improvements in RF electrode design and power delivery algorithms (using up to 250 W) have increased the size of the coagulation zone created during a single RF power application to 3−6 cm. The need for increasing power during RF ablation procedures will likely persist, since increasing coagulation zone size and decreasing treatment times continue to be of clinical interest. Recent in vivo studies have demonstrated the potential benefit of creating larger coagulation zones with commercially available electrodes and higher generator power (up to 1000 W, and 4 A) [11], [12].
The increase in the maximum power used during clinical RF ablation procedures has led to an increase in the incidence of skin burns due to ground pad heating, with incidence rates in the literature ranging from 0.1% to 3.2% for severe skin burns (2nd or 3rd degree) and from 5% to 33% for mild skin burns (1st degree) [13]-[19]. However, other recent studies suggest that the incidence of skin burns after RF ablation may be under-reported [18], [20]. In addition to RF tumor ablation devices, other electrosurgical devices may cause excessive skin heating near ground pads in pediatric patients where available skin area is limited [21].
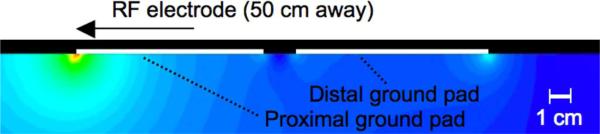
During RF ablation and electrosurgery procedures, it is well documented that maximum current density, and thus, maximum temperature rise at the ground pads occurs along the edges [21], [22]. In particular, due to the specific geometric relationship between the RF electrode and ground pads, maximum current density and heating occur at the so-called “leading edge” of the ground pad [the edge nearest to the RF electrode (Fig. 2)] [22]. Therefore, the leading edge of the ground pad closest to the RF electrode is the location where burns are most likely to occur during RF ablation [23]-[25].
Fig. 2.
Current density distribution from a previous 2-D modeling study. In this collinear pad arrangement, current flows preferentially to the leading edge of the proximal pad, resulting in little heating elsewhere at the proximal pad or at the distal pad. In this example, each pad was 8.5 cm long and the pads were spaced 1.5 cm apart. (reproduced with permission from [28]).
The size and number of ground pads used during RF ablation procedures has increased over time in order to safely disperse the increased RF power, with today's systems typically employing two or four pads (two on each thigh); however, this approach has reached a practical limit since there is little room to effectively add additional ground pad surface area, either by making the pads larger or by placing additional ground pads equidistant from the RF electrode. Equidistant placement of the ground pads is necessary because RF current preferentially flows to the closest ground pad, especially the leading edge (Fig. 2); the placement of additional ground pads further away from the RF electrode or increasing the overall area of the ground pads away from the leading edge provides little to no reduction in the maximum temperature reached in the tissue near the ground pads.
Recent attempts at preventing ground pad burns during RF ablation have included altering the shape of the ground pads to reduce heating along the edges [21], [26], applying ice packs to the ground pads to reduce temperature rise at the leading edge [20], dividing circular pads into annular segments and using resistors to equilibrate current at each segment [27], and monitoring temperature at the leading edge of the ground pads [23]. Two manufacturers have included monitoring features in their latest RF devices in an effort to reduce the incidence of skin burns. One system monitors temperature at the leading edge of the pads as described earlier, and alerts the user or terminates RF power application if the temperature at any of the ground pads exceeds a threshold. The other commercial system measures the RF current that flows to each ground pad, verifying for the operator that the power dispersed at each pad is balanced.
While these monitoring schemes are helpful in preventing skin burns, they do not address the fundamental roadblock to increased power levels during RF ablation, namely the uneven distribution of current density underneath the ground pads due to the leading edge effect. We have previously demonstrated that sequential activation of ground pads at different distances from the RF electrode leads to lower overall temperatures below the ground pads than the standard methodology (in which all ground pads are simultaneously connected) [28]. In this computer modeling study, we use the same sequential activation method with a single ground pad that is segmented into between two and five separate ground electrodes. For each number of ground electrodes, we determined the configuration that resulted in the lowest maximum tissue temperatures.
II. Materials and Methods
A. Finite-Element Method (FEM) Software
We used PATRAN 2005 r2 (The MacNeal-Schwendler Company, Los Angeles, CA) to create the model geometry, perform meshing, and assign all boundary conditions, including voltage, temperature, convection, and radiation. The nonuniform mesh ranged in size from 8 mm (along distal edges away from ground electrodes) to 0.1 mm (near the ground electrodes); in all, the model contained ∼83 000 elements and ∼43 000 nodes. The PATRAN software generated a data file suitable for the ABAQUS/STANDARD 6.5 solver software (Hibbitt, Karlsson, & Sorensen, Inc., Pawtucket, RI). For postprocessing, we used the built-in POST module in ABAQUS to create profiles of electric potential, current density, temperature, and thermal damage. We used a Dell Optiplex GX620 workstation with 3 GB of RAM to run all simulations.
B. FEM Model Parameters and Equations
1) Bioheat Equation
In this study, we examine the temperature rise due to Joule heating (which occurs whenever electrical current passes through a material) that occurs in the tissue under each ground electrode during RF ablation. The magnitude of this rise is governed by the bioheat equation [29]
| (1) |
where ρ is the density (in kilogram per cubic meter), c is the specific heat (in joules per kilogram per kelvin, and k is the thermal conductivity (in watts per meter per kelvin). J is the current density (in amperes per square meter) and E is the electric field intensity (in volts per meter). Tbl is the temperature of blood, ρbl is the blood density (in kilogram per cubic meter), cbl is the specific heat of the blood (in joules per kilogram per kelvin), and wbl is the blood perfusion (in liter per second). Qm (in watts per cubic meter) denotes the energy generated by metabolic processes, which was neglected since it is small compared to the other terms [30]. We included temperature-dependent effects in calculating the magnitude of the perfusion term [ρblcblwbl(T – Tbl)] in each tissue type (Section II-B3.a).
2) Description of the Model Geometry
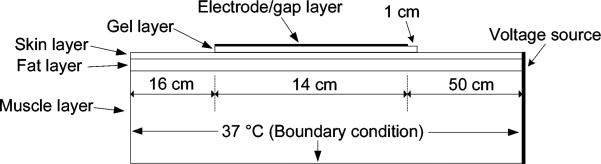
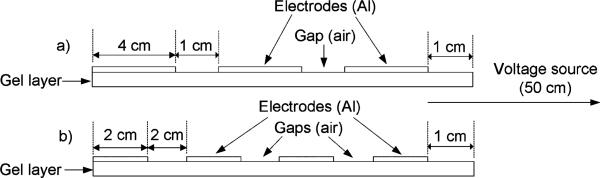
Fig. 3 next shows the overall geometry of our FEM model. We included three tissue layers in the model (muscle, fat, and skin) and two layers that represent typical ground pad construction (aluminum foil and adhesive gel). The thickness of each layer is shown in Table I. The aluminum layer (i.e., electrode/gap layer in Fig. 3) consists of a varying number of aluminum segments, with varying size and distance as described next (see Fig. 5). The total length of the aluminum layer was held constant at 14 cm, which is the length of a commonly used commercial ground pad (Valleylab, Boulder, CO). Similar to the commercial pad, the gel layer lined up evenly with the rear edge of the distal ground electrode, but extended 1 cm in front of the proximal ground electrode (Figs. 3 and 5).
Fig. 3.
Ground pad model setup (not to scale). Voltage was applied along the right boundary of the model, 50 cm from the leading edge of the electrode/gap layer. A temperature boundary condition (37 °C) was applied to the left, right, and bottom edges of the model.
TABLE I.
Thermal and Electrical Material Properties (at 37 °C)
| Material | ρ (kg/m3) | c (J/kg·K) | k (W/m·K) | σ (S/m) | layer thickness (cm) |
|---|---|---|---|---|---|
| Electrode (A1) | 2700 | 900 | 237 | 3.8 × 104 | 0.01 |
| Gel layer | 1010 | 4182 | 0.600 | 0.03 | 0.1 |
| Skin | 1010 | 3663 | 0.290 | 0.015 | 0.1 |
| Fat | 900 | 1500 | 0.160 | 0.04 | 0.6 |
| Muscle | 1060 | 3600 | 0.512 | 0.4 | 7.0 |
| Blood | N/A | 3500 | N/A | N/A | N/A |
Fig. 5.
Two sample electrode/gap configurations (not to scale). In the top case (a), the three ground electrodes are each 4 cm in length and the two gaps are each 1 cm (14 cm total). In the bottom case (b), the four ground electrodes are each 2 cm in length and the three gaps are each 2 cm (14 cm total). In all cases, the gel layer extended 1 cm in front of the proximal electrode.
3) Material Properties
We used published values of electrical and thermal properties in the model (Table I) [31]-[36]. Additionally, we measured the electrical conductivity (σ) of the gel layer on a typical commercial ground pad using the four-electrode method [37] and included that value in our model.
We included temperature dependence for the thermal conductivity (k) of each tissue, as published in a previous study [38], and a temperature coefficient of 2%/°C for the electrical conductivity of each tissue [31].
a) Perfusion
We included temperature-dependent perfusion of skin, muscle, and fat tissue in our model, which were implemented in FORTRAN subroutines. For fat and muscle tissue, perfusion changes with temperature according to a sigmoidal profile with a plateau above 45 °C [(2) and (3)] [32].
| (2) |
| (3) |
For skin tissue, we assumed that the relative change in perfusion with temperature in the human model is similar to a previous study in the rat model [39], and used a previously published value for human baseline skin perfusion (4) [40]
| (4) |
b) Convection and radiation
We included convective and radiative heat loss in this model, assigning the heat fluxes as boundary conditions to the skin and ground pad exterior surfaces, according to (5) and (6)
| (5) |
| (6) |
where qconv equals convective heat flux, qrad equals radiative heat flux, hf equals the convective heat transfer coefficient of skin [hf = 2.68 W/(m2 °C)] [41]), σ equals the Stefan–Boltzmann constant (σ = 5.67 × 10−8 W/(m2 K4)), ε equals the emissivity of skin (ε = 0.98) [42], and Tair equals the temperature of the air in contact with the skin and ground pad (Tair = 22 °C). Note that in (6) the temperatures are in Kelvin.
C. FEM Model Geometry and Algorithm
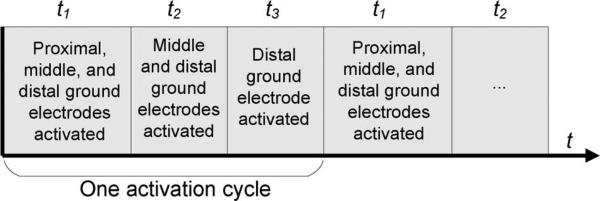
In our sequential activation algorithm, different subsets of ground electrode segments located at varying distances from the RF voltage source are activated in a repeating cycle (Fig. 4). In general, the pattern of the activation cycle is the same for any configuration of n electrode segments (i.e., all segments activated during t1, all segments except the most proximal activated during t2,..., only the most distal segment activated during tn. The result of this sequential activation is that during each period of the cycle (t1, t2, t3 in the example in Fig. 4), a different ground electrode segment is the activated ground electrode proximal to the RF electrode. Since the leading edge of the proximal activated ground electrode is the location of maximum heating, this algorithm more uniformly distributes tissue heating among all ground electrodes, resulting in lower maximum tissue temperature. The period that each electrode subset is activated is adjusted to produce equal temperatures at the leading edge of each ground electrode.
Fig. 4.
Sequential activation algorithm: Example with three ground electrodes. During each part of the activation cycle, tissue heating occurs primarily at the closest activated ground electrode (in this case, proximal during t1 , middle during t2, and distal during t3).
For each simulation, we adjusted the model geometry based on the desired number of ground electrode segments and the desired electrode length, distributing the remaining length of the electrode/gap layer evenly among the gaps. Two examples of electrode and gap configurations are shown in Fig. 5.
We simulated a total of 16 different configurations with two to five ground electrode segments, as well as the standard case (a nonsegmented commercial ground pad). Since the computer model is a cross-sectional 2-D model, we made some assumptions in order to estimate the total current for a 3-D system. The calculated current in a 2-D model effectively represents the current per unit width (e.g., using the units from our model, in amperes per millimete), where the width extends orthogonal to the 2-D model. By assuming a certain ground pad width, and further assuming that current is uniform along this width (i.e., neglecting corner effects), we can estimate the total current for the 3-D case as the current per unit width times the ground pad width. This estimate is justified in this study due to the large width of the ground pad in comparison to the region where corner effects result in higher current. Therefore, we assumed the width of the ground pad in this study was 23 cm (which is the width of another commercial ground pad (Thermopad, Rita Medical Systems, Mountain View, CA)), and multiplied this width by the current per unit width determined from the 2-D model to obtain total current. When we discuss total current in the subsequent text, we are always referring to this estimated total current for the 3-D case as described here.
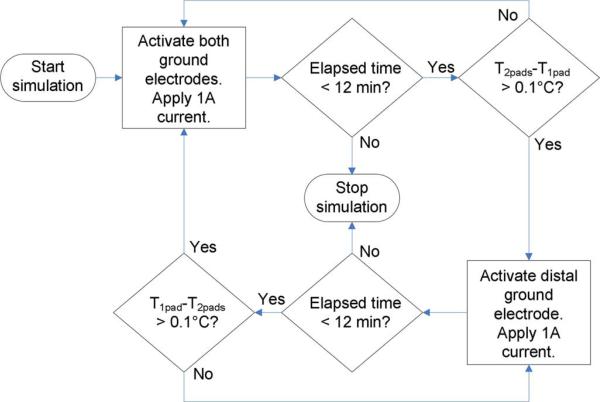
We set the initial temperature of the tissue and the boundary temperature of the model to 37 °C. We did not model the region around the RF electrode in this study, since the current density profile in the region of interest (underneath the ground electrodes) should be practically independent of the location and orientation of the RF electrode. This is due to the relatively large distance between the RF electrode and the ground electrodes in a typical RF ablation; the RF electrode (voltage source) would be located in the abdominal cavity and the ground pad would be located on the patient's thigh (Fig. 1). Therefore, we set the voltage source (simulating the RF electrode) at the model boundary 50 cm from the leading edge of the proximal pad (Fig. 3). The ground potential (0 V) was applied to the activated subset of ground electrodes. For each configuration, we first ran the simulation for 24 min without applying RF current to allow all tissue temperatures to reach steady state, since radiation and convection reduce tissue temperature near the skin (to ∼32.5 °C). After this initial simulation, we set the applied voltage to produce an RF current of 1 A. Assuming the same pad arrangement is used on the other thigh, this would correspond to 2 A total current, which is the maximum current output for typical commercial systems [11], [12]. The RF current was kept constant at 1 A during each simulation by changing the magnitude of the applied voltage at the voltage source using FORTRAN subroutines built-in to ABAQUS. For each configuration, we ran a preliminary simulation with each ground electrode subset activated to determine the node for each subset (hereafter referred to as “control node”) that reached the highest temperature after 12 min (a typical duration for clinical procedures). After determining the control nodes for a given configuration, we ran the main simulation for 12 min using the sequential activation algorithm (Fig. 4). FORTRAN routines recorded the temperature at the control node for each electrode subset, and paused the simulation if the control node of the activated subset reached a temperature 0.1 °C higher than any of the other control nodes at the end of a time step. Subsequently, a C++ program (Microsoft Visual Studio, Redmond, WA) activated the next electrode subset in the cycle (Fig. 4) and restarted the simulation. A flowchart demonstrating the simulation procedure for a case with two ground electrodes is shown in Fig. 6, and the location of the control nodes for sample simulations with two and four ground electrode segments is shown in Fig. 10. This method of determining the switching periods (using the “hottest” nodes at each ground electrode for temperature feedback) ensured that the maximum temperature rise for each electrode subset was approximately equal in each simulation.
Fig. 6.
Flowchart of simulation procedure for a two-ground-electrode configuration. T2pads and T1pad represent the temperature at the control nodes for the front (both electrodes subset) and rear (distal electrode only subset) ground electrodes, respectively. After each simulation time step, the elapsed time is checked to determine if the simulation should continue. If so, the control node temperature differential is checked to determine which electrode subset should be activated during the subsequent time step.
Fig. 10.
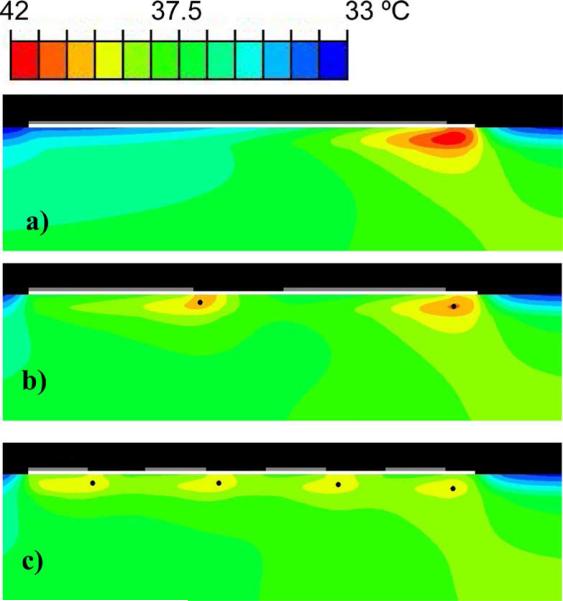
Temperature distribution after 12 min for (a) the single-electrode case, (b) a two-electrode simulation (5.5 cm electrodes, 3 cm gap), and (c) a four-electrode simulation (2 cm electrodes, 2 cm gaps). The temperatures at the control nodes (black dots) are used to control the switching periods. Temperature rise occurs primarily at the leading edges of the electrodes (gray) underneath the gel layer (white). Sequential activation of the electrodes leads to a significant decrease in maximum temperature.
The time steps during the solution of the FEM started at 0.05 s each time the model was restarted with a new activated electrode subset; they were subsequently automatically controlled by the solver software so that the maximum temperature change at any node in the model during one time step was below 0.1 °C. This threshold kept the time steps relatively short so that the control nodes did not significantly overshoot the temperature differential (also 0.1 °C, above) used to control the switching during the simulation.
D. Analysis
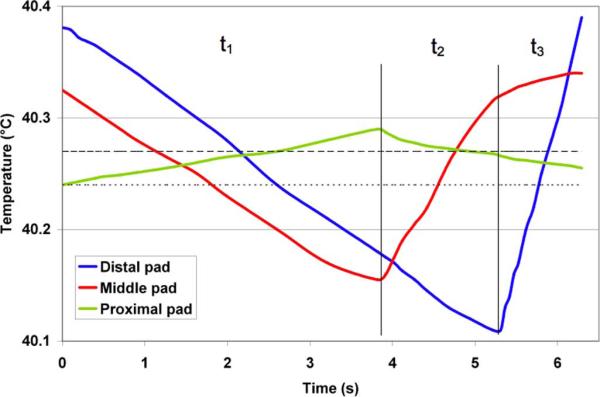
To determine the reported temperature rise for each simulation, we first calculated the temporal average temperature at each control (i.e., “hottest”) node over the last complete cycle, and then averaged the temporal values for all of the control nodes. A sample calculation from a simulation with three ground electrodes is shown in Fig. 7. We compared the simulations by average temperature at the control nodes instead of maximum temperature because the two values will theoretically be similar in the ideal case with very short switching periods and negligible ripple in the temperature time course (the switching periods were comparatively long in this study to reduce computational times).
Fig. 7.
Computation of reported temperature values. The graph displays the temperature at the control (i.e., hottest) nodes during the last cycle for a sample three-electrode case (4-cm-long electrodes, 1-cm-long gaps). The time periods t1, t2, and t3 correspond to the switching periods in Fig. 4. The dotted line (40.24 °C) represents the calculated average temperature for the distal electrode control node (blue), while the dashed line (40.27 °C) shows the calculated average temperature for the middle and proximal electrodes hottest nodes (red and green). The overall average maximum temperature rise reported for this simulation is the average of these three values, or 40.26 °C (Table II).
In addition to reporting maximum temperature rise during each trial, we used the commonly used parameter of thermal isoeffective dose to compare thermal damage between trials (7) [43]:
| (7) |
where CEM43 is the cumulative equivalent minutes at 43 °C, dti is the duration of the model time-step i in minutes, Ti is the temperature during time-step i (in degree celsius), and R is a factor describing the number of minutes needed to produce an equivalent amount of damage for a temperature change of 1 °C (typically 0.25 for temperatures below 43 °C, as in this study) [43]. The calculation of CEM43 at each node was performed during each simulation using a FORTRAN subroutine. The thermal dose is generally better suited than temperature alone for quantitative comparison in situations where tissue temperature changes during a procedure, since it takes the exponential relationship between damage and temperature into account.
During each activation cycle, a portion of the total current passes through the inactive ground electrodes that are between the proximal activated ground electrode and the voltage source (Fig. 8). This is because the aluminum in the ground electrodes has much higher electrical conductivity than the tissue or gel layer (Table I) and effectively acts as a short circuit (i.e., current preferentially flows through the inactive electrodes instead of nearby tissue). This current flow through the inactive electrodes leads to additional tissue heating (and therefore, higher temperatures) at the leading edges of the inactive electrodes. We calculated the percentage of the total current that passes through the adjacent inactive electrode when only the most distal electrode is activated using (8)
| (8) |
Fig. 8.
Example of “short circuit” effect in a two-electrode case. When only the rear electrode is activated, some of the total current passes through the inactive front electrode (arrows) instead of the surrounding tissue on its way to the rear electrode. This leads to increased leading edge heating at the front electrode, since current is flowing into the electrode even when it is inactive. This phenomenon becomes more pronounced as the distance between the electrodes is decreased (Table III).
Where Jmax is the maximum current density in the aluminum layer of the adjacent inactive electrode (in amperes per cubic meter), A is the area of the element with maximum current density (in square meter), w is the width of the model ground pad (0.23 m), and Itot is the total applied current (A).
E. Limitations
We did not include the time-dependent nature of temperature-dependent perfusion in our model to simplify calculations. We also did not take into account any thermally insulating effects that the foam backing of a typical commercial ground pad may have on temperatures underneath the pad. These simplifications may lead to inaccurate results.
III. Results
Including the control case (i.e., one 14 cm electrode), we simulated 17 different electrode/gap configurations in this study. The maximum tissue temperature rise (averaged over the final activation cycle) for each configuration is shown in Table II.
TABLE II.
Summary of Results
| Number of electrodes | Electrode length (cm) | Gap length (cm) | Max. CEM43 (min) | Maxi. temperature (°C) |
|---|---|---|---|---|
| 1 | 14.0 | NA | 0.523 | 41.71 |
| 2 | 5.0 | 4.00 | 0.151 | 40.70 |
| 2 | 5.5 | 3.00 | 0.122 | 40.55 |
| 2 | 6.0 | 2.00 | 0.132 | 40.60 |
| 2 | 6.5 | 1.00 | 0.198 | 40.93 |
| 3 | 2.0 | 4.00 | 0.142 | 40.67 |
| 3 | 2.5 | 3.25 | 0.072 | 40.17 |
| 3 | 3.0 | 2.50 | 0.051 | 39.90 |
| 3 | 3.5 | 1.75 | 0.053 | 39.93 |
| 3 | 4.0 | 1.00 | 0.081 | 40.26 |
| 4 | 1.5 | 2.67 | 0.044 | 39.81 |
| 4 | 2.0 | 2.00 | 0.031 | 39.54 |
| 4 | 2.5 | 1.33 | 0.035 | 39.59 |
| 4 | 3.0 | 0.67 | 0.056 | 39.98 |
| 5 | 1.0 | 2.25 | 0.031 | 39.54 |
| 5 | 1.5 | 1.63 | 0.024 | 39.33 |
| 5 | 2.0 | 1.00 | 0.028 | 39.44 |
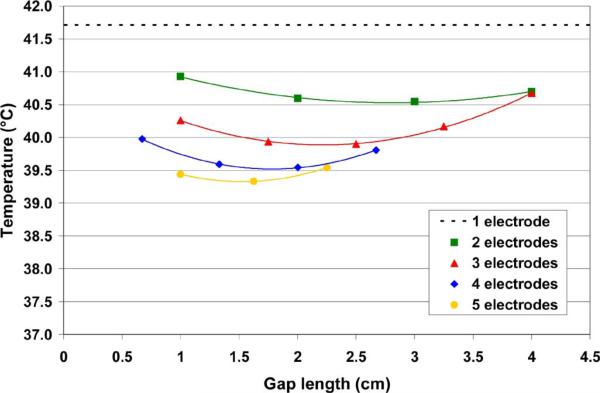
For each number of ground electrodes, there is a parabolic relationship between the gap length and maximum tissue temperature (Fig. 9).
For a given number of electrodes, the maximum temperature varied with gap length in an approximately parabolic fashion (Fig. 9). As the gap length was decreased (and the electrode length was correspondingly increased), the increased area of the ground electrodes initially led to lower tissue temperatures. However, as the gap length was further decreased and the electrodes got increasingly close to one another, the heating areas for adjacent ground electrodes began to overlap, leading to higher temperatures. Additionally, as the electrodes were brought closer together, an increasing amount of current passed through the inactive ground electrodes in front of the proximal activated pad (the “short circuit” effect, Fig. 8). Table III shows the percentage of the total current that passed through the adjacent inactive electrode when only the most distal electrode was activated for several sample cases.
Fig. 9.
Maximum temperature (averaged over the final cycle) versus gap length for all simulations. The dashed line at the top represents the maximum temperature achieved in the control case (one electrode). The color curves represent the 2nd-order polynomial approximations for each number of electrodes.
TABLE III.
“Short Circuit” Current Through Inactive Electrodes
| Number of electrodes | Electrode length (cm) | Gap length (cm) | Total current through adjacent inactive electrode, % |
|---|---|---|---|
| 2 | 5.0 | 4.00 | 13.5% |
| 2 | 6.5 | 1.00 | 31.0% |
| 3 | 2.0 | 4.00 | 11.4% |
| 3 | 4.0 | 1.00 | 33.2% |
| 4 | 1.5 | 2.67 | 16.6% |
| 4 | 3.0 | 0.67 | 41.5% |
| 5 | 1.0 | 2.25 | 20.1% |
| 5 | 2.0 | 1.00 | 35.3% |
For a given number of electrodes, as the gap length decreases, a greater proportion of the total current flows through the adjacent inactive electrodes, leading to higher tissue temperatures.
From the plot in Fig. 9, we determined a 2nd-order polynomial approximation of the maximum temperature versus gap length data for each number of electrodes. Using this approximation, the ideal configuration and lowest predicted maximum temperature rise for each number of ground electrodes is shown in Table IV.
TABLE IV.
Optimal Electrode and Gap Lengths for Each Number of Electrodes
| Number of electrodes | Optimal electrode length (cm) | Optimal gap length (cm) | Estimated max. temperature |
|---|---|---|---|
| 2 | 5.60 | 2.81 | 40.53 |
| 3 | 3.19 | 2.22 | 39.89 |
| 4 | 2.17 | 1.78 | 39.52 |
| 5 | 1.58 | 1.52 | 39.33 |
The temperature distribution in the tissue below the ground electrodes is shown next in Fig. 10 for the control case (single electrode), a two-electrode simulation, and a four-electrode simulation. The maximum tissue temperature after 12 min decreased as the number of ground electrodes was increased.
IV. Discussion
Skin burns due to ground pad heating are a common complication during RF tumor ablation [13]-[19], and are a limiting factor preventing further increase in RF power. Two recent studies show that even with today's RF electrodes, applying greater RF power than what is currently available clinically results in larger ablation zone size [11], [12]. Presently, up to four ground pads are placed on the patient equidistant from the active RF electrode to ensure equal current density (and therefore, heating) at each ground pad. This standard method has several limitations. First, the requirement of equidistant placement means that the process is operator dependent. If one or more of the pads are placed closer to the electrode than the others, a disproportionate amount of current may flow to this pad (assuming that closer distances result in lower impedance between electrode and pad) resulting in a skin burn. Alternately, the placement of a pad over a metallic device such as a hip prosthesis may create a low resistance path (short circuit) to the nearest part of the ground pad, resulting in a skin burn. A second limitation of the standard method is that further reduction of tissue temperatures by adding more ground pads is not possible because there is no more available skin area equidistant from the active RF electrode. Lastly, in this method, the majority of current flows through a relatively small area of tissue compared to the total ground pad area, creating high temperatures and possibly burns; in other words, little of the surface area of the ground pad is effectively utilized to disperse the RF current. While the recent introduction of current- and temperature-monitoring features into commercial RF systems are useful in decreasing the skin burn incidence rate using the standard grounding method, these monitoring features do not reduce ground pad heating. Therefore, the ineffective utilization of ground pad surface area in the standard grounding method remains a barrier to the safe use of higher power levels during RF tumor ablation procedures.
We have previously found experimentally that in a system with multiple ground pads placed at varied distances from the RF electrode, sequential activation leads to lower overall temperatures than standard simultaneous activation [28]. In this paper, we compared the sequential activation of a single-segmented commercial ground pad (Fig. 5) to the standard activation of a single nonsegmented pad. During sequential activation, subsets of the ground electrodes were activated for different time periods (Fig. 4) based on temperature feedback, in order to achieve equal heating below each ground electrode and lower overall tissue temperatures. It is important to note that segmentation of a ground pad can only reduce tissue temperatures if used with the sequential activation scheme (not with simultaneous activation), since the sequential method does not require equidistant placement of ground electrodes. We found that the maximum tissue temperature after 12 min of power application decreased as the ground pad was segmented into an increasing number of separate ground electrodes using the optimal segment size and distance (Fig. 9, Table IV), with a more uniform temperature distribution in the tissue as the number of segments was increased (Fig. 10). This is because current density and the corresponding tissue heating is more evenly distributed as the number of ground electrodes (and therefore, number of leading edges) increases. Additionally, as the number of ground electrodes increases, each ground electrode is the proximal activated electrode for a shorter time period, and therefore, undergoes less leading edge heating.
However, it is important to note that there are diminishing returns as the number of ground electrodes is increased (see Table IV, Fig. 9); i.e., there is a greater temperature reduction by going from one electrode to two electrodes (best case: 41.7 °C vs. 40.6 °C) than by going from three-electrode to four (best case: 39.9 °C vs. 39.5 °C). In all likelihood, it will be necessary to balance the temperature improvement gained by adding more ground electrodes against the resulting increase in both fabrication and system complexity. Furthermore, equilibrating the maximum temperature rise in the tissue at all ground electrodes during sequential activation will likely be more difficult in practice than in the model, since (unlike the model) the temperature feedback will not always be optimally located at the point of maximum temperature rise for each ground electrode. The length of the time periods used in conjunction with the sequential activation method is also an important consideration. The control algorithm used in this study (Fig. 6) led to relatively long switching periods (up to 10 s) at times, which resulted in considerable tissue temperature variation (i.e., temperature ripple) during each cycle. For example, in Fig. 7, the temperature ripple was approximately 0.3 °C for the one-pad control node (blue curve) over the course of the cycle. The switching time periods in a practical implementation may need to be shorter than those used in this study in order to reduce the temperature ripple and associated peak tissue temperatures. A reduction in ripple is advantageous due to the exponential temperature–damage relationship; i.e., a smaller ripple will result in a lower isoeffective thermal dose. Lastly, we examined the most basic segmented ground pad geometry in which all electrode segments and gaps were of same size in this study. It is possible that using varied segment sizes and gaps would allow for more uniform current between segments and allow further reduction in skin temperatures.
Because of the dynamic control over switching periods via temperature feedback, the sequential activation algorithm could be used to limit the heating of multiple ground pads (each segmented into multiple ground electrodes) placed arbitrarily on the skin surface—virtually anywhere on the patient's body. In addition to more effectively utilizing the surface area of the currently used ground pad configuration (leading to lower tissue temperatures), this means that additional pads could be used to further reduce skin heating. The ability to place pads in arbitrary locations also reduces the possibility of operator error, since nonequidistant placement will no longer result in an increased potential for burns.
V. Conclusion
Sequential activation of a segmented commercial ground pad during RF tumor ablation creates more uniform distribution of current density under the pad, and therefore, leads to considerably lower maximum tissue temperatures and lower isoeffective thermal dose. Computational models allowed us to examine the effect of segment size and distance between the segments to determine the optimal parameters for a given number of segments. The use of segmented ground pads may allow for increased maximum RF generator power and a reduction of the incidence rate of skin burns during RF tumor ablation procedures. In addition to tumor ablation, this method may be useful for other electrosurgical devices, especially in pediatric patients, where there is limited skin surface area.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant C06 RR018823 from the Extramural Research Facilities Program of the National Center for Research Resources, and in part by the National Institutes of Health under Grant R01 CA118990. Asterisk indicates corresponding author.
Biography
 David J. Schutt was born in Wyandotte, MI, on April 2, 1977. He received the B.S. degree from the Department of Electrical Engineering, University of Wisconsin, Madison, in 2000, and the M.S. degree from the Department of Biomedical Engineering, University of Wisconsin, in 2005.
David J. Schutt was born in Wyandotte, MI, on April 2, 1977. He received the B.S. degree from the Department of Electrical Engineering, University of Wisconsin, Madison, in 2000, and the M.S. degree from the Department of Biomedical Engineering, University of Wisconsin, in 2005.
He is currently a Research Specialist in the Division of Pediatric Cardiology, Medical University of South Carolina, Charleston. His current research interests include tumor ablation, cardiac ablation, and biomedical instrumentation.
 Dieter Haemmerich (S'00–A'02–M'03) received the Ph.D.B.M.E. degree from the University of Wisconsin, Madison in 2001, and the Ph.D.E.E. degree from the Vienna University of Technology, Vienna, Austria, in 2003.
Dieter Haemmerich (S'00–A'02–M'03) received the Ph.D.B.M.E. degree from the University of Wisconsin, Madison in 2001, and the Ph.D.E.E. degree from the Vienna University of Technology, Vienna, Austria, in 2003.
He is currently an Assistant Professor of Pediatric Cardiology at the Medical University of South Carolina, Charleston, and Adjunct Faculty of Bioengineering at Clemson University, Clemson, SC. His current research interests include thermal ablation, biomedical instrumentation, measurement of thermal and dielectric tissue properties, and computational modeling of bioheat transfer problems.
REFERENCES
- 1.Farrell MA, Charboneau WJ, DiMarco DS, Chow GK, Zincke H, Callstrom MR, Lewis BD, Lee RA, Reading CC. Imaging-guided radiofrequency ablation of solid renal tumors. AJR Amer. J. Roentgenol. 2003 Jun.180:1509–1513. doi: 10.2214/ajr.180.6.1801509. [DOI] [PubMed] [Google Scholar]
- 2.Gervais DA, McGovern FJ, Arellano RS, McDougal WS, Mueller PR. Renal cell carcinoma: Clinical experience and technical success with radio-frequency ablation of 42 tumors. Radiology. 2003 Feb.226:417–424. doi: 10.1148/radiol.2262012062. [DOI] [PubMed] [Google Scholar]
- 3.Mayo-Smith WW, Dupuy DE. Adrenal neoplasms: CT-guided radiofrequency ablation—preliminary results. Radiology. 2004 Apr.231:225–230. doi: 10.1148/radiol.2311031007. [DOI] [PubMed] [Google Scholar]
- 4.Neeman Z, Wood BJ. Radiofrequency ablation beyond the liver. Tech. Vasc. Interv. Radiol. 2002 Sep.5:156–163. doi: 10.1053/tvir.2002.36419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rosenthal DI, Hornicek FJ, Torriani M, Gebhardt MC, Mankin HJ. Osteoid osteoma: Percutaneous treatment with radiofrequency energy. Radiology. 2003 Oct.229:171–175. doi: 10.1148/radiol.2291021053. [DOI] [PubMed] [Google Scholar]
- 6.Wood BJ, Abraham J, Hvizda JL, Alexander HR, Fojo T. Radiofrequency ablation of adrenal tumors and adrenocortical carcinoma metastases. Cancer. 2003 Feb. 197:554–560. doi: 10.1002/cncr.11084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dewhirst MW, Viglianti BL, Lora-Michiels M, Hanson M, Hoopes PJ. Basic principles of thermal dosimetry and thermal thresholds for tissue damage from hyperthermia. Int. J. Hyperthermia. 2003 May–Jun.19:267–294. doi: 10.1080/0265673031000119006. [DOI] [PubMed] [Google Scholar]
- 8.Breen MS, Breen M, Butts K, Chen L, Saidel GM, Wilson DL. MRI-guided thermal ablation therapy: Model and parameter estimates to predict cell death from MR thermometry images. Ann. Biomed. Eng. 2007 Aug.35:1391–1403. doi: 10.1007/s10439-007-9300-3. [DOI] [PubMed] [Google Scholar]
- 9.Rossi S, Fornari F, Pathies C, Buscarini L. Thermal lesions induced by 480 KHz localized current field in guinea pig and pig liver. Tumori. 1990 Feb. 2876:54–57. doi: 10.1177/030089169007600114. [DOI] [PubMed] [Google Scholar]
- 10.Cady B, Jenkins RL, Steele GD, Jr., Lewis WD, Stone MD, McDermott WV, Jessup JM, Bothe A, Lalor P, Lovett EJ, Lavin P, Linehan DC. Surgical margin in hepatic resection for colorectal metastasis: A critical and improvable determinant of outcome. Ann. Surg. 1998 Apr.227:566–571. doi: 10.1097/00000658-199804000-00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brace CL, Laeseke PF, Sampson LA, Frey TM, Mukherjee R, Lee FT., Jr. Radiofrequency ablation with a high-power generator: Device efficacy in an in vivo porcine liver model. Int. J. Hyperthermia. 2007 Jun.23:387–394. doi: 10.1080/02656730701397858. [DOI] [PubMed] [Google Scholar]
- 12.Solazzo SA, Ahmed M, Liu Z, Hines-Peralta AU, Goldberg SN. High-power generator for radiofrequency ablation: larger electrodes and pulsing algorithms in bovine ex vivo and porcine in vivo settings. Radiology. 2007 Mar.242:743–750. doi: 10.1148/radiol.2423052039. [DOI] [PubMed] [Google Scholar]
- 13.Bleicher RJ, Allegra DP, Nora DT, Wood TF, Foshag LJ, Bilchik AJ. Radiofrequency ablation in 447 complex unresectable liver tumors: Lessons learned. Ann. Surg. Oncol. 2003 Jan./Feb.10:52–58. doi: 10.1245/aso.2003.03.018. [DOI] [PubMed] [Google Scholar]
- 14.Bowles BJ, Machi J, Limm WM, Severino R, Oishi AJ, Furumoto NL, Wong LL, Oishi RH. Safety and efficacy of radiofrequency thermal ablation in advanced liver tumors. Arch. Surg. 2001 Aug.136:864–869. doi: 10.1001/archsurg.136.8.864. [DOI] [PubMed] [Google Scholar]
- 15.Goette A, Reek S, Klein HU, Geller JC. Case report: Severe skin burn at the site of the indifferent electrode after radiofrequency catheter ablation of typical atrial flutter. J. Interv. Card Electrophysiol. 2001 Sep.5:337–340. doi: 10.1023/a:1011481104053. [DOI] [PubMed] [Google Scholar]
- 16.Livraghi T, Solbiati L, Meloni MF, Gazelle GS, Halpern EF, Goldberg SN. Treatment of focal liver tumors with percutaneous radiofrequency ablation: Complications encountered in a multicenter study. Radiology. 2003 Feb.226:441–451. doi: 10.1148/radiol.2262012198. [DOI] [PubMed] [Google Scholar]
- 17.Mulier S, Mulier P, Ni Y, Miao Y, Dupas B, Marchal G, De Wever I, Michel L. Complications of radiofrequency coagulation of liver tumours. Br. J. Surg. 2002 Oct.89:1206–1222. doi: 10.1046/j.1365-2168.2002.02168.x. [DOI] [PubMed] [Google Scholar]
- 18.Steinke K, Gananadha S, King J, Zhao J, Morris DL. Dispersive pad site burns with modern radiofrequency ablation equipment. Surg. Laparosc. Endosc. Percutan. Tech. 2003 Dec.13:366–371. doi: 10.1097/00129689-200312000-00003. [DOI] [PubMed] [Google Scholar]
- 19.Wood TF, Rose DM, Chung M, Allegra DP, Foshag LJ, Bilchik AJ. Radiofrequency ablation of 231 unresectable hepatic tumors: Indications, limitations, and complications. Ann. Surg. Oncol. 2000 Sep.7:593–600. doi: 10.1007/BF02725339. [DOI] [PubMed] [Google Scholar]
- 20.Machi J. Prevention of dispersive pad skin burns during RFA by a simple method. Surg. Laparosc. Endosc. Percutan. Tech. 2003 Dec.13:372–373. doi: 10.1097/00129689-200312000-00004. [DOI] [PubMed] [Google Scholar]
- 21.Tan KS, Hinberg I. Temperature distribution beneath pediatric electrosurgical dispersive electrodes: A model study. Biomed. Instrum. Technol. 1993 Nov.–Dec.27:506–513. [PubMed] [Google Scholar]
- 22.Goldberg SN, Solbiati L, Halpern EF, Gazelle GS. Variables affecting proper system grounding for radiofrequency ablation in an animal model. J. Vasc. Interv. Radiol. 2000 Sep.11:1069–1075. doi: 10.1016/s1051-0443(07)61341-4. [DOI] [PubMed] [Google Scholar]
- 23.de Baere T, Risse O, Kuoch V, Dromain C, Sengel C, Smayra T, Gamal El Din M, Letoublon C, Elias D. Adverse events during radiofrequency treatment of 582 hepatic tumors. AJR Amer. J. Roentgenol. 2003 Sep.181:695–700. doi: 10.2214/ajr.181.3.1810695. [DOI] [PubMed] [Google Scholar]
- 24.McGahan JP, Dodd GD., III Radiofrequency ablation of the liver: Current status. AJR Amer. J. Roentgenol. 2001 Jan.176:3–16. doi: 10.2214/ajr.176.1.1760003. [DOI] [PubMed] [Google Scholar]
- 25.Rhim H, Dodd GD, III, Chintapalli KN, Wood BJ, Dupuy DE, Hvizda JL, Sewell PE, Goldberg SN. Radiofrequency thermal ablation of abdominal tumors: Lessons learned from complications. Radiographics. 2004 Jan.–Feb.24:41–52. doi: 10.1148/rg.241025144. [DOI] [PubMed] [Google Scholar]
- 26.Krasteva VT, Papazov SP. Estimation of current density distribution under electrodes for external defibrillation. Biomed. Eng. Online. 2002 Dec. 161:7. doi: 10.1186/1475-925X-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wiley JD, Webster JG. Distributed equivalent-circuit models for circular dispersive electrodes. IEEE Trans. Biomed. Eng. 1982 May;29(5):385–389. doi: 10.1109/TBME.1982.324911. [DOI] [PubMed] [Google Scholar]
- 28.Haemmerich D, Schutt DJ. Sequential activation of multiple grounding pads reduces skin heating during radiofrequency tumor ablation. Int. J. Hyperthermia. 2007 Nov.23:555–566. doi: 10.1080/02656730701697778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. 1948. J. Appl. Physiol. 1998 Jul.85:5–34. doi: 10.1152/jappl.1998.85.1.5. [DOI] [PubMed] [Google Scholar]
- 30.Chato JC. Heat transfer to blood vessels. J. Biomech. Eng. 1980 May;102:110–118. doi: 10.1115/1.3138205. [DOI] [PubMed] [Google Scholar]
- 31.Ck FA. Chapter 6: Electrical properties of tissue. In: Duck FA, editor. Physical Properties of Tissue: A Comprehensive Reference Book. Du Academic; London, U.K.: 1990. pp. 167–223. [Google Scholar]
- 32.Erdmann B, Lang J, Seebass M. Optimization of temperature distributions for regional hyperthermia based on a nonlinear heat transfer model. Ann. N. Y. Acad. Sci. 1998 Sep. 11858:36–46. doi: 10.1111/j.1749-6632.1998.tb10138.x. [DOI] [PubMed] [Google Scholar]
- 33.Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996 Nov.41:2231–2249. doi: 10.1088/0031-9155/41/11/001. [DOI] [PubMed] [Google Scholar]
- 34.Golombeck MA, Dossel O, Raiser J. Improvement of patient return electrodes in electrosurgery by experimental investigations and numerical field calculations. Med. Biol. Eng. Comput. 2003 Sep.41:519–528. doi: 10.1007/BF02345313. [DOI] [PubMed] [Google Scholar]
- 35.Lide DR. CRC Handbook of Chemistry and Physics. 87th ed. Taylor & Francis; Boca Raton, FL: 2006. [Google Scholar]
- 36.Tamura T, Tenhunen M, Lahtinen T, Repo T, Schwan HP. Modelling of the dielectric properties of normal and irradiated skin. Phys. Med. Biol. 1994 Jun.39:927–936. doi: 10.1088/0031-9155/39/6/001. [DOI] [PubMed] [Google Scholar]
- 37.Tsai JZ, Will JA, Hubbard-Van Stelle S, Cao H, Tungjitkusolmun S, Choy YB, Haemmerich D, Vorperian VR, Webster JG. In-vivo measurement of swine myocardial resistivity. IEEE Trans. Biomed. Eng. 2002 May;49(5):472–483. doi: 10.1109/10.995686. [DOI] [PubMed] [Google Scholar]
- 38.Valvano JW, Cochran JR, Diller KR. Thermal conductivity and diffusivity of biomaterials measured with self-heated thermistors. Int. J. Thermophys. 1985;6:301–311. [Google Scholar]
- 39.Song CW. Effect of local hyperthermia on blood flow and microenvironment: A review. Cancer Res. 1984 Oct.44:4721s–4730s. [PubMed] [Google Scholar]
- 40.Gowrishankar TR, Stewart DA, Martin GT, Weaver JC. Transport lattice models of heat transport in skin with spatially heterogeneous, temperature-dependent perfusion. Biomed. Eng. Online. 2004 Nov. 173:42. doi: 10.1186/1475-925X-3-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kim Y, Webster JG, Tompkins WJ. Simulated and experimental studies of temperature elevation around electrosurgical dispersive electrodes. IEEE Trans. Biomed. Eng. 1984 Nov.31(11):681–692. doi: 10.1109/TBME.1984.325391. [DOI] [PubMed] [Google Scholar]
- 42.Mall G, Hubig M, Beier G, Buttner A, Eisenmenger W. Energy loss due to radiation in postmortem cooling. Part B: Energy balance with respect to radiation. Int. J. Legal Med. 1999;112:233–240. doi: 10.1007/s004140050242. [DOI] [PubMed] [Google Scholar]
- 43.Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. Int. J. Radiat. Oncol. Biol. Phys. 1984 Jun.10:787–800. doi: 10.1016/0360-3016(84)90379-1. [DOI] [PubMed] [Google Scholar]