Conditional Tests for Localizing Trait Genes

Abstract

Background/Aims

With pedigree data, genetic linkage can be detected using inheritance vector tests, which explore the discrepancy between the posterior distribution of the inheritance vectors given observed trait values and the prior distribution of the inheritance vectors. In this paper, we propose conditional inheritance vector tests for linkage localization. These conditional tests can also be used to detect additional linkage signals in the presence of previously detected causal genes.

Methods

For linkage localization, we propose to perform inheritance vector tests conditioning on the inheritance vectors at two positions bounding a test region. We can detect additional linkage signals by conducting a further conditional test in a region with no previously detected genes. We use randomized p values to extend the marginal and conditional tests when the inheritance vectors cannot be completely determined from genetic marker data.

Results

We conduct simulation studies to compare and contrast the marginal and the conditional tests and to demonstrate that randomized p values can capture both the significance and the uncertainty in the test results.

Conclusions

The simulation results demonstrate that the proposed conditional tests provide useful localization information, and with informative marker data, the uncertainty in randomized marginal and conditional test results is small.

1. Introduction

The goals of genetic linkage analysis [1] include detecting and localizing genes that are causal to a trait. The trait of interest can be quantitative, such as lipid levels, or qualitative, such as disease affectation status. This paper concerns linkage analysis using pedigree data.

In pedigree-based linkage analysis, data available to us include trait values and genetic marker data on observed individuals in a collection of pedigrees, and inheritance vectors [2] play a central role. When inheritance vectors can be completely determined from the genetic marker data, they and the observed trait values are sufficient for both linkage detection and gene localization. Individuals with the same genotype at a causal locus tend to have similar mean trait values or disease penetrances, and the probability for two individuals in a pedigree to have the same genotype at a locus depends on the inheritance vector at that locus. So when there are one or more causal loci in a genomic region, the posterior distribution of the inheritance vectors S_j at positions j in the region given observed trait values Y will deviate from their prior distribution. The theme of this paper is to measure and explore this deviation in order to achieve linkage detection and gene localization goals.

For clarity, in this paper, loci refer specifically to genetic trait or marker loci, while a position is simply a generic location in the genome. Posterior/prior refer to conditional/unconditional on trait values, while conditional refers to conditional on inheritance vectors at nearby genomic positions or conditional on genetic marker data. Throughout the paper, we follow the notational convention of using capital letters for random variables and corresponding lower case letters for their values. In expressions involving probabilities, we use shorthands such as Pr(s_j ∣ y) to mean Pr(S_j = s_j ∣ Y = y).

The main focus of this paper is to introduce conditional inheritance vector tests for linkage localization. Traditionally, linkage localization is often treated as an interval estimation problem. Papachristou and Lin [3] constructed confidence sets for the location of a disease gene by inverting hypothesis testing results. Their method requires that the effect of the disease gene be specified or accurately estimated. If more than one disease gene is involved, the interactions between the genes must also be incorporated. Liang et al. [4] discussed point and interval estimation of the location of a disease gene under the GEE framework [5], considering single disease gene models. Biernacka et al. [6] extended the method of Liang et al. [4] to work with two linked disease genes. These GEE methods will estimate the effects of the disease genes together with their locations, but it is still crucial to correctly specify the number of disease genes. These GEE methods are developed for affected-sib-pair data and rely on asymptotic results to have correct confidence interval coverage probabilities. Confidence interval approaches have intrinsic difficulties. To construct a confidence interval for the location of a disease gene, one has to include the location as a parameter in a model and has to consider the number and effects of the disease genes. The validity of the resulting confidence interval inevitably depends on correct specification or estimation of these number and effects.

We propose a different strategy for linkage localization. In this strategy, we conduct an inheritance vector test conditioning on the inheritance vectors at two positions bounding a test region. This conditional test has many appealing features. First, the test provides a statistically valid way to accurately interpret the localization information in the data. The test will only show significance when there are one or more casual loci in the specified test region. When there is no causal locus in the test region, the test has the correct type-I error. The validity of the test does not rely on asymptotic results. Second, being focused on the distribution of the inheritance vectors, our conditional tests rely much less on trait model assumptions. For the test to work, it is not required to specify the number or effects of the disease genes. Third, the proposed conditional tests can be implemented for both quantitative traits and qualitative traits, and are applicable to general pedigrees, not just affected relative pairs.

The proposed conditional tests can also be used to detect extra linkage signals in the presence of one or more previously detected causal genes on the same chromosome. Once linkage signals have been detected and successfully localized to small regions, we can perform further conditional tests in regions with no previously detected linkage signal. We condition out the effects of previously detected genes by excluding these genes from the test region.

In the context of detecting extra linkage signals, the idea of conditioning has been explored before: Delepine et al. [7] detected a new linkage signal for type I diabetes (IDDM) by conditioning on the IBD state at a previously discovered gene on the same chromosome. Farrall [8], Cordell et al. [9], Biernacka et al. [10], and Barber et al. [11] discussed incorporating previously detected genes by including their estimated locations in the likelihood (LOD score) or GEE estimation equations for estimating the location of the undetected gene. One distinctive feature of our proposed conditioning strategy is that it does not require point estimates of the locations of previous detected genes. We just need to exclude the localized gene regions from the test region of the conditional test. As pointed out by many (for example, Biernacka et al. [10]), the point estimate of the location of a causal gene is often unreliable, especially when the number of possible causal genes is unknown. Another feature of our conditional tests is that we explicitly condition on inheritance vectors. In this regard, the method of Delepine et al. [7] is most similar to ours. However, Delepine et al. [7] considered only affected sib pairs with genotyped parents (in this situation, the IBD states of the sib pairs are equivalent to inheritance vectors). Our method applies to general pedigrees. Also, by using randomized p values [12, 13], our test draws information from all pedigrees even when inheritance vectors cannot be completely determined.

Our conditional inheritance vector test method shares some features with the composite interval mapping (CIM) method of Zeng [14, 15]. Both methods involves choosing two bounding positions to specify a test region and then using a conditional test to examine linkage evidence in the specified test region. There are, however, important differences between our method and Zeng's CIM method. First, the CIM method relies on the Markov chain structure of the genotypes along a chromosome to work. This Markov chain structure of genotypes exists in backcross or intercross populations, but not in general pedigrees, so the CIM method cannot be validly applied to general pedigrees. Our conditional inheritance vector tests use the Markov chain structure of the inheritance vectors, which holds in general pedigrees under the assumption of no genetic interference [16], so our conditional tests are applicable to general pedigrees. Second, in designed crosses, the state space of the genotype at a genomic position is very small, so conditional tests in CIM can be effectively performed by regressing the trait values on the genotypes at multiple positions and testing whether certain multiple regression coefficient is 0. The state space of the inheritance vector at a genomic position is huge and regression method is not applicable to inheritance-vector-based tests. Different techniques are needed for implementing tests based on inheritance vectors.

Conditional inheritance vector tests are the main focus of this paper, although for comparison purpose, we also discuss marginal inheritance vector tests. In our implementation of these marginal and conditional tests, when the inheritance vectors cannot be fully determined from the marker data, we do not integrate the test statistic over imputed inheritance vectors. Instead, we summarize the test results using randomized p values [12, 13]. Using randomized p values allows us to decouple the uncertainly in the test results due to latent inheritance vectors from the lack of evidence for linkage detection or localization.

In the rest of this paper, Section 2 describes the Markov chain structure of the inheritance vectors and introduces the marginal and conditional inheritance vector tests. The section starts by assuming known inheritance vectors, and later discusses how to use randomized p-values [12, 13] to extend the tests using an MCMC sample of the inheritance vectors when the inheritance vectors cannot be fully determined from the genetic marker data. Section 3 presents simulation results to compare the properties of the marginal tests and the conditional tests. We also evaluate the effects of uncertainty in latent inheritance vectors on both the marginal and the conditional tests. Section 4 concludes the paper with discussion.

2. Methods

2.1. Markov Structure of the Inheritance Vectors

At each genomic position, each individual has two alleles, a paternal allele and a maternal allele. A random copy of one of the two alleles will be chosen to be copied to each child of the individual. A meiosis indicator [17] S_ij indicates whether the paternal allele or the maternal allele is copied to the child from the parent:

$$s_{ij}=\{\begin{array}{c}1,\hspace{0.17em}\text{if parent's paternal allele is copied to the child}\\ 0,\hspace{0.17em}\text{if parent's maternal allele is copied to the child}\end{array}$$ (1)

where i = 1, …, I indexes meioses in a pedigree and j = 1, …, J indexes positions along a genomic region of interest. An inheritance vector [2] at a position is the set of all meiosis indicators at that position:

$$S_J=\left(S_{1j},\dots ,S_{Ij}\right).$$ (2)

With multiple pedigrees, S_j will represent the multiple-pedigree inheritance vector resulting from concatenating inheritance vectors of individual pedigrees. The inheritance vector S_j fully specifies how founder alleles descend in each pedigree at position j.

When inheritance vectors S = (S₁, …, S_J) at positions j = 1, …, J are completely determined, then S together with trait values Y are jointly sufficient for both linkage detection and linkage localization. Under the assumption of no genetic interference [16], the prior distribution of (S₁, …, S_J) is simple: S₁, …, S_J form a Markov chain with state space $\mathcal{S}$, $\mathcal{S}$ being the set of all possible inheritance vector configurations at a single position, common to all j. The distribution of this Markov chain is well-characterized: Mendel's First Law states that meioses are independent, so the meiosis indicators S_ij, i = 1, …, I, at any position j are independent, and that Pr(S_ij = 0) = Pr(S_ij = 1) = 1/2. As a corollary, at each position j, the marginal distribution of S_j = (S_1j, …, S_Ij) is uniform over $\mathcal{S}$. Within each meiosis, at different positions j and j′, meiosis indicators can be different. When S_ij ≠ S_ij′, there is recombination between positions j and j′ at meiosis i. The farther apart the positions are, the more probable it is that there will be recombination between them. The transition probability Pr(s_{j+ 1} ∣ s_j) of the Markov chain is determined by the probability of having recombination between positions j and j + 1.

Assume we have observed trait values y on a subset of individuals in the pedigrees and complete inheritance vectors s = (s₁, …, s_J) at linked positions j = 1, …, J along a chromosome region. When no causal locus is linked to the chromosome region under investigation, observing trait values y should not affect the posterior distribution of the inheritance vectors. So the posterior distribution of the inheritance vectors given observed trait values should be the same as the prior distribution of the inheritance vectors, and the following global null hypothesis should hold:

H₀ : (s₁, …, s_J) follows a Markov chain distribution with uniform marginal distribution and transition probability Pr(s_{j+ 1}∣ s_j). (3)

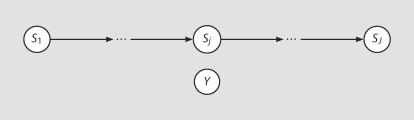
This global null is about the joint distribution of inheritance vectors at all positions. A graphical representation [18] of this global null is shown in figure 1.

Fig. 1.

A graphical representation of the global null model H₀.

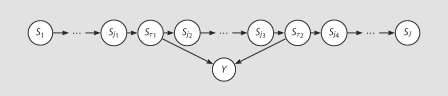
Figure 2 shows a graphical representation of one possible alternative model, in which there are two causal loci τ₁ and τ₂ in the region. A general alternative model can be quite complicated, but under any alternative model, there should be more ‘connection’ between the inheritance vectors $\mathcal{S}$ and the trait values Y. Observing trait values Y = y will affect the posterior distribution of the inheritance vectors, and the posterior distribution of the inheritance vectors (S₁, …, S_J) given the observed trait values y will deviate from the prior distribution of (S₁, …, S_J). Our task is to measure and explore the discrepancy between the posterior distribution of the inheritance vectors given the trait values and the prior distribution of the inheritance vectors.

Fig. 2.

A graphical representation of one possible alternative model.

2.2. Marginal Inheritance Vector Tests

For linkage detection, we want to see whether the data collected provide significant evidence against the global null (3). Since it is difficult to tackle the joint distribution of (S₁, …, S_J) under a general alternative, linkage detection is often achieved using marginal tests. The global null (3) implies the following marginal null hypothesis at all j:

$$H_{0,j}:s_j\hspace{0.17em}\text{follows a uniform distribution over}\hspace{0.17em}\mathcal{S}$$ (4)

A valid test for H_0,j at any j is also a valid test for the global null. To test H_0,j at a single position j, we need a test statistic t(S_j; y) that measures the connection between the inheritance vectors at the test position j and the observed trait values y. The null distribution of S_j is uniform over $\mathcal{S}$. If we sample s_j^(h), h = 1, …, N, uniformly from $\mathcal{S}$, then t(s_j^(h); y) will provide an empirical null distribution of the test statistic. Assuming large values of the test statistic t(s_j; y) indicate deviation from H_0,j, we can compute a valid Monte Carlo p value for testing H_0,j by counting the proportion of t(s_j^(h); y) that are greater than the observed value t(s_j; y) of the test statistic,

$$p=\frac{{\sum }_{h=1}^{N}1\left\{t\left(s_j^{\left(h\right)};y\right)\ge t\left(s_j;y\right)\right\}+1}{N+1},$$ (5)

where 1{·} is an indicator function taking value 1 if the expression in the curly braces in true, 0 otherwise.

Inheritance vectors at linked positions tend to be similar and marginal inheritance vector tests at linked positions are correlated. As a consequence, marginal inheritance vector tests can show significance at positions that are not those of causal loci, but only linked to the true causal loci. A significant marginal test result does not provide specific linkage localization information.

2.3. Conditional Inheritance Vector Tests

For linkage localization, we propose to perform inheritance vector tests conditioning on the inheritance vectors at two positions j₁ and j₂ bounding a test region. If there is no causal locus in the test region, observing the trait values y should not affect the posterior conditional distribution of (S_j ∣ S_j1 = s_j1, S_j2 = s_j2) at any position j between j₁ and j₂, so the following conditional null hypothesis should hold

H^cond_0,j: s_j follows the distribution of (S_j ∣ S_j1 = s_j1, S_j2 = s_j2) as determined by the Markov chain distribution in (3). (6)

To test H^cond_0,j we can compare the observed test statistic t(s_j; y) to the conditional distribution of (t(S_j; y) ∣ S_j1 = s_j1, S_j2 = s_j2). If we sample s_j^(h), h = 1, …, N, from the conditional distribution of

$$\left(S_j|S_{j_1}=s_{j_1},S_{j_2}=s_{j_2}\right)$$

corresponding t(s_j^(h); y) will provide an empirical null distribution of the test statistic. Again, we can compute a Monte Carlo p value for testing H^cond_0,j by counting the proportion of t(s_j^(h); y) that are greater than the observed value of the test statistic, as in equation (5).

The conditional inheritance vector tests provide a statistically valid way to accurately assess the gene localization information in the data. When the above conditional test shows significance, it indicates that there are one or more causal loci between positions j₁ and j₂. The p value of the test gives the probability of having a false positive. This conditional test does not require the specification of the number or effects of the causal genes, and the validity of the test does not rely on such model assumptions. When j₁ or j₂ is close to j, there can be too few meioses with recombinations between j₁ or j₂ and j, and thus not much variability in (S_j ∣ S_j1 = s_j1, S_j2 = s_j2). To improve power, we can perform the test conditioning on more distant positions. As a trade-off, the localization information provided by the conditional test will then be less precise.

2.4. Detecting Additional Linkage Signals

A conditional inheritance vector test can be used also to detect additional linkage signals in the presence of previously detected causal genes. Suppose a causal gene has been detected and localized to the genomic region bounded by positions (j₁, j₂). We can perform a further conditional test conditioning on inheritance vectors at positions (j₃, j₄), the region bounded by which does not overlap with the region (j₁, j₂). This way, we condition out the effect of the previously detected gene by excluding it from the test region of the further conditional test. The test will have the correct type-I error if there is no causal locus in the region (j₃, j₄).

Note that this approach does not require precise point estimates of the locations of previously detected causal genes. This feature is important, since relying on a wrongly estimated gene position may lead to invalid test significance. In our conditional test, we only need to exclude regions that contain any previously detected causal loci. These regions may be available from previous studies or found using our conditional tests.

When the test regions of two conditional tests do not overlap, our simulation results suggest that the p values of the two tests are close to uncorrelated, so adjusting for multiple testing is simple. One could, for example, use a Bonferroni correction [19]. In theory, we can repeat the procedure after a new gene is localized. However, due to power-precision trade-off, we may have to use a wide test region to detect genes with weak effect. This will limit the number of the causal loci that we may resolve.

2.5. Latent Inheritance Vectors

In practice, we cannot observe inheritance vectors. However, there are well established methods on drawing Markov Chain Monte Carlo (MCMC) samples from the conditional distribution of the inheritance vectors given observed genetic marker data [17]. Marginal inheritance vector tests and conditional inheritance vector tests can be extended using an MCMC sample of S = (S₁, …, S_J), when these inheritance vectors cannot be fully determined by the genetic marker data.

Let s^(h*), h* = 1, …, N*, be an MCMC sample from the conditional distribution of S given observed marker genotypes at multiple genetic marker loci. At position j, a p value p(s_j^(h*)) can be computed for each s_j^(h*) according to (5). The collection of p values for all s_j^(h*), h* = 1, …, N*, provides an empirical distribution of a randomized p value [13]. At any nominal level α, this randomized p value leads naturally to a randomized test for H_0,j (see (4)), in which we reject the null with probability

$$\frac{1}{N^{*}}\sum _{h*=1}^{N^{*}}1\left\{p\left(s^{\left(h*\right)}\right)<\alpha \right\}.$$ (7)

When H_0,j holds, the power of this randomized marginal test is α up to discretization error [13].

Conditional inheritance tests can also be performed using an MCMC sample of S. At position j, we can compute a p value for each s_j^(h*), conditional on S_j1 = s_j^(h ₁^*) and S_j2 = s_j^(h₂^*). The p values computed for h* = 1, …, N* will provide us an empirical distribution of a randomized p value for testing H^cond_0,j (see (6)). A valid randomized test can be designed accordingly.

The uncertainty in the latent inheritance vectors may result in power loss. Using randomized p values allows us to decouple the uncertainty in the test results due to latent inheritance vectors from the lack of evidence for linkage detection or localization.

2.6. Test Statistics

In the marginal and the conditional inheritance vector tests, we need a test statistic t(s_j; y) to measure the connection between the inheritance vectors and the observed trait values. Allele-sharing statistics for qualitative traits [20,21,22,23], and variance components estimated using Haseman-Elston regression [24] or more general variance components methods [25, 26], are all functions of inheritance vectors and trait values. They can be used as test statistics for our marginal or conditional tests. However, many allele-sharing statistics use information from affected individuals only, and Haseman-Elston regression or variance components methods aggregate information in relative pairs and ignore the effects of higher-order sharing on trait values. In an attempt to use the data more efficiently, we introduce a test statistic, w-score, that draws information from all individuals with trait values and takes higher order gene sharing into consideration.

We will define the test statistic conditioning on the trait values y. Pedigrees collected in practice are often ascertained and y is often part of the ascertainment criteria, but information on ascertainment criteria is often vague. Conditioning the test on y makes the test more robust to ascertainment [27].

As a motivating example, we first consider a model-based approach. At any potential trait locus j, the inheritance vector S_j specifies how founder alleles have descended in a pedigree. S_j, together with the allelic types A_j of all founder alleles, will determine the genotypes g(S_j, A_j) of all the individuals in the pedigree. Assuming a simple trait model in which locus j is the single causal locus and genotypes at j determine the trait values. Let p_D be the minor allele frequency at the locus j. Let θ be the parameters of the trait model. In a quantitative model, θ can be the genotype-specific mean trait values. In a qualitative trait model, this θ can be the genotype-specific probabilities of being affected. We can measure the connection between s_j and y using Pr(s_j ∣ y). It is not hard to see

$$Pr\left(s_j|y;\theta ,p_D\right)\propto |Pr\left(s_j,y;\theta ,p_D\right)$$ (8)

$$\propto Pr\left(y|s_j;\theta ,p_D\right)$$ (9)

$$=\sum _{a_j}Pr\left(y|g\left(s_j,a_j\right);\theta \right)Pr\left(a_j;p_D\right).$$ (10)

(8) holds since we condition on Y = y, and (9) holds since Pr(s_j) is constant. Note that, if viewed as a function of the location of locus j, this model-based score is simply the likelihood (up to a constant) of the location of the causal gene under the one-locus trait model described above.

The model-based score (10) is not practical, since usually we will not know the trait model parameters θ. So we propose another score, which we call w-score,

$$w\left(s_j,y;p_D\right)=\sum _{a_j}Pr\left(y|g\left(s_j,a\right);\stackrel{‸}{\theta }\left(g\left(s_j,a_j\right),y\right)\right)Pr\left(a_j;p_D\right).$$ (11)

That is, for each (s_j, a_j), we estimate $\stackrel{‸}{\theta }$ based on the observed trait values y and genotypes g(s_j, a_j). Note $\stackrel{‸}{\theta }$ in (11) is not an MLE, since we will estimate a different $\stackrel{‸}{\theta }$ for each different assignment of a_j. Here we are not interested in the values of $\stackrel{‸}{\theta }$. For each possible assignment of founder allelic types, we simply use

$$Pr\left(y|g\left(s_j,a_j\right);\stackrel{‸}{\theta }\left(g\left(s_j,a_j\right),y\right)\right)$$

as a measure of trait value similarity among individuals with same genotypes. We weight the contributions from each possible a_j by its probability.

The w-score is not specific to a particular trait model, it draws information from all individuals with observed trait values in the pedigrees, and it can be implemented for both qualitative and quantitative traits and for general pedigree structures. To compute the w-score for qualitative traits, we need both affected and unaffected individuals, so w-score will not work for affected-sib-pair data. For affected-sib-pair data, an alternative test statistic, such as S_pairs could be used in our marginal or conditional tests.

The qualitative behavior of the marginal and conditional tests will not depend on the test statistic used. It will be of practical interest to know the relative power resulted from different test statistics, but this is not the focus of this paper. In our simulation study, we present a brief comparison of w-score with LOD score computed using a variance component method.

3. Simulation Studies

In this section, we present results of two simulation studies. In the first study, we assume that the inheritance vectors are completely determined. We use this study to demonstrate the differences between marginal tests and conditional tests. In the implementation of the marginal and conditional tests, the newly developed w-score (Section 2.6) was used as the test statistic. To provide a comparison with standard methods, we compare the w-scores with variance component LOD scores computed using the software SOLAR [26]. In the second study, we assume that the inheritance vectors are latent and we need to use dense genetic marker data to infer their distributions. The focus there is to investigate the effects of the uncertainty in the inheritance vectors on both marginal and conditional tests.

3.1. Known Inheritance Vectors

In this first simulation study, we assumed that the inheritance vectors are known. We simulated data on identical copies of a three-generation 12-member pedigree (fig. 3). For each pedigree, we simulated quantitative trait values on the 8 non-founders and inheritance vectors at 21 evenly spaced positions at 0, 5, 10, …, 100 cM along a 100 cM chromosome as shown in figure 4. We first simulated inheritance vectors at two causal loci at 37.5 and 62.5 cM on the chromosome. The inheritance vectors at the 21 positions were then simulated respecting constraints on recombination probabilities. The trait values of the 8 non-founders were simulated based on the genotypes determined by the inheritance vectors at the two causal loci and randomly simulated founder allelic types, and according to the two locus trait model shown in table 1. In this model, locus τ₂ has a stronger effect on trait values and there are interactions between the causal effects of the two loci. Sung and Wijsman [28] used this model to study a two QTL method. To be able to see reasonable powers, in each data set, we simulated 200 pedigrees. For power simulations, we simulated 1000 data sets.

Fig. 3.

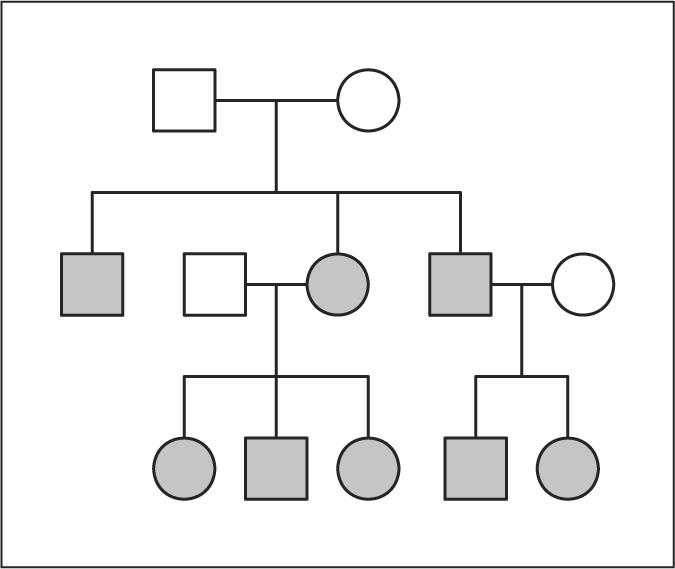
The ped12 pedigree used in the simulation studies.

Fig. 4.

The chromosome simulated in the simulation studies. The two crosses indicate the two causal loci.

Table 1.

A two-locus quantitative trait model

Locus τ1	Locus τ2
	dd	dD	DD
dd	–1.0	7.0	15.0
dD	1.0	3.5	6.0
DD	3.0	0.0	–3.0

Allele frequencies of D at τ₁ and τ₂ are 0.3 and 0.4 respectively.

Let j index the 21 positions on the chromosome. For each data set, at each position j, we performed three tests using the simulated trait values and inheritance vectors: a marginal test and two conditional tests, one conditional on the inheritance vectors s_{j− 1} and s_{j+ 1} at the two positions immediately next to the test position j, the other conditional on the inheritance vectors s_j−2 and s_{j+ 2} at two positions that are one position removed from the test position j. We did not perform tests directly at the causal loci. At each position j, we also computed a variance component LOD score using the software SOLAR [26].

When computing the w-score for a set of pedigrees, we take the product of the w-scores of individual pedigrees to be the multiple-pedigree w-score. For each pedigree, to compute (11), we need to determine

$$Pr\left(y|g\left(s_j,a_j\right);\stackrel{‸}{\theta }\left(g\left(s_j,a_j\right),y\right)\right)Pr\left(a_j;p_D\right)$$ (12)

for each possible founder allelic type assignment a_j. We assumed the rare allele frequency p_D to be 0.3. Previous simulation results (not shown) show that test results are reasonably robust to the specification of p_D. For a quantitative trait, other parameters involved in (12) include the mean trait values (β_DD, β_Dd, β_dd) for different genotypes and the variance of the trait values σ ², which we assumed to be common to all three genotype groups. For each a_j, we estimated (β_DD, β_Dd, β_dd) based on g(s_j, a_j) and y. However, estimating σ² from a small number of individuals will generate very variable estimates and can result in disproportionate contributions to the multiple-pedigree w-score by a few pedigrees. So, instead, we specify the ${\stackrel{‸}{\sigma }}^2$ to be the total variance of observed trait values. This approach will overestimate σ², but the bias will be small unless the genetic variance is large relevant to the total variance, in which case, the causal loci will be easy to detect.

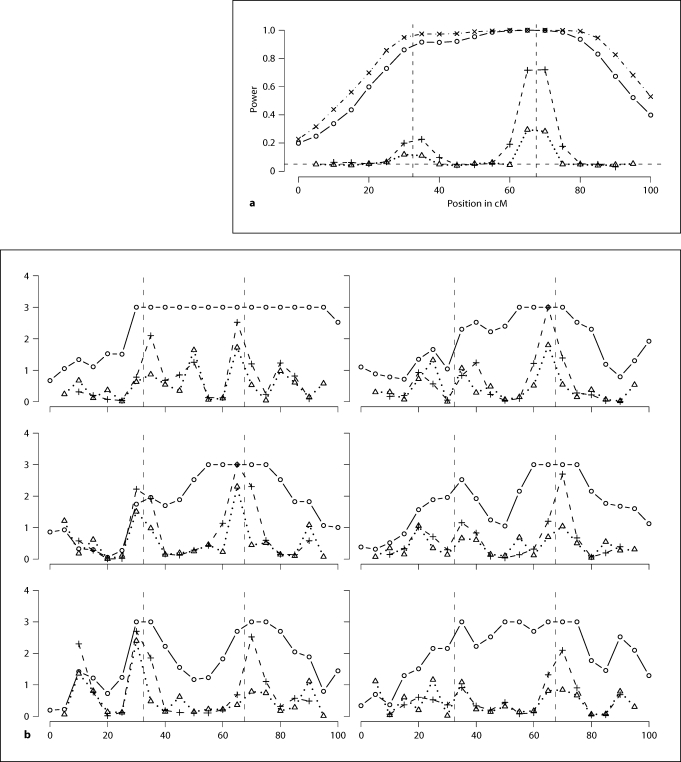
Figure 5 compares the marginal and the conditional tests. Figure 5a summarizes the powers of the marginal and conditional tests. A p value cutoff of 0.05 is used to compute these powers. Figure 5b summarizes the p values of the marginal and conditional tests based on w-scores for six data sets randomly chosen from the 1000 simulated data sets. From the power and the p value curves, we can see that the conditional inheritance vector tests show very specific localizing information. The test conditional on s_{j− 1} and s_{j+ 1} only shows significance when there is a causal locus between j − 1 and j + 1. The p value of the test represents the probability of having a false positive when there is no causal locus between s_{j− 1} and s_{j+ 1}. The conditional tests have the correct type-I errors, as can be seen from the power curves in figure 5a. For the conditional tests, there is a trade-off between power and precision. The tests conditional on s_j−2 and s_{j+ 2} are more powerful, but less precise. When this test shows significance, we can only claim that there is a causal locus between positions j − 2 and j + 2.

Fig. 5.

a Powers of the marginal tests and the conditional tests, nominal level α = 0.05. b −log p values of the marginal tests and the conditional tests for 6 randomly chosen data sets. Two vertical dashed lines correspond to the two causal loci τ₁ and τ₂. The horizontal dashed line in a corresponds to α = 0.05. Solid line with circles: marginal tests. Dotted line with triangles: tests conditional on S_{j − 1} and S_{j + 1}. Dashed line with pluses: tests conditional on S_{j − 2} and S_{j + 2}. In a, dot-dashed line with crosses: powers corresponding to SOLAR LOD scores.

In contrast, the marginal tests show power at all test positions and show strong power at all test positions between τ₁ and τ₂. The p value curves for individual data sets show that a significant marginal test result does not provide specific localization information. We computed the test p values by comparing observed w-score to 1000 simulated null w-scores, so the smallest achievable p value is 0.001. To see more detailed information, we can look at the test statistics. For the six data sets corresponding to figure 5b, we show linearly transformed (details below) log w-scores on figure 6. We see that a log w-score curve can have multiple peaks. Not all peaks correspond to positions of the causal genes and it is difficult to distinguish the peaks. Also, a marginal test statistic curve does not give clear information about the number of possible causal genes in the region.

Fig. 6.

Comparing log w-scores to SOLAR LOD scores. The data sets correspond to figure 5b. The y-axis is on the LOD score scale. The log w-scores were linearly transformed so that they have the same range as the LOD scores. Solid line with circles: log w-scores. Dot-dashed line with crosses: SOLAR LOD scores.

We also compare w-scores with the SOLAR variance component LOD scores. For a power comparison, we converted the LOD scores to approximate p values by first converting the scores to natural logarithm and then comparing twice the converted values to a 50 : 50 mixture of a chi-square distribution with 1 degree of freedom and a point mass at 0. The resulting powers corresponding to the LOD scores are also shown on figure 5a. To compare the test statistics, we linearly transformed the log w-score so that the range of the log w-scores match that of the LOD scores. In figure 6, we see that the variance component LOD scores and the log w-scores show similar qualitative behavior. In Marchani et al. [29], we also saw similar qualitative behavior of w-scores and SOLAR LOD scores in analysis of a large real data set [30] of multiple pedigrees.

We have also performed extensive simulations under other quantitative trait models and under qualitative trait models. The results all show similar patterns in comparisons of p values and of powers between conditional and marginal tests.

3.2. Latent Inheritance Vectors

When the inheritance vectors are latent, we can draw MCMC samples of the inheritance vectors based on dense genetic marker data and summarize inheritance vector test results using randomized p values. Next, we present a simulation study to explain how the randomized p values provide information about both the significance and the uncertainty in a test result, and to demonstrate that the marginal and conditional tests can still provide useful information when the inheritance vectors cannot be completely determined.

In this study, we simulated trait values and dense SNP marker data. We simulated data on one set of 200 pedigrees that are identical copies of the pedigree shown in figure 3. For each pedigree, we simulated inheritance vectors at the two causal loci τ₁ and τ₂ and quantitative trait values on the 8 non-founder individuals the same way as in the last study. To simulate the SNP marker data, we first simulated inheritance vectors at marker positions, respecting constraints on recombination probabilities between marker positions and the two trait loci, and then simulated SNP variants at the markers by gene dropping. Two sets of dense SNP markers along the chromosome region were simulated. One set consisted of evenly spaced SNPs that are 0.25 cM apart. The other set consisted of SNP blocks that are 1 cM apart and have 3 SNPs per block. The recombination rates between adjacent SNPs within a block are 10^–6. Each SNP block is comparable to a microsatellite marker. We set the rare allele frequency for each SNP to be 0.2. The polymorphism and density of these two marker sets are typical of currently available studies.

Conditional on each SNP marker set, we used a version of the MORGAN program lm_auto (http://www.stat.washington.edu/thompson/Genepi/MORGAN/Morgan.shtml) to draw an MCMC sample of size 1000 of the inheritance vectors jointly across the test positions. Other types of genetic marker data, such as microsatellite markers, can also be used in this MORGAN program. The types of markers used influence the marginal and conditional tests only through the variability in the resulting MCMC sample of the inheritance vectors. In this study, SNPs were simulated assuming linkage equilibrium. When SNPs are in linkage disequilibrium, we would need to estimate hyplotype frequencies within LD blocks and use (for example) the clustered SNPs approach of MERLIN [31]. In practice, appropriately chosen tag SNPs [32] that are in linkage equilibrium will often provide sufficient information about the inheritance vectors.

Based on the MCMC sample of the inheritance vectors and the simulated trait values, we performed the marginal and conditional inheritance vector tests at test positions that are evenly spaced and 1 cM apart on the chromosome. Note that the test positions can be chosen independently from the marker positions and test positions do not have to be as dense as the marker positions. For the marginal and the conditional test, at each test position, we computed 1000 p values based on the 1000 sampled inheritance vectors. The collection of these 1000 p values provides an empirical distribution of a randomized p value. For the conditional tests, we conditioned each test on two positions that are 10 cM apart from the test position.

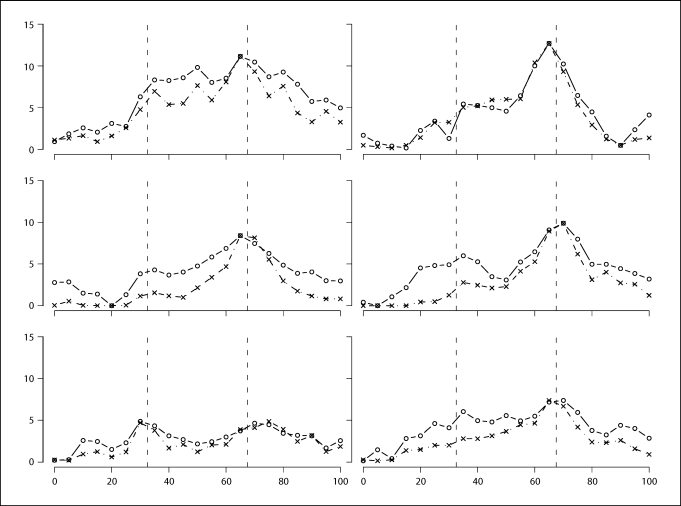
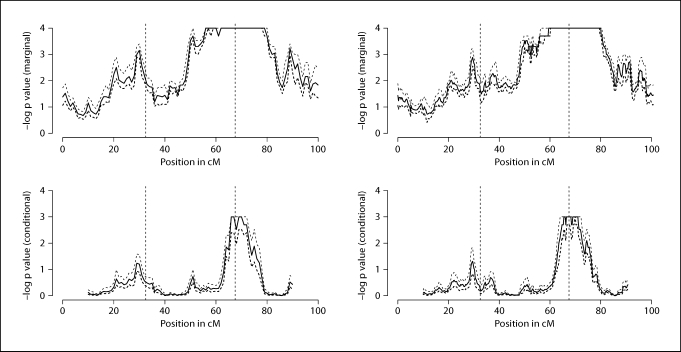
In figure 7, we show the 10-th, 50-th and 90-th percentiles of the randomized p values for the marginal and conditional tests at all applicable test positions. From the randomized p value plots, we see that with such informative marker data, the uncertainty in the marginal and conditional test results is small. With this amount of uncertainty, the marginal and conditional tests can still reveal useful linkage and localization information. For example, for this data set, we can successfully localize causal locus τ₂, since 90-th percentile of the conditional test p value at a nearby locus is below 0.01.

Fig. 7.

10-th, 50-th, and 90-th percentiles of the −log randomized p values for the marginal and conditional tests. The top two plots are for the marginal tests, the bottom two plots are for the conditional tests. For results on the left, the marker data used to infer the distribution of the inheritance vectors are SNP blocks that are 1 cM apart and have 3 SNPs per block with recombination rates 10⁻⁶ between adjacent SNPs in a block. On the right, the marker data used are evenly spaced SNPs that are 0.25 cM apart.

4. Discussion

In this paper, we introduced conditional inheritance vector tests and demonstrated using simulation studies that these conditional tests provide useful information for gene localization. Conditional inheritance vector tests provide a statistically valid way to accurately assess linkage localization information in a data set. These conditional tests are robust to trait model assumptions: they do not rely on correct specification of the number and effects of the causal genes to work. These conditional tests are applicable to general pedigrees and can be implemented for both qualitative and quantitative traits.

We can contrast the conditional test approach with the confidence interval approach to gene localization by comparing the different questions they answer. In a confidence interval approach, the investigators specify a significance level, the resulted confidence interval provides the localization precision. In our conditional test approach, we specify the desired localization precision, which is the size of the test region, the test p value will inform us whether the data provide enough evidence to achieve this localization precision.

We compared conditional tests with marginal tests (Section 3.1). Any marginal test reflects linkage information about the entire chromosome. A significant marginal test result does not provide specific localization information. There are also difficulties in interpreting extreme values of the marginal test statistic (linkage peaks) as corresponding to the locations of causal genes. First, in the simulation study, we saw that the marginal test statistic curve can have many peaks, not all corresponding to causal genes. Second, assuming a single causal gene, Cordell [33] discussed how sample sizes and the effect of the gene can influence the location of a linkage peak. Third, with two causal genes, Hauser et al. [34] demonstrated that a linkage peak may not occur at either gene position. With the number and effects of the genes unknown, the linkage peaks will be even less interpretable.

In contrast, results of the conditional tests are easy to interpret and provide specific localization information. When a conditional test shows significance, the result indicates there is a causal locus in the specified test region. Conditional tests are less powerful than the marginal tests performed at the same positions. The relative lack of power in conditional tests, however, is a reflection of the fact that linkage localization is a more challenging task than linkage detection. In practice, we recommend using marginal tests to scan for linkage signal and then using conditional tests on chromosomes with detected linkage signals to extract more specific localization information. For linkage detection, a more stringent p value could be used.

Precise gene localization will demand substantially more data than linkage detection. The conditional test approach enables us to specify the localization precision according to the amount of data available. It is possible that the conditional tests may not be able to localize genes with small effect at the pre-specified localization precision. In a situation where a strong causal locus is successfully detected and then localized to a small region, we can perform a further conditional test in a region with no previously detected gene to detect additional linkage signals (Section 2.4). This further conditional test could use a wider test region to increase power for detection.

When the inheritance vectors are latent and cannot be fully determined from genetic marker data, we use randomized p values to extend both marginal tests and conditional tests using an MCMC sample of the inheritance vectors. This randomized p values summarize both the significance and the uncertainly in the test results (Section 3.2). Our simulation results show that with highly informative marker data, the uncertainty in randomized p values for both marginal and conditional tests is small and these tests can still reveal useful linkage and localization information.

In the simulation studies, we used the w-score as the test statistic. Other test statistics can be used in our marginal or conditional tests. The qualitative behavior of the marginal and conditional tests will not depend on the test statistic used. The comparison between the w-scores and the variance component LOD scores confirms this (Section 3.1). It will be of practical interest to know the relative power resulted from different test statistics. In future work, we will systematically compare w-scores with other possible test statistics.