Computer-assisted time-averaged holograms of the motion of the surface of the mammalian tympanic membrane with sound stimuli of 0.4 to 25 kHz

Abstract

Time-averaged holograms describing the sound-induced motion of the tympanic membrane (TM) in cadaveric preparations from three mammalian species and one live ear were measured using opto-electronic holography. This technique allows rapid measurements of the magnitude of motion of the tympanic membrane surface at frequencies as high as 25 kHz. The holograms measured in response to low and middle-frequency sound stimuli are similar to previously reported time-averaged holograms. However, at higher frequencies (f > 4 kHz), our holograms reveal unique TM surface displacement patterns that consist of highly-ordered arrangements of multiple local displacement magnitude maxima, each of which is surrounded by nodal areas of low displacement magnitude. These patterns are similar to modal patterns (two-dimensional standing waves) produced by either the interaction of surface waves traveling in multiple directions or the uniform stimulation of modes of motion that are determined by the structural properties and boundary conditions of the TM. From the ratio of the displacement magnitude peaks to nodal valleys in these apparent surface waves, we estimate a Standing Wave Ratio of at least 4 that is consistent with energy reflection coefficients at the TM boundaries of at least 0.35. It is also consistent with small losses within the uniformly stimulated modal surface waves. We also estimate possible TM surface wave speeds that vary with frequency and species from 20 to 65 m/s, consistent with other estimates in the literature. The presence of standing wave or modal phenomena has previously been intuited from measurements of TM function, but is ignored in some models of tympanic membrane function. Whether these standing waves result either from the interactions of multiple surface waves that travel along the membrane, or by uniformly excited modal displacement patterns of the entire TM surface is still to be determined.

Introduction

Sound-induced motion of the tympanic membrane (TM) is the first stage in the transformation of airborne environmental sound into the hydro-mechanical stimulus to the sensory cells within the auditory inner ear. While there are a multitude of detailed models of TM function (e.g. Funnell & Laszlo 1977; Rabbitt and Holmes 1986; Rabbitt 1988; Funnell & Decraemer 1996; Gan et al. 2002; Koike et al. 2002; Fay et al. 2005; Fay, Puria & Steele 2006; Parent & Allen 2007) there is a relative paucity of data describing sound-induced motion of the entire TM, especially at frequencies above 8 kHz. The most detailed descriptions of the motion of the mammalian TM to date come from time-averaged holograms collected in cats (Khanna & Tonndorf 1972), cadaveric humans (Tonndorf & Khanna 1972; Bally 1978; Fritze, Kreitlow & Tinger 1978), cadaveric dogs (Naito 1990; Okano 1990; Suehiro 1990; Maeta 1991) and live humans (Løkberg, Høgmoen & Holje 1979). These data generally provide good qualitative descriptions of the magnitude of sound-induced motions of the mammalian TM surface. There are also more modern quantitative measurements that use either speckle holography (Wada et al. 2002) or scanning laser Doppler vibrometry (Konrádsson, Ivarsson & Bank 1987; Huber et al. 1997; Decraemer, Khanna & Funnell 1999) to study the sound-induced motion of the surface of the TM but the published data using these techniques are few.

Because of the lack of published data, we have not been able to answer fundamental questions of TM function. One major question that has been the subject of differing opinions in the literature is how the TM contributes to high-frequency hearing. Several older reports (Tonndorf & Khanna 1970, 1972; Shaw & Stinson 1983) suggest that the complex patterns of TM motion observed with stimulus frequencies above 4 kHz indicate a ‘break-up’ of the TM similar to the complex motion patterns of microphone diaphragms and loudspeaker cones with sounds above the high-frequency limit of effective sound transduction in these devices (Fletcher 1992). A more recent report opines that the complexity is due to a plethora of modes with closely spaced natural frequencies that can sum to provide efficient TM response to high-frequency stimulation (e.g. Fay et al. 2006). A second major question is whether surface waves on the TM contribute to sound conduction by the middle ear, specifically whether predictions of the transmission of TM surface waves from the periphery to the center contributes to observations of ‘middle-ear delay’ (Puria & Allen 1998; Olson 1998; Parent and Allen 2007). A third major question is whether the observations or predictions of wave-like phenomena on the TM surface (e.g. Puria and Allen 1998; Fay et al. 2005) result from traveling transverse surface waves, or are the consequence of uniformly driven modal motions in a lossy membrane; a complication to this distinction is that equations describing modal behavior can be used to describe traveling waves and vice-versa. While, the data we present do not directly answer these questions, they place limits on the answers.

Over the last two years our group – including personnel from the Worcester Polytechnic Institute (WPI) and the Massachusetts Eye and Ear Infirmary (MEEI) – has worked to apply modern computer-assisted high-speed Opto-Electronic Holography (OEH) to the study of the vibration of the TM (Furlong et al. 2006; Rosowski et al. 2007; Furlong et al. 2009; Hernández-Montes et al. in press). The main benefits of OEH are that the holographic interference patterns are recorded by a digital camera, and the computation of the reconstructed holographic images is accelerated by the use of computer-controlled variations in the length of the optical path of one of the interfering beams (Furlong & Pryputniewicz 1995, 1998). We have used OEH to produce time-averaged holograms (TAHs) that describe the magnitude of the sound-induced motion of the surface of the TM of cadaveric and live animals to tones of varied frequency and level, where the digital-optical processing techniques (described below) allow independent computations of surface motion patterns at rates of 10 holograms per second. We use these TAHs to quantify patterns of TM surface motion produced by sound frequencies between 0.4 and 25 kHz. Two advantages of OEH derived time-averaged holography are (1) the high spatial resolution of the measurement; we image the whole surface of the TM with a pixel size equivalent to an area of (45 micrometers)²; 2) the optical measurements, holographic computations and display occur at video rates. Therefore, one can sweep frequency or level and observe real-time changes in the displacement pattern of the entire TM.

A unique feature of our results is the demonstration of ‘ordered’ modal displacement patterns on the surface of the TM at frequencies above 8 kHz. The observation of these patterns depends on the high-spatial resolution of the OEH technique. The displacement patterns produced by sound frequencies above 2 kHz describe clear nodes (regions where the motion is minimal) on the TM surface that are indicative of strong modal patterns, e.g. standing waves, on the TM surface. Such modal patterns are not a primary feature of several existing models of TM surface displacement (Fay et al. 2005; Fay, Puria & Steele 2006; Parent & Allen 2007). The recognition of the presence of modes or standing waves, and descriptions of their frequency dependence and associated wave-propagation velocities and TM losses will lead to refinements of our understanding of TM motion.

Methods

Computer-Assisted Laser Holography

Computer-assisted Opto-Electronic Holography (OEH) uses a digital camera synchronized with an optical phase shifter to capture multiple interference images while stepping the optical phase of one of the interfering beams in cyclic steps of 90° (Furlong and Pryputniewicz 1995, 1998). The optical interference images captured by the digital camera describe variations in the optical path length between a beam of coherent light that is reflected from a moving object (the reflected object beam) and a fixed coherent reference beam (Kreis 2005).

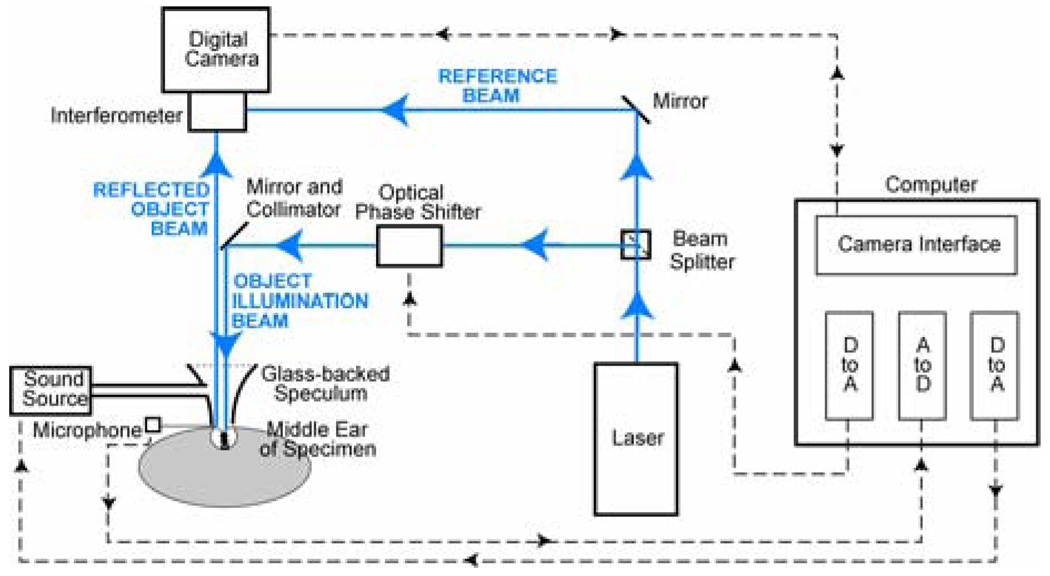
An overview of the OEH system we use is schematized in Figure 1 and summarized here. Details of the systems design and construction have been published elsewhere (Hernández-Montes et al. in press). The output of a collimated laser source is split into reference and object beams. One of these beams is also subjected to an optical phase shift of 0, 90, 180 or 270 degrees via a computer-controlled piezo-electric mirror system that changes the optical path length by an appropriate fraction of the optical wave length (either 0, 0.25, 0.5 or 0.75 times the wavelength of the laser light). These path-length changes are synchronized to the frame rate of the digital camera, such that any four successive images are captured at four different phase-shifter settings. The object beam illuminates the surface of the TM. The reflected object beam is combined in the interferometer with the fixed reference beam and the resultant interferogram is recorded by the camera, which has a functional imaging area of 360² pixels. The holographic image is reconstructed from the digitized interferograms as we describe later. The controlling computer also produces an analog signal to drive the sound stimulus and uses an analog-to-digital converter to measure the output of a probe-microphone positioned at the edge of the TM surface.

Figure 1.

Time-averaged Holography (TAH) via Computer-assisted Opto-Electronic Holography (OEH). Details of the systems design and construction have been published elsewhere (Hernández-Montes et al. in press). The output of a collimated laser source (473 nm, 15 mW) is split into a reference and object beam. One of these beams is also subjected to an optical phase shift of 0, 90, 180 or 270 degrees, via a computer-controlled piezo-electric mirror system that changes the optical path length by an appropriate fraction of the optical wavelength. The object beam is directed to illuminate the surface of the TM. The reflected object beam is combined in the interferometer with the fixed reference beam and a digital camera records the interferogram. The controlling computer also produces an analog signal to drive the sound stimulus and uses an analog-to-digital converter to measure the signal produced by a probe-microphone near the surface of the TM.

Digital manipulation of the four phase-stepped time-averaged interference patterns yields one time-averaged hologram for every 4 camera frames. In the present system, the camera frame rate is limited to about 40 frames per second allowing the calculation of an independent TAH image every 0.1 s; however, the use of a rolling computation scheme produces a new holographic image with every successive frame. This rapid computation rate reduces the effects of very low-frequency motion noise in the system and permits the observation of changes in TM motion patterns at video rates. Since the imaged TM area of 40 to 70 mm² takes up about 40,000 pixels, the system is therefore capable of determining the magnitude of the displacement of the entire TM with a spatial resolution of about 45 microns in 1/10^th of a second: A spatial and temporal resolution that is far superior to scanning laser vibrometry.

Computation of the Holograms

Interference images acquired by the digital camera are processed by computer to provide quantitative measurements of the deformation of the tympanic membrane. The computation is based on spatial and temporal intensity distributions, I (x,y,t), captured by the camera and defined at the surface of the camera’s backplane (x,y), i.e.,

$$I(x,y,t)=I_o(x,y,t)+I_r(x,y,t)+2\sqrt{I_o(x,y,t)I_r(x,y,t)}\text{cos}[\mathrm{\Delta }\varphi (x,y,t)+\Omega (x,y,t)],$$ Eqn. (1)

where I_o (x,y,t) and I_r (x,y,t) represent temporal variations in the intensities of the two interfering beams (the beam reflected from the object and the reference beam), and (x,y,t) represents spatial variations in the optical phase difference between the two beams when the system is at rest. The fringe locus, Ω(x,y,t) , is related to displacements and deformations of the samples of interest that vary in time (Furlong & Pryputniewicz 1995, 1998; Kreis 2005).

In time-averaged mode, a periodic motion of the object modulates the path length of the object beam, and the light intensity at each camera coordinate is averaged over multiple periods of the stimulus. Quantitative measurements are obtained by performing continuous exposure of the camera during image acquisition to provide intensity distributions of the form

$$\overline{I}(x,y)=\frac{1}{\mathrm{\Delta }t}{\displaystyle {\int }_t^{t+\mathrm{\Delta }t}I(x,y,t)\mathit{\text{dt}},}$$ Eqn. (2)

where t is the exposure time of the camera. By varying the optical path length of either the reference or object light path by n = 0, 1, 2, or 3 quarters of a wavelength using the piezo-controlled mirror system, the n-th intensity distribution in time-averaged mode is

$${\overline{I}}_n(x,y)={\overline{I}}_o(x,y)+{\overline{I}}_r(x,y)+2\sqrt{{\overline{I}}_o(x,y){\overline{I}}_r(x,y)}\text{cos}\left[\mathrm{\Delta }¯\varphi (x,y)+{\theta }_n\right].M[\overline{\Omega }t(x,y)],$$ Eqn. (3)

where _n is the optical phase change associated with the nth alteration in the optical path length, and M[Ω̄t (x,y)] is the characteristic function determined by the temporal motion of the sample under investigation. For the case of a sample excited by sinusoidal functions with period much shorter than the exposure time of the camera,

$$M[\overline{\mathrm{\Omega }}t(x,y)]=J_o[\overline{\Omega }t(x,y)],$$ Eqn. (4)

where J₀ is the zero-order Bessel function of the first kind (Stetson and Brohinsky 1988; Pryputniewicz 1994; Furlong and Pryputniewicz 1995).

The digitally reconstructed holographic image has the form:

$${\overline{I}}_d(x,y)=4\sqrt{{\overline{I}}_o(x,y){\overline{I}}_r(x,y)}\left|M[\overline{\Omega }t(x,y)]\right|,$$ Eqn. (5)

and can be computed from the intensities of the interference patterns made at the four different optical phases

$${\overline{I}}_d(x,y)=\sqrt{\left({\overline{I}}_0(x,y)-{\overline{I}}_2{(x,y)}^2\right)+{\left({\overline{I}}_1(x,y)-{\overline{I}}_3(x,y)\right)}^2.}$$ Eqn. (6)

Time-Averaged Holograms (TAH)

In our system, the computed TAH describes the magnitude of the component of object displacement orthogonal to the camera plane that is perpendicular to the nearly parallel illuminating and reflected object beams. The TAH is a gray-scaled surface map in which the magnitudes of the displacements at different points on the imaged surface d(x,y), averaged over the exposure frame of the camera, are coded as variations in image intensity. Specifically, the averaged intensity at each x and y position on the image surface Ī_d (x,y) is proportional to the square of the 0^th order Bessel function of the first kind of the product of the averaged displacement magnitude d(x,y) and the wave number k associated with the wavelength of the light produced by the laser, where k = 2 /. In the case of collinear illumination and reflected object beams (as in our system, Figure 1), IR(x,y), the ratio of the measured light intensity at any point I_d(x,y) and the illuminating intensity of the laser I₀(x,y) is:

$$\mathit{\text{IR}}(x,y)=\frac{{\overline{I}}_d(x,y)}{{\overline{I}}_0(x,y)}\propto {\left(J_0\left(2kd(x,y)\right)\right)}^2,$$ Eqn. (7)

where J₀ is the 0^th order Bessel function of the first kind and the factor of 2 in the function argument accounts for the equal effects of object motion on the path length of both the illuminating and reflected object beams (Kreis 2005).

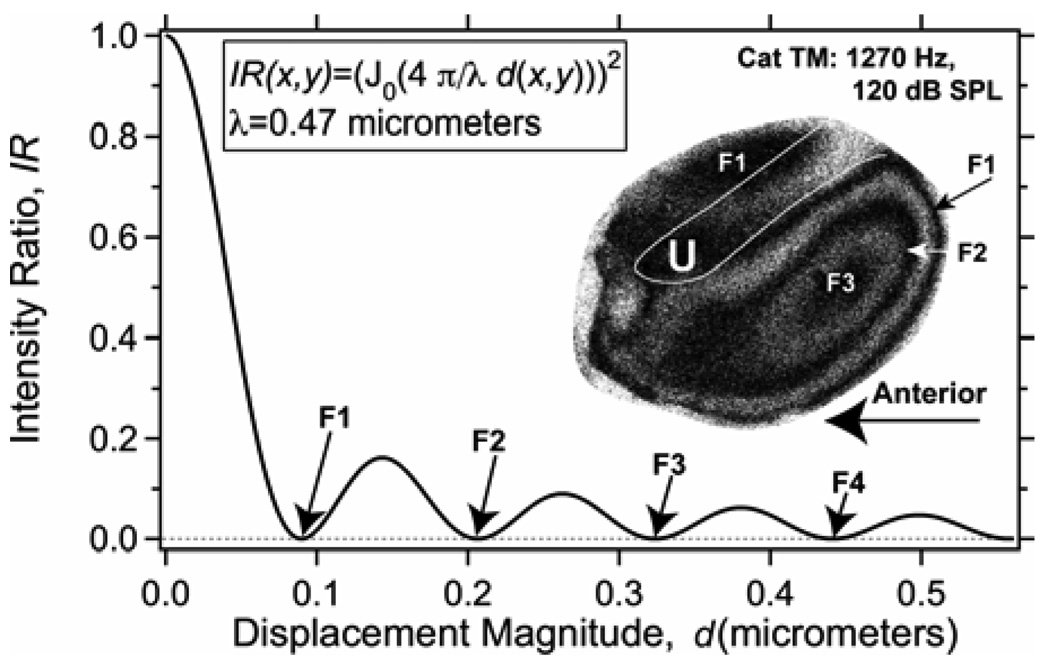
Figure 2 describes the mapping between the intensity of the TAH image and magnitude of displacement, which couples the smallest displacement magnitudes with the highest IR (the brightest parts of the image). If we were to vary our sinusoidal stimulus intensity, such that the magnitude of the displacement increases from 0 to 0.5 micrometers at any one location, the image intensity at that location would go through a series of minima and relative maxima. This periodicity of the mapping function with displacement magnitude is responsible for a series of alternating dark and brighter fringes observed in the inset TAH measured in a cat ear. Each of the dark holographic fringes, defines a spatial contour of displacement magnitude that produces a zero in the resultant intensity, where these fringes occur at the displacement magnitudes of 0.09, 0.21, and 0.33 micrometers. The smallest motions (d < 0.05 micrometers) on the membrane surface are coded by the highest intensity on the image, e.g. the bright spot in the upper right hand corner of the TM near the ‘lateral process’ at the intersection of the manubrium (or handle) of the malleus and the tympanic ring. The regions of largest motion magnitude (of about 0.3 micrometers) are coded by the dark spot in the middle of the posterior half of the TM (labeled F3) that is surrounded by two dark fringes.

Figure 2.

The mapping between the Intensity Ratio on the image surface IR(x,y) and the displacement magnitude along the surface d(x,y) (Equation 7) for our blue laser system with = 0.47 micrometers. The Inset shows fringes of displacement amplitude on a cat tympanic membrane stimulated by a sound of 1270 Hz and 120 dB SPL. The white outline line shows the outline of the ossicular handle (the manubrium of the malleus) that is attached to the membrane. The ‘lateral process’ of the manubrium is located at the intersection of the manubrium and the tympanic ring. The ‘U’ labels the umbo, the tip of the handle. The F1, F2 and F3 label black ‘fringes’ related to the zeros in the IR at 0.09, 0.21 and 0.33 micrometers, respectively.

Sample Preparation

The ears of cadaveric chinchillas, cats and humans and the ear of a live anesthetized chinchilla were prepared in a similar manner. The middle-ear air spaces of each specimen were widely opened to enable assessment of the normality of the TM and ossicles. The cartilaginous ear canal was resected and the bony external ear canal was drilled away until 85% to 95% of the lateral surface of the TM was visible. (Attempts to remove more bony canal usually perforated the TM near its rim.) To increase the amount of light reflected from the TM surface, the TM was lightly painted with a solution of TiO₂ powder in saline. The painted and widely exposed TM was placed against a sound coupler integrated into the interferometer head and oriented such that the surface of the TM was perpendicular to the object beam of the laser (Figure 1). The sound coupler tip was a truncated speculum that came into irregular contact with the bone surrounding the TM, but was not sealed to the bone. The reflected object beam was focused in the interferometer where it was combined with the reference beam to produce interferograms.

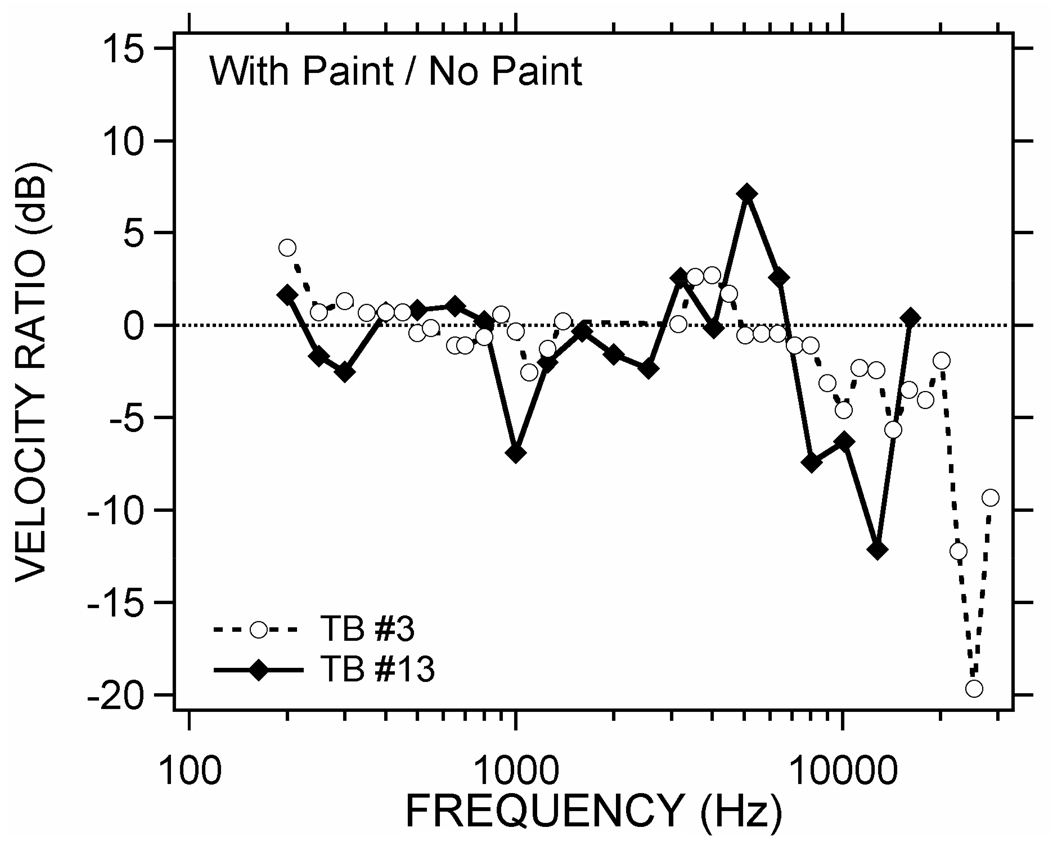
Laser Doppler vibrometer (LDV) measurements of sound-induced stapes motion before and after painting the tympanic membrane (using the techniques of Chien et al. 2007) have been used to quantify the effect of painting on middle-ear function in two temporal bones. Illustrated in Figure 3 are ratios of two sets of stapes-velocity measurements. Each set consists of a sound-induced velocity measured after painting the TM in an excised temporal bone that is normalized by a measurement of velocity made before painting. These ratios (in dB) suggest the effects of paint on middle-ear transmission can be less than a few dB across a broad frequency range dB, but there are frequency regions where the effects are as large as 10 to 20 dB. The larger paint-induced changes occur at the higher frequencies, but the data do not suggest a simple monotonic reduction in TM displacement with increasing frequency, and the frequency range of the biggest changes varies between the two preparations. While suggestive of generally small-to-moderate effects of the paint on stapes velocity, these data do not address the possibility that the paint influences the pattern of vibration of the TM in a significant manner without influencing stapes motion. Such a possibility is a point of later discussion.

Figure 3.

Effect of paint on stapes motion. Ratios of the sound-induced velocity of the stapes in two temporal bones (TB #3 & 13) measured before and after painting the TM with TiO₂. The ratio of the velocity measured after painting to that measured before painting has been converted to decibels, where the dB value = 20 × log10(the velocity ratio).

Sound Stimulation and Capture of the TAH

Continuous sinusoids at frequencies between 0.4 and 25 kHz and RMS (root-mean square) levels between 0.7 mV and 7 volts were generated by a stimulus generator controlled by the computer. The sound stimulus was produced by a Beyer-Dynamic DT-48 earphone, and a calibrated Knowles hearing-aid microphone and probe-tube mounted within 1 mm of the edge of the TM (see Figure 4) produced a measure of sound pressure. Stimulus frequency and intensity were varied while observing the stream of reconstructed TAH images generated every 0.025 seconds (40/s) on a computer monitor. Images at selected frequencies and levels were stored for later analysis.

Figure 4.

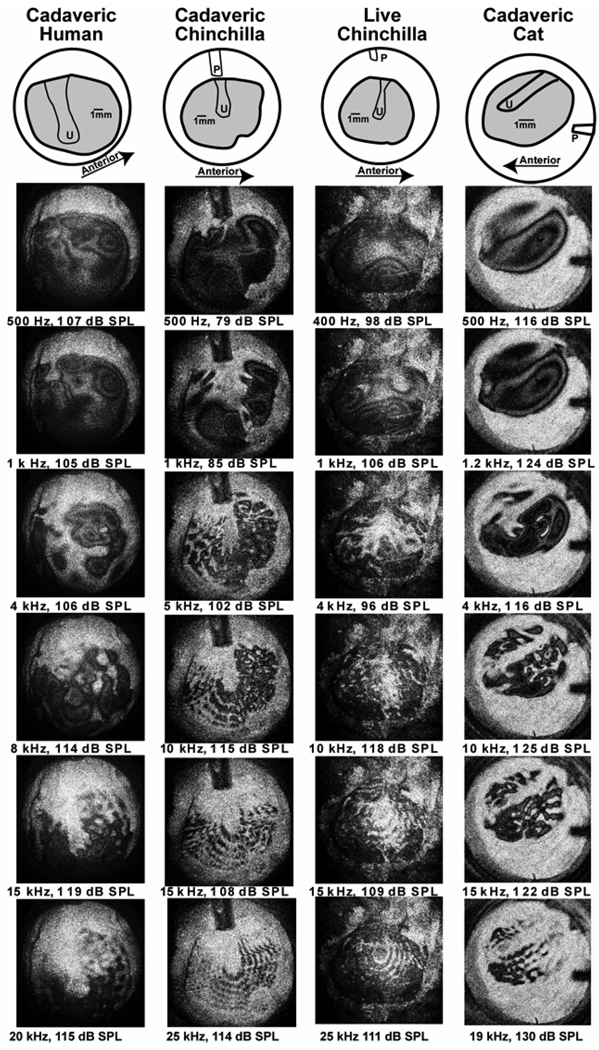
Time-averaged holograms measured in four specimens: the left-handed column contains TAHs measured in cadaveric humans, the next in cadaveric chinchilla, the third from the left in live chinchilla, and the right-hand column in cadaveric cat. The top row contains cartoons showing the exposed area of the TM (in gray), the location of the handle of the malleus on the medial surface of the imaged TMs, the umbo (U) and the probe tube. The scale bars show a 1 mm length in each image. The TAHs are arranged from top to bottom in order of the sound frequency of the stimulus. The rows group similar stimulus frequencies.

The stimulus levels used to produce the measured holographic patterns varied from 80 dB SPL to 130 db SPL. In general, it was necessary to increase the stimulus level with higher stimulus frequencies to overcome the decline in the displacement of the TM and ossicles produced by constant level stimuli as frequency increased above 1000 Hz (Guinan and Peake 1967; Saunders and Johnstone 1972; Goode et al. 1994). At 130 dB, Fourier analysis of the sound-pressure waveform revealed distortions; however, the level of distortion was at least 20 dB below the stimulus level. The distortions were even less significant at lower stimulus levels.

There is a second issue associated with the use of high stimulus levels: Do sound pressures of 120 to 130 dB SPL produce nonlinear motion of the TM? We argue that nonlinearity is not an issue in our measurements in that ossicular motion has been demonstrated to grow linearly with stimulus levels as high as 124–130 dB SPL (Guinan and Peak 1967; Goode et al. 1994). Also, all of the patterns of motion we describe develop along a simple progression as stimulus level increases from 80 to 130 dB SPL, such that what is observable at high stimulus levels is evident at lower stimulus levels. Finally, most of the data we show were gathered with stimulus levels of 116 dB SPL or less.

Another potential concern, especially with stimulus frequencies above 10 kHz where the dimensions of the TM are a significant fraction of the wavelength of the sound stimulus, is whether the probe-microphone measurements made at one location near the rim of the TM are a reasonable approximation of the sound pressure across the TM surface. To address this concern we made control measurements of the sound produced at 16 points on the surface of an artificial membrane, whose area and maximum displacements were similar to the TM. The measurements were made with a probe microphone mounted on a micromanipulator, where the position of the probe opening was moved across two diameters (a vertical and a diagonal diameter) of the circular membrane. Results indicated that at frequencies of 20 kHz or less, the sound pressure magnitude varied by less than 3 dB, and the phase angle of the pressure varied by less than 0.05 cycles from the pressure measured at the rim. In general, the sound pressures were larger in the center, than toward the rim. Variations in sound pressure of as large as 20 dB were seen at frequencies between 20 and 30 kHz.

Results

Variations in TAHs with stimulus frequency

Figure 4 shows TAHs of the sound-induced TM displacements of a cadaveric human (left-most column), a cadaveric chinchilla (second to the left), live chinchilla (third from the left) and cadaveric cat (right column), at selected frequencies from about 400 Hz (the top row of TAHs) to near 20 kHz (the bottom row). The stimulus intensities (in dB SPL) were selected to produce a moderate level of TM motion in each TAH. At the top of each column is a cartoon depicting the orientation of the exposed TM surface (the gray area) with the handle of the malleus outlined in black and the umbo labeled (U). The tip of the probe-tube microphone is clearly visible at the top of the chinchilla images (near 12 o’clock), and at 3 o’clock in the cat TM images. The prominent white areas at the top of each image in the three left-most columns and at the bottom in the right-hand column are the non-moving bony ring that supports the TM.

The TAHs in the 3 species and 2 conditions have several features in common. At the lowest frequencies in each column (the top rows), the displacement patterns are fairly simple: The entire membrane, including the part attached to the manubrium of the malleus, is generally set into motion (the entire membrane is colored moderate gray or black) with one-to-three displacement maxima (the center area of a group of concentric fringes) occurring at different membrane locations. At 4 kHz in cat and human, and near 1 kHz in the chinchilla, the TAHs show a more complicated pattern with interdigitating areas of concentric rings that are separated by bright areas that correspond to ‘nodal’ regions of reduced motion.

At frequencies above 4 kHz in chinchilla and above 8 kHz in cat and human, the patterns become more ordered, with an increase in the number of dark local motion maxima surrounded by white nodal areas. The small dark gray/black areas of measurable motion are arranged in circular and radial patterns on the membrane surface, and appear as dark pearls on multiple concentric nested strings. The structure of these pearls is best observed as stimulus level is varied and will be discussed in the next section. As frequency increases, (a) the number of pearls increases, (b) the spacing between the center of the pearls decreases, and (c) the space between the nested strings decreases. Another feature of the high-frequency membrane displacement patterns, independent of the arrangement of nodes, is that those parts of the TM lateral to the manubrium of the malleus generally appear fairly bright because they move much less than most other areas on the TM, especially as frequency increases above 1 kHz. This decreased motion of the ossicular attachment in the TM has been noted by others (e.g. Tonndorf & Khanna 1970, 1972; Khanna & Tonndorf 1972; Decreamer et al. 1999).

Variations in TAHs with stimulus level

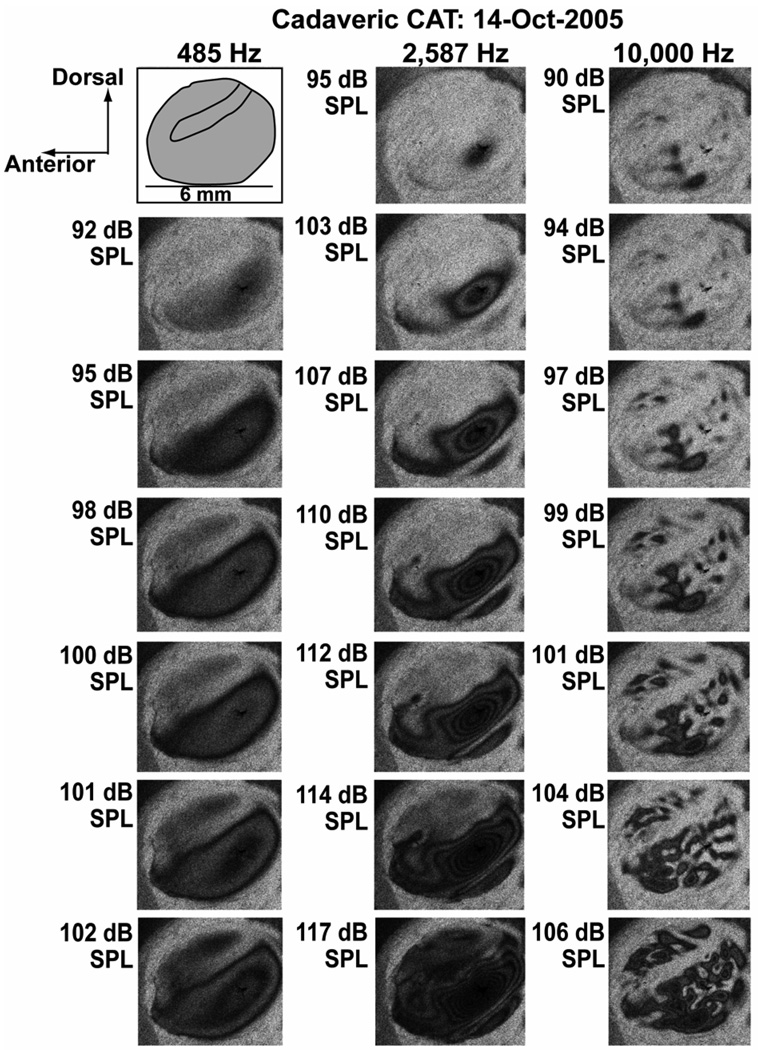
Examples of how TAH patterns vary with stimulus level are illustrated by a level series measured at three frequencies in a cadaveric cat (Figure 5). The simple displacement pattern observed with 485 Hz tones contains two modal regions marked by local displacement maxima, one modal region is ventral and posterior to the manubrium and becomes apparent between 92 and 95 dB SPL; the second modal region is dorsal and anterior to the manubrium and appears at levels above 100 dB SPL.

Figure 5.

Time-averaged holograms measured in a cadaveric cat ear at three frequencies and 6 or 7 levels at each frequency. The cartoon in the upper left hand corner describes the area of the TM (in gray), the dimensions and the location of the manubrium. Each of the three columns describes data taken at one frequency. The stimulus levels vary between 90 and 117 dB SPL.

The ‘complex’ displacement patterns observable with 2587 Hz stimulation in Figure 5 show three modal regions of larger motion with at least one clear ‘nodal’ region of reduced motion separating two of the modal areas. The most sensitive mode appears at sound levels greater than 95 dB SPL in a position posterior and ventral to the manubrium, but its shape is irregular compared to the similarly positioned modal maximum seen at 485 Hz. With stimulus levels above 105 dB at 2587 Hz, we observe a second long-thin modal maximum positioned at the extreme ventral rim of the exposed TM, and this long-thin mode is separated from the first modal region of local maximal displacement by a thin ‘white’ nodal region of minimal displacement. As stimulus level increases above 110 dB SPL each of the visible modal areas gets larger as increased areas of the membrane move with displacements large enough to create fringes and the number of concentric fringes within each modal region increases. At 117 dB, the two ventral modal areas are still separated by a nodal minimum, and we begin to see fringes developing in the anterior-dorsal region of the membrane. The THA measured at 2587 Hz and 117 dB SPL is also the only TAH in the series illustrated in Figure 5 that shows significant darkening of the TM over the manubrium.

The right-most column of Figure 5 illustrates the development of ‘ordered’ motion patterns in the cat. With a 90 dB SPL 10000 Hz stimulus, we clearly see three dark ‘pearls’ (small local motion maxima surrounded by regions of lower motion) in the ventral area of the TM that are arranged along a dorsal-ventral projection. There are also hints of other smaller pearls in the posterior ventral and dorsal quadrant. As stimulus level increases, the more prominent dark pearls grow slowly in size, but also develop clear fringes, where at 99 dB SPL the largest pearl shows two clear fringes. At the same level we also see over a dozen smaller pearls scattered over the membrane surface. At 104 dB SPL some of the larger pearls have broken into smaller pearls, and the pearls in the ventral half of the TM are roughly arranged in three lines or ‘strings’ that parallel the manubrium of the malleus. We also see multiple strings of pearls in the dorsal membrane. At 106 dB SPL, some of the regions separating the pearls along each string have begun to displace enough to fill in the areas along each string with dark fringes; however, the strings are still separated from each other by scattered nodal regions

In general, the area of each pearl is defined by a contiguous area in which the displacement magnitude is large enough to produce a ‘dark’ region in the computed THA, surrounded by a ‘light’ region of low displacement magnitude. The pearls are arranged in strings across the TM surface that parallel the manubrium in cat, or roughly radiate from the umbo in chinchilla and man (Figure 4). Once the stimulus level is large enough to define the pearls, the location and spacing of their centers varies little with level, though Figure 5 shows examples of the splitting and latter rejoining of pearls. Also as stimulus level increases the ‘brighter’ areas of reduced motion that separate pearls along strings tend to get smaller and even disappear, while the brighter areas that separate the strings are somewhat more resilient.

Variations across species

The comparisons of Figure 4 also suggest some across species differences. The TM of the chinchilla and human TMs are nearly round with a manubrium that is nearly vertical in the skull, while the cat TM is more oval, with a relatively longer manubrium that is more horizontal in its position. The scale bars in the top row of the images point out that the chinchilla and human TM are of similar dimension, while the cat TM is smaller. As noted above the ‘complex’ and ‘ordered’ modal patterns occur at lower frequencies in chinchilla than they do in either human or cat. Also, while all three species show clear ‘strings of pearls’ patterns with high-frequency stimuli, the identification of individual pearls is more difficult in the human TAHs, though some of this difference may be related to the choice of stimulus levels.

Discussion

Comparison to previous studies

The time-averaged holograms in Figure 4 show similarities and differences with TAHs that have been previously described. The best-described set of TAH data is that of Khanna and Tonndorf (1972) in cat and Tonndorf and Khanna (1972) in human temporal bone. In those groundbreaking studies Khanna and Tonndorf described simple patterns of TM surface displacement that occurred at frequencies of less than 2 kHz, where the displacement patterns were consistent with in-phase displacement of the entire membrane surface with one to three spatial maxima located on the membrane surface. At frequencies between 2 and 8 kHz, the patterns of displacement became more complicated; the number of local maxima increased, the shape of each maxima increased in complexity and the different maxima where separated by high light intensity (bright) regions of greatly reduced motion (nodes).

These two distinct patterns are observable in our data. We see simple patterns of displacement in chinchillas at frequencies less than 0.8 kHz, and in cat and human at frequencies less than 2 kHz. The complex patterns with multiple maxima separated by nodal lines of negligible motion and high light intensity occur in chinchillas at frequencies between 1 and 3 kHz and at frequencies between 2 and 8 kHz in cat and human. In addition, our data demonstrate that at higher frequencies, all of the specimens show a transition from complex to ordered patterns where a large number of local displacement maxima are orderly arranged on the membrane surface. As we will see, these ordered patterns of displacement are consistent with modal displacement patterns in a simple acousto-mechanical system.

While we describe three step-like differences in displacement pattern (simple, complex, ordered), these different classifications describe prominent positions along a progression of patterns. For example, once we recognized the existence of the ordered pattern at higher frequencies, we could trace its origin back in frequency into what we originally considered the complex domain. Indeed, one of the major differences between complex and ordered is not in the position or shape of the node-separated modal maxima (the ‘pearls’ and ‘strings’) but in their number and size. The larger the number of the pearls and strings and the smaller the dimensions of the pearls, the more apparent is their ordered arrangement.

Consistent with a progression of displacement pattern, the ordered patterns show additional order in how they vary with increasing frequency. As stimulus frequency increases the patterns show regular changes consistent with an increase in the number (or density) of the local maxima (the pearls) as well as an increase in the orderliness of their arrangement. The increase in density is also associated with a decrease in the spatial area of each local maxima. The regular variation in the size, number and location of these local maxima as frequency increase, makes it unlikely that their location and size are tied to inhomogeneities within the structure of the membrane such as variations in the membrane thickness or in the density of radial or circumferential fibers within the central layer of the TM (Lim 1968, 1970; Funnell & Laszlo 1982; Decraemer & Funnell 2008).

Methodological Issues and Potential Artifacts

The effects of painting the TM surface

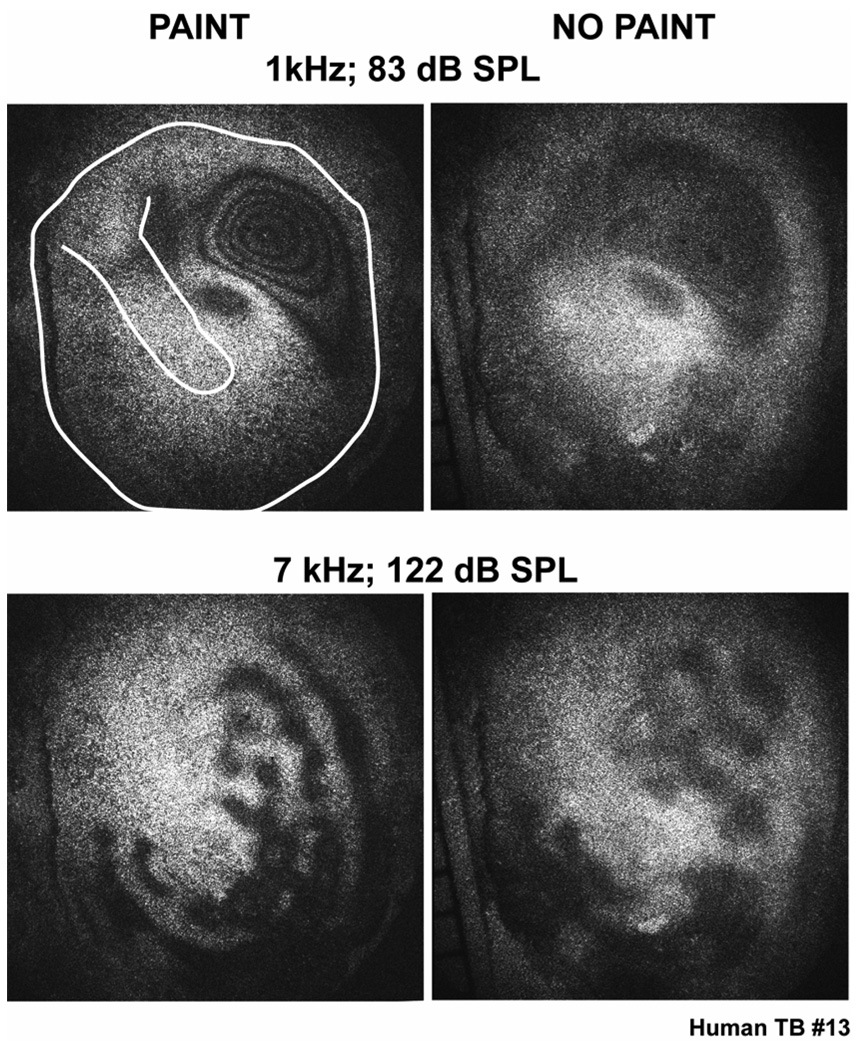
Another point of commonality between this study and most holographic studies of TM motion (the exception is Løkberg et al. 1979) was the need to coat the TM surface with an opaque paint or metal powder in order to decrease the transparency of the measurement surface. We have presented laser-Doppler vibrometer data (Figure 3) that demonstrate that the effect of our TiO₂ painting procedures on sound-induced stapes velocity is relatively small at frequencies below 8000 Hz, but it can produce narrow-band reductions in stapes velocity magnitude of as much as 20 dB at higher frequencies. An unanswered question is: How the coating affects the patterns of TM displacement? We have made some preliminary measurements in human temporal bones of TAHs with and without painting. The thicker epidermal layer of the human tympanic membrane is more opaque than in animals (especially in older humans) and like Løkberg et al. (1979), we were able to obtain a few ‘muddy’ TAHs with more poorly defined fringes without painting the membrane (Figure 6). With low-frequency stimulation the painted and non-painted TMs show similar-sized areas of gray in similar locations, though no fringes are visible within the gray area of the unpainted TM. With high frequencies the typical ‘pearl and string’ pattern is visible in the unpainted TMs and the location of the pearls and strings is comparable to that observed after painting. The pearls on the unpainted membrane are less well defined and appear larger. We conclude from these measurements that painting the TM does not evoke the basic patterns of displacement that we observe; it does however make them visible.

Figure 6.

A comparison of the time-averaged holograms measured with a cadaveric human temporal bone at two frequencies before and after applying a thin layer of TiO2 paint on the TM surface. The TM is oriented in an identical manner in each figure. The line drawings added to the upper-left hand panel show the boundaries of the TM and orientation of the manubrium of the malleus.

The need for high sound levels

Because (1) the THA is a measure of the sound-induced displacement of the TM and our blue laser requires a relatively large displacement value of 0.1 micrometers to evoke the first holographic fringe, and (2) the displacement of the TM produced by a constant SPL decreases as frequency increases, the TAHs we illustrate were gathered with the high sound levels of 80 to 130 dB SPL. At the highest levels of this range, we expect measurable nonlinear responses, visible as harmonic distortion: in the sound source, in the microphone, in the sound-field itself, as well as in the middle ear’s response to sound. Measures of distortion made with the probe microphone noted visible harmonic distortion, but such distortions were at least 20 dB smaller than the stimulus-frequency at 130 dB, and smaller at lower stimulus levels. Also measures of ossicular motion show responses consistent with low-distortion (at least 20 dB down) at stimulus levels that approach 130 dB SPL (Guinan and Peake 1967; Goode et al. 1994). It has also been noted that most of the measurements we illustrate were gathered at sound levels less than 116 dB SPL, and that all of the patterns of motion that we describe are visible in ears at sound levels less than 100 dB SPL. Therefore, the basic results of this report are not greatly affected by nonlinearities in the sound stimulus or in the TM’s response to high-level sound.

Spatial variations in the high-frequency sound field

Another potential acoustic artifact in our results that we have discussed is the presence of variations in the sound field in space, specifically variations between the sound pressure at different points on the membrane surface and at the probe microphone placed within 1 mm of the TM’s rim. Such variations are expected to be more significant at high frequencies where the dimensions of the TM (4.5 mm radius for chinchilla and human and 3–3.5 mm radius for cat) are a significant fraction of the sound wave length: The wave length of a 20 kHz tone in air at standard temperature and pressure is 17 mm, and wavelength varies inversely with frequency. While we have not investigated spatial variations in the sound field acting on our experimental membranes, the methods summarize some control measurements made on an artificial membrane of similar dimensions and displacement magnitudes. These controls suggest that spatial variations in pressure are smaller than 3 dB in magnitude at frequencies of 20 kHz and less, but do also describe more significant variations at higher sound frequencies. Descriptions of the motion of the human, chinchilla and cat at frequencies above 20 kHz will require better understanding of such variations.

Nodes and natural frequencies

The holographic patterns we see on the various TMs measured in response to low-frequency stimuli appear as areas of gray punctuated with black contours. This pattern suggests that at these low frequencies, the entire membrane is set into motion with distinct areas moving with larger magnitude. As frequency increases, the number of local displacement maxima increases and we start to see these areas separated by brighter regions with an intensity similar to that of the non-moving bone that surrounds the TMs. These delimiting areas of reduced motion are reminiscent of nodes in response patterns that result from the combination of ‘natural’ responses of the membrane to the stimulus, where each natural response of the membrane is best elicited by a stimulus at a ‘natural frequency’.

The natural modes of motion of a lossless circular membrane of uniform mechanical properties and radius a that is bound at its rim are described by Equations 8 and 9, which define the signed amplitude of displacement at any point on the surface of the membrane d(r,) in terms of two integer “mode numbers”, m and n, a wave number k_mn (determined by the mechanical properties of the membrane), and the radial distance r and angular position from the center of the membrane (Kinsler et al. 1982; Fletcher 1992), where:

$$d(r,\theta )=M_{\mathit{\text{mn}}}{J}_m(k_{\mathit{\text{mn}}}r)\text{cos}(m\theta ),$$ Eqn. (8)

and

$$J_m(k_{\mathit{\text{mn}}}a)=0.$$ Eqn. (9)

and J_m is the m^th -ordered Bessel function of the first kind. Equation 9 constrains the values of k_mn to satisfy the boundary condition of zero motion at the membrane’s rim (r=a), thereby restricting the possible values of k_mn to natural frequencies (f_mn), where k_mn = 2 / _mn describes the spacing of the different modal maxima and minima, and _mn is the wave length associated with the spacing of the maxima and minima. If these modal patterns result from the interference of traveling transverse waves on the membrane surface, then _mn = c_mn / f_mn, and c_mn is equivalent to the propagation velocity of surface waves moving along the membrane for a specific natural frequency. The Bessel function term (J_m) in Equation 8 defines a series of n circular regions of zero displacement (nodal circles), while the cosine term defines a series of m diameters of zero displacement (nodal diameters) that separate the TM into similarly-sized wedges (Kinsler et al.1982; Fletcher 1992).

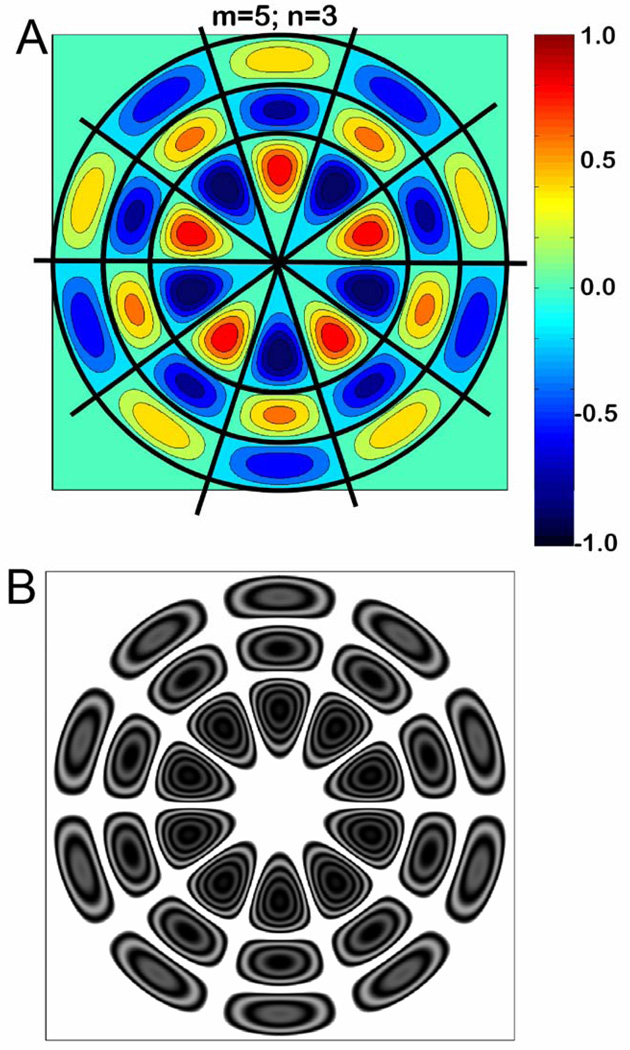
An example of a ‘natural’ modal pattern is illustrated in Figure 7A. In this figure we see 5 regularly spaced nodal diameters (m=5) and 3 nodal circles (n=3), where d(r, ) =0. The modal pattern in Figure 7A, and the computed TAH associated with it (Figure 7B), approximate the ‘ordered’ holographic patterns seen at higher frequency in all four specimens of Figure 4. The computed modal pattern and the TAH both show a collection of regions of large displacement magnitude separated by nodal regions zero displacement. The regions of large motion magnitude, the ‘pearls’, are circularly arranged on ‘strings’. The largest magnitudes of motions, the deepest blues (outward motions) and reds (inward motions) in 7A and the highest concentrations of concentric dark fringes in 7B, occur near the center of the membrane while the local displacement maxima and minima are of smaller magnitude closer to the TM rim. One difference between the computed modal pattern (Fig. 7A) with its associated nodes and the TAH (Fig. 7B) is the rectification that occurs in the TAH computation, where the TAH image intensity is the square of the Bessel function of the displacement (Equation 7). Because of this rectification, the TAH gives no information about the relative phases of the different maxima, whereas the computed modal patterns displayed in Fig 7A predict that positive outward moving modal maxima are surrounded by negative inward moving modal maxima, with nodal regions of zero displacement separating the modal peaks and valleys.

Figure 7.

The modal pattern of displacement of a circular membrane computed from equations 8 and 9, with m=5 and n=3. (A.) The signed magnitude of the displacement is coded by color as a function of position, with zero displacement coded as a pale blue-green. The three black concentric circles describe the three circular nodes (n=3) at which the magnitude of membrane motion is 0, and includes the outer rim of the membrane. The five diagonal nodes (m=5) are also emphasized by black lines. The signed magnitudes of the displacements switch from positive to negative, or vice versa, across any nodal boundary. (B.) A computed time averaged histogram (using Eqn. 7) that assumes the maximal displacement is equivalent to the laser wavelength (470 nm).

Estimating node numbers

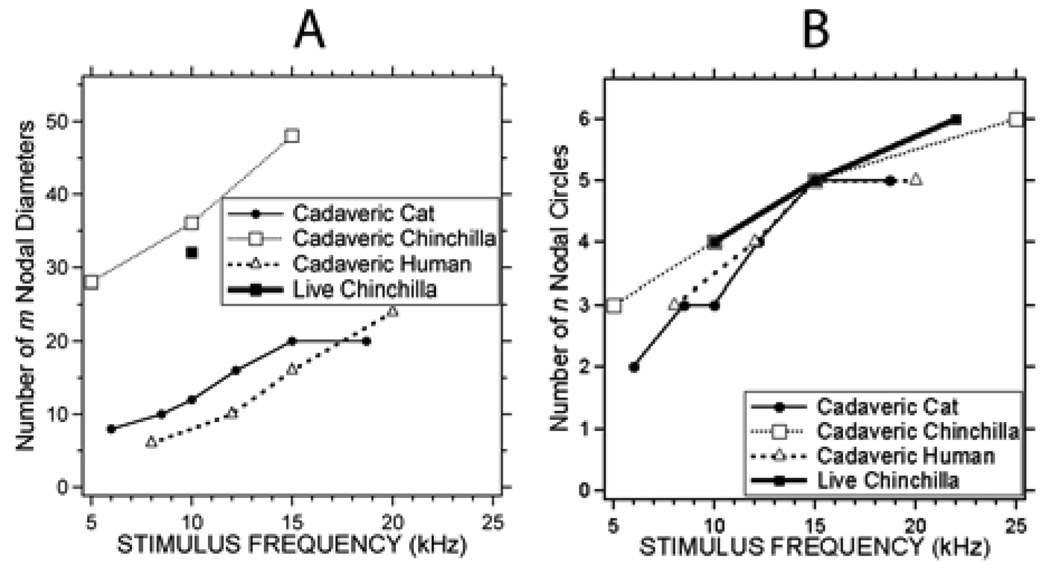
While the TM is certainly more complicated in structure than a flat circular lossless membrane, the similarity of Figures 7A&B and the lower rows of Figure 4 suggest that we can use counts of nodal circles and diameters to describe the modal patterns visible in the TAHs of Figure 4. (An analysis of such node counts assumes that the measured TAH primarily reflect a single natural modal pattern. The strength of this assumption is a point of later discussion.) We counted the nodal circles and diameters on the four specimens of Figure 4 for a range of stimulus frequencies from 5 to 25 kHz. Figure 8A shows the number of ‘m’ nodal diameters we counted in each specimen at the varied stimulus frequencies; Figure 8B illustrates the number of ‘n’ nodal circles in the same specimens. While the ‘n’ value was rather easy to count in each specimen at frequencies greater than 1–4 kHz, it was more difficult to count ‘m’: We could not always see a distribution of m nodal diameters and modal maxima at all locations on the membrane surface, and when we did, it was sometimes difficult to separate one local displacement maxima from another. (This ‘blurring’ of the nodal diameters is responsible for the fewer data points in Figure 8A.) Because of these difficulties, our estimates of ‘m’ are often based on extrapolations of counts made over known segments (about one-quarter) of the TM surface.

Figure 8.

Estimates of the ‘m’ and ‘n’ node numbers from the measured TAHs in our four specimens as a function of frequency.

Figure 8A indicates a strong frequency dependence in the number of ‘m’ nodal diameters in our 4 specimens, where m in chinchilla is about 2 to 3 times that observed in human and cats at similar frequencies, with m varying from 27 to almost 50 in chinchilla, and between 5 and 25 in human and cat. The increase in m with frequency is consistent with the observations that the size and separation of the ‘pearls’ on the strings decreased as frequency increased. Figure 8B indicates that the number of ‘n’ circular nodes we observed was independent of the species we used but highly dependent on sound frequency (correlation coefficient of 0.926); n varied from 2 to 6 as the sound frequency was varied from 5 to 25 kHz. The increase in n with frequency quantifies the observation that the number of the strings of pearls in the TAHs increased as stimulus frequency increased.

The analysis of m and n nodes used above assumes that the TAHs we record are dominated by a single modal pattern with a natural frequency nearby the stimulus frequency. In actuality, the TAHs we record represent the summation of the weighted response of a group of modal patterns. One weighting factor is inversely proportional to the difference between the frequency of the stimulus and the natural frequency of each pattern, and generally the modes with natural frequencies nearest the stimulus frequency dominate. However, other weighting factors, such as the average displacement of the membrane at each modal frequency, also play a role and may interfere with our assumption (Fletcher 1992).

Nodes, modes and standing waves

The presence of nodes, locations of decreased motion, on the surface of the TM is consistent with the presence of modes or standing waves that result either (1) from the cancellation of multiple transverse waves on the surface of the TM, or (2) from instantaneous excitation of modal surface-motion patterns on the TM. However, these two possibilities are not easily separable. For example waves on a string produced either by (1) an oscillating displacement source at the one end of the string or (2) instantaneously produced waves that result from plucking a string fixed at both ends, can both be described either in terms of the localized summation and cancellation of bi-directional traveling waves as they reflect at the boundaries and propagate back and forth along the string, or in terms of the summation of a family of temporally invariant standing waves.

Regardless of their derivation, we can use observations of the displacement patterns to quantify parameters relevant to either model of TM response. One measure of the relative magnitude of the reflections occurring at the boundaries of a wave-conducting media, or the losses within the media, is the standing wave ratio or SWR: the ratio of the time averaged magnitudes of the (mode associated) spatial displacement maximum and the nodal displacement minimum. In our TAH images we often see displacement magnitude maxima with TAH patterns that include at least 3 holographic fringes. For the blue laser used in our system, Figure 2 suggests that the third fringe corresponds to a magnitude of 320 nm. While imperfect knowledge of the illuminating intensity prevents us from precisely defining the magnitude minima within the nodal ‘white’ areas in the TAHs of Figure 4, it is clear from Figure 2 and the holograms in the middle and lower rows of Figure 4 that the nodal ‘white’ areas have gray values that are least half the maximum intensity of the gray areas observed between fringes 1 and 2. This suggests that the nodal magnitude is smaller than 80 nm. Therefore, the SWR is greater than 4 (320/80).

In the surface-wave model of TM excitation (case 1), a standing wave ratio of 4 or greater implies that at least 36% of the energy in any surface wave traveling along the membrane is reflected at the wave boundaries (Kinsler et al. 1982). In the ordered regime, the boundaries seem to include not only the rim of the TM, but also the attachment of the TM to the relatively immobile malleus. The demonstration of a significant SWR in our specimens is consistent with some models of TM function that suggest significant surface standing waves on the TM (e.g. Puria and Allen 1998) but not consistent with models that suggest the TM acts as a lossless, matched transmission line in which there is little reflection as waves progress from the membrane rim to its center (e.g. Parent and Allen 2007).

In the instantaneous-excitation model (case 2), a standing wave ratio of 4 implies the presence of energy losses within the membrane or its attachments. The magnitude of these losses is described by one minus the power-reflection coefficient. Since we estimate a power reflectance of at least 36%, we place an upper limit on power absorption (1 minus power reflection) of 64%. This estimate suggests that such losses are significant.

Waves on the TM surface?: Estimates of wave speed and wave delay

The TAH technique we use describes the magnitude of motion of each point on the TM surface averaged over the time it takes to collect four camera frames. With this instrument, pure radially traveling waves of constant amplitude along the membranes surface will produce changes in light intensity that are uniform along the membrane surface, where the magnitude of the measured intensity would depend on the magnitude of displacement and the Bessel function that relates the two (Figure 2, Equation 7). Realistically, such unidirectional traveling waves cannot occur in a membrane that is rigidly supported at its rim, where interactions of traveling waves with the rim will produce reflected traveling waves moving in the opposite direction. The interactions of such bidirectional traveling waves will produce standing waves with local spatial minima (nodes), consistent with the nodes observed in Figure 4. While we have argued that the nodal minima we observe could also result from uniform stimulation of the entire membrane surface that produces natural modal patterns of excitation, we will at this point use our measurements to produce estimates of surface wave travel for comparison with other estimates in the literature.

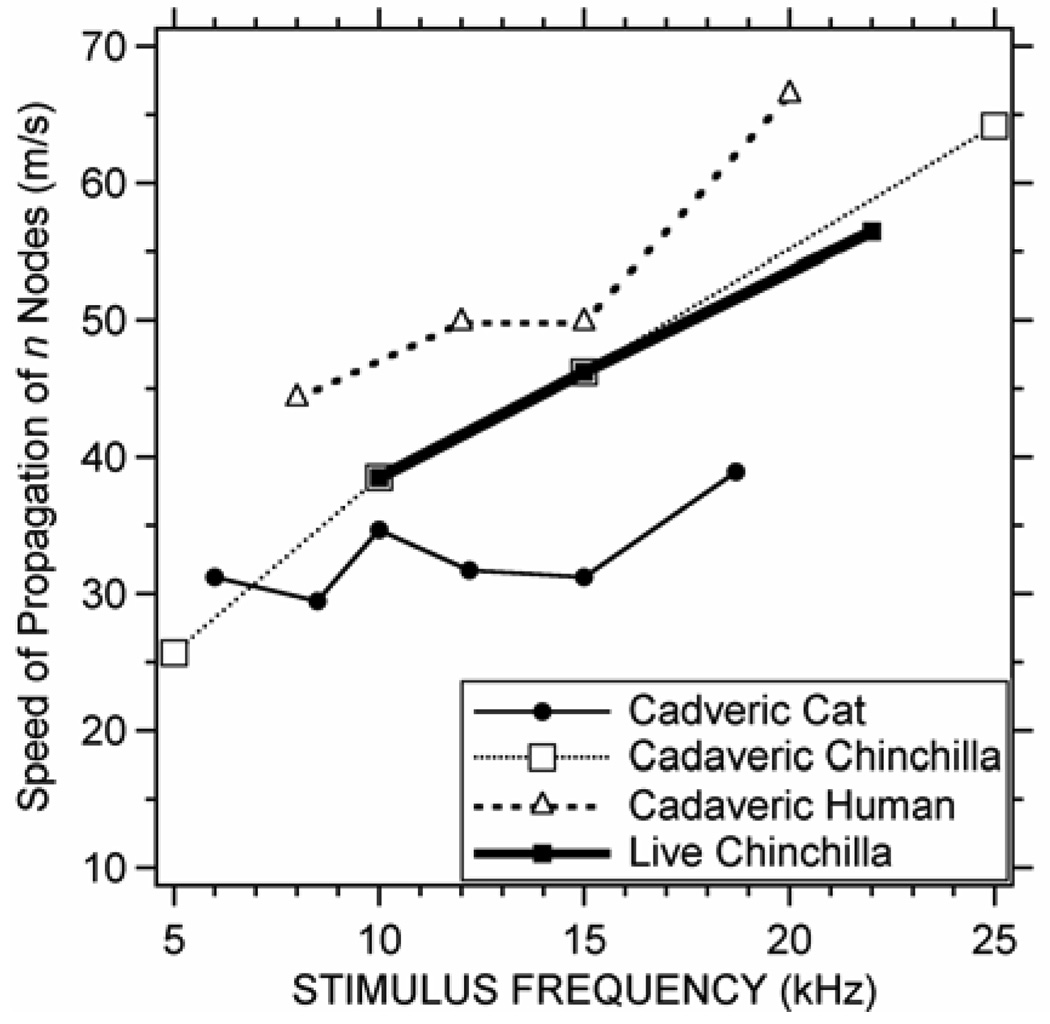
The strongest arguments for traveling TM surface waves are the observations of delay in middle-ear transmission (as estimated from measurements of group-delay in middle-ear transfer functions: Olson 1998; Overstreet & Ruggero 2002; Ravicz, Cooper & Rosowski. 2008) and the use of TM surface delays to fit functional middle-ear data (Puria & Allen 1998; O’Connor & Puria 2008). We can use our data to estimate the phase velocity of waves propagating radially along the TM surface by assuming that the distance between the easily-recognized circular nodes n (counted in Figure 8B) is half of a wavelength, i.e. c = f = 2f n. Figure 9 shows estimates of the speed of propagations computed from the circular (n) nodal patterns we observe on the four specimens. These velocities vary from 25 to 65 m/s and in general, the estimated phase velocity increases as frequency increases. The phase velocities we estimate in cat vary less with frequency and tend to be lower than the phase velocities computed from the human and chinchilla TAHs at similar frequencies. The 30 to 40 m/s phase velocities we compute in cat fall in between phase velocities determined for cat TM by others (Puria & Allen 1998; Fay et al. 2005). (It should be noted that our estimate of wave velocity based on a count of the number of waves lengths along a radius of the TM, produces an average measure of wave velocity along that radius and does not account for variations in velocity along the radius. It also does not account for the compression of wavelength with radial distance that is predicted by the Bessel functions we use to model the radial modal patterns.)

Figure 9.

Speed of propagation of radially traveling waves on the 4 TMs based on counts of ‘n’ nodal circles in Figure 7b.

The hypothesized propagation delay (Puria & Allen 1998; Parent and Allen 2007; O’Connor and Puria 2008) for the travel of radial waves on the TM surface can be estimated by the ratio of the radial distance of the TM and the group velocity. Table 1 lists estimates of the wave delay (based on the phase velocities of Figure 9) associated with radial travel along TMs that are 4 mm in radius for chinchilla and human, and 3 mm for cat. These delays vary from 0.06 to 0.16 ms in chinchilla, and from 0.06 to 0.09 ms in human and 0.075 to 0.1 cat, with the longer times at the lower frequencies. The delays we estimate in chinchilla are 1.5 to 6 times larger than the 0.025 to 0.040 ms middle-ear transmission delays observed in gerbil and cats, while the delays we estimate for cat are about twice the estimated middle-ear delay (Puria & Allen 1998; Olson 1998; Overstreet & Ruggero 2002; Ravicz, Cooper & Rosowski 2008), but the calculated delays in human TM are similar to the 0.04 to 0.09 ms delays predicted from models of TM sound transmission (O’Connor & Puria 2008) and measurements of middle-ear function in human temporal bones (Nakajima et al. 2009).

TABLE 1.

Species	Estimate of middle-ear delay	Source	reference
Cat	0.036 ms	Analysis of middle-ear input admittance measurements	Puria & Allen 1998
Gerbil	0.032 ms	Group delay in inner-ear to TM sound pressure ratio	Dong & Olson 2006
Human temporal bones	0.038 to 0.093 ms	Analysis of middle-ear functional measurements	O’Connor & Puria 2008
Gerbil	0.030 ms	Stapes velocity to TM sound pressure Group delay	Overstreet & Ruggero 2002
Gerbil	0.020 to 0.039 ms	Stapes velocity to TM sound pressure Group delay	Ravicz, Copper & Rosowski 2008
Human temporal bone	0.083 ms	Group delay in inner-ear to TM sound pressure ratio	Nakajima et al. 2009
Human temporal bones	0.06 to 0.089 ms*	Estimated from computed wave propagation velocity and 4 mm TM radius	This study
Cat	0.075 to 0.100 ms*	Estimated from computed wave propagation velocity and 3 mm TM radius	This study
Chinchilla	0.060 to 0.160 ms*	Estimated from computed wave propagation velocity and 4 mm TM radius	This study

^*Delay varies inversely with frequency

There is a significant difference in the methods we have used to quantify the delay associated with wave travel across the TM. The other reports in the literature in the literature (e.g. Olson 1998; Overstreet & Ruggero 2002) estimated the group delay based on measurements of changes in response phase with changes in frequency. Such delays can be associated with delays in energy transmission ((Brillouin 1960). Our estimates of delay come from estimates of velocity based on observations of wavelength and phase delay using tonal (single-frequency) stimulation. The relationship between our measured phase delays and velocity of energy transmission is not clear cut, and the differences between previous delay estimates and those we calculate may reflect some of those complexities. Better estimates of group delays on the surface of the TM would come from observations of the TM surface displacements produced by transient stimuli.

Transverse waves versus modal displacements

While the existence of nodes in the patterns of TM surface displacement measured by the TAH technique is consistent with the presence of standing transverse waves on the TM surface, whether the nodes are produced by transverse surface waves is unclear. Repeating our earlier analogy of a string: A modal or standing-wave pattern can be produced on a string either by (a) the interaction of a forward-going and reflected transverse wave, when one end of the string is driven while the other is constrained, or (b) by initially plucking a string, which is bound at both ends, along its entire length thereby evoking a modal pattern of displacement. In either case, the steady-state motion along the length of the string can be described mathematically either in terms of multiple modal standing waves whose interactions produce traveling waves, or by bidirectional traveling waves whose interactions produce standing waves. Others have argued that the existence of middle-ear delay is suggestive of significant transverse wave travel along the surface of the TM (Puria & Allen 1998; Fay et al . 2005, 2006; Parent & Allen 2007). An argument in favor of the patterns resulting from more instantaneous modal displacement of the surface is the disparity in the wave speeds estimated for transverse waves traveling along the surface of the TM (generally less than 70 m/s) and the significantly higher wave speed of sound in air at body temperature and standard pressure (nearly 350 m/s). The TAH technique we employ is unable to distinguish between these possibilities. However, future applications of stroboscopic holography techniques in which one can estimate the magnitude and phase of TM surface motion (e.g. Furlong et al. 2009) will address this issue more directly.

Significance and Conclusions

The ordered patterns of displacements we describe in time-averaged holograms measured at stimulus frequencies above 8 kHz are unique: They have not been described before, except for some preliminary reports (Furlong et al. 2006; Rosowski et al. 2007; Furlong, et al. 2009). The description of standing wave-like modal patterns on the TM, is not new (e.g. Khanna & Tonndorf 1972; Funnell and Laszlo 1977) but the existence of such standing-waves on the TM surface is not generally appreciated, and our new estimates of wave speed and Standing Wave Ratio set limits on the both the mechanical parameters of the membrane and the absorption of power within the membrane and the ossicular chain, and will help theorists better understand the workings of the TM and middle ear.

In the future, OEH can be used to shed light on other fundamental questions in TM function, including the contribution of ‘peripheral’ parts of the TM to the function of the ear at middle and high frequencies. TM surface displacement measurements made with artificial ossicular pathologies, e.g. ossicular fixations or interruptions, will identify how gross changes in ossicular load affect the motion of the entire surface of the TM over a broad frequency range. Other measurements made before and after controlled TM perforations or slits (e.g. Voss, Rosowski, Merchant & Peake 2001; O'Connor, Tam, Blevins & Puria 2008)) can define how interruptions in the TM structure at one location, affect the motion of the ossicles as well as motion at other TM locations. Such new data will help distinguish between the competing theories of the ‘dissonant tympanic membrane’ in which the multitude of closely-spaced natural frequencies of the TM are thought to boost the high-frequency response of the middle ear (Fay et al. 2006) and older ideas concerning the uncoupling of the peripheral TM from the ossicles at higher frequencies (Tonndorf & Khanna 1970, 1972; Shaw & Stinson 1983). OEH may also prove useful in the diagnosis of middle-ear disorders.

In this paper, we have demonstrated (i) frequency dependences of the patterns of sound-induced displacement in the TM of cadaveric and live mammals at frequencies that are higher than in any other reports; (ii) at frequencies above 5 kHz, the patterns of displacement are roughly consistent with nodal circles and diameters; (iii) the presence of nodes implies the presence of modes or standing waves on the surface of the TM; (iv) the estimates of wave propagation velocity along the TM surface are comparable to other estimates for those species. but we also see a significant species dependence in wave velocity; (iv) the Standing Wave Ratios we estimate from our nodal patterns suggest that the that there is significant reflection of any waves traveling on the membrane surface at the membrane boundaries, including the manubrium of the malleus, and suggest that TM models, which assume wave reflectance at the boundaries of the TM is small, need revision; (v) the holographic data we present are also consistent with near instantaneous modal displacements of the TM surface that do not depend on the transmission of sound energy from the rim of the membrane to its center; (vi) while the techniques we describe are capable of rapid determinations of the pattern of TM displacements produced by tones, they require relatively high stimulus levels and are insensitive to differences in the relative phase of displacement between locations on the TM. Because of this insensitivity to phase, they cannot distinguish between wave travel along the TM surface or instantaneous modal stimulation; however, related techniques being developed in our lab (Furlong et al. 2009; Hernandez-Montes et al. in press) will enable future tests of these two competing hypotheses.