Analytical Ultracentrifugation: Sedimentation Velocity and Sedimentation Equilibrium

Abstract

Analytical ultracentrifugation (AUC) is a versatile and powerful method for the quantitative analysis of macromolecules in solution. AUC has broad applications for the study of biomacromolecules in a wide range of solvents and over a wide range of solute concentrations. Three optical systems are available for the analytical ultracentrifuge (absorbance, interference and fluorescence) that permit precise and selective observation of sedimentation in real time. In particular, the fluorescence system provides a new way to extend the scope of AUC to probe the behavior of biological molecules in complex mixtures and at high solute concentrations. In sedimentation velocity, the movement of solutes in high centrifugal fields is interpreted using hydrodynamic theory to define the size, shape and interactions of macromolecules. Sedimentation equilibrium is a thermodynamic method where equilibrium concentration gradients at lower centrifugal fields are analyzed to define molecule mass, assembly stoichiometry, association constants and solution nonideality. Using specialized sample cells and modern analysis software, researchers can use sedimentation velocity to determine the homogeneity of a sample and define whether it undergoes concentration-dependent association reactions. Subsequently, more thorough model-dependent analysis of velocity and equilibrium experiments can provide a detailed picture of the nature of the species present in solution and their interactions.

I. Introduction

For over 75 years, analytical ultracentrifugation (AUC) has proven to be a powerful method for characterizing solutions of macromolecules and an indispensable tool for the quantitative analysis of macromolecular interactions (Cole and Hansen, 1999; Hansen et al., 1994; Hensley, 1996; Howlett et al., 2006; Scott and Schuck, 2005). Because it relies on the principle property of mass and the fundamental laws of gravitation, AUC has broad applicability and can be used to analyze the solution behavior of a variety of molecules in a wide range of solvents and over a wide range of solute concentrations. In contrast to many commonly-used methods, during analytical ultracentrifugation samples are characterized in their native state under biologically-relevant solution conditions. Because the experiments are performed in free solution, there are no complications due to interactions with matrices or surfaces. Because it is nondestructive, samples may be recovered for further tests following AUC. For many questions, there is no satisfactory substitute method of analysis.

Two complementary views of solution behavior are available from AUC. Sedimentation velocity provides first-principle, hydrodynamic information about the size and shape of molecules (Howlett et al., 2006; Laue and Stafford, 1999; Lebowitz et al., 2002). Sedimentation equilibrium provides first-principle, thermodynamic information about the solution molar masses, stoichiometries, association constants, and solution nonideality (Howlett et al., 2006; Laue, 1995). Different experimental protocols are used to conduct these two types of analyses. This chapter will cover the fundamentals of both velocity and equilibrium AUC.

A. Types of problems that can be addressed

Analytical ultracentrifugation provides useful information on the size and shape of macromolecules in solution with very few restrictions on the sample or the nature of the solvent. The fundamental requirements for the sample are: 1) that it has an optical property that distinguishes it from other solution components, 2) that it sediments or floats at a reasonable rate at an experimentally achievable gravitational field and 3) that it is chemically compatible with the sample cell. The fundamental solvent requirements are its chemical compatibility with the sample cell and its compatibility with the optical systems. The range of molecular weights suitable for AUC exceeds that of any other solution technique, from a few hundred Daltons (e.g. peptides, dyes, oligosaccharides), to several hundred-million Daltons (e.g. viruses, organelles).

Different sorts of questions may be addressed by AUC depending on the purity of the sample. Detailed analyses are possible for highly purified samples with only a few discrete macromolecular components. Some of the thermodynamic parameters that can be measured by AUC include the molecular weight, association state and equilibrium constants for reversibly-interacting systems. AUC can also provide hydrodynamic shape information. For samples containing many components, or containing aggregates or lower molecular weight contaminants, or high concentration samples, size distributions and average quantities may be determined. While these results may be more qualitative than those from more purified samples, the dependence of the distributions on macromolecular concentration, ligand binding, pH and solvent composition can provide unique insights into macromolecular behavior.

II. Basic Theory

Mass will redistribute in a gravitational field until the gravitational potential energy exactly balances the chemical potential energy at each radial position. If we monitor the rate at which boundaries of molecules move during this redistribution, then we are conducting a sedimentation velocity experiment. If we determine the concentration distribution after equilibrium is reached, then we are conducting an equilibrium sedimentation experiment.

A. Sedimentation Velocity

We can understand a sedimentation velocity experiment by considering the forces acting on a molecule during a sedimentation velocity experiment. The force on a particle due to the gravitational field is just M_pω²r, where M_p is the mass of the particle, ω is the rotor speed in radians per second (ω= 2π•rpm/60), and r is the distance from the center of the rotor. A counterforce will be exerted on the particle by the mass of solvent, M_s, displaced as the particle sediments, M_sω²r. The net force is (M_p − M_s)ω²r. The mass of solvent displaced is just the M_p times partial specific volume of the particle, v̄(cm³/g), times the density of the solvent, ρ (g/cm³). So the effective, or buoyant mass of the particle is M_b = M_p(1 − v̄ρ). The last force to consider is the frictional force developed by the motion of the particle through the solvent, which given by fv, where f is the frictional coefficient and v is the velocity. Balancing these forces we obtain the following relationship (see e.g. references (Fujita, 1975; Tanford, 1961; Williams et al., 1958)):

$$s\equiv \frac{v}{{\omega }^{2}r}=\frac{M_b}{f}$$ (1)

which is also definition of the sedimentation coefficient, s, as the ratio of the velocity to the centrifugal field. In terms of molecular parameters, equation 1 indicates that s is proportional to the buoyant molar mass, M_b, and inversely proportional to the frictional coefficient, f. Diffusion causes the sedimenting boundary to spread with time. Hence by monitoring the motion and shape of a boundary it is possible to determine both the sedimentation coefficient and the translation diffusion coefficient, D. From the Stokes-Einstein relationship, we know that D = RT/N_af, where R is the gas constant (erg/mole °K), T the absolute temperature and N_a is Avogadro’s number.

The time evolution of the radial concentration distribution during sedimentation is given by the Lamm equation (see e.g. references (Fujita, 1975; Williams et al., 1958)):

$$\frac{\partial c}{\partial t}=D\left[\frac{{\partial }^{2}c}{\partial r^2}+\frac{1}{r}\frac{\partial c}{\partial r}\right]-s{\omega }^2\left[r\frac{\partial c}{\partial r}+2c\right]$$ (2)

where c is the weight concentration of macromolecules and t is time. The optical systems on the analytical ultracentrifuge supply the radial concentration distribution at time intervals during the course of an experiment, c(r,t), and the instrument provides the rotor speed, ω. The quantities sought in a velocity sedimentation experiment are s and D. There are no exact solutions to the Lamm equation: approximate (Behlke and Ristau, 1997; Philo, 1994) and numerical (Demeler and Saber, 1998; Schuck, 1998; Stafford and Sherwood, 2004) solutions form the basis of many sedimentation velocity analysis programs used to extract s and D from AUC data. By taking the ratio s/D, the frictional contribution to these parameters is removed and the result is proportional to the buoyant molar mass, M_b, through the Svedberg equation

$$\frac{s}{D}=\frac{M_b}{RT}$$ (3)

Both the Lamm and Svedberg equations, as presented above, are starting points for the equations that apply to real chemical systems. The equations for real systems are presented below, along with the assumptions and simplifications often used to extract information.

B. Sedimentation Equilibrium

When the centrifugal force is sufficiently small, an equilibrium concentration distribution of macromolecules is obtained throughout the cell where the flux due to sedimentation is exactly balanced by the flux due to diffusion. The shape of this concentration gradient can be derived using a variety of approaches (Fujita, 1975; Tanford, 1961; Williams et al., 1958). For an ideal single non-interacting species, the equilibrium radial concentration gradient, c(r), is given by

$$c(r)=c_{0}exp\left[\frac{M_b{\omega }^2}{RT}\left(\frac{r^2-r_0^2}{2}\right)\right]=c_{0}exp\left[\sigma \left(\frac{r^2-r_0^2}{2}\right)\right]$$ (4)

where c₀ is the concentration at an arbitrary reference distance r₀. The term M_bω²/RT is often referred to as the reduced molecular weight, σ. Sedimentation equilibrium experiments provide a very accurate way to determine M and consequently the oligomeric state of biomolecules in solution. Deviations from the simple exponential behavior described by equation 4 can result from the presence of either multiple non-interacting or interacting macromolecular species, or thermodynamic nonideality.

III. Dilute Solution Measurements

For dilute solutions containing a single macromolecular component, detailed information is available from both sedimentation equilibrium and sedimentation velocity analysis (Cole and Hansen, 1999; Hansen et al., 1994; Hensley, 1996; Howlett et al., 2006; Laue and Stafford, 1999; Lebowitz et al., 2002; Scott and Schuck, 2005). What constitutes a dilute solution depends somewhat on the nature of the macromolecule being studied and the solvent it is in. For this review, we will consider a system dilute if there is not significant hydrodynamic or thermodynamic nonideality (below), and if gradients in the solvent component concentrations are small enough to be neglected in the analysis. For globular proteins of moderate charge (z < ~15) at physiological salt concentrations, protein concentrations less than 2–3 mg/ml can be considered dilute. On the other hand, nucleic acids or polysaccharides form may form highly nonideal solutions at concentrations < 0.1 mg/ml. It should be noted that only electrically neutral particles sediment. For proteins and nucleic acids in near physiological salt concentrations (ionic strengths > 100 mM), there are sufficient counter ions in the immediate surroundings that the sedimentation coefficient is relatively insensitive to salt concentration. However, at lower ionic strengths (< 10 mM), a greater region of solution is required to produce a neutral particle that can sediment. That is, the apparent radius of a protein or nucleic acid will increase at low ionic strength and, consequently, the sedimentation coefficient will decrease. The slowing of sedimentation at low ionic strength is called the primary charge effect (Fujita, 1975; Williams et al., 1958).

Solvents that contain components at high concentrations that sediment sufficiently to form a significant gradient (e.g. 10% sucrose or 8 M urea) will affect sedimentation rates (Schuck, 2004). Even for dilute solutions, a series of experiments should be conducted at different macromolecular concentrations so that the concentration dependence of s and D may be determined. If these quantities are invariant or weakly dependent on macromolecular concentration, then the analysis below is appropriate. Under these conditions and using the analysis methods and computer programs listed below, s and D (hence M, through the Svedberg equation) may be obtained with good accuracy (s to within 2%, D to within 5% and M to within 5%). Note that analysis using the Svedberg equation is only valid for a single, noninteracting species, or a mixture of noninteracting species.

The frictional coefficient obtained from sedimentation measurements is often interpreted in terms of the molecular size and shape through the Stokes relationship:

$$f=6\pi \eta R_S$$ (5)

where η is the solution viscosity and R_S is the Stokes radius, which contains contributions from both molecular asymmetry and solvation (Williams et al., 1958). In order to interpret R_S in terms of molecular asymmetry, it is necessary to have a good estimate of the solvation, usually expressed as the number of grams of solvent bound per gram of macromolecule. Although estimates of the hydration (i.e. bound water) of macromolecules are available (Perkins, 2001) these values neglect the amount of other solvent components that may be bound, and they do not reflect the physical meaning of R_S, which includes coupling of the macromolecular flow with flows of other solvent components. If the macromolecule is ionic, then flow-coupling with solvent ions will contribute significantly to R_S. This is particularly true at low ionic strengths where a large R_S is required to maintain electroneutrality during sedimentation. Sometimes, the frictional parameters are further interpreted using simple structural models consisting of ellipsoids of revolution or cylinders to assess molecular asymmetry (Cantor and Schimmel, 1980; Tanford, 1961). Hydrodynamic properties can also be interpreted using more complex structural models composed of assemblies of spherical beads (Byron, 2000; Garcia De La Torre et al., 2000; Rai et al., 2005). It is important to realize that there are pitfalls associated with interpreting s or R_S in terms of molecular dimensions determined by application of these models (see chapter by O. Byron). That said, changes in R_s (e.g. with addition of a ligand) usually reflect changes in molecular size. Using the technique of difference sedimentation, changes in R_s of only a few Angstroms may be detected (Richards and H.K., 1957). Furthermore, the concentration dependence of the sedimentation coefficient can be useful in assessing the relative asymmetry of different molecules (Hattan et al., 2001).

For a sample containing only one type of molecule, a useful quantity to report is the standard sedimentation coefficient, s^o_20,w. This quantity is obtained by extrapolating sedimentation coefficients determined at finite concentrations to zero concentration (i.e. s^o = lim_c→0 s), then adjusting s^o for the solvent density and viscosity to the density and viscosity of water at 20 °C. Values of s^o_20,w are useful (e.g. 30 s or 50 s ribosomal subunits) since they are a primary quantity. Thus, any differences in s^o_20,w, for example due to changes in pH, reflect differences in the molecule.

One common application of AUC to dilute solutions is to determine the sedimentation coefficient distribution of macromolecules (e.g. g(s) or c(s)). Analysis methods and programs for obtaining g(s) and c(s) are described below. For solutions containing a single component, the abundance and sedimentation coefficients of irreversible aggregates or of degradation products may be determined. Often a simple relationship between s and M may be used to identify particular peaks as belonging to certain oligomers (e.g. dimer, trimer, etc.) or certain fragments of the monomer. Sedimentation coefficient distributions are used widely in the pharmaceutical industry to assess the stability of protein formulations and to characterize preparations of inherently heterogeneous samples (e.g. vaccines based on bacterial cell wall preparations).

IV. Concentrated and Complex Solutions

If a solution contains a single macromolecular component at high concentration, then one may use sedimentation equilibrium analysis to extract thermodynamic information. In particular, the concentration dependence of the apparent molecular weight, M_app, divided into the actual molecular weight (i.e. M/M_app) yields the activity coefficient, γ. The product of the activity coefficient and weight concentration yields the chemical activity (or apparent concentration). For an ideal solution, γ = 1, and the apparent concentration equals the actual concentration. For a macromolecule that undergoes self-association, γ will be < 1, whereas γ will be > 1 for a macromolecule that repels itself (e.g. due to excluded volume or charge-charge repulsion). While a more quantitative description of a macromolecule’s behavior may be desired (e.g. what is the association stoichiometry and strength), for many questions simply knowing a macromolecule’s qualitative behavior may be sufficient. More quantitative analysis at high concentration is best performed using SE (Harding et al., 1992; Roark and Yphantis, 1969).

The sedimentation coefficient depends on the total macromolecular concentration. In the simplest analysis, the viscosity of solutions increases with increasing concentration (above); hence the observed sedimentation coefficient decreases. However, any specific interactions between molecular species also must be considered (14).

The availability of a fluorescence detector for the XLI analytical ultracentrifuge (AU-FDS, Aviv Biomedical, Lakewood, NJ) allows the rigor and power of AUC to be applied to complex, concentrated solutions, such as cell lysates, serum, cerebral spinal fluid, urine and cell culture media. As currently used, analytical ultracentrifugation is applied primarily to dilute solutions. For dilute solutions, s^o_20,w and D^o_20,w are considered to be properties of a molecule. In fact, however, s and D are system properties whose values depend on the concentrations of all other components in the solution. Thus, the interpretation of the data for many of the most interesting applications of the AU-FDS will require more detailed analysis than is available currently. Even now, however, phenomenological analysis of sedimentation data from complex, concentrated solutions will provide useful insights into the solution behavior of appropriately labeled molecules. For example, a mass action association between components A^* and B, where A^* is the only labeled component, will lead to an apparent increased sedimentation coefficient of A over what would be expected simply on the basis of the viscosity (Kroe, 2005).

V. Instrumentation and Optical Systems

The analytical ultracentrifuge is similar to a high-speed preparative centrifuge in that a spinning rotor provides a gravitational field large enough to make molecular-sized particles sediment. What distinguishes the Beckman Coulter (Fullerton, California) XL-I analytical ultracentrifuge from a high-speed preparative centrifuge is the specialized rotors, sample holders and optical systems that permit the observation of samples during sedimentation. To view the sample, the analytical rotor has holes through it to hold sample containers commonly called cells. Each cell contains a centerpiece, with chambers (called channels) to hold the liquid samples. The centerpiece, in turn, is sealed between windows to permit the passage of light through the channels, thus allowing the cell contents to be viewed. Centerpieces are made out of a variety of tough, inert materials, such as epoxy, anodized aluminum or titanium. For biological materials, the epoxy-based centerpieces are used most frequently. The epoxy contains a small amount of either charcoal or aluminum powder filler (~5% by weight) for improved thermal conductance. With very few exceptions, either centerpiece type may be used. Depending on the type of experiment that will be performed, centerpieces are available that can hold several samples each. Rotors for the XLI are available that hold either four or eight cells, hence many samples may be analyzed at once.

The fundamental measurements in AUC are radial concentration distributions. These concentration distributions, called “scans”, are acquired at intervals ranging from minutes (for velocity sedimentation) to hours (for equilibrium sedimentation). As the rotor spins, each cell passes through the optical paths of detectors capable of measuring the concentration of molecules at closely spaced radial intervals in the cell. There are three commercially available optical detectors for the XLI to measure the concentration distributions: an absorbance spectrophotometer and Rayleigh interferometer from Beckman Coulter (Fullerton, California), and the fluorescence detector from Aviv Biomedical (Lakewood, New Jersey). All subsequent analysis of sedimentation data relies on the quantity and quality of data available from these detectors. A comparison of the capabilities of the three optical systems is provided in Table 1. As can be seen from these data, the three optical systems are complementary. Each optical system has its strengths and weaknesses (Table 2). A more detailed comparison of the absorbance and interference optical systems is available (Laue, 1996). A summary of the properties of each optical system is presented below. In addition to these real-time optical systems, for SE experiments tracer sedimentation methods have been described where the concentration gradients of labeled molecules are determined following centrifugation using a microfractionator (Howlett et al., 2006; Rivas and Minton, 2003).

Table 1.

Capabilities of optical systems.

	Absorbance	Interference	Fluorescence
Sensitivitya	0.1 OD	0.1 mg/ml	100 pM
Rangeb	2–3 logs	3–4 logs	6–8 logs
Precisionc	Good	Excellent	Good

^aThe sensitivity is the minimum amount of signal needed to obtain good results. For the interference optical system, the signal is relatively insensitive to the type of biological material, so that a 1 mg/ml sample results in a displacement of ~3.25 fringes. Sensitivity of the fluorescence system is for fluorescein (molar extinction coefficient ~65,000 at 488 nm, quantum yield ~0.9).

^bThe range refers to the concentration range accessible by the optical system.

^cThe precision of the optical system is estimated by comparing the signal to noise ratio. For the absorbance and fluorescence detectors, this ratio is ~100 (e.g. the uncertainty in a 1 OD reading is about 0.01 OD, and the uncertainty in a fluorescence intensity reading is about 1% of the signal). For the current interference optical system, this ratio is closer to 1000.

Table 2.

Strengths and weaknesses of optical systems.

Characteristic	Absorbance	Interference	Fluorescence
Radial resolutiona	20–50	10	20–50
Scan timeb	60–300	1–10	60–90
When to usec	Selectivity Sensitivity Non-dialyzable components	Solvent absorbs light Solute does not absorb light Accuracy needed Short solution columns	Selectivity Sensitivity Small sample quantities Non-dialyzable components

^aApproximate spacing (in microns) between data points such that each measurement can be considered an independent estimate of the concentration.

^bThe minimum time (in seconds) required to complete one radial scan. The time listed for the fluorescence system is the time needed to scan all of the samples (Laue, 2006).

^cSelectivity refers to the absorbance and fluorescence systems’ ability to discriminate between components based on their spectral properties. Since the Rayleigh interference optics relies on differences in the refractive index of the sample and reference solutions, it provides no selectivity. On the other hand, the interference optics do not require that samples have an appropriate chromophore, and may be used so long as the solvent does not absorb light at ~670 nm. The interference optics require that samples are at dialysis equilibrium with the reference solution; hence, they should not be used for samples containing non-dialyzable components (e.g. detergents). The greater radial resolution of the interference optics allows them to be used with the eight-channel “short column” centerpieces (Yphantis, 1960).

A. Absorbance

Absorbance is the most frequently used detector for the analytical ultracentrifuge (Laue, 1996). This optical system is the easiest to use and operates as a standard double-beam spectrophotometer. Under conditions where the Beer-Lambert law holds, the absorbance signal is directly proportional to solute concentration: A = εcl, where e is the solute’s weight extinction coefficient, c is the weight concentration and l is the sample pathlength (1.2 cm for standard centerpieces). The rated precision of the absorbance system is ±0.01 OD, although it is usually better than this. The noise is primarily stochastic. Hence, the noise appears as a high-frequency “fuzz” around the signal. The scans typically contain little systematic noise that is either radially-independent (e.g. the entire scan is shifted up or down) or time-independent (e.g. a feature, such as a scratch, that does not move from scan to scan). As described below, the other optical systems will have very different noise characteristics.

Although the absorbance optics are useable over a wavelength range from 190 to 800 nm, limited light intensity may restrict the useable range for two reasons. First, many standard biological solvent components absorb strongly at short wavelengths (e.g. disulfides, carbonyl oxygens, nitrogenous compounds, some detergents), so that solvent components should be selected with care when data collection at short wavelengths is desired. A simple rule of thumb is that the solvent absorbance at the desired operating wavelength should be less than ~0.5 OD, using water as the reference. Second, output from the Xe light source is blue-rich and “spiky,” with the maximum output at 230 nm, and very low red light output. If there uncertainty about what wavelength to use, one can perform a wavelength scan using the XLA. It is best to view these data as both intensities and absorbencies to ensure the data will have a good signal to noise ratio (Laue, 1996).

When preparing samples for the absorbance system, it is best if they have an absorbance between 0.2 and 1.0 OD. If you are interested in gathering data over a wide concentration range, you may want to scan different samples at different wavelengths. While this is permitted, the XLA wavelength selector is notoriously imprecise (±3 nm) at setting the monochromator back to the same wavelength. Consequently, if your experimental protocol involves scanning samples at different wavelengths, you should make sure the wavelengths used are in “flat” portions of the sample’s absorbance spectrum, at peaks and valleys, and not in spectral regions where the absorbance is changing rapidly with wavelength. Otherwise, absorbance readings will not be reproducible from scan to scan. While some analysis programs (e.g. ULTRASCAN) have built in routines to adjust data for these variations, it is best to avoid the problem.

Of the three optical systems, the absorbance system requires the longest to complete a scan. For sedimentation equilibrium, long scan times are not a problem. However, for sedimentation velocity experiments, the long scan times may limit the amount of data that can acquired over the course of an experiment. In particular, at rotor speeds above 6000 rpm, the repetition rate of the pulsed Xe lamp (100 Hz) limits the data acquisition rate. Consequently, absorbance protocols for velocity experiments typically use a fairly coarse radial step size (0.003 cm) with no data averaging. Improvements to the absorbance system are being developed to overcome the scan speed limitation, as well as the poor precision of the wavelength selection mechanism.

When used in a traditional double beam mode (each sample having a corresponding reference solution), up to three (four hole rotor) or seven (eight hole rotor) samples may be analyzed. It is also possible to the use intensity data for sedimentation velocity analysis (Kar et al., 2000), thus doubling the number of samples per experiment. You should make sure the material in the sample and reference channels have approximately the same absorbance reading, and that the absorbance is not too high (< 0.5 OD). Otherwise, the automatic gain control logic of the XLA may result in low intensity readings from the sample channel, or it may change the gain settings from one scan to the next, resulting in unusable data.

B. Interference

The signal from the Rayleigh interference optical system consists of equally-spaced horizontal fringes whose vertical displacement, ΔY, is directly proportional to the optical path difference between light beams passing through the sample and reference solutions. Any refractive index difference, Δn, between the two solutions contributes to the optical path length so that: ΔY = Δnl/λ, where l is the optical path length and λ is the wavelength of the light source (Richards and Schachman, 1959; Yphantis, 1964). For a non-dialyzable solution component, the refractive index difference is proportional to the refractive index increment: Δn = c(dn/dc) and the extinction coefficient e is replaced by

$$\mathcal{E}\to \left(\frac{dn}{dc}\right)\frac{M}{\lambda }$$ (6)

For proteins, dn/dc is relatively independent of composition with an average value of 0.186 ml/g (Huglin, 1972). For the XLA λ = ~670 nm and the sample pathlength is 1.2 cm, so that a 1 mg/ml sample results in a fringe displacement of ~3.25 fringes (Laue, 1996).

Because the signal from interference optical system does not rely on a chromophore, colorless compounds (e.g. polysaccharides and lipids) may be characterized by AUC. Indeed, any material having a refractive index different from the reference will contribute to the signal. This is both a useful characteristic and poses possible problems if a sample contains a non-dialyzable substance (e.g. detergents, lipid micelles). Thus, while the molecular weights and partial specific volumes of detergents may be characterized using the interference optics (Reynolds and McCaslin, 1985), samples containing detergents are best studied using either absorbance or fluorescence optics.

Unlike the absorbance system, the interference signal has very little stochastic noise. However, since any pathlength difference between the sample and reference beams contributes to the fringe displacement, even tiny optical imperfections (dust, oil, dirt, scratches on the lenses and mirrors) are visible in the signal. Consequently, there is significant time-independent systematic noise. Furthermore, the conversion of the interference image to fringe displacement measurements uses a Fourier analysis to determine the fractional fringe displacement (DeRosier et al., 1972) for which the first radial position is arbitrarily assigned a zero fringe displacement. Since the fringes cannot be traced through certain image features (e.g. menisci), fringe displacement data also contain radially-independent systematic noise. Both types of systematic noise must be removed prior to data analysis (Fujita, 1975; Schuck and Demeler, 1999; Stafford, 1992).

The precision and accuracy of the interference optical system places a premium on the optical components. Any variation in the window or centerpiece flatness > 0.01 λ will cause a vertical shift in the image. A severe enough wedge (> 30 λ) will result in severe degradation or even loss of the image as the entire diffraction envelope can be displaced from the camera sensor. Stress on the optical components also may lead to refractive index changes. For this reason, sapphire windows must be used with the interference optical system. Also, in order to achieve the full accuracy of the interference optics, careful alignment and focusing are necessary (Richards et al., 1971; Yphantis, 1964). It is not that the interference optics are particularly fussy with respect to focusing. However, they offer precision and accuracy well beyond the other optical systems, hence, require that more attention be paid to focus and alignment. Once properly aligned and focused, they remain stable. Changes that will require realignment are few (e.g. new light source mounting, new drive motor). Re-focusing should be done if there is a switch from 12-mm to 3-mm cell pathlength centerpieces and high-accuracy work is desired.

C. Fluorescence

The fluorescence optical system is the most recent addition to the XLI. The AU-FDS (Aviv Biomedical, Lakewood, NJ) may be added to an existing XLI, and is based on previously described prototypes (Laue, 2006; MacGregor et al., 2004). Although the fluorescence optics are not as well characterized as the absorbance and interference systems, some features are known that impact experiment designs.

A laser light source must be used in order to achieve sufficient radial resolution (~20–50 microns). Currently the AU-FDS laser provides excitation at 488 nm. It is likely that more excitation wavelengths will become available as solid state lasers that meet the size and power dissipation requirements become available. Because a 488 nm source is used, the fluorescence system ordinarily is used with extrinsically labeled compounds. Suitable labels include fluorescein, BODIPY, NBD, green fluorescent protein (GFP), and the many derivatives of these labels used for fluorescence microscopy. Information about specific labels and the chemistries available for attaching them to biomolecules may be found on the web (see http://probes.invitrogen.com/handbook/). In our experience, Alexa488 is an excellent choice due to its large extinction coefficient (~80,000), insensitivity to pH, resistance to photobleaching and because of the many coupling chemistries for covalently attaching the dye to specific functional groups on proteins and nucleic acids. The many variants of GFP may be used to generate transcriptionally-labeled material for the AU-FDS. Due to the extraordinary sensitivity and selectivity of fluorescence detection, it is possible to characterize the sedimentation behavior of GFP-labeled proteins in cell lysates without further purification (Kroe, 2005).

The emitted light passes through a pair of long-pass (> 505 nm) dichroic filters. This choice of filters captures the maximum amount of emitted light, providing good sensitivity, but offers no opportunity to select a label by its emission characteristics. Thus, there is currently no simple way to use multiple labels in the AU-FDS (e.g. for fluorescence resonance energy transfer).

The noise characteristics of the fluorescence detector are a combination of the high-frequency stochastic noise found in the absorbance detector, with the low-frequency systematic noise observed with the interference optics. The similarity of fluorescence noise to absorbance noise stems from their mutual reliance on measuring light intensities and their use of similar photo detectors. Our experience is that the stochastic noise on an intensity reading is about 1% of the value. This observation holds over a wide range of sample concentrations and detector gain settings. The systematic noise tends to be time-independent and arises from two sources. First, fluorescent material may stick to the windows, particularly in places where there once was an air-liquid boundary. Hence, there can be regions where label stuck to the window while the cell was being handled (e.g. filled, put in the rotor). The severity of this problem depends strongly on the nature of the sample, with some proteins exhibiting little sticking while other proteins and other materials (especially lipids) leaving an uneven coating over most of the window. While most analysis programs remove time-invariant noise, the resultant loss of materials to surfaces will affect the concentration of the labeled material (discussed below). The second source of time-invariant noise is background fluorescence from cell components (particularly epoxy centerpieces). This source of noise tends to be of lower magnitude and more uniform than that from adsorbed label, and also is removed during data analysis. Sources of radially-independent noise include variation in the source intensity and variation in detector sensitivity. In our experience, both of these noise sources are small.

The conversion from fluorescence intensity to concentration is not trivial. So long as the signal is directly proportional to concentration, one can determine the sedimentation coefficient, diffusion coefficient and molecular weight without needing to convert the data. Likewise, there are many qualitative observations (e.g. the sedimentation coefficient increases or decreases in response to some stimulus) that require only relative knowledge of the concentration. For these purposes data collected using the AU-FDS may be handled in the same manner as absorbance or interference data. However, if one wishes to obtain concentration-dependent data (e.g. an association constant, or non-ideality coefficient), fluorescence detection poses some difficulties.

The fluorescence intensity is proportional to the concentration, F = I_o Qεc, where ε is the extinction coefficient (either molar or weight, depending on the concentration units used for c), Q is the quantum yield (the fraction of photons absorbed that result in a fluorescence signal) and I_o is the incident intensity of the excitation beam. While ε is relatively constant, Q is sensitive to the peculiarities of the immediate surroundings of the dye (e.g. local dielectric constant, polarizability and any dipole moments) and to the specific solution conditions (e.g. how many and how uniform are the labels attached to the molecule of interest, are quenchers present). This means that it is more difficult to relate the fluorescence intensity to concentration than it is the absorbance or fringe displacement. Comparison of fluorescence intensities to standards is one way to do this, and special calibration centerpieces are available to hold several standards (Spin Analytical, NH). Even using standards is not without problems (MacGregor et al., 2004).

Collisional quenching decreases Q, hence decreases the fluorescence intensity. Removing quenchers uniformly (both sample to sample and radially) is essential for good sensitivity and good reproducibility. While most common biological solvents do not contain quenching agents, some reagents (e.g. cesium ions, acetate ions, heavy metals, iodide, acrylamide) should be avoided (see http://probes.invitrogen.com/handbook/). The most common quencher is molecular oxygen, which should be removed from samples by a nitrogen sparge or placing the samples under vacuum for a few minutes. It has been our limited experience that biological samples (e.g. serum, cell lysates) do not contain large quantities of quenchers.

One of the most common applications of AUC is the detection and characterization of molecular interactions. While it is straightforward to detect binding as changes in the sedimentation coefficient or changes in apparent molecular weight, determining an accurate association constant may be difficult. Specifically, if a label’s local surroundings change on association (e.g. with respect to polarizability, dipole moments, etc.), the quantum yield may be affected, and the fluorescence intensity will not be linear with concentration. At present, only one analysis program (SEDANAL) is equipped to handle changes in the quantum yield upon molecular association). If one simply wants to get a ballpark idea of the association constant, the wide dynamic range of the AU-FDS system typically allows a complete titration curve (S_W versus c) to be obtained. The midpoint of the transition of the curve provides an estimate of the binding energy (as ln c), and it may be possible to fit the titration curve to more sophisticated models (Correia, 2000; Schuck, 2003).

While the fluorescence optics may be used over a very broad concentration range, special care must be exercised when using samples containing at very low concentrations (< 10 nM) or high concentrations (> 5 μM) of labeled material. For low concentrations, loss of material to surfaces can be a problem. Proteins, lipids, nucleic acids and polysaccharides can be “sticky” and form a monolayer (or thicker layer) on surfaces in contact with the solution. At low concentrations, the stuck material may be a significant fraction of the total material put in the sample cell. The degree of “stickiness” varies from substance to substance. For the AUC sample holders, there are three surfaces to consider: the walls of the centerpiece, the cell windows and the air-liquid meniscus. The simplest way to minimize these effects is to include some non-labeled “carrier” protein in the sample buffer. Low concentration (0.1 mg/ml) ovalbumin, serum albumin and kappa casein have all been used as carrier proteins. It is worthwhile to try more than one type of carrier protein to make sure the carrier protein does not interact with the labeled material.

The confocal design of the AU-FDS allows the detector to provide usable data at fairly high concentrations of dye (MacGregor et al., 2004). Nonetheless, absorbance of the excitation beam by dye molecules not in the observation volume will reduce I_o (inner filter effect) and lead to a nonlinear relationship between the concentration and fluorescence intensity. A similar problem will occur if the emitted light is absorbed by the fluorophore. The easiest fix for this is to reduce the concentration of the dye, either by diluting labeled material with unlabeled material or by decreasing the number of labels per molecule.

D. High Concentrations and High Concentration Gradients

It is sometimes desirable to characterize high concentration samples using AUC. The signal for both the absorbance and interference optics is dependent on the optical pathlength. Decreasing the sample pathlength is the best way to extend their concentration range to high concentrations. Special 3-mm thick centerpieces (and the adapters to use them with standard windows and cell housings) are available (Spin Analytical, NH; Beckman Coulter, CA) for this purpose. If accurate concentration-dependent parameters (equilibrium constants, nonideality coefficients) are sought, consideration must be given to the optical focus when using these centerpieces, particularly when high concentration gradients are present (Yphantis, 1964). Although the interference (Richards et al., 1971; Yphantis, 1964) and fluorescence (http://rasmb.bbri.org/rasmb/AOS) systems may be refocused, no procedure exists to refocus the absorbance optics.

Snell’s law says that light will bend from a region of lower refractive index into a region of higher refractive index. The concentration gradients developed during sedimentation also are refractive index gradients that may affect any of the optical systems. The collimated light used in the absorbance and interference optical systems will be bent towards the base of the cell (for a sedimenting boundary, but towards the meniscus for a floating boundary). Ordinarily, the imaging optics will correct this distortion and bring the deviated light back to the correct radial position. However, if the gradient is steep enough and the optics improperly focused, the correction may not be entirely accurate (Yphantis, 1964). If the gradient is steep enough, light even may be deviated entirely out of the optical path. A simple test for the absorbance system is to scan the cell at a non-absorbing wavelength (e.g. 320 nm for a protein solution). This scan should be a flat line at 0 OD. If a too-steep gradient is present, this scan will have a “bump” in it centered at the boundary position. The height of the bump will diminish as the boundary spreads (Dhami et al., 1995; Laue, 1996). The only way to obtain accurate data is to reduce the steepness of the gradient. In some cases, this may be done by sedimenting a lower rotor speeds to let diffusion spread the boundary, or just using data later in the run for analysis when the boundary has spread.

VI. Sample Requirements

Often, the first question that we face when planning an AUC experiment is “do we have enough material?” The sample requirements for AUC typically lie somewhere between crystallography/NMR and biochemical assays, but they can vary greatly depending on the nature of the experiment, the optical detection system and the extinction coefficient. The sample volumes required for AUC analysis are quite low. SV experiments are generally performed using two sector cells which require 420 μL/sample, but for the fluorescence detection system cells with volumes of 60 μL/sample are available (Spin Analytical, NH). Typical SE experiments are performed in six sector centerpieces which require 110 μL/channel; however, short column measurements require lower volumes. In particular, the eight-channel centerpieces only use 14 μL/channel. For lower molecular weight solutes it is often useful to perform SE measurements using longer columns (4–5 mm) in two-sector cells.

The choice of sample concentrations can be challenging and involves balancing the biological and biochemical relevance, sensitivity and linearity of the AUC detection optics and limitations imposed by the physical chemistry of the macromolecules being investigated. One usually attempts to investigate proteins near their physiologically relevant concentrations. In many cases, however, these concentrations are not known and one simply wants to establish whether a sample is homogeneous, define the dominant association state and possible obtain some shape information. Here, the concentration range will be dictated by the optimal conditions for the AUC measurements. The low concentration limit for an AUC measurement is limited by the sensitivity of the detection system and the optical properties of the sample. The highest accessible concentrations are determined by the linearity of optical system, optical artifacts occur at high concentration gradients and by thermodynamic and hydrodynamic nonideality which becomes more pronounced at higher concentrations. Typical RMS noise levels for the absorption system are ~ 0.005 OD, and for the interference system the noise is ~ 0.01 fringes. Thus, reasonable signal/noise levels require a minimum sample concentration corresponding to ~0.1 OD or 0.2 fringes. For a typical protein with a specific absorbance near 1 (mg/ml) ⁻¹cm⁻¹, 0.1 OD corresponds to a concentration of ~ 0.08 mg/ml (note that the usual centerpiece optical path is 1.2 cm). For the interference system, 0.2 fringes corresponds to about 0.06 mg/ml and the sensitivity interference optics is roughly comparable to that of the of the absorbance system operating at 280 nm. However, using the absorption optics, higher sensitivity measurements can be achieved at shorter wavelengths. In the XL-I, it is useful work at 229–230 nm where the flash lamp has a strong output and the protein absorbance is ~5–7-fold higher than at 280 nm. Reasonably good signal/noise can be obtained at this wavelength with protein concentrations as low as 10–15 μg/ml.

In experiments designed to measure the equilibrium constants for reversible associating systems, the concentration ranges must be chosen such that each of the species which participates in the equilibrium is present at an appreciable concentration. Thus, precise determination of K_d values for high affinity reactions requires low sample concentrations which may lie below the detection limits discussed above. On the other end of the scale, weak interactions require high concentrations where nonideality and optical artifacts can become problematic. The best way to choose sample concentrations and other experimental conditions, and to determine whether the equilibrium constants are even experimentally accessible for a given system, is by simulation. Synthetic data are generated using the appropriate molecular parameters, experimental conditions and estimated equilibrium constants. Noise is added to the data to simulate the optical system being used. The data are then fit to determine whether the correct equilibrium constants can be recovered with reasonable confidence. Simulation routines are implemented in many AUC analysis software packages such as HETEROANALYSIS, SEDANAL, SEDFIT/SEDPHAT and ULTRASCAN.

VII. Sample Preparation

The admonition from the late Efraim Racker “Don’t waste clean thinking on dirty enzymes” (Schatz, 1996) applies well to AUC. Rather than trying to interpret complicated and ambiguous AUC data obtained using impure or heterogeneous samples, we find that the time is much better spent on improved purification protocols. In practice, proteins should be at least 95% pure by SDS polyacrylamide gel electrophoresis and the mass spectrum should correspond to a single species consistent with the predicted molecular weight. Many proteins tend to form irreversible aggregates during purification or storage. Gel filtration is a good last purification step to remove such aggregates as well as low molecular weight contaminants that may not be resolved on polyacrylamide gels. Some proteins can aggregate with time or upon freeze/thaw cycles, so that it may be necessary to run a gel filtration column immediately before AUC analysis. Aggregation or proteolytic degradation can also occur during long SE experiments. These problems can be diagnosed by analysis of the sample after the AUC experiment. We have also encountered sticky samples that bind to the windows or centerpiece. This loss of soluble material can be assessed by measuring the OD at low speed (3000 rpm) after loading the sample.

Samples should be equilibrated into the experimental buffer such that the composition of the reference and sample solutions is identical. This can be accomplished by conventional gel filtration, as mentioned above, small volume gel filtration spin columns or by dialysis. Buffer matching is most critical when using interference optics, where any mismatch of salts or other buffer components contributes to the fringe displacement. Most of the commonly used buffer components are compatible with AUC experiments. As described above, the major issues to keep in mind are ionic strength, absorbance (when using absorbance detection), viscosity and generation of density gradients (Schuck, 2004). The salt concentration should be at least 20–50 mM to shield electrostatic interactions that contribute to thermodynamic nonideality. For absorbance measurements, the OD of the buffer at the detection wavelength of should be minimized. Reductants such as mercaptoethanol and dithiothreitol absorb at 280 nm upon oxidation; however, TCEP (Tris(2-carboxyethyl)phoshine) is essentially transparent at this wavelength. At shorter wavelengths, e.g., 230 nm, many buffer constituents absorb and a buffer vs. water spectrum should be recorded. Highly viscous buffers slow sedimentation in SV experiments and extend the time to achieve equilibrium in SE and should be avoided. Finally, density and viscosity gradients produced at high solute concentrations should be taken into account for SV experiments (Schuck, 2004).

Two critical parameters for interpretation of AUC experiments are ρ and v̄. Typically, ρ is calculated from the composition using SEDNTERP (Laue et al., 1992) or measured using a high-precision density meter (automated instruments are available from Anton-Paar). For proteins lacking prosthetic groups or posttranslational modification, v̄ is commonly calculated from the amino acid composition (Laue et al., 1992). However, these calculated values should be used with caution. Some buffer components are either excluded (e.g. glycerol) or concentrated (e.g. guanidine HCl) at the protein hydration layer, which affects v̄ (Timasheff, 2002). The effects of glycerol (Gekko and Timasheff, 1981), salts and amino acids (Arakawa and Timasheff, 1985) guanidine HCl (Lee and Timasheff, 1974; Lee and Timasheff, 1974) and urea (Prakash and Timasheff, 1985) on v̄ have been tabulated. v̄ can also be affected by changes in the water density in the hydration layer and by changes in protein packing density, and in some cases the origin of an anomalous value of v̄ may not be apparent from the protein structure (Philo et al., 2004). Thus, in some circumstances, it may be necessary to measure partial specific volumes experimentally. Ideally, v̄ can be obtained from the variation in solvent density with protein concentration using a high-precision density meter. In this regard, Eisenberg (Eisenberg, 2000) suggests replacing the buoyancy term used in analytical ultracentrifugation experiments M(1−ῡρ), by the more thermodynamically rigorous density increment (∂ρ/∂_c2)_p,μ, where c₂ is the protein concentration and the subscript μ indicates a constant chemical potential of all other solute components. Alternatively, in the Edelstein-Schachman method, v̄ is calculated from the linear change in the buoyant molecular weight in sedimentation equilibrium experiments performed in buffers where the density is increased by adding D₂0 (Edelstein and Schachman, 1973).

VIII. Sedimentation Velocity

A. Instrument Operation and Data Collection

Sedimentation velocity experiments are carried out in two channel cells with sector shaped compartments (Figure 1) in order to prevent convection, which would occur if the cell walls were not parallel to radial lines. The usual protocol in our laboratories is to run three sample concentrations spanning at least an order of magnitude, e.g. 0.1, 0.3, and 1.0 mg/ml.

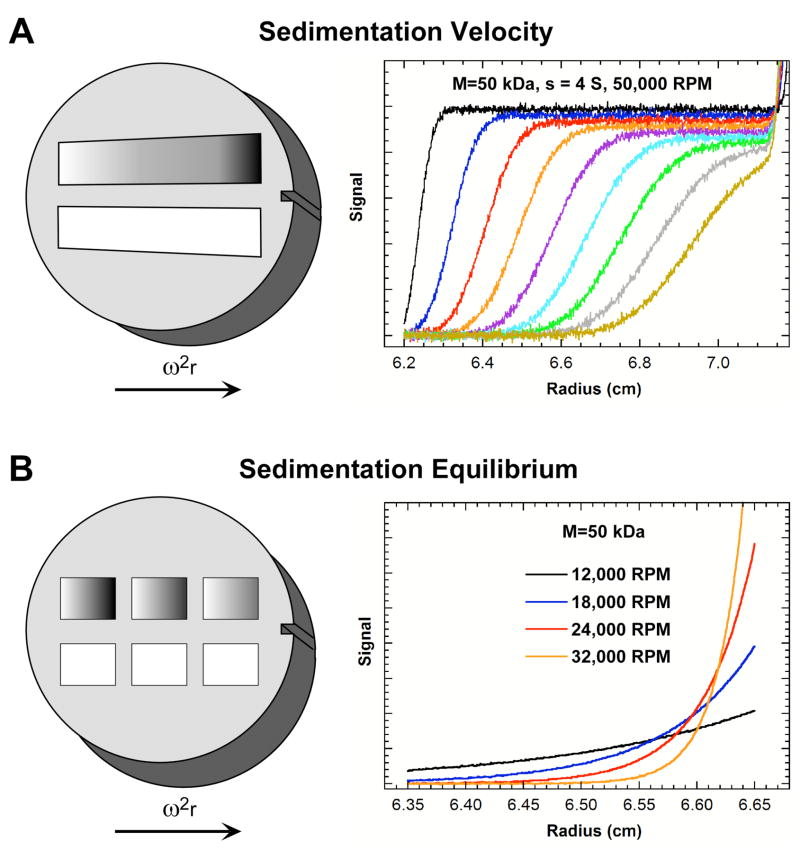
Figure 1.

Basic analytical ultracentrifugation experiments. Simulations are for a protein of 50 kDa with a sedimentation coefficient of 4 S. A) SV experiment. Velocity sedimentation is usually performed using a two-sector cell and scans are recorded at fixed intervals during the run. The simulation is for a rotor speed of 50,000 RPM and scans are displayed at 20 minute intervals. B) SE experiment. Equilibrium measurements usually employ a six sector cell with three loading concentrations. The equilibrium concentration gradients are simulated for four rotor speeds ranging between 12,000–32,000 RPM, corresponding to values of ranging from ~ 0.8 to ~ 6 cm⁻². The 32,000 RPM scan is truncated at the base.

For SV experiments using absorbance optics the cells are assembled using standard double-sector centerpieces and quartz windows. The cells are filled with 430 μL of buffer in the reference sector and 420 μL of sample solution in the sample sector. The XL-A (or XL-I) monochromator may not reproducibly return to the same wavelength if scans are performed at multiple wavelengths. Because of this potential problem we choose to limit SV experiments to using a single wavelength and choose concentrations of the sample that will yield ODs of 1.2, 0.4, and 0.1 at the selected wavelength. The rotor, with the cells and a correctly weighted counterbalance, is loaded into the centrifuge and the vacuum system is started. At this point the speed is set to “0” and the run is started, though the rotor will be stationary. This procedure will turn on the diffusion pump and allow the vacuum to drop below 100 microns, at which point the temperature reading will accurately reflect the rotor temperature. Once the rotor temperature has reached the set point we allow the rotor to equilibrate for an additional hour before starting the run. This, in turn, will minimize the effects of convection due to temperature gradients.

The protocol for SV experiments using interference optics is somewhat different due to the fact that interference data will reflect any refractive index differences between the sample and reference sectors, including differences in the buffer gradient if the column heights are mismatched. In order to eliminate this possible problem we use double-sector synthetic boundary, capillary-type centerpieces. The cells are assembled using sapphire windows because this optical system is focused only for this type of window, and the interference fringe pattern tends to blur at higher speeds if quartz windows are used. In addition, we perform a test run of the cells filled with water in order to preset the scan configurations for each cell and to perform a radial calibration. This test run will also allow checking of the cells for leaks, thus preventing the possible loss of sample material. It will also make it possible to start collecting data during the actual run as soon as the rotor reaches speed. Once the test run is finished the cells are removed from the rotor, the water is aspirated from the cells and the assembled cells are dried in a vacuum chamber. One can also now replace the interference counterbalance with a fourth cell containing an additional sample dilution since the radial calibration has already been performed. For the actual run each synthetic boundary cell is loaded with 430 μL of buffer in the reference sector and 420 μL of sample solution in the sample sector. The cells are placed in the rotor and the rotor is placed in the chamber, along with the monochromator/laser assembly. The rotor is accelerated to ~12,000 rpm and the interference fringe pattern, for each cell, is checked to confirm that the excess buffer has transferred over to the sample sector from the reference side. At this point the rotor is stopped, removed from the centrifuge, and then gently inverted to thoroughly mix the contents of each cell. Now the rotor is placed back in the centrifuge and the temperature is equilibrated as previously described. A typical concentration series for four cells would be 1.5, 0.9, 0.3, and 0.1 mg/ml. Sample dilutions may be made immediately prior to the SV run unless it is suspected that slowly reversible reactions are taking place. In that case dilutions are made and then sufficient time allowed for complete equilibration at the experimental temperature.

The instrument operating parameters include: the temperature, the rotor speed, time after speed is reached before the first scan is taken, the time interval between scans, and how many scans are to be acquired. For sedimentation velocity analysis, there should be no delay before data are acquired. Likewise, there is no reason to wait between scans, so there should be no interval between scans. These two parameters (scan delay and scan interval) should be set to zero in the method for either the Beckman Coulter ProteomeLab or the Aviv-AOS software to maximize the number of data sets available for analysis.

The listed operating temperature range of the XLI is 0 – 40 °C. However, excessive oil vapor at operating temperatures above 35°C and difficulty maintaining temperatures below 4 °C limit the useful temperature range. Replacing the oil diffusion pump with a turbomolecular pump allows operation to 40 °C, and reduces optical fouling. A kit for upgrading the XLI vacuum system is being developed (Beckman Coulter, CA). Most experiments are conducted at 20 °C, thus simplifying correction of the sedimentation and diffusion coefficients to standard conditions. For a sedimentation velocity experiment, one wants to make sure the samples have stabilized at the desired temperature prior to rotor acceleration. For this reason, many people allow the system to stabilize at temperature for an hour or so before acceleration. For high accuracy work, it is desirable to calibrate the XLI temperature sensor (Liu and Stafford, 1995).

Choosing the correct rotor speed for a sedimentation velocity experiment depends what you want to know about your sample, what the expected component size distribution is, and which optical systems will be used. These considerations lead to competing needs. The resolution of solution components is proportional to ω², indicating you should use the highest rotor speed possible, especially if you are trying to determine how many components there are in a solution. Thus, for samples with s < 10 S (the units of s are Svedbergs (S) with 1 S = 10⁻¹³ s), it makes sense to use the highest rotor speeds (55,000–60,000 RPM). However, with modern global analysis software it is also beneficial to obtain a large number of scans. Thus, lower rotor speeds are required if components of interest are very large with large sedimentation coefficients. Also, the absorbance optics have long scan times and when scanning multiple samples and wavelengths it may be useful to reduce rotor speeds. Although there is no simple formula for optimizing the rotor speed, we can use the definition of the sedimentation coefficient, (equation 2) to determine reasonable rotor speeds. It should take a boundary at least 2 hours to sediment the full length of the cell (1.5 cm maximum), to ensure sufficient scans will be acquired. Based on this criterion, the maximum recommended rotor speeds for various sedimentation coefficients are presented in Table 3. In addition, when using the absorbance system it is necessary to consider the longer scan times and adjust the rotor speed so that at least 30–40 scans are recorded during the movement of the boundary across the cell.

Table 3.

Maximum rotor speeds for sedimentation velocity experiments.

Sa	Mbapproximate	RPMc
10	200,000	55,000
15	400,000	50,000
30	1,000,000	30,000
90	5,000,000	20,000
270	25,000,000	10,000

^aMaximum allowed rotor speed may be used for solutions where all components have sedimentation coefficients < 10 S. However, acquiring absorbance data at multiple wavelengths will greatly increase scan times, thus decreasing the number of scans acquired at a particular wavelength over the course of an experiment. For experiments requiring multi-wavelength scanning, one may wish to spin at a lower rotor speed.

^bThese are only approximate values estimated for spherical proteins. If the molecules are asymmetric or a highly solvated, then a higher molecular weight will correspond to a given sedimentation coefficient.

^cAbout two hours of data acquisition will be available at the listed rotor speed. Be sure the maximum speed rating for the centerpiece is not exceeded. For example, the Epon-based centerpieces from Beckman Coulter have a maximum speed rating of 44,000 RPM, whereas the Spin Analytical Epon centerpieces are rated to 60,000 RPM.

B. Data Analysis

Methods for analysis of SV experiments have evolved rapidly in recent years and many alternative approaches and software packages are available. Here, we will outline an approach that we have found useful in the initial stages of analyzing an unknown system. At the early stages, it is useful to examine the data using methods that require the fewest assumptions about the nature of the system being investigated. Simple put, the goal of these “model-free” approaches is to determine how many species are present and whether they interact. Later, this information can be used to construct models and obtain starting parameters for more detailed analyses.

In the “dc/dt” method, a closely spaced group of SV scans are subtracted in pairs to approximate the time derivative of the data and thereby determine how much material is sedimenting at various rates (Stafford, 1992). This subtraction removes the systematic noise in the data, which is particular useful for interference data. The radial variable is then transformed to an apparent sedimentation coefficient (s*) and the data are averaged among several pairs to enhance the signal to noise ratio. Finally a data transformation yields the apparent sedimentation coefficient distribution function g(s*). These algorithms have been implemented in several software packages: we find that DCDT+ is particularly easy to use and convenient. The g(s*) distributions resemble chromatographs and can be visually examined to determine whether the sample appears pure (one peak) or heterogeneous (multiple peaks or shoulders). It is important to inspect the distributions at multiple loading concentrations to check for reversible interactions. A shift in peak position to higher s* with increasing concentration is evidence for mass-action equilibrium where the species interact the timescale of sedimentation. In this case, the peak represents a “reaction boundary” and cannot be treated as a species. Alternatively, the peak positions may remain constant or shift only slightly, but the relative area of the higher s* feature may increase with loading concentration. This behavior is diagnostic for slowly reversible interactions and it is important to fully equilibrate such samples prior to AUC analysis. For homogeneous species or mixtures of noninteracting species, the width of each peak is related to D, and one can fit the distribution to obtain D and thus the molecular mass of each component. This fitting process can also be useful to determine whether the peak is truly homogeneous. Recent advances have improved the fitting function (Philo, 2000) and extended the scan range (Philo, 2006) than can be used in this analysis.

The main advantage of the dcdt method is simplicity. No models are assumed in the analysis. Also, the subtraction and averaging results in noise reduction, allowing lower sample concentrations. The chief disadvantages are the limitations in the number of scans to avoid distortion of the peak shape, and the diffusional broadening of the peaks that can hide heterogeneity. Also, it is difficult to cover a large range of sedimentation coefficients using this approach and the method does not work well with low molecular weight solutes (molar masses less than 10 kDa or s < 2S).

Alternatively, in the c(s) method implemented in the programs SEDFIT and SEDPHAT, the sedimentation coefficient distribution function is obtained from a direct fit to the data (Dam and Schuck, 2004; Schuck, 2000). Here, we describe the most basic implementation of the c(s) method. First, the program creates a grid of sedimentation coefficients covering the expected range of interest. By assuming a constant shape, and consequently an equal frictional ratio (f/f₀), for all species, a scaling relationship is created between s and D. The program then simulates the sedimentation boundaries for each point using a numerical solution of the Lamm equation. Finally, the data are fit to a sum of these Lamm solutions using a least-squares fitting procedure to define the concentration of each species in the grid. During this process, the systematic noise of the baseline (time invariant noise) and the vertical displacements (jitter and integral fringe jumps) are removed by treating them as additional linear fitting parameters. The resulting c(s) function is often quite “spiky” and a regularization procedure is performed to produce a smoother distribution function. Like the g(s*) distribution, the c(s) distribution can be visually interpreted by looking at how many peaks are present and how they depend on loading concentration. For the c(s) models, one can also check whether the model of a sum of noninteracting species provides a good fit to the experimental data. A poor fit can indicate reversible interactions. Although the c(s) distribution can be converted to a distribution of molar masses (c(M) distribution), the derived masses will only be accurate if there is one dominant species present or if all the species have equal frictional ratios. More complex analysis procedures that do not assume a single value of f/f₀ are also implemented in SEDFIT and SEDPHAT.

The main advantages of the c(s) method are the excellent resolution and sensitivity. In contrast to the dc/dt method, there is no restrictions on the number of scans that can be included in the analysis, and the diffusional broadening is deconvoluted from the c(s) distribution based on the scaling relationship between s and D. The c(s) method is thus very useful for characterizing homogeneity and quantitating impurities and aggregates. The main disadvantage of this approach is that it assumes a noninteracting mixture and particular care must be exercised in the analysis of self- or hetero-associating systems where the resulting distributions are developed from an incorrect model. Nonetheless, for a system undergoing rapid association and dissociation, the distributions are reminiscent of those expected by limiting models (57), and useful semi-quantitative information may be extracted (53, 54). For interacting systems undergoing reactions on the timescale of the SV experiment, peaks in the c(s) distribution may not correspond to true molecular species (Dam et al., 2005). Provided that the c(s) distribution is a good fit to the data, it is always feasible to extract thermodynamic parameters from the data by integration of the distribution and analyzing the dependence of weight average sedimentation coefficients on the loading concentrations (Correia, 2000; Correia et al., 2005; Schuck, 2003). The only requirement for this analysis to be accurate is that all association reactions are at equilibrium prior to the start of sedimentation. This criterion may be met by incubating the sample dilutions a sufficient amount of time (e.g. overnight) at the sedimentation temperature prior to sedimentation.

The van Holde – Weischet approach (van Holde and Weischet, 1978) is also used for the initial, qualitative analysis of SV experiments. Because sedimentation is proportional to the first power of time whereas diffusion is proportional to the square root of time, graphic extrapolation of the boundary to infinite time yields an integral sedimentation coefficient distribution, G(s) in which the diffusional contribution has been removed. This method is implemented in ULTRASCAN, SEDFIT and the Beckman-Coulter software. Recent advances have extended this method for the analysis highly heterogeneous systems. (Demeler and van Holde, 2004).

Although the information obtained from the model-free approaches may be enough to answer the relevant questions about the macromolecular system being studied, we often find it useful to analyze the system using model-dependent procedures. For analysis of mixtures, the goal is usually to obtain the concentration, sedimentation coefficient and mass of each species. These parameters are recovered with greater precision by using a fitting model of a mixture of several discrete species rather than continuous distribution approaches. The available software uses either approximate (SVEDBERG, LAMM) or numerical (SEDANAL, SEDFIT/SEDPHAT, ULTRASCAN) solutions to the Lamm equation to fit data as a superposition of noninteracting species. We often find it useful to improve the precision of the fitted parameters by globally analyze data sets obtained at several loading concentrations using SEDANAL or SEDPHAT. The absence of systematic deviations in global fit also confirms that there are no mass action reactions over the concentration range examined. For systems that contain a mixture of well-defined discrete species and poorly resolved aggregates or low molecular weight impurities, it can be useful to fit the data to a hybrid c(s)-discrete species model in SEDPHAT where the poorly resolved material is accounted for in the continuous distribution.

Analysis of reversible interactions by SV is a complex problem (Dam and Schuck, 2005; Dam et al., 2005; Rivas et al., 1999; Schuck, 2003; Stafford, 2000; Stafford and Sherwood, 2004). However, SV may be the only feasible approach for systems that are intrinsically unstable or that do not come to equilibrium in SE experiments. For interacting systems, the boundaries do not generally correspond to discrete species. Because the concentrations are changing throughout the cell during sedimentation, particularly where there are boundaries, the species composition is continuously varying due to the mass action equilibria. Consequently, the apparent sedimentation coefficients and boundary shapes are complex functions of the sedimentation coefficients of the species participating in the equilibrium, their concentrations, and the equilibrium and kinetic constants governing their interactions (Cann, 1970; Dam and Schuck, 2005; Gilbert and Jenkins, 1956). As alluded to above, the traditional approach to analyzing interacting systems by SV is to measure weight average sedimentation coefficients as a function of loading concentrations (Correia, 2000; Correia et al., 2005; Schachman, 1959; Schuck, 2003). An advantage of this method is that the weight average sedimentation coefficient is a thermodynamically valid parameter that is determined the sample composition in the plateau and is independent of the kinetics of the interactions, provided that the sample is at equilibrium prior to sedimentation. Examples of this approach can be found in studies of CMV protease dimerization (Cole, 1996) and the complex association reactions of tubulin (Correia, 2000; Sontag et al., 2004) and HIV rev (Surendran et al., 2004). Interacting systems can also be characterized calculation of g(s*) distributions using the time-derivative method (Stafford, 2000). More recently, direct boundary fitting methods for interacting systems have been implemented in SEDANAL, SEDPHAT and ULTRASCAN. When compared, this approach gives comparable results to those obtained using weight-average analysis (Sontag et al., 2004). Some recent examples of direct boundary analysis to define the energetics of associating systems can be found in (Connaghan-Jones et al., 2006; Correia et al., 2005; Dam et al., 2005; Gelinas et al., 2004; Snyder et al., 2004).

IX. Sedimentation Equilibrium

The big advantage of sedimentation equilibrium, SE, is that it removes all hydrodynamic effects, so that purely thermodynamic analysis is possible. The requirements for sample purity and homogeneity are much stricter for SE measurements that for velocity experiments. In the latter case, the boundaries associated with each species separate during the sedimentation run so that it is possibly to isolate contaminants from the species of interest. In contrast, different species are incompletely fractionated in an SE gradient. Furthermore, as shown below, fitting SE concentration gradients requires deconvolution of multiple exponential functions, which is a challenging mathematical operation that becomes increasingly difficult with larger numbers of species.

A. Instrument Operation and Data Collection

There are three commercially available centerpiece styles that are commonly used when conducting SE experiments. The choice of which style to use will be determined by the information that is being sought. The short-column centerpiece has 8 channels which can hold four sample-reference pairs. Each channel requires only 15 μL of solution, resulting in a column height of 700- to 800 μm, and will typically reach equilibrium within an hour or two (Yphantis, 1960). This type of centerpiece is useful for conducting a rapid survey over a wide range of concentrations and/or conditions (Laue, 1992). The standard long-column centerpiece has 6 channels, which can hold three sample-reference pairs (Figure 1B). Each of these channels requires approximately 120 μL of solution, which will result in a column height of ~3 mm. Long-column experiments are useful for accurately determining molecular weights, self-associations, hetero-associations, etc., by direct fitting of data from multiple concentrations (or multiple mixing ratios) at multiple speeds using global, model-dependent, nonlinear least squares analysis.

A version of the 6 channel centerpieces is available that, along with a custom cell housing, allows the cells to be loaded and unloaded without disassembly (Ansevin et al., 1970). These “external loading” cells are particularly useful with the interference optics because they facilitate blank subtraction. Prior to acquiring blanks, each cell must be “aged” in order to bring the cell, centerpiece, and windows into a mechanically stable configuration. First assemble the external loading cell according to specifications (typically sealed at between 120 and 140 inch-pounds of torque). Fill each of the reference sectors with 150 μL of water and each sample sector with 140 μL of water and seal the filling holes with a gasket and screw. Centrifuge the cells at the maximum speed that will be used during your experiment for at least 1 hour. Stop the run, remove the cells, and re-torque them to specifications. Place the cells back in the rotor and centrifuge them at the same speed as before for another hour. Repeat this at least one more time for a total of three acceleration/deceleration cycles. In our experience three or four cycles is sufficient to bring the cell into a stable state. To acquire the blank, the cells are filled with water and run at the same temperature and rotor speeds as will be used during the experiment. At each rotor speed, scans are acquired every 5 minutes or so until no changes in the fringe patterns are apparent. After the blanks have been acquired the water is removed, the cells dried, and the samples loaded. The “blank” scans are subtracted from the data scans to remove the systematic noise. Because they do not need disassembly, the blank correction from external loader cells (above) can result in 10-fold lower noise (Ansevin et al., 1970). Specialized methods for washing the external loading cells without disassembly have been described (Ansevin et al., 1970). An automated cell washer recently became available (Spin Analytical, NH). Also, Beckman Coulter produces centerpieces that facilitate cell cleaning by incorporating two holes per sector.

In order to characterize a system over a wide concentration range, different sample loading concentrations must be used. It is recommended that 1:1, 1:3 and 1:9 dilutions be used with the 6-channel cells, and 1:1, 1:2, 1:4, 1:8 dilutions be used in the 8-channel cells. Cells are loaded so that the highest concentration sample will be closest to the rotor center and the most dilute sample will be towards the rotor’s edge. This way, advantage will be taken of the gravitational field to concentrate the more dilute samples while minimizing the concentration gradients in the highest concentration sample. A layer of dense, colorless fluid should be used to create an artificial base of each sample. This layer allows data acquisition at the highest concentration region with less interference from reflections from the centerpiece base. The recommended fluid is FC-43 (3M, Inc., MN). For 2-channel and 6-channel centerpieces, 10 μL of FC-43 is used whereas 5 μL is used for 8-channel centerpieces. It has been found that certain proteins (e.g. tubulin) will denature and aggregate at the interface between the aqueous solution and the FC-43. Thus, while it is generally inert, it is worthwhile checking to make sure FC-43 is compatible with the solution components.

Other than the cells that are employed, there is no change in the instrumentation from SV for SE experiments. However the operating parameters are different. Unlike SV, it is usually not critical to allow temperature equilibration prior to starting the rotor spinning. It is important to collect data at multiple loading concentrations and rotor speeds to assess if the sample is homogeneous, if mass action-driven self-association is occurring, or if thermodynamic nonideality is significant. The complete data set can be used subsequently in global curve fitting programs to obtain the most precise parameters from the data. Many researchers perform sedimentation equilibrium experiments using rotor speeds that are too low (e.g, the 12,000 RPM trace in figure 1B). For a typical experiment using the standard 3 mm column heights, we recommend choosing the lowest speed such that σ ~ 2 cm⁻² for the monomer (e.g., the 18,000 RPM trace in Figure 1B). Assuming a typical protein v̄ ~ 0.74 cm³/g this speed can be estimated as

$$\mathit{RPM}\approx 4\times {10}^6\sqrt{1/M_p}$$ (7)

There are times when you may want to start a protocol at a rotor speed which produces σ less than 2 cm⁻² (e.g. for systems exhibiting large stoichiometries or for longer solution columns). A typical experimental protocol will produce data at three or four rotor speeds using 1.2-fold to 1.5-fold intervals between speeds, with the highest rotor speed yielding σ as high as 10–15 cm⁻². In combination with the recommended cell loading described above, this protocol will produce data over a very broad concentration range that will enhance the reliability of the analysis. The experimental protocol must go from lowest to highest rotor speed. If a lower rotor speed is used after a higher one, the system will not reach equilibrium in a reasonable time (Roark, 1976).

B. Monitoring Approach to Equilibrium

The time to achieve equilibrium is dependent on a number of experimental factors, including the mass and shape of the particle, the solvent viscosity and the distance between the meniscus and the base (column height). In particular, the equilibrium time is proportional to the square of column height. Although theoretical expressions are available for the simplest systems (van Holde and Baldwin, 1958), the actual time to equilibrium may be extended by slow association and dissociation rates and other factors. Thus, the approach to equilibrium is often monitored experimentally by taking the difference between successive scans and looking for the absence of systematic deviations. A better procedure is to use WINMATCH or the Match utility in HETEROANALYSIS. These programs do least-squares comparison of the scans allowing for displacements in the vertical and horizontal directions. The RMS deviations decrease as a function of time until at equilibrium they reach a constant level corresponding to the noise level in the data. Although the equilibrium method in the Beckman-Coulter XL-I control software allows one to insert a delay prior to recording data, we recommend collecting data immediately at regular 15 – 30 minute intervals to monitor the approach to equilibrium. When using the absorbance system, we typically record scans using a coarse point spacing of 0.003 cm with only one reading/point to monitor the approach to equilibrium. Once equilibrium is achieved, the sample is then scanned using the maximal point spacing of 0.001 cm with about 10 readings/point. Slow aggregation can cause a loss of material in successive scans and prevent achievement of equilibrium. Other potential problems in equilibrium experiments can include sample hydrolysis or denaturation. In some cases, problematic samples can be stabilized by altering the buffer composition, temperature or changing the protein construct. However, it may be necessary to reduce the column height to achieve rapid equilibrium or use more rapid techniques, such as SV.

C. Data Analysis

There are several ways to analyze SE data. The old fashioned method calculates σ as the slope of a graph of lnC versus r²/2 (i.e. σ = dlnc/dr²/2). While this method is no longer widely used, it highlights a problem that must be addressed by all analysis methods, namely that one must have an accurate estimate of the concentration. It is tempting to substitute the absorbance, fringe displacement or fluorescence intensity signal since each of these is proportional to the concentration. Before they can be used, however, it is necessary to adjust the signal to be zero at zero concentration. This adjustment is accomplished by subtracting a baseline offset. For absorbance data, one can determine the offset experimentally by increasing the rotor speed to ~40,000 RPM at the end of the run to pellet the solutes and then measuring the residual absorbance in the solution column. Alternatively, the offsets may be treated as fitting parameters in nonlinear least squares analysis software. With interference data the offsets must be treated as fitting parameters.

Data analysis can be divided into two general methods- molecular weight moment determination and nonlinear least squares fitting. Both of these methods are useful, depending on what information is sought. Molecular weight moments can be determined directly from the data using the ratio of the different concentration moments (Harding et al., 1992; Roark and Yphantis, 1969; Stafford, 1980). For example, at any point in the sample, the weight average molecular weight (as σ_W), is the local concentration slope, dc(r)/dr²/2, divided by the local concentration, σ_W(r) = (dc(r)/dr²/2c(r). Because the determination of c(r) is subject to uncertainty due to the baseline offset, the z-average, calculated as the ratio of the curvature of the data to the slope, (σ_Z(r) = (d²c(r)/dr^{2 2}/dc(r)/dr²)) is particularly useful since it does not require knowledge of the concentration. No model needs to be specified for these calculations, so they are particularly useful for the analysis of complex systems. Graphs of σ_W(r) or σ_Z(r) as a function of c(r) or r can provide useful diagnostics about interacting systems (Roark and Yphantis, 1969). In particular, overlapping curves of σ_W(r) versus c(r) for samples at different loading concentrations and analyzed at different rotor speeds are thermodynamic proof that the system is homogeneous and undergoes reversible mass-action association. Programs are available specifically for calculating molecular weight moments (Table 4).

Table 4.

AUC analysis programs and utilities

Method	Application	Sourcea	References
SV:
Time Derivative (dc/dt)	DCDT+	1	(Philo, 2006; Philo, 2000; Stafford, 1992)
c(s)	SEDFIT	2	(Dam and Schuck, 2004; Schuck, 2000)
Van Holde-Weischet	ULTRASCAN	3	(Demeler, 2005; Demeler and van Holde, 2004; van Holde and Weischet, 1978)
	SEDFIT	2
Discrete Species: Approximate Lamm Solution	SVEDBERG	1,4	(Philo, 1997; Philo, 1994)
	LAMM	4	(Behlke and Ristau, 1997)
Discrete Species: Numerical Lamm Solution	SEDFIT	2	(Schuck, 1998)
	ULTRASCAN	3	(Demeler, 2005)
Global Analysis of Interacting Systems	SEDANAL	4	(Stafford and Sherwood, 2004)
	SEDPHAT	2	(Schuck, 2003)
Hydrodynamic Modeling	HYDRO, HYDROPRO	5	(Garcia De La Torre et al., 2000)
	ATOB	4	(Byron, 1997)
	SOMO	4	(Rai et al., 2005)
SE:
Test for Equilibrium	WINMATCH	6,4
	HETEROANALYSIS	6,4	(Cole, 2004)
Nonlinear Least Squaresb	WINNONLIN	6,4	(Johnson et al., 1981)
	HETEROANALYSIS	6,4	(Cole, 2004)
	ULTRASPIN	8
Molecular Weight Moment Analysis	SEDANAL	4	(Roark and Yphantis, 1969; Stafford and Sherwood, 2004)
	ULTRASPIN	7
	MSTAR	4	(Harding et al., 1992)
Utilities
Data Acquisition	AOS	4
Realtime Display and Analysis	SEDVIEW	4
	SEDFIT	2
Graphics	XLGRAPH	1,4
Calculations	SEDNTERP	1,4	(Laue et al., 1992)
	ULTRASCAN	3	(Demeler, 2005)

^aWebsites where software can be downloaded:

1. http://www.jphilo.mailway.com

2. http://analyticalultracentrifugation.com

3. http://www.cauma.uthscsa.edu

4. http://www.rasmb.bbri.org/rasmb

5. http://leonardo.fcu.um.es/macromol

6. http://biotech.uconn.edu/auf/

7. http://ultraspin.mrc-cpe.cam.ac.uk

^bThe programs listed are specifically designed for analysis of SE data. Several general AUC analysis programs (SEDANAL, SEDPHAT, ULTRASCAN) can also be used for nonlinear least squares fitting of SE data.

Nonlinear least squares analysis of sedimentation data have been performed for over 40 years (Johnson et al., 1981; Yphantis, 1964). Most nonlinear least squares fitting programs directly fit the experimental data to particular models, such as a single ideal species:

$$S(r,\lambda )={\delta }_{\lambda }+{\mathcal{E}}_{\lambda }{c}_{0}exp\left[\frac{M_b{\omega }^2}{RT}\left(\frac{r^2-r_0^2}{2}\right)\right]$$ (8)

where S(r, λ) is the signal (absorbance, fringe displacement, fluorescence) at radius r and wavelength λ, δ_λ, is the wavelength-dependent baseline offset and ε_λ is the extinction coefficient. Modern SE analysis software data can incorporate data obtained at multiple rotor speeds using multiple signals for global analysis (Table 4). Notice that σ (or M_bω²/RT) is in the exponent of the fitting function. As σ gets smaller and smaller, S(r, λ) approaches a straight line. For values of σ less than 2 cm⁻² or so, the correlation between c_o and δ for individual data sets becomes so great that fitted values of σ tend to be unreliable (e.g., the trace at 12,000 RPM in figure 1B). Therefore we recommend using rotors speeds such that σ ≥ 2 cm⁻² and, for absorbance data, fixing the baseline offsets using values of δ obtained from scans acquired after pelleting the material at the end of the run. More complex models are required for analyzing data for associating systems and for systems exhibiting thermodynamic non-ideality (Johnson et al., 1981). The newer analysis packages are capable of analyzing heteroassociation reactions involving two or more components. These models involve a large number of adjustable parameters and it is often necessary to constrain the fitting process by incorporating multiple signals (Cole, 2004; Howlett et al., 2006) and by invoking mass-conservation algorithms (Philo, 2000; Vistica et al., 2004).

It should be stressed that SE does not have the resolving power of SV, and reliable analysis of SE data by nonlinear least squares fitting methods requires pure samples free of aggregated material or contaminants. Depending on the size of the aggregates, it may be possible to pellet them while still analyzing the remaining sample. However, the presence of aggregates or contaminants will lead to inconsistencies in the data analysis Thus, it is critical to characterize samples by SV prior to SE experiments. In some cases, contaminants or aggregates identified by the SV measurements can be removed by preparative gel filtration prior to SE analysis.

X. Discussion and Summary

Analytical ultracentrifugation is a versatile and rigorous technique for characterizing the molecular mass, shape and interactions of biological molecules in solution. In particular, the size distribution analysis available with SV is more flexible, is applicable to more chemical systems, spans a much wider range of sizes and provides higher resolution than size exclusion chromatography. The hydrodynamic information available with SV is complemented by thermodynamic analysis by SE. The availability of interference (refractive), absorbance and fluorescence detectors makes AUC applicable to a wide variety of questions in cell biology. In particular, the fluorescence system provides a new way to extend the scope of AUC to probe the behavior of biological molecules under physiological conditions.

As we have described above, modern AUC users can choose from a broad array of experimental techniques and data analysis methods, and it can be difficult to decide how to best apply AUC methods when confronted with a new sample. Although the best strategy will depend considerably on the nature of the sample and the kinds of questions that need to be answered, Figure 2 shows a typical workflow that we use for characterizing a new sample by AUC. It is strongly recommended that new samples are first analyzed by SV at several concentrations. These measurements are crucial for deciding whether the sample is homogeneous and suitable for more detailed analysis. The SV data should first be analyzed using model-free methods: we typically examine g(s*) and c(s) distributions. If contaminants or aggregates are present that differ appreciably in size from the molecule of interest, the sample can often be purified by preparative gel filtration. In fact, we typically gel filter sample prior to AUC analysis. It should also be noted that although dynamic light scattering (DLS) lacks the resolving power of AUC, it a fast and sensitive method to determine whether aggregates are present and we often use DLS as a quality-control step prior to AUC.

Figure 2.

Typical workflow for a analytical ultracentrifugation analysis of an unknown sample. For details see the text.

The next step is to determine whether the sample undergoes reversible, mass-action association. A convenient method is to superimpose normalized g(s*) distributions obtained at different concentrations: reversible association will shift the distributions to higher s* with increasing concentration, whereas hydrodynamic nonideality will shift the distributions to lower s^*. For a non-interacting system, the SV data can be analyzed to obtained s and D for the species of interesting and the data can be interpreted to obtain the molar mass and shape parameters. It should be stressed that this analysis cannot be done for an interacting system: here, more sophisticated analysis is required to measure the sedimentation coefficients of the interacting species and to define the kinetics and thermodynamics of the interaction. If the system is stable, the interaction can be characterized by SE. Similarly, for a stable noninteracting system, reliable measurement of the molar mass and stoichiometry can be obtained by SE.

Throughout this review we have described a large number of data analysis packages available for both SV and SE. Table 4 lists the websites where this software may be obtained along with references describing the analysis algorithms and their applications. Table 4 also includes a number of utility programs that perform useful calculations or graphics. It should also be mentioned that the RASMB (Reversible Associations in Structural and Molecular Biology) group also maintains an email list-server that facilitates communication among researchers interested in analytical ultracentrifugation (http://www.bbri.org/RASMB/rasmb.html). The RASMB also maintains a software archive where many of the programs can be obtained.

Abbreviations

AUC

analytical ultracentrifugation

SE

sedimentation equilibrium

SV

sedimentation velocity