The effect of recovery time and test conditions on viscoelastic measures of tensile damage in cortical bone

Abstract

Stiffness degradation and strength degradation are often measured to monitor and characterize the effects of damage accumulation in bone. Based on evidence that these properties could be affected by not only damage magnitude but also test conditions the present study investigated the effect of hold condition and recovery time on measures of tensile damage.

Machined human femoral cortical bone specimens were subjected to tensile tests consisting of a pre-damage diagnostic loading cycle, a damage loading cycle and post-damage cycle. Controlled variables were recovery time (1, 10, 100 minutes) and hold condition (zero load or zero strain) after the damage cycle. Damage measures were calculated as the ratio of each post-damage cycle to the pre-damage value for loading modulus, secant modulus, unloading modulus stress relaxation and strain (stress) recovery at 1 minute post-diagnostic time.

The damage cycle caused reductions in all measures and some measures varied with recovery time and hold condition. Apparent modulus degradation for both hold conditions decreased with recovery time. Stress relaxation was unaffected by recovery time for both hold conditions. Zero-strain hold conditions resulted in lower values for degradation of modulus and change of relaxation. Stress or strain recovery after the damage cycle was evident through 100 minutes, but 90% of the recovery occurred within 10 minutes. The results demonstrate that choice of test conditions can influence the apparent magnitude of damage effects. They also indicate that 10 minutes recovery time was sufficient to stabilize most measures of the damage state.

Introduction

Bone damage has been widely studied because it plays a major role in mechanical failure and biological behavior of bone (Burr et al., 1997; Burr et al., 1998; Carter et al., 1977; Jepsen and Davy, 1997). Damage, most often recognized by histological means as micro-scale linear microcracks (Zioupos and Currey, 1994; Schaffler et al., 1995; Norman et al., 1998) and diffuse damage (Schaffler et al., 1994; Vashishth et al., 2000), has long been recognized as a normally occurring phenomenon that is present in increasing quantities with aging and with increased loading. Increased in situ damage may contribute to an increased risk of fracture, particularly for the elderly or individuals with bone metabolic disease (Burr et al., 1997; Zioupos and Currey, 1998). Therefore, understanding of the bone damage process has direct relevance to clinical orthopaedics. While many studies have focused on purely mechanical issues, a number of studies of bone damage have examined the coupling of damage and biology (Burr and Martin, 1993; Lanyon, 1993; Weinbaum et al., 1994; Martin, 2003; Fleck and Eifler, 2003; Carter and Spengler, 1978), which reflects its perceived importance to the bone biology.

Damage can affect most measurable mechanical properties of bone. The most common mechanical measures of damage are stiffness loss or strength loss. However, damage manifests itself in other ways. For example, creep or low-cycle fatigue studies show that viscous properties, as measured by changes in the rate and magnitude of relaxation, are more sensitive to damage than modulus (Jepsen and Davy, 1997; Martin, 2003; Fondrk et al., 1988; Fondrk et al., 1999; Currey, 1965; Knott et al, 2000; Lakes and Katz, 1979).

In our previous studies as well as studies by others, damage effects on viscoelastic and strength properties have been examined by loading bone into the damaging (post-yield) strain range and comparing post-damage properties to pre-damage properties (Akkus et al., 2003; Choi and Goldstein, 1992; Jepsen et al., 2001; Jepsen and Davy, 1997; Kotha and Guzelsu, 2003; Pidaparti and Vogt, 2002; Zioupos and Currey, 1994). However, the interpretation of damage effects, particularly in terms of their magnitude, may be influenced by the test conditions that are used, such as recovery time and the diagnostic loading protocol. These factors often vary among studies.

To address these issues conducted an experimental study using a protocol based on previous studies to observe tensile damage effects on cortical bone, in terms of changes of stiffness, viscous relaxation and energy dissipation (Jepsen and Davy, 1997; Jepsen et al., 2001; Pattin et al., 1996). We examined whether the length of the recovery period after damage (1, 10, or 100 minutes) and the boundary conditions (zero-load hold or zero-strain hold) would influence the apparent measures of damage in human cortical bone in tensile loading mode.

Methods

Experimental specimens were obtained from the left femur of a 42 year old female donor with no known skeletal pathologies. The femur was machined into the final dog-bone shape specimens with gage dimensions of 1.0×3.0×15.0 mm (Figure 1) using a band saw (Model 11, Biro Manufacturing, Marblehead. OH) and a side mill (Tensilkut I, Tensilkut, Knoxville, TN). Eight specimens were randomly assigned to each of six test groups. Total 48 specimen were individually placed in a bag containing saline solution and stored at −20 °C until testing.

Figure 1.

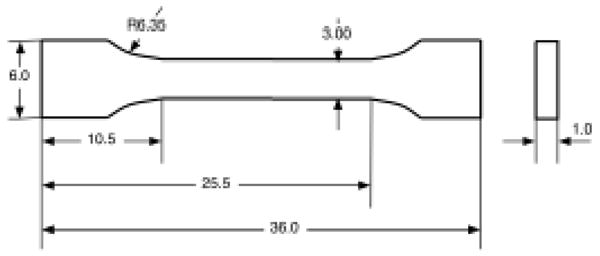
Schematic diagram of the specimen geometry. All dimensions are in millimeters. The front view is in the longitudinal plane and the side view in the radial-circumferential plane of the cortical diaphysis.

Each specimen was positioned in pre-aligned grips on a servohydraulic materials testing machine (Instron, model 8501, Instron Corp., Canton, MA). An extensometer (model 2620-530, Instron Corp., Canton, MA) was used to measure axial strain over the middle 10mm of the specimen. Testing was performed in an environment chamber at 37°C, and the specimen was kept wet by a 37°C saline solution drip. Axial load was measured using a 500lb (2224N) load cell with 100Hz sampling rate through a GPIB data-acquisition board. Wavemaker software (Instron, Instron Corp., Canton, MA) was used for test control and data acquisition.

The experimental tests consisted of a 3-cycle loading protocol similar to that used previously (Jepsen and Davy, 1997). Each specimen was loaded in uniaxial tension and subjected to a series of three trapezoidal pulses, which were a pre-damage diagnostic cycle, a damaging cycle and a post-damage diagnostic cycle (Figure 1).

Six experimental groups were tested (Table 1). Controlled variables were recovery times (1, 10 or 100 minutes) after the damage cycle and holding conditions at recovery time after each cycle (hold at zero strain or hold at zero stress). In all groups samples were loaded under strain control during the three load-hold-unload cycles. In groups 1–3, samples were held at zero strain under strain control during the post-damage recovery period (Figure 2; (Knott et al., 2000)). In groups 4–6, samples were held at zero load under load control during the recovery period (Table 1).

Table 1.

Experimental Groups. N=8 for each test group.

Group	1	2	3	4	5	6
Hold condition after damage loading	Zero strain	Zero strain	Zero strain	Zero stress	Zero stress	Zero stress
Recovery time after damage loading [min]	1	10	100	1	10	100

Figure 2.

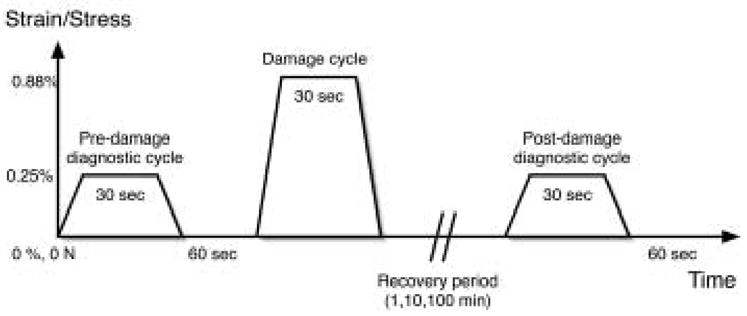
Three-cycle tensile loading protocol. Mechanical properties were compared between Pre and Post-Damage diagnostic cycles. Recovery over one of three times was at either zero strain (shown) or zero stress (not shown).

The load and unload ramps during all testing were at constant strain rate of 1% per second. In the pre-damage diagnostic cycle, the specimen was held at 0.25% strain for 30 seconds, unloaded to zero strain or zero stress and held 60 seconds (Knott et al., 2000). In preliminary studies we confirmed the previous result of Knott et al (2000) that 0.25% strain does not induce measurable damage in the bone specimens and 60 seconds was enough time to allow residual strains or residual stresses to fully recover. In the damage diagnostic cycle, the sample was loaded to 0.88% strain, held for 30 second’s and unloaded to either zero strain or zero stress for damage recovery. This was maintained for 1, 10 or 100 minutes. Prior studies showed that 0.88% strain exceeded the yield point in tension and induced measurable damage within the samples (Knott et al., 2000). The post-damage diagnostic cycle was identical to the pre-damage diagnostic cycle was run as a post-damage diagnostic cycle (Figure 1).

For each diagnostic cycle we calculated loading modulus (E_U), secant modulus (E_S, stress at the end of the loading period/total strain) and unloading modulus (E_U). The unloading modulus was calculated over the same stress range as for the loading modulus (Figure 3). For each diagnostic cycle, we also determined total stress relaxation over the 30 second hold period (σ_rel) and stress or strain recovery over the 1, 10 and 100 minute recovery periods (σ_rec or ε_rec). To examine whether the diagnostic cycle induced damage, we compared the loading modulus of the pre-damage diagnostic cycle with the damage cycle.

Figure 3.

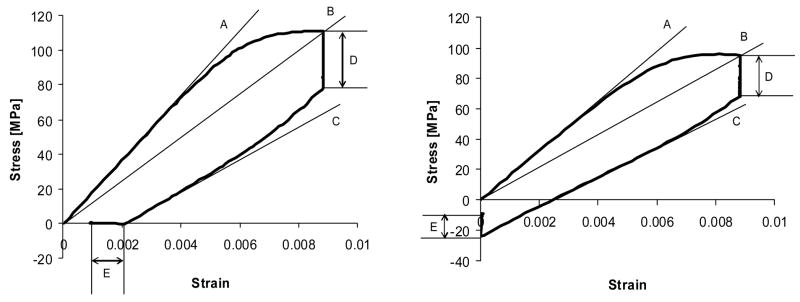
Stress-strain curve for typical damage cycles of zero-stress hold condition (left) and zero-strain hold condition (right). Thin lines represent measured mechanical properties: Loading modulus (slope of A), Secant modulus (slope of B) and Unloading modulus (slope of C), Stress relaxation (D), Strain recovery (E on left graph) and Stress recovery (E on right graph). These same mechanical properties were also measured for pre and post-damage diagnostic cycles.

The changes in mechanical properties following damage induction were defined as R = (P_Post-damage−P_pre-damage)/P_Pre-damage, where P_post-damage is measured property from post-damage diagnostic cycle and P_pre-damage is measured property from pre-damage diagnostic cycle. For the loading, secant and unloading modulus degradation, the parameter, D, was defined as D = −R. D is referred to as a damage parameter, because it corresponds to simple parameter so identified for modulus decrease in other studies (Akkus et al., 2003; Choi and Goldstein, 1992; Jepsen et al., 2001; Jepsen and Davy, 1997; Kotha and Guzelsu, 2003; Pidaparti and Vogt, 2002; Zioupos and Currey, 1994). The parameter D normally increased from zero for properties that degraded, i.e. P_post-damage < P_pre-damage. Since the stress relaxation and stress or strain recovery were actually increased due to the damage cycle, this would lead to negative values in D. Therefore, R is reported for stress relaxation (R_rel) and stress or strain recovery (R_rec-stress or R_rec-strain) while D is reported for loading (D_L), secant (D_S) and unloading modulus (D_U).

Effects of recovery times and hold conditions during recovery time were investigated statistically (MINITAB Inc., State College, PA) using a 2-way ANOVA and t-tests with Bonferroni correction.

Results

The loading modulus for the first (pre-damage diagnostic) cycle showed a mean value±S.D. of 19.54±1.97 GPa (n=48) and did not vary among groups (p > 0.14, Table 2 & 3), which was expected for samples that were randomly assigned to groups. The corresponding mean value for the initial loading modulus during the second (damage) cycle was 18.86±1.96 GPa (n=48) and there was no significant change between cycle 1 and cycle 2 (p > 0.11).

Table 2.

Mechanical properties change of pre- and post-damage diagnostic cycles by damage under zero-strain hold condition.

	1 minute recovery time		10 minutes recovery time		100 minutes recovery time
	Pre-damage	Post-damage	Pre-damage	Post-damage	Pre-damage	Post-damage
Loading Modulus [GPa]	19.22±1.30	18.08±1.42	19.36±0.54	18.97±0.39	17.69±1.65	17.50±2.16
Secant Modulus [GPa]	18.88±1.00*	17.46±1.21*	18.56±0.66^	17.66±0.58^	17.46±2.20†	17.01±2.01†
Unloading Modulus [GPa]	18.92±1.27*	16.98±1.32*	18.59±0.61^	17.70±0.68^	17.36±2.26†	16.47±2.20†
Stress Relaxation [MPa]	2.94±0.51*	5.55±1.11*	2.93±0.44^	6.47±0.92^	2.54±0.74†	5.41±1.41†
Stress Recovery [MPa]	2.99±0.47*	6.42±1.05*	2.71±0.37^	5.19±0.82^	2.73±0.52†	4.92±0.21†

^{* , ^ and †} represent p < 0.05 between measures.

Table 3.

Mechanical properties change of pre- and post-damage diagnostic cycles by damage under zero-stress hold condition.

	1 minute recovery time		10 minutes recovery time		100 minutes recovery time
	Pre-damage	Post-damage	Pre-damage	Post-damage	Pre-damage	Post-damage
Loading Modulus [GPa]	19.92±2.45*	18.00±2.16*	19.72±2.52^	18.74±2.52^	18.33±1.97†	17.79±1.83†
Secant Modulus [GPa]	19.52±2.38*	17.59±1.97*	19.27±2.40^	17.87±2.43^	18.23±1.84†	17.13±1.64†
Unloading Modulus [GPa]	19.66±2.97*	16.76±1.97*	19.25±2.65^	17.67±2.69^	18.13±1.95†	16.18±1.36†
Stress Relaxation [MPa]	2.92±0.36*	6.01±0.70*	2.98±0.56^	6.51±1.41^	2.90±0.21†	5.87±1.34†
Strain Recovery [%]	0.01±0.00*	0.04±0.01*	0.03±0.03^	0.03±0.01^	0.01±0.00†	0.02±0.01†

^{*, ^ and †}represent p < 0.05 between measures.

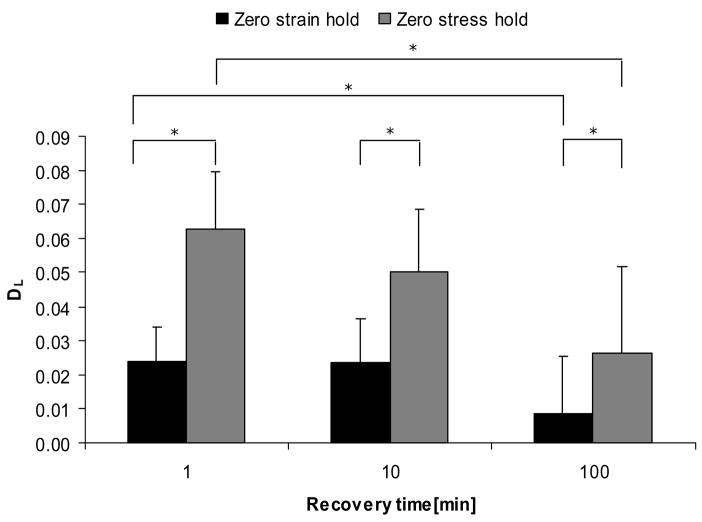
The damage cycle caused changes in all measured mechanical properties, and some measures varied with recovery time and hold conditions after the damage cycle (Table 2, Table 3). The loading modulus parameter, D_L, was significantly different between hold conditions at 1 minute recovery time, and between 1 minute zero stress hold condition and 100 minutes zero strain hold condition (Figure 4). For all recovery times, D_L in zero strain hold showed lower degradation than zero stress hold condition.

Figure 4.

Loading modulus degradation by recovery times and hold conditions. Plot of parameter D_L = [(E_L)_pre−(E_L)_post]/(E_L)_pre. * indicates p < 0.05.

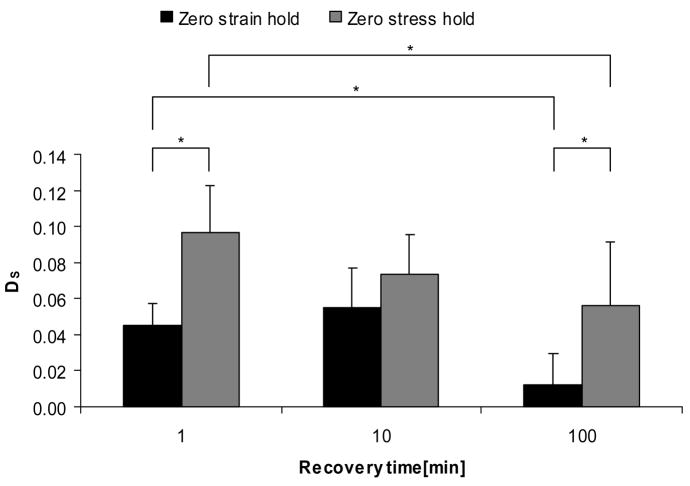
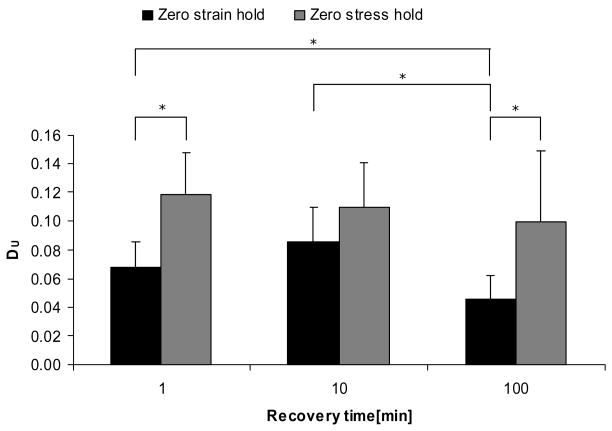
The secant modulus parameter, D_S, showed similar trends, and significant differences between 1 min and 100 min recovery time in zero strain hold condition, and between hold conditions at 100 minutes recovery time (Figure 5). Also, D_S for zero strain hold condition at 100 minutes was significantly different from zero-stress hold condition at 1 minute and 10 minutes. The unloading modulus parameter, D_U, only showed significant differences between 1 minute zero stress hold condition and 100 minutes zero strain hold condition, and showed no significant differences among recovery times for both hold conditions (Figure 6). For all recovery times there were trends toward larger degradations in stiffness measures for the zero-stress hold condition than for the zero-strain hold condition, although not all were significant (Figures 4–6).

Figure 5.

Secant modulus degradation by recovery times and hold conditions. Plot of parameter D_S = [(E_S)_pre−(E_S)_post]/(ES)_pre. * indicates p < 0.05.

Figure 6.

Unloading modulus degradation by recovery times and hold conditions. Plot of parameter D_U = [(E_U)_pre−(E_U)_post]/(E_U)_pre. * indicates p < 0.05.

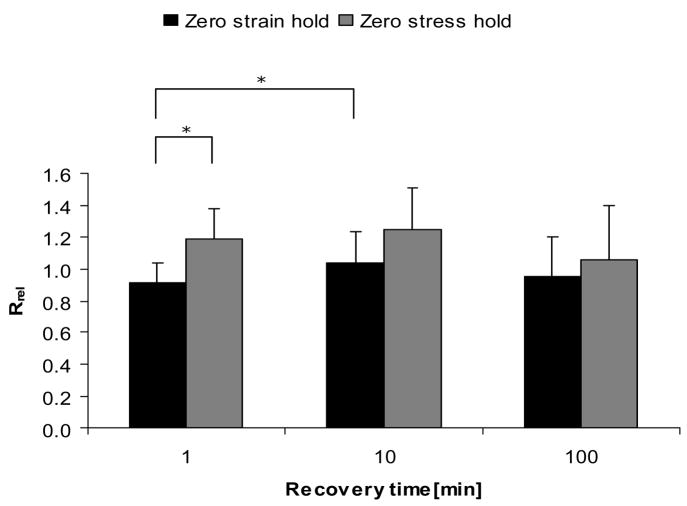
The stress relaxation parameters, R_rel, were not significantly different among recovery times in each hold condition, and between hold conditions in each recovery time. (Figure 7). However, change of magnitude was much higher than changes in modulus. The stress and strain recovery parameters (R_rec-stress or R_rec-strain) showed trends to decrease with increasing recovery time (Table 2, Table 3). However, the ratios were not significantly different among recovery times.

Figure 7.

Stress relaxation change during 30 sec hold by recovery times and hold conditions. Plot of parameter R_rel = [(σ_rel)_post−(σ_rel)_pre]/(σ_rel)_pre. * indicates p < 0.05.

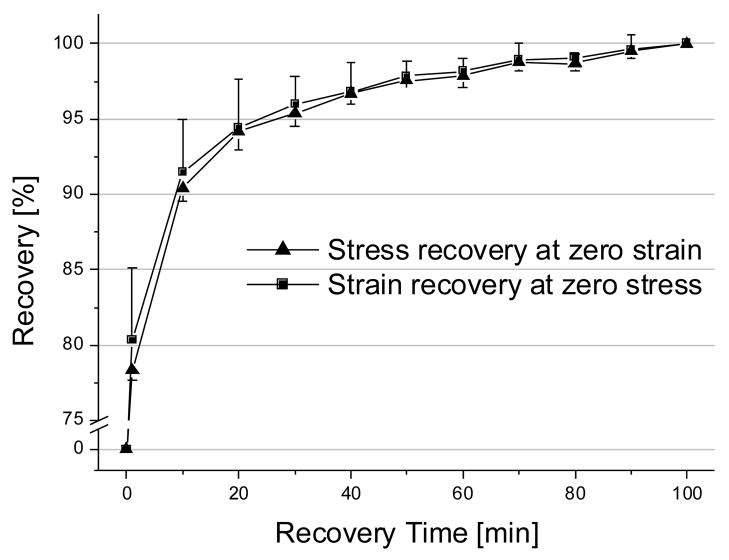
For the 100 minute recovery group, we examined the recovery of residual stresses at zero-strain or residual strains at zero-stress following the damage load cycle. Both measures tended to decrease with recovery time at similar rates (Figure 8). For both measures, values were significantly different only between 1 and 100 minutes recovery time. Both strain and stress recovery showed around 80% recovery (79.36% for stress recovery and 81.23% for strain recovery) at 1 minute recovery time and around 90% recovery (89.43% for stress recovery and 90.47% for strain recovery) at 10 minutes recovery time with respect to its recovery at 100 minutes.

Figure 8.

Histories of stress recovery (zero-strain hold group) and strain recovery (zero-stress hold group) during 100 minutes recovery period after damage cycle. Note the data were normalized to the maximum recovery value of each group. Recovery of strain and stress were similar to each other after 10 minutes of recovery time. All values are mean±SD (n=8). The curve fitting showed y = 79.356x^0.0519, R² = 0.9831 for stress recovery; y = 81.229x^0.0468, R² = 0.9858 for strain recovery, where x is recovery time in seconds, and y is percent decrease in residual stress or strain

Discussion

Overall, the results showed that the recovery conditions (recovery time and holding condition) following the induction of tensile damage alter the apparent effects of the induced damage on mechanical properties of human cortical bone. The results of this study showed that longer recovery times led to lower measures of stiffness degradation following tensile damage induction. Holding at zero-strain after the damage cycle typically produced significantly smaller changes in mechanical properties compared to holding at zero-stress. The one major exception was the changes in stress relaxation. As shown in Figure 7, length of recovery time had no effect on the measured change in viscous properties associated with damage accumulation, and hold conditions had no effect as well.

Modulus and strength degradation have been widely used as mechanical evidence of damage accumulation in bone (Burr et al., 1998; Carter et al., 1977; Jepsen and Davy, 1997; Zioupos and Currey, 1994; Schaffler et al., 1995; Norman et al., 1998; Schaffler et al., 1994; Vashishth et al., 2000). We found that the apparent modulus loss recovered with time. Our data showed transient effects that altered these values between 1 and 10 minutes of recovery. The results demonstrate that when examining stiffness as a measure of damage, these effects can come into play.

Unloading to zero stress or to zero strain following the damage cycle had a substantially larger effect on the measured property changes than did the length of the recovery period. The apparent changes in any stiffness measure were significantly less for the zero-strain hold condition than for the zero-stress hold condition at all times. Holding at zero strain resulted in residual compressive stresses, and holding at zero stress resulted in residual tensile strains. The smaller stiffness decrease at zero-strain would be consistent with the occurrence of some crack closure and some recovery of slip due to the induced compressive stresses (Figure 4, 5 and 6, Table 2 and 3).

We also observed that the actual changes in loading modulus were relatively small for the damage protocol used. This is consistent with a number of observations that loading modulus is relatively little affected by damage, even when other parameters show considerably greater changes (Jepsen and Davy, 1997). Secant modulus was somewhat more affected by damage and showed similar patterns of recovery as modulus with recovery time and recovery hold conditions.

The actual mechanisms for these could occur at scales associated with nano- or micro-structural organization such as fibrils, fibril arrays, interfaces between mineral phase and matrix, lamellar interfaces and cement lines. A reduction in the number of collagen cross links has been associated with reduced bone strength, and elongation of collagen molecules when bone is damaged (Kotha and Guzelsu, 2003). At the macroscopic level, interface cracks are clearly observed by histologic means (Jepsen et al., 2001). The opening and sliding of new interfaces at any scale would produce residual strains at zero stress and residual compressive stresses at zero strain. The time dependent recovery of mechanical properties as well as creep recovery implies existence of internal stresses, which may stem from the same source. However, the actual processes remain to be elucidated.

In a previous study (Jepsen and Davy, 1997) found that torsional viscous property changes were more sensitive to damage compared to modulus changes. In this study, viscous property changes as represented by the stress relaxation ratio were also significantly larger than modulus changes after damage. However, as noted above, viscous property changes were the least affected by recovery conditions. The stress relaxation values increased at least 90% after damage for all recovery times and hold conditions (Figure 7), while modulus changes were at most 12% (Figure 6). A number of sources for the viscoelastic behavior have been suggested, including matrix viscoelasticity (Lakes and Katz, 1979; Christiansen et al., 2000; Jager and Fratzl, 2000), cement line or lamellar interfaces (Lakes and Katz, 1979), or fluid flow (Currey, 1965; Smit et al., 2002; Knothe Tate and Knothe, 2000). The mechanisms underlying the damage effects on viscoelastic properties are not yet elucidated.

The residual compressive stress at zero strain and the residual tensile strains at zero stress persisted at 100 minutes after the damage cycle, but they appeared to continue to trend downward (Figure 8). It is possible that the recovery represents viscoelastic behavior unrelated to added damage. In our studies, we have found primary viscous relaxation time scales to be much shorter (Jepsen and Davy, 1997; Fondrk et al., 1988), although relatively long relaxation times have been reported by others (Iyo et al., 2004; Sasaki and Enyo, 1995). In spite of this stress or strain recovery, viscoelastic properties were not significantly changed.

One major limitation of the present study is the single damage level. The extent to which a higher strain level might have altered the outcome is unknown, so the results must be viewed in that light. However, the amount of property degradation is consistent with several studies (Jepsen and Davy, 1997; Zioupos and Currey, 1994; Fondrk et al, 1988; Lakes and Katz, 1979), and the results provide some insight into the potential role of recovery conditions on these typical measures of tensile damage.

A second limitation is the restriction to tensile loading only. The recovery conditions could have effects in other loading modes such as compression and torsion testing. However, it is known that the damage morphologies in these loading modes are different, so the results cannot be directly applied to those circumstances. As well, this study has not looked at the effects of repeated load cycles, as is often done in fatigue studies. It is interesting to note that property degradation is often done using the cyclic loading data without interrupting the test, so any possible recovery of the properties due to unloading is excluded (Pattin et al, 1996; Yeni and Fyhrie, 2002; Fleck and Eifler, 2003).

The choice of a single donor femur could be viewed as a limitation. However, we deliberately chose to use a single source in order to focus on the single issue of effects of test conditions. This had the advantage of excluding inter-specimen variability in the basic behavior. The observed behaviors represent consistent qualitative effects and allow us to draw conclusions accordingly. However the results do not reveal the quantitative variations of these effects across large numbers of tests.

The results of this study suggest guidelines regarding the diagnosis of the presence of damage using mechanical properties as a surrogate measure. Our results show that as much as 90% of the non-permanent change of strain or stress was recovered by 10 minutes (Figure 8). However, if the post-damage hold conditions or if recovery times less than 10 minutes are not matched it is inappropriate to compare results between studies. Obviously, this conclusion does not negate the comparisons within any given experimental design using fixed recovery conditions. However, it does reflect the fact that different recovery conditions may lead to different conclusions about the magnitude of damage effects. Although one property (secant modulus degradation at zero strain hold) varied between 10 minutes and 100 minutes, a nominal 10 minute recovery appears to be a reasonable minimum recovery for cross-study comparisons.

The relative merit of choosing to hold at zero load or to zero strain after damage accumulation is a more difficult issue to resolve. The two conditions clearly produce different final internal states of the material which manifest themselves primarily in lower measured stiffness changes for the zero strain recovery. If, as speculated above, this is due to crack closure and internal friction, it is likely that the zero-strain recovery state underestimates the actual damage state of the material. On this basis, the choice to recover at zero stress may offer a more realistic and consistent way to characterize the mechanical effects of damage.