Fretting about FRET: Failure of the Ideal Dipole Approximation

Abstract

With recent growth in the use of fluorescence-detected resonance energy transfer (FRET), it is being applied to complex systems in modern and diverse ways where it is not always clear that the common approximations required for analysis are applicable. For instance, the ideal dipole approximation (IDA), which is implicit in the Förster equation, is known to break down when molecules get “too close” to each other. Yet, no clear definition exists of what is meant by “too close”. Here we examine several common fluorescent probe molecules to determine boundaries for use of the IDA. We compare the Coulombic coupling determined essentially exactly with a linear response approach with the IDA coupling to find the distance regimes over which the IDA begins to fail. We find that the IDA performs well down to roughly 20 Å separation, provided the molecules sample an isotropic set of relative orientations. However, if molecular motions are restricted, the IDA performs poorly at separations beyond 50 Å. Thus, isotropic probe motions help mask poor performance of the IDA through cancellation of error. Therefore, if fluorescent probe motions are restricted, FRET practitioners should be concerned with not only the well-known κ² approximation, but also possible failure of the IDA.

Introduction

Fluorescence-detected resonance energy transfer (FRET) has become a popular tool for studying the structures of and interactions between proteins and nucleic acids in biology (1–11) as well as novel materials (12–16). A number of approximations are often made in analysis of FRET data, though they are rarely treated with care. One of those, the ideal dipole approximation (IDA), is widely accepted to fail when the fluorescent probe molecules are “too close” to each other. However, a quantitative definition for what is meant by “too close” is not known. In this work, we seek such a definition and show that, for molecules commonly employed in contemporary FRET studies, the IDA is questionable for distances of 20 Å or less when isotropically averaged and for distances >50 Å for particular orientations.

The utility of FRET as a tool for structural biology was first demonstrated by Stryer and Haugland in the late 1960s (6,7,17,18). In many of today's studies, as in those classic works, two fluorescent probes are covalently attached to the biomolecule(s) of interest. One of those, the energy donor (D), is electronically excited by a lamp or laser and if conditions are right, that excitation energy can transfer nonradiatively through space via a resonant energy transfer (RET) mechanism to the energy acceptor (A). Observing the fluorescence emission from the D and/or the A reports on the efficiency (rate) of RET. Because the RET rate (k_RET) depends strongly on distance (see below), this measurement reports on the intermolecular separation of the D and A and, therefore, the structure of the biomolecules(s) of interest.

FRET was developed as an experimental technique through careful work in several laboratories throughout the 1970s and early 1980s (6,17–23). These studies showed the approximations needed to make FRET a useful tool for structural biology were reasonable for a variety of biological systems and types of experiments, such that application of these approximations (e.g., IDA) became standard practice. With the arrival of FRET as a common laboratory tool in the late 1990s and continuing through today, it is being applied to a vast array of systems of interest in both biology and materials science that are quite different from those studied in the 1970s and 1980s. In addition, a range of different experimental techniques are being employed, including single-molecule methods. Yet, while the scope of systems and techniques has expanded tremendously since the foundational days of FRET, little attention has been paid to the viability of the common FRET approximations across this range of application.

Thus, we have begun to examine several of the common FRET approximations in the context of modern experiments (24). In this work, we focus on the IDA and its effects on analysis of FRET data for several FRET probes in common use today. In particular, we seek to identify the distances over which the IDA transitions from a sound approximation to one that is questionable for these molecules. We begin with a discussion of the theoretical underpinnings of RET including the pertinent approximations. This is followed by description of our computational methods, presentation of results, and discussion of the implications to FRET experiments.

Theory

In the weak coupling limit, in which the line shapes of the D and A are not noticeably affected by their electronic interaction, the rate of RET is given by

$$k_{\text{RET}}=\frac{2\pi }{\hslash }{\left|V\right|}^2{J}_{\text{DA}},$$ (1)

where V is the electronic coupling between the donor and acceptor and J_DA is the overlap of the Frank-Condon envelopes that are responsible for the line shapes of the D and A transitions. In the 1940s, Förster laid the foundation for FRET by theoretically describing the RET process (25–27). He used a transition dipole-transition dipole interaction to describe the electronic coupling and used the emission spectrum of D and the absorption spectrum of A to represent the line shapes such that

$$\begin{array}{c}V\approx V_{\text{Coul}}\approx V_{\text{dip-dip}}=\frac{\kappa \left|{\overrightarrow{\mu }}_{\text{D}}\right|\left|{\overrightarrow{\mu }}_{\text{A}}\right|}{4\pi {\varepsilon }_0{n}^2{R}_{\text{DA}}^3}\\ \text{and}\\ J_{\text{DA}}=\frac{1}{h}\int d\nu \frac{C_{\text{D}}{f}_{\text{D}}\left(\nu \right)}{{\nu }^3}\frac{C_{\text{A}}{\varepsilon }_{\text{A}}\left(\nu \right)}{\nu },\end{array}$$ (2)

where κ is the orientation factor ($\kappa ={\widehat{\mu }}_{\text{D}}\cdot {\widehat{\mu }}_{\text{A}}-3\left({\widehat{\mu }}_{\text{D}}\cdot {\widehat{R}}_{\text{DA}}\right)\left({\widehat{\mu }}_{\text{A}}\cdot {\widehat{R}}_{\text{DA}}\right)$), ${\overrightarrow{\mu }}_{\text{i}}$ are transition dipole moments (${\widehat{\mu }}_{\text{i}}$, unit vectors), ${\widehat{R}}_{\text{DA}}$ is the unit vector along the line connecting the centers of the D and A, R_DA is the distance between the D and A, n is the index of refraction, ν is frequency, and C_i are normalization factors such that the integrals of C_Df_D(ν)ν⁻³ and C_Aɛ_A(ν)ν⁻¹ are unity. Förster then went on to blend the coupling and overlap terms to arrive at an equation—known as the Förster equation—that is used in contemporary FRET studies essentially unchanged (though written in a variety of forms depending on desired units),

$$k_{\text{RET}}=\frac{9\left(\ln 10\right){\kappa }^2{\mathit{\varphi }}_{\text{D}}}{128{\pi }^5{N}_{\text{A}}{n}^4{R}_{\text{DA}}^6{\tau }_{\text{D}}}{\int }_0^{\mathrm{\infty }}d\tilde{\nu }N{f}_{\text{D}}\left(\tilde{\nu }\right){\varepsilon }_{\text{A}}\left(\tilde{\nu }\right){\tilde{\nu }}^{-4}\text{.}$$ (3)

Thus, to arrive at Eq. 3, several approximations have been called into play, including the IDA. In addition, most researchers further assume that all of the spectral parameters (ϕ_D, τ_D, f_D(ν), and ɛ_A(ν) are the same for all D-A pairs in the ensemble as well as constant with respect to structural/solvent fluctuations, that D and A sample orientation space isotropically such that 〈κ²〉 = 2/3, and that fluctuations in κ and R_DA are not correlated (24,28–30). Of primary concern in this work is the representation of the electronic coupling, V, as the transition dipole-transition dipole coupling, V_dip-dip. This involves two levels of approximation. The first is that the total electronic coupling can be represented by the Coulombic coupling, V ≈ V_Coul. Except at very large distances where radiative mechanisms begin to dominate (31) and at very small distances where orbital-overlap-driven mechanisms become important (32,33), the Coulombic interaction is the dominant mechanism for coupling. Thus, for the intermediate distances that are of most relevance to FRET, 10–100s of Å, V is very well approximated by V_Coul.

The second approximation is that V_Coul ≈ V_dip-dip. This results from first defining a center for each molecule and then expanding the transition density about that point. This gives the familiar multipole representation of each transition density:

$$M=M_{\text{mono}}+M_{\text{dip}}+M_{\text{quad}}+\dots \text{.}$$ (4)

After interacting D and A and retaining the first nonzero term (M_mono = 0 for transition densities), we have the transition dipole-transition dipole coupling given in Eq. 2. If the D and A are far apart then this is also an accurate approximation. However, as the D and A get closer together, the IDA begins to fail.

Several different methods have been used as alternatives to V_dip-dip. The first description of Coulomb-driven resonance energy transfer beyond the IDA was given by Golebiewski and Witkowski, who described the interaction of polyenes using the transition monopole method in which the transition density of a molecule is represented by individual charges (monopoles) placed on each atomic center (34). This monopole description followed from London's use of monopoles to represent molecular polarizability (35), later extended by Haugh and Hirschfelder (36). Transition monopoles were later used by Chang to carefully test the IDA for several chlorophylls. She found that the IDA was in large error at distances ≤12 Å, but that it was reasonable for larger distances especially if several D-A were averaged approximating an isotropic distribution (37). Nearly two decades later, similar monopoles (38) were applied by Sauer and co-workers to calculate the interactions between chlorophylls in a photosynthetic light-harvesting complex, where they found small deviations between the IDA and the monopole-derived coupling. However, for idealized orientations where the orientation factor (κ) is nearly zero, they found large deviations even at 50–60 Å distances (39). Later, Fleming and co-workers expanded the transition monopole approach to include the full molecular transition density, called the transition density cube method, in which the molecular transition density (40) is integrated into a large three-dimensional grid of volume elements (41). They also examined a photosynthetic light-harvesting system and showed significant failures of the IDA, especially between carotenoids (long polyenes) and chlorophylls (41). Different groups have advanced the ideas of the monopole and transition density cube methods further by enabling basis-level descriptions of the transition densities, either at the semiempirical (42,43) or ab initio level (32,44), such that the Coulombic coupling can now be calculated quickly and with an accuracy that is limited only by the description of the ground and excited-state wavefunctions. Further, the work by Iozzi et al. (44) also includes orbital overlap-dependent contributions to the coupling and exchange (45) components. More importantly, this linear response (LR) approach includes the ability to properly account for solvent effects (at the integral equation formalism, polarizable continuum model, IEFPCM, level (46)) at all stages of the wavefunction determination and evaluation of the interaction (47,48). While we do not address solvent effects in this work, we do utilize the last approach to examine the electronic coupling for seven different fluorescent probes. The set of molecules, shown in Fig. 1, encompasses several commonly-used FRET probes and provides some diversity in molecular size and shape.

Figure 1.

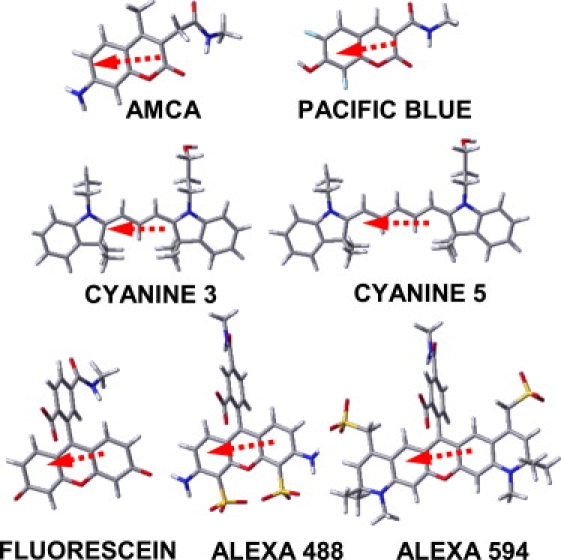
Chemical structures of the seven probes examined in this work. All of the probes include an amide group on a short alkyl chain representing a tether for attachment of the probe to a biomolecule. The arrows indicate the directions of the transition dipole moments. In the images, C is gray, H white, O red, N blue, S yellow, and F cyan.

Methods

Details of the calculation of the Coulombic interaction are given elsewhere (44,47), though we present a brief overview here. The key step is the interaction of the D and A transition densities

$$V_{\text{Coul}}=\int d{\overrightarrow{r}}_{\text{D}}\int d{\overrightarrow{r}}_{\text{A}}\frac{{\mathit{\rho }}_{\text{A}}^{\text{T}\ast }\left({\overrightarrow{r}}_{\text{A}}\right){\mathit{\rho }}_{\text{D}}^{\text{T}}\left({\overrightarrow{r}}_{\text{D}}\right)}{4\pi {\varepsilon }_0\left|{\overrightarrow{r}}_{\text{D}}-{\overrightarrow{r}}_{\text{A}}\right|},$$ (5)

in which the ${\mathit{\rho }}_{\text{i}}^{\text{T}}\left({\overrightarrow{r}}_{\text{i}}\right)$ are the transition densities that retain the three-dimensional structural information of the molecules. In the dipole-dipole interaction given in Eq. 2, the details of the individual D and A transition densities are first averaged into the transition dipoles, such that those details are lost, and then the interaction is determined. In the Coulombic interaction used here (Eq. 5), the full structural details of the individual D and A transition densities are accounted for during calculation of the interaction.

In addition, the total coupling presented here (44,47) includes the Coulombic interaction above (Eq. 5) as well as exchange and correlation contributions (though the correlation contribution must also be supported by the quantum mechanical method, e.g., with TD-DFT; see below) and overlap interactions, such that the total coupling within this linear response approach is

$$V_{\text{LR}}=\int d{\overrightarrow{r}}_{\text{D}}\int d{\overrightarrow{r}}_{\text{A}}{\rho }_{\text{A}}^{\text{T}\ast }\left({\overrightarrow{r}}_{\text{A}}\right)\left(\frac{1}{4\pi {\varepsilon }_0\left|{\overrightarrow{r}}_{\text{D}}-{\overrightarrow{r}}_{\text{A}}\right|}+g_{\text{xc}}\left({\overrightarrow{r}}_{\text{A}},{\overrightarrow{r}}_{\text{D}}\right)\right)\times {\rho }_{\text{D}}^{\text{T}}\left({\overrightarrow{r}}_{\text{D}}\right)-{\omega }_{\text{D}/\text{A}}\int d{\overrightarrow{r}}_{\text{D}}\int d{\overrightarrow{r}}_{\text{A}}{\rho }_{\text{A}}^{\text{T}\ast }\left({\overrightarrow{r}}_{\text{A}}\right){\rho }_{\text{D}}^{\text{T}}\left({\overrightarrow{r}}_{\text{D}}\right),$$ (6)

where ω_D/A is the common transition energy of both monomers and g_xc is the exchange-correlation operator.

The transition densities can be determined by different quantum mechanical methods. Here we compare three methods: the semiempirical ZINDO/s method (49,50), the configuration interaction-singles (CIS) method (51), and the time-dependent density functional theory (TD-DFT) method employing the B3LYP functional (52,53). For the two ab initio methods, the 6-31G(d) basis set (54,55) is used for most calculations. For comparison (see the Supporting Material), select calculations were performed with the CIS/6-31+G(d,p), TD-B3LYP/6-31+G(d,p), TD-CAM-B3LYP/6-31+G(d,p) (56), and the symmetry-adapted cluster/configuration interaction (57) (SAC-CI)/6-31+G(d,p) model chemistries. For the latter method, we carried out SAC-CI SD-R calculations with energy thresholds of 5 × 10⁻⁶ and 5 × 10⁻⁷ a.u. for the ground and excited states, respectively. Regardless of the method used to determine the (gas-phase) ground and excited state wavefunctions (and therefore the transition densities), molecular geometries were always determined at the B3LYP/6-31G(d) level. Most geometries were determined with a gas phase environment. However, gas-phase geometry optimizations of the xanthene dyes gave structures in which the acid group bonded to the tertiary sp² carbon atom of the xanthene moiety, turning it into an sp³ carbon and creating a five-membered ring. These structures are not expected in a polar condensed phase where the free acid group is stabilized by solvent. For these molecules, geometries were determined at the B3LYP/6-31G(d) level including a IEFPCM representation of water (46), which gave the anticipated structures in which all of the xanthene carbons are sp². All calculations were performed with a special version of Gaussian03 (58) into which the code for evaluating the D-A coupling (Eq. 6) had been added.

The relative orientations of the D and A molecules are defined using a vector, which represents the relative positions of the centers of the molecules, and a rotation, which represents the relative angular positions of the molecules, similar in spirit to the coordinate system employed by Knox (59). In effect, the D is kept fixed at the origin and the A (originally superimposed on the D) is translated by the vector (specified by R_DA, θ₁, ϕ₁) then rotated according to θ₂ and ϕ₂ as shown in Fig. 2. Throughout this article, specific orientations will be referenced using a quintuple of (R_DA, θ₁, ϕ₁, θ₂, ϕ₂). Choosing a large number of random values for the four angles confirms that this is a suitable coordinate system as 〈κ²〉 = 2/3. To approximate an isotropic distribution using a modest number of structures, 14 sets of θ/ϕ angles were chosen. If the D is oriented with its transition dipole along the +z axis, then these 14 orientations correspond to: ± the x, y, and z axes as well as approximately the eight diagonal directions. In fact, for these diagonal directions the polar angle was increased slightly from 45° to magic angle, ≈54.7° (or decreased from 180°—45° for the lower quadrants). Using these same 14 sets of θ/ϕ angles for the translation vector and the A rotation results in 196 unique relative orientations for each value of R_DA. This set of orientations constitutes a good representation of an isotropic average, and reproduces 〈κ²〉 = 2/3 with high accuracy. In the actual calculations, the original transition dipole was not always perfectly aligned with the +z axis, leading to slight deviations (<0.003) from 2/3.

Figure 2.

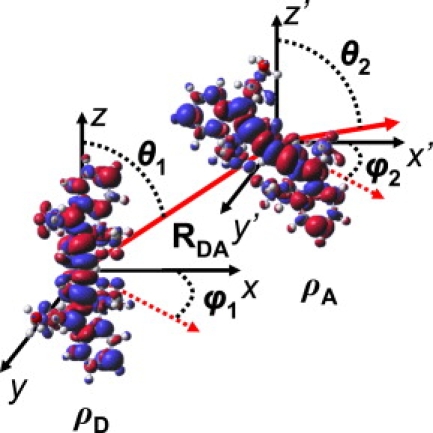
Coordinate system used to define the relative orientations of D and A. R, θ₁, and ϕ₁ define a vector for translating the A dye relative to the D dye. θ₁ is the polar angle and ϕ₁ is the azimuthal angle. After translation, the A is rotated according to θ₂ and ϕ₂.

Results and Discussion

In the following we discuss the difference between V_LR and V_dip-dip averaged over all 196 relative orientations as a function of distance. Results from selected specific orientations will then be presented, followed by a discussion of the implication of all of these results on analysis of FRET experiments. We note that an analysis of the performance of different quantum mechanical methods (and basis sets) on the coupling is reported in the Supporting Material; the conclusions coming from that analysis are consistent with those reported in a recent article by Muñoz-Losa et al. (60).

Error in IDA—isotropic average

To examine the performance of the IDA we define the relative error in the IDA, given by

$$Er{r}_{\text{IDA}}=\frac{\langle V_{\text{dip-dip}}^2\rangle -\langle V_{\text{LR}}^2\rangle }{\langle V_{\text{LR}}^2\rangle }\text{.}$$ (7)

Fig. 3 shows the relative error in the IDA (Err_IDA) for homodimers of the six primary molecules of study: AMCA, PB, Cy3, Cy5, Fluor, and AF488. At each distance, Err_IDA was calculated as in Eq. 7 where the $\langle V_{\text{LR}}^2\rangle$ and $\langle V_{\text{dip-dip}}^2\rangle$ were each averages of the complete set of 196 relative orientations, approximating an isotropic distribution. If the IDA is performing badly, V_LR might be either larger or smaller than V_dip-dip depending on the particular spatial arrangement of the donor and acceptor. Thus, while particular relative orientations might exhibit very poor performance of the IDA (detailed in the next section), these will generally be balanced by opposing poor orientations such that the average, $\langle V_{\text{dip-dip}}^2\rangle$, remains reasonably accurate. Significant errors will only be found when the IDA is performing badly in the same direction (e.g., underestimating the coupling) for most or all relative orientations. In other words, the orientationally averaged data are a very conservative measure of errors in the IDA.

Figure 3.

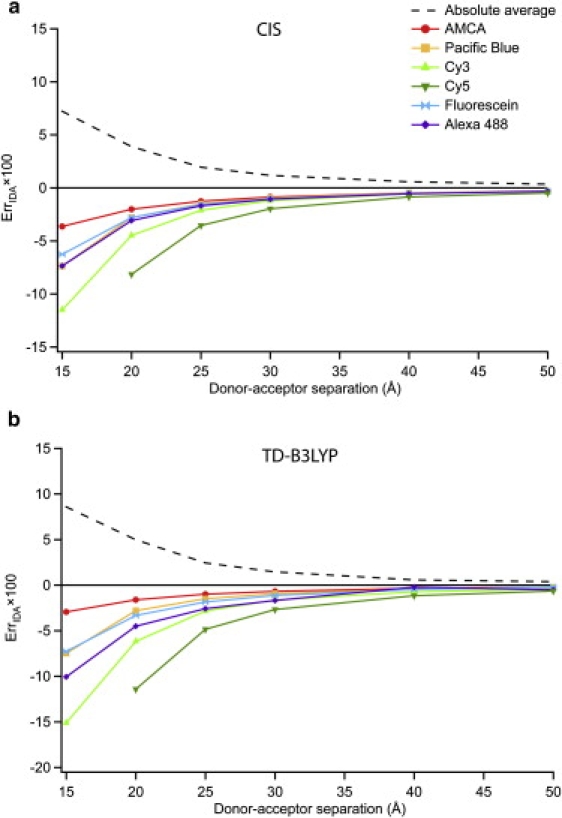
Relative error in the IDA (Err_IDA) for orientationally averaged homodimers of the six primary molecules examined (see Fig. 1) as a function of distance: a and b refer to CIS and TD-B3LYP, respectively.

One observation from Fig. 3 is that all of the datapoints for CIS and TD-B3LYP indicate negative errors. That is, the IDA tends to underestimate the strength of the coupling. Thus, the actual R_DA would be larger than one would infer from a simple Förster analysis of experimental data. The extent of the error in coupling is modest for these molecules (<5% except for Cy3 and Cy5, which are <12%) provided that the separation is >20 Å. However, under 20 Å the magnitude of the error dramatically increases. Not surprisingly, Cy5 (the longest molecule; see Fig. 1) exhibits the largest error and AMCA (the shortest molecule) the smallest. PB exhibits significantly larger Err_IDA than the structurally similar AMCA; presumably the electron withdrawing groups on the periphery of PB either make the transition density larger (spatially) or reduce its symmetry such that the orientational averaging is less able to wash out errors. In contrast, Fluor and AF488—an analogous pair to PB and AMCA—show very similar errors in the IDA.

Failure of the IDA is often discussed in terms of the molecular separation compared to the size of the molecule. Following this logic, it may be that the different sizes of the molecules under investigation lead to the slightly different error-versus-distance behaviors seen in Fig. 3. To examine this more carefully, these data have been replotted using a unitless distance axis in which the intermolecular separation is divided by the size of the molecule. The size that is relevant to the multipole description of the transition density is not the physical molecular size, but rather the spatial extent of the transition density itself. That said, these sizes were rather crudely estimated by measuring the length of the longest axis of an ellipsoid that approximately encloses the atoms involved in the transition through visual inspection of the density. The results, given in Fig. 4, do not collapse onto a single line. In fact, while the AMCA data overlay the other molecules a bit better, the onset of poor IDA behavior for Cy3 and Cy5 is now at a much smaller separation than the other molecules. This is likely because Cy3 and Cy5, as mainly linear polyenes, have very different shapes than the other dyes, which are all fused aromatic ring systems. Thus, a single size parameter does not adequately represent the sizes of the transition densities for the diversity of molecules studied here. In addition, the CIS data given in Fig. 3 are already remarkably similar, so adjusting by any size parameter is unlikely to improve the similarity. We do note that a similar treatment of the TD-DFT data yields a more noticeable coalescence of the Err_IDA data. In fact, the Err_IDA-versus-molecular units data show very similar behavior in the region where the IDA just begins to fail; that is, from three-to-six molecular units (with the exception of Cy3 and Cy5, which are far removed). The TD-DFT data also show more spread when plotted in Å so there is greater contrast between the Å and molecular unit representations of the data.

Figure 4.

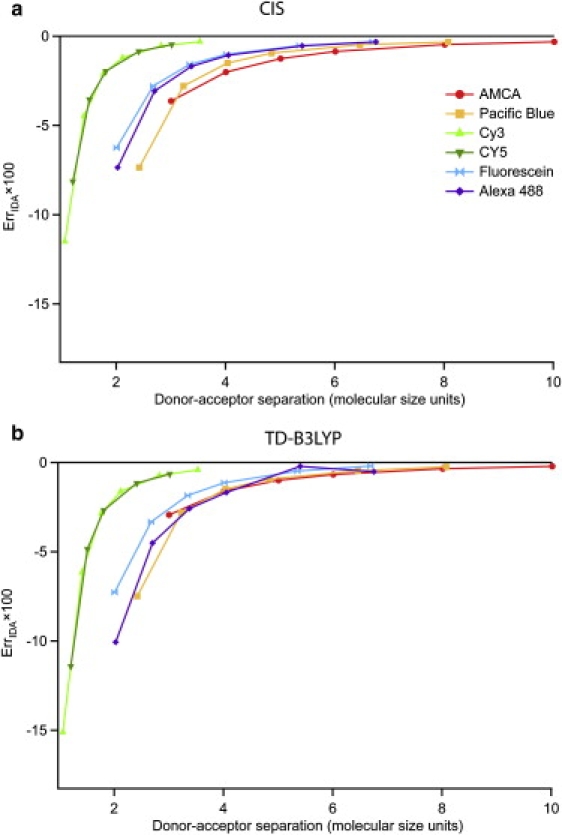
Same results as in Fig. 3, but replotted with the distance axis in units of molecular size. This size is given by the intermolecular separation divided by the approximate sizes of the transition densities of each molecule (namely 4.99 Å for AMCA, 6.19 Å for PB, 7.47 Å for fluorescein, 7.40 Å for AF488, 14.15 Å for Cy3, and 16.57 Å for Cy5). Graphs a and b refer to CIS and TD-B3LYP, respectively.

While the above data demonstrate breakdown of the IDA at molecular separations <20 Å, these calculations were all performed on energy transfer pairs in which the donor and acceptor molecules are the same (homodimers). While this is convenient for a theoretical investigation, it does not mimic a typical system in a FRET experiment. To more closely model FRET experiments, three heterodimer donor-acceptor pairs were investigated: AMCA-Fluorescein, Cy3-Cy5, and AF488-AF594. All three of these pairs are in common use in FRET experiments with the Cy3-Cy5 and AF488-AF594 pairs being especially popular in single-molecule fluorescence experiments (61). The resulting Err_IDA versus R_DA are shown in Fig. 5.

Figure 5.

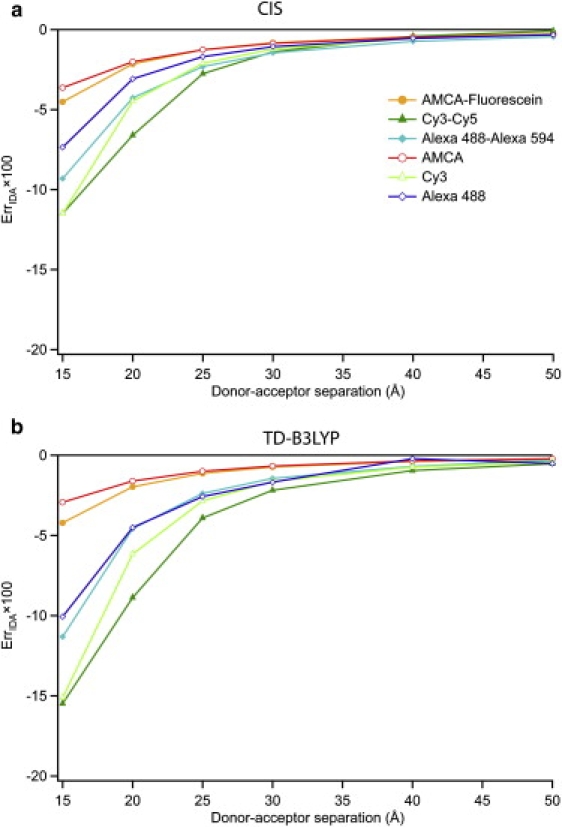
Relative error in the IDA (Err_IDA) for the three orientationally averaged heterodimers (AMCA-Fluorescein, Cy3-Cy5, and AF488-AF594—see Fig. 1) as a function of distance: a and b refer to CIS and TD-B3LYP, respectively. The homodimer data for AMCA, Cy3, and AF488 (identical to Fig. 3) are also given for comparison.

As might be expected, the Err_IDA data lie about midway between the Err_IDA from the respective homodimer cases. Thus, the orientationally averaged heterodimer results are generally consistent with the homodimer results, suggesting that the IDA begins to fail at molecular separations <20 Å.

Error in IDA—specific orientations

While the results presented above provide a reasonable representation of the case of orientationally averaged fluorophores, there are experimental situations in which the donor or acceptor (or both) are limited in their orientational freedom. For instance tryptophan, GFP, FlAsH, or similar probe molecules are all inherently fixed in space. Even for probes that are free to reorient, it is generally accepted that the presence of the covalent linker and the biomolecule (or other substrate) of interest place some limits on the orientational freedom of the fluorophore. Thus, in addition to the above analysis of averages over 196 relative orientations, we also explore averages over smaller subsets of orientations.

To illustrate the effect, we average over all orientations of one probe (θ₂ and ϕ₂) for individual values of the translational vector (θ₁ and ϕ₁). This approximates the case where one probe might be fixed in space (e.g., GFP) while another is free to reorient. The left-hand plots of Fig. 6 show Err_IDA as a function of distance for the homodimer pairs of AMCA, Fluorescein, and Cy3.

Figure 6.

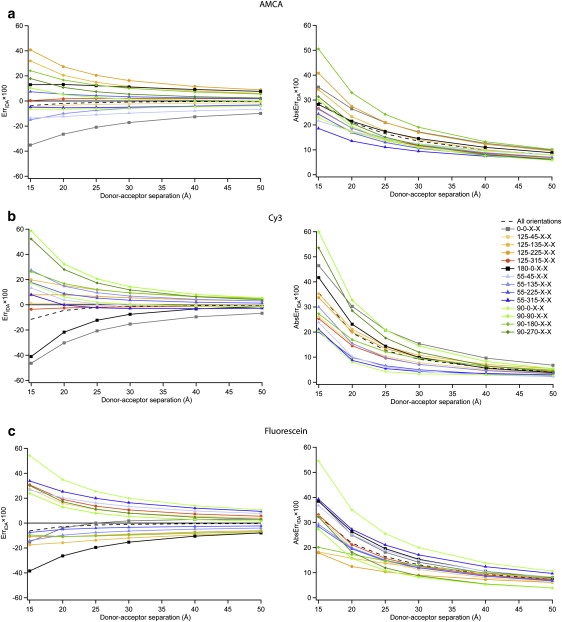
Error in the IDA for specific translation vectors, i.e., specific values of θ₁ and ϕ₁, as obtained at the CIS level. For each translation vector, the other probe was allowed to take on all possible orientations, that is (θ₂, ϕ₂) took on all 14 values described in the text. (Left) The relative error in the IDA (Err_IDA) versus distance. (Right) The average absolute relative error in the IDA (AbsErr_IDA) versus distance.

Note that the errors are now quite large at short distance (exceeding 50% in some cases at 15 Å) and that they exceed 10% for multiple orientations even at 50 Å separation. Thus, the results show that keeping the orientation of one dye fixed dramatically increases the Err_IDA. This is clearly a consequence of a reduced cancellation of errors between the different orientations sampled by the second dye, i.e., the errors of these orientations must be mostly of the same sign. In the right-hand plots, the orientational averaging has been further removed by finding the average of the magnitude of the error for each orientation. That is,

$${\mathit{AbsErr}}_{\text{IDA}}=\frac{\langle \left|V_{\text{dip-dip}}^2-V_{\text{LR}}^{\text{2}}\right|\rangle }{\langle V_{\text{LR}}^2\rangle }\text{.}$$ (8)

These AbsErr_IDA values are remarkably similar in absolute value to the Err_IDA results. This similarity confirms that the errors in the 14 orientations sampled by the second dye must be mainly of the same sign. It is also notable that the largest errors observed are quite similar for AMCA, Cy3, and Fluorescein, and that the AbsErr_IDA is ∼10% even at the maximum separation of 50 Å, where one would expect the IDA to perform well, particularly in the case of AMCA where this corresponds to roughly 10 molecular size units.

This effect is also illustrated in Fig. 7 where the AbsErr_IDA, averaged over all 196 orientations, is shown for each of the homodimers. These are the identical coupling data as in Fig. 3, but now the magnitudes of the errors (i.e., unsigned) have been averaged together so there is no cancellation. In this case we also find that AbsErr_IDA values for all molecules are ∼10% at the largest separation of 50 Å.

Figure 7.

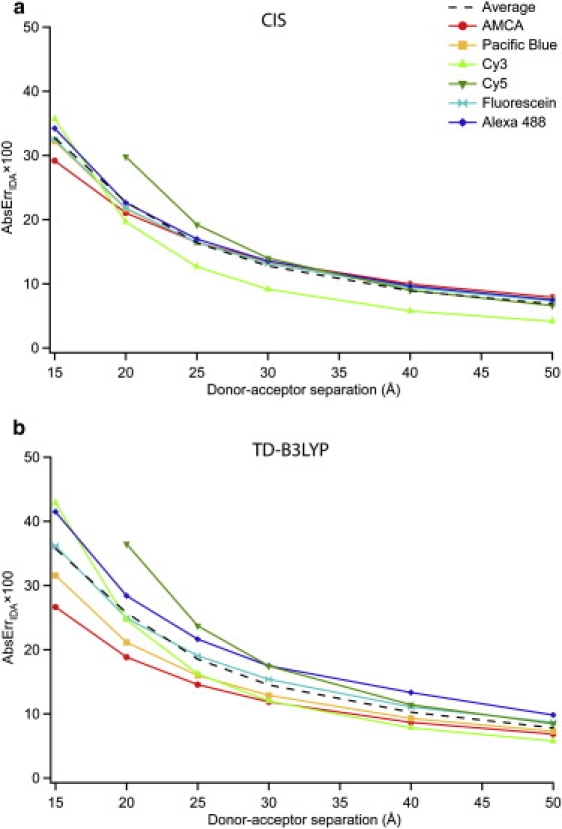
Average absolute relative error in the IDA (AbsErr_IDA) for orientationally averaged homodimers of each molecule examined as a function of distance. Graphs a and b refer to CIS and TD-B3LYP results, respectively. These curves are generated from the same data used to generate Fig. 3, but have been calculated using Eq. 8 rather than Eq. 7.

Fig. 7 underscores the fact that the IDA itself does not perform well for typical FRET probes, even at distances of 50 Å. While the AbsErr_IDA is clearly converging at large distances, errors >10% are still seen in several molecules. Thus, the appearance of accuracy in Fig. 3 is the result of orientational averaging, which masks the poor performance of the IDA. This highlights the critical importance of orientational mobility of the probe molecules to a FRET experiment; not only is rapid reorientation needed to enable the 〈κ²〉 = 2/3 approximation, but it also allows the IDA to be utilized in the 20–50 Å regime, where it does not generally perform well.

Implications to FRET experiments

Above, we have examined the breakdown of the IDA in two extreme contexts: an approximately isotropic distribution of relative orientations and specific individual relative orientations. Below we describe the impact of the IDA on FRET experiments in which the donor and acceptor truly sample space isotropically followed by experiments with less complete sampling.

As shown in Figs. 3–5, the IDA performs quite well when both the donor and acceptor sample space isotropically. Err_IDA is <10%, provided the intermolecular separation is larger than approximately three times the size of the molecule, or 20–25 Å for the pairs studied here. This small error in the coupling strength corresponds to an even smaller error in the usual FRET analysis where the measured FRET efficiency is used to estimate the separation. In this case, the R_DA³ in Eq. 2 and the V² in Eq. 1 lead to the error in distance being the sixth-root of the error in rate. Thus, a maximum 10% error in the rate leads to <2% error in distance.

While the IDA appears to be accurate in the ideal case when both the donor and acceptor sample many orientations, it must be remembered that this is the result of cancelation of error. It is not the case that the IDA is generally performing well; it is simply the case that the errors are both positive and negative such that averaging over a large number of relative orientations greatly reduces the overall error. Thus, if the donor and acceptor do not sample space isotropically, this not only causes potential difficulty with the 〈κ²〉 = 2/3 approximation, but it also allows errors in the IDA to come to the forefront. For instance, if an experiment utilized a system in which two probes were in a T configuration (perpendicular to each other, matching our R-90-0-90-X or R-0-0-90-X or R-180-0-90-X configurations), then κ is exactly zero. However, the coupling is significant (>10 cm⁻¹) even at separations as large as 15 Å for the probes studied here. Alternatively if the two probes were in an H configuration (parallel or antiparallel to each other, but perpendicular to the separation vector, matching our R-90-X-0-0 and R-90-X-180-0 configurations), then we find that the error in the IDA coupling becomes acceptable (<10%) at distances >25 Å.

This latter situation is similar to that recently found when Cy3 and Cy5 are bound to DNA using short C3 linkers (62,63). In that situation the dihedral angles between the transition dipoles are not precisely 90 (the T configuration), or 0/180 (H) as they are here, but rotate roughly in a plane that includes those extremes. In particular, the probes are shown to stack on the ends of the double-stranded DNA, exhibiting little orientational freedom as confirmed by nuclear magnetic resonance and fluorescence anisotropy experiments. Iqbal et al. (62) examined DNA samples ranging from 10 to 24 basepairs, or roughly 40–90 Å. In this context, our results for the Cy3-Cy5 pair at 50 Å suggest that use of the IDA leads to AbsErr_IDA values of 109% and 11% for the subset of datapoints that fit the T or H configurations, respectively. These errors would not affect the overall conclusions of the Iqbal work, as they were based largely on the qualitative shapes of the FRET efficiency versus basepair curves and because we still predict effective κ² values close to 0 (<0.01) for T orientations based on our quantum mechanical calculations. In other words, because the magnitude of the total coupling is small for the T orientation, even a large relative error leads to a small magnitude error in the total coupling. However, incorporating V_LR into their model would change the quantitative details of their modeling results and, therefore, would affect the connection between FRET efficiency and distance in this system. Within the scope of our current work, we simply note that it may be useful for researchers utilizing Cyanine dyes with DNA or RNA to properly treat the electronic coupling to take full advantage of the known orientations of Cy3 and Cy5 in these systems. Similar suggestions would apply to those experiments that utilize FlAsH-type probes (64) or any of the various GFP probes (65).

Summary

We have examined the accuracy of the IDA for several common fluorescent molecules that are used in a wide variety of FRET experiments. For systems in which the donor and acceptor both sample orientation space effectively, the IDA appears to work very well (Err_IDA < 10%) at intermolecular separations of 20 Å or larger. However, this seemingly good performance of the IDA is the result of cancellation of error from orientational averaging, as was suggested in previous studies (66,67). In fact, the errors from the IDA are significant out beyond molecular separations of 50 Å (the largest separations tested here) for some specific relative orientations. For instance, relative orientations in which the donor and acceptor are perpendicular to each other have κ = 0, and therefore V_dip-dip = 0 at all distances, whereas V_LR is nonzero at all distances. Thus, orientational freedom of the donor and acceptor is critical in a FRET experiment to enable both the 〈κ²〉 = 2/3 approximation as well as to mask errors in the IDA. Researchers who wish to take advantage of situations in which the relative orientations of the donor and acceptor may be known, for instance, with FlAsH probes or Cy3/Cy5 attached to DNA/RNA (62), should take care in treating the coupling between the probes, as use of the IDA in these situations is particularly problematic.

Supporting Material

An analysis of the performance of different quantum mechanical methods (and basis sets) on the coupling, including two tables, is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00782-6.