A Mathematical Analysis of Obstructed Diffusion within Skeletal Muscle

Abstract

Molecules are transported through the myofilament lattice of skeletal muscle fibers during muscle activation. The myofilaments, along with the myosin heads, sarcoplasmic reticulum, t-tubules, and mitochondria, obstruct the diffusion of molecules through the muscle fiber. In this work, we studied the process of obstructed diffusion within the myofilament lattice using Monte Carlo simulation, level-set and homogenization theory. We found that these intracellular obstacles significantly reduce the diffusion of material through skeletal muscle and generate diffusion anisotropy that is consistent with experimentally observed slower diffusion in the radial than the longitudinal direction. Our model also predicts that protein size has a significant effect on the diffusion of material through muscle, which is consistent with experimental measurements. Protein diffusion on the myofilament lattice is also anomalous (i.e., it does not obey Brownian motion) for proteins that are close in size to the myofilament spacing. The obstructed transport of ${\text{Ca}}^{2+}$ and ATP-bound ${\text{Ca}}^{2+}$ through the myofilament lattice also generates smaller ${\text{Ca}}^{2+}$ transients. In addition, we used homogenization theory to discover that the nonhomogeneous distribution in the troponin binding sites has no effect on the macroscopic ${\text{Ca}}^{2+}$ dynamics. The nonuniform sarcoplasmic reticulum ${\text{Ca}}^{2+}$-ATPase pump distribution also introduces small asymmetries in the myoplasmic ${\text{Ca}}^{2+}$ transients.

Introduction

Actin and myosin myofilaments are responsible for generating force in skeletal muscle. These myofilaments form a regular lattice, linked together by myosin heads. However, the myofilament lattice impedes the diffusion of molecules such as ${\text{Ca}}^{2+}$ through the muscle fiber. Furthermore, the mitochondria, t-tubules, and sarcoplasmic reticulum (SR) also obstruct diffusion within skeletal muscle. In this work, we examine this process of obstructed diffusion within skeletal muscle using mathematical and Monte Carlo simulation modeling techniques. We find that these intracellular obstacles significantly reduce the diffusion of material through skeletal muscle.

The microstructure of biological tissue limits the flow of solutes through it in a manner dependent on the geometry of the tissue. The resistive properties of tissue are described by tortuosity factors, which have been calculated for a number of different tissue types and different fixed regular geometries (1,2). The tortuosity factor, τ, is defined in this article by the homogenized diffusion equation (3,4)

$$\frac{\partial c}{\partial t}=\tau D{\nabla }^{2}c=D_{\text{eff}}{\nabla }^{2}c,$$ (1)

where D is the solute diffusion coefficient in free solution, c is the solute concentration in the tissue, $D_{\text{eff}}$ is the effective diffusion coefficient, and t is time. This equation describes the macroscopic transport of the solute through the tissue. The mean-squared displacement (MSD) of the solute is then

$$\langle r^2\left(t\right)\rangle =2d\tau Dt,$$ (2)

where d is the spatial dimensionality, which can be used to calculate the tortuosity factor.

The tortuosity factor for skeletal muscle has been measured in a number of different species, and it has been observed that diffusion in skeletal muscle is anisotropic, with diffusion slower in the radial than the longitudinal direction. Engel et al. (5) suggested that the anisotropic arrangement of diffusion obstacles such as myofilaments and mitochondria is responsible for this direction-dependent transport phenomenon. In this article, we use mathematical modeling techniques to show that the myofilaments and myosin heads within skeletal muscle generate diffusion anisotropy consistent with experimental data.

The tortuosity factor for protein diffusion in skeletal muscle is also dependent on protein size (6,7). This effect of protein size on tortuosity is believed to be due to structural barriers within the myoplasm acting as obstacles to diffusion (7,8). We investigated this theory using both Monte Carlo simulation and homogenization theory. Our model predicts that protein size has a significant effect on both the longitudinal and radial tortuosity factors in a manner consistent with experimental measurements. Our modeling approach is therefore useful for understanding the effect of cellular structural organization on the transport of different metabolites in skeletal muscle (9).

Methods and Results

Myofilament lattice geometry

The myofilament lattice geometry is shown in Fig. 1 A. The myosin filaments lie on a hexagonal mesh with six actin filaments surrounding each myosin filament (10). Myofilaments are assumed to be cylindrical, with a diameter of ∼11 nm, and actin filaments have a diameter of ∼6 nm (10–12). The distance between the surfaces of the myosin and actin filaments is ∼8 nm (10,13), and therefore, the distance between the centers of the myosin and actin filaments is ∼16.5 nm (14,15).

Figure 1.

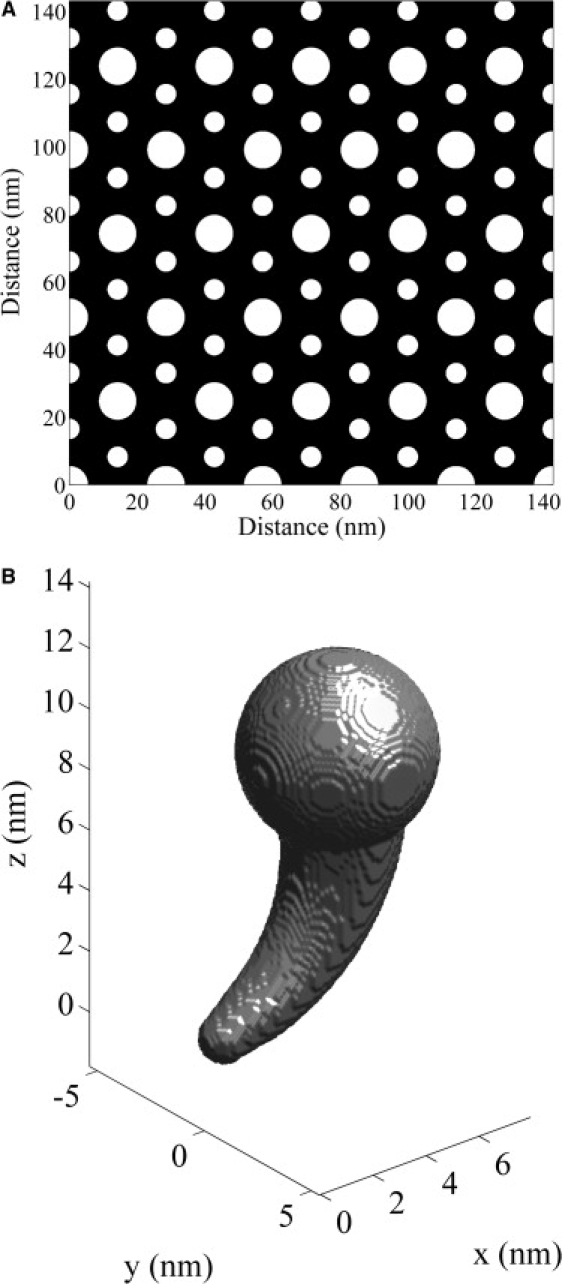
(A) The myofilament lattice geometry. The actin myofilaments are larger in diameter than the myosin myofilaments. (B) The myosin head geometry.

The myosin head geometry is shown in Fig. 1 B. This geometry is based on the model of the myosin head developed by Skubiszak and Kowalczyk (12), which was based on the three-dimensional myosin head structure measured by Rayment and Holden (16). The myosin head length is ∼15 nm (10,17). The spatial positioning of the myosin heads is not completely resolved (14,18,19) and we use a myosin head configuration similar to that of Skubiszak and Kowalczyk, (12). The myosin head placements on a myosin filament are shown in Fig. 2. The arrangement of the cross-bridges is described by the three-stranded model, where the myosin heads are located on a three-stranded 9/1 helix of cross-bridges (10). In this model, the six myosin heads located within each 13 nm axial subunit is termed a crown. The distance between successive crowns is therefore 13 nm, and the rotation between successive crowns is 40° (14,20). The complete three-dimensional myofilament lattice geometry is shown in Fig. 3.

Figure 2.

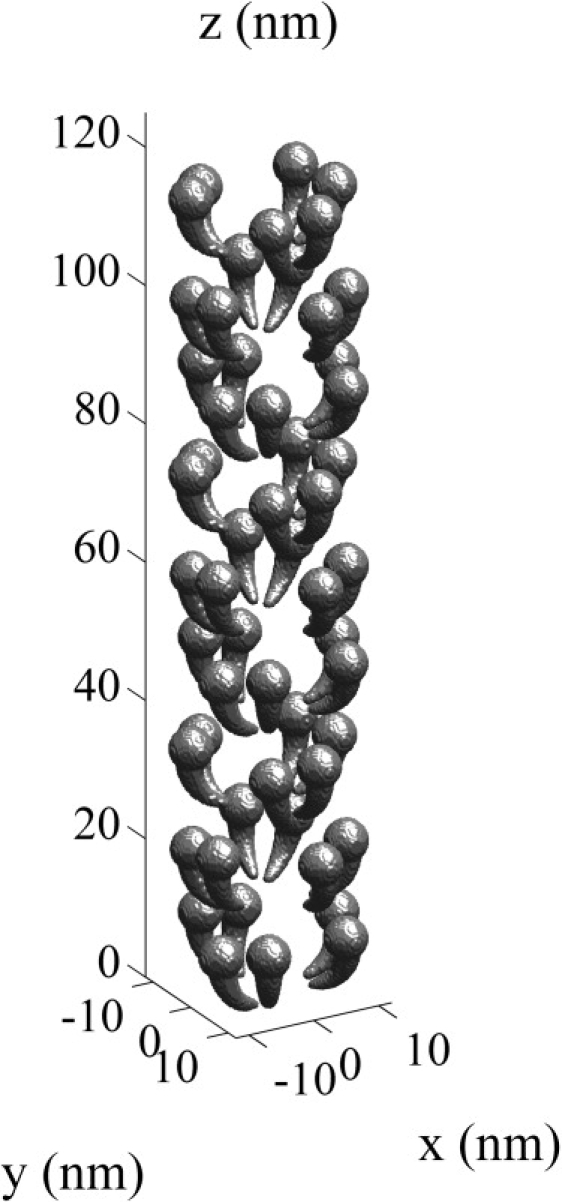
The location of the myosin heads on a single actin myofilament.

Figure 3.

The three-dimensional myofilament lattice geometry.

Monte Carlo method

The structure of biological tissue impedes the diffusion and transport of material through the tissue and this is referred to as obstructed diffusion (21). A Monte Carlo random-walk simulation technique to investigate obstructed diffusion has been proposed by Saxton (22) and Olveczky and Verkman, (23). With this technique, tracers move by random walk throughout a cubic mesh that defines an obstacle-free domain. Tracers are obstructed by the obstacles, and a particle to be moved across an obstacle remains in its original position, which indicates that the particle is reflected at the obstacle boundary. If the obstacles in a three-dimensional domain are defined by $\hat{\Omega }$, then a random walk, $\mathbf{x}\left(t\right)$, on this domain is given by

$$\begin{array}{l}{\tilde{\mathbf{x}}}_{j+1}={\mathbf{x}}_j+{\mathbf{\eta }}_j\sqrt{6D\Delta t},\\ t_{j+1}=t_j+\Delta t,\\ {\mathbf{x}}_{j+1}\left(t_{j+1}\right)=\{\begin{array}{c}{\tilde{\mathbf{x}}}_{j+1},\begin{array}{cc}& \text{if}\end{array}\begin{array}{cc}& \end{array}\left({\tilde{\mathbf{x}}}_{j+1}+\Psi \right)\cap \hat{\Omega }=\varphi \\ {\mathbf{x}}_j,\begin{array}{cc}& \text{if}\end{array}\begin{array}{cc}& \end{array}\left({\tilde{\mathbf{x}}}_{j+1}+\Psi \right)\cap \hat{\Omega }\ne \varphi ,\end{array}\end{array}$$ (3)

where $\Delta x=\sqrt{6D\Delta t}$ is the mesh size, $\Delta t$ is the time step size, ${\mathit{\eta }}_j$ is a random unit vector in one of the six Cartesian axis directions, ϕ denotes the empty set and Ψ is a set that defines the geometry of the spherical diffusing tracer ($\Psi =\left\{y\in {\Re }^3:\Vert y\Vert <d/2\right\}$, where d is the diameter of the tracer). An ensemble of tracer paths can then be used to calculate the mean-squared displacement $\left(\langle r^2\left(t\right)\rangle \right)$ and the effective diffusion coefficient, respectively (24):

$$\begin{array}{l}\langle r_i^2\left(t\right)\rangle =\langle {\Vert x_i\left(t\right)-x_{i0}\Vert }_2^2\rangle ,\\ {\tau }_i=\frac{D_{\text{eff}}^i}{D}=\underset{t\to \mathrm{\infty }}{\lim }\frac{\langle r_i^2\left(t\right)\rangle }{2Dt},\end{array}$$ (4)

where $\mathbf{x}\left(t\right)=\left[\begin{array}{ccc}{x}_1\left(t\right)& x_2\left(t\right)& x_3\left(t\right)\end{array}\right]$ and ${\mathbf{x}}_0=\left[\begin{array}{ccc}{x}_{10}& x_{20}& x_{30}\end{array}\right]$. We applied this technique to calculate random walks on the myofilament lattice geometry in Fig. 3 ($\Delta x$ = 0.5 nm, D = $7.7\times {10}^{-6}$${\text{cm}}^2/\text{s}$).

Homogenization method

Homogenization theory can also be used to calculate the effective diffusion coefficients of point tracers diffusing through a porous medium (3). If the void myoplasmic space is defined by the neighborhood Ω then homogenization involves solving a system of equations for a small periodic component in the concentration field (ω) (25,26):

$$\begin{array}{l}{\nabla }^2{\omega }_i=0,\begin{array}{cc}& \end{array}\mathbf{x}\in \Omega \\ {\omega }_i\left(\mathbf{x}\right)=0,\begin{array}{cc}& \end{array}\mathbf{x}\in C_i\\ \frac{\partial {\omega }_i}{\partial y}\left(\mathbf{x}\right)=0,\begin{array}{cc}& \end{array}\mathbf{x}\in C_j,\begin{array}{c}\end{array}j\ne i\\ \widehat{\mathbf{n}}·\nabla {\omega }_i=\widehat{\mathbf{n}}·{\widehat{\mathbf{e}}}_i,\begin{array}{cc}& \end{array}\mathbf{x}\in {\Omega }^{\prime }\end{array},$$ (5)

where ${\Omega }^{\prime }$ denotes the surface of the myofilament lattice, $\widehat{\mathbf{n}}$ is the outward unit normal at the surface of the myofilament lattice, ${\widehat{\mathbf{e}}}_i$ is the macroscopic diffusion direction in the ith Cartesian coordinate direction, and $C_i$ are the planar faces of the rectangular box, $C_i=\left\{\mathbf{x}=[x_1,x_2,x_3]\in {\Re }^3|x_i=x_{i0}\begin{array}{c}\end{array}\text{or}\begin{array}{c}\end{array}{x}_i=x_{i1}\right\}$ that define the boundary of Ω. The geometric tortuosity factor in the direction of ${\widehat{\mathbf{e}}}_i$ is then given by

$${\tau }_i=\frac{1}{A}\underset{\Omega }{\int }\left(1-{\widehat{\mathbf{e}}}_i·\nabla {\omega }_i\right)d\Omega ,$$ (6)

where A is the volume of the void myoplasmic space defined by Ω.

Homogenization theory can also be used to calculate the effective diffusion coefficients of spherical tracers diffusing through a porous medium. If the tracer has diameter d, then the tortuosity factor can be calculated using Eqs. 5 and 6 with a restricted myoplasmic void space ${\Omega }_d=\left\{y\in \Omega :\left(y+\Psi \right)\cap \hat{\Omega }=\varphi \right\}$, where ϕ denotes the empty set, Ψ is the set that defines the geometry of the spherical diffusing tracer ($\Psi =\left\{y\in {\Re }^3:\Vert y\Vert <d/2\right\}$, and $\hat{\Omega }$ defines the obstacles in the three-dimensional domain. The restricted myoplasmic void space, ${\Omega }_d$, can be calculated directly using this definition or by solving the level-set equation for $\psi \left(\mathbf{x},t\right)$:

$$\begin{array}{l}\frac{d\psi }{dt}+\left|\nabla \psi \right|=0,\begin{array}{cc}& \end{array}\\ \psi \left(\mathbf{x},t=0\right)=0,\begin{array}{cc}& \end{array}\mathbf{x}\in {\Omega }_{}^{\prime }\\ \psi \left(\mathbf{x},t=0\right)>0,\begin{array}{cc}& \end{array}\mathbf{x}\in \Omega \\ {\Omega }_d^{\prime }=\left\{\mathbf{x}:\psi \left(\mathbf{x},t=d/2\right)=0\right\}\\ {\Omega }_d^{}=\left\{\mathbf{x}:\psi \left(\mathbf{x},t=d/2\right)>0\right\}\end{array},$$ (7)

where $\psi \left(\mathbf{x},t=0\right)$ represents the signed distance to the boundary of the myoplasmic void space (${\Omega }_{}^{\prime }$) and ${\Omega }_d^{\prime }$ denotes the boundary of the restricted myoplasmic void space. Fast methods for solving the level-set equation are described by Sethian (27). The myoplasmic void space boundary (${\Omega }_{}^{\prime }$) is shown in Fig. 4 A, and the boundary of the restricted myoplasmic void space for a 6-nm spherical particle (${\Omega }_6^{\prime }$) calculated using Eq. 7 is shown in Fig. 4 B. This demonstrates how the arrangement of the myoplasmic void space changes as the particle size increases.

Figure 4.

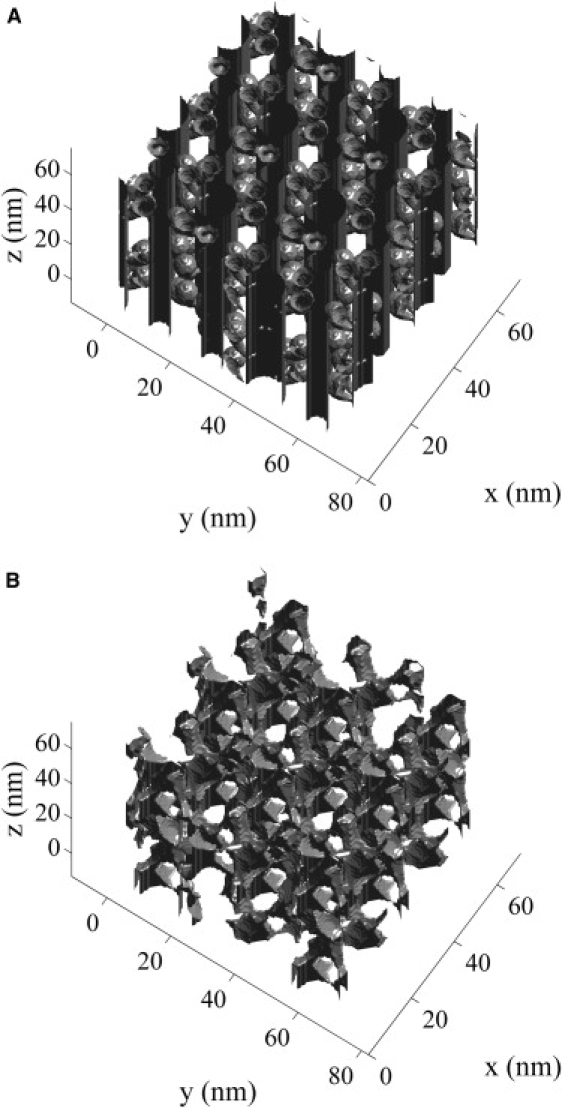
(A) The boundary of the myoplasmic void space (${\Omega }^{\prime }$). (B) The boundary of the restricted myoplasmic void space for a 6-nm spherical particle (${\Omega }_6^{\prime }$) calculated using the level-set equation (Eq. 7).

Anisotropic diffusion on the myofilament lattice

Engel et al. (5) observed that rat cardiomyocytes are anisotropic with respect to ${\text{Ca}}^{2+}$ transport. They found that ${\text{Ca}}^{2+}$ waves traveled faster in the axial than in the radial direction and that the ratio of radial to axial velocity was 0.74 at 27°C. Engel at al. (5) suggested that the anisotropic arrangement of diffusion obstacles such as myofilaments and mitochondria is responsible for the direction-dependent ${\text{Ca}}^{2+}$ wave propagation velocities. Cleveland et al. (28) also found that the diffusion of water in skeletal muscle was anisotropic, with $D_x/D_z=D_y/D_z=0.72$. Kinsey et al. (8) also measured the anisotropic diffusion of phosphocreatine (0.8-nm diameter; relative molar mass (Mr) = 226) within fast- and slow-twitch fish muscle fibers. They found that ${\tau }_x={\tau }_y=0.58$, ${\tau }_z=0.90$, and $D_x/D_z=D_y/D_z=0.64$ in the fast fibers, and ${\tau }_x={\tau }_y=0.5$, ${\tau }_z=0.80$, and $D_x/D_z=D_y/D_z=0.63$ in the slow fibers. Diffusion in skeletal muscle is therefore highly anisotropic.

Aliev and Tikhonov (29) investigated the anisotropic diffusion of low-molecular particles within a skeletal muscle cell using a three-dimensional computer simulation model. Their model included a regular lattice of actin and myosin (without the myosin heads), the membranes of the SR, and mitochondria surrounding the myofibrils and sets of myofibrils within a muscle cell. They found that ${\tau }_x={\tau }_y=0.80$, ${\tau }_z=1.0$, and $D_x/D_z=D_y/D_z=0.80$ when the SR and mitochondria obstacles are ignored. This indicates that the anisotropic arrangement of diffusion obstacles such as myofilaments and mitochondria produces anisotropic diffusion in skeletal muscle.

Using our model, which included not only the myofilaments but also the myosin heads, we calculated that $D_x/D_z=D_y/D_z=0.78$, which is consistent with the findings of Engel et al. (5) and Cleveland et al. (28). We also found that ${\tau }_x={\tau }_y=0.73$ and ${\tau }_z=0.93$, and therefore the myofilaments and myosin heads significantly impede diffusion in skeletal muscle. When the myosin heads were not included in our simulations, we found, using both Monte Carlo and homogenization methods, that ${\tau }_x={\tau }_y=0.81$ and ${\tau }_z=1.0$, which is consistent with the results of Aliev and Tikhonov (29). This small difference between our tortuosity factor and that calculated by Aliev and Tikhonov (29) is due to slightly different myofilament geometries. The numerical solution of Eq. 5 with ${\widehat{\mathbf{e}}}_i$ aligned with the x axis for a point particle is shown in Fig. 5 A. Because of symmetry, the solution is only shown on the repeating unit of the myofilament lattice. Our simulations therefore show that the myofilaments and myosin heads within skeletal muscle generate diffusion anisotropy.

Figure 5.

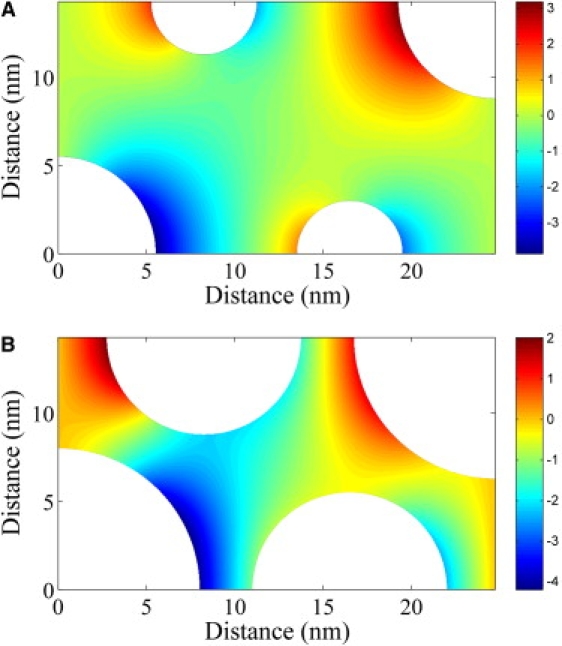
(A) The numerical solution of Eq. 5 for a point particle with ${\widehat{\mathbf{e}}}_i$ aligned with the x axis for the myofilament geometry excluding the myosin heads. The tortuosity factor is $\tau =0.79$. (B) The numerical solution of Eq. 5 for a protein of diameter 5 nm with ${\widehat{\mathbf{e}}}_i$ aligned with the x axis for the myofilament geometry excluding the myosin heads. The tortuosity factor is $\tau =0.63$.

Protein diffusion on the myofilament lattice

Papadopoulos et al. (7) measured the longitudinal diffusion of protein (e.g., cytochrome c, myoglobin, and hemoglobin) in rat extensor digitorum longus muscle within an aqueous solution at 22°C. Kinsey et al. (8) also measured the longitudinal and radial diffusion of phosphocreatine within fast- and slow-twitch fish muscle fibers. The radial diffusion coefficients of a range of different molecules (e.g., ATP, phosphocreatine, and aequorin) have also been measured in other skeletal muscle fibers (6,30,31). Those authors found that molecule size had a significant effect on tortuosity, and their measurements are shown in Fig. 6 (tortuosity factor relative to a 24 g/dl protein solution). This effect of molecule size on tortuosity is believed to be due to structural barriers within the myoplasm acting as obstacles to diffusion (7,8) and can be investigated with our mathematical model. The numerical solution of Eq. 5 with ${\widehat{\mathbf{e}}}_i$ aligned with the x axis for a protein of diameter 5 nm is shown in Fig. 5 B (compare with Fig. 5 A). For this scenario, we found that ${\tau }_x={\tau }_y=0.63$ using both Monte Carlo and homogenization methods. The model simulated effect of molecule size on tortuosity is shown in Fig. 6 for longitudinal and radial protein diffusion on the myofilament lattice with and without the myosin heads. Calculations were made using both Monte Carlo and homogenization methods to check model computations. We found that the myosin heads have a significant effect on the tortuosity factor for protein diffusion in skeletal muscle. Molecules with a diameter >7.3 nm are unable to diffuse through the myofilament lattice that contains the myosin heads. This threshold molecule size of 7.3 nm is slightly smaller than our assumed distance between the surfaces of the myosin and actin filaments of 8 nm (10,13). We note that the measured distance between the surfaces of the myosin and actin filaments is variable, ranging from 8 to 15 nm (7), and this is consistent with the observation that larger molecules, such as ferritin (12.2 nm diameter), are able to diffuse within skeletal muscle (7).

Figure 6.

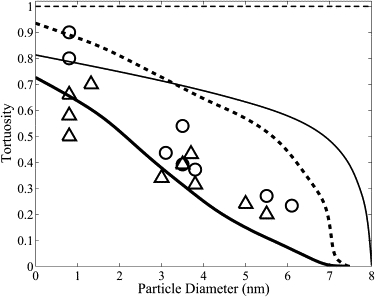
The model effect of protein size on radial tortuosity (${\tau }_x$) in a myofilament lattice with (thick line) and without (thin line) the myosin heads, along with the effect of protein size on longitudinal tortuosity (${\tau }_z$) in a myofilament lattice with (thick dotted line) and without (thin dotted line) the myosin heads. Also shown are experimental measurements in skeletal muscle of the effect of protein size on the radial tortuoisty factor (Δ) (6,8,30,31,33) and the longitudinal tortuosity factor (○) (7,8,33). Protein size has a significant effect of tortuosity.

Our model is consistent with experimental measurements of the radial tortuosity factor for a range of molecules (6,8,30,31,33) and of the longitudinal tortuosity factor for small molecules (8). However, the model does not explain the measured longitudinal tortuosity factors for large molecules such as cytochrome c, myoglobin, and hemoglobin (7). The myoplasmic diffusion data for larger molecules, such as myoglobin, indicates that diffusion of large molecules is isotropic (7,33,34). The model predicts that the longitudinal and radial diffusion coefficients for large proteins in skeletal muscle are significantly different, with a different dependence on protein diameter. Therefore, our model, based on the steric hindrance to diffusion by the myoplasmic structures, explains the observed anisotropy for small molecules such as phosphocreatine, but does not explain the isotropic diffusion of larger molecules such as myoglobin. This indicates that factors not included in our model are responsible for this observed isotropic diffusion of larger molecules within the myoplasm. Possible factors include obstruction due to the Z-band, M-band, and C-protein structures and hydrodynamic wall effects that come into play for large molecules diffusing in confined spaces.

Anomalous diffusion on the myofilament lattice

We also observed that protein diffusion on the myofilament lattice is anomalous (i.e., it does not obey Brownian motion) for proteins that are close in size to the myofilament spacing. The MSD for anomalous diffusion is characterized by

$$\langle r^2\left(t\right)\rangle =K_{\alpha }{t}^{\alpha },\begin{array}{cc}& \alpha \ne 1\end{array},$$ (8)

where $K_{\alpha }$ is a generalized transport coefficient and α is the anomalous exponent, which is a measure of the irregular movement of the protein. Anomalous diffusion is referred to as subdiffusion if $\alpha <1$ and superdiffusion if $\alpha >1$. In three dimensions, anomalous diffusion is a localized phenomenon if α is greater than the percolation threshold, $\tilde{\alpha }=0.543$ (35). Therefore, for $\alpha >\tilde{\alpha }$, diffusion is anomalous over short distances, whereas over large distances it is normal. The crossover length ($R^{\ast }$) between anomalous and normal diffusion is defined by (24)

$$\langle r^2\left(t\right)\rangle \sim \{\begin{array}{c}{t}^{\alpha }\\ t^{}\end{array},\begin{array}{cc}& \end{array}\begin{array}{c}r<R^{\ast }\\ r>R^{\ast }\end{array}\text{.}$$ (9)

The relationship between the protein diameter (d) and α in radial and longitudinal directions is shown in Fig. 7. We found that the anomalous diffusion exponent is different in radial (${\alpha }_r$) and longitudinal directions (${\alpha }_z$) and that proteins with a diameter larger than $\tilde{d}=$ 7.4 nm are unable to diffuse through the myofilament lattice. The difference between the ${\alpha }_r$ and ${\alpha }_z$ is only significant for proteins with a diameter near $\tilde{d}$. The anomalous diffusion is said to be obstructed if $d<\tilde{d}$ and confined if $d>\tilde{d}$.

Figure 7.

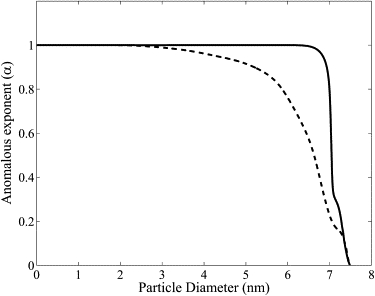
The relationship between the protein diameter (d) and the anomalous diffusion exponent (α) in radial (dotted line) and longitudinal (solid line) directions.

Anomalous diffusion cannot be described by Eq. 1, but must be described by the fractional diffusion equation (21)

$$\frac{\partial c}{\partial t}={}_{0}D_t^{1-{\alpha }_r}{K}_{{\alpha }_r}\frac{{\partial }^{2}c}{\partial r^2}+{}_{0}D_t^{1-{\alpha }_z}{K}_{{\alpha }_z}\frac{{\partial }^{2}c}{\partial z^2},$$ (10)

where the Riemann-Liouville operator ${}_{0}D_t^{1-\alpha }$, for $0<\alpha <1$, is defined by

$${}_{0}D_t^{1-\alpha }x\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}\frac{\partial }{\partial t}\underset{0}{\overset{t}{\int }}\frac{x\left(s\right)}{{\left(t-s\right)}^{1-\alpha }}\text{d}s,$$ (11)

where $\Gamma \left(\alpha \right)$ is the gamma function. Experiments that examine the diffusion of large proteins through the myofilament lattice over a short time period must therefore be analyzed using a fractional diffusion equation.

The effect of mitochondria and sarcoplasmic reticulum on myoplasmic diffusion

The mitochondria and SR also obstruct diffusion in skeletal muscle. Aliev and Tikhonov (29) have modeled the obstruction to diffusion by the mitochondria and SR by a semipermeable cylindrical sheath. They found that this semipermeable cylindrical sheath had no effect on ${\tau }_z$ but a significant effect on ${\tau }_x$ and ${\tau }_y$, depending on the porosity of the sheath. However, Aliev and Tikhonov (29) did not specify an appropriate level of porosity for the semipermeable cylindrical sheath. Here, we estimate the appropriate level of porosity using structural information about the mitochondria and SR in skeletal muscle.

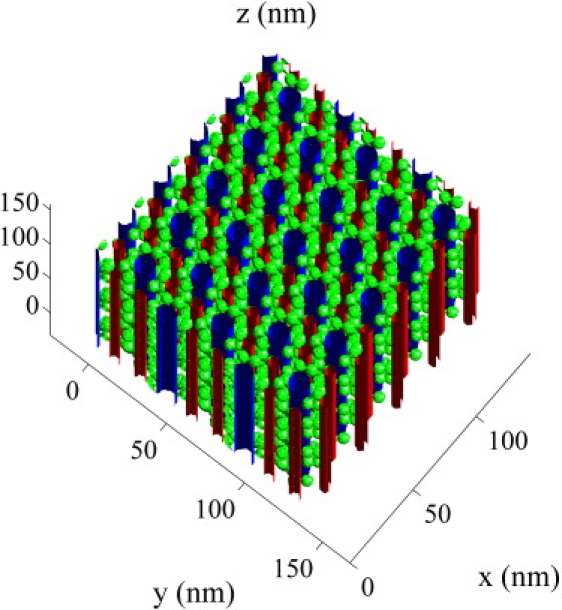
The structure of the mitochondria, t-tubules, and SR in fast- and slow-twitch fibers has been imaged by Ogata and Yamasaki (36), and a scanned reconstruction is shown in Fig. 8 for a slow-twitch fiber. Myofibrils are approximately cylindrical, with a diameter of 1 $\mu \text{m}$ (37) and are packed on a hexagonal lattice (38). Using our model, we found that ${\tau }_x={\tau }_y=0.91$ and ${\tau }_z=0.97$ for a slow-twitch fiber with mitochondria, t-tubules, and SR, but without myofilaments. Mitochondria, t-tubules, and SR therefore have a small but significant effect on intermyofibril diffusion in skeletal muscle.

Figure 8.

The structure of the mitochondria (blue), t-tubules (red), and SR (green) in slow-twitch fibers based on the reconstruction by Ogata and Yamasaki (36).

Obstructed diffusion due to the myofilaments and myosin heads occurs on a nanometer spatial scale, whereas obstructed diffusion due to the SR and mitochondria occurs on a micrometer spatial scale. Because these two spatial scales are significantly different, the two obstructed diffusion processes are largely independent. The combined effect of the myofilament lattice, mitochondria, and sarcoplasmic reticulum on myoplasmic diffusion can therefore be calculated using homogenization theory. In this case, there are nanoscopic, microscopic, and macroscopic spatial scales. Homogenization theory allows the dynamics on a microscopic scale to be incorporated into a macroscopic description of the system dynamics. The idea is to undertake homogenization twice, first incorporating the structure at a nanoscopic level into a homogenized description at the microscopic level and then incorporating the structure at the microscopic level into a homogenized description at the macroscopic level. If the void myoplasmic space defined by the myofilaments is ${\Omega }_m$ with volume $A_m$ and the void space defined by the mitochondria and sarcoplasmic reticulum is ${\Omega }_{\text{SR}}$ with volume $A_{\text{SR}}$, then the geometric tortuosity factor in the direction of ${\widehat{\mathbf{e}}}_i$ at the macroscopic level is given by

$${\tau }_i={\tau }_m\times {\tau }_{SR}=\frac{1}{A_m}\underset{{\Omega }_m}{\int }\left(1-{\widehat{\mathbf{e}}}_i·\nabla {\omega }_i\left({\Omega }_m\right)\right)d\Omega \times \frac{1}{A_{SR}}\underset{{\Omega }_{SR}}{\int }\left(1-{\widehat{\mathbf{e}}}_i·\nabla {\omega }_i\left({\Omega }_{SR}\right)\right)d\Omega$$ (12)

where ${\omega }_i(\Omega )$ denotes the solution to Eq. 5. Thus, for diffusion of a point particle on the muscle fiber spatial scale, our model predicts that ${\tau }_x={\tau }_y=0.73\times 0.91=0.66$ and ${\tau }_z=0.93\times 0.97=0.90$.

The effect of Ca²⁺ buffering and binding to troponin on Ca²⁺ diffusion

${\text{Ca}}^{2+}$ is highly buffered within the myoplasm by parvalbumin and ATP, and these buffers play an important role in ${\text{Ca}}^{2+}$ dynamics (39). Assuming mass-action kinetics, the transport equations for ${\text{Ca}}^{2+}$ (c) and buffer (b) are (40)

$$\begin{array}{l}\frac{\partial c}{\partial t}=\nabla ·{\mathbf{D}}_{\text{c}}^{\mathrm{muscle}}\nabla c+k_{-}b-k_{+}^{}c\left(b_t-b\right),\begin{array}{cc}& x\in \Omega \end{array}\\ \frac{\partial b}{\partial t}=\nabla ·{\mathbf{D}}_{\text{b}}^{\text{muscle}}\nabla b-k_{-}^{}b+k_{+}^{}c\left(b_t-b\right),\begin{array}{cc}& x\in \Omega \end{array}\\ \nabla c·\widehat{\mathbf{n}}=0,\begin{array}{cc}& \text{on}\begin{array}{c}\end{array}{\Omega }^{\prime }\end{array}\\ \nabla b·\widehat{\mathbf{n}}=0,\begin{array}{cc}& \text{on}\begin{array}{c}\end{array}{\Omega }^{\prime }\end{array}\end{array},$$ (13)

where D is the corresponding diffusion tensor, Ω denotes the void space characterized by the myofilament lattice, $k^{+}$ and $k^{-}$ are the association and dissociation rate constants, and $b_{\text{t}}$ is the total concentration of buffer. Homogenization of Eq. 13 to account for the structure of the myofilament lattice yields (41)

$$\begin{array}{l}\frac{\partial c}{\partial t}=\nabla ·\Gamma {\mathbf{D}}_{\text{c}}^{\text{muscle}}\nabla c+k_{-}b-k_{+}^{}c\left(b_{\text{t}}-b\right),\begin{array}{cc}& x\in {\Re }^3\end{array}\\ \frac{\partial b}{\partial t}=\nabla ·\Gamma {\mathbf{D}}_{\text{b}}^{\text{muscle}}\nabla b-k_{-}^{}b+k_{+}^{}c\left(b_{\text{t}}-b\right),\begin{array}{cc}& x\in {\Re }^3\end{array}\end{array}$$ (14)

where Γ is the geometric tortuosity tensor. If it is assumed that the buffer is immobile and the buffer kinetics are rapid, reaching equilibrium at each location before significant diffusion occurs, then (42)

$$\begin{array}{l}\frac{\partial c}{\partial t}=\frac{1}{1+\theta }\nabla ·\Gamma {\mathbf{D}}_{\text{c}}^{\text{muscle}}\nabla c,\begin{array}{cc}& x\in {\Re }^3\end{array}\\ \theta =\frac{K{b}_t}{{\left(K+c\right)}^2}\end{array},$$ (15)

where $K=k^{-}/k^{+}$. We show in Appendix A that Eq. 15 can also be derived from Eq. 13 if the order of assumptions is reversed—i.e., if it is assumed first that the buffer is immobile and that the buffer kinetics are rapid, before undertaking homgenization. There is therefore no interaction between the assumptions of fast buffering and homgenization.

Anisotropic diffusion of ${\text{Ca}}^{2+}$ and ${\text{Ca}}^{2+}$ buffers will have an important effect on the ${\text{Ca}}^{2+}$ dynamics. ${\text{Ca}}^{2+}$ (diameter 0.36 nm) has a diffusion coefficient of $D_{\text{Ca}}^{\text{water}}=7.78\times {10}^{-6}$${\text{cm}}^2/\text{s}$ in free solution at 25°C (43). The viscosity of the myoplasm is believed to be about twice that of water (44). It follows that the ${\text{Ca}}^{2+}$ diffusion coefficient in skeletal muscle at 25°C is $D_{\text{Ca}}^{\text{muscle}}=3.89\times {10}^{-6}$${\text{cm}}^2/\text{s}$, and from Fig. 6,

$${\Gamma }_{\text{c}}{\mathbf{D}}_{\text{c}}^{\text{muscle}}=3.89\times {10}^{-6}\left[\begin{array}{ccc}0.70& 0.70& 0\text{.}\end{array}91\right]\mathbf{I}\begin{array}{c}\end{array}{\text{cm}}^2\text{/s,}$$ (16)

where ${\mathbf{I}}_n$ is the $n\times n$ identity matrix. Diffusion of ${\text{Ca}}^{2+}$ in the longitudinal direction is less impaired than in the radial direction.

ATP and parvalbumin are myoplasmic ${\text{Ca}}^{2+}$ buffers that are both mobile. ATP (∼1.32 nm diameter; Mr = 507) has a diffusion coefficient of $D_{\text{ATP}}^{\text{water}}=3.54\times {10}^{-6}$${\text{cm}}^2\text{/s}$ in free solution at 25°C (31) and parvalbumin (∼3 nm diameter, Mr = 12,000) has a diffusion coefficient of $D_{\text{Parv}}^{\text{water}}=1.48\times {10}^{-6}$${\text{cm}}^2\text{/s}$ in free solution at 20°C (34). It follows that $D_{\text{ATP}}^{\text{muscle}}=1.77\times {10}^{-6}$${\text{cm}}^2\text{/s}$ and $D_{\text{Parv}}^{\text{muscle}}=0.75\times {10}^{-6}$ at 25°C, and from Fig. 6,

$$\begin{array}{l}{\Gamma }_{\text{ATP}}{\mathbf{D}}_{\text{ATP}}^{\text{muscle}}=1.77\times {10}^{-6}\left[\begin{array}{ccc}0.60& 0\text{.60}& 0\text{.}\end{array}86\right]\mathbf{I}\begin{array}{c}\end{array}{\text{cm}}^2\text{/s}\\ {\Gamma }_{\text{Parv}}{\mathbf{D}}_{\text{Parv}}^{\text{muscle}}=0.75\times {10}^{-6}\left[\begin{array}{ccc}0\text{.38}& 0\text{.38}& 0\text{.}\end{array}73\right]\mathbf{I}\begin{array}{c}\end{array}{\text{cm}}^2\text{/s}\end{array}\text{.}$$ (17)

The anisotropic diffusion not only of ${\text{Ca}}^{2+}$ but of ${\text{Ca}}^{2+}$ buffers within the myoplasm therefore has a significant effect on the ${\text{Ca}}^{2+}$ dynamics.

The binding of myoplasmic ${\text{Ca}}^{2+}$ to troponin on the myofilaments generates cross-bridge cycling and force generation. The troponin binding sites are located on each myosin head and two ${\text{Ca}}^{2+}$ ions must bind to troponin to activate the cross-bridges. The troponin binding sites are therefore nonhomogeneous in their spatial distribution, and we investigate the effect of this nonhomogeneous distribution on the macroscopic ${\text{Ca}}^{2+}$ dynamics. We show in Appendix B using homogenization that the nonhomogeneous distribution in the troponin binding sites has no effect on the macroscopic ${\text{Ca}}^{2+}$ dynamics. The binding sites of the buffers ATP and parvalbumin are also nonhomogeneous in their distribution. This is because the size of ATP and parvalbumin is significant relative to the myofilament geometry, and therefore the concentration of binding sites is significantly lower in zones around the myofilaments. Our result in Appendix B also applies in this situation, and the nonhomogeneous binding site distribution has no effect on the macroscopic ${\text{Ca}}^{2+}$ dynamics.

Ca²⁺ transport in skeletal muscle

In this section, we investigate the effect of the structure of the myofilaments and the SR on ${\text{Ca}}^{2+}$ transport within the myoplasm. We assume that the myofilaments are arranged to produce maximum isometric tension so that the bridge regions of the myosin filaments completely overlap with the actin filaments. Our model of ${\text{Ca}}^{2+}$ transport within the half-sarcomere is based on the model by Baylor and Hollingworth (39) and incorporates ${\text{Mg}}^{2+}$ competition for ${\text{Ca}}^{2+}$ binding sites on ATP and parvalbumin:

$$\begin{array}{l}\frac{\partial \text{Ca}}{\partial t}=D_{\text{Ca}}^{}\left({\Gamma }_x^{\text{Ca}}{\nabla }_x^2+{\Gamma }_r^{\text{Ca}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\text{Ca}-k_{\text{T}}^{\text{on}}\text{Ca}\left(T_{\text{tot}}-\left[{\text{Ca}}_{}^{\text{T}}\right]\right)+k_{\text{T}}^{\text{off}}\left[C{a}_{}^{\text{T}}\right]\\ -k_{\text{CATP}}^{\text{on}}\text{Ca}\left[\text{ATP}\right]+k_{\text{CATP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{ATP}}\right]-k_{\text{CP}}^{\text{on}}\text{Ca}\left[\text{P}\right]+k_{\text{CP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{P}}\right],\begin{array}{cc}& 0<x<L,\end{array}\begin{array}{cc}& 0<r<R,\end{array}\\ \frac{\partial \left[\text{ATP}\right]}{\partial t}=D_{\text{ATP}}^{}\left({\Gamma }_x^{\text{ATP}}{\nabla }_x^2+{\Gamma }_r^{\text{ATP}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[\text{ATP}\right]-k_{\text{CATP}}^{\text{on}}\text{Ca}\left[\text{ATP}\right]+k_{\text{CATP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{ATP}}\right]\\ -k_{\text{MATP}}^{\text{on}}\text{Mg}\left[\text{ATP}\right]+k_{\text{MATP}}^{\text{off}}\left[{\text{Mg}}_{}^{\text{ATP}}\right],\\ \frac{\partial \left[{\text{Ca}}_{}^{\text{ATP}}\right]}{\partial t}=D_{\text{ATP}}^{}\left({\Gamma }_x^{\text{ATP}}{\nabla }_x^2+{\Gamma }_r^{\text{ATP}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[{\text{Ca}}_{}^{\text{ATP}}\right]+k_{\text{CATP}}^{\text{on}}\text{Ca}\left[\text{ATP}\right]-k_{\text{CATP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{ATP}}\right],\\ \frac{\partial \left[\text{P}\right]}{\partial t}=D_{\text{P}}^{}\left({\Gamma }_x^{\text{P}}{\nabla }_x^2+{\Gamma }_r^{\text{P}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[\text{ATP}\right]-k_{\text{CP}}^{\text{on}}\text{Ca}\left[\text{P}\right]+k_{\text{CP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{P}}\right]-k_{\text{MP}}^{\text{on}}\text{Mg}\left[\text{P}\right]+k_{\text{MP}}^{\text{off}}\left[{\text{Mg}}_{}^{\text{P}}\right],\\ \frac{\partial \left[{\text{Ca}}_{}^{\text{P}}\right]}{\partial t}=D_{\text{P}}^{}\left({\Gamma }_x^{\text{P}}{\nabla }_x^2+{\Gamma }_r^{\text{P}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[{\text{Ca}}_{}^{\text{P}}\right]+k_{\text{CP}}^{\text{on}}\text{Ca}\left[\text{P}\right]-k_{\text{CP}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{P}}\right],\\ \frac{\partial \left[{\text{Mg}}_{}^{\text{ATP}}\right]}{\partial t}=D_{\text{ATP}}^{}\left({\Gamma }_x^{\text{ATP}}{\nabla }_x^2+{\Gamma }_r^{\text{ATP}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[{\text{Mg}}_{}^{\text{ATP}}\right]+k_{\text{MATP}}^{\text{on}}\text{Mg}\left[\text{ATP}\right]-k_{\text{MATP}}^{\text{off}}\left[{\text{Mg}}_{}^{\text{ATP}}\right],\\ \frac{\partial \left[{\text{Mg}}_{}^{\text{P}}\right]}{\partial t}=D_{\text{P}}^{}\left({\Gamma }_x^{\text{P}}{\nabla }_x^2+{\Gamma }_r^{\text{P}}\left[\frac{1}{r}{\nabla }_r^{}+{\nabla }_r^2\right]\right)\left[{\text{Mg}}_{}^{\text{P}}\right]+k_{\text{MP}}^{\text{on}}\text{Mg}\left[\text{P}\right]-k_{\text{MP}}^{\text{off}}\left[{\text{Mg}}_{}^{\text{P}}\right],\\ \frac{\partial \left[{\text{Ca}}_{}^{\text{T}}\right]}{\partial t}=\left(k_{\text{T}}^{\text{on}}\text{Ca}\left(T_{\text{tot}}-\left[{\text{Ca}}_{}^{\text{T}}\right]\right)-k_{\text{T}}^{\text{off}}\left[{\text{Ca}}_{}^{\text{T}}\right]\right)\end{array},$$ (18)

where $\text{Ca},\left[\text{ATP}\right],\left[{\text{Ca}}_{}^{\text{ATP}}\right],\left[\text{P}\right],\left[{\text{Ca}}_{}^{\text{P}}\right],\left[{\text{Mg}}_{}^{\text{ATP}}\right],\left[{\text{Mg}}_{}^{\text{P}}\right],\text{and}\left[{\text{Ca}}_{}^{\text{T}}\right]$ denote the concentrations of ${\text{Ca}}^{2+}$, ATP, ATP-bound ${\text{Ca}}^{2+}$, parvalbumin, parvalbumin-bound ${\text{Ca}}^{2+}$, ATP-bound ${\text{Mg}}^{2+}$, parvalbumin-bound ${\text{Mg}}^{2+}$, and troponin-bound ${\text{Ca}}^{2+}$. Model parameter values and definitions are defined in Table 1. There is no flux of material across the Z-line (x = 0) or M-line (x = L), so that

$${\frac{\partial Y}{\partial x}|}_{x=0}={\frac{\partial Y}{\partial x}|}_{x=L}=0,\begin{array}{cc}& \end{array}Y\in \left\{\text{Ca},\left[\text{ATP}\right],\left[{\text{Ca}}_{}^{\text{ATP}}\right],\left[\text{P}\right],\left[{\text{Ca}}_{}^{\text{P}}\right],\left[{\text{Mg}}_{}^{\text{ATP}}\right],\left[{\text{Mg}}_{}^{\text{P}}\right]\right\}\text{.}$$ (19)

Table 1.

Model parameter values and definitions

Parameter	Unit	Definition (equation)	Value	Source
${\upsilon }_{\text{SR}}$	$\mu \text{M}\mu {\text{m ms}}^{-1}$	SR ${\text{Ca}}^{2+}$ pump uptake rate	0.5	This work
$K_{\text{SR}}$	$\mu \text{M}$	SR ${\text{Ca}}^{2+}$ pump Michaelis constant	1	(39)
$L_e$	$\mu {\text{m ms}}^{-1}$	SR ${\text{Ca}}^{2+}$ leak constant	0.000014	(46)
$C{a}_{}^{\text{SR}}$	$\mu \text{M}$	SR [${\text{Ca}}^{2+}$]	1500	(46)
L	$\mu \text{m}$	Half-sarcomere length (Z-line to M-line)	1.1	(46)
R	$\mu \text{m}$	Sarcomere radius	0.5	(46)
$\Delta C$	$\mu \text{m}$	Width of terminal cisternae	0.1	This work
${\Gamma }_x^{\text{Ca}}$	—	Longitudinal tortuosity factor for ${\text{Ca}}^{2+}$	0.91	This work
${\Gamma }_r^{\text{Ca}}$	—	Radial tortuosity factor for ${\text{Ca}}^{2+}$	0.7	This work
${\Gamma }_x^{\text{ATP}}$	—	Longitudinal tortuosity factor for ATP	0.86	This work
${\Gamma }_r^{\text{ATP}}$	—	Radial tortuosity factor for ATP	0.6	This work
${\Gamma }_x^P$	—	Longitudinal tortuosity factor for parvalbumin	0.73	This work
${\Gamma }_r^{\text{P}}$	—	Radial tortuosity factor for parvalbumin	0.38	This work
$D_{\text{Ca}}^{}$	$\mu {\text{m}}^2{\text{ms}}^{-1}$	Calcium diffusion coefficient	0.389	(43)
$D_{\text{ATP}}^{}$	$\mu {\text{m}}^2{\text{ms}}^{-1}$	ATP diffusion coefficient	0.177	(31)
$D_{\text{P}}^{}$	$\mu {\text{m}}^2{\text{ms}}^{-1}$	Parvalbumin diffusion coefficient	0.075	(45)
$k_{\text{T}}^{\text{on}}$	$\mu {\text{M}}^{-1}{\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ binding to troponin	0.0885	(39)
$k_{\text{T}}^{\text{off}}$	${\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ dissociation from troponin	0.115	(39)
$T_{\text{tot}}$	$\mu \text{M}$	Total concentration of troponin binding sites	140	(46)
$k_{\text{CP}}^{\text{on}}$	$\mu {\text{M}}^{-1}{\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ binding to parvalbumin	0.0417	(39)
$k_{\text{CP}}^{\text{off}}$	${\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ dissociation from parvalbumin	0.0005	(39)
$P_{\text{tot}}$	$\mu \text{M}$	Total concentration of parvalbumin binding sites	1500	(39)
${\tau }_{\text{on}}$	ms	Time constant for RyR channel opening	1.5	(39)
${\tau }_{\text{off}}$	ms	Time constant for RyR channel closing	1.9	(39)
A	$\mu \text{M}\mu {\text{m ms}}^{-1}$	Maximum RyR ${\text{Ca}}^{2+}$ permeability	550	This work
[${\text{Mg}}^{2+}$]	$\mu \text{M}$	${\text{Mg}}^{2+}$ concentration	1000	(39)
${\text{ATP}}_{\text{tot}}$	$\mu \text{M}$	Total concentration of ATP binding sites	8000	(39)
$k_{\text{MP}}^{\text{on}}$	$\mu {\text{M}}^{-1}{\text{ms}}^{-1}$	Rate of ${\text{Mg}}^{2+}$ binding to parvalbumin	0.000033	(39)
$k_{\text{MP}}^{\text{off}}$	${\text{ms}}^{-1}$	Rate of ${\text{Mg}}^{2+}$ dissociation from parvalbumin	0.003	(39)
$k_{\text{CATP}}^{\text{on}}$	$\mu {\text{M}}^{-1}{\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ binding to ATP	0.15	(39)
$k_{\text{CATP}}^{\text{off}}$	${\text{ms}}^{-1}$	Rate of ${\text{Ca}}^{2+}$ dissociation from ATP	30	(39)
$k_{\text{MATP}}^{\text{on}}$	$\mu {\text{M}}^{-1}{\text{ms}}^{-1}$	Rate of ${\text{Mg}}^{2+}$ binding to ATP	0.0015	(39)
$k_{\text{MATP}}^{\text{off}}$	${\text{ms}}^{-1}$	Rate of ${\text{Mg}}^{2+}$ dissociation from ATP	0.15	(39)

The ${\text{Ca}}^{2+}$ transport between the myoplasm and the SR is described by

$$\begin{array}{l}{\Gamma }_r^{\text{Ca}}{D_{\text{Ca}}^{}\frac{\partial Ca}{\partial r}|}_{r=R}=\left[L_e\left({\text{Ca}}_{}^{\text{SR}}-\text{Ca}(x,R)\right)-\frac{{\nu }_{\text{SR}}\text{Ca}(x,R)}{\text{Ca}(x,R)+K_{\text{SR}}}\right]\frac{\Psi \left(x\right)}{\overline{\Psi }}+W\left(t\right)\Sigma \left(x\right),\\ {\frac{\partial \text{Ca}}{\partial r}|}_{r=0}=0,\end{array}$$ (20)

where ${\text{Ca}}_{}^{\text{SR}}$ is the SR [${\text{Ca}}^{2+}$], the function $\Psi \left(x\right)$ defines the SR density,

$$\begin{array}{l}\Psi \left(x\right)=\{\begin{array}{c}1.0,\begin{array}{cc}& 0<x\le 0.25\begin{array}{c}\end{array}\begin{array}{cc}& \end{array}\end{array}\\ 0.25,\begin{array}{cc}& 0.25<x\le 0.55\begin{array}{c}\end{array}\end{array}\\ 0.05,\begin{array}{cc}& 0.55<x\le L=1.1\end{array}\end{array}\\ \overline{\Psi }={\int }_0^L\Psi \left(x\right)dx,\end{array}$$ (21)

which is based on human SR images by Ogata and Yamasaki (36), and the function $\Sigma \left(x\right)$ defines the location of the terminal cisternae

$$\Sigma \left(x\right)=\{\begin{array}{c}0,\begin{array}{cc}& 0<x\le \frac{1}{2}L-\frac{1}{2}\Delta C\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{cc}& \begin{array}{c}\end{array}\end{array}\end{array}\\ 1,\begin{array}{cc}& \frac{1}{2}L-\frac{1}{2}\Delta C<x\le \frac{1}{2}L+\frac{1}{2}\Delta C\mu \mathrm{m}\end{array}\\ 0,\begin{array}{cc}& \frac{1}{2}L+\frac{1}{2}\Delta C<x\le L\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{cc}& \end{array}\end{array}\end{array},$$ (22)

where $\Delta C$ is the width of the terminal cisternae. The SR ${\text{Ca}}^{2+}$ pump uptake rate (${\upsilon }_{\text{SR}}$) was chosen so that the ${\text{Ca}}^{2+}$ removal rate is 1.5 $\mu {\text{M ms}}^{-1}$ over the entire half-sarcomere (39). The release of ${\text{Ca}}^{2+}$ from the SR occurs at the midpoint of the actin filaments in mammalian muscle (36) and can be described by (46)

$$W\left(t\right)=A\left(1-\exp \left(-t/{\tau }_{\text{on}}\right)\right)\exp \left(-t/{\tau }_{\text{off}}\right)\text{.}$$ (23)

The effects of obstructed diffusion due to the myofilaments on the myoplasmic ${\text{Ca}}^{2+}$ transients are shown in Fig. 9. Shown are the ${\text{Ca}}^{2+}$ and ATP-bound ${\text{Ca}}^{2+}$ (${\text{Ca}}^{2+}$-ATP) transients at the terminal cisternae (x = 0.55 $\mu \text{m}$) at t = 0.5 ms. The myofilament lattice significantly obstructs the transport of ${\text{Ca}}^{2+}$ and ATP-bound ${\text{Ca}}^{2+}$ into the myoplasm. ${\text{Ca}}^{2+}$-ATP plays a significant role in the transport of Ca²⁺ within the myoplasm (39). A smaller flux of ${\text{Ca}}^{2+}$ away from the SR during a ${\text{Ca}}^{2+}$ transient ensures that ${\text{Ca}}^{2+}$ is more quickly pumped back into the SR and therefore generates a smaller ${\text{Ca}}^{2+}$ transient. Obstructed diffusion due to the myofilaments therefore plays a role in the distribution of myoplasmic ${\text{Ca}}^{2+}$.

Figure 9.

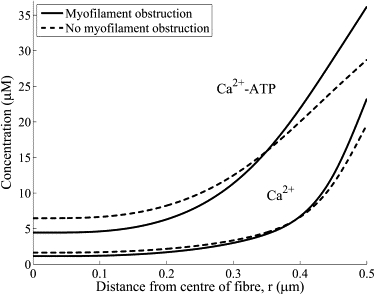
The effect of obstructed diffusion due to the myofilaments on the myoplasmic Ca²⁺ transients. Shown are typical Ca²⁺ and ATP-bound Ca²⁺ (Ca²⁺-ATP) transients (solid line) that account for the obstructed diffusion along with the transients without obstructed diffusion (dotted line). Transients are shown for x = 0.55 $\mu \text{m}$ (i.e,. at the terminal cisternae) and t = 0.5 ms. The myofilament lattice significantly obstructs the transport of Ca²⁺ and ATP-bound Ca²⁺ into the myoplasm.

The significant asymmetric distribution in the SR density (36) and, consequently, the SR ${\text{Ca}}^{2+}$-ATPase pump density (Fig. 10) is expected to generate an associated asymmetric ${\text{Ca}}^{2+}$ distribution. The effect of the nonuniform SR ${\text{Ca}}^{2+}$-ATPase pump distribution on the myoplasmic ${\text{Ca}}^{2+}$ distribution near the surface of the SR (r = R) is shown in Fig. 10. The nonuniform SR ${\text{Ca}}^{2+}$-ATPase pump distribution introduces only very small asymmetries in the myoplasmic ${\text{Ca}}^{2+}$ transients. The reason for this small asymmetry in the myoplasmic ${\text{Ca}}^{2+}$ distribution is that ${\text{Ca}}^{2+}$ diffusion and buffering is fast enough to counteract any asymmetry introduced by the asymmetric SR density.

Figure 10.

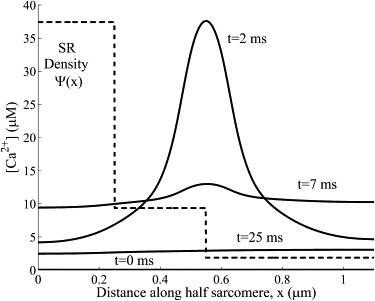
The myoplasmic Ca²⁺ distribution near the surface of the SR (r = R). The nonuniform SR Ca²⁺-ATPase pump distribution (dotted line) introduces very small asymmetries in the myoplasmic Ca²⁺ transients (solid line).

Discussion

The diffusion of small molecules in skeletal muscle has been observed to be highly anisotropic (5,8,28,47). For example, Kinsey et al. (8) measured the anisotropic diffusion of phosphocreatine within fish fast- and slow-twitch muscle fibers and found that ${\tau }_x={\tau }_y=0.58$ and ${\tau }_z=0.90$ in the fast fibers, and ${\tau }_x={\tau }_y=0.5$ and ${\tau }_z=0.80$ in the slow fibers. The anisotropic diffusion of molecules within skeletal muscle is important for determining whether intracellular gradients in energy metabolites such as phosphocreatine occur during muscle fatigue in large-diameter skeletal muscle fibers (8). Using our mathematical modeling approach, we found that the myofilaments, myosin heads, SR, t-tubules, and mitochondria significantly impede diffusion in skeletal muscle. Because obstructed diffusion due to the myofilaments and myosin heads occurs on a spatial scale significantly smaller than that of obstructed diffusion due to the SR, t-tubules, and mitochondria, it follows that these two obstructed diffusion processes are independent. For diffusion on the muscle fiber spatial scale, our model therefore predicts that ${\tau }_x={\tau }_y=0.73\times 0.91=0.66$ and ${\tau }_z=0.93\times 0.97=0.90$ for a point particle and ${\tau }_x={\tau }_y=0.58$ and ${\tau }_z=0.85$ for phosphocreatine, which is consistent with the tortuosity measurements for phosphocreatine in muscle fibers by Kinsey et al. (8).

Many biological processes within skeletal muscle, such as calcium transport, need only be considered on the myofibril scale. For diffusion on the myofibril spatial scale, the myofilaments and myosin heads are the major obstacles: the SR, t-tubules, and mitochondria do not significantly impede diffusion within an individual myofibril. For a point particle diffusing on the myofibril spatial scale, our model therefore predicts that ${\tau }_x={\tau }_y=0.73$ and ${\tau }_z=0.93$. Calcium has an atomic radius of 0.18 nm, so for calcium diffusion on the myofibril spatial scale, our model predicts that ${\tau }_x={\tau }_y=0.70$ and ${\tau }_z=0.91$. The myofilaments and myosin heads therefore significantly impede the diffusion of calcium within skeletal muscle, and this process has not been accounted for in existing models of calcium transport within skeletal muscle.

Protein size has a significant effect on tortuosity in skeletal muscle. This effect of protein size on tortuosity is believed to be due to structural barriers within the myoplasm acting as obstacles to diffusion (7,8) and was investigated with our mathematical model. We found that the myosin heads have a significant effect on the tortuosity factor for protein diffusion in skeletal muscle. Although our model predictions of the radial tortuosity factor are consistent with experimental measurements of the radial tortuosity factor (6,8,30,31,33), the model does not explain the measured longitudinal tortuosity factors for large molecules such as cytochrome c, myoglobin, and hemoglobin (7). The model also predicts that the longitudinal and radial diffusion coefficients for large molecules in skeletal muscle are significantly different and that therefore the diffusion of large molecules is anisotropic. However, the myoplasmic diffusion data for larger molecules, such as myoglobin, indicates that diffusion of large molecules is isotropic (7,33,34). Therefore, our model, based on the steric hindrance to diffusion by the myoplasmic structures, explains the observed anisotropy for small molecules such as phosphocreatine, but does not explain the isotropic diffusion of larger molecules, such as myoglobin. This indicates that factors not included in our model are responsible for this observed isotropic diffusion of larger molecules within the myoplasm. Possible explanatory factors include obstruction due to the Z-band, M-band, and C-protein structures, hydrodynamic wall effects that come into play for large molecules diffusing in confined spaces, and the molecular motion that the myosin heads and the other myofilament proteins undergo continuously.

The arrangements of the Z-band, M-band, and C-protein structures in skeletal muscle have been measured (10) and the interfilament distances within the Z-band and M-band have been estimated to be 15–20 nm (7). Although this interfilament distance is comparable to the interfilament distance within the A-band, the diffusion of large molecules through the Z-band and M-band could be significantly impeded by the α-actinin and M-bridge structures, respectively. Ferritin (12.2 nm diameter) was observed to be able to diffuse in the longitudinal direction of muscle fibers (7), so the obstruction by the α-actinin and M-bridge structures is not too restrictive. Furthermore, the Z-band and M-band lattices include obstacles that are oriented in directions both longitudinal and perpendicular to the fiber, and diffusion within the Z-band and M-band would not be expected to be significantly anisotropic. Anisotropic diffusion of large molecules in the Z-band and M-band, with preferential transport in the radial direction, would be required to counteract the preferential transport of large molecules in the longitudinal direction within the A-band that have been estimated in this article to generate isotropic diffusion through the entire fiber. Although the Z-band and M-band structures will impede the longitudinal transport of large molecules, they will most likely impede, to a similar degree, the radial transport of large molecules, and they are unlikely to completely explain the observed isotropic diffusion of large molecules in skeletal muscle.

A potential explanation of the isotropic diffusion of large molecules is the hydrodynamic wall effects that come into play for large molecules diffusing in confined spaces. There is increased hydrodynamic drag on diffusing molecules near obstacles and therefore a reduction in the mobility of the diffusing molecule (48,49,50). This hydrodynamic drag is proportional to the diameter of the diffusing molecule relative to the dimension of the porous media (49). This increased hydrodynamic drag near the boundary of an obstacle ensures that diffusion of large particles is slow in all directions relative to the boundary as opposed to being slow only in directions toward the interior of the obstacle as in the case of steric hindrance of point particles. This hydrodynamic drag effect ensures that diffusion becomes more isotropic as the size of the diffusing particle increases, as per measurements of diffusion in skeletal muscle. Another potential contributing factor for the isotropic diffusion of large molecules is the continuous molecular motion that the myosin heads and the other myofilament proteins undergo, which results in localized mixing of the large molecules. The effect of mixing on the transport of large molecules is expected to be isotropic in nature and more significant for larger molecules.

The mitochondria, t-tubules, and SR also obstruct diffusion in skeletal muscle. However, the level of obstructed diffusion due to these obstacles is unknown. We estimated this level of obstruction using a scanned reconstruction of an image of the mitochondria, t-tubules, and SR in muscle fibers by Ogata and Yamasaki (36). Using our model, we found that ${\tau }_x={\tau }_y=0.91$ and ${\tau }_z=0.97$ for a slow-twitch fiber with mitochondria, t-tubules, and SR but without myofilaments. Mitochondria, t-tubules, and SR therefore have a small but significant effect on intermyofibril diffusion in skeletal muscle. Furthermore, differences in the structure of the SR, t-tubules, mitochondria, and myofilaments between fiber types will have a small but significant effect on tortuosity that could potentially be characterized using our model. Our modeling study is therefore useful for understanding the role of cellular structural organization on the transport of different metabolites in skeletal muscle.

Homogenization theory allows the dynamics on a microscopic scale to be incorporated into a macroscopic description of the system dynamics. Homogenization of microscopic spatial structure and fast buffer kinetics are assumptions that are used to simplify models of ${\text{Ca}}^{2+}$ transport. We found that theoretical models based on both of these assumptions are independent of the order in which the assumptions are applied. There is therefore no interaction between the assumptions of fast buffering and homgenization. We also investigated the effect of the nonhomogeneous spatial distribution in the troponin binding sites on the macroscopic myoplasmic ${\text{Ca}}^{2+}$ dynamics. Using homogenization theory, we found that the nonhomogeneous distribution in the troponin binding sites has no effect on the macroscopic ${\text{Ca}}^{2+}$ dynamics.

We also investigated the effect of the nonhomogeneous SR distribution on the myoplasmic ${\text{Ca}}^{2+}$ transients. The significant asymmetric distribution in the SR density and, consequently, the SR ${\text{Ca}}^{2+}$-ATPase pump density are expected to generate an associated asymmetric ${\text{Ca}}^{2+}$ distribution. However, we found that the nonuniform SR ${\text{Ca}}^{2+}$-ATPase pump distribution introduces only very small asymmetries in the myoplasmic ${\text{Ca}}^{2+}$ transients. The reason for this small asymmetry in the myoplasmic ${\text{Ca}}^{2+}$ distribution is that ${\text{Ca}}^{2+}$ diffusion and buffering are fast enough to counteract any asymmetry introduced by the asymmetric SR density.

The effect of the structure of the myofilaments and the SR on ${\text{Ca}}^{2+}$ transport within the half-sarcomere was also characterized. Our model of ${\text{Ca}}^{2+}$ transport within the half-sarcomere is based on the model by Baylor and Hollingworth (39) and incorporates ${\text{Mg}}^{2+}$ competition for ${\text{Ca}}^{2+}$ binding sites on ATP and parvalbumin. We found that the myofilament lattice significantly obstructs the transport of ${\text{Ca}}^{2+}$ and ATP-bound ${\text{Ca}}^{2+}$ into the myoplasm. ${\text{Ca}}^{2+}$-ATP plays a significant role in the transport of Ca²⁺ within the myoplasm (39), even though ATP is obstructed by the myofilament lattice to a greater degree than ${\text{Ca}}^{2+}$ due to its larger size. A smaller flux of ${\text{Ca}}^{2+}$ away from the SR during a ${\text{Ca}}^{2+}$ transient ensures that ${\text{Ca}}^{2+}$ is more quickly pumped back into the SR and therefore generates a smaller ${\text{Ca}}^{2+}$ transient. Obstructed diffusion due to the myofilaments therefore plays a role in the distribution of myoplasmic ${\text{Ca}}^{2+}$.

Appendix A

Our homogenization analysis proceeds along the lines described by Goel et al. (41). If it is assumed that the buffer is immobile and the buffer kinetics are rapid, reaching equilibrium at each location before significant diffusion occurs, then the ${\text{Ca}}^{2+}$ dynamics are described by (42)

$$\begin{array}{l}\frac{\partial c}{\partial t}=\frac{1}{1+\theta }\nabla ·A\nabla c,\begin{array}{cc}& x\in \Omega \end{array}\\ \theta =\frac{K{b}_t}{{\left(K+c\right)}^2};\begin{array}{cc}& \end{array}A=\Gamma {\mathbf{D}}_{\text{c}}^{\text{muscle}}\\ \nabla c·\widehat{\mathbf{n}}=0,\begin{array}{cc}& \text{on}\begin{array}{c}\end{array}{\Omega }^{\prime }\end{array}\end{array},$$ (A1)

where Ω denotes the void myoplasmic space and $K=k^{-}/k^{+}$. We visualize the myofilament lattice as forming a periodic network with period ɛ and domain ${\Omega }_{\varepsilon }$. The ${\text{Ca}}^{2+}$ concentration within this domain is denoted by $c_{\varepsilon }$ (where the subscript ɛ denotes a quantity dependent on the period ɛ of the domain) and we consider a family of problems and their solutions in the limit $\varepsilon \to 0$. It follows that

$$\begin{array}{l}\frac{\partial c_{\varepsilon }}{\partial t}=\frac{1}{1+\theta }\nabla ·A_{\varepsilon }\nabla c_{\varepsilon },{\begin{array}{cc}& x\in \Omega \end{array}}_{\varepsilon }\\ \theta =\frac{K{b}_t}{{\left(K+c_{\varepsilon }\right)}^2}\\ A_{\varepsilon }\nabla c_{\varepsilon }·{\widehat{\mathbf{n}}}_{\varepsilon }=0,\begin{array}{cc}& \text{on}\begin{array}{c}\end{array}{\Omega }_{\varepsilon }^{\prime }\end{array}\end{array},$$ (A2)

where $A_{\varepsilon }=a_{ij}\left(x/\varepsilon \right)$ denotes the diffusion coefficient and ${\widehat{\mathbf{n}}}_{\varepsilon }$ denotes the exterior normal to the boundary ${\Omega }_{\varepsilon }^{\prime }$. We introduce the periodic unit cube with microscopic variable $y=[y_1,y_2,y_3]=x/\varepsilon$, $y_i\in [0,1]$ and define $y\in {\Omega }_c$ if $x=y\varepsilon \in {\Omega }_e$. We assume that $c_{\varepsilon }$ is a function of both $x\in \Omega$ and $y\in {\Omega }_c$:

$$c_{\varepsilon }=c(x,y,t),$$ (A3)

with asymptotic expansion

$$\begin{array}{l}{c}_{\varepsilon }=c_0(x,y,t)+\varepsilon c_1(x,y,t)+{\varepsilon }^2{c}_2(x,y,t)+\dots \\ c_n(x,y,t)=c_n(x,y+1,t)\end{array}\text{.}$$ (A4)

Defining $\nabla =\partial /\partial x_i+{\varepsilon }^{-1}\partial /\partial y_i$ we obtain

$$\nabla ·A_{\varepsilon }\nabla =\left(\frac{\partial }{\partial x_i}+{\varepsilon }^{-1}\frac{\partial }{\partial y_i}\right)a_{ij}\left(y\right)\left(\frac{\partial }{\partial x_j}+{\varepsilon }^{-1}\frac{\partial }{\partial y_j}\right)={\varepsilon }^{-2}{A}_0+{\varepsilon }^{-1}{A}_1+A_2,$$ (A5)

where the operators $A_i$ are

$$\begin{array}{l}{A}_0=\frac{\partial }{\partial y_i}\left(a_{ij}\left(y\right)\frac{\partial }{\partial y_j}\right)\\ A_1=\frac{\partial }{\partial y_i}\left(a_{ij}\left(y\right)\frac{\partial }{\partial x_j}\right)+\frac{\partial }{\partial x_i}\left(a_{ij}\left(y\right)\frac{\partial }{\partial y_j}\right)\\ A_2=a_{ij}\left(y\right)\frac{{\partial }^2}{\partial x_i\partial x_j}\end{array}\text{.}$$ (A6)

It follows from Eqs. A2, A3, and A5 that

$$\begin{array}{l}\frac{\partial c_{\varepsilon }}{\partial t}=\frac{1}{1+\theta \left(c_{\varepsilon },x\right)}\left[{\varepsilon }^{-2}{A}_0+{\varepsilon }^{-1}{A}_1+A_2\right]c_{\varepsilon },\begin{array}{cc}& x\in \Omega \end{array},\begin{array}{c}\end{array}y\in {\Omega }_c^{}\\ a_{ij}^{\varepsilon }\left(\frac{\partial }{\partial x_i}+{\varepsilon }^{-1}\frac{\partial }{\partial y_i}\right)n_{\varepsilon i}=0,\begin{array}{cc}& x\in {\Omega }_{\varepsilon }^{\prime }\end{array},\begin{array}{c}\end{array}y\in {\Omega }_c^{\prime },\end{array}$$ (A7)

where $n_i$ denotes the exterior normal to the boundary ${\Omega }_c^{\prime }$. Sinceit

$$\begin{array}{l}\frac{1}{1+\theta \left(c_0+\varepsilon c_1+{\varepsilon }^2{c}_2+\dots \right)}=\frac{1}{1+\theta \left(c_0\right)+\varepsilon c_1{\theta }^{\prime }\left(c_0\right)+{\varepsilon }^2{c}_2{\theta }^{\prime }\left(c_0\right)+\dots }\\ =\frac{1}{1+\theta \left(c_0\right)}\left[1-\frac{\varepsilon c_1{\theta }^{\prime }\left(c_0\right)}{1+\theta \left(c_0\right)}-\frac{{\varepsilon }^2{c}_2{\theta }^{\prime }\left(c_0\right)}{1+\theta \left(c_0\right)}+{\left(\frac{\varepsilon c_1{\theta }^{\prime }\left(c_0\right)}{1+\theta \left(c_0\right)}\right)}^2+\dots \right]\\ =\frac{1}{1+\theta \left(c_0\right)}\left[1-\varepsilon {\varphi }_1+{\varepsilon }^2{\varphi }_2+\dots \right],\begin{array}{cc}& \end{array}\text{where}\begin{array}{c}\end{array}{\varphi }_1=\frac{c_1{\theta }^{\prime }\left(c_0\right)}{1+\theta \left(c_0\right)},\begin{array}{cc}& \end{array}{\varphi }_2={\left(\frac{c_1{\theta }^{\prime }\left(c_0\right)}{1+\theta \left(c_0\right)}\right)}^2\end{array},$$ (A8)

if follows that

$$\begin{array}{l}\frac{\partial (c_0+\varepsilon c_1+{\varepsilon }^2{c}_2+\dots )}{\partial t}=\frac{1}{1+\theta \left(c_0\right)}\left[1-\varepsilon {\varphi }_1+{\varepsilon }^2{\varphi }_2+\dots \right]\left[{\varepsilon }^{-2}{A}_0+{\varepsilon }^{-1}{A}_1+A_2\right](c_0+\varepsilon c_1+{\varepsilon }^2{c}_2+\dots )\\ a_{ij}^{\varepsilon }\left(\frac{\partial }{\partial x_i}+{\varepsilon }^{-1}\frac{\partial }{\partial y_i}\right)n_{\varepsilon i}=0,\begin{array}{cc}& x\in {\Omega }_{\varepsilon }^{\prime }\end{array},\begin{array}{c}\end{array}y\in {\Omega }_c^{\prime }\end{array}.$$ (A9)

We proceed by equating coefficients of ɛ in Eq. A9. The equation at order ${\varepsilon }^{-2}$ require

$$A_0{c}_0=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c,$$ (A10)

and the boundary conditions at order ${\varepsilon }^{-1}$ require that

$$a_{ij}\left(y\right)\frac{\partial c_0}{\partial y_j}{n}_i=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c^{\prime }\text{.}$$ (A11)

Since $c_n(x,y,t)=c_n(x,y+1,t)$ it follows that $c_0=c_0(x,t)$. The equation at order ${\varepsilon }^{-1}$ require

$$A_1{c}_0+A_0{c}_1^{}=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c,$$ (A12)

and the boundary conditions at order ${\varepsilon }^0$ require

$$a_{ij}\left(y\right)\left(\frac{\partial c_0}{\partial x_j}+\frac{\partial c_1}{\partial y_j}\right)n_i=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c^{\prime }\text{.}$$ (A13)

If we define ω to be the solution to

$$\begin{array}{l}\frac{\partial }{\partial y_j}\left[a_{ij}\left(y\right)\left(\frac{\partial {\omega }_k}{\partial y_j}+{\delta }_{jk}\right)\right]=0,y\in {\Omega }_c\\ a_{ij}\left(y\right)\left(\frac{\partial {\omega }_k}{\partial y_j}+{\delta }_{jk}\right)n_i=0,y\in {\Omega }_c^{\prime }\\ {\omega }_k\left(x,y,t\right)={\omega }_k\left(x,y+1,t\right)\end{array},$$ (A14)

then

$$c_1={\omega }_i\frac{\partial c_0}{\partial x_i}+{\overline{c}}_1(x,t)\text{.}$$ (A15)

The equation at order ${\varepsilon }^0$ requires that

$$\left[1+\theta \left(c_0\right)\right]\frac{\partial c_0}{\partial t}=\left(A_2{c}_0+A_1{c}_1^{}+A_0{c}_2\right),\begin{array}{cc}& \end{array}y\in {\Omega }_c,$$ (A16)

and the boundary conditions at order ${\varepsilon }^1$ require that

$$a_{ij}\left(y\right)\left(\frac{\partial c_1}{\partial x_j}+\frac{\partial c_2}{\partial y_j}\right)n_i=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c^{\prime }\text{.}$$ (A17)

Integrating the left-hand side of Eq. A16 over ${\Omega }_c$ yields

$${\int }_{{\Omega }_c}\left[1+\theta \left(c_0\right)\right]\frac{\partial c_0}{\partial t}dy=\left[1+\theta \left(c_0\right)\right]\frac{\partial c_0}{\partial t}{\gamma }_c,$$ (A18)

where ${\int }_{{\Omega }_c}dy$ denotes the volume of ${\Omega }_c$ within the unit cell. Integrating Eq. A16 over ${\Omega }_c$ yields

$${\int }_{{\Omega }_c}\left(A_2{c}_0+A_1{c}_1^{}+A_0{c}_2\right)dy={\int }_{{\Omega }_c}\frac{\partial }{\partial x_i}\left(a_{ij}\left(y\right)\left(\frac{\partial c_0}{\partial x_j}+\frac{\partial c_1^{}}{\partial y_j}\right)\right)dy+{\int }_{{\Omega }_c}\frac{\partial }{\partial y_i}\left(a_{ij}\left(y\right)\left(\frac{\partial c_1^{}}{\partial x_j}+\frac{\partial c_2}{\partial y_j}\right)\right)dy,$$ (A19)

and substituting Eq. A15 into the first term on the right-hand side of Eq. A19 yields

$$\begin{array}{l}{\int }_{{\Omega }_c}\frac{\partial }{\partial x_i}\left(a_{ij}\left(y\right)\left(\frac{\partial c_0}{\partial x_j}+\frac{\partial }{\partial y_j}\left({\omega }_i\frac{\partial c_0}{\partial x_i}+{\overline{c}}_1\left(x,t\right)\right)\right)\right)dy\\ ={\int }_{{\Omega }_c}\frac{\partial }{\partial x_i}\left(a_{ij}\left(y\right)\left({\delta }_{jk}+\frac{\partial {\omega }_k}{\partial y_j}\right)\frac{\partial c_0}{\partial x_k}\right)dy\\ =\frac{\partial }{\partial x_i}\left({\tilde{a}}_{ik}\left(y\right)\frac{\partial c_0}{\partial x_k}\right),\begin{array}{cc}& \end{array}\text{where}\begin{array}{cc}& \end{array}{\tilde{a}}_{ik}\left(y\right)={\int }_{{\Omega }_c}{a}_{ij}\left(y\right)\left({\delta }_{jk}+\frac{\partial {\omega }_k}{\partial y_j}\right)dy,\end{array}$$ (A20)

where ${\delta }_{jk}$ is the Kronecker delta. By applying the divergence theorem to the second term on the right-hand side of Eq. A19 and using Eq. A17 we obtain

$${\int }_{{\Omega }_c}\frac{\partial }{\partial y_i}\left(a_{ij}\left(y\right)\left(\frac{\partial c_1^{}}{\partial x_j}+\frac{\partial c_2}{\partial y_j}\right)\right)dy=0\text{.}$$ (A21)

From Eqs. A18–A21, we arrive at

$$\left[1+\theta \left(c_0\right)\right]\frac{\partial c_0}{\partial t}{\gamma }_c=\frac{\partial }{\partial x_i}\left({\tilde{a}}_{ik}\left(y\right)\frac{\partial c_0}{\partial x_k}\right),$$ (A22)

where ${\tilde{a}}_{ik}\left(y\right)/{\gamma }_c$ are the effective diffusion coefficients for the homogenized problem.

Appendix B

The troponin binding sites are nonhomogeneous in their spatial distribution and are located within the domain Ψ. We assume that the immobile binding sites are located periodically in space and that the buffer kinetics are rapid, reaching equilibrium at each location before significant diffusion occurs. The ${\text{Ca}}^{2+}$ dynamics are then described by

$$\begin{array}{l}\frac{\partial c}{\partial t}=\left(1+\left(\frac{1}{1+\theta }-1\right)H\left(x\right)\right)\nabla ·A\nabla c,\begin{array}{cc}& x\in \Omega ={\Re }^3\end{array}\\ \theta =\frac{K{b}_t^{\ast }}{{\left(K+c\right)}^2};\begin{array}{ccc}& & \end{array}{b}_t^{\ast }=b_t^{}/\alpha ,\end{array}$$ (B1)

where α is the fraction of the domain occupied by the binding sites and $H\left(x\right)=1$ if $x\in \Psi$ and $H\left(x\right)=0$ if $x\notin \Psi$. We visualize the binding sites as forming a periodic arrangement with period ɛ and domain ${\Omega }_{\varepsilon }$ and introduce the periodic unit cube with microscopic variable $y=[y_1,y_2,y_3]=x/\varepsilon$, $y_i\in [0,1]$ and $y\in {\Omega }_c$ if $x=y\varepsilon \in {\Omega }_e$. We define $H\left(y\right)=1$ if $x=y\varepsilon \in \Psi$ and $H\left(y\right)=0$ if $x=y\varepsilon \notin \Psi$. The ${\text{Ca}}^{2+}$ concentration within the domain ${\Omega }_{\varepsilon }$ is denoted by $c_{\varepsilon }$ (where a subscript ɛ denotes a quantity dependent on the period ɛ of the domain) and we consider a family of problems and their solutions in the limit $\varepsilon \to 0$. We assume that $c_{\varepsilon }$ is a function of both $x\in \Omega$ and $y\in {\Omega }_c$:

$$c_{\varepsilon }=c(x,y,t),$$ (B2)

with asymptotic expansion

$$\begin{array}{l}{c}_{\varepsilon }=c_0(x,y,t)+\varepsilon c_1(x,y,t)+{\varepsilon }^2{c}_2(x,y,t)+\dots \\ c_n(x,y,t)=c_n(x,y+1,t).\end{array}$$ (B3)

It follows that

$$\begin{array}{l}\frac{\partial c_{\varepsilon }}{\partial t}=\left[{\varepsilon }^{-2}{A}_0+{\varepsilon }^{-1}{A}_1+A_2\right](c_0+\varepsilon c_1+{\varepsilon }^2{c}_2+\dots )\left[1-H\left(y\right)\right]\\ +\frac{1}{1+\theta \left(c_0\right)}\left[1-\varepsilon {\varphi }_1+{\varepsilon }^2{\varphi }_2+\dots \right]\left[{\varepsilon }^{-2}{A}_0+{\varepsilon }^{-1}{A}_1+A_2\right](c_0+\varepsilon c_1+{\varepsilon }^2{c}_2+\dots )H\left(y\right),\begin{array}{cc}& y\in {\Omega }_c,\end{array}\end{array}$$ (B4)

where $A_i$ and ${\varphi }_i$ are defined in Eqs. A6 and A8, respectively. We proceed by equating coefficients of ɛ in Eq. B4. The equation at order ${\varepsilon }^{-2}$ requires that

$$\begin{array}{l}{A}_0{c}_0\beta \left(y\right)=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c\\ \beta \left(y\right)=[1-H\left(y\right)]+\frac{H\left(y\right)}{1+\theta \left(c_0\right)}\end{array},$$ (B5)

and since $c_n(x,y,t)=c_n(x,y+1,t)$ it follows that $c_0=c_0(x,t)$. The equation at order ${\varepsilon }^{-1}$ requires that

$$A_1{c}_0+A_0{c}_1^{}=0,\begin{array}{cc}& \end{array}y\in {\Omega }_c,$$ (B6)

as in Appendix A. The equation at order ${\varepsilon }^0$ requires

$$\frac{1}{\beta \left(y\right)}\frac{\partial c_0}{\partial t}=\left(A_2{c}_0+A_1{c}_1^{}+A_0{c}_2\right),\begin{array}{cc}& \end{array}y\in {\Omega }_c\text{.}$$ (B7)

Integrating the left-hand side of Eq. B7 over ${\Omega }_c$ yields

$$\begin{array}{l}{\int }_{{\Omega }_c}\frac{1}{\beta \left(y\right)}\frac{\partial c_0}{\partial t}dy={\int }_{{\Omega }_c}\frac{(1+\theta )}{(1+\theta )[1-H\left(y\right)]+H\left(y\right)}\frac{\partial c_0}{\partial t}dy\\ =(1+\theta )\frac{\partial c_0}{\partial t}{\int }_{{\Omega }_c}\frac{1}{(1+\theta )[1-H\left(y\right)]+H\left(y\right)}dy\\ =(1+\theta )\frac{\partial c_0}{\partial t}\left[\alpha +\frac{1-\alpha }{1+\theta }\right]\\ =(1+{\theta }^{\ast })\frac{\partial c_0}{\partial t};\begin{array}{ccc}& & \end{array}{\theta }^{\ast }=\theta \alpha =\frac{K{b}_t^{}}{{\left(K+c\right)}^2},\end{array}$$ (B8)

and it follows that

$$\begin{array}{l}\frac{\partial c}{\partial t}=\frac{1}{1+{\theta }^{\ast }}\nabla ·A\nabla c,\begin{array}{cc}& x\in {\Re }^3\end{array}\\ {\theta }^{\ast }=\frac{K{b}_t}{{\left(K+c\right)}^2}.\end{array}$$ (B9)