Abstract
Neuronal growth is an extremely complex yet reliable process that is directed by a dynamic lamellipodial structure at the tip of every growing neurite, called the growth cone. Lamellipodial edge fluctuations are controlled by the interplay between actin polymerization pushing the edge forward and molecular motor driven retrograde actin flow retracting the actin network. The leading edge switches randomly between extension and retraction processes. We identify switching of “on/off” states in actin polymerization as the main determinant of lamellipodial advancement. Our analysis of motility statistics allows for a prediction of growth direction. This was used in simulations explaining the amazing signal detection capabilities of neuronal growth by the experimentally found biased stochastic processes. Our measurements show that the intensity of stochastic fluctuations depend on changes in the underlying active intracellular processes and we find a power law η = a∗xα with exponent α = 2.63 ± 0.12 between noise intensity η and growth cone activity x, defined as the sum of protrusion and retraction velocity. Differences in the lamellipodial dynamics between primary neurons and a neuronal cell line further suggests that active processes tune the observed stochastic fluctuations. This hints at a possible role of noise intensity in determining signal detection sensitivity.
Introduction
Neuronal growth is a fundamental process for the correct development of the central nervous system as well as for neuronal plasticity and nerve regeneration. During growth, neuronal cells form long extensions, called neurites, which are guided toward their target sites by a motile structure at their tip, the growth cone (Fig. 1, A and F). Morphological changes driving this growth process are controlled by cytoskeletal activity within the lamellipodium, a flat actin rich structure at the periphery of the growth cone (1). Neuronal growth has been studied extensively from a molecular biology perspective revealing many details about signaling pathways (2), whereas cell biology has identified the detailed structure of neuronal growth cones (3). Actin turnover plays a crucial role for neuronal growth dynamics. It was shown that actin is polymerized into a dense network at the leading edge of the lamellipodium that pushes the membrane forward resulting in lamellipodium protrusion (4). Simultaneously, polymerization is antagonized by the retrograde actin flow, a continuous centripetal movement of the actin network away from the leading edge (3,5). During this retrograde transport, the actin gradually depolymerizes, freeing new monomers to repolymerize. In contrast to the dense and flat actin network in the lamellipodium, growth cones also show filopodia that consist of actin bundles extending finger-like from the lamellipodium. The actin transport and polymerization processes that determine the growth dynamics in filopodia were studied in detail previously (5), showing that the polymerization velocity at the filopodial tip is controlled independently from the retrograde flow. More recent work suggests a similar mechanism for growth cone lamellipodia, where leading edge actin polymerization is regulated independently from the myosin motor driven retrograde flow, and dominates the dynamics of lamellipodial extensions (6).
Figure 1.
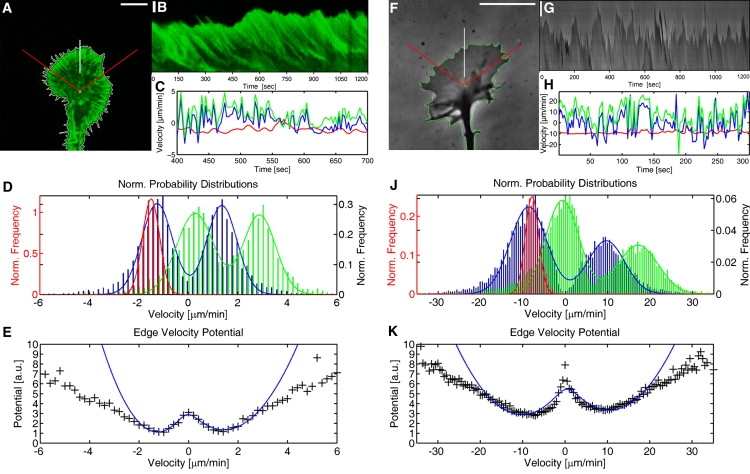
Edge dynamics of NG108-15 and primary embryonic rat growth cones recorded for 20 min in 3- and 2-s time steps, respectively. (A) Fluorescence image of GFP-actin labeled growth cone at start of time series, and (F) phase contrast image of primary growth cone. Data presented are related to the front sector of the growth cone. Vertical lines indicate regions cropped for the kymograph in (B and G). Scale bar = 10 μm. (B and G) Kymographs display the leading edge's time evolution. Scale bar = 2 μm. (C and H) Temporal development of edge velocity (blue), polymerization (green), and retrograde flow (red) along the direction shown in the kymographs. (D and J) Normalized mean velocity distributions of edge retraction and extension phases (blue), of polymerization (green), and of retrograde flow (red). The histograms are fitted with a double Gaussian for the edge velocity and the fit values are listed in Table 1. (E and K) Underlying potentials of the probability landscape for the mean edge velocity during extension and retraction phases, data (black) and fit (blue).
Nevertheless, how the interplay between leading edge actin polymerization and retrograde actin flow can lead to controlled growth cone turning is still not resolved fully. We have shown previously (7,8) that lamellipodial edge dynamics can be quantitatively described by a random walk of forward and backward steps where the stochastic weight determines whether the growth cone advances or retracts. The central role of stochastic processes in growth cone motility is intriguingly counterintuitive considering the importance of correct neuronal path finding. Furthermore, a recent theoretical investigation by deGennes suggests that random processes might be important for the collective behavior of many growth cones influencing each other (9).
Material and Methods
Cell culture and image acquisition
Experiments were conducted with primary embryonic rat neurons, prepared as described previously (12,13) and with NG108-15 cells, transfected with a pEGFP-actin vector (Clontech, Mountain View, CA) to fluorescently label the actin cytoskeleton. The transfection of the NG108-15 cells was carried out using Nanofectin (PAA, Pasching, Austria) according to the product manual. Cells were cultured in Dulbecco's modified Eagle's medium (PAA) supplemented with 10% fetal bovine serum (PAA), 100 U/mL penicillin/streptomycin (Sigma, St. Louis, MO) and 10 mM HEPES (Sigma), and plated on laminin coated glass coverslips 24–48 h before observation. During the observation period, cell viability was ensured by controlling pH and temperature stability in a custom cell chamber. Fluorescence image time series for 5 to 20 min time periods with 3 to 6 s/frame time resolution were recorded using an oil immersion objective (63× 1.4 NA; Leica Microsystems, Bensheim, Germany) on a confocal laser scanning microscope (TCS SP2 AOBS; Leica Microsystems) with a resolution of 1024 × 1024 pixels and 4× line average in bidirectional mode. Considering the Nyquist sampling theorem, we sample two to three times faster than the observed protrusion and retraction phases that have a characteristic timescale in the order of 10 s (7).
Primary neuronal cultures were prepared from embryonic Wistar rat brain at the developmental stage of 16–18 days according to standard protocols (12). In brief, the telencephalic cortical hemispheres were dissected from embryonic brain. Cell dissociation was achieved by mild trypsination for 5 min at 37°C (0.12% trypsin/EDTA solution, 1:250; Gibco, Eggenstein, Germany with DNase, 10 μg/mL) and stopped with fetal calf serum. Pieces of tissue were triturated through a small pipette and filtration through a sterile cell strainer (40 μm Nylon; Falcon, BD, Franklin Lakes, NJ). The resulting cell suspension was centrifuged for 5 min at 200 × g and the cell pellet was resuspended in Neurobasal medium (Gibco) supplemented with 2% B27 (Gibco), 500 μM L-glutamine, 50 μg/mL gentamycin, and 2% fetal calf serum (Biochrom AG, Berlin, Germany). Cells were seeded in laminin-coated tissue culture dishes. After 1 day in culture the medium was exchanged with the above specified medium but without fetal bovine serum. Phase contrast time series of 10–20 min with a time resolution of 1–2 s and a spatial resolution of 1344 × 1024 pixels have been recorded with a Hamamatsu ORCA-285 IEEE 1394 -Based Digital Camera in 12-bit using an oil immersion objective (100× 1.35 NA OIL PH3, Leica Microsystems) in combination with a 2× C-mount on a standard inverted microscope (DMIRB, Leica).
Data analysis
For analysis, images are turned to always have the same upward directionality of the growth cone in the subsequent analysis. A threshold algorithm with repeated dilation and erosion is used to extract a first binary shape of the growth cone. The pixel-based center of mass (COM) with each pixel having the same mass density is calculated from this binary shape and the average COM of successive images is defined as COM for the image pair being analyzed. Relative to this COM the edge points in 500 angular directions are obtained with subpixel resolution in the following way (Fig. 2): the image is smoothed with a 7 × 7 Gaussian kernel and the derivative of the intensity values along the line from the COM to the edge in each direction of the smoothed intensity profile is fitted with a Gaussian and the maximum of this fit function is defined as edge point (7). The change in the edge point position along each direction in successive images gives the lamellipodium extension and retraction.
Figure 2.
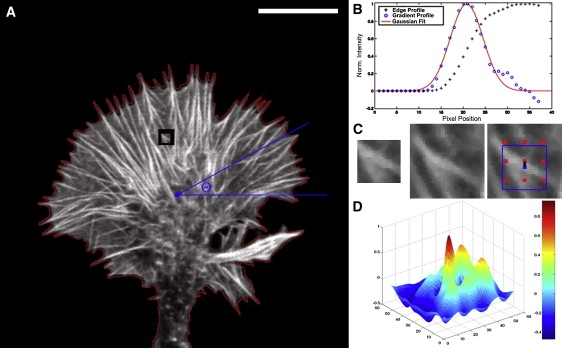
Edge detection and retrograde flow extraction from successive images. (A) Fluorescence image of growth cone showing the second frame, the detected edge, the mesh grid, the center of mass, the angular direction Θ, and the displacement in a search area at an example grid point. Scale bar = 10 μm. (B) Intensity profile along line from outside the edge to the COM. The intensity values rise at the edge. The derivative of the profile is fitted with a Gaussian and the fit maximum is set as edge position giving subpixel resolution. (C) Left: Mask area cropped from first frame (not shown). Mask size = 1 μm. Middle: Search area cropped from second frame (A). Right: Overlay of search area and mask showing the detected new mask position and the grid. (D) Surface plot of the cross-correlation value. The peak value gives the center position of the displaced mask.
A mesh grid with a distance of 0.5 μm between grid points is defined on the growth cone image within the detected shape. At each grid point a template pixel area (MASK) of size 1.0 μm is cropped. For grid points at which all pixels of MASK are within the shape, the MASK is overlaid onto each pixel of a larger search area (SEARCH) at the same grid point in the successive image and the cross-correlation value for each SEARCH pixel is calculated. The size of SEARCH is set to the sum of the mask size and the pixel distance corresponding to a maximum retrograde flow speed of 10 μm/min. This calculation finds the pixel area within SEARCH that is most identical to the MASK and the position of the maximum cross-correlation value defines the displacement vector at this grid point. In this way the movement of a specific structure in the time from image 1 to image 2 within SEARCH is identified at each grid point and results in a discrete displacement vector field. A three-dimensional convolution kernel on the filtered discrete displacement field is used for interpolation to obtain the final retrograde flow field. This three-dimensional convolution kernel is a normalized Gaussian ranging ±2 frames in time and with a radius of 5 μm in space decreasing to 1/e in intensity at 1.0 μm. The convolution is only done for cross-correlation values exceeding a threshold value of 0.6 and the kernel values are linearly weighted with the respective retrograde flow value and cross-correlation value at each point. In this way only the most reliable values enter the convolution and the best detected ones have the highest significance for the calculation.
The polymerization rate in each direction is calculated from the respective retrograde flow value at the edge and the lamellipodium extension/retraction value using Eq. 1.
| (1) |
where vEgde is the edge extension/retraction rate along the direction of the COM to the edge, vRetrograde Flow,‖ is the retrograde flow rate component parallel to this direction and vPolymerization is the resulting polymerization rate along the same line.
Histograms of Fig. 1, D and J, are obtained by separating the data into growth and retraction phases of the edge in the forward direction (Θ = 36–144°) and calculating the mean value of the edge velocity, the polymerization and the retrograde flow for each phase respectively. This procedure ensured that the detection noise did not obscure the phase behavior.
Simulation of a neuronal growth cone
The simulation consists of a Monte-Carlo simulation, in which the movement of the edge is modeled by numerical simulation of the Langevin equation presented previously:
| (2) |
which was numerically solved using the Euler method. In Eq. 2 v is the edge velocity, V(v) is the velocity dependent potential, η is the noise intensity, and ζ(t) represents Gaussian white noise.
The iterative method starts with a set value v0 and calculates the following value by interpolating the integration of Δt with a constant value of the right side of Eq. 2:
| (3) |
Thus, the (i +1)th step is:
| (4) |
In the simulation, this scheme is used at 50 edge positions that are angularly equally spaced, and the actual state of the edge point n at the time i is denoted by . Because the analytical expression of the real bistable potential is unknown, the potential was approximated by
| (5) |
The influence of external signals is introduces by tilting this potential to favor growth in the direction of increasing external signal strength. This is implemented in the simulation by adding a linear term to the potential. In a real growth cone it is known that the growth direction is influenced by chemical gradients. To account for this it was assumed that the potential tilt at any edge position depends on the difference between an external signal and the mean of this external signal over the whole growth cone. In a mathematical way, this can be expressed by adding the linear term to the potential in Eq. 5, where denotes the external gradient at the time i and at the edge position n. Thus, we get the final potential for the simulation
| (6) |
with the negative derivative
| (7) |
The simulation starts with an initial edge velocity for all edge positions and a starting COM-edge distance . Then the program first calculates the subsequent edge velocities according to Eq. 4. Subsequently the new edge velocity is used to get the updated COM-edge distance . So far, no line tension and area conservation have been included in the simulation. Both constraints are reasonable, because the cell membrane smooth the edge contour and the volume of a growth cone should be conserved due to material conservation. To include these constraints, we first smoothed the simulated edge velocity by a moving average of width ɛ = 4, and calculate the next updated COM-edge () distance by:
| (8) |
where the second term ensures a smooth contour, whereas the nonlinear last term allows small changes in overall growth cone volume, but prevents large fluctuations (the parameter κ allows to adjust the influence of the volume conservation, and R is the desired radius that should be conserved).
Due to the last term in Eq. 8, the simulated growth cone tends to keep a COM-edge distance in the order of R. This means, that the COM that is used to define all , needs to be repositioned to allow the simulated growth cone to move. Hence, the new COM is calculated using the new and the growth cone is moved to be centered on the newly calculated COM. To not modify the spatial position of the edge, the change of the COM is compensated by changing the accordingly. In the final step, this new COM-edge distance is used to draw the new contour, and the whole scheme is repeated as illustrated in Fig. 3. For the analysis of optimal noise, we applied the described experimental data analysis method on the simulated data and recovered the potential used in the simulation. This leads to the noise value that was used in the representation of noise over signal detection capabilities as shown in Fig. 4 D.
Figure 3.
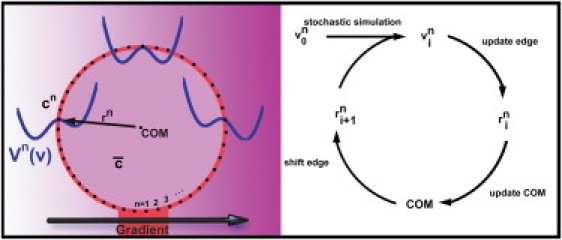
Illustration of the in silico growth cone properties that are used in the simulation. The edge is defined by a set of edge points n that are equally spaced. At each edge point a potential Vn(ν) is defined and the tilting of this potential depends on the difference between the external signal strength cn and the average signal strength over the growth cone . During the simulation the actual edge velocity is calculated using the potential, and an updated COM-edge distance for the next step is calculated. To ensure that the COM is always in the center, the COM is first updated, and then the resulting COM-edge distances are calculated. Finally the new shape is drawn and the same scheme is repeated.
Figure 4.
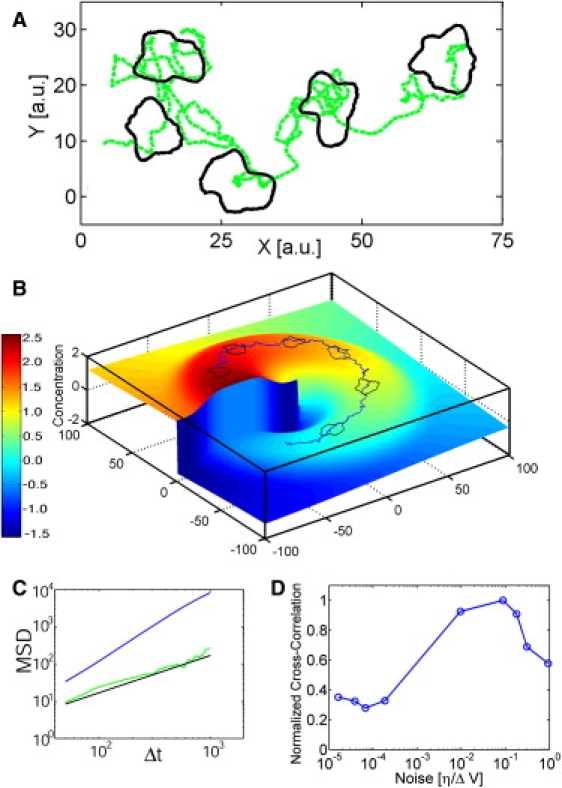
Motion of in silico growth cones. (A) Simulated movement of a growth cone without external field (i.e., chemical gradient) (Movie S4). The green line represents the center of mass movement, whereas the black shapes represent the growth cone at different times. (B) Movement of a simulated growth cone in a field caused by a gradient of an external growth signal (Movie S5). The height and the color coding represent the signal intensity and the blue line is the path of the growth cone. (C) The scaling of the mean-square displacement with time is a measure for random nature of the movement. The green line represents the simulated data of A that fits to an exponent β = 1 in the fit function msd(Δt) = 4DΔtβ. This scaling is characteristic for a random walker. The blue line represents the scaling for the motion of the growth cone in B that is superdiffusive (β > 1), i.e., it is directed. (D) Correlation between the path of the growth cone and the optimal signal path for various noise values. The peak at ηopt = 0.09∗ΔV shows that the growth cone has its optimum signal detection capabilities at a weak noise intensity compared to the potential barrier, well in agreement with Kramers approximation on which the data analysis is based.
Results and Discussion
We sought to better understand growth cone motility by measuring the dynamics of the actin cytoskeleton in the lamellipodium. We used eGFP-actin (10) transfected neuronal cells (NG108-15 (11)) to fluorescently visualize the actin-based internal growth cone dynamics (Fig. 1 A). Because neuronal cell lines often differ in their behavior from primary neurons, yet primary cells cannot be stably transfected with eGFP-actin, phase contrast recordings of primary embryonic rat cortical neurons were used to validate the physiological relevance of our results (Fig. 1 F) (12). Time series of primary cells were recorded with a time resolution of 1–2 s using phase contrast microscopy (DMIRB, Leica) and fluorescent time series of eGFP-actin transfected NG108-15 cells were acquired with a time resolution of 3–6 s using a confocal laser scanning microscope (TCS SP2 AOBS, Leica Microsystems) (Supporting Material, Movie S1 and Movie S2). Leading edge velocity, actin polymerization at the leading edge, and inward actin flow, i.e., retrograde flow, were analyzed with high resolution edge detection algorithms (7) together with fluorescence and phase contrast pseudo speckle microscopy (14).
As illustrated in the kymographs in Fig. 1, B and G, our measurements indicate that the edge of the lamellipodium fluctuates between protrusion and retraction phases whereas the retrograde flow remains almost stationary (Fig. 1, C and H). To further quantify these dynamics, we separated the data into growth and retraction phases along 500 equally spaced angular directions with respect to the pixel based center of mass (COM). Subsequently, we determined the probability distribution of the respective mean rates of edge velocity, polymerization and retrograde flow as shown in Fig. 1, D and J. Like the edge velocity, the polymerization switches between two prominent states as indicated by the double peak distributions. In contrast, the retrograde flow is peaked around a single average value. The main difference between the embryonic rat cortical neurons and the NG108 line is the pace. The measured velocities for edge fluctuations, actin polymerization and retrograde flow are ∼3–4 times faster in primary cells (Table 1). The widths of the fitted Gaussian distribution for the primary cells are also 3–4 times larger than that of the cell line. Nevertheless, besides the increased velocities, the observed behavior is similar in cell lines and primary cells, as can be seen in Fig. 1, D and J. These collective properties demonstrate that our statistical analysis on NG108 cell lines is also relevant for the description of growth cones from primary cells and suggest that the underlying processes controlling the edge dynamics are similar in both cell types.
Table 1.
Lamellipodium dynamics for NG108-15 and primary rat neuronal cells
| Cell type | n | cedge,pol | cedge, retro | cretro,pol | vedge,retr [μm/min] | vedge,prot [μm/min] | vpol,off [μm/min] | vpol,on [μm/min] | vretro [μm/min] |
|---|---|---|---|---|---|---|---|---|---|
| NG108-15 | 44 | 0.91 ± 0.02 | −0.05 ± 0.05 | −0.11 ± 0.07 | −1.55 ± 0.61 | 2.04 ± 0.68 | −0.14 ± 0.38 | 3.38 ± 1.00 | −1.46 ± 0.54 |
| Primary rat | 26 | 0.92 ± 0.02 | −0.08 ± 0.05 | −0.03 ± 0.05 | −8.83 ± 1.55 | 10.68 ± 2.48 | −2.38 ± 1.47 | 16.66 ± 2.43 | −6.43 ± 0.80 |
| Fig. 1, NG108 | 1 | 0.91 ± 0.04 | −0.06 ± 0.04 | −0.14 ± 0.04 | −1.26 ± 0.04 | 1.36 ± 0.04 | 0.21 ± 0.06 | 2.75 ± 0.05 | −1.42 ± 0.01 |
| Fig. 1, primary rat | 1 | 0.91 ± 0.03 | −0.06 ± 0.04 | −0.04 ± 0.04 | −8.68 ± 0.20 | 9.62 ± 0.32 | −0.75 ± 0.17 | 17.13 ± 0.35 | −7.87 ± 0.04 |
Values are given as mean ± SD except for the velocity values of the individual growth cones from Fig. 1 where the errors represent the 95% confidence interval of the Gaussian fits. cedge,pol denotes correlation values between edge velocity and polymerization, cedge,retro between edge velocity and retrograde flow, and cretro,pol between polymerization and retrograde flow. vedge,retr is the most probable velocity of edge retraction phases, vedge,prot of edge protrusion phases, vpol,off of polymerization “off” state, vpol,on of polymerization “on” states, and vretro of the retrograde flow.
In contrast to previous studies of the random movement of neurons and cells that focused on the overall path of growth cones (15,16), we analyze the local intracellular movement in the entire growth cone's leading edge. First, we are interested in the edge velocity. The fluctuating movement of the leading edge switching between advancement and retraction can be quantitatively explained as a stochastic process in a velocity dependent potential V(v) that is perturbed by a stochastic noise with intensity η (7). Using this description, the potential V(v) (Fig. 1, E and K) can be related to the mean edge velocity histograms by p(ν) = const×exp(−V(ν)/η), where p(v) is the probability distribution of the mean velocities as measured in the histogram (Fig. 1, D and J), V(v)/η is the potential scaled by the stochastic noise η and const is a normalization constant. The resulting bistable potential is obtained using V(ν)/η = const − ln(p(ν)). Kramers theory (17) applied to V(v)/η is used to calculate a Kramers rate for the random hopping process between protrusion and retraction (7). Strictly speaking, Kramers theory is only valid if the potential barrier is large compared to the noise. As shown in our previous work (7), this is only partially valid in the experimental analysis, where the potential barrier is about twice the noise intensity. However, in this analysis we ignore the error that we make, as it is expected to account for only ∼30% (18) of the measured ratio between noise and potential barrier. The error is systematic, and not of importance in the current analysis as we are focusing not on absolute values but rather a qualitative, relative comparison. The derived Kramers rates allow us to quantify the edge fluctuation's noise intensity and the absolute potential V(v) (8). Hence, the local movement of the growth cone edge can be understood as a stochastic process that evolves in this potential that follows the Langevin equation (8,19): . This is a stochastic equation of motion including Gaussian white noise, represented by the function ζ(t). Final edge movement is determined by the interplay between the bistable potential and the stochastic noise. Consequently, the growth cone edge acts as a random walker and the shape and depth of the two minima of the potential V(v) determine the probabilities for the edge's advancement or retraction. Thus, the edge fluctuations reflect which direction a growth cone will take.
It should be noted that this model does not account for lateral waves that have been reported previously in different cell types (20,21). In our measurements, we see lateral movements of filopodia, which are detected as extreme values in edge velocity. Such lateral movements originate from filopodia alignment that is not radial, but diagonal to the edge. Lateral filopodia movement is well known (22), and does not represent real lamellipodia growth. Hence, such movements are not lateral polymerization waves but filopodia moving through the line profile that is used for edge detection. They show up in the edge velocity analysis as a brief moment of high positive edge velocity immediately followed by a negative phase. This can be seen in Fig. S1, which gives the spatial-temporal map of the measured edge velocities of the growth cone shown in Fig. 1 A. In this study we exclude filopodia and focus on a description of the lamellipodium dynamics.
Characteristics of growth cone turns
The experimental relevance of the extracted potential can be directly validated in a turning growth cone. For this purpose we measured how the potential differs in the direction of advancement with respect to the opposite direction. Fig. 5 shows a time series of a NG108 growth cone turning to the right (Movie S3). The fitted potentials are presented for both the turning and the opposite direction. As presented in Fig. 5, the potential in the direction of the turn favors edge protrusion as compared to the potential in the opposing direction. During the three time intervals presented in Fig. 5 we find that the potential in the direction of growth is tilted to favor protrusion over retraction in the growth direction with respect to the opposite direction. The tilting can result in different characteristic potential shapes as represented in Fig. 5. We find pure tilt of the potential (Fig. 5 A), a tilt with a widening of the potential for the protrusion processes (Fig. 5 B) and a tilt with a deeper potential well for the protrusion (Fig. 5 C). Whether the integrated area of the extension part or the retraction part of the bistable potential is larger determines if the growth cone advances or retracts in the respective direction. This is reflected in the mean velocity that corresponds to given potential as presented in Fig. 5. The mean velocity is always larger in the direction of extension than in the stationary direction. Hence, the turning of a growth cone is the outcome of changes in the stochastic processes that control its edge dynamics, substantiating our description of growth cone motility by a Langevin equation. Table S1 shows that in extending growth cones, the overall dynamics in the direction of the extension is systematically higher as compared to the full growth cone. Additionally, the respective values for stationary growth cones are provided.
Figure 5.
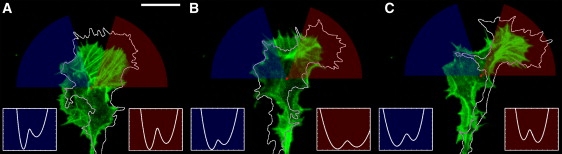
Growth cone time evolution while turning to the right and corresponding potential landscapes in the direction of extension and in the opposite direction, shown in time intervals of 300 s. (A–C) Images of a GFP-actin labeled growth cone shown at the beginning (0, 300, 600 s) and the corresponding growth cone perimeter outlines (white line) at the end (300, 600, 900 s) of time intervals. Colored cones illustrate direction of extension (red) and the opposite direction (blue), and matching colored insets show the respective potentials. The potential's shape determined the direction of protrusion. This is reflected by the mean velocity in each direction, which is negative/positive for the direction of retraction/extension, respectively (A: blue, −0.89 μm/min; red, 0.25 μm/min; B: blue, −0.98 μm/min; red, 0.49 μm/min; C: blue, −1.62 μm/min; red, 0.80 μm/min). Scale bar = 10 μm.
Stochasticity increases the reliability of neuronal path finding
The characteristic tilting of the potential opens the possibility of enhancing the growth cone's sensitivity to chemotaxis. Thus, it could possibly explain the neuronal growth cone's amazing signal detection capabilities that was shown to permit a sensitivity close to the single molecule level even in noisy environments (23). Nonlinear potentials modulated by external signals can significantly enhance signal detection in stochastic processes (24). For this recently discovered possibility the term stochastic resonance has been coined. In stochastic resonance the signals vary temporally, whereas for a growth cone, guidance cue signals change spatially. Because we find that a tilting of the potential correlates with growth direction (Fig. 5) we consider that an external signal (e.g., guidance cue) can tilt the potential by modifying the stochastic fluctuations. To generate an in silico growth cone in a Monte Carlo simulation (Fig. 4) we used the derived Langevin equation, which explains our experimental observations. At each edge point of the simulated growth cone we defined a bistable potential analog to the measured potentials (Fig. 1). This potential was tilted to the same degree as we found in turning growth cones on the side where the leading edge of the growth cone experienced an external signal intensity. Surface tension and conservation of area were included to achieve a smooth growth cone contour. Because we exclusively focus on the dynamics of the lamellipodium, filopodia are excluded from the simulation.
Based on our experimental measurements, it was possible to simulate growth cones that show the same statistical characteristics as real growth cones. The simulation results in a random walk of the growth cone in the absence of an external guidance cue (Fig. 4 A, Movie S4). However, if an external signal tilts the potential as experimentally observed (Fig. 5), the simulated growth cone follows this signal while the edge still fluctuates (Fig. 4 B, Movie S5). The random nature of the growth cone motility is reflected in the mean-squared displacement of the growth cone's path (Fig. 4 C), defined by the relation msd(Δt) = 4DΔtβ. Without external signal, the in silico growth cone exhibits normal diffusion (exponent β = 1), whereas an external signal shifts the characteristics to superdiffusive behavior (β > 1). Moreover, the simulation shows that the stochastic detection of an external signal depends dramatically on the actively acting noise. Signal detection was quantified by calculating the correlation value between the simulated and the optimal growth path. The noise intensity was measured by analyzing the simulated growth cone contours using the same method that was applied to the experimental growth cones. This allowed the extraction of the same characteristic noise as measured previously. As shown in Fig. 4 D, optimal signal detection occurs not at minimal noise, but at a noise intensity of about ηopt = 0.09×ΔV, where ΔV is the potential barrier between the bistable states. At such small noise intensities, Kramers approximation of weak noise is valid. If the system is exposed to nonoptimal noise, the simulated growth cone still detects the initial external signal, but is not able to adapt to changes of the external signal. If the added noise intensity is too high, the growth cone effectively remains stationary. The simulations show that stochastic signal amplification by noise tuning (24,25) is feasible for migrating growth cones in spatial gradient of external stimuli. However, it remains to be shown by independent experiments that the noise intensity is indeed controlled by the cell as a response to an extracellular signal. Nonetheless, the simulation shows that the proposed stochastic model would allow for optimal signal detection at an optimal noise level.
The possibility that certain noise intensity is increasing signal detection in stochastic processes poses the questions of whether and how growth cones regulate their internal noise intensity. Nontunable thermal noise is inherent due to the small size of the growth cone and the general weak binding constants in biochemistry. Furthermore, ATP consuming processes like motor activity and actin polymerization result in an activity-dependent (i.e., tunable) increase of stochastic fluctuations called active noise (26–28). Thus, we suspect that noise intensity depends on the growth cone's overall activity. To consider both activities, actin polymerization and retrograde flow, we define as a measure of activity the distance between peaks in the edge velocity distribution as the maximal change in velocity (Fig. 1, D and J, blue) (8). This definition was chosen because it incorporates the two ATP consuming processes of polymerization and myosin motor activity in a single quantitative parameter. Plotting the measured noise intensity over the so defined activity, shows a surprising scaling behavior with a scaling coefficient of α = 2.63 ± 0.12. In previous work, we reported the dependence of noise on the activity for NG108 cells (8). However, investigation of the lamellipodium dynamics in primary embryonic rat cortical neurons showed dramatically higher activity values for the latter. Combining the data of NG108 and primary cells shows the scaling behavior of the noise intensity on the activity across different cell types and allows for a much more reliable determination of the power law. Hence, we now clearly find a nonlinear dependence between noise intensity and the growth cones' activity, as show in Fig. 6 for 44 NG108-15 and 26 primary growth cones, all combined in one graph. This is a remarkable result, because it gives a direct quantitative description of the active noise in a biological system and simultaneously describes the data of two different neuronal cell types. According to this data growth cones can control noise intensity by modulating their activity. Thus, we conclude that growth cones can indeed control their stochastic noise, which might be used for optimal signal detection. Such a mechanism would include an increase of actin polymerization alone or in combination with an increase in retrograde flow in response to small guidance signals. Unfortunately, the current state of knowledge on the signal detection remains limited.
Figure 6.
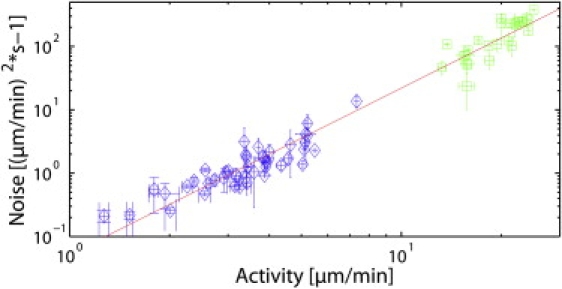
Log-log plot of the noise intensity over activity as measured in 44 NG108-15 (diamond) and 26 primary rat (square) growth cones. The straight line represents a fitted power-function a∗xα with a = 0.05 ± 0.01 and an exponent α = 2.63 ± 0.12, that represents all measurements of the two cell types by a single power law. This shows how growth cones of different cell types can tune their internal noise to optimize signal detection. By changing their retrograde flow and the actin polymerization velocity, cells can vary their internal noise following the reported power-law, which provides a physical mechanics for intracellular noise tuning.
Changes in actin polymerization control leading edge motion
The movement of the lamellipodium results from the additive interplay of retrograde flow that retracts the network and leading edge actin polymerization, which pushes against the membrane (29). To understand the role of these processes for stochastic switching between leading edge protrusion and retraction, we measured the correlation between time-series of leading edge velocity, polymerization, and retrograde flow. For the 44 NG108 (and 26 primary) growth cones investigated, we find a high mean correlation between the actin polymerization and the edge velocity cpol,edge = 0.91 ± 0.02 (0.92 ± 0.02), whereas correlations between the retrograde flow and the edge velocity cretro,edge = −0.05 ± 0.05 (−0.08 ± 0.05) or between retrograde flow and the polymerization cretro,pol = −0.11 ± 0.07 (−0.03 ± 0.05) are very minor (Table 1). The high correlation between actin polymerization and edge movement means that the dynamics of the edge is controlled by actin polymerization and not by retrograde actin flow. This is further supported by the histograms of retrograde flow and actin polymerization velocities (Fig. 1, D and J). The probability distribution of actin polymerization velocity shows a double peak distribution similar to edge velocity but shifted to higher values. In the investigated cases of a NG108 and a primary growth cone, the left peak is centered at a polymerization speed of 0.21 ± 0.06 μm/min and −1.75 ± 0.19 μm/min, respectively. The right peak is found at 2.75 ± 0.05 μm/min and 16.5 ± 0.79 μm/min, respectively. However, the retrograde flow only shows a single Gaussian peak at −1.41 ± 0.01 μm/min and −7.39 ± 0.04 μm/min, respectively. As mentioned previously, besides the three to four times faster dynamics of primary growth cones, both cell types show similar characteristics in the statistical analysis. The polymerization is mostly independent from retrograde flow, because polymerization and retrograde flow do not correlate (see above). Furthermore, the lack of correlation between retrograde flow and actin polymerization agrees with recent results stating that in growth cones, retrograde flow is not principally driven by polymerization but by myosin motors (6).
The independence of actin polymerization and retrograde flow in filopodia was shown previously (5). Our investigation finds similar results for the polymerization dynamics within the lamellipodium, where actin polymerization switches between “on” and “off” states. The polymerization distribution peaks for its on state at high velocities, whereas the peak for its off state is naturally found around zero because in the off state solely minimal polymerization occurs (Table 1). The peak for leading edge extension is the sum of the peak for the polymerization on state and the peak for the counteracting retrograde flow. The retraction peak coincides with the retrograde flow peak indicating that actin polymerization is switched off during retraction and the actin network is pulled back by molecular motors. Thus, for a growth cone the observed stochastic edge fluctuations are the superposition of a steady retrograde flow and an actin polymerization switching between on and off states.
To investigate this polymerization-related instability, we manipulated actin polymerization in a controlled experiment by applying substochiometric amounts of cytochalasin D (CD). CD is a strong actin filament capper that binds the polymerizing F-actin barbed ends with high affinity, preventing further addition of actin monomers (30,31). CD was applied at miniscule concentrations of 5–20 nM, and the concentration dependent response of the growth cones was measured. We quantified the effect of CD by measuring the change in growth cone area 10 min after application. It was expected that CD blocks actin polymerization, thus leading to a retraction of the lamellipodium. This was observed at concentrations above 12 ± 1 nM CD (Fig. 7, Movie S6). The concentration dependent effect as presented in Fig. 7 shows that CD concentrations below a threshold did not influence the area of the growth cone, whereas a sharp transition was observed at the threshold concentration. This effect is unusual as compared to the concentration dependent response of other cell types to CD (32). In all observed growth cones, the transition to growth cone collapse happened sharply at the same critical concentration. Whether the observed sharp transition is due to collective biochemical effects or a sign of a stochastic instability of actin polymerization remains to be investigated. A stochastic instability would be consistent with the found on/off states of the polymerization. In this context, the miniscule concentrations of CD might affect the mechanism responsible for stochastic switching, driving it to the point where the polymerization becomes unfavorable, thus resulting in a sharp transition. However, a cooperative biochemical effect could also explain the observed transition, and further investigation will help in understanding the nonlinear response of growth cone area to CD concentration.
Figure 7.
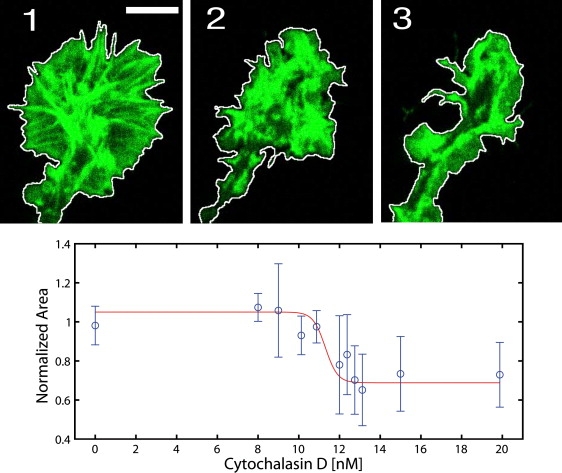
Effect of CD (that inhibits the actin polymerization by capping the polymerizing actin filament ends) on the lamellipodium of a growth cone. The time series visualize the collapse of a growth cone at (1) 0 min, (2) 5 min, and (3) 10 min after application of 20 nM CD. The line marks the detected outline of the growth cone. The growth cone area decreases to 62%, which is calculated by dividing the collapsed growth cone area (3) by the initial, untreated growth cone area (1). Moreover, the change in growth cone area was measured in dependence of the applied concentration of CD. As shown in the plot, the normalized area decreases sharply at a CD concentration of 12 ± 1 nM to a final area of ∼70%. Thus, there is a critical CD concentration that induces growth cone collapse.
Conclusion
Growth cone extension and retraction is determined by whether the rate of actin polymerization or retrograde flow is higher. On the timescales investigated, we find that leading edge motion does not depend on changes in the retrograde flow velocity. Instead, forward and backward motions are controlled by the activity of actin polymerization switching randomly between on and off states. Inherently, small systems like neuronal growth cones are subject to strong thermal and chemical fluctuations. To reliably operate, these systems have to tolerate this intrinsic noise. The stochastic nature of growth cone dynamics provides significant advantages for the growth cone because it is robust against errors in the growth cone's intracellular molecular processes, allowing for immediate error corrections through its fluctuations. Moreover, the noise might be exploited to provide an increased sensitivity to signals through noise tuning (33), which could explain the incredible chemosensitivity (23) of neuronal growth.
Supporting Material
Six movies, a figure, and a table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00796-6.
Supporting Material
Acknowledgments
We thank U. Behn for helpful discussion and J. Gerdelmann for his help concerning primary cultures and amplification of the vectors.
This work was supported by the Deutsche Forschungsgemeinschaft-Graduiertenkolleg Interneuro, Specific Targeted Research Project of the European Union, called Active Biomics, and Marianne Duda.
Footnotes
Timo Betz and Daniel Koch contributed equally to the work.
References
- 1.Chilton J.K. Molecular mechanisms of axon guidance. Dev. Biol. 2006;292:13–24. doi: 10.1016/j.ydbio.2005.12.048. [DOI] [PubMed] [Google Scholar]
- 2.Song H., Poo M. The cell biology of neuronal navigation. Nat. Cell Biol. 2001;3:E81–E88. doi: 10.1038/35060164. [DOI] [PubMed] [Google Scholar]
- 3.Lin C.H., Forscher P. Growth cone advance is inversely proportional to retrograde F-actin flow. Neuron. 1995;14:763–771. doi: 10.1016/0896-6273(95)90220-1. [DOI] [PubMed] [Google Scholar]
- 4.Dent E.W., Gertler F.B. Cytoskeletal dynamics and transport in growth cone motility and axon guidance. Neuron. 2003;40:209–227. doi: 10.1016/s0896-6273(03)00633-0. [DOI] [PubMed] [Google Scholar]
- 5.Mallavarapu A., Mitchison T. Regulated actin cytoskeleton assembly at filopodium tips controls their extension and retraction. J. Cell Biol. 1999;146:1097–1106. doi: 10.1083/jcb.146.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Medeiros N.A., Burnette D.T., Forscher P. Myosin II functions in actin-bundle turnover in neuronal growth cones. Nat. Cell Biol. 2006;8:215–226. doi: 10.1038/ncb1367. [DOI] [PubMed] [Google Scholar]
- 7.Betz T., Lim D., Kas J.A. Neuronal growth: a bistable stochastic process. Phys. Rev. Lett. 2006;96:098103. doi: 10.1103/PhysRevLett.96.098103. [DOI] [PubMed] [Google Scholar]
- 8.Betz T., Koch D., Stuhrmann B., Ehrlicher A., Kaes J. Statistical analysis of neuronal growth: edge dynamics and the effect of a focused laser on growth cone motility. N.J. Phys. 2007;9:426. [Google Scholar]
- 9.de Gennes P.G. Collective neuronal growth and self organization of axons. Proc. Natl. Acad. Sci. USA. 2007;104:4904–4906. doi: 10.1073/pnas.0609871104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ballestrem C., Wehrle-Haller B., Imhof B.A. Actin dynamics in living mammalian cells. J. Cell Sci. 1998;111:1649–1658. doi: 10.1242/jcs.111.12.1649. [DOI] [PubMed] [Google Scholar]
- 11.Hamprecht B., Glaser T., Reiser G., Bayer E., Propst F. Culture and characteristics of hormone-responsive neuroblastoma X glioma hybrid cells. Methods Enzymol. 1985;109:316–341. doi: 10.1016/0076-6879(85)09096-6. [DOI] [PubMed] [Google Scholar]
- 12.Hansson E., Ronnback L. Regulation of glutamate and GABA transport by adrenoceptors in primary astroglial cell cultures. Life Sci. 1989;44:27–34. doi: 10.1016/0024-3205(89)90214-2. [DOI] [PubMed] [Google Scholar]
- 13.Ueberham U., Ueberham E., Bruckner M.K., Seeger G., Gartner U. Inducible neuronal expression of transgenic TGF-beta1 in vivo: dissection of short-term and long-term effects. Eur. J. Neurosci. 2005;22:50–64. doi: 10.1111/j.1460-9568.2005.04189.x. [DOI] [PubMed] [Google Scholar]
- 14.Vallotton P., Danuser G., Bohnet S., Meister J.J., Verkhovsky A.B. Tracking retrograde flow in keratocytes: news from the front. Mol. Biol. Cell. 2005;16:1223–1231. doi: 10.1091/mbc.E04-07-0615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maskery S., Shinbrot T. Deterministic and stochastic elements of axonal guidance. Annu. Rev. Biomed. Eng. 2005;7:187–221. doi: 10.1146/annurev.bioeng.7.060804.100446. [DOI] [PubMed] [Google Scholar]
- 16.Schienbein M., Franke K., Gruler H. Random walk and directed movement: comparison between inert particles and self-organized molecular machines. Phys. Rev. E. 1994;49:5462–5471. doi: 10.1103/physreve.49.5462. [DOI] [PubMed] [Google Scholar]
- 17.Kramers H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 18.Drozdov A.N., Talkner P. Activated rate processes in a double well coupled to a slow harmonic mode: finite-barrier effects. Phys. Rev. E. 1996;54:6160–6173. doi: 10.1103/physreve.54.6160. [DOI] [PubMed] [Google Scholar]
- 19.Gardiner C.W. Springer; Berlin: 2004. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. [Google Scholar]
- 20.Dobereiner H.G., Dubin-Thaler B.J., Hofman J.M., Xenias H.S., Sims T.N. Lateral membrane waves constitute a universal dynamic pattern of motile cells. Phys. Rev. Lett. 2006;97:038102. doi: 10.1103/PhysRevLett.97.038102. [DOI] [PubMed] [Google Scholar]
- 21.Lacayo C.I., Pincus Z., VanDuijn M.M., Wilson C.A., Fletcher D.A. Emergence of large-scale cell morphology and movement from local actin filament growth dynamics. PLoS Biol. 2007;5:e233. doi: 10.1371/journal.pbio.0050233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Oldenbourg R., Katoh K., Danuser G. Mechanism of lateral movement of filopodia and radial actin bundles across neuronal growth cones. Biophys. J. 2000;78:1176–1182. doi: 10.1016/S0006-3495(00)76675-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rosoff W.J., Urbach J.S., Esrick M.A., McAllister R.G., Richards L.J. A new chemotaxis assay shows the extreme sensitivity of axons to molecular gradients. Nat. Neurosci. 2004;7:678–682. doi: 10.1038/nn1259. [DOI] [PubMed] [Google Scholar]
- 24.Gammaitoni L., Hänggi P., Jung P., Marchesoni F. Stochastic resonance. Rev. Mod. Phys. 1998;70:223–287. [Google Scholar]
- 25.Collins J.J., Chow C.C., Capela A.C., Imhoff T.T. Aperiodic stochastic resonance. Phys. Rev. E. 1996;54:5575–5584. doi: 10.1103/physreve.54.5575. [DOI] [PubMed] [Google Scholar]
- 26.Gov N. Membrane undulations driven by force fluctuations of active proteins. Phys. Rev. Lett. 2004;93:268104. doi: 10.1103/PhysRevLett.93.268104. [DOI] [PubMed] [Google Scholar]
- 27.Manneville J.B., Bassereau P., Ramaswamy S., Prost J. Active membrane fluctuations studied by micropipet aspiration. Phys. Rev. 2001;64:021908. doi: 10.1103/PhysRevE.64.021908. [DOI] [PubMed] [Google Scholar]
- 28.Nadrowski B., Martin P., Julicher F. Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc. Natl. Acad. Sci. USA. 2004;101:12195–12200. doi: 10.1073/pnas.0403020101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mogilner A., Oster G. Polymer motors: pushing out the front and pulling up the back. Curr. Biol. 2003;13:R721–R733. doi: 10.1016/j.cub.2003.08.050. [DOI] [PubMed] [Google Scholar]
- 30.Carlier M.F., Criquet P., Pantaloni D., Korn E.D. Interaction of cytochalasin D with actin filaments in the presence of ADP and ATP. J. Biol. Chem. 1986;261:2041–2050. [PubMed] [Google Scholar]
- 31.Pollard T.D., Blanchoin L., Mullins R.D. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu. Rev. Biophys. Biomol. Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- 32.Wakatsuki T., Schwab B., Thompson N.C., Elson E.L. Effects of cytochalasin D and latrunculin B on mechanical properties of cells. J. Cell Sci. 2001;114:1025–1036. doi: 10.1242/jcs.114.5.1025. [DOI] [PubMed] [Google Scholar]
- 33.Wiesenfeld K., Moss F. Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature. 1995;373:33–36. doi: 10.1038/373033a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


