Metabolic Inhibition Strongly Inhibits Na⁺-Dependent Mg²⁺ Efflux in Rat Ventricular Myocytes

Abstract

We measured intracellular Mg²⁺ concentration ([Mg²⁺]_i) in rat ventricular myocytes using the fluorescent indicator furaptra (25°C). In normally energized cells loaded with Mg²⁺, the introduction of extracellular Na⁺ induced a rapid decrease in [Mg²⁺]_i: the initial rate of decrease in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) is thought to represent the rate of Na⁺-dependent Mg²⁺ efflux (putative Na⁺/Mg²⁺ exchange). To determine whether Mg²⁺ efflux depends directly on energy derived from cellular metabolism, in addition to the transmembrane Na⁺ gradient, we estimated the initial Δ[Mg²⁺]_i/Δt after metabolic inhibition. In the absence of extracellular Na⁺ and Ca²⁺, treatment of the cells with 1 μM carbonyl cyanide p-(trifluoromethoxy)phenylhydrazone, an uncoupler of mitochondria, caused a large increase in [Mg²⁺]_i from ∼0.9 mM to ∼2.5 mM in a period of 5–8 min (probably because of breakdown of MgATP and release of Mg²⁺) and cell shortening to ∼50% of the initial length (probably because of formation of rigor cross-bridges). Similar increases in [Mg²⁺]_i and cell shortening were observed after application of 5 mM potassium cyanide (KCN) (an inhibitor of respiration) for ≥90 min. The initial Δ[Mg²⁺]_i/Δt was diminished, on average, by 90% in carbonyl cyanide p-(trifluoromethoxy)phenylhydrazone-treated cells and 92% in KCN-treated cells. When the cells were treated with 5 mM KCN for shorter times (59–85 min), a significant decrease in the initial Δ[Mg²⁺]_i/Δt (on average by 59%) was observed with only a slight shortening of the cell length. Intracellular Na⁺ concentration ([Na⁺]_i) estimated with a Na⁺ indicator sodium-binding benzofuran isophthalate was, on average, 5.0–10.5 mM during the time required for the initial Δ[Mg²⁺]_i/Δt measurements, which is well below the [Na⁺]_i level for half inhibition of the Mg²⁺ efflux (∼40 mM). Normalization of intracellular pH using 10 μM nigericin, a H⁺ ionophore, did not reverse the inhibition of the Mg²⁺ efflux. From these results, it seems likely that a decrease in ATP below the threshold of rigor cross-bridge formation (∼0.4 mM estimated indirectly in the this study), rather than elevation of [Na⁺]_i or intracellular acidosis, inhibits the Mg²⁺ efflux, suggesting the absolute necessity of ATP for the Na⁺/Mg²⁺ exchange.

Introduction

Intracellular free Mg²⁺ concentration ([Mg²⁺]_i) plays a pivotal role in numerous cellular functions in cardiac myocytes, including enzymatic activities (e.g., ATPases), the gating of ion channels (1,2), excitation-contraction coupling (3), and the sensitivity with which Ca²⁺ binds to intracellular buffer sites, including those on myofilaments (4,5). In basal conditions, [Mg²⁺]_i is thought to lie in the range of 0.8–1.0 mM (6,7). Large deviation of [Mg²⁺]_i from the normal range could significantly upregulate or downregulate intracellular reactions, which may either lead to cell death or, in some cases, protect the cells by inhibition of chain reactions that lead to cell death. During myocardial ischemia, [Mg²⁺]_i rises to high levels (>2 mM) and slowly declines after reperfusion (8); sustained elevation of [Mg²⁺]_i may protect myocardium from Ca²⁺ overloading and oxidative injury by free radicals (9).

[Mg²⁺]_i levels of normally energized myocytes are thought to be tightly regulated by active extrusion from the cells through a pathway coupled to Na⁺ influx, i.e., putative Na⁺/Mg²⁺ exchange (10–13). Previous studies have characterized activation/inhibition of the Na⁺/Mg²⁺ exchange by primary intracellular and extracellular ions (Na⁺, K⁺, Mg²⁺, Ca²⁺, and Cl⁻). Among these various ions, the Mg²⁺ extrusion transport appears to be activated only by intracellular Mg²⁺ and extracellular Na⁺ with half maximal activation at 1.5 mM and 55 mM, respectively, whereas the transport is significantly inhibited only by intracellular Na⁺ and extracellular Mg²⁺ with half inhibitory concentrations at ∼40 mM and 10 mM, respectively (7,14,15). It is not known, however, whether gradients of Na⁺ and Mg²⁺ concentrations across the cell membrane are the only requisites for the Mg²⁺ transport. Frenkel et al. (16), examining the Na⁺-dependent Mg²⁺ extrusion from lysed and resealed “ghosts” of human red blood cells, found that ATP was an absolute requirement for transport, and suggested that hydrolysis of ATP might supply energy for a directional cation movement (Mg²⁺ efflux and Na⁺ influx). Thus, this study was designed to study involvement of cellular metabolism in the Na⁺/Mg²⁺ exchange in cardiac myocytes. We measured [Mg²⁺]_i of rat ventricular myocytes with the fluorescent indicator furaptra (also called mag-fura-2). The rates of Mg²⁺ efflux were estimated in de-energized cells, and were compared with those in normally energized Mg²⁺-loaded cells.

Portions of this work have appeared previously in abstract form (17,18).

Methods

General

Hearts were excised from Wistar rats (9–12 weeks) under deep anesthesia with pentobarbital, and single ventricular myocytes were isolated enzymatically as described previously (5,11). Cells were superfused with normal Tyrode's solution composed of (mM): 135 NaCl, 5.4 KCl, 1.0 CaCl₂, 1.0 MgCl₂, 0.33 NaH₂PO₄, 5.0 glucose, and 10 HEPES (pH 7.40 at 25°C by NaOH) in a superfusion bath on the stage of an inverted microscope (TE300; Nikon, Tokyo, Japan) that was used to measure cell fluorescence. After the background fluorescence was measured, the cells were incubated at room temperature with either 5 μM furaptra AM (mag-fura-2 AM) for 14–20 min or 20 μM sodium-binding benzofuran isophthalate (SBFI) AM plus 0.02% pluronic for 2 h. The AM ester of the indicator was then washed out with Ca-free Tyrode's solution (Table S1 in the Supplementary Material), and subsequent measurements of the indicator fluorescence were carried out in Ca²⁺-free conditions at 25°C. Use of Ca²⁺-free solutions should help minimize Ca²⁺ overloading of the cells and any potential interference in the furaptra fluorescence signal by an increase in cytoplasmic [Ca²⁺].

Experimental equipment and methods for time-resolved fluorescence measurements have been described previously (7,12,14). Briefly, fluorescence emitted at 500 nm (25 nm FWHM) was detected by a photomultiplier tube from the entire volume of single cells with excitation wavelengths (slit width 5 nm) of 350 nm and 382 nm for furaptra, and 340 nm and 382 nm for SBFI switched at 100 Hz (CAM230; JASCO, Tokyo, Japan). At each excitation wavelength, the background fluorescence was subtracted from the total fluorescence measured after the indicator loading to give indicator fluorescence intensity, and thereby permit calculation of the ratio of the indicator fluorescence intensities (R).

Measurements and analyses of furaptra signals

The ratio (R) of furaptra fluorescence intensities excited at 382 nm and 350 nm [R = F(382)/F(350)] was converted to [Mg²⁺], as described previously (7,12,14), according to the equation:

$$\left[\mathrm{M}{\mathrm{g}}^{2+}\right]=K_{\text{D}}\frac{R-R_{\text{min}}}{R_{\text{max}}-R}\text{,}$$ (1)

where K_D is the dissociation constant of furaptra for Mg²⁺ in the cytoplasm, and R_min and R_max are the R values at zero [Mg²⁺] and saturating [Mg²⁺], respectively. We used the parameter values estimated previously in rat ventricular myocytes at 25°C: K_D = 5.30 mM, R_min = 0.969, and R_max = 0.223 (19). [Mg²⁺]_i refers to the spatially averaged Mg²⁺ concentration in the entire cell volume.

Because many of the experimental procedures used in this study could be expected to cause intracellular acidification (metabolic inhibition, removal of NH₄Cl) or alkalization (application of NH₄Cl), we examined effects of pH on the furaptra fluorescence with a spectrofluorometer (FP6500, JASCO) by measuring F(382)/F(350) of 0.5 μM furaptra in a 1-cm quartz cell (Fig. S1 A). Because the furaptra calibration parameters (K_D, R_min, and R_max) were essentially unchanged within the pH range of 6.5–7.7 (this finding consistent with the apparent pK of ∼5 reported by Raju et al. (20)), we did not correct calibration of furaptra signals for changes in intracellular pH (pH_i).

Measurements and analyses of SBFI signals

For measurements of intracellular Na⁺ concentration ([Na⁺]_i), we used the ratio (R) of SBFI fluorescence intensities excited at 382 nm and 340 nm, and SBFI R [= F(382)/F(340)] was converted to [Na⁺] with an equation analogous to Eq. 1, as described previously (14). This form of the equation can be applied for SBFI R, because 340 nm is very close to an isosbestic wavelength of intracellular SBFI for Na⁺ (14,21). For intracellular values of K_D, R_min, and R_max, we used the parameter values previously estimated in rat ventricular myocytes at 25°C: K_D = 22.7 mM, R_min = 0.530, R_max = 0.242 (14).

With spectrofluorometric measurements of SBFI fluorescence, we found that the K_D of SBFI was sensitive to pH, whereas R_min and R_max stayed nearly constant (Fig. S1 B). We used the pH dependence of the fitted exponential function (solid line in Fig. S1 B, upper panel) to correct intracellular K_D of SBFI for pH changes. It has been reported that pH_i of cardiac myocytes decreases from ∼7.1 to reach ∼6.8 when cells are in rigor after exposure to anoxia (22) or a mitochondrial uncoupler carbonyl cyanide 3-chlorophenylhydrazone (CCCP) (23). According to the pH dependence in Fig. S1 B, a decrease in pH from 7.1 to 6.8 caused a 12% increase in the K_D value. We therefore set the intracellular K_D value of SBFI to 25.4 mM (= 22.7 mM × 1.12) for cells in rigor after metabolic inhibition.

Fluorescence imaging

In some experiments, fluorescence images of furaptra were collected from the cells by a cooled charge-coupled device system (EM-CCD C9100, Hamamatsu Photonics, Hamamatsu, Japan) with a 20× objective (Plan Fluor 20× 0.50 DIC M, Nikon) of an inverted microscope (TE300, Nikon). With excitation at 345 nm and 380 nm (slit width 15 nm, 27.3 ms exposure for each wavelength with a 2-ms gap between the 345 nm and 380 nm images), furaptra fluorescence images at wavelengths longer than 470 nm were acquired at 5-s intervals, and digitized data were analyzed with an image analysis software (Aquacosmos/Ratio, Hamamatsu Photonics). We chose 345 nm as an excitation wavelength (rather than 350 nm), because we found that it was an isosbestic wavelength in the optics used for fluorescence imaging.

The ratio of F(380) and F(345) was calibrated in terms of [Mg²⁺] as described above with some modifications. Among three calibration parameters, R_min and R_max are optics-dependent, and must be determined for each instrument. For the imaging optics, lack of estimates for intracellular R_min and R_max led us to take an alternative approach. First, we assumed that resting levels of [Mg²⁺]_i averaged 0.9 mM (19) in five cells from which fluorescence images were taken. We also assumed that F(380) decreased to 23% on Mg²⁺ binding, as observed for F(382) in the optics for the time-resolved fluorescence measurements (i.e., R_max/R_min = 0.23). With these assumptions, R_min can be calculated by rearrangement of Eq. 1:

$$R_{\text{min}}=R_{\text{rest}}\frac{K_{\text{D}}+{\left[{\text{Mg}}^{2+}\right]}_{\text{rest}}}{K_{\text{D}}+{\left[{\text{Mg}}^{2+}\right]}_{\text{rest}}\times (R_{\text{max}}/R_{\text{min}})}\text{,}$$ (2)

where R_rest and [Mg²⁺]_rest are, respectively, R and [Mg²⁺]_i values in the resting myocytes. With the mean R_rest measured before metabolic inhibition in the five cells and intracellular K_D of 5.3 mM, values of R_min (= 4.80) and R_max (= R_min× 0.23) were obtained, and Eq. 1 was then applied to calculate [Mg²⁺] pixel by pixel.

Solutions and experimental procedure

The extracellular solutions used for this study are listed in Table S1. For observation of Mg²⁺ efflux in normally energized myocytes, the cells were first loaded with Mg²⁺ by incubation in the solution of high-Mg²⁺ and low-Na⁺ concentrations for 3–6 h. Mg²⁺ concentration of the solution for Mg²⁺ loading was either 93 mM (Mg-loading solution in Table S1) or 24 mM (1:3 mixture of Mg-loading solution and Na-depleting solution in Table S1). After [Mg²⁺]_i was elevated to ∼2.5 mM, Mg²⁺ efflux was induced by superfusion with the Ca²⁺-free Tyrode's solution that contained 140 mM Na⁺ (Table S1). For experiments in which myocytes were depolarized by extracellular 140 mM K⁺, Mg²⁺-loaded cells were first superfused by hypertonic 0 Na solution (Table S1) that contained 140 mM K⁺ and 70 mM N-methyl-d-glucamine (NMDG) for several minutes. Mg²⁺ efflux was then induced by equimolar substitution of N-methyl-d-glucamine in the superfusion solution with Na⁺ (hypertonic 70 Na solution in Table S1).

The initial rate of change in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) was analyzed as an index of the rate of Mg²⁺ efflux. On addition of 140 mM or 70 mM extracellular Na⁺, the initial Δ[Mg²⁺]_i/Δt was estimated by linear regression of data points spanning 120 s (30–150 s after solution exchange; see solid lines in Figs. 2, 5, and 6). Because our previous work showed that the initial Δ[Mg²⁺]_i/Δt values depend strongly on [Mg²⁺]_i levels (7), comparisons of the initial Δ[Mg²⁺]_i/Δt values were made at comparable initial [Mg²⁺]_i (defined as [Mg²⁺]_i at the first point of the fitted line).

Figure 2.

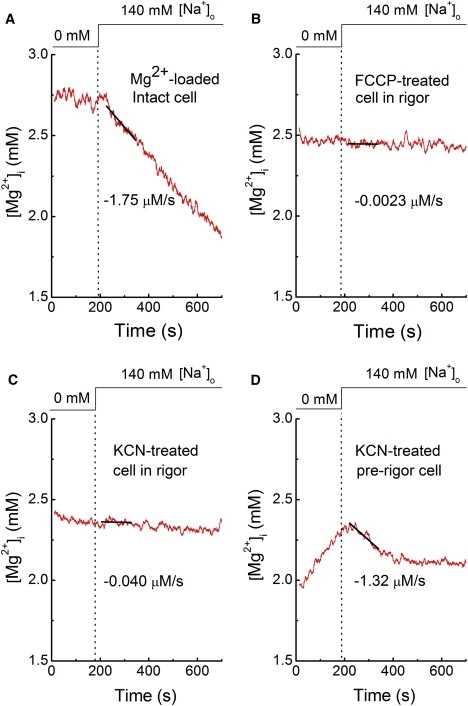
Records from four separate experiments. Initial Δ[Mg²⁺]_i/Δt measurements in a normally energized cell loaded with Mg²⁺ in the Mg-loading solution (Table S1) for 6 h: (A) cells in rigor after treatment with 1 μM FCCP for 10 min, (B) or 5 mM KCN for 93 min, and (C) a cell just before rigor formation after treatment with 5 mM KCN for 75 min (prerigor). Cells were initially incubated in the Na⁺-depleting solution (Table S1), and extracellular Na⁺ concentration was raised to 140 mM, as shown at the top. Solid lines were drawn by the least-squares fit to data points 30–150 s after solution exchange; values of the initial Δ[Mg²⁺]_i/Δt estimated from the slopes are indicated near the traces. In this and Figs. 4–6, traces of [Mg²⁺]_i or [Na⁺]_i were smoothed with adjacent averaging of 51 data points (10 s) to reduce the noise of the graphic display. Only unsmoothed traces were used for the analysis.

Figure 5.

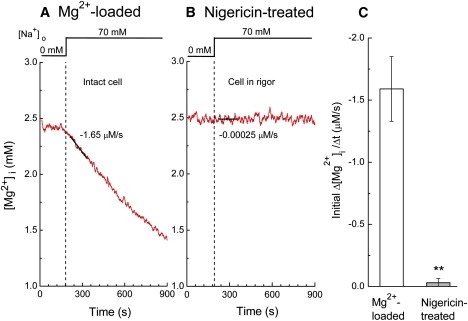
Measurements of initial Δ[Mg²⁺]_i/Δt in (A) a Mg²⁺-loaded normally energized cell, and (B) a cell in rigor after treatment with 10 μM nigericin. Cells were incubated initially in hypertonic 0 Na solution that contained 140 mM K⁺, 70 mM N-methyl-d-glucamine, and 1 mM Mg²⁺ (Table S1) for ∼5 min. Mg²⁺ efflux was induced by raising extracellular Na⁺ concentration to 70 mM, as shown at the top, by substituting N-methyl-d-glucamine by Na⁺. The pH of the extracellular solutions was 7.15. Estimated values of the initial Δ[Mg²⁺]_i/Δt are indicated near the traces. (C) Summary of the initial Δ[Mg²⁺]_i/Δt obtained from the type of experiments shown in A and B. Columns represent mean ± SE of 3 Mg²⁺-loaded cells (left) and 4 nigericin-treated cells (right). ^∗∗p < 0.01 versus Mg²⁺-loaded normally energized cells.

Figure 6.

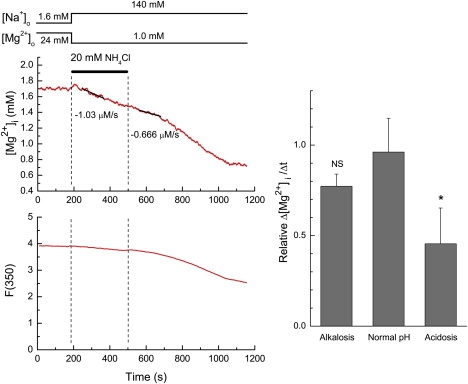
Effects of intracellular acidosis and alkalosis on the initial Δ[Mg²⁺]_i/Δt in normally energized cells. (Left) A record taken from a Mg²⁺-loaded cell. After Mg²⁺ loading, Mg²⁺ efflux was induced by extracellular 140 mM Na⁺, as shown at the top. Superfusion solutions also contained EIPA throughout the run (see text). Application and removal of NH₄Cl are indicated by a horizontal bar. The least-squares fitted lines for data points 30–150 s after solution exchange are drawn in solid, and values of the initial Δ[Mg²⁺]_i/Δt estimated from the slopes are indicated near the traces. (Right) Summary of relative Δ[Mg²⁺]_i/Δt (see text for definition) during intracellular alkalosis and acidosis induced by addition and removal of NH₄Cl (4 cells). Values for normal pH were obtained in separate experiments without NH₄Cl application (6 cells). Columns represent mean ± SE. ^∗p < 0.05 versus normal pH. NS, not significantly different from normal pH.

Carbonyl cyanide p-(trifluoromethoxy)phenylhydrazone (FCCP), nigericin, or 5-(N-ethyl-N-isopropyl)amiloride (EIPA) was added to the solutions with 0.1% ethanol as a solvent, which did not affect the fluorescence measurements. 2,3-buthandione monoxime (BDM) was directly dissolved in the superfusion solutions at 30 mM concentration. To test direct effects of 30 mM BDM on furaptra fluorescence, F(350) and F(382) were measured in quartz capillaries (internal diameter ∼50 μm) that contained the furaptra solution at 0, 1, 2, 4, 8, 50 mM [Mg²⁺] (see Fig. S1 legend). BDM (30 mM) equally quenched F(350) and F(382) of furaptra by 24%, and did not significantly change the furaptra R at any [Mg²⁺] tested. We therefore did not correct the calibration of furaptra R in terms of [Mg²⁺]_i for the fluorescence quenching effect of BDM. For modification of pH_i of normally energized cells, we simply added 20 mM NH₄Cl to Ca-free Tyrode's solution without compensation for osmolality, which made the solution slightly hypertonic (by 13%).

Data analysis

Linear and nonlinear least-squares fittings were carried out with the program Origin (Ver. 8, OriginLab, Northampton, MA). Statistical values are expressed as the mean ± SE for the number of cells indicated. Statistical significance was tested by Student's two-tailed t-test with the significance level set at p < 0.05.

Results

Effect of FCCP and potassium cyanide on the cell autofluorescence

To deplete intracellular ATP, we used FCCP, an uncoupler of mitochondria. FCCP dissipates H⁺ gradient across the mitochondrial inner membrane, and stimulates ATP hydrolysis by F₁F_o ATPase. We found that cell autofluorescence excited at either 350 nm or 382 nm quickly decreased exponentially to the lower level (Fig. S2 A). After potassium cyanide (KCN) treatment, the ultraviolet-illuminated cell autofluorescence increased transiently, and then slowly decayed with time constants of 60–80 min (Fig. S2 B). The subsequent analysis of the indicator R measured from the cell after FCCP or KCN treatment included correction for the time-dependent decay of cell autofluorescence; we calculated, at each excitation wavelength, the autofluorescence at any time during the fluorescence measurement runs using the fitted exponential (plus constant) functions for the decay (Fig. S2, A and B). For correction of the autofluorescence after application of nigericin (an H⁺ ionophore), we somewhat arbitrarily used the steady-state nadir values reached after FCCP treatment, because FCCP and nigericin were thought to deplete cellular ATP by a common mechanism (i.e., dissipation of mitochondrial H⁺ gradient, see below).

Effects of FCCP on [Mg²⁺]_i

Fig. 1 shows the results of an experiment in which fluorescence images of furaptra were followed from a cell that was superfused with Na⁺-depleting solution that did not contain glucose. On application of 1 μM FCCP, [Mg²⁺] within the region of interest (white square frame in Fig. 1 A), as well as other parts of the cells, rapidly increased to ∼2 mM, and then crept up to a quasi-steady level of ∼3 mM. The rise of [Mg²⁺] was probably due to breakdown of intracellular ATP and release of Mg²⁺ from Mg-ATP (24–26). The late part of the second rise of [Mg²⁺] coincided with cell shortening to ∼50% of the initial length, which was probably attributable to depletion of intracellular ATP and formation of rigor cross-bridges. Because only a small additional rise of [Mg²⁺] was observed during the shortening, the rigor formation appears to be associated with a small decrease in residual ATP. Similar results were obtained in four other cells. In a total of five cells, [Mg²⁺]_i reached 2.80 ± 0.124 mM when the cells were in complete rigor, and stayed relatively constant thereafter. Thus, FCCP treatment induced a large and, eventually, steady increase in [Mg²⁺]_i without requiring the Mg²⁺-loading procedure used previously in normally energized cells (12).

Figure 1.

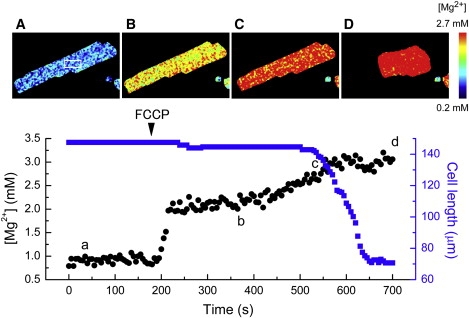
An example of simultaneous measurements of [Mg²⁺] and cell length from single cells. Fluorescence of intracellular furaptra was measured at wavelengths longer than 470 nm with sequential illumination at 345 nm and 380 nm. [Mg²⁺] was then calculated from F(380)/F(345), as described in text, pixel by pixel. (A–D) Pseudo-color images of [Mg²⁺] taken at the times indicated in the lower panel. The lower panel shows changes in mean [Mg²⁺] (black dots) in the fixed ROI set inside the cell image (shown in the upper leftmost image) and cell length (blue solid squares) followed at 5-s intervals. The cell was initially incubated in the Na⁺-depleting solution (Table S1), and 1 μM FCCP was applied at the time indicated by the arrow head.

Measurements of the initial rates of Mg²⁺ efflux after metabolic inhibition

For the following experiments, the initial rates of Mg²⁺ efflux were estimated with the time-resolved fluorescence measurements from the entire cell volume (see above). Experiments of metabolic inhibition used the following protocol: 1), the cells were incubated in the Na⁺-depleting solution that contained 5 mM glucose (Table S1) for 30 min to deplete the cells of Na⁺; 2), FCCP was applied in the Na⁺-depleting solution that did not contain glucose for ∼10 min, by which time nearly all cells went into rigor; and 3), the fluorescence measurement run was started, and extracellular Na⁺ concentration was raised to 140 mM by superfusing Ca²⁺-free Tyrode's solution that was free of glucose in the continuous presence of FCCP.

As a control, normally energized cells were incubated in the Mg²⁺-loading solution (Table S1) until [Mg²⁺]_i reached the levels similar to those found in the FCCP-treated cells (∼2.5 mM), and 140 mM extracellular Na⁺ was applied to induce Mg²⁺ efflux (Fig. 2 A). In five normally energized cells, the initial Δ[Mg²⁺]_i/Δt was −2.08 ± 0.126 μM/s from the initial [Mg²⁺]_i of 2.44 ± 0.115 mM. Fig. 2 B shows the result of a fluorescence measurement run obtained from an FCCP-treated cell. In eight cells treated with 1 μM FCCP, the initial Δ[Mg²⁺]_i/Δt was −0.201 ± 0.077 μM/s from the initial [Mg²⁺]_i of 2.59 ± 0.092 mM.

Cellular ATP could be also depleted by application of 5 mM KCN, instead of FCCP, for 90–168 min in the Na⁺-depleting solution that did not contain glucose. Mg²⁺ efflux on addition of 140 mM Na⁺ (in the continuous presence of KCN) was markedly reduced (Fig. 2 C), as observed in the FCCP-treated cells. In four KCN-treated cells in rigor, the initial Δ[Mg²⁺]_i/Δt was −0.165 ± 0.063 μM/s from the initial [Mg²⁺]_i of 2.38 ± 0.051 mM. The furaptra concentration in these cells, as reflected in the value of F(350) measured from the entire volume, stayed relatively constant even after rigor cell shortening, suggesting that cell membrane integrity was maintained in de-energized cells.

Four other cells were treated with KCN (5 mM) for shorter time periods (59–85 min, prerigor), and the fluorescence measurements were started when the cell length was equal to, or only slightly shorter than, the initial length measured before KCN treatment (on average, 93 ± 5% of the initial length). When observed just after the fluorescence measurement runs, however, all of these cells were in rigor. Fig. 2 D shows an example of [Mg²⁺]_i measurements in the cell treated with 5 mM KCN for 75 min in the Na-depleting solution. We did not note any shortening of the cell at the beginning of the fluorescence measurement run, but it was decreased by 34% at the end (∼20 min later), suggesting that the residual ATP was depleted during the run. In the essential absence of extracellular Na⁺ (Na-depleting solution, Table S1), [Mg²⁺]_i slowly rose higher than 2.3 mM (Fig. 2 D), which was probably caused by breakdown of ATP and release of Mg²⁺, as observed in FCCP-treated cells. Addition of extracellular 140 mM Na⁺ induced Mg²⁺ efflux only for a short period, and [Mg²⁺]_i stayed at a high level (∼2.1 mM) thereafter (Fig. 2 D). Similar results were obtained in another cell treated with KCN for 85 min. In two other cells treated with KCN for 59 min and 70 min, Mg²⁺ efflux was largely inhibited without any clear observation of a transient decrease in [Mg²⁺]_i on introduction of extracellular Na⁺. In the total of four cells, the initial Δ[Mg²⁺]_i/Δt averaged −0.850 ± 0.416 μM/s from the initial [Mg²⁺]_i of 2.31 ± 0.088 mM.

Fig. 3 A summarizes the rates of Mg²⁺ efflux thus obtained at the initial [Mg²⁺]_i of ∼2.5 mM with or without metabolic inhibition. The initial Δ[Mg²⁺]_i/Δt was not significantly different from zero in the absence of extracellular Na⁺ either in the normally energized cells or in the FCCP-treated cells, confirming that Mg²⁺ extrusion is dependent on extracellular Na⁺. The rate of Na⁺-dependent Mg²⁺ efflux was markedly reduced in the cells in rigor, induced either by FCCP or KCN, to levels that were not significantly different from zero, whereas it was reduced to intermediate levels (on average, by 59%) in the cells with residual small amounts of ATP present after treatment by KCN for shorter time periods (prerigor, Fig. 3 A). Further analyses using data from individual cells show a steep relation between the rate of Mg²⁺ efflux and cell lengths, i.e., levels of intracellular ATP (Fig. 3 B). Thus, the Mg²⁺ efflux was apparently intracellular ATP-dependent.

Figure 3.

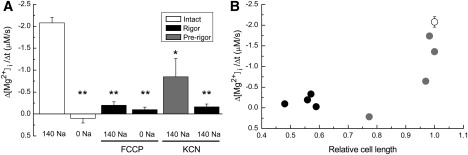
(A) Summary of initial Δ[Mg²⁺]_i/Δt estimated from the type of experiments shown in Fig. 2. The leftmost two columns show data obtained from Mg²⁺-loaded normally energized cells at 140 mM and 0 mM extracellular Na⁺, respectively. The third and fourth columns were obtained from cells in rigor after treatment with 1 μM FCCP at 140 mM and 0 mM extracellular Na⁺, respectively. The fifth and sixth columns are data obtained from KCN-treated cells in the presence of 140 mM extracellular Na⁺, respectively, ∼10 min before (prerigor) and after development of rigor. Columns represent mean ± SE of (from left to right) five, three, eight, five, four, and four cells. (B) Relation between initial Δ[Mg²⁺]_i/Δt (ordinate) and relative cell length (abscissa) estimated in the cells in rigor (black dots) and prerigor cells (gray dots) after treatment by 5 mM KCN for various times. In each cell, cell length at the beginning of the fluorescence measurement run was normalized to the initial cell length (measured before KCN treatment) to yield relative cell length. Mean ± SE obtained from Mg²⁺-loaded normally energized cells was also shown (open circle). ^∗≤0.01 p < 0.05; ^∗∗p < 0.01 versus Mg²⁺-loaded normally energized cells.

Effects of cell structure changes on Mg²⁺ efflux

Because ATP depletion causes cell shortening by ∼50% of the initial cell length (55.3 ± 1.1% in FCCP-treated cells [n = 5]; 45.0 ± 2.4% in KCN-treated cells [n = 4]), it is possible that the marked inhibition of Mg²⁺ efflux is due to severe changes in cell structure, rather than intracellular ATP. To address this possibility, we measured the initial Δ[Mg²⁺]_i/Δt of the ATP-depleted cells in which rigor cell shortening was minimized by BDM, an inhibitor of myosin ATPase activity. In the presence of 30 mM BDM, FCCP-induced cell shortening (rigor) was significantly reduced to 15.7 ± 5.0% of the initial length, but the rise of [Mg²⁺]_i (2.6–3.0 mM) was similar to that observed in the absence of BDM. The initial Δ[Mg²⁺]_i/Δt was −0.040 ± 0.288 μM/s, which was not significantly different from zero, from the initial [Mg²⁺]_i of 2.79 ± 0.097 mM (n = 4). In normally energized cells loaded with Mg²⁺, Mg²⁺ efflux was clearly observed in the presence of 30 mM BDM with the initial Δ[Mg²⁺]_i/Δt of −1.53 ± 0.245 μM/s at the initial [Mg²⁺]_i of 2.44 ± 0.252 mM (n = 3). Thus, it seems unlikely that changes in cell structure caused by extreme cell shortening are primarily responsible for the inhibition of Mg²⁺ efflux.

Measurements of [Na⁺]_i during Mg²⁺ efflux

Besides ATP, many changes of cytoplasmic constituents likely occur in de-energized cells. For example, [Na⁺]_i is expected to rise because of impaired activity of Na⁺/K⁺ ATPase. Because the Na⁺-dependent Mg²⁺ efflux is inhibited by intracellular Na⁺ with the half maximal inhibition of ∼40 mM (14), the diminished Mg²⁺ efflux observed in the rigor cells (above) could be explained by a rise of [Na⁺]_i up to levels much higher than 40 mM.

Fig. 4 shows examples of [Na⁺]_i measurements in two different cells (Fig. 4, A and B) during the experimental protocol used to estimate the initial Δ[Mg²⁺]_i/Δt; the cells were first incubated in the Na⁺-depleting solution for 30 min, and FCCP was applied in the Na⁺-depleting solution for ∼10 min before extracellular 140 mM Na⁺ was applied (above). In four FCCP-treated myocytes in rigor, the mean [Na⁺]_i measured in the Na⁺-depleting solution was 0.75 ± 0.78 mM, which was not significantly different from zero. The mean [Na⁺]_i estimated 30 s and 150 s after the Na⁺ addition (the first and the last points of the linear regression line) were, respectively, 5.0 ± 1.25 mM and 10.5 ± 4.76 mM. Thus, in the time period of the initial Δ[Mg²⁺]_i/Δt, the [Na⁺]_i levels (5–11 mM) were found to be much lower than that required for 50% inhibition of the Mg²⁺ efflux (40 mM).

Figure 4.

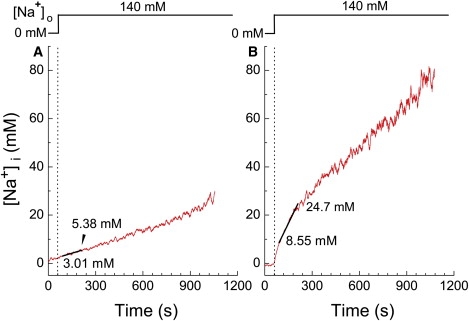
Time-dependent changes in [Na⁺]_i after addition of 140 mM extracellular Na⁺. SBFI-loaded cells were initially incubated in a Na⁺-free solution (Na-depleting solution, Table S1) to deplete the cells of Na⁺ before 1 μM FCCP was applied. [Na⁺]_i was measured from cells in rigor in the continuous presence of FCCP. In each cell, data points between 30 s and 150 s after application of 140 mM Na⁺ were least-squares fitted by a linear function. (A and B) Examples of the [Na⁺]_i measurements obtained from two different cells, in which relatively slow (A) and fast (B) rises of [Na⁺]_i were observed after addition of 140 mM extracellular Na⁺, as indicated above. In A and B, the linear regression lines are shown in solid, and fitted [Na⁺]_i values at the beginning and at the end of the 120-s period are indicated near the traces.

Effects of pH_i on the rate of Mg²⁺ efflux

During metabolic inhibition, pH_i of cardiac myocytes decreases from its normal value, typically ∼7.4, down to ∼6.8 when the cells are in rigor (22,23). If intracellular acidosis is mainly responsible for the diminished Mg²⁺ efflux, elevation of pH_i should restore the efflux. To normalize pH_i, we used nigericin, a H⁺ ionophore, in combination with cell membrane depolarization by 140 mM extracellular K⁺ (hypertonic Na solution, Table S1). This procedure should equilibrate pH_i with extracellular pH, and has been used for intracellular calibration of pH indicators (27).

We found that treatment of the myocytes with 10 μM nigericin caused a rise of [Mg²⁺]_i (to ∼2.5 mM) and cell shortening (rigor), which was attributed to the drug's uncoupling effect on mitochondria and depletion of ATP, as seen with FCCP. Fig. 5 compares the Mg²⁺ efflux induced by 70 mM extracellular Na⁺ in a normally energized cell (Fig. 5 A) and a nigericin-treated cell (Fig. 5 B), and clearly indicates that the marked reduction of the initial Δ[Mg²⁺]_i/Δt in the rigor cells is not reversed by normalization of pH_i (Fig. 5 C). The results suggest that inhibition of Mg²⁺ efflux cannot be primarily attributed to intracellular acidosis caused by metabolic inhibition.

To examine the effect of an increase or a decrease in pH_i on the rate of Mg²⁺ efflux in metabolically normal cells, we changed pH_i with a pulse of NH₄Cl (Fig. 6). Application of NH₄Cl is expected to cause a rise of pH_i to ∼7.4–7.5, whereas removal of NH₄Cl should decrease pH_i to 6.7–6.8 at 37°C (28) and 25°C (29,30). To prolong intracellular acidosis induced by NH₄Cl removal (30), we treated the cells with EIPA, an inhibitor of the Na⁺/H⁺ exchange, during Mg²⁺ loading ∼5 min before the Mg²⁺ efflux was induced by superfusion of Ca²⁺-free Tyrode's solution that also contained 5 μM EIPA. The initial Δ[Mg²⁺]_i/Δt obtained after simultaneous application of NH₄Cl with 140 mM Na⁺ was, on average, −1.13 ± 0.14 μM/s from the initial [Mg²⁺]_i of 1.81 ± 0.09 mM (n = 4), whereas the Δ[Mg²⁺]_i/Δt obtained after removal of NH₄Cl was, on average, −0.61 ± 0.14 μM/s at the initial [Mg²⁺]_i of 1.55 ± 0.08 mM (n = 4).

Because the [Mg²⁺]_i levels were substantially lower at the time of NH₄Cl removal than those at the time of NH₄Cl addition, comparisons of the initial Δ[Mg²⁺]_i/Δt values should be adjusted for variations of the initial [Mg²⁺]_i levels. We calculated relative Δ[Mg²⁺]_i/Δt using the standard relation between the initial Δ[Mg²⁺]_i/Δt and the initial [Mg²⁺]_i constructed previously (solid curve in Fig. 2 of Tursun et al. (7)) as a standard curve; any value of the initial Δ[Mg²⁺]_i/Δt was normalized to the standard value on the curve at a given initial [Mg²⁺]_i. Relative Δ[Mg²⁺]_i/Δt values thus obtained after addition of NH₄Cl (intracellular alkalosis with slight hypertonicity) were not significantly different from those obtained at normal pH_i, whereas relative Δ[Mg²⁺]_i/Δt values after removal of NH₄Cl (intracellular acidosis) were significantly lower than the control values (Fig. 6, right). Thus, intracellular acidosis seems to inhibit the Mg²⁺ efflux by ∼50%.

We noted that the decrease in [Mg²⁺]_i was initially slow after removal of NH₄Cl as described above, but was accelerated in the later time periods (Fig. 6, left upper panel). The late change in [Mg²⁺]_i decay may be due to slow recovery of pH_i that could occur even in the presence of EIPA (30), but may also be attributed to ultraviolet-damage of the cells exposed to the NH₄Cl pulse, because it accompanied an accelerated decrease in F(350) (Fig. 6, left, lower panel) that were not observed in the control cells.

Discussion

The aim of this study was to examine the contribution of high-energy-phosphate compounds to active Mg²⁺ extrusion in cardiac myocytes via a putative Na⁺/Mg²⁺ exchange. We found that the rate of extracellular Na⁺-dependent Mg²⁺ efflux was markedly reduced in the de-energized cells, when cellular metabolism was inhibited by either mitochondrial uncouplers (FCCP, nigericin) or an inhibitor of electron transport in mitochondria (KCN). The results strongly suggest the absolute requirement of intact cellular metabolism, in addition to concentration gradients of Na⁺ and Mg²⁺, for the Mg²⁺ transport.

Although cells underwent rigor shortening of cell length (by ∼50% of the initial length) after depletion of ATP, it is unlikely that inhibition of Mg²⁺ efflux is primarily caused by gross structural changes, because Mg²⁺ efflux in de-energized cells was not restored by reduction of cell shortening with BDM to the levels observed during physiological twitch responses (∼16% of the initial length). Although we cannot completely exclude the possibility that small changes in cell length (<16% of the initial length) somehow mechanically influence the Mg²⁺ transport activity, experimental evidence so far obtained does not support a putative Na⁺/Mg²⁺ exchanger that is highly mechanosensitive. For example, cell shrinkage by superfusion with hypertonic solutions that had ∼40% higher osmolality did not diminish the Mg²⁺ efflux in this study (Fig. 5 A).

Metabolic inhibition not only causes depletion of high-energy-phosphate compounds, but also alters other cytoplasmic constituents, such as concentrations of small ions and metabolites. Among primary intracellular ions, the Na⁺/Mg²⁺ exchange is inhibited by Na⁺ (14) and H⁺ (present study). Measurements of [Na⁺]_i shown in Fig. 4 suggest that [Na⁺]_i is not high enough to significantly inhibit the Mg²⁺ efflux under these experimental conditions; [Na⁺]_i shortly after application of extracellular Na⁺ was only 5–11 mM (see above), whereas we previously reported that 50% inhibition occurred at ∼40 mM [Na⁺]_i (14). Intracellular acidification to pH_i 6.7–6.8 inhibited the Mg²⁺ efflux by ∼50% (Fig. 6), and therefore may partly account for reduced Mg²⁺ efflux rates after metabolic inhibition, by which pH_i is expected to fall to ∼6.8 (22). However, it is unlikely that intracellular acidosis is primarily responsible for the impaired Mg²⁺ efflux, because the transport was not restored by normalization of pH_i (Fig. 5).

Requirement of ATP for the Mg²⁺ efflux

Metabolic inhibition causes depletion of high energy phosphate compounds (creatine phosphate, ATP, ADP) and accumulation of metabolites (AMP, inorganic phosphate) (31). Reduction of ATP concentration to very low levels leads to formation of rigor cross-bridges and cell shortening. In this study, we showed that the Mg²⁺ efflux was strongly inhibited after the onset of rigor shortening, as shown by the steep relation between the initial Δ[Mg²⁺]_i/Δt and cell length (Fig. 3 B). The inhibition occurred rather abruptly (within 100–120 s) during the fluorescent measurement runs, after which the cells were in rigor (Fig. 2 D). These results leave ATP as the most likely candidate for the primary regulator of the Mg²⁺ efflux during metabolic inhibition, although it is possible that changes in concentrations of other high-energy-phosphate compounds and/or metabolites may play an additional role.

Frenkel et al. (16) studied Na⁺-dependent Mg²⁺ efflux (the putative Na⁺/Mg²⁺ exchange) in human erythrocyte ghosts (i.e., cells resealed after hemolysis). They reported many properties of the Mg²⁺ transport similar to those found in cardiac myocytes in previous studies and this study: absolute requirement of ATP (above), inhibition by intracellular Na⁺ (14) and preferential outward transport of Mg²⁺ with net movement in the reverse direction difficult to bring about experimentally (15). By incorporation of ATP analogs in the resealed cells, Frenkel et al. (16) found that adenylyl(β,γ-methylene)diphosphonate (AMP-PCP) and AMP could not substitute for ATP, which led them to conclude that hydrolysis of ATP must supply energy for transport rather than activating transport by protein phosphorylation or by binding. Further studies are required to determine if a similar ATP-driven Na⁺/Mg²⁺ exchange is taking place in cardiac myocytes.

Further quantitative considerations

As inhibition of the Mg²⁺ efflux roughly coincided with cell shortening (Fig. 3 B), the Mg²⁺ efflux appears to decline steeply as the ATP concentration falls into the range at which rigor occurs. Because ATP has high affinity for Mg²⁺ (apparent K_D for Mg²⁺ = 0.19 mM for pH 6.8, 150 mM K⁺, 10 nM Ca²⁺, and 25°C (32)), most (93%) of ATP molecules are expected to be in Mg-bound form (Mg-ATP) at 2.5 mM [Mg²⁺]_i. When Mg-ATP is hydrolyzed, Mg²⁺ is released with a 1:1 stoichiometry. It follows that the approximate ATP concentration just before rigor cell shortening can be assessed from the associated increase in [Mg²⁺]_i that accompanies rigor cell shortening by assuming that 1), intracellular ATP is completely depleted when the cell has shortened to the quasi-steady length at time point d in Fig. 1 (24), and 2), Mg²⁺ transport across the cell membrane and membranes of intracellular organelles is negligible during the time of the rigor cell shortening. The second assumption could be justified by very small influx of Mg²⁺ even with 24–93 mM Mg²⁺ in the extracellular solutions (7), and lack of any significant efflux in the absence of extracellular Na⁺ (14). Mg²⁺ transport across the mitochondrial inner membrane is also unlikely, because mitochondrial membrane potential should be dissipated by FCCP (7). However, Mg²⁺ released from (or bound to) binding sites other than ATP must be considered, as described below.

In the experiments of the type shown in Fig. 1, [Mg²⁺]_i averaged 2.44 ± 0.105 mM at the onset of cell shortening (Fig. 1 c), and 2.80 ± 0.124 mM at the quasi-steady level of cell length after cell shortening (Fig. 1 d) with the mean difference (Δ[Mg²⁺]_i) of 0.36 ± 0.119 mM. In de-energized cells, the most important Mg²⁺ buffers are probably ATP, ADP, AMP, and P_i. To obtain quantitative information on Mg-ATP concentration at the onset of rigor contraction, we used a mathematical model developed by Allen and Orchard (31), as described in Appendix S1. The model calculated total concentrations of creatine phosphate ([PCr_tot]), creatine ([Cr_tot]), ADP ([ADP_tot]), AMP ([AMP_tot]), and P_i ([P_{i tot}]) at various total ATP concentrations ([ATP_tot]) (Fig. 7 A). Mg²⁺ binding to each buffer was then estimated with an equilibrium dissociation constant for Mg²⁺ assumed for pH 6.8 and 25°C (32,33; Appendix S1). Estimated changes in Mg²⁺-bound concentrations that are associated with hydrolysis of ATP (and the resultant rise in [Mg²⁺]_i) can then be calculated. These are negative for [MgATP], [MgADP] and [MgPCr], indicating net Mg²⁺ release from these buffers, whereas Mg²⁺ binding to AMP and P_i increases. Values of the sum (solid line in Fig. 7 B), which are thought to approximate −Δ[Mg²⁺]_i during the final depletion of ATP, varies between −0.13 mM and −0.72 mM, depending on the levels of initial [ATP_tot] between 0.2 mM and 0.8 mM, respectively, just before rigor cell shortening. The mean Δ[Mg²⁺]_i of 0.36 mM (i.e., −Δ[Mg²⁺]_i of −0.36 mM) obtained in this study (above) is most consistent with the initial [ATP_tot] of ∼0.4 mM (Fig. 7 B). Thus, our current best estimate suggests that ∼0.4 mM total ATP (i.e., MgATP slightly lower than 0.4 mM) is required to fully activate the Na⁺/Mg²⁺ exchange.

Figure 7.

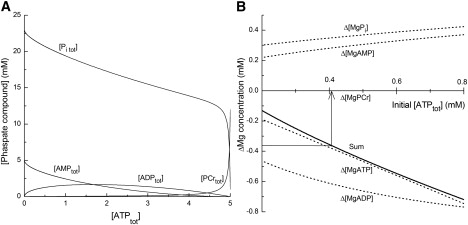
Concentrations of cytoplasmic phosphate compounds and their Mg²⁺ binding. (A) Total concentrations of phosphate compounds [P_{i tot}], [AMP_tot], [ADP_tot], and [PCr_tot] calculated by the model (see Appendix S1), and plotted as a function of [ATP_tot]. (B) Changes in concentrations of Mg²⁺-bound buffers. For initial conditions of the model calculation, [Mg²⁺]_i was set at 2.44 mM and initial [ATP_tot] (abscissa) was varied between 0.2 mM and 0.8 mM. For the final condition, [Mg²⁺]_i was 2.80 mM and [ATP_tot] was 0 mM. The model calculated [MgATP], [MgADP], [MgAMP], [MgP_i], and [MgPCr] at the initial and the final conditions, and the differences (the values at the final conditions minus those at the initial conditions) were defined as Δ[MgATP], Δ[MgADP], Δ[MgAMP], Δ[MgP_i], and Δ[MgPCr], respectively. The differences in values were plotted as a function of initial [ATP_tot] (dotted lines) with the sum, Δ[MgATP] + Δ[MgADP] + Δ[MgAMP] + Δ[MgP_i] + Δ[MgPCr], shown by a solid line. Note that a dotted line for Δ[MgPCr] is not seen because of superimposition on the horizontal axis. An arrow indicates that the sum value of −0.36 mM (ordinate) corresponds to 0.405 mM initial [ATP_tot] (abscissa) on the solid curve.

Possible pathophysiological implications

After prolonged ischemia or hypoxia, intracellular concentration of ATP falls to the levels below the threshold for rigor cross-bridge formation. Depletion of ATP affects various pumps and transporters; failure of the Ca²⁺ pumps and the Na⁺/Ca²⁺ exchanger leads to a rise in intracellular Ca²⁺ concentration, and failure of the Na⁺/Mg²⁺ exchange (that is stimulated by ATP) results in sustained high levels of [Mg²⁺]_i, as suggested by the results of this study.

It is well established that cytoplasmic Mg²⁺ inhibits L-type Ca²⁺ channels (2), a primary Ca²⁺ influx pathway in cardiac myocytes. Reduction of Ca²⁺ influx, as well as a decrease in Ca²⁺ sensitivity of myofilaments (4) by high levels of [Mg²⁺]_i is expected to counter Ca²⁺ overload and hypercontracture of the cells, and thus may play protective roles. High [Mg²⁺]_i could also inhibit free radical production associated with postischemic injury (9). It should be noted that in vivo situations of ischemia or hypoxia also involve extracellular acidosis and continuous presence of high extracellular Na⁺ concentrations (140 mM). Under such conditions, augmented changes in pH_i and [Na⁺]_i, in addition to ATP depletion, may also contribute to maintaining [Mg²⁺]_i at high levels.

Supporting Material

Nine equations, one table, and two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00565-7.