Binding Thermodynamics of Ferredoxin:NADP⁺ Reductase: Two Different Protein Substrates and One Energetics

Abstract

The thermodynamics of the formation of binary and ternary complexes between Anabaena PCC 7119 FNR and its substrates, NADP⁺ and Fd, or Fld, has been studied by ITC. Despite structural dissimilarities, the main difference between Fd and Fld binding to FNR relates to hydrophobicity, reflected in different binding heat capacity and number of water molecules released from the interface. At pH 8, the formation of the binary complexes is both enthalpically and entropically driven, accompanied by the protonation of at least one ionizable group. His²⁹⁹ FNR has been identified as the main responsible for the proton exchange observed. However, at pH 10, where no protonation occurs and intrinsic binding parameters can be obtained, the formation of the binary complexes is entropically driven, with negligible enthalpic contribution. Absence of the FMN cofactor in Fld does not alter significantly the strength of the interaction, but considerably modifies the enthalpic and entropic contributions, suggesting a different binding mode. Ternary complexes show negative cooperativity (6-fold and 11-fold reduction in binding affinity, respectively), and an increase in the enthalpic contribution (more favorable) and a decrease in the entropic contribution (less favorable), with regard to the binary complexes energetics.

Introduction

The flavoenzyme FNR catalyses the two-ET from two independent Fd molecules, previously reduced by Photosystem I, to a single NADP⁺ molecule through the formation of a ternary Fd·FNR·NADP⁺ complex (1–3). In the case of some algae and cyanobacteria, Fld, an FMN-dependent protein, replaces Fd under iron-deficient conditions, also acting as a single-electron carrier (2). Fd and Fld are able to play a similar role in this ET chain, interacting with the same partners, despite having different molecular size, topology, and redox cofactors (2,4)

Anabaena Fd is a 12 kDa acidic protein folded in four β-strands surrounded by three short α-helices and contains a [2Fe-2S] center (5). Anabaena Fld is a 17 kDa α/β protein formed by a five parallel β-strand central core surrounded by five α-helices and contains a noncovalently bound FMN as redox center (6). Both proteins dock to the same site in FNR (7,8). A transient interaction between a preformed FNR·NADP⁺ complex and the electron donor protein (Fd or Fld) has been proposed to be produced for efficient ET to take place (3,4,9). Electrostatic interactions between certain key positive residues on the FNR surface and acidic residues on Fd contribute to the protein-protein recognition within the cell (4,10–15), whereas the hydrophobic effect contributes to the reorganization of this initial interaction to produce an optimal complex for ET (12–14,16). The crystal structures reported for the Fd·FNR interaction confirm such assumptions (16,17). Despite a crystal structure for the Fld·FNR interaction remains elusive, models for this interaction have been theoretically constructed, and in all of them Fld is proposed to bind to the same region in FNR than Fd (8,18). These models show a short distance between the cofactors on both proteins, and suggest multiple orientations/configurations of Fld on the FNR surface without considerably altering such distance. Moreover, individual replacements of negatively charged or hydrophobic side chains on the Fld surface indicated that these side chains, despite contributing to modulate the orientation and tightening of the Fld·FNR complex, are not involved in crucial specific interactions (14,15,19,20). Therefore, the interaction of FNR with Fld appears to be less specific than that with Fd.

The thermodynamics of the interaction between FNR and Fd from spinach was previously analyzed by ITC (21,22). The complex formation was shown to be dominated by a favorable entropy change, linked to the release of several water molecules from the complex interface. This fact, together with the negative binding heat capacity, indicated a large contribution of the hydrophobic effect in the binding process. An additional study with mutant FNRs also concluded that the dehydration of the complex interface contributed to the stability (22). It is also known that, during the binding process, a protonation event must be taking place involving some ionizable group(s) located either on the FNR or on the Fd binding surfaces (23).

A preliminary study of the energetics of the interaction of Anabaena FNR with NADP⁺, Fd, and Fld was recently reported (24). However, this study was rather focused into the methodology for characterizing heterotropic cooperative interactions in ligand binding, and the buffer-independent parameters were not determined. In this work, the thermodynamics of the formation of binary and ternary complexes of NADP⁺, Fd, and Fld binding to Anabaena FNR has been further studied to address several questions:

• 1.What is the intrinsic (buffer- and pH-independent) binding energetics of Fd and Fld binding to FNR? What is the energetics of the ternary complex formation? How similar are the FNR systems from spinach and Anabaena?
• 2.How are Fd and Fld able to bind to the same protein target and play the same physiological roles? Are there any features in the binding energetics related to their structural differences?
• 3.Which is(are) the ionizable group(s) involved in the proton exchange process coupled to Fd and Fld binding to FNR?
• 4.How important is the presence of the Fld FMN cofactor in binding to FNR?

ITC is an experimental technique especially suited for obtaining the information needed to answer these questions: 1), it allows determining the binding affinity and enthalpy, and, therefore, it provides a direct and complete characterization of the energetics of the binding process into enthalpic and entropic contributions; 2), protonation and other coupled processes can be readily assessed by evaluating the impact of environmental variables (temperature, buffer ionization enthalpy, pH, osmotic stress, etc.) into binding affinity and enthalpy; 3), because enthalpy and entropy reflects intermolecular interactions of very different nature, the impact of changes in the environmental variables or the interacting molecules on the binding Gibbs energy, and its partition into enthalpic and entropic contributions, provide useful direct information about the binding process.

Materials and Methods

Production of proteins: FNR, Fd, and Fld

Proteins were produced as previously described (25,26). ApoFld was obtained by treating Fld with trichloroacetic at 4°C in the presence of dithiothreithol as previously described (27). Trichloroacetic acid, dithiothreitol and NADP⁺ were purchased from Sigma (Madrid, Spain).

Spectral analysis

Ultraviolet-visible spectra were obtained on a Cary-Bio 100 spectrophotometer (Varian, Palo Alto, CA) and were used to estimate purity and protein concentration. Extinction coefficients were ɛ_{458 nm} = 9.4 mM⁻¹ cm⁻¹ for wild-type and H299F FNRs (28), ɛ_464nm = 8.8 mM⁻¹ cm⁻¹ for Fld (29,30), and ɛ_{423 nm} = 9.7 mM⁻¹ cm⁻¹ for Fd (28).

High-sensitivity ITC

ITC experiments were conducted using a high-precision VP-ITC system (MicroCal LLC, Northampton, MA). Measurements were performed with the oxidized forms of FNR, NADP⁺, Fd, or Fld. For binary complexes, buffered solutions of FNR (∼20 μM) were titrated with NADP⁺, Fd, or Fld (250–300 μM) in the same buffer. In the case of ternary complexes, NADP⁺ (∼50 μM) was added to the FNR solution in the calorimetric cell. Because of the wealth of experimental data at pH 8 (2,7,24,25), experiments were performed at this pH.

The binding enthalpy (ΔH), the association constant (K_A), and the stoichiometry of the binding are simultaneously estimated through nonlinear least squares regression of the experimental data employing a methodology applicable to both binary and ternary complex formation, as described previously (24).

Binding parameters for binary complexes

ΔH, K_A and, thus, the binding Gibbs energy, ΔG (24,31), determined in the ITC experiments allow the calculation of the entropy of binding, ΔS, according to:

$$\Delta G=\Delta H-T\Delta S\text{.}$$ (1)

The heat capacity change upon binding, ΔC_P, was determined from linear regression of the binding enthalpy values obtained at different temperatures (20°C, 25°C, and 30°C), according to:

$$\Delta C_{\text{P}}={\left(\frac{\partial \Delta H}{\partial T}\right)}_{\text{P}}\text{.}$$ (2)

If a binding process is coupled to the exchange of protons between ionizable groups and the bulk solvent, then, the measured binding enthalpy contains a contribution from the ionization of the buffer (32,33). The association constant does not contain any buffer contribution as long as the pH of the experiment is close enough to the pK_a of the employed buffer. The buffer-independent binding enthalpy, ΔH⁰, can be obtained by eliminating the contribution of the buffer ionization, ΔH_ion, from the observed binding enthalpy, ΔH, according to:

$$\Delta H=\Delta H^{\text{0}}+n_{\text{H}+}\Delta H_{\text{ion}},$$ (3)

where n_H+ is the net number of protons exchanged between the complex and the bulk solution. If n_H+ is positive, the complex formation occurs with the capture of protons from the solvent; if n_H+ is negative, it takes places releasing of protons to the solvent. To estimate both, ΔH⁰ and n_H+, buffers with different ionization enthalpies were also used: EPPS, 5.10 kcal/mol; Tricine, 7.50 kcal/mol; and Tris, 11.35 kcal/mol (21,34,35).

If a binding process is coupled to the exchange of a certain type of molecule (proton, ion, water, etc.) between the complex and the bulk solution, then, there is a dependence of the binding association constant on the activity of such molecule through a linkage equation (36). In particular, if experiments are done at different osmotic stress conditions using several osmolyte concentrations, linear regression analysis of lnK_A as a function of osmolality allows estimating the net number of water molecules exchanged between the complex and the solution, n_w, according to (37):

$$\frac{\partial \ln K_{\text{A}}}{\partial \text{osmolality}}=-\frac{n_{\text{W}}}{\text{55}.\text{6}}\text{.}$$ (4)

Sucrose was employed as the osmotic stress generating agent in the experiments reported here. Other reagents, such as glycerol, may be employed. In the case of glycerol, due to the particular nature of the water-water, glycerol-glycerol, and water-glycerol interactions, the mixing of glycerol and water is strongly exothermic, and calorimetric experiments in the presence of glycerol may distort the thermodynamic parameters if water is released or captured at the binding interface (21). On the contrary, sucrose behaves as an ideal solute: it forms hydrogen bonds with water with similar energetics to that of water-water, and it does not change the apparent density of water (38). Therefore, the mixing of water and sucrose is less energetic and will have a smaller influence. Sucrose buffered solutions of 1 M and 2 M concentration were prepared and then 1:1 mixed with buffer and protein solutions to achieve the appropriate molality (0.56, and 1.28 mol/kg).

pH-independent binding parameters

Experiments were done mainly at pH 8, but higher pH values (pH 10), where no proton exchange was observed, were used to obtain the pH-independent thermodynamic binding parameters. According to well-known equations, if a binding process is coupled to the exchange of protons between ionizable groups and the bulk solvent, K_A and ΔH⁰ depend on the pH and the pK_a values of those ionizable groups (32):

$$\begin{array}{l}{K}_{\text{A}}=K_{\text{A},\text{int}}\prod _{\text{i}}\left(\frac{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{C}}-\text{pH}}}{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{F}}-\text{pH}}}\right)\\ \Delta H^{\text{0}}=\Delta H_{\text{int}}+\sum _{\text{i}}\left(\frac{{\text{10}}^{{\text{pK}}_{\text{a},\text{i}}^{\text{C}}-\text{pH}}}{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{C}}-\text{pH}}}\Delta H_{\text{p},\text{i}}^{\text{C}}-\frac{{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{F}}-\text{pH}}}{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{F}}-\text{pH}}}\Delta H_{\text{p},\text{i}}^{\text{F}}\right)\\ n_{\text{H}+}=\sum _{\text{i}}\left(\frac{{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{C}}-\text{pH}}}{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{C}}-\text{pH}}}-\frac{{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{F}}-\text{pH}}}{\text{1}+{10}^{{\text{pK}}_{\text{a},\text{i}}^{\text{F}}-\text{pH}}}\right),\end{array}$$ (5)

once the influence of the buffer has been removed, where K_A,int and ΔH_int are the pH-independent intrinsic association constant and binding enthalpy, respectively, pK_a,i^F and pK_a,i^C are the pK_a values of a given ionizable group in the free species and the complex, and ΔH^F_p,i and ΔH^C_p,i are the ionization enthalpy of a given ionizable group in the free species and the complex. Therefore, only those groups undergoing a pK_a change upon ligand binding will be involved in proton exchange. If pH is high enough (higher than the pK_a values of the ionizable groups involved in proton exchange), then no proton exchange is observed and the measured binding parameters will coincide with the intrinsic pH-independent binding parameters (Eq. 5). Experiments were performed at pH 10 (glycine and carbonate, with ionization enthalpies of 10.57 kcal/mol and 3.52 kcal/mol, respectively (21)), to estimate the pH-independent binding parameters.

Global analysis of the temperature dependence of the binding parameters

K_A and ΔH are temperature dependent according to:

$$\begin{array}{l}{K}_{\text{A},\text{int}}\text{(}T\text{)}=K_{\text{A},\text{int}}\text{(}{T}_{\text{0}}\text{)}\text{exp}\left(-\frac{\Delta H_{\text{int}}(T_{\text{0}}\text{)}}{R}\left(\frac{\text{1}}{T}-\frac{\text{1}}{T_{\text{0}}}\right)-\frac{\text{Δ}{C}_{\text{P}}}{R}\left(\text{1}-\frac{T_{\text{0}}}{T}-\text{ln}\left(\frac{T}{T_{\text{0}}}\right)\right)\right)\\ \Delta H_{\text{int}}\text{(}T\text{)}=\Delta H_{\text{int}}\text{(}{T}_{\text{0}}\text{)}+\Delta C_{\text{P}}\text{(}T-T_{\text{0}})\end{array},$$ (6)

where T₀ is a reference temperature (e.g., 298.15 K) and, K_A(T₀) and ΔH(T₀) are the association constant and the binding enthalpy at this reference temperature. It has been assumed that ΔC_P is constant and does not depend on the temperature, at least within the temperature range considered. If K_A and the ΔH are measured at different temperatures, then K(T₀), ΔH(T₀), and ΔC_P can be estimated through global analysis based on Eq. 6. This procedure is more reliable than performing just one determination at a given single temperature value (very important if the enthalpy exhibits a small value and the relative error is large).

Binding parameters for ternary complexes

The formation of ternary complexes has been studied here by applying the formalism for heterotropic interactions (24). ΔH and ΔG for the formation of the ternary complex can be expressed as:

$$\begin{array}{l}\Delta H_{\text{AB}}=\Delta H_{\text{A}}+\Delta H_{\text{B}}+\Delta h\\ \Delta G_{\text{AB}}=-RT\text{ln}\left(\alpha K_{\text{A}}{K}_{\text{B}}\right)=\Delta G_{\text{A}}+\Delta G_{\text{B}}+\Delta g,\end{array}$$ (7)

where ΔH_A and ΔH_B, and ΔG_A and ΔG_B are the enthalpies and the Gibbs energies associated with the formation of each binary complex. The parameters α, Δg, and Δh are the cooperativity interaction constant, the cooperativity Gibbs energy, and the cooperativity enthalpy, respectively, associated with the formation of the ternary complex: if α > 1 (Δg < 0), the binding of A and B presents positive cooperativity; if 0 < α < 1, the binding of A and B presents negative cooperativity (Δg > 0); if α = 1, the binding of A and B is independent (Δg = 0); if α = 0, the binding of A and B presents maximal negative cooperativity (purely competitive or mutually excluding; Δg = +∞).

Structure-based calculations

Thermodynamic binding parameters may be estimated by empirical correlations based on structural properties of the complexes. The most successful correlations are based on changes in solvent ASA upon binding (39–41). According to the work by Freire et al., (39–41) in the absence of coupled protonation processes, ΔC_p and ΔH (60°C) may be estimated from changes in polar and apolar solvent ASA (ΔASA) elicited upon binding, according to:

$$\begin{array}{l}\Delta C_{\text{P}}=\text{0.45}\Delta {\text{ASA}}_{\text{apolar}}-\text{0.26}\Delta {\text{ASA}}_{\text{polar-no OH}}+\text{0.17}\text{Δ}{\text{ASA}}_{\text{OH}}\\ \Delta H(\text{60}°\text{C})=-\text{8.44}\text{Δ}{\text{ASA}}_{\text{apolar}}+31.4\Delta {\text{ASA}}_{\text{polar}},\end{array}$$ (8)

where ΔASA is measured in Ų. Solvent accessible apolar and polar surface areas (ASA_apolar and ASA_polar) were calculated by using the Lee & Richard's algorithm (42). ΔASA were obtained by subtracting the ASA of the two individual partners (FNR, Fd, or Fld) from the ASA of the corresponding binary complex. The crystallographic structure of Fd·FNR (PDB code 1EWY) (16), and theoretical models reported for Fd·FNR and Fld·FNR were used: the docking Fd·FNR complex (8), and the two Fld·FNR models obtained by homology modeling with the cytochrome P450 reductase structure (18), and by docking (8).

Results

Thermodynamics of binary interactions of FNR with its substrates

ITC measurements for the titration of Anabaena FNR with NADP⁺ (Table 1 and Fig. 1 A) indicated that, at pH 8, NADP⁺ binds to Anabaena FNR with K_A of 2.6 × 10⁵ M⁻¹, a value similar to that reported in the literature (25). Linear regression of the measured ΔH in different buffers (Fig. 2 A, Table 1) yielded a ΔH⁰ of −4.6 kcal/mol, and a net number of protons exchanged of 0.36, suggesting there is, at least, one ionizable group being protonated. Linear regression of the measured ΔH at different temperatures (Fig. 2 B) yielded a ΔC_P of −200 cal/K·mol, indicating a major contribution to the binding from the hydrophobic effect, in agreement with the role played by hydrophobic protein chains, particularly Leu²⁶³, in the interaction with this substrate (43). The formation of the FNR·NADP⁺ complex is both enthalpically and entropically driven (Table 1).

Table 1.

Thermodynamic parameters for the interaction of FNR with its substrates

	KA† (M−1)	KD‡ (M)	ΔG (kcal/mol)	ΔH0§ (kcal/mol)	−TΔS (kcal/mol K)	nH+	nw	ΔCP (cal/K mol)
NADP+ → FNR	2.6 · 105	3.8 · 10−6	−7.4	−4.6	−2.8	0.36	—	−200
Fd → FNR	7.6 · 105	1.3 · 10−6	−8.0	−4.9	−3.1	1.13	−29.5	−170
Fld → FNR	3.5 · 105	2.9 · 10−6	−7.6	−5.1	−2.5	0.91	−21.1	−115
apoFld → FNR	1.1 · 105	9.1 · 10−6	−6.9	−1.2	−5.7	0.13	—	−40
Fld → FNRH299F	7.0 · 104	1.4 · 10−5	−6.7	−2.5	−4.2	0.31	—	—
Fd→ FNR¶	4.8 · 106	2.2 · 10−7	−9.1	−0.4	−8.7	—	—	−166
Fld → FNR¶	2.2 · 106	4.5 · 10−7	−8.6	−0.4	−8.2	—	—	−106

	α†	Δg (kcal/mol)	Δh§ (kcal/mol)	−TΔs (kcal/mol)	nH+	ΔGAB (kcal/mol)	ΔHAB (kcal/mol)	−TΔSAB (kcal/mol)
Fd → FNR presence of NADP+	0.17	1.1	−2.4	3.5	0.65	−14.3	−11.9	−2.4
Fld → FNR presence of NADP+	0.090	1.4	−5.7	7.1	0.60	−13.6	−15.4	1.8

Data from experiments in three different buffers (50 mM, pH 8, 25°C).

Typically, relative errors in K_A, K_D, and α are 10–15%, absolute error in Gibbs energy values is 0.1 kcal/mol, and in enthalpy and entropy values are 0.3 kcal/mol. Absolute error in n_H+ is 0.02, in n_w is 2, and in ΔC_P is 20 cal/K·mol.

^†Average of values measured with three different buffers (50 mM, pH 8, 25°C).

^‡K_D = (K_A)^-1.

^§Buffer-independent enthalpy obtained by linear regression (Eq. 3).

^¶Data at pH 10 (glycine 50 mM, pH 10, 25°C) ΔH_int.

Figure 1.

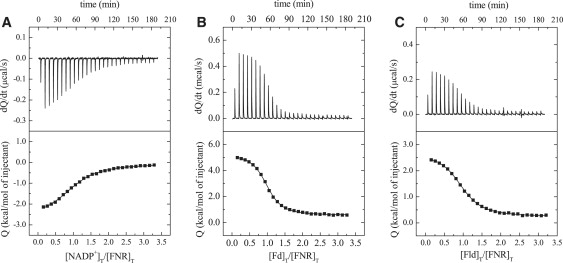
Selected experimental calorimetric titrations from the characterization of the binary complexes formed between FNR and either NADP⁺, Fd, or Fld. Titration of FNR (21.7 μM in the calorimetric cell) with NADP⁺ (336 μM in the syringe) in EPPS 50 mM, pH 8, at 25°C (A); FNR (19.5 μM) with Fd (298 μM) in Tricine 50 mM, pH 8, at 20°C (B); and FNR (20 μM) with Fld (299 μM) in Tricine 50 mM, pH 8, at 20°C (C).

Figure 2.

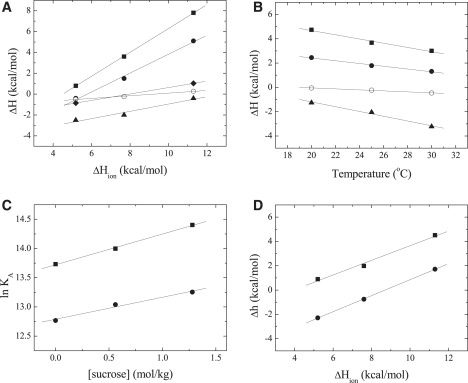
(A) Dependence of the measured enthalpy of binary complex formation, ΔH, on the buffer ionization enthalpy, ΔH_ion, for FNR binding to NADP⁺ (solid triangles), Fd (solid squares), Fld (solid circles), apoFld (open circles), and H299F FNR binding to Fld (solid diamonds), in EPPS, Tricine, and Tris 50 mM, pH 8 at 25°C. The lines are best fits according to Eq. 3. (B) Dependence of the measured enthalpy of binary complex formation on the temperature for FNR binding to NADP⁺ (solid triangles), Fd (solid squares), Fld (solid circles), and apoFld (open circles), in Tricine 50 mM, pH 8 at 20°C, 25°C, and 30°C. The lines are best fits according to the Eq. 2. (C) K_A dependence for binary complex formation on the solution osmolality for FNR binding to Fd (solid squares) and Fld (solid circles). Sucrose concentrations (0, 0.56, and 1.28 mol/kg), in Tricine 50 mM, pH 8 at 25°C. Lines are best fits to Eq. 4. (D) Dependence of the Δh on the ionization heat of the buffer for FNR:NADP⁺ binding to Fd (solid squares) and Fld (solid circles), in EPPS, Tricine, and Tris 50 mM, pH 8 at 25°C. Lines are best fits according to Eq. 3. Estimated values of parameters derived from plots are shown in Table 1.

The interaction of Fd or Fld with FNR was also analyzed varying buffer, temperature, and pH conditions (Table 1 and Figs. 1, B and C, 2, and 3). At pH 8, Fd and Fld bind to FNR with a K_A of 7.6 × 10⁵ and 3.5 × 10⁵ M⁻¹, respectively (Table 1), similar values to those reported (25). ΔH⁰ values of −4.9 and −5.1 kcal/mol and 1.13 and 0.91 protons exchanged upon binding were estimated for Fd and Fld, respectively (Fig. 2 A, Table 1), suggesting that, at least, one ionizable group is protonated. A ΔC_P of −170 cal/K·mol for Fd binding and −115 cal/K·mol for Fld were determined (Fig. 2 B), indicating also a major contribution of the hydrophobic effect to the binding of both proteins to FNR. The formation of Fd·FNR and Fld·FNR complexes are both enthalpically and entropically driven (Table 1). However, these buffer-independent parameters still contain the contribution from the proton exchange involving ionizable groups in the proteins. Experiments under osmotic stress (Fig. 2 C, Table 1) indicated that Fd binding releases 30 water molecules from the binding interface, whereas Fld binding releases only 20 water molecules.

Figure 3.

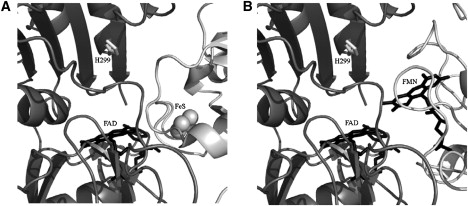
Interaction interface of the complexes (A) Fd·FNR (PDB code 1EWY) (16), and (B) Fld·FNR (18). FNR is drawn in dark gray, and Fd and Fld in light gray. Residue H299 is indicated in white. Cofactors FAD for FNR and FMN for Fld are shown in black and the [2Fe-2S] center for Fd in balls.

Measurements carried out at pH 10 for Fd binding to FNR in buffers with different ionization enthalpies yielded similar measured ΔH, indicating that at this pH there is not a net proton exchange process. The same effect was observed for Fld binding to FNR. ΔH_int (Table 1 and in the Supporting Material) is small and negative for both Fd and Fld (−0.4 kcal/mol), indicating that the intrinsic binding of Fd or Fld to FNR is entropically driven (−TΔS = −8.7 and −8.2 kcal/mol, respectively). Because the enthalpy value is quite small, the binding parameters were estimated by global analysis of the temperature dependence (Eq. 6). The ΔC_P values estimated at pH 10 and pH 8 are almost equal (Table 1).

Because at pH 8 binding of Fd or Fld to FNR is accompanied by the capture of 1.13 or 0.91 protons, binding at pH 10 should become weaker, unless other phenomena influence it. However, our results indicate that the binding process is sixfold more favorable at the higher pH: K_A values of 4.8 × 10⁶ and 2.2 × 10⁶ M⁻¹ at pH 10, compared with 7.6 × 10⁵ and 3.5 × 10⁵ M⁻¹ at pH 8 (Table 1 and Supporting Material). These changes in affinity of FNR for Fd or Fld correspond to an additional −1 kcal/mol in ΔG.

Calculations of the ΔH and ΔC_p values based on the structures of the Fd·FNR and Fld·FNR complexes are listed in Table 2. The results for the crystallographic Fd·FNR complex and for the theoretical homology Fld·FNR model (based on the cytochrome P450 reductase structure) are in reasonable agreement with the experimental ones (considering the implicit assumptions in the empirical relationships used and the extrapolation errors). Both complexes show a small interface (ΔASA < 1200 Ų). The binding interface appears to be more apolar in the case of the Fd·FNR complex than that of the Fld·FNR complex (640 Ų, compared to 380 Ų). Thus, 61% of the binding interface in the Fd·FNR complex is apolar, whereas this percentage decreases to 44% in the Fld·FNR complex. Therefore, a more negative value of ΔC_P for Fd binding to FNR is expected. If we base our calculations on the docking complex models, larger binding interfaces, ΔH and ΔC_P values result, but, again, the binding interface in the Fd·FNR complex is more apolar than that of the Fld·FNR one.

Table 2.

Changes in solvent ASA and estimated thermodynamic binding parameters for the interaction of FNR with Fd and Fld

	ΔASAapolar (Å2)	ΔASApol-no OH (Å2)	ΔASAOH (Å2)	ΔASApol (Å2)	ΔCP∗ (cal/K·mol)	ΔH† (kcal/mol)
Fd → FNR‡	−640	−410	0	−410	−180	−1.4 (−1.0)
Fd → FNR§	−1470	−970	−50	−1020	−420	−13.6 (−5.0)
Fld → FNR¶	−380	−460	−20	−480	−50	−7.8 (−10.0)
Fld → FNR§	−1100	−840	−80	−930	−290	−15.9 (−9.8)

^∗Calculated using Eq. 8.

^†Calculated using Eq. 8 and extrapolating to 25°C using the experimental ΔC_P (in parenthesis, extrapolating to 25°C using the theoretical ΔC_P).

^‡Crystallographic complex (16).

^§Docking complex (8).

^¶Homology complex from (18).

Because ΔC_P is determined in buffered solutions, the observed binding heat capacity contains a contribution from the ionization heat capacity of the corresponding buffer, ΔC_Pion (−12.7 cal·K/mol and −13.6 cal/K·mol for Tricine at pH 8, and glycine at pH 10, respectively). As a first approximation, this contribution is equal to n_H+ΔC_Pion. Then, the correction is not larger than 15 cal/K·mol in the case of Tricine (n_H+ is close to 1), and negligible in the case of glycine (n_H+ is zero). There is another correcting term, ΔH_iondn_H+/dT, but this correction, which reflects differences in fluctuation of the proton saturation fraction of the protein ionizable groups involved in proton exchange upon binding, is also small.

Role of the Fld prosthetic group, the FMN, in the Fld·FNR interaction

Titration of FNR with apoFld showed that the absence of the FMN cofactor in Fld only slightly modulated the affinity, making the interaction threefold weaker than that of the Fld·FNR complex (Table 1 and Fig. 2 A). Nevertheless, the partition of ΔG into its components resulted in a considerable less favorable enthalpic and a more favorable entropic contributions (Table 1). Moreover, this interaction occurred with the net exchange of only 0.13 protons and with a ΔC_P of −40 cal/K·mol (Fig. 2, A and B), values much smaller that those for Fld.

Nature of the protonated residue upon interaction of FNR with the protein partner

Because the protonation effect is roughly similar upon Fd or Fld binding to FNR, the proton exchange was expected to implicate mainly ionizable groups on the FNR interacting surface. Moreover, because this protonation effect was observed at pH 8 but not at pH 10, the group(s) involved must undergo a pK_a change upon binding from a pK_a below 8 in the free state (pK_a^F) toward a pK_a above 8 in the complex (pK_a^C). Then, the reasonable candidate was a histidine. Inspection of the available structural models for the Fd·FNR and Fld·FNR interactions points to His²⁹⁹ as the main candidate (8,16,18) (Fig. 3). Previous work on Fd binding to FNR from spinach also suggested a His from FNR to be the responsible for proton exchange (21). Replacement of His²⁹⁹ with Phe in FNR weakened the binding affinity between Fld and FNR by 0.7 kcal/mol with respect to that of wild-type FNR, with a reduction of the favorable enthalpic contribution that was not compensated with the more favorable entropic one (Table 1). The estimated number of protons exchanged upon binding was 0.31 (Table 1 and Fig. 2 A). Therefore, His²⁹⁹ in FNR seems to be responsible for 60% of the protonation produced upon Fld binding.

Energetics of the ternary interactions FNR·NADP⁺·Fd and FNR·NADP⁺·Fld

Titrations of the FNR·NADP⁺ complex (NADP⁺ at saturating concentration) with Fd or Fld were carried out in different buffers to estimate the buffer-independent cooperativity binding parameters (Table 1). According to the affinity of NADP⁺ binding to FNR and the concentrations of FNR (∼20 μM) and NADP⁺ (50 μM) in the calorimetric cell, more than 90% of FNR was bound to NADP⁺. Besides, the methodology employed for estimating the cooperativity parameters does not require complete saturation (24). At pH 8, Fd and Fld bind to FNR·NADP⁺ with cooperativity constants of 0.17 and 0.09, respectively (Table 1), similar values to those previously reported (24), indicating that the binding affinities of Fd and Fld are reduced by 6-fold and 11-fold, respectively, when NADP⁺ is prebound to FNR. Analysis of the measured cooperativity enthalpies in different buffers on the basis of Eq. 5 (Table 1 and Fig. 2 D), yielded Δh⁰ values of −2.4 kcal/mol and −5.7 kcal/mol, and n_H+ of 0.65 and 0.60, for Fd and Fld, respectively. These data indicate that, for both protein carriers, the heterotropic effect involves the protonation of, at least, one additional ionizable group respect to the protonation process corresponding to the binary complex formation.

Discussion

Similar features are obtained at pH 8 for the binding of both Fd and Fld to Anabaena FNR. Both Fd and Fld bind to FNR with moderate affinity corresponding to ΔG values of −8.0 and −7.6 kcal/mol. After removal of the influence of the buffer ionization, ΔG partitions into both favorable enthalpic and entropic contributions. In both cases, at least one proton is captured from the bulk solution upon binding. This coupled proton exchange makes the binding parameters pH-dependent, because they contain the contributions from the ionizable group(s) involved in such protonation.

ΔC_P values for the FNR interaction with Fd and, especially, with Fld are low compared to that of the binding of the smaller NADP⁺ coenzyme to FNR (Table 1). Despite these values being remarkably low for a protein-protein interaction, the size of a protein-protein interface does not necessarily correlate with the size of the proteins involved (44). In our particular case, Fd, smaller than Fld, appears to bind to FNR through a larger binding site than Fld. Studies on redox complexes have demonstrated that their protein-protein interfaces are poorly packed, exhibiting low geometric complementarity and small surface areas (45). These characteristics are advantageous because protein-protein interactions in redox reaction must be transient and exhibit fast k_off values. The lower ΔC_P value for Fld binding suggests an interaction interface in the Fld·FNR complex smaller than in the Fd·FNR complex. This is also in agreement with the reduced number of water molecules released upon Fld binding. ΔC_P values estimated at pH 8 and pH 10 are similar, suggesting similar surface area burial from the solvent and conformational change, if any, upon binding.

Stronger binding for both Fd and Fld to FNR is observed upon increasing the osmotic stress, again indicative of a net release of water molecules from the protein-protein interface. As expected, ΔH did not change significantly in the experiments done at different sucrose concentrations, and the effect of the osmotic stress was mainly entropic.

The lack of protonation coupled to binding at pH 10 allows estimating the intrinsic pH-independent binding parameters. Unexpectedly, the binding affinity slightly increases, corresponding to a ∼1 kcal/mol more favorable ΔG compared to the value obtained at pH 8. Because at pH 8 the binding of Fd or Fld to FNR is linked to a proton capture, at pH 10 the interaction was expected to be weaker due to the depletion in the free proton concentration available to be captured during binding. This inconsistency is not well understood, and further work beyond the scope of this study must be done to address this matter. At pH 10, ΔH_int is almost negligible (−0.4 kcal/mol), being the process clearly dominated by the entropic contribution (−8.7 and −8.2 kcal/mol for Fd and Fld, respectively) (Table 1). Therefore, the uptake of a proton at pH 8 significantly modulates the enthalpic and entropic contribution, and most of the contribution to the experimentally ΔH measured at pH 8 is due to the protonation event.

Previous work on spinach FNR showed similar results for Fd binding: binding entropically driven with a negligible binding enthalpy, a small ΔC_P upon binding (−160 cal/K·mol), and a protonation process coupled to the binding (21). Besides a His residue in FNR, the E92 residue from spinach Fd was also suggested to be involved in the proton exchange (22). According to the experimental analysis here presented (Table 1 and Fig. 2 A), His²⁹⁹ accounts for 60% of the protonation effect observed for the interaction at pH 8. The substitution of His²⁹⁹ by Phe also leads to a significant decrease in the binding affinity (ΔΔG = +1 kcal/mol), with a less favorable binding enthalpy (ΔΔH = +2.6 kcal/mol) and a more favorable binding entropy (−TΔΔS = −1.7 kcal/mol). This is the expected effect when replacing a polar residue involved in binding with an apolar residue: larger hydrophobic desolvation associated with an enthalpic penalty and an entropic gain.

The intrinsic binding enthalpy and binding heat capacity can be theoretically estimated from changes in the solvent ASA upon binding. These have been calculated using the crystallographic structure of the Fd·FNR complex and the modeled structures (homology modeling and docking calculations) of the Fd·FNR and Fld·FNR complexes (Table 2). The Anabaena Fd·FNR complex was previously classified into complexes with standard interface size (1600 ± 400 Ų), with a calculated value for ΔASA of 1660 Ų and showing a polarity of the interface equally polar and apolar (50:50) (45). However, according with our calculations the crystallographic Anabaena Fd·FNR model (16) and homology Fld·FNR model (18) belong to the redox complex group with small binding interface, and do not show equally distributed polar-apolar areas. Surprisingly, the reported docking models for both Fd·FNR and Fld·FNR show much larger binding interfaces, correlating in less extension with the experimental binding parameters (Table 2).

Despite differences in structure, shape, and redox cofactor, Fd and Fld bind to FNR with a very similar energetics. ΔC_P and n_w are the main differences detected so far. These two parameters are directly related to the hydrophobic character of the binding interface in the complex, and they reflect the different partition into polar and apolar surface area of the binding interface in the Fd·FNR and Fld·FNR complexes: both parameters, ΔC_P and n_w, are larger for the Fd·FNR complex, and it has been already mentioned that this complex contains a larger amount and percentage of apolar surface area. These results agree with previous studies based on mutations in hydrophobic residues of Fd and Fld (12–16,19,20).

Our data suggest that binding of apoFld to FNR is only slightly weaker than that of Fld (ΔΔG = +0.6 kcal/mol). However, all other thermodynamic parameters show significant changes. The binding enthalpy is less favorable (ΔΔH = +3.9 kcal/mol), whereas the binding entropy is more favorable (−TΔΔS =−3.2 kcal/mol). Besides, ΔC_P and n_H+ are very small compared to those of Fld. These values might arise from a reduced binding interface between apoFld and FNR or from a different relative binding orientation, resulting in a smaller desolvation and/or a lower conformational entropy penalty. This observed enthalpy-entropy compensation may reflect a conformational change upon binding different than that in holoFld interaction. This is also in agreement with the weaker interaction reported for the apoFld·FNR interaction when only changes in the FNR cofactor environment were monitored (20).

The influence of NADP⁺ on the binding of Fd and Fld to the preformed FNR·NADP⁺ complex shows strong negative cooperativity in both cases, corresponding to Δg values of −1.1 and −1.4 kcal/mol, respectively (Table 1). The energetics of the cooperativity phenomenon in the formation of both ternary complexes at pH 8 is rather similar. The cooperativity enthalpy is favorable (Δh of −2.4 kcal/mol and −5.7 kcal/mol, respectively), whereas the cooperativity entropy is unfavorable (−TΔs of 3.5 kcal/mol and 7.1 kcal/mol, respectively). The Gibbs energy penalty for the simultaneous binding of NADP⁺ and any of the protein carriers is not larger due to enthalpy-entropy compensation. If the global energetics of the ternary complexes formation is calculated, then, some differences appear: although the global Gibbs energy is similar (ΔG_AB values of −14.3 and −13.6 kcal/mol, respectively), the process is enthalpically driven (ΔH_AB values of −11.9 and −15.4 kcal/mol, respectively), and the global binding entropy is favorable for the Fd·FNR·NADP⁺ complex, whereas it is unfavorable for the Fld·FNR·NADP⁺ (−TΔS_AB values of −2.4 and +1.8 kcal/mol, respectively) (Table 1). This is in agreement with previous equilibrium studies showing that NADP⁺ decreases the association of spinach Fd with FNR (9). The sources of the negative cooperativity may be either direct ligand-ligand interactions (steric or electrostatic) or indirect ligand-ligand interactions produced through a conformational change elicited by the binding of the first ligand, both of them originating an energetic penalty for the binding of the second ligand. Previous kinetic studies showed that the oxidation-reduction state of Fd strongly affects its association with FNR, increasing the K_D at least 30-fold on Fd reduction (23). This observation has been related with conformational changes observed on the Fd interacting surface upon reduction (5) and suggests that conformational changes taking place during the ET process in the complex components will modulate the cooperativity. Fast kinetic studies also indicated that occupation of the NADP⁺ binding site of FNR by NADP⁺ greatly increased the rate of ET from Fd_rd to FNR, relieving inhibition by the produced Fd_ox, and suggested that substrate binding must be ordered during the physiological FNR action (3). All these observations point to an important role of the negative ternary interaction cooperativity to keep the high ET efficiency that characterizes FNR by facilitating the dissociation of either Fd or Fld once they have transferred the electron to the enzyme.

Differences and similarities in the cooperativity of Fd and Fld binding to FNR·NADP⁺ may be easily seen in a concentration-concentration phase diagram (Fig. 4), which is constructed from the calculation of the populations of the different FNR species (unbound FNR, binary complexes, and ternary complexes) at different concentrations (related to the chemical potential) of free Fd, Fld, and NADP⁺. The negative cooperativity (α < 1) in the binding of NADP⁺ and Fd or Fld to FNR is reflected in the asymmetry of the plots and the increase in the dissociation constants with NADP⁺ concentration, and the slightly larger cooperativity for Fld is observed in the slightly larger asymmetry in the Fld plot. According to the energy conservation principle, the effect of NADP⁺ at saturating concentration on the binding affinity of Fd (or Fld) to FNR is equal to the effect of Fd (or Fld) at saturating concentration on the binding affinity of NADP⁺ to FNR, and is given by the parameter α.

Figure 4.

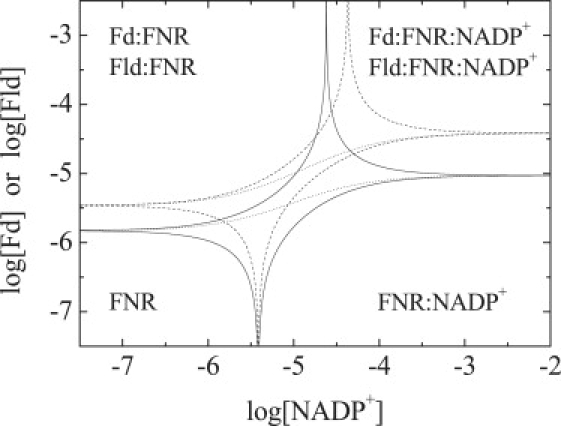
Phase diagram for the ternary equilibrium of the FNR system constructed concentrations of NADP⁺ and Fd, or Fld, as independent variables. The lines define the regions where a given species (free FNR, FNR·NADP⁺, Fd·FNR or Fld·FNR, Fd·FNR·NADP⁺, or Fld·FNR·NADP⁺) is populated at least 50% of the total FNR concentration (continuous lines for Fd and dashed lines for Fld). The intercepts with the left and right y axis are the dissociation constants for Fd and Fld interacting with FNR in the absence and the presence (at saturating concentration) of NADP⁺, respectively. The intercepts with the lower and upper x axis are the dissociation constants for NADP⁺ interacting with FNR in the absence (K_D,_Fd and K_D,_Fld) and the presence of NADP⁺ at saturating concentration (K_D,_Fd/α and (K_D,_Fld/α), respectively, of Fd or Fld. The sigmoidal dotted lines outline the dependence of the dissociation constant for Fd or Fld interacting with FNR as a function of NADP⁺ concentration.

Conclusions

Formation of the Fd·FNR and Fld·FNR complexes at pH 8 is both enthalpically and entropically driven, and characterized by a moderate affinity. The binding is coupled to the protonation of, at least, one ionizable group, and His²⁹⁹ on FNR has been identified as the main responsible for the proton uptake. However, the intrinsic pH-independent binding is dominated by the entropic contribution, with a negligible enthalpy. Therefore, the protonation process at pH 8 dictates the observed binding enthalpy at this pH. The interaction surfaces of Fd and Fld with FNR are small, with an important contribution from the hydrophobic effect to the binding, typical from redox transient protein-protein interactions. Additionally, the interaction between Fd and Fld with FNR is also coupled to the release of water molecules from the binding interface upon binding. The energetics of ApoFld binding to FNR does not relate to that of Fld. This suggests a different binding mode, and supports a direct role of the FMN molecule in the interaction of Fld with FNR.

The formation of the ternary complexes Fd·FNR·NADP⁺ and Fld·FNR·NADP⁺ is characterized by negative cooperativity. At pH 8, the formation of both ternary complexes is mainly enthalpically driven, being the total entropic effect small. Despite being structurally different, Fd and Fld bind to FNR with similar energetics: binding affinity, enthalpy, and entropy. Significant differences are only related to the somewhat different polarity and size of the binding interface when bound to FNR: ΔC_P and the number of water molecules released upon binding. Fld binds to a smaller region in FNR, and its residues are less critical in the interaction, in good agreement with previous studies (2,18,20).

Supporting Material

One figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00682-1.