Stability and Liquid-Liquid Phase Separation in Mixed Saturated Lipid Bilayers

Abstract

The phase stability of a fluid lipid bilayer composed of a mixture of DC₁₈PC, (DSPC), and a shorter ${\text{DC}}_{n_{\mathrm{s}}}$ PC, with n_s from 8 to 17, has been studied using a self-consistent field theory that explicitly includes molecular details and configurational properties of the lipid molecules. Phase separation between two liquid phases was found when there was a sufficient mismatch between the hydrophobic thicknesses of the two bilayers composed entirely of one component or the other. This occurs when n_s ≤ 12 and there is a sufficient concentration of the shorter lipid. The mixture separates into a thin bilayer depleted of DSPC and a thick bilayer enriched in DSPC. Even when there is no phase separation, as in the cases when there is either insufficient concentration of a sufficiently short lipid or any concentration of a lipid with n_s > 12, we observe that the effect of the shorter lipid is to increase the susceptibility of the system to fluctuations in the concentration. This is of interest, given that a common motif for the anchoring of proteins to the plasma membrane is via a myristoyl chain, that is, one with 14 carbons.

Introduction

There is much evidence that lateral lipid heterogeneities play an important role in many cell processes, such as signal transduction and membrane trafficking (1). To clarify the nature of these inhomogeneities, model membranes consisting of ternary mixtures of lipids and cholesterol have been studied, resulting in clear evidence that such systems undergo separation into two distinct, coexisting, liquid phases (2–9). Whether the heterogeneities in biological membranes reflect an incomplete phase separation, or is, instead, a local, spatially limited fluctuation, is uncertain. Indeed, the hypothesis that the plasma membrane itself contains many inhomogeneous regions remains a controversial one (10–13).

Instability of a liquid phase to coexisting liquid and gel phases is common and has been extensively studied (2,14–16). For example fluid-gel domain formation in mixtures of di-12:0 or dilauroyl phosphatidylcholine (DLPC) and di-18:0 or distearoyl PC (DSPC), have been studied by Leidy et al. (17). More recently, high-resolution imaging secondary-ion mass spectroscopy experiments on fluid-gel phase-separated DLPC-DSPC mixtures demonstrated composition variations within domains (18). Coexisting liquid and gel phases in DLPC-DSPC supported lipid bilayers have been investigated using atomic force microscopy and fluorescence microscopy experiments (19).

More relevant to biological membrane function is instability of the liquid phase to liquid-liquid coexistence, but evidence of its occurrence in binary lipid mixtures is rare. Only quick-freeze differential scanning calorimetry experiments have indicated, in di-14:0 or dimyristoyl PC (DMPC)-DSPC and DMPC-di-20:0 or di-arachidic PC (DAPC) mixtures, such phase coexistence (20). Other binary combinations of lipids investigated experimentally have been found to mix homogeneously in the liquid phase. For example, complete fluid phase miscibility has been reported in mixed DMPC-DSPC multilamellar suspensions using high sensitivity differential scanning calorimetry experiments (15). Fluorescence depolarization experiments employing di-7:0 PC (DHPC) to monitor the gel-fluid phase transition on two-component large multilamellar and small unilamellar liposomes suggested that di-16:0 or dipalmitoyl PC (DPPC) and DMPC randomly mix (21). Homogeneous mixing on fluid phase 1:1 DPPC-DLPC giant unilamellar vesicles was indicated by a two-photon excitation fluorescence microscopy study (22). Random mixing was also observed in fluid DMPC-DSPC mixtures by small-angle neutron scattering experiments (23).

Why miscibility in the liquid phase should be the general rule in most systems investigated is not completely clear, although the lack of a liquid-liquid transition might, of course, result from its preemption by the liquid-gel transition.

Given the possible biological importance of liquid instabilities, it is not surprising that the fluid phase of mixtures of PCs has been the subject of several theoretical studies. Jorgensen et al. (24) performed model simulations as well as calorimetry experiments on different two-component mixtures of DLPC, DMPC, DSPC, and DAPC, and found clustering of like lipids for the case of DAPC-DLPC, for which the difference in the chain length of the two species is the largest. Mean-field theory and Monte Carlo simulations applied to DMPC-DPPC, DMPC-DLPC, and DLPC-DSPC mixtures found that nonideal mixing of lipids increases as the chain length difference between the lipids increases (25).

These last two studies suggest that, of the many possible causes of liquid inhomogeneities, the case of hydrophobic mismatch merits further investigation. This concept (26) was first introduced to explain the fact that integral membrane proteins are fully active only if the hydrophobic thickness of the lipid bilayer host roughly matches the size of the hydrophobic region of the spanning protein. However, the influence of hydrophobic mismatch can also be observed in mixtures of lipid molecules alone (25,27). Lehtonen et al. (27) observed the mismatch-induced domain formation of 1-palmitoyl-2-[(pyren-1-yl)]decanoyl-sn-glycero-3-PC (PPDPC) in fluid bilayers of monounsaturated PCs with chain length ranging from 14 to 24 methyl segments. These authors suggested that lateral lipid organization is influenced by the length of the chain, and that hydrophobic mismatch induces lateral heterogeneities, which perhaps explains the presence in biological membranes of such a variety of lipids with different chain lengths. It is also known that sufficient mismatch can induce phase separation in systems of other amphiphiles, such as block copolymers (28,29).

As a consequence of the above, we have studied a homologous series of lipids to determine whether the effect of hydrophobic mismatch by itself could bring about phase separation in the liquid phase of a binary system of lipids. A molecular mean-field theory was used to evaluate the stability and concentration-dependent properties of planar, fluid-phase bilayers consisting of a binary mixture of DSPC and shorter chain PCs. The molecular theory explicitly incorporates the conformational degrees of freedom of the lipid molecules as well as molecular details of the different lipid species. The headgroup contributions are accounted for by a surface tension term. The theory accounts for the inhomogeneous distribution of the different molecules within the lipid bilayer which results from the hydrophobic packing repulsions as well as from the interfacial energy between the hydrophobic lipid core and the hydrophilic regions that confine the lipid layer. It has been previously shown to predict quantitatively the structure and conformational properties of lipid layers (30–33) in agreement with experiments (34,35) and molecular simulations (36,37). The theory we employ does not describe the gel phase, although it can be extended to do so (33).

In the next section, the molecular theory is presented. There follows a description of the numerical methodology used to solve the equations which result from the theory. A phase diagram is then obtained for the mixture as a function of concentration of one of the lipids. We find that a mixture of lipids ${\text{DC}}_{n_s}$ PC and DC₁₈PC (DSPC) can undergo phase separation when there is sufficient concentration of the shorter lipid provided that n _s ≤ 12. Even when there is no phase separation, as in the cases when there is either insufficient concentration of a sufficiently short lipid, or any concentration of a lipid with n _s > 12, we observe that the effect of the shorter lipid is to increase the susceptibility of the system to concentration fluctuations. Consequently, even if the liquid phase of the system does not undergo phase separation for whatever reason, including preemption by a liquid-gel transition, it is more readily driven to such separation by the addition of another short-chain lipid. This is of interest to the problem of raft formation given that a common motif for the anchoring of proteins to the plasma membrane is via a myristoyl chain, that is, one with only 14 carbons.

Molecular Theory

Consider a fluid, planar, lipid bilayer of thickness L, that is composed of N molecules of which a fraction x _l are lipids with two long, saturated, hydrophobic chains and a fraction x _s = 1−x _l are lipids with two short, saturated chains. (See schematic in Fig. 1.) The contributions to the free energy of the lipid hydrophobic hydrocarbon chains and that of the hydrophilic polar headgroups will be considered separately. To compute the contribution to the free energy from the system of interacting chains is, of course, an extremely difficult problem. However, as the main effect of the interactions is to produce a hydrophobic core of a density which is essentially constant throughout, it is reasonable to approximate the free energy of the system of interacting chains by one in which the chains do not interact, but in which the density is constrained to be constant (31,38). The assumption that the chains are independent permits the total free energy density per lipid, F/N, to be written in the form

$$\frac{\beta F}{N}=x_{\mathrm{l}}\sum _{{\alpha }_{\mathrm{l}}}P\left({\alpha }_{\mathrm{l}}\right)\left[\ln P\left({\alpha }_{\mathrm{l}}\right)+\beta \varepsilon \left({\alpha }_{\mathrm{l}}\right)\right]+x_{\mathrm{s}}\sum _{{\alpha }_{\mathrm{s}}}P\left({\alpha }_{\mathrm{s}}\right)\left[\ln P\left({\alpha }_{\mathrm{s}}\right)+\beta \varepsilon \left({\alpha }_{\mathrm{s}}\right)\right]+x_{\mathrm{l}}\ln x_{\mathrm{l}}+x_{\mathrm{s}}\ln x_{\mathrm{s}}+\beta {\gamma }_0\frac{A}{N},$$ (1)

where β = 1/k _B T, the sums are over the lipid conformations, α _i (i = l, s) of a single chain, and P(α _i) is the probability of finding the molecular species i in conformation α _i. One recognizes the first term in the sums as the conformational entropy of the long and short chains, respectively. The second term in each sum is the internal energy of the chain, ɛ(α _i), in the conformation α _i, an energy that arises from the gauche bonds whose energies exceed that of the trans configuration. The third and fourth terms are the entropy of mixing of the different lipids. The last term accounts for the surface free energy, at both interfaces, between the hydrophobic region within the lipid bilayer and the aqueous environment outside the layer. The total area of the system, including both interfaces, is A, and the water-hydrocarbon interfacial tension is γ ₀. The effect of the headgroups is included in the above only to the extent that their interactions affect the area per lipid, a role taken by the parameter γ ₀, and they tend to keep the density of the hydrophobic core constant even up to those carbons closest to the water interface. We have ignored terms in the free energy that are linear in the number of lipids of either length, as such terms simply alter the zero of the lipid chemical potentials.

Figure 1.

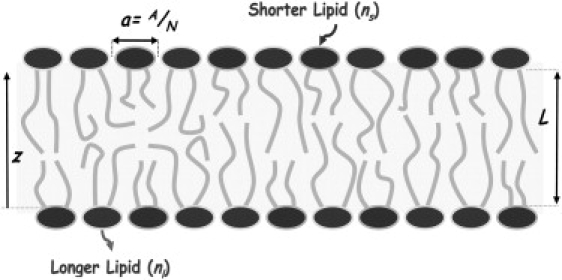
Schematic representation of the system containing a mixture of long and short lipids. The drawing represents a lipid bilayer that is a mixture of two double-chained lipids with acyl-chain lengths n_l (long, n_l = 18 corresponding to DSPC) and n_s (short, n_s = 8, 9, …, 17). The fraction of long lipids is x_l.

The constraint of constant density throughout the core must still be imposed. This constraint requires that

$$x_{\mathrm{l}}\langle {\varphi }_{\mathrm{l}}\left(z\right)\rangle dz+(1-x_{\mathrm{l}})\langle {\varphi }_{\mathrm{s}}\left(z\right)\rangle dz=\frac{V}{NL}dz;0\le z\le L\text{.}$$ (2)

The terms on the left-hand side of Eq. 2 are the fraction of the total volume per molecule occupied by long and short lipids between z and z + dz. The volumes 〈ϕ _i(z)〉 dz are those that independent chains of species i would occupy between z and z + dz; note that the total volume of a lipid species i is given by $v_{\text{i}}={\int }_0^{\mathrm{l}}\langle {\varphi }_{\text{i}}\left(z\right)\rangle dz\left(i=l,s\right)$. The brackets, 〈…〉, denote ensemble averages over the corresponding probability-density functions. It should be observed that the packing constraint as expressed in Eq. 2 assumes that any variation in the density of the different chains can only arise in the z direction, perpendicular to both interfaces. This is an assumption we shall consider more closely later.

The probability-density functions for both lipid molecules are obtained through minimization of the free energy, Eq. 1, subject to the hydrophobic packing constraint, Eq. 2. For this, position-dependent Lagrange multipliers, π(z), are introduced and one obtains for the long-lipid molecules

$$P\left({\alpha }_{\mathrm{l}}\right)=\frac{1}{q_{\mathrm{l}}}\exp \left[-\beta \varepsilon \left({\alpha }_{\mathrm{l}}\right)-\int \beta \pi \left(z\right){\varphi }_{\mathrm{l}}({\alpha }_{\mathrm{l}};z)dz\right],$$ (3)

where q _l is the partition function defined as

$$q_{\mathrm{l}}=\sum _{{\alpha }_{\mathrm{l}}}\exp \left[-\beta \varepsilon \left({\alpha }_{\mathrm{l}}\right)-\int \beta \pi \left(z\right){\varphi }_{\mathrm{l}}({\alpha }_{\mathrm{l}};z)dz\right]\text{.}$$ (4)

This ensures that the probability density function of the long-lipid species is properly normalized. The volume that the long-lipid hydrocarbon chain occupies in configuration α _l between z and z + dz is ϕ _l(α _l;z)dz, such that $\langle {\varphi }_{\mathrm{l}}\left(z\right)\rangle =\sum _{{\alpha }_{\mathrm{l}}}P\left({\alpha }_{\mathrm{l}}\right){\varphi }_{\mathrm{l}}({\alpha }_{\mathrm{l}};z)$. A similar expression is obtained for the short lipids

$$P\left({\alpha }_{\mathrm{s}}\right)=\frac{1}{q_{\mathrm{s}}}\exp \left[-\beta \varepsilon \left({\alpha }_{\mathrm{s}}\right)-\int \beta \pi \left(z\right){\varphi }_{\mathrm{s}}({\alpha }_{\mathrm{s}};z)dz\right],$$ (5)

where q _s is the partition function of the short lipids and ϕ _s(α _s;z)dz is the volume that a chain in configuration α _s occupies in the region between z and z + dz.

The Lagrange multipliers, π(z), can be interpreted as the z-dependent, repulsive, average fields acting on the molecule such that the packing constraint is fulfilled at all z. Note, that these average fields are determined self-consistently from the ensemble average of the volume elements of all the different molecular species. For more detailed discussions on the interpretation of the Lagrange multipliers and the thermodynamic consequences of the incompressibility assumption, the reader is referred to the literature (31,32,38).

Lipid models and numerical methodology

The calculation of the total free energy of the system and, consequently, any quantity of interest, essentially reduces to the numerical evaluation of the z-dependent lateral pressure, π(z). This quantity is obtained by substituting the expressions for the probability distribution functions of both lipids, Eqs. 3 and 5, into the packing constraint equation, Eq. 2. In practice, the continuous bilayer is discretized into layers of thickness δ and integrals are replaced by sums over these layers. As a result of this discretization, a finite set of equations is obtained which expresses the packing constraint at particular, discrete, values of the coordinate z. These equations require as inputs the long-lipid concentration, x _l, and the volume distribution for the different conformations of both lipids. For the latter, a molecular model for the lipid species needs to be introduced. The lipid molecules are modeled as double-chained saturated hydrocarbon chains where both chains in each lipid are equally long and contain (n _i − 2) CH₂ groups and a terminal CH₃. The number of carbon atoms, n _i, in the chain is also referred to as the size, or length, of the lipid. Each CH₂ group has a volume, v ₀ = 27 ų, while the CH₃ groups are modeled as having a volume equal to 2v ₀ (39). An example of the experimental system modeled here is a planar-supported bilayer consisting of a mixture of DSPC and DLPC. In our model, this combination corresponds to n _l = 18 (DSPC) and n _s = 12 (DLPC). We consider binary mixtures of DSPC and a lipid with shorter chains as a function of the length of the chains of the short lipid, which is varied from 8 ≤ n _s ≤ 17.

The lipid chains are characterized within the rotational isomeric model (40) in which each carbon segment can assume three different configurations: trans, gauche-plus, and gauche-minus. The energy of a gauche configuration is greater than that of the trans conformation by 0.84 k _B T for a temperature T = 300 K. After a chain conformation, α _i, for species i is generated, the discretized volume distribution ϕ _i(α _i, j), j = 1, 2, …, M is obtained by simply counting the number of segments contained within each layer and multiplying this by the volume of the group. In other words, ${\varphi }_{\text{i}}({\alpha }_{\text{i}},j)={\tilde{n}}_{\text{i}}({\alpha }_{\text{i}},j)v_0$, where ${\tilde{n}}_{\text{i}}({\alpha }_{\text{i}},j)$ is the number of segments contained within the planes z = (j − 1)δ and z = jδ for that particular chain and δ is set equal to 2 Å. Changing the value of δ between 1 and 2.5 Å does not change any of the results.

To generate all the configurations of the lipid chains that we employ, we first generate the whole set of bond sequences for the given number of chain segments. The Cartesian coordinates of each segment, for a given sequence, are obtained by matrix multiplication and the first segment is placed at the origin of the coordinate system, i.e., at the interface. Then, we check that all segments in the chain are self-avoiding. After this step, a number of rotations (typically 12 or 24) about randomly selected axes that intersect the origin of coordinates are attempted for both types of lipid molecules. Finally, if the chain does not extend into the surrounding water, but is completely contained within the planes z = 0 and z = L, the configuration is accepted and the distribution of volumes is calculated. Note that the two tails of each lipid are considered independent of each other. The chain model used here as well as the independent tails approximation have been shown to provide very good agreement with predictions from full atomistic MD simulations (32).

As both kinds of lipids are treated as noninteracting, the total probability of a configuration is simply the product of the probabilities of each chain in that configuration. The contribution of the hydrophilic polar headgroups of the lipids is included by means of the surface tension term in the free energy; see Eq. 1. The phenomenological surface tension, γ ₀, is taken as 0.1 k _B T Å⁻², which corresponds to 41 dynes/cm at T = 300 K. This value is of the order of the experimental one for the oil-water interfacial tension (41). The dependence of our results on the value of γ ₀ on the stability of the mixed bilayer is studied.

After discretization of the set in Eq. 2, we are left to solve

$$x_{\mathrm{l}}\sum _{{\alpha }_{\mathrm{l}}}P\left({\alpha }_{\mathrm{l}}\right){\tilde{n}}_{\mathrm{l}}({\alpha }_{\mathrm{l}},j)+(1-x_{\mathrm{l}})\sum _{{\alpha }_{\mathrm{s}}}P\left({\alpha }_{\mathrm{s}}\right){\tilde{n}}_{\mathrm{s}}({\alpha }_{\mathrm{s}},j)=\frac{V}{NM{v}_0};j=1,2,\dots ,M,$$ (6)

which, as the probability distribution functions of Eqs. 3 and 5 depend on the lateral pressure at all levels j, constitute a set of M nonlinear, coupled equations for the pressure π(j). Note that for a calculation at a particular value of x _l, the right-hand side of Eq. 6 is constant for all j = 1, 2, …, M. The probability distribution function of the long-lipid molecules reduces, in its discrete form, to

$$P\left({\alpha }_{\mathrm{l}}\right)=\frac{1}{q_{\mathrm{l}}}\exp \left[-\beta \varepsilon \left({\alpha }_{\mathrm{l}}\right)-\sum _{\mathrm{j}=1}^M\beta \pi \left(j\right){\tilde{n}}_{\mathrm{l}}({\alpha }_{\mathrm{l}};j)v_0\right],$$ (7)

and the partition function is now

$$q\left({\alpha }_{\mathrm{l}}\right)=\sum _{{\alpha }_{\mathrm{l}}}\exp \left[-\beta \varepsilon \left({\alpha }_{\mathrm{l}}\right)-\sum _{\mathrm{j}=1}^M\beta \pi \left(j\right){\tilde{n}}_{\mathrm{l}}({\alpha }_{\mathrm{l}};j)v_0\right]\text{.}$$ (8)

A similar expression is obtained for the probability distribution function of the short lipid species.

Note that as the volume of the bilayer core of a given lipid mixture is fixed, specifying a particular value for the bilayer thickness also specifies the average area per lipid headgroup a = A/N. For a given concentration, x _l, we perform calculations for different bilayer thicknesses and thereby obtain the free energy of the mixture as a function of the area per lipid headgroup, for each concentration (see Fig. 2 A). The optimal mixed lipid bilayer is that which minimizes the free energy as a function of the area per lipid headgroup, at the given x _l; i.e., at the area per lipid at which the surface tension γ vanishes.

Figure 2.

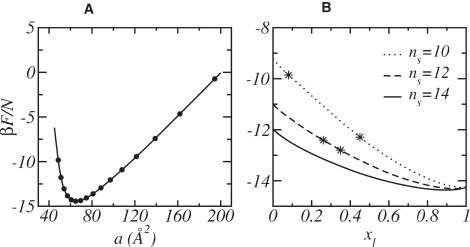
(A) Free energy per lipid as a function of the area per headgroup, a, for a mixed lipid bilayer with n_s = 16 and x_l = 0.50. (B) Free energy per lipid as a function of the concentration, x_l, of the longer lipid. For each composition, the values of the free energy correspond to the tensionless membrane, i.e., the area at which the free energy is minimal (see A). The different curves correspond to different short lipids, as denoted in the figure. The stars show the compositions of coexistence between the two lipid layers.

This procedure has been repeated for different long-lipid concentrations from x _l = 0 to 1 in intervals of Δx _l = 0.01. The results for the free energy per lipid at vanishing surface tension as a function of concentration is shown in Fig. 2 B for three different lengths of the short chains. The absolute value of the free energy is not of interest as it is only defined to within an arbitrary additive constant. In the case of n _s = 14 the free energy shows a positive curvature at all compositions and thus, the binary mixture is stable. However, for the two shorter chain lengths there is a region of compositions, whose limits are denoted in the figure by stars, where the mixtures are unstable, i.e., the curvature of the free energy is negative. For compositions within this unstable region, the system separates into two macroscopic phases with the compositions marked by the stars. It is interesting to note the highly nonideal mixing that arises from the different packing of the two chains. As the only ideal contribution to the free energy is given by the entropy of mixing, x _l lnx _l + x _s lnx _s, the shape of the free energy is dominated by the highly nonideal conformational free energy of the lipids.

Configurational or thermodynamic properties of the mixed lipid bilayer shown in this study are those of the optimal system at the given concentration. For a more detailed explanation of this optimization procedure as well as of the thermodynamic analysis used to evaluate the stability of the mixture, see Longo et al. (42).

Results

We find that, at T = 300 K, a mixture of ${\text{DC}}_{n_{\mathrm{s}}}$ PC and DC₁₈PC (DSPC) is stable to phase separation at all concentrations when the chain lengths do not differ significantly, n _s > 12, but do phase-separate over some range of concentrations when the mismatch between chain lengths is larger. Fig. 3 shows a phase diagram at fixed temperature for mixtures of DSPC and shorter PCs as a function of concentration of DSPC, x _l. The binodal curve, shown in Fig. 3, separates the stable and metastable phase regimes. The stability of the mixed bilayer depends on the size of the short lipid, n_s, and the DSPC concentration, x _l. In the cases that a phase separation is predicted, the mixture is stable both at very low DSPC concentrations and at high concentrations, >∼0.5. The range of concentrations over which the system is unstable increases as the disparity between the chain lengths of the two components increases. The phase diagram is quite asymmetric with a low concentration of long-chain lipids in the phase rich in short-chain lipids, but a significant fraction of short-chain lipids in the phase rich in long-chain lipids. This results from the fact that the gain in translation entropy achieved when long-chain lipids enter a bilayer rich in short-chain lipids does not make up for the loss in configurational entropy of the long chains when they do so. The reverse is true when short-chain lipids enter a bilayer rich in long-chain lipids. The occurrence of such asymmetries is well known for polymer brushes exposed to a solution of similar polymers but of a different polymerization index (43).

Figure 3.

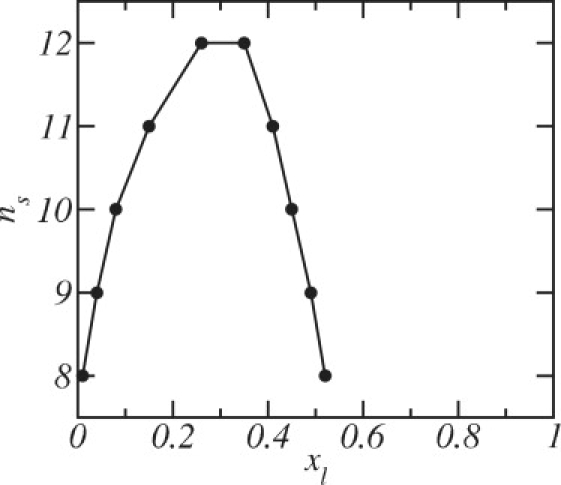
Stability diagram for fluid phase mixtures of DSPC of composition x_l and short lipids of chain length n_s. The region outside the binodal correspond to concentrations at which the mixture is stable. The points in the binodal curve represent the DSPC concentrations of stable bilayers at coexistence.

Fig. 4 displays the thickness of the mixed bilayer as a function of the size of the shorter PC at coexistence. The figure shows that the difference in membrane thickness between the thin and thick phases increases as the difference between the lengths of the two chains increases. These values for the thicknesses of the lipid bilayers represent the size of the hydrophobic region only and are not to be compared with the total thickness of lipid layers often reported in experiments, a thickness that includes both the hydrophobic and hydrophilic regions of layers that are in contact with an external aqueous medium.

Figure 4.

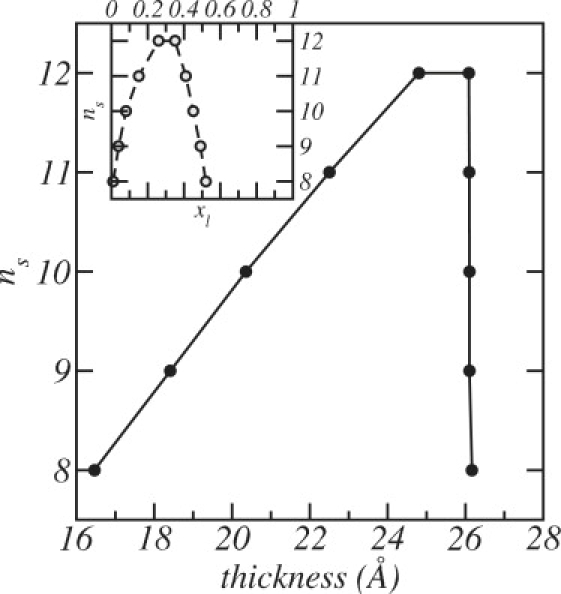
The thicknesses of the lipid bilayer versus n_s for concentrations that correspond to coexistence between the two liquid phases. The DSPC concentrations at coexistence of each bilayer can be obtained from Fig. 3, which is reproduced in the inset.

An interesting feature of Fig. 4 is that the thickness of the DSPC-rich bilayer is relatively constant (≈26 Å), independent of the size of the short lipid, while the thickness of the thin, or DSPC-poor, phase increases almost linearly with the size of the short lipid chain.

This linear increase in the thickness of the DSPC-poor phase with the chain length of the majority component is similar to the increase of the thickness of pure bilayers with the length of the chain of the single component, a dependence shown in Fig. 5. Thus the results of Fig. 4 indicate that the thickness of the mixed bilayer is essentially determined by its majority component. Our results suggest, therefore, that the origin of the phase behavior observed in Fig. 3 is associated with the difference in membrane thickness of the pure lipid bilayers; i.e., that hydrophobic mismatch between short and long lipid molecules is the driving force of the liquid-liquid phase separation.

Figure 5.

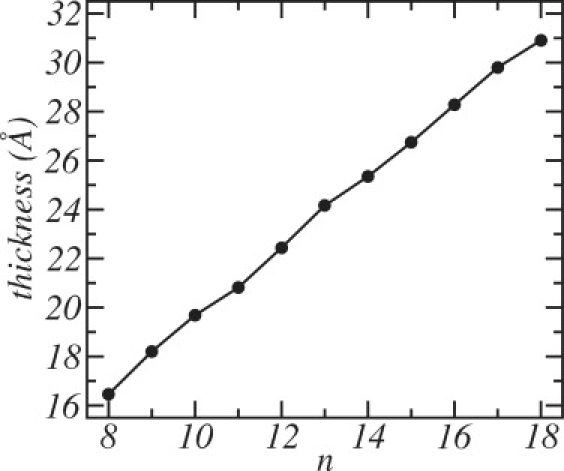
The thickness of pure bilayers as a function of the lipid chain length, n.

Were the length, n _s, of the shorter lipid chain a continuous, rather than a discrete, variable, the stability diagram of Fig. 3 would exhibit a critical point at which the difference in thickness of coexisting liquid phases would vanish. Although such a critical point cannot be reached because the chain lengths are discrete, it is expected to have real consequences in the physical systems. In particular, one expects that even when the system does not undergo phase separation, concentration fluctuations should be very large when the chain length is near the critical value, which is somewhat larger than 12. To verify this, we plot in Fig. 6 the isothermal composition susceptibility at constant, vanishing, surface tension

$${\kappa }_{T,\gamma =0}\equiv \frac{1}{N}{\left(\frac{\partial (N_{\mathrm{l}}-N_{\mathrm{s}})}{\partial ({\mu }_{\mathrm{l}}-{\mu }_{\mathrm{s}})}\right)}_{T,\gamma =0}$$ (9)

$$={\left(\frac{{\partial }^2{f}_N}{\partial x_{\mathrm{l}}^2}\right)}_{T,\gamma =0}^{-1},$$ (10)

where f_N is the free energy per particle of the system. We show in the Appendix that this quantity is related to the fluctuations in the composition via

$${\kappa }_{T,\gamma }=\frac{N}{kT}\left[{\langle {\hat{x}}_{\mathrm{l}}^2\rangle }_{T,\gamma }-{\langle {\hat{x}}_{\mathrm{l}}\rangle }_{T,\gamma }^2\right],$$ (11)

where the brackets denote an ensemble average, and ${\hat{x}}_{\mathrm{l}}$ is a fluctuating variable with ensemble average of x _l. When the size of the lipids roughly match (n _s = 17; open diamonds), the mixing is nearly ideal and the main contribution to the isothermal composition susceptibility is the mixing entropy term in the free energy, Eq. 1. As n _s and x _l approach critical values, however, larger fluctuations in concentration are indeed observed in Fig. 6.

Figure 6.

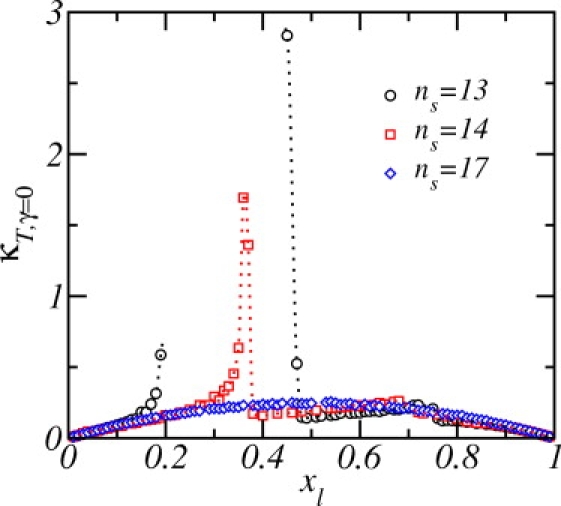
Isothermal composition susceptibility at vanishing surface tension in the liquid phase as a function of the concentration of long lipids, x_l, for various lengths of the shorter chain. The dotted lines are simply guides for the eyes.

Note that the data shown in Fig. 6 was calculated numerically from curves f _N versus x _l (see for example, Fig. 2 B). Because the quantity of interest, κ _{T, γ=0} , is the inverse of the second derivative of f_N(x _l) and because this susceptibility diverges at the critical point, the numerical errors involved in calculating κ _{T, γ=0} are large near the critical point. In particular, for n _s = 13 (open black circles), only a few points could be obtained in its vicinity. The shape of the curve and the trends observed in the figure, however, allows us to conclude that the fluctuations in concentration are, in fact, very large over a considerable region spanning the critical composition. In other words, short lipids in a concentration not necessarily near the critical one can nevertheless induce large fluctuations in the stable mixed lipid bilayer.

There are no adjustable parameters in our molecular theory; however, the phenomenological value of the hydrocarbon-water interfacial tension, γ ₀, does play a role in determining the actual shape of the phase diagram. The value of γ ₀ used in all the calculations shown above is 0.1 k _B T Å⁻², which corresponds to 41 dyn/cm at T = 300 K. The experimental values for γ ₀ at room temperature are between 30 and 50 dyn/cm (41). In reality, γ ₀ is an effective surface tension since it includes in it the effect of the repulsions between the headgroups. For the lipids treated here, the repulsions between the tails are more dominant that the headgroup repulsions. This can be seen by the predicted area per lipid at equilibrium (Fig. 2 A), which is in very reasonable agreement with the experimental values in the liquid phase.

Fig. 7 shows stability diagrams n _s versus x _l using different values of the water-oil interfacial tension. The cases where βγ ₀ = 0.08, 0.10, and 0.12 Å⁻² are considered, which correspond to γ ₀ = 33, 41, and 49 dyn/cm at T = 300 K, respectively. When βγ ₀ = 0.10 Å⁻², the phase diagram is the same as that presented in Fig. 3. A change in the value of the water-oil interfacial tension has an important effect on the quantitative results such that the phase diagram is shifted vertically and horizontally. However, the qualitative nature of the mismatch-induced phase separation remains the same. Consider the case βγ ₀ = 0.10 Å⁻² as a reference. If the strength of the interfacial tension is increased to βγ ₀ = 0.12 Å⁻², the stability diagram moves its symmetry axis to a lower DSPC concentration because a smaller area per headgroup with its concomitant increase in the bilayer thickness is now favored. This increased thickness favors the DSPC, so less of it is needed to destabilize the liquid rich in short lipids. In contrast, if the strength of the interfacial tension is weakened to βγ ₀ = 0.08 Å⁻², the phase diagram is shifted downward because this tension now favors the thinning of the mixed bilayer and, with the concomitant increase in the area per lipid, the influence of the hydrophobic mismatch is reduced.

Figure 7.

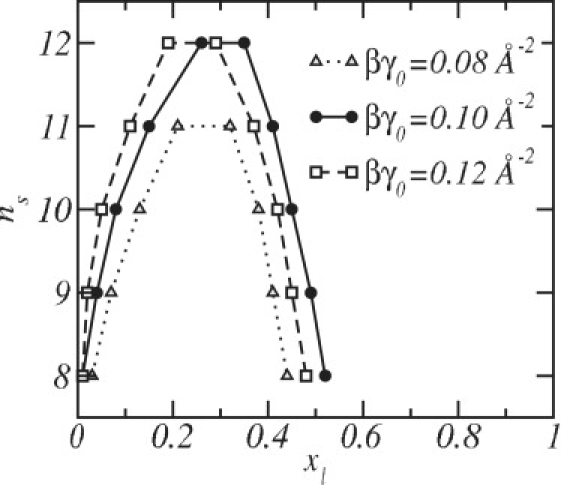
Stability diagrams using different values of the oil-water surface tension, γ₀.

Discussion

A molecular, mean-field theory has been employed to study the influence of thickness mismatch on the stability of planar lipid bilayers. We considered mixtures of DC₁₈PC, or DSPC, and a shorter lipid ${\text{DC}}_{n_{\mathrm{s}}}$ PC, with n _s = 8, 9, …, 17. As noted earlier, we have assumed that the thickness of the mixed bilayer is uniform in any phase. This assumption deserves some justification, as it is conceivable that a mixture of two lipids of different lengths might aggregate locally. If so, they would do so to increase the interaction energy between similar lipids, a gain characterized by some energy per unit area σ. Of course, this also entails a penalty of creating a boundary between the region and its surroundings which, being of different composition, will be of different thickness. This boundary costs an energy λ per unit length. Balancing these two contributions, one finds a characteristic size of such a region of R ₀ ≈ λ/σ, and a characteristic energy E ₀ ≈ πR ₀ λ. One knows that if E ₀ ≈ k _B T, then such patches are thermally excited. The effect of such fluctuations are manifest in the broadening of the distribution function of areal densities within the membrane, and in the behavior of the density-density correlation function. Precisely this behavior has recently been observed in the vicinity of a critical point (44,45); but, except near critical points, such fluctuations are observed to be small (44), so that one can conclude πR ₀ λ << k _B T. Taking a typical value of line tension in membranes to be of ∼0.2 pN (44), one finds that at biological temperatures R ₀ < < 6 nm, and can, therefore, be ignored. This conclusion is in agreement with the work of Dewa et al. (46), who looked for local clustering in a mixture of DMPC and DSPC but found none.

A phase diagram for such mixtures at T = 300 K was calculated. The binary mixture undergoes phase separation in the cases for which n _s is ≤12, which corresponds to DLPC. The coexisting phases are stable at very low DSPC concentrations where the majority component of short lipid primarily determines the thickness of the mixed bilayer, and at large concentrations of DSPC where this majority component again determines the thickness of the stable bilayer. The instability of the liquid phase is driven by the hydrophobic mismatch of the two components, and the difference in thickness of coexisting bilayers increases as this mismatch increases. The instability vanishes when the mismatch in chain lengths is less than six CH₂ segments. However. the precise value at which it vanishes is sensitive to factors affecting the area per lipid, such as the interactions between polar headgroups. These results are consistent with experimental results, which suggest that systems mix homogeneously when the difference in the chain lengths of the components is less than six. In particular, our results are in agreement with the observation that mixtures of DSPC and DMPC (an n _s of 14) do not phase-separate (23,46).

The prediction that binary mixtures with a larger mismatch should phase-separate assumes, of course, that such a transition has not been preempted by a liquid-gel transition. That the liquid-liquid separation in DLPC-DSPC mixtures at T = 100 K indicated in Fig. 3 is, in fact, preempted by a liquid-gel transition is clear from the phase diagram of this system (15). However, even if the transition does not occur, either because the mismatch is too small or because it is preempted, we have shown that the presence of shorter lipids in a bilayer composed of longer ones increases the susceptibility of the bilayer to fluctuations of composition. Given that one common motif for the anchoring of proteins to the plasma membrane is via a short myristoyl anchor and that lipid rafts may simply be due to local fluctuations of composition (10,11), our results suggest the possibility that the very mechanism of protein anchoring may induce the formation of the raft to which it anchors and may explain the very dynamic nature of the domains (47).

Appendix

Consider a bilayer system of two components, l and s. Its surface-excess free energy (48,49), F(T, N _l, N _s, A), is

$$F={\mu }_1{N}_1+{\mu }_{\mathrm{s}}{N}_{\mathrm{s}}+\gamma A,$$ (12)

$$dF=-SdT+{\mu }_{1}d{N}_1+{\mu }_{\mathrm{s}}d{N}_{\mathrm{s}}+\gamma dA\text{.}$$ (13)

Introduce the variables

$$N=N_{\mathrm{l}}+N_{\mathrm{s}},$$ (14)

$$\delta N=\frac{1}{2}(N_{\mathrm{l}}-N_{\mathrm{s}})\text{.}$$ (15)

The free energy expressed in terms of these variables, F(T, N, δN, A), is

$$F=\frac{{\mu }_{\mathrm{l}}+{\mu }_{\mathrm{s}}}{2}N+\delta \mu \delta N+\gamma A,$$ (16)

$$dF=-SdT+\frac{{\mu }_{\mathrm{l}}+{\mu }_{\mathrm{s}}}{2}dN+\delta \mu d\delta N+\gamma dA,$$ (17)

where δμ ≡ μ _l − μ _s. Because the surface tension will be held fixed, it is convenient to rewrite the above in terms of the independent variables T, N _l, N _s, and γ,

$$dF=-\left[S+\gamma {\left(\frac{\partial A}{\partial T}\right)}_{N,\delta N,\gamma }\right]dT+\left[\frac{{\mu }_l+{\mu }_{\mathrm{s}}}{2}+\gamma {\left(\frac{\partial A}{\partial N}\right)}_{T,\delta N,\gamma }\right]dN+\left[\delta \mu +\gamma {\left(\frac{\partial A}{\partial \delta N}\right)}_{T,N,\gamma }\right]d\delta N+\gamma {\left(\frac{\partial A}{\partial \gamma }\right)}_{T,N,\delta N}d\gamma \text{.}$$ (18)

Thus, when the surface tension is held fixed at the value zero,

$$\delta \mu ={\left(\frac{\partial F}{\partial \delta N}\right)}_{T,N,\gamma =0}\text{.}$$ (19)

Introducing the concentration

$$x_{\mathrm{l}}=\frac{N_{\mathrm{l}}}{N}=\frac{\delta N}{N}+\frac{1}{2}$$ (20)

and the surface free energy per lipid f _N = F/N, we can write the above as

$$\delta \mu ={\left(\frac{\partial f_N}{\partial x}\right)}_{T,\gamma =0}\text{.}$$ (21)

From an additional derivative with respect to the composition, we obtain the isothermal composition susceptibility at zero surface tension

$${\kappa }_{T,\gamma =0}={\left(\frac{\partial x}{\partial \delta \mu }\right)}_{T,\gamma =0},$$ (22)

$$={\left[{\left(\frac{{\partial }^2{f}_N}{\partial x_{\mathrm{l}}^2}\right)}_{T,\gamma =0}\right]}^{-1},$$ (23)

which is Eq. 10 in the text.

More generally, the isothermal composition susceptibility at arbitrary, but constant, surface tension is obtained by considering the system when both the composition and area fluctuate, their average values being determined by δμ and γ, respectively. The thermodynamic potential which is a natural function of T, N, δμ, and γ is

$$J=F-\delta \mu \delta N-\gamma A=\frac{{\mu }_{\mathrm{l}}+{\mu }_{\mathrm{s}}}{2}N,$$ (24)

$$dJ=-SdT+\frac{{\mu }_{\mathrm{l}}+{\mu }_{\mathrm{s}}}{2}dN-\delta Nd\delta \mu -Ad\gamma ,$$ (25)

where Eqs. 16 and 17 have been used. From this potential, it follows that

$$\delta N=-{\left(\frac{\partial J}{\partial \delta \mu }\right)}_{T,N,\gamma },$$ (26)

$${\kappa }_{T,\gamma }\equiv {\left(\frac{\partial x}{\partial \delta \mu }\right)}_{T,\gamma },$$ (27)

$$=-{\left(\frac{{\partial }^2{j}_N}{\partial {\delta }^2\mu }\right)}_{T,\gamma },$$ (28)

where j_N = J/N.

We now determine the fluctuations to which κ is related. Because the free energy F is obtained from

$$\exp [-\beta F]=Tr\exp [-\beta \hat{H}],\beta \equiv 1/k_{\mathrm{B}}T,$$ (29)

with $\hat{H}$ the Hamiltonian of the system, and because the thermodynamic potential J is related to F by J = F − δμδN − γA, it follows that

$$\exp \left[-\beta J\right]=Tr\exp \left[-\beta (\hat{H}-\delta \mu \delta \hat{N}-\gamma \hat{A})\right],$$ (30)

where $\hat{A}$ is a fluctuating variable to be integrated over and $\delta \hat{N}$ a discrete variable to be traced over. From this it follows that

$${\langle \delta \hat{N}\rangle }_{T,N,\gamma }=-{\left(\frac{\partial \beta J}{\partial \beta \delta \mu }\right)}_{T,N,\gamma }=\delta N,$$ (31)

and

$${\langle {\left(\delta \hat{N}\right)}^2\rangle }_{T,N,\gamma }-{\langle \delta \hat{N}\rangle }_{T,N,\gamma }^2=-{\left(\frac{{\partial }^2\beta J}{\partial {\left(\beta \delta \mu \right)}^2}\right)}_{T,N,\gamma }={\left(\frac{\partial \delta N}{\partial \beta \delta \mu }\right)}_{T,N,\gamma }\text{.}$$ (32)

Define the fluctuating variable $\hat{x}\equiv \hat{\delta }N/N$, so that the above equation yields

$${\langle {\hat{x}}^2\rangle }_{T,\gamma }-{\langle \hat{x}\rangle }_{T,\gamma }^2=-\frac{1}{N}{\left(\frac{{\partial }^2\beta j_N}{\partial {\left(\beta \delta \mu \right)}^2}\right)}_{T,\gamma }=\frac{1}{N\beta }{\left(\frac{\partial x}{\partial \delta \mu }\right)}_{T,\gamma }$$ (33)

$$=\frac{{\kappa }_{T,\gamma }}{N\beta },$$ (34)

which is Eq. 11 in the text.