Abstract
A charge transport (CT) mechanism has been proposed in several articles to explain the localization of base excision repair (BER) enzymes to lesions on DNA. The CT mechanism relies on redox reactions of iron-sulfur cofactors that modify the enzyme's binding affinity. These redox reactions are mediated by the DNA strand and involve the exchange of electrons between BER enzymes along DNA. We propose a mathematical model that incorporates enzyme binding/unbinding, electron transport, and enzyme diffusion along DNA. Analysis of our model within a range of parameter values suggests that the redox reactions can increase desorption of BER enzymes not already bound to lesions, allowing the enzymes to be recycled—thus accelerating the overall search process. This acceleration mechanism is most effective when enzyme copy numbers and enzyme diffusivity along the DNA are small. Under such conditions, we find that CT BER enzymes find their targets more quickly than simple passive enzymes that simply attach to the DNA without desorbing.
Introduction
The genomes of all living things can be damaged by ionizing radiation and oxidative stress. These factors can cause mismatches in the DNA strand, resulting in localized lesions. The role of base excision repair (BER) enzymes is to locate and remove these lesions. If the lesions are allowed to persist, they can give rise to mutations and ultimately diseases such as cancer.
The localization of BER enzymes to lesions is physically related to the binding of transcription factors to promoter regions that regulate gene expression. In 1970, experiments by Riggs et al. (1,2) showed that the association rate of the LacI repressor to its operator is ∼100 times faster than the maximum rate predicted by Debye-Smoluchowski theory. This theory assumes that LacI is transported to its target on DNA via three-dimensional diffusion. To explain the experimental observations, the theory was modified to account for facilitated diffusion (3–5). In this process, the LacI repressor can spend part of its time attached to the DNA and perform a one-dimensional random walk before detaching and diffusing in three dimensions again (see Fig. 1). Provided the protein spends approximately half its time on the DNA and half its time in solution, and the diffusivities in one and three dimensions are comparable, the predicted search time can be reduced by as much as 100-fold (6). However, these conditions are very restrictive, as the protein can spend up to 99.99% of its time associated to the DNA (7) and the diffusion constant along DNA (in one dimension) is, in general, much smaller than the one in the cytoplasm (in three dimensions) (8). Therefore, many modifications of the basic facilitated diffusion theory have been proposed, including intersegmental transfers (9), the effect of DNA conformation (10), directed sliding (11), and finite protein concentration (12).
Figure 1.
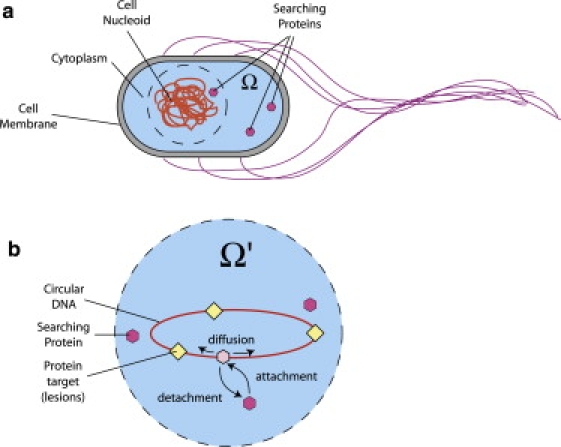
(a) Target search on prokaryotic DNA, which is tightly coiled up into a nucleoid. Proteins in the bulk can diffuse to the DNA through the cytoplasm to locate their targets. (b) Searching proteins (hexagons) locate targets (diamonds) by sliding along DNA, punctuated by attachment and detachment. The symbol Ω represents the cell volume while Ω′ represents all points in the vicinity of the nucleoid. Enzymes within Ω′ can engage in direct adsorption onto the DNA.
A series of recent articles (13–15) have revealed a special kind of long-ranged interaction for certain BER enzymes based on charge transport (CT) along DNA. MutY, a type of DNA glycosylase, contains a [4Fe-4S]2+ cluster that is very sensitive to changes in its environment. Specifically, its redox potential is modified depending on whether it is in a polar environment (when the enzyme is in solution) or in a more hydrophobic one (when the enzyme is attached to DNA). In solution, the [4Fe-4S]2+ cluster is resistant to oxidation. However, when attached to DNA, the cluster is more easily oxidized through the reaction [4Fe-4S]2+ → [4Fe-4S]3+ + e−. Furthermore, the 3+ form has a binding affinity ∼10,000 times greater than the 2+ form (15).
A model for the scanning of BER enzymes along DNA, aided by CT, was proposed in the literature (13–15), and is depicted in Fig. 2. When a BER enzyme adsorbs to DNA, it oxidizes and releases an electron along the strand (see Fig. 2 a). Distal enzymes, already adsorbed onto the DNA can absorb these electrons, become reduced and desorb. Hence, binding and unbinding of enzymes are associated with oxidation and reduction of their iron-sulfur clusters. CT along DNA can be disrupted by the presence of defects that affect electron transport. For example, guanine radicals (i.e., oxoGs), formed under oxidative stress, can absorb electrons: see Fig. 2 b. By acting as sites of reduction, they promote the adsorption of BER enzymes (13,16). Once the radical has absorbed an electron, it converts to a normal guanine base and no longer participates in CT. However, permanent defects, or lesions, can also exist on DNA, which can absorb more than a single electron (see Fig. 2 c). For example, oxoGs can erroneously pair with adenine bases when the DNA replicates. Such lesions may continuously absorb electrons with a certain probability, or otherwise reflect them. In contrast to the oxoG-cytosine case, the removal of oxoG-adenine lesions require MutY to be present at the damaged site.
Figure 2.
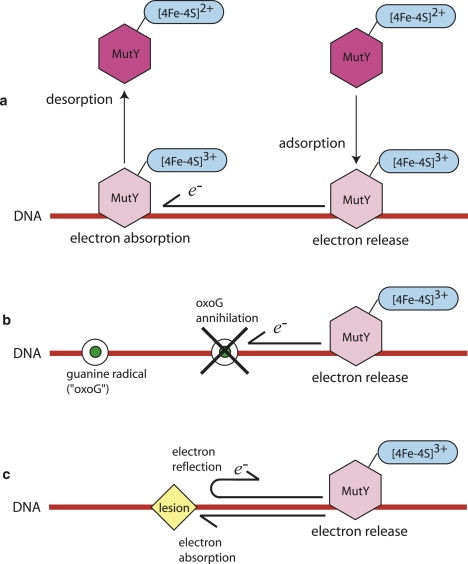
Charge transport (CT) mechanism proposed in the literature (13–15). (a) A repair enzyme (in solution) is in the 2+ state and adsorbs onto the DNA. Its iron-sulfur cluster oxidizes in the process, releasing an electron along the DNA. A repair enzyme (already adsorbed on the DNA) is in the 3+ state and accepts an incoming electron. Its iron-sulfur cluster reduces and the enzyme desorbs. (b) Guanine radicals (i.e., oxoGs) can absorb free electrons on the DNA. These radicals are annihilated upon absorbing an electron. (c) Lesions can partially reflect and absorb electrons.
In this article, we develop a model of CT-mediated BER enzyme kinetics that includes enzyme diffusion along DNA, a binding rate that depends on electron dynamics, and the effects of finite enzyme copy number. Our key finding is that the proposed charge transport mechanism employed by BER enzymes accelerates their search for targets along DNA in real finite enzyme copy number systems. In the next section, we derive the governing equations of enzyme kinetics. These equations are rendered nondimensional and key parameters are defined and estimated. In section following that, we numerically solve our model equations under various conditions and estimate the time for the binding of an enzyme to a localized lesion. We end with a discussion of our results.
Mathematical Model
Derivation of kinetic equations
Consider the diffusion and adsorption-desorption kinetics of repair enzymes in a bacterium such as E. coli: see Fig. 1. The chromosome in bacteria is circular but tightly coiled up into a nucleoid that has an effective volume of ∼8 × 107 nm3. If a repair enzyme is associated with the DNA strand, it can diffuse freely along the DNA to find lesions. These associated enzymes can spontaneously desorb from the strand, but they can also become oxidized, leading to tighter binding to the DNA. If the enzyme is reduced later on, its association with the DNA weakens and it can quickly dissociate from the DNA. Localized lesions prevent the passage of electrons (released along the DNA by oxidation of associated repair enzymes) by either reflecting or absorbing them.
We write mass-action equations for the reactions occurring in Fig. 3, coupled to equations that determine the electron dynamics. We assume that the enzyme density in the bulk, Rb(t) (where t is time), is well mixed and has no spatial dependence. The density of DNA-adsorbed BER enzymes in the reduced and oxidized state are denoted by Ra(x, t) and Q(x, t), respectively, where 0 ≤ x ≤ L is the coordinate along the DNA and lesions are located at x = 0 and x = L. The density of guanine radicals is g(x, t) and the density of rightward and leftward electrons is N+(x, t) and N–(x, t). Note that Rb(t) has units of inverse volume, while Ra(x, t), Q(x, t), N± (x, t), and g(x, t) carry units of inverse length. The governing equations corresponding to the processes depicted in Figs. 2 and 3 are
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Figure 3.
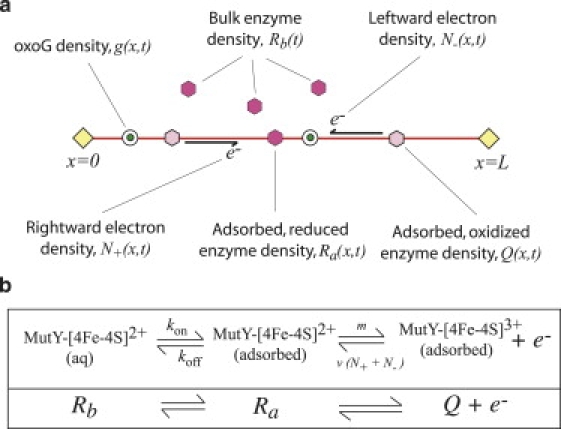
(a) Summary of the CT model, described by Eqs. 1–6. Bulk enzymes, with density Rb(t), can attach to the DNA and oxidize to release rightward and leftward electrons with densities N+(x, t) and N–(x, t), respectively. Guanine radicals with density g(x, t) act as electron absorbers. Upon adsorption, oxidized enzymes with density Q(x, t) are formed with Ra(x, t) as a transient, intermediate quantity. Fixed lesions are located at x = 0 and x = L. (b) Redox reaction diagram for the MutY repair enzyme. MutY2+ in solution is represented by Rb(t), MutY2+ adsorbed onto DNA is represented by Ra, and MutY3+ adsorbed onto DNA is represented by Q.
These equations must be solved subject to the boundary conditions
| (7) |
and initial conditions
| (8) |
In Eqs. 1–6, D+ is the diffusivity of adsorbed MutY3+ along the DNA; D– is the diffusivity of adsorbed MutY2+; v is the speed of electrons along DNA; m is the electron release (oxidation) rate of adsorbed MutY2+; koff is the intrinsic desorption rate of MutY2+; kon is the intrinsic adsorption rate of MutY2+ to the DNA from solution; Ω is the cell volume; L is the arc-length of the DNA; and f is the electron flip rate (see below). In the expressions in Eq. 7, r is the electron reflectivity of lesions, which we describe in more detail later. In the expressions in Eq. 8, n0 is the copy number of MutY, and g0 is the initial number of guanine radicals on the DNA. The definitions of all constants are summarized in Table 1.
Table 1.
| Symbol | Definition | Typical value | Reference |
|---|---|---|---|
| D± | Diffusivity of adsorbed enzymes | 5 × 106 bp2/s | (17) |
| υ | Electron velocity | 1010 bp/s | (18) |
| f | Electron flip rate | 109–1010 s−1 | ∗ |
| m | Electron release rate | ∼106 s−1 | (19) |
| Ω | Bacterium volume | 3.7 × 108nm3 | (20) |
| L | Length of DNA | 5 × 106 bp | |
| kon | MutY2+ attachment rate | 2000 s−1 | (16) |
| koff | MutY2+ detachment rate | 7 × 10−3 s−1 | † |
| n0 | Copy number of MutY in E. coli | 20–30 | (21,22) |
| r | Electron reflectivity of lesions | 0–1 | — |
| g0 | Number of oxoGs on E. coli DNA | ∼30 | ‡ |
The mean free path of an electron is estimated to be λ ∼ 1–10 basepairs and the flip rate approximated as υ/λ.
Estimated using the time taken for the restriction endonuclease BsoBI to unbind from DNA (23), toff = 150 s and taking koff = 1/toff. This value of toff may not be an accurate value for the unbinding time for MutY.
Assumes that ∼1 in 40,000 guanine bases are oxoGs (24) and the length of E. coli DNA is L = 5 × 106 bp.
We now give a brief justification of Eqs. 1–6 and the conditions in Eqs. 7 and 8. The form of the first three equations can be understood from Fig. 3 b, which summarizes the reactions among the three species Rb, Ra, and Q. Equation 1 describes the time rate of change of adsorbed MutY3+ due to oxidation of adsorbed MutY2+ (+ mRa) and reduction by incoming electrons (–v(N+ + N–)Q). The first term on the right-hand side represents diffusion along the DNA. Equation 2 describes the evolution of adsorbed MutY2+ in terms of the reduction of MutY3+ (+ v(N+ + N–)Q), spontaneous desorption into solution (– koffRa), adsorption of aqueous MutY2+ (kon(Ω/L)Rb), and oxidation into MutY3+ (– mRa). Since MutY2+ binds to DNA less strongly than MutY3+, it is possible that D+ is appreciably smaller than D–. Equation 3 is an equation for the concentration of MutY2+ in solution which can decrease by enzymes binding to the DNA (– konRb) and increase by enzymes unbinding from the DNA (represented by the integral term). Because we assume enzymes in the bulk solution are well mixed, any increases in bulk concentration are due to an integrated DNA-adsorbed density: the bulk solution does not distinguish between enzymes that are released from different positions along the DNA, but only sees the total number of enzymes that desorb.
Equations 4 and 5 describe the electron dynamics. In our model, right- and left-moving electrons (see Fig. 3 a) propagate along the DNA with speed v; this process is represented by the two convective terms on each of the left-hand sides. Also, electrons are lost when they are absorbed by MutY3+ or by guanine radicals, and produced when released by adsorbed MutY2+. These processes are represented by the third and fourth terms on the right-hand side of Eqs. 4 and 5, respectively. Finally, leftward and rightward electrons can interconvert (16) by scattering off inhomogeneities and thermally induced conformational changes in the DNA (25,26). This process is represented by the first and second terms on the right-hand side. The flip rate f characterizes how frequently a traveling electron changes direction. If f is large, the electron moves diffusively, but if f is small, it moves in a ballistic manner. Finally, Eq. 6 represents the evolution of the guanine radical population. OxoGs are annihilated when they absorb electrons as represented by the –v(N+ + N–)g term. Radicals might also be spontaneously generated and modeled by a source term on the right-hand side of Eq. 6. In this article, we neglect spontaneous oxoGs generation.
Equations 1–8 use a mean-field approximation that neglects stochastic fluctuations in enzyme, electron, and guanine number. The effect of noise in the system could be included through the use of a chemical master equation (27); however, generalizing the equation to account for spatial variations along the DNA is beyond the scope of this article (28). Nonetheless, we expect our results for lesion targeting by enzymes will be qualitatively accurate.
Lesions at x = 0 and x = L (see Fig. 3 a) define the domain of solution for Eqs. 1–6, which are subject to the boundary conditions in Eq. 7. In the first expression in Eq. 7, leftward traveling electrons are converted to rightward traveling ones by the lesion that reflects leftward electrons with probability r. If r = 0, leftward electrons are absorbed by the lesion. On the other hand, if r = 1, the lesion is fully reflective and the rightward and leftward electron densities are equal. Similar considerations apply to the lesion at x = L. Since we will eventually use our mean-field mass action equations to estimate the mean time for a repair enzyme to find a lesion, we assume that the lesions are perfectly absorbing for enzymes and set Q = Ra = 0 at the lesion positions. Our simulations are performed on a domain with g0 oxoG radicals and a bulk solution that contains n0 enzymes (see the expressions in Eq. 8); hence the adsorbed oxoG density is g0/L and the bulk concentration is n0/Ω.
Model reduction and nondimensionalization
Before nondimensionalizing Eqs. 1–6, we can make one important simplification. On the right-hand side of Eq. 2, the sizes of the second, third, fourth, and fifth terms are approximately v/L2, koff/L, kon/L, and m/L (in units of bp−1 s−1), respectively. Guided by Table 1, we assume the term mRa dominates. Since the oxidation rate is large, adsorbed MutY2+ quickly oxidizes into the 3+ form upon adsorption onto DNA. More generally, for times t ≫ 1/m and rates koff + m ≫ v/L, kon, Eq. 2 gives Ra(x,t) ≪ 1 for all 0 ≤ x ≤ L and we can neglect spatial gradients in Ra as well as ∂Ra/∂t. Therefore, we approximate Eq. 2 with
| (9) |
Upon substitution of Eq. 9 into Eqs. 1, 4, and 5, we eliminate the equations for Ra and find a reduction analogous to one commonly used in deriving the steady-state limit of Michaelis-Menten kinetics (29).
We now nondimensionalize our equations by measuring time in units of kon−1, length in units of L, concentration of adsorbed species in units of 1/L, and concentration of bulk species in units of 1/Ω. Our final set of reduced and nondimensionalized equations that describe the transport and kinetics of MutY repair enzymes, right- and left-moving electrons, and guanine radicals is
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where we have defined the dimensionless quantities
| (15) |
and
| (16) |
which can be estimated using Table 2. As we discuss later, the parameter σ represents the effective binding rate in terms of the competition between the electron release rate m and the desorption rate of DNA-bound MutY2+ koff, and lies between 0 and 1. The dimensionless boundary and initial conditions are
| (17) |
and
| (18) |
Table 2.
Dimensionless parameters in Eqs. 10–14
| Parameter | Definition | Calculated value |
|---|---|---|
| η | D+/(konL2) | ≲∼10−10 |
| U | v/(konL) | 5 |
| σ | m/(m + koff) | ∼1 |
| F | f/kon | 5 × 105–5 × 106 |
Our model can approximate the case of infinite enzyme copy number when the transport of bulk enzymes is diffusion-limited. Although most of the enzymes cannot immediately adsorb onto the DNA as they are too far away, we assume that a certain number, Rb, are in the vicinity of the nucleoid, say within a volume Ω′ (see Fig. 1), and are able to directly engage in adsorption. However, instead of being depleted over time, Rb is continuously replenished by far enzymes that diffuse into Ω′ ⊂ Ω to keep Rb fixed. Therefore, to obtain the infinite copy number limit, we hold Rb constant in Eqs. 10, 12, and 13, and Eq. 11 no longer applies. To summarize, we model the infinite copy number case by holding Rb constant. In the finite copy number case, Rb(t) is allowed to vary in time through Eq. 11. Finally, note that equations describing a simple diffusing enzyme that does not undergo CT can be recovered from Eqs. 10–14 by setting U = 0. In this case, the equations for Q(x, t) and Rb(t) decouple from the rest.
Repair enzyme binding affinity σ
In Eqs. 10–14, the rate of creation of reduced, adsorbed enzyme Ra from reduced bulk enzyme Rb is exactly Rb since we measure time in units of 1/kon. However, the overall rate of the compound reaction Rb ↔ Ra → Q is σRb. Consider a MutY3+ that is adsorbed onto the DNA. If it absorbs an incoming electron, it can either desorb into the bulk or it can release an electron back along the DNA and remain oxidized. The parameter σ in Eq. 16 is the probability of electron release. When koff ≫ m, a MutY3+ that absorbs an electron will preferentially desorb (Ra → Rb), but when koff ≪ m, a MutY3+ will simply release the electron it just absorbed to stay adsorbed onto the DNA (Ra → Q). These limiting behaviors are realized by taking σ → 0 and σ → 1, respectively.
If σ ∼0, a bulk reduced enzyme that adsorbs onto the DNA quickly desorbs back into the bulk, while if σ ∼1, MutY2+ on the DNA prefers to oxidize and stay adsorbed rather than go into solution. Once it is oxidized, any further electrons that are absorbed will be reemitted in a random direction. Hence, the electron changes direction with probability 1/2 whenever it encounters an adsorbed MutY3+: when σ = 1, the terms with prefactors (1 − σ/2) and σ/2 in Eqs. 12 and 13 add to the F(N– – N+) terms to yield an effective flip rate of F + UQ/2. The seeding of oxidized enzymes on the DNA increases the effective electron-flipping rate because these enzymes can absorb electrons and immediately release them back along the DNA in the direction they came from or in the direction they were going.
We end this section with the comment that the model for the CT redox process in Fig. 2 is not exactly equivalent to the reaction scheme in Fig. 3 b. In Fig. 2, a bulk MutY2+ (Rb) adsorbs onto a DNA and immediately oxidizes, releasing an electron along the DNA. DNA-bound MutY3+ (Q) remains adsorbed until it absorbs an incoming electron, whereupon it reduces and immediately desorbs into the bulk. For this model to hold, the reaction kinetics in Fig. 3 b must be non-Markovian. Specifically, consider the intermediate quantity Ra in Fig. 3 b. An Ra enzyme oxidizes to a Q enzyme (Ra → Q) only if it “remembered” that it was originally created via a Rb → Ra reaction. Likewise, an Ra enzyme desorbs (Ra → Rb) only if it “remembered” that it was originally created through a Q → Ra reaction.
Results and Discussion
We now compute and analyze solutions to Eqs. 10–14 and conditions 17–18 for the infinite and finite copy number cases. The equations are solved numerically using second-order finite differences on a nonuniform grid that clusters grid points near the boundaries and a trapezoidal rule to approximate the integrals. MatLab's stiff solver ode15s (The MathWorks, Natick, MA) was used to integrate the equations in time. In the infinite case, Rb is held at the value n0 and in the finite case, Rb(t) is included in the dynamics with initial condition Rb(0) = n0. Furthermore, in each case we consider the dynamics associated with CT enzymes where U > 0, and the dynamics associated with passive, non-CT enzymes where U = 0. Setting U = 0 decouples the equations for electron and guanine radical dynamics (Eqs. 12–14) from the equation for Q(x, t), the density of DNA-bound enzymes (Eq. 10).
We shall explore the behavior of Eqs. 10–14, and the associated search times defined below, with respect to:
σ, the effective binding affinity. Generally we have 0 < σ < 1. From the values of m and koff in Table 1, we have σ ≈1 − 10−8. This value of σ renders the desorption term – U(1 − σ)(N+ + N–)Q in Eq. 10 insignificant, making the effect of CT negligible. Therefore, a necessary requirement for an effective CT mechanism is that σ is not too close to 1. In our simulations for the MutY system, we take σ = 0.9, bearing in mind that the value of koff in Table 1 is for BsoBI and not MutY.
η, the diffusivity of MutY3+ along DNA. The value in Table 2 of η = 10−10 is based on the diffusive sliding of a human glycosylase, hOgg1, which has a diffusivity of ∼5 × 106 bp2/s (17). However, this value may not necessarily be an accurate value for MutY. Therefore we will explore a range of diffusivities η near 10−10.
g0, the initial guanine radical density. There are ∼30 oxoGs at any given time on E. coli DNA, but this number depends on environmental conditions. Hence we explore a range of g0 values centered at ≈30.
r, the lesion reflectivity. The interaction between electrons and lesions depends on unknown molecular factors at the lesion and in the bulk cytoplasm. Hence, we explore a full range of r-values between 0 and 1.
F, the electron flip rate. The precise dynamics of electrons on DNA is a very complicated process; our estimate for F in Table 2 makes many simplifications and may not be accurate. We will explore a range of F-values centered at ∼105.
Fig. 4 shows snapshots of adsorbed enzyme, guanine, and electron density profiles for a finite enzyme copy number (n0 = 30) system. The profiles are shown near the lesion at x = 0 at times t = 2 and t = 5. The electron density is generally smaller at the lesions and larger in the middle of the domain, resulting in a larger enzyme desorption rate away from lesions (the desorption rate in Eq. 10 is proportional to the total electron density N+ + N–). Thus, the CT enzyme density is smaller than that for passive enzymes away from lesions. The enhanced desorption of CT enzymes from the interior continuously replenishes the number of enzymes in solution so that Rb(t) decreases less rapidly than for passive enzymes. For intermediate times, the net deposition rate is larger for CT enzymes; the enzyme density near the lesions is also larger (Fig. 4 a), and grows in time (Fig. 4 b). For long times, the density vanishes everywhere: this is the trivial steady-state solution to Eqs. 10–14 and 17.
Figure 4.
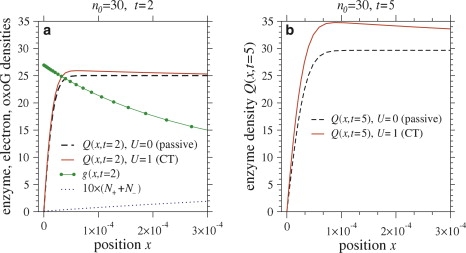
Density profiles for enzyme, guanine, and electrons on DNA in a finite enzyme copy number system (Rb(0) = n0 = 30) at time (a) t = 2 and (b) t = 5. Dashed lines show density profiles of passive enzymes in which the CT mechanism is absent. Parameters used were σ = 0.9, η = 10−10, g0 = 28, and F = 105.
Fig. 5 shows the DNA-bound enzyme density at t = 40. In Fig. 5 a, there is a sharp spike in the CT enzyme density near the lesion at x = 0, but otherwise the enzyme density is relatively small. Note that all densities are symmetric about x = 1/2. In Eq. 10, CT enzymes desorb with a rate proportional to the total electron density N+ + N– and as seen in Fig. 4 a, this density is usually smallest at the lesions. Therefore the enzyme density near x = 0 and x = 1 grows more quickly compared to the interior density. The inset shows a rapid variation in Q of ∼600 within a boundary layer of width ∼10−3. Using a nonuniform grid that clusters the mesh points near the boundaries, we are able to resolve these boundary layers to calculate the flux of enzymes through the lesions. In Fig. 5 b, CT (U = 1) and passive (U = 0) enzyme densities are compared when the copy number is finite. The CT-enzyme density has sharp maxima near the lesions, while the passive enzyme density does not. Compared to the infinite copy number case, the size of the maxima is smaller since the number of enzymes in the bulk (and hence the deposition rate) decreases with time. Because of the maxima, the flux of enzymes into the lesion,
| (19) |
is greater compared to the passive case. Fig. 5 c compares the current for CT (U = 1) and passive enzymes (U = 0) when the copy number is infinite. The passive enzyme current is always greater than the CT enzyme current because for a constant deposition rate, any desorption reduces the number of enzymes on the DNA and the flux of enzymes into the lesion. Therefore, for infinite copy number systems, search by passive enzymes will always be faster than CT enzymes. In contrast, when the bulk contains a finite number of enzymes, Fig. 5 d shows that the CT current is always greater than the passive current. This is due to free electrons on the DNA that determine the local desorption rate. In the CT mechanism, enzymes are knocked off the DNA by incoming electrons and on average, desorb from lesion-free portions of the DNA and readsorb at positions closer to the lesion. The result is that for intermediate times (t ≳ 10), the current experiences a second growth phase, a behavior that is never seen for the passive case. Ultimately, we have J(t) → 0 as t → ∞ for both passive and CT enzymes, but CT ensures that this behavior occurs at a much later time.
Figure 5.

Enzyme profiles and currents for infinite (a and c) and finite (b and d) copy numbers. In each figure, the profile or current is plotted for passive (dashed) enzymes where U = 0 and CT (solid) enzymes where U = 1. Insets show the large gradients in enzyme density within a thin boundary layer near the lesions. Parameters used were σ = 0.9, η = 10−10, g0 = 28, r = 0.5, F = 105, and n0 = 30.
Next, we consider the typical time for the first enzyme to reach a lesion. Since the enzyme density is symmetric about x = 1/2, the total flux can be found by using twice the enzyme flux to one lesion defined in Eq. 19. The typical search time τs is then approximated by integrating 2J(t) until one enzyme has diffused into the lesion:
| (20) |
From solving the full set of Eqs. 1–8 numerically, we find that the gradients in Ra(x, t) at the lesions are negligible compared to those of Q(x, t), verifying the validity of eliminating Ra and using J(t) ≈ η(∂Q(x, t)/∂x)x=0 as the total enzyme current. In the mean-field limit, an alternative definition of the search time is . We have computed τs using this mean-field approximation and find negligible qualitative differences from τs computed using Eq. 20.
Fig. 6 a shows that the search times are extremely sensitive to the initial number of oxoGs g0. In particular, there is a rapid increase in τs as g0 increases past the enzyme copy number n0 = 30. The CT mechanism relies on the presence of free electrons that cause enzymes to desorb from lesion-free portions of the strand and readsorb near lesion sites, while oxoGs suppress CT by absorbing free electrons. When g0 > n0, all enzymes from the bulk adsorb onto the DNA and any released electrons are absorbed by nearby guanine radicals. Instead of participating in CT-mediated redistribution and localization, the enzymes cannot desorb and must rely on slow diffusive sliding along the DNA strand to find their targets. When g0 < n0, at least one enzyme is always in solution and is transported through the cytoplasm. Since three-dimensional transport is assumed to be fast, the search time is correspondingly small. Also in this plot, τs increases as r increases but the search time is much more sensitive to g0: the search time changes by ∼20% for g0 ≈ 0 and by ∼0.05% for g0 ≈ 50 over the whole range of r. In our model, the search time is not greatly affected by whether lesions reflect or absorb electrons; what is important is that the lesions prevent their passage along the DNA.
Figure 6.
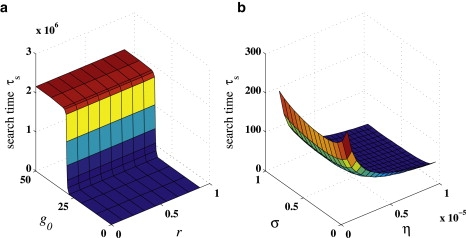
Search time τs for CT enzymes, for copy number n0 = 30, electron flip rate F = 105, and electron speed U = 1. The actual search time in seconds can be recovered by dividing by kon, whose value is estimated in Table 1. (a) Search time as a function of initial guanine density g0 and lesion electron reflectivity r. Parameters used were σ = 0.9 and η = 10−10. (b) Search time τs as a function of enzyme binding affinity σ and enzyme diffusivity along DNA, η. Parameters used were g0 = 30 and r = 0.5.
Fig. 6 b shows that for the range of η-values explored, there is a value 0 < σ∗ < 1 for which the search time τs is minimum. To understand why there is an optimal σ∗, consider the CT mechanism's dependence on the binding affinity σ. If σ = 1, enzymes strongly bind onto the DNA. Even when they absorb electrons, they will re-emit them to stay adsorbed on the strand. Hence, there is no desorption, no fast transport through the cytoplasm and acceleration of the search. On the other hand, if σ = 0, enzymes do not stay on the DNA long enough to even slide into lesions and the search is correspondingly slow. Our results show that the search is optimal when 0 < σ ≪ 1, and the electron release rate is small compared to the intrinsic desorption rate. From the data in Tables 1 and 2, it seems that real cells do not operate near this optimal regime. In Fig. 6 b, we computed most of the search times using unrealistically large values of η to clearly show the minimum with respect to σ. For smaller η-values we have σ∗ → 0+, but the dependence of τs on σ does not change qualitatively. For larger η-values, enzymes do not rely on CT to localize to lesions and can find their targets quickly using diffusive sliding. In this case, the search is most efficient if as many enzymes as possible adsorb on the DNA; this situation is realized by taking σ = 1 and τs monotonically increases as σ gets smaller.
Fig. 7 a shows how the search time varies as a function of one-dimensional enzyme diffusivity along the DNA. Notice that the search time for CT enzymes (U = 1) is much smaller than that for passive enzymes (U = 0). Indeed, τs can be reduced by several orders of magnitude when the effects of CT are included. If fewer oxoGs are initially present, the search occurs more quickly. Consistent with Fig. 6 a, the search time is extremely sensitive to the initial number of guanine radicals on the DNA. For passive enzymes, τs scales as O(η−1). For CT enzymes, the O(η−1) behavior switches to τs = O(η−1/3) for sufficiently large η with the crossover dependent on g0.
Figure 7.
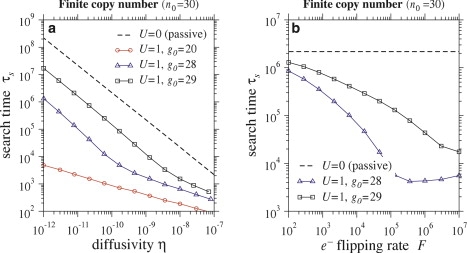
(a) Search time τs of passive enzymes (U = 0) compared with CT enzymes (U > 0) as a function of enzyme diffusivity η for various initial guanine densities g0. Parameters used were σ = 0.9, r = 0.5, F = 105, and n0 = 30. (b) Search time of passive enzymes compared with CT enzymes for different electron flip rates F. Parameters used were σ = 0.9, r = 0.5, η = 10−10, and n0 = 30. For both plots, the actual search time in seconds can be recovered by dividing by kon, whose value is estimated in Table 1.
For finite copy number, Fig. 7 b again shows that the search time decreases if CT is included, but this time for different flip rates. For the large values of F used in Fig. 7, one can show that the effective diffusion coefficient of the electron density scales as 1/F (16). Therefore, as F increases, the electron density dissipates more slowly through the partially absorbing lesions. A greater density of free electrons implies more enzyme desorption, more transport through the cytoplasm, and faster search times. In the F → ∞ limit, we expect the enzymes to self-desorb independently of the oxoG density. This can be seen from Eqs. 12 and 13 where the dominant terms on the right-hand side are ±F(N– – N+) and σRb/2. In principle, as F → ∞, one can approximate N± in terms of Rb(t) and substitute into –U(1 − σ)(N+ + N–)Q in Eq. 10 to further reduce the system to only two equations for Q(x, t) and Rb(t).
Although both plots in Fig. 7 are for the finite copy number case, we also performed analogous simulations for the infinite copy number limit. We found that including the effects of CT by taking U = 1 always led to an increase in the search time compared to the passive case: for fixed η and F, increasing U always increased τs regardless of the value of g0.
Conclusions
Our key finding is that charge-transport (CT) dynamics mediated by redox reactions can significantly reduce search times of repair enzymes in real cells where the copy number is finite and the diffusivity along the DNA is small. In theoretical systems where the copy number is infinite, CT actually slows down the search. The speed-up in finite systems arises because of a spatially dependent desorption rate. Specifically, the desorption is greater along intact portions of the DNA but smaller near lesions. As a result, CT-induced enzyme-enzyme interactions recycle enzymes so that they desorb from lesion-free parts of the DNA and reattach closer to lesion sites. Our proposed mechanism is illustrated in Fig. 8. A related mechanism has been implicated in mRNA translation where ribosomes are recycled, enhancing protein production rates (30).
Figure 8.
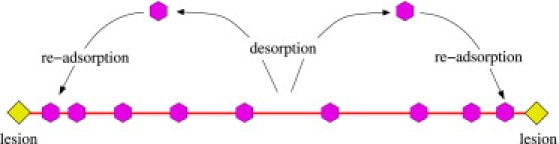
Recycling of enzymes via the CT mechanism. In a finite copy number system, the mechanism increases the enzyme desorption rate for intact portions of DNA but decreases it near lesions. Therefore, on average, enzymes are recycled to lesion sites by three-dimensional transport through the cytoplasm. In many cell systems, this method of finding lesions is faster than a one-dimensional search by diffusive sliding.
If we redimensionalize the search times by using an estimated value of kon = 2000 s−1, we find that passive enzymes with diffusivity η ∼10−10 have long search times τs of ∼15 min (see Fig. 7), comparable to the lifecycle time of E. coli. With the CT mechanism and g0 = 28 initial oxoGs, the search time drops to a few seconds. For smaller values of η, the difference in search times between passive and CT enzymes becomes greater. Using g0 = 20, we calculate τs to be ∼30 h and 2 s, respectively, for passive and CT enzymes that have diffusivity η ∼10−12. Therefore, for realistic enzyme diffusivities, we think that CT is an indispensable mechanism that allows enzymes such as MutY to locate lesions on the DNA in a reasonable amount of time.
When the initial number of oxoGs exceeded the enzyme copy number, we found a large increase in the search time. In this case, search takes place mostly through slow diffusive sliding along the DNA. However, when the copy number (number of potential electron emitters) exceeds the number of electron absorbers, we find that the search time decreased drastically, with the search taking place mainly through the transport of enzymes through the cytoplasm. Therefore, we predict that the spontaneous generation of electron absorbing defects (such as oxoG) would significantly slow down the search and conversely, the presence of other redox-active proteins (such as the transcription factor SoxR (31)) would speed up the search. Although such proteins may not be directly involved in lesion search, they may be upregulated when the cell is oxidatively stressed, increasing the population of electron emitters in the system. The iron-sulfur cluster responsible for CT in MutY is also found in other repair enzymes like EndoIII (32). Hence EndoIII could also participate in CT, emit electrons to promote the desorption of MutY, and speed up the search.
Recall that classical facilitated diffusion theory (3–5) predicts a large reduction in the search time of proteins, providing equal amounts of time are spent in one and three dimensions. However, most proteins are strongly associated with DNA so that the speed-up is not achieved in practice. The passive enzyme system considered in this study can be thought of as a suboptimal search by facilitated diffusion: with U = 0, a MutY that oxidizes and binds to the DNA cannot desorb back into the cytoplasm and the protein spends much more time diffusing in one dimension. However, when U > 0, bound oxidized MutY can be knocked off the strand by electrons. CT therefore provides a mechanism for MutY to spend more time in three dimensions than it otherwise would. In other words, CT-aided MutY could be one system where the conditions required for speed-up are actually satisfied. In addition, when MutY binds near lesions, it may diffusively slide along the DNA into its target: the target size is effectively increased with the DNA acting like an antenna (10). This antenna effect is enhanced by enzymes preferentially oxidizing and adsorbing onto parts of the DNA that are near lesion sites.
Extensions to our model may include spatial gradients in the bulk enzyme concentration, more careful treatment of electron dynamics, and adding fluctuations in copy number. Nonetheless, our simple deterministic model describes mechanisms and yields results qualitatively consistent with findings in the literature (13,14).
Acknowledgments
P.-W. Fok is grateful for helpful discussions with A. K. Boal and J. Geneveaux.
The authors acknowledge support from the National Science Foundation (DMS-0349195) and the National Institutes of Health (K25AI058672).
References
- 1.Riggs A.D., Bourgeois S., Cohn M. The Lac repressor-operator interaction. 3. Kinetic studies. J. Mol. Biol. 1970;53:401–417. doi: 10.1016/0022-2836(70)90074-4. [DOI] [PubMed] [Google Scholar]
- 2.Riggs A.D., Suzuki H., Bourgeois S. The Lac repressor-operator interaction. 1. Equilibrium studies. J. Mol. Biol. 1970;53:401–417. doi: 10.1016/0022-2836(70)90219-6. [DOI] [PubMed] [Google Scholar]
- 3.Berg O.G., Winter R.B., von Hippel P.H. Diffusion-driven mechanism of protein translocation on nucleic acids. 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 4.Winter R.B., Berg O.G., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli Lac repressor-operator interaction: kinematic measurements and conclusions. Biochemistry. 1989;20:6961–6977. doi: 10.1021/bi00527a030. [DOI] [PubMed] [Google Scholar]
- 5.von Hippel P.H., Berg O.G. Facilitated target location in biological systems. J. Biol. Chem. 1989;264:675–678. [PubMed] [Google Scholar]
- 6.Slutsky M., Mirny L.A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophys. J. 2004;87:4021–4035. doi: 10.1529/biophysj.104.050765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wunderlich Z., Mirny L.A. Spatial effects on the speed and reliability of protein-DNA search. Nucleic Acids Res. 2008;36:3570–3578. doi: 10.1093/nar/gkn173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang Y.M., Austin R.H., Cox E.C. Single molecule measurements of repressor protein 1D diffusion on DNA. Phys. Rev. Lett. 2006;97 doi: 10.1103/PhysRevLett.97.048302. 048302. [DOI] [PubMed] [Google Scholar]
- 9.Sheinman, M., and Y. Kafri. 2008. The effects of intersegmental transfers on target location by proteins. Physical Biology. 6:016003. [DOI] [PubMed]
- 10.Hu T., Grosberg A.Y., Shklovskii B.I. How proteins search for their specific sites on DNA: the role of DNA conformation. Biophys. J. 2006;80:2731–2744. doi: 10.1529/biophysj.105.078162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Loverdo C., Bénichou O., Moreau M., Voituriez R. Enhanced reaction kinetics in biological cells. Nat. Phys. 2008;4:134–137. [Google Scholar]
- 12.Cherstvy A.G., Kolomeisky A.B., Kornyshev A.A. Protein-DNA interactions: reaching and recognizing the targets. J. Phys. Chem. 2008;112:4741–4750. doi: 10.1021/jp076432e. [DOI] [PubMed] [Google Scholar]
- 13.Yavin E., Boal A.K., Stemp E.D.A., Boon E.M., Livingston A.L. Protein-DNA charge transport: redox activation of a DNA repair protein by guanine radical. Proc. Natl. Acad. Sci. USA. 2005;102:3546–3551. doi: 10.1073/pnas.0409410102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Boon E.M., Livingston A.L., Chmiel M.H., David S.S., Barton J.K. DNA-mediated charge transport for DNA repair. Proc. Natl. Acad. Sci. USA. 2003;100:12543–12547. doi: 10.1073/pnas.2035257100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Boal A.K., Yavin E., Lukianova O.A., O'Shea V.K., David S.S. DNA-bound redox activity of DNA repair glycosylases containing [4Fe-4S] clusters. Biochemistry. 2005;44:8397–8407. doi: 10.1021/bi047494n. [DOI] [PubMed] [Google Scholar]
- 16.Fok P.W., Chou T. Charge transport mediated recruitment of DNA repair enzymes. J. Chem. Phys. 2008;129:235101. doi: 10.1063/1.3026735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blainey P.C., van Oijen A.M., Banerjee A., Verdine G.L., Xie X.S. A base-excision DNA-repair protein finds intrahelical lesion bases by fast sliding in contact with DNA. Proc. Natl. Acad. Sci. USA. 2006;103:5752–5757. doi: 10.1073/pnas.0509723103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Turro N.J., Barton J.K. Paradigms, supermolecules, electron transfer and chemistry at a distance. What's the problem? The science of the paradigm. J. Biol. Inorg. Chem. 1998;3:201–209. [Google Scholar]
- 19.Lin J.-C., Singh R.R.P., Cox D.L. Theoretical study of DNA damage recognition via electron transfer from the [4Fe-4S] complex of MutY. Biophys. J. 2008;95:3259–3268. doi: 10.1529/biophysj.108.132183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Woldringh C.L., Nanninga N. Academic Press; London, UK: 1985. Molecular Cytology of E. coli. [Google Scholar]
- 21.Bai H., Lu A.-L. Physical and functional interactions between Escherichia coli MutY glycosylase and mismatch repair protein MutS. J. Bacteriol. 2007;189:902–910. doi: 10.1128/JB.01513-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Demple B., Harrison L. Repair of oxidative damage to DNA: enzymology and biology. Annu. Rev. Biochem. 1994;63:915–948. doi: 10.1146/annurev.bi.63.070194.004411. [DOI] [PubMed] [Google Scholar]
- 23.Koch S.J., Wang M.D. Dynamic force spectroscopy of protein-DNA interactions by unzipping DNA. Phys. Rev. Lett. 2003;91 doi: 10.1103/PhysRevLett.91.028103. 028103. [DOI] [PubMed] [Google Scholar]
- 24.Helbock H.J., Beckman K.B., Shigenaga M.K., Walter P.B., Woodall A.A. DNA oxidation matters: the HPLC-electrochemical detection assay of 8-oxo-deoxyguanosine and 8-oxo-guanine. Proc. Natl. Acad. Sci. USA. 1998;95:288–293. doi: 10.1073/pnas.95.1.288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.D'Orsogna M.R., Rudnick J. Two-level system with a thermally fluctuating transfer matrix element: application to the problem of DNA charge transfer. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;66 doi: 10.1103/PhysRevE.66.041804. 041804. [DOI] [PubMed] [Google Scholar]
- 26.Bruinsma R., Gruner G., D'Orsogna M.R., Rudnick J. Fluctuation-facilitated charge migration along DNA. Phys. Rev. Lett. 2000;85:4393–4397. doi: 10.1103/PhysRevLett.85.4393. [DOI] [PubMed] [Google Scholar]
- 27.Rao C.V., Wolf D.M., Arkin A.P. Control, exploitation and tolerance of intracellular noise. Nature. 2002;420:231–237. doi: 10.1038/nature01258. [DOI] [PubMed] [Google Scholar]
- 28.Isaacson S.A., Peskin C.S. Incorporating diffusion in complex geometries into stochastic chemical kinetics simulations. SIAM J. Sci. Comput. 2006;28:47–74. [Google Scholar]
- 29.Murray J.D. Springer-Verlag; New York: 1989. Mathematical Biology. [Google Scholar]
- 30.Chou T. Ribosome recycling, diffusion and mRNA loop formation in translational regulation. Biophys. J. 2003;85:755–773. doi: 10.1016/S0006-3495(03)74518-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hidalgo E., Demple B. An iron-sulfur center essential for transcriptional activation by the redox-sensing SoxR protein. EMBO J. 1994;13:138–146. doi: 10.1002/j.1460-2075.1994.tb06243.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Parikh S.S., Mol C.D., Tainer J.A. Base excision repair enzyme family portrait: integrating the structure and chemistry of an entire DNA repair pathway. Structure. 1997;5:1543–1550. doi: 10.1016/s0969-2126(97)00303-1. [DOI] [PubMed] [Google Scholar]


