Abstract
The network of interactions underlying liver regeneration is robust and precise with liver resections resulting in controlled hyperplasia (cell proliferation) that terminates when the liver regains its lost mass. The interplay of cytokines and growth factors responsible for the inception and termination of this hyperplasia is not well understood. A model is developed for this network of interactions based on the known data of liver resections. This model reproduces the relevant published data on liver regeneration and provides geometric insights into the experimental observations. The predictions of this model are used to suggest two novel strategies for speeding up liver mass recovery and a strategy for enabling liver mass recovery in cases where a resection leaves <20% of the liver that would otherwise result in complete loss of liver mass.
Introduction
The liver's ability to regenerate has been known since ancient times and has been the subject of scientific study since the early 20th century (1). After a partial hepatectomy (removal of a section of the liver), liver cells reenter the cell cycle and replicate until the liver recovers its lost mass, within a precision of 10% (2). Although numerous studies have investigated the molecular mechanisms of liver regeneration, including the roles of cytokines, growth factors, matrix remodeling, and metabolic signals (3,4), several basic questions remain. How does the liver integrate signals from different signaling pathways and from metabolic stresses, including detoxification functions, in order to control cell replication? How does liver regeneration stop once the liver reaches its original mass, and how does the liver avoid an oscillatory cycle of overgrowth and apoptosis? This article proposes a simple mathematical model for liver regeneration to answer these questions.
In a healthy adult liver, only ∼1 hepatocyte in 20,000 (0.005%) is in the cell cycle (5). The rest are quiescent, in the G0 state. After partial hepatectomy, hepatocytes reenter the cell cycle by going from the G0 state to the G1 phase. Cells in the early G1 phase progress, driven by growth factors, through the G1/S restriction point, after which cells are committed to progress to mitosis, even in the absence of the G1 growth factors. However, cells in early G1 phase that have not reached the restriction point can return to quiescence in the absence of growth factors (6). Following Fausto and Riehle (3), we consider three subpopulations of hepatocytes in our model: quiescent cells (Q), primed cells (P), and replicating cells (R).
In the priming phase of liver regeneration, multiple immediate-early genes such as c-fos and c-jun are induced (7). These immediate-early genes (IE) take liver cells from the G0 phase to the G1 phase of the cell cycle. The level of expression of immediate-early genes, in turn, is controlled in large part by a network of cytokines (8,9). Levels of tumor necrosis factor (TNF) increase after partial hepatectomy (10). TNF binds to its receptor on Kupffer cells, which activates the transcription factor nuclear factor-κB, which leads to increased interleukin-6 (IL-6) transcription and production. IL-6 binds to its receptor on hepatocytes. The receptor interacts with gp130 and activates two Janus kinase (JAK) proteins. JAK phosphorylates monomeric signal transducer and activator of transcription 3 (STAT3), which then immediately homodimerizes to the active form (11). JAK also activates the mitogen-activated protein kinase pathway. STAT3 promotes transcription of many immediate-early genes, including suppressor of cytokine signaling 3 (SOCS3), which binds to JAK proteins and blocks further signaling through competitive inhibition with inactive STAT3 (12). Thus, the negative feedback mechanism of SOCS3 ensures an initial spike in transcription, after which quiescent cells can no longer enter the cell cycle.
Once cells have entered the G1 phase, their progression through the cell cycle to the proliferating phase is driven by growth factors (GF). The most important growth factor for liver regeneration is hepatocyte growth factor (HGF), which binds to the c-met receptor (13,14). Pro-HGF, an inactive form of HGF, is depleted from the extracellular matrix during the first three hours after partial hepatectomy, after which it is produced by nonparenchymal cells (15). Urokinase-type plasminogen activator activates pro-HGF and is detected within the first 5 min after partial hepatectomy (16). Other growth factors include epidermal growth factor (EGF) (17), transforming growth factor α (18), and heparin-binding EGF-like growth factor (HB-EGF) (19). In the absence of growth factors, cells return to quiescence. Once cells are in the replicating phase, the length of the cell cycle is fairly fixed.
The extracellular matrix (ECM) plays an important role in the regulation of liver regeneration (20). After partial hepatectomy, the ECM is degraded by matrix metalloproteinases (MMP), which are activated by TNF and other cytokines (21). The ECM is then produced again by nonparenchymal cells after most hepatocytes have divided. The ECM has the capacity to anchor growth factors to itself, thus preventing them from being activated. This constitutes an indirect inhibition of cell proliferation. In addition, the ECM may be directly responsible for replicating cells returning to quiescence through mitoinhibitory signaling in conjunction with integrins or transforming growth factor β1 (4,20).
The causes of the initial rise in activity of cytokines and growth factors remains a mystery. The volume of blood in the portal vein increases threefold after 2/3 partial hepatectomy. It has been suggested that the increase in shear stress after partial hepatectomy could trigger regeneration by activating urokinase-type plasminogen activator (22). Fluid shear stress has also been shown to stimulate mitogen-activated protein kinases in endothelial cells (23). Portal blood flow has been proposed as a hepatostat, whereby increases and decreases in portal pressure would control the stimuli for liver growth (4). However, blood pressure cannot be the only factor initiating regeneration, because liver growth has been stimulated in parabiotic animals; these have a surgically united circulation, in which the portal pressure in the animal with the intact liver is not the same as the blood pressure in the animal with the removed liver (24,25).
Another hypothesis is that elements of the innate immune system are responsible for the start trigger. Increased portal flow may cause an increase in lipopolysaccharide (LPS), which is produced in the gut. LPS interacts with the LPS receptor on Kupffer cells and may stimulate production of TNF and IL-6 (26).
Increases in the concentration of amino acids in the blood may also facilitate liver regeneration by upregulating mammalian-target-of-rapamycin (mTOR) and increasing protein translation. Amino-acid deprivation and treatment with rapamycin, an inhibitor of mTOR, have been shown to inhibit hepatocyte proliferation (27,28), though this inhibition is not specific to liver regeneration.
Although the exact nature of the start signal is not clear, it appears that it involves the metabolic load upon the liver, whether this manifests itself in mechanical stress or increased concentrations of nutrients and innate immune system components or increased detoxification demands. In our model, we take the trigger for the production of TNF and growth factors to be the metabolic load (including detoxification) per hepatocyte M/N, where M is a constant load that depends on the entire body's metabolic needs, and N is the total number of cells. This supposition entails that larger partial hepatectomies will result in larger metabolic loads and faster regenerative responses. This has indeed been observed: the expression of immediate-early protooncongenes increases with the size of the partial hepatectomy (except for partial hepatectomies larger than 90%, which result in apoptosis (29)).
Finally, it has been observed that hepatectomies >75% are lethal (30). This may be due to excessive detoxification stress on the remaining hepatocytes, with contributions from an overincrease in the shear stress and pressure in the portal vein (31), which may also affect the immune response through Kupffer cell dysfunction (30).
To better understand liver regeneration, we have developed a model that considers cells in quiescent, primed, and replicating phases, and in which the crucial quantity is the metabolic load per cell. Our model confirms and explains much of the liver regeneration behavior that has been observed until this point. It results in a simple geometric picture from which we make predictions that suggest strategies for speeding up liver mass recovery and for enabling liver recovery in cases where an overly small liver is liable to fail.
Methods
Liver regeneration is not, strictly speaking, regeneration: The resected lobe(s) of the liver do not reappear. Instead, the remaining lobe(s) of the liver grow until the entire liver has a mass equal to the mass of the original liver. Therefore, our model will assume that the compensatory hyperplasia occurs homogeneously throughout the remaining lobe(s), a good first approximation. With this assumption, the equations of the model are ordinary differential equations.
Cellular equations
The rates of change of cell number are modeled in terms of signaling molecules interacting with cells in each state Q, P, and R. The simplest assumption for these reactions is that they proceed following the law of mass action. As such, the transition rate between states is proportional to the number of signaling molecules and to the fraction of cells in the state affected by the signal. This leads to second-order steps in the transition equations. Higher-order interactions may also be present involving multiple signaling molecules binding to a cell in principle, but we found excellent agreement with experimental observations using just second-order mass action kinetics for cellular transitions due to signaling events. Such higher-order interactions could arise, for example, from saturation-binding regulated kinetics when expanded in a perturbation series. However, the agreement we found with experimental observations using just the lowest second-order form suggests that the number of receptors is large enough to allow the neglect of higher-order terms. The signals themselves have nonlinear rates of increase and decrease governed by Michaelis-Menten dynamics, and are given in the next subsection.
The equations for different cell types are
| (1) |
| (2) |
| (3) |
where [IE] – [IE]0 and [GF] – [GF]0 are the excess levels of immediate-early genes and growth factors; [ECM] is the size of the extracellular matrix; k Q, k P, and k R are rates of progression out of Q, P, and R; k prol, k req, and k ap are the rates of proliferation, requiescence, and apoptosis; σ req and σ ap are sigmoidal functions describing the threshold for requiescence and apoptosis; and N = Q + P + R. [IE], [GF], and [ECM] are considered as number of molecules per cell, normalized to stable state values.
This scheme is a simplification in that we are reducing all of the transitions between different cellular states to depend on the levels of three elements. In reality, k Q[IE] is a short-hand notation for ∑i k Q,i [IEi]: There are numerous factors IE i with different coefficients k i, all performing the same function of priming quiescent cells.
Molecular equations
The main molecular pathways can be represented by the following equations, which consider seven elements, each of which represents multiple compounds: TNF, JAK, STAT3, SOCS3, immediate early genes (IE), growth factors (GF), and ECM. In addition to the relations between elements, we give each element a half-life κ. Several molecular reactions in these pathways are enzyme-mediated and occur over timescales much shorter than changes in enzyme concentrations. As such, following the standard quasi-steady-state approximation, we assume Michaelis-Menten kinetics for these reactions.
Under normal physiological conditions, there are low constant levels of each of the seven factors described in Eqs. 4–10. We normalize the number of molecules to these levels, so that in the stable state, with an intact liver, each element has a number of 1. To use these units, however, we need to have constant production or degradation terms k 1…k 7 in each equation, so that the time-derivative of each element is 0 under normal conditions. Biologically, these terms simply correspond to homeostatic influxes or outfluxes of elements in and out of the liver and have nothing to do with the liver regeneration mechanisms.
TNF, which represents various inflammatory cytokines including TNF and IL-6, is produced in response to the excess metabolic load. TNF activates the IL-6 receptor, which interacts with the two gp-130 subunits and activates two JAK proteins. We represent the entire activated gp130-JAK complex as JAK, which should not be confused with individual JAK proteins:
| (4) |
| (5) |
Active, homodimeric STAT3 (i.e., STAT3) forms when two monomeric STAT3s (i.e., proSTAT3) are phosphorylated by the two activated JAK proteins in the gp130-JAK complex. The two phosphorylated STAT3s then immediately homodimerize—in fact, the two steps are almost simultaneous (11). The reaction occurs at a rate V ST3 and with Michaelis-Menten constant k M ST3. ProSTAT3 also competes with SOCS3, which raises k M ST3 by a factor of 1+[SOCS3]/K I SOCS3, where K I SOCS3 is the dissociation constant of SOCS3: K I SOCS3 = [SOCS3][JAK] / [SOCS3 · JAK] at equilibrium (32). STAT3 activation requires proSTAT3 binding to both JAK proteins, so SOCS3 binding to only one JAK protein inhibits STAT3 formation. We assume that the number of molecules of monomeric STAT3 remains constant:
| (6) |
STAT3 activates immediate early genes IE and SOCS3, thereby creating a negative feedback, ensuring a spike of IE:
| (7) |
| (8) |
The ECM is degraded by TNF—it is an initial degradation, because levels of TNF quickly decrease—and is produced at a constant rate k 6 per hepatocyte by nonparenchymal cells:
| (9) |
Growth factors are produced in response to the excess metabolic load; they are taken up by the ECM at a rate k up:
| (10) |
A set of parameters for the model, along with references, is found in Tables 1–3. Parameters were chosen assuming a partial hepatectomy of 2/3 (fraction of liver remaining = 0.32) in the rat. Although the model does not represent individual molecules but rather groups of molecules that perform the same function, values that were suggested by the scientific literature for sample molecules were used as parameters whenever possible.
Table 1.
Model parameters 1
| Comment/Reference | ||
|---|---|---|
| N | Fraction of liver mass. N = 1 for the intact liver. | |
| M | 16.8 | Metabolic load. |
| kTNF | 1.5 | TNF production. Changes in TNF protein levels have not been detected after partial hepatectomy (see (39) and references within). An increase of ≈20-fold has been measured after liver injury (40). The entire priming phase ends 5–6 h after partial hepatectomy (12). |
| κTNF | 9 × 10−1 | TNF mRNA has a half-life of 45 min after stimulation with LPS (41). |
| VJAK | 2 × 104 | JAK activation. |
| kMJAK | 1 × 104 | |
| κJAK | 4 × 10−1 | JAK degradation based on Siewert et al. (42). |
| [proSTAT3] | 2 | Concentration of monomeric STAT3. |
| VST3 | 7.5 × 102 | STAT3 levels increase 30-fold after 2/3 partial hepatectomy (43). STAT3 degradation based on Siewert et al. (42). |
| kMST3 | 4 × 10−1 | |
| κST3 | 1 × 10−1 | |
| VSOCS3 | 2.4 × 104 | SOCS3 is induced 40-fold after 2/3 partial hepatectomy (12). SOCS3 degradation based on Siewert et al. (42). |
| kMSOCS3 | 7 × 10−4 | |
| κSOCS3 | 4 × 10−1 | |
| kISOCS3 | 1.5 × 10−2 | SOCS3 inhibition constant. |
| VIE | 2.5 × 102 | Typical IE gene expression levels increase 20- to 50-fold (7). c-fos mRNA has a very short half-life (<10 min) (44). |
| kMIE | 18 | |
| κIE | 5 | |
| kdeg | 7 | ECM degradation by TNF-activated MMPs. |
| κECM | 33 | ECM degradation. |
Units: time in hours, numbers normalized to stable-state numbers, cell populations as fractions of normal liver size.
Table 2.
Model parameters 2
| Comment/Reference | ||
|---|---|---|
| kGF | 1.13 × 10−1 | GF production, degradation, and uptake of GF by the ECM. After 2/3 partial hepatectomy, HGF increases 20-fold, peaking at 12 h; other growth factors increase less and peak at 24 h (18,19,45). |
| κGF | 2.3 × 10−1 | |
| kup | 6 × 10−2 | |
| kQ | 7 × 10−3 | >90% of cells enter the cell cycle after 2/3 partial hepatectomy (46). |
| kP | 4.4 × 10−3 | The number of cells changes as described in Brues et al. (38); in particular, after 2/3 partial hepatectomy, the number of cells doubles within three days. The original mass is fully recovered after 7–10 days. |
| kR | 5.4 × 10−2 | |
| kprol | 2.0 × 10−2 | The length of the mitotic cycle is between 30 and 40 h (47). |
| kreq | 1 × 10−1 | Requiescence rate. Without growth factors, primed cells return quickly to quiescence between 24 and 48 h after administration of TNF (48). |
| θreq | 8 | . Increasing θreq leads to earlier requiescence and slower growth and vice versa. Values of θreq between 5 and 12 give reasonable behavior. |
| βreq | 3 | |
| kap | 1 × 10−2 | Apoptosis rate. Liver failure occurs within 48 h of massive hepatectomy (49). |
| θap | 9 × 10−3 | . A 75% partial hepatectomy should not lead to liver failure, although larger ones should (30). |
| βap | 4.5 × 10−3 |
Units: time in hours, numbers normalized to stable-state numbers, cell populations as fractions of normal liver size.
Table 3.
Model parameters 3
| k1 | −22.30 |
| k2 | −1.60 |
| k3 | 2.39 × 104 |
| k4 | 2.40 × 104 |
| k5 | −8.16 |
| k6 | 40 |
| k7 | −1.60 |
Units: time in hours, numbers normalized to stable-state numbers, cell populations as fractions of normal liver size.
Equations were integrated using MatLab's ode15s solver (The MathWorks, Natick, MA).
Results
Liver regeneration model
Our model considers three populations of cells: quiescent (Q), primed (P), and replicating (R). Only cells in the R phase can proliferate. We take the rate of transition of Q cells to P cells to be proportional to the level of expression of immediate-early genes (IE). These in turn are controlled by a network of cytokines triggered by TNF, itself produced proportionally to the metabolic load per cell M/N. The rate of transfer of cells from the P phase to the R phase is proportional to the concentration of growth factors (GF), which are also produced proportionally to the metabolic load per cell. In the absence of growth factors, cells return from the P phase to the Q phase at a constant requiescence rate. R cells have a constant replicating term. The rate of transition from R to Q is proportional to the density of the ECM, which is degraded by TNF. Growth factors are inactivated by the ECM. We also include an apoptosis term in our equations for Q, P, and R cells that is activated by excess metabolic stress per cell.
The model is concerned with the interplay between large groups of factors (growth factors and cytokines), as opposed to the actions of particular factors. Of the many experiments involving knockout mice and rats, only a single factor, hepatocyte growth factor (HGF), has been found to be essential to liver regeneration (14). Most knockout trials show only a delay in regeneration (20), suggesting that multiple pathways often perform a similar function. Although the model considers the number of molecules per cell of seven factors in addition to the levels of the three cell types, these numbers should be taken to represent large groups of factors as opposed to specific factors. For example, k[GF] should be taken as a short-hand for ∑i k i[GFi]: each individual growth factor has its own number of molecules and its own rate coefficient.
The full details of the model can be found in Methods. The model parameters were chosen based on the known phenomenology of 2/3 liver resections.
Fig. 1 is a schematic of the interactions included in the model.
Figure 1.
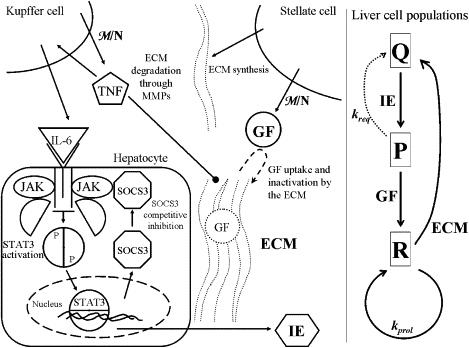
Schematic of liver regeneration model. The left side shows molecular interactions, whereas the right side represents the cellular kinetics. Molecular interactions: TNF is produced by Kupffer cells in response to the increased metabolic load and leads to the activation of IL-6. IL-6 binds to its receptor on hepatocytes and activates JAK. JAK phosphorylates the transcription factor STAT3, which dimerizes and induces the transcription of multiple immediate-early genes (IE), as well as SOCS3, which binds to JAK and inhibits STAT3 phosphorylation. TNF degrades the extracellular matrix (ECM), which is produced by stellate cells. Growth factors GF are also produced in response to the metabolic load (HGF is produced primarily by stellate cells). The ECM binds and inactivates growth factors. Cellular kinetics: Quiescent cells Q are taken to the primed state P through the action of IE. Primed cells can either progress to the replicating state R or return to the quiescent state. Replicating cells proliferate at a constant rate and return to the quiescent state through the action of the ECM.
Liver regeneration profiles
The modeled responses of the liver after partial hepatectomies of 85%, 68%, 45%, and 25% are shown in Fig. 2.
Figure 2.
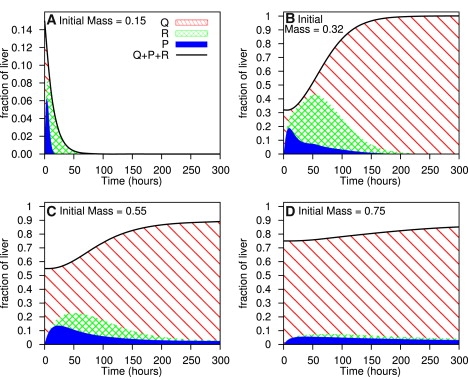
Liver regeneration after varying degrees of partial hepatectomy. The diagonal, cross-hatched, and blue solid areas represent quiescent, primed, and replicating cells, respectively.
The model successfully reproduces the significant features of liver regeneration after a 2/3 partial hepatectomy (Fig. 2 B). In addition, the model correctly predicts liver regeneration behavior after other degrees of partial hepatectomy. Partial hepatectomies >75% (Fig. 2 A) result in liver failure, as described in Panis et al. (30). Partial hepatectomies between 40% and 70% (Fig. 2 C) have a fairly rapid regenerative response, with a well-defined peak in proliferative activity, as found by Bucher and Swaffield (33). Partial hepatectomies <40% (Fig. 2 D) have a much slower regenerative response, with a low, fairly constant level proliferative activity throughout the response (33). Regenerative growth is significantly impaired (19). Finally, for partial hepatectomies <10%, there is an extremely minute regenerative response; for a 5% hepatectomy, the total number of cells only increases by 0.5% after 300 h (data not shown). This corresponds to what MacDonald et al. (34) describe as “a threshold amount of liver, of ∼9–12%, which must be removed to elicit a statistically significant response in DNA synthesis.” The model thus agrees with the different regimes of liver regeneration that have previously been described.
Fig. 3 shows the time required to recover half of the lost mass as a function of the fraction of liver remaining after partial hepatectomy. The different regimes described in Fig. 2 are readily recognizable. Partial hepatectomies leaving <25% lead to liver failure and those leaving between 25 and 60% have a fairly short time of regeneration. Hepatectomies removing <40% have a much longer time of regeneration, and those leaving >80% have very little growth even after long periods of time.
Figure 3.
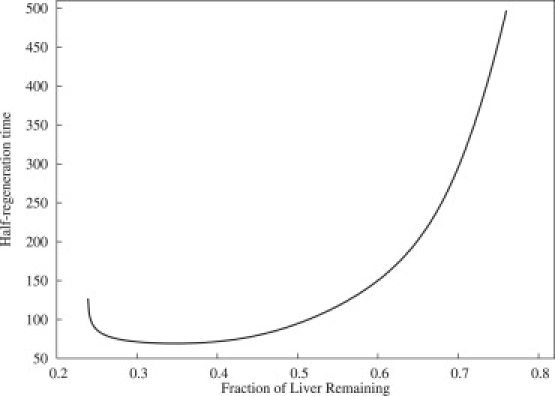
Regeneration time per hepatocyte. Time required to recover half of lost mass as a function of the fraction of liver remaining after partial hepatectomy. Fractions <25% resulted in liver failure; those >80% did not recover half of the lost mass within 500 h (≈3 weeks).
Mutant analysis
Table 4 shows the half-regeneration times for different mutants of the liver regeneration model. Since liver regeneration is a complex process, with multiple equivalent pathways, experiments that knock out one particular gene only succeed, in general, in slowing the liver regeneration process. We can simulate knock-out experiments or overstimulation experiments by varying the kinetic parameters of the model. Here, we either multiply or divide parameters by a factor of two.
Table 4.
Half-regeneration times for selected mutants after 2/3 partial hepatectomy
| Mutant type | Half-regeneration time (h) | Comment/Reference |
|---|---|---|
| Regular model | 70.0 | This article. |
| 1/2 VST3 | 78.9 | STAT3 knockouts have diminished DNA synthesis and induction of IE genes (35). |
| 1/2 kGF | 95.4 | Met (HGF-receptor) knockouts have increased mortality and liver failure (13). |
| 1/2 kdeg | 80.7 | Mice with collagenase-resistant collagen have impaired recovery to CCl4 damage (36). |
Decreasing the rate of production of STAT3 and GF lengthens the regeneration time, confirming knockout experiments that suggest that these elements are crucial for liver regeneration (13,35). Decreasing the rate at which TNF-activated MMPs degrade the ECM also delays regeneration, as shown previously in Issa et al. (36).
The model also confirms the importance of the metabolic load. Increasing the metabolic load M by 25% without partial hepatectomy induces a liver growth of 10% within 300 h; for an increase of 50%, the liver grows by 25%. Similarly, Mead et al. have observed (37) that protein-deprived rats that are refed amino acids undergo a burst in hepatic DNA activity, without undergoing partial hepatectomy. On the other hand, small increases in the metabolic load do not change the liver size significantly: a 10% increase only results in 1% liver growth after 300 h.
Model sensitivity
Although we modeled cellular apoptosis and requiescence using hyperbolic tangent functions, any other sigmoidal function with the same mean and width gives similar results. Substituting the hyperbolic tangent function with the Gompertz function, the error function, or the functions , did not change our results.
We performed a sensitivity analysis on the mean and width of sigmoidal functions θ req, βr eq, θ ap, and β ap, and on the cell-cycle parameters k Q, k P, and k R. We considered the cell populations as a function of time for four resections with initial fractions 0.15, 0.32, 0.55, and 0.75, as in Fig. 2. We chose 20 time points; at each we calculated the sum of the squares of the difference among the values of Q, P, and R evaluated at the vector of model parameter values x 0 and the vector of the evaluated values x. Our cost function C(x) is this quantity summed over the 20 time points and over the four resections:
| (11) |
The parameter ranges can be approximated by the diagonal entries of the inverse of the Hessian of C(x), evaluated at x 0. The parameter ranges, normalized to the model parameter values, are shown in Table 5. The cell-cycle parameters have sensitivities of ∼1%, while the sigmoid function parameters have sensitivities between 10 and 150%. The fact that the parameters associated with the sigmoidal functions have wide latitudes whereas the cellular rate constants are well determined is consistent with the precise sigmoidal functional form being unimportant for our conclusions.
Table 5.
Parameter ranges normalized to model values
| kQ | 0.0118 |
| kP | 0.0091 |
| kR | 0.0245 |
| θreq | 0.4606 |
| βreq | 1.5697 |
| θap | 0.5445 |
| βap | 0.1020 |
Geometric interpretation
The dynamics observed in the liver regeneration model can be more easily understood in terms of a geometric picture in the two-dimensional phase plane involving R and Q cells. We can motivate this picture by observing a projection of the full dynamics onto the Q–R plane as shown in Fig. 4 and considering a systematic reduction of the full system while preserving the geometric structure. In the Q–R projection there seem to be attracting fixed points located near Q = 1, R = 0 and R = 0, Q = 0, with a separatrix between them. In a reduced description, continuity of the trajectories would require that there be an unstable fixed point, whose stable manifold would correspond to the separatrix. The fact that a range of liver resting states are possible implies that there exists a line attractor along the Q axis (i.e., attracting invariant one-dimensional manifold).
Figure 4.
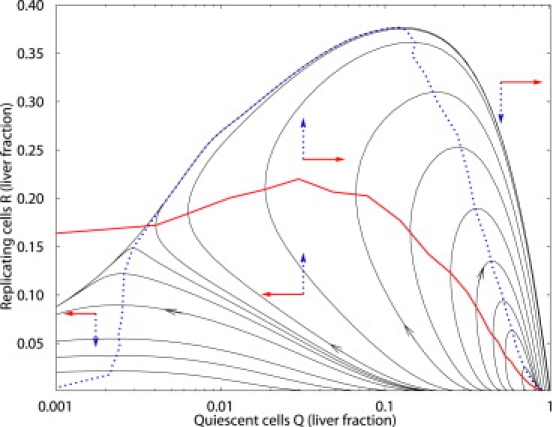
Q–R plane projection of sample liver regeneration trajectories. The dark solid and dotted lines represent the Q and R nullclines, respectively. The smooth nullclines are approximated by piecewise linear interpolation from turning points of selected trajectories. The solid and dotted arrows show the direction of the vector field explicitly in each region.
We can observe these features by performing a systematic reduction of the dynamics as is often done in excitable membrane dynamics. These approximations are intended to only preserve the geometric properties of the vector field governing the dynamics. We first assume that all the dynamical equations other than those for Q and R (i.e., P, ECM, GF, IE, and intracellular mediators) are much faster, and can thus be presumed to be quasistationary. We then observe that, at rest, almost all cells are in state Q, so we can replace N by Q. We can then express all the quasistationary variables as functions of Q, resulting in a two-dimensional autonomous dynamical system for Q and R. The resulting equations will have the form
| (12) |
| (13) |
where ψ and ϕ are fairly complicated functions of Q and R. However, these functions can be simplified considerably and still preserve the main geometric structure in the phase-plane. We propose that the following system captures the main features of the liver regeneration model,
| (14) |
| (15) |
where f(x) is any decreasing sigmoidal function, and k and c are free parameters. The nullclines, given by and , are shown in Fig. 5. The Q-nullcline is composed of two disjoint curves. One is given by Q = 0 and the other is given by R = f(Q). The R-nullcline is given by R = cf(Q)Q.
Figure 5.
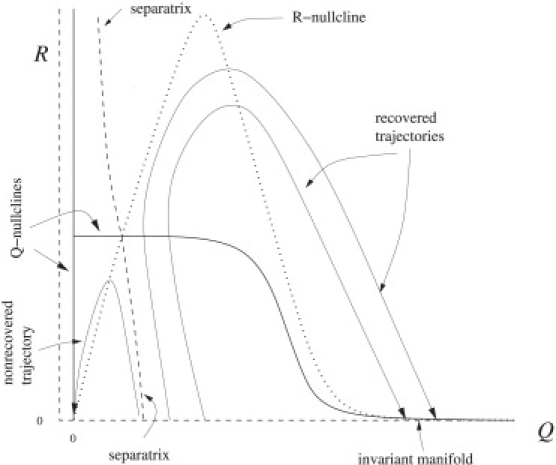
Q–R plane of reduced model, with f(x) = 1 + tanh(10(0.65 – x)), k = 0.2, c = 4.
The intersections of the nullclines of Pediaditakis et al. (15) give the invariant sets of the phase plane. Both nullclines converge toward zero for large Q, defining an invariant manifold along the Q axis or line attractor, which is attracting in the R direction but marginally stable along Q. Thus, the liver can exist at a number of sizes. There is a stable fixed point at the origin and a saddle point for R and Q > 0. Trajectories below the Q-nullcline will flow toward the left and those above will flow to the right. Simultaneously, trajectories below the R-nullcline will flow upwards while those above will flow downwards. The stable manifold of the saddle point defines the separatrix between the basins of attraction of the origin (no recovery) and the line attractor (full recovery). From these properties, the fate of all initial conditions can be understood.
Trajectories with initial conditions for Q values below the line attractor (but not too low) will increase in R and decrease in Q until they cross the Q-nullcline, from which they will then increase in Q. When the liver trajectory crosses the R nullcline, R will begin to decrease and return to the liver to the line attractor. The continuity of the trajectory in the phase plane implies that trajectories cannot cross, so this implies that the more Q is reduced initially, the faster R will rise and the further out in Q the trajectory will terminate. Hence, small reductions will always result with smaller livers than large reductions (provided the reduction is not so large as to cross the separatrix). If the initial reduction in Q takes it below the separatrix, then the trajectory will cross the R nullcline before the Q nullcline, causing R to decrease and thus, the liver trajectory will end up at the origin (obviously the animal would die before the liver shrank to zero size).
The geometric picture can provide the intuition to design interventions for liver recovery. For example, the model suggests that if any intervention could move the location of the unstable fixed point and hence the separatrix, then it may be possible to save a damaged liver that might otherwise not recover. Lowering the Q-nullcline and/or raising the R-nullclines would decrease the threshold for nonrecoverable excision. These possibilities are explored in the following section.
Predictions
In addition to matching several experimental results, the model makes predictions for future experiments. These predictions stem from the geometric picture of liver regeneration and involve moving the starting point of the liver regeneration to locations that are not on the Q axis or moving the location of the unstable fixed point.
First, the model gives striking results for multiple-resection experiments: counterintuitively, multiple resections can result in faster growth. For example, if, 48 h after a 45% partial hepatectomy, a liver is again resected so as to return to 55% of its normal weight, the liver recovers 25% faster than it would have if the excess growth had not been removed. The total recovery time is shortened because of the fast recovery after the second resection. The recovery after the second resection is faster than the one after the first—even though they both start with the same number of cells—because the second recovery begins with large populations of replicating and primed cells, as well as with higher numbers per cell of IE and GF. This headstart results in an extremely rapid regeneration, which more than compensates for the initial wasted 48 h. Fig. 6 shows the recovery time as a function of the interval between successive partial hepatectomies, for various degrees of partial hepatectomy. The second resection in a repeated resection experiment must be physiologically feasible in terms of the lobular structure of the remaining liver, since liver regeneration does not resurrect the resected lobe(s). Repeated resections may be best tested in a parabiotic experiment, in which a second resection is performed on the other animal in a parabiotic pair of animals without multiple resections on the animal that undergoes the first resection.
Figure 6.
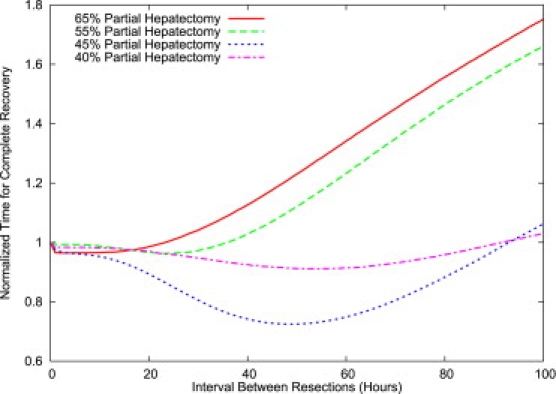
Recovery times for double hepatectomies: normalized total time of recovery as a function of the interval between hepatectomies (in hours). The time of recovery, defined as the time to reach 90% of normal size, is normalized to the recovery time for a single hepatectomy. The second hepatectomy consists of reducing the liver size to the size after the first hepatectomy; it affects all cell types equally. The 45% repeated hepatectomy results in a significant reduction in recovery time over a single hepatectomy.
Secondly, the model predicts that increasing the metabolic load before partial hepatectomy will lead to a faster recovery. For example, doubling the metabolic load 48 h before 75% partial hepatectomy ( Fig. 7) leads to a complete and rapid recovery, as compared to an extremely slow recovery under regular conditions (Fig. 1 D). This is because the increased metabolic load leads to increases in primed and proliferating cells, which places the system in a different part of the phase space in which it recovers much faster. Increasing the metabolic load before partial hepatectomy, through increased diet or even perhaps controlled toxification, should lead to more rapid recoveries in experimental settings.
Figure 7.
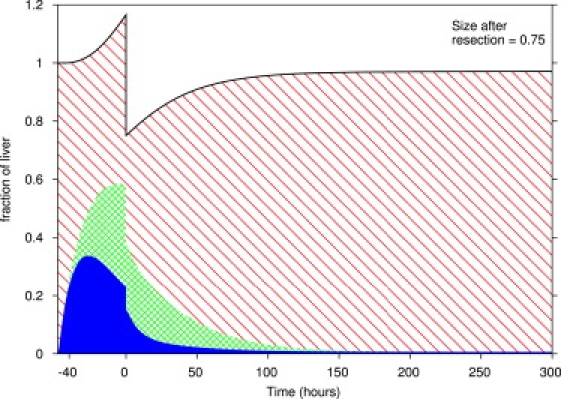
Liver regeneration in response to increased metabolic load followed by partial hepatectomy. The metabolic load was doubled for 48 h before partial hepatectomy and was normal after partial hepatectomy. The 75% partial hepatectomy at time 0 affects all cell types equally. The diagonal, cross-hatched, and solid areas represent quiescent, primed, and replicating cells, respectively.
Finally, the model proposes a way to salvage livers that are too small to perform basic functions and are liable to failure. Decreasing the metabolic load M will decrease the metabolic load per cell M/N so that the liver is not in the apoptotic range. The liver can then grow sufficiently so that it can survive under a regular metabolic load. Halving the metabolic load for 48 h after 85% partial hepatectomy successfully brought the liver to full recovery ( Fig. 8). Experimentally, decreasing the metabolic load through starvation and detoxification should help prevent liver failure in cases of overly small livers.
Figure 8.
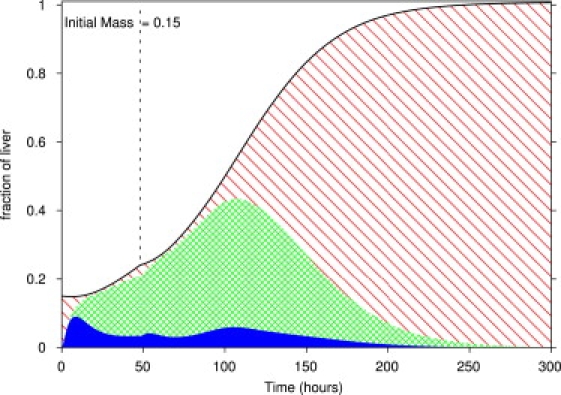
Liver regeneration under decreased metabolic load. After an 85% partial hepatectomy, the metabolic load was halved for 48 h before being raised to normal at time 48 h (dashed line). The diagonal, cross-hatched, and solid areas represent quiescent, primed, and replicating cells, respectively.
In these latter two contexts, it is crucial to experimentally determine specifically which of the myriad metabolic demands on the liver are most important as factors in the overall quantity we have characterized as the metabolic load M.
Discussion
Our model relies on distinguishing between three cell phases, as suggested by Fausto et al. (9): quiescent cells, primed cells and replicating cells. The addition of a primed phase, in addition to the traditional quiescent and replicating phases, allows for much greater control of cell proliferation. The initial cytokine burst, the size of which depends on the metabolic load, takes cells from the quiescent state to the primed state. One important control mechanism is that after the initial burst, cells can no longer be primed: once cells return to quiescence, they cannot enter the cell cycle again. Another control mechanism is that primed cells can make a decision between proceeding to the replicating phase and returning to the quiescent phase. Under elevated levels of growth factors, primed cells continue to the replicating phase; under low levels of growth factors, they return to quiescence. The level of growth factor depends on the size of the liver both in terms of growth factor production, which is proportional to the metabolic load, and in terms of growth factor inactivation, which is proportional to the size of the ECM. Finally, the number of cells in the proliferating state depends on the balance between the body's metabolic needs and the size of the ECM, which grows back as the metabolic load decreases.
DNA synthesis occurs at different times in liver parenchymal and nonparenchymal cells (8). Since the ECM is produced by nonparenchymal cells, whereas the metabolic load is relieved by the growth of parenchymal cells, it is possible to envisage a model in which the control of liver growth depends on a coordination between the parenchymal and nonparenchymal cell cycles. Our model does not distinguish between different types of liver cells, suggesting that the difference in cell cycle parameters is not necessary for liver regeneration to occur.
Our model shows a steady and smooth regrowth of the liver. However, early studies of liver regeneration (1,38) report several waves of liver growth, presumably corresponding to different rounds of cell division (after a 2/3 resection, each cell reproduces on average 1.6 times). This aspect of liver regeneration, though not included in our model of regeneration, could easily be captured in a stochastic version of our model.
While liver regeneration is a complex process (4,8) at the molecular level, the simplicity of our mathematical model suggests that liver regeneration is not a complex process in the mathematical sense: it involves (excluding degeneracies) a small number of pathways that relate liver growth to the body's metabolic needs and elegantly succeed in tightly controlling the regenerative process. The framework that we have developed here may help guide the development of future experiments and therapies.
Acknowledgments
This research was supported by the Intramural Research Program of the U.S. National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases.
References
- 1.Higgins G., Anderson R. Restoration of the liver of the white rat following partial surgical removal. Arch. Pathol. (Chic) 1931;12:186–202. [Google Scholar]
- 2.Fausto N. Hepatocytes break the rules of senescence in serial transplantation studies—is there a limit to their replicative capacity? Am. J. Pathol. 1997;151:1187–1189. [PMC free article] [PubMed] [Google Scholar]
- 3.Fausto N., Riehle K.J. Mechanisms of liver regeneration and their clinical implications. J. Hepatobiliary Pancreat. Surg. 2005;12:181–189. doi: 10.1007/s00534-005-0979-y. [DOI] [PubMed] [Google Scholar]
- 4.Michalopoulos G.K. Liver regeneration. J. Cell. Physiol. 2007;213:286–300. doi: 10.1002/jcp.21172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mangnall D., Bird N.C., Majeed A.W. The molecular physiology of liver regeneration following partial hepatectomy. Liver Int. 2003;23:124–138. doi: 10.1034/j.1600-0676.2003.00812.x. [DOI] [PubMed] [Google Scholar]
- 6.Heath J.K. Blackwell Science; Oxford, UK: 2000. Principles of Cell Proliferation. [Google Scholar]
- 7.Su A.I., Guidotti L.G., Pezacki J.P., Chisari F.V., Schultz P.G. Gene expression during the priming phase of liver regeneration after partial hepatectomy in mice. Proc. Natl. Acad. Sci. USA. 2002;99:11181–11186. doi: 10.1073/pnas.122359899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Taub R. Liver regeneration: from myth to mechanism. Nat. Rev. Mol. Cell Biol. 2004;5:836–847. doi: 10.1038/nrm1489. [DOI] [PubMed] [Google Scholar]
- 9.Fausto N., Campbell J.S., Riehle K.J. Liver regeneration. Hepatology. 2006;43:S45–S53. doi: 10.1002/hep.20969. [DOI] [PubMed] [Google Scholar]
- 10.Iwai M., Cui T.-X., Kitamura H., Saito M., Shimazu T. Increased secretion of tumor necrosis factor and interleukin 6 from isolated, perfused liver of rats after partial hepatectomy. Cytokine. 2001;13:60–64. doi: 10.1006/cyto.2000.0797. [DOI] [PubMed] [Google Scholar]
- 11.Levy D.E., D J., Jr. STATs: transcriptional control and biological impact. Natl. Rev. 2002;3:651–662. doi: 10.1038/nrm909. [DOI] [PubMed] [Google Scholar]
- 12.Campbell J.S., Prichard L., Schaper F., Schmitz J., Stephenson-Famy A. Expression of suppressors of cytokine signaling during liver regeneration. J. Clin. Invest. 2001;107:1285–1292. doi: 10.1172/JCI11867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huh C.-G., Factor V.M., Sanchez A., Uchida K., Conner E.A. Hepatocyte growth factor/c-met signaling pathway is required for efficient liver regeneration and repair. Proc. Natl. Acad. Sci. USA. 2004;101:4477–4482. doi: 10.1073/pnas.0306068101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmidt C., Bladt F., Goedecke S., Brinkmann V., Zschiesche W. Scatter factor/hepatocyte growth factor is essential for liver development. Nature. 1995;373:699–702. doi: 10.1038/373699a0. [DOI] [PubMed] [Google Scholar]
- 15.Pediaditakis P., Lopez-Talavera J.C., Petersen B., Monga S.P.S., Michalopoulos G.K. The processing and utilization of hepatocyte growth factor/scatter factor following partial hepatectomy in the rat. Hepatology. 2001;34:688–693. doi: 10.1053/jhep.2001.27811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mars W.M., Liu M.-L., Kitson R.P., Goldfarb R.H., Gabauer M.K. Immediate early detection of urokinase receptor after partial hepatectomy and its implications for initiation of liver regeneration. Hepatology. 1995;21:1695–1701. [PubMed] [Google Scholar]
- 17.Olsen P.S., Boesby S., Kirkegaard P., Therkelsen K., Almdal T. Influence of epidermal growth factor on liver regeneration after partial hepatectomy in rats. Hepatology. 1988;8:992–996. doi: 10.1002/hep.1840080503. [DOI] [PubMed] [Google Scholar]
- 18.Mead J.E., Fausto N. Transforming growth factor-α may be a physiological regulator of liver regeneration by means of an autocrine mechanism. Proc. Natl. Acad. Sci. USA. 1989;86:1558–1562. doi: 10.1073/pnas.86.5.1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mitchell C., Nivison M., Jackson L.F., Fox R., Lee D.C. Heparin-binding epidermal growth factor-like growth factor links hepatocyte priming with cell cycle progression during liver regeneration. J. Biol. Chem. 2005;280:2562–2568. doi: 10.1074/jbc.M412372200. [DOI] [PubMed] [Google Scholar]
- 20.Mohammed F.F., Khokha R. Thinking outside the cell: proteases regulate hepatocyte division. Trends Cell Biol. 2005;15:555–563. doi: 10.1016/j.tcb.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 21.Serandour A., Loyer P., Garnier D., Courselaud B., Theret N. TNF-α-mediated extracellular matrix remodeling is required for multiple division cycles in rat hepatocytes. Hepatology. 2005;41:478–486. doi: 10.1002/hep.20602. [DOI] [PubMed] [Google Scholar]
- 22.Sokabe T., Yamamoto K., Ohura N., Nakatsuka H., Qin K. Differential regulation of urokinase-type plasminogen activator expression by fluid shear stress in human coronary artery endothelial cells. Am. J. Physiol. Heart Circ. Physiol. 2004;287:H2027–H2034. doi: 10.1152/ajpheart.00260.2004. [DOI] [PubMed] [Google Scholar]
- 23.Tseng H., Peterson T.E., Berk B.C. Fluid shear stress stimulates mitogen-activated protein kinase in endothelial cells. Circ. Res. 1995;77:869–878. doi: 10.1161/01.res.77.5.869. [DOI] [PubMed] [Google Scholar]
- 24.Moolten F.L., Bucher N.L.R. Regeneration of rat liver: transfer of humoral agent by cross circulation. Science. 1967;158:272–274. doi: 10.1126/science.158.3798.272. [DOI] [PubMed] [Google Scholar]
- 25.Fisher B., Szuch P., Levine M., Fisher E.R. A portal blood factor as the humoral agent in liver regeneration. Science. 1971;171:575–577. doi: 10.1126/science.171.3971.575. [DOI] [PubMed] [Google Scholar]
- 26.Cornell R.P. Gut-derived endotoxin elicits hepatotrophic factor secretion for liver regeneration. Am. J. Physiol. 1985;249:R551–R562. doi: 10.1152/ajpregu.1985.249.5.R551. [DOI] [PubMed] [Google Scholar]
- 27.Nelsen C.J., Rickheim D.G., Tucker M.M., Hansen L.K., Albrecht J.H. Evidence that cyclin D1 mediates both growth and proliferation downstream of TOR in hepatocytes. J. Biol. Chem. 2003;278:3656–3663. doi: 10.1074/jbc.M209374200. [DOI] [PubMed] [Google Scholar]
- 28.Nelsen C.J., Rickheim D.G., Tucker M.M., McKenzie T.J., Hansen L.K. Amino acids regulate hepatocyte proliferation through modulation of cyclin D1 expression. J. Biol. Chem. 2003;278:25853–25858. doi: 10.1074/jbc.M302360200. [DOI] [PubMed] [Google Scholar]
- 29.Moser M., Gong Y., Zhang M., Johnston J., Lipschitz J. Immediate-early protooncogene expression and liver function following various extents of partial hepatectomy in the rat. Dig. Dis. Sci. 2001;46:907–914. doi: 10.1023/a:1010791915733. [DOI] [PubMed] [Google Scholar]
- 30.Panis Y., McMullan D.M., Emond J.C. Progressive necrosis after hepatectomy and the pathophysiology of liver failure after massive resection. Surgery. 1997;121:142–149. doi: 10.1016/s0039-6060(97)90283-x. [DOI] [PubMed] [Google Scholar]
- 31.Sato Y., Koyama S., Tsukada K., Hatakeyama K. Acute portal hypertension reflecting shear stress as a trigger of liver regeneration following partial hepatectomy. Surg. Today. 1997;27:518–526. doi: 10.1007/BF02385805. [DOI] [PubMed] [Google Scholar]
- 32.Berg J.M., Tymoczko J.L., Stryer L. Biochemistry. 6th Ed. W.H. Freeman; New York: 2007. Chapter 8. [Google Scholar]
- 33.Bucher N.L., Swaffield M.N. The rate of incorporation of labeled thymidine into the deoxyribonucleic acid of regenerating rat liver in relation to the amount of liver excised. Cancer Res. 1964;24:1611–1625. [PubMed] [Google Scholar]
- 34.MacDonald R.A., Rogers A.E., Pechet G. Regeneration of the liver: relation of regenerative response to size of partial hepatectomy. Lab. Invest. 1962;11:544–548. [Google Scholar]
- 35.Li W., Liang X., Kellendonk C., Poli V., Taub R. STAT3 contributes to the mitogenic response of hepatocytes during liver regeneration. J. Biol. Chem. 2002;277:28411–28417. doi: 10.1074/jbc.M202807200. [DOI] [PubMed] [Google Scholar]
- 36.Issa R., Zhou X., Trim N., Millward-Sadler H., Krane S. Mutation in collagen-I that confers resistance to the action of collagenase results in failure of recovery from CCl4-induced liver fibrosis, persistence of activated hepatic stellate cells, and diminished hepatocyte regeneration. FASEB J. 2003;17:4749–4759. doi: 10.1096/fj.02-0494fje. [DOI] [PubMed] [Google Scholar]
- 37.Mead J.E., Braun L., Martin D.A., Fausto N. Induction of replicative competence (“priming”) in normal liver. Cancer Res. 1990;50:7023–7030. [PubMed] [Google Scholar]
- 38.Brues A.M., Drury D.R., Brues M.C. A quantitative study of cell growth in regenerating liver. Arch. Pathol. (Chic) 1936;22:658–673. [Google Scholar]
- 39.Campbell J.S., Riehle K.J., Brooling J.T., Bauer R.L., Mitchell C. Proinflammatory cytokine production in liver regeneration is Myd88-dependent, but independent of Cd14, Tlr2, and Tlr4. J. Immunol. 2006;176:2522–2528. doi: 10.4049/jimmunol.176.4.2522. [DOI] [PubMed] [Google Scholar]
- 40.Klein C., Wüstefeld T., Assmus U., Roskams T., Rose-John S. The IL-6gp130STAT3 pathway in hepatocytes triggers liver protection in T-cell mediated liver injury. J. Clin. Invest. 2005;115:860–869. doi: 10.1172/JCI200523640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gao J.J., Xue Q., Papasian C.J., Morrison D.C. Bacterial DNA and lipopolysaccharide induce synergistic production of TNF-α through a post-transcriptional mechanism. J. Immunol. 2001;166:6860–6877. doi: 10.4049/jimmunol.166.11.6855. [DOI] [PubMed] [Google Scholar]
- 42.Siewert E., Müller-Esterl W., Starr R., Heinrich P.C., Schaper F. Different protein turnover of interleukin-6-type cytokine signaling components. Eur. J. Biochem. 1999;265:251–257. doi: 10.1046/j.1432-1327.1999.00719.x. [DOI] [PubMed] [Google Scholar]
- 43.Cressman D.E., Diamond R.H., Taub R. Rapid activation of the Stat3 transcription complex in liver regeneration. Hepatology. 1995;21:1443–1449. [PubMed] [Google Scholar]
- 44.Rahmsdorf H.J., Schönthal A., Angel P., Litfin M., Rüther U. Posttranscriptional regulation of c-fos mRNA expression. Nucleic Acids Res. 1987;15:1643–1659. doi: 10.1093/nar/15.4.1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zargenar R., DeFrances M.C., Kost D.P., Lindroos P., Michalopoulos G.K. Expression of hepatocyte growth factor mRNA in regenerating rat liver after partial hepatectomy. Biochem. Biophys. Res. Commun. 1991;177:559–565. doi: 10.1016/0006-291x(91)92020-k. [DOI] [PubMed] [Google Scholar]
- 46.Stöcker E., Heine W.-D. Regeneration of liver parenchyma under normal and pathological conditions. Beitr. Pathol. 1971;144:400–408. [PubMed] [Google Scholar]
- 47.Alison M.R. Regulation of hepatic growth. Physiol. Rev. 1986;66:499–541. doi: 10.1152/physrev.1986.66.3.499. [DOI] [PubMed] [Google Scholar]
- 48.Webber E.M., Bruix J., Pierce R.H., Fausto N. Tumor necrosis factor primes hepatocytes for DNA replication in the rat. Hepatology. 1998;28:1226–1234. doi: 10.1002/hep.510280509. [DOI] [PubMed] [Google Scholar]
- 49.Emond J., Capron-Laudereau M., Meriggi F., Bernuau J., Reynes M. Extent of hepatectomy in the rat. Eur. Surg. Res. 1989;21:251–259. doi: 10.1159/000129034. [DOI] [PubMed] [Google Scholar]


