Molecular Renormalization Group Coarse-Graining of Polymer Chains: Application to Double-Stranded DNA

Abstract

Coarse-graining of atomistic force fields allows us to investigate complex biological problems, occurring at long timescales and large length scales. In this work, we have developed an accurate coarse-grained model for double-stranded DNA chain, derived systematically from atomistic simulations. Our approach is based on matching correlators obtained from atomistic and coarse-grained simulations, for observables that explicitly enter the coarse-grained Hamiltonian. We show that this requirement leads to equivalency of the corresponding partition functions, resulting in a one-step renormalization. Compared to prior works exploiting similar ideas, the main novelty of this work is the introduction of a highly compact set of Hamiltonian basis functions, based on molecular interaction potentials. We demonstrate that such compactification allows us to reproduce many-body effects, generated by one-step renormalization, at low computational cost. In addition, compact Hamiltonians greatly increase the likelihood of finding unique solutions for the coarse-grained force-field parameter values. By successfully applying our molecular renormalization group coarse-graining technique to double-stranded DNA, we solved, for the first time, a long-standing problem in coarse-graining polymer systems, namely, how to accurately capture the correlations among various polymeric degrees of freedom. Excellent agreement is found among atomistic and coarse-grained distribution functions for various structural observables, including those not included in the Hamiltonian. We also suggest higher-order generalization of this method, which may allow capturing more subtle correlations in biopolymer dynamics.

Introduction

Many exciting biological processes occur over time- and length-scales that are not amenable to computational modeling using all-atom (AA) molecular dynamics (MD) simulations. To study these complex biological systems, coarse-grained (CG) models are developed from either experimental data or atomistic simulations. For example, to address the million-fold compaction of DNA into a highly organized structure called chromatin (1,2), one needs to deal with dozens of nucleosomal core particles connected by linker DNA chains. Each nucleosome core particle is a nucleoprotein complex, with ∼150 DNA basepairs wrapped around a protein histone core of ∼1200 residues. In addition, each histone protein projects out a flexible histone tail, whose interactive dynamics with the rest of the nucleosome core particle can have a significant impact on the higher-order chromatin organization. Therefore, because of the enormous number of atoms in even the shortest chromatin fiber segments, a simplified CG representation is required for computational modeling. Prior efforts in this area were based on the use of a phenomenological wormlike chain Hamiltonian and continuum electrostatics approach (3,4) or computational models derived from experimental structural data (5). An alternative approach, based on coarse-graining of high-resolution AA force fields, such as AMBER (6), has not been yet pursued. In this work, we make a significant step in that direction, by developing an accurate CG model of a double-stranded DNA chain, playing the role of a linker DNA segment in the chromatin. Our technique is general and can be effectively used in a straightforward manner to coarse-grain various molecular systems, including polymer chains.

DNA electrostatics, particularly at short distances, plays a key role in chromatin folding (7). Moreover, conformational preferences of the semiflexible linker DNA are critically important, since the vast majority of the chromatin backbone conformational degrees of freedom reside in the linker DNA. To accurately capture these essential properties of the DNA molecule, we derive an effective Hamiltonian for a simplified CG DNA model from AA MD simulations. This implies, first, that we do not rely only on interactions derived from continuum electrostatics (as is customary), which are inapplicable at short distances (8,9). Second, our approach of accurate matching of the relevant fluctuations between the AA and CG systems allows us to move beyond phenomenological elastic models used in prior works and reproduce various DNA chain anharmonicities. Finally, we report a novel polymer chain coarse-graining technique, based on renormalization group (RG) ideas (10), which systematically accounts for correlations among various polymer degrees of freedom, including bonding, bending angle, and dihedral angle interactions. Fukunaga et al. demonstrated that even in case of a simple polyethylene chain, these CG degrees of freedom appeared to be highly correlated at room temperature (11). Although the interaction potentials in their study have been approximated by the potentials of mean force (PMF) derived from all-atom MD simulation, they suggested that a significant improvement of CG polymer models could be achieved by accounting for cross-correlations among various CG variables. This problem, which is well recognized, has been solved in this work using novel molecular basis functions within the RG-inspired coarse-graining approach developed in prior works (12,13).

Although numerous optimization techniques exist to account for cross-correlations in CG models either self-consistently or explicitly, they have not been applied to complex polymer systems. For example, a widely used Inverse Monte Carlo technique, belonging to the first class of the above algorithms, was first successfully applied in deriving the effective interaction potentials by iterative inversion of the radial distribution functions (RDF) in one-component simple liquids (14,15). This scheme was later generalized to many-component systems and applied to simple polymers, such as polyisoprene (16,17). The main deficiency of this optimization technique is a slow convergence associated with an implicit way of accounting for correlations among various types of effective interactions. Furthermore, the choice of RDFs to match between AA and CG simulations is often ad hoc. Another systematic coarse-graining technique, multiscale coarse-graining method based on force matching (18–20), has been recently applied to the coarse-graining of mixed lipid bilayers, peptides, and ionic liquids (21). A different approach, parameter optimization based on the ideas of RG theory, was applied by Lyubartsev and Laaksonen to explicitly account for cross-correlations in CG systems (13). This technique, which is distinct from Inverse Monte Carlo, was adapted from the Monte Carlo RG method developed by Swendsen to compute critical exponents in three-dimensional Ising models (12). It was applied in coarse-graining of a number of molecular systems, such as aqueous solution of Na⁺ and Cl⁻ (13), liquid water (22), and lipid bilayers (23).

While the Lyubartsev-Laaksonen (LL) technique is theoretically sound, it has only been applied to molecular systems with simple pairwise interactions (13,22,23). For example, the hydrocarbon tails in lipid systems were modeled without bending and dihedral angle potentials, or some equivalent interactions, which, in turn, would preclude a realistic description of hydrocarbon tail's conformational preferences (23). Consequently, a thinner CG membrane resulted, compared to the AA simulations (23). This unresolved discrepancy points to the conceptual difficulty of incorporating polymer degrees of freedom and other many-body interactions into the LL optimization scheme. As elaborated below, degeneracy of obtained solutions, and unreasonable large computer memory load demand to deal with many-body effects, are serious drawbacks of the LL technique. Since a number of key polymeric interactions, such as bending rigidity and torsional angle potentials, represent three- and four-body interactions, respectively, the LL optimization scheme represents an impractical tool for building an accurate CG model for polymers. In summary, existing optimization techniques do not provide a straightforward path to deriving an accurate CG model for double-stranded DNA, a polymer characterized by high rigidity, anharmonicities, and other many-body effects.

In this work, we generalize further Swendsen's RG method (12) and demonstrate that not only it can be used to develop interaction potentials for monoatomic and simple molecular systems, but also successfully applied in coarse-graining of various polymer systems. Our approach is based on matching various order correlators between CG and AA systems, for dynamical observables that explicitly enter the CG Hamiltonian. As elaborated below, these observables are compact molecular basis functions that directly enter the polymer Hamiltonian, allowing us to account not only for pairwise interactions, as in the literature (13,22,23), but treat many-body effects. This, in turn, ensures significant equivalence of the corresponding partition functions. In this sense, coarse-graining is based on the RG theory (10), where the reduction of a system's number of degrees of freedom is accompanied by renormalization of the interactions between particles, leaving the partition function and, thus, the character of fluctuations, unchanged. Hence, passing from the detailed AA system to a simplified CG representation corresponds to one-step renormalization. In coarse-graining, however, integrating out the solvent, mobile ion and irrelevant DNA degrees of freedom in detailed AA system results in a form of a Hamiltonian that is not explicitly known. A physically plausible Hamiltonian form should be guessed, followed by parameter optimization. As customary, the corresponding PMFs may serve as a starting point for parameter optimization (11,24).

In the following section, we first introduce our molecular renormalization group coarse-grained (MRG-CG) model of a double-stranded DNA chain. Next, we elaborate on the details of our optimization scheme that explicitly takes into account the correlations among various polymer degrees of freedom. The application to DNA chain is demonstrated. We subsequently provide field-theoretical arguments to show the close relationship between the MRG-CG scheme and the RG theory and also discuss on the possibility of achieving even higher accuracy with higher order expansions of partition functions. The applicability of the MRG-CG technique to other complex molecular systems and polymers is suggested.

A Coarse-Grained Model for Double-Stranded DNA

Our coarse-grained model of DNA is based on representing each DNA basepair by two beads of the same type, where each bead is placed in the geometric center of the corresponding basepair nucleotide. This leads to an ∼30-fold reduction of DNA degrees of freedom while preserving the major and minor groove structural patterns. We used the Biochemical Algorithms Library to build the DNA model (25). Such a homopolymeric two-bead model can easily be extended by introducing all four types of DNA nucleotides. Then, it would be possible to study, for example, a sequence-dependent melting and hybridization (so-called bubble dynamics (26)). In this work, however, we are focusing on developing a simpler DNA model with identical monomer units.

We used the following effective Hamiltonian to describe DNA chain interactions:

$$\mathcal{H}={\mathcal{U}}_{\text{bond}}+{\mathcal{U}}_{\text{ang}}+{\mathcal{U}}_{\text{fan}}+{\mathcal{U}}_{\text{el}}\text{.}$$ (1)

In this expression, the first two terms indicate bond and bending angle potential energies, respectively. While these contributions reflect connectivity of each DNA strand and represent intrastrand interactions, a nonstandard third term (we call it fan interactions) is responsible for maintenance of the DNA double-strand formed by two polynucleotides. As shown in Fig. 1, these interstrand interactions represent a superposition of basepairing and stacking forces. The last term in Eq. 1 corresponds to electrostatic energy between nonbonded pairs. The proposed Hamiltonian is somewhat similar to one used in a related recent work on DNA coarse-graining (27); however, this particular set of structural contributions was selected from systematically probing a variety of Hamiltonians with our optimization scheme. The Hamiltonian (Eq. 1) has led to a good agreement between AA and CG distributions for different molecular degrees of freedom, even for those not included in a Hamiltonian explicitly (discussed below and in Fig. 2).

Figure 1.

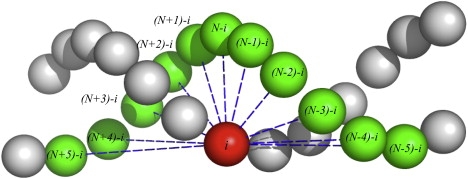
Fan interactions in the two-bead DNA model: Beads are placed in geometric centers of the AA nucleotides. Dashed lines indicate interactions between a given bead i located on one strand and a number of beads [(N ± 0..5) − i] located on the other strand, N being the total number of particles. There are 11 such interactions associated with basepairing and stacking of two polynucleotides.

Figure 2.

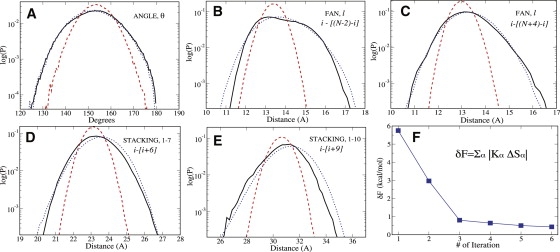
Semilog plots of distributions are shown for (A) DNA bending angle; (B and C) some of the fan constraints; and (D and E) intrastrand distances between particles separated by six and nine nucleotides (1–7 and 1–10 interactions). Solid, dashed, and dotted lines represent the reference AA, initial CG, and the corrected-by-optimization final CG distributions, respectively. Initial CG distributions are those generated by PMFs and correspond to accuracy of the CG polymer model developed by Fukunaga et al. (11). The 1–7 and 1–10 interactions do not enter the Hamiltonian equation (Eq. 1), indicating that other structural properties are also well reproduced. Panel F demonstrates the reduction of the total free energy difference δF between AA and CG models with optimization iterations.

To capture a nonsymmetric shape of DNA structural fluctuations (anharmonicities), we have chosen the following polynomial forms for individual energetic contributions,

$$U_{\begin{array}{l}\text{bond},\hfill \\ \text{fan}\hfill \end{array}}=\sum _{\alpha =2}^4{K}_{\alpha }{(l-l_0)}^{\alpha },U_{\text{ang}}=\sum _{\alpha =2}^4{K}_{\alpha }{(\theta -{\theta }_0)}^{\alpha },$$ (2)

where l and l₀ in the first formula are fluctuating and equilibrium interparticle separations for individual bond and fan interactions, respectively. The values θ and θ₀ play analogous roles for the angular potential in the second expression. As customary, equilibrium values l₀ and θ₀, as well as the initial set of coefficients {K_α⁽⁰⁾}, can be obtained by fitting these polynomials to the corresponding PMFs, extracted from AA MD simulations (24). To obtain these, we analyzed the dynamics of 16-basepair DNA oligomer solvated in explicit water with added physiological NaCl salt buffer, a system studied in our prior works (8,28,29). A brief summary of the all-atom MD simulation protocol is given in the Appendix.

We derived an effective bead-to-bead electrostatic potential from a separate series of extensive AA MD simulations, where two in-parallel oriented 16-basepair DNA oligomers at the same NaCl concentration were brought into proximity (9). In this work, we used the following expression, effective electrostatic energy of two in-parallel CG DNA molecules, to match the PMF for interacting AA DNA oligomers,

$${\mathcal{U}}_{\text{el}}=\sum _{ij}\left[A\frac{{\text{e}}^{-\kappa {\gamma }_{ij}}}{{\gamma }_{ij}^4}+\frac{q_i^{\text{eff}}{\text{e}}^{-\kappa ({\gamma }_{ij}-a)}{q}_j^{\text{eff}}}{4\pi {\varepsilon }_0\varepsilon {\gamma }_{ij}(1+a\kappa )}\right]$$ (3)

where the last term represents the long-range interactions approximated by the Debye-Hückel (DH) potential for beads of size a = 5 Å. The Debye length κ⁻¹ = 9 Å corresponds to physiological conditions. The bead charge was taken to be a quarter of the bare DNA nucleotide charge, q_eff = −0.25 (30). This assumption allowed us to set the absolute scale of the inter-DNA free energy curves (PMF), by equating the free energy for two DNA at the largest separation in our AA simulations to the interaction energy calculated from the analytical DH potential. The first term in Eq. 3 accounts for repulsive short-range interactions underestimated by the DH potential (9). The only adjustable parameter, A, was found to be 22.7 × 10³ kcal × mol⁻¹ × Å⁻⁴ from fitting to the AA PMF (9).

Optimizing Force-Field Parameters Using an RG-Inspired Approach

As mentioned in the Introduction, the optimization scheme used in this work closely follows the Monte Carlo RG method developed by Swendsen to compute critical exponents in Ising models (12). To proceed with mathematical formulation of the problem, we first introduce an effective CG Hamiltonian $\mathcal{H}\left(\left\{K_{\alpha }\right\}\right)$, defined by a parameter set, {K_α}, α = 1…N; and a set of observables of interest, {S_α({K_α})}, subject to canonical averaging over $\mathcal{H}\left(\left\{K_{\alpha }\right\}\right)$. Then, the difference, Δ〈S_α〉 ≡ 〈S_α〉_CG − 〈S_α〉_AA, between the expectation values of an observable, S_α, averaged over CG and AA systems may be expressed as

$$\Delta \langle S_{\alpha }\rangle =\sum _{\gamma }\frac{\partial {\langle S_{\alpha }\rangle }_{CG}}{\partial K_{\gamma }}\Delta K_{\gamma }+O(\Delta K^2),$$ (4)

which is simply an expansion of 〈S_α〉_CG around some point in space of the Hamiltonian {K_α}. The derivative in Eq. 4 is given by (CG subscripts are omitted)

$$\frac{\partial \langle S_{\alpha }\rangle }{\partial K_{\gamma }}=-\frac{1}{k_{\text{B}}T}\left[\langle S_{\alpha }\frac{\partial \mathcal{H}}{\partial K_{\gamma }}\rangle -\langle S_{\alpha }\rangle \langle \frac{\partial \mathcal{H}}{\partial K_{\gamma }}\rangle \right]$$ (5)

and represents susceptibility of observable 〈S_α〉 to the change of parameter K_γ (α and γ may be different). Hence, Eq. 4 may be viewed as a system's linear response to an external potential ΔK. This analogy is particularly beneficial in the case of Hamiltonians linear in {K_α}, having the form $\mathcal{H}={\sum }_{\alpha }{K}_{\alpha }{S}_{\alpha }$. Then, Eq. 4 reduces to

$$\Delta \langle S_{\alpha }\rangle =-1/\left(k_{\text{B}}T\right)\sum _{\gamma }\left[\langle S_{\alpha }{S}_{\gamma }\rangle -\langle S_{\alpha }\rangle \langle S_{\gamma }\rangle \right]\Delta K_{\gamma },$$ (6)

being expressed in terms of cross-correlators of various observables, as expected for susceptibilities. The following parameter optimization scheme may be used to decrease Δ〈S_α〉. First, the 〈S_αS_γ〉_CG correlators are obtained from MD simulations of the CG system using some trial set of Hamiltonian parameters, {K_α⁽⁰⁾}, followed by the calculation of the deviations Δ〈S_α〉 of each CG variable from their corresponding reference AA values. Subsequently, the system of linear equations in Eq. 6 is solved to yield the corrections for the Hamiltonian parameters, ΔK_α⁽⁰⁾, which define a new parameter set K⁽¹⁾_α = K⁽⁰⁾_α + ΔK⁽⁰⁾_α for the next CG iteration. The procedure is repeated until the convergence of all CG variables is reached, i.e., 〈S_α〉_CG ≈ 〈S_α〉_AA.

In the above discussion, K_α may be understood as fields conjugate to S_α which, in turn, represent various combinations of collective order parameters characterizing the CG system. For example, in Swendsen's original work (12), S_α values indicated various cumulative spin products, corresponding to interactions between nearest-neighbor and distant spins, as well as many-spin interactions (generated by RG). Analogously, in this work we relate S_α values to various collective modes associated with different types of effective molecular interactions in a DNA chain, as explained in the next section. In contrast, Lyubartsev and Laaksonen (13) expressed ionic RDFs in terms of S_α values, where the latter were positional Dirac delta functions. From this perspective, S_α can be viewed as a set of basis functions over which an effective Hamiltonian is spanned. A completeness of the given basis set is consistent with all Δ〈S_α〉s nearly vanishing after parameter optimization.

Compact Basis Set Allows the Inclusion of Many-Body Interactions

Compared to the LL approach, the principal novelty we introduce is the many-fold reduction of the Hamiltonian positional basis set, where the new basis set is spanned by functions of different dimensions (units). Such compactification is not just a matter of basis choice but may be viewed as a projection onto the relevant set of the collective dynamical modes, which enables us to explicitly account for cross-correlations between polymer degrees of freedom in a very efficient way. As follows from the previous section, each type of the effective DNA interactions is described by a very small number of physical observables, which are structure-based collective order parameters. Indeed, it follows from Eq. 2 that observables {S_α}, entering $\mathcal{H}={\sum }_{\alpha }{K}_{\alpha }{S}_{\alpha }$, are represented by various combinations of the structural order parameters, following from the functional form of polynomials defining our CG Hamiltonian. For example, three collective order parameters for bonds are $S_1^{\text{bond}}={\sum }_{\text{all}\text{bonds}}{(l-l_0)}^2$, $S_2^{\text{bond}}={\sum }_{\text{all}\text{bonds}}{(l-l_0)}^3$, and $S_3^{\text{bond}}={\sum }_{\text{all}\text{bonds}}{(l-l_0)}^4$, where l and l₀ enter Eq. 2. Analogously, collective observables for bending angles are $S_1^{\text{angle}}={\sum }_{\text{all}\text{angles}}{(\theta -{\theta }_0)}^2$, $S_2^{\text{angle}}={\sum }_{\text{all}\text{angles}}{(\theta -{\theta }_0)}^3$, and $S_3^{\text{angle}}={\sum }_{\text{all}\text{angles}}{(\theta -{\theta }_0)}^4$, etc. Aside from electrostatics, 39 K_α constants enter the DNA Hamiltonian, since there are 13 types of structural interactions (bond, angle, and fan), each characterized by three S_α values (see Eq. 2). We did not include electrostatics in our optimization scheme aimed to improve U_bond, U_ang, and U_fan potentials, because the former turned out to be substantially uncoupled from the structural degrees of freedom. Indeed, we verified that inter-DNA PMF, a chosen characteristic to calibrate the electrostatics, is reproduced in CG system at different stages of optimization procedure with no changes in the initial value of the parameter A in Eq. 3.

Next, we provide an estimate of the scale of the reduction of the total number of degrees of freedom upon the compactification of the CG Hamiltonian basis set compared with the positional Dirac delta function basis set in the LL formalism. In positional basis, each interaction potential was tabulated with resolution of 0.05 Å (13). Such a high resolution is apparently needed because of the potential instability of simulations associated with discontinuities of tabulated potentials. Thus, having a typical range of 10 Å, each type of interaction would be defined by ∼200 observables (instead of three, in our case), in terms of positional Dirac delta functions. Since our DNA model is described by >10 interaction potentials (see above), such representation would require us to deal with ∼4000 variables, necessitating inversion of a matrix of ∼10⁷ elements to solve the set of linear equations in Eq. 6. Representing bending angle potentials, which are three-body interactions, is even more problematic in the positional basis, resulting in serious computational difficulty because of the necessity of dealing with very large arrays. Note also that had we included the four-body dihedral potential in the consideration, the corresponding matrices would be even larger. On the other hand, within our approach this computational difficulty is bypassed by projecting such a large many-dimensional array into a very compact two-dimensional array defined in a set of basis functions of different dimensions (our S_α values). We elaborate next on the nontrivial inverse problem that needs to be solved when the covariance matrix, 〈S_αS_γ〉 − 〈S_α〉〈S_γ〉, contains noise and the basis functions have dissimilar physical units.

Solving the Inverse Problem

Eigenvalues of the covariance matrix in Eq. 6 indicate how changes in various dynamical modes affect different effective potentials. For the DNA problem, it turns out that the covariance matrix is nearly singular, resulting in the degeneracy of solutions that represent various sets of parameters. Apparently, this problem is caused by the redundancy of interaction potential functions as well as the noise which is normally present in the input data obtained from MD simulations (22,23). When too many observables are used to describe the CG system, larger uncertainty in the covariance matrix inversion results, and, thus, the stronger the degeneracy of the resulting set of CG Hamiltonian parameters. This implies, in particular, a significant advantage of using our compact set of 39 basis functions. Further reduction in the degeneracy can be achieved by eliminating those matrix eigenvectors which superfluously affect Hamiltonian parameters. Singular value decomposition (SVD) could have been directly used to address this issue if the elements of the covariance matrix in Eq. 6 had identical physical units. For example, the matrix element 〈S₂^bond·S₃^angle〉 − 〈S₂^bond〉〈S₃^angle〉 has a dimension of [ų·Rad⁴], while the diagonal element $\langle {\left(S_2^{\text{bond}}\right)}^2\rangle -{\langle S_2^{\text{bond}}\rangle }^2$ is measured in units of [Å⁶]. Therefore, to use SVD at each iteration, we reduced the corresponding covariance matrix to a dimensionless form by appropriately rescaling vectors ΔK_α and Δ〈S_α〉. Then, in matrix notation, the rescaled Eq. 6 takes the form

$$\sum _{\text{j}}\frac{M_{\text{ij}}}{\sqrt{q_{\text{i}}{q}_{\text{j}}^{\text{T}}}}\cdot \left[X_{\text{j}}\sqrt{q_{\text{j}}}\right]=\frac{B_{\text{i}}}{\sqrt{q_{\text{i}}}},q_{\text{i}}\equiv M_{\text{ii}},$$ (7)

with M, X, and B standing for the covariance matrix, vector of the corrections ΔK_α, and the vector of deviations Δ〈S_α〉, respectively. As follows from the second equation, vector q is composed from the diagonal elements of the original matrix M. Hence, the latter is reduced to a dimensionless form (with unit elements on the diagonal) after its element-by-element division by the tensor elements, $\sqrt{q_{\text{i}}{q}_{\text{j}}^{\text{T}}}$. After filtering out near-zero eigenvalues and performing a subsequent matrix inversion, the original units of the elements ΔK_α were obtained by reverse transformation. The optimized set of parameter values is given in the Supporting Material.

Comparison to All-Atom Results

As mentioned in A Coarse-Grained Model for Double-Stranded DNA, the initial Hamiltonian parameters, {K_α⁽⁰⁾}, were derived from fitting the polynomials in Eq. 2 to the corresponding AA PMFs approximating the effective potentials. As expected (11), these parameters generated distributions for all CG variables (l, θ) differing substantially from the corresponding AA results (see Fig. 2). We optimized the CG Hamiltonian parameters by solving the systems in Eq. 6 according to the technique outlined in the previous section. MD simulations of the CG system were carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS) (31). The details of the simulation protocol are provided in the Appendix.

The current MRG-CG optimization scheme has worked well, as illustrated in Fig. 2. For clarity, we show here a few distributions only at initial and final stages of the optimization procedure and compare them with the reference AA results (the remaining results and the Hamiltonian parameters are available upon request). The agreement is excellent not only for S_α values that entered the CG Hamiltonian, but also for those whose conjugate fields were not optimized. This is exemplified by 1–7 and 1–10 intrastrand interactions in Fig. 2, D and E.

We can estimate the change in the total free energy difference, $\delta F={\sum }_{\alpha }{K}_{\alpha }\Delta S_{\alpha }$, between AA and CG systems in the course of optimization procedure. Since our method is aimed at matching only the first moments in distributions of S_α values, we express δF in terms of the average deviations Δ〈S_α〉 of each CG variable from their corresponding reference AA value. Hence, the free energy difference is approximated by the leading term in the cumulant expansion,

$$\delta F=-k_{\text{B}}T\ln \langle {\text{e}}^{-\Delta \mathcal{H}/k_{\text{B}}T}\rangle =\langle \Delta \mathcal{H}\rangle +\frac{1}{2}\left[\langle \Delta {\mathcal{H}}^2\rangle -{\langle \Delta \mathcal{H}\rangle }^2\right]+\cdots ,$$ (8)

where $\Delta \mathcal{H}\equiv \delta F={\sum }_{\alpha }{K}_{\alpha }\Delta S_{\alpha }$, and the angular brackets indicate the canonical averaging over the ensemble of CG system states. To go beyond this linear approximation, higher order correlators of S_α values must be computed to estimate other terms in Eq. 8. We discuss this possibility below. As illustrated in the last panel of Fig. 2, only five iterations are needed to reduce the (average) total free energy difference between AA and CG systems to a small value within the statistical error of the simulation (〈δF〉 ∼0.5 k_BT). The discrepancies between the thermally averaged individual CG and AA terms, |K_αS_α|, were ∼0.01 k_BT, indicating excellent agreement between CG and AA Hamiltonians.

Generalizing Swendsen's RG Scheme

We suggest that the RG-CG scheme possesses significant advantages when compared with other commonly used optimization methods. Interestingly, prior works using this method for spin and ionic systems did not clearly elaborate on the specifics of its close relationship to the RG theory. Here, we point out these connections, and demonstrate how to generalize the method to achieve an arbitrarily high accuracy. We start by noticing that representing Hamiltonian as a linear decomposition over observables S_α allows us to interpret the partition function, $\mathcal{Z}\left(\left\{K\right\}\right)\propto \sum \exp \left[-1/\left(k_{\text{B}}T\right){\sum }_{\alpha =1}^N{K}_{\alpha }{S}_{\alpha }\right]$, as a generating function which can be differentiated to obtain all correlation functions (10),

$$\langle S_1\cdots S_n\rangle \propto \frac{{\delta }^n\ln \mathcal{Z}}{\delta K_1\cdots \delta K_n}\text{.}$$ (9)

Again, K_α here may be viewed as the fields conjugate to the observables S_α. We propose that these relations be used to define the degree of equivalency of CG and the partially integrated AA partition functions. Particularly, if two partition functions generate two identical sets of various auto- and cross-correlators of order n and less (hence, identical n^th derivatives of the free energies), we can think of n as a degree of similarity between two generating functions. From this perspective, Swendsen's optimization method, which matches only first moments in distributions over observables S_α, corresponds to order n = 1 of equivalency between CG and AA systems. Within this framework, it is straightforward to achieve higher accuracy in CG system description by demanding the coincidence of higher moments in S_α. This, in turn, would require computing (cross) correlators of order n + 1, to be used in equations equivalent to Eq. 6.

For example, we can use the condition Δ〈S_αS_γ〉 ≈ 0 to match various second-order correlators. In that case, the system of N linear equations, from the set of expressions in Eq. 6, would be supplemented by N(N − 1)/2 equations for Δ〈S_αS_γ〉 expressed in terms of various correlators of the third order. Since our system is characterized by a relatively small number of observables, N ≲ 10², it is computationally feasible to solve such an extended system of (still linear) equations. In an ongoing work, we are applying this higher order technique to coarse-grain highly inhomogeneous molecular systems, where accounting for the second moments of the collective order parameter distribution functions is essential.

Discussion and Conclusions

Our generalization of Swendsen's method compares favorably with many other commonly used alternative schemes aimed at matching certain ad hoc structural characteristics (see (24) and references therein), but not partition functions. It is well known from the RG theory that a renormalization step might lead to the introduction of extra many-body terms to the functional form of the original Hamiltonian. In a complex system, consisting of water, ions, and DNA, there is no simple procedure to determine the rigorous functional form of the CG Hamiltonian. Furthermore, many-body nonbonded terms would result in great computational inefficiency. Therefore, as a practical matter, one has to use physical intuition to construct a plausible form of the CG Hamiltonian. In our experience, a poor guess leads to problems with the optimization convergence. For example, to capture anharmonicities in DNA motion, we included polynomials up to quartic terms (see Eq. 2), which allowed us to reproduce complex correlations along the DNA chain. We also experimented with various ways to connect neighboring beads, finding that the fan potential described previously leads to satisfactory results. To facilitate parameter optimization procedure, it is convenient that parameters enter the Hamiltonian linearly, as discussed above. This, however, is not a strict requirement. Compactness of the Hamiltonian is also very important, mainly to increase the likelihood of obtaining a unique set of CG force-field parameters. Noncompact functional forms are expected to produce highly degenerate solutions sets, where, without any further guidance for how to choose the final parameter set, the technique becomes largely impractical.

The combination of topological constraints aimed to preserve the desired structure of the system may result in either quick convergence of the optimization scheme or no convergence at all. Thus, while the functional forms of the individual Hamiltonian contributions are dictated by their physical plausibility (and by common sense), it is the performance of the optimization technique that enables us to discriminate among the quality of various sets of the structural constraints imposed on the system. For example, we introduced the intrastrand and interstrand DNA interactions, represented by bond and bending angle potentials, and the fan interactions, respectively (see A Coarse-Grained Model for Double-Stranded DNA). As stated above, our optimization procedure led to a good agreement not only for the S_α values associated with these structural constraints, but also for those not imposed on a system and, hence, not considered explicitly in the effective Hamiltonian (see Fig. 2). At the same time, when we tried other combinations of structural constraints, for example, by introducing the interactions among distant beads of DNA chain belonging to the same strand, the results turned out to be unsatisfactory: the method showed poor convergence even for those constraints included into optimization, while other structural characteristics were not reproduced. In the worst case scenario, the structure of the double-stranded DNA was not stable at all. To summarize this issue, we emphasize that the application of the present technique to various systems will be greatly facilitated by careful selection of a physically sound CG Hamiltonian and the appropriate combination of the topological constraints, which, in turn, would allow maintaining the desired system structure and reproducing important motions.

Next, we discuss and summarize the advantages of the Hamiltonian linearity and compactness, which are the novel and principal features of our method. First, the Hamiltonian linearity enables us to avoid dealing with derivatives appearing explicitly in Eq. 5. Instead, we need to compute the various pair-correlators for the physical observables entering a much simpler Eq. 6, as demonstrated in Optimizing Force-Field Parameters Using an RG-Inspired Approach. These correlators can readily be obtained from the analysis of MD trajectory. In addition, the linearity of the Hamiltonian is very beneficial when the problem is viewed in light of field-theoretical arguments: as the parameters, K_α, correspond to the fields conjugate to physical observables, S_α, Eq. 6 appears naturally in the context of the fluctuation-dissipation theorem in the linear regime, when the system is slightly perturbed by the external fields, ΔK_α. Interestingly, it can be formally shown that representing the Hamiltonian in terms of the collective order parameters, ${\sum }_{\alpha }{K}_{\alpha }{S}_{\alpha }$, where only first moments of the distributions of these collective observables are reproduced, corresponds to addressing the problem on the level of mean-field approximation (see, for example, (10)). This means, in particular, that in this formalism, the resulting fields K_α appear as mean fields acting on the corresponding CG degrees of freedom, assuring the coincidence of the expectation values for the collective structure order parameters in AA and CG systems. Hence, the further generalization of the method proposed in Generalizing Swendsen's RG Scheme—by considering higher moments in distributions of S_α values—is an attempt to go beyond the mean-field approach. Again, this statement is formally justified by the correction to the mean-field approximation, known as the mean-field expansion (10).

Importantly, the possibility of incorporating these corrections into the MRG-CG optimization scheme relies heavily on the compactness of the Hamiltonian, which is another principal feature of our approach. Indeed, we have shown that because of the Hamiltonian compactness, our method is readily applicable to systems possessing important many-body effects which cannot be captured within the mean-field approximation. The double-stranded DNA chain studied in this work is an example of a system characterized by many-body interactions associated with the polymeric nature of the molecule. For instance, bending angle potentials appearing in our Hamiltonian are three-body interactions in a positional representation. To treat such interaction forms in this optimization scheme, we needed to develop a nontrivial inversion technique for tensors defined in space of basis functions of different dimensionality. On the other hand, the necessity of utilizing the extended approach of Generalizing Swendsen's RG Scheme arises when we are concerned with the correlations, more subtle than those among various types of CG degrees of freedom. For example, one would pose the problem of reproducing the correlations between the sets of structural constraints belonging to spatially different regions of the macromolecule. Interestingly, a very similar problem was encountered in our ongoing work on incorporating the mobile ions into the CG model of DNA chain developed here. In particular, we have found that to accurately capture the coupling between the dynamics of the DNA chain and the surrounding ionic atmosphere, the latter being strongly inhomogeneous along the macromolecule, it is necessary to ensure matching of the second order correlators (to be published elsewhere).

Finally, it is worth noting that reproducing higher order correlations acts as an efficient suppressor of the degeneracy in the resulting set of Hamiltonian parameters. Indeed, by capturing more subtle system correlations, it is possible to discriminate between those parameter sets which generate the same mean-field picture and, thus, belong to the same uncertainty class. Given the discussion of Solving the Inverse Problem, we can define a hierarchy of approaches to reduce the degeneracy of the Hamiltonian parameters. First, the Hamiltonian compactness is characterized by the total numbers of both the CG degrees of freedom and the corresponding conjugate parameters. One expects that the smaller number of parameters would result in a lower rate of degeneracy. Next, we use the SVD technique to truncate those eigenvectors of the covariance matrix (see Eq. 6), which have little effect on the system Hamiltonian, resulting in a further significant reduction of the parameter manifold. Finally, reproducing higher-order correlations on top of the mean-field picture serves as potentially powerful tool for calibrating the Hamiltonian parameters.

In summary, by developing a two-bead double-stranded DNA model, we demonstrated for the first time that the present technique can be successfully applied to coarse-grain complex polymer systems with correlated degrees of freedom, where correlations between bonds and angles along the polymer chain are accurately taken into account. The problem of accounting for polymer chain correlations in coarse-graining has been posed by Fukunaga et al. (11). As opposed to prior related works in this area based on using a large basis set of Dirac delta functions, where the uniqueness of the obtained solutions and the method's convergence were not established (13,23), we demonstrated convergence of our optimization procedure based on compact molecular basis sets and estimated the accuracy of our CG Hamiltonian for DNA to be ∼0.01 k_BT per elementary interaction (see Fig. 2 F). By utilizing field theoretical arguments and showing the close relationship between the presented optimization technique and the RG theory, we suggest that the MRG-CG approach may allow achieving high accuracy in CG system description. In general, we expect this technique would allow coarse-graining of many biological molecules and other polymers, where strong correlations exist among internal degrees of freedom. In a recent work, which will be reported elsewhere, we have also applied this approach to develop an accurate coarse-grained model for electrolyte solutions, such as aqueous NaCl and KCl. It will be interesting to compare our method with other systematic coarse-graining efforts, for example force matching (18–20), in terms of accuracy, uniqueness of the solutions, and computational efficiency.

Appendix

MD simulation of AA system

The starting point for AA simulation was a canonical B-form of a 16-basepair DNA oligomer [d(CGAGGTTTAAACCTCG)]₂ (32). We built an ideal DNA chain model and carried out an MD simulation in explicit, TIP3P water (33) using the AMBER 8.0 suite of programs (34) and the refined AMBER parmbsc0 force field for nucleic acids (35). The initial structure was first neutralized by 15 Na⁺ ions. An extra ∼0.12 M of NaCl buffer (14 additional Na⁺ ions and 14 Cl⁻ ions), corresponding to physiological concentrations, was then added to the system. The initial positions of the ions were determined from the computed electrostatic potential using LEaP (34). The system was further solvated in >6500 TIP3P water molecules in a cubic box, having dimensions 60 × 60 × 60 Å. As a result, two DNA segments from neighboring periodic images were at least 35 Å apart. The overall number of atoms in the system was ∼20,000 in the periodic box. We used a multistage equilibration process, reported by Shields et al. (36), to equilibrate the starting structure. The subsequent production run was carried out at constant temperature (300 K) and pressure (1 bar) using the Langevin temperature equilibration scheme (see the AMBER 8 manual), the weak-coupling pressure equilibration scheme (37), and periodic boundary conditions. The translational center-of-mass motion was removed every 2 ps. We used the SHAKE algorithm (38) to constrain all bonds involving hydrogens, which allows all MD simulations to use an increased time step of 2 fs without any instability. The particle-mesh Ewald method (39) was used to treat long-range interactions with a 9 Å nonbonded cutoff. The production run was carried out for 60 ns to ensure the equilibration of ions. It was shown in prior works (40,41) that 50 ns MD was enough to equilibrate the Na⁺ atmosphere around DNA in a smaller system comprised of ∼16,000 atoms. Given the slightly larger size of our systems (∼20,000 atoms), we used extra 10 ns of MD to ensure equilibration.

MD simulation of CG system

We used the large-scale atomic/molecular massively parallel simulator (LAMMPS) (31) to carry out MD simulations of our CG double-stranded DNA. The macromolecule was comprised of 200 beads (100 basepairs) whose initial coordinates were the geometric centers of the corresponding all-atomistic basepair nucleotides. The Biochemical Algorithms Library (25) was used to build such a model. Initially the system was minimized according to the standard steepest-descent algorithm. Then it was heated up to 300 K during the 5 ns and subsequently equilibrated for another 10 ns in a large periodic box having dimensions ∼600 × 600 × 600 Å. We used the canonical NVT integration scheme (Nosé-Hoover temperature thermostat) to update particle positions and velocities at each timestep (42). To determine the biggest timestep we can afford to simulate the CG system with no instabilities, we used the criteria of the total energy conservation, the latter being the energy of the CG system complemented by the contribution from the Nosé-Hoover Hamiltonian (26). It appeared that it was safe to use the time steps of up to 10 fs, so we used this upper limit in our MD simulations. The production run for each optimization iteration was 20 ns to ensure the convergence of the covariance matrix in Eq. 6. We verified the convergence at each iteration by comparing the data generated by two halves of the MD trajectory.