Growth Pattern of Single Fission Yeast Cells Is Bilinear and Depends on Temperature and DNA Synthesis

Abstract

Cell growth and division have to be tightly coordinated to keep the cell size constant over generations. Changes in cell size can be easily studied in the fission yeast Schizosaccharomyces pombe because these cells have a cylindrical shape and grow only at the cell ends. However, the growth pattern of single cells is currently unclear. Linear, exponential, and bilinear growth models have been proposed. Here we measured the length of single fission yeast cells with high spatial precision and temporal resolution over the whole cell cycle by using time-lapse confocal microscopy of cells with green fluorescent protein-labeled plasma membrane. We show that the growth profile between cell separation and the subsequent mitosis is bilinear, consisting of two linear segments separated by a rate-change point (RCP). The change in growth rate occurred at the same relative time during the cell cycle and at the same relative extension for different temperatures. The growth rate before the RCP was independent of temperature, whereas the growth rate after the RCP increased with an increase in temperature, leading to clear bilinear growth profiles at higher temperatures. The RCP was not directly related to the initiation of growth at the new end (new end take-off). When DNA synthesis was inhibited by hydroxyurea, the RCP was not detected. This result suggests that completion of DNA synthesis is required for the increase in growth rate. We conclude that the growth of fission yeast cells is not a simple exponential growth, but a complex process with precise rates regulated by the events during the cell cycle.

Introduction

Symmetrically dividing cells have to double their size between two consecutive divisions to ensure a constant average cell size during proliferation over many generations. Therefore, cell growth and division are strongly correlated and tightly controlled (1,2). The unicellular eukaryote Schizosaccharomyces pombe provides an excellent model for investigating the growth profile of single cells because the cells of this yeast are cylindrical, with a constant diameter, and grow by extending at the ends (3). The cell length is thus a good measure of the size (volume and mass) of these cells.

After a medial division of an S. pombe cell, each of the two daughter cells starts to grow by extension at the old end, i.e., the end that existed before the last division. Later during interphase, growth is also initiated at the new end, i.e., the end created during the last division, in a process called new end take-off (NETO) (3). The total cell length increases for the first ∼75% of the cell cycle. The growth slows down in the remaining ∼25% of the cycle, when mitosis and cytokinesis occur (3).

It is unclear what type of growth profile these cells follow. In earlier studies, exponential, linear, and bilinear models were fitted to the cell length as a function of time (3–6). Exponential models assume that the rate of growth is proportional to the existing cell size, whereas linear models assume a constant growth rate, and multilinear models introduce different constant rates separated by rate-change points (RCPs). A controversy arose regarding which model provides the best fit (7,8). This was a consequence of the relatively low temporal and spatial resolution of the data obtained using time-lapse photomicrography, which was the best technique available at the time (9).

Mitchison and Nurse (3) suggested a bilinear model in which the cell grows linearly during two time intervals separated by an RCP at ∼0.34 of the cell cycle in wild-type cells, which coincides with NETO. Wee1 mutants also show bilinear behavior, but with NETO occurring later, when the cell has reached a threshold length. Cells that were blocked in early G2 phase did not show NETO. The authors concluded that a cell has to successfully pass an event in G2 and reach a threshold length (9–9.5 μm) for NETO to occur. The bilinear pattern was also proposed in a later study (10).

However, Cooper (4,7) reanalyzed the data from Sveiczer et al. (10) and found that a single exponential model fits the data as well as a bilinear model. Since the exponential model is simpler than a bilinear one, the author advocated the use of the simpler model by invoking Occam's razor (7).

A similar debate has been going on for over 40 years regarding the growth law of single Escherichia coli cells. Contradictory results were again obtained as a result of limited experimental precision. Exponential (11), bilinear (12), and interrupted (13) models were suggested. Recently, Reshes et al. (14) measured the growth profile of single Escherichia coli cells using phase contrast and fluorescence time-lapse microscopy, and found that it shows a bilinear or a trilinear pattern.

To obtain more precise measurements of the cell length in fission yeast, we used laser scanning confocal microscopy to image single fission yeast cells with a green fluorescent protein (GFP)-labeled cell membrane throughout the cell cycle. We found that, after cell division, the cells grew rapidly during the first few minutes, most likely because of the reshaping of the new cell end. Afterward, the cell length increased in a bilinear manner until mitosis occurred, at which point the growth slowed down or ceased. In the bilinear growth pattern, only the second linear segment showed a temperature-dependent rate. Finally, using hydroxyurea (HU), we found that the growth rate was constant when the cells were blocked in S-phase.

Materials and Methods

Choice of strain

We used a strain with a GFP-tagged plasma and nuclear membrane (Fig. 1, a and b). The strain PG2747 (h⁹⁰ leu1-32 ura4-D18 ade6-216 [D817]) was a kind gift from Genevieve Thon (University of Copenhagen, Denmark). The cells carry the plasmid D817 (15), which contains the GFP-tagged N-terminal 275 amino acid residues of P450 cytochrome reductase (16), including a single potential transmembrane segment (15).

Figure 1.

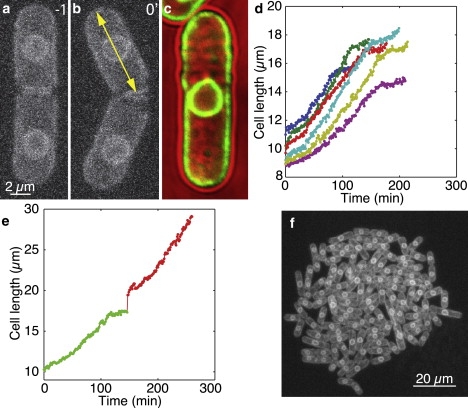
Growth of cells with GFP-labeled nuclear and plasma membrane. (a) MIP showing a cell with GFP-labeled membranes (strain PG2747). A septum shortly before the separation of the two daughter cells (t = −1 min) is visible at the cell center. (b) The same cells as in a, directly after separation. Cell birth (t = 0 min) is defined here as the separation of the daughter cells. The arrow indicates how the cell length was measured. (c) Overlay of the images obtained using fluorescence (green) and transmitted light (red) of the same cell shows that the outer fluorescently labeled membrane follows the cell wall. (d) Length of six cells from birth to subsequent division from a single experiment, plotted as a function of time. The cell length increases during the first ∼75% of the cell cycle, with a fast increase during the first few minutes. The cell does not grow substantially for the last ∼25% of the cell cycle, where nuclear division and cytokinesis occur. The cells were imaged every 1 min at 32°C. (e) Length of a single cell from birth to division (green), followed by the sum of the length of the two resulting daughter cells (red), showing that the cells grew for more than one generation under our imaging conditions. The cells were imaged every 1 min at 32°C. (f) Microcolony of the cells with GFP-labeled membranes. The observed equal fluorescence intensity among the cells indicates that the number of plasmids in each cell does not change significantly through generations.

To confirm plasma membrane staining, a fluorescence image was overlaid on a transmitted light image (Fig. 1 c). This allowed the cell outline and the cell length across the middle plane of the cell to be determined (see “Microscopy” below). Nuclear membrane staining allowed precise determination of the timing of mitosis.

Cell preparation

To prevent loss of the plasmid, the cells were grown in liquid Edinburgh minimal media (EMM) plus supplements at 25°C, 28°C, or 32°C until log phase. For microscopy, a plastic 35-mm dish with a hole in the middle of the bottom was used. A coverslip was glued with silicone inside the dish on the bottom. The dish was turned upside down and a drop of liquid agar was poured onto the coverslip. The agar patch was covered with another coverslip to obtain a flat surface of the agar. When the agar solidified, the second coverslip was carefully removed and 3–4 μL of the cell culture were added onto the agar. When the liquid medium dried out, the agar was covered with a new coverslip and sealed with Vaseline.

Microscopy

We used confocal microscopy to acquire z-stacks of images, which ensures imaging of the whole cell along the z axis even when the sample moves out of the focal plane during long-term time-lapse imaging. Since the cells are shaped as cylinders with hemispherical caps that lie horizontally at the bottom of the dish, the cell outline in the resulting z-projections reflects the image of the middle plane of the cell. Thus, the measurement of the cell length in the z-projection ensures that the length is measured across the middle of the cell. Moreover, taking fluorescent images of the cell nucleus allows accurate determination of the timing of mitosis.

Imaging was performed with a Zeiss Axiovert inverted laser scanning confocal microscope using a 488 nm argon laser line and a Plan Apochromat 63×/1.4 NA oil DIC objective (Zeiss, Jena, Germany). The laser power was set to 0.5–1% (of 30 mW maximum). Typically, a cell with a septum was found and imaged until the second division occurred, and z-stacks of five optical sections, with a pixel size of 40 nm and a z-distance of 1 μm, were taken either every 2 min, 1 min, or 30 s. The scanning time per pixel was 0.64–0.80 μs. The temperature was maintained at (25 ± 0.5)°C, (26 ± 0.5)°C, (27 ± 1)°C, (28 ± 0.5)°C, or (32 ± 0.5)°C using a Bachhoffer chamber (Tempcontrol 37; H. Saur Laborbedarf, Reutingen, Germany).

HU treatment

To block the cells in S-phase, HU (Sigma-Aldrich, St. Louis, MO) was added to the solid medium 1 h before imaging at a final concentration of 11 mM (17) as follows: 4% agar (Becton, Dickinson and Co., Sparks, MD) was added to liquid EMM plus supplements, heated, and stirred until the agar melted; then 2 mL of the liquid agar was pipetted into an Eppendorf tube and kept at 60°C. Vitamins were added, and HU to a final concentration of 11 mM. Using the agar with HU, a microwell dish was prepared as described above. The prepared sample was kept at 32°C until imaging.

For experiments in which cell growth was observed both in the presence of HU and after HU washout, a coverslip was coated with ∼5 μL of 2 mg/mL lectin BS-1 (Sigma-Aldrich) in PBS. The coverslip was glued with silicone beneath a plastic dish, as described above; ∼300 μL of the cell culture was added to the lectin spot. After the cells settled down, the dish was carefully filled with ∼2 mL of EMM plus HU. The time between acquisition of z-stacks was 2 min. HU was washed out after 2 h of imaging. All HU experiments were performed at 32°C.

Control experiments

As a control for potential artifacts due to GFP labeling and laser scanning, we used two wild-type strains: L972 and NCYC132 (Fig. 2). The unlabeled wild-type strain L972 was imaged with the same microscope used for strain PG2747 (Zeiss Axiovert inverted laser scanning confocal microscope) with the following differences in the settings: Only transmitted light z-stacks were acquired, at a time interval of 2 min. The sample was illuminated with the 514 nm line of an argon laser at the minimum laser power (0.1% of 30 mW maximum). The scanning time per pixel was 0.57 μs.

Figure 2.

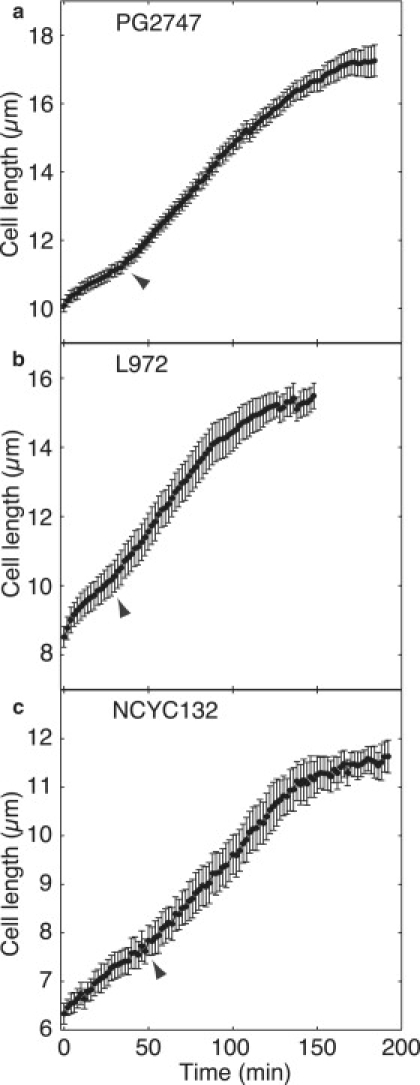
Control experiments. Mean cell length is shown as a function of time for the (a) PG2747 strain and two unlabeled wild-type strains: (b) L972 and (c) NCYC132. All three strains show a change in growth rate at 30–50 min after birth (arrows). The temperature was 32°C for PG2747 and L972, whereas NCYC132 was observed at 30°C; n = 40 (PG2747), n = 16 (L972), and n = 5 (NCYC132). The error bars represent SE.

Strain NCYC132 (18) was imaged on thin yeast extract (YE)-4% agarose pads at 30°C using a Zeiss Axiovert 200 microscope with a Micromax NTE/CCD-1024-EB camera, at 600× magnification (Plan-Neofluar 60×/1.40 Oil). Bright-field images were acquired every minute.

Image processing

Images were analyzed using ImageJ (National Institutes of Health) and programs written in MATLAB (The MathWorks, Natick, MA). A maximum-intensity projection (MIP) was made from each stack of five optical sections. The coordinates of the cell tips were determined manually by clicking on the two extreme points of the cell in the MIP using ImageJ (see Fig. 1 b). The length was then calculated with MATLAB and plotted as a function of time (see Fig. 1 d).

Data analysis

For each cell the following parameters were calculated (Table 1):

• 1.Birth length, where birth is defined as the event of daughter cell separation.
• 2.Division length, measured as the mean length of the last five data points before division, i.e., when the cell separates into two daughter cells.
• 3.Generation time, defined as the time between birth and division.
• 4.Growth time, defined as the time between birth and nuclear division (early anaphase B).

Table 1.

Birth length, division length, generation time, and growth time for cells growing at different temperatures

	25°C	28°C	32°C	p-Value from a t-test comparing 25°C and 32°C
Birth length (μm)	7.5 ± 0.5 (n = 24)	8.6 ± 1.1 (n = 24)	10.2 ± 1.2 (n = 40)	8 × 10−15
Division length (μm)	15.8 ± 1.6 (n = 12)	16.3 ± 1.1 (n = 19)	17.3 ± 1.3 (n = 36)	0.0029
Generation time (min)	310 ± 40 (n = 12)	211 ± 85 (n = 19)	177 ± 36 (n = 36)	3 × 10−14
Growth time (min)	278 ± 40 (n = 20)	176 ± 84 (n = 20)	135 ± 35 (n = 39)	3 × 10−20
Generation time – growth time (min)	45 ± 12 (n = 12)	39 ± 3 (n = 19)	40 ± 6 (n = 36)	0.02

Data are shown as mean ± SD; n is the number of cells. The cells were divided into three groups with respect to temperature. For definitions of the parameters, see Materials and Methods.

The cells were divided into three groups with respect to temperature. The group of cells denoted as “25°C” consisted of 20 cells imaged at 25°C and four cells imaged at 26°C. The group denoted as “28°C” consisted of four cells imaged at 26.5°C, six cells imaged at 27°C, and 14 cells imaged at 28°C. The group denoted as “32°C” consisted of 40 cells observed at 32°C.

The cell length, L, was measured from birth (t = 0) until the subsequent division. At each time point the mean value of the length of all the cells in one group, and the mean ± SE were calculated and plotted as a function of time (see Figs. 2–5 and 8).

Figure 3.

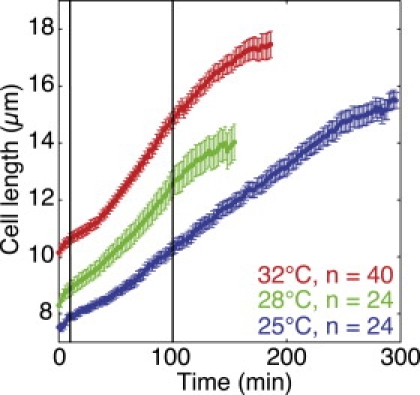
Cell growth at different temperatures. Mean cell length is shown as a function of time for a group of cells of the PG2747 strain at 25°C (blue, n = 24), 28°C (green, n = 24), and 32°C (red, n = 40). The data are plotted from the birth of each cell (t = 0 min) until the time when the first divisions were observed in each group. Error bars represent SE. The vertical lines mark the fitting interval, t = 10–100 min, used in Fig. 5. The data for the cells at 28°C are shown only for t < 158 min because by that time a substantial fraction of the cells (7/24) divided and hence could not be included in the calculation of the mean value.

Figure 4.

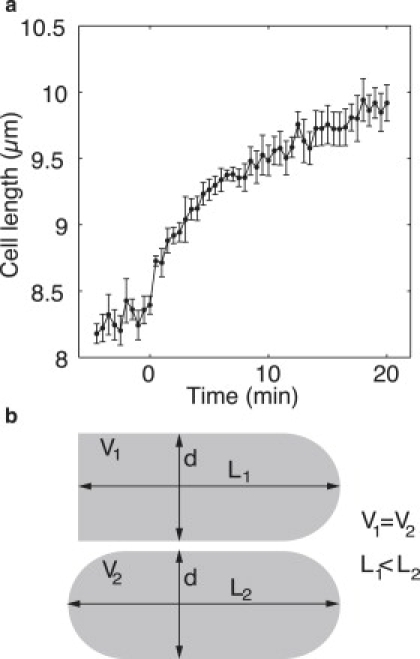
Cell growth during the first few minutes. (a) Mean cell length is shown as a function of time before and after separation of the daughter cells (t = 0 min) for two pairs of daughter cells imaged every 30 s at 32°C. The cell length does not increase substantially before the separation, but grows rapidly during the first few minutes after the separation. The growth slows down afterward. Error bars represent SE. (b) Schematic drawing of the idealized cell shape. (Top) The shape of one daughter cell shortly before separation with the septum on the left (flat end of the cell). (Bottom) The same cell after separation, when the new end has formed a hemispherical tip. The volume V and the diameter d are constant, whereas the length increases by 8.6% for L₁ = 8.3 μm and d = 4.3 μm.

Figure 5.

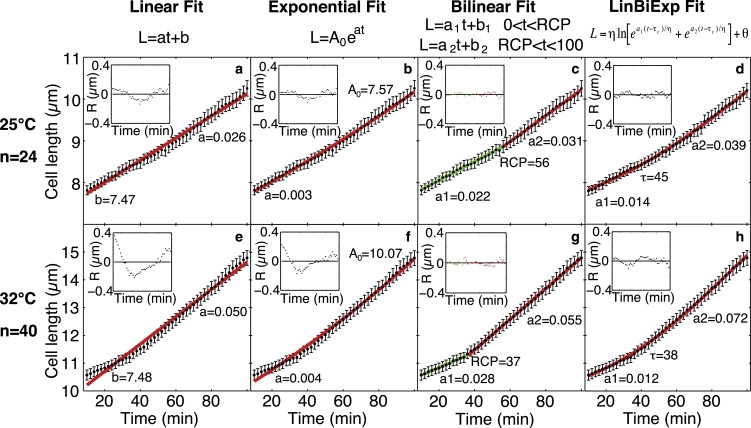
Fitting of linear, exponential, bilinear, and linear biexponential models to the mean cell length at two different temperatures. (a and e) Linear model, L = at + b. (b and f) Exponential model, L = A₀e^at. (c and g) Bilinear model, L = a₁t + b₁ (10 ≤ t < RCP), L = a₂t + b₂ (RCP ≤ t ≤ 100). For the bilinear fits, the segment of the fit before and after the RCP is shown in green and red, respectively. (d and h) Linear biexponential model, $L=\eta \ln \left[e^{a_1(t-{\tau }_c)/\eta }+e^{a_2(t-{\tau }_c)/\eta }\right]+\theta$, where a₁ and a₂ correspond to the two slopes from the bilinear model, and τ_c corresponds to the RCP. (a–d) 25°C (n = 24), (e–h) 32°C (n = 40). The data are represented as mean ± SE. Insets show the residuals (R = data − fit) for each fit; the x axis in the insets is the same as in the main panels.

Figure 8.

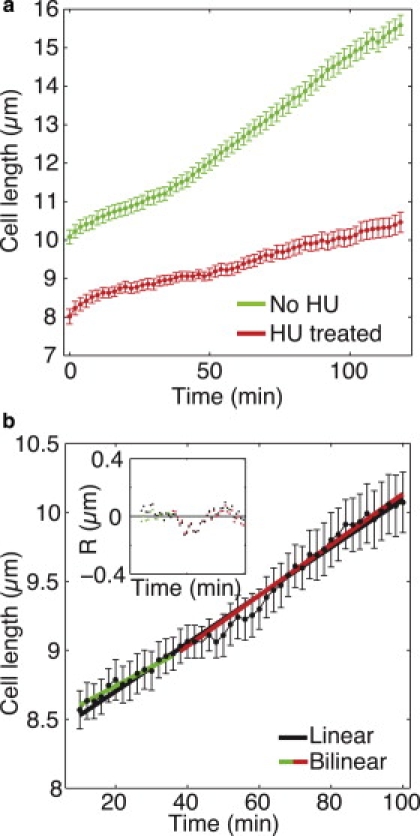
Growth of cells blocked in S-phase by HU. (a) Mean cell length is shown as a function of time for the HU-treated cells (red) and the untreated cells (green), both growing at 32°C. Error bars represent SE. (b) Linear (black) and bilinear (green and red) fits to the mean length data of HU-treated cells. The inset shows the residuals for both fits in corresponding colors. The fitting was performed for t = 10–100 min.

The fitting of models to the cell length as a function of time was performed in MATLAB using the polyfit and lsqcurvefit functions. The fits are least-squares fits. The interval t = 10–100 min was chosen for fitting because the growth in the first 10 min was different and thus was treated separately. At t > 100 min, nuclear division, and the accompanying slow-down of growth, was observed in individual cells, which changed the mean cell length of the population.

The linear fit had the form L = at + b. The exponential fit, L = A₀e^at, was performed by fitting a line to the natural logarithm of the data. The biexponential model had the form L = Ae^bt + Ce^(d–b)t.

We define the bilinear model by L = a₁t + b₁ for t < RCP; L = a₂t + b₂ for t > RCP. This model consists of two connected linear segments. The term “bilinear” may not be appropriate for this model, since this term is typically used in mathematics for the form f(x,y) = (mx + b)(ny + c). The model described here may be considered as “linear with an RCP”; however, for simplicity we will refer to this model as bilinear.

For the bilinear model, one line was fitted to the first two data points and another line to the remaining points, then one line to the first three points, and so forth. The fit with the minimum χ² (the sum of squared differences between the data and the fitted values) was chosen as the best fit. The bilinear fit yielded four parameter values: the two slopes a₁ and a₂, and the two y-intercepts b₁ and b₂. From these values, the RCP was calculated as the intersection of the two lines. We denote the x coordinate (the time) of the RCP by RCP, and the corresponding cell length by L_RCP; RCP = (b₂ − b₁) / (a₁ − a₂) and L_RCP = a₂RCP + b₂. From the bilinear fits, we report a₁, a₂, RCP, and L_RCP.

The linear biexponential model (LinBiExp) had the form $L=\eta \ln \left[e^{a_1(t-{\tau }_c)/\eta }+e^{a_2(t-{\tau }_c)/\eta }\right]+\theta$ (19). This is a generalized bilinear model in which the transition between the two linear segments is smooth.

The quality of the fits was estimated by plotting the residuals of the best fit for each model, as well as by χ². Fitting was performed both on the mean length data (see Figs. 5 and 8; Tables 3 and 6) and on length data from single cells (see Tables 5 and 7).

Table 3.

Values obtained from different model selection criteria showing that the bilinear model best fits the mean cell length as a function of time

	25°C	32°C
Single linear: L = at + b
χ2	0.2357	0.9654
r2	0.9897	0.9878
AIC	−62.47	2.38
SBIC	−58.81	6.04
Single exponential: L = A0eat
χ2	0.1177	0.3987
r2	0.9949	0.9950
AIC	−94.41	−38.30
SBIC	−90.76	−34.64
Biexponential: L = Aebt + Ce(d−b)t
χ2	0.0732	0.2126
r2	0.9968	0.9973
AIC	−112.26	−63.23
SBIC	−104.94	−55.92
Bilinear: L = a1t + b1, 0 < t < RCP; L = a2t + b2, RCP < t < 100
χ2	0.0248	0.0331
r2	0.9989	0.9996
AIC	−162.14	−148.79
SBIC	−154.82	−141.48
LinBiExp: $L=\eta \ln \left[e^{a_1(t-{\tau }_c)/\eta }+e^{a_2(t-{\tau }_c)/\eta }\right]+\theta$
χ2	0.0415	0.1122
r2	0.9982	0.9986
AIC	−136.39	−90.61
SBIC	−127.25	−83.34

We fitted five different models (linear, single exponential, biexponential, bilinear, and linear biexponential) to the mean cell length, L, as a function of time for t = 10–100 min. As an estimation of goodness of fit, we calculated the sum of squared errors (χ²), correlation coefficient (r²), AIC, and SBIC. The latter two show that a bilinear model provides the best fit to the data.

Table 6.

Parameters obtained by fitting a bilinear and a linear model to the mean length data of cells blocked in S-phase with HU

HU-treated, mean data, 32°C
Bilinear fit L = a1t + b1, t < RCP; L = a2t + b2, t ≥ RCP	a1 (μm/min)	0.014
	a2 (μm/min)	0.020
	RCP (min)	39
	LRCP (μm)	9.0
	χ2	0.1136
	r2	0.9904
	AIC	−92.07
	SBIC	−84.75
Linear fit L = at + b	a (μm/min)	0.019
	b (μm)	8.3
	χ2	0.1791
	r2	0.9849
	AIC	−71.11
	SBIC	−63.79

The fitting interval was t = 10–100 min, χ² is the sum of the squared differences between the data and the fit, and r² is the correlation coefficient; n = 16 cells.

Table 5.

Parameters obtained by fitting a bilinear model to the length data of each single cell

Bilinear fit, single cells	25°C(n = 16)	32°C(n = 34)	p, 25°C and 32°C
a1 (μm/minute)	0.021 ± 0.010	0.025 ± 0.010	0.16
a2 (μm/minute)	0.035 ± 0.014	0.057 ± 0.012	5 × 10−7
p, comparing a1 and a2	0.004	6 × 10−18
RCP (minutes)	59 ± 27	39 ± 15	0.0029
LRCP (μm)	9.0 ± 1.0	11.4 ± 1.3	6 × 10−8
a2/a1	1.91 ± 0.88	2.79 ± 1.71	0.058
RCP/generation time	0.17 ± 0.10 (n = 6)	0.23 ± 0.10 (n = 30)	0.14
LRCP/division length	0.58 ± 0.05 (n = 6)	0.65 ± 0.08 (n = 30)	0.009
(LRCP−Lbirth)/ (Ldivision−Lbirth)	0.14 ± 0.10 (n = 6)	0.17 ± 0.11 (n = 30)	0.60

A linear model with a change in growth rate was fitted to the data of cell length, L, as a function of time for t = 10–100 min: 0 < t < RCP: L = a₁t + b₁; RCP < t < 100 min: L = a₂t + b₂. Although the growth time of cells at 25°C was ∼280 min, the data were fitted up to 100 min because typically there was a clear RCP within this time interval. The results are shown as mean ± SD. Data from cells that could not be fitted well with a bilinear model, i.e., the RCP was outside the fitting interval (n = 8 for 25°C and n = 5 for 32°C), as well as those with a₁ < 0 (n = 1 for 32°C and n = 0 for 25°C), were excluded from this analysis. The number of analyzed cells was n = 16 at 25°C and n = 34 at 32°C. To calculate the ratios in the last three rows, we used only the cells that divided during the observation time and were not excluded from fitting. p-Values from t-tests comparing the data from 25°C and 32°C are shown in the last column.

Table 7.

Parameters obtained by fitting a bilinear and a linear model to the length data of each single cell blocked with HU

HU-treated, single cells, 32°C
Bilinear fit L = a1t + b1, t < RCP; L = a2t + b2, t ≥ RCP (n = 13)	a1 (μm/min)	0.019 ± 0.013
	a2 (μm/min)	0.023 ± 0.017
	p, comparing a1 and a2	0.49
	RCP (min)	167 ± 384
	LRCP (μm)	10.7 ± 4.1
Linear fit L = at + b (n = 16)	a (μm/min)	0.017 ± 0.012
	b (μm)	8.4 ± 0.7
	p, comparing a1 and a	0.78
	p, comparing a2 and a	0.31

The fitting interval was t = 10–100 min. Cells with a₁ < 0 (n = 1), a₂ < 0 (n = 1), and an outlier cell with a₁ ∼20 SD away from the mean (n = 1) were excluded from the statistics of the bilinear fit.

For HU experiments, including the HU washout, the data before and after HU washout were analyzed separately. The data before the washout were fitted in the interval t = 0–98 min, and after the washout in the interval t = 0–94 min, where in the latter case t = 0 is the first image after the washout.

An alternative way to perform a bilinear fit is to fit a step function to the derivatives of the data (dL/dt) (see Fig. 6). The advantage of this method is that it uses only three parameters: a₁, a₂, and RCP.

Figure 6.

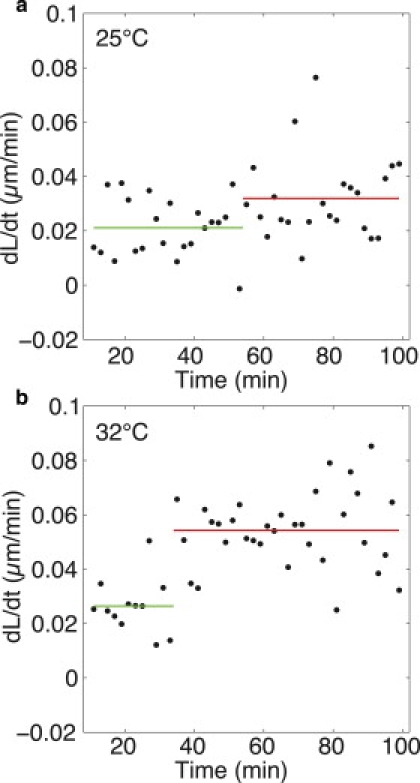
Bilinear fit of the instantaneous growth rates. Derivatives of the mean cell length data are shown for 25°C (a) and 32°C (b). A step function was fitted to the data (horizontal lines). The resulting values for the growth rates (a₁ = 0.021, a₂ = 0.032 and a₁ = 0.026, a₂ = 0.054 μm/min for 25°C and 32°C, respectively) and RCP (54 and 34 min for 25°C and 32°C, respectively) were similar to those obtained by fitting a bilinear fit to the length data (Table 3; Fig. 5, c and g). Note that the two outliers in a (dL/dt > 0.05) affect the resulting change in growth rate. Fitting the data without these outliers yielded a₁ = 0.023 and a₂ = 0.043 μm/min; RCP = 90 min. This further emphasizes that although the growth pattern is clearly bilinear at 32°C, it is less so at 25°C.

Statistical analysis

Results are expressed as either the mean ± SE or the mean ± SD, as indicated. For comparison of the mean values of two data sets, two-tailed t-tests at a 5% significance level were used. Paired t-tests were performed when the two data sets were paired, i.e., when they were measured on the same set of cells (Table 2). In all other cases, nonpaired t-tests were used.

Table 2.

Diameters of the mother cell and its two daughter cells

d, Mother, left side (μm)	d, Daughter, left (μm)	d, Mother, right side (μm)	d, Daughter, right (μm)
4.48	4.37	3.99	4.09
3.93	3.76	3.78	3.83
4.44	4.28	4.48	4.10
5.00	4.97	4.16	4.08
5.11	4.88	4.25	4.10
4.64	4.68	4.38	4.42
4.32	4.13	4.34	4.16
4.17	4.12	4.36	4.46
3.88	3.85	3.92	3.99
4.07	4.05	4.44	4.26
4.40 (mean)	4.31 (mean)	4.21 (mean)	4.15 (mean)
p = 0.62		p = 0.54

The diameter d of the mother cell was measured on the last image before separation, at positions that correspond to the center of the left daughter cell (mother, left side) and the center of the right daughter cell (mother, right side). The diameter of the daughter cells was measured at the cell center in the first image after separation. p-Values from paired t-tests comparing the diameter on each side of the mother cell and the respective daughter cell are also shown.

Model selection criteria

Correlation coefficient (r²)

$$r^2=1-\frac{SSE}{S{S}_y}=1-\frac{\sum _i{(y_i-y_{i,pred})}^2}{\sum _i{(y_i-y_{mean})}^2}\text{.}$$

Here, SSE is the sum of squared errors, SS_y is the overall (total) variance, y_i is the ith data point, y_i,pred is the ith point predicted by the model, and y_mean is the mean value of all data points. The correlation coefficient does not consider the number of parameters in the model. It is therefore not an appropriate measure for comparison of models with different numbers of parameters.

Akaike information criteria (AIC)

$$\text{AIC}=n_{obs}\ln \left(\text{SSE}\right)+2n_{par}\text{.}$$

Here, n_obs is the number of observations and n_par the number of parameters.

Schwarz Bayesian information criteria (SBIC)

$$\text{SBIC}=n_{obs}\ln \left(\text{SSE}\right)+n_{par}\ln \left(n_{obs}\right)$$

AIC and SBIC (5,19) take the number of parameters, as well as the size of the data set, into account. The lower the value of AIC or SBIC, the better the model describes the given data set. All three criteria (r², AIC, and SBIC) were calculated using custom-made fitting programs in MATLAB.

Results

Control experiments

We used a strain with GFP-labeled cell membrane and nuclear membrane to observe cell growth and nuclear division, respectively (strain PG2747). An overlay of a transmitted light image and a fluorescence image of the same cell shows that the outer fluorescently labeled membrane structure follows the cell wall. Therefore, the outer membrane represents the plasma membrane (Fig. 1 c).

Since the plasmid carrying fluorescence in the strain PG2747 can be present in many copies, we tested whether the plasmid number varies among the cells by measuring the variation of the fluorescence intensity. The cells in the same generation coming from the same mother cell showed a coefficient of variation (c.v.) of 3.7 ± 2.2% just after the division of the mother cell, indicating that the fluorescent proteins were distributed equally to the newly born sister cells. A similarly small variation in fluorescence (c.v. = 2.9 ± 1.8%) was observed between fully grown sister cells before they underwent mitosis. This suggests that sister cells synthesize a similar amount of fluorescent proteins and therefore inherit a similar number of plasmids. Furthermore, images of a whole microcolony of membrane-labeled cells, which were the descendents of a single cell after more than four generations, did not show any significant variation in fluorescence (Fig. 1 f). These results indicate that the plasmid copy number does not change considerably through several divisions.

We tested whether the GFP labeling affected general cell growth. Optical density measurements of exponentially growing liquid cultures showed that the doubling time of the labeled strain PG2747 was similar to that of the nonlabeled wild-type strain L972 (215 ± 3 min and 196 ± 3 min, respectively; mean ± SD; n = 10 cultures per strain at 32°C). This result indicates that cell growth was not impaired by the fluorescent labeling.

Next, we tested whether GFP labeling and laser scanning affected the growth of single cells. We used two wild type-strains, L972 and NCYC132 (18), neither of which carries GFP. Single cells of strain L972, which were observed using a confocal microscope with a low laser power, showed a generation time similar to that of PG2747 (159 ± 30 min, n = 14, and 177 ± 36, n = 36, respectively; mean ± SD, p-value from a t-test = 0.10, at 32°C; Fig. 2, a and b). A similar result was obtained with strain NCYC132 using wide-field transmitted light microscopy (generation time of 205 ± 20 min at 30°C, n = 5; Fig. 2 c). Moreover, the cells of all three strains showed a change in the growth rate at 30–50 min after birth (arrows in Fig. 2).

Finally, while following the growth of single cells of strain PG2747, we observed two or sometimes even three consecutive cell divisions. This suggests that the laser-induced damage was not significant under our imaging conditions (Fig. 1 e).

Growth of single cells at different temperatures

We observed cells growing at 25°C, 28°C, and 32°C (Fig. 3 and Supporting Material). Consistent with previous studies (3), the cells growing at higher temperatures were born longer, divided at a longer length, and grew and divided faster than the cells at a lower temperature (Table 1). The period of constant cell length, corresponding to mitosis and septation, was largely independent of temperature (Table 1).

The initial increase in cell length reflects the rounding-up of the new cell end

During the first few minutes after the separation of the two daughter cells, we observed a rapid increase in length: the cell grew by ∼1 μm in 5 min (Fig. 4 a). To investigate this growth pattern more precisely, we performed experiments with a higher time resolution, i.e., we acquired a stack of images every 30 s. We observed that the cell diameter before the separation of the sister cells did not differ from that after the separation (Table 2).

To test whether the observed increase in length might be due to reshaping of the cell, we calculated the increase in length for reshaping of a cylindrical object with one hemispherical cap into a cylindrical object with two hemispherical caps, while keeping the diameter and the volume constant (Fig. 4 b). The calculated increase in length was 8.6%. Here, the value for the length before separation was L₁ = 8.3 μm (Fig. 4 a), and cell diameter d = 4.3 μm (Table 2). The measured increase in cell length from t = 0 to t = 2 min (Fig. 4 a) was 7.5%, which is similar to the value calculated above.

Cell growth follows a bilinear pattern

To investigate which model best describes the growth pattern of single-fission yeast cells, we fitted five models to the data representing the mean cell length as a function of time for the cells imaged at 25°C and 32°C. The tested models included linear, exponential, biexponential, bilinear, and linear biexponential models (Table 3). Fig. 5 shows the fitted models (except for the biexponential one) together with the data.

For cells growing at 32°C, the bilinear model, which consists of two linear segments with an RCP between them, provided the best fit to the data. This conclusion is supported by the plot of residuals (insets in Fig. 5): the residuals are small and randomly distributed around zero for the bilinear fit, whereas their values are larger and their distribution patterned for the other models. Moreover, the minimal values of the model selection criteria (AIC and SBIC) were associated with the bilinear model. This suggests that the bilinear model is the most appropriate of the five tested models (Table 3).

In a bilinear model, the cell grows at a constant rate until the RCP occurs, after which it grows at another constant rate. The bilinear fit showed that the growth rate increased approximately twice at the RCP (a₁ = 0.028 and a₂ = 0.055 μm/min). The RCP occurred at t = 37 min and a cell length of 11.3 μm (Table 4). Similar values of the corresponding parameters were obtained by fitting the linear biexponential model (Table 4), which was the next best model after the bilinear (Table 3).

Table 4.

Parameters obtained by fitting a bilinear and a linear biexponential model to the mean length of cells growing at either 25°C or 32°C

Mean length data	25°C	32°C
Bilinear: 0 < t < RCP: L = a1t + b1; RCP < t < 100 min: L = a2t + b2
a1 (μm/min)	0.022	0.028
a2 (μm/min)	0.031	0.055
RCP (min)	56	37
LRCP (μm)	8.90	11.30
a2/a1	1.41	1.96
RCP/generation time	0.18	0.21
LRCP/division length	0.57	0.67
(LRCP − Lbirth) /(Ldivision − Lbirth)	0.17	0.16
LinBiExp: $L=\eta \ln \left[e^{a_1(t-{\tau }_c)/\eta }+e^{a_2(t-{\tau }_c)/\eta }\right]+\theta$
a1 (μm/min)	0.014	0.012
a2 (μm/min)	0.039	0.072
τc (min)	45	38
Lτ (μm)	8.56	11.51

The models were fitted to the data of the mean cell length, L, as a function of time for t = 10–100 min (see Fig. 5). At each temperature, all cells observed for >100 min after birth were included in the fit (n = 24 at 25°C and n = 40 at 32°C).

We also fitted the bilinear model to the length data of each single cell for t = 10–100 min (Table 5). The growth rates before and after the RCP were significantly different (a₁ = 0.025 and a₂ = 0.057 μm/min, p = 6 × 10⁻¹⁸; Table 5). The variation (measured as SD) in the RCP was 15 min, which is small compared to the generation time of 177 min for cells growing at 32°C. This explains why the RCP was not smeared out in the data representing the mean cell length (Fig. 3).

The growth rate after the RCP is temperature-dependent

Cells that grew at lower temperatures had a longer generation time and a smaller cell size at birth and at division (Table 1). Similarly to the cells that grew at 32°C, we investigated the growth pattern at 25°C by fitting the five models to the mean length data from t = 10–100 min (Fig. 5 and Table 3). The bilinear model was fitted to the length data of each cell in the same time interval (Table 5). For the mean length data at 25°C, the best fit was a bilinear fit (Table 3). The bilinear fit yielded a ∼1.4-fold increase in the growth rate at the RCP for 25°C (Table 4). This increase in the growth rate was smaller than at 32°C (∼2-fold). Taken together, these results show that the growth has a clearly bilinear pattern with two significantly different slopes at 32°C, whereas the difference in the slopes and thus the bilinear nature of growth are less pronounced at lower temperatures.

Next, we explored the temperature dependence of the growth rates and the RCP by comparing the results from the bilinear fit at 25°C and 32°C (Table 5). The growth rate before the RCP did not change significantly with temperature. In contrast, the growth rate after the RCP increased significantly with an increase in temperature (1.6-fold increase, p = 5 × 10⁻⁷; Table 5). The absolute time when the rate change occurred, RCP, was shorter at the higher temperature, but the relative time (i.e., the time between birth and rate change divided by the generation time) was independent of temperature within experimental error (the rate change occurred at ∼0.2 of the cell cycle at both temperatures). Similarly, the length in micrometers at the RCP was different at the two temperatures, but the relative extension (i.e., the growth in length from birth to the RCP divided by the total growth) was largely independent of temperature (Table 5).

To reduce the number of parameters in the bilinear fit from four to three, we fitted a step function to the instantaneous growth rates (Fig. 6). The resulting values for the growth rates (a₁ = 0.021, a₂ = 0.032 and a₁ = 0.026, a₂ = 0.054 μm/min for 25°C and 32°C, respectively) and RCP (54 and 34 min for 25°C and 32°C, respectively) were similar to those obtained by the bilinear fit described above.

For completeness, we fitted the models described above to the cell length data obtained at 28°C. The resulting values of the fitting parameters typically fell between the corresponding values for the cells at 25°C and 32°C (data not shown).

The change in the growth rate does not correspond to NETO

We sought to determine whether the observed change in the growth rate was correlated to the beginning of growth at the new cell end (NETO). We measured the length of the new and old cell ends by measuring the distance between the birth scar and the tips of the new and old cell ends, respectively. We performed these measurements using the transmitted light images taken simultaneously with the fluorescence images. Examples of growth of the new and old cell ends are shown in Fig. 7. An increase in the growth rate of the new end (NETO) was clearly visible in only a subset of the cells. The old end, on the other hand, typically showed an increase in the growth rate at the time close to the RCP measured for the total cell length as described above. These results suggest that the observed RCP for the total cell length is more closely related to a change in the growth rate of the old cell end than that in the new cell end.

Figure 7.

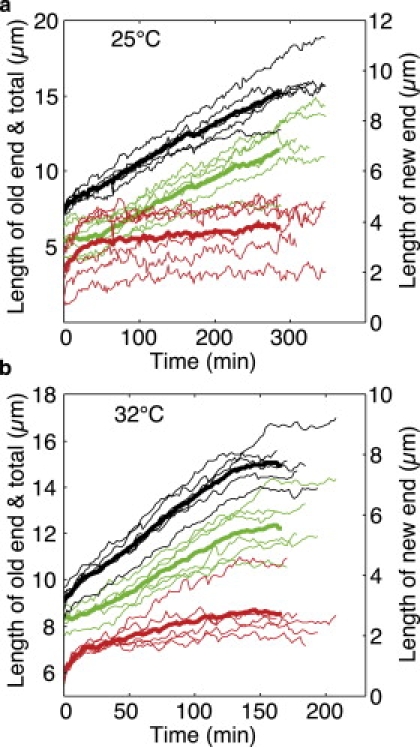
Growth of the new and old cell ends. For cells grown at 25°C (a) and 32°C (b), the growth of the new and old cell ends was measured separately using transmitted light images. Red lines show the new end, green lines indicate the old end, and black lines show the sum of the new plus the old end. Thin lines represent data from single cells, and thick lines show the mean value for each cell end (red and green) and the total cell length (black). To show the growth of the new end in more detail, the new-end data are plotted on a different scale, which is indicated on the right side of each panel.

The change in the growth rate depends on DNA synthesis

To investigate whether the increase in growth rate depends on DNA synthesis, we blocked the cells in S-phase using HU (Fig. 8) (20). We added 11 mM HU to an exponentially growing culture 1 h before imaging to acquire septating cells blocked in S-phase at the beginning of the imaging. Imaging was performed at 32°C following the same protocol used for the cells on HU-free agar pads.

We first tested whether cells growing on HU pads exhibited a cell cycle block under our experimental conditions. None of the 16 HU-treated cells showed nuclear division at t < 182 min, whereas in untreated cells nuclear division occurred at t = 135 ± 35 min (see growth times in Table 1). In two HU-treated cells, nuclear division was observed at t = 208 and 216 min, whereas the other 14 cells showed no nuclear division during the whole observation time, which ranged from 182 to 316 min. Moreover, we observed cell growth on agar pads with HU for ∼6 h using transmitted-light microscopy. The HU-treated cells were, on average, significantly longer than untreated cells (data not shown). Taken together, these results provide evidence that the cells growing on HU pads were blocked in interphase.

The length data of HU-treated cells (Fig. 8 b) were analyzed in the interval of t = 0–100 min, as for the HU-free cells. Linear and bilinear models were used to test for the existence of an RCP. The model selection criteria (AIC and SBIC) favored the bilinear model over the linear one (Table 6). However, the growth rates before and after the RCP, obtained by the bilinear model, were not significantly different (Table 7). To further test whether the data from HU-treated cells were consistent with linear growth, we compared the rates obtained by the bilinear fit with the rate from the linear fit. There was no significant difference between the linear and bilinear rates (Table 7). These growth rates were also similar to the growth rates of the HU-free cells before the RCP. We conclude that the growth pattern of the cells blocked in S-phase is consistent with linear growth.

For the untreated cells, we measured the growth of the new and old cell ends for HU-treated cells (Fig. 9). NETO was not observed in the first 100 min of growth, but it occurred in a subset of cells at later times.

Figure 9.

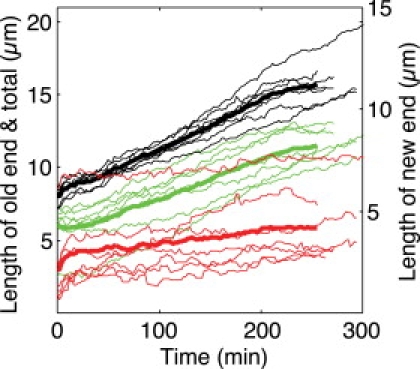
Growth of the new and old cell ends for HU-treated cells. Similarly to Fig. 7, the growth rates of the new (red) and old (green) ends, and the sum of the new and old ends (black) are shown for cells treated with HU. The lengths were measured using transmitted light images. Thin lines represent single cells, and thick lines show the mean value. The new end is plotted on a smaller scale, which is indicated on the right.

After ∼2 h of growth, which corresponds to >3 h after the addition of HU, some cells started to grow more rapidly. This is most likely a consequence of leakage from the block in the cell cycle. To investigate the growth after the release from the cell cycle block in a controlled manner, we treated the cells with HU and observed them in liquid medium for 2 h, followed by washing out of HU and continuation of imaging. The results from the cells growing in liquid medium with HU were similar to those obtained from cells on agar pads with HU, with bilinear and linear growth rates of ∼0.02 μm/min. The bilinear model fitted the data better than the linear model, but the growth rates before and after the RCP, a₁ and a₂, were not significantly different (p = 0.48). There was also no significant difference between the linear and bilinear rates (p = 0.52 and 0.13), which is consistent with the linear growth model.

For the cell length data after the HU washout, the model selection criteria (AIC and SBIC) indicated that the linear model was more appropriate than the bilinear model. This result suggests that the growth pattern of cells released from the S-phase block is also consistent with linear growth. The growth rate after the HU washout was ∼30% higher than before the washout.

In conclusion, cells blocked in S-phase by HU grow in a linear manner. These results provide evidence that DNA synthesis is required for a change in the cell growth rate.

Discussion

Confocal imaging of the cell outline

The main factor underlying the debate about the growth pattern of single-fission yeast cells is the precision of the data. Precise measurements of the cell length require images of the cell outline with high spatial precision, as well as a good temporal resolution.

The shape of the fission yeast cell can be approximated by a cylinder plus two hemispherical caps. We acquired images of five planes spaced by 1 μm using a confocal microscope and projected them into an MIP, thereby ensuring that the image with the maximum cell length was included. Confocal images were taken with a pixel size of 40 nm, and thus the spatial precision of these measurements was of a similar magnitude. The time interval between consecutive length measurements was typically 2 min, which was short enough to capture the cell growth (at the typical growth rates observed, the cells grew 1–3 pixels between two measurements) and long enough to avoid damage caused by the laser.

Initial cell growth results from rounding-up of the new cell end

During the first minutes after cell separation, the cells increased in length rapidly but the diameter did not change. We assume that during this short time interval (∼2 min) the cells do not increase in volume, but only change their shape. Before separation, the new cell end is flat, whereas after separation the minimization of surface energy leads to rounding-up of the new cell end. Simple geometrical considerations suggest that the observed increase in cell length is consistent with the notion that a cylinder with one hemispherical cap is reshaped into a cylinder with two hemispherical caps while the diameter and volume are kept constant. We conclude that the increase in cell length during the first minutes does not reflect cell growth in volume, but rather a change in cell shape due to rounding-up of the new end.

Bilinear growth pattern of single cells and the effect of temperature

To investigate the growth pattern of single cells, we fitted five models (linear, exponential, biexponential, bilinear, and linear biexponential) to the cell length data as a function of time. The bilinear model, which consists of two linear segments separated by an RCP, provided the best fit to the data for cells growing at 32°C. The growth rate increased twofold at one-fifth of the cell cycle. At lower temperatures, the increase in growth rate was smaller, and thus the bilinear pattern was less evident. Of interest, the growth rate before the RCP was independent of temperature, whereas the growth rate after the RCP depended strongly on temperature, increasing 1.8-fold from 25°C to 32°C (Fig. 10).

Figure 10.

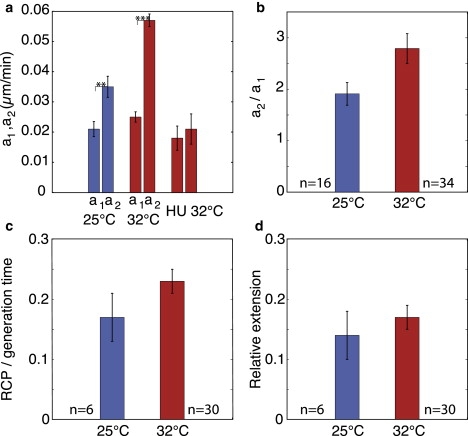
Summary of the results. Data are shown as mean ± SE. Blue bars represent the data at 25°C, and red bars represent the data at 32°C. Statistically significant differences are marked by ^∗∗ (0.0005 < p < 0.005) and ^∗∗∗ (p < 0.0005). (a) Mean values of the growth rates obtained by fitting the bilinear model to each single cell at 25°C, 32°C, and for HU-treated cells at 32°C. In each pair of bars, the left bar represents a₁ and the right bar a₂. (b) Growth rate after the RCP divided by the growth rate before the RCP, for untreated cells 25°C and 32°C. (c) RCP divided by the generation time, for untreated cells. RCP occurs at the same stage of the cell cycle at 25°C and 32°C. (d) Extension of the cell from birth to RCP (L_RCP − L_birth) divided by the total extension (L_division− L_birth), for untreated cells. RCP occurs at the same relative extension at 25°C and 32°C.

The difference in temperature dependence between the first and second growth rates indicates that the growth in these two intervals is controlled by different mechanisms. The growth in the first part may be “basal” growth that occurs independently of temperature changes and DNA synthesis (see below). This growth may be driven by enzymes, which show only a modest increase in reaction rates with an increase in temperature, for temperatures close to 30°C. In contrast, growth in the second interval may be governed by processes with reaction rates that depend strongly on temperature in the physiological temperature range.

The RCP is not directly correlated to NETO

Even though the cell length, average growth rate, and cycle time differed for the three temperatures investigated, the RCP occurred at 0.2 of the cell cycle regardless of the temperature. It was tempting to speculate that this change in the cell growth rate results from the initiation of growth at the new end (NETO). Indeed, the RCP was previously found to coincide with NETO in wild-type cells (3). However, other studies have demonstrated that not all cells undergo NETO, and that only rarely do the RCP and NETO of an individual cell coincide (21–23).

In this work, the RCP was not correlated to NETO. In cells where the RCP and NETO do not coincide, the starting of growth at the new end may have to be balanced by a reduced rate of growth at the old end. However, we observed a clear NETO event only in a fraction of the cells; the majority showed a clear RCP. After the initial fast growth of the new end, which is related to a shape change of this end, the growth of the new end was much slower than the growth of the old end. On the other hand, the old end not only grew to a larger extent, it also showed an RCP that roughly coincided with the RCP of the total cell growth (Fig. 7). Thus, under our experimental conditions, the change in the total growth rate resulted mainly from a change in the growth rate of the old end, and was independent of NETO.

The change in growth rate depends on DNA synthesis

As regards the cell length, a similar bilinear pattern with a doubling in rate at a “critical point” at one-fifth of the cell cycle was previously observed for the synthesis of the enzymes sucrase, acid phosphatase, and alkaline phosphatase (18,24). DNA synthesis occurs near the time of cell division, between 0.95 of one cell cycle and 0.05 of the next cycle (18). The delay between DNA synthesis and the “critical point” for enzyme synthesis was previously attributed to a delay between chemical and “functional” replication of the genome (24).

We speculate that a similar delay may be responsible for the doubling in growth rate at one-fifth of the cell cycle found here. One could predict that blocking of DNA synthesis should also prevent an increase in the growth rate. This was indeed observed in our experiments when the cells were blocked in S-phase by HU, which stops DNA replication by inhibiting the enzyme ribonucleotide reductase (20,25). Thus, completion of DNA synthesis is required for an increase in the cell growth rate. The delay between DNA synthesis and the growth rate change may reflect the time interval when the enzymes and material necessary for a faster growth are synthesized.

In conclusion, growth of fission yeast cells does not follow a simple linear or exponential law. This growth is, instead, a rather complex process, the regulation of which will continue to intrigue researchers for some time to come.