Impedance Control and Its Relation to Precision in Orofacial Movement

Abstract

Speech production involves some of the most precise and finely timed patterns of human movement. Here, in the context of jaw movement in speech, we show that spatial precision in speech production is systematically associated with the regulation of impedance and in particular, with jaw stiffness—a measure of resistance to displacement. We estimated stiffness and also variability during movement using a robotic device to apply brief force pulses to the jaw. Estimates of stiffness were obtained using the perturbed position and force trajectory and an estimate of what the trajectory would be in the absence of load. We estimated this “reference trajectory” using a new technique based on Fourier analysis. A moving-average (MA) procedure was used to estimate stiffness by modeling restoring force as the moving average of previous jaw displacements. The stiffness matrix was obtained from the steady state of the MA model. We applied this technique to data from 31 subjects whose jaw movements were perturbed during speech utterances and kinematically matched nonspeech movements. We observed systematic differences in stiffness over the course of jaw-lowering and jaw-raising movements that were correlated with measures of kinematic variability. Jaw stiffness was high and variability was low early and late in the movement when the jaw was elevated. Stiffness was low and variability was high in the middle of movement when the jaw was lowered. Similar patterns were observed for speech and nonspeech conditions. The systematic relationship between stiffness and variability points to the idea that stiffness regulation is integral to the control of orofacial movement variability.

INTRODUCTION

What is the means by which the nervous system achieves movement accuracy and thus regulates variation in movement? One possibility is that precision is achieved by iteratively optimizing control signals on an ongoing basis using information from sensory feedback (Todorov and Jordan 2002). A related possibility is that the nervous system selects motor commands to restrict variation that affects final outcomes while allowing ample variation in variables that have little or no effect on final values (Latash et al. 2002). There is also evidence from measures taken under stationary conditions (Gribble et al. 2003; Lametti et al. 2007; Osu et al. 2004; Selen et al. 2006; Shiller et al. 2002) that movement variability is controlled through neural signals that modify the limb's resistance to displacement, a phenomenon known as impedance control (Hogan 1985). However, it is unknown whether precision is regulated in a similar fashion during movement.

To address this question we have examined movement variability and impedance in speech production, which is characterized by some of the smallest and most precise movements that humans produce. Speech is of particular interest in this context because it tests the possible application of impedance control at the limits of human movement precision. To deal with the small movement amplitude and rapid time course of speech movements, it was necessary to develop new techniques to estimate impedance. Using these techniques, we show here that impedance varies systematically over the course of movement and that variability in speech varies directly with differences in impedance. Moreover, the patterns of both impedance change and kinematic variation that we observe are not restricted to speech movements but occur in a similar fashion in matched nonspeech movements. The consistent linkage that is observed between impedance and movement variability suggests that impedance regulation is an integral component in the control of precision in the orofacial system.

In studies of stiffness control in arm movements it has been possible to estimate stiffness during movement either by applying displacements to the arm that are position servo-controlled with respect to estimates of the unperturbed trajectory (Burdet et al. 2001; Darainy et al. 2007) or by using open-loop force control (Frolov et al. 2006; Gomi and Kawato 1997; Mah 2001). A servo-control procedure has not been possible in the case of jaw movement as a result of the small amplitude and duration of movement. Accordingly, we developed a new procedure based on the application of brief force pulses to the jaw and a Fourier-transform–based interpolation technique that estimates the required reference trajectory, that is, the trajectory that would have been followed in the absence of load.

Subjects in the present study were tested with speech utterances and with matched nonspeech movements, which were equated in terms of amplitude and duration. Impedance estimates were based on the pattern of sagittal plane jaw displacement and measured resistive forces that occurred in response to small force perturbations at various points along the movement trajectory and in various directions.

METHODS

Thirty-one young adults participated in the experiments (17 females and 14 males between the ages of 18 and 32 yr). Subjects were screened for temporomandibular joint dysfunction and speech motor disorders. All experimental procedures were approved by the Institutional Review Board of McGill University.

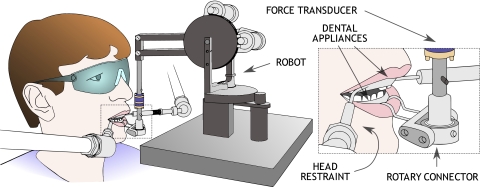
Stiffness is a measure that depends on geometrical and mechanical factors in conjunction with neural control. Stiffness reflects the combined effects of muscle properties, musculoskeletal geometry, force arising due to reflex mechanisms, and the contribution of force due to active motor units (Hogan 1985; Laboissière et al. 1996). Jaw stiffness was estimated in the present study using a small robotic device (Phantom 1.0; Sensable Technologies) that permits unrestricted movement of the jaw in three spatial dimensions and the recording of jaw position and subject-generated force (Fig. 1). The subject's jaw was connected to the robot by means of a custom-built dental appliance that was attached to a rotary connector at the end of the robot arm. A second appliance, attached to the maxillary teeth, was used for head stabilization during testing. Jaw position was measured using encoders in the robotic device. Subject-generated force was measured using an ATI Nano-17 force–torque sensor that was mounted at the distal end of the robot arm. Position and force were both recorded at 1 kHz and low-pass filtered at 30 Hz.

FIG. 1.

Experimental setup.

Stiffness estimates were obtained in a speech condition and a matched nonspeech condition with the order of testing balanced over subjects. The testing was carried out on two successive days. In the speech condition, subjects were instructed to repeat the utterance see sassy at a conversational rate and normal volume. In the nonspeech condition, subjects were asked to produce individual jaw-lowering and jaw-raising movements that were matched to the movement for sass in the speech condition in terms of amplitude and duration. The experimenter provided the subject with constant verbal feedback on these values based on a real-time display. In each case, an audio signal was given as a cue to start the trial.

The speech condition began with a practice run of 30 repetitions. This was followed by three blocks of 180 repetitions each. During the experimental sequence, the robot delivered 48-ms, 1-N perturbations to the jaw, on average one trial in five, with perturbations acting in six equally spaced directions about a circle in the sagittal plane. The start time of the perturbation varied such that perturbations were distributed throughout the jaw-lowering and -raising movements associated with the sass portion of the utterance.

The procedure for the nonspeech condition was basically similar. An initial practice run of 30 movements was followed by three blocks of jaw-lowering and -raising movements of 180 trials each. As in the speech condition, perturbations were 48 ms in duration, 1 N in magnitude, and delivered at random on a one trial in five basis. Perturbations were similarly delivered in six equally spaced directions about a circle, with perturbations distributed throughout the lowering and raising movements.

For subjects that were tested in the nonspeech condition first, a short run of 30 speech trials was collected at the very start of the procedure to obtain estimates of jaw amplitude and duration. These gave values needed to provide feedback on amplitude and duration during the nonspeech movements.

A Fourier-transform–based procedure was used to obtain estimates of the reference trajectory for each perturbed movement (see the appendix for details). The basic idea is that position and force data outside of the perturbation interval are used to predict the form the signal would have taken within the perturbed part had there been no perturbation. To prevent noise from propagating into the predicted positions and forces, we use a low-pass filtered version of the signal in the unperturbed part of the movement to generate the interpolated signal within the perturbation interval. The low-pass filtering is implemented using a variant of the Fourier transform in which Fourier coefficients are determined in the unperturbed part of the signal alone, at frequency values up to a specified cutoff frequency. The obtained Fourier coefficients are used to reconstruct the reference trajectory both within and outside the perturbation interval (see Fig. 2 for example). The restoring force vector (δF_x, δF_y) and the displacement vector (δx, δy) both measured at the mandibular incisors (see methods) are determined by taking the difference within the perturbation interval between the actual signal and the computed reference trajectory.

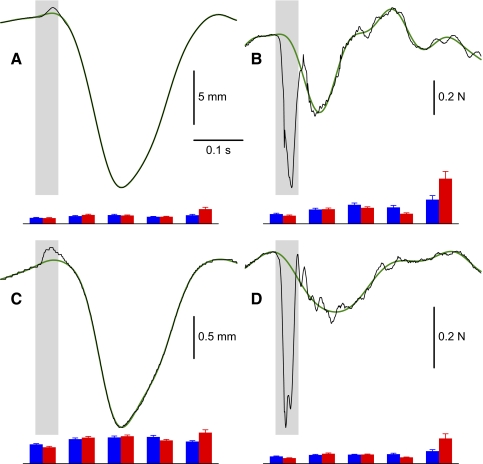
FIG. 2.

Reference trajectory estimation. An example of vertical (A) and horizontal (C) jaw position and vertical (B) and horizontal (D) force signals for a representative subject in a perturbed trial (shown in black) in the speech condition. The superimposed reference trajectories derived using a Fourier-based procedure are shown in green. The cutoff frequencies used in these examples are 12 Hz for the position signals and 10 Hz for the force signals. The perturbation interval is shown with the gray rectangles. Estimates of error are shown at the bottom of each panel. The speech condition is represented in blue and nonspeech is in red. The height of each bar is the mean of the maximum error when the Fourier-based procedure is applied to known signals (null-field trials) in each of 5 phases of movement shown from left to right (start, peak opening velocity, maximum aperture, peak closing velocity, and end). The error estimates were computed using a set of 20 null trials selected at random for each subject in both speech and nonspeech conditions. The scale for the force errors is the same as that for the force plots. For visualization purposes the position errors were multiplied by 10, in relation to the position scale bars. The SEs for each value are also given.

We have also developed a new method for stiffness estimation that is based on a moving-average (MA) procedure. The currently available techniques for estimating stiffness from data based on force pulses require that the inertial contribution to the measured restoring force be removed (Gomi and Kawato 1997). This in turn requires a mechanical model of the system. The technique used here avoids the need for an explicit mechanical model. Estimates of stiffness can be derived by modeling restoring force as the moving average of previous jaw displacements according to the following expression

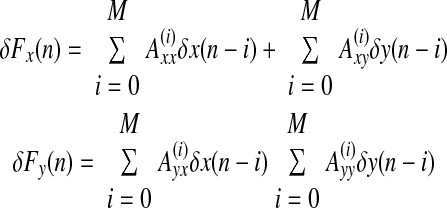(1)

where δF_x and δF_y are restoring forces in the horizontal and vertical directions and δx and δy are horizontal and vertical displacements. A_xx, A_xy, A_yx, and A_yy are coefficients of the moving average model; M + 1 is the order of the model; and n goes from M until N, where N is the number of samples in the perturbation interval. As shown in methods, stiffness estimates are derived directly from values of the moving average coefficients.

The moving-average model was used to obtain jaw stiffness estimates on the basis of the force opposing the perturbation and the associated change in the position. The discretized system given in Eq. 1 can be written in the z domain as

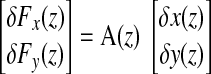(2)

where

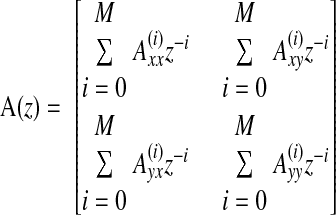(3)

The stationary condition is obtained at z = 1

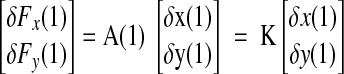(4)

where δF_x(1), δF_y(1), δx(1), and δy(1) are the stationary values for changes in force and position and K = A(1) is the stiffness matrix.

An iterative procedure that is reminiscent of the expectation–maximization (EM) algorithm (Dempster et al. 1977) was used to jointly estimate the reference trajectory and the coefficients of the moving average model. In the expectation step of the algorithm, cutoff frequencies for reference trajectory estimation were assumed fixed. Then, using values for position and force change due to the perturbation, the moving-average model coefficients shown in Eq. 4 were computed through linear regression. In the maximization step, the moving-average model was considered fixed and, for each perturbed trial, the combination of cutoff frequencies was found that best predicted δF_x and δF_y (given the moving-average coefficients and model order, M). The procedure continued until values for cutoff frequencies converged. The procedure was repeated on a per subject basis, separately for speech and nonspeech conditions and also separately for each movement phase (start, apex, and end).

When executing the maximization step, linear regressions were computed for model order M going from 10 until 20. The optimal order was the one that resulted in the smallest value for the Bayesian Information Criterion (BIC; see Schwarz 1978), a measure that takes into account both the goodness of fit and the number of free parameters in the model. The BIC is given as

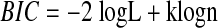(5)

where L is the maximized value of the likelihood function for the estimated model, k is the number of parameters to be estimated, and n is the number of observations. Selecting the model order based on this criterion prevents overfitting the data with models that have an unnecessarily high number of parameters (e.g., high moving-average model orders M or high cutoff frequencies).

The estimates of stiffness in the present study are dependent on the ability to adequately estimate the reference trajectory and importantly on the assumption that the subject does not voluntarily intervene over the course of the perturbation. Voluntary intervention is unlikely, at least during the perturbation interval. The perturbations are delivered at random points over the course of a movement and only on a subset of trials. Moreover, the perturbations are exceedingly small both in amplitude (∼1 mm) and duration (48 ms from start to end). Voluntary response can presumably be ruled out under these conditions.

RESULTS

Estimates of sagittal plane jaw stiffness and kinematic variability were obtained from repetitions of a single speech utterance and matched nonspeech movements. We verified that movement amplitude and duration were comparable in speech and nonspeech conditions. As is typical of speech movements, mean jaw movement amplitude for the sass portion of the utterance (±SE) was 18.0 ± 0.77 mm and mean duration for the same movement (±SE) was 366 ± 8.6 ms. For the nonspeech movements, the mean amplitude for the matched jaw-lowering and -raising movements (±SE) was 17.9 ± 0.77 (SE) and the mean duration (±SE) was 382 ± 9.7 ms. There were no statistically reliable differences between speech and nonspeech conditions in terms of either amplitude (P > 0.5) or movement duration (P > 0.19).

Figure 2 gives a representative single-movement trial in which a perturbation is delivered just before the start of movement. The figure shows jaw position and force trajectories over the course of the trial and the associated “reference trajectory,” which estimates what the movement path would have been in the absence of load. We evaluated the Fourier-based interpolation procedure that was used to estimate the reference trajectory in the case of perturbed movements by applying the technique to null-field trajectories in which the form of the actual trajectory was known throughout. We produced estimates of the reference trajectory for both position and for force at each of five intervals, which were centered at movement start, maximum lowering velocity, maximum jaw aperture, maximum raising velocity, and movement end. We did this for all subjects using a randomly selected subset of 20 null-field trials and we repeated the procedure separately for both speech and nonspeech movements. As is the case with the experimental data, we computed a reference trajectory using an estimation interval that was longer than the actual perturbation (75-ms reference trajectory estimation vs. 48-ms force perturbation). The reason for computing a reference trajectory that extended beyond the perturbation was to ensure that the estimated trajectory covered an interval that allowed both resistive force and jaw position to return to baseline values following the end of the perturbation. In each of these cases, we chose from a set of candidate trajectories produced by the Fourier interpolation procedure the one that minimized the root-mean-square (RMS) difference between the actual and the estimated movement interval. This is called the reference trajectory. Overall, we found that the best cutoff frequencies ranged from 17 to 22 Hz for the position signals and from 8 to 13 Hz for force signals (based on minimum RMS difference between null-field movements and estimated reference trajectories).

We assessed the error that results when the interpolation procedure is applied to known movements. We found that the Fourier-based interpolation procedure generates estimated reference trajectories that closely approximate those observed empirically. We carried out a quantitative evaluation of the error that results from this procedure by computing over subjects the average value of the maximum absolute difference between the computed trajectory estimate and the actual data. The maximum values were in all cases quite small (see Fig. 2; scale bars show position error × 10, force error × 1). The average over subjects of the maximum error for speech trials was 0.069 and 0.029 mm for vertical and horizontal jaw positions, respectively, and 0.092 and 0.028 N for vertical and horizontal forces, respectively. For nonspeech trials the corresponding values were 0.078 and 0.029 mm for jaw position and 0.086 and 0.032 N for force. The computed reference trajectories thus produce quite a reasonable approximation to test data drawn from null-field measurements.

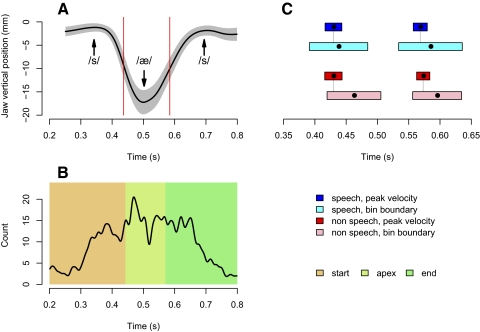
Jaw stiffness estimates were obtained for three intervals over the course of movement by partitioning the set of perturbations for a given subject and condition (speech/nonspeech) into three bins of equal size based on their time of occurrence. On average, each bin contained data from about 40 perturbations. Figure 3, A and B shows for a representative subject the distribution of perturbations at each phase of the movement. The vertical lines divide the data set into bins of equal size for purposes of analysis. Figure 3C shows the correspondence between the resulting bin boundaries and maximum jaw-lowering and -raising velocity averaged over subjects. It can be seen that by partitioning the data based on the distribution of perturbations we get (approximately) one phase preceding maximum lowering velocity, a second phase from maximum lowering to maximum raising velocity (including maximum aperture), and a final phase beyond maximum raising velocity. Note that it was necessary to divide the data set in this fashion to ensure an adequate amount of data in each phase of movement for purposes of stiffness estimation. The procedure results in a composite estimate that characterizes impedance over the estimation interval. However, as seen Fig. 4, even when estimated in this manner, the technique is sensitive to differences in stiffness over the course of movement.

FIG. 3.

Pattern of applied perturbations during jaw movement. A: jaw vertical position during speech for a selected subject. The black line indicates the mean trajectory computed using all null-field trials. The gray-shaded area represents ±1SD about the mean (no time normalization was applied). The red vertical lines indicate the mean location of maximum velocity for this subject in the speech condition. Positions corresponding to the sounds /s/ and /æ/ are indicated. B: distribution of perturbations for the same subject across time. The vertical axis shows the number of perturbations. The histogram has been smoothed by a low-pass filter for purposes of display. The zones chosen for the start, apex, and end phases for this particular subject are shown in different colors. C: dispersion of the temporal location of the velocity peaks and the bin boundaries for selection of movement phases for both opening movements (left) and closing movements (right), computed across all subjects. The results are shown separately for the speech (blue and cyan) and the nonspeech (red and pink) conditions. The rectangles represent ±1SD about the mean, which is represented by a black dot.

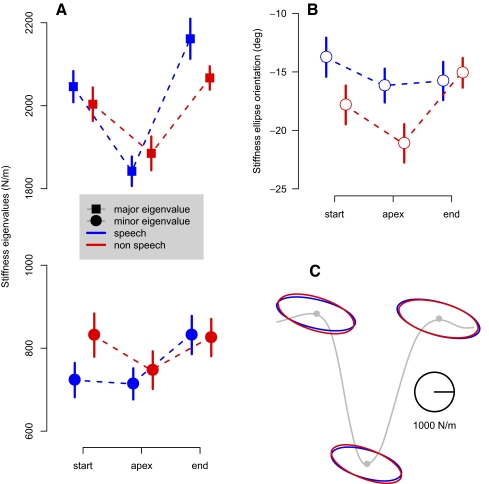
FIG. 4.

Jaw stiffness is modulated over the course of orofacial movement. A: eigenvalues of the stiffness matrices are shown for each phase of the movement in both speech and nonspeech conditions. The points (squares for the major eigenvalue and dots for the minor eigenvalue) represent the mean values for each phase and each condition across the subjects. The vertical bars show ±1SE, after removal of individual differences. For presentation purposes, the points for the nonspeech condition are displaced to the right with respect to the points for speech. B: orientation of the major axis of jaw stiffness ellipses. Negative is downward relative to the horizontal. C: mean stiffness ellipses for each phase of movement (jaw protrusion/retraction is in the horizontal direction and jaw raising/lowering is along the vertical axis; subjects are facing to the right). For display purposes, the ellipses are superimposed on a representative plot of jaw vertical position vs. time.

With the data set partitioned into bins, estimates of position change and force change due to the perturbations were used to compute three separate stiffness estimates for each subject in speech and nonspeech conditions. An iterative procedure based on a moving-average model was used to obtain estimates of stiffness. Figure 4A shows average magnitudes of stiffness for the major and minor axes of the jaw stiffness ellipse in each phase of movement. It can be seen that similar patterns are observed in speech and nonspeech movements. In each case, for the direction of greatest stiffness (protrusion and retraction), stiffness is high in the early and late phases of movement and lower in the middle (by about 80 N/m on average). For the direction of least stiffness (raising and lowering) there is no phase-dependent change in the observed magnitude of stiffness. Repeated-measures ANOVA with factors phase (beginning, middle, end) and condition (speech, nonspeech) confirmed that, in the direction of greatest stiffness, measured stiffness values differed over the course of movement [F_(2,150) = 17.7, P < 0.0001], such that values for stiffness were less in the middle of movement than those at either the beginning [F_(1,90) = 14.7, P < 0.001] or at the end [F_(1,90) = 35.2, P < 0.001], as assessed by Bonferroni-corrected comparisons. Stiffness values at movement start and end were not found to differ [F_(1,90) = 2.65, P > 0.1]. For the direction of least stiffness, no modulation of stiffness values was observed [F_(2,150) = 2.01, P > 0.1]. In addition, there were no statistically reliable differences in the pattern of stiffness between speech and nonspeech movements [F_(1,150) = 0.80, P > 0.35; F_(1,150) = 1.27, P > 0.25, for major and minor axes, respectively].

Figure 4B gives the orientation of the major axis of the stiffness ellipse for the same three phases of movement. Repeated-measures ANOVA found no differences in orientation over the three phases [F_(2,150) = 2.13, P > 0.1]. There was a small but significant difference in orientation between speech and nonspeech movements [F_(2,150) = 3.96, P < 0.05], with the stiffness ellipse tilted further from the horizontal axis in the nonspeech condition, by 1.375°.

We assessed the relationship between jaw stiffness and kinematic variability by computing, for each subject, composite measures of stiffness and variability. For stiffness, we calculated 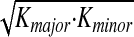, a measure that varies monotonically with stiffness ellipse area, for each of the three phases of movement shown in Fig. 3, where K_major and K_minor are the magnitudes of the major and minor axes. The calculation was done for each subject separately and was repeated to have values for both speech and for nonspeech movements.

We computed an analogous measure for kinematic variability, again on a per subject basis, and also for each movement phase separately. The pattern of kinematic variability was fit with a 1SD confidence ellipse that was derived using principal components analysis (see Fig. 5). The orientation and magnitude of the major axis of the ellipse corresponds to the direction and magnitude of maximum kinematic variability. The minor axis shows the direction and magnitude of minimum kinematic variability. A global measure of kinematic variability, analogous to the area of the ellipse, was obtained by computing the square root of the product of the magnitude of the major and minor axes, 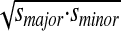, where s_major and s_minor are SDs on the two axes of kinematic variability.

FIG. 5.

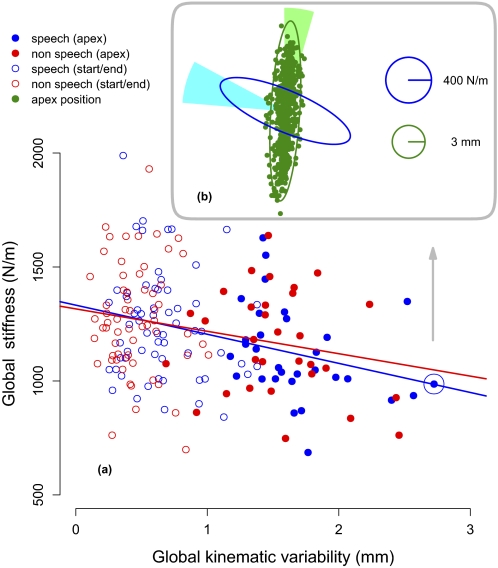
Kinematic variability in jaw movement is inversely related to stiffness. A: scatterplot of global stiffness against global kinematic variability for all subjects in both conditions (speech and nonspeech). Jaw positions at the apex of the movement are shown with filled circles. Start and end positions have unfilled circles. Global stiffness is defined as the geometric mean of the eigenvalues of the stiffness matrix. Global kinematic variability is obtained from the 1SD dispersion matrix of jaw positions by computing the geometric mean of its eigenvalues. Regression lines are shown separately for speech and nonspeech conditions. B: null-field positions for jaw movements in the sagittal plane for a selected subject in the speech condition, corresponding to the highlighted point in A. The 95% confidence ellipse is drawn in green around the points. The corresponding stiffness ellipse is shown in blue. The 2 conical sections represent ±1SD for the orientation of the major axis of the stiffness and kinematic variability ellipses, computed for all subjects in both conditions: kinematic variability (light green) and stiffness (cyan).

Figure 5 shows the relationship between jaw stiffness and kinematic variability, where each point represents an individual subject in either the speech or the nonspeech condition. The individual stiffness and variability estimates come from all three phases of the movement. As can be seen, stiffness during movement is systematically related to kinematic variability such that variability is high when stiffness is low and vice versa. The overall correlation between stiffness and variability (r = −0.29) was significant (P < 0.001). The correlation was likewise significant when stiffness and associated variability measures were computed for each axis separately (r = −0.30, P < 0.0001 and r = −0.18, P < 0.02, for the major and minor axes of the stiffness ellipse, respectively). The correlation for speech was −0.32 (P < 0.001) and for nonspeech −0.24 (P < 0.02). There was no indication that the intercept or the slope of the relation between stiffness and variability differed for speech and nonspeech conditions (P > 0.5 in both cases). Overall, the mean angle (±SE) between the major axes of the stiffness and kinematic variability ellipses in speech was 81.61 ± 1.38° and for nonspeech the angle was 80.99 ± 2.35°.

Since jaw stiffness varies over the course a movement it is possible that the relationship between stiffness and variability actually reflects differences that arise in different phases of movement. We examined this possibility using ANOVA by fitting a model to the data that assessed the linear dependence of stiffness on movement phase, kinematic variability, and speech versus nonspeech testing. This analysis indicated a reliable dependence of stiffness on phase [F_(2,144) = 5.50, P < 0.005] and on movement variability [F_(1,144) = 3.97, P < 0.05]. None of the other possible effects was statistically reliable, including interactions between phase, variability, and speech and nonspeech conditions (P > 0.15 in all cases). Thus overall, even after accounting for differences in stiffness that are dependent on the phase of the movement, there is still a reliable dependence of stiffness on variability.

DISCUSSION

Impedance control (Hogan 1985)—the capacity to voluntarily modify patterns of stiffness—has been reported previously in the context of human arm movement, both under static conditions (Darainy et al. 2004; Gomi and Osu 1998; Perreault et al. 2002) and also during movement (Burdet et al. 2001; Franklin et al. 2003). In each of these reports, subjects have been shown to modify stiffness in an adaptive fashion to counteract environmental instabilities or in responding to biofeedback manipulations. Stiffness control has also been observed using similar manipulations in the context of orofacial movement (Shiller et al. 2005). In studies of both limb movement and in speech, a link has been documented between stiffness and kinematic variability. Variability is observed to be less in situations involving higher levels of cocontraction and higher stiffness (Gribble et al. 2003; Selen et al. 2006; Shiller et al. 2002). Variability and stiffness are likewise linked in an adaptive fashion when subjects make movements to targets of different shape (Lametti et al. 2007).

In the present study, we find that impedance is modulated over the course of movement and that the pattern of stiffness change is comparable for speech and matched nonspeech movements. The modulation observed over the course of movement is basically similar to the pattern of stiffness modulation under stationary conditions where stiffness is greater at more elevated positions of the jaw and less for lower positions (Shiller et al. 2002). However, in comparison with measures taken when the jaw is stationary, stiffness during movement is higher by a factor of about two, particularly in the direction of jaw protrusion–retraction. The demonstration differs from previous examples of impedance control in that modulation of stiffness is observed in the absence of experimentally imposed instability and indeed in the absence of any specific requirement to regulate stiffness for purposes of environmental interaction.

We have seen that jaw stiffness is inversely related to kinematic variability and that stiffness is high in directions where variability is low and visa versa. Previous demonstrations of the relationship between either stiffness or muscle cocontraction and variability have been obtained at movement end (Gribble et al. 2003; Lametti et al. 2007; Shiller et al. 2002) and may thus have been influenced by the unique stability requirements that arise at the end of movements. The results of the present study suggest that stiffness and variability are more globally linked and thus that stiffness regulation is a basic part of normal movement control.

We have not found differences between speech and matched nonspeech movements, either in patterns of stiffness or in kinematic variability. The analyses show that this is not for lack of statistical power. We can readily detect differences when they are present, as for example between the middle and the ends of the movement. Moreover, given the large sample size (31 subjects tested in both speech and nonspeech conditions), we are fairly satisfied that the absence of a speech/nonspeech difference is real. Nevertheless, we think it is important to emphasize that speech and nonspeech movements differ in important respects that are perhaps not evident when movements in the two conditions are matched for experimental purposes. Even in the case of the jaw, speech movements tend to be smaller than other orofacial movements and certainly faster. Thus speech and nonspeech movements may be distinguished more by the part of the orofacial workspace that they inhabit than by the basic rules that govern their behavior. Other articulators such as the tongue and the lips are also important in speech production and may present patterns of stiffness modulation over the course of movement that are different from those observed for the jaw. An examination of stiffness in these articulators would be informative.

The present finding—that changes in variability are systematically related to differences in impedance—is correlational in nature and thus on the basis of the present data alone, little can be concluded about the underlying causality. Nevertheless, the findings are consistent with a number of other reports for speech production and for human arm movement (Gribble et al. 2003; Lametti et al. 2007; Selen et al. 2006a,b; Shiller et al. 2002), in which it is shown that variability changes in systematic ways with differences in stiffness and muscle cocontraction. The present results, taken in the context of these other findings, are consistent with the view that stiffness control plays an important role in the regulation of variability.

It may seem paradoxical that stiffness control is used to achieve movement accuracy, since increasing stiffness, of necessity, results in an increase in force output and thus an increase in variation in individual muscle force. Stiffness control is presumably effective for purposes of regulation of movement accuracy because the stabilizing effects of increased stiffness outweigh the negative effects due to increased force variability in individual muscles (Faisal et al. 2008).

Differences in stiffness were observed between closed and open jaw positions. In the case of speech movements, it is possible that tongue–palate contact during closed jaw positions leads to higher values for stiffness. However, the presence of the same pattern of stiffness modulation in nonspeech conditions, where palate contact is presumably less of an issue, argues against the idea that peripheral mechanical factors are the source of the stiffness difference between raised and lowered jaw positions.

The stiffness modulation observed in the present study occurs over the course of an ongoing movement. Whether the present modulation is set on-line or established prior to a movement cycle is not known. However, in other instances, it has been observed that changes to stiffness and cocontraction control take place primarily from one movement to the next. Cocontraction increases on trials following an increase in error and decreases when error is reduced (Franklin et al. 2008). Similarly, measures of stiffness are modulated on a trial-by-trial basis to produce changes in required accuracy (Mottet and Bootsma 1999).

We have taken an approach to variability in the present study that differs from that proposed in the so-called uncontrolled manifold formulation. In the latter approach (Latash et al. 2002), variability is decomposed into combinations of variables that have little effect on precision and other combinations that lead to a reduction in precision. The present approach uses a composite measure of variability. This is justified by the fact that separate measures of variability in directions of greatest and least stiffness show the same basic relation to impedance. Variability is high where stiffness is low and vice versa. At least in the present case, a single composite measure of variability captures the overall result.

It is important to note that, in the present data, measures of stiffness and variability are independent and thus the observed correlation between these variables is not a consequence of their reliance on similar kinematic measures. A potential concern is the possibility of a part–whole correlation between displacement measures used for stiffness calculation and kinematic variability measures obtained from jaw trajectories. This is not an issue in the present study. The stiffness calculation is conducted in relation to a reference trajectory that is computed on a trial-by-trial basis. This removes any influence of trial-to-trial variability from the displacement measures, δx and δy, that are used to estimate stiffness. Thus the computation of stiffness explicitly excludes an effect of trial-to-trial variation. Had we used a global mean reference trajectory this would not have been the case.

The computation of stiffness in the present study is based on the assumption that the complex structures that characterize this nonlinear system can be approximated by a locally linear system. Although we have not assessed whether the perturbations used here (1-mm displacement and 1 N in force) are small enough to stay in the linear portion of the system, given their magnitudes we presume this is a reasonable assumption. The possible effects, on stiffness estimates, of time delays in reflex loops is a related concern regarding the adequacy of the linear approximation. Because of the short time windows (48 ms) that were used for the perturbations, the contribution of reflexes to measured stiffness is presumably restricted to short-latency phasic reflexes and changes in activation due to the tonic stretch response. The moving-average procedure used for stiffness estimation helps account for delays between the position and force signals because the parameters relating the dependence of force on position take into account the preceding 10 to 20 values of jaw position in computing the optimal model order.

The observed correlation between stiffness and variability was statistically significant but the numerical magnitude of the correlation measure was low. We suspect that the low r-values are due to intersubject variation that is not parceled out in the correlation analysis that we did. Individual differences in factors such as movement amplitude, individual morphology, or speaking patterns may well affect the stiffness and variability estimates that were obtained from a single subject and are reflected in the overall value of the correlation that we report.

GRANTS

This work was supported by National Institutes of Health Grants DC-04669 and HD-048924. R. Laboissière is Chargé de Recherche at Centre National de la Recherche Scientifique, France.

APPENDIX

Fourier-based procedure for reference trajectory estimation

Stiffness values were obtained by determining the deviations of measured force and position signals from estimated unperturbed records (reference trajectories). The reference trajectories were derived using a Fourier-based procedure in which the portions of the signal outside the perturbation interval were used to estimate the form of the signal in the absence of a perturbation. The technique is reminiscent of algorithms for reconstruction and interpolation of missing samples from oversampled band-limited signals (Ferreira 1992).

To interpolate the missing samples of a one-dimensional signal from its known parts, a basic assumption is made that the low-frequency components extracted from the known portion of the signal contain enough information to interpolate the missing portion. We then partition the time domain T of the discrete signal x of length N into two disjoint subsets: T_m for the missing portion and T_k for the known portion. The Fourier coefficients A_j of the known part of the signal are obtained by solving the following underdetermined linear system, in a least-squares sense

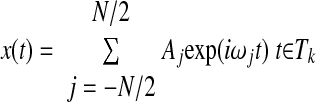(A1)

where w_j = j2πf_s/N and f_s is the sampling frequency (for the sake of simplicity, N is assumed to be even). In the case where T_k = T, which means to a fully known signal, the solution of the above-cited system is fully equivalent to the usual discrete Fourier transform.

Once the coefficients A_j are determined, the missing part of the signal can be derived using

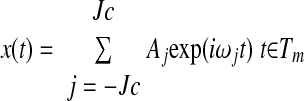(A2)

where the index J_c corresponds to the desired cutoff frequency of the signal. A value for the cutoff frequency that is too high may result in undesirable oscillations in the interpolated portion of the signal. On the other hand, choosing an excessively low value for the cutoff frequency may yield poor fitting even in the known portion of the signal.

Since there is no principled way of choosing the appropriate cutoff frequency for the jaw position and force signals in the present study, we consider a range of possible frequencies for each signal and the final choice is made using the EM procedure, as described in methods.

We evaluated the reference trajectory estimation procedure for vertical and horizontal positions and also vertical and horizontal forces. The analysis was carried out for speech and nonspeech movements separately. For each subject and for each variable, 20 null-field trials were randomly selected. We evaluated the reference trajectory fit at five points in each null-field movement: movement start, midway in time through the jaw lowering phase, maximum aperture, midway in time through jaw raising, and movement end. Intervals of 50 ms, corresponding to the duration of the perturbation, were used to obtain estimates at these points.

For each estimated trajectory, the maximum deviation from the actual or known trajectory was computed over the estimation interval. For purposes of this computation, we used cutoff frequencies from 8 to 23 Hz for position signals and from 5 to 20 Hz for force signals. The minimum across frequencies of the maximum deviation was used as a measure of “worst error in the best fit case.” For each subject, each measurement variable (vertical and horizontal position and vertical and horizontal force), each condition (speech/nonspeech), and for each of five phases of the null-field movement, the average of the minimal–maximal deviations was computed across the 20 trials.

Evaluation of the MA estimation procedure

We conducted a simulation study to assess the extent to which the MA procedure is able to correctly recover stiffness of a known two-dimensional, second-order linear system with the following equation of motion

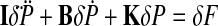(A3)

where δP and δF are the position and force change vectors, respectively. I, B, and K are the inertia, viscosity, and stiffness matrices. Successful recovery of stiffness in these simulations means that if the MA procedure is applied to real-world cases in which local linearity of stiffness, viscosity, and inertia holds, then correct values for the stiffness matrix can obtained.

The stiffness matrix used in the simulations was taken from that of an average subject and has the following values: major axis 2,440 N/m, minor axis 608 N/m, curl term 44.6 N/m, ellipse orientation −10.5°. The inertia matrix was diagonal with values of 0.05 kg for the diagonal terms. This value was obtained using our jaw model (Laboissière et al. 1996) to compute the apparent jaw mass at the lower incisors using values of mass and inertia given by Zhang et al. (2002). The formula b = 2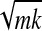 was applied to obtain viscosity values for the major and minor axes in the critically damped case. The viscosity matrix was further rotated such that it was aligned with the stiffness matrix.

To test a range of situations in the simulations, values for b were multiplied by 0.5 (underdamped case) and 2.0 (overdamped case). We used the damping factors of 0.5, 1.0, and 2.0 for both the major and minor axis viscosities, which gave us nine combinations in total. As input to the model (δF), cosine-shaped pulses, 48 ms in duration, were used. For each of the simulated systems, six trials were generated, for each of the following directions in the sagittal plane: 0, 60, 120, 180, 240, and 300°. A 1-N pulse was applied at the beginning of the simulation and the output was evaluated until t = 80 ms, sampled at 1 kHz. This closely approximates the experimental conditions.

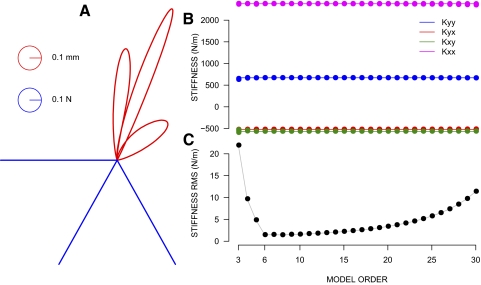
Figure A1 gives the results for the case involving critically damped viscosity. All of the other cases yielded similar results. The left panel shows simulated perturbations in the sagittal plane. The right panel gives the estimated values of the stiffness matrix for varying orders of the MA procedure. Note that for orders 6 to beyond order 30 the estimates are close to the actual value. The bottom panel of Figure A1 summarizes the RMS difference between actual and estimated stiffness values averaged across all nine cases and all matrix components. It can be seen that there is a model order at which fitting error is minimized. By order 6, the MA model is able to precisely recover stiffness values. The RMS error is well under 1% for this linear second-order system.

FIG. A1.

Evaluation of the moving-average (MA) estimation procedure. A: trajectories of the position signal (red curves) obtained by simulating a 2-dimensional critically damped 2nd-order linear system fed with 3 different force pulses (blue lines) at angles 180, 240, and 200°. Stiffness values 2,440 N for the major axis and 608 N for the minor axis were used in this example. The curl component was equal to 44.6 N and the matrix was oriented at −0.183 rad. These values are close to the values estimated empirically for the jaw. B: the estimated values of the 4 components of the stiffness matrix [K_xx, K_xy; K_yx, K_yy] for different orders of the MA estimation procedure between 3 to 30 are shown in dots. The horizontal lines correspond to the actual value of each component. C: root mean square (RMS) of the stiffness estimation error. For each MA order, the RMS value was computed by pooling together the estimation errors of the 4 components of the matrix across the different viscosity factors (0.5, 1.0, and 2.0) as well as the 3 different combinations of stiffness values for the major and minor axes.

We also ran simulations for systems with zero stiffness, using the viscosity and inertia values determined earlier. The procedure was able to estimate values very close to zero for the components of the stiffness matrix. The optimal RMS value under these conditions was 0.035 N/m, for order 7 of the MA procedure. Thus the ability of the model to extract zero stiffness is comparable to its ability to extract more typical stiffness values.